New exponential operation laws and operators for interval-valued q-rung orthopair fuzzy sets in group decision making process

Abstract

The paper aims to introduce the novel concept of q-connection number (q-CN) for interval-valued q-rung orthopair fuzzy set (IVq-ROFSs) and thus to develop a method for solving the multiple-attribute group decision making (MAGDM) problem. The IVq-ROFS is a tool to represent the uncertain information with an integer parameter $q\ge 1$, while the connection number (CN) processes the uncertainties and certainties into a single system with three degrees, namely “identity”, “contrary” and “discrepancy”. Driven by these required properties, this paper introduces a q-CN for IVq-ROFSs to represent the information in a more concise way. To this end, we divide the paper into three aspects. First, we define q-CN and a scoring function to evaluate the numbers. Second, we give some new q-exponential operation laws (q-EOLs) and operators over q-CNs in which bases are real numbers and exponents are q-CNs. Moreover, we define an operator based on these laws and derive their properties. Third, a novel MAGDM method for solving decision problems with IVq-ROFS information is illustrated with several examples. The advantages and superiority analysis of the proposed framework are also given to assert the results.

1 Introduction

Multiple attribute group decision-making (MAGDM) is an important topic in the field of decision science, where the challenge is to select the most appropriate objects among various limited resources. A group of experts is available to evaluate the objects with some numerical values under the presence of different attributes. It is further analyzed that, in human cognition mechanisms, it is often found difficult to model the work situations using the primitive data processing techniques based on crisp numbers. These methods lead the decision-makers to vague conclusions as well as uncertain decisions. Therefore, in order to deal with uncertain and fuzzy situations in the real world, the decision-makers must have such theories that allow them to consider fuzzy data values and maintain their decision-criteria in accordance with the particular situation, whether it is human cognition or pattern recognition. To address this problem, Zadeh [1] introduced the theory of fuzzy sets (FSs), in which each object is measured using the degree of membership to reduce the ambiguity of information. After its existence, several extensions of FSs were explored by researchers, such as intuitionistic fuzzy set (IFS) [2], interval-valued IFS (IVIFS) [3], pythagorean fuzzy set (PFS) [4], interval-valued PFS (IVPFS) [5, 6].

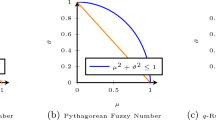
In most practical decision problems, there are two main critical tasks. The first is how to choose the right preference values to evaluate the given objects, while the other is how to combine these values efficiently. To address the first task, researchers always believe to represent the preferences in interval form instead of a single real number. For this purpose, the theories of IVIFS and IVPFS are well suited. In IVIFS, each element is assigned two degrees, denoted as belonging, $[{\underline{\vartheta }}, {\overline{\vartheta }}]$ and non-belonging $[{\underline{\varphi }}, {\overline{\varphi }}]$, with the restriction that ${\overline{\vartheta }}+{\overline{\varphi }}\le 1$ for any number lying between [0,1]. However, in IVPFS, this constraint is relaxed from ${\overline{\vartheta }}+{\overline{\varphi }}\le 1$ to ${\overline{\vartheta }}^2 + {\overline{\varphi }}^2 \le 1$. It is clear that the feasible region of IVIFS is a triangle, while IVPFS is a quarter circle, and therefore, the range of ${\overline{\vartheta }}^2 + {\overline{\varphi }}^2 \le 1$ is larger than ${\overline{\vartheta }}+{\overline{\varphi }}\le 1$. After its appearance, several works have been done to solve the given problem by defining different types of aggregation operators (AOs) and ranking methods. For example, in [7, 8], the authors have presented averaging and geometric operators for IVIFSs, while such operators for IVPFSs are presented by the authors in [5, 6, 9]. Using the concept of divergence to compute the weight vector, Liang et al. [10] developed weighted operators for IVPFSs. Wang and Li [11] developed the continuous aggregation operators for IVPFSs. Besides these operators to describe the acquisition information, there is also a need to defuzzify it into a crisp number. For this purpose, the score and accuracy functions are well suited and widely used by researchers. For example, Xu [8] has given a score function under the IFS environment, while Garg [12], Zhang et al. [13], Yang et al. [14] present a generalized improved score function for IVIFSs. Also, some accuracy functions and modified score functions for ranking IVIFSs are presented by the authors in [15, 16]. On the other hand, the score function for IVPFS is presented by Peng and Yang [5], while the improved score function is presented in Ref. [17]. Regarding the accuracy function for IVPFSs, we refer the reader to the articles in Ref. [6, 18]. A similarity measure for IVPFSs is discussed by Peng and Li [19] for solving the MAGDM problems.

The authors have used the above approaches to solve the MAGDM problems with constraints ${\overline{\vartheta }}+{\overline{\varphi }}\le 1$ or ${\overline{\vartheta }}^2+{\overline{\varphi }}^2\le 1$. But, with the increasing complexity of information nowadays, it is sometimes difficult to satisfy the expert rating during the evaluation. For example, if an expert gives a score as ([0.5, 0.7], [0.6, 0.8]), then neither $0.7+0.8 \le 1$ nor $0.7^2+0.8^2\le 1$ is sufficient. Therefore, the algorithm given above does not work in such cases and hence the algorithms under IVIFS and IVPFS have restricted their access. To get a broader information, Ju et al. [20] introduced the notion of interval-valued q-rung orthopair fuzzy set (IVq-ROFS) with membership $[{\underline{\vartheta }}, {\overline{\vartheta }}]$ and non-membership $[{\underline{\varphi }}, {\overline{\varphi }}]$ together with the constraint ${\overline{\vartheta }}^q + {\overline{\varphi }}^q\le 1$, $q\ge 1$ is an integer. Here, for scoring ([0.5, 0.7], [0.6, 0.8]), we see that $0.7^3+0.8^3\le 1$ for the smallest value of q as 3. Thus, the parameter q is more flexible for experts to assign scores independently. Moreover, setting $q=1$ and $q=2$ reduces the considered IVq-ROFS to IVIFS and IVPFS, respectively. Considering the advantages of IVq-ROFSs, various algorithms were developed by the researchers to solve MAGDM problems. In this direction, the averaging operators of Ju et al. [20] were first developed. A concept of Muirhead mean was integrated into the IVq-ROFS by Xu et al. [21] to solve the MAGDM problems. Later, a concept of Maclaurin symmetric mean is embedded in IVq-ROFS and studied by Wang et al. [22] to solve decision-making problems (DMPs). However, some hybrid aggregation operators were initiated by Wang and Li [11]. Recently, a new possibility degree measure was defined by Garg [23] for IVq-ROFSs.

In addition to the above theories, Zhao [24] presented a theory of uncertainty analysis in 1989, by combining dialectical reasoning and mathematical tools, which is called SPA (“set pair analysis”) theory. This theory differs from traditional probabilistic and fuzzy set theory in that it coordinates the structure of certainty and uncertainty in a single analysis. The main component of this theory is the connection number (CN), which is composed of three perspectives, namely “identity (a)”, “discrepancy (b)”, and “contrary (c)” with $a+b+c=1$. Jiang et al. [25] discussed the basic concept, while Liu et al. [26] defined basic operation laws for CNs and studied their properties. Garg and Kumar [27] presented more generalized operations for the different CNs. Instead of applying the SPA theory to solve other covenants, it is also widely used in DMPs. For example, Yang et al. [28] defined the similarity and distance measures between the two CNs. Lü and Zhang [29] developed the multi-attribute decision making (MADM) approach based on SPA theory. Xie et al. [30] solved the decision problems based on SPA theory under interval fuzzy number environment. However, Kumar and Garg [31, 32] introduced various forms of CNs to solve the decision problems using TOPSIS method (technique for order preference by similarity to ideal solution). Fu and Zhou [33] used the SPA theory for a triangular fuzzy number to solve the problems. Cao et al. [34] defined a stochastic method under the IVIF environment based on the SPA theory. Garg and Kumar [35] introduced power geometric operators based on the CNs of IFS. Su et al. [36] developed a groundwater quality assessment and prediction model based on SPA and Markov chain theory, in which SPA was used to measure groundwater quality.

The literature listed above shows that there are several algorithms that address the problem of MAGDM. However, all these studies are valid considering that the exponent of the numbers is a real number of unit length and therefore, not applicable under the cases where the exponents are interval numbers. To address this, some exponential operation laws (EOLs) [37,38,39,40] were developed by the researchers under the manifold fuzzy environment. For example, in [37, 38], the authors developed an algorithm to solve the DMPs using EOLs for IFS and IVIFS features. Garg [39] presented algorithms for solving the DMPs by proposing EOLs for IVPFS, while Peng et al. [40] extended them to q-rung orthopair fuzzy sets (q-ROFSs). Recently, some generalized and compensating operators were developed by Garg and Rani [41] for complex IFS. All these theories are well suited for DMPs with IVIFS or IVPFS, but they are not able to deal with IVq-ROFS properties.

Another hurdle covered in MAGDM is ranking the given objects by selecting the appropriate defuzzification method such as score or accuracy. From the study, that the existing score functions under IVIFS [12] or IVPFS [5, 6] may give undesirable results (see Table 1) to rank the numbers. Therefore, there is a need to present a novel ranking function for them, which not only overcomes the weakness of the existing studies but also provides some advantages for ranking the interval numbers. Moreover, the shortcoming of the existing studies [31, 32, 34, 35] with respect to CNs is that they are limited in access with the condition $a+bi+cj$, where $0\le a,\,b,\,c\le 1$ and $a+b+c=1$. However, in many practical problems, the condition $a+b+c$ may be $>1$. Therefore, it is necessary to pay more attention to it by extending the feasible domain of the problem to describe the information more flexibly and comprehensively.

Considering all points about IVq-ROFSs and CNs from SPA, this paper introduces a new notion of q-CN for IVq-ROFSs with three degrees, namely “identity (a)”, “discrepancy (b)” and “contrary (c)” with $a^q+b^q+c^q=1$. The main advantage of the presented q-CN is that it combines the pairs of certainty and uncertainty in a single place. Moreover, we have given its basic properties for the study and defined new subtraction and division operations as well as the score function using the sigmoidal function to compare the given set. Apart from that, we have represented the EOLs for the given q-CNs under IVq-ROFSs by taking an exponent as q-CNs. Based on these operations, we defined a set of operators to manage the collective information into one and thus a MAGDM algorithm for DMPs. Finally, we explain the validation of the proposed algorithm by comparing its results with some existing methods and present their advantages. To the best of our knowledge, no research has been done so far toward the development of operators under IVq-ROFS environment.

To summarize the entire discussion, the basic objectives of this article are as follows.

• (1) To introduce a new concept called q-CNs for IVq-ROFSs and to investigate their properties.

• (2) To define a new subtraction and division operation and a sigmoid-based score function by overcoming the weakness of existing sets under IVq-ROFSs properties.

• (3) Propose new EOLs, operators and their fundamental relations for the pair of q-CNs.

• (4) Design a MAGDM algorithm for solving DMPs based on the above-stated work.

• (5) Validate the work with several numerical examples and state their advantages.

The remainder of the article is as follows. In Sect. 2, a basic notation is given about the existing studies. In Sect. 3, the concept of q-CN and the score function are introduced. In Sect. 4, new subtraction, division and EOL operators are introduced, along with their aggregation operators, and their properties are studied. In Sect. 5, an algorithm based on MAGDM problems is presented based on the proposed aggregation operators and demonstrated with several numerical examples. The superiority of the approach is explained in Section 6. Finally, a concluding remark is given in Sect. 7.

2 Preliminaries

In this section, we review some basic notions about the existing studies on the set ${\mathcal {U}}$.

Definition 1

[3] An IVIFS ${\mathcal {I}}$ in ${\mathcal {U}}$ is defined as

$$\begin{aligned} {\mathcal {I}}=\{(u, \vartheta _{{\mathcal {I}}}(u), \varphi _{{\mathcal {I}}}(u)) \mid u\in {\mathcal {U}} \}, \end{aligned}$$

(1)

where $\vartheta _{{\mathcal {I}}}(u) = [{\underline{\vartheta }}_{{\mathcal {I}}}(u), {\overline{\vartheta }}_{{\mathcal {I}}}(u)] \subseteq [0, 1]$ and $\varphi _{{\mathcal {I}}}(u) = [{\underline{\varphi }}_{{\mathcal {I}}}(u)$, ${\overline{\varphi }}_{{\mathcal {I}}}(u)] \subseteq [0, 1]$ describe the membership degrees (MDs) and non-membership degrees (NMDs) such that $0\le {\overline{\vartheta }}_{{\mathcal {I}}}(u)$ + ${\overline{\varphi }}_{{\mathcal {I}}}(u)\le 1$ for all $u\in {\mathcal {U}}$. For accessibility, a pair ${\mathcal {I}}=([{\underline{\vartheta }}_{\mathcal {I}}, {\overline{\vartheta }}_{\mathcal {I}}], [{\underline{\varphi }}_{\mathcal {I}}, {\overline{\varphi }}_{\mathcal {I}}])$ is called an interval-valued intuitionistic fuzzy number (IVIFN) with the requirement that $[{\underline{\vartheta }}_{\mathcal {I}}, {\overline{\vartheta }}_{\mathcal {I}}]$, $[{\underline{\varphi }}_{\mathcal {I}}, {\overline{\varphi }}_{\mathcal {I}}]\subseteq [0,1]$ and ${\overline{\vartheta }}_{\mathcal {I}}+{\overline{\varphi }}_{\mathcal {I}}\le 1$.

Definition 2

[5, 6] An IVPFS ${\mathcal {P}}$ is stated as

$$\begin{aligned} {\mathcal {P}}=\{(u, \vartheta _{\mathcal {P}}(u), \varphi _{\mathcal {P}}(u)) \mid u\in {\mathcal {U}} \} \end{aligned}$$

(2)

where $\vartheta _{{\mathcal {P}}}(u) = [{\underline{\vartheta }}_{{\mathcal {P}}}(u), {\overline{\vartheta }}_{{\mathcal {P}}}(u)] \subseteq [0, 1]$ and $\varphi _{{\mathcal {P}}}(u) = [{\underline{\varphi }}_{{\mathcal {P}}}(u), {\overline{\varphi }}_{{\mathcal {P}}}(u)] \subseteq [0, 1]$ with $0\le {\overline{\vartheta }}_{{\mathcal {P}}}^2(u)+ {\overline{\varphi }}_{{\mathcal {P}}}^2(u)\le 1$ for all $u\in {\mathcal {U}}$. We call ${\mathcal {P}}=([{\underline{\vartheta }}, {\overline{\vartheta }}], [{\underline{\varphi }}, {\overline{\varphi }}])$ as IVPFN (“interval-valued Pythagorean fuzzy number”).

Definition 3

[20] An IVq-ROFSs ${\mathcal {Q}}$ on ${\mathcal {U}}$ is stated as

$$\begin{aligned} {\mathcal {Q}} =\{(u, \vartheta _{\mathcal {Q}}(u), \varphi _{\mathcal {Q}}(u)) \mid u\in {\mathcal {U}}\}, \end{aligned}$$

(3)

where $\vartheta _{{\mathcal {Q}}}(u) = [{\underline{\vartheta }}_{{\mathcal {Q}}}(u), {\overline{\vartheta }}_{{\mathcal {Q}}}(u)] \subseteq [0, 1]$ and $\varphi _{{\mathcal {Q}}}(u) = [{\underline{\varphi }}_{{\mathcal {Q}}}(u), {\overline{\varphi }}_{{\mathcal {Q}}}(u)] \subseteq [0, 1]$ with $0\le {\overline{\vartheta }}_{{\mathcal {Q}}}^q(u)+ {\overline{\varphi }}_{{\mathcal {Q}}}^q(u)\le 1$ for all $u\in {\mathcal {U}}$. We call ${\mathcal {Q}}=([{\underline{\vartheta }}, {\overline{\vartheta }}], [{\underline{\varphi }}, {\overline{\varphi }}])$ as IVq-ROFN (“interval-valued q-rung orthopair fuzzy number”) with ${\overline{\vartheta }}^q + {\overline{\varphi }}^q \le 1$ for $q\ge 1$ and an integer.

Remark 1

From Definition 3, we see that

• (1) If $q=1$, then it becomes Definition 1.

• (2) If $q=2$, then it becomes Definition 2.

Definition 4

[20] The score function ${\mathcal {S}}$ of ${\mathcal {Q}}=([{\underline{\vartheta }}, {\overline{\vartheta }}], [{\underline{\varphi }}, {\overline{\varphi }}])$ is defined as

$$\begin{aligned} S({\mathcal {Q}}) = ({\underline{\vartheta }}^q+{\overline{\vartheta }}^q - {\underline{\varphi }}^q - {\overline{\varphi }}^q)/2, \end{aligned}$$

(4)

and ${\mathcal {H}}$ (“an accuracy function”) is

$$\begin{aligned} H({\mathcal {Q}}) = ({\underline{\vartheta }}^q+{\overline{\vartheta }}^q + {\underline{\varphi }}^q + {\overline{\varphi }}^q)/2 \end{aligned}$$

(5)

Definition 5

A relation between two IVq-ROFNs ${\mathcal {I}}$ and ${\mathcal {J}}$ written by ${\mathcal {I}} \succ {\mathcal {J}}$ holds, if either i) $S({\mathcal {I}})>S({\mathcal {J}})$, or ii) $S({\mathcal {I}})=S({\mathcal {J}})$ and $H({\mathcal {I}})>H({\mathcal {J}})$ satisfy.

Definition 6

[24] A pair of sets ${\mathcal {Y}}$ between the two sets ${\mathcal {P}}$ and ${\mathcal {Q}}$ is denoted by ${\mathcal {Y}}({\mathcal {P}}, {\mathcal {Q}})$ and the CN for a problem ${\mathcal {W}}$ written by ${\mathcal {C}}n({\mathcal {Y}},{\mathcal {W}})$ is defined as

$$\begin{aligned} {\mathcal {C}}n = ({\mathcal {L}}/{\mathcal {F}}) + ({\mathcal {M}}/{\mathcal {F}})i + ({\mathcal {N}}/{\mathcal {F}}) j \end{aligned}$$

(6)

where ${\mathcal {F}}$ is the “total number of features” in which ${\mathcal {L}}$, ${\mathcal {M}}$ and ${\mathcal {N}}$ represent the “identity”, “discrepancy” and “contrary” features. Equation (6) can also be written as ${\mathcal {C}}n=a+bi+cj,$ where $a={\mathcal {L}}/{\mathcal {F}}$, $b={\mathcal {M}}/{\mathcal {F}}$ and $c={\mathcal {N}}/{\mathcal {F}}$ denote the “identity”, “discrepancy” and “contrary” degrees such that $0\le a,b,c\le 1$ and $a+b+c=1$. Furthermore, $i\in [-1,1]$ and j are the “discrepancy coefficient” and “coefficients of contrary” degrees, respectively.

3 Proposed q-CN for IVq-ROFS

This section discusses the concept of q-CN for IVq-ROFS with $q\ge 1 \in {\mathbb {N}}$. Moreover, we propose the novel score function to rank them.

3.1 Concept of q-CN

In this section, we introduce the notion of q-connection number set (q-CNS) for the given IVq-ROFS. To do so, we first consider two IVq-ROFSs ${\mathcal {I}}$ and ${\mathcal {J}}$ such that $S({\mathcal {I}})\ne S({\mathcal {J}})$ and $H({\mathcal {I}})\ne H({\mathcal {J}})$, then the q-CNS is defined as

Definition 7

A q-CNS with $q\ge 1$ corresponding to IVq-ROFS ${\mathcal {I}}=\{(u_t, [{\underline{\vartheta }}_{\mathcal {I}}(u_t), {\overline{\vartheta }}_{\mathcal {I}}(u_t)]$, $[{\underline{\varphi }}_{\mathcal {I}}(u_t)$, ${\overline{\varphi }}_{\mathcal {I}}(u_t)])\mid u_t \in {\mathcal {U}}\}$ is defined as

$$\begin{aligned} {\mathcal {C}}n=\{(u_t, a_{\mathcal {I}}(u_t) + b_{\mathcal {I}}(u_t) i + c_{\mathcal {I}}(u_t)j) \mid u_t \in {\mathcal {U}}\}, \end{aligned}$$

(7)

where for each $u_t\in {\mathcal {U}}$,

$$\begin{aligned} &a_{\mathcal {I}}= \left( \frac{{\underline{\vartheta }}_{\mathcal {I}}^q + {\overline{\vartheta }}_{\mathcal {I}}^q }{2}\right) ^{1/q} \root q \of {1- \frac{{\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q}{2}}, \\ &b_{\mathcal {I}}= \root q \of {\frac{1+\left( 1-{\underline{\vartheta }}_{\mathcal {I}}^q - {\overline{\vartheta }}_{\mathcal {I}}^q \right) \cdot \left( 1-{\underline{\varphi }}_{\mathcal {I}}^q - {\overline{\varphi }}_{\mathcal {I}}^q \right) }{2} } , \\& \text {and } ~~ c_{\mathcal {I}}= \left( \frac{{\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q }{2}\right) ^{1/q} \root q \of {1- \frac{{\underline{\vartheta }}_{\mathcal {I}}^q+ {\overline{\vartheta }}_{\mathcal {I}}^q}{2}} \end{aligned}$$

such that $a^q_{\mathcal {I}}+b^q_{\mathcal {I}}+c^q_{\mathcal {I}}=1$ and $0\le a_{\mathcal {I}}, b_{\mathcal {I}}, c_{\mathcal {I}}\le 1$, $q\ge 1 \in {\mathbb {N}}$ for all $u_t\in {\mathcal {U}}$.

If in a given situation, for two different q-ROFSs ${\mathcal {I}}$ and ${\mathcal {J}}$, it holds that $S({\mathcal {I}})=S({\mathcal {J}})$, we construct the q-CNS by uniting the degree of hesitation and define as follows.

Definition 8

If ${\mathcal {I}}=\{(u_t, [{\underline{\vartheta }}_{\mathcal {I}}(u_t), {\overline{\vartheta }}_{\mathcal {I}}(u_t)], [{\underline{\varphi }}_{\mathcal {I}}(u_t), {\overline{\varphi }}_{\mathcal {I}}(u_t)]) \mid u_t \in {\mathcal {U}}\}$ be IVq-ROFS, then q-CNS corresponding to ${\mathcal {I}}$ is given as follows ${\mathcal {C}}n=\{(u_t, a_{\mathcal {I}}(u_t) + b_{\mathcal {I}}(u_t) i + c_{\mathcal {I}}(u_t)j ) \mid u_t \in {\mathcal {U}}\},$ where

$$\begin{aligned} a_{\mathcal {I}}&= \left( \frac{{\underline{\vartheta }}_{\mathcal {I}}^q\left( 1-{\overline{\vartheta }}_{\mathcal {I}}^q - {\overline{\varphi }}_{\mathcal {I}}^q\right) + {\overline{\vartheta }}_{\mathcal {I}}^q\left( 1-{\underline{\vartheta }}_{\mathcal {I}}^q - {\underline{\varphi }}_{\mathcal {I}}^q\right) }{2} \right) ^{1/q} \times \\&\quad \root q \of {1- \frac{{\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q}{2}} \\ c_{\mathcal {I}}&= \left( \frac{{\underline{\varphi }}_{\mathcal {I}}^q\left( 1-{\overline{\vartheta }}_{\mathcal {I}}^q - {\overline{\varphi }}_{\mathcal {I}}^q\right) + {\overline{\varphi }}_{\mathcal {I}}^q\left( 1-{\underline{\vartheta }}_{\mathcal {I}}^q - {\underline{\varphi }}_{\mathcal {I}}^q\right) }{2} \right) ^{1/q} \times \\&\quad \root q \of {1- \frac{{\underline{\vartheta }}_{\mathcal {I}}^q + {\overline{\vartheta }}_{\mathcal {I}}^q}{2}} \\ b_{\mathcal {I}}&= \left( 1-a_{\mathcal {I}}^q-c_{\mathcal {I}}^q\right) ^{1/q} \end{aligned}$$

Here ${\underline{\pi }}_{\mathcal {I}} = \root q \of {1-{\overline{\vartheta }}_{\mathcal {I}}^q - {\overline{\varphi }}_{\mathcal {I}}^q}$ and ${\overline{\pi }}_{\mathcal {I}} = \root q \of {1-{\underline{\vartheta }}_{\mathcal {I}}^q - {\underline{\varphi }}_{\mathcal {I}}^q}$ are the degrees of hesitancies.

To justify the above q-CNSs are valid or not, we see in the following result.

Theorem 1

For an IVq-ROFS, the set described in Definition 7is a q-CNS.

Proof

To ascertain whether the set given in Eq. (7) is a q-CNS or not for the IVq-ROFS ${\mathcal {I}}=\{(u_t, [{\underline{\vartheta }}_{\mathcal {I}}(u_t), {\overline{\vartheta }}_{\mathcal {I}}(u_t)]$, $[{\underline{\varphi }}_{\mathcal {I}}(u_t)$, ${\overline{\varphi }}_{\mathcal {I}}(u_t)])\mid u_t\in {\mathcal {U}}\}$, we check the following two conditions:

• (P1) $0\le a_{\mathcal {I}}(u_t), b_{\mathcal {I}}(u_t), c_{\mathcal {I}}(u_t)\le 1$.

• (P2) $a^q_{\mathcal {I}}(u_t)+b^q_{\mathcal {I}}(u_t)+c^q_{\mathcal {I}}(u_t)=1$ for all $u_t$.

Since ${\mathcal {I}}$ is IVq-ROFS which implies that ${\underline{\vartheta }}_{\mathcal {I}}(u_t)$, ${\overline{\vartheta }}_{\mathcal {I}}(u_t)$, ${\underline{\varphi }}_{\mathcal {I}}(u_t)$, ${\overline{\varphi }}_{\mathcal {I}}(u_t)\in [0,1]$ and ${\overline{\vartheta }}_{\mathcal {I}}^q(u_t)+{\overline{\varphi }}_{\mathcal {I}}^q(u_t)\le 1$ for all $u_t\in {\mathcal {U}}$. Then, we have

• (P1) For given ${\underline{\vartheta }}_{\mathcal {I}}$, ${\overline{\vartheta }}_{\mathcal {I}}$, ${\underline{\varphi }}_{\mathcal {I}}$, ${\overline{\varphi }}_{\mathcal {I}}$, we have $\frac{{\underline{\vartheta }}_{\mathcal {I}}^q + {\overline{\vartheta }}_{\mathcal {I}}^q}{2}, \frac{{\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q}{2} \in [0,1]$ and hence $\left( \frac{{\underline{\vartheta }}_{\mathcal {I}}^q + {\overline{\vartheta }}_{\mathcal {I}}^q}{2}\right) ^{1/q}$, $\root q \of {1-\frac{{\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q}{2}} \in [0,1]$. Thus, we get $a_{\mathcal {I}}\in [0,1]$. Similarly, we obtain $c_{\mathcal {I}}\in [0,1]$. Further, $0\le {\underline{\vartheta }}_{\mathcal {I}}^q + {\overline{\vartheta }}_{\mathcal {I}}^q \le 2$ and $0\le {\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q \le 2$ which implies that $-1\le 1-{\underline{\vartheta }}_{\mathcal {I}}^q - {\overline{\vartheta }}_{\mathcal {I}}^q \le 1$ and $-1\le 1-{\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q \le 1$. Hence, $b_{\mathcal {I}}= \root q \of {\frac{1+\left( 1-{\underline{\vartheta }}_{\mathcal {I}}^q - {\overline{\vartheta }}_{\mathcal {I}}^q \right) \cdot \left( 1-{\underline{\varphi }}_{\mathcal {I}}^q - {\overline{\varphi }}_{\mathcal {I}}^q \right) }{2}} \in [0,1]$. Thus, P1) exists.

• (P2) By Eq. (7), we have

  $$\begin{aligned}&a^q_{\mathcal {I}} + b^q_{\mathcal {I}} + c^q_{\mathcal {I}} = \left( \frac{{\underline{\vartheta }}_{\mathcal {I}}^q + {\overline{\vartheta }}_{\mathcal {I}}^q }{2}\right) \left( 1- \frac{{\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q}{2}\right) \\&\qquad +\frac{1+\left( 1-{\underline{\vartheta }}_{\mathcal {I}}^q - {\overline{\vartheta }}_{\mathcal {I}}^q \right) \cdot \left( 1-{\underline{\varphi }}_{\mathcal {I}}^q - {\overline{\varphi }}_{\mathcal {I}}^q \right) }{2} \\&\quad = \frac{{\underline{\vartheta }}_{\mathcal {I}}^q + {\overline{\vartheta }}_{\mathcal {I}}^q + {\underline{\varphi }}_{\mathcal {I}}^q + {\overline{\varphi }}_{\mathcal {I}}^q}{2}\\&\qquad - \frac{({\underline{\vartheta }}_{\mathcal {I}}^q + {\overline{\vartheta }}_{\mathcal {I}}^q)({\underline{\varphi }}_{\mathcal {I}}^q +{\overline{\varphi }}_{\mathcal {I}}^q)}{2} \\&\qquad + \frac{1+\left( 1-{\underline{\vartheta }}_{\mathcal {I}}^q - {\overline{\vartheta }}_{\mathcal {I}}^q \right) \cdot \left( 1-{\underline{\varphi }}_{\mathcal {I}}^q - {\overline{\varphi }}_{\mathcal {I}}^q \right) }{2} = 1. \end{aligned}$$

  $\therefore$ P2) exists.

$\square$

Theorem 2

The set defined in Definition 8is also a q-CNS.

Proof

Obtained similarly from above theorem. $\square$

To demonstrate the above definition more surely, consider an example as follows.

Example 1

Let ${\mathcal {I}}=([0.6, 0.7], [0.2, 0.4])$ and ${\mathcal {J}}$=([0.4, 0.6], [0.3, 0.4]) be two IVq-ROFNs with $q=2$. Since $S({\mathcal {I}})=\frac{0.6^2+0.7^2-0.2^2-0.4^2}{2}=0.3250$ and $S({\mathcal {J}})=\frac{0.4^2+0.6^2-0.3^2 - 0.4^2}{2} = 0.1350$ and we get $S({\mathcal {I}})\ne S({\mathcal {J}})$. For ${\mathcal {I}}$, the values of $a_{\mathcal {I}}$, $b_{\mathcal {I}}$ and $c_{\mathcal {I}}$ are computed by Definition 7 as

$$\begin{aligned} &a_{\mathcal {I}}= \left( \frac{0.6^2+0.7^2}{2}\right) ^{1/2} \sqrt{1-\frac{0.2^2+0.4^2}{2}} = 0.6185, \\ &b_{\mathcal {I}}= \left( \frac{1+(1-0.6^2-0.7^2)(1-0.2^2-0.4^2)}{2}\right) ^{1/2} = 0.7483, \\ \text { and }~ &c_{\mathcal {I}}= \left( \frac{0.2^2+0.4^2}{2}\right) ^{1/2} \sqrt{1-\frac{0.6^2+0.7^2}{2}} = 0.2398. \end{aligned}$$

and get ${\mathcal {C}}n_{\mathcal {I}}= 0.6185 + 0.7483 i + 0.2398 j$. Similarly, q-CN of ${\mathcal {J}}$ is ${\mathcal {C}}n_{\mathcal {J}}=0.4770 + 0.8246 i + 0.3041 j$.

Example 2

Let ${\mathcal {I}}=([0.3, 0.4], [0.4, 0.5])$ and ${\mathcal {J}}$=([0.2, 0.3], [0.35, 0.35]) be two IVq-ROFN with $q=1$ such that $S({\mathcal {I}})=S({\mathcal {J}})$. Hence, for ${\mathcal {I}}$ and by Definition 8, we can construct the q-CNs as ${\mathcal {C}}n_{\mathcal {I}}=0.0412 + 0.8970 i + 0.0617 j$ and similarly for ${\mathcal {J}}$, we have ${\mathcal {C}}n_{\mathcal {J}}=0.0666 + 0.8284 i + 0.1050 j$.

Example 3

Let ${\mathcal {I}}=([0, 0.5], [0.1, 0.7])$ and ${\mathcal {J}}$=([0.3, 0.4], [0.5, 0.5]) be two IVq-ROFNs with $q=2$. Then, clearly seen that $S({\mathcal {I}})=S({\mathcal {J}})=-0.1250$. Thus, by Definition 8, the q-CNs for given pairs are constructed as ${\mathcal {C}}n_{\mathcal {I}}=0.3047+0.8330i + 0.4619j$ and ${\mathcal {C}}n_{\mathcal {J}}=0.2440 + 0.8965 i +0.3698 j$.

Definition 9

For two CNSs ${\mathcal {C}}n=\{u, a_{\mathcal {C}}(u)+ b_{\mathcal {C}}(u)i + c_{\mathcal {C}}(u)j\mid u\in {\mathcal {U}}\}$ and ${\mathcal {D}}n=\{u, a_{\mathcal {D}}(u)+ b_{\mathcal {D}}(u)i + c_{\mathcal {D}}(u)j\mid u\in {\mathcal {U}}\}$, we have

• (i) ${\mathcal {C}}n\subseteq {\mathcal {D}}n$ if $a_{\mathcal {C}}(u) \le a_{\mathcal {D}}(u)$, $b_{\mathcal {C}}(u)\ge b_{\mathcal {D}}(u)$, $c_{\mathcal {C}}(u)\ge c_{\mathcal {D}}(u)$.

• (ii) ${\mathcal {C}}n = {\mathcal {D}}n$ if $a_{\mathcal {C}}(u) = a_{\mathcal {D}}(u)$, $c_{\mathcal {C}}(u) = c_{\mathcal {D}}(u)$.

3.2 A new score function

In order to make a clear decision in our modern life, it is necessary to consider simultaneously the identity and contrary degrees in the analysis. Furthermore, it is obvious that for q-CN ${\mathcal {C}}n=a_{\mathcal {I}}+b_{\mathcal {I}}i+c_{\mathcal {I}}j$ corresponding to IVq-ROFN ${\mathcal {I}}$, a more likely decision to support the statement if $a_{\mathcal {I}} > c_{\mathcal {I}}$ while if $a_{\mathcal {I}} < c_{\mathcal {I}}$ then will have an opposite effect on the decision. It will thus be necessary to include the degree of indeterminacy $b_{\mathcal {I}}$ in the analysis, which will show the influence of the degrees on the decision. To this end, one has taken an S-shaped sigmoidal function $f(x)=\frac{e^x}{1+e^x}$ and defined the score function for q-CN of IVq-ROFN ${\mathcal {I}}$ as follows:

Definition 10

For q-CN ${\mathcal {C}}n_{\mathcal {I}}=a_{\mathcal {I}}+b_{\mathcal {I}}i+c_{\mathcal {I}}j$, a score function is defined as

$$\begin{aligned} {\mathcal {S}}({\mathcal {C}}n_{\mathcal {I}})=\left( a_{\mathcal {I}}^q-c_{\mathcal {I}}^q\right) +\left( \frac{e^{a_{\mathcal {I}}^q - c_{\mathcal {I}}^q}}{1 + e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}}-\frac{1}{2}\right) b_{\mathcal {I}}^q \end{aligned}$$

(8)

Definition 11

For two q-CNs ${\mathcal {C}}n_1$ and ${\mathcal {C}}n_2$, an order relation between them, denoted by ${\mathcal {C}}n_1\succ {\mathcal {C}}n_2$, is defined if either one of the conditions satisfies (i) ${\mathcal {S}}({\mathcal {C}}n_1)>{\mathcal {S}}({\mathcal {C}}n_2)$ or (ii) if ${\mathcal {S}}({\mathcal {C}}n_1)={\mathcal {S}}({\mathcal {C}}n_2)$ and $b_1<b_2$.

Proposition 1

For a q-CN ${\mathcal {C}}n_{\mathcal {I}}=a_{\mathcal {I}}+b_{\mathcal {I}} i + c_{\mathcal {I}} j$, ${\mathcal {S}}({\mathcal {C}}n_{\mathcal {I}})$ monotonically increases with respect to $a_{\mathcal {I}}$ and monotonically decreases with respect to $b_{\mathcal {I}}$.

Proof

Differentiate ${\mathcal {S}}$ with respect to $a_{\mathcal {I}}$ and $c_{\mathcal {I}}$, we can get

$$\begin{aligned} \frac{\partial {\mathcal {S}}}{\partial a_{\mathcal {I}}}&= q a_{\mathcal {I}}^{q-1} \left[ \frac{3}{2} + \frac{e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}}{\left( 1+e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}\right) ^2} b_{\mathcal {I}}^q -\frac{e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}}{1+e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}} \right] \\ \frac{\partial {\mathcal {S}}}{\partial c_{\mathcal {I}}}&= -q c_{\mathcal {I}}^{q-1} \left[ \frac{1}{2} + \frac{e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}}{\left( 1+e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}\right) ^2} b_{\mathcal {I}}^q +\frac{e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}}{1+e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}} \right] \end{aligned}$$

Since $\frac{e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}}{\left( 1+e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}\right) ^2} b_{\mathcal {I}}^q \ge 0$ and $\frac{e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}}{1+e^{a_{\mathcal {I}}^q-c_{\mathcal {I}}^q}} b_{\mathcal {I}}^q \in [0,1]$, we can have $\frac{\partial {\mathcal {S}}}{\partial a_{\mathcal {I}}} \ge 0$ and $\frac{\partial {\mathcal {S}}}{\partial c_{\mathcal {I}}}\le 0$. Consequently, we get the desired result. $\square$

Proposition 2

For a q-CN ${\mathcal {C}}n=a+bi+cj$, a proposed function ${\mathcal {S}}({\mathcal {C}}n)$ satisfies:

• (1) $-1\le {\mathcal {S}}({\mathcal {C}}n)\le 1$.

• (2) ${\mathcal {S}}({\mathcal {C}}n)=1$ iff ${\mathcal {C}}n=1$ and ${\mathcal {S}}({\mathcal {C}}n)=-1$ iff ${\mathcal {C}}n=1j$.

Proof

• (1) For a q-CN ${\mathcal {C}}n=a+bi+cj$ such that $0\le a,b,c\le 1$ and $a^q+b^q+c^q=1$ and the property of S-shaped function, we have $\frac{-1}{2} \le \frac{e^{a^q-c^q}}{1+e^{a^q-c^q}}-\frac{1}{2}\le \frac{1}{2}$ which gives $\frac{-1}{2}b^q \le \left( \frac{e^{a^q-c^q}}{1+e^{a^q-c^q}}-\frac{1}{2}\right) b^q\le \frac{1}{2}b^q$ and hence $a^q - c^q + \frac{-1}{2}b^q \le a^q - c^q +\left( \frac{e^{a^q-c^q}}{1+e^{a^q-c^q}}-\frac{1}{2}\right) b^q \le a^q - c^q + \frac{1}{2}b^q$. Also, $-1=-a^q -b^q- c^q \le a^q-c^q-\frac{1}{2}b^q$ and $a^q-c^q+\frac{1}{2}b^q \le a^q+b^q+c^q = 1$ and consequently, we have $-1\le {\mathcal {S}}({\mathcal {C}}n)\le 1$.

• (2) Using the monotonicity of the score function described in Proposition 1, we can easily conclude that ${\mathcal {S}}({\mathcal {C}}n)$ reaches the maximum value at $a=1$ and $c=0$ and the minimum value at $a=0$ and $c=1$. Thus, we consequently have ${\mathcal {S}}({\mathcal {C}}n)=1$ iff ${\mathcal {C}}n=1$ and ${\mathcal {S}}({\mathcal {C}}n)= -1$ iff ${\mathcal {C}}n=1j$.

$\square$

Proposition 3

Let ${\mathcal {C}}n=a+bi+cj$ be a q-CN and ${\mathcal {C}}n^c=c+bi+aj$, then ${\mathcal {S}}({\mathcal {C}}n^c)=-{\mathcal {S}}({\mathcal {C}}n)$.

Proof

Consider a function $f(x)=\frac{e^x}{1+e^x}-\frac{1}{2}$ which is symmetrical about origin and hence $f(-x)=-f(x)$. Thus, by taking $x=a^q-c^q$, we get $\frac{e^{-a^q+c^q}}{1+e^{-a^q+c^q}}-\frac{1}{2} = -\frac{e^{a^q-c^q}}{1+e^{a^q-c^q}}+\frac{1}{2}$ which implies that $-a^q + c^q + \left( \frac{e^{-a^q+c^q}}{1+e^{-a^q+c^q}}-\frac{1}{2}\right) b^q = -a^q + c^q + \left( -\frac{e^{a^q-c^q}}{1+e^{a^q-c^q}}+\frac{1}{2}\right) b^q$ and hence ${\mathcal {S}}({\mathcal {C}}n^c)=-{\mathcal {S}}({\mathcal {C}}n)$.

$\square$

To examine the applicability of the proposed ${\mathcal {S}}$ for ranking the IVq-ROFNs, several numbers are taken and their results are presented in comparison with the existing functions in Table 1. Thus, we conclude that the proposed function can overcome the shortcomings of the existing score functions defined under IVIFSs [8, 12, 15, 16] and IVPFS [5, 6, 17, 18]. Therefore, the proposed ${\mathcal {S}}$ is more reliable and valid to solve the DMPs.

Table 1 Comparison of score functions

4 Exponential operational laws and operators for q-CNs

In this section, as a supplement of the existing operators, we introduce the new q-exponential operation laws (EOLs) and operators over q-CNs, in which the bases $\zeta$ are real positive numbers and the exponents are q-CNs.

4.1 New exponential operational laws

Definition 12

For a given q-CNS ${\mathcal {C}}n=\{(u_t, a(u_t) + b(u_t) i + c(u_t) j) \mid u_t\in {\mathcal {U}}\}$, the q-EOL of the q-CN ${\mathcal {C}}n$ has the following form:

$$\begin{aligned} \zeta ^{{\mathcal {C}}n} = {\left\{ \begin{array}{ll} \left\{ \left( \begin{aligned} &{} u_t, \root q \of {\zeta ^{1-a^q(u_t)}} + \root q \of {\zeta ^{c^q(u_t)}-\zeta ^{b^q(u_t)+c^q(u_t)}} i \\ &{} \qquad + \root q \of {1-\zeta ^{c^q(u_t)}} j \end{aligned} \right) \mid u_t\in {\mathcal {U}}\right\} &{}; \zeta \in (0,1) \\ \\ \left\{ \left( \begin{aligned} &{} u_t, \root q \of {\left( \frac{1}{\zeta }\right) ^{1-a^q(u_t)}} + \root q \of {\left( \frac{1}{\zeta }\right) ^{c^q(u_t)}-\left( \frac{1}{\zeta }\right) ^{b^q(u_t)+c^q(u_t)}} i \\ &{} \qquad + \root q \of {1-\left( \frac{1}{\zeta }\right) ^{c^q(u_t)}} j \end{aligned} \right) \mid u_t\in {\mathcal {U}}\right\} &{}; \zeta \ge 1 \end{array}\right. } \end{aligned}$$

Definition 13

For a q-CN ${\mathcal {C}}n=a + b i + c j$, the q-EOL of ${\mathcal {C}}n$ is defined as

$$\begin{aligned} \zeta ^{{\mathcal {C}}n} = {\left\{ \begin{array}{ll} \root q \of {\zeta ^{1-a^q}} + \root q \of {\zeta ^{c^q}-\zeta ^{b^q+c^q}} i + \root q \of {1-\zeta ^{c^q}} j &{}; \zeta \in (0,1) \\ \\ \root q \of {\left( \frac{1}{\zeta }\right) ^{1-a^q}} + \root q \of {\left( \frac{1}{\zeta }\right) ^{c^q}-\left( \frac{1}{\zeta }\right) ^{b^q+c^q}} i + \root q \of {1-\left( \frac{1}{\zeta }\right) ^{c^q}} j &{}; \zeta \ge 1 \end{array}\right. } \end{aligned}$$

We can easily prove that $\zeta ^{{\mathcal {C}}n}$ is also q-CN.

• (1) For a q-CN ${\mathcal {C}}n=a + b i + c j$ with $0\le a,b,c\le 1$ and $a^q+b^q+c^q=1$. Consider the case when $\zeta \in (0,1)$ then $\left( \root q \of {\zeta ^{1-a^q}}\right) ^q + \left( \root q \of {\zeta ^{c^q}-\zeta ^{b^q+c^q}}\right) ^q + \left( \root q \of {1-\zeta ^{c^q}}\right) ^q = \zeta ^{1-a^q}+\zeta ^{c^q} - \zeta ^{b^q+c^q} + 1-\zeta ^{c^q} = \zeta ^{1-a^q} - \zeta ^{b^q+c^q} + 1 = 1$

• (2) When $\zeta \ge 1$ then $1/\zeta \in (0,1)$ and hence it is also q-CN.

Remark 2

It should be noted here that the operations defined as ${\mathcal {C}}n^{\lambda }$ and $\zeta ^{{\mathcal {C}}n}$ are entirely different. In the first operation, the base is a q-CN, while in the second operation, the base is a real number. Moreover, in the first operation, the exponent is a real number, while in the second operation, it is a CN. In other words, we can say that the position of CN and the real number changes in the proposed operations.

Remark 3

It is clear from Definition 13 that when $\zeta \in (0,1)$ then $\zeta ^{{\mathcal {C}}n}$ increases along with the increase in $\zeta$. Thus, we have obtained the following special values of $\zeta ^{{\mathcal {C}}n}$.

• (1) If $\zeta =1,$ then $\zeta ^{{\mathcal {C}}n} = 1+0i+0j$.

• (2) If ${\mathcal {C}}n = 1+0i+0j$, then $\zeta ^{{\mathcal {C}}n} = \root q \of {\zeta ^{1-a^q}} + \root q \of {\zeta ^{c^q}-\zeta ^{b^q+c^q}} i$ + $\root q \of {1-\zeta ^{c^q}} j = 1+0i+0j$.

• (3) If ${\mathcal {C}}n = 0+0i+1j$, then $\zeta ^{{\mathcal {C}}n} = \root q \of {\zeta ^{1-a^q}} + \root q \of {\zeta ^{c^q}-\zeta ^{b^q+c^q}} i$ + $\root q \of {1-\zeta ^{c^q}} j = \root q \of {\zeta }+0i+\root q \of {1-\zeta }j$.

From the point (1), if $\zeta =1$, we always get the largest q-CN given as $1+0i+0j$, no matter what value ${\mathcal {C}}n$ we take. Similarly, in point (2), if we set q-CN as the largest CN, then after applying the q-EOL, we always get the largest q-CN $\zeta ^{{\mathcal {C}}n}=1+0i+0j$, no matter what value we take for the real number $\zeta$. However, in (3), for the smallest q-CN ${\mathcal {C}}n = 0+0i+1j$, we have $\zeta ^{{\mathcal {C}}n} = \root q \of {\zeta }+0i+\root q \of {1-\zeta }j$ which shows that it depends on a real parameter $\zeta$. Moreover, it clearly shows that the larger the value of $\zeta$, the larger the value of $\zeta ^{{\mathcal {C}}n}$.

Next, we discuss the properties of EOL-q-CNs for the case when $\zeta \in (0,1)$ and similarly we can obtain for $\zeta \ge 1$.

Proposition 4

Let ${\mathcal {C}}n_k$, $k=1,2,3$ be three q-CNs and $\zeta \in (0,1)$ be a real number, then

• (1) ${\zeta ^{{\mathcal {C}}n_1} \oplus \zeta ^{{\mathcal {C}}n_2} = \zeta ^{{\mathcal {C}}n_2} \oplus \zeta ^{{\mathcal {C}}n_1} }$.

• (2) $\zeta ^{{\mathcal {C}}n_1} \otimes \zeta ^{{\mathcal {C}}n_2} = \zeta ^{{\mathcal {C}}n_2} \otimes \zeta ^{{\mathcal {C}}n_1}$.

• (3) $\left( \zeta ^{{\mathcal {C}}n_1} \otimes \zeta ^{{\mathcal {C}}n_2}\right) \otimes \zeta ^{{\mathcal {C}}n_3} = \zeta ^{{\mathcal {C}}n_1} \otimes \left( \zeta ^{{\mathcal {C}}n_2}\otimes \zeta ^{{\mathcal {C}}n_3}\right)$.

• (4) $\left( \zeta ^{{\mathcal {C}}n_1} \oplus \zeta ^{{\mathcal {C}}n_2}\right) \oplus \zeta ^{{\mathcal {C}}n_3} = \zeta ^{{\mathcal {C}}n_1} \oplus \left( \zeta ^{{\mathcal {C}}n_2}\oplus \zeta ^{{\mathcal {C}}n_3}\right)$.

Proof

It is trial. $\square$

Let ${\mathcal {C}}n_1$ and ${\mathcal {C}}n_2$ be two q-CNs with $q\ge 1$ formulated either by Definitions 7 or 8 accordingly whether score values are equal or not, then we define some operation between them as follows.

Definition 14

Let ${\mathcal {C}}n_1=a_1+b_1i+c_1j$ and ${\mathcal {C}}n_2=a_2+b_2i + c_2j$ be two q-CNs over IVq-ROFSs with $q\ge 1$. Then, the operations on them are stated as

• (i) $\begin{aligned} {\mathcal {C}}n_1 \oplus {\mathcal {C}}n_2= & {} \root q \of {\left( a_1^q+c_1^q\right) \left( a_2^q+c_2^q\right) -c_1^q c_2^q} \\&+ \left( \root q \of {1-\left( 1-b_1^q\right) \left( 1-b_2^q\right) } \right) i + c_1c_2 j \end{aligned}$

• (ii) $\begin{aligned}&{\mathcal {C}}n_1\otimes {\mathcal {C}}n_2 = a_1a_2 + \left( \root q \of {1-\left( 1-b_1^q\right) \left( 1-b_2^q\right) } \right) i\\&\quad + \left( \root q \of {\left( a_1^q+c_1^q\right) \left( a_2^q+c_2^q\right) -a_1^qa_2^q}\right) j \end{aligned}$

• (iii) $\begin{aligned} \lambda {\mathcal {C}}n_1 = \root q \of {\left( a_1^q+c_1^q\right) ^\lambda -\left( c_1^q\right) ^\lambda }+ \left( \root q \of {1-\left( 1-b_1^q\right) ^\lambda } \right) i + c_1^\lambda j \end{aligned}$

• (iv) $\begin{aligned} {\mathcal {C}}n_1^\lambda = a_1^\lambda + \left( \root q \of {1-\left( 1-b_1^q\right) ^\lambda } \right) i + \left( \root q \of {\left( a_1^q+c_1^q\right) ^\lambda -\left( a_1^q\right) ^\lambda }\right) j \end{aligned}$

where $\lambda >0$ is a real number.

Definition 15

For two q-CNs ${\mathcal {C}}n_1=a_1+b_1i + c_1j$ and ${\mathcal {C}}n_2=a_2+b_2i + c_2j$, the subtraction and division operations are defined under the restriction that.

• (1) ${\mathcal {C}}n_1 \oslash {\mathcal {C}}n_2 = \dfrac{a_1}{a_2} + \left( \dfrac{b_1^q-b_2^q}{1-b_2^q}\right) ^{1/q} i + \left( \dfrac{a_2^q c_1^q - a_1^q c_2^q}{a_2^q(a_2^q+c_2^q)}\right) ^{1/q} j$, provided $a_2, c_1\ne 0$; $a_1\le \min \left\{ a_2,\frac{c_1a_2}{c_2}\right\}$, $b_1\ge b_2$.

• (2) ${\mathcal {C}}n_1 \ominus {\mathcal {C}}n_2 = \left( \dfrac{c_2^q a_1^q - c_1^q a_2^q}{c_2^q(a_2^q+c_2^q)}\right) ^{1/q} + \left( \dfrac{b_1^q-b_2^q}{1-b_2^q}\right) ^{1/q} i + \dfrac{c_1}{c_2} j$, provided $a_1, c_2\ne 0$; $c_1\le \min \left\{ c_2,\frac{a_1c_2}{a_2}\right\}$, $b_1\ge b_2$.

Theorem 3

Let ${\mathcal {C}}n_1$ and ${\mathcal {C}}n_2$ be two q-CNs, $\zeta \in (0,1)$ and $\kappa >0$ be real numbers. Then

• (1) $\kappa \left( \zeta ^{{\mathcal {C}}n_1} \oplus \zeta ^{{\mathcal {C}}n_2}\right) = \kappa \zeta ^{{\mathcal {C}}n_1} \oplus \kappa \zeta ^{{\mathcal {C}}n_2}$

• (2) $\left( \zeta ^{{\mathcal {C}}n_1} \otimes \zeta ^{{\mathcal {C}}n_2}\right) ^{\kappa } = \left( \zeta ^{{\mathcal {C}}n_1}\right) ^{\kappa } \otimes \left( \zeta ^{{\mathcal {C}}n_2}\right) ^{\kappa }$

• (3) $\kappa \left( \zeta ^{{\mathcal {C}}n_1} \ominus \zeta ^{{\mathcal {C}}n_2}\right) = \kappa \zeta ^{{\mathcal {C}}n_1} \ominus \kappa \zeta ^{{\mathcal {C}}n_2}$, provided $a_1, c_2\ne 0$; $c_1\le \min \left\{ c_2,\frac{a_1c_2}{a_2}\right\}$, $b_1\ge b_2$.

• (4) $\left( \zeta ^{{\mathcal {C}}n_1} \oslash \zeta ^{{\mathcal {C}}n_2}\right) ^{\kappa } = \left( \zeta ^{{\mathcal {C}}n_1}\right) ^{\kappa } \oslash \left( \zeta ^{{\mathcal {C}}n_2}\right) ^{\kappa }$, provided $a_2, c_1\ne 0$; $a_1\le \min \left\{ a_2,\frac{c_1a_2}{c_2}\right\}$, $b_1\ge b_2$.

Proof

Let ${\mathcal {C}}n_k = a_k + b_k i +c_k j$ $(k=1,2)$ be two q-CNs and $\zeta \in (0,1)$.

• (1) By operations defined in Definition 14, we get

  $$\begin{aligned}&\zeta ^{{\mathcal {C}}n_1} \oplus \zeta ^{{\mathcal {C}}n_2} \\&\quad = \left( \left( \zeta ^{1-a_1^q} + 1-\zeta ^{c_1^q}\right) \left( \zeta ^{1-a_2^q} + 1-\zeta ^{c_2^q}\right) \right. \\&\qquad \left. - \left( 1-\zeta ^{c_1^q} \right) \left( 1-\zeta ^{c_2^q}\right) \right) ^{1/q}\\&\qquad + \left( 1-\left( 1-\zeta ^{c_1^q}+\zeta ^{b_1^q+c_1^q}\right) \left( 1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}\right) \right) ^{1/q} i \\&\qquad + \left( \root q \of {1-\zeta ^{c_1^q}} \root q \of {1-\zeta ^{c_2^q}}\right) j \end{aligned}$$

  and

  $$\begin{aligned}&\kappa \left( \zeta ^{{\mathcal {C}}n_1} \oplus \zeta ^{{\mathcal {C}}n_2} \right) \\&\quad = \left( \left( \zeta ^{1-a_1^q} + 1-\zeta ^{c_1^q}\right) ^{\kappa }\left( \zeta ^{1-a_2^q} + 1-\zeta ^{c_2^q}\right) ^{\kappa } \right. \\&\qquad \left. - \left( 1-\zeta ^{c_1^q} \right) ^{\kappa }\left( 1-\zeta ^{c_2^q}\right) ^{\kappa } \right) ^{1/q} \\&\qquad + \left( 1-\left( 1-\zeta ^{c_1^q}+\zeta ^{b_1^q+c_1^q}\right) ^{\kappa } \left( 1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}\right) ^{\kappa } \right) ^{1/q} i \\&\qquad + \left( \root q \of {1-\zeta ^{c_1^q}} \root q \of {1-\zeta ^{c_2^q}}\right) ^{\kappa } j\\&\quad = \left( \begin{aligned}&\root q \of {\left( \zeta ^{1-a_1^q} + 1-\zeta ^{c_1^q}\right) ^{\kappa } - \left( 1-\zeta ^{c_1^q}\right) ^{\kappa }} + \root q \of {1-\left( 1-\zeta ^{c_1^q}+\zeta ^{b_1^q+c_1^q}\right) ^{\lambda }} i \\&\qquad \qquad \qquad \qquad + \left( \root q \of {1-\zeta ^{c_1^q}} \right) ^{\kappa } j \end{aligned} \right) \\&\qquad \qquad \qquad \oplus \left( \begin{aligned}&\root q \of {\left( \zeta ^{1-a_2^q} + 1-\zeta ^{c_2^q}\right) ^{\kappa } - \left( 1-\zeta ^{c_2^q}\right) ^{\kappa }} + \root q \of {1-\left( 1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}\right) ^{\lambda }} i \\&\qquad \qquad \qquad \qquad + \left( \root q \of {1-\zeta ^{c_2^q}} \right) ^{\kappa } j \end{aligned} \right) \\&\quad = \kappa \zeta ^{{\mathcal {C}}n_1} \oplus \kappa \zeta ^{{\mathcal {C}}n_2} \end{aligned}$$

• (4) By using Definition 15 for q-CNs ${\mathcal {C}}n_k$’s, we have

  $$\begin{aligned} \zeta ^{{\mathcal {C}}n_1} \oslash \zeta ^{{\mathcal {C}}n_2}&= \left( \frac{\zeta ^{1-a_1^q}}{\zeta ^{1-a_2^q}}\right) ^{1/q} \\&\quad + \left( \frac{\zeta ^{c_1^q}-\zeta ^{b_1^q+c_1^q}-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}}{1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}} \right) ^{1/q} i\\&+ \left( \frac{\zeta ^{1-a_2^q}\left( 1-\zeta ^{c_1^q}\right) - \zeta ^{1-a_1^q}\left( 1-\zeta ^{c_2^q}\right) }{\zeta ^{1-a_2^q}\left( \zeta ^{1-a_2^q} + 1-\zeta ^{c_2^q}\right) } \right) ^{1/q} j \end{aligned}$$

  Thus,

  $$\begin{aligned} \left( \zeta ^{{\mathcal {C}}n_1} \oslash \zeta ^{{\mathcal {C}}n_2}\right) ^{\kappa }&= \left( \root q \of {\frac{\zeta ^{1-a_1^q}}{\zeta ^{1-a_2^q}}}\right) ^{\kappa } + \root q \of { 1- \left( 1-\frac{\zeta ^{c_1^q}-\zeta ^{b_1^q+c_1^q}-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}}{1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}} \right) ^\kappa } i \\&\quad + \root q \of { \left( \frac{\zeta ^{1-a_1^q}}{\zeta ^{1-a_2^q}} + \frac{\zeta ^{c_1^q}-\zeta ^{b_1^q+c_1^q}-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}}{1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}} \right) ^{\kappa } - \left( \frac{\zeta ^{1-a_1^q}}{\zeta ^{1-a_2^q}}\right) ^{\kappa } } j\\&= \left( \root q \of {\frac{\zeta ^{1-a_1^q}}{\zeta ^{1-a_2^q}}}\right) ^{\kappa } + \root q \of { \frac{\left( 1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}\right) ^{\kappa } - \left( 1-\zeta ^{c_1^q}+\zeta ^{b_1^q+c_1^q}\right) ^{\kappa } }{\left( 1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}\right) ^{\kappa }} } i\\&\qquad + \root q \of { \left( \frac{\zeta ^{1-a_1^q}+1-\zeta ^{c_1^q}}{1-\zeta ^{c_2^q}+\zeta ^{1-a_2^q}}\right) ^\kappa -\left( \frac{\zeta ^{1-a_1^q}}{\zeta ^{1-a_2^q}}\right) ^{\kappa } } j \\&= \left( \root q \of {\frac{\zeta ^{1-a_1^q}}{\zeta ^{1-a_2^q}}}\right) ^{\kappa } + \root q \of { \frac{\left( 1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}\right) ^{\kappa } - \left( 1-\zeta ^{c_1^q}+\zeta ^{b_1^q+c_1^q}\right) ^{\kappa }}{\left( 1-\zeta ^{c_2^q}+\zeta ^{b_2^q+c_2^q}\right) ^{\kappa }} }i \\&\quad + \root q \of { \frac{\left( \zeta ^{1-a_2^q}\right) ^{\kappa } \left( \zeta ^{1-a_1^q}+1-\zeta ^{c_1^q}\right) ^\kappa - \left( \zeta ^{1-a_1^q}\right) ^{\kappa } \left( \zeta ^{1-a_2^q}+1-\zeta ^{c_2^q}\right) ^\kappa }{ \left( \zeta ^{1-a_2^q}\right) ^{\kappa } \left( \zeta ^{1-a_1^q}+1-\zeta ^{c_1^q}\right) ^\kappa } } j \\&= \left( \zeta ^{{\mathcal {C}}n_1}\right) ^{\kappa } \oslash \left( \zeta ^{{\mathcal {C}}n_2}\right) ^{\kappa } \end{aligned}$$

  Hence, $\left( \zeta ^{{\mathcal {C}}n_1}\oslash \zeta ^{{\mathcal {C}}n_2}\right) ^{\kappa } = \left( \zeta ^{{\mathcal {C}}n_1}\right) ^{\kappa } \oslash \left( \zeta ^{{\mathcal {C}}n_2}\right) ^{\kappa }$.

$\square$

Theorem 4

Let ${\mathcal {C}}n$ be q-CN and $\kappa _1,\kappa _2>0$, $\zeta \in (0,1)$ are real numbers, then

• (1) $\kappa _1 \zeta ^{{\mathcal {C}}n} \oplus \kappa _2 \zeta ^{{\mathcal {C}}n} = (\kappa _1+\kappa _2) \zeta ^{{\mathcal {C}}n}$.

• (2) $\left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _1} \otimes \left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _2} = \left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _1 + \kappa _2}$

• (3) $\kappa _1 \zeta ^{{\mathcal {C}}n} \ominus \kappa _2 \zeta ^{{\mathcal {C}}n} = (\kappa _1-\kappa _2)\zeta ^{{\mathcal {C}}n}$ iff $\kappa _1\ge \kappa _2$

• (4) $\left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _1} \oslash \left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _2} = \left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _1-\kappa _2}$ iff $\kappa _1\ge \kappa _2$.

Proof

For a EOL-q-CN $\zeta ^{{\mathcal {C}}n} = \root q \of {\zeta ^{1-a^q}}+\root q \of {\zeta ^{c^q} - \zeta ^{b^q+c^q}} i + \sqrt{1-\zeta ^{c^q}}j$. For real $\kappa _1,\kappa _2>0$,

• (2) By Definition 14, we have

  $$\begin{aligned}&\left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _1} \otimes \left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _2} = \left( \root q \of {\zeta ^{1-a^q}}\right) ^{\kappa _1} \left( \root q \of {\zeta ^{1-a^q}}\right) ^{\kappa _2} \\&\qquad +\root q \of {1- \left( 1-\zeta ^{c^q} + \zeta ^{b^q+c^q}\right) ^{\kappa _1}\left( 1-\zeta ^{c^q} + \zeta ^{b^q+c^q}\right) ^{\kappa _2}} i \\&\qquad + \left[ \left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _1} \left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _2} \right. \\&\left. - \left( \zeta ^{1-a^q}\right) ^{\kappa _1}\left( \zeta ^{1-a^q}\right) ^{\kappa _2}\right] ^{1/q} j \\&\quad = \left( \root q \of {\zeta ^{1-a^q}}\right) ^{\kappa _1+\kappa _2} + \left( 1- \left( 1-\zeta ^{c^q} + \zeta ^{b^q+c^q}\right) ^{\kappa _1+\kappa _2}\right) ^{1/q} i \\&\qquad + \left( \left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _1+\kappa _2} - \left( \zeta ^{1-a^q}\right) ^{\kappa _1+\kappa _2}\right) ^{1/q} j \\&= \left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _1+\kappa _2} \end{aligned}$$

• (4) By Definition 15, we get

  $$\begin{aligned}&\left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _1}\oslash \left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _2} \\&\quad = \frac{\left( \root q \of {\zeta ^{1-a^q}}\right) ^{\kappa _1}}{\left( \root q \of {\zeta ^{1-a^q}}\right) ^{\kappa _2}}\\&\qquad +\left( \frac{\left( 1-\zeta ^{c^q} + \zeta ^{b^q+c^q}\right) ^{\kappa _2}-\left( 1-\zeta ^{c^q} + \zeta ^{b^q+c^q}\right) ^{\kappa _1}}{\left( 1-\zeta ^{c^q} + \zeta ^{b^q+c^q}\right) ^{\kappa _2}} \right) ^{1/q} i \\&\qquad + \left( \frac{ \begin{aligned} \left( \zeta ^{1-a^q}\right) ^{\kappa _2}\left[ \left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _1} - \left( \zeta ^{1-a^q}\right) ^{\kappa _1}\right] \\ - \left( \zeta ^{1-a^q}\right) ^{\kappa _1}\left[ \left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _2} - \left( \zeta ^{1-a^q}\right) ^{\kappa _2}\right] \end{aligned}}{ \left( \zeta ^{1-a^q}\right) ^{\kappa _2}\left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _2}} \right) ^{1/q} j\\&\quad = \left( \root q \of {\zeta ^{1-a^q}}\right) ^{\kappa _1 - \kappa _2} + \left( 1-\left( 1-\zeta ^{c^q} + \zeta ^{b^q+c^q}\right) ^{\kappa _1-\kappa _2}\right) ^{1/q} i \\&\qquad + \left( \frac{\left( \zeta ^{1-a^q}\right) ^{\kappa _2}\left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _1} - \left( \zeta ^{1-a^q}\right) ^{\kappa _1}\left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _2}}{ \left( \zeta ^{1-a^q}\right) ^{\kappa _2}\left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _2}} \right) ^{1/q} j\\&\quad = \left( \root q \of {\zeta ^{1-a^q}}\right) ^{\kappa _1 - \kappa _2} + \left( 1-\left( 1-\zeta ^{c^q} + \zeta ^{b^q+c^q}\right) ^{\kappa _1-\kappa _2}\right) ^{1/q} i \\&\qquad + \left( \left( \zeta ^{1-a^q} + 1-\zeta ^{c^q}\right) ^{\kappa _1-\kappa _2} - \left( \zeta ^{1-a^q}\right) ^{\kappa _1-\kappa _2}\right) ^{1/q} j\\&\quad = \left( \zeta ^{{\mathcal {C}}n}\right) ^{\kappa _1-\kappa _2} \end{aligned}$$

$\square$

Theorem 5

Let ${\mathcal {C}}n_k$, $k=1,2$ be two q-CNs and $\zeta \in (0,1)$ then

• (1) $\left( \zeta ^{{\mathcal {C}}n_1} \ominus \zeta ^{{\mathcal {C}}n_2}\right) \oplus \zeta ^{{\mathcal {C}}n_2} = \zeta ^{{\mathcal {C}}n_1}$, provided $a_1, c_2\ne 0$; $c_1\le \min \left\{ c_2,\frac{a_1c_2}{a_2}\right\}$, $b_1\ge b_2$.

• (2) $\left( \zeta ^{{\mathcal {C}}n_1} \oslash \zeta ^{{\mathcal {C}}n_2}\right) \otimes \zeta ^{{\mathcal {C}}n_2} = \zeta ^{{\mathcal {C}}n_1}$ provided $a_2, c_1\ne 0$; $a_1\le \min \left\{ a_2,\frac{c_1a_2}{c_2}\right\}$, $b_1\ge b_2$.

4.2 Proposed Exponential operators for q-CNs

Based on the EOLs, as defined in Definition 13, we define new exponential operators, for q-CNs ${\mathcal {C}}n=a+bi+cj$ derived either by using Definitions 7 or 8 for IV-q-ROFS. Let $\varOmega$ be family of q-CNs.

Definition 16

For “n” q-CNs and real $\zeta _k\in (0,1)$. A $q\text {-CNWEA}: \varOmega ^n \rightarrow \varOmega$ is defined as

$$\begin{aligned}&q\text {-CNWEA}({\mathcal {C}}n_1,{\mathcal {C}}n_2,\ldots ,{\mathcal {C}}n_n) \nonumber \\&\quad = \omega _1 \left( \zeta _1^{{\mathcal {C}}n_1}\right) \oplus \omega _2\left( \zeta _2^{{\mathcal {C}}n_2}\right) \oplus \ldots \oplus \omega _n \left( \zeta _n^{{\mathcal {C}}n_n}\right) \end{aligned}$$

(9)

and called as q-CN weighted exponential average operator, where $\omega _k>0, \sum \nolimits _{k=1}^n \omega _k = 1$ is the vector of $\left( \zeta _k\right) ^{{\mathcal {C}}n_k}$.

Theorem 6

For a collection of “n” q-CNs ${\mathcal {C}}n_k=a_k+b_ki+c_kj$, the aggregated value by using q-CNWEA operator is also q-CN, where

(10)

Proof

Let q-CN ${\mathcal {C}}n_k = a_k + b_k i + c_k j$ with $a_k^q + b_k^q + c_k^q = 1$ and $\zeta _k\in (0,1)$ be a real number. By Definition 13, we have

$$\begin{aligned} \zeta _k^{{\mathcal {C}}n_k} = \root q \of {\zeta _k^{1-a_k^q}} + \left( \zeta _k^{c_k^q} - \zeta _k^{b_k^q + c_k^q}\right) ^{1/q} i + \root q \of {1-\zeta _k^{c_k^q}} j \end{aligned}$$

For real $\omega _k>0$, and by Definition 14, we have

$$\begin{aligned} \omega _k \left( \zeta _k^{{\mathcal {C}}n_k}\right)&= \root q \of { \left( \zeta _k^{1-a_k^q} + 1-\zeta _k^{c_k^q}\right) ^{\omega _k} - \left( 1-\zeta _k^{c_k^q}\right) ^{\omega _k}} \\&\quad + \root q \of { 1-\left( 1-\zeta _k^{c_k^q} + \zeta _k^{b_k^q + c_k^q} \right) ^{\omega _k} }i + \left( \root q \of {1-\zeta _k^{c_k^q}}\right) ^{\omega _k} j \end{aligned}$$

which implies that

$$\begin{aligned}&\bigoplus _{k=1}^n \omega _k \left( \zeta _k^{{\mathcal {C}}n_k}\right) \\&\quad = \root q \of { \prod \limits _{k=1}^n \left( \zeta _k^{1-a_k^q} + 1-\zeta _k^{c_k^q}\right) ^{\omega _k} - \prod \limits _{k=1}^n \left( 1-\zeta _k^{c_k^q}\right) ^{\omega _k}}\\&\qquad + \root q \of { 1-\prod \limits _{k=1}^n \left( 1-\zeta _k^{c_k^q} + \zeta _k^{b_k^q + c_k^q} \right) ^{\omega _k} }i \\&\qquad + \root q \of {\prod \limits _{k=1}^n \left( 1-\zeta _k^{c_k^q}\right) ^{\omega _k}} j \end{aligned}$$

which is the desired result. $\square$

Example 4

Let ${\mathcal {I}}_1$=([0.3, 0.4], [0.3, 0.5]), ${\mathcal {I}}_2$=([0.2, 0.4], [0.4, 0.5]), ${\mathcal {I}}_3$=([0.6, 0.7], [0.4, 0.5]) and ${\mathcal {I}}_4$=([0.5, 0.6], [0.4, 0.5]) be four IVq-ROFNs with $q=2$ and $\omega =(0.3, 0.2, 0.1, 0.4)$. Assume that $\zeta _1=0.2$, $\zeta _2=0.5$, $\zeta _3=0.3$ and $\zeta _4=0.7$ such that $\zeta _k\in (0,1)$. To implement q-CNWEA operator to aggregate the given numbers, we compute the q-CN for each ${\mathcal {I}}_k$. For it, we firstly compute the score values of ${\mathcal {I}}_k$ and get $S({\mathcal {I}}_1)=-0.0450$, $S({\mathcal {I}}_1)=-0.1050$, $S({\mathcal {I}}_1)=0.2200$ and $S({\mathcal {I}}_4)=0.1000$. Since $S({\mathcal {I}}_1)\ne S({\mathcal {I}}_2)\ne S({\mathcal {I}}_3)\ne S({\mathcal {I}}_4)$, thus, q-CNs are derived by Definition 14 and get ${\mathcal {C}}n_1 = 0.3221 + 0.8646 i + 0.3857j$; ${\mathcal {C}}n_2 = 0.2820 + 0.8579 i + 0.4295j$; ${\mathcal {C}}n_3 = 0.5813 + 0.7377 i + 0.3433j$; and ${\mathcal {C}}n_4 = 0.4924 + 0.7843 i + 0.3775j$. Now, the terms

$$\begin{aligned}&\prod \limits _{k=1}^4 \left( \zeta _k^{1-a_k^q}+1-\zeta _k^{c_k^q}\right) ^{\omega _k} \\&\quad = \left( (0.2)^{1-0.3221^2}+1-(0.2)^{0.3857^2}\right) ^{0.2} \\&\qquad \times \left( (0.5)^{1-0.2820^2}+1-(0.5)^{0.4295^2}\right) ^{0.4} \\&\qquad \times \left( (0.3)^{1-0.5813^2}+1-(0.3)^{0.3433^2}\right) ^{0.3} \\&\qquad \times \left( (0.7)^{1-0.4924^2}+1-(0.7)^{0.3775^2}\right) ^{0.1} \\&\quad =0.5969 \\&\prod \limits _{k=1}^4 \left( 1-\zeta _k^{c_k^q}\right) ^{\omega _k} \\&\quad = \left( 1-(0.2)^{0.3857^2}\right) ^{0.2} \times \left( 1-(0.5)^{0.4295^2}\right) ^{0.4} \\&\qquad \times \left( 1-(0.3)^{0.3433^2}\right) ^{0.3} \times \left( 1-(0.7)^{0.3775^2}\right) ^{0.1} \\&\quad = 0.1269 \end{aligned}$$

Thus, by Eq. (10), we get $q\text {-CNWEA}({\mathcal {C}}n_1,{\mathcal {C}}n_2,{\mathcal {C}}n_3,{\mathcal {C}}n_4)$ $= \left( 0.5969 - 0.1269\right) ^{1/2} + \left( 1-0.5969\right) ^{1/2} i +\left( 0.1269\right) ^{1/2} j$ $= 0.6856 + 0.6349 i + 0.3562j$.

Further, if we take $\zeta _1=3$, $\zeta _2=2$, $\zeta _3=5$ and $\zeta _4=4$ then $\prod \nolimits _{k=1}^4 \left( \left( \frac{1}{\zeta _k}\right) ^{1-a_k^q}+1-\left( \frac{1}{\zeta _k}\right) ^{c_k^q}\right) ^{\omega _k} = 0.5690$ and $\prod \nolimits _{k=1}^4 \left( 1-\left( \frac{1}{\zeta _k}\right) ^{c_k^q}\right) ^{\omega _k} = 0.1459$. Hence, by definition of q-CNWEA operator, we get $q\text {-CNWEA}({\mathcal {C}}n_1,{\mathcal {C}}n_2,{\mathcal {C}}n_3,{\mathcal {C}}n_4)=0.6505 + 0.6565 i + 0.3819j$.

Definition 17

Let ${\mathcal {C}}n_k$ be the collection of “n” q-CNs and $\zeta _k$ be real numbers. A $q\text{-CNWEG}: \varOmega ^n \rightarrow \varOmega$ is defined as

$$\begin{aligned}&q\text{-CNWEG}({\mathcal {C}}n_1,{\mathcal {C}}n_2,\ldots ,{\mathcal {C}}n_n) \nonumber \\&\quad = \left( \zeta _1^{{\mathcal {C}}n_1}\right) ^{\omega _1} \otimes \left( \zeta _2^{{\mathcal {C}}n_2}\right) ^{\omega _2} \otimes \ldots \otimes \left( \zeta _n^{{\mathcal {C}}n_n}\right) ^{\omega _n} \end{aligned}$$

(11)

and called as q-CN weighted exponential geometric operator.

Theorem 7

For a collection of “n” q-CNs ${\mathcal {C}}n_k=a_k + b_k i + c_k j$, the value obtained through q-CNWEG operator is also q-CN, where

(12)

Proof

Same as Theorem 6. $\square$

Next, we investigate some properties of q-CNWEA operator by considering $\zeta _1=\zeta _2=\ldots =\zeta _n=\zeta \in (0, 1)$ only here. As similar to this, other cases can be easily derived.

Proposition 5

For ‘n’ q-CNs ${\mathcal {C}}n_k$. If ${\mathcal {C}}n_k={\mathcal {C}}n=a + bi + cj$ for all k, then

$$\begin{aligned} q\text {-CNWEA}({\mathcal {C}}n_1,{\mathcal {C}}n_2,\ldots ,{\mathcal {C}}n_n) = \zeta ^{{\mathcal {C}}n} \end{aligned}$$

Proof

By Theorem 6, for q-CNs ${\mathcal {C}}n_k={\mathcal {C}}n = a + b i +cj$ and $\zeta \in (0,1)$, we have $q\text {-CNWEA}({\mathcal {C}}n_1,{\mathcal {C}}n_2,\ldots ,{\mathcal {C}}n_n) = \omega _1 \left( \zeta ^{{\mathcal {C}}n}\right) \oplus \omega _2\left( \zeta ^{{\mathcal {C}}n}\right) \oplus \ldots \oplus \omega _n \left( \zeta ^{{\mathcal {C}}n}\right) = (\omega _1+\omega _2+\ldots +\omega _n) \zeta ^{{\mathcal {C}}n} = \zeta ^{{\mathcal {C}}n}$. $\square$

Proposition 6

For two collections of q-CNs ${\mathcal {C}}n_k=a_{{\mathcal {C}}_k} + b_{{\mathcal {C}}_k} i + c_{{\mathcal {C}}_k} j$ and ${\mathcal {D}}n_k=a_{{\mathcal {D}}_k} + b_{{\mathcal {D}}_k} i + c_{{\mathcal {D}}_k} j$ and a real number $\zeta \in (0,1)$. If $a_{{\mathcal {C}}_k} \le a_{{\mathcal {D}}_k}$, $b_{{\mathcal {C}}_k} \ge b_{{\mathcal {D}}_k}$ and $c_{{\mathcal {C}}_k} \ge c_{{\mathcal {D}}_k}$ for all k, then $q\text {-CNWEA}({\mathcal {C}}n_1,{\mathcal {C}}n_2,\ldots ,{\mathcal {C}}n_n) \le q\text {-CNWEA}({\mathcal {D}}n_1,{\mathcal {D}}n_2,\ldots ,{\mathcal {D}}n_n)$, which is called the monotonicity.

Proof

If $a_{{\mathcal {C}}_k} \le a_{{\mathcal {D}}_k}$, $b_{{\mathcal {C}}_k} \ge b_{{\mathcal {D}}_k}$ and $c_{{\mathcal {C}}_k} \ge c_{{\mathcal {D}}_k}$ for all k, then for $\zeta \in (0,1)$, we have $\zeta ^{a_{{\mathcal {C}}}^q} \ge \zeta ^{a_{{\mathcal {D}}}^q}$, $\zeta ^{b_{{\mathcal {C}}}^q} \le \zeta ^{b_{{\mathcal {D}}}^q}$ and $\zeta ^{c_{{\mathcal {C}}}^q} \le \zeta ^{c_{{\mathcal {D}}}^q}$ which implies that $\zeta ^{b_{{\mathcal {C}}}^q} -1\le \zeta ^{b_{{\mathcal {D}}}^q}-1$ and $\zeta ^{c_{{\mathcal {C}}}^q}\left( \zeta ^{b_{{\mathcal {C}}}^q}-1\right) \le \zeta ^{c_{{\mathcal {D}}}^q}\left( \zeta ^{b_{{\mathcal {D}}}^q}-1\right)$, i.e., $\zeta ^{b_{{\mathcal {C}}}^q+c_{{\mathcal {C}}}^q}-\zeta ^{c_{{\mathcal {C}}}^q} \le \zeta ^{b_{{\mathcal {D}}}^q+ c_{{\mathcal {D}}}^q}-\zeta ^{c_{{\mathcal {D}}}^q}$. Therefore, $\zeta ^{1-a_{{\mathcal {C}}}^q}-\zeta ^{c_{{\mathcal {C}}}^q} \le \zeta ^{1-a_{{\mathcal {D}}}^q}-\zeta ^{c_{{\mathcal {D}}}^q}$ and hence $\prod \nolimits _{k=1}^n \left( \zeta ^{1-a_{{\mathcal {C}}}^q}+1-\zeta ^{c_{{\mathcal {C}}}^q} \right) ^{\omega _k} \le \prod \nolimits _{k=1}^n \left( \zeta ^{1-a_{{\mathcal {D}}}^q}+1-\zeta ^{c_{{\mathcal {D}}}^q}\right) ^{\omega _k}$. Similarly, we can obtain

$$\begin{aligned} \prod \limits _{k=1}^n \left( 1-\zeta ^{c_{{\mathcal {C}}}^q}\right) ^{\omega _k} \ge \prod \limits _{k=1}^n \left( 1-\zeta ^{c_{{\mathcal {D}}}^q}\right) ^{\omega _k} \end{aligned}$$

and

$$\begin{aligned} 1-\prod \limits _{k=1}^n \left( \zeta ^{1-a_{{\mathcal {C}}}^q}+1-\zeta ^{c_{{\mathcal {C}}}^q} \right) ^{\omega _k} \ge 1-\prod \limits _{k=1}^n \left( \zeta ^{1-a_{{\mathcal {D}}}^q}+1-\zeta ^{c_{{\mathcal {D}}}^q}\right) ^{\omega _k} \end{aligned}$$

which further implies that

$$\begin{aligned}&\prod \limits _{k=1}^n \left( \zeta ^{1-a_{{\mathcal {C}}}^q}+1-\zeta ^{c_{{\mathcal {C}}}^q} \right) ^{\omega _k} - \prod \limits _{k=1}^n \left( 1-\zeta ^{c_{{\mathcal {C}}}^q}\right) ^{\omega _k} \\&\qquad \le \prod \limits _{k=1}^n \left( \zeta ^{1-a_{{\mathcal {D}}}^q}+1-\zeta ^{c_{{\mathcal {D}}}^q}\right) ^{\omega _k} - \prod \limits _{k=1}^n \left( 1-\zeta ^{c_{{\mathcal {D}}}^q}\right) ^{\omega _k}. \end{aligned}$$

Now, by Theorem 6, we denote $q\text {-CNWEA}({\mathcal {C}}n_1, {\mathcal {C}}n_2$, $\ldots ,{\mathcal {C}}n_k)=a_{\mathcal {C}} + b_{\mathcal {C}} i +c_{\mathcal {C}} j$ and $q\text {-CNWEA}({\mathcal {D}}n_1, {\mathcal {D}}n_2$, $\ldots$, ${\mathcal {D}}n_k)=a_{\mathcal {D}} + b_{\mathcal {D}} i +c_{\mathcal {D}} j$. Hence, by above inequalities, we get $a_{\mathcal {C}} \le a_{\mathcal {D}}$, $c_{\mathcal {C}} \ge c_{\mathcal {D}}$. Thus, by order relation, we get $q\text {-CNWEA}({\mathcal {C}}n_1$, ${\mathcal {C}}n_2$, $\ldots$, ${\mathcal {C}}n_n)$ $\le$ $q\text {-CNWEA}({\mathcal {D}}n_1$, ${\mathcal {D}}n_2$, $\ldots$, ${\mathcal {D}}n_n)$. $\square$

Proposition 7

For a collection of q-CNs ${\mathcal {C}}n_k=a_k + b_k i + c_k j$. Let ${\mathcal {C}}n^- =a^- + b^- i + c^- j$, ${\mathcal {C}}n^+ =a^+ + b^+ i + c^+ j$, $a^- = \left( \zeta ^{1-\left( \min _k\{a_k\}\right) ^q} -\zeta ^{\left( \min _k\{c_k\}\right) ^q} +\zeta ^{\left( \max _k \{c_k\}\right) ^q } \right) ^{1/q}$; $a^+ = \left( \zeta ^{1-\left( \max _k\{a_k\}\right) ^q} -\zeta ^{\left( \max _k \{c_k\}\right) ^q } +\zeta ^{\left( \min _k\{c_k\}\right) ^q} \right) ^{1/q}$; $c^- = \left( 1-\zeta ^{\left( \min _k\{c_k\}\right) ^q}\right) ^{1/q}$; $c^+ = \left( 1-\zeta ^{\left( \max _k \{c_k\}\right) ^q } \right) ^{1/q}$; $b^- = \root q \of {1-(a^-)^q - (c^-)^q}$ and $b^+ = \root q \of {1-(a^+)^q - (c^+)^q}$. Then, we have

$$\begin{aligned} {\mathcal {C}}n^- \le q\text {-CNWEA}({\mathcal {C}}n_1, {\mathcal {C}}n_2, \ldots , {\mathcal {C}}n_n)\le {\mathcal {C}}n^+ \end{aligned}$$

which is called the boundedness.

Proof

Easily follows from the above. $\square$

Definition 18

Let ${\mathcal {C}}n_k$ be collection of “n” q-CNs, and $w=(w_1,w_2,\ldots ,w_n)^T$ is the associated weighting vector for the ordered weighted averaging with $w_k>0$, $\sum _{k=1}^n w_k=1$. A q-CNOWEA operator of dimension n is a mapping $q\text {-CNOWEA}: \varOmega ^{n} \rightarrow \varOmega$, defined as

$$\begin{aligned} q\text {-CNOWEA}({\mathcal {C}}n_1,{\mathcal {C}}n_2,\dots {\mathcal {C}}n_n) = \bigoplus _{k=1}^n {w_k} \left( \zeta _k^{{\mathcal {C}}n_{\sigma (k)}}\right) \end{aligned}$$

(13)

where ${\mathcal {C}}n_{\sigma (k)}$ is the $k^{th}$ largest q-CN of all q-CNs ${\mathcal {C}}n_k$ and $\sigma$ is the permutation map.

Theorem 8

Let ${\mathcal {C}}n_k= a_k + b_k i + c_k j$ be a collection of “n” q-CNs, then their aggregated value by q-CNOWEA operator is also a q-CN with $q\in {\mathbb {N}}$ and given by

(14)

The proof of this theorem is similar to Theorem 6.

q-CNOWEA operator also satisfies Propositions 5–7. In addition, we have

• (1) If $w=(1,0,\ldots ,0)^T$, we have $q\text {-CNOWEA}({\mathcal {C}}n_{1}$, ${\mathcal {C}}n_{2}$, $\ldots$, ${\mathcal {C}}n_{n})$= $\zeta _1^{{\mathcal {C}}n_{\sigma (1)}}$ = $\max \{\zeta _1^{{\mathcal {C}}n_1}$, $\zeta _2^{{\mathcal {C}}n_2}$, $\ldots$, $\zeta _n^{{\mathcal {C}}n_n}\}$.

• (2) If $w=(0,0,\ldots ,1)^T$, we have $q\text {-CNOWEA}({\mathcal {C}}n_{1}$, ${\mathcal {C}}n_{2}$, $\ldots$, ${\mathcal {C}}n_{n})$= $\zeta _1^{{\mathcal {C}}n_{\sigma (n)}}$ = $\min \{\zeta _1^{{\mathcal {C}}n_1}$, $\zeta _2^{{\mathcal {C}}n_2}$, $\ldots$, $\zeta _n^{{\mathcal {C}}n_n}\}$.

Definition 19

Let ${\mathcal {C}}n_k$ be a collection of “n” q-CNs. If a mapping $q\text {-CNOWEG} : \varOmega ^{n} \rightarrow \varOmega$ satisfies

$$\begin{aligned} q\text {-CNOWEG}({\mathcal {C}}n_{1},{\mathcal {C}}n_{2},\dots {\mathcal {C}}n_{n})= \bigotimes _{k=1}^n \left( \zeta _k^{{\mathcal {C}}n_{\sigma (k)}}\right) ^{w_k} \end{aligned}$$

(15)

then q-CNOWEG is called q-CN ordered weighted exponential geometric operator.

Theorem 9

Let ${\mathcal {C}}n_k= a_k + b_k i + c_k j$ be a collection of “n” q-CNs, then the value obtained by q-CNOWEG operator is also a q-CN, and is given by

(16)

where $w_k > 0$, $\sum _{k=1}^nw_k=1$ be the weight vector of q-CNOWEG operator, and $q\in {\mathbb {N}}$.

Definition 20

Let ${\mathcal {C}}n_k$ be a collection of “n” q-CNs, $w=(w_{1}, w_{2},\ldots ,w_{n})^{T}$ is the associated weight vector for the ordered weighted averaging with $w_k >0$ and $\sum _{k=1}^n w_k=1$, and $\omega _k>0$, $\sum _{k=1}^n \omega _k=1$ be the weighting vector of $\zeta _1^{{\mathcal {C}}n_1}, \zeta _2^{{\mathcal {C}}n_2},\ldots , \zeta _n^{{\mathcal {C}}n_n}$. If a mapping $q\text {-CNHEA} : \varOmega ^{n} \rightarrow \varOmega$ of dimension n satisfies

$$\begin{aligned} q\text {-CNHEA}({\mathcal {C}}n_1,{\mathcal {C}}n_2,\dots {\mathcal {C}}n_n) =\bigoplus _{k=1}^n w_k \left( \dot{\zeta }_k^{{\mathcal {C}}n_{\sigma (k)}}\right) \end{aligned}$$

(17)

then $q\text {-CNHEA}$ is called an q-CN hybrid exponential averaging operator, where $\dot{\zeta }_k^{{\mathcal {C}}n_k}={n\omega _{k}}\lambda _k^{{\mathcal {C}}n_k}$ and given as $\dot{\zeta }_k^{{\mathcal {C}}n_k}={\dot{a}}_k + {\dot{b}}_k i + {\dot{c}}_k j$, $(k=1,2,\ldots ,n)$.

Theorem 10

The overall value for “n” q-CNs ${\mathcal {C}}n_k= a_k + b_k i +c_k j$ by using Definition 20is also q-CN as

(18)

Remark 4

The following special cases observed.

• By taking $w=(\frac{1}{n},\frac{1}{n},\ldots ,\frac{1}{n})^{T}$, then $q\text {-CNHEA}$ reduces to $q\text {-CNWEA}$ operator.

• By taking $\omega =(\frac{1}{n},\frac{1}{n},\ldots ,\frac{1}{n})^{T}$, the $q\text {-CNHEA}$ reduced to the $q\text {-CNOWEA}$.

Definition 21

Let ${\mathcal {C}}n_k$ be a finite collection of q-CNs. If a mapping $q\text {-CNHEG} : \varOmega ^{n} \rightarrow \varOmega$ of dimension n satisfies

$$\begin{aligned} q\text {-CNHEG}({\mathcal {C}}n_{1},{\mathcal {C}}n_{2},\dots {\mathcal {C}}n_{n})= \bigotimes _{k=1}^n \left( \dot{\zeta }_k^{{\mathcal {C}}n_{\sigma (k)}}\right) ^{w_{k}} \end{aligned}$$

(19)

then $q\text {-CNHEG}$ is called q-CN hybrid exponential geometric operator, where $\dot{{\mathcal {C}}n}_{\sigma (k)}$ is the $k^{th}$ largest of all q-CNs $\dot{\zeta }_k^{{\mathcal {C}}n_k} = \left( \zeta _k^{{\mathcal {C}}n_k}\right) ^{n\omega _{k}} = {\dot{a}}_k + {\dot{b}}_k i + {\dot{c}}_k j$.

Theorem 11

For “n” q-CNs ${\mathcal {C}}n_k= a_k + b_k i + c_k j$, the value obtained by q-CNHEG operator is again a q-CN, and given by

(20)

Further, such operators q-CNOWEA, q-CNOWEG, q-CNHEA, and q-CNHEG satisfy the boundary, monotonicity and commutativity properties.

5 Group decision making approach based on EOL-q-CN under IVq-ROFS information

Here, a MAGDM algorithm is presented based on the stated EOL-q-CN followed by several numerical examples.

5.1 Proposed approach

A group DMP consists of ‘m’ alternatives ${\mathcal {K}}_1,{\mathcal {K}}_2,\ldots ,{\mathcal {K}}_m$ evaluated under the ‘n’ attributes ${\mathfrak {V}}_1$, ${\mathfrak {V}}_2$, $\ldots$, ${\mathfrak {V}}_n$ by ‘l’ experts ${\mathcal {D}}_1,{\mathcal {D}}_2,\ldots ,{\mathcal {D}}_l$. Each expert ${\mathcal {D}}_p(p=1,2,\ldots ,l)$ gives his preferences in terms of IVq-ROFNs denoted by ${\mathcal {I}}_{kt}^{(p)}=([{\underline{\vartheta }}_{kt}^{(p)}, {\overline{\vartheta }}_{kt}^{(p)}], [{\underline{\varphi }}_{kt}^{(p)}, {\overline{\varphi }}_{kt}^{(p)}])$, with the conditions $({\overline{\vartheta }}_{kt}^{(p)})^q$ + $({\overline{\varphi }}_{kt}^{(p)})^q$ $\le 1$, $[{\underline{\vartheta }}_{kt}^{(p)}, {\overline{\vartheta }}_{kt}^{(p)}], [{\underline{\varphi }}_{kt}^{(p)}, {\overline{\varphi }}_{kt}^{(p)}] \subseteq [0,1]$ and $q\in {\mathbb {N}}$. Here $[{\underline{\vartheta }}_{kt}^{(p)}, {\overline{\vartheta }}_{kt}^{(p)}]$ represents the “intensity degree of preferred” to ${\mathcal {K}}_k$ under ${\mathfrak {V}}_t$, where $[{\underline{\varphi }}_{kt}^{(p)}, {\overline{\varphi }}_{kt}^{(p)}]$ be “degree against the satisfaction level” of ${\mathcal {K}}_k$ under ${\mathfrak {V}}_t$. All the values of the expert ${\mathcal {D}}_p$ are displayed in matrix ${\mathcal {R}}^{(p)}=({\mathcal {I}}_{kt}^{(p)})_{m\times n}$, while $\wedge =(\zeta _{kt})$ gives the exponent base indices. Therefore, an IVq-ROF decision matrix can be taken as

To select the optimal alternative(s), the procedure steps are written as follows:

• Step 1: Formulate a decision matrix ${\mathfrak {R}}$ for each expert ${\mathfrak {D}}$.

• Step 2: Discrete the attributes into cost $(F_1)$ and the benefit $(F_2$) types and hence normalize ${\mathcal {I}}_{kt}^{(p)}$ into $r_{kt}^{(p)}$ as

  $$\begin{aligned} r_{kt}^{(p)} = {\left\{ \begin{array}{ll} \left( [{\underline{\varphi }}_{kt}^{(p)}, {\overline{\varphi }}_{kt}^{(p)}], [{\underline{\vartheta }}_{kt}^{(p)}, {\overline{\vartheta }}_{kt}^{(p)}] \right) &{}; \text {for } F_1 \text { attribute} \\ \left( [{\underline{\vartheta }}_{kt}^{(p)}, {\overline{\vartheta }}_{kt}^{(p)}], [{\underline{\varphi }}_{kt}^{(p)}, {\overline{\varphi }}_{kt}^{(p)}] \right) &{}; \text {for } F_2 \text { attribute} \\ \end{array}\right. } \end{aligned}$$

  (21)

• Step 3: Construct the q-CNs for each $r_{kt}^{(p)}$ by either Definition 7 or Definition 8. For instance, by taking Definition 7, we formulated a q-CN decision matrix ${\mathcal {Q}}^{(p)} = (\lambda _{kt}^{(p)})_{m\times n} = \left( a_{kt}^{(p)} + b_{kt}^{(p)} i + c_{kt}^{(p)}j\right) _{m\times n}$ where

  $$\begin{aligned} a_{kt}^{(p)}&= \left( \frac{\left( {\underline{\vartheta }}_{kt}^{(p)}\right) ^q + \left( {\overline{\vartheta }}_{kt}^{(p)}\right) ^q }{2}\right) ^{1/q}\\&\quad \root q \of {1- \frac{\left( {\underline{\varphi }}_{kt}^{(p)}\right) ^q + \left( {\overline{\varphi }}_{kt}^{(p)}\right) ^q}{2}},\\ b_{kt}^{(p)}&= \root q \of {\frac{1+\left( 1-\left( {\underline{\vartheta }}_{kt}^{(p)}\right) ^q - \left( {\overline{\vartheta }}_{kt}^{(p)}\right) ^q \right) \cdot \left( 1-\left( {\underline{\varphi }}_{kt}^{(p)}\right) ^q - \left( {\overline{\varphi }}_{kt}^{(p)}\right) ^q \right) }{2}}, \\ c_{kt}^{(p)}&= \left( \frac{\left( {\underline{\varphi }}_{kt}^{(p)}\right) ^q + \left( {\overline{\varphi }}_{kt}^{(p)}\right) ^q }{2}\right) ^{1/q}\\&\quad \root q \of {1- \frac{\left( {\underline{\vartheta }}_{kt}^{(p)}\right) ^q+ \left( {\overline{\vartheta }}_{kt}^{(p)}\right) ^q}{2}} \end{aligned}$$

• Step 4: Aggregate preferences of experts $\lambda _{kt}^{(p)}=a_{kt}^{(p)}+b_{kt}^{(p)} i + c_{kt}^{(p)}j$ into $\lambda _{kt}=a_{kt}+b_{kt} i + c_{kt} j$ with weight vector $w_p>0$ by using appropriate AOs namely q-CNWEA or q-CNWG. The obtained decision matrix is denoted by ${\mathcal {D}}=(\lambda _{kt})_{m\times n}$. For instance, by q-CNWEA operator, we have

  $$\begin{aligned} \lambda _{kt} = q\text {-CNWEA}\left( \lambda _{kt}^{(1)}, \lambda _{kt}^{(2)}, \ldots , \lambda _{kt}^{(l)}\right) \end{aligned}$$

  (22)

• Step 5: If attribute weights are known a priori, use them. Otherwise, if some information about the attribute weights is partially known, denoted by H or completely unknown, then we formulate an optimization model, to compute it, as

  $$\begin{aligned}&\max ~ f = \sum _{t=1}^n \sum _{k=1}^m \omega _t {\mathcal {S}}_{kt} \nonumber \\ &\text{ s.t. }\sum _{t=1}^n \omega _t=1 ; \omega _t \ge 0 ; \omega \in H \end{aligned}$$

  (23)

  where ${\mathcal {S}}_{kt}= {\mathcal {S}}(\zeta _{kt}^{\lambda _{kt}})$ represents the score value of q-CN $\zeta _{kt}^{\lambda _{kt}}$. If $\sum _{k=1}^m {\mathcal {S}}_{kt}=1$ then compute the accuracy values and hesitancy degrees. After solving this model (23), we get the weight vector $\omega =(\omega _1,\omega _2,\ldots ,\omega _n)^T$.

• Step 6: Compute the collective value of $\lambda _{kt}$ as $\lambda _k =a_k + b_k i+ c_k j$ for $k=1,2,\ldots ,m$ using either of the stated operator. For instance, if we utilize q-CNWEG operator, then $\lambda _k$ is computed as

  $$\begin{aligned} \lambda _k = q\text{-CNWEG}(\lambda _{k1}, \lambda _{k2}, \ldots , \lambda _{kn}) \end{aligned}$$

  (24)

• Step 7: Find defuzzifier value of the $\lambda _k = a_k + b_k i + c_k j$, $k=1,2,\ldots ,m$ by using Eq. (25).

  $$\begin{aligned} {\mathcal {S}}(\lambda _k)= a_k^q - c_k^q + \left( \frac{e^{a_k^q - c_k^q}}{1+e^{a_k^q - c_k^q}}-\frac{1}{2}\right) b_k^q \end{aligned}$$

  (25)

• Step 8: Apply Definition 11 to rank ${\mathcal {K}}_k (k=1,2,\ldots ,m)$ and select the best alternative(s).

5.2 Illustrative case

The stated algorithm has been demonstrated with an illustrative example as follows.

Jharkhand is the eastern state of India, which has the 40 percent mineral resources of the country and second leading state of the mineral wealth after Chhattisgarh state. It is also known for its vast forest resources. Jamshedpur, Bokaro and Dhanbad cities of the Jharkhand are famous for industries all over the world. After that, it is the widespread poverty state of India because it is primarily a rural state as 76 percent of the population lives in the villages which depend on the agriculture and wages. Only 30 percent of villages are connected by roads, while only 55 percent of villages have accessed to electricity and other facilities. But in today’s life, everyone is changing fast to himself for a better life; therefore, everyone moves to the urban cities for a better job. To stop this emigration, Jharkhand government wants to set up the industries based on agriculture in the rural areas. For this, the government has been organized MOMENTUM JHARKHAND global investor submit 2017 in Ranchi to invite the companies for investment in the rural areas. Government announced the various facilities for setting up five food processing plants in the rural areas and consider the six attributes required for company selection to setup them, namely project cost $({\mathfrak {B}}_{1})$, completion time $({\mathfrak {B}}_{2})$, technical capability $({\mathfrak {B}}_{3})$, financial status $({\mathfrak {B}}_{4})$ and assign the weights of relative importance of each attributes. The five companies have taken as in the form of the alternatives, namely, Surya Food and Agro Pvt. Ltd. $({\mathcal {K}}_{1})$, Mother Dairy Fruit and Vegetable Pvt. Ltd. $({\mathcal {K}}_{2})$, Parle Products Ltd. $({\mathcal {K}}_{3})$, Heritage Food Ltd. $({\mathcal {K}}_{4})$ and Reliance Fruits Pvt. Ltd. $({\mathcal {K}}_{5})$ interested for these projects. Then, the main object of the government is to choose the best company among them for the task. To it, the steps as defined in Sect. 5.1 are executed as follows.

• Step 1: The evaluation matrix of the alternatives ${\mathcal {K}}_k$ provided by an authority is reviewed in Table 2.

• Step 2: Utilize Eq. (21) for the cost attributes ${\mathfrak {B}}_1$ and ${\mathfrak {B}}_2$ and the transformed matrix is furnished in Table 3.

• Step 3: The q-CNs for each expert rating are formulated by using Definitions 7 or 8 and listed in Table 4.

• Step 4: With experts weight $w=(0.35,0.40,0.25)$ and q-CNWEA operator, the resultant numbers ($\lambda _{kt}$) are summarized as

  

• Step 5: Formulate a score matrix of q-CN $\lambda _{kt}$ as

  

  Formulate the optimization model by Eq. (23), by taking the partial information of the attribute importance as $H=\{0.20\le \omega _1 \le 0.25$, $0.25\le \omega _2 \le 0.35$, $0.20\le \omega _3 \le 0.40$, $0.10 \le \omega _4 \le 0.20$, $\omega _1+\omega _3\le 2\omega _2$, $\omega _1+2\omega _4\le \omega _3 \}$, as

  $$\begin{aligned}& \max ~~f = 2.0873 \omega _1 + 2.9383 \omega _2 + 3.0202 \omega _3 + 2.2148 \omega _4 \\&\text {s.t. } \sum \limits _{t=1}^4 \omega _t=1; \omega \in H \end{aligned}$$

  and hence after solving it, we can get $\omega = (0.2$, 0.3, 0.4, 0.1).

• Step 6: Aggregate the ratings ($\lambda _{kt}$) with q-CNWEA operator and hence the q-CNs for the given alternatives are computed as $\lambda _1 = 0.7209 + 0.6518 i + 0.2355 j$, $\lambda _2 = 0.8434 + 0.5029 i + 0.1894 j$, $\lambda _3 = 0.8851 + 0.4497 i + 0.1195 j$, $\lambda _4 = 0.8256 + 0.5508 i + 0.1225 j$ and $\lambda _5 = 0.8857 + 0.4450 i + 0.1324 j$.

• Step 7: By Eq. (25), the score values of $\lambda _k$’s are computed as ${\mathcal {S}}(\lambda _1)=0.5127$, ${\mathcal {S}}(\lambda _2)=0.7165$, ${\mathcal {S}}(\lambda _3)=0.8063$, ${\mathcal {S}}(\lambda _4)=0.7153$ and ${\mathcal {S}}(\lambda _5)=0.8031$.

• Step 8: Since ${\mathcal {S}}(\lambda _3)> {\mathcal {S}}(\lambda _5)> {\mathcal {S}}(\lambda _2)> {\mathcal {S}}(\lambda _4) > {\mathcal {S}}(\lambda _1)$ and hence ordering of the given alternative is ${\mathcal {K}}_3 \succ {\mathcal {K}}_5 \succ {\mathcal {K}}_2 \succ {\mathcal {K}}_4\succ {\mathcal {K}}_1$. Thus, ${\mathcal {K}}_3$ is the best alternative.

Table 2 Rating of the alternatives

Table 3 Normalized data of Table 2

Table 4 q-CNs of the given IVq-ROFNs

5.3 Impact of q and AOs on the outcomes

To examine the influence of the parameter q on the given algorithm, we tested it by setting different values of q. The results using q-CNWEA and q-CNWEG operators are summarized in Table 5. From this table, it can be seen that we can obtain the different best alternatives for different values of q. For example, when $q=1,2$, the best alternative is ${\mathcal {K}}_3$ while for $q\ge 3$, ${\mathcal {K}}_5$ is the best alternative. Thus, a decision-maker can choose the desired alternative depending on the nature of the parameter q.

Table 5 Impact of q on alternatives

How does one choose the smallest q for analysis that satisfies the constraint ${\overline{\vartheta }}^q+{\overline{\varphi }}^q\le 1$? To address it, an analyst can choose according to his evaluation column under this constraint. For example, if an expert suggests the value ([0.6,0.8], [0.5,0.8]) in the evaluation, then clearly $0.8^3+0.8^3\ge 1$ and $0.8^4+0.8^4\le 1$. So, the smallest integer q is 4.

Moreover, to investigate the impact of the proposed AOs on the decision-making method, we implement the steps of the recommended algorithm with different AOs. For this, we change the AOs in Step 4 and Step 6 and the optimal values of the alternatives are checked in Table 6. It is determined that if an analyst uses the q-CNWEA operator to aggregate the expert preferences while q-CNOWEG on the attribute, then its effect on the optimal degree of membership is shown in it. Similarly, for the other cases, we can analyze the impact of the proposed AOs on the process.

Table 6 Influence of various AOs on ranking

5.4 Validation and Comparative analysis

Here, we give exceptional examples to validate the efficiency of the given algorithm. In this analysis, we have assumed $\zeta _1=\zeta _2=\ldots =\zeta _n=0.5$.

Example 5

Consider a MAGDM problem regarding the setup of new library building in a university. For it, an authority of the university decides to increase the number of infrastructure in the library and hence to fulfill it, they listed the four builders ${\mathcal {K}}_i, i=1,2,3,4$. To access the best builders among them, each builder (considered as alternative) is evaluated from four attributes namely ${\mathfrak {V}}_1$ (social influence), ${\mathfrak {V}}_2$ (quality), ${\mathfrak {V}}_3$ (reputation) and ${\mathfrak {V}}_4$ (service reputation). The weights given to them are $\omega =(0.3, 0.4, 0.1, 0.2)$. The three experts from the civil engineering and human resources departments are requested to evaluate them. The experts weight are taken as $w=(0.32, 0.45, 0.23)$ and their rating under IVq-ROFNs features with $q=1$ given in Tables 1–3 (for more details, we refer to see [42]). The results for diverse MAGDM methods with the several others existing approaches [5,6,7,8,9,10,11, 20, 23, 42, 43] are listed in Table 7. From this, we can see that ${\mathcal {K}}_2$ is the best one.

Table 7 Outcomes of Example 5

Example 6

Consider a MADM problem with five alternatives ${\mathcal {K}}_1,{\mathcal {K}}_2,{\mathcal {K}}_3, {\mathcal {K}}_4$ and ${\mathcal {K}}_5$ drawing the patients, who are affected with the bugs and necessitate to be diagnosed from the four manifestations (attributes) of the viruses namely, ${\mathfrak {V}}_1$ (vital signs, including heart rate and blood pressure), ${\mathfrak {V}}_2$ (body temperature), ${\mathfrak {V}}_3$ (the frequency of the cough) and ${\mathfrak {V}}_4$ (the frequency of hemoptysis) with $\omega$=(0.2,0.1, 0.3, 0.4). The doctor proffers the evaluation values of all the patients under the signs by using IVIFNs (i.e., $q=1$ of IVq-ROFNs) and their judgment matrix is represented in Eq. (26).

(26)

The ranking outcomes to this problem are listed in Table 8 concurrently with the several others existing approaches [5,6,7,8,9,10,11, 20, 23, 42, 43].

Table 8 Outcomes of Example 6

Example 7

[10, 11] Consider a DMP regarding the selection of the best high-tech enterprise with the lowest risk of technologic invention. For this, a management constitute a committee with three experts who acts as a decision-makers having weights w=(0.40, 0.35, 0.25), whose responsibility is to evaluate the given four alternatives $\{{\mathcal {K}}_1, {\mathcal {K}}_2, {\mathcal {K}}_3, {\mathcal {K}}_4\}$. To access them completely, they considered the six attributes namely ${\mathfrak {V}}_1$ (policy risk), ${\mathfrak {V}}_2$ (financial risk), ${\mathfrak {V}}_3$ (technological risk), ${\mathfrak {V}}_4$ (production risk), ${\mathfrak {V}}_5$ (market risk) and ${\mathfrak {V}}_6$ (managerial risk) to evaluate the given four alternatives. The weight vector of the attributes is taken as $\omega$=(0.1894, 0.1841, 0.1361, 0.1257, 0.1753, 0.1894). The judgment matrices are furnished by the experts, (see [10, 11], Tables 1-3) under IVq-ROFNs with $q=2$. The result obtained by the proposed and the existing approaches [5,6,7,8,9,10,11, 20, 23, 43] are listed in Table 9.

Table 9 Outcomes of Example 7

Example 8

[19] Consider that there are five emergency plans ${\mathcal {K}}_1, {\mathcal {K}}_2, {\mathcal {K}}_3, {\mathcal {K}}_4, {\mathcal {K}}_5$ pondered for an explosion hazard in coal mine. An expert evaluate it under the set of five benefit attributes namely ${\mathfrak {V}}_1$ (Gas), ${\mathfrak {V}}_2$ (Casualties), ${\mathfrak {V}}_3$ (Smoke), ${\mathfrak {V}}_4$ (Viability), and ${\mathfrak {V}}_5$ (Facility). The weight vector of ${\mathfrak {V}}$’s is $\omega$=(0.3, 0.2, 0.14, 0.16, 0.2) and the rating of them is given in Eq. (27).

(27)

Stated and the existing [5,6,7,8,9,10,11, 19, 20, 23, 43] algorithms have been implemented and the results are recorded in Table 10.

Table 10 Outcomes of Example 8

Example 9

Consider a person which wants to invest their certain money in one of the five markets denoted by ${\mathcal {K}}_1$, ${\mathcal {K}}_2$, $\ldots$, ${\mathcal {K}}_5$. For it, they hired an expert to select the best market under the five different attributes namely ${\mathfrak {V}}_1$ (risk analysis); ${\mathfrak {V}}_2$ (growth analysis); ${\mathfrak {V}}_3$ (environmental impact analysis); ${\mathfrak {V}}_4$ (social-political impact analysis) and ${\mathfrak {V}}_5$ (development of the society). The weight vector of them is considered as $\omega =(0.3, 0.2, 0.14, 0.16, 0.2)$. The normalized rating value of each alternative given by an expert in terms of IVq-ROFNs is summarized in Eq. (28). Based on such information, an investigation has been done and their complete results are listed in Table 11.

(28)

From this table, we can quickly understand that the most suitable alternative obtained by the proposed approach is consistent with these existing measures. Therefore, this analysis shows the usefulness of the intended method for determining the DMPs.

Table 11 Outcomes of Example 9

5.5 Further comparative studies

The validity of the stated algorithm was verified using Examples 5–9. However, to signify the advantages of the algorithm with the studies [5,6,7,8,9,10,11, 20, 43], we have explained it as follows.

Example 10

Consider a case study as presented in section 5.2 and recorded the outcomes (the steps are excluded here) using methods [5,6,7,8,9,10,11, 20, 43] in Table 12. From this, we obtain the best alternative as ${\mathcal {K}}_3$. However, from Tables 7, 8, 9, 10, 11, 12, we can see that the order of the alternatives may be different from the proposed one due to the following reasons.

• (1) The approaches under IVIFS and IVPFS and IVq-ROFS environment to solve the DMPs have made a restriction only to the MD and NMD. However, the given theory provides an alternative space to the distribution with the problem with three degrees namely “contrary”, “identity” and “discrepancy” of the q-CNs such that their $q^{th}$ power sum should be equal to one. The compatibility between the SPA and IVq-ROFS, gives a suitable procedure to transform the given IVq-ROFNs into q-CNs, which is described in Definition 7 and Definition 8. Therefore, the given work is more suitable to solve modern decision-making problems, and there is a some reduction of information loss during the execution process.

• (2) The traditional operators under the IVq-ROFS environment work under the condition that the exponents are real numbers and the bases are IVq-ROFNs. Therefore, such operators do not work when these conditions are reversed. To address this, a proposed q-CNWEA or q-CNWEG operator is well suited, where the bases are considered to be real numbers, while the exponents are the q-CNs formulated from the given IVq-ROFNs.

• (3) In the existing work, the real number $\zeta$ plays no role and therefore, there may be a change in the ranking of the given objects derived from the given and existing algorithm. This change occurs due to the importance and position of IVq-ROFN ${\mathcal {I}}$ and q-CN $\zeta ^{{\mathcal {C}}n}$.

• (4) From Table 1, we see that there are significant weaknesses in the score functions for ranking the numbers, since they do not taken into account the degree of hesitation. However, in the proposed work, a score function based on the sigmoidal function $f(x)=\frac{e^x}{1+e^x}$ is defined in Eq. (8) and hence the ranking is done based on it. Moreover, it is found that the proposed score function successfully and efficiently solves the DMPs by fixing the parameter q. Thus, the proposed algorithm is more comprehensive than the algorithms based on IVIFSs or IVPFSs.

Table 12 Outcomes of the main example

Example 11

From Examples 6–9, it can be seen that the given algorithm has a wider scope for simplifying the DMPs than the algorithm in [5,6,7,8,9,10,11], due to the adjusting parameter q in the constraint ${\overline{\vartheta }}^q+{\overline{\varphi }}^q\le 1$. To give further benefits of this, we take small changes to the values of ${\mathcal {I}}_{12}, {\mathcal {I}}_{21}, {\mathcal {I}}_{32}$, ${\mathcal {I}}_{44}$ and ${\mathcal {I}}_{53}$ with ([0.6, 0.8], [0.5, 0.7]) of Example 6, and then implemented the given and existing [5,6,7,8,9,10,11, 20] algorithms. The final results of them are recorded in Table 13 and it can be seen that the results obtained in [5,6,7,8,9,10,11] are not able to handle the DMP, because it fails to fulfill ${\overline{\vartheta }}+{\overline{\varphi }}\le 1$ and ${\overline{\vartheta }}^2+{\overline{\varphi }}^2\le 1$. Therefore, the approaches [5,6,7,8,9,10,11] are narrow, while the approaches [20, 43] ${\overline{\vartheta }}^q+{\overline{\varphi }}^q\le 1$ satisfy, where q is naturally adjusted.

In addition to that, in the computational study, we see the best alternative resemblance with the results of [20, 43] but the whole execution process of their algorithms is different. In the following, we describe some highlights between the given algorithm and the existing algorithms of [20, 43].

• (1) In [20, 43], the decision is solely taken with score values without including the hesitancy degree in the computation process. Counter to this, in the proposed algorithm, we recognize the same by accompanying the q-CNs and the novel score function defined in Definition 10.

• (2) The proposed q-CNWEA, q-CNWEG and several existing IVq-ROFWA, IVq-ROFWG, IVIFWG, IVIFWA, IVPFWA, IVPFWG, etc., operators are applied at different disciplines based on the fulfillment of ${\overline{\vartheta }}+{\overline{\varphi }}\le 1$ or ${\overline{\vartheta }}^2+{\overline{\varphi }}^2\le 1$ or ${\overline{\vartheta }}^q+{\overline{\varphi }}^q\le 1$.

• (3) The existing operators IVq-ROFWA, IVq-ROFWG, IVIFWG, IVIFWA, IVPFWA, IVPFWG etc., work under the conditions that the exponent is a real number of [0, 1] and the bases are interval-numbers. When these conditions are reversed, all these operators are no longer applicable. However, the proposed q-CNWEA or q-CNWEG operator is well suited when the bases are considered as real numbers and the exponents are the q-CNs formulated from the given IVq-ROFNs.

• (4) In the existing work, there is no role of real number $\zeta$’s and hence due to this, there may be a change in the ranking order of the given objects derived from stated and existing algorithm. This change occur due to the significance and position of IVq-ROFN ${\mathcal {I}}$ and q-CN $\zeta ^{{\mathcal {C}}n}$. For instance, the q-CNWEA operator is $q\text {-CNWEA}({\mathcal {C}}n_1$, ${\mathcal {C}}n_2$, $\ldots$, ${\mathcal {C}}n_n)=\omega _1(\zeta _1^{{\mathcal {C}}n_1})\oplus \ldots \oplus \omega _n(\lambda _n^{{\mathcal {C}}n_n})$ where $\zeta _i\in [0,1]$, while IVq-ROFWA operator is $q\text {-ROFWA}({\mathcal {I}}_1$, ${\mathcal {I}}_2$, $\ldots$, ${\mathcal {I}}_n)=\omega _1{\mathcal {I}}_1\oplus \ldots \oplus \omega _n{\mathcal {I}}_n$ where ${\mathcal {I}}_i\in \text {IVq-ROFNs}$ and $\omega _i\in [0,1]$.

Table 13 Outcomes of the updated Example 11

6 The advantages of the proposed MADM method

Using IVq-ROFS features, we have some examples as given below to assert the advantages of the algorithm over the studies [5,6,7,8,9,10, 20, 43].

Example 12

Consider a problem with three alternatives ${\mathcal {K}}_1$, ${\mathcal {K}}_2$, ${\mathcal {K}}_3$ and four attributes ${\mathfrak {B}}_1$, ${\mathfrak {B}}_2$, ${\mathfrak {B}}_3$ and ${\mathfrak {B}}_4$ with weight $\omega =(0.3,0.2,0.2,0.3)$. An expert gave their rating of each alternative as

With the given weight vector and by using the existing AOs [5,6,7, 9, 20, 43], the aggregated values of ${\mathcal {K}}$’s are summarized in Table 14 along with their ranking order with existing score function. Clearly, the ordering of the given alternatives becomes ${\mathcal {K}}_1\sim {\mathcal {K}}_2 \sim {\mathcal {K}}_3$. But from their rating values, we see that ${\mathcal {K}}_1 \not \sim {\mathcal {K}}_2 \not \sim {\mathcal {K}}_3$.

However, in order to implement the proposed operator to the given data, we firstly construct the q-CN (with q = 2) by using Definition 7 or 8 and get

Aggregate these values into $r_k$ by using q-CNWEG operator with $q=2$ and we get $r_1= 0.7492 + 0.5966 i + 0.2876 j$, $r_2= 0.7185 + 0.6202 i + 0.3148 j$ and $r_3= 0.7600 + 0.5869 i + 0.2792 j$. The score values of them are ${\mathcal {S}}(r_1)=0.5204$, ${\mathcal {S}}(r_2)= 0.4567$ and ${\mathcal {S}}(r_3)= 0.5418$. Since ${\mathcal {S}}(r_3)> {\mathcal {S}}(r_1) > {\mathcal {S}}(r_2)$, thus ordering of given alternatives is ${\mathcal {K}}_3 \succ {\mathcal {K}}_1 \succ {\mathcal {K}}_2$ which is logical.

Table 14 Computed results of Example 12

Example 13

For a MADM problem with two alternatives ${\mathcal {K}}_1$ and ${\mathcal {K}}_2$ under four attributes ${\mathfrak {B}}_1$, ${\mathfrak {B}}_2$, ${\mathfrak {B}}_3$ and ${\mathfrak {B}}_4$ with weights $\omega =(0.4, 0.3, 0.1, 0.2)$. The ratings of an expert are recorded as:

With the given weight vector and by using the existing AOs [6, 7, 9, 43], the aggregated values of ${\mathcal {K}}$’s are summarized in Table 15. Here, we can see that the overall value in these existing approaches is ([0,0], [1,1]) which means that the existing measures such as score and accuracy functions give the same results. Consequently, the order of the given alternatives ${\mathcal {K}}_1\sim {\mathcal {K}}_2$. But from their score values, it is clear that ${\mathcal {K}}_1 \not \sim {\mathcal {K}}_2$.

On contrary to these, if we utilized the proposed MADM approach to this given information, then we construct the q-CNs of the given q-ROFS with $q=2$. The computed q-CNs are summarized in Eq. (29)

(29)

Based on the information, aggregating the results by using q-CNWEG operator and utilizing the proposed score function, we get the optimal degree of ${\mathcal {K}}$’s are ${\mathcal {S}}(r_1)= 0.5418$ and ${\mathcal {S}}(r_2)= 0.4940$. Since ${\mathcal {S}}(r_1) > {\mathcal {S}}(r_2)$ and thus ${\mathcal {K}}_1$ is better than ${\mathcal {K}}_2$. Therefore, the proposed MADM method work well under those cases also, where the existing approaches and measures fail to rank them.

Table 15 Computed results of Example 13

Example 14

Consider a DMP with four alternatives ${\mathcal {K}}_1$, ${\mathcal {K}}_2$, ${\mathcal {K}}_3$ and ${\mathcal {K}}_4$ and attributes ${\mathfrak {B}}_1$, ${\mathfrak {B}}_2$, ${\mathfrak {B}}_3$ and ${\mathfrak {B}}_4$. The expert choices on them are furnished as

With $\omega =(0.2,0.3,0.2,0.3)$ of ${\mathfrak {B}}_t$’s, we implement averaging operators [5, 8,9,10, 20] and the proposed q-CNWEA operators, and hence arrange the overall ordering of the alternatives in Table 16. From it, we can see the stated algorithm has overcome the drawbacks of the existing algorithms [5, 8,9,10, 20] and get ${\mathcal {K}}_2$ is the optimal one.

Table 16 Computed results of Example 14

7 Conclusion

The chief augmentation of the work is compiled below.

• (1) A new concept of q-CNs for the IVq-ROFSs is formed by combining the features of “identity”, “contrary” and “discrepancy” degrees of the set into the one consolidated system. The explained q-CN ${\mathcal {C}}n=a+bi+cj$ based on the SPA theory affords an alternative way to trade with the uncertainties such that $a^q+b^q+c^q=1$ where $q\ge 1$ is integer.

• (2) It has been noted that the existing models such as the score function for ranking the given numbers among the IVIFSs, IVPFS or IVq-ROFSs do not hit the objects. The shortcomings of these are shown in Table 1. To defeat the drawbacks, a generalized scoring function for the pairs of q-CNs is constructed to match the given objects. Also, the superiority, as well as the interests of the proposed score function, is confirmed by the examples as given in Examples 12–14. Furthermore, the proposed ones estimate more objective information in terms of q-CN degrees, thus preventing any information loss.

• (3) The MAGDM algorithm based on the recommended exponential operators is explained, which is more generalized and flexible with parameter q for the decision-maker. In it, q-CNs are taken as the exponent, while the bases are arbitrary real numbers. The importance of the parameter q and the different AOs on the final ranking are shown in detail (Tables 5, 6). In conjunction with the various existing MAGDM algorithms (Tables 7,12,13,15) under different fuzzy environments, the benefits are (i) to obtain the best alternatives by considering all degrees such as “contrary”, “identity” and “discrepancy”, (ii) without counter-intuitive cases [5,6,7,8,9,10,11, 20, 43] (given in Tables 14, 15, 16), and (iii) employ the novel S-shaped score function to order the given alternatives rather than existing score function which may give the effects sometimes irregular as demonstrated in Table 1.

In the future, we expect to work in operating the proposed approaches in some other real-life scenarios such as medical diagnosis, pattern recognition, and brain hemorrhage [44,45,46,47] under extensions of the fuzzy environment.