1 Introduction

Since extreme learning machine (ELM) has been proposed by Huang et al. [18, 19], there has been great attention by researchers in many disciplines and real-world applications such as medical/biomedical [1, 48, 56], computer vision [9, 34], image/video processing [2, 4, 44], text classification [36, 59], system modeling and prediction [6, 33, 51, 52, 58], control and robotics [39], chemical process [7, 50], fault detection and diagnosis [10], time-series analysis [3] and remote sensing [17, 45]. For some comprehensive review studies on ELM theory and applications, the readers are referred to Huang et al. [22], Huang et al. [24] and Deng et al. [11]. The underlying reasons for attention are its superior properties like extremely fast learning speed, simplicity and convincing performance in different learning problems including supervising [22], unsupervising [20] and semisupervising tasks [20]. Although ELM produces successful results in many real-world applications, it has several drawbacks caused by its learning nature. As a result of structural risk minimization approach [47], ELM may provide poor results in terms of stability, generalization performance and sparsity perspectives. In some situations, even the ELM presents efficient convergence in theory, its results may be overfitted or underfitted compared to what it should be in reality. Besides, the performance of the ELM significantly depends on the number of the hidden layer nodes. The selection of optimal node number is a complicated issue because of the possibility of overfitting or underfitting [30].

In order to deal with the ELM drawbacks, alternative variants of the ELM have been proposed to improve performance. Some of them have been mentioned in this study. A majority of these studies are based on regularization methods including the norms like \(L_{2}\) (i.e., Tikhonov, ridge) and \(L_{1}\) (i.e., Lasso).

When collinearity exists among the columns of the output matrix of hidden layer, multicollinearity exists. In case of multicollinearity, ELM results cannot be obtained or they will be unstable. The ridge estimator was proposed by Hoerl and Kennard [18] to deal with multicollinearity problem in linear models. The first appearance of ridge estimator in the context of ELM has been presented by Deng et al. [12] and later proposed by Li and Niu [25] in a regular form. Li and Niu [25] proposed an enhanced ELM algorithm based on the ridge regression (RR-ELM) and showed that RR-ELM may provide more stable and generalizable results than the conventional ELM. Cao et al. [5] proposed a suitable method for both classification and regressional studies called as stacked sparse denoising autoencoder—ridge regression (SSDAE-RR) to obtained more stable and generalizable network model. Shao et al. [43] developed a new regularized ELM based on leave-one-out cross-validation (LOO-CV) to determine the optimal model and get better learning performance. Chen et al. [8] proposed a two-stage method based on uninformative variable elimination and ridge regression to carry on a ridge-based ELM with the most informative feature. Yu et al. [57] developed a novel dual adaptive regularized online sequential extreme learning machine (DA-ROS-ELM) to deal with ill-posing and over-fitting on problems related to network intrusion. Wang and Li [49] presented one of the first studies on ELM for survival data and proposed a new method called as ELMCoxBAR (a kernel ELM Cox model regularized by an L-0-based broken adaptive ridge) to reduce the computational cost for high-dimensional survival data. Yıldırım and Özkale [54] have found that the performance of ELM algorithms based on the ridge and almost unbiased ridge estimators [35] depends on the selection method of the parameter and they proposed different criteria including Akaike information criterion (AIC), Bayesian information criterion (BIC) and cross-validation (CV) for the selection of the tuning parameter in the context of ELM. Luo et al. [29] presented a weighted extreme learning machine with distribution optimization using ridge regression to classify user behavior prediction. Yan et al. [53] proposed a new algorithm called as artificial bee colony algorithm-based kernel ridge regression to provide more efficient results on insurance fraud identification. Raza et al. [38] presented k-sparse ELM to select the most informative features to obtain more compact model. In this study, it is shown that the selection method of parameter is effective on the performance of ridge-based algorithms. ELM algorithms based on ridge regression improve ELM performance in a certain extent.

Although ELM algorithms in regression studies based on \(L_{2}\)-norm have been widely adapted by researchers, there are alternatives to the ridge estimator. Liu estimator [27] is one of the alternatives which is effective for dealing with multicollinearity problem. The advantage of Liu estimator over the ridge estimator is to have a linear form of the tuning parameter unlike the nonlinear form in the ridge estimator. This property gives the possibility to determine the tuning parameter easier and faster than ridge. Therefore, the superiority of Liu estimator can be beneficial to dealing with the instability and poor generalization performance of ELM. Hence, Yıldırım and Özkale [55] proposed an enhanced ELM algorithm based on Liu (Liu-ELM) with different selection methods for tuning parameter and showed that the proposed algorithm generally provides more stable and generalizable results than ELM and RR-ELM.

RR-ELM has been widely used in different fields due to its superiorities like stability, predictive performance and functionality on high-dimensionality settings over ELM. However, it does not present a sparse (i.e., compact) model which is quite important to deal with high-dimensional data sets including irrelevant or noisy features. In other words, RR-ELM does not carry out a variable selection process and affects on the compactness of the model. This yields less interpretable model compared to its competitors. Lasso regression proposed by Tibshirani [46] could be a remedy for these drawbacks of RR-ELM.

To make further, particularly in the presence of irrelevant features, \(L_{1}\)-norm has been considered in learning process of ELM. Miche et al. [31] proposed a pruning algorithm called optimally pruned extreme learning machine (OP-ELM) to obtained more robust results than ELM. Later on, in order to benefit from the advantages of \(L_{1}\) and \(L_{2}\) regularizations, several studies have been carried out. Firstly, Miche et al. [32] proposed a double-regularized ELM called Tikhonov-regularized OP-ELM (TROP-ELM) and obtained better results than OP-ELM [31] and the basic ELM. Afterward, Martinez et al. [30] proposed a regularized ELM to select the optimal number of hidden layer nodes and they adapted the elastic net method in ELM training phase and the results have been given comparatively. Luo et al. [28] proposed a unified form of ELM algorithm based on \(L_{1}\) and \(L_{2}\) forms to be used in regression and classification tasks. Shan et al. [42] proposed a new method called as interval LASSO-based ELM to determine the appropriate nodes of network and avoid from the overfitting problem. Li et al. [26] presented a new regularized algorithm based on \(L_{2,1}\)-norm for deal with noises and outliers to obtain more robust and compact networks. Preti et al. [37] developed novel online sequential extreme learning machine based on \(L_{2,1}\)-norm to improve the processing time and memory usage for process real-time sequential data. Fan et al. [15] proposed two different algorithms based on \(L_{1/2}\)-norm having both group and smoothing group regularization to present more compact networks with effective learning capability.

The advantage of Lasso method is that it shrinks some of the weights exactly to zero. Thus, a much sparser model is obtained. Both RR-ELM and lasso-ELM shrink the weights matrix with proportional to the tuning parameters, but Lasso also carries out variable selection by setting some weights to zero. Due to these properties, Lasso and its variants have been attracted in many disciplines. Due to the impossibility of closed-form solution, several algorithms [14, 16, 40] have been proposed to obtain solution in Lasso-type problems. Although Lasso is well in high-dimensional data, there are some drawbacks of Lasso regression which are pointed out by Zou and Hastie [60]. In order to overcome the drawbacks of Lasso, Zou and Hastie [60] proposed elastic net as a regularization and variable selection method. In elastic net, the superiorities of both ridge and Lasso methods have been used in a unified model. Thus, an effective variable selection process can be carried out by considering the grouping effect (the relationships between variables).

Liu-ELM was proposed as an alternative to RR-ELM, and it has the disadvantage of that it does not do variable selection. However, when we combine Liu-ELM with \(L_{1}\)-norm, it does variable selection because of the feature of \( L_{1}\)-norm penalization. Thus, it may be more efficient and convenient than Liu-ELM and Lasso-based ELM algorithms. With the sparsity property of \(L_{1}\)-norm, the results may be more convincing for dealing with ELM’s drawbacks. Taken together, the drawbacks mentioned above can be briefly summarized as follows:

  • The performance results may present poor generalization and stability performance.

  • Some of algorithms such as Liu-ELM and RR-ELM do not carry a variable (i.e., node in the context of ELM) selection process. Therefore, they do not have the sparsity property.

  • Ridge-type algorithms are based on a parameter selection which do not have a generally accepted way and could be adversely effective on the speed of algorithm.

In this study, we present a new algorithm which is a cascade of two regularization types including Liu estimator and \(L_{1}\)-norm to improve the ELM and its variants based on \(L_{1}\)- and \(~L_{2}\)-norms in terms of stability and generalization performance. We called this novel algorithm as Liu–Lasso extreme learning machine (LL-ELM) algorithm. The main contributions of the proposed algorithm can be listed as follows:

  • The new method produces a solution to the multicollinearity problem like Liu-ELM and RR-ELM as well as its superiority compared to Liu-ELM and RR-ELM is that it does variable selection.

  • The new method does variable selection like Lasso; however, instead of shrinking the components toward the origin as Lasso does, it shrinks toward d times ELM results where d is a parameter between 0 and 1.

  • The new method, like Enet-ELM, does variable selection and depends on two tuning parameters, but the selection of the new tuning parameter is mathematically easier than that of Enet-ELM.

In the rest of the paper, a brief review of algorithms is presented in Sect. 2. The details of the proposed algorithm are given in Sect. 3. In Sect. 4, the details of parameter and model selection are provided. An experimental study is carried out to investigate the performances of all algorithms on the real data sets in Sect. 5. The discussions and conclusions are summarized in Sect. 6.

2 A brief review of algorithms

2.1 Extreme learning machine (ELM)

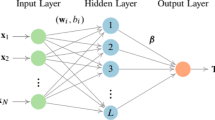
This section shortly presents ELM algorithm proposed by Huang et al. [30, 31]. The main property of ELM is to give a chance to select the number of hidden layer neurons and biases arbitrary (i.e., randomly). As a result of random selection, the estimation problem of the neural network is reduced to find a solution of a linear system which can be easily obtained analytically. Therefore, ELM provides faster and simpler learning and estimation processes than other learning algorithms like backpropagation. Consider a group of samples \(\left( x_{i},t_{i}\right) ,\) where \( x_{i}=\left( x_{i1},x_{i2},...,x_{in}\right) ^{\rm{T}}\in {\mathbb {R}} ^{n}\) and \(t_{i}=\left( t_{i1},t_{i2},...,t_{im}\right) ^{\rm{T}}\in {\mathbb {R}} ^{m}\) to be estimated in a problem. For a given activation function \(\left( g\right) \) and a number of hidden layer neurons \(\left( K\right) \), the mathematical model of estimation based on a single-layer feedforward neural network (SLFN) can be written as follows:

$$\begin{aligned} {\mathbf{t}}_{j}^{\rm{T}}=\sum \limits _{i=1}^{K}{\varvec{\beta }}_{i}^{\rm{T}}g\left( {\mathbf{w}}_{i}.{\mathbf{x}}_{j}+b_{i}\right) ,~j=1,2,\ldots ,N, \end{aligned}$$
(1)

where \({\mathbf{x}}_{j}^{\rm{T}}=\left[ x_{j1},x_{j2,...,}x_{jn}\right] \) is the input values corresponding to the original data points, \({\mathbf{t}}_{j}^{\rm{T}}= \left[ t_{j1},t_{j2,...,}t_{jm}\right] \) is the outputs of neural network, \( {\mathbf{w}}_{i}=\left[ w_{i1},w_{i2},\ldots ,w_{im}\right] ^{T}\) and \(b_{i}\) are the learning parameters between the ith hidden node and the input nodes. \( \varvec{\ \beta }_{i}=\left[ \beta _{i1},\beta _{i2},...,\beta _{im} \right] ^{\rm{T}}\) is the weight vector linking the ith hidden node and the output nodes. \({\mathbf{w}}_{i}.{\mathbf{x}}_{j}\) corresponds to the inner product between \({\mathbf{w}}_{i}\) and \({\mathbf{x}}_{j}\) [30, 31]. Generally, n is equal to the number of explanatory variables and m is equal to the number of response variables which is commonly taken as one in most practical applications. ELM algorithm as a SLFN claims that it can converge with zero error to the actual values of N samples. In other words, there are always a group of optimal parameters (i.e., weight and bias values) to provide \( \sum \nolimits _{i=1}^{K}\) \(\left\| {\mathbf{y}}_{j}-t_{j}\right\| =0\). Equation (1) can be written more compactly as

$$\begin{aligned} {\mathbf{H}}{\varvec{\beta }}={\mathbf{T}}, \end{aligned}$$
(2)

where

$$\begin{aligned} {\mathbf{H}}=\left[ \begin{array}{ccc} g\left( {\mathbf{w}}_{1}.{\mathbf{x}}_{1}+b_{1}\right) &{} ... &{} g\left( {\mathbf{w}} _{K}.{\mathbf{x}}_{1}+b_{K}\right) \\ \vdots &{} ... &{} \vdots \\ g\left( {\mathbf{w}}_{1}.{\mathbf{x}}_{N}+b_{1}\right) &{} ... &{} g\left( {\mathbf{w}} _{K}.{\mathbf{x}}_{N}+b_{K}\right) \end{array} \right] _{N\times K} \end{aligned}$$

is the output matrix of hidden layer in the neural network,

$$\begin{aligned} {\varvec{\beta }}=\left[ \begin{array}{c} \beta _{1}^{\rm{T}} \\ \vdots \\ \beta _{K}^{\rm{T}} \end{array} \right] _{K\times m} \end{aligned}$$

corresponds to the weights and

$$\begin{aligned} {\mathbf{T}}=\left[ \begin{array}{c} {\mathbf{t}}_{1}^{\rm{T}} \\ \vdots \\ {\mathbf{t}}_{N}^{\rm{T}} \end{array} \right] _{N\times m} \end{aligned}$$

is the output values of neural network.

By selecting the learning parameters randomly, the weight matrix \(\left( \beta \right) \) can be obtained via a classical least squares approach. Therefore, the estimation of \({\varvec{\beta }}\) in ELM, say \(\hat{\beta }_{{{\text{ELM}}}}\), is equivalent to obtain the solution of the following objective function:

$$\begin{aligned} {\hat{\varvec{\beta }}}_{\rm{ELM}}=\arg \min \limits _{{\varvec{\beta }} }\left\| {\mathbf{H}}{\varvec{\beta }}-{\mathbf{T}}\right\| _{2}^{2}, \end{aligned}$$
(3)

where \(\left\| \mathbf{.}\right\| _{2}^{2}\) denotes the \(L_{2}\)-norm.

In order to find the solution of Eq. (3), the classical inverse can be used if \({\mathbf{H}}\) matrix has full-column rank. In this case, \(\varvec{\ \beta }\) is estimated as \({\hat{\varvec{\beta }}}_{\rm{ELM}}=\left( {\mathbf{H}} ^{\rm{T}}{\mathbf{H}}\right) ^{-1}{\mathbf{H}}^{\rm{T}}{\mathbf{\rm{T}}}\).

2.2 The variants of ELM based on \(L_{1}\)- and \(L_{2}\)-Norms

In the presence of multicollinearity, H will not be full-column rank. The RR-ELM proposed by Li and Niu [25] as a solution of this problem has the closed-form solution

$$\begin{aligned} {\hat{\varvec{\beta }}}_{\rm{RR-ELM}}\varvec{=}\left( {\mathbf{H}}^{\rm{T}}\mathbf{ \ H+}k{\mathbf{I}}\right) ^{-1}{\mathbf{H}}^{\rm{T}}{\mathbf{T}}, \end{aligned}$$

where \({\mathbf{I}}\) is the identity matrix and \(k>0\) refers to the tuning parameter for RR-ELM

The \(L_{1}\) minimization of system (2) that Miche et al. [30, 31] presented is the solution of

$$\begin{aligned} {\hat{\varvec{\beta }}}_{\rm{Lasso-ELM}}\varvec{=}\arg \min \limits _{ {\varvec{\beta }}}\left\{ \left\| {\mathbf{H}}{\varvec{\beta }}-\mathbf{ \ T}\right\| _{2}^{2}+\lambda \left\| {\varvec{\beta }}\right\| _{1}\right\} , \end{aligned}$$

where \(\left\| \mathbf{.}\right\| _{1}\) denotes the \(L_{1}\)-norm and \( \lambda \) is the tuning parameter.

The elastic net is the solution of [30, 32]:

$$\begin{aligned} {\hat{\varvec{\beta }}}_{\rm{Enet-ELM}}\varvec{=}\arg \min \limits _{ {\varvec{\beta }}}\left\{ \left\| {\mathbf{H}}{\varvec{\beta }}-\mathbf{ \ T}\right\| _{2}^{2}+k\left\| {\varvec{\beta }}\right\| _{2}^{2}+\lambda \left\| {\varvec{\beta }}\right\| _{1}\right\} , \end{aligned}$$

where k and \(\lambda \) are the tuning parameters representing the size of \( L_{1}\)- and \(L_{2}\)-norms, respectively.

If the parameters of elastic net \(\left( k\text {~and}~\lambda \right) \) are tuned carefully, both more predictive and sparse results can be obtained than Lasso or ridge regression. One of the parameters which should be tuned in elastic net is the ridge tuning parameter \(\left( k\right) \). However, there is no consensus on the appropriate selection of k parameter. There has been an extensive study for determination of optimal \(\left( k\right) \) parameter. As a remedy of this problem, an alternative method called Liu estimator was proposed by Liu [27]. Similar to ridge regression, Liu can deal with multicollinearity problem by using a different parameter on the learning process. The difference between Liu and ridge is the form of tuning parameter. Although ridge includes a nonlinear form of k biasing parameter, Liu offers a linear form of its d parameter. The linear form makes Liu better and easier than ridge in terms of calculations and speed. Therefore, Liu estimator can be considered as an alternative to ridge in elastic net model. In this study, we propose a new regularization and variable selection method which is based on Liu and Lasso methods. In the following section, we present some details of Liu and the form of the proposed method called Liu–Lasso ELM (LL-ELM).

3 The proposed algorithm: LL-ELM

Liu and ridge deal with multicollinearity by shrinking coefficient with a tuning parameter and provide more stable and generalizable results than classical ELM model. Although both estimators are effective on accounting the variables with high correlations, Liu estimator is faster and easier than ridge in terms of selecting tuning parameters because of having linear form of tuning parameter. The objective function of Liu estimator can be defined as [55]

$$\begin{aligned} {{\displaystyle {\hat{\varvec{\beta }}}_{\rm{Liu-ELM}}\varvec{=}\arg \min \limits _{{\varvec{\beta }}}\left\{ \left\| {\mathbf{H}}\varvec{\beta }-{\mathbf{T}}\right\| _{2}^{2}+\left\| d{\hat{\varvec{\beta }}}_{\rm{ELM}}-\varvec{\beta }\right\| _{2}^{2}\right\} ,~0<d<1 }}, \end{aligned}$$
(4)

where d refers to the Liu tuning parameter. The solution of Eq. (4) is obtained in a closed form as follows:

$$\begin{aligned} {\hat{\varvec{\beta }}}_{\rm{Liu-ELM}}\varvec{=}\left( {\mathbf{H}}^{T}\mathbf{ \ H}\varvec{+I}\right) ^{-1}\left( {\mathbf{H}}^{T}{\mathbf{H}}\varvec{+} d{\hat{\varvec{\beta }}}_{\rm{ELM}}\right) ,~0<d<1. \end{aligned}$$

Similar to elastic net method, the solution of Eq. (4) can be obtained via an augmented data set, which is defined as follows:

$$\begin{aligned} \tilde{{\mathbf{H}}}=\left( {\begin{array}{c}{\mathbf{H}}\\ {\mathbf{I}}\end{array}}\right) \quad \text {and } {\tilde{\mathbf{T}}}=\left( {\begin{array}{c}{\mathbf{T}}\\ d{\hat{\varvec{\beta }}}_{\rm{ELM}}\end{array}}\right) . \end{aligned}$$
(5)

Then, the Liu estimator in Eq. (4) can be redefined in augmented form as

$$\begin{aligned} {\hat{\varvec{\beta }}}_{\rm{Liu-ELM}}\varvec{=}\arg \min \limits _{ {\varvec{\beta }}}\left\{ \left\| {\tilde{\mathbf{H}}}{\varvec{\beta }}- {\tilde{\mathbf{T}}}\right\| _{2}^{2}\right\} . \end{aligned}$$

When multicollinearity exists, the ELM estimates often have low bias but large variance, which results in prediction difficulty. Besides, when there exist a large number of nodes, interpolation problem occurs with the ELM estimates. Shrinkage estimation methods and variable selection methods are the standard techniques for improving the ELM in these cases. RR-ELM and Liu-ELM are such shrinkage estimation methods. Although RR-ELM and Liu-ELM give more stable results, they do not set any weight to zero and do not give an easily interpretable model. Lasso-ELM was proposed as a competitor to RR-ELM which shrinks some weights and sets others to zero. Similar to RR-ELM, Liu-ELM shrinks the weights, resulting in good prediction accuracy, but does not select weights; in other words, it does not set some weights to zero. To obtain more interpretable estimates, we here aim to combine the idea of Lasso-ELM and Liu-ELM and propose a new algorithm called Liu–Lasso ELM (LL-ELM). By inspiring the objective functions of Enet-ELM and Liu-ELM, the objective function of our proposed method is as

$$\begin{aligned} {\hat{\varvec{\beta }}}_{LL-ELM}\varvec{=}\arg \min \limits _{\varvec{ \ \beta }}\left\{ \left\| {\mathbf{H}}{\varvec{\beta }}-{\mathbf{T}} \right\| _{2}^{2}+\left\| d{\hat{\varvec{\beta }}}_{ELM}-\varvec{ \beta }\right\| _{2}^{2}+\lambda \left\| {\varvec{\beta }} \right\| _{1}\right\} . \end{aligned}$$
(6)

The objective function given by Eq. (6) is proposed in such a way that the new method has length closer to the true parameter vector than ELM and carries the properties of Enet-ELM. Furthermore, it has the sparsity property of Lasso in virtue of Eq.(6). The objective function given by Eq. (6) can also be defined with augmented form as:

$$\begin{aligned} {\hat{\varvec{\beta }}}_{LL-ELM}\varvec{=}\arg \min \limits _{\varvec{ \ \beta }}\left\{ \left\| {\tilde{\mathbf{H}}}{\varvec{\beta }}-\mathbf{\ \tilde{T}}\right\| _{2}^{2}+\lambda \left\| {\varvec{\beta }} \right\| _{1}\right\} . \end{aligned}$$
(7)

where \({\tilde{\mathbf{H}}}\) and \({\tilde{\mathbf{T}}}\) are defined in Eq (5) and \(\lambda \) is any fixed non-negative parameter.

By defining the proposed method (LL-ELM) in Eq. (7), the problem is reduced to a Lasso problem, so that similar to the approach of elastic net, LARS-EN algorithm [60] can be used to estimate the \({\varvec{\beta }}\) . In our study, we adopted the approach of Sjöstrand et al. [31] and LARS-EN algorithm with piecewise linear regularization path proposed by Rosset and Zhu [40]. For fixed d, LL-ELM problem is equivalent to a Lasso problem on the augmented data set. So LARS which is originally proposed by Efron et al. [11] and its variants can be directly used to compute the weights of LL-ELM.

In order to present the sparsity property of LL-ELM, a simple experiment has been carried out on the body fat data set which is also used in the experiment section. The solution paths of the coefficients (i.e., weights) of LL-ELM are given in Fig. 1 where s corresponds to the fraction of \(\ L_{1}\)-norm of coefficients \(\left( s\right) \) which is defined as \(\left\| {\hat{\varvec{\beta }}}_{\rm{ELM}}\right\| /\max \left( {\hat{\varvec{\beta }}} _{\rm{ELM}}\right) \) and has a range in [0, 1]. The d tuning parameter and the number of hidden layer nodes have been arbitrarily selected as 0.5 and 20, respectively. The node number is deliberately chosen to be small for a better visuality. It is expected that the solution paths are piecewise linear because of the property of the LARS-EN algorithm which is explained by Zou and Hastie [60]. Figure 1 shows the points at which the variables enter into the model. Therefore, according to Fig. 1, it can be said that the proposed algorithm can be considered a beneficial tool to obtain sparse models. The following algorithm can be used for experiments:

Algorithm 1

LL-ELM.

Input: Training set \(\left\{ \left( x_{i},t_{i}\right) \right\} \), the maximum number of the hidden neurons\(\left\{ K\right\} \), an activation function \(\left\{ g\left( .\right) \right\} \), the number of trials \(\left\{ L\right\} .\)

Output: The \(\beta \) weight matrix.

1

Generate the initial parameters \({\mathbf{w}}_{i}\) and \(b_{i}\), \(1\le i\le K\), randomly.

2

Calculate the hidden layer output matrix \(\left\{ {\mathbf{H}}\right\} \) via Eq. (3)

 

and obtain the ELM solution.

3

Find the optimal Liu parameters \(\left\{ {\hat{d}}\text { }\right\} \) via Eq. (8) or

 

Eq. (9), respectively.

4

Solve the equation \({\varvec{\beta }}_{LL-ELM}\varvec{=}\arg \min \limits _{{\varvec{\beta }}}\left\{ \left\| {\tilde{\mathbf{H}}} {\varvec{\beta }}-{\tilde{\mathbf{T}}}\right\| _{2}^{2}+\lambda \left\| {\varvec{\beta }}\right\| _{1}\right\} \)

 

by using LARS-EN algorithm as \({\varvec{\beta }}=\)LARS-EN\(\left( {\tilde{H},\tilde{T},\hat{d}} \right)\)

5

for \(1\le t\le size\left( \beta \right) \) do

6

Calculate BIC\(\left( t\right) \) using each possible model using Eq. (10).

7

end

8

Find the \(t^{*}\) corresponding to the minimum BIC value among all

 

possible models of \(\beta \) vector.

9

Select the optimum weights vector as \(\beta _{Best}=\beta \left( t^{*}\right) \).

4 Parameter and model selection

As seen from Eq. (7) that LL-ELM depends on two tuning parameters d and \( \lambda \) and the objective function given by Eq. (7) is same with that of Lasso-ELM when d is fixed. Therefore, the method for the selection of \( \lambda \) can be same with that of Lasso-ELM when d is fixed. Since first two terms in Eq. (7) are same with that of Eq. (6) which corresponds to the objective function of Liu-ELM, the LL-ELM could follow with Liu-ELM for the initialization of tuning parameter d.

Fig. 1
figure 1

The coefficient estimates of LL-ELM based on the range of s

Full size image

It is clear that the selection of Liu tuning parameter is effective on the performance of Liu-ELM and LL-ELM. In the context of ELM, Yıldırım and Özkale [55] proposed the following methods:

$$\begin{aligned} {\hat{d}}_{1}=1-{\hat{\sigma }}^{2}\left[ \left( \sum \limits _{i=1}^{K}\frac{1}{ \lambda _{i}\left( \lambda _{i}+1\right) }\right) /\left( \sum \limits _{i=1}^{K}\frac{{\hat{\alpha }}_{i}^{2}}{\left( \lambda _{i}+1\right) ^{2}}\right) \right] \end{aligned}$$
(8)

and

$$\begin{aligned} {\hat{d}}_{2}=1-{\hat{\sigma }}^{2}\left[ \left( \sum \limits _{i=1}^{\tilde{N}} \frac{1}{\left( \lambda _{i}+1\right) }\right) /\left( \sum \limits _{i=1}^{ \tilde{N}}\frac{\lambda _{i}{\hat{\alpha }}_{i}^{2}}{\left( \lambda _{i}+1\right) ^{2}}\right) \right] , \end{aligned}$$
(9)

where \(\lambda _{1},\lambda _{2},...,\lambda _{K}\) correspond to the eigenvalues of the \({\mathbf{H}}^{\rm{T}}\mathbf{H\ }\)matrix. \({\hat{\alpha _{i}}}\) is the ith element of \(\widehat{\alpha }={\mathbf{P}}^{\rm{T}}{\hat{\varvec{\beta }}}_{\rm{ELM}}\) and \({\mathbf{P}}_{KxK}\) is the orthogonal matrix whose columns are the eigenvectors of \({\mathbf{H}}^{T}{\mathbf{H}}\). \({\hat{\sigma }}^{2}\) is the estimate of the variance of residuals which are the residents between actual and model output values. Yıldırım and Özkale [55] presented \({\hat{d}}_{1}\) as the minimizer of the scalar mean square error of \( {\hat{\varvec{\beta }}}_{Liu-ELM}\) and \({\hat{d}}_{2}\) as the minimizer of the \(C_{p}\) statistic under \({\hat{\varvec{\beta }}}_{Liu-ELM}\) which was defined as

$$\begin{aligned} C_{p}=\frac{\rm{SS}_{{\rm{Re}}s,d}}{{\hat{\sigma }}^{2}}+2\rm{tr}\left( {\mathbf{M}}_{d}\right) -(n-2), \end{aligned}$$

where \(M_{d}={\mathbf{H}}\left( {\mathbf{H}}^{\rm{T}}{\mathbf{H}}+I\right) ^{-1}\left( {\mathbf{H}}^{\rm{T}}{\mathbf{H}}+\rm{d}I\right) \left( {\mathbf{H}}^{T}{\mathbf{H}}\right) ^{-1}{\mathbf{H}}^{T}\) is the quasi-projection matrix and \(\rm{SS}_{{\rm{Re}}s,d}\) is the residual sum of squares using \({\hat{\varvec{\beta }}}_{\rm{Liu-ELM}}\).

In Liu-ELM, \({\hat{d}}_{1}\) and \({\hat{d}}_{2}\) values given in Eq. (8) and Eq. (9) are obtained using training data and used for measuring testing performance. For the proposed algorithm (LL-ELM), same \({\hat{d}}_{1}\) and \( {\hat{d}}_{2}\) values with Liu-ELM can be used for the initial parameters. For each fixed \({\hat{d}}_{1}\) and \({\hat{d}}_{2}\), the \(\lambda \) parameter is needed to be tuned carefully. There are various ways like AIC, BIC and CV to determine it. All of these methods have been widely used in the literature. Among these methods, BIC tends to produce more parsimonious models (i.e., more compact). This property of BIC may guarantee an optimal model instead of underfitted or overfitted one. The optimal \(\lambda \) value is determined via BIC, which is defined as follows:

$$\begin{aligned} \varvec{BIC}_{t}\varvec{=}\left\| {\mathbf{T}}-{\mathbf{H}} {\varvec{\beta }}_{t}\right\| _{2}^{2}+\log \left( N\right) {\hat{\sigma }} ^{2}L_{t}, \end{aligned}$$
(10)

where \({\varvec{\beta }}_{t}\) is the tth model obtained with each possible combination of \(\left( d,\lambda \right) \), N is the size of training set, \({\hat{\sigma }}^{2}\) is mean of squares of residuals and \(L_{t}\) is the number of positive elements in \({\varvec{\beta }}_{t}\) vector. The \( \left( d,\lambda \right) \) combination providing minimum BIC value is selected for each d value, and an overall examination among all \(\left( d\right) \) values is carried out. The best \(\left( d,\lambda \right) \) pair is selected for final model and used for obtaining testing results.

5 Experimental study: real data sets

In this section, a performance comparison has been carried out on several benchmark data sets to investigate the effectiveness of the algorithms. All data sets have been obtained from UCI repository [13] and standardized to have zero mean and unit variance. For LL-ELM, the effect of standardization is to avoid from the adverse effect of magnitude of each variable and to get more reasonable constraints which is also effective on the performance of the model. Standardization has a common usage for training Lasso-based models. That is why, it is deliberately preferred not to use the data sets including mostly categorical variables for testing LL-ELM algorithm and is aimed to compare the algorithms under same conditions which they are firstly proposed. Also, it is assumed that the dependent variable spans sufficient enough through the attribute space. The properties of data set are given in Table 1.

Table 1 The properties of data sets used in this study
Full size table

Both hold-out and k-fold cross-validation approaches have been separately conducted to validate the efficiency of the algorithms. For hold-out approach, each data set is split into training and testing data sets with the ratios 70 and 30%, respectively. On the other side, fivefold CV is applied for k-fold CV approach. Twenty trials have been conducted to eliminate the randomness effect of initial parameters assignments. The initial number of the hidden layer nodes is fixed as 100, and sigmoid activation function is used for all data sets and experiments.

The experiments have been carried out via R software. In order to train LL-ELM, ELM variants based on Lasso and elastic net algorithms, LARS-EN algorithm with piecewise linear regularization path proposed by Rosset and Zhu [40] has been used. All coding processes of each algorithm have been carried out from scratch in the R platform.

In Lasso-ELM, instead of tuning \(\lambda \), it is suggested to use the fraction of \(\ L_{1}\)-norm of coefficients \(\left( s\right) \) which is defined as \(\left\| {\hat{\varvec{\beta }}}_{\rm{ELM}}\right\| /\max \left( {\hat{\varvec{\beta }}}_{\rm{ELM}}\right) \). Here, \(\max \left( {\hat{\varvec{\beta }}}_{\rm{ELM}}\right) \) actually corresponds to the ELM solution which is the \(L_{1}\)-norm of low-bias model solution. From the point of optimization perspective, there is a \(\lambda \) value corresponding to each s value and the solutions obtained via any form of this optimization problem are exactly the same each other. In other words, the \( {\hat{\varvec{\beta }}}\) solution corresponding to any \(\lambda \) value in Lagrangian form solves the problem which has the bound of \(s=\left\| {\hat{\varvec{\beta }}}_{\lambda }\right\| \). The advantage of s over \( \lambda \) is to have values within \(\left[ 0,1\right] \). Similar to the process in LL-ELM, BIC is used to determine optimal s value by using fixed \({\hat{d}}_{1}\) and \({\hat{d}}_{2}\) parameters as initial parameters. On the other hand, the ridge tuning parameter k is selected from the sequence of \(\left( 10^{-15},10^{-14},...,10^{1}\right) \). In RR-ELM, the k value minimizing the training error is used to obtain training and testing results. In order to get the ELM results based on elastic net, for each fixed k value, the optimal s value minimizing BIC is calculated and the \(\left( k,s\right) \) values giving the global minimum among all possible combinations are used for the final model’s performance.

In addition to the performance results of each algorithm, the optimal parameters for both hold-out and fivefold CV approaches are presented in Table 2. In Table 2, the third and fourth columns correspond to the average d values and their standard deviations which are calculated based on all trials. The k and s columns refer to the best parameters corresponding to the optimal \(\left( k,s\right) \) or \(\left( d,s\right) \) combination giving the overall minimum value of BIC. In the last column, the mean node number throughout all trials is reported.

Table 2 The results of optimal tuning parameters for each algorithm
Full size table
Table 3 Comparison of all algorithms in terms of training and testing RMSE
Full size table

When the sparsity results are examined, Lasso-ELM and Enet-ELM generally give more parsimonious models than LL-ELM. For bank domains and abalone data, LL-ELM based on \({\hat{d}}_{2}\) provides more sparse models. Table 3 shows the training and testing results of all algorithms based on data sets given in Table 1. The training and testing performance with their standard deviations is calculated by taking the averages of 20 trials. Based on the results for hold-out approaches in Table 3, the following interpretations can be said:

  • LL-ELM for at least one Liu tuning parameter overperforms to all algorithms in terms of training performance except bank domains data set.

  • According to the testing RMSE values, the proposed algorithm with \( {\hat{d}}_{1}\) parameter is more generalizable than other algorithms for body fat and energy data sets. Similarly, LL-ELM is seen as stable in terms of standard deviation of testing performance. It provides best results for body fat and bank domains data sets. Liu-ELM is better than LL-ELM in terms of testing performance for fish, bank domains and abalone data sets. Additionally, Liu-ELM and LL-ELM are compared based on 100 trials with the random assignments of Liu tuning parameters within range \(\left[ 0,1 \right] \), and the results are given in Fig. 1. In Fig. 1, it is seen that there is at least one Liu tuning parameter where LL-ELM overperforms Liu-ELM for all data sets except Bank Domains.

On the other side, fivefold CV approaches contribute some additional insights about the performances of the proposed algorithms. These insights can be listed as follows:

  • Considering LL-ELM and Liu-ELM in all data sets, there is one d value which gives better fivefold CV results in terms of either RMSE or SD than hold-out results.

  • In all data sets, fivefold CV results for LL-ELM according to \(d_{1}\) give higher reduction rate in testing RMSE values than Lasso-ELM and Enet-ELM when compared to hold-out results. Additionally, this is also true for the SD criterion with one exception of Lasso-ELM results for Bank Domains data set.

  • In all data sets, according to SD criterion, LL-ELM for \(d_{2}\) gives better reduction rate values than ELM and RR-ELM in fivefold CV criterion than hold-out criterion.

Table 4 Norm comparison of Liu-ELM and LL-ELM algorithms
Full size table

In order to present an insight into the regularization level of each algorithm, the norm values of coefficients obtained via Liu-ELM and LL-ELM are calculated for these data sets and are given in Table 4. Although Liu-ELM has lower testing RMSE value, the mean norm value for Liu-ELM is higher than that for LL-ELM for all data sets for both hold-out and fivefold CV approaches. This means that the proposed algorithm shrinks more severe than Liu-ELM.

Fig. 2
figure 2

The performance comparison of Liu-ELM and LL-ELM based on random biasing parameter

Full size image

6 Discussion and conclusions

In this paper, we proposed a novel regularization and variable selection algorithm to improve the conventional extreme learning machine and its variants. The proposed algorithm combines the benefits of Liu and Lasso regression methods to deal with the drawbacks of ELM like the instability, poor generalizability and under or overfitting problems. The experimental studies based on both hold-out and k-fold cross-validation approaches show that LL-ELM generally improves the training and testing performance of ELM and overperforms the well-known competitors. It is seen that LL-ELM has a notable shrinkage property compared with other algorithms, particularly Liu-ELM. Although LL-ELM does not carry out a hard variable selection (i.e., node selection) process like Lasso or elastic net, the level of shrinkage with an amount of sparsity is better to give good generalization performance. The norm of estimated coefficients is lower than other algorithms. This means that LL-ELM may guarantee lower norm estimated which can provide more stable and accurate results in terms of generalization performance. It should be noted that the level of LL-ELM’s sparsity property can be improved by considering alternative ways of parameter selection methods. Besides, the proposed algorithm is a tool for both regressional and classification tasks in data-oriented studies.

The limitation LL-ELM is that it cannot be applied to high-dimensional data. Therefore, our next study will focus on solving this limitation.