Plant intelligence based metaheuristic optimization algorithms

Abstract

Classical optimization algorithms are insufficient in large scale combinatorial problems and in nonlinear problems. Hence, metaheuristic optimization algorithms have been proposed. General purpose metaheuristic methods are evaluated in nine different groups: biology-based, physics-based, social-based, music-based, chemical-based, sport-based, mathematics-based, swarm-based, and hybrid methods which are combinations of these. Studies on plants in recent years have showed that plants exhibit intelligent behaviors. Accordingly, it is thought that plants have nervous system. In this work, all of the algorithms and applications about plant intelligence have been firstly collected and searched. Information is given about plant intelligence algorithms such as Flower Pollination Algorithm, Invasive Weed Optimization, Paddy Field Algorithm, Root Mass Optimization Algorithm, Artificial Plant Optimization Algorithm, Sapling Growing up Algorithm, Photosynthetic Algorithm, Plant Growth Optimization, Root Growth Algorithm, Strawberry Algorithm as Plant Propagation Algorithm, Runner Root Algorithm, Path Planning Algorithm, and Rooted Tree Optimization.

1 Introduction

Most of the optimization algorithms need mathematical models for system modelling and objective function. Establishment of a mathematical model is mostly hard for complex systems. Even though the model is established, it cannot be used due to high cost of solution time. Classical optimization algorithms are insufficient in large-scale combinational and non-linear problems. Such algorithms are not effective in adaptation a solution algorithm for a given problem. In most cases, this requires some assumptions whose approval of validity can be difficult. Generally, because of natural solution mechanism of classical algorithms, significant problem is modeled the way that algorithm can handle it. Solution strategy of classical optimization algorithms generally depends on type of objective and constraints (linear, non-linear etc.) and depends on type of variables (integer, real) used in modelling of problem. Furthermore, effectiveness of the classical algorithms highly depends on solution space (convex, non-convex etc.), the number of decision variable, and the number of constraints in problem modelling.

Another important deficiency is that; if there are different types of decision variables, objectives, and constraints, general solution strategy is not presented for implemented problem formulation. In other words, most of algorithms solve models which have certain type of object function or constraints. However, optimization problems in many different areas such as management science, computer, and engineering require concurrently different types of decision variables, object function, and constraints in their formulation. Therefore, metaheuristic optimization algorithms are proposed. These algorithms become quite popular methods in recent years, due to their good computation power and easy conversion. In other words, a metaheuristic program, written for a specific problem with a single objective function, can be adapted easily to a multi objective version of this problem or a different problem.

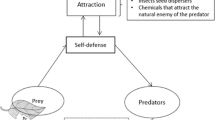
Studies in recent years indicate that plants also exhibit intelligent behaviors. According to this, it is thought that plants have nervous system. For example, in roots, imported light and poison information are transmitted to growth center in root tips and the roots perform orientation according to that. Additionally, it is thought that plants make contact with external world using electric current. An example for this is defense mechanism which is shown against to aphid or caterpillar by plants. After the first developed attack, plants produce secretions which can make worse taste or which can poison their enemy.

Inspiring by the flow pollination process of flowery plants, Flower Pollination Algorithm (FPA), has been developed in 2012 by Yang (2012). Invasive Weed Optimization (IWO), inspired from the phenomenon of colonization of invasive weeds in nature, has been proposed by Mehrabian and Lucas (2006). It is based on ecology and weed biology. Paddy Field Algorithm (PFA), which simulates growth process of paddy fields, is another plant based metaheuristic algorithm and has been proposed by Premaratne et al. (2009). Root Mass Optimization (RMO) is based on the process of root growth and has been proposed by Qi et al. 2013. Artificial Plant Optimization Algorithm (APOA) simulates growth model of plants which includes photosynthesis and phototropism mechanism (Zhao et al. 2011). Sapling Growing up Algorithm (SGuA) is a computational method based on cultivating, growing up, and mating of saplings and it is developed for efficient solutions to search and optimization problems (Karci 2007a).

Photosynthetic Algorithm (PA) is based on the processes of Calvin–Benson cycle and photorespiration cycle for the plants (Murase 2000). Plant Growth Optimization (PGO) is proposed to simulate plant growth with a realistic way considering the spatial occupancy, account branching, phototropism, and leaf growth. The main purpose of the model is to select active point by comparing the morphogen concentration for increasing the L-system (Cai et al. 2008). Root Growth Algorithm (RGA) is another plant based metaheuristic algorithm and simulates root growth of plants based on L-system (Zhang et al. 2014).

Strawberry algorithm has been proposed as an exemplar of Plant Propagation Algorithm (PPA). It maps an optimization problem onto survival optimization problem of strawberry plant and adopts strategy of survival in the environment for searching points in the search space which give the best values and ultimately the best value (Salhi and Fraga 2011). Runner Root Algorithm (RRA) is inspired by plants such as strawberry and spider plants which are spread through their runners and also which develop roots and root hairs for local search for minerals and water resources (Merrikh-Bayat 2015). Path Planning Algorithm is based on plant growth mechanism (PGPP) which uses phototropism, negative geotropism, apical dominance, and branching as basic rules (Zhou et al. 2016). One of the most recent plant based algorithm is Rooted Tree Optimization (RTO) and it is based on the intelligent behaviors of roots which select their orientation according to the wetness (Labbi et al. 2016). Researches about new versions and applications of these algorithms incrementally continue.

In this work, in the second part, the information is given about metaheuristic optimization and it is mentioned that why metaheuristic algorithms are needed. In the third part, plant intelligence is mentioned; optimization algorithms developed inspired by plant intelligence are examined and related works with these algorithms are described. FPA, IWO, PFA, RMO Algorithm, APOA, SGuA, PA, PGO, RGA, Strawberry Algorithm as PPA, RRA, PGPP, and RTO are explained. In the fourth part, discussions about general evaluations of these algorithms are presented and in the fifth part, the work is concluded along with future works.

2 Metaheuristic optimization

In most of the real life problems, solution space of the problem is infinite or it is too large for assessment of all the solutions. Therefore, with evaluating solutions, a good solution is needed to be found in acceptable time. Actually, for such problems, evaluating solutions in acceptable time has the same meaning with evaluating “some solutions” in the whole solution space. Selection of some solutions depending on what and how they are selected changes according to metaheuristic method. It cannot be guaranteed that optimal solution is included in the solutions which get involved in the evaluation. Therefore, the solution, proposed by metaheuristic methods for an optimization problem, must be perceived as a good solution, not as an optimal solution (Cura 2008).

They are criteria or computer methods identified in order to decide effective ones of various alternative movements for achieving any purpose or the goal. Such algorithms have convergence property, but they cannot guarantee exact solution, they can only guarantee a solution which closes to exact solution.

The reasons of why metaheuristic algorithms are needed are as follows:

• (a) Optimization problem can have a structure that the process of finding the exact solution cannot be defined

• (b) Metaheuristic algorithms can be much simpler from the point of decision maker, in terms of comprehensibility.

• (c) Metaheuristic algorithms can be used as a part of process of finding the exact solution, and learning purpose.

• (d) Generally, the most difficult parts of real world problems (which purposes and which restrictions must be used, which alternatives must be tested, how problems data must be collected) are neglected in the definitions made with mathematical formulas. Faultiness of the data used in process of determining model parameters can cause much larger errors than sub-optimal solution produced by metaheuristic approach (Karaboğa 2011).

General purposed metaheuristic methods are evaluated in eight different groups which are biology based, physic based, swarm based, social based, music based, chemistry based, sport based, and math based. Furthermore, there are hybrid methods which are combination of these. These mentioned methods are presented in Fig. 1. Genetic Algorithm (GA) (Holland 1975), differential evolution algorithm (Storn and Price 1995), and biogeography-based optimization (Simon 2008) are biology based; parliamentary optimization algorithm (Borji 2007), teaching-learning-based optimization (Ghasemi et al. 2015; Rao et al. 2011), and imperialist competitive algorithm (Atashpaz-Gargari and Lucas 2007a, b; Ghasemi et al. 2014) are social based; artificial chemical reaction optimization algorithm (Alatas 2011a) and chemical reaction optimization (Lam and Li 2010) are chemistry based; harmony search algorithm (Geem et al. 2001) is music based; gravitational search algorithm (Rashedi et al. 2009), intelligent water drops algorithm (Shah-Hosseini 2009), and charged system search (Kaveh and Talatahari 2010) are physics based; Particle Swarm Optimization (PSO) algorithm (Kennedy and Eberhart 1995), cat swarm optimization (Chu et al. 2006), ant colony algorithm (Dorigo et al. 1991), monarch butterfly optimization (Wang et al. 2015), group search optimizer (He et al. 2006, 2009), and cuckoo search via Levy flights (Yang and Suash 2009) are swarm based; league championship algorithm (Kashan 2009) is sport based; and base optimization algorithm (Salem 2012), and Matheuristics (Maniezzo et al. 2009) are math based algorithms and methods. Cultural algorithm (Jin and Reynolds 1999) and colonial competitive differential evolution (Ghasemi et al. 2016) can be classified as both biology based and social based algorithm.

Although there are many successful search and optimization algorithms and techniques in the literature; design, development, and implementation of new techniques is an important task under the philosophy of improvement in the scientific field and always searching to design better. The best algorithm that gives the best results for all the problems has not yet been designed, that is why constantly new artificial intelligence optimization algorithms are proposed or some efficient additions or modifications have been performed to the existing algorithms.

Fig. 1

Metaheuristic methods

3 Plant intelligence optimization algorithms

As a result of previous studies, it is observed that plants have gender identity and immune system. Furthermore, recent studies show that plants exhibit intelligent behavior. According to this, it is thought that plants have nervous system. For example, in roots, imported light and poison data are transmitted to growth centers in root tips, and roots perform orientation according to this. As another consideration, plants are considered to be contacting with the external world by electric currents. Defense mechanism, which is shown against to aphid or caterpillar by plants, can be shown as an example for this. After the first attack takes place, plants will worsen their taste or produce secretions which can poison their enemy.

The metaheuristic optimization algorithms which are developed by inspiration from plant intelligence have been shown in Fig. 2 and explained in subsections.

Fig. 2

Plant intelligence metaheuristic optimization algorithms

3.1 Flower Pollination Algorithm (FPA)

3.1.1 Characteristic of flower pollination

It is estimated that, in nature, there are over a quarter of a million types of flowery plants. Approximately 80 % of all plant species are flowery plant. Flowery plants have been evolving for more than 125 million years. The main objective of a plant is reproducing through pollination. About 90 % of pollens are transferred by biotic pollinators such as animals and insects and about 10 % of pollens are transferred by abiotic pollinators such as wind. Biotic pollinators visit only some types of flowers. Therefore, pollen transfer of same types of flowers will be maximum. This provides advantages for pollinators in terms of research cost and limited memory. Focusing on some unpredictable but potentially more rewarding new flower species can give better results (Yang et al. 2013).

Pollination can be achieved by cross-pollination or self-pollination. Cross-pollination, or hybridization can occur from a flowers plant of a different plant. Self-pollination occurs from the same flowers pollen or different flowers of the same plant. Biotic cross-pollination can occur in long-distance, because of long distance flight of birds, bats, bees, etc. Thus, this is considered as global pollination. In addition to this, bees and birds are able to move with the Levy flight behavior (Yang et al. 2013).

3.1.2 FPA

FPA, inspired by the flow pollination process of flowery plants, was developed in 2012 by Yang (2012). The following 4 rules are used as a matter of convenience.

• (1) Biotic cross-pollination can be thought as global pollination process. Pollen-carrying pollinators move according to a Levy flight process (Rule 1).

• (2) Self-pollination and local pollination are used for local pollination (Rule 2).

• (3) Pollinators such as birds and bees can develop flower persistence (Rule 3).

• (4) A switch probability $p\in \left[ {0,1} \right]$, which is slightly biased towards local pollination, can control the switching or interaction of global and local pollination (Rule 4).

The above rules must be converted to appropriate updating equations for formulation of updating formulas. For example, flower pollen gametes are moved by pollinators such as birds and bees in the global pollination process. Pollen can be transferred over a long distance, because pollinators can often fly and move over a much longer range. Therefore, Rule 1 and Rule 3 (flower persistence) can be represented mathematically as (1).

$$\begin{aligned} x_i ^{t+1}=x_i ^{t}+\gamma L\left( \lambda \right) \left( {g_*-x_i ^{t}} \right) \end{aligned}$$

(1)

$x_i ^{t}$, is the pollen i, or $x_i$ solution vector in iteration t, $\gamma$ is a scale factor to control the step size. $L\left( \lambda \right)$ is the parameter corresponding to the pollination power, more specially it is the Levy-flights based step size, $g_*$ is the current best solution found among all solutions at the current iteration/generation. Levy flight can be used effectively to simulate pollinators’ movements (Yang et al. 2013).

$$\begin{aligned} L\sim \frac{\lambda \Gamma \left( \lambda \right) \sin \left( {\pi \lambda /2} \right) }{\pi }\frac{1}{s^{1+\lambda }},\left( {s\gg s_0 >0} \right) \end{aligned}$$

(2)

Here ${\Gamma }\left( \lambda \right)$ is the standard gamma function and this distribution is valid for large steps $s>0$. It must be $\left| {s_0 \gg 0} \right|$ in theory, but in practice, $s_0$ can be as small as 0.1. However, it is not trivial to generate pseudo-random step sizes which conform to the Levy distribution. There are a few methods for drawing these type pseudo-random numbers. One of the most efficient methods is using two Gaussian distributions U and V, which is the so-called Mantegna algorithm for drawing step size s.

$$\begin{aligned} s=\frac{U}{\left| V \right| ^{1/\lambda }},U\sim N\left( {0,\sigma ^{2}} \right) ,\quad V\sim N\left( {0,1} \right) \end{aligned}$$

(3)

In (3), $U\sim \left( {0,\sigma ^{2}} \right)$ means that the samples are drawn from a Gaussian normal distribution with a variance of $\sigma ^{2}$ and a zero mean. The variance can be calculated as (4) (Yang et al. 2013).

$$\begin{aligned} \sigma ^{2}=\left\{ {\frac{\Gamma \left( {1+\lambda } \right) }{\lambda \Gamma \left[ {\left( {1+\lambda } \right) /2} \right] }.\frac{\sin \left( {\pi \lambda /2} \right) }{2^{\left( {\lambda -1} \right) /2}}} \right\} ^{1/\lambda } \end{aligned}$$

(4)

This formula seems complicated, but for a given $\lambda$ value it is only a constant. For example, if $\lambda =1$, than the gamma functions become $\Gamma \left( {1+\lambda } \right) =1,\Gamma \left( {\left[ {1+\lambda /2} \right] } \right) =1$.

$$\begin{aligned} \sigma ^{2}=\left\{ {\frac{1}{1x1}.\frac{\sin \left( {\pi x1/2} \right) }{2^{0}}} \right\} ^{1/1}=1 \end{aligned}$$

(5)

It is proved mathematically that Mantegna algorithm can produce random samples which obey the required distribution (2) correctly (Yang et al. 2013).

Both of rules (2) and (3) can be represented as (6) for local pollination.

$$\begin{aligned} x_i ^{t+1}=x_i ^{t}+\in \left( {x_j ^{t}-x_k ^{t}} \right) \end{aligned}$$

(6)

Here $x_j ^{t}$ and $x_k ^{t}$ are pollens in different flowers of the same plant species. This essentially mimics flower constancy in a limited neighborhood. Mathematically, if $x_j ^{t}$ and $x_k ^{t}$ are selected from the same population or come from the same species; this equivalently becomes a local random walk if $\in$ is drawn from a uniform distribution in [0, 1].

In principle, flower pollination activities can occur both at local and global levels, at all scales. However, substantially, the flowers in the not-far-away or adjacent flower patches are more likely to be pollinated by local flower pollen than those far away. Therefore, value of the switch probability can be taken as $p=0.8$. The pseudo code of FPA is shown in Fig. 3.

3.1.3 Studies with FPA

Yang et al. (2013, (2014) used FPA for solving multi-objective optimization problems. Proposed algorithm was tested in multi-objective test functions and it has been seemed that this algorithm has a better convergence speed compared to other algorithms Lenin (2014) proposed a hybrid algorithm, which is a combination of chaotic harmony search algorithm and FPA, for solving reactive power dispatch problem. Standard FPA was integrated with the harmony search algorithm to improve the search accuracy .

Fig. 3

Pseudo code of FPA

Wang and Zhou (2014) proposed dimension by dimension improvement based FPA, for multi-objective optimization problem. They also applied local neighborhood search strategy in this improved algorithm for enhancing the local searching ability. Yang et al. (2013) indicated that, it is important to balance exploration and exploitation for any metaheuristic algorithm. Because, interaction of these two components could significantly affect the efficiency. Therefore, they studied FPA with Eagle Strategy.

Abdel-Raouf et al. (2014a) used FPA with chaos theory for solving definite integral. Additionally, they proposed a hybrid method which was a combination of FPA and PSO for improving search accuracy. They used it for solving constrained optimization problems (Abdel-Raouf et al. 2014b). They also proposed a new hybrid algorithm combined with FPA and chaotic harmony search algorithm, to solve Sudoku puzzles (Abdel-Raouf et al. 2014c). Sundareswaran et al. proposed a modification for steps of traditional GA, used for PVM inverter, by imitating flower pollination and subsequent seed production in plants (Sulaiman et al. 2014). Prathiba et al. set the real power generations using FPA, for minimizing the fuel cost, in economic load dispatch, which is the main optimization task in power system operation (Prathiba et al. 2014).

Łukasik and Kowalski (2015) studied FPA for continuous optimization and they compared solutions with PSO. Platt used FPA in the calculation of dew point pressures of a system exhibiting double retrograde vaporization. The main idea was to apply a new algorithmic structure in a hard nonlinear algebraic system arising from real-world situations (Platt 2014). Kanagasabai and RavindhranathReddy (2014) proposed a combination of FPA and PSO for solving optimal reactive power dispatch problem. Sakib et al. 2014 compared FPA with Bat Algorithm. They tested these two algorithms on both unimodal and multimodal, low and high dimensional continuous functions and they observed that FPA gave better results.

3.2 Invasive Weed Optimization (IWO)

3.2.1 The inspiration phenomenon

IWO, inspired from the phenomenon of colonization of invasive weeds in nature, is proposed by Mehrabian and Lucas (2006). IWO is based on ecology and weed biology. It was seemed that mimicking invasive weeds properties, leads a powerful optimization algorithm. In a cropping field, weed colonization’s behavior can be explained as follows:

Weeds invade a cropping system by the way of disperse. They occupy suitable fields between plants. Each invasive weed takes the unused resources in the field, and becomes a flowering plant, and produces new invasive weeds independently. Number of new invasive weed produced by each flowering herb depends on fitness of flowering plants in the colony. These weeds provide better adaptation to the environment and grow faster by taking more unused resources and produce more seeds. The new produced weeds randomly spread over the field and grow to flowering plants. This process continues until reaching the maximum number of weed in the field because of limited resources. Weeds with better fitness can only survive and can produce new plants. The competition between weeds causes them to become well adapted and evolved over time (Karimkashi and Kishk 2010).

3.2.2 Algorithm

The new key terms used for explaining this algorithm should be introduced, before considering the algorithm process. Some of these terms are shown in Table 1. Each individual or agent is called as a seed, or a set containing a value of each optimization variable. Each seed grows to a flowering plant in colony. The meaning of a plant is an individual or an agent after evaluating its fitness. Therefore, growing a seed to a plant corresponds to evaluating the fitness of an agent (Karimkashi and Kishk 2010).

Table 1 Some of the key terms used in IWO

For simulating the colonizing behavior of weeds following steps are accepted and flow-chart of the simulation is shown in Fig. 4.

• 1. Primarily, N parameters (variable) that need to be optimized must be selected. Then, in N-dimensional solution space, a maximum and a minimum value must be assigned for each of these variables (Defining the solution space) (Karimkashi and Kishk 2010).

• 2. A finite number of seeds are distributed randomly on the defined solution space. In another words, each seed randomly takes position in N-dimensional solution space. Position of each seed is an initial solution, which contains N values for the N variables, of optimization problem (Initializing a population).

• 3. Each of initial seed grows to a flowering plant. The fitness function, defined for representing goodness of the solution, returns a fitness value for each seed. Seed is called as a plant, after assigning the fitness value to the corresponding seed (Evaluate fitness of each individual) (Karimkashi and Kishk 2010).

• 4. Flowering plants are ranked according to fitness value assigned to them, before they produce new seeds. Then, each flowering plant produces seeds according to its ranking in the colony. In other words, the number of seed production of each plant depends on its fitness value or ranking and it increases from the minimum possible seeds ($S_{min})$ to maximum possible seeds ($S_{max})$. These seeds, which solve the problem better correspond the plants which are more adapted to the colony and therefore, they produce more seed. This step, by allowing all of the plants to participate in the reproduction contest, adds an important property to the algorithm (Ranking population and producing new seeds) (Karimkashi and Kishk 2010).

• 5. In this step, produced seeds are spread to location of produced plant with equal-average by normally distributed random numbers on the search space. At the present time step, the standard deviation (SD) can be expressed by (7).

  $$\begin{aligned} \sigma _{iter} =\frac{\left( {iter_{max} -iter} \right) ^{n}}{\left( {iter_{max} } \right) ^{n}}\left( {\sigma _{iinitial} -\sigma _{final} } \right) +\sigma _{final} \end{aligned}$$

  (7)

  Here, $iter_{max}$ is number of maximum iteration. $\sigma _{iinitial}$ and $\sigma _{final}$ are initial and final standard deviation respectively, and n is nonlinear modulation index. Algorithm starts with a high initial SD which can be explored by optimizer through the whole solution space. By increasing the number of iterations, for finding the global optimal solution, SD value is decreased gradually to search around the local minimum or maximum (Dispersion) (Karimkashi and Kishk 2010).

• 6. New seeds grow to flowering plant, after all seeds have found their positions on the search space, and then, they are ranked with their parents. The plants in low rankings in the colony are eliminated for reaching number of maximum plant in the colony ($P_{max} )$. The number of fitness evaluation, population size, is more than the maximum number of plants in the colony (Competitive exclusion) (Karimkashi and Kishk 2010).

• 7. Survived plants produce new seeds according to their ranking in the colony. The process is repeated at step 3, until the maximum number of iteration is reached or fitness criterion is met (Repeat) (Karimkashi and Kishk 2010).

Fig. 4

Flowchart of IWO algorithm

3.2.3 Selection of control parameter values

Three parameters among all parameters affect the convergence of the algorithm; initial SS, $\sigma _{iinitial}$, final SS, $\sigma _{final}$, and nonlinear modulation index, n, must be tuned carefully for obtaining proper value of SS in each iteration according to (7). A high initial standard deviation must be chosen aggressively for allowing algorithm to discover the whole search space.

3.2.4 Studies with IWO

Mallahzadeh et al. (2008) used IWO for antenna configurations. Feasibility, efficiency and effectiveness of algorithm were examined with a set of antenna configurations for optimization of antenna problems. Karimkashi and Kishk (2010) applied IWO for different electromagnetic problems. They used IWO in linear array antenna synthesis, in the design of aperiodic thinned array antennas, and U-slot patch antenna for desired dual-band characteristics. Rad and Lucas (2007) did work on recommender system which makes personalization according to features of user-profile. For each user, they used IWO to find the optimal priorities.

Roy et al. (2011) presented IWO for the design of non-uniform, planar, and circular antenna array which can achieve minimum side lobe levels for a specific first null beam width. For current application, they introduced more explorative routine which changes standard deviation of the seed population of classical IWO algorithm. Basak et al. (2010) used IWO to solve real parameter optimization problem which was related to design of time-modulated linear antenna arrays with Main Lobe Beam Width, ultra-low Side Lobe Level, and Side Band Level. They included properties to classical IWO which were two parallel populations and a more explorative routine of changing the mutation step-size with iterations. Monavar and Komjani (2011) proposed a new approach using Jerusalem cross-shaped frequency selective surfaces as an artificial magnetic ground plane, for improving the bandwidth of a micro-strip patch antenna. They used IWO to achieve optimal sizes of the JC_FSS element and the patch antenna.

Zaharis et al. (2012) introduced the improved adaptive beamforming technique of antenna arrays. This technique was implemented by IWO with adaptive dispersion. Unlike conventional IWO, seeds, produced by a weed, were distributed in the search space with a standard deviation, determined by fitness value of weed; and in this way they increased the convergence speed. Main purposes of Kostrzewa and Josiński (2009) study were to adapt the idea of the IWO to the problem of predetermining the progress of distributed data merging process, and to compare the results with the results obtained from evolutionary algorithm. Mehrabian and Yousefi-Koma (2007) developed a new approach for optimization of piezoelectric actuators in vibration suppression. They used IWO for maximizing of the frequency response function peaks, which reduced the vibration of smart fin. Ahmadi and Mojallali (2012) introduced a novel hybrid optimization algorithm using advantage of the stochastic properties of chaotic search and IWO. In order to deal with the weakness of conventional method, they presented chaotic IWO which incorporated the capabilities of chaotic search methods.

Nikoofard et al. (2012) presented a proposal for multi-objective IWO based on non-dominant solutions ranking. This proposed algorithm was evaluated through a number of well-known benchmarks for multi-objective optimization. Li et al. (2011) mentioned that there was no analytical formula for the Yagi-Uda antenna design. Therefore, for getting the highest directivity, they integrated full-wave solver with IWO to optimize the variable parameters of Yagi-Uda antenna. Pourjafari and Mojallali (2012) used IWO for solving non-linear equations systems and they could find all real and complex root of a system. Ghasemi et al. (2014) presented a chaotic IWO algorithm based on chaos theory. They investigated its performance for control variables of optimal power flow with non-smooth and non-convex generator fuel cost curves.

3.3 Paddy Field Algorithm (PFA)

PFA was proposed by Premaratne et al. (2009) in 2009. PFA is a novel biology based algorithm which simulates growth process of paddy fields. Multi-objective optimization problem is considered as the growth process of rice in the PFA. Standard paddy field process can be divided into five parts: initialization, selection, sowing, pollination, and distribution. Considering a terminating condition, these five parts generate a cycle. When stopping criterion is reached, the cycle is terminated. Most seed-producing plant has a chance to survive and to reproduce. The selected plant offers the best solution in multi-objective optimization problems. Standard PFA was proposed to solve multi-objective optimization problem (Premaratne et al. 2009).

When seeds are sowed in a non-uniform area, the fertile soil and soil moisture have an effect on the growth of seeds. The seeds, which fall on the area with fertile soil and soil moisture, grow as the best plants which produce most seed. When seeds grow to plant, pollination affects reproduction. Generally, the pollen carried by the wind is related with population density. High population density of plants gets more pollen and produces more seeds. Highest seed-producing plants are considered as the optimal solution of the optimization problem. PFA simulates the growth process of paddy field; candidate solutions make growth towards optimal solution. PFA is similar to GA, but it does not mean that there are cross-over between individuals. Therefore, it is easy to direct PFA by the programs. The flowchart of PFA is shown in Fig. 5 (Premaratne et al. 2009; Wang et al. 2011).

Fig. 5

Flowchart of PFA

PFA works on principle of reproduction based on proximity to the general solution and population density similar to the plant population (Premaratne et al. 2009).

Assume that fitness function $y=f\left( x \right)$, $x=\left[ {x_1 ,x_2 ,\ldots ,x_n } \right]$. Each vector $x=x_i$ is known as a seed or a plant, and its fitness value can be represented by y. Each dimensionality of seed must be in the range of $x_j \in \left[ {a,b} \right]$.

Standard PFA, which simulates growth process, contains five main parts. These five main parts are: initiation, selection, sowing, pollination, and distribution. Bad seeds are eliminated at the end of an iteration count. After the good seeds are stored, better seeds are produced. Candidate solutions move toward the optimal solution during the cycle (Premaratne et al. 2009).

Step 1 Initialization

Each seed in the standard PFA represents a candidate solution. In a multi-objective optimization problem, seed is a vector. Algorithm initially works by distributing seeds randomly in the parameter space, to keep the seed variety (Premaratne et al. 2009).

Step 2 Selection

PFA is similar to GA. During evolution, populations, which cannot adapt to the environment, are eliminated. Generally, an objective function of a multi-objective problem is seen as a fitness function. After calculating fitness value of each seed, the best plants are selected according to a threshold value. nth most appropriate individual can be selected as the threshold operator. Plants will be eliminated whose fitness value is lower than the threshold value (Kong et al. 2012).

Step 3 Sowing

Seeds are distributed randomly and the soil is non-uniform; therefore some lucky seeds are growing with fertile soil and good drainage. The probability of producing more seeds is high. Seeds in the best location would be the best plants which produce the most amounts of seed and expressed as $q_{max}$. Therefore, fitness value can be associated with production capacity of plants. Greater fitness value means plants produce more seeds. The total amount of seeds produced by plants can be expressed as a function associated with fitness of plant and maximum number of seeds:

$$\begin{aligned} s=q_{max} *\left[ {\frac{y-y_t }{y_{max} -y_t }} \right] \end{aligned}$$

(8)

$y_{max}$ is the maximum fitness value, y indicates fitness value of each seed, and $y_{t}$ is the most appropriate nth individual selected as the threshold value (Kong et al. 2012).

Step 4 Pollination

Seed is available only if it is pollinated. Pollination depends on density of population. The neighbors’ number of a plant can indicate the density of population. Therefore, the number of active seed produced by a plant can be expressed as:

$$\begin{aligned} S_v =U*s \end{aligned}$$

(9)

where $0\le U\le 1$ and $u\left( {x_j ,x_k } \right) =\Vert x_j -x_k\Vert -a<0$ (Kong et al. 2012).

To obtain the number of neighbors of a plant, a sphere of radius a is used. Two plants such as $x_j$ and $x_k$ will be neighbors if they are in the sphere, and thus, neighbors’ number of each plant $v_j$ can be determined. The maximum neighbors’ number of the plant in the population can be expressed as $v_{max}$ (Kong et al. 2012).

After calculating the number of neighbors for each individual and the maximum neighbors’ number of the best plant, pollination factor for this plant can be obtained as:

$$\begin{aligned} U_j =e^{\left| {\frac{v_j }{v_{max} }-1} \right| } \end{aligned}$$

(10)

Step 5 Distribution

The new seed can be distributed according to a Gaussian distribution, and the cycle starts again from the selection process.

$$\begin{aligned} X_{seed}^{i+1} =N\left( {x^{i},\delta } \right) \end{aligned}$$

(11)

Gaussian distribution is determined by average and variance. In PFA, $v_i$ represents average, $\delta$ is often coefficient of experimental set emission. During the emission, according to a Gaussian distribution, a $v_i$ plant produces $S_v$ vector. Thus, $X_{seed}^{i+1}$ is a matrix. The number of lines is determined by the number of viable seeds of each plant ($S_v )$, and the number of columns is determined by the size of a plant. Distribution process, if the best plant corresponds to a local optimum, provides to drop distributed seeds into the parameter space corresponding to the general optimum. Older plants selected in the selection process and new plants produced in the distribution process create new generations. Then, the cycle continuous until the termination conditions are achieved (Premaratne et al. 2009).

3.3.1 Studies with PFA

Kong et al. (2012) reported that when the number of solutions was over the range in PFA, due to executing a lot of redundant iterations, the efficiency of algorithm became low. Therefore, they proposed a hybrid algorithm composed by PFA and Pattern Search Algorithm. Final results were found by pattern search based on the result of PFA. Wang et al. (2011) proposed PFA for the selection of Radial Basis Functions neural network center parameters. Cheng et al. (2011) used PFA for designing of PID controller of a high-order system.

3.4 Plant Root Growth

3.4.1 Root Mass Optimization (RMO) Algorithm

Root growth offers a great inspiration to propose a novel optimization algorithm. The objective function is considered as growth environment of the plant roots. The apices of the initial root forms a root mass. Each root apex can be considered as a solution of the problem. The roots turn the direction where provides optimal soil, water, and fertilizer conditions; thus they can reproduce. This process can be simulated as an optimizing process in the soil replaced with an objective function. According to this view, Qi et al. (2013) proposed RMO algorithm.

Some rules make improvements in the root growth behavior of RMO:

• (1) All root apices forms a root mass. Two operators, including the root regrowth and the root branching, need to improve root growth behavior. Each root apex grows using one of these two operators.

• (2) Root mass are divided into three groups according to their fitnesses. The group with better fitness is called as re-growing group. The group with worse fitness, called as stop group, stops growing. The group, remaining from the root mass, is called as branching group. The meaning of the two operators, including root growth and root branching, are listed below (Qi et al. 2013).

  • (a) Root Growth: This operator means root apex growth in the original direction. The root apex can migrate to the best position where provides the optimal soil water and fertilizer conditions. This operator can be formulated using (12).

    $$\begin{aligned} n_i =x_i +r+\left( {g_{best} -x_i } \right) \end{aligned}$$

    (12)

    r is a random vector whose each element is in the range of [1, 1]. $n_i$ is the new location of the ith root apex. $x_i$ is the original position of the ith root apex. $g_{best}$ is the root apex with the best fitness in each generation (Qi et al. 2013).

  • (b) Root Branching: This operator means that root apex produces a new growth point instead of growing along the original direction. The growth point can be produced with a random angle $\beta$, in a random position of original root. This operator can be formulated using (13).

    $$\begin{aligned} n_i =\beta \alpha x_i \end{aligned}$$

    (13)

    $\alpha$ is a random number in the range of [0,1]. $n_i$ is the new position of ith root apex. $x_i$ is the original position of ith root apex. $\beta$ can be calculated using (14).

    $$\begin{aligned} \beta =\lambda \Big /\sqrt{\lambda _i ^{T}\lambda _i } \end{aligned}$$

    (14)

    $\lambda _i$ is a random vector (Qi et al. 2013).

The pseudo code of RMO is listed in Fig. 6. In each generation, root apices are ranked in descending order. The selection of the root apices which will participate in the next generation uses linear descending path according to (15). This way makes a better root growth or root branching with better fitness performance and inhibits the growth of the bad ones. In the selection process, a percentage of root apices is selected from the front and these root apices (growing group) are allowed to grow using the root growth operator; the remaining part of the root apices (branching group) branches using the root branching operator (Qi et al. 2013).

$$\begin{aligned} ratio=sRatio-\left( {sRatio-eRation} \right) \frac{eva}{mEva} \end{aligned}$$

(15)

eva is number of current function evaluation and mEva is maximum number of function evaluation. sRatio is the initial percentage and eRation is the final percentage (Qi et al. 2013).

Fig. 6

The pseudo code of RMO

3.5 Artificial Plant Optimization Algorithm (APOA)

3.5.1 Main method

An important issue for simulating phenomena of plant growth is to peer this process into the optimization problem. Light intensity which guides to search direction in the problem space can be seen as fitness value due to guiding growth direction of plants and supplying significant energy by photosynthesis. Furthermore, a point can be seen as a branch and search strategy can be considered as growing curve. Because this new algorithm simulates growth model of plants which includes photosynthesis and phototropism mechanism, it is called briefly as APOA (Zhao et al. 2011).

Basic APOA pseudocode is given in Fig. 7.

Fig. 7

Basic APOA pseudocode

3.5.2 Photosynthesis operator

Photosynthesis is a process which converts carbon dioxide to organic compounds (especially sugar) using the energy from sunlight. Photosynthesis occurs from algae in plants. Photosynthetic organisms are called as photoautotrophs as long as they established their own food. In plants and algae, photosynthesis uses carbon dioxide and water; it produces oxygen as a waste product.

Photosynthesis is vital for all aerobic life on Earth. In addition to maintaining the normal oxygen level in the atmosphere, almost all life is dependent to photosynthesis directly as an energy source or indirectly as an ultimate energy source of their food (chemoautotroph living in rock or around the deep-sea hydrothermal vents) (Zhao et al. 2011).

Because of being different fitness value range for each branch, to avoid confusion, predefined [0, 1] range is required. (16) is designed to narrow this field:

$$\begin{aligned} Score_u \left( t \right) =\frac{f\left( {x_u \left( t \right) } \right) -f_{worst} \left( t \right) }{f_{best} \left( t \right) -f_{worst} \left( t \right) } \end{aligned}$$

(16)

where $f_{worst} \left( t \right)$ and $f_{best} \left( t \right)$ are the worst and the best original light intensity at time t, respectively, $f\left( {x_u \left( t \right) } \right)$ denotes the branch u’s original light intensity (Zhao et al. 2011).

Photosynthesis rate plays an important role in measuring how much energy is produced. Until today, many models have been proposed such as rectangular hyperbolic model, and non-rectangular hyperbolic model. As the most important model, rectangular hyperbolic model is used successfully and extensively to simulate photosynthesis rate. For instance, rectangular hyperbolic model is used to measure the energy received for each branch.

$$\begin{aligned} PR_u \left( t \right) =\frac{\alpha Score_u \left( t \right) \cdot P_{max} }{\alpha Score_u \left( t \right) +P_{max} }-R_d \end{aligned}$$

(17)

where $PR_u \left( t \right)$ represents photosynthesis rate of u branch at time t, $Score_u \left( t \right)$ represents the light intensity, $\alpha$ is the initial quantum efficiency, $P_{max}$ is the maximum net photosynthetic rate, and $R_d$ is dark respiration rate. $\alpha$, $P_{max}$, and $R_d$ are three parameters which control the size of the photosynthesis rate (Zhao et al. 2011).

In each iteration, all branches grow with the energy obtained from photosynthesis according to (17). Steps of photosynthesis operator are listed as shown in Fig. 8 (Zhao et al. 2011).

Fig. 8

Steps of photosynthesis operator in APOA

3.5.3 Phototropism operator

Phototropism is usually seen in plants, but also can occur in other organisms like fungi. The cells on the plants far from the light, have a chemical that reacts when phototropism occurs. Therefore plants have elongated cells on the farthest side from the light. Phototropism is one of the tropism or movements that plants respond to external stimuli. Growth away from light is called as negative phototropism and growth towards a light source is a positive phototropism. Most plants exhibit positive phototropism, while their roots usually exhibit negative phototropism. Some vine shoot tips which allow growth towards to darkness, suspended solids and climbing, exhibit negative phototropism (Zhao et al. 2011).

Each branch will be attracted by these positions with high light intensity; therefore, branch u in iteration t will take the following action:

$$\begin{aligned} x_u \left( t \right) =x_u \left( {t-1} \right) +G_p \cdot F_u \left( t \right) \cdot rand() \end{aligned}$$

(18)

where $G_p$ is a parameter reflecting the conversion rate and used for controlling the growth rate per unit time. $F_u$ is the growth force which is directed by photosynthesis rate, rand() represents a random number sampled with a uniform dispersion (Zhao et al. 2011).

For each branch u, $F_u \left( t \right)$ is calculated as (19):

$$\begin{aligned} F_u \left( t \right) =\frac{F_u^{total} \left( t \right) }{\Vert F_u^{total} \left( t \right) \Vert } \end{aligned}$$

(19)

$F_u^{total} \left( t \right)$ is calculated as (20):

$$\begin{aligned} F_u^{total} \left( t \right) =\mathop \sum \limits _{u\ne j} F_{u,j} \left( t \right) \end{aligned}$$

(20)

and

$$\begin{aligned} F_{u,j} \left( t \right) =\left\{ {{\begin{array}{ll} 0,&{}\quad if\;\Vert x_u \left( t \right) -x_j \left( t \right) \Vert =0\\ coe \cdot \frac{e^{-dimPR_j \left( t \right) }-e^{-dimPR_u \left( t \right) }}{\Vert x_u \left( t \right) -x_j \left( t \right) \Vert },&{}\quad otherwise \\ \end{array} }} \right. \end{aligned}$$

(21)

where dim represents the dimensionality of the problem, coe is a parameter used to control direction of movement.

$$\begin{aligned} coe=\left\{ {{\begin{array}{ll} 1,&{}\quad if\; f\left( {x_u \left( t \right) } \right) -f\left( {x_j \left( t \right) } \right) >0, \\ -1,&{}\quad otherwise \\ \end{array} }} \right. \end{aligned}$$

(22)

Furthermore, a small probability pm is introduced to reflect some random events

$$\begin{aligned} x_u \left( t \right) =L+\left( {U-L} \right) \cdot rand_1 (),if\left( {rand_2 (),pm} \right) \end{aligned}$$

(23)

where L and U are the lower and upper limits in the problem space, $rand_1 ()$ and $rand_2 ()$ are two random numbers with uniform distribution, respectively. The steps of phototropism operator are listed as shown in Fig. 9 (Zhao et al. 2011).

Fig. 9

The steps of phototropism operator

3.5.4 Studies with APOA

The structure prediction of Toy model of protein folding is one of the bioinformatics problems. Cui et al. (2012) proposed APOA which could reach the local optimum easily and could find the global optimum with a larger probability. Furthermore, they used splitting strategy to improve the performance. Cui et al. (2013a) reported that in standard APOA, photosynthesis operator was selected only as rectangular hyperbolic, and some light-responsive curves could increase the photosynthesis sensitivity. They used three different curves for it. In another study, they used Gravitropism mechanism (Cui et al. 2013b). Liu and Cui (2013) proposed a new hybrid APOA based Golden Section which increased the population density for protein folding problem. Furthermore; a famous local search strategy, Limited Memory Broyden–Fletcher–Shanno, was used to make an effective local search. Yu et al. 2013 proposed APOA with correlation branch which was no direct communication between branches unlike standard APOA.

Cai et al. (2012) chose seven classic models for research. These were rectangular hyperbolic model, non-rectangular hyperbolic model, updated rectangular hyperbolic model, parabolic model, straight-line model and, two exponential curve models. Cai et al. (2013) designed binary-coded version of APOA and used this in Hydrophobic-Polar model which was simplest grid model in the protein structure prediction problem. Cui et al. (2014) designed a new dynamic local search strategy because exploitation capability is not suffice in APOA. Cai et al. (2014) indicated that in standard APOA there is no branching in each branch, on the contrary, in the real tree there are many branches in each branch. They incorporate two selection strategies into standard version for avoiding to this, and they tested it in DV-Hop algorithm. Zhao et al. (2011) proposed APOA to solve constrained optimization problems.

3.6 Sapling Growing up Algorithm (SGuA)

It is a computational method based on cultivating, growing up, and mating of saplings which is developed for searching and optimization problems. SGuA is discovered by Karci and his colleagues in 2006.

As a first step for this method, in sowing sapling, there must be equal length distance to each direction to each other. There are four operators for SGuA: Mating, Branching, Vaccinating, and Surviving (Karci 2007a, b, c; Karci and Alatas 2006).

The processes of SGuA can be explained by the following two phases:

Sowing Phase—Uniformed sampling: Saplings are scattered evenly to solution space.

Growing up Phase—This phase contains three operators: Mating operator aims to generate new saplings by mating of currently available saplings. Mating operator is a global search operator based on data exchange between two saplings (Karci 2007a, b, c; Karci and Alatas 2006).

Branching operator aims to generate new saplings from currently available saplings by using probabilistic method to determine the branching position of currently available saplings. Vaccinating operator aims to generate new saplings from currently available similar saplings. Vaccinating operator is a search operator which uses similar saplings (Karci 2007a, b, c; Karci and Alatas 2006).

3.6.1 Sowing saplings

In the first place, a solution space Z is defined as $\hbox {Z}=\left\{ {z_0 ,\hbox {}z_1 ,\hbox {}\ldots ,\hbox {}z_{s-1} } \right\}$ and it is assumed that this solution space is in binary. In this solution space, assuming that each sapling has two branches, then it is in the form $\hbox {Z}=\left\{ {00,\hbox {}01,\hbox {}10,\hbox {}11} \right\}$ (Karci 2007a, b, c; Karci and Alatas 2006).

Firstly, two saplings $S_0$ and $S_1$ are arranged as $S_0 =\left\{ {u_1 ,u_2 ,\ldots ,u_n } \right\}$ and $S_1 =\left\{ {l_1 ,l_2 ,\ldots ,l_n } \right\}$. n is the length of the sapling and this case is assumed as $k=1$. $u_i$, $1\le i\le n$, is the upper bound for the corresponding variable, and $l_i$, $1\le i\le n$, is the lower bound for the corresponding variable. Then a dividing factor, k, is determined. Firstly, $k=2$ and two extra saplings $S_3$, $S_4$ are derived from $S_0$, $S_1$. $S_0$ is divided into two parts of equal length, by this way 4 saplings $\left( {2^{2}=4} \right)$ are derived from $S_0$. But one becomes similar to $S_0$, and one becomes similar to $S_1$. Then two saplings different from $S_0$ and $S_1$ are derived (Karci 2007a, b, c; Karci and Alatas 2006).

$$\begin{aligned} S_3= & {} \left\{ l_1 +\left( {u_1 -l_1 } \right) *r,l_2 +\left( {u_2 -l_2 } \right) *r,\ldots ,l_{n/2}\right. \nonumber \\&\left. +\left( {u_{n/2} -l_{n/2} } \right) *r,l_{n/2+1} +\left( {u_{n/2+1} -l_{n/2+1} } \right) *r,l_{n/2+2} +\left( {u_{n/2+2} -l_{n/2+2} } \right) *r \right\} \nonumber \\ \end{aligned}$$

(24)

and

$$\begin{aligned} S_4= & {} \left\{ l_1 +\left( {u_1 -l_1 } \right) *\left( {1-r} \right) ,l_2 +\left( {u_2 -l_2 } \right) *\left( {1-r} \right) ,\ldots ,l_{n/2} +\left( {u_{n/2} -l_{n/2} } \right) \right. \nonumber \\&\left. *\left( {1-r} \right) ,l_{n/2+1} +\left( {u_{n/2+1} -l_{n/2+1} } \right) *\left( {1-r} \right) ,l_{n/2+2} +\left( {u_{n/2+2} -l_{n/2+2} } \right) *\left( {1-r} \right) \right\} \nonumber \\ \end{aligned}$$

(25)

Here, r is a random number in the range of $0\le r<1$. Same method will be applied to remaining saplings in the garden by increasing the value of k. In case of $k=3$, there will be 6 saplings obtained from $S_1$ (Karci 2007a, b, c; Karci and Alatas 2006).

$$\begin{aligned} S_5= & {} \left\{ l_1 +\left( {u_1 -l_1 } \right) *r,\ldots ,l_{2n/3} +\left( {u_{2n/3} -l_{2n/3} } \right) *r,l_{2n/3+1}\right. \nonumber \\&\left. +\left( {u_{2n/3+1} -l_{2n/3+1} } \right) *\left( {1-r} \right) ,\ldots ,l_n +\left( {u_n -l_n } \right) *\left( {1-r} \right) \right\} \end{aligned}$$

(26)

$$\begin{aligned} S_6= & {} \left\{ l_1 +\left( {u_1 -l_1 } \right) *r,\ldots ,l_{n/3} +\left( {u_{n/3} -l_{n/3} } \right) *r,l_{n/3+1} +\left( {u_{n/3+1} -l_{n/3+1} } \right) \right. \nonumber \\&*\left( {1-r} \right) ,\ldots ,l_{2n/3} +\left( {u_{2n/3} -l_{2n/3} } \right) \nonumber \\&\left. *\left( {1-r} \right) ,l_{2n/3+1} +\left( {u_{2n/3+1} -l_{2n/3+1} } \right) *r,\ldots , \right\} l_n +\left( {u_n -l_n } \right) *\left( {1-r} \right) \end{aligned}$$

(27)

$$\begin{aligned} S_7= & {} \left\{ l_1 +\left( {u_1 -l_1 } \right) *r,\ldots ,l_{n/3} +\left( {u_{n/3} -l_{n/3} } \right) *r,l_{n/3+1} +\left( {u_{n/3+1} -l_{n/3+1} } \right) \right. \nonumber \\&\left. *\left( {1-r} \right) ,\ldots ,l_n +\left( {u_n -l_n } \right) *\left( {1-r} \right) \right\} \end{aligned}$$

(28)

$$\begin{aligned} S_8= & {} \left\{ l_1 +\left( {u_1 -l_1 } \right) *\left( {1-r} \right) ,\ldots ,l_{n/3} +\left( {u_{n/3} -l_{n/3} } \right) *\left( {1-r} \right) ,l_{2/3+1}\right. \nonumber \\&\left. +\left( {u_{n/3+1} -l_{n/3+1} } \right) *r,\ldots ,l_n +\left( {u_n -l_n } \right) *r \right\} \end{aligned}$$

(29)

$$\begin{aligned} S_9= & {} \left\{ l_1 +\left( {u_1 -l_1 } \right) *\left( {1-r} \right) ,\ldots ,l_{n/3} +\left( {u_{n/3} -l_{n/3} } \right) *\left( {1-r} \right) ,l_{n/3+1}\right. \nonumber \\&+\left( {u_{n/3+1} -l_{n/3+1} } \right) *r,\ldots ,l_{2n/3} +\left( {u_{2n/3} -l_{2n/3} } \right) *r,l_{2n/3+1}\nonumber \\&\left. +\left( {u_{2n/3+1} -l_{2n/3+1} } \right) *\left( {1-r} \right) ,\ldots , \right\} l_n +\left( {u_n -l_n } \right) *\left( {1-r} \right) \end{aligned}$$

(30)

$$\begin{aligned} S_{10}= & {} \left\{ l_1 +\left( {u_1 -l_1 } \right) *\left( {1-r} \right) ,\ldots ,l_{2n/3} +\left( {u_{2n/3} -l_{2n/3} } \right) *\left( {1-r} \right) ,l_{2n/3+1}\right. \nonumber \\&\left. +\left( {u_{2n/3+1} -l_{2n/3+1} } \right) *r,\ldots ,l_n +\left( {u_n -l_n } \right) *r \right\} \end{aligned}$$

(31)

In binary case, current value is complemented instead of multiplying of a random value by the current value. Sapling derivation goes on up to fulfilling the population. Pseudo code of initially generated saplings in SGuA is shown in the Fig. 10 (Karci 2007a, b, c; Karci and Alatas 2006).

Fig. 10

Generating of initial saplings in SGuA

3.6.2 Growing up saplings

Growing up phase contains three operators: Mating, Branching, and Vaccinating. If the garden G(), contains |G| number of saplings, then the current garden is replaced by the |G| number of the best saplings of the offspring garden and the current garden. In other words, there isn’t any stochastic process in selection of the next generation garden (Karci 2007a, b, c; Karci and Alatas 2006).

(a) Mating: The purpose of the mating operator is generating a new sapling from the currently available saplings by replacing the currently available information with the makeshifts. $S_1 =\left\{ {s_{1,1} ,s_{1,2} ,\ldots ,s_{1,i} ,\ldots ,s_{1,n} } \right\}$ and $S_2 =\left\{ {s_{2,1} ,s_{2,2} ,\ldots ,s_{2,i} ,\ldots ,s_{2,n} } \right\}$ are two saplings. The distance between $S_1$ and $S_2$ affects the mating process by taking place or by not taking place in the process and it depends on the distance between the current pair. $P_m (S_1 ,S_2 )$, is the mating probability of $S_1$ and $S_2$ saplings and it can be linear or exponential. The pseudo code of mating operator is given in the Fig. 11 (Karci 2007a, b, c; Karci and Alatas 2006).

Fig. 11

Mating process in SGuA

(b) Branching: $S_1 =\left\{ {s_{1,1} ,s_{1,2} ,\ldots ,s_{1,i} ,\ldots ,s_{1,n} } \right\}$ is a sapling. If one of the branch occurs in the point $s_{1,i}$, then the probability of occurring of a branch in the point $s_{1,i}$, $i\ne j$, can be calculated in two ways: linear and non-linear. The distance between $s_{1,i}$ and $s_{1,j}$ can be considered as $\left| {i-j} \right|$ or $\left| {j-i} \right|$. This process is shown in Fig. 12 (Karci 2007a, b, c; Karci and Alatas 2006).

(c) Vaccinating: Vaccinating process is performed between two saplings in the case of dissimilarities of these saplings in this algorithm. Dissimilarities of saplings affects the performance of vaccinating process and at the same time performance of vaccinating process is proportional in the case of dissimilarities of these two saplings. The pseudo code of vaccinating operator is given in Fig. 13 (Karci 2007a, b, c; Karci and Alatas 2006).

Fig. 12

Branching process in SGuA

Fig. 13

Vaccinating process in SGuA

3.6.3 SGuA

SGuA uses the similarity in the garden to generate the better saplings (Mating process). This is a cultural interaction process. Vaccinating process is the opposite of mating by the fact that vaccinating operator uses the dissimilarity in the garden. That is why; it is also the opposite of cultural interaction. Branching process is a unary operator which aims to embed the new information to the current solution set and to delete the information from the current solution set. Steps of SGuA are listed in the Fig. 14.

For determining the quality of saplings, objective function is used. Objective function is denoted as a function which considers each sapling as a solution and used as a solution for the problem and the obtained results are the values of the objective function (Karci 2007a, b, c; Karci and Alatas 2006).

Fig. 14

Pseudocode of SGuA

3.7 Photosynthetic Algorithm (PA)

Photosynthesis is one of the most important biochemical events. The most interesting photosynthetic reactions are considered as “dark reactions”. Dark reactions consist of a biochemical process which are combinations of Calvin–Benson cycle and photorespiration. The product of dark reaction is carbohydrates, like DHAP. PA uses the rules which regulate the conversion of carbon molecules from one substance to another in Calvin–Benson cycle, and photorespiration reactions. Replaced parts or shuffling are used to simulate the PA. PA is firstly proposed in 2000 by Murase. They chose analysis of the invert finite element to test the performance of PA as a typical optimization or parameter estimation (Murase 2000). Okayama and Murase (2002) chose Vizier problem as a typical optimization problem to show the performance of PA. Alatas (2011b) used PA in bioinformatics problems such as discovering association rules in biomedical data and multiple-sequence alignment.

Fig. 15 shows the diagram of Calvin–Benson cycle. In this diagram, each row represents conversion of each molecule of each metabolite. Cycle can be separated into three phases.

• (1) Fixation of $\hbox {CO}_{2}$ by ribulose bisphosphate carboxylase (Rubisco) and formation of 3 phosphoglycerate.

• (2) Reduction of 3 phosphoglycerate to triose-P by the actions of glycerate-3-P kinase and NADP-dependent glyceraldehyde-P dehydrogenase.

• (3) Regeneration of ribulose 1,5 bisphosphate by conversion of five $\hbox {C}_{3}$ units into three $\hbox {C}_{5}$ units (Alatas 2011b).

Fig. 15

Calvin–Benson cycle in PA

Rubisco (Ribulose-1,5-bisphosphate carboxylase/oxygenize) is a bi-functional key enzyme which fixes $\hbox {CO}_{2}$ in chloroplasts of organisms that photosynthesize by their own carboxylase operation. In addition to carboxylation, Rubisco can also be bind to the $\hbox {O}_{2}$. $\hbox {CO}_{2}$ and $\hbox {O}_{2}$ compete with each other in the active region of Rubisco. Rubisco fixes the carbon dioxide when carbon dioxide concentration is high. However, when oxygen concentration is high, Rubisco binds oxygen instead of carbon dioxide. To catalyze this oxygen activity Rubisco’s tendency increases much with temperature than its carboxylase activity. Rubisco would prefer 100 more $\hbox {O}_{2}$ than $\hbox {CO}_{2}$; however, $\hbox {O}_{2}$ concentration in the atmosphere is much higher than $\hbox {CO}_{2}$’s concentration, that is why; Rubisco fixes one molecule of $\hbox {O}_{2}$ for each three molecule of $\hbox {CO}_{2}$. In active parts of Rubisco, one molecule of phosphoglycerate and one molecule of phosphoglycolate form a toxic product when $\hbox {O}_{2}$ is substituted instead of $\hbox {CO}_{2}$. Plants can metabolize the phosphoglycolate by photorespiration process. For this reason, glycolate metabolism is correlated with photorespiration. Energy is required in this process and also it is the reason of reduced carbon as $\hbox {CO}_{2}$. Fig. 16 shows the part of the photorespiratory pathway depends to Rubisco (Alatas 2011b).

Fig. 16

Photorespiration in PA

In the first stage of Calvin–Benson cycle, the rules that are regulating conversion of carbon molecules from one substance to another and the reaction located in chloroplast subcellular compartment for photorespiration are used by PA. DHAP, the product of photosynthesis, serves to provide information strings of the algorithm. When it is not possible to improve the quality of products, then the optimum point is reached. The quality of a product is evaluated according to the fitness value. Fig. 17 shows a flow diagram of the processes of the PA.

Algorithm starts with the random generation of intensity of light. Fixation rate of $\hbox {CO}_{2}$ is evaluated according to the (32) which is based on the light intensity.

Either Calvin–Benson cycle or photorespiration cycle is selected for the next processing according to the fixation rate. Bits, values or parts of strings are exchanged or shuffled according to the recombination of carbon molecules in photosynthetic pathways in both cycles. GAPs, the intermediate information strings, are generated after some iterations. Each GAP consists of appropriate bits, strings, or values. The fitness of these GAPs are then evaluated. The best fitting GAP proceeds as a DHAP (Alatas 2011b).

Fig. 17

Flow diagram of PA

One of the unique features of the algorithm is production of stimulation function. Randomly changing light intensity which alters the influence degree on renewing elements of RuBP by photorespiration creates the stimulation. The frequency of the stimulation cycle by photorespiration can be calculated with the $\hbox {CO}_{2}$ fixation rate in (32).

$$\begin{aligned} C=\frac{V_{max} }{1+\frac{A}{L}} \end{aligned}$$

(32)

C: $\hbox {CO}_{2}$ Fixation rate

$V_{max}$: Maximum $\hbox {CO}_{2}$ fixation rate

A: Affinity of $\hbox {CO}_{2}$

L: Light intensity

All parameters that are given in (32) can be determined; however, these values can be assigned within a realistic range and they don’t need to be empirical. Light intensity might be randomly generated by the computer when PA is executed. Time-varying actual light intensity might be used as an alternative with on-line measuring system. For this phase, chaotic sequences may also be used. Change of light intensity as a stimuli is effective in reducing the occurring of local minimum traps in the search process. $\hbox {CO}_{2}$ concentration in the leaf varies according to the $\hbox {CO}_{2}$ fixation rate. $\hbox {O}_{2}$ and $\hbox {CO}_{2}$ concentration ratios are evaluated to determine the ratio of calculation frequency of Calvin–Benson cycle to the photorespiration cycle (Alatas 2011b).

3.8 Plant Growth Optimization (PGO)

PGO, which is simple but effective algorithm, is proposed to simulate plant growth with a realistic way considering the spatial occupancy, account branching, phototropism, and leaf growth. The main purpose of the model is to select active point by comparing the morphogen concentration for increasing the L system (Cai et al. 2008).

PGO has some major differences from natural plant growth process. PGO takes the solution space as growth areas of artificial plant, a point of plant as a potential solution for problem. The algorithm searches optimal point in solution space according two behaviors:

• 1. Produce new points with branching to search in optimal area which consists of the optimal solution;

• 2. The growth of leaves around the branching point to find accurate solutions in the local area;

Fig. 18

Pseudocode of PGO Algorithm

Considering the definitions given in the previous section, the pseudocode of PGO algorithm is shown in Fig. 18 (Cai et al. 2008).

$$\begin{aligned} A_i= & {} \left\{ {{\begin{array}{ll} 1-\frac{f\left( {x_i } \right) -f_{min} }{\mathop \sum \nolimits _{j=1}^N \left[ {f\left( {x_j } \right) -f_{min} } \right] },&{} f\left( {x_i } \right) >f_{min} \\ 1,&{} f\left( {x_i } \right) =f_{min} \\ \end{array} }} \right. \;i=1,2,\ldots ,N \end{aligned}$$

(33)

$$\begin{aligned} \alpha= & {} \alpha /0.9~\beta =\beta /0.9 \end{aligned}$$

(34)

One execution of procedure from Step 2 through Step 6 is called as a generation or a cycle (Cai et al. 2008).

3.9 Root Growth Algorithm (RGA)

3.9.1 Description for growth behaviors of root system

A plant starts from a seed, and root growth is indispensable for the plant growth. All the roots of a plant can be seen as a system composed of a large number of root hairs and root apices. In the late 1960s, Lindenmayer proposed L-systems for modeling of the plant growth process. L-Systems are based on simple rewrite rules and branching rules, and make a formal definition successfully for plant growth. In this algorithm, L-Systems are used for describing growth behavior of the root system (Zhang et al. 2014):

• (1) A seed sprouts in the soil, and partly realizes growth as a plant stem above the soil surface. The other part of the seed grows downward to be the plant’s root system. The new root hairs grow from the root apex.

• (2) The newer root hairs grow from the root apices of old root hairs. Repeated behavior of root system is called as branching of root apices.

• (3) Most of the root hairs and root apices are similar. All of the plant’s root system has a self-similar structure. Root system of each plant consists of large number of root apices and root hairs with similar structure (Zhang et al. 2014).

3.9.2 Plant morphology

The effects of the root and rhizosphere characteristics on the plant resource efficiency are important. Uneven concentration of nutrients in the soil makes root hair growing in different directions. This characteristic of root growth is associated with the model of morphology in the biological theory. The formation of model can be considered as a complex process that cells are differentiated and create new spatial structure. When the rhizomes of the root system grows, three or four growth points with different rotation direction will be formed at each root apex. The rotation diversifies the growth direction of root apex. Root hairs contain cells whose root apices in the germinating place are undifferentiated. These cells are regarded as fluid bags in which there are homogeneous chemical components. One of the chemical components is a version of growth hormone called as morphactin. Morphactin concentration is a parameter of morphogenesis model. The parameter ranges between 0 and 1. The morphactin concentration determines whether cells start to divide or not. When cells start to divide, root hairs are visible (Zhang et al. 2014).

As regards to the root growth process, in biology, there are following consequences:

• (1) If the plant root system has more than one root apex which can germinate, root hairs depends on their morphactin concentration. The probability of germination of new root hairs is higher from the root apices with larger morphactin concentration than root apices with less one.

• (2) Morphactin concentration in the cell is not static, but it depends on its surrounding, in other words spatial distribution of nutrients in the soil. After the new root hairs germinate and grow, morphactin concentration will be reallocated between new root apices in parallel with new concentration of nutrients in the soil (Zhang et al. 2014).

To simulate the above process, it is assumed that the multicellular closed system is constant (considered as 1) in morphactin state space. If there are n root apices $x_i \hbox {}\left( {i=1,\hbox {}2,\hbox {}\ldots ,\hbox {}n} \right)$ which are D-dimensional vectors, morphactin concentration of any cell is defined as $E_i \hbox {}\left( {i=1,\hbox {}2,\hbox {}\ldots ,\hbox {}n} \right)$. Morphactin concentration of each root apex can be expressed as follows:

$$\begin{aligned} E_i =\frac{1/f\left( {x_i } \right) }{\mathop \sum \nolimits _{i=1}^n 1/f\left( {x_i } \right) } \end{aligned}$$

(35)

$f\left( {x_i } \right)$ is the objective function which shows the spatial distribution of nutrients in the soil. In (35), themorphactin concentration of each root apex is determined by relative position of each point and environmental information in this position (objective function value). Therefore, n root apices correspond to the n morphactin concentration values. When root hairs germinate, morphactin concentration can be changed (Zhang et al. 2014).

3.9.3 Branching of the root tips

Branching of the root apices, proposed in root growth model, is important for simulation and embodied algorithm. There are four rules for root branching as follows (Zhang et al. 2014):

• (1) Plant growth begins from seed.

• (2) In each cycle of growth process, some excellent root apices which have larger morphactin concentration (fitness value in the embodied algorithm) are selected for branching.

• (3) Distance should not be close between selected root apices in order to make spatial distribution wider and increase the diversity of fitness value.

• (4) If number of selected root apices is equal to predefined value, the cycle of selection process ends (Zhang et al. 2014).

In memory, to produce a new growth point from the old root apex, the proposed model uses following statement:

$$\begin{aligned} pg_{lj} =f\left( x \right) =\left\{ {{\begin{array}{ll} x_{ij} +\left( {2\times \delta _{ij} -1} \right) ,&{}\quad j=k \\ x_{ij} ,&{}\quad j\ne k \\ \end{array} }} \right. \end{aligned}$$

(36)

$k\in \left\{ {1,2,\ldots ,D} \right\}$ and $j\in \left\{ {1,2,\ldots ,D} \right\}$ are randomly selected indexes. $pg_l \left( i=1,2,\ldots ,\right.$ $\left. S \right)$ are S new growth point. $\delta _{ij}$ is a random number within the range $\left[ {-1,1} \right]$ (Zhang et al. 2014).

3.9.4 Root hair growth

After new growth points are produced, root hairs begin to grow from these growth points. Root hair growth depends on its growth angle and growth length. Growth angle is a vector to measure the growth direction of the root hair. Randomly generated growth angle $\varphi _i \left( {i=1,2,\ldots ,n} \right)$ can be expressed as follows:

$$\begin{aligned} (\phi _1 ,\phi _2 ,\ldots ,\phi _D )=rand\left( D \right) \end{aligned}$$

(37)

$$\begin{aligned} \varphi _i =\frac{(\phi _1 ,\phi _2 ,\ldots ,\phi _D )}{\sqrt{\upphi _1^2 +\upphi _2^2 +\ldots +\upphi _D^2 }} \end{aligned}$$

(38)

The growth length of each root hair is defined as $\delta _i \left( {i=1,2,\ldots ,n} \right)$, which is an important parameter in root growth model. Some strategies of tuning parameter can produce multiple versions of the root growth model. After growth, a new root apex can be obtained by the following expression (Zhang et al. 2014):

$$\begin{aligned} x_i =x_i +\delta _i \varphi _i \end{aligned}$$

(39)

Some rules are defined as follows to simulate the trophotropism of the root system:

• (1) If the morphactin concentration (fitness) of the new root apex is better than the old one in the same t cycle, the root apex will continue to grow. A new root apex in the inner loop can be expressed as:

  $$\begin{aligned} x_i^t =x_i^t +\delta _i \varphi _i \end{aligned}$$

  (40)

  However, the number of iterations in the inner loop is a predefined value. If the number of iterations in the inner loop is equal to a predefined value, the inner loop stops (Zhang et al. 2014).

• (2) If the morphactin concentration of the new root apex is worse than the old one in the same t cycle, the root apex will stop growing and $t=\hbox {}t+1$. A new root apex can be expressed as:

  $$\begin{aligned} x_i^{t+1} =x_i^{t+1} +\delta _i \varphi _i \end{aligned}$$

  (41)

Fig. 19

The flowchart of the RGA

3.9.5 RGA

The proposed root growth model is embodied as RGA for simulating root growth of plants and optimization of higher-dimensional numerical functions. The growth length of each root hair and the threshold of distance between the roots apices are important parameters for RGA. The flowchart of RGA is shown in Fig. 19. The pseudo-code for RGA is listed in Fig. 20 (Zhang et al. 2014).

Fig. 20

Pseudocode for the RGA

3.10 The Strawberry Algorithm as Plant Propagation Algorithm (PPA)

Strawberry plants belong to the rose family. Strawberry-growing industry began in Paris in the 17th century by European diversity. Amede-Francois Freizer, who was a mathematician and an engineer, was hired by Louis XIV in 1714 for drawing the map of South America, and he returned from Chile with Chilean strawberry plant which gives large fruits.

It is assumed that, strawberry plants, as well as other plants, have an underlying propagation strategy. This strategy is developed over time for ensuring to survive in species. In other words, a plant makes an effort to have children in areas which provide essential nutrients and growth potential. When a plant is in a good point, it sends lots of short runner, and when a plant is in a weak point, it sends longer runners for searching better points. Long runners are few, because they are investments. The plant may not have sufficient resource for sending many types of runners (Salhi and Fraga 2011).

It is predictable that with these observations and assumptions, strawberry plants and other plants can solve survival problem to grow in a particular environment. The mentioned approaches here contain mapping an optimization problem onto survival optimization problem of strawberry plant and adopting strategy of survival in the environment for searching points in the search space which give best values and ultimately the best value.

The strawberry algorithm is an exemplar of PPA. There are two features to emit all successful algorithms/heuristics for global optimization: concentration or intensification and diversification or exploration. While diversification provides searching to prevent jamming in a review of local optimum, concentration provides local search and convergence to a local optimum. This two features are contradictory and the success of any implementation of a search algorithm depends on the balance between these two features (Salhi and Fraga 2011).

This strawberry approach applies concentration by sending a large number of short runners from good solutions. It sends less but longer runner from the less good solutions to apply diversification. The full algorithm is presented in Fig. 21.

As many algorithms of this nature, PPA requires customization through the introduction of some auxiliary functions and assignment of values to a set of parameters. These parameters and functions for PPA are: size of population, a fitness function, the number of runners will be created for each solution, and distance for each runners (Salhi and Fraga 2011).

PPA is based on population of shoots each of which represents a solution in the search space. It is assumed that each shoot is taken to be equivalent to evaluated objective function. Each shoot will subsequently be sent to explore the solution space around it. The number of shoots is given by this parameter and it is shown as m in the algorithm. Algorithm is repeatedly run with sending runners from shoots in each generation. This parameter provides a termination condition based on how many times runners are transmitted, and is represented by $g_{max}$.

The solutions in the population will be sorted according to their fitness. This fitness will naturally be a function of value of objective function. However, the real relationship between fitness and objective function can be tailored for discussed specific problem. Although this is recommended for algorithm representation of fitness value supported by $f\left( x \right)$ function, $f\left( x \right) \in \left[ {0,1} \right]$, if not, the equations used to determine the number of runners and the distance to be run for each runner should be modified (Salhi and Fraga 2011).

Fig. 21

The pseudo code of PPA

Functions are used to determine the number of runners and the distance each of which should be traveled by runners are described below. They require that fitness values lie strictly in (0, 1). To ensure this, the fitness value $f\left( x \right)$ described above is mapped:

$$\begin{aligned} N\left( x \right) =\frac{1}{2}\left( {\tanh \left( {4f\left( x \right) -2} \right) +1} \right) \end{aligned}$$

(42)

The number of runners produced by a solution should be proportional with its fitness. By default, function in (43) can be used:

$$\begin{aligned} n_r =\lceil n_{max} N_i r \rceil \end{aligned}$$

(43)

$n_r$ is the number of runners produced for generating solution i in current iteration, after sorting; $n_{max}$ is the number of runners to generate. $N_i$ is mapped fitness of solution i; and $r\in \left[ {0,1} \right]$ is a randomly selected number for each individual in each generation. The combination of the fitness mapping function and ceiling operator provides that all solution generates at least one runner, even for the fittest solutions, ones with $f_i \left( x \right) \equiv 0$. The fittest solutions will generate at most $n_{max}$ runners (Salhi and Fraga 2011).

The distance of each runner is inversely proportional with its growth as (44):

$$\begin{aligned} d_{r,j} =2\left( {1-N_i } \right) \left( {r-0.5} \right) \end{aligned}$$

(44)

$j=1,\ldots ,n. \quad n$ is the size of the search space. Each $d_{r,j}$ will be in the range $\left[ {-1,1} \right]$. $d_{r,j}$ is computed and which runner and what extend it spreads are determined. The calculated distance will be used for updating i solution based on the limit on $x_j$.

$$\begin{aligned} x_j^*=x_j +\left( {b_j -a_j } \right) d_{r,j} ) \end{aligned}$$

(45)

This $x_j^{*}$ values are set to make sure that new produced points are within the limits $\left[ {a_j ,\hbox {}b_j } \right]$ (Salhi and Fraga 2011).

3.10.1 Studies with PPA

Sulaiman et al. (2014) used modified PPA for constrained engineering optimization problems. Sulaiman et al. (2016) introduced a robust and efficient version of PPA and they provided more effective and improved variants of it on standard continuous optimization test problem in high sizes. Birds and animals provide dispersion of the seeds into the environment, while they are feeding from plants. Sulaiman and Salhi presented a seed based PPA by modelling this situation (Sulaiman and Salhi 2015).

3.11 Runner Root Algorithm (RRA)

RRA is inspired by plants such as strawberry and spider plants which are spread through their runners and also which develop roots and root hairs for local search for minerals and water resources. Similar to other metaheuristics, RRA does not apply same number of function evaluation at all iterations. More precisely, for optimal solution (exploitation procedure) in RRA, global search is performed at all iterations, while local search is performed only when global search does not lead to a significant improvement in the value of cost function. The only similarity between this algorithm and PPA is in using the idea of runners (Merrikh-Bayat 2015).

Obviously, in order to arrive at a numerical optimization algorithm inspired by plants such as strawberry, it is needed to model the behavior of these plants by simple but effective rules. In this algorithm, it is assumed that the behaviors of such plants can be effectively modelled through the following three facts:

• Each strawberry mother plant spreads through their runners. These runners rise randomly and each one leads to a new daughter plant (global search with big steps for resources).

• Each strawberry mother plant improves its roots and root hairs randomly (local search with relatively big steps and small steps for resources).

• Daughter strawberry plants which have access to rich resources, produce more runners and roots, grow fast, and, therefore, cover larger areas. On the other hand, daughter plants which move to poor resources will probably die (Merrikh-Bayat 2015).

3.11.1 Mathematical Description of RRA

Similar to other metaheuristic optimization algorithm, this algorithm, begins with a uniformly distributed random initial population, each called a mother plant in domain of the problem. The number of the mother plants is considered to be equal to $N_{pop}$. Then, any mother plant at each iteration, except the fittest one, produces a daughter plant randomly in the domain of the problem (global search for better solutions). The distance of this each daughter plant from the mother plant is controlled by a parameter called $d_{runner}$. The fittest mother plant produces a daughter plant exactly at the same location as itself. $N_{pop}$ daughter plants are produced using this procedure. It is assumed that in RRA, at each iteration each mother plant is moved to a position referred by the daughter plant. If at least one of these daughter plants provides a significant improvement in the value of cost function compared with one of those obtained from the beginning of the algorithm, all of the mother plants required for the next iteration are selected from these daughter plants using a combination of elite and roulette wheel selection methods. More precisely, in this case, one of the necessary $N_{pop}$ mother plants of the next iteration is considered to be equal to fittest daughter plant of the current iteration (elite selection), and the others are obtained by applying the roulette wheel method. In other words, while a significant decrease is observed in the value of cost function, the algorithm continuously examines the domain of the problem for better solutions through runners which improve only around the available solution. The amount of this improvement is measured by a parameter called tol.

However, if none of the resulting daughter plants leads to a pretty good value for cost function, algorithm starts to local search procedure through roots and root hairs. In this case, the algorithm assumes that the fittest daughter plant is in the same valley as the unknown global best solution. Therefore, if any improvements observed by applying a random change to each variable of this daughter plant, the algorithm accepts it. In other words, if the change which applies to some of the variables of the fittest daughter plant leads to a better solution, the algorithm accepts it and applies a random change to the other variable of the resulted daughter plant. If not, the previous value of this variable is retained and a random change is applied to the next variable of that daughter plant. This procedure is applied to all of the variables of the fittest daughter plant. This strategy guarantees that the general movement of the fittest daughter plant, which may be the global best solution, will be towards to the nearest minimum point in the same valley. From this case, the fittest daughter plant may be located in a valley that too flat or narrow, and both large and small random changes should be applied to each variable of the fittest daughter plant. In conclusion, in each iteration, a global search procedure is performed and a daughter plant is produced for all of the each mother plant. If none of the resulting daughter plant provides a significant improvement at the cost function value, the variables of the fittest daughter plant are subjected to random changes with both small and large steps (Merrikh-Bayat 2015).

The local search is not applied to all daughter plants which can significantly save the number of function evaluations and at all iterations. In addition to this, to increase the functionality, algorithm needs to be equipped with a restart strategy, because algorithm may be falling into the point trap of local optimum. For this purpose, after the global and potential local search, if the relative improvement is less than tol, value of the counter called stall_coune is incremented by 1; if not, value of the counter is equal to 0. If the value of this counter is equal to a predefined stall_max value, the algorithm is started with a random initial population. In other words, in this case, all the solutions obtained so far are discarded, and only the fittest solution obtained at the last iteration is memorized for comparison with the solutions previously or subsequently obtained to determine the best solution.

For following unconstrained optimization problem $minf\left( x \right)$

$$\begin{aligned} x_l \le x\le x_u ) \end{aligned}$$

(46)

$f:\mathbb {R}^{m}\rightarrow {\mathbb {R}}$ is m-variable cost function to be minimized, $x^{*}=argminf\left( x \right) \in {\mathbb {R}}^{m}$ is the best global solution to be calculated, and $x_l ,x_u \in {\mathbb {R}}^{m}$ are two vectors indicating the lower and upper bound of variables. In case of dealing with a constrained optimization problem, standard methods can be used for converting to an unconstrained equivalent. As previously mentioned, RRA begins with a set of $N_{pop}m$-dimensional randomly generated vectors in the domain of problem each serves as an initial mother plant. Then, in each iteration, any mother plant except the fittest one randomly generates a daughter plant and the fittest mother plant generates a daughter plant exactly equal to itself. Let $x_{mother}^k \left( i \right)$ is the location of the kth mother plant $k=1,\ldots ,N_{pop}$ at the ith iteration where $x_{mother}^1 \left( i \right)$ is the fittest daughter plant of the previous iteration and $x_{daughter}^k \left( i \right) \quad k=2,\ldots ,N_{pop}$ are the mother plants selected among the daughter plants of the last iteration using the roulette wheel method. Thus, with using this notation, the location of the kth daughter plant at the ith iteration, $x_{daughter}^k \left( i \right)$, is calculated as:

$$\begin{aligned} x_{daughter}^k \left( i \right) =\left\{ {{\begin{array}{ll} x_{mother}^1 \left( i \right) ,&{}\quad k=1 \\ x_{mother}^k \left( i \right) +d_{runner} \times r_k ,&{}\quad k=2,\ldots , N_{pop} \\ \end{array} }} \right. \end{aligned}$$

(47)

where, $r_k \in {\mathbb {R}}^{m}$ is a vector whose entries are random numbers with uniform in the range [-0.5, 0.5], and $d_{runner}$ is a scaler which represents the maximum distance of daughter plants to its mother plant. According to (47), the best daughter plant of the last iteration is considered as a mother plant in current iteration. In addition, to calculate any daughter plant, a random vector $r_k$ should be created (Merrikh-Bayat 2015).

The cost function is considered at the location of daughter plant as calculated in (47). If at least one of these daughter plant leads a significant improvement in the value of the cost function compared with the best daughter plant of the previous iteration, for instance, if the inequality

$$\begin{aligned} \left| {\frac{\mathop {\min }\nolimits _{k=1,\ldots ,N_{pop} } f\left( {x_{daughter}^k \left( i \right) } \right) -\mathop {\min }\nolimits _{k=1,\ldots ,N_{pop} } f\left( {x_{daughter}^k \left( {i-1} \right) } \right) }{\mathop {\min }\nolimits _{k=1,\ldots ,N_{pop} } f\left( {x_{daughter}^k \left( {i-1} \right) } \right) }} \right| \ge tol \end{aligned}$$

(48)

is satisfied, algorithm does not start to local search as long as (48) means that global search is still effective. If the cost function is defined as if denominator of (48) has a chance to be equal to zero, the absolute difference can be used instead of the term side of it. But, if (48) is not satisfied, local search should be performed. For this purpose, let the best daughter plant from those calculated is represented as $x_{daughter,best} \left( i \right)$, and a vector obtained by applying a random change to kth entry of $x_{daughter,best} \left( i \right)$ is represented as $x_{perturbed,k}$, for example

$$\begin{aligned} x_{perturbed,k} =diag\left\{ {1,1,\ldots ,1,1+d_{runner} n_k ,1,\ldots ,1} \right\} \times x_{daughter,best} \left( i \right) \end{aligned}$$

(49)

$d_{runner}$ is the same as before, $n_k \left( {k=1,\ldots ,m} \right)$ is a random number with normally distributed $(\mu =0$ and $\sigma =1)$, and $diag\left\{ {1,1,\ldots ,1,1+d_{runner} n_k ,1,\ldots ,1} \right\}$ is a diagonal matrix whose all diagonal elements, except kth element, are equal to unity, and kth one is equal to $1+d_{runner} n_k$. To make local search, for $k=1$, $x_{perturbed,k}$ is calculated from (49). If $f\left( {x_{perturbed,1} } \right) <f(x_{daughter,best} \left( i \right) )$, then $x_{daughter,best} \left( i \right) \leftarrow x_{perturbed,1}$, else $x_{daughter,best} \left( i \right)$ is remained unchanged. Then, $x_{perturbed,k}$ is calculated for $k=2$ from (49) using calculated $x_{daughter,best} \left( i \right)$. Again if, $f\left( {x_{perturbed,2} } \right) <f(x_{daughter,best} \left( i \right) )$, then $x_{daughter,best} \left( i \right) \leftarrow x_{perturbed,2}$, else $x_{daughter,best} \left( i \right)$ is remained unchanged. This procedure is repeated for all m variables of $x_{daughter,best} \left( i \right)$. So far, local search with large steps (model of the root functions in nature) is completed. Now, a local search with small steps (model of root hairs function in nature) should be treated. (50) is used for this task:

$$\begin{aligned} x_{perturbed,k} =diag\left\{ {1,1,\ldots ,1,1+d_{root} r_k ,1,\ldots ,1} \right\} \times x_{daughter,best} \left( i \right) \end{aligned}$$

(50)

$d_{root}$ is a constant scalar which is considered as much smaller than $d_{runner}$, $x_{daughter,best} \left( i \right)$ is final result of local search with random large steps which is done before, and $r_k \left( {k=1,\ldots ,m} \right)$ is a random number with uniform distribution in the range $\left[ {-0.5,0.5} \right]$ (Merrikh-Bayat 2015).

After local search is performed (if necessary), mother plants of next iteration are selected among the daughter plants of current iteration using a combination of elite and roulette wheel selection. Elite selection can be as simple as the following:

$$\begin{aligned} x_{mother}^1 \left( {i+1} \right) \leftarrow x_{daughter,best} \left( i \right) \end{aligned}$$

(51)

Before applying roulette wheel method to select the remaining required mother plant of next iteration, the fitness of kth daughter plant is calculated as follows:

$$\begin{aligned} fit\left( {x_{daughter}^k \left( i \right) } \right) =\frac{1}{a+f\left( {x_{daughter}^k \left( i \right) } \right) -f\left( {x_{daughter,best} \left( i \right) } \right) } \end{aligned}$$

(52)

a is a positive real constant controlled the selection pressure. After calculating the fitness value, the selection probability of kth daughter plant as a mother plant of next iteration, $p_k$, is calculated as follows:

$$\begin{aligned} p_k =\frac{fit\left( {x_{daughter}^k \left( i \right) } \right) }{\mathop \sum \nolimits _{j=1}^{N_{pop} } fit\left( {x_{daughter}^j \left( i \right) } \right) } \end{aligned}$$

(53)

The pseudo code of RRA is presented in Fig. 22 (Merrikh-Bayat 2015).

Fig. 22

The pseudo code of RRA

3.12 Path Planning Algorithm based on Plant Growth Mechanism (PGPP)

PGPP is established by extracting data processing mechanism in plant growth process. PGPP takes the plant bud as the main computing unit to search optimal plant. The growth of buds at different speeds and directions in PGPP embodies the group search capability. PGPP defines the seed germ as starting point and the light source as destination. PGPP discretizes plant growth period and replaces it with iterative calculations. During each iteration, it is assumed that plant growth behaviors remain the same. With the plant growth, the path which reaches the light source first is the best growth path. The path is planned according to this.

PGPP extracts phototropism, negative geotropism, apical dominance, and branching in plant growth as basic rules (Zhou et al. 2016).

Phototropism is the phenomenon consisting only towards the glare of one direction light source, and represents the plant adaptive mechanism to poor lighting. It is induced by the changes of the oxygen concentration in the light side and dark side. In PGPP, phototropism is summarized as follows: bud growth direction depends on the ambient light intensity in a limited reference area. Light intensity of calculation point is inversely proportional to the square of the distance between calculation point and destination point. Moreover, in order to pay attention to the shadow of the barrier in the reference range, the light intensity of the points under it requires a correction. The calculated light intensity is used for determining the growth rate and the growth direction of the bud.

Negative geotropism is the characteristic that front end of plant grows away from the ground and toward the sky. It is the complement of phototropism mechanism. Gravity vector introduces the effect of negative geotropism into PGPP. The line between the starting point and the ending point is defined as the vertical direction. Gravity vector becomes pointed from destination point to starting point. Both of negative geotropism and phototropism have an effect on the growth direction of the bud (Zhou et al. 2016).

Apical dominance is restraining effect on the growth in buds of lateral branches and is sprouting caused by apical bud of main branch which includes effect on the growth angle of lateral branches. It is due to the effect of two aspects. One of these is polarity of auxin transport. The other one is different response of the bud to auxin concentration. The polarity transport causes the buds of branches have a high oxygen concentration. Meanwhile, apical bud of main branch has appropriate auxin concentration to promote its growth, and apical dominance occurs. The transport amount of auxin polarity is determined by the differences between ages of branches.

Branch means sprouting new branches from main branch to absorb the sunlight. Branching is used to perform the search path diversity. It provides to PGPP for finding optimal path rather than a suboptimal path. When branches grow to branching age, PGPP judges whether to branch in a random way. The growth direction of the bud in the new branch depends on light intensity distribution of bud in original branch. The light intensity of new bud in new branch is randomly selected from the top five large light intensity values of original bud (Zhou et al. 2016).

Fig. 23

The flowchart of PGPP

3.12.1 Basic processes

PGPP includes six basic steps. The flowchart of PGPP is shown in Fig. 23.

• Step 1: Initialization. Initialize variables such as plant and light intensity. Indicate the map data. Set the starting point as the growth point of the first bud.

• Step 2: Calculation of light intensity. Calculate the light intensity in the reference range.

• Step 3: Random branching. If the main branch reaches the branching condition, randomly create new branches.

• Step 4: Calculation of growth vector. Calculate growth vector of light intensity and auxin concentration of the all buds. Then, to obtain the new growth vector, calculate weighted sum of the last period growth vector, gravitational growth vector, and light intensity growth vector.

• Step 5: Plant growth. Each bud performs cell division until a new cell reaches the destination according to its growth vector. If any cell reaches the destination, route search ends and then proceeds to the next step. Otherwise, all the buds no sooner finish the growth of this period than go back to the second step.

• Step 6: Way output. Way planning ends. The optimal way can be established from the start point to the destination point through being searched the parent cell by cell (Zhou et al. 2016).

3.13 Rooted Tree Optimization (RTO)

3.13.1 Roots look for water

A root has a limited capacity, but a group of roots can find together the best location to get water and their density positions around this location or around the way which connects the water resource with the plant. To create the algorithm, a presumptive behavior which is a way how the roots decide together, is added for selecting their orientation according to the wetness degree where the root head is in. These roots move randomly, but when one or more of them finds the wetness, to get the original location of the water and to strengthen their presence around this location, they call other roots. According to RTO algorithm, the solutions remote from water resources are omitted or replaced with the new roots oriented randomly. Moreover, the solutions remote from water resources can be changed by the roots which are next to the best root of the previous generation. The roots with significant wetness degree retain their orientation (Labbi et al. 2016).

3.13.2 RTO

Similar to other methods, the proposed algorithm starts by randomly creating an initial population. Some terms used for determining how initial population of RTO algorithm moves to a new one, are:

• Root: a candidate or proposed solution

• Degree of wetness ($D_w )$: a term that evaluates a candidate and gives fitness degree between population segments (Labbi et al. 2016).

3.13.2.1 The rate of the nearest root to water ($R_n$)

It is the rate which represents number of candidates according to the total population that need rally around the wetter locations. The new population of root, which is the closest to the water is calculated as follows:

$$\begin{aligned} x^{new}\left( {i,It+1} \right) =x^{best}\left( {It} \right) +c_1 \times D_w \left( i \right) \times randn\times l/\left( {N\times It} \right) \end{aligned}$$

(54)

It is a step in the iteration. $x^{new}\left( {It+1} \right)$ is the new candidate for the iteration $\left( {It+1} \right)$; $x^{best}\left( {It} \right)$ is the best solution from the previous generation. i is the number of candidate, N is the population scale.l is the upper bound of parameter, and randn is a random number in the range of $\left[ {-1,1} \right]$. Then a new point $x^{new}$ is lower and upper bounded (Labbi et al. 2016).

3.13.2.2 The rate of the continuous root in its orientation ($R_c$)

It is the rate of members which are directed from the previous way because of closing to the water. The new population of the random root is calculated as:

$$\begin{aligned} x^{new}\left( {i,It+1} \right) =x\left( {i,It} \right) +c_2 \times D_w \left( i \right) \times rand\times \left( {x^{best}\left( {It} \right) -x\left( {i,It} \right) } \right) \end{aligned}$$

(55)

$x\left( {It} \right)$ is the previous candidate for the iteration It, and rand is a random number in the range of $\left[ {0,1} \right]$ (Labbi et al. 2016).

3.13.2.3 The rate of the random root $(R_r$)

It is the rate which represents the number of candidates according to the total population that is randomly distributed at search area, in order to increase the uptake rate of the general solution. In addition, it changes roots with a weak wetness degree from the last generation. The new population of random root is calculated as:

$$\begin{aligned} x^{new}\left( {i,It+1} \right) =x_r \left( {It} \right) +c_3 \times D_w \left( i \right) \times randn\times l/It \end{aligned}$$

(56)

$x_r$ is randomly selected individual from the previous generation; $c_1$, $c_2$, and $c_3$ are configurable parameters.

$R_n ,R_r ,$ and $R_c$ ratios are experimentally determined according to the investigated problem. These ratios are considered as variables affecting the convergence. $R_r$ value is always small compared with others, because it aims to reserve the randomness to be far from local solutions. $D_w$ value is added from the search function of roots for determining a search area according to candidate force (Labbi et al. 2016).

3.13.3 RTO algorithm

The steps of RTO algorithm can be summarized as follows:

• Step 1: Randomly create the first generation which consists of N candidates within variable limits in the search area, and set the numerical values of $R_n$, $R_r$, and $R_c$ ratios.

• Step 2: Evaluate the whole population members for measuring $D_w$ as following:

  $$\begin{aligned} D_w \left( \hbox {i} \right) =\left\{ {{\begin{array}{l} \frac{\hbox {f}_i }{\hbox {max}\left( {\hbox {f}_i } \right) }\quad \hbox {for the maximum objective} \\ 1-\frac{\hbox {f}_i }{\hbox {max}\left( {\hbox {f}_i } \right) }\quad \hbox {for the minimum objective} \\ \end{array} }} \right. ,\quad i=1,2,\ldots ,N \end{aligned}$$

  (57)

  or directly use the fitness regardless of the suitable formula.

• Step 3: Reproduce and replace with the new population. According to $R_n$, $R_r$, and $R_c$ reorder the population using the (54)-(56), according to wetness degree to replace with the new population.

• Step 4: If the termination conditions are not reached, go back to step 2 (Labbi et al. 2016).

Fig. 24 shows the pseudocode of RTO algorithm. It includes two basic procedures: (a) start (b) repeated body until termination conditions cannot be reached.

Fig. 24

The pseudocode of RTO algorithm

4 Discussions

Depending on the source of inspiration, all of the plant based metaheuristic algorithms in the literature have been searched and collected for the first time to present a relatively comprehensive list and to inspire further research. One of the research works in the related literature consist of comparing one of these plant based algorithms to the other nature inspired algorithms. These works have experimentally shown that some plant intelligence based algorithms are better than other nature inspired methods although it is still not quite understood why. Especially, the older plant intelligence based algorithms have been compared with GA and PSO. Algorithms which lack certain basic capabilities such as the mixing and diversity among the solutions can be thought as badly designed. Most of the plant based metaheuristic search and optimization algorithms which have been searched and collected for the first time in this paper have been developed relatively more recently and there is not any work about comparing all of their performances in the selected complex benchmark or engineering problems satisfying the equal conditions. Equal conditions mean using the same starting and termination criterion, equal number of starting search points, the same benchmark function with equal dimensions and intervals for these dimensions, same hardware running the algorithms, same programming languages, and maybe the same programmer. Thus, it can be concluded that there is not a single software available for evaluating all these new plant based algorithms over different types of benchmark functions; this provides an opportunity for the research community to develop the unified software that could be used to simulate the performance of these algorithms over benchmark problems used for search and optimization.

Software which can be developed in near future can also be extended for solving various other types of discrete, combinatorial, NP hard, multi-objective, complex optimization problems etc. It can be concluded that metaheuristic algorithms inspired from plant behaviors have much room to grow since this research community is quite young. Thus, this paper would act as a boon to the research community in identifying the research prospects in the field of metaheuristic optimization.

If more works are performed in relatively more recent plant based algorithms, they can have both mixing and diversity control so that the algorithms can explore the vast search space efficiently, while converge relatively more quickly. Some good and relatively old algorithms such as FPA and SGuA have both global search and intensive local search capabilities, which balance the exploration and exploitation, and they seem partly more efficient in unimodal and multimodal functions or problems. Their solution quality in terms of mean objective value is much better and the value of the standard deviation indicates that the results obtained from them are more consistent due to the huge number of works on their performances. More works should be performed for more recent algorithms such as RTO and PGPP which have been proposed in 2016, RRA and PPA which have been proposed in 2015 in order to increase the performance in terms of convergence, precision, robustness, and general performance.

In future, more comprehensive evaluation of all plant inspired metaheuristic algorithms with graphical and tabular analysis may be focused on. Their variants containing multi objectivity, dynamic parameter selection, different initial population methods, different termination criterion, discrete versions, and their hybrids with other metaheuristic or heuristic methods may be proposed for efficient solutions as these plant based metaheuristic algorithms have high potential to solve various search and optimization problems in different areas. Researchers should be encouraged to implement a detailed performance analysis of these algorithms truly to pick up the best methods for different types of hard problems. Therefore, searching and collecting all of the plant based metaheuristic algorithms in the literature for the first time and inspiring more research to gain better insight into efficient algorithms and solve large-scale real-world problems has been aimed with this paper.

5 Conclusions

Although there are many successful search and optimization algorithms and techniques in the literature; design, development, and implementation of new techniques is an important task under the philosophy of improvement in the scientific field and always searching to design better. Best algorithm that gives the best results for all of the problems have not yet been designed, that is why constantly new artificial intelligence optimization algorithms are proposed or some efficient additions or modifications have been performed to the existing algorithms.

In recent years, researchers have shown that plants exhibit intelligent behaviors. Although there are thirteen different plant intelligence based metaheuristic search and optimization algorithms, they are not known by the researchers of the related area. However, they seem to be very popular in solving of high-dimensional and hard problems due to their efficiency and robustness.

In this paper, all of the metaheuristic algorithms inspired from plant intelligence have been firstly searched, collected, and their properties are introduced in a smooth way. In this way, the main algorithm and source of inspiration are introduced. Besides, the basic steps of the plant intelligence based optimization algorithms are demonstrated. Consequently, studies about related algorithms are shown to reveal how those algorithms helped solving of complex problems.

This paper will help the related researchers to rapidly gain information about novel techniques, the differences between these techniques, and adopting them for different types of complex search and optimization problems.