Novel multi-objective, multi-item and four-dimensional transportation problem with vehicle speed in LR-type intuitionistic fuzzy environment

Abstract

In this paper, we present some novel multi-objective, multi-item and four-dimensional transportation problems in LR-type intuitionistic fuzzy environment. Here, for the first time, the speed of different vehicles and rate of disturbance of speed due to the road condition of different routes for the time minimization objective are introduced. Furthermore, three models are presented under three different conditions. The reduced deterministic models are obtained on implementation of a defuzzification approach by using the accuracy function. Moreover, a new method for converting multi-objective problem into single-objective one is proposed and also we use convex combination method. The models are illustrated by some numerical examples and optimal results are presented.

1 Introduction

It is well known that the traditional transportation problem [1] is an optimization problem, which offers huge potential in decreasing costs involving two kinds of constraints taken into consideration, i.e., availability constraint and demand constraint. Afterward, many researchers have studied this problem from various viewpoints and acquired some important results such as [2,3,4,5]. However, in real-life situation, we have to deal with another constraint besides source constraint and destination constraint, which is conveyance constraint. To obtain minimum total cost, an appropriate mode of transportation is to be resolved at each source. Subsequently, as an extension of the traditional TP, the TP with the conveyance constraint is known as solid transportation problem (STP), which was introduced by Haley [6]. Thereafter, the STP has been taken much into consideration and numerous models have been investigated. In the real situation, the solid transportation problem (STP) plays a very important role in global competition for minimizing solid transportation cost, time, distance, road condition and providing service. For example, Bhatia [7] offered an algorithm to solve a STP with indefinite quadratic objective function. Again Pandian et al. [8] presented a new method applying the principle of zero-point method to find an optimal solution of the STP. Pandian et al. [9] also offered a new method named as bound technique to find cost sensitivity ranges of STP (cf. Pramanik et al. [10]).

In real-life problems, there may be various routes/paths to move from a source to a destination. Some of the roads may be in good condition, whereas others may be in bad condition. Distance may differ in a wide range. Again if the transported item in a transportation system is breakable, it may depend on the type of the vehicle, condition of the road and the distance of the path. So it is more realistic to consider the choice of routes along with the vehicles in a STP. Thus, if along with different vehicles, different routes are also considered in a TP, then the STP is changed to a four-dimensional TP (4DTP) (cf. Bera et al. [11]). As a result, the distance of different routes from different sources to different destinations is necessary to be considered in 4DTPs, which is not considered in traditional TPs or STPs. In addition, if one has to deal with a time minimization problem, then it is obvious to consider the speed of different vehicles as it is not exact for all types of vehicles. So far, none has considered this fact. If time is to be minimized, then short route is to be considered. Again it may happen that the short routes are in bad condition or may be in traffic jump problem most of the time. Accordingly, the speed of the vehicle may be disturbed due to this. Hence, rate of disturbance of speed due to different routes plays an important role in case of time minimization problem in TPs. This phenomenon is also not considered by any researchers till now. Moreover, in a 4DTP, if different types of item are considered, then the TP becomes a multi-item 4DTP (MI4D-TP). For example, normally a constraint on a resource, say, capacity for expenditure, is forced in the model.

Many researchers studied the TP in deterministic environment, and the related parameters are considered as constant numbers. But, in real life, due to the complexity of the social and economic environment, the relevant parameters in the STPs are often treated as uncertain variables to manage the practical situations. In reality, there exists uncertainty everywhere in practical life problems. As a result, it is not suitable to describe the relevant parameters as constant numbers. Nowadays, the researchers are in a rising interest to model and solve the TPs in which all of the parameters are considered in imprecise environment such as random environment and fuzzy environment. The fuzzy programming approach was introduced by Zimmermann [12] for solving linear programming problem with several objective functions. Numerous works on TP have been executed in imprecise environment.

In real-life optimization problems, one may suppose that an object belongs to a set to a certain degree; however, it is possible that he is not sure regarding this. In other words, there may be hesitation or uncertainty about the membership degree. The main point is that the parameters’ demands across the problem are uncertain. However, they are known to fall within a prescribed uncertainty set with some attributed degree. In fuzzy set theory, there is no means to incorporate this hesitation in the membership degree. To incorporate the hesitation in the membership degree, intuitionistic fuzzy sets (IFSs) proposed by Atanassov in 1986 are an extension of type 1 fuzzy set theory. For example, Jimanez et al. [13] developed uncertain solid transportation problems where uncertainty appears in the problem as interval solid transportation problem and fuzzy solid transportation problem. A multi-objective STP in imprecise environments was presented and solved by Pramanik et al. [14]. Again Pramanik et al. [15] considered a fixed-charge multi-objective STP in random fuzzy environment and got the solution. Pramanik et al.[16] also developed a multi-objective solid transportation problem in fuzzy, bi-fuzzy environment via genetic algorithm. Samanta et al. [17], Jana et al. [18] have made some contributions in this field.

Nowadays, fuzzy set theory has been broadly developed and much effort has been given to generalize the ordinary fuzzy set theory concept. As a result, different generalizations and modifications have appeared. For example, an extension of the ordinary fuzzy set theory concept, namely the intuitionistic fuzzy set theory concept, was introduced by Atanassov [19]. Such a concept generalizes the idea of ordinary fuzzy sets by separately considering not only the degree of membership of the elements to a given set, but also the degree of nonmembership along with the degree of hesitation. Thus, the intuitionistic fuzzy set (IFS) concept offers a richer representation to handle the present uncertainty as compared to the ordinary fuzzy sets concept. Angelov [20] introduced an application of the IFSs to optimization problems based on the technique of maximizing the degree of membership and minimizing the degree of nonmembership. Several researchers like Yager [21], Guha et al. [22], Beliakov [23], Hajiagha et al. [24], Chakraborty et al. [25] worked on IFSs. Using chance operator, Chakraborty et al. [26] offered a new approach for solving multi-objective multi-choice, multi-item Atanassova’s intuitionistic fuzzy TP. Again Chakraborty et al. [27] also developed arithmetic operations on generalized intuitionistic fuzzy number and applied them to TP. Chakraborty et al. [28] developed the expected value of intuitionistic fuzzy number (IFN) using credibility measures and used this to solve a multi-objective, multi-item, intuitionistic fuzzy solid transportation problems for damageable items. Jana [29] developed novel arithmetic operations on type 2 intuitionistic fuzzy environment and used them to solve a transportation problem. So far we know, there is no method in the literature for solving STP in LR-type intuitionistic fuzzy environments, though Singh et al. [30] developed and optimized the unrestricted LR-type intuitionistic fuzzy mathematical programming problems. Again Kaur et al. [31] solved fully fuzzy linear programming problems in which the relevant parameters are represented by unrestricted $L{-}R$ flat fuzzy numbers. Ghanbari et al. [32] offered a method for characterization and also presented an approach to solve the fuzzy linear systems with $L{-}R$ fuzzy variables.

The main contributions of this paper are summarized as follows:

• For the first time, some multi-objective, multi-item 4DTPs in LR-type intuitionistic fuzzy environment are formulated.

• Also for the first time, the speed of different vehicles and rate of disturbance of speed due to different routes for the time minimization objective function are considered.

• We present three models; the first model is about transportation of breakable items which depends on different conveyances along different routes and the type of the item, the second one is about transportation of damageable items which depends on only its type, and the third one considers nonbreakable/damageable items.

• The reduced deterministic models are obtained on implementation of a defuzzification approach by using the accuracy function..

• We propose a new method for converting multi-objective optimization problem into single-objective one and also use convex combination method

• The models are illustrated by some numerical examples, and optimal results are presented in tabular forms.

The rest of the paper is organized as follows.

In Sect. 2, the proposed method for converting multi-objective optimization problem into single-objective problem is described. In Sect. 3, notations for the proposed models are listed. In Sect. 4, we formulate the models considered in this paper. Equivalent crisp models are obtained in Sect. 5. The numerical illustration is provided in Sect. 6, and a set of optimal solutions are shown here. In Sect. 7, the practical implication has been given. The concluding remarks are given in Sect. 8. The paper ends with “Appendix,” which reviews some basic definitions and theorems related to IFNs and LR-type IFNs and the convex combination method.

2 Novel method for conversion of multi-objective into single objective

Preliminary ideas on LR-type TIFN, arithmetic operations on LR-type TIFN and convex combination method (CCM) are given in the “Appendix” section.

In this section, a new approach for multi-objective optimization problem is offered. The proposed approach has been motivated by Zimmermann [12] concepts and the CCM.

Let us consider the following multi-objective decision-making model in Eq. (1) as:

$$\begin{aligned} \left\{ \begin{array}{ll} \max &{} \quad {f}_{i}(x); \ i=1, 2, \ldots ,m' \\ \min &{} \quad {f}_{j}(x), \ j=m'+1, m'+2, \ldots ,m\\ \hbox {s.t} &{} \left\{ \begin{array}{ll} {g}_{r}(x) \le {c}_{r} ;\quad r=1, 2, \ldots ,n' \\ {g}_{r}(x) \ge {c}_{r} ;\quad r=n'+1, n'+2, \ldots ,n \\ x \ge 0 \\ \end{array} \right. \\ \end{array} \right. \end{aligned}$$

(1)

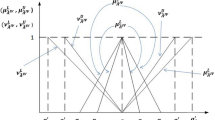
The objective functions $f_{i}(x); i=1, 2, \ldots ,m'$, of model in Eq. (1) are to be maximized. So for each objective, we introduce the membership function as

$$\begin{aligned} \mu _{i}(f_{i}(x))= \left\{ \begin{array}{ll}1 &{} \quad \hbox { for }\quad f_{i}(x) > U^{i} \\ \frac{f_{i}(x)-L^{i}}{U^{i}-L^{i}} &{} \quad \text{ for } \ L^{i} \le f_{i}(x)\le U^{i} \\ 0 &{} \quad \hbox { for }\ f_{i}(x) <L^{i} \end{array} \right. \end{aligned}$$

(2)

where $L^{i}$ and $U^{i}$ are the lower and upper bounds for each objective. Again some of the objective functions $f_{j}(x); j=m'+1, m'+2, \ldots ,m$ of model (1) are to be minimized, so for each objective we introduce the membership function as

$$\begin{aligned} \mu _{j}(f_{j})=\left\{ \begin{array}{ll} 0 &{} \quad \text{ for } f_{j}(x)\ge U^{j} \\ \frac{ U^{j}-f_{j}(x)}{ U^{j}- L^{j}}&{} \quad \text{ for } L^{j}\le f_{j}(x)\le U^{j} \\ 1 &{} \quad \text{ for } f_{j}\le L^{j} \end{array} \right. \end{aligned}$$

(3)

Currently, our major objective is to increase the level of satisfaction of the decision maker, i.e., the membership functions for both the maximizing objective functions and minimizing objective functions. So problem (1) can be modeled as:

$$\begin{aligned} \left\{ \begin{array}{ll} \max &{} [\mu _{i}(f_{i}(x)), \ \quad \quad i=1,2, \ldots , m] \\ \hbox {s.t} &{} \left\{ \begin{array}{ll} {g}_{r}(x) \le {c}_{r} ; \quad r=1, 2, \ldots ,n' \\ {g}_{r}(x) \ge {c}_{r} ; \quad r=n'+1, n'+2, \ldots ,n \\ x \ge 0 \\ \end{array} \right. \\ \end{array} \right. \end{aligned}$$

(4)

This model can be reduced to the single-objective problem as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \max &{} \sum \limits _{i=1}^{m}\alpha _{i}\mu _{i}(f_{i}(x)),\quad \text{ where } \sum \limits _{i=1}^{m}\alpha _{i}=1, 0<\alpha _{i}<1;i=1, 2, \ldots ,m \\ \hbox {s.t} &{} \left\{ \begin{array}{ll} {g}_{r}(x) \le {c}_{r} ;\quad r=1, 2, \ldots ,n' \\ {g}_{r}(x) \ge {c}_{r} ;\quad r=n'+1, n'+2, \ldots ,n \\ x \ge 0 \\ \end{array} \right. \\ \end{array} \right. \end{aligned}$$

(5)

where $\alpha _{i}$ is the weight function of membership function of the ith objective.

Corresponding x and $f_{i}(x)$ of Eq. (5) are the solutions of the problem in Eq. (1).

3 Notations

To formulate the multi-objective, multi-item and four-dimensional transportation model, the following notations are used:

• (i) m = number of sources.

• (ii) n = number of destinations.

• (iii) K = number of conveyances, i.e., different modes of the transportation problem.

• (iv) Q = number of routes.

• (v) T = number of items.

• (vi) ${Z}_k^I$ = the objective functions, where $k=1,2$.

• (vii) ${p}_{it}^I$ = the purchasing price of tth item at the ith origin.

• (viii) ${s}_{jt}^I$ = the selling price of tth item at the jth destination.

• (ix) ${c}_{ijkqt}^I$ = the unit transportation cost of tth item from ith source to jth destination by kth conveyance via qth route per unit distance.

• (x) $x_{ijkqt}$ = the decision variable which is the amount of the tth item to be transported from ith source to jth destination by kth conveyance via qth route.

• (xi) $\beta _{ijkqt}$ = the rate of breakability per unit distance of the tth item from ith source to jth destination by kth conveyance via qth route.

• (xii) $d_{ijq}$ = distance from ith source to jth destination via qth route.

• (xiii) ${v}_{k}$ = speed of the kth conveyance .

• (xiv) ${\delta }_{ijq}$ = Rate of disturbance of speed due to qth route from ith source to jth destination.

• (xv) ${\gamma }_{ijkt}^I$ = loading and unloading time of the tth item with respect to the transportation activity from ith source to jth destination by kth conveyance.

• (xvi) ${a}_{it}^I$ = the amount of the tth item available at the ith origin.

• (xvii) ${b}_{jt}^I$ = the demand of the tth item at the jth destination.

• (xviii) ${e}_k^I$ = capacity of a single vehicle of kth conveyance.

4 Model formulation

We assume that there are m origins (or sources) $O_{i}$$(i=1,2,\ldots ,m)$, n destinations(or demands) $D_{j} (j=1,2,\ldots ,n)$, K conveyances $E_{k} (k=1,2,\ldots ,K),$ i.e., different modes of transport may be trucks, cargo flights, goods trains, ships, etc., Q routes $G_{q} (q=1,2,\ldots ,Q)$ and T items $P_{t} (t=1,2,\ldots ,T)$. Moreover, in this model, the objectives are to maximize the profit incurred by the transportation activities and also to minimize the total transportation time. At the present situation, it is not so simple for anyone to estimate the exact amount of related parameters. Practically, in application of TP, decision makers may face different uncertainties such as availability of raw materials in the sources, demands in the destinations and unit transportation cost due to various unmanageable factors. These unmanageable factors in a TP may be as follows: (1) There exists uncertainty regarding the product availability at a source due to the time factors, (2) there exists some sort of vagueness about the total demand of a newly launched product to the market, (3) there may not be a decision maker who exactly knows the unit transportation cost of the first-time transportation operation.

Considering this fact, we take the problem under LR-type Intuitionistic fuzzy environment, which aims to make service strategies on the tactical planning level. So, we formulate the problem assuming that parameters are all LR-type trapezoidal intuitionistic fuzzy variables.

Furthermore, the transported item is likely to be broken or damaged during the time of transportation. There are several causes for this damageability.

• This damageability may depend on different conveyances along different routes and the type of the items. There are some items mainly made of glass such as ceramics and China clay. These types of items depend on the above conditions.

• Moreover, there are some items where the damageability depends on only its type.

• Again there are a number of items which are not damageable.

So, keeping all these in mind, here we present three models. The first model is about transportation of breakable items which depend on different conveyances along different routes and its type. So here we use $\beta _{ijkqt}$ as the rate of breakability per unit distance of the tth item from ith source to jth destination by kth conveyance via qth route. The second one is about damageable items which depend on only their type. Here, we use $\beta _{t}^I$ as the rate of breakability per unit distance of the tth item. And the third one considers nonbreakable/damageable items.

4.1 Model 1: model with breakable items which depend on conveyances, routes and items

The First objective of the problem is to maximize the total profit, which is as follows:

$$\begin{aligned} \max \,\,\,\, {Z}_1^I= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T}\bigg [({s}_{jt}^I(1-\beta _{ijkqt} d_{ijq}) -{p}_{it}^I-{c}_{ijkqt}^I d_{ijq})\,\,\,x_{ijkqt}\bigg ] \end{aligned}$$

The other objective is to minimize the total transportation time, which is as follows:

$$\begin{aligned} \min \,\,\,\, {Z}_2^I= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\frac{1}{{v}_{k} (1-\delta _{ijq})}d_{ijq} {y}_{ijkq}+ \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T} {\gamma }_{ijkt}^Ix_{ijkqt} \end{aligned}$$

Here, if the items are transported from ith source to jth destination by kth conveyance via qth route, then only the transporting time will be taken. So, we introduce a binary relation as

$$\begin{aligned} y_{ijkq}= & {} \left\{ \begin{array}{llll} 1, \quad \text{ if } \sum \limits _{t=1}^{T}x_{ijkqt}>0;\\ 0, \quad \text{ if } \sum \limits _{t=1}^{T}x_{ijkqt}=0\end{array} \right. \end{aligned}$$

Now, the constraints are the supply constraints, demand constraints and capacity constraints. As the quantity of a item from a source cannot exceed the supply capacity, so we have

$$\begin{aligned}&\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}x_{ijkqt}\le {a}_{it}^I,\quad i=1,2,3,\ldots ,m; t=1,2,\ldots ,T \end{aligned}$$

Again the quantity of a item transported to a destination should not be less than its demand, that is

$$\begin{aligned}&\sum _{i=1}^{m}\sum _{k=1}^{K}\sum _{q=1}^{Q}(1-\beta _{ijkqt} d_{ijq})x_{ijkqt}\ge {b}_{jt}^I,\quad j=1,2,3,\ldots ,n; t=1,2,\ldots ,T \end{aligned}$$

The third constraint requires the total amount of items transported from different sources to different destinations by conveyance k to be not greater than its transportation capacity. So we have

$$\begin{aligned}&\sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{q=1}^{Q}\sum _{t=1}^{T}x_{ijkqt}\ge {e}_{k}^I, \quad k=1,2,\ldots ,K \end{aligned}$$

It is usual to have the nonnegativity of decision variable $x_{ijkqt}$, that is

$$\begin{aligned}&x_{ijkqt}\ge 0,\quad i=1,2,3;\, j=1,2,3,\ldots ,n; k=1,2,\ldots ,K; q=1,2,\ldots ,Q; t=1,2,\ldots ,T \end{aligned}$$

So, the multi-objective, multi-item and four-dimensional transportation problem can be written as:

$$\begin{aligned} \max \,\,\,\, {Z}_1^I= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T}\bigg [({s}_{jt}^I(1-\beta _{ijkqt} d_{ijq}) -{p}_{it}^I-{c}_{ijkqt}^I d_{ijq})\,\,\,x_{ijkqt}\bigg ] \end{aligned}$$

(6)

$$\begin{aligned} \min \,\,\,\, {Z}_2^I= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\frac{1}{{v}_{k}(1-\delta _{ijq})}d_{ijq} {y}_{ijkq}+ \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T}{\gamma }_{ijkt}^Ix_{ijkqt} \end{aligned}$$

(7)

where

$$\begin{aligned} y_{ijkq}= & {} \left\{ \begin{array}{llll} 1, \quad \text{ if } \sum \limits _{t=1}^{T}x_{ijkqt}>0;\\ 0, \quad \text{ if } \sum \limits _{t=1}^{T}x_{ijkqt}=0\end{array} \right. \end{aligned}$$

(8)

subject to

$$\begin{aligned}&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q}x_{ijkqt}\le {a}_{it}^I,\quad i=1,2,3,\ldots ,m; t=1,2,\ldots ,T \end{aligned}$$

(9)

$$\begin{aligned}&\sum \limits _{i=1}^{m}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q}(1-\beta _{ijkqt} d_{ijq})x_{ijkqt}\ge {b}_{jt}^I, \quad j=1,2,3,\ldots ,n; t=1,2,\ldots ,T \end{aligned}$$

(10)

$$\begin{aligned}&\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{n}\sum \limits _{q=1}^{Q}\sum \limits _{t=1}^{T}x_{ijkqt}\ge {e}_{k}^I,\quad k=1,2,\ldots ,K \end{aligned}$$

(11)

$$\begin{aligned}&x_{ijkqt}\ge 0,\quad i=1,2,3\ldots ,m;\, j=1,2,3,\ldots ,n;\, k=1,2,\ldots ,K; \nonumber \\&\quad q=1,2,\ldots ,Q;\, t=1,2,\ldots ,T \end{aligned}$$

(12)

4.2 Model 2: model with breakable items which depend on only their type

Now, we formulate a problem where we select some items where the damageability depends on only its type. So here we use $\beta _{t}$ as the rate of breakability per unit distance of the tth item instead of $\beta _{ijkqt}$ which is taken in the previous model. So the first objective and the second constraint are changed. The rest are same as the previous model. As a result, the multi-objective, multi-item and four-dimensional transportation problem can be written as:

$$\begin{aligned} \left\{ \begin{array}{ll} \max \,\,\,\, {Z}_1^I = \sum \limits _{i=1}^{m}\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{K} \sum \limits _{q=1}^{Q}\sum \limits _{t=1}^{T}\bigg [({s}_{jt}^I(1-\beta _{t} d_{ijq}) -{p}_{it}^I-{c}_{ijkqt}^I d_{ijq})\,\,\,x_{ijkqt}\bigg ]\\ \text{ with } \text{ Eqs. } \text{(7) } \text{ and } \text{(8) } \end{array} \right. \end{aligned}$$

(13)

subject to

$$\begin{aligned} \left\{ \begin{array}{ll} \text{ Equations } \text{(9), } \text{(11), } \text{(12) } \text{ and }\\ \sum \limits _{i=1}^{m}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q}(1-\beta _{t} d_{ijq})x_{ijkqt}\ge {b}_{jt}^I,\quad j=1,2,3,\ldots ,n; t=1,2,\ldots ,T \end{array} \right. \end{aligned}$$

(14)

4.3 Model 3: model with no breakable items

Here, we present a model where we select some items where no damageability occurs. So, we do not consider any rate of breakability in this case. The multi-objective, multi-item and four-dimensional transportation problem becomes:

$$\begin{aligned} \left\{ \begin{array}{ll} \max \,\,\,\, {Z}_1^I = \sum \limits _{i=1}^{m}\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q}\sum \limits _{t=1}^{T}\bigg [({s}_{jt}^I -{p}_{it}^I-{c}_{ijkqt}^I d_{ijq})\,\,\,x_{ijkqt}\bigg ]\\ \text{ with } \text{ Eqs. } \text{(7) } \text{ and } \text{(8) } \end{array} \right. \end{aligned}$$

(15)

subject to

$$\begin{aligned} \left\{ \begin{array}{ll} \text{ Equations } \text{(9), } \text{(11), } \text{(12) } \text{ and }\\ \sum \limits _{i=1}^{m}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q}x_{ijkqt}\ge {b}_{jt}^I,\quad j=1,2,3,\ldots ,n; \quad t=1,2,\ldots ,T \end{array} \right. \end{aligned}$$

(16)

5 Equivalent crisp problem

The above TP with imprecise market supplies, demands, capacities, costs and loading and unloading time can be stated as equivalent deterministic problem by using the accuracy function, which is given as follows.

5.1 For Model 1

The deterministic form is as follows:

$$\begin{aligned} \max f[{Z}_1^I]= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T}\bigg (f[{s}_{jt}^I](1-\beta _{ijkqt} d_{ijq}) -f[{p}_{it}^I]-f[{c}_{ijkqt}^I] d_{ijq}\bigg )x_{ijkqt} \end{aligned}$$

(17)

$$\begin{aligned} \min f[{Z}_2^I]= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\frac{1}{{v}_{k}(1-\delta _{ijq})} d_{ijq} {y}_{ijkq}+ \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T}f[{\gamma }_{ijkt}^I]x_{ijkqt} \end{aligned}$$

(18)

where

$$\begin{aligned} y_{ijkq}= & {} \left\{ \begin{array}{llll} 1, \quad \text{ if } \sum \limits _{t=1}^{T}x_{ijkqt}>0;\\ 0, \quad \text{ if } \sum \limits _{t=1}^{T}x_{ijkqt}=0\end{array} \right. \end{aligned}$$

(19)

subject to

$$\begin{aligned}&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q}x_{ijkqt}\le f[{a}_{it}^I], \quad i=1,2,3,\ldots ,m; \,t=1,2,\ldots ,T \end{aligned}$$

(20)

$$\begin{aligned}&\sum \limits _{i=1}^{m}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q} (1-\beta _{ijkqt}d_{ijq})x_{ijkqt}\,\ge\, f[{b}_{jt}^I],\quad j=1,2,3,\ldots ,n; t=1,2,\ldots ,T \end{aligned}$$

(21)

$$\begin{aligned}&\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{n}\sum \limits _{q=1}^{Q} \sum \limits _{t=1}^{T}x_{ijkqt}\ge f[{e}_{k}^I], \quad k=1,2,\ldots ,K \end{aligned}$$

(22)

$$\begin{aligned}&x_{ijkqt}\ge 0, \quad i=1,2,3;\, j=1,2,3,\ldots ,n;\, k=1,2,\ldots ,K; q=1(Q);\, t=1(T). \end{aligned}$$

(23)

Here, ${s}_{jt}^I$${p}_{it}^I$, ${c}_{ijkqt}^I$, ${\gamma }_{ijkt}^I$, ${a}_{it}^I$, ${b}_{jt}^I$ and ${e}_{k}^I$ are considered as LR-type TIFNs; these can be denoted as: ${s}_{jt}^I=(s_{jt}^1,s_{jt}^2;s_{jt}^l,s_{jt}^r;s_{jt}^{l'},s_{jt}^{r'})$, ${p}_{it}^I=(p_{it}^1,p_{it}^2;p_{it}^l,p_{it}^r;p_{it}^{l'},p_{it}^{r'})$, ${c}_{ijkqt}^I=(c_{ijkqt}^1,c_{ijkqt}^2;c_{ijkqt}^l,c_{ijkqt}^r;c_{ijkqt}^{l'},c_{ijkqt}^{r'})$, ${\gamma }_{ijkt}^I=({\gamma }_{ijkt}^1,{\gamma }_{ijkt}^2;{\gamma }_{ijkt}^l,{\gamma }_{ijkt}^r;{\gamma }_{ijkt}^{l'},{\gamma }_{ijkt}^{r'})$, ${a}_{it}^I=(a_{it}^1,a_{it}^2;a_{it}^l,a_{it}^r;a_{it}^{l'},a_{it}^{r'})$, ${b}_{jt}^I=(b_{jt}^1,b_{jt}^2;b_{jt}^l,b_{jt}^r;b_{jt}^{l'},b_{jt}^{r'})$, ${e}_{k}^I=(e_{k}^1,e_{k}^2;e_{k}^l,e_{k}^r;e_{k}^{l'},e_{k}^{r'}),$ respectively. Then, the above model in Eqs. (17)–(23) can be written in the following form by using Eq. (55):

$$\begin{aligned} \max \,\,\,\, f[{Z}_1^I]= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T} \bigg [\frac{2s_{jt}^1+2s_{jt}^2-\frac{s_{jt}^l}{2}+\frac{s_{jt}^r}{2} -\frac{s_{jt}^{l'}}{2} +\frac{s_{jt}^{r'}}{2}}{4}\times \bigg (1- \beta _{ijkqt} d_{ijq}\bigg )\nonumber \\&- \frac{2p_{it}^1+2p_{it}^2-\frac{p_{it}^l}{2}+\frac{p_{it}^r}{2}-\frac{p_{it}^{l'}}{2}+\frac{p_{it}^{r'}}{2}}{4} \nonumber \\ {}- & {} \bigg (\frac{2c_{ijkqt}^1+2c_{ijkqt}^2-\frac{c_{ijkqt}^l}{2} +\frac{c_{ijkqt}^r}{2}-\frac{c_{ijkqt}^{l'}}{2}+\frac{c_{ijkqt}^{r'}}{2}}{4}\bigg ) \times \bigg (d_{ijq}\bigg )\bigg ]\,\,\,x_{ijkqt} \end{aligned}$$

(24)

$$\begin{aligned} \min \,\,\,\, f[{Z}_2^I]= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\frac{1}{{v}_{k} (1-\delta _{ijq})} d_{ijq} {y}_{ijkq}\nonumber \\&+\sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T} \frac{2\gamma _{ijkt}^1+2\gamma _{ijkt}^2-\frac{\gamma _{ijkt}^l}{2} +\frac{\gamma _{ijkt}^r}{2}-\frac{\gamma _{ijkt}^{l'}}{2}+\frac{\gamma _{ijkt}^{r'}}{2}}{4}x_{ijkqt} \end{aligned}$$

(25)

where

$$\begin{aligned} y_{ijkq}= & {} \left\{ \begin{array}{llll} 1, \quad \text{ if } \sum \limits _{t=1}^{T}x_{ijkqt}>0;\\ 0, \quad \text{ if } \sum \limits _{t=1}^{T}x_{ijkqt}=0\end{array} \right. \end{aligned}$$

(26)

subject to

$$\begin{aligned}&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q} x_{ijkqt}\le \frac{2a_{it}^1+2a_{it}^2-\frac{a_{it}^l}{2}+\frac{a_{it}^r}{2} -\frac{a_{it}^{l'}}{2}+\frac{a_{it}^{r'}}{2}}{4}, \quad i=1(m); t=1,2,\ldots ,T \end{aligned}$$

(27)

$$\begin{aligned}&\sum \limits _{i=1}^{m}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q} (1-\beta _{ijkqt}d_{ijq})x_{ijkqt}\ge \frac{2b_{jt}^1+2b_{jt}^2-\frac{b_{jt}^l}{2} +\frac{b_{jt}^r}{2}-\frac{b_{jt}^{l'}}{2}+\frac{b_{jt}^{r'}}{2}}{4},\quad j=1(n); t=1(T) \end{aligned}$$

(28)

$$\begin{aligned}&\sum \limits _{i=1}^{m}\sum \limits _{j=1}^{n}\sum \limits _{q=1}^{Q} \sum \limits _{t=1}^{T}x_{ijkqt}\ge \frac{2e_{k}^1+2e_{k}^2-\frac{e_{k}^l}{2} +\frac{e_{k}^r}{2}-\frac{e_{k}^{l'}}{2}+\frac{e_{k}^{r'}}{2}}{4}, \quad k=1,2,\ldots , K \end{aligned}$$

(29)

$$\begin{aligned}&x_{ijkqt}\ge 0,\quad i=1,2,3;\, j=1,2,3,\ldots ,n;\, k=1,2,\ldots ,K; q=1,2,\ldots ,Q. \end{aligned}$$

(30)

5.2 For Model 2

Here, all the parameters are the same as Model 1 except the rate of breakability, i.e., ${\beta }_{t}^I$. We consider the rate of breakability as ${\beta }_{t}^I=({\beta }_{t}^1,{\beta }_{t}^2;{\beta }_{t}^l,{\beta }_{t}^r;{\beta }_{t}^{l'},{\beta }_{t}^{r'})$, By using the accuracy function values as stated in Eq. (55), the deterministic equivalent form of Model 2 can be written as follows:

$$\begin{aligned} \max \,\,\,\, f[{Z}_1^I]= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T} \bigg [\bigg (\frac{2s_{jt}^1+2s_{jt}^2-\frac{s_{jt}^l}{2}+\frac{s_{jt}^r}{2} -\frac{s_{jt}^{l'}}{2} +\frac{s_{jt}^{r'}}{2}}{4}\bigg )\times (1-\beta _{t}d_{ijq})\nonumber \\&-\frac{2p_{it}^1+2p_{it}^2-\frac{p_{it}^l}{2}+\frac{p_{it}^r}{2} -\frac{p_{it}^{l'}}{2}+\frac{p_{it}^{r'}}{2}}{4} \nonumber \\&-\bigg (\frac{2c_{ijkqt}^1+2c_{ijkqt}^2-\frac{c_{ijkqt}^l}{2} +\frac{c_{ijkqt}^r}{2}-\frac{c_{ijkqt}^{l'}}{2}+\frac{c_{ijkqt}^{r'}}{2}}{4}\bigg ) \times \bigg (d_{ijq}\bigg )\bigg ]\,\,\,x_{ijkqt} \end{aligned}$$

(31)

with Eqs. (25) and (26) subject to Eqs. (27), (29), (30) and

$$\begin{aligned}&\sum \limits _{i=1}^{m}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q}(1-\beta _{t} d_{ijq})x_{ijkqt}\ge \frac{2b_{jt}^1+2b_{jt}^2-\frac{b_{jt}^l}{2} +\frac{b_{jt}^r}{2}-\frac{b_{jt}^{l'}}{2}+\frac{b_{jt}^{r'}}{2}}{4},\nonumber \\&j=1,2,3,\ldots ,n; t=1,2,\ldots ,T \end{aligned}$$

(32)

5.3 For Model 3

Here, the deterministic equivalent form of Model 3 is as follows:

$$\begin{aligned} \max \,\,\,\, f[{Z}_1^I]= & {} \sum _{i=1}^{m}\sum _{j=1}^{n}\sum _{k=1}^{K}\sum _{q=1}^{Q}\sum _{t=1}^{T} \bigg [\frac{2s_{jt}^1+2s_{jt}^2-\frac{s_{jt}^l}{2}+\frac{s_{jt}^r}{2} -\frac{s_{jt}^{l'}}{2} +\frac{s_{jt}^{r'}}{2}}{4}\nonumber \\&-\frac{2p_{it}^1+2p_{it}^2-\frac{p_{it}^l}{2}+\frac{p_{it}^r}{2} -\frac{p_{it}^{l'}}{2}+\frac{p_{it}^{r'}}{2}}{4} \nonumber \\&-\bigg (\frac{2c_{ijkqt}^1+2c_{ijkqt}^2-\frac{c_{ijkqt}^l}{2} +\frac{c_{ijkqt}^r}{2}-\frac{c_{ijkqt}^{l'}}{2}+\frac{c_{ijkqt}^{r'}}{2}}{4}\bigg ) \times \bigg (d_{ijq}\bigg )\bigg ]\,\,\,x_{ijkqt} \end{aligned}$$

(33)

with Eqs. (25) and (26) subject to Eqs. (27), (29), (30) and

$$\begin{aligned}&\sum \limits _{i=1}^{m}\sum \limits _{k=1}^{K}\sum \limits _{q=1}^{Q}x_{ijkqt}\ge \frac{2b_{jt}^1+2b_{jt}^2-\frac{b_{jt}^l}{2}+\frac{b_{jt}^r}{2}-\frac{b_{jt}^{l'}}{2}+\frac{b_{jt}^{r'}}{2}}{4}, j=1(n); t=1(T). \end{aligned}$$

6 Numerical experiment

In this segment, the following example of a multi-objective, multi-item and four-dimensional transportation problem to illustrate the efficiency and effectiveness of the proposed approach is considered. The selling prices, purchasing costs of different items, availabilities of these items in the corresponding origins, demands in the destinations, capacity of each vehicle, unit transportation costs of different items per unit distance and loading and unloading time are assumed as LR-type TIFNs, which are as follows:

6.1 Input data

In this experiment, we assume two origins or sources, two destinations, two conveyances, two routes from each source to each destination and two items, i.e., $m =2,\, n =2, \,K =2,\, Q=2$ and $T=2$.

The availabilities of items in the origins, the demands of items in the destinations and the capacity of conveyances are given in Tables 1, 2 and 3.

Table 1 Availabilities in the sources

Table 2 Demands in the destinations

Table 3 Capacities of the two types for conveyances

Table 4 Purchasing prices for different items

Now, the purchasing price, selling price of different items and unit transportation cost of different items per unit distance between different origins and destinations by different conveyances via different routes are given in Tables 4, 5 and 6.

Table 5 Selling prices for different items

Table 6 Unit transportation costs of different items per unit distance

Again rate of breakability of different items per unit distance, distance between different origins and destinations via different routes, speed of the different conveyances, rate of disturbance of speed due to different routes between different origins and destinations are given in Tables 7, 8, 9 and 10.

Table 7 Rate of breakability of different items per unit distance

Table 8 Distance from the sources to the destinations via different routes

Table 9 Speed of the two types of conveyances

Table 10 Rate of disturbance of speed due to two routes

On addition, the loading and unloading times with respect to the transportation activity of two items from different sources to different destinations by different conveyances are given in Table 11.

Table 11 Loading and unloading times

6.2 Optimum results

The generalized reduced gradient method (GRG) technique is a method for solving NLP and LPP problems for handling equality as well as inequality constraints in an optimization problem. The solution techniques used here are the generalized reduced gradient (GRG) technique (using LINGO-14.0 solver).

6.2.1 For Model 1

The deterministic optimization problems of Model 1 given by Eqs. (24)–(30) are solved for the above data. We have calculated the values of $U^{i}$ and $L^{i}, \,i=1,2.$ for each objective separately. These values are given as follows:

$$\begin{aligned} U^{1}=23512.71,\quad L^{1}=13634.39,\quad U^{2}=103.07,\quad L^{2}=43.85 \end{aligned}$$

As the first objective is to maximize and the second objective is to minimize, using Eqs. (2) and (3) the membership functions $\mu _{1}(Z_1(x))$ and $\mu _{2}(Z_2(x))$ are defined as follows:

$$\begin{aligned} \mu _{1}(Z_1(x))&= \left\{ \begin{array}{ll} 1 & \quad \text{ for } Z_1(x)\ge 23512.71 \\ \frac{Z_1(x)-13634.39}{23512.71-13634.39}&{}\quad \text{ for } 13634.39\le Z_1(x)\le 23512.71 \\ 0 &\quad \text{ for } Z_1(x)\le 13634.39 \end{array} \right. \\ \mu _{1}(Z_2(x))&= \left\{ \begin{array}{ll} 0 &\quad \text{ for } Z_2(x)\ge 103.07 \\ \frac{103.07-Z_2(x)}{103.07-43.85}&{}\quad \text{ for } 43.85\le Z_2(x)\le 103.07 \\ 1 &\quad \text{ for } Z_2(x)\le 43.85 \end{array} \right. \end{aligned}$$

Now to get an efficient solution, we compute the following reduced deterministic single-objective problem with the constraints in Eqs. (27)–(30).

$$\begin{aligned} \begin{array}{ll} \max &{} \alpha _{1}\mu _{1}(Z_{1}(x))+\alpha _{2}\mu _{2}(Z_{2}(x)), \text{ where }\,\, \alpha _{1}+\alpha _{2}=1, 0<\alpha _{i}<1\\ \end{array} \end{aligned}$$

(34)

After solving this, we obtain the solutions for total profit $(Z_1)$ and total transportation time $(Z_2)$ of the proposed Model 1 Eqs. (6)–(12) for the above data. The solutions are listed in Table 12. We also obtain the solutions for Model 1 after conversion of multi-objective into single objective by using CCM, which is given in Table 13.

Table 12 Optimum results with different values of $\alpha _{1}$, $\alpha _{2}$ via proposed method for Model 1

Table 13 Optimum results via convex combination method for Model 1

6.2.2 For Model 2

To get the optimum results for this model, we use the above data except the rate of breakability, i.e., $\beta _{ijkqt}$. The corresponding values are $\beta _{1}=0.005$, $\beta _{2}=0.01$. With respect to the deterministic optimization problems of Model 2 given by Eqs. (25)–(27) and (29)–(32) using these data, the calculated values of $U^{i}$ and $L^{i}, \,i=1,2.$ are given as follows:

$$\begin{aligned} U^{1}=36331.59,\quad L^{1}=13026.18,\quad U^{2}=182.76,\quad L^{2}=39.25 \end{aligned}$$

Consequently, we formulate the membership functions $\mu _{1}({Z}_{1})$ and $\mu _{2}({Z}_{2})$. Then, after getting the reduced deterministic single-objective problem, we obtain the solutions of Model 2 (Eqs. (13) and (14)), which are listed in Table 14. Again Table 15 contains the solutions of Model 2 after conversion of multi-objective into single objective by using CCM.

Table 14 Optimum results with different values of $\alpha _{1}$, $\alpha _{2}$ via proposed method for Model 2

Table 15 Optimum results via convex combination method for Model 2

6.2.3 For Model 3

At last, we get the optimum results for Model 3 by using the same input data as given in Sect. 6.1 except the rate of breakability, because in this model we consider nonbreakable/damageable items. In this case, the calculated values of $U^{i}$ and $L^{i}, \,i=1,2.$ are given as follows:

$$\begin{aligned} U^{1}=48250.95,\quad L^{1}=13634.39,\quad U^{2}=263.50,\quad L^{2}=49.99 \end{aligned}$$

Here also, we formulate the membership functions $\mu _{1}({Z}_{1})$ and $\mu _{2}({Z}_{2})$. Then, after getting the reduced deterministic single-objective problem, we obtain the solutions of Model 3 given by Eqs. (15) and (16), which are listed in Table 16. Again Table 17 contains the solutions of Model 3 after conversion of multi-objective into single objective by using CCM.

Table 16 Optimum results with different values of $\alpha _{1}$, $\alpha _{2}$ via proposed method for Model 3

6.3 Discussion

Tables 12, 14 and 16 give the optimum results for Model 1, Model 2 and Model 3, respectively, by our proposed method of conversion of multi-objective optimization problem into single-objective optimization problem. Here, the optimum results are presented for different values of the weight functions of the membership functions of two objectives. While we increase the weight function of the membership function of the first objective, i.e., $\alpha _1,$ and decrease the weight function of the membership function of the second objective, i.e., $\alpha _2,$, we observe that the profit increases and the time also increases which is an expected phenomenon as we have to maximize profit and minimize time. Also we observe that the membership functions of the objective functions change as we desire. Again Tables 13, 15 and 17 give the optimum results for Model 1, Model 2 and Model 3, respectively, by CCM.

In Model 1, considering the highest value of $\alpha _1$ and the lowest value of $\alpha _2$ among all the taken values, the optimum profit is $23,461.33 and optimum time is 94.03 min. Again considering the lowest value of $\alpha _1$ and the highest value of $\alpha _2$ among all the taken values, the optimum profit is $13,634.39 and optimum time is 55.81 min. However, in the second model for the highest value of $\alpha _1$ and for the lowest value of $\alpha _2$ among all the considering values, the optimum profit is $36,196.62 and optimum time is 146.76 min. Again for the lowest value of $\alpha _1$ and the highest value of $\alpha _2$ among all the taken values, the optimum profit is $13,026.18 and optimum time is 39.25 min. In Model 3 for the highest value of $\alpha _1$ and the lowest value of $\alpha _2$ among all the taken values, the optimum profit is $48,063.95 and optimum time is 156.83 min. Again for the lowest value of $\alpha _1$ and the highest value of $\alpha _2$ among all the considering values, the optimum profit is $44,058.75 and optimum time is 85.58 min. From these results, we have observed that for Model 1, we get maximum profit. Again considering Model 3, we get minimum profit, whereas a moderate profit is obtained for Model 2, which is expected. This is because in Model 1, damage of the items occurs and it depends on different conveyances along different routes and the type of the item, in Model 2 damage of the items occurs but it depends on only its type and in Model 3, no damage occurs.

Table 17 Optimum results via convex combination method for Model 3

7 Practical implication

The proposed model is very much helpful in the real-world business sectors. A retailer, Mr. Parimal Das, has outlets of different types of glass containers at three different places Haldia, Kharagpur and Panskura in West Bengal, India. He collects the products from different manufacturing companies situated in Kolkata, Howrah and Durgapur in West Bengal, India. The products can be transported from different manufacturing companies to the retailer through different paths such as NH-4, NH-6 (NH: National Highway) and other village paths using different conveyances like lorry, tempo, truck, etc. Since there are different paths between one manufacturing company and one retailer, the distances will differ. Moreover, as glass container is a breakable item, depending on the path and the type of the conveyance, rate of breakability will be different. On the other hand, as there are different types of conveyances between one manufacturing company and one retailer, the speed of each conveyance is different, which will affect the time minimization objective. Furthermore, depending on the path, the speed of each conveyance will vary due to the road condition. As a result, rate of disturbance of speed occurs. As customers’ mood is unpredictable, the availabilities at different manufacturing companies vary, different prices, times vary; these parameters can be represented as uncertain or imprecise quantities by LR-type TIFNs. Hence, the present investigation will be helpful to execute the above real-life phenomena.

8 Conclusions

Here, we concentrate on dealing with novel multi-objective, multi-item 4DTP with the relevant parameters in $L{-}R$-type intuitionistic fuzzy environment. To the best of our knowledge, this is not done so far. It is more realistic to consider the choice of routes along with the vehicles in a TP, as we have done here. As a result, the distance of different routes from different sources to different destinations is taken into consideration. For the first time, the speed of different vehicles and rate of disturbance of speed due to different routes for the time minimization objective are introduced which are quite realistic. The reduced deterministic models are obtained on implementation of a defuzzification approach by using the accuracy function. We propose a new method for converting multi-objective problem into single objective one. Here, we present three models: The first model is about transportation of breakable items which depends on different conveyances along different routes and the type of the item, the second one is about transportation of damageable items which depends on only its type, and the third one considers nonbreakable/damageable items. The models are illustrated by some numerical examples, and optimal results are presented in tabular forms for all the models. In the future, this approach can be applied for different realistic problems such as supply chain network design, transportation problems including space constraints, price discounts on the basis of amount of transported units. As a direction for future research, more investigation can be carried out to develop a multi-choice, multi-objective 4DTP and also to include the aspects related to the sustainability in the 4DTP as well.

Appendix

1.1 Preliminaries

In this section, we recall some basic definitions and results which will be used in the next sections of this paper.

Definition 1

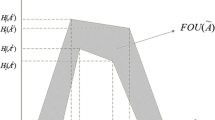
An intuitionistic fuzzy set (IFS) is a generalization of the ordinary fuzzy sets, which is characterized by a membership function and a nonmembership function. Let $X=\{ x_1 , x_2 ,\ldots , x_n \}$ be a collection of some objects, then an intuitionistic fuzzy set $A^{I}$ in X is defined as the form of an ordered triplet $A^{I} = \{\langle x_i,\mu _{A^{I}}(x_i), \nu _{A^{I}}(x_i)\rangle / x_i \in X \}$, where $\mu _{A^{I}}(x_i): X \rightarrow [0, 1]$ is called the membership function or grade of membership of $x_i$ in $A^{I}$ and $\nu _{A^{I}}(x_i): X [0, 1]$ is called the nonmembership function or grade of nonmembership of $x_i$ in $A^{I}$ satisfying the condition $0 \le \mu _{A^{I}}(x_i) + \nu _{A^{I}}(x_i) \le 1$. $\pi _{A^{I}}(x)=1-\mu _{A^{I}}(x) - \nu _{A^{I}}(x)$ represents the degree of hesitation or the degree of indeterminacy of $x_i$ being in $A^{I}$ in X and $0\le \pi _{A^{I}}\le 1$.

Definition 2

The $\alpha$-cut of an IFS $A^{I}$ is denoted as $A^{I}_{\alpha }$ and is given by:

$$\begin{aligned} A^{I}_{\alpha } = \{x\in X:\mu _{A^{I}}(x)\ge \alpha \}, \quad \forall \alpha \in [0,1] \end{aligned}$$

Definition 3

The $\beta$-cut of an IFS $A^{I}$ is denoted as $A^{I}_{\beta }$ and is given by:

$$\begin{aligned} A^{I}_{\beta } = \{x\in X:\nu _{A^{I}}(x)\le \beta \}, \quad \forall \beta \in [0,1] \end{aligned}$$

Definition 4

The $(\alpha ,\beta )$-cut of an IFS $A^{I}$ is denoted as $A^{I}_{\alpha , \beta }$ and is given by:

$$\begin{aligned} A^{I}_{\alpha , \beta } = \{x\in X:\mu _{A^{I}}(x)\ge \alpha , \nu _{A^{I}}(x)\le \beta ; \alpha +\beta \le 1\}, \quad \forall \alpha , \beta \in [0,1] \end{aligned}$$

Definition 5

An IFS $A^{I} = \{\langle x,\mu _{A^{I}}(x), \nu _{A^{I}}(x)\rangle / x \in {\mathfrak {R}}\}$ is called an intuitionistic fuzzy number (IFN) if the following hold

• (i) There exists $m \in {\mathfrak {R}}$ such that $\mu _{A^{I}}(m)=1$ and $\nu _{A^{I}}(m)=0$ (m is called the mean value of $A^{I}$)

• (ii) The membership function $\mu _{A^{I}}$ and nonmembership function $\nu _{A^{I}}$ are piecewise continuous functions from R to the closed interval [0, 1] and $0 \le \mu _{A^{I}}(x) + \nu _{A^{I}}(x)\le 1,$ ,$\forall x\in {\mathfrak {R}}$. $\mu _{A^{I}}$, $\nu _{A^{I}}$ are of the following forms:

  $$\begin{aligned} \mu _{A^{I}}(x)= \left\{ \begin{array}{ll} f_{1}(x), &{} \quad \text{ for } m-l< x< m\\ 1,&{} \quad \text{ for } x=m \\ f_{2}(x),&{} \quad \text{ for } m< x <m+r\\ 0, &{} \quad \text{ otherwise } \end{array} \right. \end{aligned}$$

  and

  $$\begin{aligned} \nu _{A^{I}}(x)= \left\{ \begin{array}{ll} g_{1}(x), &{} \quad \text{ for } m-l'< x< m; 0\le f_{1}(x)+g_{1}(x)\le 1\\ 0,&{}\quad \text{ for } x=m \\ g_{2}(x),&{} \quad \text{ for } m< x <m+r'; 0\le f_{2}(x)+g_{2}(x)\le 1\\ 1, &{} \quad \text{ otherwise } \end{array} \right. \end{aligned}$$

Here, $f_{1}$ and $f_{2}$ are piecewise continuous, strictly increasing and strictly decreasing functions in $(m-l, m)$ and $(m, m+r),$ respectively. Again $g_{1}$ and $g_{2}$ are piecewise continuous, strictly decreasing and strictly increasing functions in $(m-l', m)$ and $(m, m+r'),$ respectively. l and r are the left and right spreads of membership function $\mu _{A^{I}},$ respectively. Again $l'$ and $r'$ are the left and right spreads of nonmembership function $\nu _{A^{I}},$ respectively. The IFN $A^{I}$ is represented by $(m; l, r; l', r')$.

Definition 6

An IFN $A^{I}$ is called trapezoidal intuitionistic fuzzy number (TIFN) if its membership function $\mu _{A^{I}}$ and nonmembership function $\nu _{A^{I}}$ are as follows:

$$\begin{aligned} \mu _{A^{I}}(x)= \left\{ \begin{array}{ll} \frac{x-r_{1}}{r_{2}-r_{1}}, &{} \quad \text{ for } r_{1}\le x\le r_{2} \\ 1,&{} \quad \text{ for } r_{2}\le x\le r_{3} \\ \frac{r_{4}-x}{r_{4}-r_{3}},&{} \quad \text{ for } r_{3}\le x \le r_{4}\\ 0, &{} \quad \text{ otherwise } \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \nu _{A^{I}}(x)= \left\{ \begin{array}{ll} \frac{r_{2}-x}{r_{2}-r_{1}'}, &{} \quad \text{ for } r_{1}'\le x\le r_{2} \\ 0,&{} \quad \text{ for } r_{2}\le x\le r_{3} \\ \frac{x-r_{3}}{r_{4}'-r_{3}},&{} \quad \text{ for } r_{3}\le x \le r_{4}'\\ 1, &{} \quad \text{ otherwise } \end{array} \right. \end{aligned}$$

where $r_{1}'\le r_{1}\le r_{2}\le r_{3}\le r_{4}\le r_{4}'$. The TIFN $A^{I}$ in ${\mathfrak {R}}$ is represented as $(r_{1}, r_{2},r_{3}, r_{4};r_{1}',r_{2}, r_{3}, r_{4}')$ with its membership function $\mu _{A^{I}}$ and nonmembership function $\nu _{A^{I}}$.

Definition 7

A function$f:[0,\infty )\rightarrow [0,1]$ is called a shape function if the following conditions hold:

• (a) $f(0)=1$

• (b) f is continuous function on $[0,\infty )$

• (c) f is decreasing on $[0,\infty )$ and

• (d) $\lim \nolimits _{x\rightarrow \infty }f(x)=0.$

Definition 8

An IFN $A^{I}$ is called LR-type IFN, so that for membership function $\mu _{A^{I}}(x)$ and nonmembership function $\nu _{A^{I}}(x)$, $0 \le \mu _{A^{I}}(x) + \nu _{A^{I}}(x)\le 1$ holds and is defined as follows:

$$\begin{aligned} \mu _{A^{I}}(x)= \left\{ \begin{array}{ll} L\left(\frac{m-x}{l}\right), &{} \quad \text{ for } x\le m \\ R\left(\frac{x-m}{r}\right),&{} \quad \text{ for } x \ge m \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \nu _{A^{I}}(x)= \left\{ \begin{array}{ll} 1-L\left(\frac{m-x}{l'}\right), &{}\quad \text{ for } x\le m \\ 1-R\left(\frac{x-m}{r'}\right),&{} \quad \text{ for } x \ge m \end{array} \right. \end{aligned}$$

Definition 9

The LR-type representation of a TIFN $A^{I}=(r_{1}, r_{2},r_{3}, r_{4};r_{1}',r_{2}, r_{3}, r_{4}')$ is given by $A^{I}=(r_{2}, r_{3};r_{2}-r_{1}, r_{4}-r_{3};r_{2}-r_{1}', r_{4}'-r_{3}),$ and its membership function $\mu _{A^{I}}$ and nonmembership function $\nu _{A^{I}}$ are defined by

$$\begin{aligned} \mu _{A^{I}}(x)= \left\{ \begin{array}{ll} L\left(\frac{r_{2}-x}{r_{2}-r_{1}}\right), &{} \quad \text{ for } x\le r_{2} \\ 1,&{} \quad \text{ for } r_{2}\le x\le r_{3} \\ R\left(\frac{x-r_{3}}{r_{4}-r_{3}}\right),&{} \quad \text{ for } x \ge r_{3} \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \nu _{A^{I}}(x)= \left\{ \begin{array}{ll} 1-L\left(\frac{r_{2}-x}{r_{2}-r_{1}'}\right), &{} \quad \text{ for } x\le r_{2} \\ 0,&{} \quad \text{ for } r_{2}\le x\le r_{3} \\ 1-R\left(\frac{x-r_{3}}{r_{4}'-r_{3}}\right),&{} \quad \text{ for } x \ge r_{3} \end{array} \right. \end{aligned}$$

where $L(x)=R(x)=\max \{0,1-x\}$; $r_{2}-r_{1}$ and $r_{4}-r_{3}$ are the left spread and right spread of the membership function $\mu _{A^{I}},$ respectively, whereas $r_{2}-r_{1}'$ and $r_{4}'-r_{3}$ are the left spread and right spread of the nonmembership function $\nu _{A^{I}} ,$ respectively.

Theorem 1

The$\alpha$-cut and$\beta$-cut of a TIFN$A^{I}=(r_{1}, r_{2},r_{3}, r_{4};r_{1}',r_{2}, r_{3}, r_{4}')$are given by$A^{I}_{\alpha }=[r_1+(r_2-r_1)\alpha , r_4-(r_4-r_3)\alpha ]$and$A^{I}_{\beta }=[r_2-(r_{2}-r_{1}')\beta , r_3+(r_4'-r_3)\beta ]$, $\forall \alpha ,\beta \in (0,1]]$

Proof

For $\alpha \in (0,1]$,

$$\begin{aligned}\ \mu _{A^{I}}(x)\ge \alpha\Rightarrow & {} \frac{x-r_1}{r_2-r_1}\ge \alpha , \frac{r_4-x}{r_4-r_3}\ge \alpha \\\Rightarrow & {} x\ge r_1+(r_2-r_1)\alpha , x\le r_4-(r_4-r_3)\alpha \\\Rightarrow & {} r_1+(r_2-r_1)\alpha \le x\le r_4-(r_4-r_3)\alpha \\\Rightarrow & {} A^{I}_{\alpha }=[r_1+(r_2-r_1)\alpha , r_4-(r_4-r_3)\alpha ] \end{aligned}$$

Now for $\beta \in (0,1]$,

$$\begin{aligned} \nu _{A^{I}}(x)\le \beta\Rightarrow & {} \frac{r_{2}-x}{r_{2}-r_{1}'}\le \beta , \frac{x-r_{3}}{r_{4}'-r_{3}}\le \beta \\\Rightarrow & {} x\ge r_2-(r_{2}-r_{1}')\beta , x\le r_3+(r_4'-r_3)\beta \\\Rightarrow & {} r_2-(r_{2}-r_{1}')\beta \le x\le r_3+(r_4'-r_3)\beta \\\Rightarrow & {} A^{I}_{\beta }=[r_2-(r_{2}-r_{1}')\beta , r_3+(r_4'-r_3)\beta ] \end{aligned}$$

Hence, it is proved. $\square$

Theorem 2

The$(\alpha , \beta )$-cut of a TIFN$A^{I}=(r_{1}, r_{2},r_{3}, r_{4};r_{1}',r_{2}, r_{3}, r_{4}')$is given by$A^{I}_{\alpha , \beta }=[r_1+(r_2-r_1)\alpha , r_4-(r_4-r_3)\alpha ]\cap [r_2-(r_{2}-r_{1}')\beta , r_3+(r_4'-r_3)\beta ]$, $\forall \alpha , \beta \in (0,1]]$

Proof

For $\alpha \in (0,1]$, the $\alpha$-cut of a TIFN $A^{I}=(r_{1}, r_{2},r_{3}, r_{4};r_{1}',r_{2}, r_{3}, r_{4}')$ is given by $A^{I}_{\alpha }=[r_1+(r_2-r_1)\alpha , r_4-(r_4-r_3)\alpha ]$.

For $\beta \in (0,1]$, the $\beta$-cut of the TIFN $A^{I}=(r_{1}, r_{2},r_{3}, r_{4};r_{1}',r_{2}, r_{3}, r_{4}')$ is given by $A^{I}_{\beta }=[r_2-(r_{2}-r_{1}')\beta , r_3+(r_4'-r_3)\beta ]$, $\forall \beta \in (0,1]]$.

So by Definition 4, $A^{I}_{\alpha , \beta }=[r_1+(r_2-r_1)\alpha , r_4-(r_4-r_3)\alpha ]\cap [r_2-(r_{2}-r_{1}')\beta , r_3+(r_4'-r_3)\beta ]$, $\forall \alpha \in (0,1], \alpha +\beta \le 1]$.

Hence, it is proved. $\square$

Theorem 3

Let$A^{I}=(m, n;l, r;l', r')$be a LR-type TIFN, wherelandrare the left spread and right spread of the membership function$\mu _{A^{I}}$, $l'$and$r'$are the left spread and right spread of the nonmembership function$\nu _{A^{I}}$. Then, its$\alpha$-cut and$\beta$-cut are given by$A^{I}_{\alpha }=[m-lL^{-1}(\alpha ), n+rR^{-1}(\alpha )]$and$A^{I}_{\beta }=[m-l'L^{-1}(1-\beta ), n+rR^{-1}(1-\beta )]$, $\forall \alpha ,\beta \in (0,1]$

Proof

For $\alpha \in (0,1]$,

$$\begin{aligned}\ \mu _{A^{I}}(x)\ge \alpha\Rightarrow & {} L\bigg (\frac{m-x}{l}\bigg )\ge \alpha , R\bigg (\frac{x-n}{r}\bigg )\ge \alpha \\\Rightarrow & {} x\ge m-lL^{-1}(\alpha ), x\le n+rR^{-1}(\alpha )\\\Rightarrow & {} m-lL^{-1}(\alpha ) \le x\le n+rR^{-1}(\alpha )\\\Rightarrow & {} A^{I}_{\alpha }=[m-lL^{-1}(\alpha ), n+rR^{-1}(\alpha )] \end{aligned}$$

Now for $\beta \in (0,1]$,

$$\begin{aligned} \nu _{A^{I}}(x)\le \beta\Rightarrow & {} 1-L\bigg (\frac{m-x}{l'}\bigg )\le \beta , 1-R\bigg (\frac{x-n}{r'}\bigg )\le \beta \\\Rightarrow & {} x\ge m-l'L^{-1}(1-\beta ), x\le n+r'R^{-1}(1-\beta )\\\Rightarrow & {} m-l'L^{-1}(1-\beta ) \le x\le n+r'R^{-1}(1-\beta )\\\Rightarrow & {} A^{I}_{\beta }=[m-l'L^{-1}(1-\beta ), n+r'R^{-1}(1-\beta )] \end{aligned}$$

Hence, it is proved. $\square$

Theorem 4

Let$A^{I}=(m, n;l, r;l', r')$be a LR-type TIFN. Then, its$(\alpha , \beta )$-cut is given by$A^{I}_{\alpha , \beta }=[m-lL^{-1}(\alpha ), n+rR^{-1}(\alpha )]\cap [m-l'L^{-1}(1-\beta ), n+r'R^{-1}(1-\beta )]$, $\forall \alpha , \beta \in (0,1]$and$\alpha +\beta \le 1$.

Proof

For $\alpha \in (0,1]$, The $\alpha$-cut of a LR-type TIFN $A^{I}=(m, n;l, r;l', r')$ is given by $A^{I}_{\alpha }=[m-lL^{-1}(\alpha ), n+rR^{-1}(\alpha )]$ For $\beta \in (0,1]$, The $\beta$-cut of the LR-type TIFN $A^{I}=(m, n;l, r;l', r')$ is given by $A^{I}_{\beta }=[m-l'L^{-1}(1-\beta ), n+rR^{-1}(1-\beta )]$, $\forall \beta \in (0,1]]$.

So by definition, $A^{I}_{\alpha , \beta }=[m-lL^{-1}(\alpha ), n+rR^{-1}(\alpha )]\cap [m-l'L^{-1}(1-\beta ), n+r'R^{-1}(1-\beta )]$, $\forall \alpha , \beta \in (0,1], \alpha +\beta \le 1$. Hence, it is proved. $\square$

Arithmetic Operations on LR -type TIFN

Proposition 1

(Addition) If${A_{1}}^{I}=(m_{1}, n_{1};l_{1}, r_{1};l_{1}', r_{1}')$and${A_{2}}^{I}=(m_{2}, n_{2};l_{2}, r_{2};l_{2}', r_{2}')$are two LR-type TIFNs, then${A_{1}}^{I} +{A_{2}}^{I}= (m_{1}+m_{2}, n_{1}+n_{2};l_{1}+l_{2}, r_{1}+r_{2};l_{1}'+l_{2}', r_{1}'+r_{2}')$.

Proof

For $\alpha \in (0,1]$ and $\beta \in (0,1]$, the $\alpha$-cut and $\beta$-cut of the LR-type TIFNs ${A_{1}}^{I}=(m_{1}, n_{1};l_{1}, r_{1};l_{1}', r_{1}')$ and ${A_{2}}^{I}=(m_{2}, n_{2};l_{2}, r_{2};l_{2}', r_{2}')$ are given by ${A_{1}}^{I}_{\alpha }=[m_{1}-l_{1}L^{-1}(\alpha ), n_{1}+r_{1}R^{-1}(\alpha )]$, ${A_{2}}^{I}_{\alpha }=[m_{2}-l_{2}L^{-1}(\alpha ), n_{2}+r_{2}R^{-1}(\alpha )]$ ; ${A_{1}}^{I}_{\beta }=[m_{1}-l_{1}'L^{-1}(1-\beta ), n_{1}+r_{1}'R^{-1}(1-\beta )]$, ${A_{2}}^{I}_{\alpha }=[m_{2}-l_{2}'L^{-1}(1-\beta ), n_{2}+r_{2}'R^{-1}(1-\beta )],$ respectively Now,

$$\begin{aligned} ({A_{1}}^{I}+{A_{2}}^{I})_{\alpha }&= {A_{1}}^{I}_{\alpha }+{A_{2}}^{I}_{\alpha }\nonumber \\&= [m_{1}-l_{1}L^{-1}(\alpha ), n_{1}+r_{1}R^{-1}(\alpha )]+[m_{2}-l_{2}L^{-1}(\alpha ), n_{2}+r_{2}R^{-1}(\alpha )]\nonumber \\&= [(m_{1}+m_{2})-(l_{1}+l_{2})L^{-1}(\alpha ), (n_{1}+n_{2})+(r_{1}+r_{2})R^{-1}(\alpha )] \end{aligned}$$

(35)

Since L and R are decreasing functions on $[0,\infty ]$ with $L(0)=R(0)=1$, $\exists$ some $\alpha =\alpha _0\in (0,1]$ such that $L^{-1}(\alpha _0)=R^{-1}(\alpha _0)=1$.

Therefore,

$$\begin{aligned} ({A_{1}}^{I}+{A_{2}}^{I})_{\alpha _0}&= [(m_{1}+m_{2})-(l_{1}+l_{2}), (n_{1}+n_{2})+(r_{1}+r_{2})] \end{aligned}$$

(36)

Now, by putting $\alpha =1$ in Eq. (35), we get the model point of ${A_{1}}^{I}+{A_{2}}^{I}$, which is given by

$$\begin{aligned} ({A_{1}}^{I}+{A_{2}}^{I})_{1}&= [m_{1}+m_{2}, n_{1}+n_{2}] \end{aligned}$$

(37)

Again

$$\begin{aligned}&({A_{1}}^{I}+{A_{2}}^{I})_{\beta }={A_{1}}^{I}_{\beta }+{A_{2}}^{I}_{\beta }\nonumber \\&\quad =[m_{1}-l_{1}'L^{-1}(1-\beta ), n_{1}+r_{1}'R^{-1}(1-\beta )]\nonumber \\&\qquad +\,[m_{2}-l_{2}'L^{-1}(1-\beta ), n_{2}+r_{2}'R^{-1}(1-\beta )]\nonumber \\&\quad =[(m_{1}+m_{2})-(l_{1}'+l_{2}')L^{-1}(1-\beta ), (n_{1}+n_{2})+(r_{1}'+r_{2}')R^{-1}(1-\beta )] \end{aligned}$$

(38)

Since L and R are decreasing functions on $[0,\infty ]$ with $L(0)=R(0)=1$, $\exists$ some $\beta =\beta _0\in (0,1]$ such that $L^{-1}(1-\beta _0)=R^{-1}(1-\beta _0)=1$.

Therefore,

$$\begin{aligned} ({A_{1}}^{I}+{A_{2}}^{I})_{\beta _0}&= [(m_{1}+m_{2})-(l_{1}'+l_{2}'), (n_{1}+n_{2})+(r_{1}'+r_{2}')] \end{aligned}$$

(39)

Since ${A_{1}}^{I}, {A_{2}}^{I}$ are two LR-type TIFNs, $0 \le l_{1} \le l_{1}'$, $0\le l_{2}\le l_{2}'$, $0 \le r_{1} \le r_{1}'$ and $0\le r_{2}\le r_{2}'$, so $0 \le l_{1} + l_{2}\le l_{1}' + l_{2}'$ and $0 \le r_{1} + r_{2}\le r_{1}' + r_{2}'$

So, from Eqs. (36), (37) and (39), we have ${A_{1}}^{I} +{A_{2}}^{I}= (m_{1}+m_{2}, n_{1}+n_{2};l_{1}+l_{2}, r_{1}+r_{2};l_{1}'+l_{2}', r_{1}'+r_{2}')$.

Hence, it is proved. $\square$

Proposition 2

(Subtraction) If${A_{1}}^{I}=(m_{1}, n_{1};l_{1}, r_{1};l_{1}', r_{1}')$and${A_{2}}^{I}=(m_{2}, n_{2};l_{2}, r_{2};l_{2}', r_{2}')$are two LR-type TIFNs, then${A_{1}}^{I} -{A_{2}}^{I}= (m_{1}-n_{2}, n_{1}-m_{2};l_{1}+r_{2}, r_{1}+l_{2};l_{1}'+r_{2}', r_{1}'+l_{2}')$.

Proof

The $\alpha$-cut and $\beta$-cut of the LR-type TIFNs ${A_{1}}^{I}=(m_{1}, n_{1};l_{1}, r_{1};l_{1}', r_{1}')$ and ${A_{2}}^{I}=(m_{2}, n_{2};l_{2}, r_{2};l_{2}', r_{2}')$ are given by

$$\begin{aligned} {A_{1}}^{I}_{\alpha }&= [m_{1}-l_{1}L^{-1}(\alpha ), n_{1}+r_{1}R^{-1}(\alpha )],\\ {A_{2}}^{I}_{\alpha }&= [m_{2}-l_{2}L^{-1}(\alpha ), n_{2}+r_{2}R^{-1}(\alpha )] ;\\ {A_{1}}^{I}_{\beta }&= [m_{1}-l_{1}'L^{-1}(1-\beta ), n_{1}+r_{1}^{'}R^{-1}(1-\beta )],\\ {A_{2}}^{I}_{\alpha }&= [m_{2}-l_{2}'L^{-1}(1-\beta ), n_{2}+r_{2}'R^{-1}(1-\beta )], \end{aligned}$$

respectively. Now,

$$\begin{aligned} ({A_{1}}^{I}-{A_{2}}^{I})_{\alpha }&= {A_{1}}^{I}_{\alpha }-{A_{2}}^{I}_{\alpha }\nonumber \\&= [m_{1}-l_{1}L^{-1}(\alpha ), n_{1}+r_{1}R^{-1}(\alpha )]-[m_{2}-l_{2}L^{-1}(\alpha ), n_{2}+r_{2}R^{-1}(\alpha )]\nonumber \\&= [m_{1}-n_{2}-(l_{1}L^{-1}(\alpha )+r_{2}R^{-1}(\alpha )), n_{1}-m_{2}+(r_{1}R^{-1}(\alpha )+l_{2}L^{-1}(\alpha ))] \end{aligned}$$

(40)

Since L and R are decreasing functions on $[0,\infty ]$ with $L(0)=R(0)=1$, $\exists$ some $\alpha =\alpha _0\in (0,1]$ such that $L^{-1}(\alpha _0)=R^{-1}(\alpha _0)=1$.

Therefore,

$$\begin{aligned} ({A_{1}}^{I}-{A_{2}}^{I})_{\alpha _0}&= [(m_{1}-n_{2})-(l_{1}+r_{2}), (n_{1}-m_{2})+(r_{1}+l_{2})] \end{aligned}$$

(41)

Now, by putting $\alpha =1$ in Eq. (40), we get the model point of ${A_{1}}^{I}-{A_{2}}^{I}$, which is given by

$$\begin{aligned} ({A_{1}}^{I}-{A_{2}}^{I})_{1}&= [m_{1}-n_{2}, n_{1}-m_{2}] \end{aligned}$$

(42)

Again

$$\begin{aligned} ({A_{1}}^{I}-{A_{2}}^{I})_{\beta }&= {A_{1}}^{I}_{\beta }-{A_{2}}^{I}_{\beta }\nonumber \\&= [m_{1}-l_{1}'L^{-1}(1-\beta ), n_{1}+r_{1}'R^{-1}(1-\beta )]\nonumber \\&-[m_{2}-l_{2}'L^{-1}(1-\beta ), n_{2}+r_{2}'R^{-1}(1-\beta )]\nonumber \\&= [m_{1}-n_{2}-(l_{1}'L^{-1}(1-\beta )+r_{2}'R^{-1}(1-\beta )), n_{1}\nonumber \\&-m_{2}+(r_{1}'R^{-1}(1-\beta )+l_{2}'L^{-1}(1-\beta ))] \end{aligned}$$

(43)

Since L and R are decreasing functions on $[0,\infty ]$ with $L(0)=R(0)=1$, $\exists$ some $\beta =\beta _0\in (0,1]$ such that $L^{-1}(1-\beta _0)=R^{-1}(1-\beta _0)=1$.

Therefore,

$$\begin{aligned} ({A_{1}}^{I}-{A_{2}}^{I})_{\beta _0}&= [(m_{1}-n_{2})-(l_{1}'+r_{2}'), (n_{1}-m_{2})+(r_{1}'+l_{2}')] \end{aligned}$$

(44)

Since ${A_{1}}^{I}, {A_{2}}^{I}$ are two LR-type TIFNs, $0 \le l_{1} \le l_{1}'$, $0\le l_{2}\le l_{2}'$, $0 \le r_{1} \le r_{1}'$ and $0\le r_{2}\le r_{2}'$, so $0 \le l_{1} + r_{2}\le l_{1}' + r_{2}'$ and $0 \le r_{1} + l_{2}\le r_{1}' + l_{2}'$.

Therefore, from Eqs. (41), (42) and (44), we have

$$\begin{aligned} {A_{1}}^{I} - {A_{2}}^{I}= (m_{1}-n_{2}, n_{1}-m_{2};l_{1}+r_{2}, r_{1}+l_{2};l_{1}'+r_{2}', r_{1}'+l_{2}'). \end{aligned}$$

Hence, it is proved.

Proposition 3

(Scalar multiplication) If${A_{1}}^{I}=(m_{1}, n_{1};l_{1}, r_{1};l_{1}', r_{1}')$is a LR-type TIFN and$\lambda$is any real number, then$\lambda {A_{1}}^{I} = (\lambda m_{1}, \lambda n_{1};\lambda l_{1}, \lambda r_{1};\lambda l_{1}', \lambda r_{1}')$, when$\lambda \ge 0$.

$\lambda {A_{1}}^{I} = (\lambda n_{1}, \lambda m_{1};-\lambda r_{1}, -\lambda l_{1};-\lambda r_{1}', -\lambda l_{1}')$, when$\lambda < 0$.

Proof

The $\alpha$-cut and $\beta$-cut of the LR-type TIFN ${A_{1}}^{I}=(m_{1}, n_{1};l_{1}, r_{1};l_{1}', r_{1}')$ are given by ${A_{1}}^{I}_{\alpha }=[m_{1}-l_{1}L^{-1}(\alpha ), n_{1}+r_{1}R^{-1}(\alpha )]$, ${A_{1}}^{I}_{\beta }=[m_{1}-l_{1}'L^{-1}(1-\beta ), n_{1}+r_{1}'R^{-1}(1-\beta )]$, respectively

Case I$\lambda \ge 0$

$$\begin{aligned} (\lambda {A_{1}}^{I})_{\alpha }&= \lambda {A_{1}}^{I}_{\alpha }\nonumber \\&= \lambda [m_{1}-l_{1}L^{-1}(\alpha ), n_{1}+r_{1}R^{-1}(\alpha )]\nonumber \\&= [\lambda m_{1}-\lambda l_{1}L^{-1}(\alpha ), \lambda n_{1}+\lambda r_{1}R^{-1}(\alpha )] \end{aligned}$$

(45)

Since L and R are decreasing functions on $[0,\infty ]$ with $L(0)=R(0)=1$, $\exists$ some $\alpha =\alpha _0\in (0,1]$ such that $L^{-1}(\alpha _0)=R^{-1}(\alpha _0)=1$.

Therefore,

$$\begin{aligned} (\lambda {A_{1}}^{I})&= [\lambda m_{1}-\lambda l_{1}, \lambda n_{1}+\lambda r_{1}] \end{aligned}$$

(46)

Now, by putting $\alpha =1$ in Eq. (45), we get the model point of $\lambda {A_{1}}^{I}$, which is given by

$$\begin{aligned} (\lambda {A_{1}}^{I})_{1}&= [\lambda m_{1}, \lambda n_{1}] \end{aligned}$$

(47)

Again

$$\begin{aligned} (\lambda {A_{1}}^{I})_{\beta }&= \lambda {A_{1}}^{I}_{\beta }\nonumber \\&= [\lambda m_{1}-\lambda l_{1}'L^{-1}(1-\beta ), \lambda n_{1}+ \lambda r_{1}'R^{-1}(1-\beta )] \end{aligned}$$

(48)

Since L and R are decreasing functions on $[0,\infty ]$ with $L(0)=R(0)=1$, $\exists$ some $\beta =\beta _0\in (0,1]$ such that $L^{-1}(1-\beta _0)=R^{-1}(1-\beta _0)=1$.

Therefore,

$$\begin{aligned} (\lambda {A_{1}}^{I})_{\beta _0}&= [\lambda m_{1}-\lambda l_{1}', \lambda n_{1} + \lambda r_{1}'] \end{aligned}$$

(49)

Since ${A_{1}}^{I}$ are LR-type TIFN and $\lambda > 0$, $0 \le l_{1} \le l_{1}'$ and $0 \le r_{1} \le r_{1}'$. So $0 \le \lambda l_{1}\le \lambda l_{1}'$ and $0 \le \lambda r_{1} \le \lambda r_{1}'$

So, from Eqs. (46), (47) and (49), we have

$$\begin{aligned} \lambda {A_{1}}^{I} = (\lambda m_{1}, \lambda n_{1};\lambda l_{1}, \lambda r_{1};\lambda l_{1}', \lambda r_{1}') \end{aligned}$$

Hence, it is proved.

Case II$\lambda < 0$

$$\begin{aligned} (\lambda {A_{1}}^{I})_{\alpha }&= \lambda {A_{1}}^{I}_{\alpha }\nonumber \\&= \lambda [m_{1}-l_{1}L^{-1}(\alpha ), n_{1}+r_{1}R^{-1}(\alpha )]\nonumber \\&= [\lambda n_{1}+\lambda r_{1}R^{-1}(\alpha ), \lambda m_{1}-\lambda l_{1}L^{-1}(\alpha )] \end{aligned}$$

(50)

Since L and R are decreasing functions on $[0,\infty ]$ with $L(0)=R(0)=1$, $\exists$ some $\alpha =\alpha _0\in (0,1]$ such that $L^{-1}(\alpha _0)=R^{-1}(\alpha _0)=1$.

Therefore,

$$\begin{aligned} (\lambda {A_{1}}^{I})&= [\lambda n_{1}+\lambda r_{1}, \lambda m_{1}-\lambda l_{1}] \end{aligned}$$

(51)

Now, by putting $\alpha =1$ in Eq. 50, we get the model point of $\lambda {A_{1}}^{I}$, which is given by

$$\begin{aligned} (\lambda {A_{1}}^{I})_{1}&= [\lambda n_{1}, \lambda m_{1}] \end{aligned}$$

(52)

Again

$$\begin{aligned} (\lambda {A_{1}}^{I})_{\beta }& = \lambda {A_{1}}^{I}_{\beta }\nonumber \\&= [\lambda n_{1}+ \lambda r_{1}'R^{-1}(1-\beta ), \lambda m_{1}-\lambda l_{1}'L^{-1}(1-\beta )] \end{aligned}$$

(53)

Since L and R are decreasing functions on $[0,\infty ]$ with $L(0)=R(0)=1$, $\exists$ some $\beta =\beta _0\in (0,1]$ such that $L^{-1}(1-\beta _0)=R^{-1}(1-\beta _0)=1$.

Therefore

$$\begin{aligned} (\lambda {A_{1}}^{I})_{\beta _0}&= [\lambda n_{1} + \lambda r_{1}', \lambda m_{1}-\lambda l_{1}'] \end{aligned}$$

(54)

Since ${A_{1}}^{I}$ are LR-type TIFN and $\lambda < 0$, $0 \le l_{1} \le l_{1}'$ and $0 \le r_{1} \le r_{1}'$. So $0 \le -\lambda l_{1}\le -\lambda l_{1}'$ and $0 \le -\lambda r_{1} \le -\lambda r_{1}'$

So, from Eqs. (51), (52) and (54), we have

$$\begin{aligned} \lambda {A_{1}}^{I} = (\lambda n_{1}, \lambda m_{1};-\lambda r_{1}, -\lambda l_{1};-\lambda r_{1}', -\lambda l_{1}'). \end{aligned}$$

Hence, it is proved. $\square$

Definition 10

[33] Let the $(\alpha ,\beta )$-cut of a LR-type TIFN be given by

$$\begin{aligned} A^{I}_{\alpha , \beta }=[A_{1}(\alpha ),A_{2}(\alpha )]\cap [{A'}_{1}(\beta ),A'_{2}(\beta )]; \alpha +\beta \le 1, \forall \alpha , \beta \in [0,1]; \end{aligned}$$

where $A_{1}(\alpha )=m-lL^{-1}(\alpha )$, $A_{2}(\alpha )=n+rR^{-1}(\alpha )$, ${A'}_{1}(\beta )=m-l'L^{-1}(1-\beta )$ and ${A'}_{1}(\beta )=n+r'R^{-1}(1-\beta )$. Then, by mean of $(\alpha , \beta )$-cut method, the representation of membership function is

$$\begin{aligned} R_{\mu }(A^{I})=\frac{1}{2}\int _{0}^{1}\bigg [A_{1}(\alpha )+A_{2}(\alpha )\bigg ]{\mathrm{d}}\alpha . \end{aligned}$$

Again by mean of $(\alpha , \beta )$-cut method, the representation of nonmembership function is

$$\begin{aligned} R_{\nu }(A^{I})=\frac{1}{2}\int _{0}^{1}\bigg [{A'}_{1}(\beta )+A'_{2}(\beta )\bigg ]{\mathrm{d}}\beta . \end{aligned}$$

The accuracy function of $A^{I}$ is denoted by $f(A^{I})$ and defined by

$$\begin{aligned} f(A^{I})=\frac{R_{\mu }(A^{I})+R_{\nu }(A^{I})}{2}, \end{aligned}$$

to defuzzify the given numbers as deterministic one.

Theorem 5

Let$A^{I}=(m, n;l, r;l', r')$be a LR-type TIFN. Then, its accuracy function is given by$f(A^{I})=\frac{2m+2n-\frac{l}{2}+\frac{r}{2}-\frac{l'}{2}+\frac{r'}{2}}{4}$.

Proof

By definition, the accuracy function of $A^{I}$ is defined by

$$\begin{aligned} f(A^{I})&= \frac{R_{\mu }(A^{I})+R_{\nu }(A^{I})}{2}\\&= \frac{\frac{1}{2}\int _{0}^{1}\bigg [A_{1}(\alpha )+A_{2}(\alpha )\bigg ] {\mathrm{d}}\alpha +\frac{1}{2}\int _{0}^{1}\bigg [{A'}_{1}(\beta )+A'_{2}(\beta )\bigg ]{\mathrm{d}}\beta }{2}\\&= \frac{1}{4}\bigg [\int _{0}^{1}\bigg \{m-lL^{-1}(\alpha )+n+rR^{-1}(\alpha ) \bigg \}{\mathrm{d}}\alpha \\ &\quad+\,&\int _{0}^{1}\bigg \{m-l'L^{-1}(1-\beta )+n+r'R^{-1}(1-\beta ) \bigg \}{\mathrm{d}}\beta \bigg ] \end{aligned}$$

Now, by Definition 9 for a TIFN, $L(x)=R(x)=max\{0,1-x\}, \forall x\ge 0$;

Since $\alpha \in (0,1]$, $L(1-\alpha )=\alpha \Rightarrow L^{-1}(\alpha )=\alpha$ and $R(1-\alpha )=\alpha \Rightarrow R^{-1}(\alpha )=\alpha$ Similarly, $L(\beta )=1-\beta \Rightarrow L^{-1}(1-\beta )=\beta$ and $R(\beta )=1-\beta \Rightarrow R^{-1}(1-\beta )=\beta$

$$\begin{aligned} f(A^{I})&= \frac{1}{4}\bigg [\int _{0}^{1}\bigg \{m-l(1-\alpha )+n+r(1-\alpha )\bigg \}{\mathrm{d}}\alpha +\int _{0}^{1}\bigg \{m-l'\beta +n+r'\beta \bigg \}{\mathrm{d}}\beta \bigg ]\nonumber \\ \Rightarrow f(A^{I})&= \frac{2m+2n-\frac{l}{2}+\frac{r}{2}-\frac{l'}{2}+\frac{r'}{2}}{4} \end{aligned}$$

(55)

Hence, it is proved. $\square$

Theorem 6

Let${A_{1}}^{I}=(m_{1}, n_{1};l_{1}, r_{1};l_{1}', r_{1}')$, ${A_{2}}^{I}=(m_{2}, n_{2};l_{2}, r_{2};l_{2}', r_{2}')$be any two LR-type TIFNs and$\lambda _{1}$and$\lambda _{2}$be any two real numbers, then$f(\lambda _{1}{A_{1}}^{I}+\lambda _{2}{A_{2}}^{I})=\lambda _{1} f({A_{1}}^{I})+\lambda _{2} f({A_{2}}^{I})$

Proof

Let $\lambda \ge 0$, now by using propositions 2 and 3, $\lambda {A_{1}}^{I}+\lambda {A_{2}}^{I}=(\lambda _{1}m_{1}+\lambda _{2}m_{2}, \lambda _{1}n_{1}+\lambda _{2}n_{2}; \lambda _{1}l_{1}+\lambda _{2}l_{2}, \lambda _{1}r_{1}+\lambda _{2}r_{2}; \lambda _{1}l_{1}'+\lambda _{2}l_{2}', \lambda _{1}r_{1}'+\lambda _{2}r_{2}')$ Thus, by using Eq. (55),

$$\begin{aligned}&f(\lambda {A_{1}}^{I}+\lambda {A_{2}}^{I})\nonumber \\&\quad =\frac{2(\lambda _{1}m_{1}+\lambda _{2}m_{2})+2(\lambda _{1}n_{1}+\lambda _{2}n_{2})- \frac{\lambda _{1}l_{1}+\lambda _{2}l_{2}}{2}+\frac{\lambda _{1}r_{1}+\lambda _{2}r_{2}}{2}- \frac{\lambda _{1}l_{1}'+\lambda _{2}l_{2}'}{2}+\frac{\lambda _{1}r_{1}'+\lambda _{2}r_{2}'}{2}}{4} \end{aligned}$$

(56)

Again $f({A_{1}}^{I})= \frac{2m_{1}+2n_{1}-\frac{l_{1}}{2}+\frac{r_{1}}{2}-\frac{l_{1}'}{2}+\frac{r_{1}'}{2}}{4}$ and $f({A_{2}}^{I})= \frac{2m_{2}+2n_{2}-\frac{l_{2}}{2}+\frac{r_{2}}{2}-\frac{l_{2}'}{2}+\frac{r_{2}'}{2}}{4}$ So,

$$\begin{aligned}&\lambda _{1} f({A_{1}}^{I})+\lambda _{2} f({A_{2}}^{I})\\&\quad =\lambda _{1}\bigg (\frac{2m_{1}+2n_{1}-\frac{l_{1}}{2}+\frac{r_{1}}{2}-\frac{l_{1}'}{2}+\frac{r_{1}'}{2}}{4}\bigg )+ \lambda _{2}\bigg (\frac{2m_{2}+2n_{2}-\frac{l_{2}}{2}+\frac{r_{2}}{2}-\frac{l_{2}'}{2}+\frac{r_{2}'}{2}}{4}\bigg )\\&\quad \Rightarrow \lambda _{1} f({A_{1}}^{I})+\lambda _{2} f({A_{2}}^{I})\\&\quad =\frac{2(\lambda _{1}m_{1}+\lambda _{2}m_{2})+2(\lambda _{1}n_{1}+\lambda _{2}n_{2})- \frac{\lambda _{1}l_{1}+\lambda _{2}l_{2}}{2}+\frac{\lambda _{1}r_{1}+\lambda _{2}r_{2}}{2}- \frac{\lambda _{1}l_{1}'+\lambda _{2}l_{2}'}{2}+\frac{\lambda _{1}r_{1}'+\lambda _{2}r_{2}'}{2}}{4} \end{aligned}$$

Thus, from Eqs. (56) and (57), for $\lambda _{1}\ge 0$ and $\lambda _{2}\ge 0$$f(\lambda _{1}{A_{1}}^{I}+\lambda _{2}{A_{2}}^{I})=\lambda _{1} f({A_{1}}^{I})+\lambda _{2} f({A_{2}}^{I}).$ In the same way, it can be proved for any value of $\lambda _{1}$ and $\lambda _{2}$.

Hence, it is proved. $\square$

1.2 Conversion technique for multi-objective into single objective

In this segment, we will present a discussion about conversion techniques for multi-objective into single objective. Now we discuss about convex combination method

1.3 Convex combination method (CCM)

We consider the multi-objective optimization problem together with some constraints as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \max & \quad [f_{i}(x),\ i=1,2, \ldots , M] \\ \hbox {s.t} &{} \quad g_{j}\ge 0; \ j=1,2,\ldots , N\\ &{} \quad x\in X \end{array} \right. \end{aligned}$$

(57)

Subsequently, by the convex combination method (Tanino et al. [34]), we shift the above problem into the following form as:

$$\begin{aligned} \left\{ \begin{array}{ll} \max &{} \quad {\sum \limits _{i=1}^{M}w_{i}f_{i}(x)}, \text{ where } \sum \limits _{i=1}^{M}w_{i}=1, 0<w_{i}<1\\ \hbox {s.t} &{} \quad g_{j}\ge 0; j=1,2,\ldots , N \\ &{} \quad x\in X \end{array} \right. \end{aligned}$$

(58)

where $w_{i}$ is the weight function of ith objective. Then, the corresponding x and $f_{i}(x)$ are the solutions of the problem in Eq. (57).