Mean and CV reduction methods on Gaussian type-2 fuzzy set and its application to a multilevel profit transportation problem in a two-stage supply chain network

Abstract

The transportation problem (TP) is an important supply chain optimization problem in the traffic engineering. This paper maximizes the total profit over a three-tiered distribution system consisting of plants, distribution centers (DCs) and customers. Plants produce multiple products that are shipped to DCs. If a DC is used, then a fixed cost (FC) is charged. The customers are supplied by a single DC. To characterize the uncertainty in the practical decision environment, this paper considers the unit cost of TP, FC, the supply capacities and demands as Gaussian type-2 fuzzy variables. To give a modeling framework for optimization problems with multifold uncertainty, different reduction methods were proposed to transform a Gaussian type-2 fuzzy variable into a type-1 fuzzy variable by mean reduction method and CV reduction method. Then, the TP was reformulated as a chance-constrained programming model enlightened by the credibility optimization methods. The deterministic models are then solved using two different soft computing techniques—generalized reduced gradient and modified particle swarm optimization, where the position of each particle is adjusted according to its own experience and that of its neighbors. The numerical experiments illustrated the application and effectiveness of the proposed approaches.

1 Introduction

A transportation problem (TP) is often associated with additional costs (termed as fixed costs) besides transportation cost. The fixed-charge transportation problem, first proposed by Hirsch and Dantzig [1], considers two types of costs (say direct cost and fixed charge). These fixed-charge costs may be due to permit fees, toll charges, etc. Since the introduction of TPs by Hitchcock [2], there have been lots of developments in this area by several researchers. Chanas et at. [3] formulated and solved TPs with fuzzy supply and demand values (cf. Pakdaman et al. [4], Mortazavi et al. [5]). Recently, Fegad et al. [6] found optimal solutions to TPs using interval and triangular membership functions. It is sometimes difficult to determine the exact membership grades to (deterministic) represent an uncertain parameter by ordinary fuzzy set, and as a result, membership function itself is again represented by a fuzzy set (FS). Such a fuzzy set is called type-2 fuzzy set (T2FS). Due to fuzziness in membership function, the computational complexity is very high to deal with T2FS. For a T2FS, normally complete defuzzyfication process consists of two parts—type reduction and defuzzyfication proper. Type reduction is a procedure by which a T2FS is converted to the corresponding type-1 FS (i.e., ordinary fuzzy set), known as type-reduced set (TRS). Karmik and Mendel [7] proposed a centroid-type reduction method to reduce interval T2FS to T1FS. But it is very difficult to apply this method to a generalized T2FS. Some researchers (cf. Liu [8], Chen and Chang [9], Malin and Castillo [10], Yang et al. [11, 12], Liu et al. [13], Tavoosi et al. [14], Zoveidavianpoor et al. [15], Tavoosi and Badamchizadeh [16], etc.) have developed type reduction strategies for continuous generalized T2FS. Coupland [17] proposed a geometric defuzzification method for T2FSs by converting a T2FS into a geometric T2FS. Recently, Qin et al. [18] introduced three kinds of reduction methods called optimistic CV, pessimistic CV and CV reduction (critical values) of regular fuzzy variables. Figueeroa-Garce and Hernndez [19] first considered a TP with interval type-2 fuzzy demands and supplies. Recently, Kundu et al. [20] have solved fixed-charge transportation problem (FCTP) with type-2 fuzzy parameters introducing an interval approximation method of continuous type-2 fuzzy variables. Abdullah and Najib [21] have developed a new type-2 fuzzy set of linguistic variables for the fuzzy analytic hierarchy process. But they did not consider the variables as Gaussian type-2 type. It requires a different reduction method for reduction to type-1 fuzzy set (T1FS) and then a different defuzzification method (Jana et al. [22]).

Due to the complex environment during the transportation activities, some significant parameters in the solid transportation problem are always treated as uncertain variables to meet the practical situations. For instance, if one needs to make a transportation plan for the next month, the supply capacity at each source, the demand at each destination, price of product, selling price and the conveyance capacity are often required to be estimated by professional judgments or probability statistics because of no precise a priori information. In this case, it is more suitable to investigate this problem by using fuzzy or random optimization methodologies. For this purpose, type-2 fuzzy variable is introduced in STP.

Particle swam optimization (PSO) is a heuristic optimization technique based on swarm intelligent that is inspired by the behavior of bird blocking (cf. Kennedy and Eberhat [23]). Like GA, a PSO normally starts with a set of solutions (called swarm) of the decision-making problem under consideration. Individual solutions are called particles, and food is analogous to optimal solution. The particles are flown through a multidimensional search space, where the position of each particle is adjusted according to its own experience and that of its neighbors. Many studies have been made to improve modified particle swam optimization (MPSO) algorithm in continuous optimization (cf. Pedrycz et al. [24], Sadeghi et al. [25], Koulinas et al. [26]).

In this paper, we consider two fixed-charge transportation problems for a two-stage supply chain network in Gaussian fuzzy type-2 environment. The problems are formulated as maximization of profit in transporting the units from a manufacturing center to some DCs and from DCs to business centers to satisfy the demands of retailers. Here, fixed-charge costs, unit transportation costs, availabilities and demands are expressed by Gaussian type-2 fuzzy numbers. The T2FS FCTPs are reduced to crisp FCTP by CV reduction following Qin et al. [18]. The proposed models are solved by soft computing techniques GRG and MPSO. Optimum results obtained from two methods are compared. Sensitivity analyses are carried out on the basis of different optimistic labels of decision maker.

In this paper, the transportation problem with fuzzy information, we have two motivations to explore this problem within the framework of Gaussian type-2 fuzzy (GT2F) set theory. Firstly, it is more general and common to treat some critical parameters as GT2F variables because of the practical difficulties of determining their crisp membership functions. Secondly, when some parameters are assumed to be type-2 fuzzy variables, designing an effective method to handle the optimization problem is also a challenging issue. With this concern, we are particularly interested in how to formulate the transportation model and then design effective algorithms to produce the optimal transportation strategies. To this end, this study proposes two new defuzziness methods for type-2 fuzzy variables via mean reduction method. Numerical experiments are done by two different soft computing techniques MPSO and Lingo-14.0.

The structure of this paper is as follows: in Sect. 2, we give some preliminaries about T2FS. In Sect. 3, notations of the proposed models are presented. In Sect. 4, we formulate the models in fuzzy type-2 environments. The solution procedure via GRG and MPSO is presented in Sect. 5. Experimental results and discussion are presented in Sect. 6, and some sensitivity analysis is performed in Sect. 7. The paper is concluded in Sect. 8.

2 Preliminaries

2.1 Type-2 fuzzy sets

In 1975, the concept of a T2FS was introduced by Zadeh [27] as an extension of the concept of an ordinary fuzzy set (henceforth called a T1FS). A T2FS is characterized by a fuzzy membership function; i.e., the membership grade for each element of this set is a fuzzy set in [0, 1], unlike a T1FS where the membership grade is a crisp number in [0, 1]. Such sets can be used in situations where there is uncertainty about the membership grades themselves, e.g., an uncertainty in the shape of the membership function or in some of its parameters. Consider the transition from ordinary sets to fuzzy sets. When we cannot determine the membership of an element in a set as 0 or 1, we use fuzzy sets of type-1. Similarly, when the situation is so fuzzy that we have trouble determining the membership grade even as a crisp number in [0, 1], we use fuzzy sets of type-2 (cf. Li et al. [28]).

Example 1

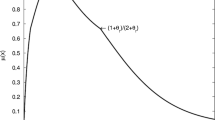
Let us consider the case of a fuzzy set characterized by a Gaussian membership function (in Fig. 1) with mean m and standard deviation $\sigma$ that can take values in $\sigma \in [\sigma _1,\sigma _2]$, i.e.,

$$\mu (x)=\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) ,\quad \sigma \in [\sigma _1,\sigma _2] $$

(1)

Let us now consider the domain elements of the primary memberships of x (denoted by $\mu _1$) and membership grades of these primary memberships which is secondary memberships of x [denoted by $\mu _2(x,\mu _1), \mu _1\in [0,1]$]. So, for a fixed x, we get a T1FS whose domain elements are primary memberships of x and whose corresponding membership grades are secondary memberships of x. If we assume that the secondary memberships follow a Gaussian with mean m(x) and standard deviation $\sigma _{m}$, as in Fig. 2, we can describe the secondary membership function for each x as

$$\mu _{2}(x, \mu _1)=\exp \left( -\frac{(\mu _1-m(x))^{2}}{2\sigma ^{2}_{m}}\right) $$

(2)

The Gaussian type-2 fuzzy set is depicted in Fig. 3 and another way of viewing type-2 membership functions is in a three-dimensional fashion, in which we can better appreciate the idea of type-2 fuzziness. The three-dimensional view of a type-2 Gaussian membership function is shown in Fig. 4.

Fig. 1

A type-2 fuzzy set representing a type-1 fuzzy set with uncertain standard deviation

Fig. 2

A type-2 fuzzy set representing a type-1 fuzzy set with uncertain mean

Definition 1

A Gaussian type-2 fuzzy set is one in which the membership grade of every domain point is a Gaussian T1FS contained in [0, 1].

Fig. 3

A type-2 fuzzy set in which the membership grade of every domain point is a Gaussian T1FS

Fig. 4

Three-dimensional view of a T2FS membership function

2.2 Possibility and credibility measures on type-2 fuzzy variables

Let $\Gamma$ be the universe of discourse. An ample field ${\mathcal {A}}$ on $\Gamma$ is a class of subsets of $\Gamma$ that is closed under arbitrary unions, intersections and complements in $\Gamma$.

Let $\hbox {Pos} : A \longrightarrow [0, 1]$ be a set function on the ample field ${\mathcal {A}}$. Pos is said to be a possibility measure if it satisfies the following conditions:

P1: $\hbox {Pos}(\Phi ) = 0$ and $\hbox {Pos}(\Gamma ) = 1$.

P2: For any subclass ${ \{ A_{i} | i \epsilon I\}}$ of ${\mathcal {A}}$ (finite, countable or uncountable),

$$\hbox {Pos}\left( \bigcup \limits _{i=I}A_{i}\right) = \sup \limits _{i=I}\hbox {Pos}(A_{i}) $$

(3)

The triplet ($\Gamma , {\mathcal {A}}$, Pos) is referred to as a possibility space, in which a credibility measure is defined as

$$\hbox {Cr}(A) = \frac{1}{2}\left( 1 + \hbox {Pos}(A) - \hbox {Pos}(A^{c})\right) , \quad A \in {\mathcal {A}} $$

(4)

If $(\Gamma ,{\mathcal {A}}$, Pos) is a possibility space, then an m-ary regular fuzzy vector $\tilde{\xi } = (\xi _{1}, \xi _{2}, \ldots , \xi _{m}$) is defined as a measurable map from $\Gamma$ to the space $[0,1]^{m}$ in the sense that for every $t = (t_{1}, t_{2}, \ldots , t_{m})\in [0, 1]^{m}$, one has

$$\begin{aligned}\left\{ \gamma \in \Gamma \mid \tilde{\xi }(\gamma )\le t\right\}& =\left\{ \gamma \in \Gamma \mid \tilde{\xi }_{1}(\gamma )\le t_{1},\tilde{\xi }_{2}(\gamma )\le t_{2},\ldots ,\right. \\&\left. \qquad \tilde{\xi }_{m}(\gamma )\le t_{m}\right\} \in {\mathcal {A}} \end{aligned}$$

(5)

When $m=1, \tilde{\tilde{\xi }}$ is called a regular fuzzy type-2 variable (RT2FV). In this paper, we denote by R([0, 1]) the collection of all RT2FVs on [0, 1].

Example 2

If $\tilde{\xi }$ has the following possibility distribution:

$$\begin{aligned} \tilde{\xi }\sim \left( \begin{array}{llll} r_{1} & r_{2} & \ldots & r_{n} \\ \mu _{1} & \mu _{2} & \ldots & \mu _{n} \\ \end{array} \right) \end{aligned}$$

where for each $i = 1, 2, \ldots , n, r_{i} \epsilon [0, 1], \xi _{i} > 0$, and $\max ^{n}_{i=1}\mu _{i} = 1$, then $\tilde{\xi }$ is a discrete RFV. If $\tilde{\xi } = (r_{1}, r_{2}, r_{3}, r_{4})$ with $0 \le r_{1} < r_{2} < r_{3} < r_{4} \le 1$, then $\tilde{\xi }$ is a trapezoidal RFV. If $\tilde{\xi } = (r_{1}, r_{2}, r_{3})$ with $0 <r_{1} < r_{2} < r_{3} \le 1$, then $\tilde{\xi }$ is a triangular RFV.

Fig. 5

Fuzzy type-2 variable $\tilde{A}$

For example (in Fig. 5), if $\tilde{\xi }$ is defined as

$$\begin{aligned} \tilde{\xi }=\left\{ \begin{array}{ll} 1, & \hbox {with possibility}\,\, (0.1,\, 0.2,\, 0.4) \\ 4, & \hbox {with possibility }\tilde{1} \\ 8, & \hbox {with possibility}\,\, (0.1,\, 0.3,\, 0.5,\, 0.7) \\ \end{array} \right. \end{aligned}$$

then $\tilde{\xi }$ is a type-2 fuzzy variable that takes on the values 1, 4 and 8 with possibilities $(0.1, 0.2, 0.4), \tilde{1}$ and (0.1, 0.3, 0.5, 0.7), respectively.

3 Defuzzification methods for type-2 fuzzy variables (T2FVs)

For application purpose, some detailed defuzzification methods for T2FVs will be introduced in this section, which can be conceived as a simplification process for twofold uncertain information. Based on this, a type-2 fuzzy variable can be easily converted into a type-1 fuzzy variable with the aid of reduction methods (1) mean reduction method and (2) CV reduction method.

3.1 Mean reduction methods

A type-2 fuzzy number should be defuzzified before applying in practical problems. For this purpose, some defuzzification methods have been presented in the literature such as Karnik and Mendel [7] and Liu [8]. In this section, we suggest a new reduction methods for a type-2 fuzzy variable. Compared with the existing methods in the literature, the proposed methods are easy to use in building the model with type-2 fuzzy coefficients. We call the above methods as the mean reduction methods for the type-2 fuzzy variable $\xi$. According to the definition of the expectation (Qin et al. [18]) of fuzzy variables, if $\tilde{\xi }=(r_1,r_2,r_3)$ is a triangular RT2FV, then we have

$$\begin{aligned} E^{*}[\xi ]=\frac{r_2+r_3}{2}, \quad E_{*}[\xi ]=\frac{r_1+r_2}{2},\quad E[\xi ]=\frac{r_1+2r_2+r_3}{4} \end{aligned}$$

(6)

In the following, we discuss the mean reductions for a T2FVs.

Theorem 1

Let $\tilde{\eta }$ be a GT2FV $N(\mu , \sigma ^2; \theta _l ,\theta _r)$. Then, we have

• (1) With $E^{*}$ reduction method, the reduction $\eta _1$ of $\widetilde{\eta }$ has the following distribution

  $$\begin{aligned} \mu _{\eta _{1}(x)}= \left\{ \begin{array}{ll} \frac{(2+\theta _{r})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{2}, & \hbox {if }\, x\le \mu -\sigma \sqrt{2\ln 2}\, \hbox { or }\, x\ge \mu +\sigma \sqrt{2\ln 2} \\ \frac{(2-\theta _{r})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) +\theta _r}{2}, & \hbox {if }\, \mu -\sigma \sqrt{2\ln 2} < x < \mu +\sigma \sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

• (2) With $E_{*}$ reduction method, the reduction $\eta _2$ of $\widetilde{\eta }$ has the following distribution

  $$\begin{aligned} \mu _{\eta _{2}(x)}= \left\{ \begin{array}{ll} \frac{(2-\theta _{l})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{2}, & \hbox {if }\, x\le \mu -\sigma \sqrt{2\ln 2} \,\hbox { or } \,x\ge \mu +\sigma \sqrt{2\ln 2} \\ \frac{(2+\theta _{l})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) -\theta _l}{2}, & \hbox {if } \,\mu -\sigma \sqrt{2\ln 2} < x < \mu +\sigma \sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

• (3) With E reduction method, the reduction $\eta _3$ of $\widetilde{\eta }$ has the following distribution

  $$\begin{aligned} \mu _{\eta _{3}(x)}= \left\{ \begin{array}{ll} \frac{(4+\theta _{r}-\theta _{l})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{4}, & \hbox {if } x\le \mu -\sigma \sqrt{2\ln 2} \,\hbox { or }\, x\ge \mu +\sigma \sqrt{2\ln 2} \\ \frac{(4-\theta _{r}+\theta _{l})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) +\theta _r-\theta _{l}}{4}, & \hbox {if } \mu -\sigma \sqrt{2\ln 2} < x < \mu +\sigma \sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

Proof

We only prove (1). The rest can be proved similarly. Since $\tilde{\eta }$ is a GT2FV, the secondary possibility distribution $\mu _{\tilde{\eta }}(x)$ of $\tilde{\xi }$ is the following RFV

$$\begin{aligned}&\left( \exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) -\theta _l\min \left\{ 1-\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) ,\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) \right\} ,\, \exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) ,\right. \\&\left. \exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) +\theta _r\min \left\{ 1-\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) ,\,\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) \right\} \right) \end{aligned}$$

For any $x\in {\mathcal {R}}$. If we denote $\eta _1$ as E reduction of $\tilde{\eta }$, then by (6), we have

$$\begin{aligned} \mu _{\eta _1}& = \hbox {Pos}\{\eta _1=x\}=\frac{r_2+r_3}{2}\\ & = \frac{ \exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) + \exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) +\theta _r\min \left\{ 1-\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) ,\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) \right\} }{2} \\& = \left\{ \begin{array}{ll} \frac{(2+\theta _{r})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{2}, & \hbox {if } x\le \mu -\sigma \sqrt{2\ln 2} \hbox { or } x\ge \mu +\sigma \sqrt{2\ln 2} \\ \frac{(2-\theta _{r})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) +\theta _r}{2}, & \hbox {if } \mu -\sigma \sqrt{2\ln 2} < x < \mu +\sigma \sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

which completes the proof of assertion (1).$\square$

Example 3

If $\tilde{\xi }=N(2, 0.5, 0.8, 0.2)$ be a GT2FV, then the $\mu _{\xi _1}, \mu _{\xi _2}, \mu _{\xi _3}$ of mean reduction method are graphically represented in Fig. 6 and the corresponding support of $\tilde{\xi }$ in Fig. 7.

Fig. 6

$\mu _{\xi _1}, \mu _{\xi _2}, \mu _{\xi _3}$ of mean reduction method

Fig. 7

Support of $\xi$ in Example 2

Example 4

Let $\tilde{\xi }$ be a GT2FV defined as $\tilde{\xi }=N(2, 0.5, 0.2, 0.8)$, and suppose $\xi _1, \xi _2,$ and $\xi _3$ are $E^{*}, E_*$ and E reductions of $\tilde{\xi }$. respectively. Then according to Theorem 1, we have

$$\begin{aligned} \mu _{\xi _{1}(x)}= \left\{ \begin{array}{ll} \frac{2.8 \exp \left( -\frac{(x-2)^{2}}{0.5}\right) }{2}, & \hbox {if } x\le 2-0.5\sqrt{2\ln 2} \hbox { or } x\ge 2+0.5\sqrt{2\ln 2} \\ \frac{0.9 \exp \left( -\frac{(x-2)^{2}}{0.5}\right) +0.8}{2}, & \hbox {if } 2-0.5\sqrt{2\ln 2} < x < 2+0.5\sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

• (2) With $E_{*}$ reduction method, the reduction $\xi _2$ of $\widetilde{\xi }$ has the following distribution

  $$\begin{aligned} \mu _{\xi _{2}(x)}= \left\{ \begin{array}{ll} \frac{1.8 \exp \left( -\frac{(x-2)^{2}}{0.5}\right) }{2}, & \hbox {if } x\le 2-0.5\sqrt{2\ln 2} \hbox { or } x\ge 2+0.5\sqrt{2\ln 2} \\ \frac{2.2 \exp \left( -\frac{(x-2)^{2}}{0.5}\right) -0.2}{2}, & \hbox {if } 2-0.5\sqrt{2\ln 2} < x < 2+0.5\sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

• (3) With E reduction method, the reduction $\xi _3$ of $\widetilde{\xi }$ has the following distribution

  $$\begin{aligned} \mu _{\xi _{3}(x)}= \left\{ \begin{array}{ll} \frac{4.6 \exp \left( -\frac{(x-2)^{2}}{0.5}\right) }{4}, & \hbox {if } x\le 2-0.5\sqrt{2\ln 2} \hbox { or } x\ge 2+0.5\sqrt{2\ln 2} \\ \frac{3.4 \exp \left( -\frac{(x-2)^{2}}{0.5}\right) +0.6}{4}, & \hbox {if } 2-0.5\sqrt{2\ln 2} < x < 2+0.5\sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

Theorem 2

Let $\xi _i$ be E reduction of the GT2FV $\tilde{\xi _i}=N(\mu _i, \sigma ^{2}_{i},\theta _{l,i},\theta _{r,i})$. Suppose $\xi _{1}, \xi _{2}, \ldots , \xi _{n}$ are mutually independent, and $\theta _{r,1}-\theta _{l,1}\le \theta _{r,2}-\theta _{l,2}\le \cdots \le \theta _{r,n}-\theta _{l,n}$ and $k_i\ge 0$ for $i= 1, 2,\ldots ,n$.

• (1) if $\alpha \in (0,( 4+\theta _{r,1}-\theta _{l,1})/16]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i-\sigma _{i} \sqrt{2\ln (4+\theta _{r,i}-\theta _{l,i})-2\ln 8\alpha } \right) \le t \end{aligned}$$

• (2) if $\alpha \in ((4+\theta _{r,n}-\theta _{l,n})/16, 0.05]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i-\sigma _{i} \sqrt{2\ln (4-\theta _{r,i}+\theta _{l,i}))-2\ln (8\alpha -\theta _{r,i}+\theta _{l,i})} \right) \le t \end{aligned}$$

• (3) if $\alpha \in (0.5, (12-\theta _{r,n}-\theta _{l,n})/16]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i+\sigma _{i} \sqrt{2\ln (4-\theta _{r,i}+\theta _{l,i})-2\ln 2(8(1-\alpha )-\theta _{r,i}+\theta _{l,i})} \right) \le t, \end{aligned}$$

• (4) if $\alpha \in ((12-\theta _{r,n}-\theta _{l,n})/16, 1]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i+\sigma _{i} \sqrt{2\ln (4+\theta _{r,i}-\theta _{l,i})-2\ln 8(1-\alpha )} \right) \le t \end{aligned}$$

Proof

We only prove (3) and (4). The rest can be proved similarly. Since $\xi$ is the E reduction of the type-2 normal fuzzy variable $\tilde{\xi }_i$ for $i=1,2,\ldots ,n$, their possibility distributions are as follows

$$\begin{aligned} \mu _{\xi _{3}(x)}= \left\{ \begin{array}{ll} \frac{(4+\theta _{r,i}-\theta _{l,i})\exp \left( -\frac{(x-\mu _{i})^{2}}{2\sigma ^{2}_{i}}\right) }{4}, & \hbox {if } x\le \mu _{i}-\sigma _{i}\sqrt{2\ln 2} \hbox { or } x\ge \mu _{i}+\sigma _{i}\sqrt{2\ln 2} \\ \frac{(4-\theta _{r,i}+\theta _{l,i})\exp \left( -\frac{(x-\mu _{i})^{2}}{2\sigma ^{2}_{i}}\right) +\theta _{r,i}-\theta _{l,i}}{4}, & \hbox {if } \mu _{i}-\sigma _{i}\sqrt{2\ln 2} < x < \mu _{i}+\sigma _{i}\sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

for $i=1,2,\dots ,n$. Let $\xi =\sum \nolimits _{i=1}^{n}k_i\xi _i$, if $\alpha \ge 0.5$, then we have

$$\begin{aligned} \hbox {Cr}\left\{ \sum \limits _{i=1}^{n}k_i\xi _i\le t\right\}& = \frac{1}{2}\left( 1+\sup _{x\le t}\mu _{\xi }(x)-\sup _{x> t}\mu _{\xi }(x)\right) \\& = \frac{1}{2}\left( 1+1-\sup _{x> t}\mu _{\xi }(x)\right) \\& = \frac{1}{2}\left( 2-\sup _{x\le t}\mu _{\xi }(x)\right) \end{aligned}$$

Thus, Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

$$\begin{aligned} \sup _{x\ge t}\mu _{\xi }(x)\le (2-2\alpha ) \end{aligned}$$

If we denote $\xi _{\sup }(\alpha )=\sup \{r|\sup _{x\ge r}\mu _{\xi }(x)\ge \alpha \}$ for $\alpha \in (0, 1]$, then we have

$$\begin{aligned} \xi _{\sup }(2-2\alpha )\le t \end{aligned}$$

Since $\xi _{1},\xi _{2},\ldots ,\xi _{n}$ are mutually independent, we have

$$\begin{aligned} \xi _{\sup }(2-2\alpha )=\left( \sum \limits _{i=1}^{n}k_i\xi _i\right) _{\sup }(2-2\alpha )=\sum \limits _{i=1}^{n}k_i\xi _{i\sup }(2-2\alpha )\le t \end{aligned}$$

(7)

If $2-2\alpha \ge (4+\theta _{r,i}-\theta _{l,i})/8$, i.e., $\alpha \in (0.5,(12-\theta _{r,i}+\theta _{l,i})/16)$, then for each $i, \xi _{i, \sup }(2-2\alpha )$ is the solution of the following equation

$$\begin{aligned} \frac{(4-\theta _{r,i}+\theta _{l,i})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) +\theta _{r,i}-\theta _{l,i}}{4}-(2-2\alpha )=0 \end{aligned}$$

(8)

Solving the above equation, we have

$$\begin{aligned} \xi _{\sup }(2-2\alpha )& = \mu _i+\sigma _{i} \sqrt{2\ln (4-\theta _{r,i}+\theta _{l,i})-2\ln (8(1-\alpha )-\theta _{r,i}+\theta _{l,i})} \end{aligned}$$

(9)

On the other hand, if $2-2\alpha <(4+\theta _{r,i}-\theta _{l,i})/8$, i.e., $\alpha \in ( 12-\theta _{r,i}+\theta _{l,i})/16, 1)$. Then for each $i, \xi _{_{i,\sup }}\in (2-2\alpha )$ is the solution of the following equation

$$\begin{aligned} \frac{(4+\theta _{r,i}-\theta _{l,i})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{4}-(2-2\alpha )=0 \end{aligned}$$

Solving the above equation gives

$$\begin{aligned} \xi _{\sup }(2-2\alpha )& = \mu _i+\sigma _{i} \sqrt{2\ln (4+\theta _{r,i}-\theta _{l,i})-2\ln 8(1-\alpha )} \end{aligned}$$

Note that $\theta _{r,1}-\theta _{l,1}\le \theta _{r,2}-\theta _{l,2}\le \cdots \le \theta _{r,n}-\theta _{l,n}$ and $k_i\ge 0$ for $i= 1, 2,\dots ,n$. We have the following results. If $(4+ \theta _{r,n}-\theta _{l,n})/8\le (2-2\alpha )\le 1$, then $(2-2\alpha \ge (4+ \theta _{r,i}-\theta _{l,i})/8$, for $i=1,2,\dots ,n$. Therefore, if $\alpha \in (0.5, (12-\theta _{r,i}-\theta _{l,i})/16]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

$$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i+\sigma _{i} \sqrt{2\ln (4-\theta _{r,i}+\theta _{l,i})-2\ln 2(8(1-\alpha )-\theta _{r,i}+\theta _{l,i})} \right) \le t \end{aligned}$$

(10)

If $2-2\alpha < (4+\theta _{r,1}-\theta _{l,1})/8$, then $2-2\alpha \le (4+\theta _{r,i}-\theta _{l,i})/8$ for $i=1,2,\dots ,n$. Therefore, if $\alpha \in ((12-\theta _{r,i}-\theta _{l,i})/16, 1]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

$$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i+\sigma _{i} \sqrt{2\ln (4+\theta _{r,i}-\theta _{l,i})-2\ln 8(1-\alpha )} \right) \le t \end{aligned}$$

(11)

$\square$

3.2 CV reduction method

Because of fuzziness in membership function of T2FS, computational complexity is very high to deal with T2FS. A general idea to reduce its complexity is to convert a T2FS into a T1FS so that the methodologies to deal with T1FSs can also be applied to T2FSs. Qin et al. [18] proposed a CV-based reduction method which reduces a type-2 fuzzy variable to a type-1 fuzzy variable (may or may not be normal). Let $\xi$ be a T2 FV with secondary possibility distribution function $\widetilde{\mu }_{\xi }(x)$ (which represents a RFV). The method is to introduce the critical values (CVs) as representing values for RFV $\hbox {CV}_{*}[\widetilde{\mu }_{\xi }(x)]$, CV$^{*}[\widetilde{\mu }_{\xi }(x)]$ or CV$[\widetilde{\mu }_{\xi }(x)]$, and so corresponding type-1 fuzzy variables (T1FVs) are derived using these CVs of the secondary possibilities. Then, these methods are respectively called optimistic CV reduction, pessimistic CV reduction and CV reduction method (in Fig. 3).

3.3 Critical values for RFVs

In this section, we define three kinds of CVs for an RFV by using a fuzzy integral

Definition 2

Let $\xi$ be an RFV. Then, the optimistic CV of $\xi$, denoted by CV$^{*}[\xi ]$, is defined as

$$\begin{aligned} \hbox {CV}^{*}[\xi ] = \sup \limits _{\alpha \in [0,1]}[\alpha \wedge \hbox {Pos}({\xi \ge \alpha })], \end{aligned}$$

(12)

while the pessimistic CV of $\xi$, denoted by CV$_{*}[\xi ]$, is defined as

$$\begin{aligned} \hbox {CV}_{*}[\xi ] = \sup \limits _{\alpha \in [0,1]}[\alpha \wedge \hbox {Nec}({\xi \ge \alpha })], \end{aligned}$$

(13)

The CV of $\xi$ , denoted by CV[$\xi$], is defined

$$\begin{aligned} \hbox {CV}[\xi ] = \sup \limits _{\alpha \in [0,1]}[\alpha \wedge \hbox {Cr}({\xi \ge \alpha })], \end{aligned}$$

(14)

Example 5

Let $\xi$ be a discrete RFV with the following possibility distribution:

$$\begin{aligned} \xi \sim \left( \begin{array}{llll} 0.1 & 0.3 & 0.6 & 0.8 \\ 0.2 & 1 & 0.5 & 0.7 \\ \end{array} \right) \end{aligned}$$

Then it is easy to compute that

$$\begin{aligned}&\hbox {Pos}({\xi \ge \alpha })=\left\{ \begin{array}{ll} 1, & \hbox {if }\,\,\alpha \le 0.3 \\ 0.7, & \hbox {if }\,\,0.3 < \alpha \le 0.8 \\ 0, & \hbox {if }\,\,0.8 < \alpha \le 1\\ \end{array} \right. \\&\hbox {Nec}({\xi \ge \alpha })=\left\{ \begin{array}{ll} 1, & \hbox {if }\,\,\alpha \le 0.1 \\ 0.8, & \hbox {if }\,\,0.1 < \alpha \le 0.3 \\ 0, & \hbox {if }\,\,0.3 < \alpha \le 1 \\ \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \hbox {Cr}({\xi \ge \alpha })=\left\{ \begin{array}{ll} 1, & \hbox {if }\,\,\alpha \le 0.1 \\ 0.9, & \hbox {if }\,\,0.1 < \alpha \le 0.3 \\ 0.35, & \hbox {if }\,\,0.3 < \alpha \le 0.8 \\ 0, & \hbox {if }\,\,0.8 < \alpha \le 1 \\ \end{array} \right. \end{aligned}$$

Therefore, by the definitions of CVs, we have

$$\begin{aligned}&\hbox {CV}^{*}[\xi ]=\left\{ \begin{array}{ll} \sup \limits _{\alpha \in [0,1]}[\alpha \wedge \hbox {Pos}({\xi \ge \alpha })] \\ \sup \limits _{\alpha \in [0,0.3]}[\alpha \wedge 1] \vee \sup \limits _{\alpha \in [0.3,0.8]}[\alpha \wedge 0.7] \vee \sup \limits _{\alpha \in [0.8,1]}[\alpha \wedge 0] \\ 0.3 \vee 0.7 \vee 0 = 0.7 \\ \end{array} \right. \\&\hbox {CV}_{*}[\xi ]=\left\{ \begin{array}{ll} \sup \limits _{\alpha \in [0,1]}[\alpha \wedge \hbox {Nec}({\xi \ge \alpha })] \\ \sup \limits _{\alpha \in [0,0.1]}[\alpha \wedge 1] \vee \sup \limits _{\alpha \in [0.1,0.3]}[\alpha \wedge 0.8] \vee \sup \limits _{\alpha \in [0.3,1]}[\alpha \wedge 0] \\ 0.1 \vee 0.3 \vee 0 = 0.3 \\ \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \hbox {CV}[\xi ]=\left\{ \begin{array}{ll} \sup \limits _{\alpha \in [0,1]}[\alpha \wedge \hbox {Cr}({\xi \ge \alpha })] \\ \sup \limits _{\alpha \in [0,0.1]}[\alpha \wedge 1] \vee \sup \limits _{\alpha \in [0.1,0.3]}[\alpha \wedge 0.9] \vee \sup \limits _{\alpha \in [0.3,0.8]}[\alpha \wedge 0.35] \vee \sup \limits _{\alpha \in [0.8,1]}[\alpha \wedge 0] \\ 0.1 \vee 0.3 \vee 0.35 \vee 0 = 0.35 \\ \end{array} \right. \end{aligned}$$

The following theorem presents the formulas for CVs of a trapezoidal RFV.

Theorem 3

(Qin et al. [18]) Let $\xi$ be a type-2 normal fuzzy variable $N(\mu , \sigma ^2; \theta _l ,\theta _r)$. Then, we have

• (1) Using the optimistic CV reduction method, the reduction $\xi _1$ of $\widetilde{\xi }$ has the following possibility distribution:

  $$\begin{aligned} \mu _{\xi _{1}(x)}= \left\{ \begin{array}{ll} \frac{(1+\theta _{r})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{1+\theta _{r}\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }, & \hbox {if } x\le \mu -\sigma \sqrt{2\ln 2} \hbox { or } x\ge \mu +\sigma \sqrt{2\ln 2} \\ \frac{\theta _r+(1-\theta _{r})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{1+\theta _{r}-\theta _r \exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }, & \hbox {if } \mu -\sigma \sqrt{2\ln 2} < x < \mu +\sigma \sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

• (2) Using the pessimistic CV reduction method, the reduction $\xi _2$ of $\widetilde{\xi }$ has the following possibility distribution:

  $$\begin{aligned} \mu _{\xi _{2}(x)}= \left\{ \begin{array}{ll} \frac{\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{1+\theta _{l}\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }, & \hbox {if } x\le \mu -\sigma \sqrt{2\ln 2} \hbox { or } x\ge \mu +\sigma \sqrt{2\ln 2} \\ \frac{\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{1+\theta _{l}-\theta _l \exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }, & \hbox {if } \mu -\sigma \sqrt{2\ln 2} < x < \mu +\sigma \sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

• (3) Using the CV reduction method, the reduction $\xi _3$ of $\widetilde{\xi }$ has the following possibility distribution:

  $$\begin{aligned} \mu _{\xi _{3}(x)}= \left\{ \begin{array}{ll} \frac{(1+\theta _{r})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{1+2\theta _{r}\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }, & \hbox {if } x\le \mu -\sigma \sqrt{2\ln 2} \hbox { or } x\ge \mu +\sigma \sqrt{2\ln 2} \\ \frac{\theta _r+(1-\theta _{l})\exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }{1+2\theta _{l}-2\theta _l \exp \left( -\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right) }, & \hbox {if } \mu -\sigma \sqrt{2\ln 2} < x < \mu +\sigma \sqrt{2\ln 2} \\ \end{array} \right. \end{aligned}$$

Theorem 4

(Qin et al. [18]) Let $\xi$ be the reduction of the type-2 fuzzy variable $\xi =\widetilde{N}(\mu _i, \sigma _i^{2}, \theta _{l,i}, \theta _{r,i})$ obtained by the CV reduction method for $i = 1, 2, \dots , n$. Suppose $\xi _1, \xi _2, \ldots , \xi _n$ are mutually independent, and $k_i \ge 0$ for $i = 1, 2, \ldots , n$.

• (1) Given the generalized credibility level $\alpha \in (0, 0.5]$, if $\alpha \in (0, 0.25]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i-\sigma _{i} \sqrt{2\ln (1+(1-4\alpha )\theta _{r,i})-2\ln 2\alpha } \right) \le t, \end{aligned}$$

  if $\alpha \in (0.25, 0.50]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i-\sigma _{i} \sqrt{2\ln (1+(4\alpha -1)\theta _{r,i})-2\ln (2\alpha +4\alpha -1)\theta _{l,i}} \right) \le t, \end{aligned}$$

• (2) Given the generalized credibility level $\alpha \in (0.5, 1]$, if $\alpha \in (0.5, 0.75]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i+\sigma _{i} \sqrt{2\ln (1+(3-4\alpha )\theta _{l,i})-2\ln 2(\alpha -1)+(3-4\alpha )\theta _{r,i}} \right) \le t, \end{aligned}$$

  if $\alpha \in (0.75, 1]$, then Cr$\{\sum \nolimits _{i=1}^{n}k_i\xi _i\le t\}\ge \alpha$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^{n}k_i\left( \mu _i+\sigma _{i} \sqrt{2\ln (1+(3-4\alpha )\theta _{l,i})-2\ln 2(1-\alpha )} \right) \le t, \end{aligned}$$

Example 6

(Using the same data from Example 3) If $\tilde{\xi }=N(2, 0.5, 0.8, 0.2)$ be a Gaussian FT2 variable, then from Example 2 $\mu _{\xi _1}, \mu _{\xi _2}, \mu _{\xi _3}$ of mean reduction method are graphically represented in Fig. 8 and the corresponding support of $\xi$ in Fig. 9.

Fig. 8

$\mu _{\xi _1}, \mu _{\xi _2}, \mu _{\xi _3}$ of CV reduction method

Fig. 9

Support of $\xi$ in Example 6

Theorem 5

(Qin et al. [18]) Let $\xi$ be a Gaussian RFV with the following possibility distribution:

$$\begin{aligned} \mu _{\xi }(x)=\exp \left( -\frac{(x-\mu )^2}{2\sigma ^{2}}\right) ,\quad x\in [0,1]. \end{aligned}$$

(15)

• (1) If $\mu = 1$, then CV$^{*}[\xi ] = 1$, and if $0 \le \mu \le 1$, then CV$^{*}[\xi ]$ is the solution of the following equation:

  $$\begin{aligned} (\alpha - \mu )^2 + 2\sigma ^2\ln \alpha = 0. \end{aligned}$$

• (2) If $\mu = 0$, then CV$_{*}[\xi ] = 0$, and if $0 \le \mu \le 1$, then CV$_{*}[\xi ]$ is the solution of the following equation:

  $$\begin{aligned} (\alpha - \mu )^2 + 2\sigma ^2\ln (1-\alpha ) = 0. \end{aligned}$$

• (3) If $\mu = 0.5$, then CV$[\xi ] =0.5$, and if $0.5 \le \mu \le 1$, then CV$[\xi ]$ is the solution of the following equation:

  $$\begin{aligned} (\alpha - \mu )^2 + 2\sigma ^2\ln 2(1-\alpha ) = 0. \end{aligned}$$

Example 7

The CVs of a Gaussian RFV can be evaluated by the Newton–Rapshon method. Consider the following possibility distribution as:

$$\begin{aligned} \mu _{\xi }(x)=\exp \left( -\frac{(x-3)^2}{18}\right) ,\quad x\in [0,1]. \end{aligned}$$

(16)

Using Theorem 5, we compute CV$^{*}[\xi ]=0.7559, CV_{*}[\xi ]=0.3275$ and CV$[\xi ]=0.6336$.

4 Notations and abbreviations

In this investigation, a two-stage transportation problem (TP) consisting of manufacturer, distribution centers (DCs) and customers are considered. Here, products from each manufacturer are transported to each DC and the item from a DC is transported to a specific customer only. The purchasing and selling prices of the items and the respective transportation costs are considered, and TP is formulated as a maximization problem. In this TP, the following notations are used:

• (1) $P=$ number of product (indexed $i=1,2,\dots ,P$).

• (2) $M=$ number of origins/plants/manufacturers of the TP (indexed $j=1,2,\dots ,M$) from which the humanitarian products are shipped.

• (3) $N=$ number of distribution centers (DCs) (indexed $k=1,2,\dots , N$).

• (4) $R=$ number of customers (indexed $l=1,2,\dots , R$).

• (5) $\tilde{a}_{ij}=$ capacity for i-th product at the j-th manufacturer, which is GT2FVs in nature (ton).

• (6) $\tilde{d}_{il}=$ demand for i-th product by the l-th customer, which is GT2FVs in nature (ton).

• (7) $\tilde{c}_{ijk}=$ unit transportation cost for i-th product from j-th manufacturer to the k-th DC ($/ton).

• (8) $g_{ikl}=$ unit transportation cost for i-th product from k-th DC to the l-th customer($/ton).

• (9) $x_{ijk}=$ the amount (tons) to be transported from j-th manufacturer to k-th DC for the i-th product (decision variables).

• (10) $\tilde{f}_{k}=$ each DC has an associated fixed cost ($).

• (11) $Z_{k}=$ an open indicator, which take the value 0 or 1 by the decision maker.

• (12) $Y_{kl}=$ Each k-th customer is served by one DC.

• (13) $\tilde{s}_{k}=$ selling price of the product at the k-th destination ($/unit).

• (14) $\tilde{B}=$ total budget of the TP ($).

• (15) $\tilde{p}_{j}=$ the purchasing price of the item at jth manufacturer ($/unit).

• (16) $TF=$ total profit in the problem ($).

• (17) $RA=$ total received amount at the customer (ton).

5 Formulation of Gaussian type-2 fuzzy transportation problem (GT2FTP)

In this model, we maximize total profit (TF) over a three-tiered distribution system (in Fig. 10) consisting of plants, distribution centers and customers. Plants produce multiple products that are shipped to distribution centers. If a distribution center is used, then a fixed cost is charged. Customers are supplied by a single distribution center. The GT2FTP is formulated as

$$\begin{aligned}\max \hbox {TF}& = \sum _{i=1}^{P}\sum _{j=1}^{M}\sum _{k=1}^{N}\left\{ (\tilde{s}_{k}-\tilde{p}_{j}-\widetilde{c}_{ijk})x_{ijk}\right\} \\&\quad +\,\sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\left\{ g_{ikl}\times \tilde{d}_{il}\times Y_{kl}\right\} +\sum _{k=1}^{N}\left\{ \tilde{f}_{k}\times Z_{k}\right\} \\\text {s.t}&\quad \sum _{k=1}^{N}x_{ijk}\le \widetilde{a}_{ij}, \quad \forall ~~ i, j \\&\quad \sum _{j=1}^{M}x_{ijk} \ge \sum _{l=1}^{R}\widetilde{d}_{il}\times Y_{kl}, \quad \forall ~~ i, k \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{i=1}^{P}\sum _{j=1}^{M}\sum _{k=1}^{N} \tilde{p}_{j}~x_{ijk}\le \tilde{B} \\&\sum _{k=1}^{N}Y_{kl}=1, \quad \forall ~~ l, x_{ijk}\ge 0. \end{aligned}$$

(18)

For the objective function TF is concerning with transportation cost $\tilde{c}_{ijk}$, purchasing price $\tilde{p}_{j}$, selling price $\tilde{s}_{k}$, fixed-charge cost $\tilde{f}_{k}$, total supply $\tilde{a}_{il}$, and total demand $d_{il}$, represents GT2FVs in nature.

Fig. 10

Multiproduct transportation problem

5.1 Crisp equivalences

Suppose that the $\tilde{c}_{ijk}$, $\tilde{a}_{ij}$, $\tilde{f}_{k}$, $\tilde{d}_{il}$ are all mutually independent type-2 Gaussian fuzzy variables defined by $\tilde{c}_{ijk}=(\mu ^{c_{ijk}}, \sigma ^{2c_{ijk}}, \theta _{l}^{c_{ijk}}, \theta _{r}^{c_{ijk}})$, $\tilde{d}_{il}=(\mu ^{b_{il}}, \sigma ^{2b_{il}}, \theta _{l}^{b_{il}}, \theta _{r}^{b_{il}})$, $\tilde{f}_{k}=(\mu ^{f_{k}}, \sigma ^{2f_{k}}, \theta _{l}^{f_{k}}, \theta _{r}^{f_{k}})$, $\tilde{d}_{il}=(\mu ^{b_{il}}, \sigma ^{2b_{il}}, \theta _{l}^{b_{il}}, \theta _{r}^{b_{il}})$, respectively. Applying chance constraint programming in the above GT2FTP, we obtain the equivalent crisp problem as:

$$\begin{aligned} \min&\quad f \\ \text {s.t}&\quad \hbox {Cr}\left\{ \sum _{i=1}^{P}\sum _{j=1}^{M}\sum _{k=1}^{N}\left\{ (\tilde{s}_{k}-\tilde{p}_{j}-\widetilde{c}_{ijk})x_{ijk}\right\} \right. \\&\qquad \left. +\,\sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\left\{ g_{ikl}\times \tilde{d}_{il}\times Y_{kl}\right\} \right. \\&\qquad \left. +\,\sum _{k=1}^{N}\left\{ \tilde{f}_{k}\times Z_{k}\right\} \ge f \right\} \ge \alpha \\&\hbox {Cr}\left\{ \sum _{k=1}^{N}x_{ijk}\le \widetilde{a}_{ij}\right\} \ge \beta _{ij}, \quad \forall i,j \\&\hbox {Cr}\left\{ \sum _{j=1}^{M}x_{ijk} \ge \sum _{l=1}^{R}\widetilde{d}_{il}\times Y_{kl}\right\} \ge \gamma _{il},\quad \forall i, k \end{aligned}$$

(19)

$$\begin{aligned}&\hbox {Cr}\left\{ \sum _{i=1}^{P}\sum _{j=1}^{M}\sum _{k=1}^{N} \tilde{p}_{j}~x_{ijk}\le \tilde{B}\right\} \ge \eta \hbox { and} \,\,(18). \end{aligned}$$

(20)

where $\alpha , \beta _i, \gamma _j, \eta _k$ and $\delta$ are different optimistic levels which are to be chosen by decision maker (DM). Then, the above model can be solved by the following mean reduction method and CV reduction method.

5.1.1 Using mean reduction method

Case 1: $0 <\alpha \le 0.25$: then, the equivalent parametric programming problem for the model representation is

$$\begin{aligned} \min&\quad f \\ \text {s.t}&\quad \bigg [ \sum _{i=1}^{P}\sum _{j=1}^{M}\sum _{k=1}^{N}\bigg \{\left( \mu _j^{s_{k}}-\sigma _{j}^{s_{k}} \sqrt{2\ln (4+\theta _{r,j}^{s_{k}}-\theta _{l,j}^{s_{k}})-2\ln 8\alpha }\right) \\ - & (\mu _i^{p_{j}}-\sigma _{i}^{p_{j}} \sqrt{2\ln (4-\theta _{r,i}^{p_{j}}+\theta _{l,i}^{p_{j}})-2\ln 8\alpha }) \\- & \left( \mu _{ijk}^{c_{ijk}}-\sigma _{ijk}^{c_{ijk}} \sqrt{2\ln (4+\theta _{r,j}^{c_{ijk}}-\theta _{l,j}^{c_{ijk}})-2\ln 8\alpha }\right) \bigg \}\times x_{ijk} \\- & \sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\bigg \{ \mu _{il}^{d_{il}}-\sigma _{il}^{d_{il}} \sqrt{2\ln (4+\theta _{r,j}^{d_{il}}-\theta _{l,j}^{d_{il}})-2\ln 8\alpha } \bigg \}\times g_{ikl}\times Y_{kl} \\- & \sum _{k=1}^{N}\bigg \{ \mu _{k}^{f_{k}}-\sigma _{il}^{f_{k}} \sqrt{2\ln (4+\theta _{r,j}^{f_{k}}-\theta _{l,j}^{f_{k}})-2\ln 8\alpha }\bigg \}\times Z_{k} \bigg ]\ge f \end{aligned}$$

(21)

$$\begin{aligned} \text { and }&\quad \left\{ \begin{array}{ll} \sum \limits _{k=1}^{N}x_{ijk}\le F_{a_{ij}}, \quad \forall i,j \\ \sum \limits _{j=1}^{M}x_{ijk} \ge \sum \limits _{l=1}^{R} F_{d_{il}\times Y_{kl}}, \quad \forall i,k \\ \sum \limits _{i=1}^{P}\sum \limits _{j=1}^{M}\sum \limits _{k=1}^{N} F_{\tilde{p}_{j}}~x_{ijk}\le F_{\tilde{B}} \hbox { and} \,\,(18).\end{array} \right. \end{aligned}$$

(22)

where

$$\begin{aligned} F_{a_{ij}}& = \left\{ \begin{array}{ll} \mu _{ij}^{a_{ij}}-\sigma _{ij}^{a_{ij}} \sqrt{2\ln (4+\theta _{r,ij}^{a_{ij}}-\theta _{l,ij}^{a_{ij}})-2\ln 8\beta _{ij}} , & \hbox {if } \beta _{ij} \in \bigg [0,0.25\bigg ],\\ \mu _{ij}^{a_{ij}}-\sigma _{ij}^{a_{ij}} \sqrt{2\ln (4-\theta _{r,ij}^{a_{ij}}+\theta _{l,ij}^{a_{ij}}))-2\ln (8\beta _{ij}-\theta _{r,i}^{a_{ij}}+\theta _{l,ij}^{a_{ij}})} , & \hbox {if } \beta _{ij} \in \bigg (0.25,0.50\bigg ],\\ \mu _{ij}^{a_{ij}}+\sigma _{ij}^{a_{ij}} \sqrt{2\ln (4-\theta _{r,ij}^{a_{ij}}+\theta _{l,ij}^{a_{ij}})-2\ln (8(1-\beta _{ij})-\theta _{r,i}^{a_{ij}}+\theta _{l,ij}^{a_{ij}})} , & \hbox {if } \beta _{ij}\in \bigg (0.50,0.75\bigg ],\\ \mu _{ij}^{a_{ij}}+\sigma _{ij}^{a_{ij}} \sqrt{2\ln (4+\theta _{r,ij}^{a_{ij}}-\theta _{l,ij}^{a_{ij}})-2\ln 8(1-\beta _{ij})}, & \hbox {if } \beta _{ij}\in \bigg [0.75,1\bigg ] \end{array} \right. \\ F_{d_{il}}& = \left\{ \begin{array}{ll} \mu _{il}^{d_{il}}-\sigma _{ij}^{d_{il}} \sqrt{2\ln (4-\theta _{r,il}^{d_{il}}+\theta _{l,il}^{d_{il}})-2\ln 8\gamma _{il}} , & \hbox {if } \gamma _{il} \in \bigg [0,0.25\bigg ],\\ \mu _{il}^{d_{il}}-\sigma _{ij}^{d_{il}} \sqrt{2\ln (4+\theta _{r,i}^{d_{il}}-\theta _{l,i}^{d_{il}}))-2\ln (8\gamma _{il}+\theta _{r,il}-\theta _{l,il})} , & \hbox {if } \gamma _{il} \in \bigg (0.25,0.50\bigg ],\\ \mu _{il}^{d_{il}}+\sigma _{ij}^{d_{il}} \sqrt{2\ln (4-\theta _{r,i}^{d_{il}}-\theta _{l,i}^{d_{il}})-2\ln (8(1-\gamma _{il})+\theta _{r,il}-\theta _{l,il})} , & \hbox {if } \gamma _{il}\in \bigg (0.50,0.75\bigg ],\\ \mu _{il}^{d_{il}}+\sigma _{ij}^{d_{il}} \sqrt{2\ln (4-\theta _{r,i}^{d_{il}}+\theta _{l,i}^{d_{il}})-2\ln 8(1-\gamma _{il})}, & \hbox {if } \gamma _{il}\in \bigg [0.75,1\bigg ] \end{array} \right. \end{aligned}$$

where $F_{\tilde{p}_{j}}$ and $F_{\tilde{B}}$ can be written from the above two equations.

Case 2: $0.25 <\alpha \le 0.5$: then, the equivalent parametric programming problem for the model representation is

$$\begin{aligned} \min&\quad f \\ \text {s.t}&\quad \bigg [ \sum _{i=1}^{P}\sum _{j=1}^{M}\sum _{k=1}^{N}\bigg \{\left( \mu _j^{s_{k}}-\sigma _{j}^{s_{k}} \sqrt{2\ln \left( 4-\theta _{r,j}^{s_{k}}+\theta _{l,j}^{s_{k}}\right) -2\ln \left( 8\alpha -\theta _{r,j}^{s_{k}}+\theta _{l,j}^{s_{k}}\right) }\right) \\ &- \left( \mu _i^{p_{j}}-\sigma _{i}^{p_{j}} \sqrt{2\ln \left( 4+\theta _{r,i}^{p_{j}}-\theta _{l,i}^{p_{j}}\right) -2\ln \left( 8\alpha +\theta _{r,i}^{p_{j}}-\theta _{l,i}^{p_{j}}\right) }\right) \\ &- \left( \mu _{ijk}^{c_{ijk}}-\sigma _{ijk}^{c_{ijk}} \sqrt{2\ln \left( 4+\theta _{r,j}^{c_{ijk}}-\theta _{l,j}^{c_{ijk}}\right) -2\ln \left( 8\alpha +\theta _{r,j}^{c_{ijk}}-\theta _{l,j}^{c_{ijk}}\right) }\right) \bigg \}\times x_{ijk} \\ & -\sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\bigg \{ \mu _{il}^{d_{il}}-\sigma _{il}^{d_{il}} \sqrt{2\ln \left( 4+\theta _{r,j}^{d_{il}}-\theta _{l,j}^{d_{il}}\right) -2\ln \left( 8\alpha +\theta _{r,j}^{d_{il}}-\theta _{l,j}^{d_{il}}\right) } \bigg \}\times g_{ikl}\times Y_{kl} \\ & -\sum _{k=1}^{N}\bigg \{ \mu _{k}^{f_{k}}-\sigma _{il}^{f_{k}} \sqrt{2\ln \left( 4+\theta _{r,j}^{f_{k}}-\theta _{l,j}^{f_{k}}\right) -2\ln \left( 8\alpha +\theta _{r,j}^{f_{k}}-\theta _{l,j}^{f_{k}}\right) }\bigg \}\times Z_{k} \bigg ]\ge f \\ \text { and }&\quad (22) \end{aligned}$$

(23)

Case 3: $0.5 <\alpha \le 0.75$: then, the equivalent parametric programming problem for the model representation is

$$\begin{aligned} \min&\quad f \\ \text {s.t}&\quad \bigg [ \sum _{i=1}^{P}\sum _{j=1}^{M}\sum _{k=1}^{N}\bigg \{\left( \mu _j^{s_{k}}-\sigma _{j}^{s_{k}} \sqrt{2\ln \left( 4-\theta _{r,j}^{s_{k}}+\theta _{l,j}^{s_{k}}\right) -2\ln \left( 8(1-\alpha )-\theta _{r,j}^{s_{k}}+\theta _{l,j}^{s_{k}}\right) }\right) \\ &- \left( \mu _i^{p_{j}}-\sigma _{i}^{p_{j}} \sqrt{2\ln \left( 4+\theta _{r,i}^{p_{j}}-\theta _{l,i}^{p_{j}}\right) -2\ln \left( 8(1-\alpha )+\theta _{r,i}^{p_{j}}-\theta _{l,i}^{p_{j}}\right) }\right) \\ &- \left( \mu _{ijk}^{c_{ijk}}-\sigma _{ijk}^{c_{ijk}} \sqrt{2\ln \left( 4+\theta _{r,j}^{c_{ijk}}-\theta _{l,j}^{c_{ijk}}\right) -2\ln \left( 8(1-\alpha )+\theta _{r,j}^{c_{ijk}}-\theta _{l,j}^{c_{ijk}}\right) }\right) \bigg \}\times x_{ijk} \\ &- \sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\bigg \{ \mu _{il}^{d_{il}}-\sigma _{il}^{d_{il}} \sqrt{2\ln \left( 4+\theta _{r,j}^{d_{il}}-\theta _{l,j}^{d_{il}}\right) -2\ln \left( 8(1-\alpha )+\theta _{r,j}^{d_{il}}-\theta _{l,j}^{d_{il}}\right) } \bigg \}\times g_{ikl}\times Y_{kl} \\ &- \sum _{k=1}^{N}\bigg \{ \mu _{k}^{f_{k}}-\sigma _{il}^{f_{k}} \sqrt{2\ln \left( 4+\theta _{r,j}^{f_{k}}-\theta _{l,j}^{f_{k}}\right) -2\ln \left( 8(1-\alpha )+\theta _{r,j}^{f_{k}}-\theta _{l,j}^{f_{k}}\right) }\bigg \}\times Z_{k} \bigg ]\ge f \\ \text { and }&\quad (22) \end{aligned}$$

(24)

Case 4: $0.75 <\alpha \le 1.0$: Then, the equivalent parametric programming problem for the model representation is

$$\begin{aligned} \min&\quad f \\ \text {s.t}&\quad \bigg [ \sum _{i=1}^{P}\sum _{j=1}^{M}\sum _{k=1}^{N}\bigg \{\left( \mu _j^{s_{k}}-\sigma _{j}^{s_{k}} \sqrt{2\ln \left( 4+\theta _{r,j}^{s_{k}}-\theta _{l,j}^{s_{k}}\right) -2\ln 8(1-\alpha )}\right) \\ & -\left( \mu _i^{p_{j}}-\sigma _{i}^{p_{j}} \sqrt{2\ln \left( 4-\theta _{r,i}^{p_{j}}+\theta _{l,i}^{p_{j}}\right) -2\ln 8(1-\alpha )}\right) \\ &- \left( \mu _{ijk}^{c_{ijk}}-\sigma _{ijk}^{c_{ijk}} \sqrt{2\ln \left( 4-\theta _{r,j}^{c_{ijk}}+\theta _{l,j}^{c_{ijk}}\right) -2\ln 8(1-\alpha )}\right) \bigg \}\times x_{ijk} \\ &- \sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\bigg \{ \mu _{il}^{d_{il}}-\sigma _{il}^{d_{il}} \sqrt{2\ln \left( 4-\theta _{r,j}^{d_{il}}+\theta _{l,j}^{d_{il}}\right) -2\ln 8(1-\alpha )} \bigg \}\times g_{ikl}\times Y_{kl} \\ &- \sum _{k=1}^{N}\bigg \{ \mu _{k}^{f_{k}}-\sigma _{il}^{f_{k}} \sqrt{2\ln \left( 4-\theta _{r,j}^{f_{k}}+\theta _{l,j}^{f_{k}}\right) -2\ln 8(1-\alpha )}\bigg \}\times Z_{k} \bigg ]\ge f \\ \text { and }&\quad (22) \end{aligned}$$

(25)

5.1.2 Using CV reduction method

Case 1: $0 <\alpha \le 0.25$: Then, the equivalent parametric programming problem for the model representation is

$$\begin{aligned} \max&\quad f_1 \\ \text {s.t}&\quad \bigg [\sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{K}\bigg \{ \bigg (\mu _j^{s_{k}}-\sigma _{j}^{s_{k}} \sqrt{2\ln (1+(1-4\alpha )\theta _{r,j}^{s_{k}}))-2\ln 2\alpha } \\&-(\mu _i^{p_{j}}-\sigma _{i}^{p_{j}} \sqrt{2\ln (1+(1-4\alpha )\theta _{l,i}^{p_{j}})-2\ln 2\alpha }) \\&- (\mu _{ijk}^{c_{ijk}}-\sigma _{ijk}^{c_{ijk}} \sqrt{2\ln (1+(1-4\alpha )\theta _{l,ijk}^{c_{ijk}})-2\ln 2\alpha }\bigg )x_{ijk} \\ - & \sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\bigg \{ \mu _{il}^{d_{il}}-\sigma _{il}^{d_{il}} \sqrt{2\ln (1+(1-4\alpha )-\theta _{l,il}^{d_{il}})-2\ln 2\alpha } \bigg \}\times g_{ikl}\times Y_{kl} \\- & \sum _{k=1}^{N}\bigg \{ \mu _{k}^{f_{k}}-\sigma _{il}^{f_{k}} \sqrt{2\ln (1+(1-4\alpha )\theta _{l,k}^{f_{k}}-2\ln 2\alpha }\bigg \}\times Z_{k} \bigg ]\ge f_{_{1}} \end{aligned}$$

(26)

$$\begin{aligned} \text { and }&\quad \left\{ \begin{array}{ll} \sum \limits _{k=1}^{N}x_{ijk}\le F_{a_{ij}}, \quad \forall i,j \\ \sum \limits _{j=1}^{M}x_{ijk} \ge \sum \limits _{l=1}^{R} F_{d_{il}\times Y_{kl}}, \quad \forall i,k \\ \sum \limits _{i=1}^{P}\sum \limits _{j=1}^{M}\sum \limits _{k=1}^{N}F_{p_{j}}\times x_{ijk} \le F_{B} \hbox { and} \,\,(18) \end{array} \right. \end{aligned}$$

(27)

where $X=(\mu ^{X},\sigma ^{2X}, \theta _{r}^{X},\theta _{r}^{X})=$, $\tilde{a}_{ij}$, $\tilde{B}$, $Y=(\mu ^{Y},\sigma ^{2Y},\theta _{r}^{Y},\theta _{r}^{Y})=\tilde{p}_{i}$, $\tilde{d}_{il}$, the different optimistic labels $\lambda =\beta _{_{ij}}, \gamma _{_{il}}, \eta$ and

$$\begin{aligned} F_X& = \left\{ \begin{array}{ll} \mu _i-\sigma _{i} \sqrt{2\ln (1+(1-4\alpha )\theta _{r,i})-2\ln 2\lambda } , & \hbox {if } \lambda \in \bigg [0,0.25\bigg ],\\ \mu _i-\sigma _{i} \sqrt{2\ln (1+(4\lambda -1)\theta _{l,i}))-2\ln (2\lambda +(4\lambda -1)\theta _{l,i})} , & \hbox {if } \lambda \in \bigg (0.25,0.50\bigg ],\\ \mu _i+\sigma _{i} \sqrt{2\ln (1+(3-4\lambda )\theta _{l,i})-2\ln (2(1-\lambda )+(3-4\lambda )\theta _{l,i})} , & \hbox {if } \lambda \in \bigg (0.50,0.75\bigg ],\\ \mu _i+\sigma _{i} \sqrt{2\ln (1+(4\lambda -3)\theta _{r,i})-2\ln 2(1-\lambda )}, & \hbox {if } \lambda \in \bigg [0.75,1\bigg ] \end{array} \right. \\ F_Y& = \left\{ \begin{array}{ll} \mu _i-\sigma _{i} \sqrt{2\ln (1+(1-4\alpha )\theta _{l,i})-2\ln 2\lambda } , & \hbox {if } \lambda \in \bigg [0,0.25\bigg ],\\ \mu _i-\sigma _{i} \sqrt{2\ln (1+(4\lambda -1)\theta _{r,i}))-2\ln (2\lambda +(4\lambda -1)\theta _{r,i})} , & \hbox {if } \lambda \in \bigg (0.25,0.50\bigg ],\\ \mu _i+\sigma _{i} \sqrt{2\ln (1+(3-4\lambda )\theta _{r,i})-2\ln (2(1-\lambda )+(3-4\lambda )\theta _{r,i})} , & \hbox {if } \lambda \in \bigg (0.50,0.75\bigg ],\\ \mu _i+\sigma _{i} \sqrt{2\ln (1+(4\lambda -3)\theta _{l,i})-2\ln 2(1-\lambda )}, & \hbox {if } \lambda \in \bigg [0.75,1\bigg ] \end{array} \right. \end{aligned}$$

Case 2: $0.25 <\alpha \le 0.5$: then, the equivalent parametric programming problem for the model representation is

$$\begin{aligned} \max&\quad f_1 \\ \text {s.t}&\quad \bigg [\sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{K}\bigg \{ \bigg (\mu _j^{s_{k}}-\sigma _{j}^{s_{k}} \sqrt{2\ln (1+(4\alpha -1)\theta _{l,j}^{s_{k}})-2\ln (2\alpha +(4\alpha -1)\theta _{l,j}^{s_{k}})} \\&-(\mu _i^{p_{j}}-\sigma _{i}^{p_{j}} \sqrt{2\ln (1+(4\alpha -1)\theta _{r,i}^{p_{j}})-2\ln (2\alpha +(4\alpha -1)\theta _{r,i}^{p_{j}}}) \\&- (\mu _{ijk}^{c_{ijk}}-\sigma _{ijk}^{c_{ijk}} \sqrt{2\ln (1+(4\alpha -1)\theta _{r,ijk}^{c_{ijk}})-2\ln (2\alpha +(4\alpha -1)\theta _{r,ijk}^{c_{ijk}})})\bigg )x_{ijk} \\ - & \sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\bigg \{ \mu _{il}^{d_{il}}-\sigma _{il}^{d_{il}} \sqrt{2\ln (1+(1-4\alpha )-\theta _{l,il}^{d_{il}})-2\ln (2\alpha +(4\alpha -1)\theta _{r,il}^{d_{il}})} \bigg \}\times g_{ikl}\times Y_{kl} \\- & \sum _{k=1}^{N}\bigg \{ \mu _{k}^{f_{k}}-\sigma _{il}^{f_{k}} \sqrt{2\ln (1+(1-4\alpha )\theta _{l,k}^{f_{k}}-2 \ln (2\alpha +(4\alpha -1)\theta _{r,il}^{f_{k}})}\bigg \}\times Z_{k} \bigg ]\ge f_{_{1}} \\ \text { and }&\quad \text {(27)} \end{aligned}$$

(28)

Case 3: $0.5 <\alpha \le 0.75$: Then, the equivalent parametric programming problem for the model representation is

$$\begin{aligned} \max&\quad f_1 \\ \text {s.t}&\quad \bigg [\sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{K}\bigg \{ \bigg (\mu _j^{s_{k}}+\sigma _{j}^{s_{k}} \sqrt{2\ln (1+(3-4\alpha )\theta _{l,j}^{s_{k}})-2\ln (2(1-\alpha )+(3-4\alpha )\theta _{l,j}^{s_{k}})} \\&-(\mu _i^{p_{j}}+\sigma _{i}^{p_{j}} \sqrt{2\ln (1+(3-4\alpha )\theta _{r,i}^{p_{j}})-2\ln (2(1-\alpha )+(3-4\alpha )\theta _{r,i}^{p_{j}}}) \\&- (\mu _{ijk}^{c_{ijk}}+\sigma _{ijk}^{c_{ijk}} \sqrt{2\ln (1+(3-4\alpha )\theta _{r,ijk}^{c_{ijk}})-2\ln (2(1-\alpha )+(3-4\alpha )\theta _{r,ijk}^{c_{ijk}}})\bigg )x_{ijk} \\ - & \sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\bigg \{ \mu _{il}^{d_{il}}+\sigma _{il}^{d_{il}} \sqrt{2\ln (1+(3-4\alpha )\theta _{r,il}^{d_{il}})-2\ln (2(1-\alpha )+(3-4\alpha )\theta _{r,il}^{d_{il}})} \bigg \}\times g_{ikl}\times Y_{kl} \\- & \sum _{k=1}^{N}\bigg \{ \mu _{k}^{f_{k}}+\sigma _{il}^{f_{k}} \sqrt{2\ln (1+(3-4\alpha )\theta _{l,k}^{f_{k}}-2 \ln (2(1-\alpha )+(3-4\alpha -1)\theta _{r,il}^{f_{k}})}\bigg \}\times Z_{k} \bigg ]\ge f_{_{1}} \\ \text { and }&\quad \text {(27)} \end{aligned}$$

(29)

Case 4: $0.75 <\alpha \le 1.0$: then, the equivalent parametric programming problem for the model representation is

$$\begin{aligned} \max&\quad f_1 \\ \text {s.t}&\quad \bigg [\sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{K}\bigg \{ \bigg (\mu _j^{s_{k}}+\sigma _{j}^{s_{k}} \sqrt{2\ln (1+(4\alpha -3)\theta _{r,j}^{s_{k}})-2\ln 2(1-\alpha )} \\&-(\mu _i^{p_{j}}+\sigma _{i}^{p_{j}} \sqrt{2\ln (1+(4\alpha -3)\theta _{l,i}^{p_{j}})-2\ln 2(1-\alpha )}) \\&- (\mu _{ijk}^{c_{ijk}}+\sigma _{ijk}^{c_{ijk}} \sqrt{2\ln (1+(4\alpha -3)\theta _{l,ijk}^{c_{ijk}})-2\ln 2(1-\alpha )})\bigg )x_{ijk} \\- & \sum _{i=1}^{P}\sum _{k=1}^{N}\sum _{l=1}^{R}\bigg \{ \mu _{il}^{d_{il}}+\sigma _{il}^{d_{il}} \sqrt{2\ln (1+(4\alpha -3)\theta _{l,il}^{d_{il}})-2\ln (2(1-\alpha )} \bigg \}\times g_{ikl}\times Y_{kl} \\- & \sum _{k=1}^{N}\bigg \{ \mu _{k}^{f_{k}}+\sigma _{il}^{f_{k}} \sqrt{2\ln (1+(4\alpha -3)\theta _{l,k}^{f_{k}}-2 \ln (2(1-\alpha )}\bigg \}\times Z_{k} \bigg ]\ge f_{_{1}} \\ \text { and }&\quad \text {(27)} \end{aligned}$$

(30)

The above deterministic problems has been solved by the following soft computing technique.

5.2 Modified particle swarm optimization (MPSO)

A PSO normally starts with a set of solutions (called swarm) of the decision-making problem under consideration. Individual solutions are called particles, and food is analogous to optimal solution. The particles are flown through a multidimensional search space, where the position of each particle is adjusted according to its own experience and that of its neighbors. Each particle i has a position vector ($X_{i}(t)$), velocity vector ($V_i(t)$), the position vector at which the best fitness ($X_{{pbesti}}(t)$) encountered by the particle so far and the best position vector of all particles ($X_{gbest}(t)$) in current generation t. In generation ($t+1$), the position and velocity of the particle are changed to $X_i(t+1)$ and $V_i(t+1)$ using following rules:

$$V_i(t+1) = wV_i(t)+\mu _1r_1(X_{{pbesti}}(t)-X_i(t))+\mu _2r_2(X_{{gbest}}(t)-X_i(t))$$

(31)

$$X_i(t+1) = X_i(t)+V_i(t+1)$$

(32)

The parameters $\mu _1$ and $\mu _2$ are set to constant values, which are normally taken as 2, $r_1$ and $r_2$ are two random values uniformly distributed in [0, 1], and $w (0<w<1)$ is inertia weight which controls the influence of previous velocity on the new velocity.

In our study, this algorithm is modified by introducing diversity in the initial population, using entropy originating from information theory. After each iteration of the proposed algorithm, search space is modified depending upon the concentration of better individuals. The outline of the proposed algorithm is presented below. In the algorithm, t is generation counter, $p_c$ and $p_m$ are probability of crossover and mutation, respectively, Maxgen is maximum number of generation of the algorithm, S is population size, i.e., number of solutions in the population, $B_l(t)$ is lower boundary vector and $B_u(t)$ is upper boundary vector of initial search space, and $X_i(t)$ is i-th solution vector. Check_constraint ($X_i$) check whether solution $X_i$ satisfies the constraints of the problem or not. It returns 1 if constraints are satisfied by $X_i$ otherwise it returns 0. A separate subfunction is used for this purpose. $f(X_i(t))$ represents the fitness of solution $X_i$. $k_i$ represents reduction factor of search space for i-th variable. $X_{pbesti}(t)$ represents the position of i-th particle at which best fitness up to t-th iteration is encountered. $X_{gbest}(t)$ represents the position where best fitness is found up to generation t with respect to all the particles.

MPSO Algorithm

The proposed crisp model presented earlier is solved by the above-mentioned PSO.

6 Numerical experiment

6.1 Input data

In the experiments, assume that there are products $P=2$, three plants $M=3$, four distributions centers $N=4$ and five customers $R=5$. Let unit transportation costs, fixed-charge costs, supplies and demands are Gaussian fuzzy type-2 in nature, and these are given in Tables 1, 2, 3, 4 and 5. Here, total budget $\tilde{B}=(2500,50,\theta _l,\theta _r)$, selling price $\tilde{s_{k}}=(80,10,\theta _l,\theta _r)$ and purchasing cost $\tilde{p_{j}}=(10,2,\theta _l,\theta _r)$. Also let the left and right spreads are $\theta _l=0.5$ and $\theta _r=0.5$, respectively, for all Gaussian FT2 variables.

Table 1 Plant capacities (in ton) $\tilde{a}_{ij}$

Table 2 Unit transportation costs (in $) $\tilde{c}_{ijk}$

Table 3 Fixed-charge costs (in $) $\tilde{f}_{k}$ at each DC

Table 4 Shipping costs, DC to customer (in $) $g_{ikl}$

Table 5 Demand for the i-th product by the l-th customer (in $) $\tilde{d}_{il}$

6.2 Optimum results

With the above input data, we solve the problems derived in Sects. 5.1.1 and 5.1.2, using above-mentioned meta-heuristic technique MPSO and gradient base optimization technique-GRG (Lingo-14.0 software). The optimum results are presented in Tables 6, 7, 8 and 9. To derive the optimum results, we first use optimistic value criterion to reduce type-2 fuzzy parameters with different confidence level. Then, MPSO and GRG are used to derive the optimal solutions with different values of $\alpha$. The results are executed on a personal computer with a 2.50 GHz CPU and 4 GB memory.

Table 6 Optimistic results via GRG and PSO for Case 1

Table 7 Optimistic results via GRG and PSO for Case 2

Table 8 Optimistic results via GRG and PSO for Case 3

Table 9 Optimistic results via GRG and PSO for Case 4

Table 10 Optimistic results by changing SD of different FVs via MPSO of mean reduction method

Table 11 Optimistic results by changing SD of different FVs via MPSO of CV reduction method

7 Discussion

From the our experiments, the determined compromise solutions are different with different degrees. In order to validate the proposed models, different optimistic results and a sensitivity analyses are given in Tables 10 and 11 at the end to demonstrate the applicability of the proposed methodology (MPSO) and to provide some managerial insights. It shows that the presented algorithm is efficient in searching good solutions, and the obtained Pareto optimal solutions set is acceptable for decision support systems. For minimum transported cost, the selected unit transportation costs and the transported amounts in different cells for each model are also presented in Tables 6, 7, 8 and 9 against different optimistic labels of decision maker $(0-0.25),(0.25-0.50) (0.5-0.75), (0.75-1.0)$. It may be noted that the optimum value of TF, i.e., maximum profit for each model using mean reduction method is greater than the maximum profit using CV reduction method. A comparison of the results shows that the PSO algorithm performs better than the GRG (Lingo-14.0) algorithms in terms of the objective function values.

8 Conclusions and future research work

In this investigation, we have developed a multilevel distribution in a supply chain transportation problem (TP) under Gaussian type-2 fuzzy (GT2F) environments. Here, the supply capacities, demands and transportation capacities, unit transportation costs and fixed-charge costs are supposed to be GT2F variables due to the instinctive imprecision. Then, the TP is reformulated as profit maximization problem by the credibility optimization methods via (1) mean reduction method and (2) CV-based reduction method. The numerical experiments illustrated the application and effectiveness of the proposed approaches. The deterministic models are solved using MPSO and GRG.

The major new features of the paper include the following three aspects:

• (1) For general fuzzy variables, we defined a generalized credibility measure and discussed the properties of the reduced fuzzy variables of type-2 normal fuzzy variables.

• (2) Using the proposed two reduction methods, a new class of generalized credibility transportation problem has been established.

• (3) For the first time, we have introduced profit transportation problem in GT2F environments.

The present research work can be extended for multi-item STP and multiobjective STP in two-stage supply chain model. The presented models can be extended to different types of TPs including price discounts, transportation time constraints, breakable/deteriorating items, damageable item, transportation with restriction on transported amount, restriction with the use of DCs, operating costs for DCs.