CanSuR: a robust method for staining pattern recognition of HEp-2 cell IIF images

Abstract

The recognition of staining patterns present in human epithelial type 2 (HEp-2) cells helps to diagnose connective tissue disease. In this context, the paper introduces a robust method, termed as CanSuR, for automatic recognition of antinuclear autoantibodies by HEp-2 cell indirect immunofluorescence (IIF) image analysis. The proposed method combines the advantages of a new sequential supervised canonical correlation analysis (CCA), introduced in this paper, with the theory of rough hypercuboid approach. While the proposed CCA efficiently combines the local textural information of HEp-2 cells, derived from various scales of rotation-invariant local binary patterns, the relevant and significant features of HEp-2 cell for staining pattern recognition are extracted using rough hypercuboid approach. Finally, the support vector machine, with radial basis function kernel, is used to recognize one of the known staining patterns present in IIF images. The effectiveness of the proposed staining pattern recognition method, along with a comparison with related approaches, is demonstrated on MIVIA, SNP and ICPR HEp-2 cell image databases. An important finding is that the proposed method performs significantly better than state-of-the art methods, on three HEp-2 cell image databases with respect to both classification accuracy and F1 score.

1 Introduction

Autoimmune diseases are a group of disorders where the immune system of the affected individual malfunctions and the tissues are attacked by autoantibodies. One aspect of these diseases is the formation of self-antigens or autoantibodies. There are two general groups of autoimmune diseases, namely, organ specific and non-organ specific. In organ specific, a specific organ can be attacked, while in non-organ specific, multiple organ systems can be attacked by the autoantibodies. Hashimoto’s thyroiditis is an example of organ-specific autoimmune disease where the thyroid gland is damaged by autoantibodies. An example of a systemic autoimmune disease is systemic lupus erythematosus where the autoantibodies can attack any organ in the body. One of the standard examples of autoimmune disorders is connective tissue diseases (CTDs), which are characterized by a chronic inflammatory process concerning connective tissues.

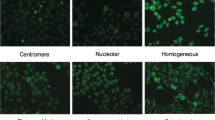
The antinuclear antibody (ANA) test is used to predict the presence of autoantibodies in nucleus of the cell. The ANAs are used as markers to detect certain chronic immuno-inflammatory diseases. The detection as well as quantitation of ANAs is pivotal to the diagnosis of many autoimmune diseases [2, 36]. The presence of ANAs can be determined by indirect immunofluorescence (IIF) [11]. The knowledge about the localization of autoantigens is provided by the IIF, which has become a standard method to predict the presence of ANA in patient serum. The most used cell substrate for IIF demonstration of ANA is human epithelial type 2 (HEp-2) cell [21, 38, 44]. Various staining patterns of ANAs, namely, centromere, cytoplasmic, golgi, homogeneous, nucleolar, speckled and other mixed patterns, can provide useful information to diagnose CTDs, as different patterns are associated with different autoimmune diseases and/or autoantigens [1, 26, 38]. So, accurate classification of these staining patterns is very essential. In real-life analysis, this process suffers from low-throughput and inter and/or intra-laboratory variance. Visual evaluation of IIF test is quite time-consuming, and subjective to the skill of experts [16]. At least two experts must examine each ANA specimen under a fluorescence microscope.

Computer-aided diagnosis (CAD) systems are used to overcome the shortcomings of manual test procedure by determining the staining patterns of a given HEp-2 cell image automatically [10, 40]. Both time and effort may be reduced by the automation of staining pattern classification of HEp-2 cell images. The automated method can make IIF analysis faster, easier and more reliable. Machine learning techniques are widely used to develop the CAD systems in the field of medicine. The goal of the CAD systems is to recognize one of the known staining HEp-2 patterns present in the IIF images. In recent past, some efforts on IIF image analysis using CAD systems have been done. However, a fully automated system to serve the purpose is yet to be developed [10, 16]. There are several approaches present in the literature, either to automate individual stages or the entire IIF diagnostic procedure. Such procedures consist of mainly five steps, namely, acquisition of images, segmentation of images, detection of mitosis, classification of fluorescence intensity and recognition of staining patterns. Soda et al. [35] reported an autofocus function to deal with photobleaching effect during image acquisition. Using a set of textural and shape features obtained from the images, the quality of fluorescence images has been evaluated in [17]. Based on statistical features, fluorescence intensity classification has been performed in [34]. Rough segmentation of HEp-2 cells from IIF images has been addressed in [3, 4, 33]. In [22], an automatic pattern recognition system using fully convolutional network has been proposed to simultaneously address the segmentation and classification problem of HEp-2 specimen images. Another framework has been developed in [12] for the classification of HEp-2 cell images by utilizing deep convolutional neural networks. A superpixel-based Hep-2 cell classification technique has been introduced in [8], based on sparse codes of image patches.

Textural features can be used to capture the information of surface of the HEp-2 cells, which have unpredictably ambiguous texture. The inherent textures in different HEp-2 cell types are quite different from each other. Moreover, the visual resemblance among the cells of different classes increases the ambiguity of IIF image analysis. These difficulties create limitations of HEp-2 pattern recognition using CAD systems. To characterize a cell image, several local texture descriptors, namely, local binary pattern (LBP) [29], rotation-invariant LBP ($\hbox {LBP}^{\mathrm{ri}}$) [30], completed LBP [15], co-occurrence of adjacent LBPs [28] and rotation-invariant co-occurrence of adjacent LBPs [27], are used in [5], while the concept of gradient-oriented co-occurrence of LBP has been introduced in [40]. In [9], a combination of morphological features and textural features extracted using LBPs is used for automatic mitotic cell recognition. In [19], the similarity-based watershed algorithm with marker techniques has been used to segment HEp-2 cells, while learning vector quantization has been used to identify the patterns. Strandmark et al. [37] have developed an automatic method, based on random forests, which classifies an HEp-2 cell image. On the other hand, Cordelli et al. [6] have proposed a method which is independent from the color model used and showed that a gray-scale representation based on the HSI model better exploits information for IIF image analysis. In [39], an automated HEp-2 cell staining pattern recognition method has been proposed by using morphological features. To capture local textural information, a modified version of uniform LBPs descriptor is incorporated in this research work. Wiliem et al. [45] have proposed a system for cell classification, comprising of nearest convex hull classifier and a dual-region codebook-based descriptor. In [5], an HEp-2 cell classification approach has been reported based on subclass discriminant analysis. In order to encode gradient and textural characteristics of the depicted HEp-2 patterns, Theodorakopoulos et al. [40] have proposed a new descriptor, based on co-occurrence of uniform LBPs along directions dictated by the orientation of local gradient. Nosaka et al. [27] have developed a method, which integrates the advantages of both support vector machine (SVM) and rotation-invariant co-occurrence among adjacent LBPs image features. In [32], an automatic HEp-2 cell classification approach has been introduced by combining multiresolution co-occurrence texture and large regional shape information.

The integration of multiple scales of same local textural features may provide better recognition of HEp-2 patterns. Due to the drastic variation of different scales and noisy nature of input HEp-2 cell images, the naive integration usually gives poor performance, which reflects in the insufficient and inaccurate staining pattern representation of these images. Multiple scales of unique cell image, on the other hand, may contain complementary information. The linkages between attributes of each HEp-2 cell images can be made by using these multiple scales of unique sample cell. The combination of multiple scales of a unique HEp-2 cell image would have more discriminatory and complete information of the inherent properties of that cell by generating improved system performance than individual scale. Hence, a proper integration method is needed to incorporate the information of local textural descriptors obtained at multiple scales. In this background, canonical correlation analysis (CCA) [18] or its several variants [7, 14, 42] provide an effective way of capturing the correlation among different multidimensional data sets. Recently, some new supervised CCA have been proposed [24, 25], which perform significantly better than the existing CCA-based approaches. However, these methods are known to have high computational complexity, which renders their application in many real-life data analysis such as classification of HEp-2 cell patterns.

In this regard, the paper presents a new method, termed as CanSuR, for automatic recognition of antinuclear autoantibodies by HEp-2 cell IIF image analysis. It judiciously integrates the advantages of canonical correlation analysis, support vector machine and rough hypercuboid approach. The proposed staining pattern recognition method has two main steps, namely feature extraction and classification. The feature extraction step consists of two levels. At first, the local textural features are extracted from HEp-2 cell images, and then combined using a novel sequential canonical correlation analysis (CCA). To integrate two multidimensional variables, consisting of local features at different scales, the proposed supervised CCA extracts features sequentially by maximizing the correlation between canonical variables, significance among the features and their individual relevance with respect to HEp-2 cell images. The theory of rough hypercuboid approach is used for computing both significance and relevance measures. Finally, the SVM with radial basis function kernel is used to recognize one of the known staining patterns present in IIF images. In this context, it should be mentioned that both proposed CCA and supervised CCA, introduced in [25] and termed as FaRoC, can extract features sequentially from two multidimensional variables. But, the proposed method explores large search space with significantly lesser amount of time than FaRoC. The effectiveness of the proposed staining pattern recognition method, along with a comparison with related approaches, is demonstrated on MIVIA, SNP and ICPR HEp-2 cell image databases.

2 A novel sequential supervised CCA

A novel feature extraction algorithm for multimodal data sets, termed as sequential CCA, is introduced in this section. It extracts maximally correlated and most significant as well as relevant latent features sequentially from two multidimensional variables ${{\fancyscript{X}}} \in \mathfrak {R}^{{\fancyscript{p}} \times n}$ and ${\fancyscript{Y}} \in \mathfrak {R}^{{{\fancyscript{q}}} \times n}$. If the number of features ${\fancyscript{p}}$ and ${\fancyscript{q}}$ of ${{\fancyscript{X}}}$ and ${\fancyscript{Y}}$, respectively, is larger than the number of samples n, that is, $n<< ({\fancyscript{p,q}})$, then the covariance matrices ${\fancyscript{C_{xx}}}$ and ${{\fancyscript{C_{yy}}}}$ become ill-conditioned. In the current work, a fast and supervised sequential CCA is proposed to address the singularity issue of covariance matrices while integrating the information of two multidimensional data sets. The proposed CCA obtains two directional basis vectors ${{\fancyscript{w_x}}} \in \mathfrak {R}^{\fancyscript{p}}$ and ${\fancyscript{w_y}} \in \mathfrak {R}^{\fancyscript{q}}$ such that the correlation between canonical variables ${\fancyscript{U}}={\fancyscript{w_x}}^{T} {\fancyscript{X}}$ and ${\fancyscript{V}}={\fancyscript{w_y}}^{T}{\fancyscript{Y}}$ is maximum, and the extracted feature ${\fancyscript{A=U+V}}$ is most relevant and significant. The correlation coefficient between the canonical variables is given as follows:

$$\begin{aligned}\fancyscript{J(w_x,w_y)}&= \max \limits _{{\fancyscript{w_x}}, {\fancyscript{w_y}}} \;\;{\fancyscript{UV}}^{T} = \max \limits _{{\fancyscript{w_x}}, {\fancyscript{w_y}}} \;\;{\fancyscript{w_x}}^{T}{\fancyscript{C_{xy}w_y}} \\&\text{ subject } \text{ to, }\quad {\fancyscript{UU}}^{T}={\fancyscript{w_x}}^{T}{\fancyscript{C_{xx}w_x}}=1; \\&\quad \text{ and }\quad {\fancyscript{VV}}^{T}={\fancyscript{w_y}}^{T}{\fancyscript{C_{yy}w_y}}=1. \end{aligned}$$

(1)

To incorporate the above two constraints into correlation coefficient-based objective function, the Lagrange multiplier is used in (1), which leads to

$$\begin{aligned} \begin{aligned} {\fancyscript{L}}(\lambda _1,\lambda _2) ={\fancyscript{w_x}}^{T}{\fancyscript{C_{xy}w_y}} -\frac{\lambda _1}{2}({\fancyscript{w_x}}^{T}{\fancyscript{C_{xx}w_x}}-1) \\ -\frac{\lambda _2}{2}({\fancyscript{w_y}}^{T}{\fancyscript{C_{yy}w_y}}-1); \end{aligned} \end{aligned}$$

(2)

where $\lambda _1$ and $\lambda _2$ are Lagrange multipliers. Differentiating ${\fancyscript{L}}$ with respect to ${\fancyscript{w_x}}$ and ${\fancyscript{w_y}}$ and setting the vectors of derivative to zero, we obtain

$$\begin{aligned}&\frac{\delta {\fancyscript{L}}}{\delta {\fancyscript{w_x}}} ={\fancyscript{C_{xy}w_y}}-\frac{\lambda _1}{2}({\fancyscript{C_{xx}w_x}} +{\fancyscript{C_{xx}}}^{T}{\fancyscript{w_x}})=0\nonumber \\&\quad \Rightarrow {\fancyscript{C_{xy}w_y}}=\lambda _1{\fancyscript{C_{xx}w_x}}; \end{aligned}$$

(3)

$$\begin{aligned}&\text{ and } \,\frac{\delta {\fancyscript{L}}}{\delta {\fancyscript{w_y}}} ={\fancyscript{C_{xy}}}^{T}{\fancyscript{w_x}}-\frac{\lambda _2}{2}({\fancyscript{C_{yy}w_y}} +{\fancyscript{C_{yy}}}^{T}{\fancyscript{w_y}})=0\nonumber \\&\quad \Rightarrow {\fancyscript{C_{yx}w_x}}=\lambda _2{\fancyscript{C_{yy}w_y}}. \end{aligned}$$

(4)

Multiplying (3) and (4) by ${\fancyscript{w_x}}^{T}$ and ${\fancyscript{w_y}}^{T}$, respectively, we obtain

$$\begin{aligned}&{\fancyscript{w_x}}^{T}{\fancyscript{C_{xy}w_y}} =\lambda _1{\fancyscript{w_x}}^{T}{\fancyscript{C_{xx}w_x}}=\lambda _1; \end{aligned}$$

(5)

$$\begin{aligned}&\text{ and } \quad {\fancyscript{w_y}}^{T} {\fancyscript{C_{yx}w_x}}=\lambda _2{\fancyscript{w_y}}^{T}{\fancyscript{C_{yy}w_y}}=\lambda _2. \end{aligned}$$

(6)

The correspondence between the Lagrange multipliers $\lambda _1$ and $\lambda _2$ can be established using (5) and (6),

$$\begin{aligned} \lambda _1=({\fancyscript{w_x}}^{T}{\fancyscript{C_{xy}w_y}})^{T} ={\fancyscript{w_y}}^{T}{\fancyscript{C_{yx}w_x}}=\lambda _2. \end{aligned}$$

(7)

From (7), it can be seen that the correlation coefficient between two canonical variables ${\fancyscript{U}} = {\fancyscript{w_x}}^{T} {\fancyscript{X}}$ and ${\fancyscript{V}} = {\fancyscript{w_y}}^{T} {\fancyscript{Y}}$ is same with the Lagrange multipliers $\lambda _1 = \lambda _2 = \lambda$. Hence, (3) and (4) can be rewritten as

$$\begin{aligned}&{\fancyscript{C_{xy}w_y}}=\lambda {\fancyscript{C_{xx}w_x}} \Rightarrow {\fancyscript{w_y}}=\lambda {\fancyscript{C}}_{\fancyscript{xy}}^{-1} {\fancyscript{C}}_{\fancyscript{xx}} {\fancyscript{w}}_{\fancyscript{x}}; \end{aligned}$$

(8)

$$\begin{aligned}&\text{ and } \quad {\fancyscript{C_{yx}w_x}}=\lambda {\fancyscript{C_{yy}w_y}} \Rightarrow {\fancyscript{w_x}}=\lambda \fancyscript{C}_{\fancyscript{yx}}^{-1}\fancyscript{C}_{\fancyscript{yy}}\fancyscript{w_y}. \end{aligned}$$

(9)

Using (4) and (8), we obtain

$$\begin{aligned} \begin{aligned} {\fancyscript{C_{yx}w_x}}=\lambda {\fancyscript{C_{yy}w_y}} ={\lambda ^{2}\fancyscript{C_{yy}C_{xy}}^{-1}\fancyscript{C_{xx}w_x}} \\ \Rightarrow {\fancyscript{C}_{\fancyscript{xx}}^{-1}\fancyscript{C}_{\fancyscript{xy}}\fancyscript{C}_{\fancyscript{yy}}^{-1}\fancyscript{C_{yx}w_x}} ={\lambda ^{2}\fancyscript{w_x}}. \end{aligned} \end{aligned}$$

(10)

Similarly, using (3) and (9), we obtain

$$\begin{aligned} \begin{aligned} {\fancyscript{C_{xy}w_y}}=\lambda {\fancyscript{C_{xx}w_x}} ={\lambda ^{2}\fancyscript{C_{xx}}\fancyscript{C}_{\fancyscript{yx}}^{-1}\fancyscript{C_{yy}w_y}} \\ \Rightarrow {\fancyscript{C}_{\fancyscript{yy}}^{-1}\fancyscript{C}_{\fancyscript{yx}}\fancyscript{C}_{\fancyscript{xx}}^{-1}\fancyscript{C_{xy}w_y}} ={\lambda ^{2}\fancyscript{w_y}}. \end{aligned} \end{aligned}$$

(11)

Hence, (10) and (11) lead to the following generalized eigenvalue problem:

$$\begin{aligned}&\begin{aligned} \left[ \begin{array}{cc} \fancyscript{C}_{\fancyscript{xx}}^{-1} \fancyscript{C}_{\fancyscript{xy}}\fancyscript{C}_{\fancyscript{yy}}^{-1}\fancyscript{C_{yx}} &{} 0 \\ 0 &{} \fancyscript{C}_{\fancyscript{yy}}^{-1} \fancyscript{C}_{\fancyscript{yx}}{\fancyscript{C}}_{\fancyscript{xx}}^{-1} \fancyscript{C_{xy}} \\ \end{array} \right] \left[ \begin{array}{l} {\fancyscript{w_x}} \\ {\fancyscript{w}}_{\fancyscript{y}} \\ \end{array} \right] ={\lambda ^{2}} \left[\begin{array}{l} {\fancyscript{w}}_{\fancyscript{x}} \\ {\fancyscript{w}}_{\fancyscript{y}} \\ \end{array} \right] ; \\ \Rightarrow \left[ \begin{array}{ll} \fancyscript{H} &{} 0 \\ 0 & \tilde{{{\fancyscript H}}} \end{array} \right] \left[ \begin{array}{l} {\fancyscript{w}}_{\fancyscript{x}} \\ {\fancyscript{w}}_{\fancyscript{y}} \\ \end{array} \right] ={\lambda ^{2}} \left[ \begin{array}{l} {\fancyscript{w}}_{\fancyscript{x}} \\ {\fancyscript{w}}_{\fancyscript{y}} \\ \end{array} \right] ; \end{aligned} \end{aligned}$$

(12)

$$\begin{aligned}&{\text{where }} {\fancyscript{H}}={\fancyscript{C}}_{\fancyscript{xx}}^{-{\rm 1}}{\fancyscript{C}}_{\fancyscript{xy}}{\fancyscript{C}}_{\fancyscript{yy}}^{-{\rm 1}} {\fancyscript{C}}_{\fancyscript{yx}} \\ &{\text{and }} \tilde{\fancyscript{H}} ={\fancyscript{C}}_{\fancyscript{yy}}^{-{\rm 1}}{\fancyscript{C}}_{\fancyscript{yx}} {\fancyscript{C}}_{\fancyscript{xx}}^{-{\rm 1}}{\fancyscript{C}}_{\fancyscript{xy}}. \end{aligned}$$

(13)

2.1 Proposed CCA

In real-life high-dimensional multimodal data analysis, the number of features is larger than the number of samples, which makes the covariance matrices ${\fancyscript{C_{xx}}}$ and ${\fancyscript{C_{yy}}}$ non-invertible. Regularized CCA (RCCA) [42] adds regularization parameters ${\mathfrak {r}}_{\fancyscript{x}}$ and ${\mathfrak {r}}_{\fancyscript{y}}$ to the diagonal elements of the covariance matrices ${\fancyscript{C_{xx}}}$ and ${\fancyscript{C_{yy}}}$ to make them invertible. On the other hand, in fast RCCA (FRCCA) [7], the values of off-diagonal elements of the matrices ${\fancyscript{C_{xx}}}$ and ${\fancyscript{C_{yy}}}$ are reduced by using shrinkage parameters $\fancyscript{s_x}$ and $\fancyscript{s_y}$ to deal with the singularity issue of these matrices. Both regularization parameters (${\mathfrak {r}}_{\fancyscript{x}}$ and ${\mathfrak {r}}_{\fancyscript{y}}$) and shrinkage parameters ($\fancyscript{s_x}$ and $\fancyscript{s_y}$) are used to correct the noise present in ${\fancyscript{X}}$ and ${\fancyscript{Y}}$. In the proposed method, both regularization and shrinkage are done simultaneously to take care of the singularity problem of ${\fancyscript{C_{xx}}}$ and ${\fancyscript{C_{yy}}}$. Here, ${\mathfrak {r}}_{\fancyscript{x}}$ and ${\mathfrak {r}}_{\fancyscript{y}}$ are varied within a range $[{\mathfrak {r}}_{\fancyscript{min}}, {\mathfrak {r}}_{\fancyscript{max}}]$, where the common differences are $\fancyscript{d_x}$ and $\fancyscript{d_y}$ for ${\mathfrak {r}}_{\fancyscript{x}}$ and ${\mathfrak {r}}_{\fancyscript{y}}$, respectively, and ${\mathfrak {r}}_{\fancyscript{min}} \leqslant {\mathfrak {r}}_{\fancyscript{x}}, {\mathfrak {r}}_{\fancyscript{y}} \leqslant {\mathfrak {r}}_{\fancyscript{max}}$. On the other hand, $\fancyscript{s_x}$ and $\fancyscript{s_y}$ can be computed as

$$\begin{aligned} \fancyscript{s_x}=\frac{\sum \nolimits _{\fancyscript{i {\ne } j}} \hat{{\mathcal {V}}}(\fancyscript{{[C_{xx}]}_{ij}})}{\sum \nolimits _{\fancyscript{i {\ne } j}} {{{[\fancyscript{C}^2_{\fancyscript{xx}}]}_{\fancyscript{ij}}}}}; \quad {\mathrm{and}} \quad \fancyscript{s_y}=\frac{\sum \nolimits _{\fancyscript{i {\ne } j}} \hat{{\mathcal {V}}}(\fancyscript{{[C_{yy}]}_{ij}})}{\sum \nolimits _{\fancyscript{i {\ne } j}} {{{[\fancyscript{C}^2_{\fancyscript{yy}}]}_{\fancyscript{ij}}}}}; \end{aligned}$$

(14)

where $\hat{{\mathcal {V}}}(\fancyscript{{[C_{xx}]}_{ij}})$ and $\hat{{\mathcal {V}}}(\fancyscript{{[C_{yy}]}_{ij}})$ are the unbiased empirical variance of $\fancyscript{{[C_{xx}]}_{ij}}$ and $\fancyscript{{[C_{yy}]}_{ij}}$, respectively. Hence, to deal with the singularity issue, the covariance matrices $\tilde{{{\fancyscript C}}}_{\fancyscript{xx}}$ and $\tilde{{{\fancyscript C}}}_{\fancyscript{yy}}$ can be redefined as follows:

$$\begin{aligned} &\tilde{{{\fancyscript C}}}_{\fancyscript{xx}}=\hat{\fancyscript{C}}_{\fancyscript{xx}}+({\mathfrak {r}}_{\fancyscript{x}}+(\fancyscript{k}-1)\fancyscript{d_x}) I \\ &\text{ and }\tilde{{{\fancyscript C}}}_{\fancyscript{yy}}=\hat{\fancyscript{C}}_{\fancyscript{yy}}+({\mathfrak {r}}_{\fancyscript{y}}+(\fancyscript{l}-1)\fancyscript{d_y}) I \end{aligned}$$

(15)

$$\begin{aligned}&\text{ where }\, [\hat{\fancyscript{C}}_{\fancyscript{xx}}]_{\fancyscript{ij}}= \left\{ \begin{array}{ll} (1-\fancyscript{s_x}){[\fancyscript{C_{xx}]}_{ij}}; &{}\mathrm{where} \;\fancyscript{i{\ne }j}\\ \fancyscript{{[C_{xx}]}_{ij}}; &{}\mathrm{where} \;\fancyscript{i{=}j} \end{array}\right. \end{aligned}$$

(16)

$$\begin{aligned}&\text{ and }\,\,\,[\hat{\fancyscript{C}}_{\fancyscript{yy}}]_{\fancyscript{ij}}= \left\{ \begin{array}{ll} (1-\fancyscript{s_y}){[\fancyscript{C_{yy}}]}_{\fancyscript{ij}}; &{}\mathrm{where} \;\fancyscript{i{\ne }j}\\ \fancyscript{{[C_{yy}]}_{ij}}; &{}\mathrm{where} \;\fancyscript{i{=}j} \end{array}\right. \end{aligned}$$

(17)

where $\forall \fancyscript{k} \in \{{1, 2}, \ldots , {\mathfrak {t}}_{{\fancyscript{x}}}\}$ and $\forall \fancyscript{l} \in \{{1, 2}, \ldots , {\mathfrak {t}}_{{\fancyscript{y}}}\}$. The parameters ${\mathfrak {t}}_{{\fancyscript{x}}}$ and ${\mathfrak {t}}_{{\fancyscript{y}}}$ denote the number of possible values of ${\mathfrak {r}}_{\fancyscript{x}}$ and ${\mathfrak {r}}_{\fancyscript{y}}$, respectively. As ${\mathfrak {r}}_{\fancyscript{x}}$ and ${\mathfrak {r}}_{\fancyscript{y}}$ are varied within a range and followed arithmetic progression, there exists a relation between the eigenvalues of covariance matrices corresponding to the first and the ${\fancyscript{t}}$-th regularization parameters for both multidimensional variables ${\fancyscript{X}}$ and ${\fancyscript{Y}}$ as follows [24]:

$$\begin{aligned}&[\hat{\fancyscript{C}}_{\fancyscript{xx}}+({\mathfrak {r}}_{\fancyscript{x}}+(\fancyscript{k}-1)\fancyscript{d_x}) I] = \varPsi _{\fancyscript{x}} (\varLambda _{\fancyscript{x}}+(\fancyscript{k}-1)\fancyscript{d_x}I) \varPsi _{\fancyscript{x}}^{T}; \end{aligned}$$

(18)

$$\begin{aligned}&[\hat{\fancyscript{C}}_{\fancyscript{yy}}+({\mathfrak {r}}_{\fancyscript{y}}+(\fancyscript{l}-1)\fancyscript{d_y}) I] = \varPsi _{\fancyscript{y}} (\varLambda _{\fancyscript{y}}+(\fancyscript{l}-1)\fancyscript{d_y}I) \varPsi _{\fancyscript{y}}^{T}. \end{aligned}$$

(19)

Here, $\varLambda _{\fancyscript{x}}$ and $\varLambda _{\fancyscript{y}}$ are the diagonal matrices, where diagonal elements are the eigenvalues of $[\hat{\fancyscript{C}}_{\fancyscript{xx}}+{\mathfrak {r}}_{\fancyscript{x}} I]$ and $[\hat{\fancyscript{C}}_{\fancyscript{yy}}+{\mathfrak {r}}_{\fancyscript{y}} I]$, respectively, and the corresponding orthonormal eigenvectors are in the columns of $\varPsi _{\fancyscript{x}}$ and $\varPsi _{\fancyscript{y}}$. The theoretical analysis, reported in [25], gives assistance to compute the matrices $\fancyscript{H}$ and $\tilde{{{\fancyscript H}}}$ with $\fancyscript{(k,l)}$-th regularization parameters of ${\mathfrak {r}}_{\fancyscript{x}}$ and ${\mathfrak {r}}_{\fancyscript{y}}$, that is, $\fancyscript{H_{kl}}$ and $\tilde{{{\fancyscript H}}}_{\fancyscript{kl}}$, as follows:

$$\begin{aligned}&\begin{aligned} {\fancyscript{H_{kl}}} = \varPsi _{\fancyscript{x}} [\varLambda _{\fancyscript{x}} + (\fancyscript{k}-1)\fancyscript{d_x}I]^{-1} \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}} \\ \varPsi _{\fancyscript{y}} [\varLambda _{\fancyscript{y}} + (\fancyscript{l}-1)\fancyscript{d_y}I]^{-1} \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}}; \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned}&\text{ and } \quad \tilde{{{\fancyscript H}}_{{\fancyscript{kl}}}} = \varPsi_{{\fancyscript{y}}} [\varLambda _{{\fancyscript{y}}} +({\fancyscript{l}}-1)\fancyscript{d}_{\fancyscript{y}}I]^{-1} \varPsi_{\fancyscript{y}}^{T} {\fancyscript{C}}_{{\fancyscript{yx}}} \\&\varPsi _{{\fancyscript{x}}} [\varLambda _{{\fancyscript{x}}} +({\fancyscript{k}}-1){\fancyscript{d}}_{\fancyscript{x}}I]^{-1} \varPsi_{{\fancyscript{x}}}^{T} {\fancyscript{C}}_{\fancyscript{{xy}}}.\end{aligned}$$

(21)

The inverse of the diagonal matrices $[\varLambda _{\fancyscript{x}} + (\fancyscript{k}-1)\fancyscript{d_x}I]$ and $[\varLambda _{\fancyscript{y}} + (\fancyscript{l}-1)\fancyscript{d_y}I]$ can be computed as

$$\begin{aligned}&[\varLambda _{\fancyscript{x}} + (\fancyscript{k}-1)\fancyscript{d_x}I]^{-1} \nonumber \\&= \varLambda _{\fancyscript{x}}^{-1} - \varLambda _{\fancyscript{x}}^{-1} (\fancyscript{k}-1)\fancyscript{d_x}I\varLambda _{\fancyscript{x}}^{-1}(I + (\fancyscript{k}-1)\fancyscript{d_x}I\varLambda _{\fancyscript{x}}^{-1})^{-1} \nonumber \\&= \varLambda _{\fancyscript{x}}^{-1} - \varLambda _{\fancyscript{x}}^{-1} (\fancyscript{k}-1)\fancyscript{d_x}\varLambda _{\fancyscript{x}}^{-1}(I + (\fancyscript{k}-1)\fancyscript{d_x}\varLambda _{\fancyscript{x}}^{-1})^{-1} \nonumber \\&= \varLambda _{\fancyscript{x}}^{-1} - \varLambda _{\fancyscript{x}}^{-1} \nabla _{\fancyscript{k}}; \end{aligned}$$

(22)

$$\begin{aligned}&[\varLambda _{\fancyscript{y}} + (\fancyscript{l}-1)\fancyscript{d_y}I]^{-1} \nonumber \\&= \varLambda _{\fancyscript{y}}^{-1} - \varLambda _{\fancyscript{y}}^{-1} (\fancyscript{l}-1)\fancyscript{d_y}I\varLambda _{\fancyscript{y}}^{-1}(I + (\fancyscript{l}-1)\fancyscript{d_y}I\varLambda _{\fancyscript{y}}^{-1})^{-1} \nonumber \\&= \varLambda _{\fancyscript{y}}^{-1} - \varLambda _{\fancyscript{y}}^{-1} (\fancyscript{l}-1)\fancyscript{d_y}\varLambda _{\fancyscript{y}}^{-1}(I + (\fancyscript{l}-1)\fancyscript{d_y}\varLambda _{\fancyscript{y}}^{-1})^{-1} \nonumber \\&= \varLambda _{\fancyscript{y}}^{-1} - \varLambda _{\fancyscript{y}}^{-1} \nabla _{\fancyscript{l}}; \end{aligned}$$

(23)

$$\begin{aligned}&\text{ where }\, \nabla _{\fancyscript{k}} = (\fancyscript{k}-1)\fancyscript{d_x}\varLambda _{\fancyscript{x}}^{-1}(I + (\fancyscript{k}-1)\fancyscript{d_x}\varLambda _{\fancyscript{x}}^{-1})^{-1}; \end{aligned}$$

(24)

$$\begin{aligned}&\text{ and }\,\, \nabla _{\fancyscript{l}} = (\fancyscript{l}-1)\fancyscript{d_y}\varLambda _{\fancyscript{y}}^{-1}(I + (\fancyscript{l}-1)\fancyscript{d_y}\varLambda _{\fancyscript{y}}^{-1})^{-1}. \end{aligned}$$

(25)

Hence, using (22) and (23), the matrix $\fancyscript{H}$ of (20) becomes

$$\begin{aligned} \fancyscript{H_{kl}}= & {} \varPsi _{\fancyscript{x}} [\varLambda _{\fancyscript{x}}^{-1} - \varLambda _{\fancyscript{x}}^{-1} \nabla _{\fancyscript{k}}] \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}} \varPsi _{\fancyscript{y}} [\varLambda _{\fancyscript{y}}^{-1} - \varLambda _{\fancyscript{y}}^{-1} \nabla _{\fancyscript{l}}] \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}} \nonumber \\= & {} \varPsi _{\fancyscript{x}} \varLambda _{\fancyscript{x}}^{-1} \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}} \varPsi _{\fancyscript{y}} \varLambda _{\fancyscript{y}}^{-1} \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}} + \fancyscript{Z_{kl}} = \fancyscript{H}_{11} + \fancyscript{Z_{kl}}; \end{aligned}$$

(26)

$$\begin{aligned}&\begin{aligned} \text{ where }\,\,\, \fancyscript{Z_{kl}} = \varPsi _{\fancyscript{x}} \varLambda _{\fancyscript{x}}^{-1} [\nabla _{\fancyscript{k}} \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}} \varPsi _{\fancyscript{y}} \varLambda _{\fancyscript{y}}^{-1} \nabla _{\fancyscript{l}} \\ - \nabla _{\fancyscript{k}} \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}} \varPsi _{\fancyscript{y}} \varLambda _{\fancyscript{y}}^{-1} - \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}} \varPsi _{\fancyscript{y}} \varLambda _{\fancyscript{y}}^{-1} \nabla _{\fancyscript{l}}] \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}}. \end{aligned} \end{aligned}$$

(27)

Similarly, using (22) and (23), the matrix $\tilde{{{\fancyscript H}}}$ of (21) becomes

$$\begin{aligned}&\tilde{{{\fancyscript H}}}_{\fancyscript{{kl}}} = \varPsi _{\fancyscript{y}} [\varLambda _{\fancyscript{y}}^{{-1}} -\varLambda _{\fancyscript{y}}^{{-1}} \nabla _{\fancyscript{l}}] \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}} \varPsi _{\fancyscript{x}} [\varLambda _{\fancyscript{x}}^{{-1}} -\varLambda _{\fancyscript{x}}^{{-1}} \nabla _{\fancyscript{k}}] \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}}\nonumber \\&= \varPsi _{\fancyscript{y}} \varLambda _{\fancyscript{y}}^{{-1}} \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}} \varPsi _{\fancyscript{x}} \varLambda _{\fancyscript{x}}^{{-1}} \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}} + \tilde{{{\fancyscript Z}}_{\fancyscript {kl}}} = \tilde{{{\fancyscript H}}}_{11} + \tilde{{{\fancyscript Z}}}_{\fancyscript {kl}}; \end{aligned}$$

(28)

$$\begin{aligned}&\begin{aligned} \text{ where }\, \tilde{{{\fancyscript Z}}}_{{\fancyscript{kl}}} = \varPsi _{\fancyscript{y}} \varLambda _{\fancyscript{y}}^{{-1}} [\nabla _{\fancyscript{l}} \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}} \varPsi _{\fancyscript{x}} \varLambda _{\fancyscript{x}}^{{-1}} \nabla _{\fancyscript{k}} \\ - \nabla _{\fancyscript{l}} \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}} \varPsi _{\fancyscript{x}} \varLambda _{\fancyscript{x}}^{{-1}} - \varPsi _{\fancyscript{y}}^{T} \fancyscript{C_{yx}} \varPsi _{\fancyscript{x}} \varLambda _{\fancyscript{x}}^{{-1}} \nabla _{\fancyscript{k}}] \varPsi _{\fancyscript{x}}^{T} {\fancyscript{C_{xy}}}. \end{aligned} \end{aligned}$$

(29)

The nonzero eigenvalues of $\fancyscript{H_{kl}}$ and $\tilde{{{\fancyscript H}}}_{{\fancyscript {kl}}}$ are same [13], and the $\fancyscript{t}$-th eigenvector $\fancyscript{w_{yt}}$ of $\tilde{{{\fancyscript H}}}_{{\fancyscript {kl}}}$ can be obtained from the $\fancyscript{t}$-th eigenvector $\fancyscript{w_{xt}}$ of $\fancyscript{H_{kl}}$ as $\fancyscript{w_{yt}} =\tilde{{{\fancyscript C}}}_{\fancyscript{yy}}^{-1} \fancyscript{C_{yx} w_{xt}}$. So, one of the matrices $\fancyscript{H_{\fancyscript {kl}}}$ and $\tilde{{{\fancyscript H}}}_{{\fancyscript {kl}}}$ is sufficient to compute the eigenvectors of both of them. Hence, either $\fancyscript{H_{kl}}$ or $\tilde{{{\fancyscript H}}}_{\fancyscript {kl}}$ will be computed by using (26) or (28), respectively, depending on whether $\fancyscript{p\leqslant q}$ or $\fancyscript{p>q}$, where $\forall \fancyscript{k} \in \{{1, 2}, \ldots , {\mathfrak {t}}_{{\fancyscript{x}}}\}$ and $\forall \fancyscript{l} \in \{{1, 2}, \ldots , {\mathfrak {t}}_{{\fancyscript{y}}}\}$.

In practical analysis, ${\fancyscript{K}}$ = $\min (\fancyscript{p, q})$ is large enough, and a small subset of extracted features is sufficient to perform a certain task. Hence, the objective of the proposed work is to find out a reduced subset of most significant and relevant extracted features. The sequential generation of each eigenvector of $\fancyscript{H_{kl}}$ and $\tilde{{{\fancyscript H}}}_{\fancyscript{kl}}$ would help to evaluate the quality of each extracted feature individually. The theoretical analysis reported next, based on deflation method [43], gives assistance to compute $(\fancyscript{t}+1)$-th basis vectors, which are the eigenvectors of matrices $\fancyscript{H}_{\fancyscript{kl}}(\fancyscript{t}+1)$ and $\tilde{{{\fancyscript H}}}_{\fancyscript{kl}}(\fancyscript{t}+1)$. Thus, the matrices $\fancyscript{H_{kl}}(\fancyscript{t}+1)$ and $\tilde{{{\fancyscript H}}}_{\fancyscript{kl}}(\fancyscript{t}+1)$ can be computed as follows:

$$\begin{aligned}&\begin{aligned} \fancyscript{H_{kl}}(\fancyscript{t}+1) = \fancyscript{H_{kl}}(1) -\sum \limits _{\fancyscript{m}=1}^\fancyscript{t} \fancyscript{{\rho _m}_{kl}} \fancyscript{{w_{xm}}_{kl}} \fancyscript{{w_{xm}}_{kl}}^T \\ = \fancyscript{H}_{11} + \fancyscript{Z_{kl}} -\sum \limits _{\fancyscript{m}=1}^\fancyscript{t} \fancyscript{{\rho _m}_{kl}} \fancyscript{{w_{xm}}_{kl}} \fancyscript{{w_{xm}}_{kl}}^T; \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned} \text{ and } \quad \tilde{{{\fancyscript H}}}_{\fancyscript {kl}}(\fancyscript{t}+1) = \tilde{{{\fancyscript H}}}_{\fancyscript {kl}}(1) -\sum \limits _{\fancyscript{m}=1}^\fancyscript{t} \fancyscript{{\rho _m}_{kl}} \fancyscript{{w_{ym}}_{kl}} \fancyscript{{w_{ym}}_{kl}}^T \\ = \tilde{{{\fancyscript H}}}_{\rm {11}} + \tilde{{{\fancyscript Z}}}_{\fancyscript{kl}} -\sum \limits _{\fancyscript{m}=1}^\fancyscript{t} \fancyscript{{\rho _m}_{kl}} \fancyscript{{w_{ym}}_{kl}} {\fancyscript {{w_{ym}}}_{kl}}^T; \end{aligned}$$

(31)

where $\rho _{\fancyscript{t_{kl}}}$ denotes eigenvalue of $\fancyscript{H_{kl}}(\fancyscript{t}+1)$ or $\tilde{{{\fancyscript H}}}_{\fancyscript {kl}}(\fancyscript{t}+1)$, $\forall \fancyscript{t} \in \{{1, 2, \ldots , \fancyscript{K}-1}\}$, ${\fancyscript{K}}$ = $\min (\fancyscript{p, q})$, $\forall \fancyscript{k} \in \{{1, 2}, \ldots , {\mathfrak {t}}_{\fancyscript{x}}\}$, and $\forall \fancyscript{l} \in \{{1, 2}, \ldots , {\mathfrak {t}}_{\fancyscript{y}}\}$. Finally, the most correlated $\fancyscript{D}$ $(<< {\fancyscript{K}})$ features $\fancyscript{{A_t}_{kl}}=\fancyscript{{w_{xt}}_{kl}}^{T}{{\fancyscript{X}}} +\fancyscript{{w_{yt}}_{kl}}^{T}{{\fancyscript{Y}}}$ are extracted from two multidimensional variables ${{\fancyscript{X}}}$ and ${{\fancyscript{Y}}}$.

The objective of this work is to extract not only the correlated features but also the most relevant and significant features. Let us assume that the set ${\mathbb {C}}$ contains all the ${\fancyscript{t}}$-th correlated features which are extracted using $\fancyscript{(k,l)}$-th regularization parameters of ${\mathfrak {r}}_{\fancyscript{x}}$ and ${\mathfrak {r}}_{\fancyscript{y}}$. If $\fancyscript{t}=1$, the most relevant feature from the set ${\mathbb {C}}$ is selected and is included into another set ${\mathbb {S}}$, initially which is empty, that is, ${\mathbb {S}} \leftarrow \emptyset$. If $\fancyscript{t}>1$, the feature which has maximum relevance (among the features of ${\mathbb {C}}$) and significance (with respect to the features of ${\mathbb {S}}$) is selected from the set ${\mathbb {C}}$ and is included to $\mathbb {S}$. Following objective function is used to select the most relevant and significant feature from the set ${\mathbb {C}}$ when $\fancyscript{t}>1$:

$$ \gamma _{\fancyscript{{A_t}_{kl}}}({\mathbb {D}})+ \frac{1}{\fancyscript{t}-1} \sum _{{{\fancyscript{A}}_{{\tilde{t}}}} \in {\mathbb {S}}} \sigma _{\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\}}({\mathbb {D}},\fancyscript{{A_t}_{kl}}). $$

(32)

To compute both significance and relevance of an extracted feature, rough hypercuboid-based hypercuboid equivalence partition matrix [23] is used in the current work. The relevance $\gamma _{\fancyscript{{A_t}_{kl}}}({\mathbb {D}})$ of a feature $\fancyscript{{A_t}_{kl}}$ with respect to the class label or decision attribute ${\mathbb {D}}$ is determined as follows [23]:

$$\begin{aligned}&\gamma _{\fancyscript{{A_t}_{kl}}}({\mathbb {D}}) = 1 - \frac{1}{n} \sum \limits _{\fancyscript{j} = 1}^n \fancyscript{v_j({A_t}_{kl}}); \end{aligned}$$

(33)

$$\begin{aligned}&\gamma _{{\fancyscript{{A_t}_{kl}}}}({\mathbb {D}})=\left\{ \begin{array}{ll} 1 &{} {\text{if}}\, \fancyscript{{A_t}_{kl}} \,{\text{totally depends on}}\, {\mathbb {D}}; \\ 0 &{} {\text{if}}\, {\fancyscript{{A_t}_{kl}}}\, {\text {does not depend on}}\, {\mathbb {D}}; \end{array}\right. \end{aligned}$$

(34)

and $\gamma _{\fancyscript{{A_t}_{kl}}}({\mathbb {D}}) \in (0,1)$ if $\fancyscript{{A_t}_{kl}}$ partially depends on ${\mathbb {D}}$. The confusion vector for the feature $\fancyscript{{A_t}_{kl}}$ is denoted as

$${\mathbb {V}}({\fancyscript{{A_t}_{kl}}}) = [{\fancyscript{v}_1}({\fancyscript{{A_t}_{kl}}}), \ldots , {\fancyscript{v_j}}({\fancyscript{{A_t}_{kl}}}), \ldots , {\fancyscript{v}_{n}}({\fancyscript{{A_t}_{kl}}})]$$

(35)

$$\text{ where }\,\, \fancyscript{v_j({A_t}_{kl})} = \min \{1, \sum \limits _{\fancyscript{i}=1}^c \fancyscript{h_{ij}({A_t}_{kl})}-1\},$$

(36)

the matrix ${\mathbb {H}}(\fancyscript{{A_t}_{kl}}) =[\fancyscript{h_{ij}(\fancyscript{{A_t}_{kl}})}]_{c \times n}$ is termed as hypercuboid equivalence partition matrix of the feature $\fancyscript{{A_t}_{kl}}$ [23], where

$$\fancyscript{h_{ij}(\fancyscript{{A_t}_{kl}})} = \left\{ \begin{array}{ll} 1 & \text{ if } {\mathcal {L}}_{\fancyscript{i}} \leqslant \fancyscript{O_j(\fancyscript{{A_t}_{kl}})} \leqslant {\mathcal {U}}_{\fancyscript{i}}\\ 0 & \text{ otherwise } \end{array} \right.$$

(37)

represents the membership of sample $\fancyscript{O_j}$ in the $\fancyscript{i}$-th class $\beta _{\fancyscript{i}}$, and c denotes the number of classes. According to the decision attribute $\mathbb {D}$, the interval of the $\fancyscript{i}$-th class $\beta _{\fancyscript{i}}$ is denoted by $[{\mathcal {L}}_{\fancyscript{i}}, \mathcal {U}_{\fancyscript{i}}]$. Each row of the $c \times n$ hypercuboid equivalence partition matrix ${\mathbb {H}}(\fancyscript{{A_t}_{kl}})$ denotes a hypercuboid equivalence class. The joint relevance $\gamma _{\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\}}({\mathbb {D}})$ of the feature set $\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\}$ can be used to compute the significance of the feature $\fancyscript{{A_t}_{kl}}$ as follows:

$$\sigma _{\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\}} ({{\mathbb {D}}}, {\fancyscript{A}}_{\fancyscript{tkl}}) = \gamma _{\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}} \}} ({\mathbb{D}})- \gamma _{{\fancyscript{A}}_{\tilde{\fancyscript{t}}}} ({{\mathbb {D}}}).$$

(38)

The joint relevance $\gamma _{\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\}}({\mathbb {D}})$ of feature set $\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\}$ is depended on $c \times n$ hypercuboid equivalence partition matrix ${{\mathbb {H}}}(\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\})$ corresponding to the set $\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\}$. Thus, the matrices ${{\mathbb {H}}}({\fancyscript{A}}_{\fancyscript{tkl}})$ and ${\mathbb H}({\fancyscript{A}}_{\tilde{\fancyscript{t}}})$ are used to compute the matrix ${{\mathbb {H}}}(\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\})$, where

$$\begin{aligned}&{{\mathbb {H}}}(\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\})= {{\mathbb {H}}}({\fancyscript{A}}_{\fancyscript{tkl}}) \cap {{\mathbb {H}}}({\fancyscript{A}}_{\tilde{\fancyscript{t}}}); \end{aligned}$$

(39)

$$\begin{aligned}&\mathrm{and} \,{\fancyscript{h}}_{\fancyscript{ij}} (\{{\fancyscript{A}}_{\fancyscript{tkl}}, {\fancyscript{A}}_{\tilde{\fancyscript{t}}}\}) = {\fancyscript{h}}_{\fancyscript{ij}} ({\fancyscript{A}}_{\fancyscript{tkl}}) \times {\fancyscript{h}}_{\fancyscript{ij}} ({\fancyscript{A}}_{\tilde{\fancyscript{t}}}). \end{aligned}$$

(40)

Fig. 1

Block diagram of the proposed method for HEp-2 cell classification

2.2 Computational complexity

Let us assume that ${\fancyscript{K}} = \min (\fancyscript{p, q})$ and $\fancyscript{M} = \max (\fancyscript{p, q})$, where the number of extracted features $\fancyscript{D}<< {\fancyscript{K}}$. The total time complexity to compute two covariance matrices ${\fancyscript{C_{xx}}}$ and ${\fancyscript{C_{yy}}}$ is $({\mathcal {O}}(\fancyscript{K}^{2}n+\fancyscript{M}^{2}n)=){\mathcal {O}}(\fancyscript{M}^{2}n)$, whereas the computational cost to calculate cross-covariance matrix ${\fancyscript{C_{xy}}}$ is ${\mathcal {O}}(\fancyscript{KM}n)$. The shrinkage parameters $\fancyscript{s_x}$ and $\fancyscript{s_y}$ can be computed with time complexity $({\mathcal {O}}(\fancyscript{K}^{2}n+\fancyscript{M}^{2}n)=)\mathcal {O}(\fancyscript{M}^{2}n)$. On the other hand, the eigenvalues $\varLambda _{\fancyscript{x}}$ and $\varLambda _{\fancyscript{y}}$, along with corresponding eigenvectors $\varPsi _{\fancyscript{x}}$ and $\varPsi _{\fancyscript{y}}$, can be calculated with computational complexity $(\mathcal {O}(\fancyscript{K}^3+\fancyscript{M}^3)=){\mathcal {O}}(\fancyscript{M}^3)$. Hence, the total time complexity to compute $\fancyscript{C_{xx}}^{-1}$ and $\fancyscript{C_{yy}}^{-1}$ is $({\mathcal {O}}(\fancyscript{K}^3+\fancyscript{M}^3)=){\mathcal {O}}(\fancyscript{M}^3)$.

Depending on $\fancyscript{p\leqslant q}$ or $\fancyscript{p>q}$, one of the matrices $\fancyscript{H}_{11}$ or $\tilde{{{{\fancyscript H}}}}_{11}$ has to be computed; hence, computational cost to compute $\fancyscript{H}_{11}$ or $\tilde{{{{\fancyscript H}}}}_{11}$ is $({\mathcal {O}}(\fancyscript{K}^3+\fancyscript{K}^2\fancyscript{M+KM}^2+\fancyscript{M}^3)=){\mathcal {O}}(\fancyscript{M}^3)$. Similarly, the computational complexity of the matrix $\nabla _{\fancyscript{k}}$ or $\nabla _{\fancyscript{l}}$ is ${\mathcal {O}}({{\fancyscript{K}}})$. Hence, the time complexity to compute matrix $\fancyscript{Z_{kl}}$ or $\tilde{{{{\fancyscript Z}}_{\fancyscript {kl}}}}$ is $({\mathcal {O}}(\fancyscript{K}^3+\fancyscript{K}^2\fancyscript{M}+\fancyscript{KM}^2)=){\mathcal {O}}(\fancyscript{KM}^2)$. Now, the time complexity to calculate the first basis vector of first multidimensional variable is ${\mathcal {O}}(\fancyscript{K}^2)$, whereas the $(\fancyscript{t}+1)$-th basis vector of first multidimensional variable can be computed with computational cost $(\mathcal {O}(\fancyscript{M}^3+\fancyscript{KM}^2+\fancyscript{tK}^2)=){\mathcal {O}}(\fancyscript{M}^3)$, where $\forall \fancyscript{t} \in \{{1, 2, \ldots , \fancyscript{K}-1}\}$. On the other hand, each basis vector of the second multidimensional variable can be computed with time complexity $(\mathcal {O}(\fancyscript{KM}^2+\fancyscript{KM})=){\mathcal {O}}(\fancyscript{KM}^2)$. The total time complexity for computing canonical variables is $(\mathcal {O}({\fancyscript{K}}n+\fancyscript{M}n)=){\mathcal {O}}(\fancyscript{M}n)$. The computational complexity to extract a feature is ${\mathcal {O}}(n)$. The time complexity to compute both relevance and significance of a feature is same, which is ${\mathcal {O}}(cn)$. Hence, the total complexity to extract all highest relevant features among all $({\mathfrak {t}}_{\fancyscript{x}} \times {\mathfrak {t}}_{\fancyscript{y}})$ combination of regularization parameters is $({\mathcal {O}}({\mathfrak {t}}_{\fancyscript{x}}{\mathfrak {t}}_{\fancyscript{y}} (\fancyscript{K}^2+\fancyscript{KM}^2+\fancyscript{M}n+n+cn))=) {\mathcal {O}}({\mathfrak {t}}_{\fancyscript{x}} {\mathfrak {t}}_{\fancyscript{y}} \fancyscript{KM}^2)$.

The complexity to extract all the $(\fancyscript{t}+1)$-th features, by maximizing both relevance and significance, among all $({\mathfrak {t}}_{\fancyscript{x}} \times {\mathfrak {t}}_{\fancyscript{y}})$ candidate features is $({\mathcal {O}}({\mathfrak {t}}_{\fancyscript{x}}{\mathfrak {t}}_{\fancyscript{y}} (\fancyscript{M}^3+\fancyscript{KM}^2+\fancyscript{M}n+n+cn))=) {\mathcal {O}}({\mathfrak {t}}_{\fancyscript{x}} {\mathfrak {t}}_{\fancyscript{y}} \fancyscript{M}^3)$. The selection of a feature from $({\mathfrak {t}}_{\fancyscript{x}} \times {\mathfrak {t}}_{\fancyscript{y}})$ candidate features by maximizing relevance and significance has complexity ${\mathcal {O}}({\mathfrak {t}}_{\fancyscript{x}} {\mathfrak {t}}_{\fancyscript{y}})$. So, total complexity to compute all $\fancyscript{D}$ maximally relevant and significant features is $({\mathcal {O}}({\mathfrak {t}}_{\fancyscript{x}}{\mathfrak {t}}_{\fancyscript{y}}(\fancyscript{KM}^2+\fancyscript{M}^3(\fancyscript{D}-1)) +{\mathfrak {t}}_{\fancyscript{x}}{\mathfrak {t}}_{\fancyscript{y}}{\fancyscript{D}})=) {\mathcal {O}}({\mathfrak {t}}_{\fancyscript{x}}{\mathfrak {t}}_{\fancyscript{y}}\fancyscript{M}^3\fancyscript{D})$. Hence, the overall computational complexity of the proposed sequential supervised CCA algorithm is $(\mathcal {O}(\fancyscript{M}^2n+\fancyscript{KM}n+\fancyscript{M}^3+{{\fancyscript{K}}}+\fancyscript{KM}^2+ {\mathfrak {t}}_{\fancyscript{x}}{\mathfrak {t}}_{\fancyscript{y}}\fancyscript{M}^3\fancyscript{D}))$, that is ${\mathcal {O}}({\mathfrak {t}}_{\fancyscript{x}}{\mathfrak {t}}_{\fancyscript{y}}\fancyscript{M}^3\fancyscript{D})$.

3 CanSuR: a new method for HEp-2 cell classification

This section presents a new method, termed as CanSuR, for staining pattern recognition of HEp-2 cell images. The proposed method has two stages, namely, extraction of features from HEp-2 cell images and classification of cells based on the extracted features using support vector machine (SVM). The feature extraction step of the proposed method has two levels. In the first level, rotation-invariant local binary patterns ($\hbox {LBP}^{\mathrm{ri}}$s) [30] are extracted directly from the input cell image. The sets of $\hbox {LBP}^{\mathrm{ri}}$ feature vectors, corresponding to scales $S_{\fancyscript{x}}$ and $S_{\fancyscript{y}}$ of all HEp-2 cells, form two modalities ${\fancyscript{X}} \in \mathfrak {R}^{\fancyscript{p} \times n}$ and ${\fancyscript{Y}} \in \mathfrak {R}^{{\fancyscript{q}} \times n}$, respectively. Here, each row in ${\fancyscript{X}}$ and ${\fancyscript{Y}}$ represents one of the $\hbox {LBP}^\mathrm{ri}$ feature vectors, and each column represents one of the n samples. These extracted feature sets ${\fancyscript{X}}$ and ${\fancyscript{Y}}$ are integrated in the second level using the proposed sequential CCA method. The proposed sequential CCA extracts maximally correlated, most relevant and significant features from two multidimensional data sets ${\fancyscript{X}}$ and ${\fancyscript{Y}}$. In the proposed HEp-2 cell staining pattern recognition method, henceforth termed as CanSuR, a set of maximally correlated and most significant as well as relevant latent local features is first extracted for each set of training data, and then, SVM is trained using this feature set. After the training, the information of training feature set is used to generate the test set and then the class label of the test sample is predicted using the SVM. The basic steps of the proposed methodology are outlined next:

• 1. Compute $\hbox {LBP}^{\mathrm{ri}}$s using scale $S_{\fancyscript{x}}$ and scale $S_{\fancyscript{y}}$ for each HEp-2 cell image to record the local textural features and generate two data sets ${\fancyscript{X}}$ and ${\fancyscript{Y}}$.

• 2. Apply the proposed sequential CCA on ${\fancyscript{X}}$ and ${\fancyscript{Y}}$ to extract maximally correlated, most significant and relevant latent local features.

• 3. Recognize the staining pattern of HEp-2 cell images using SVM based on extracted features set.

A graphical representation of the proposed HEp-2 cell classification methodology is shown in Fig. 1. The detail description of each step is presented next.

3.1 Step I: generation of local textural features

To generate the local textural features of each HEp-2 cell images, gray scale and rotation-invariant local binary texture operator $\hbox {LBP}^{\mathrm{ri}}$ is used. For a monochrome texture image, the local binary texture ${{\fancyscript{T}}}$ can be defined as [30]

$$ {\fancyscript{T}} = {\mathfrak {t(g_c,g}}_0, \ldots ,{\mathfrak {g}}_{{\mathcal{L}}-1}); $$

(41)

where ${\mathfrak {g_c}}$ and ${\mathfrak {g}}_{\fancyscript{l}}$, $\forall \fancyscript{l} \in \{{0, 1, 2}, \ldots , {\mathcal {L}}-1\}$ denote the gray values of the center and neighbor pixels of the circularly symmetric neighborhood with radius ${{\fancyscript{R}}}$. To achieve gray-scale invariance, the gray value of the center pixel ${\mathfrak {g_c}}$ has to be subtracted from the gray values of neighbor pixels ${\mathfrak {g}}_{\fancyscript{l}}({\fancyscript{l}}=0,\ldots ,\mathcal L-1)$, so

$${{\fancyscript{T}}}={\mathfrak {t(g_c,g}}_0-{\mathfrak {g_c,g}}_1-{\mathfrak {g_c}},\ldots , {\mathfrak {g}}_{{\mathcal {L}}-1}-{\mathfrak {g_c}}).$$

(42)

It is assumed that the difference $({\mathfrak {g}}_{\fancyscript{l}}-{\mathfrak {g_c}})$ does no depend on ${\mathfrak {g_c}}$. Hence, (42) can be factorized as follows:

$${{\fancyscript{T}}} \approx {\mathfrak {t(g_c)}} {\mathfrak {t(g}}_0-{\mathfrak {g_c,g}}_1-{\mathfrak {g_c}},\ldots , {\mathfrak {g}}_{{\mathcal {L}}-1}-{\mathfrak {g_c}}).$$

(43)

The overall luminance of the image ${\mathfrak {t(g_c)}}$ does not relate to local image texture and does not provide any useful information for texture analysis. Therefore, the original joint gray level distribution ${{\fancyscript{T}}}$ is dependent on joint difference distribution ${\mathfrak {t(g}}_0-{\mathfrak {g_c,g}}_1 -{\mathfrak {g_c}},\ldots ,{\mathfrak {g}}_{{\mathcal {L}}-1}-{\mathfrak {g_c}})$ [31],

$${{\fancyscript{T}}} \approx {\mathfrak {t(g}}_0-{\mathfrak {g_c,g}}_1 -{\mathfrak {g_c}},\ldots ,{\mathfrak {g}}_{{\mathcal {L}}-1}-{\mathfrak {g_c}}).$$

(44)

The occurrence of various patterns in the neighborhood of each pixel in a ${\mathcal {L}}$-dimensional histogram is recorded by this operator. In all directions, the differences are zero for constant regions and high for a spot. The highest difference is recorded in the gradient direction for a slowly sloped edge. On the other hand, any change in mean luminance does not affect the signed difference $({\mathfrak {g}}_{{\fancyscript{l}}}-{\mathfrak {g_c}})$. Hence, the joint difference distribution is invariant against gray-scale shifts. Thus, invariance with respect to the scaling of gray scale is achieved by considering the signs of the differences only,

$$\begin{aligned}&{{\fancyscript{T}}} \approx {\mathfrak {t(s(g}}_0-{\mathfrak {g_c),s(g}}_1-{\mathfrak {g_c}}),\ldots , {\mathfrak {s}}({\mathfrak {g}}_{{\mathcal {L}}-1}-{\mathfrak {g_c}}));\nonumber \\&\text{ where }\,\,{\mathfrak {s}}(x) = \left\{ \begin{array}{ll} 1, &{} x \geqslant 0\\ 0, &{} x < 0. \end{array} \right. \end{aligned}$$

(45)

For each sign ${\mathfrak {s}}({\mathfrak {g}}_{{\fancyscript{l}}}-{\mathfrak {g_c}})$, a binomial factor $2^{{\fancyscript{l}}}$ is assigned to produce a unique number that characterizes the spatial structure of the local image texture. The gray values ${\mathfrak {g}}_{{\fancyscript{l}}}$ will move along the perimeter of the circle around ${\mathfrak {g}}_0$, when the image is rotated, and produce different binary patterns for the same texture. To assign a unique identifier to each rotation-invariant local binary pattern, the following formula is used:

$${\text{LBP}}^{\rm ri} = \min \left\{{\mathcal {ROR}}\left(\sum \limits _{{\fancyscript{l}}=0}^{{\mathcal {L}}-1} {\mathfrak {s}}({\mathfrak {g}}_{{\fancyscript{l}}}-{\mathfrak {g_c}}) 2^{{\fancyscript{l}}},{\fancyscript{i}}\right) |{\fancyscript{i}} = 0,1,\ldots ,{\mathcal {L}}-1\right\};$$

(46)

where $\mathcal {ROR}(x,{\fancyscript{i}})$ performs a circular bit-wise right shift on the ${\mathcal {L}}$-bit number x ${\fancyscript{i}}$ times.

3.2 Step II: integration of local textural features

The sets of $\hbox {LBP}^{\mathrm{ri}}$ feature vectors, corresponding to scales $S_{\fancyscript{x}}$ and $S_{\fancyscript{y}}$ of all HEp-2 cells, form two modalities ${\fancyscript{X}} \in \mathfrak {R}^{\fancyscript{p} \times n}$ and ${\fancyscript{Y}} \in \mathfrak {R}^{{\fancyscript{q}} \times n}$, respectively. To integrate the information of these rotation-invariant local binary feature vector sets ${\fancyscript{X}}$ and ${\fancyscript{Y}}$, the proposed supervised sequential CCA is used. Here, the number of $\hbox {LBP}^{\mathrm{ri}}$ features of ${\fancyscript{X}}$ and ${\fancyscript{Y}}$ is same, that is, ${\fancyscript{p=q}}$ and n is the number of HEp-2 cell images. The proposed data integration method extracts latent features those are maximally correlated and most significant as well as relevant from $\hbox {LBP}^{\mathrm{ri}}$ feature vector sets ${\fancyscript{X}}$ and ${\fancyscript{Y}}$. It obtains two directional basis vectors ${\fancyscript{w_x}}$ and ${\fancyscript{w_y}}$ such that the correlation between canonical variables ${\fancyscript{U}} = {\fancyscript{w_x}}^{T} {\fancyscript{X}}$ and ${\fancyscript{V}} = {\fancyscript{w_y}}^{T} {\fancyscript{Y}}$ is maximum, and the extracted feature ${\fancyscript{A = U + V}}$ is most relevant and significant.

3.3 Step III: SVM for staining pattern classification

The support vector machine (SVM) [41] is used, in the present work, to classify the staining patterns of HEp-2 cell images by drawing an optimal hyperplane in the feature vector space. This hyperplane defines a boundary that maximizes the margin between data samples belonging to different classes. In the current study, the SVM uses radial basis function kernel to generate nonlinear decision boundary among different classes. The SVM is trained with the correlated, relevant and significant features generated for the training HEp-2 cell set and using the information of training feature set, and the staining pattern present in test HEp-2 cell is predicted.

4 Performance analysis and discussions

The performance of the proposed HEp-2 cell image classification method, termed as CanSuR, is presented in this section, along with a comparison with related approaches. The proposed method CanSuR consists of mainly three stages, namely, generation of local features using rotation-invariant LBP ($\hbox {LBP}^{\mathrm{ri}}$), integration of multiple scales of $\hbox {LBP}^{\mathrm{ri}}$ using the proposed sequential supervised CCA, and classification of HEp-2 cell images using SVM with radial basis function kernel ($\hbox {SVM}_{\mathrm{R}}$). So, the performance of $\hbox {LBP}^{\mathrm{ri}}$ is compared with that of several local texture descriptors, namely, LBP [29] and rotation-invariant uniform LBP ($\hbox {LBP}^{\mathrm{riu2}}$) [30]. Similarly, the performance of proposed sequential CCA is compared with that of several multimodal data integration methods, namely, CCA [18], regularized CCA (RCCA) [42] and CuRSaR [24]. The comparative performance analysis between $\hbox {SVM}_{\mathrm{R}}$ and other classifiers, such as extreme learning machine (ELM) [20], SVM with linear kernel ($\hbox {SVM}_{\mathrm{L}}$) and SVM with polynomial kernel ($\hbox {SVM}_{\mathrm{P}}$), is also done in the current study.

The performance of different methods is studied with respect to various scales of LBP 8-neighborhood such as 1 ($S_1$), 2 ($S_2$) and 3 ($S_3$). Both classification accuracy and F1 score on test sets are reported in this section to establish the performance of proposed method as well as existing approaches. To analyze the statistical significance of the proposed method, with respect to different existing methods, both tenfold cross-validation and training–testing are performed. For each data set, LBP, $\hbox {LBP}^\mathrm{ri}$ and $\hbox {LBP}^{\mathrm{riu2}}$ provide 256, 36 and 10 features, respectively. So, in case of naive integration between two scales of LBP, $\hbox {LBP}^{\mathrm{ri}}$ and $\hbox {LBP}^{\mathrm{riu2}}$, the total number of features used for the analysis is twice the number of features of individual scale. On the other hand, fifteen top-ranked extracted features are considered for different data integration methods, namely, CCA, RCCA, CuRSaR and proposed CCA. In the proposed data integration method, the value of two shrinkage parameters $\fancyscript{s_x}$ and $\fancyscript{s_y}$ is considered as 0.0001.

4.1 Description of data sets

This section provides some basic information about the data sets used for benchmarking the activity. These data sets are (i) ICPR 2012 HEp-2 cell classification contest data, termed as MIVIA image database [10]; (ii) ICPR 2014 HEp-2 cell classification contest data, termed as ICPR image database; and (iii) SNP HEp-2 database [45].

• (i) MIVIA database This data set contains 1455 cells from 28 images among which four images are belonging to cytoplasmic, fine speckled and nucleolar patterns, five images are belonging to coarse speckled and homogeneous, and six centromere images are there. The images have 24 bits color depth with uncompressed 1388 $\times$ 1038 pixels resolution. The data set contains 721 and 734 cell images in training and test sets, respectively.

• (ii) ICPR database This data set contains 13596 cell images almost equally distributed with respect to six different patterns, namely, centromere, homogeneous, nucleolar, speckled, nuclear membrane and golgi. The set contains 6797 and 6799 cell images in training and test sets, respectively.

• (iii) SNP database This database has five pattern classes, namely, centromere, homogeneous, coarse speckled, fine speckled and nucleolar. From 40 specimen images, there are 1884 cell images extracted. The specimen images are divided into training and testing sets with 20 images each (4 images for each pattern). In total, there are 869 and 937 cell images extracted for training and testing.

Table 1 Description of data sets used

Fig. 2

Comparative performance analysis of LBP-$\hbox {LBP}^\mathrm{ri}$ and $\hbox {LBP}^{\mathrm{riu2}}$-$\hbox {LBP}^{\mathrm{ri}}$ (top: MIVIA; middle: ICPR; and bottom: SNP)

The cell images from the above data sets were captured in different laboratory settings (e.g., different assays and microscope configurations). For instance, SNP HEp-2 used objective lens magnitude 20$\times$, while MIVIA HEp-2 used 40$\times$. The robustness of the proposed method as well as existing approaches is studied through the evaluation on these three data sets. Table 1 indicates the number of training and testing cells with respect to different HEp-2 patterns of these three data sets, which are used to evaluate the performance of the proposed algorithm as well as existing methods.

4.2 Importance of rotation-invariant LBP

Ideally, when an HEp-2 cell image is rotated, the pattern operator should produce a unique binary pattern for the same texture. In other words, the pattern operator should be rotation invariant. Figure 2a, b compares the performance of rotation-invariant LBP ($\hbox {LBP}^{\mathrm{ri}}$) with that of LBP, considering three scales, namely, $S_1$, $S_2$ and $S_3$ using $\hbox {SVM}_{\mathrm{L}}$ and $\hbox {SVM}_{\mathrm{R}}$, respectively. The results reported in Fig. 2a show that $\hbox {LBP}^{\mathrm{ri}}$ provides better classification accuracy of the $\hbox {SVM}_{\mathrm{L}}$ than LBP in most of the cases. For SNP data set, the $\hbox {LBP}^{\mathrm{ri}}$ attains classification accuracy of 0.465, 0.529 and 0.577, with respect to three scales, namely, $S_1$, $S_2$ and $S_3$, respectively, which are better than that obtained using LBP. On the other hand, for MIVIA data set, $\hbox {LBP}^{\mathrm{ri}}$ performs better than LBP for scales $S_2$ and $S_3$, where it achieves classification accuracy of 0.608 and 0.579, respectively. However, for scale $S_1$, LBP performs better than $\hbox {LBP}^{\mathrm{ri}}$. The $\hbox {SVM}_{\mathrm{L}}$ classification accuracy obtained using LBP for scale $S_1$ is 0.466, whereas the accuracy obtained using $\hbox {LBP}^{\mathrm{ri}}$ is 0.437. In case of ICPR data set, $\hbox {LBP}^{\mathrm{ri}}$ performs better than LBP only for scale $S_3$, while the performance is comparable in other two cases. The classification accuracy obtained using $\hbox {LBP}^{\mathrm{ri}}$ with respect to scales $S_1$, $S_2$ and $S_3$ is 0.5935, 0.664 and 0.709, respectively. On the other hand, the $\hbox {SVM}_{\mathrm{L}}$ classification accuracy obtained using LBP with respect to scales $S_1$, $S_2$ and $S_3$ is 0.5944, 0.675 and 0.708, respectively. The results reported in Fig. 2b show that $\hbox {LBP}^{\mathrm{ri}}$ achieves better classification accuracy using $\hbox {SVM}_{\mathrm{R}}$ than LBP in all the cases. For MIVIA data set, the $\hbox {LBP}^{\mathrm{ri}}$ attains classification accuracy of 0.482, 0.561 and 0.559 with respect to three scales, namely, $S_1$, $S_2$ and $S_3$, respectively, which are better than that obtained using LBP. In case of ICPR data set, the $\hbox {SVM}_{\mathrm{R}}$ classification accuracy obtained using $\hbox {LBP}^{\mathrm{ri}}$ with respect to scales $S_1$, $S_2$ and $S_3$ is 0.683, 0.765 and 0.801, which are better than that obtained using LBP. On the other hand, for SNP data set, $\hbox {LBP}^{\mathrm{ri}}$ performs better than LBP for all the scales $S_1$, $S_2$ and $S_3$, where it achieves classification accuracy of 0.442, 0.527 and 0.583, respectively. The results reported in Fig. 2a, b demonstrate that $\hbox {LBP}^{\mathrm{ri}}$, which is rotation-invariant LBP, performs better than LBP in 6 and 9 cases out of total 9 cases each using linear kernel and radial basis function kernel of SVM, respectively. All the results reported here thus establish the fact that $\hbox {LBP}^{\mathrm{ri}}$ performs better than LBP, irrespective of the datasets, scales and SVM kernels used.

Similarly, Fig. 2c, d compares the performance of $\hbox {LBP}^{\mathrm{ri}}$ with that of $\hbox {LBP}^{\mathrm{riu2}}$ at different scales using linear kernel and radial basis function kernel, respectively, considering three HEp-2 cell data sets. At scale $S_1$, the $\hbox {LBP}^{\mathrm{riu2}}$ provides $\hbox {SVM}_{\mathrm{L}}$ classification accuracy of 0.407, 0.559 and 0.466, on MIVIA, ICPR and SNP data sets, respectively, while it attains SVM linear kernel accuracy of 0.578, 0.620 and 0.520, respectively, for scale $S_2$. On the other hand, $\hbox {LBP}^{\mathrm{riu2}}$ achieves 0.601, 0.642 and 0.537 classification accuracy at scale $S_3$ using linear kernel. Similarly, the $\hbox {SVM}_{\mathrm{R}}$ classification accuracy obtained using $\hbox {LBP}^{\mathrm{riu2}}$ with respect to scale $S_1$ are 0.548, 0.694 and 0.446 on MIVIA, ICPR and SNP data sets, respectively. On the other hand, for scale $S_2$, $\hbox {LBP}^{\mathrm{riu2}}$ achieves 0.540, 0.767 and 0.490 accuracy using SVM radial basis function kernel on MIVIA, ICPR and SNP data sets, respectively. For scale $S_3$, the $\hbox {SVM}_{\mathrm{R}}$ classification accuracy obtained using $\hbox {LBP}^{\mathrm{riu2}}$ with respect to MIVIA, ICPR and SNP data sets is 0.486, 0.790 and 0.542, respectively. All the results reported in Fig. 2c, d validate that the $\hbox {LBP}^{\mathrm{ri}}$ performs better than $\hbox {LBP}^{\mathrm{riu2}}$ in 7 cases and 5 cases out of total 9 cases each, using linear kernel and radial basis function kernel of SVM, respectively. Hence, these results can establish the fact that $\hbox {LBP}^{\mathrm{ri}}$ performs better than $\hbox {LBP}^{\mathrm{riu2}}$, irrespective of the scales, datasets and SVM kernels used. Based on the analysis reported in Fig. 2, the $\hbox {LBP}^{\mathrm{ri}}$ is considered as the textural feature extraction operator in the current research work, as it can extract rotation-invariant local binary patterns more accurately from HEp-2 cell images than both LBP and $\hbox {LBP}^{\mathrm{riu2}}$.

4.3 Optimum scale for proposed method

In order to find out the optimum value of scale parameter for the proposed method, extensive experimentation is performed on each data set and corresponding results are reported in Fig. 3. Figure 3 compares the performance of different scales of $\hbox {LBP}^{\mathrm{ri}}$ operator using both linear kernel and radial basis function kernel of SVM. The results reported in Fig. 3 show that for both ICPR and SNP data, $\hbox {LBP}^{\mathrm{ri}}$ provides highest $\hbox {SVM}_{\mathrm{L}}$ and $\hbox {SVM}_{\mathrm{R}}$ classification accuracy with respect to scale $S_3$. It achieves highest $\hbox {SVM}_{\mathrm{L}}$ classification accuracy of 0.709 and 0.577 with respect to scale $S_3$ for ICPR and SNP data, respectively. Similarly, the highest $\hbox {SVM}_{\mathrm{R}}$ classification accuracy with respect to scale $S_3$ is 0.801 and 0.583 using ICPR and SNP data, respectively. On the other hand, the highest $\hbox {SVM}_{\mathrm{L}}$ and $\hbox {SVM}_{\mathrm{R}}$ classification accuracy obtained using $\hbox {LBP}^{\mathrm{ri}}$ with respect to scale $S_2$ is 0.608 and 0.561, respectively, for MIVIA data set. All the results reported here also confirm that $\hbox {LBP}^{\mathrm{ri}}$ attains better classification accuracy with respect to scales $S_2$ and $S_3$ than scale $S_1$ for both linear kernel and radial basis function kernel. Hence, integration of these two scales, namely, $S_2$ and $S_3$, may provide better recognition of HEp-2 patterns. In this regard, the optimum scale for the proposed method is considered as $S_2+S_3$.

Fig. 3

Performance analysis of $\hbox {LBP}^{\mathrm{ri}}$ for MIVIA, ICPR and SNP data sets at different scales

Fig. 4

Performance of proposed method at different scales for training–testing (top: MIVIA; middle: ICPR; and bottom: SNP)

Table 2 Classification accuracy and F1 score on different data sets for training–testing

Using the naive integration of scales $S_2$ and $S_3$, that is $S_2+S_3$, the $\hbox {SVM}_{\mathrm{L}}$ achieves classification accuracy of 0.584, 0.770 and 0.545, for MIVIA, ICPR and SNP data sets, respectively, whereas the classification accuracy using radial basis function kernel is 0.582, 0.826 and 0.589, for MIVIA, ICPR and SNP data sets, respectively. The results reported in Table 2 establish the fact that both $\hbox {SVM}_{\mathrm{L}}$ and $\hbox {SVM}_{\mathrm{R}}$ classification accuracy on ICPR data set is increased from 0.709 to 0.770 and 0.801 to 0.826, respectively. But, for MIVIA and SNP data sets, the $\hbox {SVM}_{\mathrm{L}}$ classification accuracy of $S_2+S_3$ lies in between that of scales $S_2$ and $S_3$, although the $\hbox {SVM}_{\mathrm{R}}$ classification accuracy of $S_2+S_3$ is increased from 0.561 to 0.582 and 0.583 to 0.589, for MIVIA and SNP data sets, respectively. Similar results can also be found in Table 2 for both LBP and $\hbox {LBP}^{\mathrm{riu2}}$. All these results indicate that naive integration, which is direct concatenation, of these two scales is not enough for integrating the information of two scales. Due to the drastic variation of two scales and noisy nature of the input HEp-2 cell images, naive integration usually gives poor performance, which causes insufficient and inaccurate staining pattern representation of the images. Moreover, multiple scales of unique cell image may contain complementary information. The linkages between attributes of each HEp-2 cell images can be made by using these multiple scales of unique sample cell. The combination of multiple scales of a unique HEp-2 cell image would have more discriminatory and complete information of the inherent properties of that cell by generating improved system performance than individual scale. Hence, a proper integration method is needed to incorporate the local textural feature information obtained at multiple scales.

Fig. 5

Comparative performance analysis of different data integration methods for training–testing (top: MIVIA; middle: ICPR; and bottom: SNP)

To integrate the information of two scales, namely, $S_2$ and $S_3$, of $\hbox {LBP}^{\mathrm{ri}}$ operator, the proposed sequential CCA is used in the current research work. Figure 4 demonstrates the results obtained using integrated scales of $S_1+S_2$, $S_1+S_3$ and $S_2+S_3$, using both linear kernel and radial basis function kernel of SVM, where the proposed sequential CCA is used to integrate the information of two scales. All the results reported in Fig. 4 establish the fact that the integrated information of scales $S_2$ and $S_3$ performs significantly better than that of other integrated scales, irrespective of the number of extracted features, SVM kernels and data sets used. The results reported in Fig. 4 also show that the proposed data integration method provides highest $\hbox {SVM}_{\mathrm{L}}$ classification accuracy of 0.507, 0.594 and 0.610, respectively, with respect to three aforementioned integrated scales on MIVIA data set. On the other hand, the highest $\hbox {SVM}_{\mathrm{R}}$ classification accuracy of 0.564, 0.616 and 0.636 is obtained using integrated scales $S_1+S_2$, $S_1+S_3$ and $S_2+S_3$ on MIVIA data set. Similarly, the highest F1 score for both $\hbox {SVM}_{\mathrm{L}}$ and $\hbox {SVM}_\mathrm{R}$ is 0.510, 0.584, 0.613 and 0.562, 0.625, 0.651, respectively, for all the combined scales of $S_1+S_2$, $S_1+S_3$ and $S_2+S_3$. For ICPR data set, the integrated scales of $S_1+S_2$, $S_1+S_3$ and $S_2+S_3$ obtain highest $\hbox {SVM}_{\mathrm{L}}$ classification accuracy and F1 score of 0.539, 0.692, 0.742 and 0.525, 0.663, 0.708, respectively. Similarly, the highest $\hbox {SVM}_{\mathrm{R}}$ classification accuracy and F1 score obtained using scales $S_1+S_2$, $S_1+S_3$ and $S_2+S_3$ are 0.702, 0.766, 0.851 and 0.681, 0.742, 0.825, respectively, on ICPR data set. On the other hand, the above-mentioned three integrated scales attain highest $\hbox {SVM}_{\mathrm{L}}$ classification accuracy and F1 score of 0.486, 0.572, 0.593 and 0.482, 0.586, 0.592, respectively, for SNP data set. Likewise, the highest $\hbox {SVM}_{\mathrm{R}}$ classification accuracy and F1 score achieved using scales $S_1+S_2$, $S_1+S_3$ and $S_2+S_3$ are 0.541, 0.557, 0.631 and 0.539, 0.579, 0.637, respectively, on SNP data set. However, Table 2 reports the classification accuracy and F1 score for fifteen top-ranked features, which may be different from the best values shown in Fig. 4.

Fig. 6

Execution time of proposed CCA and FaRoC

Fig. 7

Comparative performance analysis of different data integration methods for tenfold cross-validation (top: MIVIA; middle: ICPR; and bottom: SNP)

4.4 Performance of different methods

This section provides the comparative performance analysis, in terms of classification accuracy and F1 score, of different existing data integration methods considering several classifiers. Results are reported on three HEp-2 cell image databases. To incorporate the information of rotation-invariant local binary pattern ($\hbox {LBP}^{\mathrm{ri}}$) at scales $S_2$ and $S_3$, the CCA, RCCA, CuRSaR and the proposed sequential CCA method are used. Figure 5 depicts the variation of F1 score and classification accuracy obtained using both linear kernel and radial basis function kernel of SVM over different number of extracted features. From the results reported in Fig. 5, it can be seen that the proposed data integration method provides highest classification accuracy as well as highest F1 score for training–testing, integrating the local textural features of $\hbox {LBP}^{\mathrm{ri}}$ at scales $S_2$ and $S_3$, irrespective of the number of extracted features, SVM kernels and data sets used.

Table 2 compares the HEp-2 cell staining pattern F1 score and classification accuracy of the proposed as well as different existing methods for training–testing. The results corresponding to naive integration of scales $S_2$ and $S_3$ for LBP, $\hbox {LBP}^{\mathrm{ri}}$ and $\hbox {LBP}^{\mathrm{riu2}}$ are also studied in this table, where the number of features which are extracted by the naive integration of LBP, $\hbox {LBP}^{\mathrm{ri}}$ and $\hbox {LBP}^{\mathrm{riu2}}$ is 512, 72 and 20, respectively. On the other hand, the classification accuracy and F1 score of top fifteen features, which are extracted by using CCA, RCCA, CuRSaR and the proposed sequential CCA method, are reported in this table. All the results confirm that the proposed data integration method provides highest classification accuracy and F1 score of the SVM with radial basis function kernel on ICPR and SNP data sets. For MIVIA data set, the proposed data integration method achieves highest classification accuracy and F1 score of the SVM with linear kernel and radial basis function kernel, respectively.

Fig. 8

Box and whisker plots for different data integration methods (top: MIVIA; middle: ICPR; and bottom: SNP)

Table 3 Classification accuracy and F1 score of different data integration methods for tenfold cross-validation

All the results reported in Fig. 5 and Table 2 establish the fact that the proposed method can extract most relevant and significant features for HEp-2 cell staining pattern classification, which are also maximally correlated between two scales $S_2$ and $S_3$. To optimize the regularization parameters in the proposed data integration method, the rough hypercuboid approach is used. It helps to extract more relevant and significant local features than other multimodal data integration methods. In effect, the proposed method can facilitate higher HEp-2 cell pattern classification accuracy than other methods. Moreover, it can explore large search space to extract features sequentially from two multidimensional scales with significantly lesser amount of time than FaRoC [25]. Both FaRoC and proposed CCA extract features sequentially from two multidimensional variables, but the proposed CCA takes lesser amount of time than FaRoC. Figure 6 compares the execution time of FaRoC with proposed data integration method. It confirms that the execution time of the proposed sequential feature extraction method, presented in Sect. 2, is significantly lower than that of existing FaRoC.

4.5 Statistical significance analysis

This section presents the statistical significance analysis of staining pattern recognition of HEp-2 cell images using different multimodal data integration methods. To study the statistical significance of both accuracy and F1 score, tenfold cross-validation is performed. Figure 7 presents the variation of both tenfold accuracy and F1 score, for fifteen top-ranked extracted features. From the results presented in Fig. 7, it is clearly observed that both F1 score and classification accuracy for the proposed method increase while the number of generated features increases. Also, the F1 score and classification accuracy of the proposed algorithm, obtained using tenfold cross-validation, are significantly higher as compared to existing CCA, RCCA and CuRSaR, irrespective of the number of extracted features, classifiers and data sets used.

The comparative performance analysis of different data integration algorithms is also studied in Fig. 8, which shows the box and whisker plots for classification accuracy and F1 score obtained using tenfold cross-validation, on each HEp-2 cell data set using both linear kernel and radial basis function kernel of SVM. The lower and upper boundaries of each box represent the 75th percentile or lower quartile and 25th percentile or upper quartile, respectively, whereas the median is denoted by the central line. The whiskers are the two lines outside the box that extend to the highest and lowest observations. The outliers are plotted individually, and denoted as ‘+’. It represents the test cross-validation set for which a method obtains worse tenfold F1 score or classification accuracy than for the other test cross-validation sets of the same HEp-2 cell data set.

Wilcoxon signed-rank test (one-tailed), paired-t test (one-tailed) and Friedman test are used to compute the p values for statistical significance analysis. In case of tenfold cross-validation, the means and standard deviations of the classification accuracy and F1 score of the ELM, $\hbox {SVM}_{\mathrm{L}}$, $\hbox {SVM}_{\mathrm{P}}$ and $\hbox {SVM}_{\mathrm{R}}$ rules are computed for all data sets. Tests of significance are performed for the inequality of means obtained using the proposed method and other related algorithms compared. Since both mean pairs and variance pairs are unknown and different, a generalized version of t-test, termed as Behrens–Fisher problem in hypothesis testing, is used here. On the other hand, Wilcoxon signed-rank test computes the differences between the proposed method and other related algorithms using F1 score and accuracy for each observation. The p values are computed by using positive and negative ranks of absolute differences. Friedman test is a nonparametric statistical test which is used to detect the differences between the proposed method and other related algorithms by ranking procedure.

Table 3 reports the means and standard deviations of tenfold cross-validation F1 score and accuracy for all the methods using several classifiers. The p values of existing data integration methods are also recorded in this table with respect to the proposed sequential CCA method for three HEp-2 cell data sets. The highest mean values are pointed in bold in this table. All the results presented in Table 3 establish the fact that the proposed HEp-2 cell staining pattern recognition method, which mainly consists of the proposed sequential CCA and SVM with radial basis function kernel, attains best mean classification accuracy as well as F1 score, irrespective of the data integration methods, classifiers and data sets used. Out of total 216 cases, the proposed method attains significantly better p values (marked in bold) than other methods in 139 cases and better but not significant p values (marked in italics) in 66 cases, considering 95% confidence level.

5 Conclusion and discussions

The main contribution of this paper lies in developing a methodology, termed as CanSuR, which can be used to diagnose connective tissue disease by recognizing the staining patterns present in HEp-2 cells. When an HEp-2 cell image is rotated, the pattern operator should be rotation invariant such that it should produce a unique binary pattern for the same texture. In this context, the proposed method uses rotation-invariant local binary pattern as texture descriptor operator to extract important features from HEp-2 cell images. On the other hand, integration of two scales may provide better recognition of HEp-2 patterns. But, naive integration, which is the direct concatenation of two scales, may not be effective for integrating important information of two scales. A proper multimodal data integration method is thus needed to incorporate the information of two scales. In this regard, a new supervised CCA algorithm is proposed in the current research work to integrate the information of two scales. Finally, support vector machine with radial basis function kernel is used to recognize one of the known staining patterns present in IIF images. The proposed method takes into account the merits of rough hypercuboid approach and supervised CCA. While the proposed CCA helps to integrate local textural descriptors obtained from multimodal sources, the rough hypercuboid facilitates to extract significant and relevant features for HEp-2 pattern recognition. The effectiveness of the proposed method, along with a comparison with related approaches, has been demonstrated on several publicly available HEp-2 cell image databases.

The proposed method is basically the realization of computer-aided diagnosis system for the analysis of IIF images. The results produced by the proposed technique can be used to support the scientists’ subjective analysis. In effect, it may lead to prediction accuracy on test samples being consistent across laboratories and more reliable. So, one can use the proposed system to automatically identify the patterns present in the specimen HEp-2 cell images, in order to address the shortcomings of manual test procedure. Both scientific and industrial societies may be interested about the proposed method for automatic IIF image pattern analysis as it will reduce high labor costs and increase the reliability especially in the presence of photo-effect which bleaches the tissues severely in a few seconds. The proposed method may also avoid ambiguous results caused by subjective analysis and provide more efficient analysis report.