A novel double incremental learning algorithm for time series prediction

Abstract

Based on support vector machine (SVM), incremental SVM was proposed, which has a strong ability to deal with various classification and regression problems. Incremental SVM and incremental learning paradigm are good at handling streaming data, and consequently, they are well suited for solving time series prediction (TSP) problems. In this paper, incremental learning paradigm is combined with incremental SVM, establishing a novel algorithm for TSP, which is the reason why the proposed algorithm is termed double incremental learning (DIL) algorithm. In DIL algorithm, incremental SVM is utilized as the base learner, while incremental learning is implemented by combining the existing base models with the ones generated on the new data. A novel weight update rule is proposed in DIL algorithm, being used to update the weights of the samples in each iteration. Furthermore, a classical method of integrating base models is employed in DIL. Benefited from the advantages of both incremental SVM and incremental learning, the DIL algorithm achieves desirable prediction effect for TSP. Experimental results on six benchmark TSP datasets verify that DIL possesses preferable predictive performance compared with other existing excellent algorithms.

1 Introduction

In the past few decades, time series prediction (TSP) has been a challenging problem in machine learning. Time series forecasting is an effective means for assessing the characteristics of dynamic systems and predicting trends in complex systems. Moreover, with the development of TSP theory, its application in real life becomes more and more extensive. In recent years, TSP has been increasingly applied in many fields, such as traffic flow forecasting [1], cargo sales forecasting [2], sunspot prediction [3] and stock market forecasting [4].

Time series is defined as a vector formed by data recorded at the same time interval. The general process of TSP can be divided into three steps: (1) collect historical data; (2) design one model to study the characteristics of the data; and (3) use the model to predict future data. Among them, the second step is the most critical step.

In the early days, the common approaches for TSP were some traditional statistical models, such as exponential smoothing (ES), AutoRegressive integrated moving average (ARIMA) model and AutoRegressive conditional heteroskedasticity (ARCH), etc. [5]. However, these statistical models are only suitable to time series with linear features and cannot be applied to many complex systems with nonlinear features in the real world. Therefore, these models have great limitation in practical applications.

In the past few decades, the theories of machine learning have been gradually applied to the field of TSP, such as artificial neural networks (ANNs) [6,7,8,9,10,11], evolutionary computation [12], feed-forward neural networks (FNNs) [13,14,15] and support vector machine (SVM) [16,17,18]. Out of numerous methods, ANNs have strong learning and generalization ability, which have been in the leading position of TSP. The well-known ANNs-based models are fuzzy neural networks [9, 10], recurrent neural networks [7, 11], wavelet neural networks [8] and radial basis function (RBF) neural networks [6].

Although ANNs have many advantages, they still have some drawbacks, such as longer training periods and being easy to fall into local optimal traps. Moreover, hidden layer sizes and learning rates are also difficult to determine. These are issues that affect the generalization capacity of ANNs and are difficult to avoid [19]. However, these problems can be solved by using SVM in conjunction with statistical theory and structural risk minimization criteria.

SVM is a powerful nonlinear algorithm, having important application in many fields of scientific research. It is capable of generating nonlinear discriminant boundaries through linear classifiers, while still has simple geometric explanations. The original SVM was only applied to classification problems. With the development of theories, support vector regression (SVR) was proposed [20], so that SVM is applicable to the field of TSP. SVR is able to effectively solve high-dimensional and complicated regression problems [21], making it promising for TSP.

Ma and Laskov et al. proposed incremental SVM on the basis of SVM [22, 23], which inherits the advantages of SVM, and these advantages will be described in detail below. In addition, incremental SVM learns new data by modifying the trained SVM model rather than retraining a model, so it is better at handling streaming data, which are constantly changing over time. While time series is a kind of typical streaming data, therefore, compared with SVM, incremental SVM is more suitable for TSP. Particularly, incremental SVM avoids the repetitive training of large numbers of samples when processing stream data, so its efficiency is much higher than SVM.

The most important factors affecting the generalization performance of incremental SVM are kernel functions and their parameters. There exist several widely used kernel functions, such as RBF kernel, polynomial kernel, linear kernel, and sigmoid kernel. The RBF kernel and polynomial kernel are always able to satisfy Mercer’s theory, while other kernel functions are in a certain condition to meet the theory [24]. Since RBF kernel function can reduce the computational complexity and improve the generalization performance of models, it is adopted in the algorithm proposed in this paper.

Furthermore, we find that the combination of incremental learning paradigm and incremental SVM can further boost the performance for TSP, which motivates the proposal of the double incremental learning (DIL) algorithm in this work. Incremental learning was proposed firstly by Cauwenberghs et al. [25], which enables the algorithm to revise the previously generated model based on the new data points. The idea of incremental learning is to iteratively modify the effect of the new data point on the regression function to find its Kuhn–Tucker condition, while simultaneously keep the previously trained data points satisfying the Kuhn–Tucker condition. The method iteratively and appropriately modifies the model when a new data point is input into the generated incremental SVM, rather than retraining the model from scratch. Although it is originally proposed for classification problems, incremental learning is also well suited to solve the problems of regression [23].

With regard to the definition of incremental learning, different literatures give different definitions [26,27,28,29,30]. In this paper, we adopt a universally accepted concept of incremental learning that satisfies the following conditions [29, 30]:

• 1. It is capable of learning new knowledge from new data.

• 2. Old data used for the existing models are not necessary when training a new model.

• 3. Knowledge obtained previously could be preserved.

• 4. It should be able to accommodate the changes in the characteristics of the new data.

Until now, a variety of incremental learning algorithms has been proposed to solve a variety of different problems. In some cases, incremental learning refers to the growing or pruning of model architectures [31,32,33,34]. In other cases, some forms of controlled modification of learner weights have been proposed, which are ordinarily implemented by retraining the samples with large prediction errors [35,36,37,38]. Though algorithms introduced above can absorb additional knowledge from new data, it is hard for them to simultaneously meet all the four above-mentioned conditions of incremental learning. They either need to access the previous original data, or are unable to retain the previously obtained knowledge, or cannot adapt to the changes of the attributes of new data.

Since ensemble learning usually has preferable performance in comparison with single classifiers, we incorporate it into our proposed algorithm to obtain the final predictive values. The classical ensemble learning paradigm is divided into two stages, i.e., the generation of base models and the combination of their decisions [39, 40]. What’s more, many theoretical and experimental studies in the literature have confirmed that, when the dataset is properly divided into several subsets, compared to using the entire dataset, using each subset as the training set to generate a component model for the ensemble and integrating the decisions of the ensemble components often achieves better or, at least, similar generalization performance [41]. Later, we would analyze this from the perspective of TSP.

TSP is a research field with high practical value. For example, the forecasting of network access traffic allows the company to dispatch resources in a timely manner, so as to prevent a large number of concurrent visits, which might cause the paralysis of the website. For another example, by forecasting the sales of goods, it is possible to determine the future purchase to prevent the goods from encountering poor sales or out of stock. For still another example, investors may be able to get the maximum profit by properly predicting the stock movements. These practical applications have greatly promoted the study of TSP. However, the existing algorithms exposed some problems in practice. Therefore, double incremental learning (DIL) algorithm is proposed in this work, with the motivation being to improve the prediction effect, and to further promote the application of TSP in practice. DIL integrates incremental learning paradigm together with incremental SVM, which is where the algorithm name, i.e., double incremental learning (DIL) algorithm, comes from.

The DIL algorithm proposed in this work satisfies all of the above-mentioned four conditions. Besides, DIL differs from the traditional incremental learning algorithms in that, it generates new base models for the unknown parts of the feature space, instead of generating new nodes for each previously unknown instance. This scheme is similar to the rationale of ensemble learning paradigm, which significantly improves the performance of DIL algorithm in TSP.

Specifically, the dataset is preprocessed firstly and then divided into several appropriate subsets. For each subset of the dataset, weights are assigned for each sample, and the training and testing subset are selected according to the weights. Based on the training subset, a base model is obtained by implementing the incremental SVM algorithm. The weight of the base model is set according to its prediction error, and then the weighted majority voting rule is used to combine the generated base models to get a composite model. Finally, weights of the samples are adjusted in terms of the prediction error of the composite model. The above steps are repeated until a sufficient number of base models are obtained, and then, the final composite model is achieved by integrating all the base models using the weighted majority voting rule.

Next, the advantages, innovations and contributions of the proposed DIL algorithm will be introduced from several ways.

First of all, in the DIL algorithm, a new sample weight update rule is proposed, which updates the weights based on the performance of the composite model produced so far, rather than updates the weights based on the performance of the base models. Therefore, the update to the weights is more reasonable, and this rule is conducive to improving the generalization performance and robustness of the model.

In addition, the weighted majority voting method, which allocates the corresponding weight of the base model according to the performance of each base model, is used in the base model integration. Therefore, the base model with poor performance has lower discourse power, which allows the integrated model has better prediction performance.

Finally, since DIL has combined incremental learning paradigm with incremental SVM, it inherits several advantages from both of them. Incremental learning mainly brings two advantages to DIL. The first is that, it does not need to save historical data and can save the storage space. The second is that, it learns new data incrementally and makes full use of the learned knowledge without retraining the whole model, thus reducing learning time and improving learning efficiency.

DIL also inherits three major characteristics from incremental SVM. The first is its excellent generalization performance. The optimization goal of incremental SVM is to achieve the smallest structural risk, rather than the least empirical risk. Therefore, compared with many other excellent algorithms, it possesses better generalization performance. The second is the higher learning efficiency and better robustness, which are mainly benefited from the support vectors. The last point is, since incremental SVM itself has the characteristics of incremental learning, it has better generalization performance while processing time series data. Therefore, incremental SVM further enhances the overall performance of the DIL algorithm in handling TSP issues.

The numerical experiments are conducted based on six benchmark time series datasets, i.e., Mackey–Glass, Lorenz, Sunspot, Nikkei 225 Index (N225), Dow Jones Industrial Average Index (DJI), and Shanghai Stock Exchange Composite Index (SSE) datasets, to evaluate the effectiveness of the proposed DIL algorithm. The predictive performance of DIL is compared with some other excellent algorithms reported in the literature. From the comparison results, it can be concluded that DIL is superior to these comparative algorithms.

The rest of the paper is organized as follows. In Sect. 2, the required theoretical knowledge about SVM and incremental SVM will be described in detail. Section 3 will cover the details of the proposed DIL algorithm. The experimental results on the six benchmark time series datasets are reported in Sect. 4. Finally, in Sect. 5, the conclusions and outlook for future works are given.

2 Theoretical basis

SVM was originally a powerful algorithm for solving classification problems, which was proposed by Vapnik et al. [42]. With the development of relevant theories, Vapnik et al. proposed a kind of SVM for solving regression problems, i.e., SVR [43]. On the basis of SVM, incremental SVM is presented [22, 23], which inherits the power of SVM. Furthermore, the performance of incremental SVM is more excellent for regression problems. Therefore, incremental SVM is implemented as the base learner of the proposed DIL algorithm. In the following of this section, the principle of incremental SVM is introduced.

Let’s consider the regression problem. Assume that the training set is $\varvec{D} = \{ (\varvec{x}_{1} ,y_{1} ),(\varvec{x}_{2} ,y_{2} ), \ldots ,(\varvec{x}_{m} ,y_{m} )\}$, where $(\varvec{x}_{i} ,y_{i} ),i = 1, \ldots ,m$ are training samples, $\varvec{x}_{i} ,\;i = 1, \ldots ,m$ are feature vectors, and each element in the feature vectors is a real number; y_i ∊ ℜ, i = 1, …, m represent the target values. m indicates the size of the dataset ${\mathbf{D}}$, that is, the number of training samples. The goal of learning is to get the model shown in Eq. (1):

$$ f(\varvec{x}) =\varvec{\omega}^{\text{T}} \varvec{x} + b, $$

(1)

where $\varvec{\omega}$ and b are the model parameters. The output of the model $f(\varvec{x})$ should be as close as possible to y. Similarly, $\varvec{x}$ is a feature vector and y represents the target value.

The above model is proposed in the original feature space, but in practice, usually the kernel function is used to map the original space to high-dimensional space to facilitate the solution. Let $\phi (\varvec{x})$ denote the eigenvector after mapping $\varvec{x}$ to high-dimensional space, the model corresponding to Eq. (1) is as follows:

$$ f(\varvec{x}) =\varvec{\omega}^{\text{T}} \phi (\varvec{x}) + b. $$

(2)

According to literature [43], the solution of SVR is obtained as follows:

$$ f(\varvec{x}) = \sum\limits_{i = 1}^{m} {(\hat{\alpha }_{i} - \alpha_{i} )\kappa (\varvec{x},\varvec{x}_{i} )} + b, $$

(3)

where $\kappa (\varvec{x},\varvec{x}_{i} ) = \phi (\varvec{x})^{\text{T}} \phi (\varvec{x}_{i} )$ is the kernel function, $\hat{\alpha }_{i} ,\;\alpha_{i}$ are Lagrange multipliers.

According to Eq. (3), we can make the following marks:

$$ \upsilon_{i} = \hat{\alpha }_{i} - \alpha_{i} $$

(4)

$$ h(\varvec{x}_{i} ) = f(\varvec{x}_{i} ) - y_{i} = \sum\limits_{j = 1}^{m} {\kappa_{ij} \upsilon_{j} } - y_{i} + b $$

(5)

According to the value of υ, the training dataset can be divided into the following three subsets:

$$ \begin{aligned} \varvec{S} &= \{ \varvec{x}_{i} |0 < \left| {\upsilon_{i} } \right| < C\} \\ \varvec{E} &= \{ \varvec{x}_{i} |\left| {\upsilon_{i} } \right| = C\} \\ \varvec{R} &= \{ \varvec{x}_{i} |\left| {\upsilon_{i} } \right| = 0\} \\ \end{aligned} $$

(6)

Assume that sample $\varvec{x}_{c}$ be a sample newly added to the training set. Since the elements in set $\varvec{S}$ satisfy $\Delta h(\varvec{x}_{i} ) = 0$, the following equations can be obtained:

$$ \Delta h(\varvec{x}_{i} ) = \kappa_{ic} \Delta \upsilon_{c} + \sum\limits_{{\varvec{x}_{j} \in \varvec{S}}} {\kappa_{ij} \Delta \upsilon_{j} } + \Delta b = 0,\quad \forall \varvec{x}_{i} \in \varvec{S} $$

(7)

$$ \Delta \upsilon_{c} + \sum\limits_{{{\mathbf{x}}_{j} }} {\Delta \upsilon_{j} } = 0 $$

(8)

Assume that set $\varvec{S} = \{ \varvec{x}_{{s_{1} }} ,\varvec{x}_{{s_{1} }} , \ldots ,\varvec{x}_{{s_{l} }} \}$, then the incremental value of υ corresponding to the element in set $\varvec{S}$ should meet the following equation:

$$ \varvec{\rm H}\left( {\begin{array}{*{20}c} {\Delta b} \\ {\Delta \upsilon_{{s_{1} }} } \\ \vdots \\ {\Delta \upsilon_{{s_{l} }} } \\ \end{array} } \right) = - \left( {\begin{array}{*{20}c} 1 \\ {\kappa_{{s_{1} }} } \\ \vdots \\ {\kappa_{{s_{l} }} } \\ \end{array} } \right)\Delta \upsilon_{c} $$

(9)

where

$$ \varvec{\rm H} = \left( {\begin{array}{*{20}c} 0 & 1 & \cdots & 1 \\ 1 & {\kappa_{{s_{1} s_{2} }} } & \cdots & {\kappa_{{s_{1} s_{l} }} } \\ \vdots & \vdots & {} & \vdots \\ 1 & {\kappa_{{s_{l} s_{1} }} } & \cdots & {\kappa_{{s_{l} s_{l} }} } \\ \end{array} } \right) $$

(10)

From Eq. (9), the following equations can be obtained:

$$ \Delta b = \eta \Delta \upsilon_{c} $$

(11)

$$ \Delta \upsilon_{j} = \eta_{j} \Delta \upsilon_{c} ,\quad \forall \varvec{x}_{j} \in \varvec{S} $$

(12)

where η and η_j can be acquired by the following formula:

$$ \left( {\begin{array}{*{20}c} \eta \\ {\eta_{{s_{1} }} } \\ \vdots \\ {\eta_{{s_{l} }} } \\ \end{array} } \right) = - \varvec{\rm H}^{ - 1} \left( {\begin{array}{*{20}c} 1 \\ {y_{{s_{1} }} y_{c} \kappa_{{s_{1} c}} } \\ \vdots \\ {y_{{s_{l} }} y_{c} \kappa_{{s_{l} c}} } \\ \end{array} } \right) $$

(13)

For samples $\varvec{x}_{j}$’s that are not in set $\varvec{S}$, we can get $\eta_{j} = 0\;(\forall \varvec{x}_{j} \notin \varvec{S})$. For samples in sets $\varvec{R}$ and $\varvec{E}$, $\Delta h(\varvec{x}_{i} )$ can be obtained from:

$$ \Delta h(\varvec{x}_{i} ) = \left( {\kappa_{ic} + \sum\limits_{{{\mathbf{x}}_{j} \in S}} {\kappa_{ij} \Delta \eta_{j} } + \eta } \right)\Delta \upsilon_{c} = \gamma_{i} \Delta \upsilon_{c} $$

(14)

According to the principle of asymptotic movement, the value of Δυ_c can be calculated in four cases, and the maximum one is taken as the final value of Δυ_c. Since the detailed calculation method of Δυ_c does not fall into the focus of this paper, we will not elaborate it here. When a new sample $\varvec{x}_{c}$ is added to the set $\varvec{S}$, the matrix $\varvec{\varPsi}= \varvec{\rm H}^{ - 1}$ should be updated as follows:

$$ \varvec{\varPsi}= \left( {\begin{array}{*{20}c} {} & {} & {} & 0 \\ {} &\varvec{\varPsi}& {} & 0 \\ {} & {} & {} & \vdots \\ 0 & 0 & \cdots & 0 \\ \end{array} } \right) + \frac{1}{{\gamma_{c} }}\left( {\begin{array}{*{20}c} \eta \\ {\eta_{{s_{1} }} } \\ \vdots \\ {\eta_{{s_{l} }} } \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \eta & {\eta_{{s_{1} }} } & \cdots & {\eta_{{s_{l} }} } & 1 \\ \end{array} } \right) $$

(15)

3 Methodology

3.1 Base learner

The base learner is the cornerstone of DIL. Although the selection to the base learner is varied, it is necessary to select the appropriate base learner according to the specific problem. In this paper, incremental SVM is chosen as the base learner. We make such a choice mainly based on the following two considerations. First, incremental SVM inherits several advantages from SVM, such as good generalization performance and high robustness. Second, incremental SVM can learn new data incrementally, which makes it more suitable for TSP, as previously mentioned.

In DIL, it is necessary to implement incremental SVM to generate a base model in each iteration. The final composite model is obtained by combining all the generated base models. Based on the theoretical analysis in the previous section, the pseudocode of incremental SVM can be gained, as shown in Algorithm 1.

3.2 The proposed DIL algorithm

In this section, a detailed description of the proposed DIL algorithm is presented. In the DIL algorithm, incremental learning is implemented by combining the existing base models with the base models generated on the new data. As mentioned previously, DIL inherits some merits from both incremental SVM and incremental learning; therefore, it is particularly suitable for time series forecasting. Moreover, the strategy of DIL is similar to the rationale of the adaptive boosting (AdaBoost) algorithm, thus, it naturally inherits performance improvement attribute of AdaBoost.

One major characteristic of DIL is that, each new base learner added to the ensemble is trained on a set of samples selected based on a distribution got by normalizing the weights of the samples, which ensures that samples with larger errors have a higher probability to be selected as training samples. In general, the samples with high prediction errors are unknown samples, or samples that have not been used to train learners.

DIL generates a collection of weak learners and combines the predictive values obtained by individual learners using the method of weighted majority voting. This scheme is similar to the AdaBoost algorithm. During each iteration, DIL uses an update strategy to change the weight of the current sample, selecting different training data to obtain diverse weak learners. AdaBoost’s distribution update rule is designed to improve the accuracy of the classifier, while DIL’s distribution update strategy is optimized for learning new data incrementally and further decreasing predictive errors. For a detailed description about AdaBoost, please refer to [44].

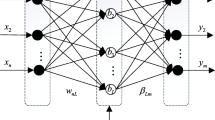
In Algorithm 2, the specific pseudo code of the DIL algorithm is presented, and its block diagram is given in Fig. 1.

Fig. 1

Block diagram of the DIL algorithm

We now give a detailed description of the DIL algorithm. The inputs of DIL are as follows:

• 1. The original time series dataset $\varvec{T} = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$. x_i, i = 1, …, n, is the value at a certain time point t_i, which is a continuous value.

• 2. Time window size tw, which is required in preprocessing the original time series dataset.

• 3. The number of data subsets K, which is used to divide the dataset. The dataset obtained by the pretreatment is divided into K parts, to obtain K data subsets.

• 4. Number of iterations T_k, which means the number of iterations implemented on each data subset, indicating, meanwhile, the number of base learners generated on each data subset.

• 5. Base learner, i.e., incremental SVM, which is implemented in each iteration.

The final model H_f is the output of the proposed algorithm. Our purpose is to get a final model H_f that possesses powerful predictive capability. In this work, we focus on the research of one-step-ahead prediction, thus H_f is used to predict the data values at the next point in time.

Let $\varvec{T} = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ be a time series and $\varvec{x}_{\varvec{i}} = \left( {x_{i} ,x_{i + 1} , \ldots ,x_{i + tw - 1} } \right)$ be the input of the i-th base learner, where tw denotes the time window size. y_i = x_i+t is regarded as the target value. Then, $\left( {\varvec{x}_{\varvec{i}} ,y_{i} } \right)$ represents a sample, and $\varvec{Data} = \left\{ {\left( {\varvec{x}_{\varvec{i}} ,y_{i} } \right),i = 1, \ldots ,N} \right\}$ is our dataset.

DIL generates an ensemble consisting of weak learners, each base learner is trained on different subsets of the currently available data subset $\varvec{S}_{\varvec{k}} ,k = 1, \ldots ,K$. All of the K data subsets are gained by dividing $\varvec{Data}$ into K parts. In each iteration, 4/45.5 of the dataset $\varvec{S}_{\varvec{k}} ,\;k = 1, \ldots ,K$ are utilized as the training data, and the remainder are used as the testing data. Each specific instance used to train the base learners is selected according to the weight of each instance in $\varvec{S}_{\varvec{k}} ,\;k = 1, \cdots ,K$. In each iteration, after updating, the weight vector $\varvec{\omega}$ is normalized, which makes the weights a distribution. The instances with higher prediction errors are more likely to be added into the training set for the next iteration. For each dataset $\varvec{S}_{\varvec{k}} ,\;k = 1, \ldots ,K$, the weight vector $\varvec{\omega}$ can be initialized as any value, while in this paper, each element value of the weight vector $\varvec{\omega}$ is initialized to 1/m, so that, initially, each instance has the same chance of being selected into the training subset.

In the tth iteration, t = 1, 2, …, T_k, the DIL algorithm first selects the training subset $\varvec{TR}$ and the testing subset $\varvec{TE}$ from $\varvec{S}_{\varvec{k}} ,\;k = 1, \ldots ,K$ according to the weight vector $\varvec{\omega}$ (Step 1). Then, appropriate parameters are selected for incremental SVM to generate base model h_t (Step 2). The error e_t of model h_t on $\varvec{S}_{\varvec{k}} = \varvec{TR} + \varvec{TE},k = 1, \ldots ,K$ is defined as:

$$ e_{t} = \sum\limits_{i = 1}^{m} {\varvec{\omega}(i) \times \left| {h_{t} (\varvec{x}_{\varvec{i}} ) - y_{i} } \right|} $$

(16)

where | · | indicates the absolute value (Step 3). That is simply the weighted sum of absolute deviations.

If e_t > ɛ, h_t will be discarded, and $\varvec{TR}$ and $\varvec{TE}$ will be rechosen, where ɛ is a threshold preset according to the distribution of the dataset. That is, whether a base model could be retained is mainly dependent on its performance over $\varvec{S}_{\varvec{k}} ,\;k = 1, \ldots ,K$. The threshold ɛ is used to measure whether h_t has reached the required level of performance. Since the value of ɛ is determined based upon the dataset, it usually owns different values for different datasets, but in general ɛ is less than 1/2.

If e_t ≤ ɛ is satisfied, then calculate the normalized error β_t(0 ≤ β_t ≤ 1) according to Eq. (17):

$$ \beta_{t} = {{e_{t} } \mathord{\left/ {\vphantom {{e_{t} } {(1 - e_{t} )}}} \right. \kern-0pt} {(1 - e_{t} )}}. $$

(17)

The rule of weighted majority voting is then used to combine the base models generated in the previous t iterations (Step 4). When voting, the weight of each base model is the logarithm of the reciprocal of the normalized error β_t. Thus, base model with a smaller error rate is assigned a higher voting weight. The composite model H_t is obtained by combining every base model as follows:

$$ H_{t} = \arg \mathop {\hbox{max} }\limits_{y} \sum\limits_{{t:\;\left| {h_{t} ({\mathbf{x}}) - y} \right| < \delta }} {\log ({1 \mathord{\left/ {\vphantom {1 {\beta_{t} }}} \right. \kern-0pt} {\beta_{t} }})} . $$

(18)

In order to make it easier for the reader to understand the weighted majority voting rule in DIL, we give a schematic diagram in Fig. 2.

Fig. 2

The weighted majority voting rule in DIL

Note that the predicted value given by H_t is the value obtained by weighted majority voting within a certain error range. That is, if the total number of votes received in the interval $\left( {y - \delta ,y + \delta } \right)$ is the highest, then the combined forecasting is y.

The composite error E_t of model H_t is computed on $\varvec{S}_{\varvec{k}} ,\;k = 1, \ldots ,K$ as:

$$ E_{t} = \sum\limits_{i = 1}^{m} {\varvec{\omega}(i) \times \left| {H_{t} (\varvec{x}_{\varvec{i}} ) - y_{i} } \right|} , $$

(19)

The composite error E_t and the error e_t have the same mathematical significance. If E_t > ɛ, then discard the current composite model H_t, select a new training subset and generate a new H_t. It is found that, in most cases, the condition E_t ≤ ɛ could be satisfied, because the performance of each base model h_t has been verified in step 3. If E_t ≤ ɛ is satisfied, the composite normalized error Γ_t will be calculated as

$$ \varGamma_{t} = {{E_{t} } \mathord{\left/ {\vphantom {{E_{t} } {(1 - E_{t} )}}} \right. \kern-0pt} {(1 - E_{t} )}}. $$

(20)

The weight vector $\varvec{\omega}$ is updated and normalized so that the weights become a distribution. And then, they are used to select the training and testing subsets, i.e., $\varvec{TR}$ and $\varvec{TE}$, respectively, for the next iteration. The specific weights update method is as follows:

$$ \varvec{\omega}(i) = \left\{ {\begin{array}{*{20}l} {\varvec{\omega}(i) \times \varGamma_{t} ,} \hfill & {{\text{if}}\;\left| {H_{t} (\varvec{x}_{\varvec{i}} ) - y_{i} } \right| < \delta } \hfill \\ {\varvec{\omega}(i),} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.. $$

(21)

Furthermore, the weight vector $\varvec{\omega}$ is normalized as:

$$ \varvec{\omega}= {\varvec{\omega}\mathord{\left/ {\vphantom {\varvec{\omega}{\sum\limits_{i = 1}^{m} {\varvec{\omega}(i)} }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{m} {\varvec{\omega}(i)} }}. $$

(22)

The weights update rule is one of the most important parts of the DIL algorithm. In order to make it easier to understand, its schematic diagram is given in Fig. 3.

Fig. 3

The weights update rule in DIL

Following this rule, if the prediction error of the composite model H_t for y_i is within a certain range, i.e., $\left| {H_{t} (\varvec{x}_{\varvec{i}} ) - y_{i} } \right| < \delta$, the corresponding weight $\varvec{\omega}(i)$ is multiplied by a factor Γ_t. According to the definition of Γ_t, its value is less than 1. If $\left| {H_{t} (\varvec{x}_{\varvec{i}} ) - y_{i} } \right| < \delta$ is not satisfied, the corresponding weight $\varvec{\omega}(i)$ will remain unchanged. According to this rule, instances with higher prediction errors are more likely to be selected into $\varvec{TR}$ in the next iteration. If we regard those instances, whose prediction errors are large, as hard instances, while the instances with small prediction errors as simple instances, then the algorithm would be more and more concerned about hard instances, and the hard instances will be further intensively studied. Therefore, the DIL algorithm belongs to the incremental learning paradigm, which is specially designed for TSP.

After generating T_k base models on each dataset $\varvec{S}_{\varvec{k}} ,\;k = 1, \ldots ,K$, all the base models generated so far are integrated by using the weighted majority voting rule to obtain the final composite model H_f. The specific form of the final composite model H_f is as follows:

$$ H_{\text{f}} = \arg \mathop {\hbox{max} }\limits_{y} \sum\limits_{k = 1}^{K} {\sum\limits_{{t:\;\left| {h_{t} (\varvec{x}) - y} \right| < \delta }} {\log \left( {{1 \mathord{\left/ {\vphantom {1 {\varGamma_{t} }}} \right. \kern-0pt} {\varGamma_{t} }}} \right)} } $$

(23)

The time complexity of the proposed DIL algorithm is O(KT_k(C_H + C_h)), where K represents the number of data subsets after dataset division, and T_k represents the number of iterations. C_h and C_H, respectively, represent the number of base models and compound models discarded during one iteration.

Note that the DIL algorithm preserves all of the generated base models; therefore, the previous data can be discarded to save storage space, without forgetting the previous knowledge. In addition, DIL has another important feature, i.e., the independence from the base learner. That is to say, any appropriate weak learner could be chosen as the base model for DIL, which has only a little effect on the overall performance of the algorithm. However, choosing the corresponding base learner according to the specific problems is helpful for DIL to achieve more desirable prediction results. Generally, the DIL algorithm is able to achieve good prediction effect for various TSP problems, which is propitious to solve many problems in reality.

3.3 A discussion about the extensions of DIL algorithm with respect to deep learning

In recent years, with the development of machine learning theory, deep learning (DL), as a new research branch, has emerged. A lot of researches and applications have verified the powerful performance of deep learning [45,46,47]. Deep learning is essentially a nonlinear combination of multi-level representation learning methods. Representation learning [48] refers to learning the feature representation from data, in order to extract useful information from the data for the purpose of classifying or forecasting. Starting from raw data, DL paradigm transforms each layer’s features into higher layers and more abstract features, so as to discover intricate structures in high-dimensional data.

In the field of DL, various deep structures have been put forward. Among them, several most classic deep structures are deep belief network (DBN) [49], deep Boltzmann machine (DBM) [50] and stacked autoencoder (SAE) [51]. DBN and DBM are obtained by stacking restricted Boltzmann machines [52]. SAE is formulated by stacking autoencoders [53]. Furthermore, researchers have proposed some excellent deep structures, recently. For example, Zhang et al. [54] developed a character-level sequence-to-sequence learning method, i.e., RNNembed, for neural machine translation.

About the extensions of the proposed DIL algorithm with respect to deep learning, we have three ideas. The first one is that, inspired by SAE, multiple incremental SVMs could be stacked together to get a deep incremental support vector machine, which could be used to replace the original base learner of the DIL algorithm to further improve its performance.

The second idea is, firstly, building a deep neural network for feature extraction from data, and then, feeding the obtained feature representation through unsupervised learning into the base models of the DIL algorithm, i.e., incremental SVMs, so that the DIL algorithm could be used to predict the trend of data.

The third thought is, it might be desirable to integrate incremental learning with deep learning paradigm, such that deep neural networks can learn data incrementally. For example, a deep neural network is used for feature learning, while an incremental learning algorithm integrates existing feature sets with newly acquired features in a particular way.

4 Numerical experiments

In order to evaluate the performance of the proposed DIL algorithm, simulation experiments based on several benchmark synthetic and real-world datasets are conducted. And the experimental results of DIL on each dataset are compared with those state-of-the-art algorithms proposed in other literatures, with the detailed experimental results and discussions given in Sect. 4.2. The experimental results have demonstrated the significant improvement to the predictive performance achieved by the proposed algorithm.

4.1 Datasets and experimental setup

4.1.1 Datasets

Simulation experiments on six benchmark datasets have been conducted in this work, including two synthetic datasets and four real-world datasets. The details of the six benchmark datasets are described in turn as below.

• (A) Mackey–Glass database

Originally, the Mackey–Glass equation was presented as a model for regulating blood cell. One of the major features of the Mackey–Glass dataset is its chaotic nature; therefore, it is one of the classical datasets in the field of chaotic TSP. The time series is generated by the following nonlinear differential equation:

$$ \frac{{{\text{d}}\varvec{x}}}{{{\text{d}}t}} = \frac{{a\varvec{x}(t - \tau )}}{{1 + \varvec{x}^{c} (t - \tau )}} - b\varvec{x}\left( t \right). $$

(24)

If τ > 16.8, then the time series is chaotic. According to the literatures [7, 55, 56], the parameters selected for generating the time series are a = 0.2, b = 0.1, c = 10, and τ = 17. According to Eq. (24), a chaotic time series dataset with the length of 10,000 is generated, with the initial value being set to 1.2, that is, $\varvec{x}(0) = 1.2$. The first 8000 values are discarded and the last 2000 values are kept for the experiments.

• (B) Lorenz database

The Lorenz time series is a three-dimensional dynamical system that exhibits chaotic flow and was found by Edward Lorenz. The equation for generating the Lorenz time series is as follows:

$$ \begin{aligned} \frac{{{\text{d}}\varvec{x}(t)}}{{{\text{d}}t}} &= \sigma \left[ {\varvec{y}(t) - \varvec{x}(t)} \right] \\ \frac{{{\text{d}}\varvec{y}(t)}}{{{\text{d}}t}} &= \varvec{x}(t)\left[ {r - \varvec{z}(t)} \right] - \varvec{y}(t) \\ \frac{{{\text{d}}\varvec{z}(t)}}{{{\text{d}}t}} &= \varvec{x}(t)\varvec{y}(t) - b\varvec{z}(t). \\ \end{aligned} $$

(25)

where σ, r and b are the dimensionless parameters. The parameters used to generate the time series are set according to the literatures [7, 55, 56], where σ = 10, r = 28 and b = 8/3. In this group of experiments, the x-coordinate of the Lorenz time series is taken as the experimental dataset. A chaotic time series dataset with the length of 10,000 can be generated according to Eq. (25). Similarly, in order to reduce the transient effect, we discard the first 8000 values and keep the last 2000 values for the experiments.

• (C) Sunspot database

The Sunspot time series is a time series that regularly records the number of sunspots, which is an important indicator for the study of the solar cycle. The solar cycle has a significant impact on the Earth’s climate, the operation of the satellite, and so on; therefore, it is of great practical significance to predict the sunspots number. However, the prediction of sunspot numbers is still a challenging task, because of its own complexity. The monthly smoothed Sunspot time series used in this paper is obtained from Sunspot Index World Data Center (SIDC) [57]. To compare the performance of the proposed DIL algorithm with the other algorithms in the literatures, the Sunspot time series from November 1834 to June 2001 is selected as our dataset, which contains 2000 data values.

• (D) Three financial datasets

In addition to the three benchmark datasets introduced above, there are three important stock index datasets, respectively, N225, DJI and SSE. These three stock indexes have a more important impact on the international financial markets, thus, it is necessary to do some research on them. The N225 dataset in the fourth group of experiments consists of monthly sampled data, which includes all the closing prices from April 1988 to March 2015, containing 324 data points [58]. The monthly closing prices of DJI from February 1985 to March 2015 are selected as the experimental data for the fifth group of experiments, including 352 data values [58]. Similarly, in the sixth group of experiments, the monthly closing prices of SSE from December 1990 to January 2015 are selected as the experimental data, containing 290 data points [58].

Furthermore, in order to facilitate comparison, it is necessary to normalize the data, that is, to adjust the data to the range of [0, 1]. The normalization formula is as follows:

$$ x_{i}^{\prime } = \frac{{x_{i} - x_{\hbox{min} } }}{{x_{\hbox{max} } - x_{\hbox{min} } }}, $$

(26)

where $x_{i}^{\prime }$ is the normalized data value, x_i is the original value, x_max and x_min are the maximum and minimum values in the original data, respectively.

4.1.2 Experimental setup

In order to carry out the experiments of this work, some parameters are required to be preset appropriately. The specific parameters of the DIL algorithm are shown in Table 1.

Table 1 The parameters of DIL

For the time window size tw, it is found by trial-and-error that, the feasible value range of the time window tw is [4, 10] for datasets with different sizes. For data partition, it is important to determine an appropriate size for the data subset $\varvec{S}_{\varvec{k}} ,k = 1, \ldots ,K$, which is usually related to the size of the original dataset. After repeated experiments, it is found that, for datasets with different sizes, when the number of subsets K is set within the range [2, 6], the subset $\varvec{S}_{\varvec{k}} ,k = 1, \ldots ,K$ will have a more appropriate size. In this paper, the original dataset is evenly divided into several subsets, that is, the sizes of $\varvec{S}_{\varvec{k}}$’s are identical. However, in fact, the DIL algorithm does not force the sizes of the subsets $\varvec{S}_{\varvec{k}}$’s to be the same. The DIL algorithm would generate T_k base models on each $\varvec{S}_{\varvec{k}} ,k = 1, \ldots ,K$. T_k should not be too large, because blindly increasing T_k is not much helpful to upgrade the model performance, and would lead to inefficiency; however, T_k should also not be too small, because a too small T_k will reduce the model performance. As shown in Table 1, the value of T_k in this work is set as 20.

In order to evaluate the performance of the proposed DIL algorithm and to compare it with the algorithms in the literatures, we need proper measurements to measure their prediction performance. In the field of TSP, there are several commonly used prediction performance measurements, among which the following four error measures, i.e., root mean squared error (RMSE), normalized mean squared error (NMSE), mean absolute error (MAE), and absolute error (Error), are employed in this work. Their specific formulas are presented as follows:

$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {x_{i} - \hat{x}_{i} } \right)^{2} } } , $$

(27)

$$ {\text{NMSE}} = \left( {\frac{{\sum\nolimits_{i = 1}^{N} {\left( {x_{i} - \hat{x}_{i} } \right)}^{2} }}{{\sum\nolimits_{i = 1}^{N} {\left( {x_{i} - \bar{x}} \right)}^{2} }}} \right), $$

(28)

$$ {\text{MAE}} = \frac{{\sum\nolimits_{i = 1}^{N} {\left| {x_{i} - \hat{x}_{i} } \right|} }}{N}, $$

(29)

$$ {\text{Error}} = x_{i} - \hat{x}_{i} , $$

(30)

where x_i and $\hat{x}_{i} ,i = 1, \ldots ,N$ represent the original data and the predicted data, respectively. $\bar{x}$ represents the average of the original data, and N denotes the size of the testing dataset.

In order to reduce the contingency of the experimental results, twenty repetitive experiments are performed on each dataset, and the average values of the repetitive experimental results are taken as the final results.

Finally, the operating environment of the experiments in this work is MATLAB R2009a. The hardware configuration is one PC with 2.4 GHz CPU and 12 GB RAM.

4.2 Results and discussion

In this section, the experimental results of the proposed algorithm on the six benchmark datasets are given, and the relevant experimental results graphics are drawn. Furthermore, the prediction performance of the DIL algorithm is compared with other excellent algorithms in the literatures.

Tables 2 and 3 show the maximum, minimum and average values of RMSE and the run times (CPU time) of the DIL algorithm in 20 independent and repetitive runs on the six benchmark datasets, which are what they have in common on each dataset. The difference between Tables 2 and 3 lies in that, Table 2 lists out the maximum, minimum and average values of NMSE on the Mackey–Glass, Lorenz and Sunspot datasets, while Table 3 displays those values of MAE on the N225, DJI and SSE datasets. The reason why the experimental results are listed out in this way is because the performance of DIL is required to be compared with other state-of-the-art algorithms. However, the comparative algorithms in some literatures provide their RMSE and NMSE results, while the comparative algorithms in other literatures provide their RMSE and MAE results.

Table 2 RMSE, NMSE and CPU time of the DIL algorithm on the first three datasets

Table 3 RMSE, MAE and CPU time of the DIL algorithm on the last three datasets

As can be seen from Tables 2 and 3, the DIL algorithm is capable to complete training and prediction on the six datasets in a short period of time. In addition, according to the minimum, maximum, mean of the RMSEs, NMSEs and MAEs, we can see that the error range of DIL on five datasets is very compact with slight fluctuation, except those on the Mackey–Glass dataset. Although the error fluctuation on the Mackey–Glass dataset is slightly larger, it is also within acceptable limits. And it can be seen from the subsequent chapters that, it is caused by very few examples. From these experimental results, a conclusion could be drawn that, the DIL algorithm possesses a relatively stable performance in most cases.

As can be seen from Figs. 4, 5, 6, 7, 8 and 9 that, the DIL algorithm has good predictive performance on all the six benchmark datasets. Figures 4a, 5a, and 6a compare the predictive values with the original values on the Mackey–Glass, Lorenz, and Sunspot datasets, respectively, which indicate that the differences between these two values are very small. Figures 7a, 8a, and 9a compare the predictive values with the original values on the N225, DJI, and SSE datasets, respectively. On these three datasets, the high degree of unpredictability of financial data causes slightly larger prediction errors. But, the forecast trend is basically consistent with the actual trend, and the prediction performance of the DIL algorithm on these three datasets also exceeds many existing algorithms.

Fig. 4

a The prediction results graph of the DIL algorithm on Mackey–Glass. b The prediction errors of the DIL algorithm on Mackey–Glass

Fig. 5

a The prediction results graph of the DIL algorithm on Lorenz. b The prediction errors of the DIL algorithm on Lorenz

Fig. 6

a The prediction results graph of the DIL algorithm on Sunspot. b The prediction errors of the DIL algorithm on Sunspot

Fig. 7

a The prediction results graph of the DIL algorithm on N225. b The prediction errors of the DIL algorithm on N225

Fig. 8

a The prediction results graph of the DIL algorithm on DJI. b The prediction errors of the DIL algorithm on DJI

Fig. 9

a The prediction results graph of the DIL algorithm on SSE. b The prediction errors of the DIL algorithm on SSE

Correspondingly, Figs. 4b, 5b, 6b, 7b, 8b, and 9b show the prediction errors (absolute errors) on the six datasets, respectively. The results show that, the absolute errors on the six datasets at most reach the value of 10⁻² or reduce to even lower values. Figure 4b shows that, very few data points fluctuate much, which confirms the results in Table 2. From these prediction errors graphs, we can conclude that, the DIL algorithm has less error fluctuation on the five datasets, and its prediction performance is stable.

As can be seen from the preceding introduction, the DIL algorithm integrates the incremental learning paradigm together with incremental SVM. In order to analyze which part has a greater impact on the overall performance of the DIL algorithm, we split the DIL algorithm into two parts. The first part is an incremental learning framework, in which, the traditional SVM is chosen as base learner, replacing the incremental SVM. This algorithm is called single incremental learning (SIL) algorithm in this paper. The second part is the base learner of the DIL algorithm, i.e., incremental SVM, which is abbreviated as ISVM.

Tables 4 and 5 show the experimental results of DIL, SIL and ISVM algorithms on the six datasets, respectively. These results are obtained by averaging the results of twenty repeated experiments. As can be seen from these two tables, the performances of SIL and DIL are relatively close to each other, while the performance of ISVM is quite different from the former two. This situation illustrates that the incremental learning framework contributes more to the overall performance of the proposed DIL algorithm, while the base learner has little impact on it.

Table 4 The results of DIL, SIL and ISVM algorithm on the first three datasets

Table 5 The results of DIL, SIL and ISVM algorithm on the last three datasets

There are some parameters in the proposed DIL algorithm, among which, the time window size tw, the number of data subsets K, and the number of iterations T_k are the three most important parameters. In order to analyze the impact of these parameters on the performance of the DIL algorithm, repeated experiments are performed on six data sets. In the course of the experiments, each parameter takes various values to carry on the experiments in turn. Through these experiments, we can determine a suitable range of each parameter values. These experiments also further verify the values intervals of the parameters setting in Sect. 4.1.2 are reasonable.

Tables 6, 7 and 8 show the results of DIL algorithm with different values of time window size tw on six datasets, while the values of the other two parameters K and T_k are set as 4 and 20, respectively, by trial-and-error. It is not difficult to find from these three tables that, the prediction results of DIL algorithm are similar when the values of tw are within the interval [4, 10]. If the tw’s value is not within the range of [4, 10], the prediction effect of DIL algorithm will be worse. This shows that, the value of tw should not be too large nor too small. If tw is too small, samples will contain too little valid information, which might lead to poor predictive performance. If the value of tw is too large, samples will contain too much noise, thus affecting the learner’s learning.

Table 6 RMSE of the DIL algorithm with different parameter tw on six datasets

Table 7 NMSE of the DIL algorithm with different parameter tw on the first three datasets

Table 8 MAE of the DIL algorithm with different parameter tw on the last three datasets

The experimental results of the DIL algorithm with different values of the number of data subsets K on six datasets are shown in Tables 9, 10 and 11, while the other two parameters tw and T_k take the values of 7 and 20, respectively, by trial-and-error. From these three tables, we can draw a conclusion similar to the previous one. The three tables show that, proper partitioning of the datasets can improve the overall performance of the algorithm. However, the size of the data subset should not be too small, since a single base model learned on an undersized dataset would have a poor overall description of the data. This also has a certain impact on the overall performance of DIL algorithm.

Table 9 RMSE of the DIL algorithm with different parameter K on six datasets

Table 10 NMSE of the DIL algorithm with different parameter K on the first three datasets

Table 11 MAE of the DIL algorithm with different parameter K on the last three datasets

Similarly, different values are set for the number of iterations T_k, and then experiments are conducted on the six datasets. In this experimental part, the values of the other two parameters tw and K are set as 7 and 4, respectively, by trial-and-error. The experimental results are presented in Tables 12, 13 and 14. It can be easily seen from the experimental results that, when the value of T_k is too small, that is, the generated base models are too little, the performance of the algorithm will be obviously decreased. This is because the number of base models is too small and the data have not been fully learned. It is not difficult to find that, when the value of T_k increases to a certain extent, if it continues to increase, the performance of the algorithm would not only not be significantly improved, but rather result in performance degradation. The reason might be that, when the value of T_k becomes too large, the diversity among the base models could decrease, while their accuracies might not be improved, simultaneously.

Table 12 RMSE of the DIL algorithm with different parameter T_k on six datasets

Table 13 NMSE of the DIL algorithm with different parameter T_k on the first three datasets

Table 14 MAE of the DIL algorithm with different parameter T_k on the last three datasets

In order to show the superiority of the proposed algorithm, the predictive performance of DIL on the six time series datasets are compared with the latest excellent algorithms in the literatures, as shown in Tables 15, 16, 17, 18, 19 and 20. For the sake of comparison, the best results are highlighted in bold. In addition, the results listed in the tables are the average values of the 20 repetitive experimental results obtained by DIL.

Table 15 Comparisons with the results from the literatures on Mackey–Glass

Table 16 Comparisons with the results from the literatures on Lorenz

Table 17 Comparisons with the results from the literatures on Sunspot

Table 18 Comparisons with the results from the literatures on N225

Table 19 Comparisons with the results from the literatures on DJI

Table 20 Comparisons with the results from the literatures on SSE

Table 15 shows the comparison between the algorithms reported in the literatures with the proposed DIL algorithm based upon RMSE and NMSE values on the Mackey–Glass dataset. It is easy to see from the table that, DIL has better performance in predicting this time series, compared with other algorithms. Obviously, compared with other algorithms, both RMSE and NMSE values have been significantly reduced by DIL.

Table 16 presents a comparison of the prediction errors on the Lorenz time series. The results show that, the DIL algorithm has much smaller RMSE and NMSE values, and more accurate prediction results.

In Table 17, the proposed DIL algorithm achieves smaller RMSE in predicting the Sunspot time series, when compared to other algorithms. The mean value of NMSE for 20 runs of DIL is minimal, although only slightly smaller than the second optimal algorithm. Table 2 shows that, the maximum NMSE of DIL is 6.24E−04 on the Sunspot dataset, which is worse than the Residual Analysis method using Hybrid Elman-NARX Neural Networks (HENNN-RA) [55] and Taguchi’s Design of Experiment (Taguchi’s DoE) [56] models. However, we can see that, the minimum and average NMSE values achieved by DIL are smaller than Taguchi’s DoE. In fact, 16 results of NMSEs are within the range of (4.07E−04, 5.03E−04) in 20 repetitive experiments. The prediction NMSEs of the proposed model are better than the second optimal model in most cases. Combining with the results of NMSE and RMSE, we have sufficient reason to believe that the performance of the proposed DIL algorithm is better than all the other comparative models.

In Tables 18, 19 and 20, the main comparisons are conducted toward the results of RMSE and MAE. Table 18 shows that, the average values of RMSE and MAE obtained by DIL are the smallest when predicting the N225 time series, which is superior to the best existing neuron model with nonlinear interactions between excitation and inhibition of dendrites (NBDM) [58]. Furthermore, we can conclude that, DIL has improved performance by at least 25% compared to NBDM. As can be seen from Table 19, when the DJI time series is predicted, the proposed DIL algorithm achieves the smallest average values of RMSE and MAE, which are 1.91E−02 and 1.42E−02, respectively. Compared to the optimal NBDM, the average values of RMSE and MAE achieved by DIL are reduced by at least 45%. In Table 20, similarly, DIL achieves the optimal average results of RMSE and MAE when predicting the SSE time series. And the average values of RMSE and MAE obtained by DIL are decreased by 19.5 and 22.4%, respectively, compared with the best NBDM.

Next, we will further verify the computational complexity of the proposed DIL algorithm through experiments. Moreover, five comparative algorithms are selected to be compared with the proposed DIL algorithm, including locally linear neurofuzzy model with locally linear model tree (LLNF-LoLiMot) algorithm [60], competitive island-based cooperative coevolution methods for two islands (CICC-two-island) [62], cooperative coevolution for training recurrent neural networks with synapse level encoding (SL-CCRNN) [7], orthogonal least squares learning algorithm for Radial Basis Function networks (RBF-OLS) [60], and cooperative coevolution for training recurrent neural networks with neuron level encoding (CCRNN-NL) [61], in terms of overall computational time on the six benchmark datasets. According to the previous analysis, the computational complexity of the proposed DIL algorithm is O(KT_k(C_h + C_H)). In the following, the computational complexities of the five selected comparative algorithms are briefly analyzed. O(2Mp⁴) is the time complexity of LLNF-LoLiMot, where M is the number of neurons, p is the dimension of the sample space. The computational complexity of SL-CCRNN is O(nsT), where n means n generations, s is equal to the total number of synapses and biases, T is the number of iterations.

O(T₁T₂D(S + N)) is the computational complexity of CICC-two-island, where T₁ represents global evolution times, T₂ means island evolution times, D is the depth of n generations, N is the number of sub-populations at neuron level, S is the number of sub-populations at synapse level. The time complexity of CCRNN-NL is O(ckm), where c is the number of cycles, k is the total number of hidden and output neurons, m is the number of generations. O(Rp) is the time complexity of RBF-OLS, where R is the number of all the candidate regressors, p represents the number of steps set in the algorithm.

Table 21 shows the overall computational times of these algorithms on the six benchmark datasets, which are also obtained by averaging the results of twenty repeated experiments. Combining the results in Table 21 and the time complexities of the comparative algorithms, the following conclusions could be drawn easily. SL-CCRNN, CCRNN-NL and DIL have similar time complexities, and their running times are also relatively close. However, the predictive performance of the DIL algorithm is much better than either of them. The time complexities of LLNF-LoLiMot and CICC-two-island are higher than DIL, and, correspondingly, their running times are much longer than DIL. Moreover, the predictive performance of DIL is better than both of them. This situation shows that, DIL is superior to the two comparative algorithms in both efficiency and performance. For RBF-OLS algorithm, its time complexity is lower than DIL, and its running time is also shorter than DIL. However, as you can see from Tables 15, 16, 17, 18, 19 and 20, DIL’s predictive performance is better than RBF-OLS.

Table 21 Comparison of the average run times (s) of the corresponding algorithms on the six benchmark datasets over 20 repetitive runs

5 Conclusions and future works

In this paper, a novel integrated algorithm, i.e., the DIL algorithm, with promising performance for TSP is presented, where incremental SVM is employed as the base leaner. In the first stage of DIL, several base models are generated, with each one generated based on a respective training data subset. Then, during training, the weighted majority voting method is used to combine the base models into a composite model. According to the composite model, the weight of one specific sample is updated by using a novel weight update rule. Finally, after all the base models have been learnt using all the training subsets, again, the weighted majority voting technique is utilized to combine them to get the final composite model. In the DIL algorithm, the most critical part is the weight update rule, which is a brand-new and powerful rule. This rule has made a great contribution to the improvement of algorithm performance.

The previous description about the advantages of DIL, including promising performance, desirable robustness, and high stability, has been fully testified in the experimental part. In addition, as mentioned earlier, since DIL saves all the trained base models, the trained historical data can be discarded, so that the storage space will be saved. These characteristics indicate that, the proposed DIL model has a broad prospect in its application to TSP problems.

Compared with some of the other excellent algorithms in the literatures, the experimental results on six benchmark time series datasets, including two synthetic and four real-world datasets, fully confirm the superiority of the DIL algorithm.

With regard to the outlook for future works, firstly, the research of this work is only focused on single-step TSP problems, while in the future, our research work can be extended to multi-step TSP ones. Besides, in this work, the parameters of DIL are determined by the trial-and-error method, while in the future, we will consider the design of self-adaptive parameters for the implementation of the algorithm. Moreover, the proposed algorithm involves the generation of multiple base models. However, ensemble pruning techniques have not been employed. Therefore, in the future, we will appropriately incorporate ensemble pruning techniques into our developed algorithm to further boost its efficiency and efficacy.