An accurate numerical method and its analysis for time-fractional Fisher’s equation

Abstract

This article aims to develop an optimal superconvergent numerical method for approximating the solution of the nonlinear time-fractional generalized Fisher’s (TFGF) equation. The time-fractional derivative in the model problem is considered in the sense of Caputo and is approximated using the $L2-1_{\sigma }$ scheme. Spatial discretization is performed using an optimal superconvergent quintic B-spline (OSQB) technique. To derive the method, a high-order perturbation of the semi-discretized equation of the original problem is generated using spline alternate relations. Convergence and stability of the method are analyzed, demonstrating that the method converges with $O(\Delta t^{2}+\Delta x^6)$, where $\Delta x$ and $\Delta t$ are step sizes in space and time, respectively. Three numerical examples are provided to demonstrate the robustness of the proposed method. Our method is compared with an existing method in the literature and the elapsed computational time for the present scheme is provided.

1 Introduction

In the present study, we consider the following nonlinear TFGF equation:

$$\begin{aligned}&\frac{\partial ^{\alpha } u(x,t)}{\partial t^{\alpha }} - u(x,t)\left( 1-u^{\beta }(x,t)\right) - \nu \frac{\partial ^{2} u(x,t)}{\partial x^{2}}\nonumber \\ {}&\quad = f(x,t), \end{aligned}$$

(1)

where $(x,t)\in \left( X_l,X_r\right) \times \left( 0,T\right) , \alpha \in (0,1).$ The above problem subjected to the initial condition (IC)

$$\begin{aligned} u(x,0)={\tilde{\mu }}(x),\, X_l\le x\le X_r \end{aligned}$$

(2)

and the boundary conditions (BCs)

$$\begin{aligned} u(X_l,t)={g}_{1}(t),\;u(X_r,t)={g}_{2}(t). \; \end{aligned}$$

(3)

Here, $\beta >0$ is an integer and $\nu$ is a viscosity parameter. The functions $f(x,t),\, {{\tilde{\mu }}}(x),\, g_{1}(t)$ and $g_{2}(t)$ are sufficiently smooth. We define the fractional derivative $\frac{\partial ^{\alpha } u(x,t)}{\partial t^{\alpha }}$ in (1) in the sense of Caputo:

$$\begin{aligned}{} & {} \frac{\partial ^{\alpha } u(x,t)}{\partial t^{\alpha }}\\ {}{} & {} \quad =\frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}(t-\phi )^{-\alpha }\frac{\partial u(x,\phi )}{\partial \phi }d\phi , \, 0<\alpha <1. \end{aligned}$$

In recent years, fractional differential equations (FDEs) have gained much attention among researchers due to their wide range of applications in applied sciences and engineering. For more details, one may refer to Podlubny (1999); Giona et al. (1992); Mainardi (1997); Bagley and Torvik (1984); Roul et al. (2021, 2022); Veeresha et al. (2020); Kumar et al. (2020); Roul (2020) and references therein. The fractional order derivatives can model complex phenomena in a better manner than the integer order derivatives.

The study of the nonlinear Fisher’s equation has attracted much attention from researchers worldwide. This equation is found in various contexts, such as modeling the spread of a viral mutant, neutron population dynamics in atomic reactors, and the proliferation of flames. Analytic solutions for most Fractional Differential Equations (FDEs) cannot be obtained explicitly, necessitating the adaptation of numerical techniques for their solutions. Numerical techniques for solving time fractional parabolic differential equations, pertinent to reaction-diffusion or convection-diffusion processes, are discussed in several works (Roul and Rohil 2022; Hamou et al. 2022; Roul and Rohil 2023; Hamou et al. 2023). Several techniques have been developed for the time-fractional Fisher’s (TFF) equation. For instance, Gupta et al. (2014) presented a numerical technique based on Haar wavelets and the Optimal Homotopy Asymptotic Method (OHAM) for approximating the solution of Burgers’ and generalized Fisher’s equations. The authors of Cherif et al. (2016) implemented the classical Homotopy Perturbation Method (HPM) for solving the space-fractional Fisher’s equation. Using the Fractional Natural Decomposition Method (FNDM), Rawashdeh (2016) obtained approximate and analytical solutions for two nonlinear FDEs, namely the time-fractional Harry Dym equation and the nonlinear TFF equation. Qurashi et al. (2017) implemented the Residual Power Series Method (RPSM) to find a series solution for the nonlinear TFF equation. Khader and Saad (2018) introduced a numerical scheme for solving the space-fractional Fisher’s equation using the spectral collocation method based on Chebyshev approximations. Majeed et al. (2020) developed a numerical technique based on cubic B-spline (CS) basis functions for TFF and Burgers’ equations. This method uses the L1 formula to approximate the Caputo fractional derivative and third-degree basis spline functions based on the Crank-Nicolson scheme for space derivatives. Additionally, a numerical scheme based on the L1 formula and the CS basis functions is presented for solving the TFGF equation (Majeed et al. 2020). Wazwaz and Gorguis (2004) obtained the series solution of the integer-order Fisher’s equation using the Adomian Decomposition Method. Recently, Tamboli and Tandel (2022) employed the Fractional Reduced Differential Transform Method (FRDTM) to solve the Time-Fractional Generalized Burger-Fisher Equation (TF-GBFE), demonstrating high accuracy through comparison with exact solutions and varying fractional orders. Choudhary et al. (2023) presented a high-order numerical scheme for the generalized time-fractional Fisher’s equation, utilizing Caputo fractional derivatives, Euler backward discretization, quasilinearization, and a compact finite difference scheme, achieving convergence of order four in space and $(2-\alpha )$ in time. Numerical methods available in the literature for time-fractional problems are typically based on the classical L1 formula, converging with an order $O(\Delta t^{2-\alpha })$. Gao et al. (2014) developed the $L1-2$ formula for approximating the Caputo fractional derivative. Roul and Rohil (2022) proposed a numerical scheme for the nonlinear TFGF equation, employing the Caputo fractional derivative of order $\alpha$ approximated using the $L1-2$ scheme, along with space derivative discretization using a collocation method based on quintic B-spline (QBS) basis functions, establishing convergence analysis with the method achieving convergence of order four in space and two in time. Recently, Alikhanov (2015) introduced a new $L2-1_{\sigma }$ scheme for approximating the Caputo fractional derivative. Numerical methods for one or two-dimensional time-fractional problems based on this scheme can be found in recent articles (Roul and Rohil 2022, 2023).

Our main objective is to develop a higher-order numerical method for solving the TFGF equation subject to initial and boundary conditions. The proposed method is based on the $L2-1_{\sigma }$ scheme for discretization of the temporal fractional derivative and the OSQB method for discretization of the spatial derivative. To derive the method, a high-order perturbation of the semi-discretized equation of the original problem is generated using spline alternate relations. The convergence and stability of this scheme are studied, proving sixth-order convergence in space and second-order convergence in time. The results of our method are compared with those of a previous method proposed by Majeed et al. (2020). To the best of our knowledge, this scheme has not been considered in the literature for the numerical approximation of the TFGF equation.

The balance of this paper is organized as follows: In Sect. 2, the proposed method is developed for the problem (1)–(3). Stability and convergence analysis of the proposed scheme are presented in Sect. 3. Numerical results are presented in Sect. 4. Finally, the conclusions are discussed in Sect. 5.

2 Description of numerical scheme

This section is devoted to the derivation of our proposed numerical scheme for the solution of the TFGF Eq. (1) with IC (2) and BCs (3).

2.1 Time discretization

We first discretize the problem (1)–(3) with respect to the time variable over [0, T]. Let $N\ge 1$ be an integer and define $t_n=n \Delta t$ with $0\le n\le N$, where $\Delta t=\frac{T}{N}$ is the step size. Let $\sigma =1-\frac{\alpha }{2}$ and denote $t_{n-1+\sigma }=(n-1+\sigma )\Delta t$.

By means of the $L2-1_{\sigma }$ scheme, the Caputo time-fractional derivative in (1) is descretized at $t=t_{n-1+\sigma }$ as Alikhanov (2015)

$$\begin{aligned}&\frac{\partial ^{\alpha } u(x,t_{n-1+\sigma })}{\partial t^{\alpha }}\nonumber \\&\quad =\frac{\Delta t^{-\alpha }}{\Gamma (2-\alpha )}\bigg [c_0^{\alpha }u(x,t_n) -\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u(x,t_l)\nonumber \\&\qquad -c^{\alpha }_{n-1}u(x,t_0)\bigg ]+O(\Delta t^{3-\alpha }), \quad n\ge 1, \end{aligned}$$

(4)

where $\text {for } n=1$, $c_0^{\alpha }=a_0^{\alpha }$ and for $n\ge 2$

$$\begin{aligned} c_l^{\alpha }= {\left\{ \begin{array}{ll} a_0^{\alpha }+b_1^{\alpha }, &{}l=0,\\ a_l^{\alpha }+b_{l+1}^{\alpha }-b_{l}^{\alpha }, &{}1\le l\le n-2,\\ a_l^{\alpha }-b_{l}^{\alpha },&{} l=n-1, \end{array}\right. } \end{aligned}$$

(5)

in which

$$\begin{aligned} a_0^{\alpha }&=\sigma ^{1-\alpha }, \quad a_{l}^{\alpha }=(l+\sigma )^{1-\alpha }-(l-1+\sigma )^{1-\alpha },\quad l\ge 1\,,\\ b_{l}^{\alpha }&=\frac{1}{2-\alpha }\left[ (l+\sigma )^{2-\alpha }-(l-1+\sigma )^{2-\alpha }\right] \\&\quad -\frac{1}{2}\left[ (l+\sigma )^{1-\alpha }+(l-1+\sigma )^{1-\alpha }\right] ,\,l\ge 1. \end{aligned}$$

The truncation error $O(\Delta t^{3-\alpha })$ in (4) can be obtained by assuming that $u(\cdot ,t) \in C^3([0, T ])$.

Lemma 1

(Alikhanov 2015) The coefficients $c^{\alpha }_l,$ $0<\alpha <1,$ satisfy

• (1) $c^{\alpha }_l>\frac{1-\alpha }{2}(l+\sigma )^{-\alpha }\ge 0,\; l\ge 0,$

• (2) $c^{\alpha }_{l-1}>c^{\alpha }_{l}, \;l\ge 1.$

Denote $u(x,t_n)=u^n(x).$ Considering (1) at $t=t_{n-1+\sigma }$ yields

$$\begin{aligned} \begin{aligned}&\frac{\partial ^{\alpha } u^{n-1+\sigma }(x)}{\partial t^{\alpha }}- u^{n-1+\sigma }(x)\left( 1-\left( u^{n-1+\sigma }(x)\right) ^{\beta }\right) \\&\quad -\nu \frac{\partial ^{2} u^{n-1+\sigma }(x)}{\partial x^2}= f^{n-1+\sigma }(x), \\&\quad X_l<x<X_r, \, n=1,2,\dots , N. \end{aligned} \end{aligned}$$

(6)

By using Eq. (4), from (6) we have

$$\begin{aligned} \begin{aligned}&\frac{\Delta t^{-\alpha }}{\Gamma (2-\alpha )}\\ {}&\quad \left[ c_0^{\alpha }u^n(x)-\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)-c^{\alpha }_{n-1}u^{0}(x)\right] \\&\quad - u^{n-1+\sigma }(x)\left( 1-\left( u^{n-1+\sigma }(x)\right) ^{\beta }\right) \\&\quad - \nu u_{xx}^{n-1+\sigma }(x) = f^{n-1+\sigma }(x)+O(\Delta t^{3-\alpha }),\quad \\ {}&\quad X_l<x<X_r, \quad n\ge 1. \end{aligned} \end{aligned}$$

(7)

Now using the Taylor’s series expansion, we can easily obtain the following:

$$\begin{aligned} u^{n-1+\sigma }(x)= & {} \sigma u^{n}(x)+(1-\sigma ) u^{n-1}(x)+O(\Delta t^{2}),\nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned} u_{xx}^{n-1+\sigma }(x)= & {} \sigma u_{xx}^{n}(x)+(1-\sigma ) u_{xx}^{n-1}(x)+O(\Delta t^{2}),\nonumber \\ \end{aligned}$$

(9)

$$\begin{aligned} \left( u^{n-1+\sigma }(x)\right) ^{\beta }= & {} \sigma \left( u^{n}(x)\right) ^{\beta }\nonumber \\{} & {} +(1-\sigma )\left( u^{n-1}(x)\right) ^{\beta }+O(\Delta t^{2}). \end{aligned}$$

(10)

Making use of (8), (9) and (10) in (7) and rearranging the terms, we obtain

$$\begin{aligned} \begin{aligned}&P_{\alpha } c_0^{\alpha }u^n(x)-\sigma u^{n}(x)+\sigma \left( u^{n}(x)\right) ^{\beta +1}-\sigma \nu u_{xx}^{n}(x)\\&\quad =P_{\alpha }\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)\\&\qquad +P_{\alpha } c^{\alpha }_{n-1}u^{0}(x)+(1-\sigma ) u^{n-1}(x)\\&\qquad -(1-\sigma )\left( u^{n-1}(x)\right) ^{\beta +1}+(1-\sigma )\nu u_{xx}^{n-1}(x)\\&\quad \quad +f^{n-1+\sigma }(x)+O(\Delta t^{2}),X_l<x<X_r, \, n\ge 1, \end{aligned} \end{aligned}$$

(11)

where $P_{\alpha }=\frac{\Delta t^{-\alpha }}{\Gamma (2-\alpha )}.$

Table 1 The values of basis functions $\Theta _{k}(x)$, $\Theta _{k}'(x)$ and $\Theta _{k}''(x)$

We use the following formula to linearize the non-linear term (Rubin and Graves 1975):

$$\begin{aligned}{} & {} \left( u^n(x)\right) ^{\beta }\nonumber \\ {}{} & {} \quad =\beta \left( u^{n-1}(x)\right) ^{\beta -1}u^n(x)-(\beta -1)\left( u^{n-1}(x)\right) ^{\beta }. \end{aligned}$$

(12)

Making use of (12) into (11) and rearranging the terms, we obtain

$$\begin{aligned} \begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( u^{n-1}(x)\right) ^{\beta }\right] u^{n}(x)-\sigma \nu u_{xx}^{n}(x)\\&\quad =P_{\alpha }\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)\\&\qquad +P_{\alpha } c^{\alpha }_{n-1}u^{0}(x)-\left[ 1-\sigma (\beta +1)\right] \left( u^{n-1}(x)\right) ^{\beta +1}\\&\qquad +(1-\sigma ) u^{n-1}(x)\\&\quad \quad +(1-\sigma )\nu u_{xx}^{n-1}(x)+f^{n-1+\sigma }(x)\\&\qquad +O(\Delta t^{2}),\, X_l<x<X_r, \, n\ge 1, \end{aligned} \end{aligned}$$

(13)

with IC

$$\begin{aligned} u(x,t_0)=u^0(x)={\tilde{\mu }}(x),\quad X_l<x<X_r \end{aligned}$$

(14)

and BCs

$$\begin{aligned}{} & {} u(X_l,t_n)=u^{n}(X_l)={g}_{1}(t_n),\;\nonumber \\ {}{} & {} u(X_r,t_n)=u^{n}(X_r)={g}_{2}(t_n). \end{aligned}$$

(15)

2.2 Space discretization

Here, we discretize (13)–(15) with respect to space variable using an OSQB scheme.

2.2.1 Quintic spline interpolation

In this subsection, we define quintic spline (QS) interpolant and derive several asymptotic relations that will be used in the formulation and the theoretical analysis of the proposed method.

Let $M\ge 1$ and $I=\bigl \{X_l = x_0<x_1<\dots < x_{M} = X_r\bigr \}$ denotes the uniform partition of the domain $\left[ X_l,X_r\right]$, where $x_{m}=m\Delta x,\,\,m=0,1,...,M$ and $\Delta x$ is the spatial step size. We consider the set of midpoints as ${\pi }_I = \{\tau _{1}<\tau _{2}<...<\tau _{M}\},$ where $\tau _{m}=\frac{x_{m-1}+x_{m}}{2}, m=1,2,...,M$. Let $S_{5,I} = \{q(x)| q(x)\in {\mathbb {C}}^4[X_l, X_r]$} be the quintic spline space (QSS). The QBS basis functions, $\Theta _{k}(x)$, $-2 \le k \le M+2$, for $S_{5,I}$ are given by De Boor (1978):

$$\begin{aligned} \Theta _{k}(x) = {\left\{ \begin{array}{ll} {\mathcal {G}}(x-x_{k-3})=a_1,\, &{} x\in [x_{k-3},x_{k-2}] \\ a_1-6{\mathcal {G}}(x-x_{k-2})=a_2,\, &{} x\in [x_{k-2},x_{k-1}] \\ a_2+15{\mathcal {G}}(x-x_{k-1}),\, &{} x\in [x_{k-1},x_{k}]\\ b_2+15{\mathcal {G}}(x_{k+1}-x), \, &{} x\in [x_{k},x_{k+1}]\\ b_1-6{\mathcal {G}}(x_{k+2}-x)=b_2, \,&{} x\in [x_{k+1},x_{k+2}]\\ {\mathcal {G}}(x_{k+3}-x)=b_1, \,&{} x\in [x_{k+2},x_{k+3}]\\ 0, \quad &{} \text {otherwise}, \end{array}\right. }\nonumber \\ \end{aligned}$$

(16)

with ${\mathcal {G}}(x)=\frac{x^5}{120\Delta x^{5}}$.

In order to facilitate the QBS basis functions, ten additional grid points as $x_{-5}<x_{-4}<x_{-3}<x_{-2}<x_{-1}<x_{0}=X_l$ and $x_{M}=X_r<x_{M+1}<x_{M+2}<x_{M+3}<x_{M+4}<x_{M+5}$, are considered outside the interval I. Let $\tilde{\Theta }=\{\Theta _{-2}(x), \Theta _{-1}(x), \Theta _{0}(x),..., \Theta _M(x),$ $\Theta _{M+1}(x), \Theta _{M+2}(x)\}$ be the set of QBS functions. All $\Theta _i(x)$ are linearly independent. Let $\Theta ^*(I)$ = span ${\tilde{\Theta }}$. Then, $\Theta ^*(I)$ is a QSS with dimension $M+5$. Observe that $\Theta ^*(I)=S_{5,I}$ (Prenter 1975). Thus, $S_{5,I}$ generates a QSS on I.

Let ${\mathcal {Z}}^{n}(x)\in S_{5,I}$ be the approximate solution of the exact solution $u^{n}(x)$ of (13)–(15), which is given by

$$\begin{aligned} {\mathcal {Z}}^n(x)=\sum _{k=-2}^{M+2}{\lambda }_{k}^{n}\Theta _{k}(x), \end{aligned}$$

(17)

where ${\mathcal {Z}}^n(x)$ satisfies the following interpolating conditions:

$$\begin{aligned} {\mathcal {Z}}^n(x_m)= & {} u_n(x_m),\hspace{0.1cm} \text {for}\hspace{0.1cm} m=0,1,...,M, \end{aligned}$$

(18)

$$\begin{aligned} {\mathcal {Z}}^n_{xxxx}(x_m)= & {} u^n_{xxxx}(x_m)-\frac{\Delta x^2}{12}u^n_{xxxxxx}(x_m)\nonumber \\{} & {} \quad +\frac{\Delta x^4}{240}u^n_{xxxxxxxx}(x_m),\hspace{0.1cm}\nonumber \\{} & {} \qquad \text {for}\hspace{0.1cm} m=0,1,M-1,M. \end{aligned}$$

(19)

The values of ${\mathcal {Z}}^n(x)$ and its first and second derivatives are obtained using (16) at the nodal points $x_m (0\le m\le M)$ and midpoints $\tau _{m} (1\le m\le M)$ as given in Table 1. With the help of Table 1, we get:

$$\begin{aligned} {\mathcal {Z}}^n(x_m)= & {} \frac{1}{120}\left( {\lambda }_{m-2}^n+26{\lambda }_{m-1}^n+66{\lambda }_{m}^n+26{\lambda }_{m+1}^n+{\lambda }_{m+2}^n\right) ,\nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned} {\mathcal {Z}}_{x}^n(x_m)= & {} \frac{1}{24\Delta x}\left( -{\lambda }_{m-2}^n-10{\lambda }_{m-1}^n+10{\lambda }_{m+1}^n+{\lambda }_{m+2}^n\right) ,\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned} {\mathcal {Z}}_{xx}^n(x_m)= & {} \frac{1}{6\Delta x^2}\left( {\lambda }_{m-2}^n+2{\lambda }_{m-1}^n-6{\lambda }_{m}^n+2{\lambda }_{m+1}^n+{\lambda }_{m+2}^n\right) ,\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned} {\mathcal {Z}}^n(\tau _m)= & {} \frac{1}{3840}\big ({\lambda }_{m-3}^n+237{\lambda }_{m-2}^n+1682{\lambda }_{m-1}^n\nonumber \\{} & {} +1682{\lambda }_{m}^n+237{\lambda }_{m+1}^n+{\lambda }_{m+2}^n\big ), \end{aligned}$$

(23)

$$\begin{aligned} {\mathcal {Z}}_{x}^n(\tau _m)= & {} \frac{1}{384 \Delta x}\big (-{\lambda }_{m-3}^n-75{\lambda }_{m-2}^n-154{\lambda }_{m-1}^n+154{\lambda }_{m}^n\nonumber \\{} & {} +75{\lambda }_{m+1}^n+{\lambda }_{m+2}^n\big ), \end{aligned}$$

(24)

$$\begin{aligned} {\mathcal {Z}}_{xx}^n(\tau _m)= & {} \frac{1}{48\Delta x^2}\left( {\lambda }_{m-3}^n+21{\lambda }_{m-2}^n-22{\lambda }_{m-1}^n \right. \nonumber \\{} & {} \left. -22{\lambda }_{m}^n+21{\lambda }_{m+1}^n+{\lambda }_{m+2}^n\right) . \end{aligned}$$

(25)

Theorem 1

Let ${\mathcal {Z}}^n(x)$ be the quintic spline interpolant (QSI) of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$. Then, for $x_{m}, 0\le m \le M,$ we have (see Theorem 2 of (Roul 2020))

$$\begin{aligned} {\mathcal {Z}}_{x}^n(x_{m})= & {} u_{x}^n(x_{m})+O({\Delta x}^{6}), \end{aligned}$$

(26)

$$\begin{aligned} {\mathcal {Z}}_{xx}^n(x_{m})= & {} u_{xx}^n(x_{m})+\frac{{\Delta x}^{4}}{720}u_{xxxxxx}^n(x_{m})+O({\Delta x}^{6}). \end{aligned}$$

(27)

Theorem 2

Let ${\mathcal {Z}}^n(x)$ be the QSI of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$. Then for ${\tau }_{m}, 1\le m \le M,$ we have

$$\begin{aligned} {\mathcal {Z}}_{x}^n({\tau }_{m})= & {} u_{x}^n({\tau }_{m})+O({\Delta x}^{6}), \end{aligned}$$

(28)

$$\begin{aligned} {\mathcal {Z}}_{xx}^n({\tau }_{m})= & {} u_{xx}^n({\tau }_{m})-\frac{7{\Delta x}^{4}}{5760}u_{xxxxxx}^n({\tau }_{m})+O({\Delta x}^{6}). \end{aligned}$$

(29)

Proof

This proof follows the same arguments as used in the proof of Theorem 2 of Roul (2020). $\square$

Theorem 3

Let ${\mathcal {Z}}^n(x)\in S_{5,I}$ be the QS interpolant of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$. Then, we have (see Theorem 3 of Roul (2020)):

$$\begin{aligned} \Vert D^{p}({\mathcal {Z}}^n(x)-u^n(x))\Vert _{\infty }\le {\mathcal {M}}\Delta x^{6-p},\; p=0,1,2, \end{aligned}$$

where $D^{p}=\frac{\partial ^p}{\partial x^p}.$

We define the difference operators $\delta$ and $\delta ^2$ as follows:

$$\begin{aligned} \delta g_m= & {} g_{m-1}-2g_m+g_{m+1},\hspace{0.1cm}m=1,2,...,M-1, \end{aligned}$$

(30)

$$\begin{aligned} \delta ^2 g_m= & {} g_{m-2}-4g_{m-1}+6g_m-4g_{m+1}\nonumber \\{} & {} +g_{m+2},\hspace{0.1cm}m=2,3,...,M-2. \end{aligned}$$

(31)

Lemma 2

Let ${\mathcal {Z}}^n(x)\in S_{5,I}$ be the QS interpolant of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$ that satisfies the interpolation conditions (18) and (19). Then, we have

$$\begin{aligned}{} & {} u_{xxxxxx}^n({x}_{m})\nonumber \\ {}{} & {} \quad =\frac{1}{\Delta x^4}\delta ^2 {\mathcal {Z}}_{xx}^n({x}_{m})+O({\Delta x}^{2}),\hspace{0.1cm} m=2,3,...,M-2.\nonumber \\ \end{aligned}$$

(32)

Proof

From (27), we have

$$\begin{aligned} \frac{{\mathcal {Z}}_{xx}^n(x_{m})}{{\Delta x}^{4}}=\frac{u_{xx}^n(x_{m})}{{\Delta x}^{4}}+\frac{1}{720}u_{xxxxxx}^n(x_{m})+O({\Delta x}^{2}). \end{aligned}$$

(33)

Applying the operator $\delta ^2$ defined in (31) on both sides of (33), we get

$$\begin{aligned} \frac{{\delta ^2 {\mathcal {Z}}}_{xx}^n(x_{m})}{{\Delta x}^{4}}= & {} \frac{\delta ^2 u_{xx}^n(x_{m})}{{\Delta x}^{4}}\nonumber \\ {}{} & {} +\frac{1}{720}\delta ^2 u_{xxxxxx}^n(x_{m})+O({\Delta x}^{2}). \end{aligned}$$

(34)

Using Taylor’s expansion on the right side of (34) and then simplifying we can obtain that

$$\begin{aligned}{} & {} \frac{1}{\Delta x^4}\delta ^2 {\mathcal {Z}}_{xx}^n({x}_{m})\\ {}{} & {} \quad = u_{xxxxxx}^n({x}_{m})+O({\Delta x}^{2}),\hspace{0.1cm} m=2,3,...,M-2. \end{aligned}$$

Corollary 1

If $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$, then the following approximations hold at the grid points $x_m$:

$$\begin{aligned} u_{x}^n(x_{m})= & {} {\mathcal {Z}}_{x}^n(x_{m})+O({\Delta x}^{6}),\hspace{0.1cm}m=0,1,...,M, \end{aligned}$$

(35)

$$\begin{aligned} u_{xx}^n(x_{m})= & {} {\mathcal {Z}}_{xx}^n(x_{m})- \frac{\delta ^2 {\mathcal {Z}}_{xx}^n(x_{m})}{720}\nonumber \\{} & {} +O({\Delta x}^{6}),\hspace{0.1cm}m=2,3,...,M-2. \end{aligned}$$

(36)

Proof

We can easily obtain the relation (35) from (26). To prove the relation (36), we substitute the value of $u_{xxxxxx}^n(x_{m})$ from (32) in (27). Thus, we have

$$\begin{aligned} {\mathcal {Z}}_{xx}^n(x_{m})= & {} u_{xx}^n(x_{m})+ \frac{\delta ^2 {\mathcal {Z}}_{xx}^n(x_{m})}{720}\\{} & {} +O({\Delta x}^{6}),\hspace{0.1cm}m=2,3,...,M-2. \end{aligned}$$

$\square$

Lemma 3

Let ${\mathcal {Z}}^n(x)\in S_{5,I}$ be the QS interpolant of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$ and it satisfies the interpolation conditions (18) and (19). Then the following relations hold near the left boundary points $(x_0, x_1)$ and the right boundary points $(x_{M-1}, x_M)$:

$$\begin{aligned} u_{xxxxxx}^n(x_{m})= & {} \frac{(3-m)\delta ^2{\mathcal {Z}}^n_{xx}(x_2)-(2-m)\delta ^2{\mathcal {Z}}^n_{xx}(x_3)}{\Delta x^4}\nonumber \\{} & {} +O(\Delta x^2),\hspace{0.1cm} m=0,1, \end{aligned}$$

(37)

$$\begin{aligned} u_{xxxxxx}^n(x_{m})= & {} \frac{(3-\lambda )\delta ^2{\mathcal {Z}}^n_{xx}(x_{M-2})-(2-\lambda )\delta ^2{\mathcal {Z}}^n_{xx}(x_{M-3})}{\Delta x^4}\nonumber \\{} & {} +O(\Delta x^2),\hspace{0.1cm} (m,\lambda )=(M-1,1),(M,0).\nonumber \\ \end{aligned}$$

(38)

Proof

First we prove (37) for $m=1$. We consider the approximation for $u_{xxxxxx}^n(x_{1})$ as follows

$$\begin{aligned} u_{xxxxxx}^n(x_{1})=2u_{xxxxxx}^n(x_{2})-u_{xxxxxx}^n(x_{3}). \end{aligned}$$

(39)

Using (32) for $m=2,3$ in above equation, we get

$$\begin{aligned} u_{xxxxxx}^n(x_{1})=\frac{2\delta ^2{\mathcal {Z}}^n_{xx}(x_{2})-\delta ^2{\mathcal {Z}}^n_{xx}(x_{3})}{\Delta x^4}+O(\Delta x^2). \end{aligned}$$

(40)

Hence, the relation (37) is obtained for $m=1$.

To prove (37) for $m=0,$ we consider an approximation for $u_{xxxxxx}^n(x_{0})$ as follows

$$\begin{aligned} u_{xxxxxx}^n(x_{0})=2u_{xxxxxx}^n(x_{1})-u_{xxxxxx}^n(x_{2}). \end{aligned}$$

(41)

By using (40) and (32) for $m=2$ in (41), we obtain

$$\begin{aligned} u_{xxxxxx}^n(x_{0})=\frac{3\delta ^2{\mathcal {Z}}^n_{xx}(x_{2})-2\delta ^2{\mathcal {Z}}^n_{xx}(x_{3})}{\Delta x^4}+O(\Delta x^2). \end{aligned}$$

Hence, relation (37) for $m=0$ is obtained. In a similar way, we can prove relation (38). $\square$

Lemma 4

Let ${\mathcal {Z}}^n(x)\in S_{5,I}$ be the QS interpolant of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$ and it satisfies the interpolation conditions (18) and (19). Then the following relations hold near the left boundary midpoint $\tau _1$ and the right boundary midpoint $\tau _M$:

$$\begin{aligned} u_{xxxxxx}^n(\tau _{1})= & {} \frac{5\delta ^2{\mathcal {Z}}^n_{xx}(x_2)-3\delta ^2{\mathcal {Z}}^n_{xx}(x_3)}{2\Delta x^4}+O(\Delta x^2), \end{aligned}$$

(42)

$$\begin{aligned} u_{xxxxxx}^n(\tau _{M})= & {} \frac{5\delta ^2{\mathcal {Z}}^n_{xx}(x_{M-2})-3\delta ^2{\mathcal {Z}}^n_{xx}(x_{M-3})}{2\Delta x^4}\nonumber \\ {}{} & {} +O(\Delta x^2).\nonumber \\ \end{aligned}$$

(43)

Proof

First we prove (42). For the purpose, we consider an approximation for $u_{xxxxxx}^n(\tau _{1})$ as follows

$$\begin{aligned} u_{xxxxxx}^n(\tau _{1})=\frac{3u_{xxxxxx}^n(x_{1})-u_{xxxxxx}^n(x_{2})}{2}. \end{aligned}$$

Using (37) for $m=1$ and (32) for $m=2$ in the above equation produces

$$\begin{aligned} u_{xxxxxx}^n(\tau _{1})=\frac{5\delta ^2{\mathcal {Z}}^n_{xx}(x_{2})-3\delta ^2{\mathcal {Z}}^n_{xx}(x_{3})}{2\Delta x^4}+O(\Delta x^2). \end{aligned}$$

Hence, relation (42) is obtained. In a similar way, we can prove (43). $\square$

2.2.2 Fully discrete scheme based on an OSQB method

Here, by means of the optimal quintic B-spline collocation method, we discretize Eqs. (13)–(15) with respect to space variable.

At the grid points $x_{m}$, (13) is discretized as

$$\begin{aligned} \begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( u^{n-1}(x_m)\right) ^{\beta }\right] u^{n}(x_m)-\sigma \nu u_{xx}^{n}(x_m)\\&=P_{\alpha }\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x_m)\\&\quad +P_{\alpha } c^{\alpha }_{n-1}u^{0}(x_m)-\left[ 1-\sigma (\beta +1)\right] \left( u^{n-1}(x_m)\right) ^{\beta +1}\\&\quad +(1-\sigma ) u^{n-1}(x_m)\\&\quad +(1-\sigma )\nu u_{xx}^{n-1}(x_m)\\&\quad +f^{n-1+\sigma }(x_m)+O(\Delta t^{2}),\quad m=0,1,\dots ,M, \, \, n\ge 1. \end{aligned} \end{aligned}$$

(44)

The discretized BCs (3) are

$$\begin{aligned} u^{n}(x_{0})={g}_{1}(t_{n}),\;u^{n}(x_{M})={g}_{2}(t_{n}). \end{aligned}$$

(45)

By using (18) and (26)–(27) in (44), we obtain

$$\begin{aligned} \begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(x_m)\right) ^{\beta }\right] {\mathcal {Z}}^{n}(x_m)\\&\quad -\sigma \nu \left( {\mathcal {Z}}^{n}_{xx}(x_m)-\frac{\Delta x^4}{720}u^{n}_{xxxxxx}(x_m)+O(\Delta x^6)\right) \\&=\phi _{m}^{n-1}+O(\Delta t^{2}),\quad m=0,1,\dots ,M, \, \, n\ge 1, \end{aligned} \end{aligned}$$

(46)

where

$$\begin{aligned} \begin{aligned} \phi _{m}^{n-1}&=P_{\alpha } \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) {\mathcal {Z}}^l(x_m)+P_{\alpha } c^{\alpha }_{n-1}{\mathcal {Z}}^0(x_m)\\&\quad -\left[ 1-\sigma (\beta +1)\right] \left( {\mathcal {Z}}^{n-1}(x_m)\right) ^{\beta +1}\\&\quad +(1-\sigma ) {\mathcal {Z}}^{n-1}(x_m)+(1-\sigma )\nu \\&\quad \left( {\mathcal {Z}}^{n-1}_{xx}(x_m)-\frac{\Delta x^4}{720}u^{n-1}_{xxxxxx}(x_m)+O(\Delta x^6)\right) \\ {}&\quad +f^{n-1+\sigma }(x_m). \end{aligned} \end{aligned}$$

In views of Lemma 2, Lemma 3 and ignoring the $O(\Delta t^{2})$ terms, from Eq. (46) we have

$$\begin{aligned}&\begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(x_0)\right) ^{\beta }\right] \\&\quad {\mathcal {Z}}^{n}(x_0)-\frac{\sigma \nu }{720}(717{\mathcal {Z}}^{n}_{xx}(x_0)+14{\mathcal {Z}}^{n}_{xx}(x_1)-26{\mathcal {Z}}^{n}_{xx}(x_2)\\&\quad +24{\mathcal {Z}}^{n}_{xx}(x_3)-11{\mathcal {Z}}^{n}_{xx}(x_4)+2{\mathcal {Z}}^{n}_{xx}(x_5))\\&=\phi _{0}^{n-1}+O\left( \Delta x^6\right) , \quad n=1,2,\dots , N, \end{aligned} \end{aligned}$$

(47)

$$\begin{aligned}&\begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(x_1)\right) ^{\beta }\right] \\&\quad {\mathcal {Z}}^{n}(x_1)-\frac{\sigma \nu }{720}(-2{\mathcal {Z}}^{n}_{xx}(x_0)+729{\mathcal {Z}}^{n}_{xx}(x_1)-16{\mathcal {Z}}^{n}_{xx}(x_2)\\&\quad +14{\mathcal {Z}}^{n}_{xx}(x_3)-6{\mathcal {Z}}^{n}_{xx}(x_4)+{\mathcal {Z}}^{n}_{xx}(x_5))\\&=\phi _{1}^{n-1}+O\left( \Delta x^6\right) , \quad n=1,2,\dots , N, \end{aligned} \end{aligned}$$

(48)

$$\begin{aligned}&\begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(x_m)\right) ^{\beta }\right] \\&\quad {\mathcal {Z}}^{n}(x_m)-\frac{\sigma \nu }{720}(-{\mathcal {Z}}^{n}_{xx}(x_{m-2})+4{\mathcal {Z}}^{n}_{xx}(x_{m-1})\\&\quad +714{\mathcal {Z}}^{n}_{xx}(x_{m})+4{\mathcal {Z}}^{n}_{xx}(x_{m+1})-{\mathcal {Z}}^{n}_{xx}(x_{m+2}))\\&\quad =\phi _{m}^{n-1}+O\left( \Delta x^6\right) , \quad \\&\quad n=1,2,\dots , N,\quad m=2,3,...,M-2, \end{aligned} \end{aligned}$$

(49)

$$\begin{aligned}&\begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(x_{M-1})\right) ^{\beta }\right] \\&\quad {\mathcal {Z}}^{n}(x_{M-1})-\frac{\sigma \nu }{720}({\mathcal {Z}}^{n}_{xx}(x_{M-5})\\ {}&\quad -6{\mathcal {Z}}^{n}_{xx}(x_{M-4})+14{\mathcal {Z}}^{n}_{xx}(x_{M-3})\\&\quad -16{\mathcal {Z}}^{n}_{xx}(x_{M-2})+729{\mathcal {Z}}^{n}_{xx}(x_{M-1})-2{\mathcal {Z}}^{n}_{xx}(x_{M}))\\&\quad =\phi _{M-1}^{n-1}+O\left( \Delta x^6\right) , \quad n=1,2,\dots , N, \end{aligned} \end{aligned}$$

(50)

$$\begin{aligned}&\begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(x_M)\right) ^{\beta }\right] \\&\quad {\mathcal {Z}}^{n}(x_{M})-\frac{\sigma \nu }{720}(2{\mathcal {Z}}^{n}_{xx}(x_{M-5})\\ {}&\quad -11{\mathcal {Z}}^{n}_{xx}(x_{M-4})+24{\mathcal {Z}}^{n}_{xx}(x_{M-3})\\&\quad -26{\mathcal {Z}}^{n}_{xx}(x_{M-2})+14{\mathcal {Z}}^{n}_{xx}(x_{M-1})+717{\mathcal {Z}}^{n}_{xx}(x_{M}))\\&\quad =\phi _{M}^{n-1}+O\left( \Delta x^6\right) , \quad n=1,2,\dots , N. \end{aligned} \end{aligned}$$

(51)

Taking into account (18), (26) and Lemma 3, it follows from (45) that

$$\begin{aligned} {\mathcal {Z}}^{n}(x_{0})= & {} {g}_{1}(t_{n}), \end{aligned}$$

(52)

$$\begin{aligned} {\mathcal {Z}}^{n}(x_{M})= & {} {g}_{2}(t_{n}). \end{aligned}$$

(53)

Equations (47)–(53) produce a linear system of $M+3$ equations having $M+5$ unknowns: ${\lambda }_{-2}^n, {\lambda }_{-1}^n, {\lambda }_{0}^n$, ...,  ${\lambda }_{M}^{n}, {\lambda }_{M+1}^n, {\lambda }_{M+2}^n$. To close this system, we require two more equations. For this purpose, we consider two auxiliary equations at the midpoints $x=\tau _1,\tau _M$. By using Eqs. (18), (28) and (29) in (44), we obtain

$$\begin{aligned} \begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(\tau _m)\right) ^{\beta }\right] {\mathcal {Z}}^{n}(\tau _m)\\&\quad -\sigma \nu \left( {\mathcal {Z}}^{n}_{xx}(\tau _m)+\frac{7\Delta x^4}{5760}u^{n}_{xxxxxx}(\tau _m)+O(\Delta x^6)\right) \\ {}&\quad =\tilde{\phi }_{m}^{n-1},\quad m=1,\,M, \, \, n\ge 1, \end{aligned}\nonumber \\ \end{aligned}$$

(54)

where

$$\begin{aligned} \begin{aligned} \tilde{\phi }_{m}^{n-1}&=P_{\alpha } \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) {\mathcal {Z}}^l(\tau _m)+P_{\alpha } c^{\alpha }_{n-1}{\mathcal {Z}}^0(\tau _m)\\&\quad -\left[ 1-\sigma (\beta +1)\right] \left( {\mathcal {Z}}^{n-1}(\tau _m)\right) ^{\beta +1}\\&\quad +(1-\sigma ) {\mathcal {Z}}^{n-1}(\tau _m)+(1-\sigma )\nu \\&\quad \left( {\mathcal {Z}}^{n-1}_{xx}(\tau _m)-\frac{\Delta x^4}{720}u^{n-1}_{xxxxxx}(\tau _m)+O(\Delta x^6)\right) \\ {}&\quad +f^{n-1+\sigma }(\tau _m). \end{aligned} \end{aligned}$$

In view of Lemma 4, from equation (54) we have

$$\begin{aligned}&\begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(\tau _1)\right) ^{\beta }\right] {\mathcal {Z}}^{n}(\tau _1)\\&\quad -\sigma \nu \Big ({\mathcal {Z}}^{n}_{xx}(\tau _1)+\frac{7}{11520}(5{\mathcal {Z}}^{n}_{xx}(x_0)-23{\mathcal {Z}}^{n}_{xx}(x_1)\\&\quad +42{\mathcal {Z}}^{n}_{xx}(x_2)-38{\mathcal {Z}}^{n}_{xx}(x_3)+17{\mathcal {Z}}^{n}_{xx}(x_4)-3{\mathcal {Z}}^{n}_{xx}(x_5))\Big )\\&\quad =\tilde{\phi }_{1}^{n-1}+O\left( \Delta x^6\right) , \quad n=1,2,\dots , N, \end{aligned} \end{aligned}$$

(55)

$$\begin{aligned}&\begin{aligned}&\left[ P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(\tau _M)\right) ^{\beta }\right] {\mathcal {Z}}^{n}(\tau _M)\\&\quad -\sigma \nu \Big ({\mathcal {Z}}^{n}_{xx}(\tau _M)+\frac{7}{11520}(-3{\mathcal {Z}}^{n}_{xx}(x_{M-5})+17{\mathcal {Z}}^{n}_{xx}(x_{M-4})\\&\quad -38{\mathcal {Z}}^{n}_{xx}(x_{M-3})+42{\mathcal {Z}}^{n}_{xx}(x_{M-2})-23{\mathcal {Z}}^{n}_{xx}(x_{M-1})+5{\mathcal {Z}}^{n}_{xx}(x_M))\Big )\\&\quad =\tilde{\phi }_{M}^{n-1}+O\left( \Delta x^6\right) , \quad n=1,2,\dots , N. \end{aligned} \end{aligned}$$

(56)

Let $\tilde{{\mathcal {Z}}}^n(x)$ denote the collocation approximation for the solution of (13)-(15) given by

$$\begin{aligned} \tilde{{\mathcal {Z}}}^n(x)=\sum _{k=-2}^{M+2}\tilde{\lambda }_{k}^{n}\Theta _{k}(x). \end{aligned}$$

(57)

We compute this approximation by satisfying the collocation equations defined by (47)-(53) and (55)-(56), after dropping the $O\left( \Delta x^6\right)$ terms. Thus, we obtain the following system of $(M+5)$ linear algebraic equations in $(M+5)$ unknowns:

$$\begin{aligned}&\begin{aligned}&(-717\sigma \nu +36\Delta x^2 p^{n-1}_0)\tilde{\lambda }_{-2}^{n}\\ {}&\qquad +(-1448\sigma \nu +936\Delta x^2 p^{n-1}_0)\tilde{\lambda }_{-1}^{n}\\&\qquad +(4300\sigma \nu +2376\Delta x^2 p^{n-1}_0)\tilde{\lambda }_{0}^{n}\\&\qquad +(-1322\sigma \nu +936\Delta x^2 p^{n-1}_0)\tilde{\lambda }_{1}^{n}+(-938\sigma \nu \\&\qquad +36\Delta x^2 p^{n-1}_0)\tilde{\lambda }_{2}^{n} -\sigma \nu (-202\tilde{\lambda }_{3}^{n}\\&\qquad +92\tilde{\lambda }_{4}^{n}-10\tilde{\lambda }_{5}^{n}-7\tilde{\lambda }_{6}^{n}+2\tilde{\lambda }_{7}^{n})=4320\Delta x^2 \phi _0^{n-1}, \quad n\\&\quad =1,2,\dots , N,\\&\quad \end{aligned} \end{aligned}$$

(58)

$$\begin{aligned}&\begin{aligned}&2\sigma \nu \tilde{\lambda }_{-2}^{n}+(-725\sigma \nu +36\Delta x^2 p^{n-1}_1)\tilde{\lambda }_{-1}^{n}\\&\qquad +(-1454\sigma \nu +936\Delta x^2 p^{n-1}_1)\tilde{\lambda }_{0}^{n}+(4396\sigma \nu \\&\qquad +2376\Delta x^2 p^{n-1}_1)\tilde{\lambda }_{1}^{n}+(-1574\sigma \nu +936\Delta x^2 p^{n-1}_1)\tilde{\lambda }_{2}^{n}\\&\qquad +(-602\sigma \nu +36\Delta x^2 p^{n-1}_1)\tilde{\lambda }_{3}^{n}\\&\qquad -\sigma \nu (50\tilde{\lambda }_{4}^{n}-4\tilde{\lambda }_{5}^{n}-4\tilde{\lambda }_{6}^{n}+\tilde{\lambda }_{7}^{n})=4320\Delta x^2 \phi _1^{n-1}, \quad n\\&\quad =1,2,\dots , N,\\&\quad \end{aligned} \end{aligned}$$

(59)

$$\begin{aligned}&\begin{aligned}&-\sigma \nu (-\tilde{\lambda }_{m-4}^{n}+2\tilde{\lambda }_{m-3}^{n})+(-728\sigma \nu +36\Delta x^2 p^{n-1}_m)\tilde{\lambda }_{m-2}^{n}\\&\qquad +(-1406\sigma \nu +936\Delta x^2 p^{n-1}_m)\tilde{\lambda }_{m-1}^{n}\\&\qquad +(4270\sigma \nu +2376\Delta x^2 p^{n-1}_m)\tilde{\lambda }_{m}^{n}\\&\qquad +(-1406\sigma \nu +936\Delta x^2 p^{n-1}_m)\tilde{\lambda }_{m+1}^{n}\\ {}&\quad +(-728\sigma \nu +36\Delta x^2 p^{n-1}_m)\tilde{\lambda }_{m+2}^{n}\\&\qquad -\upsigma \nu (2\tilde{\lambda }_{m+3}^{n}-\tilde{\lambda }_{m+4}^{n})=4320\Delta x^2 \phi _m^{n-1}, \quad n\\&\quad =1,2,\dots , N,\quad m=2,3,...,M-2,\\ \end{aligned} \end{aligned}$$

(60)

$$\begin{aligned}&\begin{aligned}&-\sigma \nu (\tilde{\lambda }_{M-7}^{n}-4\tilde{\lambda }_{M-6}^{n}-4\tilde{\lambda }_{M-5}^{n}+50\tilde{\lambda }_{M-4}^{n})\\&\qquad +(-602\sigma \nu +36\Delta x^2 p^{n-1}_{M-1})\tilde{\lambda }_{M-3}^{n}+(-1574\sigma \nu \\&\qquad +936\Delta x^2 p^{n-1}_{M-1})\tilde{\lambda }_{M-2}^{n}\\ {}&\qquad +(4396\sigma \nu +2376\Delta x^2 p^{n-1}_{M-1})\tilde{\lambda }_{M-1}^{n}\\&\qquad +(-1454\sigma \nu +936\Delta x^2 p^{n-1}_{M-1})\tilde{\lambda }_{M}^{n}\\&\qquad +(-725\sigma \nu +36\Delta x^2 p^{n-1}_{M-1})\tilde{\lambda }_{M+1}^{n}+2\sigma \nu \tilde{\lambda }_{M+2}^{n}\\&\quad =4320\Delta x^2 \phi _{M-1}^{n-1}, \quad n=1,2,\dots , N,\\ \end{aligned}\nonumber \\ \end{aligned}$$

(61)

$$\begin{aligned}&\begin{aligned}&-\sigma \nu (2\tilde{\lambda }_{M-7}^{n}-7\tilde{\lambda }_{M-6}^{n}-10\tilde{\lambda }_{M-5}^{n}+92\tilde{\lambda }_{M-4}^{n}\\&\qquad -202\tilde{\lambda }_{M-3}^{n})+(-938\sigma \nu +36\Delta x^2 p^{n-1}_{M})\tilde{\lambda }_{M-2}^{n}\\&\qquad +(-1322\sigma \nu +936\Delta x^2 p^{n-1}_{M})\tilde{\lambda }_{M-1}^{n}\\&\qquad +(4300\sigma \nu +2376\Delta x^2 p^{n-1}_{M})\tilde{\lambda }_{M}^{n}+(-1448\sigma \nu \\&\qquad +936\Delta x^2 p^{n-1}_{M})\tilde{\lambda }_{M+1}^{n}\\ {}&\qquad +(-717\sigma \nu +36\Delta x^2 p^{n-1}_{M})\tilde{\lambda }_{M+2}^{n}\\&\quad =4320\Delta x^2 \phi _{M}^{n-1}, \quad n=1,2,\dots , N,\\ \end{aligned} \end{aligned}$$

(62)

$$\begin{aligned}&\tilde{\lambda }_{-2}^{n}+26\tilde{\lambda }_{-1}^{n}+66\tilde{\lambda }_{0}^{n}+26\tilde{\lambda }_{1}^{n}+\tilde{\lambda }_{2}^{n}=120g_{1}(t_{n}), \end{aligned}$$

(63)

$$\begin{aligned}&\tilde{\lambda }_{M-2}^{n}+26\tilde{\lambda }_{M-1}^{n}+66\tilde{\lambda }_{M}^{n}+26\tilde{\lambda }_{M+1}^{n}+\tilde{\lambda }_{M+2}^{n}=120g_{2}(t_{n}),\nonumber \\ \end{aligned}$$

(64)

$$\begin{aligned}&\begin{aligned}&(-1475\sigma \nu +18\Delta x^2 {\tilde{p}}^{n-1}_1)\tilde{\lambda }_{-2}^{n}\\&\quad +(-30149\sigma \nu +4266\Delta x^2 {\tilde{p}}^{n-1}_1)\tilde{\lambda }_{-1}^{n}+(31918\sigma \nu \\&\quad +30276\Delta x^2 {\tilde{p}}^{n-1}_1)\tilde{\lambda }_{0}^{n}+(30322\sigma \nu +30276\Delta x^2 {\tilde{p}}^{n-1}_1)\tilde{\lambda }_{1}^{n}\\&\quad +(-27776\sigma \nu +4266\Delta x^2 {\tilde{p}}^{n-1}_1)\tilde{\lambda }_{2}^{n}\\&\quad +(-3680\sigma \nu +18\Delta x^2 {\tilde{p}}^{n-1}_1)\tilde{\lambda }_{3}^{n}-\sigma \nu (-994\tilde{\lambda }_{4}^{n}+98\tilde{\lambda }_{5}^{n}\\&\quad +77\tilde{\lambda }_{6}^{n}-21\tilde{\lambda }_{7}^{n})=69120\Delta x^2 \tilde{\phi }_1^{n-1}, \, n\ge 1,\\ \end{aligned}\nonumber \\ \end{aligned}$$

(65)

$$\begin{aligned}&\begin{aligned}&-\sigma \nu (-21\tilde{\lambda }_{M-7}^{n}+77\tilde{\lambda }_{M-6}^{n}+98\tilde{\lambda }_{M-5}^{n}-994\tilde{\lambda }_{M-4}^{n})\\&\qquad +(-3680\sigma \nu +18\Delta x^2 {\tilde{p}}^{n-1}_M)\tilde{\lambda }_{M-3}^{n}\\&\qquad +(-27776\sigma \nu +4266\Delta x^2 {\tilde{p}}^{n-1}_M)\tilde{\lambda }_{M-2}^{n}\\&\qquad +(30322\sigma \nu +30276\Delta x^2 {\tilde{p}}^{n-1}_M)\tilde{\lambda }_{M-1}^{n}\\&\qquad +(31918\sigma \nu +30276\Delta x^2 {\tilde{p}}^{n-1}_M)\tilde{\lambda }_{M}^{n}\\ {}&\qquad +(-30149\sigma \nu +4266\Delta x^2 {\tilde{p}}^{n-1}_M)\tilde{\lambda }_{M+1}^{n}\\ {}&\qquad +(-1475\sigma \nu +18\Delta x^2 {\tilde{p}}^{n-1}_M)\tilde{\lambda }_{M+2}^{n}\\&\quad =69120\Delta x^2 \tilde{\phi }_M^{n-1}, \quad n=1,2,\dots , N,\\ \end{aligned} \end{aligned}$$

(66)

where

$$\begin{aligned}&p^{n-1}_m=P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(x_m)\right) ^{\beta }, \quad \\&m=0,1,...,M, \\&{\tilde{p}}^{n-1}_m=P_{\alpha }c_0^{\alpha }-\sigma +\sigma (\beta +1)\left( {\mathcal {Z}}^{n-1}(\tau _m)\right) ^{\beta }, \quad \\&m=1,M. \end{aligned}$$

The following algorithm illustrates the method described above.

Step 1: Provide inputs including the number of mesh points in space (M) and time (N), the mesh size in space ($\Delta x$) and time ($\Delta t$), as well as the coefficients ${a}_l^{\alpha }$, ${b}_l^{\alpha }$, and ${c}_l^{\alpha }$ for $0\le l\le N$, along with the initial condition (IC) (2) and boundary conditions (BCs) (3).

Step 2: Formulate the system of equations given by equations (58)-(66).

Step 3: Employ the Gaussian elimination method to solve the system (58)-(66) at each time level, obtaining the unknown parameters $\lambda _m^n$, where $-2\le m\le M+2$ and $1\le n\le N$.

Step 4: Output: The approximate value of the solution u(x, t) at the grid points by utilizing the obtained values of the unknown parameters $\tilde{\lambda }_m^n$ in equation (57).

3 Stability and convergence analysis

Here, we establish stability and convergence results of the present numerical scheme for the problem (1)–(3).

3.1 Stability

In this subsection, we study the stability analysis of the present numerical scheme.

Theorem 4

The present method (58)–(66) for the problem considered is unconditionally stable.

Proof

For simplicity, the non-linear term $u^{n-1+\sigma }(x)\left( 1-(u^{n-1+\sigma }(x))^{\beta }\right)$ in the homogeneous form of (7) is linearized by setting $(u^{n-1+\sigma }(x))^{\beta }-1$ as a constant $\mu$. Then, we obtain

$$\begin{aligned}&\frac{\Delta t^{-\alpha }}{\Gamma (2-\alpha )}\nonumber \\ {}&\quad \left[ c_0^{\alpha }u^n(x)-\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)-c^{\alpha }_{n-1}u^{0}(x)\right] \nonumber \\&\qquad + \mu u^{n-1+\sigma }(x)- \nu u_{xx}^{n-1+\sigma }(x) = 0,\quad \nonumber \\&\quad X_l<x<X_r, \quad n\ge 1. \end{aligned}$$

(67)

Making use of the approximations (8) and (9) in (67), we obtain

$$\begin{aligned}&\Theta c_0^{\alpha }u^n(x)+\sigma \mu u^n(x)-\sigma \nu u_{xx}^{n}(x)\nonumber \\ {}&\quad =\Theta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)\nonumber \\&\qquad +\Theta c^{\alpha }_{n-1}u^{0}(x)-(1-\sigma )\mu u^{n-1}(x)\nonumber \\ {}&\qquad +(1-\sigma )\nu u_{xx}^{n-1}(x),\,\,\nonumber \\&\qquad X_l<x<X_r, \, n\ge 1. \end{aligned}$$

(68)

Using the OSQB, as explained in Sect. 2, in Eq. (68) yields the following equations for the mesh points $x=x_m$, $m=2,3,\dots ,M-2$:

$$\begin{aligned} \begin{aligned}&(\eta _1+\eta _2)\big (\tilde{\lambda }_{m-2}^{n}+26\tilde{\lambda }_{m-1}^{n}+66\tilde{\lambda }_{m}^{n}+26\tilde{\lambda }_{m+1}^{n}+\tilde{\lambda }_{m+2}^{n}\big )\\&\quad -\eta _3\big (-\tilde{\lambda }_{m-4}^{n}+2\tilde{\lambda }_{m-3}^{n}+728\tilde{\lambda }_{m-2}^{n}+1406\tilde{\lambda }_{m-1}^{n}\\&\quad -4270\tilde{\lambda }_{m}^{n}+1406\tilde{\lambda }_{m+1}^{n}+728\tilde{\lambda }_{m+2}^{n}+2\tilde{\lambda }_{m+3}^{n}-\tilde{\lambda }_{m+4}^{n}\big )\\&=\frac{P_{\alpha }}{120}\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \\&\quad \times \big (\tilde{\lambda }_{m-2}^{l}+26\tilde{\lambda }_{m-1}^{l}+66\tilde{\lambda }_{m}^{l}+26\tilde{\lambda }_{m+1}^{l}+\tilde{\lambda }_{m+2}^{l}\big )\\&\quad +\frac{P_{\alpha } c^{\alpha }_{n-1}}{120}\big (\tilde{\lambda }_{m-2}^{0}+26\tilde{\lambda }_{m-1}^{0}+66\tilde{\lambda }_{m}^{0}+26\tilde{\lambda }_{m+1}^{0}\\&\quad +\tilde{\lambda }_{m+2}^{0}\big )-\frac{(1-\sigma )\mu }{120}\big (\tilde{\lambda }_{m-2}^{n-1}+26\tilde{\lambda }_{m-1}^{n-1}\\&\quad +66\tilde{\lambda }_{m}^{n-1}+26\tilde{\lambda }_{m+1}^{n-1}+\tilde{\lambda }_{m+2}^{n-1}\big )+\frac{(1-\sigma )\nu }{4320\Delta x^2}\big (-\tilde{\lambda }_{m-4}^{n-1}\\&\quad +2\tilde{\lambda }_{m-3}^{n-1}+728\tilde{\lambda }_{m-2}^{n-1}+1406\tilde{\lambda }_{m-1}^{n-1}-4270\tilde{\lambda }_{m}^{n-1}\\&\quad +1406\tilde{\lambda }_{m+1}^{n-1}+728\tilde{\lambda }_{m+2}^{n-1}+2\tilde{\lambda }_{m+3}^{n-1}-\tilde{\lambda }_{m+4}^{n-1}\big ),\\&n=1,2,\dots ,N,\hspace{0.1cm} \end{aligned} \end{aligned}$$

(69)

where $\eta _1=\frac{P_{\alpha } c_0^{\alpha }}{120},$ $\eta _2=\frac{\sigma \mu }{120}$ and $\eta _3=\frac{\sigma \nu }{4320 \Delta x^2}.$ $\square$

Define the error ${\zeta }^n_m$ by

$$\begin{aligned} {\zeta }^n_m= \tilde{\lambda }_m^n- \lambda ^{*}{_{m}^{n}}, \end{aligned}$$

(70)

where $\lambda ^{*}{_{m}^{n}}$ be the solution of the perturbed system of (69). By (70), we obtain the error equations for (69):

$$\begin{aligned} \begin{aligned}&(\eta _1+\eta _2)\big (\zeta _{m-2}^{n}+26\zeta _{m-1}^{n}+66\zeta _{m}^{n}+26\zeta _{m+1}^{n}+\zeta _{m+2}^{n}\big )\\&\quad -\eta _3\big (-\zeta _{m-4}^{n}+2\zeta _{m-3}^{n}+728\zeta _{m-2}^{n}\\&\quad +1406\upzeta _{m-1}^{n}-4270\zeta _{m}^{n}+1406\zeta _{m+1}^{n}+728\zeta _{m+2}^{n}\\&\quad +2\zeta _{m+3}^{n}-\zeta _{m+4}^{n}\big )=\frac{P_{\alpha }}{120}\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \\&\quad \times \big (\zeta _{m-2}^{l}+26\zeta _{m-1}^{l}+66\zeta _{m}^{l}+26\zeta _{m+1}^{l}+\zeta _{m+2}^{l}\big )\\&\quad +\frac{P_{\alpha } c^{\alpha }_{n-1}}{120}\big (\zeta _{m-2}^{0}+26\zeta _{m-1}^{0}+66\zeta _{m}^{0}+26\zeta _{m+1}^{0}\\&\quad +\zeta _{m+2}^{0}\big )-\frac{(1-\sigma )\mu }{120}\big (\zeta _{m-2}^{n-1}+26\zeta _{m-1}^{n-1}+66\zeta _{m}^{n-1}\\&\quad +26\zeta _{m+1}^{n-1}+\zeta _{m+2}^{n-1}\big )+\frac{(1-\sigma )\nu }{4320\Delta x^2}\big (-\zeta _{m-4}^{n-1}\\&\quad +2\zeta _{m-3}^{n-1}+728\zeta _{m-2}^{n-1}+1406\zeta _{m-1}^{n-1}-4270\zeta _{m}^{n-1}\\&\quad +1406\zeta _{m+1}^{n-1}+728\zeta _{m+2}^{n-1}+2\zeta _{m+3}^{n-1}-\zeta _{m+4}^{n-1}\big ),\\&\quad n=1,2,\dots ,N,\hspace{0.1cm} m=2,3,\dots ,M-2. \end{aligned} \end{aligned}$$

(71)

The error ${\zeta }_{m}^{n}$ can be chosen as

$$\begin{aligned} {\zeta }_{m}^{n}={\xi }^{n}e^{i m\rho \Delta x}, \end{aligned}$$

(72)

where $i=\sqrt{-1}$. Inserting (72) into (71) yields

$$\begin{aligned} \begin{aligned}&{\xi }^{n}\big [(\eta _1+\eta _2)(2{\cos }(2\rho \Delta x)+52{\cos }(\rho \Delta x)+66)\\&\quad +\eta _3(2{\cos }(4\rho \Delta x)-4{\cos }(3\rho \Delta x)-1456{\cos }(2\rho \Delta x)\\&\quad -2812{\cos }(\rho \Delta x)+4270)\big ]\\ {}&\quad =\frac{P_{\alpha }}{120}\Bigg [\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) {\xi }^{l}\\&\quad +c^{\alpha }_{n-1} {\xi }^0\Bigg ](2{\cos }(2\rho \Delta x)+52{\cos }(\rho \Delta x) +66)\\&\quad -\left( \frac{1-\sigma }{\sigma }\right) \eta _2{\xi }^{n-1}(2{\cos }(2\rho \Delta x)+52{\cos }(\rho \Delta x)+66)\\&\quad -\left( \frac{1-\sigma }{\sigma }\right) \eta _3{\xi }^{n-1}(2{\cos }(4\rho \Delta x)-4{\cos }(3\rho \Delta x)\\&\quad -1456{\cos }(2\rho \Delta x)-2812{\cos }(\rho \Delta x)+4270). \end{aligned} \end{aligned}$$

(73)

From (73), we have

$$\begin{aligned} {\xi }^{n}=\frac{\frac{P_{\alpha }\gamma _1}{120}\Bigg [\displaystyle \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) {\xi }^{l}+c^{\alpha }_{n-1} {\xi }^0\Bigg ]-\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _1{\xi }^{n-1}-\left( \frac{1-\sigma }{\sigma }\right) \eta _3\gamma _2{\xi }^{n-1}}{\eta _1\gamma _1+\eta _2\gamma _1+\eta _3\gamma _2}, \end{aligned}$$

(74)

where $\gamma _1={\cos }(\rho \Delta x)+26{\cos }(\rho \Delta x)+33$ and $\gamma _2=2{\cos }(4\rho \Delta x)-4{\cos }(3\rho \Delta x)-1456{\cos }(2\rho \Delta x)-2812{\cos }(\rho \Delta x)+4270.$

We use the principle of mathematical induction to prove that

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|, n\ge 1. \end{aligned}$$

(75)

For $n=1,$ (74) leads to

$$\begin{aligned} {\xi }^{1}= \frac{\eta _1\gamma _1-\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _1-\left( \frac{1-\sigma }{\sigma }\right) \eta _3\gamma _2}{\eta _1\gamma _1+\eta _2\gamma _1+\eta _3\gamma _2}{\xi }^0. \end{aligned}$$

(76)

Since $\sigma \in \left( \frac{1}{2},1\right)$, we have

$$\begin{aligned} 0\le \left( \frac{1-\sigma }{\sigma }\right) \le 1. \end{aligned}$$

(77)

Also since $\Delta x>0,$ $\Delta t>0$, ${\nu }\ge 0$ and $0<\alpha <1,$ it follows that $\Gamma (2-\alpha )>0$ and $\eta _1,\, \eta _2,\, \eta _3$ are positive. Therefore, taking into account (77), for sufficiently small $\Delta x$, we have

$$\begin{aligned} \frac{\eta _1\gamma _1+\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _1+\left( \frac{1-\sigma }{\sigma }\right) \eta _3\gamma _2}{\eta _1\gamma _1+\eta _2\gamma _1+\eta _3\gamma _2}\le 1. \end{aligned}$$

(78)

Therefore, (76) and (78) lead to

$$\begin{aligned} |{\xi }^{1}|\le |{\xi }^0|. \end{aligned}$$

(79)

Thus, (75) is valid for $n=1$. Suppose that (75) is valid for $n\le j-1$, i.e.,

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|,\hspace{0.1cm}n=1,2,...,j-1. \end{aligned}$$

(80)

For $n=j,$ (74) leads to

$$\begin{aligned} {\xi }^{j}=\frac{\frac{P_{\alpha }\gamma _1}{120}\Bigg [\displaystyle \sum _{l=1}^{j-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{j-l}\right) {\xi }^{l}+c^{\alpha }_{j-1} {\xi }^0\Bigg ]-\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _1{\xi }^{j-1}-\left( \frac{1-\sigma }{\sigma }\right) \eta _3\gamma _2{\xi }^{j-1}}{\eta _1\gamma _1+\eta _2\gamma _1+\eta _3\gamma _2}. \end{aligned}$$

(81)

Using Lemma 1, (78) and (81), we can obtain that

$$\begin{aligned} |{\xi }^{j}|\le |{\xi }^0|. \end{aligned}$$

Hence, (75) is valid for $n=j$. Consequently, (75) is valid for every n, i.e.,

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|,\hspace{0.1cm}n\ge 1. \end{aligned}$$

(82)

Proceeding in the same manner for the grid points $x=x_m$, $m=0,\,1,\,M-1,\,M$, we can obtain

$$\begin{aligned} \xi ^n=\frac{A^{(m)}-iB^{(m)}}{C^{(m)}+iD^{(m)}}, n\ge 1, \end{aligned}$$

(83)

where $A^{(m)}=\frac{P_{\alpha }\gamma _1}{120}\Bigg [\displaystyle \sum _{l=1}^{j-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{j-l}\right) {\xi }^{l}+c^{\alpha }_{j-1} {\xi }^0\Bigg ]-\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _1{\xi }^{j-1}-\left( \frac{1-\sigma }{\sigma }\right) \eta _3{\tilde{\gamma }}_2^{(m)}{\xi }^{j-1}$, $B^{(m)}=\left( \frac{1-\sigma }{\sigma }\right) \eta _3{\tilde{\gamma }}_3^{(m)}{\xi }^{j-1}$, $C^{(m)}=\eta _1\gamma _1+\eta _2\gamma _1-\eta _3{\tilde{\gamma }}_2^{(m)}$ and $D^{(m)}=-\eta _3{\tilde{\gamma }}_3^{(m)}$,

with

$$\begin{aligned} {\tilde{\gamma }}_2^{(0)}&={\tilde{\gamma }}_2^{(M)}\\ {}&=2770{\cos }(\rho \Delta x)+1655{\cos }(2\rho \Delta x)\\&\quad -202{\cos }(3\rho \Delta x)+92{\cos }(4\rho \Delta x)-10{\cos }(5\rho \Delta x)\\&\quad -7{\cos }(6\rho \Delta x)+2{\cos }(7\rho \Delta x)-4300,\\ {\tilde{\gamma }}_2^{(1)}&={\tilde{\gamma }}_2^{(M-1)}\\ {}&=1454-3671{\cos }(\rho \Delta x)+1572{\cos }(2\rho \Delta x)\\&\quad +602{\cos }(3\rho \Delta x)+50{\cos }(4\rho \Delta x)\\&\quad -4{\cos }(5\rho \Delta x)-4{\cos }(6\rho \Delta x)+{\cos }(7\rho \Delta x),\\ {\tilde{\gamma }}_3^{(0)}&=-{\tilde{\gamma }}_3^{(M)}\\ {}&=2{\sin }(7\rho \Delta x)-7{\sin }(6\rho \Delta x)-10{\sin }(5\rho \Delta x)\\&\quad +94{\sin }(4\rho \Delta x)-202{\sin }(3\rho \Delta x)\\&\quad +221{\sin }(2\rho \Delta x)-126{\sin }(\rho \Delta x) \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\tilde{\gamma }}_3^{(1)}&=-{\tilde{\gamma }}_3^{(M-1)}\\ {}&={\sin }(7\rho \Delta x)-4{\sin }(6\rho \Delta x)-4{\sin }(5\rho \Delta x)\\&\quad +50{\sin }(4\rho \Delta x)+602{\sin }(3\rho \Delta x)\\&\quad +1576{\sin }(2\rho \Delta x)-5121{\sin }(\rho \Delta x). \end{aligned} \end{aligned}$$

Using the principle of mathematical induction, we prove that

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|, n\ge 1. \end{aligned}$$

(84)

For $n=1,$ (83) leads to

$$\begin{aligned} {\xi }^{1}= \frac{\eta _1\gamma _1-\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _1+\left( \frac{1-\sigma }{\sigma }\right) \eta _3\left( {\tilde{\gamma }}_2^{(m)}+i{\tilde{\gamma }}_3^{(m)}\right) }{\eta _1\gamma _1+\eta _2\gamma _1-\eta _3\left( {\tilde{\gamma }}_2^{(m)}+i{\tilde{\gamma }}_3^{(m)}\right) }{\xi }^0.\nonumber \\ \end{aligned}$$

(85)

Making use of (77), for sufficiently small $\Delta x$, it is clearly observed that

$$\begin{aligned} \left| \frac{\eta _1\gamma _1-\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _1+\left( \frac{1-\sigma }{\sigma }\right) \eta _3\left( {\tilde{\gamma }}_2^{(m)}+i{\tilde{\gamma }}_3^{(m)}\right) }{\eta _1\gamma _1+\eta _2\gamma _1-\eta _3\left( {\tilde{\gamma }}_2^{(m)}+i{\tilde{\gamma }}_3^{(m)}\right) }\right| \le 1.\nonumber \\ \end{aligned}$$

(86)

Therefore, (85) and (86) lead to

$$\begin{aligned} |{\xi }^{1}|\le |{\xi }^0|. \end{aligned}$$

Thus, (84) is valid for $n=1$. Suppose that (84) is valid for $n\le j-1$, i.e.,

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|,\hspace{0.1cm}n=1,2,...,j-1. \end{aligned}$$

(87)

Using Lemma 1 and (87), we can obtain that

$$\begin{aligned} \left| A^{(m)}\right| \le \left| C^{(m)}\right| |\xi ^0|\, \text { and } \, \left| B^{(m)}\right| \le \left| D^{(m)}\right| |\xi ^0|. \end{aligned}$$

(88)

Finally, making use of (88) and (83), we get

$$\begin{aligned} \begin{aligned} |{\xi }^{j}|^2=\frac{\left( A^{(m)}\right) ^2+\left( B^{(m)}\right) ^2}{\left( C^{(m)}\right) ^2+\left( D^{(m)}\right) ^2}\le |{\xi }^{0}|^2, \end{aligned} \end{aligned}$$

which gives

$$\begin{aligned} |{\xi }^{j}|\le |{\xi }^0|. \end{aligned}$$

Thus, (84) is valid for $n=j$. Consequently, (84) is valid for every n, i.e.,

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|,\hspace{0.1cm}n\ge 1. \end{aligned}$$

(89)

By (82) and (89), we conclude that the present numerical method (58)–(66) is unconditionally stable.

3.2 Convergence

A detailed analysis of convergence for proposed numerical method (58)-(66) for (1)–(3) is given here.

Theorem 5

Assume that $\tilde{{\mathcal {Z}}}^{n}(x)$ defined in (57) is the QBS approximation for the exact solution $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$ of (1)-(3). Then, we have

$$\begin{aligned} \Vert \tilde{{\mathcal {Z}}}^{n}(x)-u^{n}(x)\Vert _{\infty }\le {\mathcal {L}}\Delta x^6,\;\; \forall \; n\ge 0, \end{aligned}$$

for small enough $\Delta x$ and constant ${\mathcal {L}}$, independent of $\Delta x.$

Proof

First (7) is linearized by setting $(u^{n-1+\sigma }(x))^{\beta }-1$ as a constant $\mu$ then the terms in the resulting equation are rearranged to obtain

$$\begin{aligned} \begin{aligned}&\quad P_{\alpha } c_0^{\alpha }u^n(x)+\sigma \mu u^n(x)-\sigma \nu u_{xx}^{n}(x)\\&\quad =P_{\alpha }\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)+P_{\alpha } c^{\alpha }_{n-1}u^{0}(x)\\&\quad -(1-\sigma )\mu u^{n-1}(x)+(1-\sigma )\nu u_{xx}^{n-1}(x),\,\, X_l\\&\quad<x<X_r, \, n\ge 1. \end{aligned} \end{aligned}$$

(90)

The BCs are

$$\begin{aligned} u^{n}(X_l)=g_{1}(t_{n}),\;u^{n}(X_r)=g_{2}(t_{n}). \end{aligned}$$

(91)

Equations (90) and (91) can be rewritten in operator form as follows:

$$\begin{aligned} Lu^{n}(x)\equiv & {} P_{\alpha } c_0^{\alpha }u^{n}(x)+\sigma \mu u^n(x)-\sigma \nu u_{xx}^{n}(x)\\= & {} G^{n-1}(x)+f^{n-1+\sigma }(x), \\ Bu^{n}(x)\equiv & {} \{u^{n}(X_l)=g_{1}(t_{n}),\;u^{n}(X_r)=g_{2}(t_{n})\}, \end{aligned}$$

where

$$\begin{aligned} G^{n-1}(x)= & {} \displaystyle P_{\alpha }\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)+P_{\alpha } c^{\alpha }_{n-1}u^{0}(x)\nonumber \\{} & {} -(1-\sigma )\mu u^{n-1}(x)+(1-\sigma )\nu u_{xx}^{n-1}(x). \end{aligned}$$

(92)

Let ${{\mathcal {Z}}}^{n}(x)\in S_{5,I}$ defined by equation (17) be the QS interpolant to the exact solution of (90)–(91). Then, by using Theorems 1 and 2 we have

$$\begin{aligned}&L{{\mathcal {Z}}}^n(x_{m})=Lu^{n}(x_{m})+O(\Delta x^6),\quad m=0,1,...,M, \end{aligned}$$

(93)

$$\begin{aligned}&{{\mathcal {Z}}}^n(x_{0})=g_{1}(t_{n})+O(\Delta x^6),\;\nonumber \\ {}&{{\mathcal {Z}}}^n(x_{M})=g_{2}(t_{n})+O(\Delta x^6), \end{aligned}$$

(94)

$$\begin{aligned}&L{{\mathcal {Z}}}^n({\tau }_{m}) = Lu^{n}({\tau }_{m})+O(\Delta x^6),\quad m=1,M. \end{aligned}$$

(95)

Since $u^{n}(x_{m})=\tilde{{\mathcal {Z}}}^n(x_{m}),\hspace{0.1cm}m=0,1,...,M$ and $u^{n}({\tau }_{m})=\tilde{{\mathcal {Z}}}^n({\tau }_{m}),\hspace{0.1cm}m=1,M,$ therefore, we write the system (93) and (95) in the matrix form, as follows

$$\begin{aligned} \Big [L{{\mathcal {Z}}}^{n}(x)-L\tilde{{\mathcal {Z}}}^{n}(x)\Big ]_{x=x_{m},\hspace{0.1cm}m=0,1,...,M,\,x={\tau }_{m}\hspace{0.1cm}m=1,M}=E,\nonumber \\ \end{aligned}$$

(96)

where $E=[O(\Delta x^6), O(\Delta x^6),...,O(\Delta x^6),O(\Delta x^6)]^{T}$.

From (96), for $x=x_0,\, x_1,\, x_{M-1},\, x_{M},\,\tau _{1}$ and $\tau _{M}$, respectively, we have

$$\begin{aligned} {}&\begin{aligned}&({\tilde{\eta }}_1-717\eta _3){\lambda }_{-2}^{n}+(26{\tilde{\eta }}_1-1448\eta _3){\lambda }_{-1}^{n}\\ {}&\quad +(66{\tilde{\eta }}_1+4300\eta _3){\lambda }_{0}^{n}\\&\quad +(26{\tilde{\eta }}_1-1322\eta _3){\lambda }_{1}^{n}+({\tilde{\eta }}_1\\&\quad -938\eta _3){\lambda }_{2}^{n}+(202\eta _3){\lambda }_{3}^{n}-(92\eta _3){\lambda }_{4}^{n}+(10\eta _3){\lambda }_{5}^{n}\\&\quad +(7\eta _3){\lambda }_{6}^{n}-(2\eta _3){\lambda }_{7}^{n}-\big (({\tilde{\eta }}_1-717\eta _3)\tilde{\lambda }_{-2}^{n}\\&\quad +(26{\tilde{\eta }}_1-1448\eta _3)\tilde{\lambda }_{-1}^{n}+(66{\tilde{\eta }}_1+4300\eta _3)\tilde{\lambda }_{0}^{n}\\&\quad +(26{\tilde{\eta }}_1-1322\eta _3)\tilde{\lambda }_{1}^{n}+({\tilde{\eta }}_1-938\eta _3)\tilde{\lambda }_{2}^{n}\\&\quad +(202\eta _3)\tilde{\lambda }_{3}^{n}-(92\eta _3)\tilde{\lambda }_{4}^{n}+(10\eta _3)\tilde{\lambda }_{5}^{n}\\&\quad +(7\eta _3)\tilde{\lambda }_{6}^{n}-(2\eta _3)\tilde{\lambda }_{7}^{n}\big )=O(\Delta x^6),\\ \end{aligned} \end{aligned}$$

(97)

$$\begin{aligned} {}&\begin{aligned}&(2\eta _3){\lambda }_{-2}^{n}+({\tilde{\eta }}_1-725\eta _3){\lambda }_{-1}^{n}+(26{\tilde{\eta }}_1-1454\eta _3){\lambda }_{0}^{n}\\&\quad +(66{\tilde{\eta }}_1+4396\eta _3){\lambda }_{1}^{n}+(26{\tilde{\eta }}_1-1574\eta _3){\lambda }_{2}^{n}\\&\quad +({\tilde{\eta }}_1-602\eta _3){\lambda }_{3}^{n}-(50\eta _3){\lambda }_{4}^{n}+(4\eta _3){\lambda }_{5}^{n}+(4\eta _3){\lambda }_{6}^{n}\\&\quad -(\eta _3){\lambda }_{7}^{n}- \big ((2\eta _3)\tilde{\lambda }_{-2}^{n}+({\tilde{\eta }}_1-725\eta _3)\tilde{\lambda }_{-1}^{n}\\ {}&\quad +(26{\tilde{\eta }}_1-1454\eta _3)\tilde{\lambda }_{0}^{n}+(66{\tilde{\eta }}_1+4396\eta _3)\tilde{\lambda }_{1}^{n}\\&\quad +(26{\tilde{\eta }}_1-1574\eta _3)\tilde{\lambda }_{2}^{n}+({\tilde{\eta }}_1-602\eta _3)\tilde{\lambda }_{3}^{n}\\&\quad -(50\eta _3)\tilde{\lambda }_{4}^{n}+(4\eta _3)\tilde{\lambda }_{5}^{n}+(4\eta _3)\tilde{\lambda }_{6}^{n}-(\eta _3)\tilde{\lambda }_{7}^{n}\big )=O(\Delta x^6), \end{aligned} \end{aligned}$$

(98)

$$\begin{aligned} {}&\begin{aligned}&(-\eta _3){\lambda }_{M-7}^{n}+(4\eta _3){\lambda }_{M-6}^{n}+(4\eta _3){\lambda }_{m-5}^{n}-(50\eta _3){\lambda }_{M-4}^{n}\\&+({\tilde{\eta }}_1-602\eta _3){\lambda }_{M-3}^{n}+(26{\tilde{\eta }}_1\\&-1574\eta _3){\lambda }_{M-2}^{n}+(66{\tilde{\eta }}_1+4396\eta _3){\lambda }_{M-1}^{n}\\&+(26{\tilde{\eta }}_1-1454\eta _3){\lambda }_{M}^{n}+({\tilde{\eta }}_1-725\eta _3){\lambda }_{M+1}^{n}\\&+(2\eta _3){\lambda }_{M+2}^{n}-\big ((-\eta _3)\tilde{\lambda }_{M-7}^{n}+(4\eta _3)\tilde{\lambda }_{M-6}^{n}\\&+(4\eta _3)\tilde{\lambda }_{M-5}^{n}-(50\eta _3)\tilde{\lambda }_{M-4}^{n}+({\tilde{\eta }}_1-602\eta _3)\tilde{\lambda }_{M-3}^{n}\\&+(26{\tilde{\eta }}_1-1574\eta _3)\tilde{\lambda }_{M-2}^{n}+(66{\tilde{\eta }}_1+4396\eta _3)\tilde{\lambda }_{M-1}^{n}\\&+(26{\tilde{\eta }}_1-1454\eta _3)\tilde{\lambda }_{M}^{n}+({\tilde{\eta }}_1-725\eta _3)\tilde{\lambda }_{M+1}^{n}\\&+(2\eta _3)\tilde{\lambda }_{M+2}^{n} \big )=O(\Delta x^6),\\ \end{aligned} \end{aligned}$$

(99)

$$\begin{aligned} {}&\begin{aligned}&(-2\eta _3){\lambda }_{M-7}^{n}+(7\eta _3){\lambda }_{M-6}^{n}+(10\eta _3){\lambda }_{M-5}^{n}\\&\quad -(92\eta _3){\lambda }_{M-4}^{n}+(202\eta _3){\lambda }_{M-3}^{n}+({\tilde{\eta }}_1-938\eta _3){\lambda }_{M-2}^{n}\\&\quad +(26{\tilde{\eta }}_1-1322\eta _3){\lambda }_{M-1}^{n}+(66{\tilde{\eta }}_1+4300\eta _3){\lambda }_{M}^{n}\\&\quad +(26{\tilde{\eta }}_1-1448\eta _3){\lambda }_{M+1}^{n}+({\tilde{\eta }}_1-717\eta _3){\lambda }_{M+2}^{n}\\&\quad -\big ((-2\eta _3)\tilde{\lambda }_{M-7}^{n}+(7\eta _3)\tilde{\lambda }_{M-6}^{n}+(10\eta _3)\tilde{\lambda }_{M-5}^{n}\\&\quad -(92\eta _3)\tilde{\lambda }_{M-4}^{n}+(202\eta _3)\tilde{\lambda }_{M-3}^{n}+({\tilde{\eta }}_1\\&\quad -938\eta _3)\tilde{\lambda }_{M-2}^{n}+(26{\tilde{\eta }}_1-1322\eta _3)\tilde{\lambda }_{M-1}^{n}+(66{\tilde{\eta }}_1\\&\quad +4300\eta _3)\tilde{\lambda }_{M}^{n}+(26{\tilde{\eta }}_1-1448\eta _3)\tilde{\lambda }_{M+1}^{n}\\&\quad +(-717\eta _3+{\tilde{\eta }}_1)\tilde{\lambda }_{M+2}^{n} \big )=O(\Delta x^6),\\ \end{aligned} \end{aligned}$$

(100)

$$\begin{aligned} {}&\begin{aligned}&(\eta _1^*-1475\eta _2^*){\lambda }_{-2}^{n}+(237\eta _1^*-30149\eta _2^*){\lambda }_{-1}^{n}\\&\quad +(1682\eta _1^*+31918\eta _2^*){\lambda }_{0}^{n}+(1682\eta _1^*+30322\eta _2^*){\lambda }_{1}^{n}\\&\quad +(237\eta _1^*-27776\eta _2^*){\lambda }_{2}^{n}+(\eta _1^*-3680\eta _2^*){\lambda }_{3}^{n}\\&\quad +(994\eta _2^*){\lambda }_{4}^{n}-(98\eta _2^*){\lambda }_{5}^{n}-(77\eta _2^*){\lambda }_{6}^{n}+(21\eta _2^*){\lambda }_{7}^{n}\\&\quad -\big ((\eta _1^*-1475\eta _2^*)\tilde{\lambda }_{-2}^{n}+(237\eta _1^*-30149\eta _2^*)\tilde{\lambda }_{-1}^{n}\\&\quad +(1682\eta _1^*+31918\eta _2^*)\tilde{\lambda }_{0}^{n}+(1682\eta _1^*+30322\eta _2^*)\tilde{\lambda }_{1}^{n}\\&\quad +(237\eta _1^*-27776\eta _2^*)\tilde{\lambda }_{2}^{n}\\ {}&\quad +(\eta _1^*-3680\eta _2^*)\tilde{\lambda }_{3}^{n}+(994\eta _2^*)\tilde{\lambda }_{4}^{n}\\&\quad -(98\eta _2^*)\tilde{\lambda }_{5}^{n}-(77\eta _2^*)\tilde{\lambda }_{6}^{n}+(21\eta _2^*)\tilde{\lambda }_{7}^{n}\big )=O(\Delta x^6) \end{aligned} \end{aligned}$$

(101)

and

$$\begin{aligned} {} \begin{aligned}&(21\eta _2^*){\lambda }_{M-7}^{n}-(77\eta _2^*){\lambda }_{M-6}^{n}-(98\eta _2^*){\lambda }_{M-5}^{n}\\&\quad +(994\eta _2^*){\lambda }_{M-4}^{n}+(\eta _1^*-3680\eta _2^*){\lambda }_{M-3}^{n}+(237\eta _1^*\\&\quad -27776\eta _2^*){\lambda }_{M-2}^{n}+(1682\eta _1^*+30322\eta _2^*){\lambda }_{M-1}^{n}\\&\quad +(1682\eta _1^*+31918\eta _2^*){\lambda }_{M}^{n}+(237\eta _1^*-30149\eta _2^*){\lambda }_{M+1}^{n}\\&\quad +(\eta _1^*-1475\eta _2^*){\lambda }_{M+2}^{n}-\big ((21\eta _2^*)\tilde{\lambda }_{M-7}^{n}-(77\eta _2^*)\tilde{\lambda }_{M-6}^{n}\\&\quad -(98\eta _2^*)\tilde{\lambda }_{M-5}^{n}+(994\eta _2^*)\tilde{\lambda }_{M-4}^{n}+(\eta _1^*\\&\quad -3680\eta _2^*)\tilde{\lambda }_{M-3}^{n}+(237\eta _1^*-27776\eta _2^*)\tilde{\lambda }_{M-2}^{n}\\ {}&\quad +(1682\eta _1^*+30322\eta _2^*)\tilde{\lambda }_{M-1}^{n}\\&\quad +(1682\eta _1^*+31918\eta _2^*)\tilde{\lambda }_{M}^{n}\\&\quad +(237\eta _1^*-30149\eta _2^*)\tilde{\lambda }_{M+1}^{n}+(\eta _1^*-1475\eta _2^*)\tilde{\lambda }_{M+2}^{n}\big )\\ {}&\quad =O(\Delta x^6), \end{aligned}\nonumber \\ \end{aligned}$$

(102)

where ${\tilde{\eta }}_1=\eta _1+\eta _2,$ $\eta _1^*=\frac{P_{\alpha } c_0^{\alpha }+\sigma \mu }{3840}$ and $\eta _2^*=\frac{\sigma \nu }{69120 \Delta x^2}$.

We eliminate the unknowns ${\lambda }_{-2}^{n}, {\lambda }_{M+2}^{n}, \tilde{\lambda }_{-2}^{n}$ and $\tilde{\lambda }_{M+2}^{n}$ from (97)–(102) by using (63) and (64). Thus, at the grid point $x=x_0,$ we obtain

$$\begin{aligned} {} \begin{aligned}&(17194\eta _3){\lambda }_{-1}^{n}+(51622\eta _3){\lambda }_{0}^{n}+(17320\eta _3){\lambda }_{1}^{n}\\&\quad +(-221\eta _3){\lambda }_{2}^{n}+(202\eta _3){\lambda }_{3}^{n}-(92\eta _3){\lambda }_{4}^{n}\\&\quad +(10\eta _3){\lambda }_{5}^{n}+(7\eta _3){\lambda }_{6}^{n}-(2\eta _3){\lambda }_{7}^{n}- \big ((17194\eta _3)\tilde{\lambda }_{-1}^{n}\\&\quad +(51622\eta _3)\tilde{\lambda }_{0}^{n}+(17320\eta _3)\tilde{\lambda }_{1}^{n}\\&\quad +(-221\eta _3)\tilde{\lambda }_{2}^{n}+(202\eta _3)\tilde{\lambda }_{3}^{n}-(92\eta _3)\tilde{\lambda }_{4}^{n}+(10\eta _3)\tilde{\lambda }_{5}^{n}\\&\quad +(7\eta _3)\tilde{\lambda }_{6}^{n}-(2\eta _3)\tilde{\lambda }_{7}^{n}\big )=O(\Delta x^6). \end{aligned}\nonumber \\ \end{aligned}$$

(103)

At the grid point $x=x_1$, we obtain

$$\begin{aligned} {} \begin{aligned}&({\tilde{\eta }}_1-777\eta _3){\lambda }_{-1}^{n}+(26{\tilde{\eta }}_1-1586\eta _3){\lambda }_{0}^{n}\\&\qquad +(66{\tilde{\eta }}_1+4344\eta _3){\lambda }_{1}^{n}+(26{\tilde{\eta }}_1-1576\eta _3){\lambda }_{2}^{n}\\&\qquad +({\tilde{\eta }}_1-602\eta _3){\lambda }_{3}^{n}-(50\eta _3){\lambda }_{4}^{n}+(4\eta _3){\lambda }_{5}^{n}\\&\qquad +(4\eta _3){\lambda }_{6}^{n}-(\eta _3){\lambda }_{7}^{n} -\big (({\tilde{\eta }}_1-777\eta _3)\tilde{\lambda }_{-1}^{n}\\&\qquad +(26{\tilde{\eta }}_1-1586\eta _3)\tilde{\lambda }_{0}^{n}+(66{\tilde{\eta }}_1+4344\eta _3)\tilde{\lambda }_{1}^{n}+(26{\tilde{\eta }}_1+\\&\qquad -1576\eta _3)\tilde{\lambda }_{2}^{n}+({\tilde{\eta }}_1-602\eta _3)\tilde{\lambda }_{3}^{n}\\&\qquad -(50\eta _3)\tilde{\lambda }_{4}^{n}+(4\eta _3)\tilde{\lambda }_{5}^{n}+(4\eta _3)\tilde{\lambda }_{6}^{n}-(\eta _3)\tilde{\lambda }_{7}^{n}\big )\\ {}&\quad =O(\Delta x^6).\\ \end{aligned}\nonumber \\ \end{aligned}$$

(104)

At the grid point $x=x_2$, we obtain

$$\begin{aligned} {} \begin{aligned}&(-28\eta _3){\lambda }_{-1}^{n}+({\tilde{\eta }}_1-794\eta _3){\lambda }_{0}^{n}+(26{\tilde{\eta }}_1-1432\eta _3){\lambda }_{1}^{n}\\&\quad +(66{\tilde{\eta }}_1+4269\eta _3){\lambda }_{2}^{n}+(26{\tilde{\eta }}_1-1406\eta _3){\lambda }_{3}^{n}\\&\quad +({\tilde{\eta }}_1-728\eta _3){\lambda }_{4}^{n}-(2\eta _3){\lambda }_{5}^{n}+(\eta _3){\lambda }_{6}^{n}\\&\quad - \big ((-28\eta _3)\tilde{\lambda }_{-1}^{n}+({\tilde{\eta }}_1-794\eta _3)\tilde{\lambda }_{0}^{n}+(26{\tilde{\eta }}_1-1432\eta _3)\tilde{\lambda }_{1}^{n}\\&\quad +(66{\tilde{\eta }}_1+4269\eta _3)\tilde{\lambda }_{2}^{n}+(26{\tilde{\eta }}_1-1406\eta _3)\tilde{\lambda }_{3}^{n}\\&\quad +({\tilde{\eta }}_1-728\eta _3)\tilde{\lambda }_{4}^{n}-(2\eta _3)\tilde{\lambda }_{5}^{n}+(\eta _3)\tilde{\lambda }_{6}^{n}\big )=O(\Delta x^6).\\ \end{aligned}\nonumber \\ \end{aligned}$$

(105)

At the grid point $x=x_{m}$, $(m=3,...,M-1)$, we obtain

$$\begin{aligned} {} \begin{aligned}&(\eta _3){\lambda }_{m-4}^{n}-(2\eta _3){\lambda }_{m-3}^{n}+({\tilde{\eta }}_1-728\eta _3){\lambda }_{m-2}^{n}\\&\quad +(26{\tilde{\eta }}_1-1406\eta _3){\lambda }_{m-1}^{n}+(66{\tilde{\eta }}_1+4270\eta _3){\lambda }_{m}^{n}\\&\quad +(26{\tilde{\eta }}_1-1406\eta _3){\lambda }_{m+1}^{n}+({\tilde{\eta }}_1-728\eta _3){\lambda }_{m+2}^{n}\\&\quad -(2\eta _3){\lambda }_{m+3}^{n}+(\eta _3){\lambda }_{m+4}^{n}-\big ((\eta _3)\tilde{\lambda }_{m-4}^{n}\\&\quad -(2\eta _3)\tilde{\lambda }_{m-3}^{n}+({\tilde{\eta }}_1-728\eta _3)\tilde{\lambda }_{m-2}^{n}+(26{\tilde{\eta }}_1\\&\quad -1406\eta _3)\tilde{\lambda }_{m-1}^{n}+(66{\tilde{\eta }}_1+4270\eta _3)\tilde{\lambda }_{m}^{n}\\&\quad +(26{\tilde{\eta }}_1-1406\eta _3)\tilde{\lambda }_{m+1}^{n}+({\tilde{\eta }}_1-728\eta _3)\tilde{\lambda }_{m+2}^{n}\\&\quad -(2\eta _3)\tilde{\lambda }_{m+3}^{n}+(\eta _3)\tilde{\lambda }_{m+4}^{n} \big )=O(\Delta x^6).\\ \end{aligned} \end{aligned}$$

(106)

At the grid point $x=x_{M-2}$, we obtain

$$\begin{aligned} {} \begin{aligned}&(\eta _3){\lambda }_{M-6}^{n}-(2\eta _3){\lambda }_{M-5}^{n}+({\tilde{\eta }}_1-728\eta _3){\lambda }_{M-4}^{n}\\&\quad +(26{\tilde{\eta }}_1-1406\eta _3){\lambda }_{M-3}^{n}+(66{\tilde{\eta }}_1+4269\eta _3){\lambda }_{M-2}^{n}\\&\quad +(26{\tilde{\eta }}_1-1432\eta _3){\lambda }_{M-1}^{n}+({\tilde{\eta }}_1-794\eta _3){\lambda }_{M}^{n}\\&\quad -(28\eta _3){\lambda }_{M+1}^{n} -\big ((\eta _3)\tilde{\lambda }_{M-6}^{n}-(2\eta _3)\tilde{\lambda }_{M-5}^{n}\\&\quad +({\tilde{\eta }}_1-728\eta _3)\tilde{\lambda }_{M-4}^{n}+(26{\tilde{\eta }}_1-1406\eta _3)\tilde{\lambda }_{M-3}^{n}\\&\quad +(66{\tilde{\eta }}_1+4269\eta _3)\tilde{\lambda }_{M-2}^{n}+(26{\tilde{\eta }}_1-1432\eta _3)\tilde{\lambda }_{M-1}^{n}\\&\quad +({\tilde{\eta }}_1-794\eta _3)\tilde{\lambda }_{M}^{n}-(28\eta _3)\tilde{\lambda }_{M+1}^{n} \big )=O(\Delta x^6).\\ \end{aligned} \end{aligned}$$

(107)

At the grid point $x=x_{M-1}$, we obtain

$$\begin{aligned} {} \begin{aligned}&(-\eta _3){\lambda }_{M-7}^{n}+(4\eta _3){\lambda }_{M-6}^{n}+(4\eta _3){\lambda }_{M-5}^{n}-(50\eta _3){\lambda }_{M-4}^{n}\\&\quad +({\tilde{\eta }}_1-602\eta _3){\lambda }_{M-3}^{n}+(26{\tilde{\eta }}_1-1576\eta _3)\\&\quad \times {\lambda }_{M-2}^{n}+(66{\tilde{\eta }}_1+4344\eta _3){\lambda }_{M-1}^{n}+(26{\tilde{\eta }}_1-1586\eta _3){\lambda }_{M}^{n}\\&\quad +({\tilde{\eta }}_1-777\eta _3){\lambda }_{M+1}^{n}-\big ((-\eta _3)\tilde{\lambda }_{M-7}^{n}\\&\quad +(4\eta _3)\tilde{\lambda }_{M-6}^{n}+(4\eta _3)\tilde{\lambda }_{M-5}^{n}-(50\eta _3)\tilde{\lambda }_{M-4}^{n}\\&\quad +({\tilde{\eta }}_1-602\eta _3)\tilde{\lambda }_{M-3}^{n}+(26{\tilde{\eta }}_1-1576\eta _3)\tilde{\lambda }_{M-2}^{n}\\&\quad +(66{\tilde{\eta }}_1+4344\eta _3)\tilde{\lambda }_{M-1}^{n}+(26{\tilde{\eta }}_1-1586\eta _3)\tilde{\lambda }_{M}^{n}\\&\quad +({\tilde{\eta }}_1-777\eta _3)\tilde{\lambda }_{M+1}^{n} \big )=O(\Delta x^6).\\ \end{aligned}\nonumber \\ \end{aligned}$$

(108)

Similarly, at the grid point $x=x_M$, we obtain

$$\begin{aligned} {} \begin{aligned}&(-2\eta _3){\lambda }_{M-7}^{n}+(7\eta _3){\lambda }_{M-6}^{n}+(10\eta _3){\lambda }_{M-5}^{n}-(92\eta _3){\lambda }_{M-4}^{n}\\&\quad +(202\eta _3){\lambda }_{M-3}^{n}+(-221\eta _3){\lambda }_{M-2}^{n}\\&\quad +(17320\eta _3){\lambda }_{M-1}^{n}+(51622\eta _3){\lambda }_{M}^{n}+(17194\eta _3){\lambda }_{M+1}^{n} \\&\quad -\big ((-2\eta _3)\tilde{\lambda }_{M-7}^{n}+(7\eta _3)\tilde{\lambda }_{M-6}^{n}\\&\quad +(10\eta _3)\tilde{\lambda }_{M-5}^{n}-(92\eta _3)\tilde{\lambda }_{M-4}^{n}+(202\eta _3)\tilde{\lambda }_{M-3}^{n}\\&\quad +(-221\eta _3)\tilde{\lambda }_{M-2}^{n}+(17320\eta _3)\tilde{\lambda }_{M-1}^{n}\\&\quad +(51622\eta _3)\tilde{\lambda }_{M}^{n}+(17194\eta _3)\tilde{\lambda }_{M+1}^{n} \big )=O(\Delta x^6).\\ \end{aligned}\nonumber \\ \end{aligned}$$

(109)

At the mid point $x=\tau _{1}$, we obtain

$$\begin{aligned} {} \begin{aligned}&(211\eta _1^*+8201\eta _2^*){\lambda }_{-1}^{n}+(1616\eta _1^*+129268\eta _2^*){\lambda }_{0}^{n}\\&\quad +(1656\eta _1^*+68672\eta _2^*){\lambda }_{1}^{n}+(236\eta _1^*\\&\quad -26301\upeta _2^*){\lambda }_{2}^{n}+(\eta _1^*-3680\eta _2^*){\lambda }_{3}^{n}+(994\eta _2^*){\lambda }_{4}^{n}\\&\quad -(98\eta _2^*){\lambda }_{5}^{n}-(77\eta _2^*){\lambda }_{6}^{n}+(21\eta _2^*){\lambda }_{7}^{n}\\&\quad -\big ((211\eta _1^*+8201\eta _2^*)\tilde{\lambda }_{-1}^{n}+(1616\eta _1^*+129268\eta _2^*)\tilde{\lambda }_{0}^{n}\\&\quad +(1656\eta _1^*+68672\eta _2^*)\tilde{\lambda }_{1}^{n}+(236\eta _1^*\\&\quad -26301\eta _2^*)\tilde{\lambda }_{2}^{n}+(\eta _1^*-3680\eta _2^*)\tilde{\lambda }_{3}^{n}+(994\eta _2^*)\tilde{\lambda }_{4}^{n}\\&\quad -(98\eta _2^*)\tilde{\lambda }_{5}^{n}-(77\eta _2^*)\tilde{\lambda }_{6}^{n}+(21\eta _2^*)\tilde{\lambda }_{7}^{n}\big )=O(\Delta x^6). \end{aligned}\nonumber \\ \end{aligned}$$

(110)

At the mid point $x=\tau _{M}$, we obtain

$$\begin{aligned} {} \begin{aligned}&(21\eta _2^*){\lambda }_{M-7}^{n}-(77\eta _2^*){\lambda }_{M-6}^{n}-(98\eta _2^*){\lambda }_{M-5}^{n}\\&\quad +(994\eta _2^*){\lambda }_{M-4}^{n}+(\eta _1^*-3680\eta _2^*){\lambda }_{M-3}^{n}+(236\eta _1^*\\&\quad -26301\eta _2^*){\lambda }_{M-2}^{n}+(1656\eta _1^*+68672\eta _2^*){\lambda }_{M-1}^{n}\\&\quad +(1616\eta _1^*+129268\eta _2^*){\lambda }_{M}^{n}+(211\eta _1^*+8201\eta _2^*)\\&\quad \times {\lambda }_{M+1}^{n}-\big ((21\eta _2^*)\tilde{\lambda }_{M-7}^{n}-(77\eta _2^*)\tilde{\lambda }_{M-6}^{n}\\&\quad -(98\eta _2^*)\tilde{\lambda }_{M-5}^{n}+(994\eta _2^*)\tilde{\lambda }_{M-4}^{n}+(\eta _1^*-3680\eta _2^*)\tilde{\lambda }_{M-3}^{n}\\&\quad +(236\eta _1^*-26301\eta _2^*)\tilde{\lambda }_{M-2}^{n}\\ {}&\quad +(1656\eta _1^*+68672\eta _2^*)\tilde{\lambda }_{M-1}^{n}\\&\quad +(1616\eta _1^*+129268\eta _2^*)\tilde{\lambda }_{M}^{n}\\&\quad +(211\eta _1^*+8201\eta _2^*)\tilde{\lambda }_{M+1}^{n}\big )=O(\Delta x^6). \end{aligned}\nonumber \\ \end{aligned}$$

(111)

In matrix form, Eqs. (103)–(111) can be written as

$$\begin{aligned} R({\lambda }^{n}-\tilde{\lambda }^{n})=E. \end{aligned}$$

(112)

Here R is a square matrix of dimension $M+3$, given as

R=${\left( \begin{array}{ccccccccccccc} d^*_1&{}d^*_2&{} d^*_3&{}d^*_4&{}d^*_5&{}d^*_6&{}d^*_7&{} d^*_8&{}d^*_9&{}0 &{}\cdots &{}0&{}0\\ {\tilde{d}}_1&{}{\tilde{d}}_2&{} {\tilde{d}}_3&{}{\tilde{d}}_4&{}{\tilde{d}}_5&{}{\tilde{d}}_6&{}{\tilde{d}}_7&{} {\tilde{d}}_8&{}{\tilde{d}}_9&{}0 &{}\cdots &{}0&{}0\\ {\hat{d}}_{1}&{}{\hat{d}}_{2}&{}{\hat{d}}_{3}&{}{\hat{d}}_{4}&{}{\hat{d}}_{5}&{}{\hat{d}}_{6}&{}{\hat{d}}_7&{}{\hat{d}}_7&{}{\hat{d}}_8&{}0&{}\cdots &{}0&{}0\\ d_{6}&{}d_{7}&{}d_{8}&{}d_{9}&{}d_{4}&{}d_{3}&{}d_{2}&{}d_{1}&{}0&{}0&{}\cdots &{}0&{}0\\ d_1&{}d_2&{}d_3&{}d_4&{}d_5&{}d_4&{}d_3&{}d_2&{}d_1&{}0&{}\cdots &{}0&{}0\\ \ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots \\ 0 &{}0&{}\cdots &{} 0&{}d_1&{}d_2&{} d_{3}&{}d_{4}&{}d_{5}&{}d_{4}&{}d_{3}&{}d_{2}&{}d_1\\ 0 &{}0&{}\cdots &{} 0&{}0&{}d_{1}&{} d_{2}&{}d_{3}&{}d_{4}&{}d_{9}&{}d_{8}&{}d_{7}&{}d_6\\ 0 &{}0&{}\cdots &{} 0 &{} {\hat{d}}_{8}&{}{\hat{d}}_{7}&{}{\hat{d}}_{7}&{}{\hat{d}}_{6}&{}{\hat{d}}_{5}&{}{\hat{d}}_{4}&{}{\hat{d}}_3&{}{\hat{d}}_2&{}{\hat{d}}_1\\ 0 &{}0&{} \cdots &{}0&{}{\tilde{d}}_9&{}{\tilde{d}}_8&{} {\tilde{d}}_7&{}{\tilde{d}}_6&{}{\tilde{d}}_5&{}{\tilde{d}}_4&{}{\tilde{d}}_3&{} {\tilde{d}}_2&{}{\tilde{d}}_1\\ 0 &{}0&{} \cdots &{}0&{}d^*_9&{}d^*_8&{} d^*_7&{}d^*_6&{}d^*_5&{}d^*_4&{}d^*_3&{} d^*_2&{}d^*_1 \end{array}\right) }\,$ and ${\lambda }^{n}-\hat{\lambda }^{n}$=${\left( \begin{array}{cc} {\lambda }_{-1}^{n}-\hat{\lambda }_{-1}^{n}\\ {\lambda }_{0}^{n}-\hat{\lambda }_{0}^{n}\\ {\lambda }_{1}^{n}-\hat{\lambda }_{1}^{n}\\ {\lambda }_{2}^{n}-\hat{\lambda }_{2}^{n}\\ {\lambda }_{3}^{n}-\hat{\lambda }_{3}^{n}\\ \vdots \\ {\lambda }_{M-3}^{n}-\hat{\lambda }_{M-3}^{n}\\ {\lambda }_{M-2}^{n}-\hat{\lambda }_{M-2}^{n}\\ {\lambda }_{M-1}^{n}-\hat{\lambda }_{M-1}^{n}\\ {\lambda }_{M}^{n}-\hat{\lambda }_{M}^{n}\\ {\lambda }_{M+1}^{n}-\hat{\lambda }_{M+1}^{n} \end{array}\right) },$

where $d_1=\eta _3,\, d_2=-2\eta _3,\, d_3={\tilde{\eta }}_1-728\eta _3,\, d_4=26{\tilde{\eta }}_1-1406\eta _3,\, d_5= 66{\tilde{\eta }}_1+4270\eta _3,\, d_6=-28\eta _3,\, d_7={\tilde{\eta }}_1-794\eta _3,\, d_8= 26{\tilde{\eta }}_1-1432\eta _3,\, d_9= 66{\tilde{\eta }}_1+4269\eta _3, \,{\hat{d}}_1={\tilde{\eta }}_1-777\eta _3, \,{\hat{d}}_2=26{\tilde{\eta }}_1-1586\eta _3, \,{\hat{d}}_3=66{\tilde{\eta }}_1+4344\eta _3, \,{\hat{d}}_4=26{\tilde{\eta }}_1-1576\eta _3, \,{\hat{d}}_5={\tilde{\eta }}_1-602\eta _3, \,{\hat{d}}_6=-50\eta _3, \,{\hat{d}}_7=4\eta _3, \,{\hat{d}}_8=-\eta _3,\, {\tilde{d}}_1= 17194\eta _3,\, {\tilde{d}}_2=51622\eta _3,\, {\tilde{d}}_3=17320\eta _3,\, {\tilde{d}}_4=-221\eta _3,\, {\tilde{d}}_5=202\eta _3,\, {\tilde{d}}_6=-92\eta _3,\, {\tilde{d}}_7=10\eta _3,\, {\tilde{d}}_8=7\eta _3,\, {\tilde{d}}_9=-2\eta _3,\, d^*_1=211\eta _1^*+8201\eta _2^*,\, d^*_2=1616\eta _1^*+129268\eta _2^*,\, d^*_3=1656\eta _1^*+68672\eta _2^*,\, d^*_4=236\eta _1^*-26301\eta _2^*,\, d^*_5=\eta _1^*-3680\eta _2^*,\, d^*_6=994\eta _2^*,\, d^*_7=-98\eta _2^*,\, d^*_8=-77\eta _2^*$ and $d^*_9=21\eta _2^*.$

Let $s_{i},\ i=-1,0,1,....,{M+1}$ be the summation of the $i-$th row of R. Then, we have

$$\begin{aligned} s_{-1}= & {} \frac{177000\sigma \nu +133920(P_{\alpha } c_0^{\alpha }+\sigma \mu )\Delta x^2}{69120 \Delta x^2},\\ s_{0}= & {} \frac{ 86040\sigma \nu }{4320 \Delta x^2}, \\ s_{1}= & {} \frac{ -240\sigma \nu +4320 (P_{\alpha } c_0^{\alpha }+\sigma \mu ) \Delta x^2}{4320 \Delta x^2}, \\ s_{2}= & {} \frac{ -120\sigma \nu +4320 (P_{\alpha } c_0^{\alpha }+\sigma \mu ) \Delta x^2}{4320 \Delta x^2},\\ s_{k}= & {} P_{\alpha } c_0^{\alpha }+\sigma \mu ,\quad k=3,4,...,M-3,\\ s_{M-2}= & {} \frac{ -120\sigma \nu +4320 (P_{\alpha } c_0^{\alpha }+\sigma \mu ) \Delta x^2}{4320 \Delta x^2},\\ s_{M-1}= & {} \frac{ -240\sigma \nu +4320 (P_{\alpha } c_0^{\alpha }+\sigma \mu ) \Delta x^2}{4320 \Delta x^2},\\ s_{M}= & {} \frac{ 86040\sigma \nu }{4320 \Delta x^2},\\ s_{M+1}= & {} \frac{177000\sigma \nu +133920(P_{\alpha } c_0^{\alpha }+\sigma \mu )\Delta x^2}{69120 \Delta x^2}. \end{aligned}$$

For small enough $\Delta x,$ it follows that $s_{-1}>0, s_{0}>0, s_{k}\ge 0, k=1,...,M-1, s_{M}>0$ and $s_{M+1}>0$. Therefore, R is monotone and hence ${R}^{-1}$ exists. Let $r^{-1}_{k,j}$ be the (k, j)-th element of ${R}^{-1}.$ From the theory of matrices we have

$$\begin{aligned} \sum _{j=-1}^{M+1} r^{-1}_{k,j}s_{j}=1,\;\; \text {for}\;\;k=-1,0,1,...,M+1. \end{aligned}$$

(113)

Equation (113) yields

$$\begin{aligned} \sum _{j=-1}^{M} r^{-1}_{k,j}\le \frac{1}{s_{j}}. \end{aligned}$$

By Taylor’s expansion, we get

$$\begin{aligned} r^{-1}_{k,-1}&\le \frac{1}{s_{-1}}\\ {}&=\frac{69120\Delta x^2}{177000\sigma \nu }\left( 1+\frac{133920(P_{\alpha } c_0^{\alpha }+\sigma \mu )\Delta x^2}{177000\sigma \nu }\right) ^{-1}\\&\le \frac{69120\Delta x^2}{177000\sigma \nu }+O(\Delta x^4),\\ r^{-1}_{k,0}&\le \frac{1}{s_{0}}\\ {}&= \frac{4320 \Delta x^2}{ 86040\sigma \nu },\\ r^{-1}_{k,1}&\le \frac{1}{s_{1}}\\ {}&=-\frac{4320\Delta x^2}{240\sigma \nu }\left( 1-\frac{4320 (P_{\alpha } c_0^{\alpha }+\sigma \mu )\Delta x^2}{240\sigma \nu }\right) ^{-1}\\&\le -\frac{4320\Delta x^2}{240\sigma \nu }+O(\Delta x^4),\\ r^{-1}_{k,2}&\le \frac{1}{s_{2}}\\ {}&=-\frac{4320\Delta x^2}{120\sigma \nu }\left( 1-\frac{4320 (P_{\alpha } c_0^{\alpha }+\sigma \mu )\Delta x^2}{120\sigma \nu }\right) ^{-1}\\&\le -\frac{4320\Delta x^2}{120\sigma \nu }+O(\Delta x^4),\\ r^{-1}_{k,j}&\le \frac{1}{s_{j}}\\ {}&= \frac{1}{P_{\alpha } c_0^{\alpha }+\sigma \mu },\quad j=3,4,...,M-3,\\ r^{-1}_{k,M-2}&\le \frac{1}{s_{M-2}}\\ {}&=-\frac{4320\Delta x^2}{120\sigma \nu }\left( 1-\frac{4320 (P_{\alpha } c_0^{\alpha }+\sigma \mu )\Delta x^2}{120\sigma \nu }\right) ^{-1}\\&\le -\frac{4320\Delta x^2}{120\sigma \nu }+O(\Delta x^4),\\ r^{-1}_{k,M-1}&\le \frac{1}{s_{M-1}}\\ {}&=-\frac{4320\Delta x^2}{240\sigma \nu }\left( 1-\frac{4320 (P_{\alpha } c_0^{\alpha }+\sigma \mu )\Delta x^2}{240\sigma \nu }\right) ^{-1}\\&\le -\frac{4320\Delta x^2}{240\sigma \nu }+O(\Delta x^4),,\\&\quad r^{-1}_{k,M}\le \frac{1}{s_{M}}\\ {}&=\frac{4320 \Delta x^2}{ 86040\sigma \nu },\\ r^{-1}_{k,M+1}&\le \frac{1}{s_{M+1}}\\ {}&=\frac{69120\Delta x^2}{177000\sigma \nu }\left( 1+\frac{133920(P_{\alpha } c_0^{\alpha }+\sigma \mu )\Delta x^2}{177000\sigma \nu }\right) ^{-1}\\&\le \frac{69120\Delta x^2}{177000\sigma \nu }+O(\Delta x^4). \end{aligned}$$

By employing infinity norm, (112) reduces to

$$\begin{aligned} \Vert {\lambda }^{n}-\tilde{\lambda }^{n}\Vert _{\infty }= & {} \Vert {R}^{-1}{E}\Vert _{\infty }\\\le & {} \Vert {R}^{-1}\Vert _{\infty }\Vert {E}\Vert _{\infty }\\\le & {} \max \limits _{-1\le k \le M+1}\bigg (|\sum _{j=-1}^{M+1} r^{-1}_{k,j}|\bigg )O(\Delta x^6)\\\le & {} \max \limits _{-1\le k \le M+1}\bigg (|r^{-1}_{k,-1}|+|r^{-1}_{k,0}|+|r^{-1}_{k,1}|+|r^{-1}_{k,2}|\\{} & {} +\sum _{j=3}^{M-3} |r^{-1}_{k,j}|+|r^{-1}_{k,M-2}|\\{} & {} +|r^{-1}_{k,M-1}|+|r^{-1}_{k,M}|+|r^{-1}_{k,M+1}|\bigg )O(\Delta x^6)\\= & {} O(\Delta x^6). \end{aligned}$$

Alternatively, we may write

$$\begin{aligned} \max _{-1\le m\le M+1}\mid {\lambda }^{n}_{m}-\tilde{\lambda }^{n}_{m}\mid \le {\mathcal {K}} \Delta x^{6}, \end{aligned}$$

(114)

where $\mathcal {K}$ is a constant.

Moreover, by using (63), (64) and (114), we have

$$\begin{aligned} \mid {\lambda }^{n}_{-2}-\tilde{\lambda }^{n}_{-2}\mid = O(\Delta x^{6}),\hspace{0.2cm}\mid {\lambda }^{n}_{M+2}-\tilde{\lambda }^{n}_{M+2}\mid = O(\Delta x^{6}).\nonumber \\ \end{aligned}$$

(115)

From (17) and (57), it follows that

$$\begin{aligned} {{\mathcal {Z}}}^{n}(x)-\tilde{{\mathcal {Z}}}^{n}(x)=\sum _{k=-2}^{M+2}({\lambda }_{k}^{n}-\tilde{\lambda }_{k}^{n}) \Theta _{k}(x). \end{aligned}$$

(116)

The definition of the basis functions $\Theta _{k}$ leads to

$$\begin{aligned} \sum _{k=-2}^{M+2}| \Theta _{k}(x)|\le \frac{186}{120}. \end{aligned}$$

(117)

Operating the $L_\infty$ norm on (116) and making the use of (114), (115) and (117) leads to

$$\begin{aligned}{} & {} \Vert {{\mathcal {Z}}}^{n}(x)-\tilde{{\mathcal {Z}}}^{n}(x)\Vert _{\infty }\nonumber \\ {}{} & {} \quad \le |{\lambda }^{n}-\tilde{\lambda }^{n}|\sum _{k=-2}^{M+2} |\Theta _{k}(x)|\le {\mathcal {N}}\Delta x^6,\quad n\, \ge 1, \end{aligned}$$

(118)

where ${\mathcal {N}}=\frac{186}{120}{\mathcal {K}}$. Theorem 3 yields

$$\begin{aligned} \Vert {{\mathcal {Z}}}^{n}(x)-u^{n}(x)\Vert _{\infty }\le {\mathcal {M}}\Delta x^{6}. \end{aligned}$$

(119)

The triangle inequality gives

$$\begin{aligned}{} & {} \Vert \tilde{{\mathcal {Z}}}^{n}(x)-u^{n}(x)\Vert _{\infty }\le \Vert \tilde{{\mathcal {Z}}}^{n}(x)-{{\mathcal {Z}}}^{n}(x)\Vert _{\infty }\nonumber \\{} & {} \quad +\Vert {{\mathcal {Z}}}^{n}(x)-u^{n}(x)\Vert _{\infty }. \end{aligned}$$

(120)

Now, substituting (118) and (119) into (120), we obtain

$$\begin{aligned} \Vert \tilde{{\mathcal {Z}}}^{n}(x)-u^{n}(x)\Vert _{\infty }\le {\mathcal {L}}\Delta x^6\quad \forall \; n \ge 0. \end{aligned}$$

This completes the proof of Theorem 5. $\square$

Theorem 6

Assume that $\tilde{{\mathcal {Z}}}(x,t)$ and u(x, t), respectively, represents the B-spline approximation and the exact solution of nonlinear TFGE equation. Then, the method (58)–(66) converges with the following estimate

$$\begin{aligned} \Vert u(x,t)-\tilde{{\mathcal {Z}}}(x,t)\Vert _{\infty }=O(\Delta x^6+\Delta t^{2}). \end{aligned}$$

(121)

Proof

By using Theorem 5 and Eq. (46), we can obtain the result in (121). $\square$

4 Numerical illustrations

In this section, we consider three nonlinear examples and solve them using the present method (58)–(66) in order to illustrate the efficacy and accuracy of the method. We compute the $L_{\infty }$ norm error $({\mathcal {E}}^{M,N}_{1})$ of the present scheme. The $L_{\infty }$ norm error is defined as

$$\begin{aligned} {\mathcal {E}}^{M,N}_{1}=\max _{\begin{array}{c} 0\le m\le M\\ 0\le n\le N \end{array}}|\tilde{{\mathcal {Z}}}_m^n-u(x_m,t_n)|, \end{aligned}$$

where $u(x_m,t_n)$ is the exact solution and $\tilde{{\mathcal {Z}}}_m^n$ denote the approximate solution at $(x_m,t_n)$. We calculate the ROC (rate of convergence) of presented numerical method in space using the following formula:

$$\begin{aligned} d=\frac{\log ({\mathcal {E}}^{M,N}_{1})-\log ({\mathcal {E}}^{2M,N}_{1})}{\log (2)}\,. \end{aligned}$$

Numerical results are computed with MATLAB R2020a on AMD Ryzen 5 2500U and 2.00 GHz processor.

Example 1

We consider (1) with $\beta =3$, the IC:

$$\begin{aligned} u(x,0)=0,\, 0\le x\le 1 \end{aligned}$$

and BCs

$$\begin{aligned} u(0,t)=t^{2\alpha },\;u(1,t)=0,\, t\ge 0. \end{aligned}$$

The exact solution is given by $u(x,t)=t^{2\alpha }\left( 1-x^2\right) e^{2x}$. The source function f(x, t) can be obtained using the exact solution. We set $T=1$ and $\nu =1.$

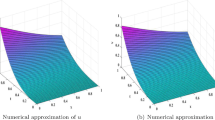
Table 2 presents the ROC in time based on $L_{\infty }$ norm errors for $\Delta x=1/1000$ and different N when $\alpha = 0.5$, 0.8, 0.95. It is observed in Table 2 that the proposed method converges with order two in time direction. Table 3 presents the ROC in space for $\Delta t=1/70,000$ and different M when $\alpha =0.95.$ It can be observed from Table 3 that the proposed method is sixth order accurate in space. Further, we can observe from Tables 2 and 3 that the experimental ROC is consistent with the theoretical ROC given in Theorem 6. The comparison of the $L_{\infty }$ error of our scheme for $\Delta t = 0.0003$ and $\Delta x=0.01$ with the method in Majeed et al. (2020) is given in Table 4. It can be observed from Table 4 that our method is more accurate than the method in Majeed et al. (2020). Figure 1 presents the two-dimensional graph of the approximate solutions for several T. In order to observe the effect of $\alpha$, we plot the approximate solution for various values of $\alpha$ when $T=0.5$ in Fig. 2. The surface plots of numerical and exact solutions when $\alpha =0.95$ and $N=M=50$ are displayed in Figs. 3 and 4, respectively. These figures confirm that the proposed method approximates the exact solution very well. The elapsed computational time (in seconds) for the OSQB scheme is presented in Table 2. From the table one can observe that the present numerical scheme is computationally efficient.

Table 2 Numerical error results (in time) with $\Delta x=1/1000$ for Example 1

Table 3 Numerical error results (in space) with $\Delta t=1/70,000$ and $\alpha = 0.95$ for Example 1

Table 4 Comparison of numerical error results for Example 1 with $\alpha =0.95$

Fig. 1

Approximate solutions for Example 1 with various values of T and $\alpha = 0.95$

Fig. 2

Approximate solutions for Example 1 with various values of $\alpha$ at T = 0.5

Fig. 3

3D plots of approximate solution for Example 1 with N=M = 50 and $\alpha = 0.95$

Fig. 4

3D plot of exact solution for Example 1 with M = N = 50 and $\alpha = 0.95$

Example 2

We consider (1) with $\beta =3$, the IC:

$$\begin{aligned} u(x,0)=x^2e^{2x},\, 0\le x\le 1 \end{aligned}$$

and BCs

$$\begin{aligned} u(0,t)=0,\;u(1,t)=e^2\left( 1+t^2\right) ,\, t\ge 0. \end{aligned}$$

The analytical solution is given by $u(x,t)=\left( 1+t^2\right) x^2e^{2x}$. The source function f(x, t) can be obtained using the exact solution. We set $T=1$ and $\nu =1.$

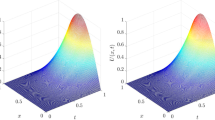
In Table 5, we give the ROC in time for $\Delta x=1/500$ and different N when $\alpha = 0.5$. As expected, it is observed in Table 5 that the proposed method converges with order two in time direction. Next, Table 6 gives the ROC in space for $\Delta t=1/70,000$ and different M when $\alpha =0.95.$ It can be seen in this table that the proposed method is sixth order accurate in space. Further, Tables 5 and 6 confirm that the experimental ROC is consistent with the theoretical one given in Theorem 6. The comparison of the $L_{\infty }$ error of our scheme for $\Delta t = 0.0003$ and $\Delta x=0.01$ with the scheme in Majeed et al. (2020) is given in Table 7 which suggests that our method is more accurate than the method in Majeed et al. (2020). Figure 5 presents the two-dimensional graph of the numerical solution for several T. Figs. 6 and 7 show the 3D plots of approximate and exact solutions, respectively, when $\alpha =0.95$ and $M=N=50$. These figures show that the numerical solution agrees very well with the exact solution.

Table 5 Numerical error results (in time) with $\Delta x=1/500$ and $\alpha = 0.5$ for Example 2

Fig. 5

Approximate solutions for Example 2 with various values of T and $\alpha = 0.95$

Fig. 6

3D plot of approximate solution for Example 2 with M = N = 50 and $\alpha = 0.95$

Fig. 7

3D plot of exact solution of Example 2 with M= N = 50 and $\alpha = 0.95$

Example 3

We consider (1) with $\beta =2$, the IC:

$$\begin{aligned} u(x,0)=0,\, 0\le x\le 1 \end{aligned}$$

and BCs

$$\begin{aligned} u(0,t)=0,\;u(1,t)=0,\, t\ge 0. \end{aligned}$$

The exact solution is given by $u(x,t)=t^2\sin (2\pi x)$. The source function f(x, t) can be obtained using the exact solution. We set $T=1$ and $\nu =1.$

Table 6 Numerical error results (in space) with $\Delta t=1/70,000$ and $\alpha = 0.95$ for Example 2

Table 7 Comparison of numerical error results with $\alpha =0.95$ for Example 2

Table 8 Numerical error results (in time) with $\Delta x=1/500$ and $\alpha = 0.5$ for Example 3

Table 9 Numerical error results (in space) with $\Delta t=1/70,000$ and $\alpha = 0.95$ for Example 3

Table 10 Comparison of numerical error results with $\alpha =0.96$ for Example 1

In Table 8, we give the ROC in time for $\Delta x=1/500$ and different N when $\alpha = 0.5$. As expected, it is observed in Table 8 that the proposed method converges with order two in time direction. Table 9 presents the ROC in space for $\Delta t=1/70,000$ and different M when $\alpha =0.95.$ It can be seen in this table that the proposed method is sixth order accurate in space. Further, Tables 8 and 9 confirm that the experimental ROC is consistent with the theoretical one given in Theorem 6. The comparison of the $L_{\infty }$ error of our scheme for $\Delta t = 0.0001$ and $\Delta x=0.01$ with the method in Majeed et al. (2020) is given in Table 10. It can be observed from Table 10 that our scheme is more accurate than the scheme in Majeed et al. (2020). Figure 8 presents the two-dimensional graph of the numerical solution for several T. In Figs. 9 and 10, we present the 3D plots of numerical and exact solutions, respectively, when $\alpha =0.95$ and $M=N=50$. Figures 9 and 10 suggest that the approximate solution agrees very well with the exact solution.

Fig. 8

Approximate solutions for Example 3 with various values of T and $\alpha = 0.95$

Fig. 9

3D plot of approximate solution for Example 3 with M = N = 50 and $\alpha = 0.95$

Fig. 10

3D plot of exact solution for Example 3 with M=N = 50 and $\alpha = 0.95$

5 Conclusions

The present paper described an accurate computational method for numerical solution of nonlinear TFGF equation. In this technique, the $L2-1_{\sigma }$ formula is used for the approximation of the Caputo fractional derivative which appears in the model problem considered. The space derivatives are approximated using the collocation technique based on an OSQB. The developed method is proved to be unconditionally stable. The convergence results indicate that the method is sixth order convergent in space direction and second order convergent in temporal direction. The experimental results indicate that the present method is very accurate and effective in solving the nonlinear TFGF equation and the experimental ROC is consistent with the theoretical one. The comparison results show that our scheme provides more accurate results than the method in Majeed et al. (2020). Moreover, the authors in Majeed et al. (2020) has not established the convergence results for their method while we proved that our method has convergence order of six in space and of order two in time. It is also observed that the order of the fractional derivative has profound effects on the solution profile of the nonlinear TFGF equation. The CPU time of the method, provided in the Tables, confirms that the method is computationally efficient. Indeed, a potential direction for future research or extension of this work could involve developing a high-order numerical method for solving the nonlinear TFGF equation with non-smooth exact solution. While the present study focuses on problems with smooth exact solutions with respect to the time variable, addressing scenarios with non-smooth solutions could enhance the applicability and robustness of the numerical method.