A high-accuracy computational technique based on $L2-1_{\sigma }$ and B-spline schemes for solving the nonlinear time-fractional Burgers’ equation

Abstract

In this article, we develop and analyze an efficient numerical technique to solve the nonlinear temporal fractional Burgers’ equation (TFBE). The temporal fractional derivative is considered in the terms of Caputo and approximated by using the $L2-1_{\sigma }$ scheme. The quintic B-spline (QBS) basis function is employed for discretization of the space derivative to obtain a fully discrete scheme. The proposed method is analyzed for its convergence and stability. Four nonlinear problems are considered to illustrate the advantage and applicability of the present method. The proposed scheme has an order of convergence $O(\varDelta t^{2}+\varDelta x^4)$, where $\varDelta t$ and $\varDelta x$ are the step sizes in time and space directions, respectively. The comparison with the corresponding results of an existing method based on cubic parametric spline functions demonstrates that the proposed method is more accurate when solving the nonlinear time-fractional Burgers’ equation. The CPU time is provided to show the computational efficiency of the method. The obtained stable and highly-accurate numerical results and low computational time collectively underscore the significance of the proposed technique in solving the nonlinear time-fractional Burgers’ equation.

1 Introduction

In recent years, the differential equations of fractional order have become center of attraction among researchers due to their wide range of applications in applied sciences and engineering. For more details, one may refer to Podlubny (1999), Giona et al. (1992), Mainardi (1997), Bagley and Torvik (1984), Roul et al. (2019b), Roul et al. (2019c), Veeresha et al. (2020), Roul et al. (2023), Roul (2020), Roul (2021), Roul and Goura (2020) and references therein. It is well known that the fractional order derivatives can model complex phenomena more accurately than the derivatives of integer order.

In this article, we deal with the following nonlinear TFBE:

$$\begin{aligned}{} & {} \frac{\partial ^{\alpha } u(x,t)}{\partial t^{\alpha }} + u(x,t)\frac{\partial u(x,t)}{\partial x} - \nu \frac{\partial ^{2} u(x,t)}{\partial x^{2}} \nonumber \\{} & {} \quad = f(x,t),\quad (x,t)\in \left( X_l,X_r\right) \times \left( 0,T\right) , \end{aligned}$$

(1)

where $\nu$ represents the viscosity parameter and f(x, t) is the source term. The initial condition (IC) is

$$\begin{aligned} u(x,0)=g(x),\, x\in [X_l, X_r] \end{aligned}$$

(2)

and the boundary conditions (BCs) are

$$\begin{aligned} u(X_l,t)={\theta }_{1}(t),\;u(X_r,t)={\theta }_{2}(t), \quad t\ge 0. \end{aligned}$$

(3)

The functions $f(x,t),\, g(x),\, {\theta }_{1}(t)$ and ${\theta }_{2}(t)$ are assumed to be sufficiently smooth. The Caputo fractional derivative $\frac{\partial ^{\alpha } u(x,t)}{\partial t^{\alpha }}$ in (1) is defined as follows:

$$\begin{aligned}{} & {} \frac{\partial ^{\alpha } u(x,t)}{\partial t^{\alpha }}=\frac{1}{\varGamma (1-\alpha )}\int _{0}^{t}(t-\kappa )^{-\alpha }\frac{\partial u(x,\kappa )}{\partial \kappa }\textrm{d}\kappa , \nonumber \\{} & {} \quad 0<\alpha <1. \end{aligned}$$

(4)

Burgers’ equation has numerous applications in various fields of science and engineering and thus the researchers worldwide have been showing keen interest in the study of this equation. More specifically, this equation describes nonlinear wave propagation effects, waves on shallow water surfaces, chemical reaction-diffusion processes and one-dimensional turbulence, see Logan (1994), Debtnath (1997), Adomian (1995), Burgers (1948). The existence and uniqueness of solutions to the Burgers’ equation of integer order have been discussed in Gyöngy (1998), Wang and Warnecke (2003). For the fractional Burgers’ equation, the existence and uniqueness of the solution is discussed by Guesmia and Daili (2010). Kolkovska (2005) considered the stochastic Burgers-type equation and studied the existence and regularity of solutions in appropriate Hilbert spaces. Vieru et al. (2021) numerically investigated the generalized time-fractional Burgers’ equation with variable coefficients, utilizing a finite-difference scheme based on integral representations of Mittag–Leffler functions. The approach is applied to specific cases, revealing numerical solutions and comparisons for different time-fractional derivatives. In Chen et al. (2021), the authors introduced a nonlinear fully discrete scheme, utilizing the nonuniform Alikhanov formula and Fourier spectral approximation, for numerically approximating the time-fractional Burgers equation with nonsmooth solutions. This scheme’s solvability is established through fixed point theorem and a priori estimate. Recently, Shafiq et al. (2022) employed cubic B-spline functions and a $\theta$-weighted scheme to numerically solve the time-fractional Burgers’ equation with the Atangana–Baleanu derivative, demonstrating its unconditional stability and second-order convergence in temporal and spatial directions through finite-difference discretization. It is well known that Burgers’ equation and Navier–Stokes equation are similar in the form of their nonlinear terms.

In most of the cases, obtaining an exact solution to the partial differential equations (PDEs) involving fractional order derivatives is a challenging task. Therefore, numerical techniques must be adapted to approximate the solution of temporal fractional order PDEs. Many authors employed various kinds of numerical methods to solve the TFBE. For instance, Mustafa Inc. Inc (2008) considered the application of variational iteration method for numerical solution of the homogeneous form of the time-fractional Burgers’ equation (1). Liu and Hou (2011) proposed the generalized differential transform method to obtain numerical solution of the space- and time-fractional coupled Burgers’ equation. In El-Danaf and Hadhoud (2012), authors developed general framework of the cubic parametric spline functions to construct a numerical technique for obtaining the approximate solution of TFBE. Yaseen and Abbas (2020) constructed a numerical method to solve the problem considered. In this method, they considered the standard finite-difference formulation to approximate the Caputo time-fractional derivative and used cubic trigonometric B-spline functions for the discretization of space variable. This method is first order convergent in time and second order convergent in space. In Majeed et al. (2020), authors presented a numerical method based on cubic B-spline finite element method to solve the TFBE. They have approximated the Caputo fractional derivative using the L1 formula for temporal discretization and then used the Crank–Nicolson scheme based on cubic B-spline basis functions for the spatial discretization. This scheme has $O(\varDelta t^{2-\alpha }+\varDelta x^2)$ convergence rate. On the other hand, various numerical techniques were used to obtain the numerical solution of Burgers equation of integer order. These methods include finite-difference method (Hassanien et al. 2005), finite element method (Kutluay et al. 2004) and B-spline collocation methods (Ramadan et al. 2005; Saka and Dag 2008).

Our main objective is to develop an efficient and high-order numerical method for solving TFBE (1)–(3). The proposed method is based on the $L2-1_{\sigma }$ scheme in temporal direction and the QBS basis function in the spatial direction. The stability and convergence of this scheme are analyzed, demonstrating that it achieves second-order convergence in time and fourth-order convergence in space. The comparison of the results obtained by the present scheme with those obtained using the method in El-Danaf and Hadhoud (2012) illustrates the advantage of the proposed method. The computational time of the present method is provided. To the best of our knowledge, this scheme has not been considered in the literature for the numerical approximation of the problem defined by (1)–(3).

This paper is organized as follows: in Sect. 2, the proposed numerical method is developed to solve the TFBE. The stability and convergence of our method are discussed in Sect. 3. The obtained numerical results are explained in Sect. 4. Section 5 discusses the conclusions.

2 Numerical scheme description

This section aims to derive a numerical scheme to solve the TFBE (1) subject to IC and BCs given in Eqs. (2) and (3), respectively.

2.1 Time discretization

First, we discretize the problem (1)–(3) in temporal direction on [0, T]. For an integer $N>1$, we set $t_n=n \varDelta t$ for $n=0,1,\ldots , N$. The uniform time step size is given by $\varDelta t=\frac{T}{N}$. Suppose that $t_{n-1+\sigma }=(n-1+\sigma )\varDelta t$, where $\sigma =1-\frac{\alpha }{2}$.

In view of the $L2-1_{\sigma }$ formula (Alikhanov 2015), the Caputo derivative defined by (4) can be approximated at $t=t_{n-1+\sigma }$ as follows:

$$\begin{aligned} \begin{aligned}&\frac{\partial ^{\alpha } u(x,t_{n-1+\sigma })}{\partial t^{\alpha }}=\frac{\varDelta t^{-\alpha }}{\varGamma (2-\alpha )}\bigg [c_0^{\alpha }u(x,t_n)\\&\quad -\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1} -c^{\alpha }_{n-l}\right) u(x,t_l)\\&\quad -c^{\alpha }_{n-1}u(x,t_0)\bigg ]+O(\varDelta t^{3-\alpha }), \quad n=1,2,\ldots ,N, \end{aligned} \end{aligned}$$

(5)

where the coefficients are defined as

$$\begin{aligned} c_0^{\alpha }=a_0^{\alpha }, \quad \text {when } n=1 \end{aligned}$$

(6)

and when $n\ge 2$

$$\begin{aligned} c_j^{\alpha }= {\left\{ \begin{array}{ll} a_0^{\alpha }+b_1^{\alpha }, &{}j=0,\\ a_j^{\alpha }+b_{j+1}^{\alpha }-b_{j}^{\alpha }, &{}1\le j\le n-2,\\ a_j^{\alpha }-b_{j}^{\alpha },&{} j=n-1, \end{array}\right. } \end{aligned}$$

(7)

where

$$\begin{aligned} a_0^{\alpha }&{=}\sigma ^{1-\alpha }, \quad a_{j}^{\alpha }{=}(j+\sigma )^{1-\alpha }{-}(j-1+\sigma )^{1-\alpha },\quad j\ge 1,\\ b_{j}^{\alpha }&=\frac{1}{2-\alpha }\left[ (j+\sigma )^{2-\alpha }-(j-1+\sigma )^{2-\alpha }\right] \\&\quad -\frac{1}{2}\left[ (j+\sigma )^{1-\alpha }+(j-1+\sigma )^{1-\alpha }\right] ,\,j\ge 1. \end{aligned}$$

The truncation error term $O(\varDelta t^{3-\alpha })$ in (5) comes under the assumption that $u(\cdot ,t) \in {\mathbb {C}}^3[0, T ]$.

Lemma 1

(Alikhanov 2015) For $c^{\alpha }_j,$ $0<\alpha <1$, the following holds true:

• (1) $c^{\alpha }_j>\frac{1-\alpha }{2}(j+\sigma )^{-\alpha }\ge 0,\; j\ge 0,$

• (2) $c^{\alpha }_{j-1}>c^{\alpha }_{j}, \;j\ge 1.$

We consider (1) at $t=t_{n-1+\sigma }$ and let $u(x,t_n)=u^n(x),$ to obtain

$$\begin{aligned} \begin{aligned}&\frac{\partial ^{\alpha } u^{n-1+\sigma }(x)}{\partial t^{\alpha }}{+}u^{n-1+\sigma }(x)\frac{\partial u^{n-1+\sigma }(x)}{\partial x}{-}\nu \frac{\partial ^{2} u^{n-1+\sigma }(x)}{\partial x^2}\\&\quad = f^{n-1+\sigma }(x), x \in (X_l,X_r), \, n=1,2,\ldots , N, \end{aligned}\nonumber \\ \end{aligned}$$

(8)

with IC

$$\begin{aligned} u(x,t_0)=u^0(x)=g(x),\quad x\in (X_l,X_r) \end{aligned}$$

(9)

and BCs

$$\begin{aligned} u(X_l,t_n){} & {} =u^{n}(X_l)={\theta }_{1}(t_{n}),\;u(X_r,t_n)=u^{n}(X_r)\nonumber \\{} & {} ={\theta }_{2}(t_{n}). \end{aligned}$$

(10)

Using Eq. (5), from (8), we have

$$\begin{aligned} \begin{aligned}&\frac{\varDelta t^{-\alpha }}{\varGamma (2-\alpha )}\left[ c_0^{\alpha }u^n(x)-\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1} \right. \right. \\&\left. \left. -c^{\alpha }_{n-l}\right) u^{l}(x)-c^{\alpha }_{n-1}u^{0}(x)\right] +\left( uu_{x}\right) ^{n-1+\sigma }(x)\\&\quad - \nu u_{xx}^{n-1+\sigma }(x) = f^{n-1+\sigma }(x)+O(\varDelta t^{3-\alpha }),\\&\quad \quad X_l<x<X_r, \quad n=1,2,\ldots , N. \end{aligned} \end{aligned}$$

(11)

Via Taylor’s expansion, we have

$$\begin{aligned}{} & {} u^{n-1+\sigma }(x)=\sigma u^{n}(x)+(1-\sigma ) u^{n-1}(x)+O(\varDelta t^{2}), \nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned}{} & {} u_{x}^{n-1+\sigma }(x)=\sigma u_{x}^{n}(x)+(1-\sigma ) u_{x}^{n-1}(x)+O(\varDelta t^{2}),\nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned}{} & {} u_{xx}^{n-1+\sigma }(x)=\sigma u_{xx}^{n}(x)+(1-\sigma ) u_{xx}^{n-1}(x)+O(\varDelta t^{2}),\nonumber \\ \end{aligned}$$

(14)

Multiplying Eqs. (12) and (13), we get

$$\begin{aligned} \begin{aligned}&\left( uu_{x}\right) ^{n-1+\sigma }(x)=\sigma ^2\left( uu_{x}\right) ^{n}(x)\\&\quad +\sigma (1-\sigma ) u^nu_{x}^{n-1}(x)+\sigma (1-\sigma )u^{n-1}u_{x}^n(x)\\&\quad +(1-\sigma )^2\left( uu_{x}\right) ^{n-1}(x)+O(\varDelta t^{2}). \end{aligned} \end{aligned}$$

(15)

Plugging (14) and (15) into (11) and rearranging the terms, we obtain

$$\begin{aligned} \begin{aligned} \varTheta&c_0^{\alpha }u^n(x)+\sigma ^2\left( uu_{x}\right) ^{n}(x)+\sigma (1-\sigma ) u^nu_{x}^{n-1}(x)\\&\qquad +\sigma (1-\sigma )u^{n-1}u_{x}^n(x)-\sigma \nu u_{xx}^{n}(x)\\&\quad =\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)\\&\qquad +\varTheta c^{\alpha }_{n-1}u^{0}(x)-(1-\sigma )^2\left( uu_{x}\right) ^{n-1}(x)\\&\qquad +(1-\sigma )\nu u_{xx}^{n-1}(x)+O(\varDelta t^{2}),\\&\quad X_l<x<X_r, \quad n=1,2,\ldots , N, \end{aligned} \end{aligned}$$

(16)

with $\varTheta =\frac{\varDelta t^{-\alpha }}{\varGamma (2-\alpha )}.$

We linearize the term $\left( uu_{x}\right) ^n(x)$ as follows Rubin and Graves (1975):

$$\begin{aligned} \left( uu_{x}\right) ^n(x)=u^nu_{x}^{n-1}(x)+u^{n-1}u_{x}^{n}(x)-\left( uu_{x}\right) ^{n-1}(x).\nonumber \\ \end{aligned}$$

(17)

Substitution of (17) into (16) and the rearrangement of the terms lead to

$$\begin{aligned} \begin{aligned}&\left( \varTheta c_0^{\alpha }{+}\sigma u_{x}^{n-1}(x)\right) u^{n}(x){+}\left( \sigma u^{n{-}1}(x)\right) u_{x}^{n}(x){-}\sigma \nu u_{xx}^{n}(x)\\&\quad =\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)\\&\qquad +\varTheta c^{\alpha }_{n-1}u^{0}(x)+(2\sigma -1)\left( uu_{x}\right) ^{n-1}(x)\\&\qquad +(1-\sigma )\nu u_{xx}^{n-1}(x)+f^{n-1+\sigma }(x)+O(\varDelta t^{2}),\,\\&\quad X_l<x<X_r, \, n=1,2,\ldots , N. \end{aligned} \end{aligned}$$

(18)

2.2 Space discretization

Here, we discretize Eq. (18) using a collocation method based on QBS basis function in spatial direction.

For a given $M>1$, we consider a uniform partition $I=\bigl \{X_l = x_0<x_1<\cdots < x_{M} = X_r\bigr \}$ over the domain $\left[ X_l,X_r\right]$, with $x_{m}=m\varDelta x,$ where $\varDelta x$ represents the spatial mesh size and $m=0,1,\ldots ,M$. We define the midpoints of the subintervals of I by $\tau _{m}=\frac{x_{m-1}+x_{m}}{2}, m=1,2,\ldots ,M$. Suppose that the set of these points be ${\pi }_I = \{\tau _{1}<\tau _{2}<\cdots <\tau _{M}\}$. Let $S_{5,I} = \{p(x)| p(x)\in {\mathbb {C}}^4[X_l, X_r]$} be the quintic-spline space (QSS). The QBS basis functions, $Q_{k}(x)$, $-2 \le k \le M+2$, for $S_{5,I}$ are given by Boor (1978)

$$\begin{aligned}{} & {} Q_{k}(x) = \frac{1}{120\varDelta x^{5}}\nonumber \\{} & {} {\left\{ \begin{array}{ll} (x-x_{k-3})^5=a_1,\, &{} x\in [x_{k-3},x_{k-2}], \\ a_1-6(x-x_{k-2})^5=a_2,\, &{} x\in [x_{k-2},x_{k-1}], \\ a_2+15(x-x_{k-1})^5,\, &{} x\in [x_{k-1},x_{k}],\\ b_2+15(x_{k+1}-x)^5, \, &{} x\in [x_{k},x_{k+1}],\\ b_1-6(x_{k+2}-x)^5=b_2, \,&{} x\in [x_{k+1},x_{_{k+2}}],\\ (x_{k+3}-x)^5=b_1, \,&{} x\in [x_{k+2},x_{k+3}],\\ 0, \quad &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(19)

To support the QBS basis functions, additional 10 grid points are included outside the interval I, denoted as $x_{-5}<x_{-4}<x_{-3}<x_{-2}<x_{-1}<x_{0}=X_l$ and $x_{M}=X_r<x_{M+1}<x_{M+2}<x_{M+3}<x_{M+4}<x_{M+5}$. Let $\tilde{Q}=\{Q_{{-}2}(x), Q_{{-}1}(x), Q_{0}(x),\ldots , Q_M(x), Q_{M{+}1}(x), Q_{M+2}(x)\}$ be the set of QBS basis functions, which is linearly independent. We define $Q^*(I)$ as the span of ${\tilde{Q}}$ over the interval I. Therefore, $Q^*(I)$ is a $M+5$ dimensional QSS. It can be observed that $Q^*(I)=S_{5,I}$ (Prenter 1975), hence, $S_{5,I}$ is a QSS over I.

Table 1 The values of $Q_{m}(x)$, $Q_{m}'(x)$ and $Q_{m}''(x)$

Let $\hat{\varPsi }^{n}(x)$ represent the approximation of the exact solution $u^{n}(x)$ of (9)–(11). It can be expressed as

$$\begin{aligned} \hat{\varPsi }^n(x)=\sum _{k=-2}^{M+2}\hat{\lambda }_{k}^{n}Q_{k}(x), \end{aligned}$$

(20)

where $\hat{\lambda }_k^n$’s are the constants that need to be determined. The values of $\hat{\varPsi }^n(x)$, as well as its derivatives upto second-order, are computed at $x=x_m$ (for $0\le m\le M$) and $x=\tau _m$ (for $1\le m\le M$), as presented in Table 1, using (19). Using the information provided in Table 1, we obtain the following relations:

$$\begin{aligned} \hat{\varPsi }^n(x_m)= & {} \frac{1}{120}\left( \hat{\lambda }_{m-2}^n+26\hat{\lambda }_{m-1}^n +66\hat{\lambda }_{m}^n\right. \nonumber \\{} & {} \left. +26\hat{\lambda }_{m+1}^n+\hat{\lambda }_{m+2}^n\right) , \end{aligned}$$

(21)

$$\begin{aligned} \hat{\varPsi }_{x}^n(x_m)= & {} \frac{1}{24\varDelta x}\left( -\hat{\lambda }_{m-2}^n-10\hat{\lambda }_{m-1}^n\right. \nonumber \\{} & {} \left. +10\hat{\lambda }_{m+1}^n+\hat{\lambda }_{m+2}^n\right) , \end{aligned}$$

(22)

$$\begin{aligned} \hat{\varPsi }_{xx}^n(x_m)= & {} \frac{1}{6\varDelta x^2}\left( \hat{\lambda }_{m-2}^n+2\hat{\lambda }_{m-1}^n\right. \nonumber \\{} & {} \left. -6\hat{\lambda }_{m}^n +2\hat{\lambda }_{m+1}^n+\hat{\lambda }_{m+2}^n\right) , \end{aligned}$$

(23)

$$\begin{aligned} \hat{\varPsi }^n(\tau _m)= & {} \frac{1}{3840}\big (\hat{\lambda }_{m-3}^n+237\hat{\lambda }_{m-2}^n +1682\hat{\lambda }_{m-1}^n\nonumber \\{} & {} +1682\hat{\lambda }_{m}^n+237\hat{\lambda }_{m+1}^n+\hat{\lambda }_{m+2}^n\big ), \end{aligned}$$

(24)

$$\begin{aligned} \hat{\varPsi }_{x}^n(\tau _m)= & {} \frac{1}{384 \varDelta x}\big (-\hat{\lambda }_{m-3}^n-75 \hat{\lambda }_{m-2}^n\nonumber \\{} & {} -154\hat{\lambda }_{m-1}^n+154\hat{\lambda }_{m}^n+75 \hat{\lambda }_{m+1}^n+\hat{\lambda }_{m+2}^n\big ),\nonumber \\ \end{aligned}$$

(25)

$$\begin{aligned} \hat{\varPsi }_{xx}^n(\tau _m)= & {} \frac{1}{48\varDelta x^2}\left( \hat{\lambda }_{m-3}^n+21 \hat{\lambda }_{m-2}^n\right. \nonumber \\{} & {} \left. -22\hat{\lambda }_{m-1}^n-22\hat{\lambda }_{m}^n+21\hat{\lambda }_{m+1}^n +\hat{\lambda }_{m+2}^n\right) . \end{aligned}$$

(26)

Theorem 1

Consider the quintic-spline interpolant (QSI) ${\varPsi }^n(x)$ of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$. Then,

$$\begin{aligned} {\varPsi }_{x}^n(x_{m})= u_{x}^n(x_{m})+O({\varDelta x}^{6}),0\le m \le M \end{aligned}$$

and

$$\begin{aligned} {\varPsi }_{xx}^n(x_{m})= & {} u_{xx}^n(x_{m})+\frac{{\varDelta x}^{4}}{720}u_{xxxxxx}^n(x_{m})\nonumber \\{} & {} +O({\varDelta x}^{6}),0\le m \le M. \end{aligned}$$

Proof

The proof of this result is analogous to the argument presented in Theorem 2.1 of Roul et al. (2019a). $\square$

Theorem 2

Consider the QSI ${\varPsi }^n(x)$ of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$. Then,

$$\begin{aligned} {\varPsi }_{x}^n({\tau }_{m})= u_{x}^n({\tau }_{m})+O({\varDelta x}^{6}), 1\le m \le M \end{aligned}$$

and

$$\begin{aligned} {\varPsi }_{xx}^n({\tau }_{m})= & {} u_{xx}^n({\tau }_{m})-\frac{7{\varDelta x}^{4}}{5760}u_{xxxxxx}^n({\tau }_{m})\nonumber \\{} & {} +O({\varDelta x}^{6}), 1\le m \le M. \end{aligned}$$

Proof

The proof of this result is analogous to the argument presented in Theorem 2.2 of Roul et al. (2019a). $\square$

Theorem 3

Consider the QSI ${\varPsi }^n(x)\in S_{5,I}$ of $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$. Then, we can obtain (refer to Theorem 2.3 of Roul et al. (2019a)):

$$\begin{aligned} \Vert D^{p}({\varPsi }^n(x)-u^n(x))\Vert _{\infty }\le {\mathcal {M}}\varDelta x^{6-p},\; p=0,1,2, \end{aligned}$$

(27)

with $D^{p}=\frac{\partial ^p}{\partial x^p}.$

Considering (18) at $x=x_m,$ one can obtain

$$\begin{aligned} \begin{aligned}&\left( \varTheta c_0^{\alpha }+\sigma u_{x}^{n-1}(x)\right) u^{n}(x_m)+\left( \sigma u^{n-1}(x_m)\right) \\&\quad u_{x}^{n}(x_m)-\sigma \nu u_{xx}^{n}(x_m)\\&\quad =\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x_m)+\varTheta c^{\alpha }_{n-1}u^{0}(x_m)\\&\qquad +(2\sigma -1)\left( uu_{x}\right) ^{n-1}(x_m)\\&\qquad +(1-\sigma )\nu u_{xx}^{n-1}(x_m)+f^{n-1+\sigma }(x_m),\,\\&\quad 0\le m\le M,\, n\ge 1. \end{aligned} \end{aligned}$$

(28)

The BCs (10) lead to

$$\begin{aligned} u^{n}(x_{0})={\theta }_{1}(t_{n}),\;u^{n}(x_{M})={\theta }_{2}(t_{n}). \end{aligned}$$

(29)

According to the collocation approach, we make $\hat{\varPsi }^n(x)$ to satisfy (28)–(29) at the nodal points. Thus, from (28) to (29), we obtain

$$\begin{aligned}{} & {} \begin{aligned}&\left( \varTheta c_0^{\alpha }+\sigma \hat{\varPsi }_{x}^{n-1}(x_m)\right) \hat{\varPsi }^{n}(x_m)+\left( \sigma \hat{\varPsi }^{n-1}(x_m)\right) \\&\quad \hat{\varPsi }_{x}^{n}(x_m)-\sigma \nu \hat{\varPsi }_{xx}^{n}(x_m)\\&\quad =\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \hat{\varPsi }^{l}(x_m)+\varTheta c^{\alpha }_{n-1}\hat{\varPsi }^{0}(x_m)\\&\qquad +(2\sigma -1)\left( \hat{\varPsi }\hat{\varPsi }_{x}\right) ^{n-1}(x_m)\\&\qquad +(1-\sigma )\nu \hat{\varPsi }_{xx}^{n-1}(x_m)+f^{n-1+\sigma }(x_m),\, \\&\quad 0\le m\le M,\, n\ge 1. \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \quad \hat{\varPsi }^{n}(x_{0})={\theta }_{1}(t_{n}),\;\hat{\varPsi }^{n}(x_{M})={\theta }_{2}(t_{n}). \end{aligned}$$

(31)

Inserting the expressions for $\hat{\varPsi }^n(x_m)$, $\hat{\varPsi }_x^n(x_m)$ and $\hat{\varPsi }^n_{xx}(x_m)$ from (21), (22) and (23), respectively, into (30) yields

$$\begin{aligned} \begin{aligned}&(p_m^{n-1}+s_m^{n-1})\hat{\lambda }_{m-2}^n+(q_m^{n-1}+v_m^{n-1})\hat{\lambda }_{m-1}^n \\&\qquad +(r_m^{n-1})\hat{\lambda }_{m}^n+(q_m^{n-1}-v_m^{n-1})\hat{\lambda }_{m+1}^n\\&\qquad +(p_m^{n-1}-s_m^{n-1})\hat{\lambda }_{m+2}^n\\&\quad =\omega _m^{n-1}{+}f^{n-1{+}\sigma }(x_m),\hspace{0.1cm} 0{\le } m\le M, \hspace{0.1cm} n=1,2,\ldots , N, \end{aligned} \end{aligned}$$

(32)

where

$$\begin{aligned} p_m^{n-1}= & {} \frac{\varTheta c_0^{\alpha }}{120}+\frac{\sigma \hat{\varPsi }_x^{n-1}(x_{m})}{120}-\frac{\sigma \nu }{6\varDelta x^2},\\ q_m^{n-1}= & {} \frac{26\varTheta c_0^{\alpha }}{120}+\frac{26\sigma \hat{\varPsi }_x^{n-1}(x_{m})}{120}-\frac{\sigma \nu }{3\varDelta x^2},\\ r_m^{n-1}= & {} \frac{66\varTheta c_0^{\alpha }}{120}+\frac{66\sigma \hat{\varPsi }_x^{n-1}(x_{m})}{120}+\frac{\sigma \nu }{\varDelta x^2}, \\ s_m^{n-1}= & {} -\frac{\sigma \hat{\varPsi }^{n-1}(x_{m})}{24\varDelta x},\quad v_m^{n-1}=-\frac{10\sigma \hat{\varPsi }^{n-1}(x_{m})}{24\varDelta x} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \omega _m^{n-1}&=\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \hat{\varPsi }^{l}(x_m)+\varTheta c^{\alpha }_{n-1}\hat{\varPsi }^{0}(x_m)\\&\quad +(2\sigma -1)\left( \hat{\varPsi }\hat{\varPsi }_{x}\right) ^{n-1}(x_m)+(1-\sigma )\nu \hat{\varPsi }_{xx}^{n-1}(x_m). \end{aligned} \end{aligned}$$

Using (21), from (31) we have

$$\begin{aligned}{} & {} \hat{\lambda }_{-2}^n+26\hat{\lambda }_{-1}^n+66\hat{\lambda }_0^n +26\hat{\lambda }_{1}^n+\hat{\lambda }_{2}^n=120{\theta }_{1}(t_{n}), \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \hat{\lambda }_{M-2}^n{+}26\hat{\lambda }_{M-1}^n+66\hat{\lambda }_{M}^n{+}26\hat{\lambda }_{M+1}^n+\hat{\lambda }_{M+2}^n{=}120{\theta }_{2}(t_{n}).\nonumber \\ \end{aligned}$$

(34)

Equations (32) and (33)–(34) form a system of $(M+3)$ linear algebraic equations with $(M+5)$ unknowns. To make the system feasible, we need two auxiliary equations. These additional equations are obtained by enforcing $\hat{\varPsi }^n(x)$ to satisfy (28) at the midpoints ${\tau }_{m}$ for $m=1, M.$ Therefore, we obtain

$$\begin{aligned} \begin{aligned}&\left( \varTheta c_0^{\alpha }+\sigma \hat{\varPsi }_{x}^{n-1}(\tau _m)\right) \hat{\varPsi }^{n}(\tau _m)+\left( \sigma \hat{\varPsi }^{n-1}(\tau _m)\right) \\&\quad \hat{\varPsi }_{x}^{n}(\tau _m)-\sigma \nu \hat{\varPsi }_{xx}^{n}(\tau _m)\\&\quad =\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \hat{\varPsi }^{l}(\tau _m)+\varTheta c^{\alpha }_{n-1}\hat{\varPsi }^{0}(\tau _m)\\&\qquad +(2\sigma -1)\left( \hat{\varPsi }\hat{\varPsi }_{x}\right) ^{n-1}(\tau _m)\\&\qquad +(1-\sigma )\nu \hat{\varPsi }_{xx}^{n-1}(\tau _m)+f^{n-1+\sigma }(\tau _m),\\&\quad m=1, M,\quad n=1,2,\ldots , N. \end{aligned} \end{aligned}$$

(35)

Making use of (24), (25) and (26) in (35) leads to

$$\begin{aligned} \begin{aligned}&({\tilde{p}}_m^{n-1}+{\tilde{s}}_m^{n-1})\hat{\lambda }_{m-3}^n+({\tilde{q}}_m^{n-1}\\&\qquad +{\tilde{v}}_m^{n-1}) \hat{\lambda }_{m-2}^n+({\tilde{r}}_m^{n-1}+{\tilde{w}}_m^{n-1})\hat{\lambda }_{m-1}^n \\&\qquad +({\tilde{r}}_m^{n-1}-{\tilde{w}}_m^{n-1})\hat{\lambda }_{m}^n\\&\qquad +({\tilde{q}}_m^{n-1}-{\tilde{v}}_m^{n-1})\hat{\lambda }_{m+1}^n+({\tilde{p}}_m^{n-1} -{\tilde{s}}_m^{n-1})\\&\quad \hat{\lambda }_{m+2}^n=\tilde{\omega }_m^{n-1}+f^n(\tau _m),\hspace{0.1cm} m=1,M,\hspace{0.1cm} n\ge 1, \end{aligned} \end{aligned}$$

(36)

where

$$\begin{aligned} {\tilde{p}}_m^{n-1}= & {} \frac{\varTheta c_0^{\alpha }}{3840}+\frac{\sigma \hat{\varPsi }_x^{n-1}(\tau _{m})}{3840}-\frac{\sigma \nu }{48\varDelta x^2},\\ {\tilde{q}}_m^{n-1}= & {} \frac{237\varTheta c_0^{\alpha }}{3840}+\frac{237\sigma \hat{\varPsi }_x^{n-1}(\tau _{m})}{3840}-\frac{21\sigma \nu }{48\varDelta x^2},\\ {\tilde{r}}_m^{n-1}= & {} \frac{1682\varTheta c_0^{\alpha }}{3840}+\frac{1682\sigma \hat{\varPsi }_x^{n-1}(\tau _{m})}{3840}+\frac{22\sigma \nu }{48\varDelta x^2},\\ {\tilde{s}}_m^{n-1}= & {} -\frac{\sigma \hat{\varPsi }^{n-1}(\tau _{m})}{384\varDelta x},\quad {\tilde{v}}_m^{n-1}=-\frac{75\sigma \hat{\varPsi }^{n-1}(\tau _{m})}{384\varDelta x},\\ {\tilde{w}}_m^{n-1}= & {} -\frac{154\sigma \hat{\varPsi }^{n-1}(\tau _{m})}{384\varDelta x} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \tilde{\omega }_m^{n-1}&=\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \hat{\varPsi }^{l}(\tau _m)+\varTheta c^{\alpha }_{n-1}\hat{\varPsi }^{0}(\tau _m)\\&\quad +(2\sigma -1)\left( \hat{\varPsi }\hat{\varPsi }_{x}\right) ^{n-1}(\tau _m)+(1-\sigma )\nu \hat{\varPsi }_{xx}^{n-1}(\tau _m). \end{aligned} \end{aligned}$$

Equations (32), (33), (34) and (36) give a linear system of $(M+5)$ equations in $(M+5)$ variables $\hat{\lambda }_{-2}^n, \hat{\lambda }_{-1}^n, \hat{\lambda }_{0}^n, \ldots ,\hat{\lambda }_{M}^{n}, \hat{\lambda }_{M+1}^n, \hat{\lambda }_{M+2}^n.$ We rewrite this system in the matrix form as follows:

$$\begin{aligned} P\hat{\lambda }^{n}=H^{n-1}+F^{n},\;\; n\ge 1, \end{aligned}$$

(37)

where $\hat{\lambda }^{n}=(\hat{\lambda }_{-2}^n, \hat{\lambda }_{-1}^n, \hat{\lambda }_0^n,\ldots ,\hat{\lambda }_{M}^{n}, \hat{\lambda }_{M+1}^n, \hat{\lambda }_{M+2}^n)^{T}$. The matrices $P, \, H^{n-1}$ and $F^{n}$ are defined as:

$$\begin{aligned} P= & {} {\begin{pmatrix} 1 &{}26&{}66&{}26&{}1&{} 0 &{}\cdots &{} 0\\ \\ \tilde{\varepsilon }_1^{n-1}&{}\tilde{\varphi }_1^{n-1}&{} \varsigma _1^{n-1}&{}\tilde{\varsigma }_1^{n-1}&{}\tilde{\varpi }_1^{n-1}&{} \tilde{\varrho }_1^{n-1}&{}\cdots &{}0\\ \\ \varepsilon _0^{n-1}&{}\varphi _0^{n-1}&{}r_0^{n-1}&{}\varpi _0^{n-1}&{}\varrho _0^{n-1}&{}0&{}\cdots &{}0\\ \\ 0&{}\varepsilon _1^{n-1}&{}\varphi _1^{n-1}&{}r_1^{n-1}&{}\varpi _1^{n-1}&{} \varrho _1^{n-1}&{}\cdots &{}0\\ \\ \ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots \\ \\ 0 &{}\cdots &{} 0 &{} \varepsilon _M^{n-1}&{}\varphi _M^{n-1}&{}r_M^{n-1}&{}\varpi _M^{n-1}&{} \varrho _M^{n-1}\\ \\ 0 &{} \cdots &{}\tilde{\varepsilon }_M^{n-1}&{}\tilde{\varphi }_M^{n-1}&{}\varsigma _M^{n-1}&{}\tilde{\varsigma }_M^{n-1}&{}\tilde{\varpi }_M^{n-1}&{} \tilde{\varrho }_M^{n-1}\\ \\ 0 &{}\cdots &{} 0 &{}1&{} 26 &{}66&{}26&{}1 \end{pmatrix}},\\ H^{n-1}= & {} {\begin{pmatrix} 0\\ \\ \tilde{\omega }_1^{n-1}\\ \\ \omega _0^{n-1}\\ \\ \omega _1^{n-1}\\ \\ \vdots \\ \\ \omega _M^{n-1}\\ \\ \tilde{\omega }_M^{n-1}\\ \\ 0 \end{pmatrix}},\quad F^{n}={\begin{pmatrix} 120{\theta }_{1}(t_{n})\\ \\ f^{n-1+\sigma }({\tau }_1)\\ \\ f^{n-1+\sigma }(x_0)\\ \\ f^{n-1+\sigma }(x_1)\\ \\ \vdots \\ \\ f^{n-1+\sigma }(x_{M})\\ \\ f^{n-1+\sigma }({\tau }_{M})\\ \\ 120{\theta }_{2}(t_{n}) \end{pmatrix}}, \end{aligned}$$

$$\begin{aligned} \varepsilon _m^{n-1}= & {} p_m^{n-1}+s_m^{n-1}, \,\varphi _m^{n-1}=q_m^{n-1}+v_m^{n-1}, \,\varpi _m^{n-1}\\= & {} q_m^{n-1}-v_m^{n-1},\, \varrho _m^{n-1}=p_m^{n-1}-s_m^{n-1}, \, \,\\ m= & {} 0,1,\ldots ,M,\,n\ge 1, \tilde{\varepsilon }_m^{n-1}\\= & {} {\tilde{p}}_m^{n-1}+{\tilde{s}}_m^{n-1},\, \tilde{\varphi }_m^{n-1}\\= & {} {\tilde{q}}_m^{n-1}+{\tilde{v}}_m^{n-1},\,\varsigma _m^{n-1} ={\tilde{r}}_m^{n-1}+{\tilde{w}}_m^{n-1},\, \tilde{\varsigma }_m^{n-1}\\= & {} {\tilde{r}}_m^{n-1}-{\tilde{w}}_m^{n-1},\, \tilde{\varpi }_m^{n-1}\\= & {} {\tilde{q}}_m^{n-1}-{\tilde{v}}_m^{n-1},\, \tilde{\varrho }_m^{n-1}\\= & {} {\tilde{p}}_m^{n-1}-{\tilde{s}}_m^{n-1},\, m=1,M,\ n=1,2,\ldots , N. \end{aligned}$$

3 Stability and convergence of the method

In this section, we analyze the stability and convergence properties of the proposed method for solving the problem (1)–(3).

3.1 Stability analysis

Here, we analyze the stability of the numerical method given by (37).

Theorem 4

The stability of the proposed method (37) for the considered problem is unconditional.

Proof

It can be seen that the right hand side function f(x, t) does not influence the stability of our proposed method. So, the proof for unconditionally stability of the method is performed in the case when $f(x,t)=0$. For simplicity, we linearize the nonlinear term $uu_x$ by setting u as a constant $\mu$ in (11). Then, we obtain

$$\begin{aligned}{} & {} \frac{\varDelta t^{-\alpha }}{\varGamma (2-\alpha )}\left[ c_0^{\alpha }u^n(x)-\sum _{l=1}^{n-1}\right. \nonumber \\{} & {} \quad \left. \left( c^{\alpha }_{n-l-1} -c^{\alpha }_{n-l}\right) u^{l}(x)-c^{\alpha }_{n-1}u^{0}(x)\right] \nonumber \\{} & {} \quad + \mu u_{x}^{n-1+\sigma }(x)- \nu u_{xx}^{n-1+\sigma }(x) = 0,\nonumber \\{} & {} \quad X_l<x<X_r, \quad n=1,2,\ldots , N. \end{aligned}$$

(38)

Using (13) and (14) in (38), we have

$$\begin{aligned}{} & {} \varTheta c_0^{\alpha }u^n(x)+\sigma \mu u_{x}^n(x)-\sigma \nu u_{xx}^{n}(x)\nonumber \\{} & {} \quad =\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)+\varTheta c^{\alpha }_{n-1}u^{0}(x)\nonumber \\{} & {} \qquad -(1-\sigma )\mu u_{x}^{n-1}(x)+(1-\sigma )\nu u_{xx}^{n-1}(x),\nonumber \\{} & {} \quad X_l<x<X_r, \, n=1,2,\ldots , N. \end{aligned}$$

(39)

Now, using the method described in Sect. 2 for Eq. (39) yields

$$\begin{aligned}{} & {} (\eta _1-\eta _2-\eta _3)\hat{\lambda }_{m-2}^n+(26\eta _1-10\eta _2-2\eta _3)\hat{\lambda }_{m-1}^n\nonumber \\{} & {} \quad +\,(66\eta _1+6\eta _3)\hat{\lambda }_{m}^n+(26\eta _1+10\eta _2-2\eta _3)\hat{\lambda }_{m+1}^n\nonumber \\{} & {} \quad +\,(\eta _1+\eta _2-\eta _3)\hat{\lambda }_{m+2}^n=\frac{\varTheta }{120}\sum _{l=1}^{n-1} \left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \big (\hat{\lambda }_{m-2}^{l}\nonumber \\{} & {} \quad +\,26\hat{\lambda }_{m-1}^{l} +66\hat{\lambda }_{m}^{l}+26\hat{\lambda }_{m+1}^{l}+\hat{\lambda }_{m+2}^{l}\big )\nonumber \\{} & {} \quad +\,\frac{\varTheta c^{\alpha }_{n-1}}{120}\big (\hat{\lambda }_{m-2}^{0}+26\hat{\lambda }_{m-1}^{0} +66\hat{\lambda }_{m}^{0}\nonumber \\{} & {} \quad +\,26\hat{\lambda }_{m+1}^{0}+\hat{\lambda }_{m+2}^{0}\big )-\frac{(1-\sigma )\mu }{24\varDelta x}\nonumber \\{} & {} \quad \big (-\hat{\lambda }_{m-2}^{n-1}-10\hat{\lambda }_{m-1}^{n-1}+10\hat{\lambda }_{m+1}^{n-1}+\hat{\lambda }_{m+2}^{n-1}\big )\nonumber \\{} & {} \quad +\,\frac{(1-\sigma )\nu }{6\varDelta x^2}\big (\hat{\lambda }_{m-2}^{n-1} +2\hat{\lambda }_{m-1}^{n-1}\nonumber \\{} & {} \quad -\,6\hat{\lambda }_{m}^{n-1}+2\hat{\lambda }_{m+1}^{n-1}+\hat{\lambda }_{m+2} ^{n-1}\big ),\, m=0,1,\ldots ,M,\hspace{0.1cm}n\ge 1,\nonumber \\ \end{aligned}$$

(40)

$$\begin{aligned}{} & {} (\eta ^*_1-\eta ^*_2-\eta ^*_3)\hat{\lambda }_{m-3}^n+(237\eta ^*_1-75\eta ^*_2-21\eta ^*_3)\hat{\lambda }_{m-2}^n\nonumber \\{} & {} \qquad +\,(1682\eta ^*_1-154\eta ^*_2+22\eta ^*_3)\hat{\lambda }_{m-1}^n\nonumber \\{} & {} \qquad +\,(1682\eta ^*_1+154\eta ^*_2+22\eta ^*_3)\hat{\lambda }_{m}^n\nonumber \\{} & {} \qquad +\,(237\eta ^*_1+75\eta ^*_2-21\eta ^*_3) \hat{\lambda }_{m+1}^n +(\eta ^*_1+\eta ^*_2-\eta ^*_3)\hat{\lambda }_{m+2}^n\nonumber \\{} & {} \quad =\,\frac{\varTheta }{3840}\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \big (\hat{\lambda }_{m-3}^{l}\nonumber \\{} & {} \qquad +\,237\hat{\lambda }_{m-2}^{l}+1682\hat{\lambda }_{m-1}^{l}+1682 \hat{\lambda }_{m}^{l}+237\hat{\lambda }_{m+1}^{l}+\hat{\lambda }_{m+2}^{l}\big )\nonumber \\{} & {} \qquad +\,\frac{\varTheta c^{\alpha }_{n-1}}{3840}\big (\hat{\lambda }_{m-3}^{0}+237\hat{\lambda }_{m-2}^{0} +1682\hat{\lambda }_{m-1}^{0}\nonumber \\{} & {} \qquad +\,1682\hat{\lambda }_{m}^{0}+237\hat{\lambda }_{m+1}^{0}+\hat{\lambda }_{m+2} ^{0}\big )-\frac{(1-\sigma )\mu }{384\varDelta x}\big (-\hat{\lambda }_{m-3}^{n-1}\nonumber \\{} & {} \qquad -\,75\hat{\lambda }_{m-2}^{n-1}-154\hat{\lambda }_{m-1}^{n-1}+154\hat{\lambda }_{m}^{n-1} +75\hat{\lambda }_{m+1}^{n-1}+\hat{\lambda }_{m+2}^{n-1}\big )\nonumber \\{} & {} \qquad +\,\frac{(1-\sigma )\nu }{48\varDelta x^2}\big (\hat{\lambda }_{m-3}^{n-1}+21\hat{\lambda }_{m-2}^{n-1}\nonumber \\{} & {} \qquad {-}\,22\hat{\lambda }_{m{-}1}^{n-1}{-}22\hat{\lambda }_{m}^{n-1}{+}21\hat{\lambda }_{m+1}^{n-1} {+}\hat{\lambda }_{m+2}^{n-1}\big ),\hspace{0.1cm} m{=}1,M,\hspace{0.1cm}n\ge 1,\nonumber \\ \end{aligned}$$

(41)

where $\eta _1=\frac{\varTheta c_0^{\alpha }}{120},$ $\eta _2=\frac{\sigma \mu }{24 \varDelta x},$ $\eta _3=\frac{\sigma \nu }{6 \varDelta x^2},$ $\eta ^*_1=\frac{\varTheta c_0^{\alpha }}{3840},$ $\eta ^*_2=\frac{\sigma \mu }{384 \varDelta x}$ and $\eta ^*_3=\frac{\sigma \nu }{48 \varDelta x^2}.$

The error ${\zeta }^n_m$ is defined by

$$\begin{aligned} {\zeta }^n_m= \hat{\lambda }_m^n- \lambda {^*}_m^n, \end{aligned}$$

(42)

with $\lambda {^*}_m^n$ representing the solution of the perturbed system of (40)–(41). Using (42), we can get the following error equations for (40)–(41):

$$\begin{aligned}{} & {} (\eta _1-\eta _2-\eta _3)\zeta _{m-2}^n+(26\eta _1-10\eta _2-2\eta _3)\zeta _{m-1}^n\nonumber \\{} & {} \qquad +\,(66\eta _1+6\eta _3) \zeta _{m}^n+(26\eta _1+10\eta _2-2\eta _3)\zeta _{m+1}^n\nonumber \\{} & {} \qquad +\,(\eta _1+\eta _2-\eta _3)\zeta _{m+2}^n=\frac{\varTheta }{120}\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1} -c^{\alpha }_{n-l}\right) \nonumber \\{} & {} \qquad \times \, \big (\zeta _{m-2}^{l}+26\zeta _{m-1}^{l}+66\zeta _{m}^{l}+26\zeta _{m+1}^{l} +\zeta _{m+2}^{l}\big )\nonumber \\{} & {} \qquad +\,\frac{\varTheta c^{\alpha }_{n-1}}{120}\big (\zeta _{m-2}^{0}+26\zeta _{m-1}^{0}+66\zeta _{m}^{0} +26\zeta _{m+1}^{0}+\zeta _{m+2}^{0}\big )\nonumber \\{} & {} \qquad -\,\frac{(1-\sigma )\mu }{24\varDelta x}\big (-\zeta _{m-2} ^{n-1}-10\zeta _{m-1}^{n-1}+10\zeta _{m+1}^{n-1}\nonumber \\{} & {} \qquad +\,\zeta _{m+2}^{n-1}\big )+\frac{(1-\sigma )\nu }{6\varDelta x^2}\big (\zeta _{m-2}^{n-1}+2\zeta _{m-1} ^{n-1}\nonumber \\{} & {} \qquad -\,6\zeta _{m}^{n-1}+2\zeta _{m+1}^{n-1}+\zeta _{m+2}^{n-1}\big ),\, n\ge 1,\, m=0,1,\dots ,M,\nonumber \\ \end{aligned}$$

(43)

$$\begin{aligned}{} & {} (\eta ^*_1-\eta ^*_2-\eta ^*_3)\zeta _{m-3}^n+(237\eta ^*_1-75\eta ^*_2-21\eta ^*_3)\zeta _{m-2}^n \nonumber \\{} & {} \qquad +\,(1682\eta ^*_1-154\eta ^*_2+22\eta ^*_3)\zeta _{m-1}^n+(1682\eta ^*_1\nonumber \\{} & {} \qquad +\,154\eta ^*_2+22\eta ^*_3)\zeta _{m}^n+(237\eta ^*_1+75\eta ^*_2-21\eta ^*_3)\zeta _{m+1}^n \nonumber \\{} & {} \qquad +\,(\eta ^*_1+\eta ^*_2-\eta ^*_3)\zeta _{m+2}^n=\frac{\varTheta }{3840}\nonumber \\{} & {} \qquad \times \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \big (\zeta _{m-3}^{l} +237\zeta _{m-2}^{l}\nonumber \\{} & {} \qquad +\,1682\zeta _{m-1}^{l}+1682\zeta _{m}^{l}+237\zeta _{m+1}^{l}+\zeta _{m+2}^{l}\big )\nonumber \\{} & {} \qquad +\,\frac{\varTheta c^{\alpha }_{n-1}}{3840}\big (\zeta _{m-3}^{0}+237\zeta _{m-2}^{0}+1682\zeta _{m-1}^{0} +1682\zeta _{m}^{0}\nonumber \\{} & {} \qquad +\,237\zeta _{m+1}^{0}+\zeta _{m+2}^{0}\big )-\frac{(1-\sigma )\mu }{384\varDelta x} \big (-\zeta _{m-3}^{n-1}\nonumber \\{} & {} \qquad -\,75\zeta _{m-2}^{n-1}-154\zeta _{m-1}^{n-1}+154\zeta _{m}^{n-1}+75\zeta _{m+1}^{n-1}+\zeta _{m+2} ^{n-1}\big )\nonumber \\{} & {} \qquad +\,\frac{(1-\sigma )\nu }{48\varDelta x^2}\big (\zeta _{m-3}^{n-1}+21\zeta _{m-2}^{n-1}\nonumber \\{} & {} \qquad -\,22\zeta _{m-1}^{n-1}-22\zeta _{m}^{n-1}+21\zeta _{m+1}^{n-1}\nonumber \\{} & {} \qquad +\,\zeta _{m+2}^{n-1}\big ),\, n=1,2,\dots ,N,\, m=1,M. \end{aligned}$$

(44)

The error ${\zeta }_{m}^{n}$ can be chosen as

$$\begin{aligned} {\zeta }_{m}^{n}={\xi }^{n}e^{i m\rho \varDelta x}, \end{aligned}$$

(45)

where $i=\sqrt{-1}$. Inserting (45) into (43) yields

$$\begin{aligned} \begin{aligned}&{\xi }^{n}e^{im\rho \varDelta x}\Big \{(\eta _1-\eta _2-\eta _3)e^{-2i\rho \varDelta x}\\&\qquad +(26\eta _1-10\eta _2-2\eta _3)e^{-i\rho \varDelta x}+(66\eta _1+6\eta _3)\\&\qquad +(26\eta _1+10\eta _2\\&\qquad -2\eta _3)e^{i\rho \varDelta x}+(\eta _1+\eta _2-\eta _3)e^{2i\rho \varDelta x}\Big \}\\&\quad =\frac{\varTheta }{120}\bigg \{\sum _{l=1}^{n-1}\big (c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\big ) {\xi }^{l}+c^{\alpha }_{n-1} {\xi }^0\bigg \}e^{im\rho \varDelta x}\\&\qquad \times \big (e^{-2i\rho \varDelta x}+26e^{-i\rho \varDelta x}+66+26e^{i\rho \varDelta x}+e^{2i\rho \varDelta x}\big )\\&\qquad -\left( \frac{1-\sigma }{\sigma }\right) \eta _2{\xi }^{n-1}e^{im\rho \varDelta x}\big (-e^{-2i\rho \varDelta x}\\&\qquad -10e^{-i\rho \varDelta x}+10e^{i\rho \varDelta x}+e^{2i\rho \varDelta x}\big )\\&\qquad +\left( \frac{1-\sigma }{\sigma }\right) \eta _3{\xi }^{n-1}e^{im\rho \varDelta x}\\&\qquad \times \big (e^{-2i\rho \varDelta x}+2e^{-i\rho \varDelta x}-6+2e^{i\rho \varDelta x}+e^{2i\rho \varDelta x}\big ). \end{aligned}\nonumber \\ \end{aligned}$$

(46)

The above equation can be rewritten as

$$\begin{aligned}{} & {} {\xi }^{n}\big [\eta _1(2{\cos }(2\rho \varDelta x)+52{\cos }(\rho \varDelta x)+66)\nonumber \\{} & {} \quad {+}\,\eta _3(6{-}2{\cos }(2\rho \varDelta x){-}4{\cos }(\rho \varDelta x)){+}i\eta _2(2\sin (2\rho \varDelta x)\nonumber \\{} & {} \quad +\,20\sin (\rho \varDelta x))\big ]\nonumber \\{} & {} =\,\frac{\varTheta }{120}\Bigg [\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) {\xi }^{l}+c^{\alpha }_{n-1} {\xi }^0\Bigg ]\nonumber \\{} & {} \quad \times \, (2{\cos }(2\rho \varDelta x)+52{\cos }(\rho \varDelta x)+66)\nonumber \\{} & {} \quad -\,i\left( \frac{1-\sigma }{\sigma }\right) \eta _2{\xi }^{n-1}(2\sin (2\rho \varDelta x)+20\sin (\rho \varDelta x))\nonumber \\{} & {} \quad -\,\left( \frac{1-\sigma }{\sigma }\right) \eta _3{\xi }^{n-1}(6-2{\cos }(2\rho \varDelta x)-4{\cos }(\rho \varDelta x)).\nonumber \\ \end{aligned}$$

(47)

From Eq. (47), we have

$$\begin{aligned} {\xi }^{n}=\frac{\frac{\varTheta \gamma _1}{120}\Bigg [\displaystyle \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1} -c^{\alpha }_{n-l}\right) {\xi }^{l}+c^{\alpha }_{n-1} {\xi }^0\Bigg ]-\left( \frac{1-\sigma }{\sigma }\right) \eta _3\gamma _2{\xi }^{n-1}-i\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _3{\xi }^{n-1}}{\eta _1\gamma _1+\eta _3\gamma _2+i\eta _2\gamma _3}, \end{aligned}$$

(48)

where $\gamma _1={\cos }(\rho \varDelta x)+26{\cos }(\rho \varDelta x)+33,$ $\gamma _2=3-{\cos }(2\rho \varDelta x)-2{\cos }(\rho \varDelta x)$ and $\gamma _3=\sin (2\rho \varDelta x)+10\sin (\rho \varDelta x).$

By means of mathematical induction, we prove that

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|. \end{aligned}$$

(49)

For $n=1,$ (48) leads to

$$\begin{aligned} {\xi }^{1}= \frac{\eta _1\gamma _1-\left( \frac{1-\sigma }{\sigma }\right) \eta _3\gamma _2-i\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _3}{\eta _1\gamma _1+\eta _3\gamma _2+i\eta _2\gamma _3}. \end{aligned}$$

(50)

Since $\sigma \in \left( \frac{1}{2},1\right)$, we have

$$\begin{aligned} 0\le \left( \frac{1-\sigma }{\sigma }\right) \le 1. \end{aligned}$$

(51)

Furthermore, as $\varDelta t>0$, $\varDelta x>0$, ${\nu }\ge 0$ and $0<\alpha <1$, it can be concluded that $\varGamma (2-\alpha )>0$ and $\eta _1,\, \eta _2,\, \eta _3$ are positive. Therefore, taking into account (51), from (50) we get

$$\begin{aligned} |{\xi }^{1}|^2=\frac{\left( \eta _1\gamma _1-\left( \frac{1-\sigma }{\sigma }\right) \eta _3\gamma _2\right) ^2 +\left( \left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _3\right) ^2}{\left( \eta _1\gamma _1+\eta _3\gamma _2\right) ^2+\left( \eta _2\gamma _3\right) ^2}\le |{\xi }^0|^2.\nonumber \\ \end{aligned}$$

(52)

Thus, (48) holds for $n=1$. Assume that (48) holds for $n\le j-1$, that is,

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|,\hspace{0.1cm}n=1,2,\ldots ,j-1. \end{aligned}$$

(53)

For $n=j,$ (48) leads to

$$\begin{aligned} \xi ^j=\frac{A-iB}{C+iD}, \end{aligned}$$

(54)

where $A=\frac{\varTheta \gamma _1}{120}\Bigg [\displaystyle \sum _{l=1}^{j-1}\left( c^{\alpha }_{j-l-1} -c^{\alpha }_{j-l}\right) {\xi }^{l}+c^{\alpha }_{j-1} {\xi }^0\Bigg ]-\left( \frac{1-\sigma }{\sigma }\right) \eta _3\gamma _2{\xi }^{j-1}$, $B=\left( \frac{1-\sigma }{\sigma }\right) \eta _2\gamma _3{\xi }^{j-1}$, $C=\eta _1\gamma _1+\eta _3\gamma _2$ and $D=\eta _2\gamma _3$.

Making use of Lemma 1 and (53), one can get

$$\begin{aligned} |A|\le |C||\xi ^0|\, \text { and } \, |B|\le |D||\xi ^0|. \end{aligned}$$

(55)

Finally, making use of (55) into (54), we get

$$\begin{aligned} |{\xi }^{j}|^2=\frac{A^2+B^2}{C^2+D^2}\le |{\xi }^{0}|^2, \end{aligned}$$

(56)

which gives

$$\begin{aligned} |{\xi }^{j}|\le |{\xi }^0|. \end{aligned}$$

(57)

Hence, the result is valid for $n=j$. Therefore, (49) is valid for every n, i.e.,

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|,\hspace{0.1cm}n\ge 1. \end{aligned}$$

(58)

Substituting (45) into (44), we obtain

$$\begin{aligned}{} & {} {\xi }^{n}e^{im\rho \varDelta x}\Big \{(\eta ^*_1-\eta ^*_2-\eta ^*_3)e^{-3i\rho \varDelta x} +(237\eta ^*_1\nonumber \\{} & {} \quad -75\eta ^*_2-21\eta ^*_3)e^{-2i\rho \varDelta x}+(1682\eta ^*_1-154\eta ^*_2\nonumber \\{} & {} \quad +22\eta ^*_3)e^{-i\rho \varDelta x}+(1682\eta ^*_1+154\eta ^*_2+22\eta ^*_3)\nonumber \\{} & {} \quad +(237\eta ^*_1 +75\eta ^*_2-21\eta ^*_3)e^{i\rho \varDelta x}+(\eta ^*_1+\eta ^*_2\nonumber \\{} & {} \quad -\eta ^*_3)e^{2i\rho \varDelta x}\Big \}=\frac{\varTheta }{3840}\bigg \{\sum _{l=1}^{n-1} \left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) \nonumber \\{} & {} \quad {\xi }^{l}+c^{\alpha }_{n-1} {\xi }^0\bigg \}e^{im\rho \varDelta x}\big (e^{-3i\rho \varDelta x}+237e^{-2i\rho \varDelta x}\nonumber \\{} & {} \quad {+}1682e^{{-}i\rho \varDelta x}{+}1682{+}237e^{i\rho \varDelta x}{+}e^{2i\rho \varDelta x}\big ) {-}\frac{(1{-}\sigma )\mu }{384\varDelta x}\nonumber \\{} & {} \quad \times \big (-e^{-3i\rho \varDelta x}-75e^{-2i\rho \varDelta x}-154e^{-i\rho \varDelta x}\nonumber \\{} & {} \quad +154+75e^{i\rho \varDelta x}+e^{2i\rho \varDelta x}\big )+\frac{(1-\sigma )\nu }{48\varDelta x^2}\big (e^{-3i\rho \varDelta x}\nonumber \\{} & {} \quad +21e^{-2i\rho \varDelta x}-22e^{-i\rho \varDelta x} -22+21e^{i\rho \varDelta x}+e^{2i\rho \varDelta x}\big ).\nonumber \\ \end{aligned}$$

(59)

Simplifying the terms in (59) yields

$$\begin{aligned}{} & {} {\xi }^{n}\Big [\eta ^{*}_1\big \{({\cos }(3\rho \varDelta x)+238{\cos }(2\rho \varDelta x) \nonumber \\{} & {} \quad {+}1929{\cos }(\rho \varDelta x){+}1682){-}i({\sin }(3\rho \varDelta x){+}236{\sin }(2\rho \varDelta x)\nonumber \\{} & {} \quad +1445{\sin }(\rho \varDelta x))\big \}+\eta ^{*}_2\big \{(154-{\cos }(3\rho \varDelta x) \nonumber \\{} & {} \quad -74{\cos }(2\rho \varDelta x)-79{\cos }(\rho \varDelta x))+i({\sin }(3\rho \varDelta x)\nonumber \\{} & {} \quad {+}76{\sin }(2\rho \varDelta x){+}229{\sin }(\rho \varDelta x))\big \}{+}\eta ^{*}_3 \big \{(22-{\cos }(3\rho \varDelta x)\nonumber \\{} & {} \quad -22{\cos }(2\rho \varDelta x)+{\cos }(\rho \varDelta x))\nonumber \\{} & {} \quad +i({\sin }(3\rho \varDelta x)+20{\sin }(2\rho \varDelta x)-43{\sin }(\rho \varDelta x))\big \}\Big ] \nonumber \\{} & {} \quad =\frac{\varTheta }{3840}\bigg [\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) {\xi }^{l}+c^{\alpha }_{n-1} {\xi }^0\bigg ]\nonumber \\{} & {} \quad {\times }\Big [({\cos }(3\rho \varDelta x){+}238{\cos }(2\rho \varDelta x){+}1919{\cos }(\rho \varDelta x){+}1682) \nonumber \\{} & {} \quad -i({\sin }(3\rho \varDelta x)+236{\sin }(2\rho \varDelta x)\nonumber \\{} & {} \quad +1445{\sin }(\rho \varDelta x))\Big ]-\left( \frac{1-\sigma }{\sigma }\right) \eta ^{*}_2{\xi }^{n-1} \nonumber \\{} & {} \quad {\times }\big \{(154{-}{\cos }(3\rho \varDelta x){-}74{\cos }(2\rho \varDelta x){-}79{\cos }(\rho \varDelta x))\nonumber \\{} & {} \quad +i({\sin }(3\rho \varDelta x)+76{\sin }(2\rho \varDelta x)+229{\sin }(\rho \varDelta x))\big \}\nonumber \\{} & {} \quad -\left( \frac{1-\sigma }{\sigma }\right) \eta ^{*}_3{\xi }^{n-1}\big \{(22-{\cos }(3\rho \varDelta x)\nonumber \\{} & {} \quad -22{\cos }(2\rho \varDelta x)+{\cos }(\rho \varDelta x))+i({\sin }(3\rho \varDelta x)\nonumber \\{} & {} \quad +20{\sin } (2\rho \varDelta x)-43{\sin }(\rho \varDelta x))\big \}.\nonumber \\ \end{aligned}$$

(60)

From (60), we have

$$\begin{aligned} {\xi }^{n}=\frac{\begin{array}{c} \frac{\varTheta }{3840}\Bigg [\displaystyle \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1} -c^{\alpha }_{n-l}\right) {\xi }^{l}+c^{\alpha }_{n-1} {\xi }^0\Bigg ](\gamma _1^*-i\gamma _2^*)\\ -\left( \frac{1-\sigma }{\sigma }\right) \left( \eta ^{*}_{2}(\beta _1+i\beta _2)+\eta ^{*}_{3} (\beta _1^*+i\beta _2^*)\right) {\xi }^{n-1} \end{array}}{\eta ^{*}_{1}(\gamma _1^*-i\gamma _2^*)+\eta ^{*}_{2} (\beta _1+i\beta _2)+\eta ^{*}_{3}(\beta _1^*+i\beta _2^*)},\nonumber \\ \end{aligned}$$

(61)

where

$$\begin{aligned} \begin{aligned} \gamma _1^*&={\cos }(3\rho \varDelta x)+238{\cos }(2\rho \varDelta x)\\&\quad +1929{\cos }(\rho \varDelta x)+1682,\\ \gamma _2^*&={\sin }(3\rho \varDelta x)+236{\sin }(2\rho \varDelta x)+1445{\sin }(\rho \varDelta x),\\ \beta _1&{=}154{-}{\cos }(3\rho \varDelta x){-}74{\cos }(2\rho \varDelta x) {-}79{\cos }(\rho \varDelta x),\\ \beta _2&={\sin }(3\rho \varDelta x)+76{\sin }(2\rho \varDelta x)+229{\sin }(\rho \varDelta x),\\ \beta _1^*&=22-{\cos }(3\rho \varDelta x)-22{\cos }(2\rho \varDelta x)+{\cos }(\rho \varDelta x)\\ \text { and }\beta _2^*&={\sin }(3\rho \varDelta x)+20{\sin }(2\rho \varDelta x)-43{\sin }(\rho \varDelta x). \end{aligned} \end{aligned}$$

Using the triangle inequality, the following estimate is obtained:

$$\begin{aligned} |{\xi }^{n}|{\le } \frac{\begin{array}{c} \frac{\varTheta }{3840}\Bigg [\displaystyle \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1} {-}c^{\alpha }_{n-l}\right) |{\xi }^{l}|{+}c^{\alpha }_{n{-}1} |{\xi }^0|\Bigg ]|\gamma _1^*{-}i\gamma _2^*| \\ {+} \left( \frac{1{-}\sigma }{\sigma }\right) \left| \eta ^{*}_{2}(\beta _1{+}i\beta _2){+}\eta ^{*}_{3}(\beta _1^*{+}i\beta _2^*) \right| |{\xi }^{n{-}1}| \end{array}}{|\eta ^{*}_{1}(\gamma _1^*-i\gamma _2^*){+}\eta ^{*}_{2} (\beta _1{+}i\beta _2){+}\eta ^{*}_{3}(\beta _1^*{+}i\beta _2^*)|}.\nonumber \\ \end{aligned}$$

(62)

Moreover, it is clearly observed that

$$\begin{aligned}{} & {} \frac{\frac{\varTheta c_0^{\alpha }}{3840}|\gamma _1^*-i\gamma _2^*|+\left( \frac{1-\sigma }{\sigma }\right) \left| \eta ^{*}_{2}(\beta _1+i\beta _2)+\eta ^{*}_{3}(\beta _1^*+i\beta _2^*)\right| }{|\eta ^{*}_{1}(\gamma _1^*-i\gamma _2^*)+\eta ^{*}_{2}(\beta _1+i\beta _2)+\eta ^{*}_{3}(\beta _1^*+i\beta _2^*)|}\nonumber \\{} & {} \le 1. \end{aligned}$$

(63)

By means of mathematical induction and (63), one can prove that

$$\begin{aligned} |{\xi }^{n}|\le |{\xi }^0|,\hspace{0.1cm}n\ge 1. \end{aligned}$$

(64)

From (58) and (64), one can conclude that the present numerical scheme (37) is unconditionally stable. $\square$

3.2 Convergence analysis

This section is devoted to the convergence analysis of the proposed scheme (37) for (1)–(3).

Theorem 5

Assume that $\hat{\varPsi }^{n}(x)$ be the QBS approximation of the solution $u^n(x)\in {\mathbb {C}}^{6}[X_l,X_r]$ for (1)–(3). Then, for sufficiently small $\varDelta x$ and a constant ${\mathcal {L}}$ independent of $\varDelta x$, we have

$$\begin{aligned} \Vert \hat{\varPsi }^n(x)-u^n(x)\Vert _{\infty }\le {\mathcal {L}}\varDelta x^4,\;\; \forall \; n\ge 0. \end{aligned}$$

(65)

Proof

Linearizing the nonlinear term $uu_x$ in (11) by taking u as a constant $\mu$, we obtain

$$\begin{aligned} \begin{aligned}&\frac{\varDelta t^{{-}\alpha }}{\varGamma (2-\alpha )}\\&\left[ c_0^{\alpha }u^n(x){-}\sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1} {-}c^{\alpha }_{n-l}\right) u^{l}(x){-}c^{\alpha }_{n-1}u^{0}(x)\right] \\&\quad + \mu u_{x}^{n-1+\sigma }(x)- \nu u_{xx}^{n-1+\sigma }(x)=f^{n-1+\sigma }(x). \end{aligned}\nonumber \\ \end{aligned}$$

(66)

From the boundary conditions, we have

$$\begin{aligned} u^{n}(X_l)={\theta }_{1}(t_{n}),\;u^{n}(X_r)={\theta }_{2}(t_{n}). \end{aligned}$$

(67)

Making use of the approximations (13) and (14) into (66) and then rearrangements of the terms leads to

$$\begin{aligned} \begin{aligned}&\varTheta c_0^{\alpha }u^n(x)+\sigma \mu u_{x}^n(x)-\sigma \nu u_{xx}^{n}(x)\\&\quad =\varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)+\varTheta c^{\alpha }_{n-1}u^{0}(x)\\&\quad -(1-\sigma )\mu u_{x}^{n-1}(x)+(1-\sigma )\nu u_{xx}^{n-1}(x)+f^{n-1+\sigma }(x),\\&\quad \,\,X_l<x<X_r, \,\, n=1,2,\ldots , N. \end{aligned} \end{aligned}$$

(68)

In operator form, Eqs. (67) and (68) can be expressed as

$$\begin{aligned} Lu^{n}(x)\equiv & {} \varTheta c_0^{\alpha }u^{n}(x)+\sigma \mu u_{x}^n(x)-\sigma \nu u_{xx}^{n}(x)\nonumber \\= & {} G^{n-1}(x)+f^{n-1+\sigma }(x), \end{aligned}$$

(69)

$$\begin{aligned} Bu^{n}(x)\equiv & {} \{u^{n}(X_l)={\theta }_{1}(t_{n}),\;u^{n}(X_r)={\theta }_{2}(t_{n})\}, \end{aligned}$$

(70)

where

$$\begin{aligned}{} & {} G^{n-1}(x)=\displaystyle \varTheta \sum _{l=1}^{n-1}\left( c^{\alpha }_{n-l-1}-c^{\alpha }_{n-l}\right) u^{l}(x)\nonumber \\{} & {} \quad +\varTheta c^{\alpha }_{n-1}u^{0}(x)-(1-\sigma )\mu u_{x}^{n-1}(x)+(1-\sigma )\nu u_{xx}^{n-1}(x).\nonumber \\ \end{aligned}$$

(71)

Let ${\varPsi }^{n}(x)\in S_{5,I}$ be the QSI to the exact solution of (68) and (67). Let ${\varPsi }^n(x)$ be given as

$$\begin{aligned} {\varPsi }^n(x)=\sum _{k=-2}^{M+2}{\lambda }_{k}^{n}Q_{k}(x). \end{aligned}$$

(72)

By means of Theorems 1 and 2, we have

$$\begin{aligned}{} & {} L{\varPsi }^n(x_{m})=Lu^{n}(x_{m})+O(\varDelta x^4),\hspace{0.1cm}m=0,1,\ldots ,M,\nonumber \\ \end{aligned}$$

(73)

$$\begin{aligned}{} & {} {\varPsi }^n(x_{0})={\theta }_{1}(t_{n})+O(\varDelta x^4),\;{\varPsi }^n(x_{M})={\theta }_{2}(t_{n})\nonumber \\{} & {} \quad +O(\varDelta x^4), \end{aligned}$$

(74)

$$\begin{aligned}{} & {} L{\varPsi }^n({\tau }_{m})=Lu^{n}({\tau }_{m})+O(\varDelta x^4),\hspace{0.1cm}m=1,M. \end{aligned}$$

(75)

As $u^{n}(x_{m})=\hat{\varPsi }^n(x_{m}),\hspace{0.1cm} 0\le m\le M$ and $u^{n}({\tau }_{m})=\hat{\varPsi }^n({\tau }_{m}),\hspace{0.1cm}m=1,M,$ thus, Eqs. (73)–(75) can be written in the matrix form, as follows:

$$\begin{aligned} \Big [L{\varPsi }^{n}(x)-L\hat{\varPsi }^{n}(x)\Big ]_{x=x_{m},\hspace{0.1cm}m=0,1,\ldots ,M,\,x={\tau }_{1},{\tau }_{M}}=E, \end{aligned}$$

(76)

where $E=[O(\varDelta x^4), O(\varDelta x^4),\ldots ,O(\varDelta x^4),O(\varDelta x^4)]^{T}$.

For $x=x_0$, from (76), we obtain

$$\begin{aligned} {}{} & {} (\eta _1-\eta _2-\eta _3){\lambda }_{-2}^n+(26\eta _1-10\eta _2-2\eta _3){\lambda }_{-1}^n\nonumber \\{} & {} \quad +(66\eta _1+6\eta _3) {\lambda }_{0}^n+(26\eta _1+10\eta _2-2\eta _3){\lambda }_{1}^n\nonumber \\{} & {} \quad +(\eta _1+\eta _2-\eta _3){\lambda }_{2}^n-\big ((\eta _1-\eta _2-\eta _3)\hat{\lambda }_{-2}^n\nonumber \\{} & {} \quad +(26\eta _1-10 \eta _2-2\eta _3)\hat{\lambda }_{-1}^n+(66\eta _1+6\eta _3)\hat{\lambda }_{0}^n\nonumber \\{} & {} \quad +(26\eta _1+10\eta _2-2\eta _3)\hat{\lambda }_{1}^n\nonumber \\{} & {} \quad +(\eta _1+\eta _2-\eta _3)\hat{\lambda }_{2}^n\big )=O(\varDelta x^4). \end{aligned}$$

(77)

For $x=x_M$, from (76), we obtain

$$\begin{aligned} {}{} & {} (\eta _1-\eta _2-\eta _3){\lambda }_{M-2}^n+(26\eta _1-10\eta _2-2\eta _3){\lambda }_{M-1}^n \nonumber \\{} & {} \quad +(66\eta _1+6\eta _3){\lambda }_{M}^n+(26\eta _1+10\eta _2-2\eta _3){\lambda }_{M+1}^n\nonumber \\{} & {} \quad +(\eta _1+\eta _2-\eta _3){\lambda }_{M+2}^n-\big ((\eta _1-\eta _2-\eta _3)\hat{\lambda }_{M-2}^n \nonumber \\{} & {} \quad +(26\eta _1-10\eta _2-2\eta _3)\hat{\lambda }_{M-1}^n+(66\eta _1+6\eta _3)\hat{\lambda }_{M}^n\nonumber \\{} & {} \quad +(26\eta _1+10\eta _2-2\eta _3)\hat{\lambda }_{M+1}^n\nonumber \\{} & {} \quad +(\eta _1+\eta _2-\eta _3) \hat{\lambda }_{M+2}^n\big )=O(\varDelta x^4). \end{aligned}$$

(78)

For $x=\tau _{1}$, from (76), we obtain

$$\begin{aligned} {}{} & {} (\eta ^*_1-\eta ^*_2-\eta ^*_3){\lambda }_{-2}^n+(237\eta ^*_1-75\eta ^*_2-21\eta ^*_3){\lambda }_{-1}^n \nonumber \\{} & {} \quad +(1682\eta ^*_1-154\eta ^*_2+22\eta ^*_3){\lambda }_{0}^n+(1682\eta ^*_1\nonumber \\{} & {} \quad +154\eta ^*_2+22\eta ^*_3){\lambda }_{1}^n+(237\eta ^*_1+75\eta ^*_2-21\eta ^*_3){\lambda }_{2}^n+(\eta ^*_1 \nonumber \\{} & {} \quad +\eta ^*_2-\eta ^*_3){\lambda }_{3}^n-\big ((\eta ^*_1-\eta ^*_2-\eta ^*_3)\hat{\lambda }_{-2}^n\nonumber \\{} & {} \quad +(237\eta ^*_1-75\eta ^*_2-21\eta ^*_3)\hat{\lambda }_{-1}^n\nonumber \\{} & {} \quad +(1682\eta ^*_1-154\eta ^*_2+22\eta ^*_3) \hat{\lambda }_{0}^n\nonumber \\{} & {} \quad +(1682\eta ^*_1+154\eta ^*_2+22\eta ^*_3)\hat{\lambda }_{1}^n\nonumber \\{} & {} \quad +(237\eta ^*_1+75\eta ^*_2-21\eta ^*_3)\hat{\lambda }_{2}^n\nonumber \\{} & {} \quad +(\eta ^*_1+\eta ^*_2-\eta ^*_3) \hat{\lambda }_{3}^n\big )=O(\varDelta x^4). \end{aligned}$$

(79)

For $x=\tau _{M}$, from (76), we obtain

$$\begin{aligned} {}{} & {} (\eta ^*_1-\eta ^*_2-\eta ^*_3){\lambda }_{M-3}^n+(237\eta ^*_1-75\eta ^*_2-21\eta ^*_3){\lambda }_{M-2}^n \nonumber \\{} & {} \quad +(1682\eta ^*_1-154\eta ^*_2+22\eta ^*_3){\lambda }_{M-1}^n\nonumber \\{} & {} \quad +(1682\eta ^*_1+154\eta ^*_2+22\eta ^*_3){\lambda }_{M}^n\nonumber \\{} & {} \quad +(237\eta ^*_1+75\eta ^*_2-21\eta ^*_3){\lambda }_{M+1}^n +(\eta ^*_1+\eta ^*_2-\eta ^*_3){\lambda }_{M+2}^n\nonumber \\{} & {} \quad -\big ((\eta ^*_1-\eta ^*_2-\eta ^*_3)\hat{\lambda }_{M-3}^n+(237\eta ^*_1-75\eta ^*_2-21\eta ^*_3)\hat{\lambda }_{M-2}^n\nonumber \\{} & {} \quad +(1682\eta ^*_1-154\eta ^*_2+22\eta ^*_3)\hat{\lambda }_{M-1}^n\nonumber \\{} & {} \quad +(1682\eta ^*_1+154\eta ^*_2+22\eta ^*_3)\hat{\lambda }_{M}^n\nonumber \\{} & {} \quad +(237\eta ^*_1+75\eta ^*_2-21\eta ^*_3)\hat{\lambda }_{M+1}^n \nonumber \\{} & {} \quad +(\eta ^*_1+\eta ^*_2-\eta ^*_3)\hat{\lambda }_{M+2}^n\big )=O(\varDelta x^4). \end{aligned}$$

(80)

By utilizing (33) and (34), the unknowns ${\lambda }_{-2}^n, {\lambda }_{M+2}^n, \hat{\lambda }_{-2}^n$ and $\hat{\lambda }_{M+2}^n$ can be eliminated from (77)–(80). Hence, for $x=x_0$, we get

$$\begin{aligned} {}{} & {} (16\eta _2+24\eta _3){\lambda }_{-1}^n+(66\eta _2+72\eta _3){\lambda }_{0}^n+(36\eta _2+24\eta _3) {\lambda }_{1}^n\nonumber \\{} & {} \qquad -\big ((16\eta _2+24\eta _3)\hat{\lambda }_{-1}^n\nonumber \\{} & {} \qquad +(66\eta _2+72\eta _3)\hat{\lambda }_{0}^n+(36\eta _2+24\eta _3)\hat{\lambda }_{1}^n\big )\nonumber \\{} & {} \quad =O(\varDelta x^4). \end{aligned}$$

(81)

For $x=x_M$, we obtain

$$\begin{aligned} {}{} & {} -2\eta _2{\lambda }_{M-2}^n-(36\eta _2-24\eta _3){\lambda }_{M-1}^n-(66\eta _2-72\eta _3){\lambda }_{M}^n \nonumber \\{} & {} \quad -(16\eta _2-24\eta _3){\lambda }_{M+1}^n-\big (-2\eta _2\hat{\lambda }_{M-2}^n\nonumber \\{} & {} \quad -(36\eta _2-24\eta _3)\hat{\lambda }_{M-1}^n-(66\eta _2-72\eta _3)\hat{\lambda }_{M}^n\nonumber \\{} & {} \quad -(16\eta _2-24\eta _3) \hat{\lambda }_{M+1}^n\big )=O(\varDelta x^4). \end{aligned}$$

(82)

For $x=\tau _{1}$, we obtain

$$\begin{aligned} {}{} & {} (211\eta ^*_1-49\eta ^*_2+5\eta ^*_3){\lambda }_{-1}^n+(1616\eta ^*_1-88\eta ^*_2 +88\eta ^*_3){\lambda }_{0}^n\nonumber \\{} & {} \quad +(1656\eta ^*_1+180\eta ^*_2+48\eta ^*_3){\lambda }_{1}^n+(236\eta ^*_1\nonumber \\{} & {} \quad +76\eta ^*_2-20\eta ^*_3){\lambda }_{2}^n+(\eta ^*_1+\eta ^*_2-\eta ^*_3){\lambda }_{3}^n \nonumber \\{} & {} \quad -\big ( (211\eta ^*_1-49\eta ^*_2+5\eta ^*_3)\hat{\lambda }_{-1}^n\nonumber \\{} & {} \quad +(1616\eta ^*_1-88\eta ^*_2 +88\eta ^*_3)\hat{\lambda }_{0}^n\nonumber \\{} & {} \quad +(1656\eta ^*_1+180\eta ^*_2+48\eta ^*_3) \hat{\lambda }_{1}^n\nonumber \\{} & {} \quad +(236\eta ^*_1+76\eta ^*_2-20\eta ^*_3) \hat{\lambda }_{2}^n\nonumber \\{} & {} \quad +(\eta ^*_1+\eta ^*_2-\eta ^*_3)\hat{\lambda }_{3}^n\big )=O(\varDelta x^4). \end{aligned}$$

(83)

For $x=\tau _{M}$, we obtain

$$\begin{aligned} {}{} & {} (\eta ^*_1-\eta ^*_2-\eta ^*_3){\lambda }_{M-3}^n+(236\eta ^*_1-76\eta ^*_2-20\eta ^*_3){\lambda }_{M-2}^n\nonumber \\{} & {} \quad +(1656\eta ^*_1-180\eta ^*_2+48\eta ^*_3){\lambda }_{M-1}^n\nonumber \\{} & {} \quad {+}(1616\eta ^*_1{+}88\eta ^*_2{+}88\eta ^*_3){\lambda }_{M}^n{+}(211\eta ^*_1{+}49\eta ^*_2{+}5\eta ^*_3){\lambda }_{M{+}1}^n\nonumber \\{} & {} \quad -\big ((\eta ^*_1-\eta ^*_2-\eta ^*_3)\hat{\lambda }_{M-3}^n\nonumber \\{} & {} \quad +(236\eta ^*_1-76\eta ^*_2-20\eta ^*_3)\hat{\lambda }_{M-2}^n\nonumber \\{} & {} \quad +(1656\eta ^*_1-180\eta ^*_2+48\eta ^*_3) \hat{\lambda }_{M-1}^n+(1616\eta ^*_1+88\eta ^*_2\nonumber \\{} & {} \quad +88\eta ^*_3)\hat{\lambda }_{M}^n+(211\eta ^*_1+49\eta ^*_2+5\eta ^*_3)\hat{\lambda }_{M+1}^n\big )=O(\varDelta x^4).\nonumber \\ \end{aligned}$$

(84)

For $x=x_m$, $m=1,2,\ldots ,M-1$, from (76), we obtain

$$\begin{aligned} {}{} & {} (\eta _1-\eta _2-\eta _3){\lambda }_{m-2}^n+(26\eta _1-10\eta _2-2\eta _3){\lambda }_{m-1}^n \nonumber \\{} & {} \quad +(66\eta _1+6\eta _3){\lambda }_{m}^n+(26\eta _1+10\eta _2-2\eta _3){\lambda }_{m+1}^n\nonumber \\{} & {} \quad +(\eta _1+\eta _2-\eta _3){\lambda }_{m+2}^n-\big ((\eta _1-\eta _2-\eta _3)\hat{\lambda }_{m-2}^n \nonumber \\{} & {} \quad +(26\eta _1-10\eta _2-2\eta _3)\hat{\lambda }_{m-1}^n+(66\eta _1+6\eta _3)\hat{\lambda }_{m}^n\nonumber \\{} & {} \quad +(26\eta _1+10\eta _2-2\eta _3)\hat{\lambda }_{m+1}^n\nonumber \\{} & {} \quad +(\eta _1+\eta _2-\eta _3)\hat{\lambda }_{m+2}^n\big )=O(\varDelta x^4). \end{aligned}$$

(85)

Equations (81)–(85) can be expressed as

$$\begin{aligned} R({\lambda }^{n}-\hat{\lambda }^{n})=E, \end{aligned}$$

(86)

where R is a $(M+3)\times (M+3)$ matrix given by

$$\begin{aligned}{} & {} R={\begin{pmatrix} {\tilde{d}}_1&{}{\tilde{d}}_2&{} {\tilde{d}}_3&{}{\tilde{d}}_4&{}{\tilde{d}}_5&{}0 &{}\cdots &{}0&{}0\\ \\ d_6&{}d_7&{}d_8&{}d_9&{}0&{}0&{}\cdots &{}0&{}0\\ \\ d_1&{}d_2&{}d_3&{}d_4&{}d_5&{}0&{}\cdots &{}0&{}0\\ \\ \ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots \\ \\ 0 &{}0&{}\cdots &{} 0&{} d_1&{}d_2&{}d_3&{}d_4&{}d_5\\ \\ 0 &{}0&{}\cdots &{} 0 &{} 0&{}-d_{9}&{}{\hat{d}}_{8}&{}{\hat{d}}_{7}&{}{\hat{d}}_{6}\\ \\ 0 &{}0&{} \cdots &{}0&{}{\tilde{d}}_{10}&{} {\tilde{d}}_9&{}{\tilde{d}}_8&{}{\tilde{d}}_7&{} {\tilde{d}}_6 \end{pmatrix}},\quad \\{} & {} {\lambda }^{n}-\hat{\lambda }^{n}={\begin{pmatrix} {\lambda }_{-1}^{n}-\hat{\lambda }_{-1}^{n}\\ \\ {\lambda }_{0}^{n}-\hat{\lambda }_{0}^{n}\\ \\ {\lambda }_{1}^{n}-\hat{\lambda }_{1}^{n}\\ \\ \vdots \\ \\ {\lambda }_{M-1}^{n}-\hat{\lambda }_{M-1}^{n}\\ \\ {\lambda }_{M}^{n}-\hat{\lambda }_{M}^{n}\\ \\ {\lambda }_{M+1}^{n}-\hat{\lambda }_{M+1}^{n} \end{pmatrix}}, \end{aligned}$$

where $d_1=\eta _1-\eta _2-\eta _3,\, d_2=26\eta _1-10\eta _2-2\eta _3,\, d_3= 66\eta _1+6\eta _3,\, d_4= 26\eta _1+10\eta _2-2\eta _3,\, d_5=\eta _1+\eta _2-\eta _3, \, d_6= 16\eta _2+24\eta _3,\, d_7 =66\eta _2+72\eta _3, \, d_8=36\eta _2+24\eta _3,\, d_9= 2\eta _2,\, {\tilde{d}}_1=211\eta ^*_1-49\eta ^*_2+5\eta ^*_3,\, {\tilde{d}}_2= 1616\eta ^*_1-88\eta ^*_2+88\eta ^*_3,\, {\tilde{d}}_3= 1656\eta ^*_1+180\eta ^*_2+48\eta ^*_3, \, {\tilde{d}}_4=236\eta ^*_1+76\eta ^*_2-20\eta ^*_3,\, {\tilde{d}}_5= \eta ^*_1+\eta ^*_2-\eta ^*_3, \, {\tilde{d}}_6=211\eta ^*_1+49\eta ^*_2+5\eta ^*_3,\, {\tilde{d}}_7= 1616\eta ^*_1+88\eta ^*_2+88\eta ^*_3, \, {\tilde{d}}_8=1656\eta ^*_1-180\eta ^*_2+48\eta _3,\, {\tilde{d}}_9=236\eta ^*_1-76\eta ^*_2-20\eta ^*_3, \, {\tilde{d}}_{10}=\eta ^*_1-\eta ^*_2-\eta ^*_3, \,{\hat{d}}_6= -16\eta _2+24\eta _3,\, {\hat{d}}_7 =-66\eta _2+72\eta _3 \,$ and $\,{\hat{d}}_8=-36\eta _2+24\eta _3.$

Let $s_{i}\, (-1\le i\le M+1)$ denote the sum of ith row of R. Thus, we obtain

$$\begin{aligned} s_{-1}= & {} \frac{3720\varTheta c_0^{\alpha }\varDelta x^2+1200\sigma \mu \varDelta x+9600\sigma \nu }{3840 \varDelta x^2},\\ s_{0}= & {} \frac{480\sigma \nu +120\sigma \mu \varDelta x}{24 \varDelta x^2},\\ s_{k}= & {} \varTheta c_0^{\alpha },\hspace{0.1cm}k=1,2,...,M-1,\\ s_{M}= & {} \frac{480\sigma \nu -120\sigma \mu \varDelta x}{24 \varDelta x^2},\\ s_{M+1}= & {} \frac{3720\varTheta c_0^{\alpha }\varDelta x^2-1200\sigma \mu \varDelta x+9600\sigma \nu }{3840 \varDelta x^2}. \end{aligned}$$

For sufficiently small $\varDelta x,$ we have $s_{-1}>0, s_{0}>0, s_{k}> 0, k=1,\ldots ,M-1, s_{M}>0$ and $s_{M+1}>0$. Thus, R exhibits monotonicity and consequently, ${R}^{-1}$ is well defined. Let $r^{-1}_{k,j}$ be the (k, j)th element of ${R}^{-1}.$ Making use of the theory of matrices, we obtain

$$\begin{aligned} \sum _{j=-1}^{M+1} r^{-1}_{k,j}s_{j}=1,\quad \text {for}\;\;k=-1,0,1,\ldots ,M,M+1. \end{aligned}$$

(87)

Using (87), we have

$$\begin{aligned} \sum _{j=-1}^{M+1} r^{-1}_{k,j}\le \frac{1}{s_{j}}. \end{aligned}$$

(88)

By Taylor’s expansion, we have

$$\begin{aligned} r^{-1}_{k,-1}\le & {} \frac{1}{s_{-1}}\le \frac{3840\varDelta x^2}{9600\sigma \nu }+O(\varDelta x^3),\\ r^{-1}_{k,0}\le & {} \frac{1}{s_{0}} \le \frac{24\varDelta x^2}{480\sigma \nu }+O(\varDelta x^3),\\ r^{-1}_{k,j}\le & {} \frac{1}{s_{j}}= \frac{1}{\varTheta c_0^{\alpha }},\hspace{0.1cm}j=1,2,\ldots ,M-1,\\ r^{-1}_{k,M}\le & {} \frac{1}{s_{M}}\le \frac{24\varDelta x^2}{480\sigma \nu }+O(\varDelta x^3),\\ r^{-1}_{k,M+1}\le & {} \frac{1}{s_{M+1}}\le \frac{3840\varDelta x^2}{9600\sigma \nu }+O(\varDelta x^3). \end{aligned}$$

From (86), we have

$$\begin{aligned} \Vert {\lambda }^{n}-\hat{\lambda }^{n}\Vert _{\infty }= & {} \Vert {R}^{-1}{E}\Vert _{\infty }\nonumber \\\le & {} \Vert {R}^{-1}\Vert _{\infty }\Vert {E}\Vert _{\infty }\nonumber \\\le & {} \max \limits _{-1\le k \le M+1}\bigg (\bigg |\sum _{j=-1}^{M+1} r^{-1}_{k,j}\bigg |\bigg )O(\varDelta x^4)\nonumber \\\le & {} \max \limits _{-1\le k \le M+1}\bigg (|r^{-1}_{k,-1}|+|r^{-1}_{k,0}|\nonumber \\+ & {} \sum _{j=1}^{M-1} |r^{-1}_{k,j}|+|r^{-1}_{k,M}|+|r^{-1}_{k,M+1}|\bigg )O(\varDelta x^4)\nonumber \\= & {} O(\varDelta x^4). \end{aligned}$$

(89)

Therefore, we have

$$\begin{aligned} \max _{-1\le m\le M+1}\mid {\lambda }^{n}_{m}-\hat{\lambda }^{n}_{m}\mid \le {\mathcal {K}} \varDelta x^{4}. \end{aligned}$$

(90)

Moreover, using (33), (34) and (90), we can obtain that

$$\begin{aligned} \mid {\lambda }^{n}_{-2}-\hat{\lambda }^{n}_{-2}\mid = O(\varDelta x^{4}),\hspace{0.2cm}\mid {\lambda }^{n}_{M+2}-\hat{\lambda }^{n}_{M+2}\mid = O(\varDelta x^{4}).\nonumber \\ \end{aligned}$$

(91)

Now, from (20) and (72), we can have

$$\begin{aligned} {\varPsi }^n(x)-\hat{\varPsi }^{n}(x)=\sum _{k=-2}^{M+2}({\lambda }_{k}^{n}-\hat{\lambda }_{k}^{n}) Q_{k}(x). \end{aligned}$$

(92)

By the definition of $Q_{k}(x)$, it is easily observed that

$$\begin{aligned} \sum _{k=-2}^{M+2}| Q_{k}(x)|\le \frac{186}{120}. \end{aligned}$$

(93)

Taking the $L_\infty$ (maximum) norm on (92) and using (90), (91) and (93), we obtain

$$\begin{aligned} \Vert \varPsi ^{n}(x)-\hat{\varPsi }^{n}(x)\Vert _{\infty }\le & {} |{\lambda }^{n}-\hat{\lambda }^{n}|\sum _{k=-2}^{M+2} |Q_{k}(x)|\nonumber \\\le & {} {\mathcal {N}}\varDelta x^4,\; n\ge 1, \end{aligned}$$

(94)

where ${\mathcal {N}}=\frac{186}{120}{\mathcal {K}}$. From Theorem 3, we have

$$\begin{aligned} \Vert {\varPsi }^n(x)-u^n(x)\Vert _{\infty }\le {\mathcal {M}}\varDelta x^{4}. \end{aligned}$$

(95)

The triangle inequality gives

$$\begin{aligned}{} & {} \Vert \hat{\varPsi }^n(x)-u^n(x)\Vert _{\infty }\le \Vert \hat{\varPsi }^n(x)-{\varPsi }^n(x)\Vert _{\infty }+\Vert {\varPsi }^n(x)\nonumber \\{} & {} \quad -u^n(x)\Vert _{\infty }. \end{aligned}$$

(96)

Using (94) and (95), from (96), we have

$$\begin{aligned} \Vert \hat{\varPsi }^n(x)-u^n(x)\Vert _{\infty }\le {\mathcal {L}}\varDelta x^4\quad \forall \; n \ge 1. \end{aligned}$$

(97)

Hence, Theorem 5 is proved. $\square$

Theorem 6

Suppose that $\hat{\varPsi }(x,t)$ and u(x, t) be the QBS approximate solution and exact solution of TFBE, respectively. Then, for $u(x,t) \in {\mathbb {C}}^{6}[X_l,X_r] \times {\mathbb {C}}^3[0,T]$, it follows that

$$\begin{aligned} \Vert u(x,t)-\hat{\varPsi }(x,t)\Vert _{\infty }=O(\varDelta x^4+\varDelta t^{2}). \end{aligned}$$

(98)

Proof

Applying Theorem 5 and utilizing Eq. (18), we can derive the expression in (98). $\square$

4 Numerical illustrations

Here, four nonlinear problems are considered to demonstrate the effectiveness and accuracy of the proposed method (37). The computed result is compared with that obtained by other method based on cubic parametric spline functions (El-Danaf and Hadhoud 2012). We compute the $L_{\infty }$ norm error $({\mathcal {E}}^{M}_{1})$ of the proposed method which is defined as

$$\begin{aligned} {\mathcal {E}}^{M}_{1}=\max _{\begin{array}{c} 0\le m\le M\\ 0\le n\le N \end{array}}|\hat{\varPsi }_m^n-u(x_m,t_n)|, \end{aligned}$$

(99)

where $u(x_m,t_n)$ and $\hat{\varPsi }_m^n$ are the exact and approximate solutions, respectively, at the grid point $(x_m,t_n)$. We calculate the OOC (order of convergence) of the present numerical method based on $L_{\infty }$ norm error by the formula:

$$\begin{aligned} d=\frac{\log ({\mathcal {E}}^{M}_{1})-\log ({\mathcal {E}}^{2M}_{1})}{\log (2)}\,. \end{aligned}$$

The numerical computations are performed in MATLAB R2020a on a computer equipped with an AMD Ryzen 5 2500U processor operating at 2.00 GHz.

Example 1

Consider the TFBE (1)–(3) with $g(x)=0,\nu =1, X_l=0,\, X_r=1, T=1, \theta _1(t)=t^2, \theta _2(t)=et^2$ and $f(x,t)=\frac{2}{\varGamma (3-\alpha )}t^{2-\alpha }e^x+t^4e^{2x}-\nu t^2e^x.$ The true solution is $u(x,t)=t^2e^x$.

Table 2 $L_{\infty }$ norm errors for Example 1 when $\varDelta x=0.01$

Table 3 $L_{\infty }$ norm errors for Example 1 when $\varDelta t=0.00005$

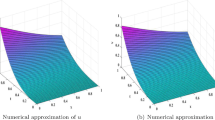
We apply the proposed method (37) to solve this problem for several values of mesh points M and N. First, we compute the rate of convergence of presented technique in temporal direction. For the purpose, we calculate the errors by varying N and fixing space step length $\varDelta x$. Table 2 gives the $L_{\infty }$ errors with different values of N when $\alpha = 0.1$, 0.5, 0.9 and $\varDelta x=0.01.$ One can observe in Table 2 that the present scheme is of order two in time. Next, to find the OOC of proposed scheme in spatial direction, we fix $\varDelta t$ and find the $L_{\infty }$ norm errors for various values of M. Table 3 shows the $L_{\infty }$ errors with various values of M when $\alpha = 0.5$, 0.9 and $\varDelta t=0.00005.$ Table 3 shows that the spatial accuracy of the proposed method is of fourth order. The OOC in Tables 2 and 3 is in good agreement with the theoretical OOC provided in Theorem 6. The CPU time of present numerical scheme is also provided in Tables 2 and 3, which confirms that our scheme is computationally efficient. The numerical solutions at various time levels $t = 0.5,\; 0.75$ and 1 are shown in Fig. 1. Figures 2 and 3 show the 3D surface plots of the numerical and exact solutions when $\alpha =0.5$. These figures indicate that the presented scheme approximates the exact solution of TFBE accurately.

Fig. 1

Numerical solution of Example 1 for $\alpha = 0.5$ and $T = 0.5, 0.75$ and 1

Fig. 2

3D graph of numerical solution of Example 1 with $N=M= 50$

Fig. 3

3D graph of exact solution of Example 1 with $N= M = 50$

Example 2

Consider the TFBE (1)–(3) with $g(x)=0, \ \nu =1, X_l=0,\, X_r=1, T=1, \theta _1(t)=t^2, \theta _2(t)=-t^2$ and $f(x,t)=\frac{2t^{2-\alpha }\cos (\pi x)}{\varGamma (3-\alpha )}-\pi t^4\cos (\pi x)\sin (\pi x)+\nu \pi ^2t^2\cos (\pi x).$ The exact solution is $u(x,t)=t^2\cos (\pi x)$.

Table 4 $L_{\infty }$ norm errors and OOC for Example 2 when $\alpha = 0.1$, 0.5, 0.9 and $\varDelta x=0.01$

Table 5 $L_{\infty }$ norm errors for Example-2 with $\varDelta t=0.0001$

Fig. 4

Numerical solution of Example 2 for $\alpha = 0.5$ and $T = 0.5$, 0.75 and 1

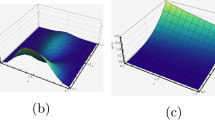
We apply present method (37) to solve this problem for several values of mesh points M and N. The $L_{\infty }$ errors when $\alpha = 0.1$, 0.5, 0.9 and $\varDelta x=0.01$ for various values of N are presented in Table 4. One can observe in Table 4 that the present scheme is of order two in time. The $L_{\infty }$ errors when $\alpha = 0.5$, 0.9 and $\varDelta t=0.0001$ for different values of M are reported in Table 5, which shows that our method has $O(\varDelta x^{4})$ convergence rate in space. This confirms that the experimental results are consistent with the theoretical estimates. The CPU timings of the scheme are also recorded, which confirm the fastness of our scheme. The numerical solutions at various time levels $t = 0.5,\; 0.75$ and 1 are plotted in Fig. 4. Figures 5 and 6 show the 3D surface plots of the numerical and exact solutions when $\alpha =0.5$. These figures confirm that the presented scheme approximates the exact solution of TFBE accurately.

Fig. 5

3D graph of numerical solution of Example 2 with $N = M = 50$

Fig. 6

3D graph of exact solution of Example 2 with $N = M = 50$

Table 6 $L_{\infty }$ norm errors with $-3\le x \le 3$, $\alpha =1$, $\mu =0.3$, $\sigma =0.4$, $\nu =0.1$ and $\lambda =0.8$ for Example 3

Example 3

In this example, we consider the TFBE (1) with IC (El-Danaf and Hadhoud 2012):

$$\begin{aligned} u(x,0)=\frac{\mu _0+\sigma _0+(\sigma _0-\mu _0)e^{\frac{\mu _0}{\nu }(x-\lambda )}}{1+e^{\frac{\mu _0}{\nu }(x-\lambda )}},\, -3\le x\le 3\nonumber \\ \end{aligned}$$

(100)

and BCs

$$\begin{aligned} u(-3,t)={\theta }_{1}(t),\;u(3,t)={\theta }_{2}(t),\, t\ge 0, \end{aligned}$$

(101)

with $f(x,t)=0$. The exact solution of this problem for $\alpha =1$ is

$$\begin{aligned} u(x,t)=\frac{\mu _0+\sigma _0+(\sigma _0-\mu _0)e^{\frac{\mu _0}{\nu }(x-\sigma _0 t-\lambda )}}{1+e^{\frac{\mu _0}{\nu }(x-\sigma _0 t-\lambda )}}. \end{aligned}$$

We compare the results of our method with those obtained by the approach presented in El-Danaf and Hadhoud (2012). This comparison is given in Table 6 where we used $\mu _0=0.3$, $\sigma _0=0.4$, $\nu =0.1$, $\lambda =0.8$ and $\varDelta x=\varDelta t =0.01$. We can observe from this Table that our method provides much more accurate solution than the method in El-Danaf and Hadhoud (2012).

Example 4

Consider the TFBE (1)–(3) with $g(x)=0, \ \nu =1, X_l=0,\, X_r=1, T=1, \theta _1(t)=0, \theta _2(t)=0$ and $f(x,t)=\frac{2t^{2-\alpha }\sin (2\pi x)}{\varGamma (3-\alpha )}+2\pi t^4\sin (2\pi x)\cos (2\pi x)+4\nu \pi ^2t^2\sin (2\pi x).$ The exact solution is $u(x,t)=t^2\sin (2\pi x)$.

Table 7 $L_{\infty }$ norm errors for Example 4 when $\varDelta x=0.005$

Table 8 $L_{\infty }$ norm errors for Example 4 when $\varDelta t=0.001$

Fig. 7

Numerical solution of Example 4 for $\alpha = 0.5$ and $T = 0.5, 0.75$ and 1

Fig. 8

3D graph of numerical solution of Example 4 with $N = M = 50$

Fig. 9

3D graph of exact solution of Example 4 with $N = M = 50$

We apply present method (37) to solve this problem for several values of grid points M and N. The $L_{\infty }$ errors when $\alpha = 0.1$, 0.5, 0.9 and $\varDelta x=0.005$ for various values of N are presented in Table 7. We can observe from Table 7 that the proposed method is of order two in time. The $L_{\infty }$ errors for various values of M when $\alpha = 0.5$, 0.9 and $\varDelta t=0.001$ are presented in Table 8. One can observe in Table 8 that the present scheme has fourth-order accuracy in spatial direction. Tables 7 and 8 confirm that the numerical results are in good agreement with the theoretical results. Tables 7 and 8 also provide the CPU timings of the method which confirm the fastness of the proposed scheme. The numerical solutions for $t = 0.5,\; 0.75$ and 1 are shown in Fig. 7. Figures 8 and 9 show the 3D surface plots of the numerical and exact solutions when $\alpha =0.5$. These figures indicate that the presented scheme approximates the exact solution of TFBE accurately.

5 Conclusions

An efficient high-order computational technique has been described and demonstrated for nonlinear TFBE. This technique is based on the $L2-1_{\sigma }$ formula which is employed for the approximation of the Caputo derivative of fractional order. We approximate the space derivatives using the collocation technique with the aid of QBS basis functions. The resulting method is unconditionally stable and exhibits fourth-order convergence in the spatial direction and second-order convergence in the temporal direction, as demonstrated by the convergence analysis. The experimental OOC confirms the theoretical results proved in Theorem 6. The experimental results indicates that the proposed method is highly accurate and efficient in dealing with the nonlinear TFBE. We have compared our results with those obtained by the method based on cubic parametric spline functions (El-Danaf and Hadhoud 2012). Comparison confirmed that the present method is more accurate than the method proposed in El-Danaf and Hadhoud (2012). The computational efficiency of the method is confirmed by the CPU time provided in the tables.