A new approach based on greedy minimizing algorithm for solving data allocation problem

Abstract

Distributed database functionality depends on sites responsible for the allocation of fragments. The aims of the data allocation problem (DAP) are to achieve the minimum execution time and ensure the lowest transaction cost of queries. The solution for this NP-hard problem based on numerical methods is computationally expensive. Despite the success of such heuristic algorithms as GA and PSO in solving DAP, the initial control parameters tuning, the relatively high convergence speed, and hard adaptations to the problem are the most important disadvantages of these methods. This paper presents a simple well-formed greedy algorithm to optimize the total transmission cost of each site-fragment dependency and each inner-fragment dependency. To evaluate the effect of the proposed method, more than 20 standard DAP problems were used. Experimental results showed that the proposed approach had better quality in terms of execution time and total cost.

1 Introduction

Recently, one of the most attractive applications has been the development of a distributed database called data allocation problem (DAP). The aim of DAP is to determine the fragments placement in various sites to reduce the total transaction cost when the query is taken from one site to another one. The optimization algorithms of performance analysis with special constraints are used for DAP with the standard test problem (Tosun 2014a; Tosun et al. 2013a). The problems of data allocation for sites are very difficult. The data for the locations of the fragments can be changed. In this situation, the data organization becomes more important. For instance, some items such as parallel query executions, network load, and the server load balancing need to be managed. DAP is an NP-hard problem, without considering the problems mentioned above. DAP can be solved by two types of algorithms: dynamic and static. The static algorithms are implemented based on data allocation on static transaction execution patterns in the target environment. These patterns are changed in the dynamic algorithm (Tosun et al. 2013a; Gu et al. 2006; Mashwani and Salhi 2012). DAP has been solved by several algorithms such as Genetic Algorithm (Tosun et al. 2013a; Mashwani and Salhi 2012), Ant colony optimization (Tosun 2014b; Adl and Rankoohi 2009), Particle Swarm Optimization (Mahi et al. 2015, 2018), and Metaheuristic methods. In this part of the paper, we have reviewed some studies on the DAP solution. Peng et al. (2022) propose an allocation scheme for the storage of data in a collaborative edge-cloud environment, with a focus on enhanced data privacy. Specifically, they first divide the datasets by fields to eliminate as much as possible the correlation between the leaked data.

Anita Brigit Mathew proposed a heuristic algorithm based on separating a database graph among nodes by defining all information on the same or adjacent nodes (Mathew 2018). This heuristic algorithm includes the best-fit decrease with Ant Colony Optimization, which refers to the data allocation in the distributed architectures of the NoSQL database graph (Mathew 2018). An effective data allocation method, which contemplates static and dynamic specifications of data centers to make more effectual datacenter resizing, was proposed by Chen et al. (2018); they used a heuristic algorithm for analyzing the current traffic in the network of data centers through first transmitting the data allocation problem into a chunk distribution tree (CDT). An improved heuristic method based on division and allocation has been proposed by Amer et al. (2012, 2017) all of the mentioned methods are combined into a single, efficient one, which has an effectual solution for Distributed Database Systems (DDBS). Nashat et al. (2018) proposed a method based on a complete taxonomy of the accessible division and allocation in the distributed database schema. Data division in the DDBS has been surveyed by Asma et al. (2017) An improved data allocation through data migration algorithm on task level (TODMA) has been presented by Du et al. (2017); Mayne and Satav (2017). Simulated annealing (SA) is done by Sen et al. to solve DAP (Sen et al. 2016). Radio Frequency Identification (RFID) tag oriented DAP as a nonlinear knapsack problem has been modeled by Wang et al. The heuristic Quadratic Assignment Problem (QAP) was designed and implemented for DAP by Tusun et al. (2013a) They proposed a fast and scalable hybrid genetic multi-start tabu search algorithm that outperformed the other well-known heuristics in terms of the execution time and solution quality (Tosun 2014a; Tosun et al. 2013a). Tosun et al. have presented a set of SA, GA, and fast ACO to solve DAP (Tosun 2014a). Nasser et al. also proposed an innovative hybrid method. Differential Evolution and Variable Neighborhood Search (DEVNS) have also been offered for solving DAP in distributed database systems (Lotfi 2019).

ACO-DAP model based on ACO and local search has been presented by Adl and Rankoohi (2009). In this approach, overcoming on RAPs has been targeted. Genetic algorithms were considered in their method and the simulation results demonstrated that its performance was good. Ulus and Uysal also presented a new dynamic DDBS called threshold algorithm (Ulus and Uysal 2003). In this approach, data reallocation has been done by changing the data access pattern. The obtained results were compared with the genetic algorithm (Tosun 2014a), Tabu search (Tosun 2014a), ant colony (Tosun 2014a), and simulated annealing (Tosun et al. 2013b) in regard to solving 20 problems with various dimensions. The execution time and the total cost were important factors. The proposed algorithm had suitable and comparable results in time; it could be inferred that Greedy-DAP execution time, in comparison with other algorithms, could be regarded as the best. In our work, we want to solve DAP through Greedy-DAP utilization and adaptation. The execution time and fragment allocation quality are investigated experimentally by Greedy-DAP. The simulation results reveal that the Greedy-DAP’s (Mahi et al. 2018) execution time together with cost could have a suitable performance in comparison with other algorithms.

Three goals for data allocation are presented, Cao (Cao 2022), minimizing the number of active servers, minimizing the average number of partitions per data, and balancing servers' workload. Li et al. (2022) are proposed demonstrates that the conventional “graph data allocation = graph partitioning” assumption is not true, and the memory access patterns of graph algorithms should also be taken into account when partitioning graph data for communication minimization. Thalij (2022), a novel high-performance data allocation approach, is designed using Chicken Swarm Optimization (CSO) algorithm. Then the CSO algorithm optimally chooses the sites for each of the data fragments without creating much overhead and data route diversions. Then, the CSO algorithm optimally chooses the sites for each of the data fragments without creating much overhead and data route diversions. Then, the CSO algorithm optimally chooses the sites for each of the data fragments without creating much overhead and data route diversions. This scenario is formulated using an optimization problem called the data allocation problem (DAP). In this paper, in addition to the fact that algorithms based on randomness are not used, we directly find the best solution to the problem in each step and refer to the next steps, and in the new step, we find the best solution and move to the next step. Of course, at each stage after the best solution for resource allocation on the site is obtained, in the matrix of costs, the column in which the part is selected, we put all the columns of that matrix as a very large number. Unfortunately, this problem is that in the next steps, maybe the best answer is again in that column, where we lose this amount. However, according to the obtained results, we have the minimum answer compared to the previous algorithms. The meaning of the best answer, according to the resource allocation matrix on the sites, is the minimum value found in the entire cost matrix. Which is done by replacing the source on the site with the lowest transaction cost. Finally, after replacing the source on the site, we put a very large number matrix in the columns of that column, so that in the next steps, the same minimum will not be found again from that column.

Section 1 serves as the introduction and the rest of the paper is structured as follows; Sect. 2 contains materials and methods of the background information for the greedy algorithm and introduces the proposed method (Greedy-DAP). Comparisons and the experimental results are presented in Sect. 3. Finally, Sect. 4 will conclude the paper.

2 Materials and methods

A greedy algorithm is a simple and intuitive algorithm used in optimization problems. It has a function that calculates the optimal choice made at each step along with finding the overall optimal method to solve the entire problem. Two examples of the problems which can be solved successfully using greedy algorithms including Huffman encoding and Dijkstra’s algorithm; these are used to compress data and find the shortest path through a graph, respectively. The greedy algorithm operates in a way that takes all of the data to a certain problem and sets a rule for the elements to add solution at each step of the algorithm (Astrachan, et al. 2002). Kadam and Kim (2022) show that it is NP-Complete and propose a greedy algorithm to solve it. Table 1 refers to the notations.

Table 1 Description of notations (Adl and Rankoohi 2009)

2.1 Data allocation problem

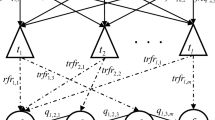
The purpose of DAP is to find the location of fragments in the best sites, to alleviate the total cost of a transaction when the query is taken from one site to another one (Adl and Rankoohi 2009; Mahi et al. 2018; Mamaghani, et al. 2010). Figure 1 shows the dependencies among sites, fragments, and transactions (Adl and Rankoohi 2009). For example, to get a query from S₁ to S₂ for obtaining the fragment j, the transaction k is necessary. Transaction access to the website is done the through site Fragment Frequency (FREQ) matrix, which included frequency values among sites transactions. Transactions to fragmentations achievements are done through the Transactions to Fragmentations (TRFR) matrix. Evaluating the amount of data transactions for fragments dependency is done through the TRFR matrix, which has some parameters. The Q matrix refers to the data between two fragments of one transaction. The size of each fragment is at interval $\left[\frac{c}{10}, \frac{20*c}{10}\right]$, which is chosen randomly. In this range, c is a value at the interval [101,000] (Adl and Rankoohi 2009).

Fig. 1

The dependences among sites, transactions and fragments (Adl and Rankoohi 2009)

The size of each fragment is calculated by Eq. (1) (Adl and Rankoohi 2009).

$$\left(\sum_{\mathrm{i}=1}^{\mathrm{n}}{p}_{i}=\mathrm{m}\right), {rf}_{i}=m-\sum_{\mathrm{q}=1}^{\mathrm{i}}{p}_{q}$$

(1)

Also, the site capacity site is calculated by Eq. (2) (Adl and Rankoohi 2009).

$${siteCap}_{i}= {p}_{i}*max{}_{1\le j\le m}({fragSize}_{j})$$

(2)

The site capacity should not be more than ${\mathrm{fragSize}}_{\mathrm{j}}*{\mathrm{x}}_{\mathrm{ij}}$ during the fragments replacement on the site, as calculated by Eq. (3) (Adl and Rankoohi 2009).

$$\sum_{\mathrm{j}=1}^{\mathrm{m}}{\mathrm{fragSize}}_{\mathrm{j}}*{\mathrm{x}}_{\mathrm{ij}}\le {\mathrm{siteCap}}_{\mathrm{i}}\mathrm{ i}=\mathrm{1,2},\dots ,\mathrm{n}$$

(3)

COST1 is calculated from the allocation of the fragments on sites according to Eq. (4)) (Adl and Rankoohi 2009). According to fragment size and site capacity, fragments are allocated to sites and the vector is created.

$${\mathrm{partialcost}1}_{\mathrm{ij}}=\sum_{\mathrm{q}=1}^{\mathrm{n}}{\mathrm{uc}}_{\mathrm{iq}}* {\mathrm{stfr}}_{\mathrm{qj}}$$

(4)

Vector (Eq. (5)) (Adl and Rankoohi 2009) is related to the COST1 calculation.

$$\text{COST}1\left(\mathrm{\psi}\right)=\sum_{\mathrm{j}=1}^{\mathrm{m}}{\text{partialcost}1}_{{\mathrm{\psi}j}^{\mathrm{j}}}$$

(5)

COST2, the parameter calculated as the query from the site j1 to j2, has been taken. The COST parameter is calculated through the matrix q. The matrix is calculated through multiplying the sum of the column with the element of the $freg$ matrix by the matrix (Eq. (6)) (Adl and Rankoohi 2009).

$${\mathrm{qfr}}_{\mathrm{kj}1\mathrm{j}2}={\mathrm{q}}_{\mathrm{kj}1\mathrm{j}2}*\sum_{\mathrm{r}=1}^{\mathrm{n}}{\mathrm{freq}}_{\mathrm{kr}}$$

(6)

FRDEP matrix is calculated based on the accumulation of the transaction cost between fragments (Eq. (7)) (Adl and Rankoohi 2009).

$${frdep}_{j1j2}=\sum_{k=1}^{l}{qfr}_{kj1j2}$$

(7)

COST2 is achieved through the FRDEP matrix and vector, as shown by Eq. (8) (Adl and Rankoohi 2009), through multiplying.

$$\mathrm{COST}2\left(\mathrm{\psi}\right)=\sum_{\mathrm{j}1=1}^{\mathrm{m}}\sum_{\mathrm{j}2=1}^{\mathrm{m}}{\mathrm{frdep}}_{\mathrm{j}1\mathrm{j}2}*{\mathrm{uc}}_{{\mathrm{\psi}}_{\mathrm{j}1}{\mathrm{\psi}}_{\mathrm{j}2}}$$

(8)

Finally, the sum of COST1 and COST2 is related to the COST according to the vector produced as Eq. (9) (Adl and Rankoohi 2009). The vector which is created to allocate fragments on sites to get the query for the algorithm in this paper is the best. The mentioned aim will be pursued by our new method, as discussed in the next section.

$$COST(\psi)=COST1(\psi)+COST2(\psi)$$

(9)

2.2 The proposed method (Greedy-DAP)

DAP solution based on greedy algorithm utilization and adaptation is the aim of this study. The method presented can be called Greedy-DAP. It is an innovative approach to solve DAP. Due to the fewer control parameters of the greedy algorithm, some parameters such as speed convergence specifications, low consuming time, and robustness against the solution space of the optimization problems are rarely used to solve the optimization problems with the same characteristics by the vector p (Deng et al. 2012; Bai 2010). To achieve this goal, the cost must be low; then, to reduce the cost of transactions, fragments must be implemented in the sites. $Vector p$ is used to compute the cost of fragments replacement in DAP. In the Greedy-DAP, the size of the vector p is $1*m$ and its structure is as follows:

	1	2	…	j	…	m	Fragment number
Vector p:	2	3	…	i	…	n	Site number of the fragment

$Vector p$ is an array, indicating that the fragment is located on the site. For example, fragment 1 is located on-site 2, fragment 2 is located on-site 3, etc. $Vector p$ shows which fragment will be placed on which site. Fragments placement on the best site to alleviate the total transaction cost is our aim. This greedy algorithm, which considers the total cost, is used to evaluate the process of fragment allocation to the sites. Fitness calculation is done by cost function in the greedy algorithm, as described in Sect. 2.1. Determination of the cost values of the vectors is done by Eq. (10), and the Max number is equal to the value of the maximum element in the Cost matrix.

$$Cost\left[i, j\right]=((partial\,Cost\left[i, k\right]*\left(frdep\left[k, j\right]\right)*\left(Uc\left[k,j\right]\right)), Max \,number = maximum \,Cost [i, j]$$

(10)

Site capacity is one of the parameters in Greedy-DAP; so, a counter is determined for each site to check the capacity of the site. Cost matrix has $n$ rows and $m$ columns, where each row and column represent a site and fragment, respectively. Firstly, the minimum value of the cost matrix is found in the $Cost\left[i, j\right]$. If the fragment size $j$ is greater than the capacity site $i$, we should find a second minimum element in the Cost matrix. We should continue finding the $k-th$ minimum until the fragment size $j$ is less than site capacity $i$ and update the site capacity by reducing the site capacity from fragment size. Secondly, if the above condition is true in the $Cost\left[i, j\right],$ then we can put j into index $i$ in the vector p. After that, the column $j$ from the Cost matrix is filled with the Max number. The Cost matrix is given in Table 2.

Table 2 Cost matrix representation

Then we will find the next minimum of the matrix; we will continue this process until all elements in the matrix are filled up to maximum value. Replace the values of the column j in a maximal matrix. The updated Cost matrix is given in Table 3.

Table 3 Updated cost matrix

Greedy-DAP pseudo-code and consequently its scripting chart are shown in Figs. 2 and 3, respectively.

Fig. 2

Pseudo-code of the Greedy-DAP

Fig. 3

The scripting chart of the Greedy-DAP

3 Experimental results

The original data set has been produced based on the cost formulation in Sect. 2.2, in order to compare DAP with other algorithms. The proposed algorithm was evaluated using three cases of comparisons in various fragments and site sizes. In the first case, the number of fragments was equal, but the number of sites was variable. In the second case, the number of sites was equal, but the number of fragments was different. The third case contained the same size of fragments and sites. It is worth noting that the proposed algorithm is a deterministic one; therefore, the results of the iterations of the algorithm were the same. However, due to using a random dataset, the cost and execution time of other algorithms are different. In order to get the minimum number of results, the program was tested in 20 iterations of executions in PSO-DAP, whereas in the case of Greedy-DAP, due to obtaining the same results in all executions, only one iteration of execution was done. PSO-DAP iteration was done in 500. Computer parameters for comparing PSO-DAP and Greedy-DAP based on an algorithm presented for DAP can be listed as follows: CPU: 1.6 GHZ, memory: 4 GB, Windows 7, and C# programming language.

3.1 State 1

The first state refers to increasing the site size from 3 to 48 and fixing the number of fragments in 48. The values of the algorithms in paper (Tosun et al. 2013a) have just been shown in the figure. The results of the cost and execution time for PSO-DAP and Greedy-DAP are shown in Tables 6 and 7, respectively. In order to compare the obtained results of the proposed algorithm with a figure in paper (Tosun et al. 2013a), we have mapped the proposed algorithm results to those charts. Considering that other algorithms used the same approach; forty-six different sites numbers were taken from the range of 3 to 48 and the number of fragments were fixed by 48. Input parameters in Table 4, as shown in bold, refer to PSO-DAP and others are common in both PSO-DAP and Greedy-DAP.

Table 4 Input parameters for PSO-DAP (Mahi et al. 2018)

Samples of the DAP cost and execution time values are shown in Table 5. The obtained results of the Greedy-DAP algorithm were compared with the other methods in the literature, namely Ant γ Algorithm (Adl and Rankoohi 2009), Ant β Algorithm (Adl and Rankoohi 2009), Ant α Algorithm (Adl and Rankoohi 2009), Evolutionary (Adl and Rankoohi 2009) and PSO-DAP minimum.

Table 5 Generate cost and execution time for increasing site numbers (n) and fragment number is fixed by 48

Tables 6 and 7 contain the cost and execution time values, respectively; the best results are shown in bold.

Table 6 Cost comparison of methods for increasing site numbers (n) and fragment number is fixed by 48 (cost values are column × 10⁹)

Table 7 Execution time (s) comparison of methods for increasing site numbers (n) and fragment number is fixed by 48

A comparison of the obtained results demonstrated that Greedy-DAP had less cost and was a less time-consuming process in comparison with PSO-DAP. DAP samples were created randomly and Greedy-DAP and PSO-DAP used them to solve problems in this paper. Datasets were created randomly according to the formula described in Sect. 2.2 for the purpose of comparison with the previous algorithm’s datasets. The results demonstrated that, among 46 obtained results, 39 were the best in terms of cost, and they were almost similar to our compared algorithm’s results in Tables 6 and 8, thereby showing that the proposed algorithm was statistically different from other methods. Consequently, PSO-DAP would consume less time than other algorithms, as shown in Table 7 (Mahi et al. 2018).

Table 8 Statistical comparison of the methods using sign test for increasing site numbers (n) with fixed fragment number (48)

Here, to show the accuracy of our method, we used the sing test (Mann 2013; Lurie et al. 2011). This test sign was done for three states. There was no significant difference between the two algorithms as the H0 hypothesis and there was a significant difference between the two algorithms as the H1 hypothesis. All calculations were implemented at a significance level of five percent. Table 8 contains the sign test results. The H1 hypotheses were accepted because the computed Z values were outside the range in all tests. The proposed algorithm and other alternatives related to comparison results are shown in the last two rows of Table 8.

In Figs. 4, 5, 6, 7, we plot the Greedy-DAP cost and the time results from comparisons with other approaches such as Ant γ Algorithm (Adl and Rankoohi 2009), Ant β Algorithm (Adl and Rankoohi 2009), Ant α Algorithm (Adl and Rankoohi 2009), Evolutionary (Adl and Rankoohi 2009) and PSO-DAP minimum (Mahi et al. 2018).

Fig. 4

Evaluating the Results achieved by the algorithms in a state 1 comparison for cost (Adl and Rankoohi 2009)

Fig. 5

Evaluating the Computation time of the algorithms in a state 1 comparison for time (Adl and Rankoohi 2009)

Fig. 6

Evaluating the Results achieved by the algorithms in a state 2 comparison for cost (Adl and Rankoohi 2009)

Fig. 7

Evaluating the Computation time of the algorithms in a state 2 comparison for time (Adl and Rankoohi 2009)

3.2 State 2

The second state of the algorithm refers to increasing the fragment size from 20 up to 50 by step 1 and fixing the number of sites in 20 (Table 9). The obtained results of the algorithm in paper (Adl and Rankoohi 2009) have not been shown in the table. The results of the cost and execution time of PSO-DAP and Greedy-DAP are shown in Tables 10 and 11. To compare the results of the paper (Adl and Rankoohi 2009), we mapped our obtained results to those charts, as shown in Figs. 6 and 7. These figures show that in comparison with other algorithms, the proposed one has the lowest cost and time. Greedy-DAP and the achieved results have been compared with other methods, such as Ant γ Algorithm (Adl and Rankoohi 2009), Ant β Algorithm (Adl and Rankoohi 2009), Ant α Algorithm (Adl and Rankoohi 2009), Evolutionary (Adl and Rankoohi 2009) and PSO-DAP (Mahi et al. 2015).

Table 9 Generate cost and execution time for increasing fragment numbers (m) and site number is fixed by 20

Table 10 Cost comparison of methods for increasing fragment numbers (m) and site number is fixed by 20

Table 11 Execution time (s) comparison of methods for increasing fragment numbers (m) and site number is fixed by 20

The DAP samples size increment in terms of the cost values and execution time is shown in Table 9.

Table 10 shows the results related to cost from three algorithms and also the standard deviation for the proposed algorithm. Table 11 shows the execution times of different methods.

The statistical comparison of the proposed method and the other method is given in the last six rows of Table 12 for increasing the fragment numbers (m) and the fixed site number, showing the acceptable results.

Table 12 For increasing fragment numbers (m) and site number is fixed by 20. Obtained results of methods comparisons with sign test

3.3 State 3

The number of fragments and sites are equal so our proposed algorithm, as implemented on an equal number of fragments and sites. DAP samples size increment cost values and execution time generations are shown in Table 13.

Table 13 Generate cost and execution time for increasing DAP instance sizes

Tables 14 and 15 present the comparison covering the cost and execution time values, respectively. The best results are shown in bold. Table 14 shows the cost of the results, which is much better than the results of the previous algorithms. In Table 15, the calculation time of resource allocation on the sites is shown that the more the number of sites with their resources, the more time it takes to get them.

Table 14 Cost comparison of methods for increasing DAP instance sizes (cost value is column × 10⁶)

Table 15 Execution time (s) comparison of methods for increasing DAP instance sizes

The statistical comparison of the proposed method and the other method is given in the last six rows of Table 16 for increasing the fragment numbers (m) and fixing the site number, showing that this algorithm has better results. To better show the results of the presented method, we have compared three data states. In the first state, we considered the number of sites varied and the number fragments fixed. For the second case, we considered the number of fragments varied and the number of sites constant. For the third state, we considered the number of sites and the number of fragments to be the same in order to better show the correct performance of the presented method. In all three states, the results of the allocated cost and especially the time consumption of the presented method are much better than the previous algorithms.

Table 16 Statistical comparison of the methods using sign test

3.4 Discussion

The aims of the data allocation problem (DAP) are to achieve the minimum execution time and ensure the lowest transaction cost of queries. The solution for this NP-hard problem based on numerical methods is computationally expensive. Despite the success of such heuristic algorithms as GA and PSO in solving DAP, the initial control parameters tuning, the relatively high convergence speed, and hard adaptations to the problem are the most important disadvantages of these methods. This paper presents a simple well-formed greedy algorithm to optimize the total transmission cost of each site-fragment dependency and each inner-fragment dependency. To evaluate the effect of the proposed method, more than 20 standard DAP problems were used. Experimental results showed that the proposed approach had better quality in terms of execution time and total cost.

4 Conclusion

In this work, we have solved DAP in non-replicated distributed database systems. The key subjective in DAP is to decrease the query execution time and the transaction cost. In this paper, as an approach based on the greedy algorithm, Greedy-DAP has been proposed to optimize query execution time and the transaction cost in DAP. To evaluate the effectiveness of the proposed algorithm, three states were considered. The first state referred to the set constant fragment size and variant site size. In addition, in the second state, the constant size of sites and variant sizes of fragments were considered. The third state contained a constant size of sites and fragments. The obtained results of the proposed algorithm based on these three states demonstrated that the presented method could have a good performance. Greedy-DAP was founded on various DAP samples in several states, obtaining effective results in comparison with other algorithms. Also, it was evaluated in terms of the query execution time and transaction cost. The obtained results demonstrated that Greedy-DAP displayed better performance in terms of query solution quality and running time. Due to the solution, space exponentially grows along with increasing the dimensionality of the problem; the performance of the approach is decreased. However, analysis of the results demonstrated that the presented approach generated results comparable with the state of art algorithms, especially in terms of execution time, due to the lower number of computations.

To solve the DAP problem that was previously solved with the PSO algorithm, it can be solved with a parallel algorithm, which can get much better results. Also, the gray wolf optimization (GWO) algorithm, the firefly optimization algorithm, the grasshopper optimization algorithm (GOA), the cuckoo optimization algorithm, and the frog leap optimization algorithm can be used in the future.