1 Introduction

The production scheduling problem is a common challenging issue faced by all production systems. It is an optimization problem that involves decisions making about machine allocation and job sequencing (Pinedo 2005) problems. Adequate production scheduling aims to account for multiple constraints to achieve timely and efficient production (Lei et al. 2017). Two significant optimization challenges in manufacturing systems are the job shop problem and the flexible problem (Zhang et al. 2022). The job shop problem involves jobs scheduling to be processed on a collection of machines, each requiring a unique sequence of machine operations (Brandimarte 1993). On the other hand, the flexible problem considers jobs assignment to machines in a way that maximizes the utilization of resources and reduces the overall production time (Song and Liu 2022).

Flexible production systems can address various complexities identifying job processing times accurately (Acevedo-Chedid et al. 2021). In this direction, analyzing uncertainty in processing times in a flexible environment is essential for optimizing production schedules in production systems (Acevedo Chedid et al. 2020). Optimal scheduling can determine the success or failure of an organization, impacting its profitability and quality of services (Kundakcı and Kulak 2016). The flexible job-shop scheduling problem may involve various constraints like machine capacity, time lags, holding times, and setup times (Boyer et al. 2021). These problems have been widely studied in the academic literature and have numerous practical applications in the manufacturing industry like assembly line production, manufacturing cell scheduling, and automated warehouse management (Boyer et al. 2021).

Although traditional scheduling problems typically assume that the processing time of each operation is a fixed value in real-world manufacturing systems, the processing time can be challenging to determine precisely in advance (Fazel Zarandi et al. 2020). Additionally, completion times may be obtained ambiguously, leading to uncertainty in the scheduling process. As a result, there is a clear need to incorporate the fuzzy concept into scheduling problems (Abdullah and Abdolrazzagh-Nezhad 2014). By considering the fuzziness in both processing time and completion time, manufacturers can create more robust scheduling algorithms that better account for the complexities of real-world production systems (Seyyedi et al. 2021). For example, considering fuzzy aspects in combination with hybrid algorithms is one of the new challenges in the literature (Kisi et al. 2023).

This study aims to explore innovative solutions to tackle the challenges of production scheduling in flexible production systems with potential implications for improving the efficiency and effectiveness of production processes. The proposed solution approach is an Adaptive Teaching–Learning-based Optimization Algorithm (TLBO-A) for solving the Flexible Job Shop Problem with partial flexibility, focusing on minimizing fuzzy makespan and fuzzy average flow. This research aims to develop a metaheuristic approach combining adaptive teaching–learning strategies with optimization techniques.

The practical relevance of modeling flexible manufacturing systems and the problem of production scheduling is a topic of great interest to researchers, and more and more manufacturing industries are investing in improving their production scheduling models. The identified advantages make it clear that as long as the organization's strategy can be visualized and executed effectively in production programming, customer loyalty can be achieved, costs can be reduced, and high-quality products can be guaranteed.

This research presents a multi-objective model that considers the uncertainty of system processes through fuzzy processing times. As with any Flexible Job Shop problem, the routing flexibility associated with the jobs and heterogeneous characteristics of the machines available in each job center is considered. The optimization objectives are expressed in a linear sum of weights, and the objectives to be evaluated are: Minimize the maximum fuzzy completion time of all the jobs processed in the system \((\mathrm{Min\, Cmax})\) and minimize the average flow time. This approach guarantees that the assignments of the jobs to the machines are carried out in a balanced way, simultaneously minimizing the maximum permanence time of the jobs in the system.

The rest of the paper is organized as follows: Sect. 2 of this paper provides a comprehensive literature review of existing solution methods, followed by a detailed description of the study problem in Sect. 3. Section 4 elaborates on the design of the proposed metaheuristic algorithm, and in Sect. 5, the obtained results and managerial implications are presented. Finally, Sect. 6 will conclude the study and discuss potential future works in this field of research.

2 Literature review

The Flexible Job Shop Scheduling Problem (FJSP) is an extension of the classic Job-Shop Scheduling Problem (JSP), which is commonly encountered in companies and is known to be an NP-hard problem (Gao et al. 2007; Kaplanoğlu 2016). The FJSP involves the flexibility of job routes among the available machines, requiring adequate sequencing, assignment, and routing of jobs (Chiang and Lin 2013). The flexibility in FJSP can be categorized as partial or total. In the case where all operations can be processed on all machines in the system, it is referred to as Total Flexible Job Shop Scheduling Problem (T-FJSP); otherwise it would be considered as a Partial Flexible Job Shop Scheduling Problem (P-FJSP) (Li et al. 2010).

Various solution methodologies have been proposed for FJSP, including conventional programming methods like exact and heuristic approaches, but their effectiveness are limited due to the combinatorial complexity associated with the problem (Chen et al. 2012; Jia and Hu 2014). The FJSP solution methods can be classified into two approaches: integration and hierarchy. The integration approach involves simultaneous sequencing and assignment, while the hierarchical approach decomposes the problem. Although the hierarchical approach may be easier to solve, the integrative approach often yields better results (Pezzella et al. 2008).

Brandimarte (1993) article pioneered a hierarchical approach to solving the FJSP. Then, various studies have been conducted to address the challenges of FJSP. Mastrolilli and Gambardella (2000) developed a taboo search heuristic with two neighborhood search functions, while Kacem et al. (2002) focused on resource allocation and used an evolutionary control approach to minimize the makespan, the flow of the most loaded machine, and the total flow of machines. Xia and Wu (2005) proposed a hybrid algorithm that combined PSO and simulated annealing as a local search algorithm to minimize makespan. Gao et al. (2007) developed a hybrid genetic algorithm with a local bottleneck search, and Gao et al. (2008) suggested a hybrid genetic algorithm with a variable neighborhood search. Xing et al. (2009) proposed a local search algorithm that combined different dispatch rules for the multi-objective FJSP with partial and complete flexibility. Finally, Zhang et al. (2011) investigated a tabu search and particle swarm optimization algorithm to address the multi-objective FJSP.

The FJSP has been tackled by several researchers using various metaheuristic algorithms. Wang et al. (2012a, b) studied an improved Pareto-based artificial bee colony algorithm, while Chiang and Lin (2013) proposed a multi-objective evolutionary algorithm that employed the Pareto approach to minimize the makespan, total flow, and maximum flow. Baykasoğlu et al. (2014) presented a solution approach for the FJSP based on a linguistically-based metaheuristic model. Li and Gao (2016) employed a hybrid algorithm that combined guided taboo search and genetic algorithm techniques. Similarly, Xu et al. (2016) presented a memetic algorithm that minimized makespan and total flow. Deng et al. (2017) developed a hybrid evolutionary bee algorithm with a genetic algorithm that minimized makespan and total and maximum flow. Gaham et al. (2018) studied an effective harmonic search which was permutation-based. Ertenlice and Kalayci (2018) executed a Kalman multi-objective heuristic algorithm that considered makespan, total flow, and critical workflow. More recently, Braune et al. (2022) developed a genetic programming approach that considered job sequencing and machine assignment in the FJSP.

Furthermore, some authors addressed uncertainty in the FJSP considering random jobs or machine breakdowns. Zhang et al. (2022) studied the dynamic flexible job shop problem (DFJSP) and proposed a two-stage algorithm that reduced makespan and the frequencies of machine breakdowns. Lei et al. (2022) included a Markov Decision Process approach in Multi-Proximal Policy Optimization Algorithm (multi-PPO). Basiri et al. (2020) considered a fuzzy processing times multi-objective model for flexible job shop scheduling and developed a metaheuristic that combines a genetic algorithm with SAW/TOPSIS methods.

Generally speaking, the completion of real systems, processing, and delivery times are often uncertain and subject to variation is essential. To address these issues, the Fuzzy Job Shop Programming Problem (fJSP) extends the JSP by introducing fuzzy variables, such as, processing times, delivery times, and constraints (Abdullah and Abdolrazzagh-Nezhad 2014). The fJSP can be divided into three main categories: the fJSP with fuzzy delivery times, the fJSP with fuzzy processing times, and the fJSP with fuzzy processing times and delivery times. Moreover, the fuzzy Job Shop problem has also been explored in flexible environments, where additional optimization criteria are considered.

The Job Shop Flexible programming problem with fuzzy behavior variables has become an increasingly popular option for tackling scheduling problems. Researchers have shown a growing interest in this problem in recent years and have proposed various solutions, albeit still in the early stages of study (Liu et al. 2015). Different models have been proposed from the classification enunciated for the fJSP, which is considered NP-Hard. The contributions of several authors in the fJSP research works are summarized in Table 1 as follows.

Table 1 Studies related to fJSP
Full size table

The current research falls under the programming environments of production in fuzzy settings for flexible job-shop scenarios. The structure of the study is detailed below. The fFJSP assumes that all jobs are initially independent and available for processing. Likewise, a machine can process only one operation, and a job can be processed by only one machine. Also, setup times are included in the processing times, and once an operation begins, it cannot be interrupted.

In this study, an Adaptive Teaching–Learning-based Optimization Algorithm (TLBO-A) is proposed to address the P-MOfFJSP with partial flexibility, where the objective is to minimize both the fuzzy makespan and the fuzzy average flow. The fuzzy behavior is modeled using Triangular Fuzzy Numbers (TFN). The practical relevance of modeling flexible manufacturing systems and production scheduling problems has caught the attention of the researchers. Many manufacturing industries are improving their production scheduling models to reduce costs and guarantee high-quality products and thus are achieving customer loyalty. Production scheduling models have been applied in various industries, such as power generation, food processing, chemical processing, automotive factories, textile industries, aeronautical industries, and steel processing (Behnamian 2017).

This study builds upon the models developed by Zhang et al. (2011), Wang et al. (2017), Kaplanoğlu (2016), Deng et al. (2017) and Kato et al. (2018), who explored multi-objective models for the Job Shop flexible scheduling problem with fuzzy processing times. The proposed models consider the routing flexibility associated with the jobs and account for heterogeneous machine characteristics at each work center. The optimization objectives are expressed as a linear sum of weights, aiming to minimize the maximum fuzzy completion time of all processed jobs (Min Cmax) and the average flow time, ensuring a balanced assignment of jobs to machines while minimizing the maximum job processing time in the system. These models account for process uncertainty, allowing for robust scheduling solutions.

The multi-objective approach of using a sum or linear combination of weights is commonly applied to solve the P-MOFfJSP problem. This technique was first proposed by Zadeh (1963), who demonstrated that solving a scalar optimization problem with the objective function as a weighted sum of the components of the original vector function can lead to efficient solutions. Reducing the problem to a single objective function allows for comparing all alternatives, enabling a comprehensive order framework. Hence, the choice of weight values \({\alpha }_{i}\) plays a crucial role in achieving the final decision. It is essential to perceive how this choice impacts the optimal points in determining the coefficients.

One of the main advantages of this method is its computational efficiency and ease of use. However, the difficulty of determining appropriate weighting coefficients without adequate information is a significant drawback. Properly scaling objectives also require considerable knowledge about the problem, which may not always be available and costly. Additionally, this method may fail to generate certain parts of the Pareto front when its shape is concave, irrespective of the weight combinations. Nonetheless, incorporating additional functions may prove helpful in obtaining an initial sketch of the Pareto front for a given problem or providing background information to be used by another approach (Chiandussi et al. 2012; Al-Janabi and Alkaimi 2020, 2022; Al-Janabi et al. 2020a, 2020b; Al-Janabi et al. 2021; Mohammed and Al-Janabi 2022). Additionally, TLBO has been used to solve supply chain problems such as inventory optimization and supplier selection (Baykasoğlu et al. 2014) and to solve transportation problems such as vehicle routing and scheduling (Jin et al. 2021). Furthermore, TLBO has shown promising results in solving complex engineering problems, such as design of truss structures and optimization of renewable energy systems (Mane et al. 2020). The versatility of TLBO in solving various optimization problems demonstrates its potential to be used in various fields. Overall, TLBO has proven to be a valuable tool in solving complex optimization problems with high efficiency and accuracy (Zou et al. 2019). For example, Xu et al. (2022) proposed a new variant of the Teaching–Learning-Based Optimization (TLBO) algorithm named Distance-Fitness Learning TLBO (DFL-TLBO). This variant employs a distance-fitness learning strategy to enhance search ability and address premature convergence and local optima entrapment issues in complex optimization problems.

The proposed methodology combines the Teaching–Learning-based Optimization (TLBO) algorithm with a Genetic Algorithm to solve the Multi-Objective Flexible Fuzzy Job Shop problem with partial flexibility (P-MOFfJSP). The Adaptive TLBO (TLBO-A) algorithm addresses the challenges associated with production scheduling in fuzzy time environments incorporating two genetic operators (mutation and crossover) with an adaptive strategy for population reconfiguration. This methodology offers several advantages over traditional metaheuristic algorithms, like genetic algorithms (Katoch et al. 2021). Firstly, TLBO-A enhances solution space exploration, ensuring the search for good solutions and avoiding premature convergence. Secondly, the hybridization of TLBO-A and GA promotes the synergy of these methods, exploiting the best of both techniques. Finally, the TLBO-A algorithm's adaptive strategy for population reconfiguration provides the ability to adapt to changes in the solution landscape, offering robustness to the algorithm.

The experimental evaluation of the proposed methodology on benchmark instances commonly used in programming problems with fuzzy variables demonstrates significant results, indicating that the TLBO-A algorithm outperforms among other state-of-the-art metaheuristic algorithms. The performance of this methodology exceeds other metaheuristic algorithms in terms of both solution quality and computational efficiency. Our methodology can effectively solve real-world production scheduling problems, such as delivery and availability times, incorporating fuzzy processing and delivery times. As a whole, our contribution lies in addressing the challenges associated with production scheduling in fuzzy time environments and proposing a practical hybrid metaheuristic approach.

3 Description of the problem

3.1 Multi-objective fuzzy flexible job shop scheduling problem with partial flexibility

Most research studies on scheduling problems focus on optimization methods to minimize makespan. However, processing times are subject to variations due to different situations. Hence, the makespan and variables associated with processing time are expected to fluctuate (Pan et al. 2014; Joo et al. 2018; Jin et al. 2021). Some studies have considered multi-objective optimizations in scheduling problems, but they have mainly worked with deterministic processing times. Therefore, the existing optimization techniques are unsuitable for solving such problems, as actual start or finish times will oscillate and create significant deviations between the actual and planned makespan. Recent research (Jin et al. 2016) has emphasized the need for optimization techniques that can handle stochastic processing times to address this issue.

Petrović et al. (2014) proposed fuzzy logic to handle imprecise information by combining fuzzy sets according to predetermined rules to generate various output values. This approach can effectively model uncertainty in real-world environments. To better represent the uncertainty inherent in the Flexible Job Shop Problem (FJSP), this study employs fuzzy sets to represent processing time and related variables like the start and end times of operations and jobs, machine utilization time, program completion time, and job processing time. It should be noted that in practical situations, the processing time for each job and operation is estimated based on the nature of the machine or the variability of personnel involved.

The multi-objective fuzzy flexible job shop scheduling problem with partial flexibility (P-MOfFJSP) consists of a set of the n jobs \({J}_{i} (i=\mathrm{1,2},3\dots n )\) and a set of the m machines \({M}_{K}(k=\mathrm{1,2},3\dots m )\). Each job \({J}_{i}\) consists of \({n}_{i}\) Operations. Several machines can process each operation \({O}_{ij}\) that indicates the operation \({j}\) of job\(i\). The processing time of the operation \({O}_{ij}\) on \({M}_{K}\) is represented as a Triangular Fuzzy Number (TFN), \({P}_{ijk}=\left({\alpha }_{ijk}^{1} ,{\alpha }_{ijk}^{2} , {\alpha }_{ijk}^{3}\right)\) (Zheng et al. 2012).The P-MOfFJSP is characterized by a finite set of machines \(M=\left\{{M}_{1}, {M}_{2} , {M}_{3}\dots {M}_{m}\right\}\) with heterogeneous characteristics and must process \(n\) jobs \(J=\left\{{J}_{1}, {J}_{2} , {J}_{3}\dots {J}_{n}\right\}\), each job \({J}_{\mathrm{i}}\) is composed of \({n}_{i}\) operations \(O=\left\{{O}_{i,1} , {O}_{i,2} , {O}_{i,3}\dots {O}_{{i,n}_{i}}\right\}\), the total number of operations \(N= \sum_{i=1}^{n}{n}_{i}\). The processing time of \({O}_{i,j}\) on the machine \({m}_{k}\) is represented by TFN, \({p}_{ijk}=\left({p}_{ijk }^{1}, {p}_{ijk }^{2} , {p}_{ijk }^{3}\right)\), where \({p}_{ijk }^{1}, {p}_{ijk }^{2}\) and \({p}_{ijk }^{3}\) represent the best, most likely, and worst processing times.

The transfer and setup time of the jobs between the different machines is included in the processing times. The fuzzy makespan of \({O}_{i,j}\) is represented by a TFN, \({\widetilde{C}}_{ijk}=\left({C}_{ijk }^{1}, {C}_{ijk }^{2} , {C}_{ijk }^{3}\right),\) and the fuzzy total flow time of the schedule for \(\widetilde{FT}=\left({FT}^{1},{FT}^{2},{FT}^{3}\right)\), where \({C}_{ijk }^{1}\) and\({FT}^{1}\), \({C}_{ijk }^{2}\) and\({FT}^{2}\), and \({C}_{ijk }^{3}\) and \({FT}^{3},\) respectively, represent the best, most probable and worst makespan and total flow time. The P-MOFfJSP aims to determine the allocation of machines and the sequencing of operations on all machines to minimize fuzzy makespan:\({\widetilde{C}}_{\mathrm{Max}}={\mathrm{max}}_{i=\mathrm{1,2},3,\dots ,n}{\widetilde{C}}_{i}\), and fuzzy average flow time: \(\overline{F }=\frac{1}{n}{\sum }_{i=1}^{n}{\widetilde{F}}_{i}\), in which \({\widetilde{C}}_{i}\) is the fuzzy makespan of job \({J}_{i}\) and \({\widetilde{F}}_{i}\) is the fuzzy flow time of job\({J}_{i}\), subject to precedence and processing constraints.

  • All jobs are available at time zero (0).

  • All machines are available at time zero (0).

  • Each job can only be executed by one machine at a time.

  • Jobs are independent of each other.

  • Jobs consist of dependent operations that cannot be interrupted. Each operation must be completed before starting another one.

  • Machines are independent (Flexible Job Shop, Heterogeneous Machines).

  • At any given time, a machine can only run one job and become available for other jobs once the current job is finished.

  • The processing times of jobs exhibit fuzzy behavior and are studied within a fuzzy interval defined by a fuzzy triangular number.

  • The flexibility of the system is partial, with not all machines capable of processing all job operations.

  • Setup times between jobs are included in processing times.

  • The completion times of jobs also exhibit fuzzy behavior.

  • Jobs are considered finished once all operations are executed.

The processing restrictions proposed in this system allow for flexible modeling of production systems, considering changes in job assignments and processing times. This increases efficiency and adaptability in response to changing customer requirements, leading to improved customer loyalty, cost reduction, and high-quality product guarantees. The fuzzy makespan is defined as \({\widetilde{C}}_{\mathrm{max}}=\underset{i=1,...,n}{\mathrm{max}}\widetilde{{\mathrm{C}}_{\mathrm{i}}}, i=1,\mathrm{ 2,3}\dots n\), where \(\widetilde{{C}_{i}}=\left({c}_{i }^{1}, {c}_{i }^{2} , {c}_{i }^{3}\right)\) is the fuzzy completion time of job i. The fuzzy average flow (\(\widetilde{\text{FP}}\)) is given by the expression \(\widetilde{\text{FP}}=({F}^{1} + 2{F}^{2} + {F}^{3} )/\left(4*n\right)\). The P-MOfFJSP involves fuzzy number operations: addition, maximum, and ranking operations to establish the objective value and the feasible schedule. Given two fuzzy triangular numbers, \(X=\left({x}_{1},{x}_{2}, {x}_{3}\right)\), \(Y=\left({y}_{1},{y}_{2}, {y}_{3}\right)\), the operation addition is expressed as\(X+Y=\left({x}_{1}+{y}_{1} ,{x}_{2}+ {y}_{2}, {x}_{3}+{y}_{3}\right)\).

For the ranking operation, different criteria are used to compare:

  • Compare the value of \({G}_{1 }\left(X\right)=\left({x}_{1}+{2x}_{2}+{x}_{3}\right)/4\,\mathrm{ and }\,{G}_{1 }\left(Y\right)=\left({y}_{1}+{2y}_{2}+{y}_{3}\right)/4\). \(\mathrm{If }\,{G}_{1 }\left(X\right)>{G}_{1 }\left(Y\right)\), then \(X >Y\).

  • If both have the same value of \({G}_{1}\), then compare the value \({G}_{2 }\left(X\right)={x}_{2}\) and \({G}_{2 }\left(Y\right)={y}_{2}\). If \({G}_{2 }\left(X\right) >{G}_{2 }\left(Y\right)\), then \(X>Y\).

  • If \({G}_{1}\) and \({G}_{2}\) are identical, then compare the value of \({G}_{3 }\left(X\right)={x}_{3}- {x}_{1} \, \mathrm{and} \, {G}_{3 } \; \left(Y\right)={y}_{3}- {y}_{1}.\) If \({G}_{3 }\left(X\right)>{G}_{3 }\left(Y\right)\), then \(X>Y\).

  • In the approximate max operation, if \(X >Y\), then \(X \bigvee Y=X\), else \(X \bigvee Y=Y\).

In this formulation, to obtain the completion time of an operation based on its start time and processing time, the max operation is utilized. Additionally, to determine the fuzzy start time of a job operation on a specific machine \({M}_{k}\), the "max" operation is employed, considering the completion time of the previous operation in the job and the completion time of the previous operation in any job developed on \({M}_{k}\). Finally, the optimal schedule for the fuzzy problem is obtained using the "ranking" method to determine the order of completion time.

In this study, to structure the mathematical model, we referred to the variable-based precedence model proposed by Özgüven et al. (2010) for FJSP and the approach developed by Li and Gao (2016) for fFJSP, which are adapted to the proposed multi-objective model that considers the uncertainty of the system processes through fuzzy processing times. The problem considers partial flexibility in job assignments and heterogeneous characteristics of the available machines at each workstation. The sets, parameters, and equations are defined as follows.

3.1.1 Sets

\(J\): Set of jobs;\(J=\left\{{J}_{1}, {J}_{2} , {J}_{3}\dots {J}_{n}\right\}\).\(i, h\): Index of the job; \(i,h=\mathrm{1,2},3...n.\)

\(M\): Set of machines; \(M=\left\{{M}_{1}, {M}_{2} , {M}_{3}\dots {M}_{k} \dots {M}_{m}\right\}\).\(k\): Index of machine; \(k=\mathrm{1,2},3\dots m\).

\(O\): Set of operations of the job \(i\); \(O=\left\{{O}_{i,1} , {O}_{i,2} , {O}_{i,3}\dots {O}_{{i,n}_{i}}\right\}\).

\({O}_{ij}\): Operation \(j\) of job \(i\).\(j, g\): Index of operation; \(j,g=\mathrm{1,2},3...{n}_{i}\).

3.1.2 Parameters

n: Number of jobs. m: Number of machines. \({n}_{i}\): Total numbers of operations of job \(i\).

\({M}_{ij}\): Set of machines available for operation; \({O}_{ij}\) \(\left({M}_{ij}\subseteq {M}_{k}\right)\).\({\widetilde{p}}_{ijk}\): Fuzzy processing time of the \({O}_{ij}\) on the machine \(k\); \(({\widetilde{p}}_{ijk} \ge (0, 0, 0))\).\(\beta :\) Relative importance of maximum fuzzy completion time on the schedule.

\(1-\beta :\) Relative importance of fuzzy average flow time on the schedule.

B: A large number.

3.1.3 Decision variables

$$ x_{{ijk}} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\;{\text{the}}\;{\text{machine}}\;k\;{\text{is}}\;{\text{selected}}\;{\text{for}}\;{\text{the}}\;{\text{run}}\;O_{{ij}} } \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right. $$
$$ y_{{ijk}} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\;{\text{the}}\;{\text{operation}}\;O_{{ij}} \;{\text{precedes}}\;{\text{operation}}\;O_{{hg}} \;{\text{on}}\;{\text{machine}}\;k} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right. $$
$$ \widetilde{t}_{{ijk}} :{\text{Fuzzy}}\;{\text{start}}\;{\text{time}}\;{\text{of}}\;{\text{the}}\;O_{{ij}} \;{\text{if}}\;{\text{run}}\;{\text{on}}\;{\text{the}}\;{\text{machine}}\;M_{k} $$
$${\widetilde{C}}_{ijk}:\text{ Fuzzy\,completion\, time \,of \,the }\,{O}_{ij}\text{ on\, the\, machine }\,{M}_{k}.$$
$${\widetilde{C}}_{i}: \text{Fuzzy completion time of job }i.$$
$${\widetilde{C}}_{max}: \mathrm{Maximum\, fuzzy\, completion\, time\, of\, jobs}.$$
$${\widetilde{F}}_{i}:\mathrm{ Fuzzy\, flow\, time\, of\, job }i.$$
$$\widetilde{FT}:\mathrm{ Fuzzy\, total\, flow\, time\, of\, schedule}.$$
$$\widetilde{\text{FP}}: \mathrm{Fuzzy\, average\, flow\, time\, of\, schedule}.$$

The mathematical model of the MOFfJSP of the research is:

$$\mathrm{Min}\; {Z}_{1}={\widetilde{C}}_{\mathrm{max}}$$
(1)
$$\mathrm{Min}\; {Z}_{2}=\widetilde{\text{FP}}$$
(2)
$$\mathrm{Min}\; {Z}_{3}=\beta {Z}_{1}+\left(1-\beta \right){Z}_{2}$$
(3)

S.t:

$${\widetilde{C}}_{\mathrm{max}}\ge {\widetilde{C}}_{i};{\forall }_{ }\left(i\right)$$
(1)
$${\widetilde{C}}_{i}\ge \sum \limits_{k\in {M}_{i,j}}{\widetilde{C}}_{i,j,k};{\forall }_{ }\left(i,j={J}_{{n}_{i}},k\right)$$
(2)
$${\widetilde{t}}_{i,j,k}+{\widetilde{C}}_{i,j,k}\le {x}_{i,j,k}*B;{\forall }_{ }\left(i,j,k\in {M}_{ij}\right)$$
(3)
$${\widetilde{C}}_{i,j,k}\ge {\widetilde{t}}_{ijk}+{\widetilde{p}}_{i,j,k}-\left(1-{x}_{i,j,k}\right)*B;{\forall }_{ }\left(i,j,k\in {M}_{ij}\right)$$
(4)
$${\widetilde{t}}_{i,j,k}\ge {\widetilde{C}}_{h,g,k}-{y}_{i,j,h,g,k}*B;{\forall }_{ }\left(i\le h,j,g,k\in {M}_{ij}\cap {M}_{hg}\right)$$
(5)
$${\widetilde{t}}_{h,g,k}\ge {\widetilde{C}}_{i,j,k}-\left(1-{y}_{i,j,h,g,k}\right)*B;{\forall }_{ }\left(i\le h,j,g,k\in {M}_{ij}\cap {M}_{hg}\right)$$
(6)
$$\sum \limits_{k\in {M}_{i,j}}{\widetilde{t}}_{i,j,k}\ge \sum \limits_{k\in {M}_{i,j}}{\widetilde{C}}_{i,j-1,k}; {\forall }\; \left(i,j = 2,...,{J}_{{n}_{i}}\right)$$
(7)
$$\sum \limits_{k\in {M}_{i,j}}{x}_{i,j,k}=1;{\forall }_{ }\left(i,j\right)$$
(8)
$${\widetilde{F}}_{i}= \sum \limits_{i=1}^{n}{\widetilde{C}}_{i,j,k};{\forall }_{ }\left(j,k\right)$$
(9)
$$\widetilde{FT}= \sum \limits_{i=1}^{n}{\widetilde{F}}_{i}$$
(10)
$$\widetilde{\text{FP}}=\frac{1}{n}\sum \limits_{i=1}^{n}{\widetilde{F}}_{i}$$
(11)
$${\widetilde{t}}_{i,j,k}\ge 0, {\widetilde{C}}_{i,j,k}\ge 0;{\forall }_{ }\left(i,j,k\right)$$
(12)
$${\widetilde{C}}_{i}\ge 0;{\forall }_{ }(i)$$
(13)
$$ x_{i,j,k} \in \left\{ {0, 1} \right\};\forall \left( {i,j,k} \right) $$
(14)
$${y}_{i,j,h,g,k}\in \left\{0, 1\right\};\forall\left(i\le h,j,g,k\in {M}_{ij}\cap {M}_{hg}\right)$$
(15)

The proposed model is formulated through constraints to optimize the flexible job shop problem with fuzzy processing times. Constraint (1) establishes the maximum completion time (fuzzy makespan) of the jobs, while Constraint (2) determines the fuzzy completion time of the final operations of the jobs. To ensure proper assignment, Constraint (3) sets the start and end fuzzy times on machine \({M}_{k}\) to zero when the operation \({O}_{ij}\) is not assigned to it. Constraint (4) guarantees that the difference between the fuzzy starting and completion times is equal to, at least, the fuzzy processing time on machine \({M}_{k}\). Constraints (5) and (6) maintain the requirements that the operation \({O}_{ij}\) and \({O}_{hg}\) cannot be conducted simultaneously on any machine in the set \({M}_{ij}\cap {M}_{hg}\). To avoid violation of precedence relationships, Constraint (7) ensures that the operations of a job are developed in the correct order. Similarly, Constraint (8) confirms that an operation is only performed on a single machine. Constraint (9) calculates the fuzzy flow time of the jobs, and Constraint (10) determines the fuzzy total flow time of the schedule. Furthermore, Constraint (11) establishes the fuzzy average flow time of the schedule. Constraints (12) and (13) secure the nonnegativity of the variables. Constraints (14) and (15) define the binary variables. Finally, to include all scenarios, the TFN values are considered individually to represent the best, most probable, and worst outcomes.

4 Optimization algorithm based on adaptive teaching–learning

Teaching Learning-Based Optimization (TLBO) is a metaheuristic algorithm inspired by the classroom teaching–learning process and individuals' social behavior (Baykasoğlu et al. 2014). Rao proposed a relatively new method that has gained widespread acceptance in solving engineering problems. The standard TLBO model involves the influence of teachers on students' learning levels during a training process, with the results being evaluated in terms of grades. In TLBO, the teacher is considered the most knowledgeable individual in the class (population), which helps improve the overall knowledge level according to their ability. The students' quality is assessed based on the mean value of the population. Initially, TLBO was designed for single-objective nonlinear optimization problems, but it has since proven effective for general engineering problems (Pickard et al. 2016). According to the study by Rao and Rai (2016), TLBO's effectiveness has been extensively verified with various performance criteria, demonstrating superior performance over other methods with less computational effort, particularly for large-scale problems.

Baykasoğlu et al. (2014) and Xu et al. (2015) conducted a study evaluating and analyzing TLBO's performance in solving two well-studied combinatorial optimization problems in the literature: the Flow Shop Problem and the Flexible Job Shop Problem. The study demonstrated the efficiency of TLBO when compared to other metaheuristics. The authors conducted also a literary review to understand the fundamental characteristics of these metaheuristics.

Several authors have proposed modifications and additional stages to TLBO to enhance its efficiency. The improved TLBO algorithm includes population division into multiple groups, training tutorials, and self-motivating learning operators (Yu et al. 2018). These modifications can be categorized into techniques used to generate the initial population, which includes learning strategies, adaptive parameters, genetic operators, neighborhood management, and population diversification (Zou et al. 2019).

Opposition-Based Learning (OBL) and the Nawaz–Encore–Ham method have been proposed as alternative methods for generating the initial population in TLBO by Shao et al. (2017). Mandal and Roy (2013) and Roy and Sarkar (2014) proposed a modification of the OBL called Quasi—Opposition-Based Learning. The adaptive parameters have been designed for TLBO. Satapathy et al. (2013) presented an adaptive weight parameter that decreases linearly in the teaching and learning phase according to the number of iterations. This study added the differential weight vector, inertial weight and acceleration coefficient, while Bulbul and Roy (2014) proposed a new TLBO method with an adaptive dynamic control mechanism for the nonlinear economic load dispatch problem.

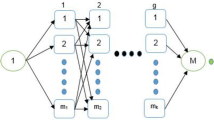
The combining of TLBO-A and an evolutionary algorithm presents a promising approach for achieving better-quality solutions in a shorter computational time. This is supported by previous literature highlighting both metaheuristics' efficiency in solving complex optimization problems. By implementing the adaptive phase approach (as shown in Figs. 1 and 4), the parameterization of feasible solutions can be fine-tuned to produce more effective results reducing the computational burden. The application of evolutionary operators in TLBO-A can further enhance the search for optimal solutions. Overall, this integration of TLBO-A and evolutionary algorithms offers a powerful optimization tool that can provide high-quality solutions in less time.

Fig. 1
figure 1

Evolutionary TLBO phases proposed

Full size image

The optimization algorithm based on Teaching–Learning-Based Optimization (TLBO) is a powerful and efficient heuristic for solving complex optimization problems. TLBO incorporates a particular encoding scheme to represent solutions and a decoding method to transfer solutions to a feasible schedule in a fuzzy sense (Baykasoğlu et al. 2014). The algorithm also integrates a two-phase crossover scheme based on the teaching and learning mechanism and special local search operators to balance exploration and exploitation capabilities. TLBO has been compared with other existing algorithms and demonstrated superior effectiveness and efficiency. In particular, TLBO can find high-quality solutions within a reasonable time, making it competitive in speed and efficiency. The TLBO can also find optimal or near-optimal solutions in most test instances, making it a competitive method in accuracy and convergence (Mane et al. 2020). In summary, TLBO is a competitive heuristic for solving complex optimization problems due to its potential for finding high-quality solutions in a reasonable time and its ability to converge to optimal or near-optimal solutions in most test instances (Jin et al. 2021).

The proposed optimization algorithm based on Teaching Learning (TLBO) is a valuable solution to solve the complex Flexible Job Shop Scheduling problem with fuzzy processing time. A specific coding scheme is always used to represent feasible solutions, eliminating the need for an additional method to decode and transfer solutions to a feasible program based on the principles of fuzzy logic. Two crossing schemes (Bi-Point, POX) and mutation were integrated through two strategies (Sequence Vector Mutation, Machine Assignment Vector Mutation) to ensure a balance between exploration and exploitation while searching for reasonable solutions. Moreover, a novel adaptation strategy is incorporated to reconfigure a portion of the population by reassigning operations to machines with less load assignment when searching for better solutions is trapped in a local optimum. The TLBO-A algorithm is also developed in a multi-objective environment, making it versatile and suitable for systems with partial or total flexibility within the work routes and available system resources. These features make it a better algorithm for developing programming schemes.

According to Ji et al. (2017), the standard TLBO algorithm is prone to get stuck in local optima when the population's diversity is lost, posing a significant problem. To address this issue, the TLBO-A algorithm is developed and experimentally tested. The tests run for single- and multi-objective problems, allowing for comparability and the algorithm's efficiency validation. In conclusion, TLBO-A is a hybrid improvement metaheuristic incorporating genetic operators to optimize non-polynomial problems such as Multi-objective Flexible Job Shop Scheduling with fuzzy processing times. TLBO-A includes two new stages: the Study Phase and the Adaptation Phase. The algorithm compares and optimizes the makespan and uncertain average flow time on each machine to obtain the most promising solution while protecting against uncertainty by defining different levels of fluctuations in completion times.

4.1 Adaptive teaching–learning-based optimization algorithm (TLBO-A)

A new adaptive strategy is proposed below to enhance the search process for optimal solutions and increase the likelihood of promising results during its evolution. This adaptive strategy is designed to improve the global and local search capacity by exploring new scenarios that provide the algorithm with greater diversity, thus preventing it from being trapped in suboptimal solutions due to premature convergence. The proposed Adaptive Teaching–Learning-based Optimization Algorithm (TLBO-A) builds on the basic principles of TLBO, incorporating two genetic operators (mutation and crossover) and an adaptive strategy for population reconfiguration, ensuring enhanced exploration of the solution space and avoidance of premature convergence. In TLBO-A, each member of the population is considered a student, representing a potential solution to the problem. A solution comprises a sequence of operation vectors and a machine assignment vector.

The sequence vector in the proposed algorithm represents the order in which operations of the different jobs are executed, and its length is equal to the total number of operations. The job index indicates the operation and its position in the sequence vector. The operations of each job are arranged in ascending order in the sequence vector. On the other hand, the machine allocation vector denotes the indices of the machines selected to process each job operation, as shown in Fig. 2.

Fig. 2
figure 2

Representation of a feasible solution

Full size image

According to Fig. 2, operation one of job one (\({O}_{11}\)) will be processed on machine four (\({M}_{4}\)). Operation two of job one (\({O}_{12}\)) will be processed on machine three (\({M}_{3}\)). Operation three of job one (\({O}_{13}\)) on machine one (\({M}_{1}\)) and job one operation four (\({O}_{14}\)) on machine two (\({M}_{2}\)).

The TLBO-A is characterized by four key parameters, namely the population size (i.e., the number of students), the number of learning levels (i.e., Levels), the percentage of top-performing students or teachers (i.e., Alpha), and the mutation percentage. In the initial phase of the algorithm, the parameters, population, and Beta parameter, which corresponds to the objective related to the makespan, are initialized. The individuals are then sorted into different learning levels, with the top group comprising the Alpha expression, representing the best students or teachers within the population. To generate the initial population, the TLBO-A algorithm considers several strategies. The sequence vector is randomly generated, while the machine allocation vector is created using different rules, each with an associated probability of occurrence. Specifically, Rule 1 involves the random selection of a machine for each operation. In Rule 2, the machines with the shortest processing time are selected from the available machines for each operation. Conversely, in Rule 3, the machines with the longest processing time are selected from the available machines for each operation. Lastly, in Rule 4, the machines with the minor load are chosen from the available machines.

Loss of population diversity can cause the traditional TLBO algorithm to fall into local optima (Ji et al. 2017). The proposed TLBO algorithm incorporates crossing and mutation operators to address this issue and enhance search space exploration. Genetic algorithms commonly use these basic operators to increase population diversity and prevent premature convergence. Typical forms of crossing include PMX (Partially Matched Crossover), OX (Ordered Crossover), and CX (Cycle Crossover) (Acevedo Chedid et al. 2020). The two-point crossing method is employed at this stage, as depicted in Fig. 3.

Fig. 3
figure 3

Example of crossing a point and bi-point

Full size image

In the proposed TLBO, the Teaching phase involves crossing each student in the population outside the top group with a randomly selected teacher to generate two new solutions using the POX crossing strategy. The first generated student is then compared to the student selected for crossing, and if the new solution is better, it replaces the previous student; otherwise, it is maintained. The exact process is repeated for the second generated student and the selected teacher for crossing. In the Learning phase, each teacher in the population crosses paths with another teacher to find a new solution using the Bi-point Crossing strategy. If the resulting solution has a better learning degree (higher fitness value), the initial teachers are replaced within the population. Otherwise, the selected individual is maintained.

The Study phase of the TLBO-A algorithm involves applying the mutation operator to the population's students to enhance their learning degree (Fitness Value). This process employs both sequence mutation strategy and machine allocation mutation strategy. The machine allocation vector mutation uses three criteria: selection of the machine with the shortest time, random selection, and selection from a machine with a higher load to one with a lower load. In the Adaptive phase of the TLBO-A algorithm, an adaptive strategy is implemented to reconfigure a percentage of the current population. This strategy applies a change criterion when the best result (the best teacher) is repeatedly obtained at certain levels. The students are ordered based on their learning degrees during this phase. Finally, the TLBO-A checks for compliance with the stop criteria. The TLBO-A metaheuristic's structure is explained in Fig. 4.

Fig. 4
figure 4

The framework of the TLBO-A for the FJSPF

Full size image

Using the Java programming language, the TLBO-A algorithm was implemented in NetBeans IDE 8.2. The corresponding pseudocodes for each stage are provided in the annexes, which detail the algorithm coding process. Appendices 1–22 specifically list the coding process for the main class, data entry, initial population generation, sequence mutation operator, assignment mutation operator, adaptive strategy, and convergence graph generation method.

The proposed Adaptive Teaching–Learning-based Optimization Algorithm (TLBO-A) is a novel approach that enhances the global and local search capacity by incorporating two genetic operators (mutation and crossover) and an adaptive strategy for population reconfiguration. The TLBO-A algorithm is based on the basic principles of TLBO, but it includes a sequence vector and a machine allocation vector to represent the order in which operations of different jobs are executed and the indices of the machines selected to process each job operation. Using these vectors in combination with the proposed adaptive strategy provides a more diverse search space and avoids premature convergence, resulting in better and more promising solutions. The TLBO-A algorithm is an effective and versatile optimization method used in multi-objective scheduling problems with fuzzy processing times, making it an ideal choice for developing programming schemes.

4.2 Validation of TLBO-A metaheuristic

For the validation stage of the TLBO-A algorithm, five were utilized instances developed by Lei (2010), each containing data on fifteen (15) jobs, ten (10) machines, and eighty (80) operations. Table 2 provides a summary of the parameters for each instance.

Table 2 Details of the instances with total flexibility by Lei (2010)
Full size table

The TLBO-A algorithm is applied to minimize the fuzzy completion time (fuzzy makespan) to compare its performance to other existing algorithms. Subsequently, an experimental design is developed to analyze the execution of TLBO-A in solving the P-MOFfJSP. The design is able to establish the influence of each parameter on the proposed algorithm through the use of an orthogonal design of Taguchi L16 (4^4), which is applied to the experimental test data of instance two (2) by Lei (2010). Table 3 summarizes the parameters and corresponding levels for the Taguchi L16 design.

Table 3 Experimental design parameters for FfJSP
Full size table

Table 3 shows the parameters and their respective levels. In each combination of parameters, 16 replicates are considered and calculated with the expression \({2}^{k}\) where k represents the factors (k = 4), a sample of 272 data is used in the design. The fuzzy makespan response variable is defined as \(\frac{({x}_{1} + 2{x}_{2} + {x}_{3} )}{4}\) which corresponds to the weighted weight of the fuzzy triangular number.

The design of experiments is developed using Statgraphics software, and the results indicated that Population, Alpha, and Levels factors are significant, with P-values less than 5% (refer to Annexure 8). The population size is the most significant factor, suggesting that a large population size allows the TLBO-A to converge slowly and achieve better results. The Alpha factor is determined to be the second most significant factor. The levels factor is also found to be significant, and it is recommended to assign large values. The mutation factor has small impact on the algorithm's functioning; higher or lower intensity values do not affect the response variable. The parameters established for the TLBO-A while minimizing the fuzzy makespan are: Population: 2000; Generations: 2000; P Mutation: 0.2; Alpha: 0.8.

The size of the population and the levels are the most significant parameters for the TLBO-A applied to the P-MOFfJSP. The Alpha factor is also essential for generating the solution, even though it is insignificant. For each parameter combination, 16 replications are conducted using a sample of 272 data. The response variables are defined as Fuzzy makespan: \(\frac{({x}_{1}, + 2{x}_{2} + {x}_{3} )}{4}\); Fuzzy average flow \(\frac{({y}_{1}, + 2{y}_{2} + {y}_{3} )}{(4*\mathrm{Number of jobs})}\). Where X is a fuzzy triangular number \(X=({x}_{1}, {x}_{2}, {x}_{3})\) that represents the fuzzy completion time associated with the job, and Y is another fuzzy triangular number \(Y=({y}_{1}, {y}_{2}, {y}_{3})\) that represents the average fuzzy flow time.

Assigning large values to the population and level factors is one way to avoid premature convergence. The behavior data of the diffuse makespan response variable and diffuse average flow concerning each factor can be observed in Annex 9, which displays the standardized effect of each factor for the fuzzy makespan response variable and the diffuse average flow response variable. Using the statistical software Statgraphics, the values that should be assigned to the TLBO-A factors were determined to minimize the objectives simultaneously, expressed through the response variables. Based on the results obtained from the experiment design, the parameterized values for the P-MOFfJSP are Population: 2000; Generation: 2000; P. Mutation: 0.4; Alpha: 0.6.

5 Experimental results

The TLBO-A is executed in 18 independent runs using the instances provided by Lei (2010) and Lin (2002), with the parameterized factors as the input. For the Total Flexibility instances by Lei (2010), the TLBO-A is executed, and the results are compared with existing algorithms applied to the production scheduling problem in the FfJSP environment, considering the minimization of the Cmax fuzzy. Table 4 compares TLBO-A with other existing algorithms applied to the fuzzy flexible environment production scheduling problem, FfJSP, for each of the five instances.

Table 4 Algorithms to minimize fuzzy makespan
Full size table

The results are also presented in Table 5 alongside those obtained with the other algorithms. Table 5 shows the results, and comparisons of the instances for the fuzzy makespan obtained with the algorithms are also shown.

Table 5 Results and comparisons of the instances for the fuzzy makespan
Full size table

When applied to FfJSP, TLBO-A yields better results than the standard TLBO algorithm in Lei's (2010) instances, except for instances 2 and 5, where it does not outperform the BSHH algorithm. In comparing the results of our proposed heuristic TLBO-A to the BSHH algorithm, it is found that the BSHH algorithm produces the best results in all instances for the fuzzy makespan problem. However, the TLBO-A heuristic shows a variation in these best results ranging from 2 to 11% across all instances. When comparing the TLBO-A heuristic to the BSHH algorithm, it outperforms the latter in instances 1, 3, and 4, with an average fluctuation of only 1% compared to the TLBO heuristic.

The best solutions obtained with TLBO-A FfJSP for instances 2 and 5 are presented in Figs. 5 and 6, respectively. Figure 5 shows the best solution, for instance 2 compared with the TLBO-A FfJSP, including the programming of the jobs for each one of the ten considered machines. In the case of job 1, its four operations must be developed on machines M6, M7, M3 and M4, respectively. Job 2 is scheduled on machines M3, M6, M9, and M8. Job 3 operations 1, 2 and 4 are produced on machine M10 and operation three on machine M5. According to the results presented in Fig. 5, the machine that develops the most jobs is M1, with six jobs, followed by M3, with five jobs and M5, with four jobs.

Fig. 5
figure 5

The best solution for instance “2” (Lei (2010)) with the TLBO-A FfJSP

Full size image
Fig. 6
figure 6

The Best solution for instance “5” (Lei (2010)) with the TLBO-A FfJSP

Full size image

Figure 6 presents the best solution for instance 5, compared with the TLBO-A FfJSP, including the programming of the jobs for each one of the ten considered machines. In the case of job 1, its five operations must be developed on machines M2, M10, M2, M1 and M5, respectively. Job 2 is scheduled on machines M8, M8, M7, M2, M6, and M5. Job 3 operations 4 and 5 are produced on machine M9, and operations 1, 2, and 3 on machines M7, M8, and M3, respectively. According to the results presented in Fig. 6, the machine that develops the most jobs is M1, with ten jobs, followed by M5 and M10, with nine jobs and M3 and M6, with eight jobs, respectively.

Figure 7 displays the TLBO-A algorithm's evolution for solving instance 2, showing the behavior of the fuzzy makespan objective against the fuzzy average flow and the Pareto frontier solutions (non-dominated solutions). The Pareto optimal solution is represented by the fuzzy triangular number (32–47–58) for the fuzzy makespan, with a weighted weight of 46.0 and a fuzzy average flow of 38.2. By varying the Beta parameter of the multicriteria function between zero (0) and one (1) with successive increments of 0.05, 21 possible solutions were obtained, resulting in the evolution presented in Fig. 7.

Fig. 7
figure 7

Evolution of TLBO-A in the best solution for instance 2 (Lei (2010))

Full size image

The P-MOFfJSP is solved by applying TLBO-A to the five instances provided by Lei (2010). Table 6 summarizes the general results obtained for each instance, including the mean, best, and worst values achieved for the considered objectives. To evaluate each instance, 18 independent runs are executed. The Gantt charts with start and end times, the sequence of operations, and the operations assigned to each machine for the best results of instances 1 and 2 are presented in Figs. 8 and 9, respectively.

Table 6 The result of the TLBO-A applied to the P-MOFfJSP
Full size table
Fig. 8
figure 8

The best solution for instance 1, obtained with the TLBO-A for the P-MOFfJSP

Full size image
Fig. 9
figure 9

The Best solution for instance 2, obtained with the TLBO-A for the P-MOFfJSP

Full size image

Figure 8 presents the best solution for instance 1, compared with the TLBO-A for the P-MOFfJSP, including the programming of the jobs for each one of the ten considered machines. In the case of job 1, its five operations must be developed on machines M6, M3, M4, and M1. Job 2 is scheduled on machines M4, M5, M6, and M9. Job 3 is scheduled on machines M3, M1, M7, and M2. According to the results presented in Fig. 8, the machine that develops the most jobs is M1, with six jobs, followed by M2, M3, M4, M5, M6, M8, and M9 with four jobs and M7 and M10, with three jobs, respectively.

Figure 9 presents the best solution for instance 2, compared with the TLBO-A for the P-MOFfJSP, including the programming of the jobs for each one of the ten considered machines. In the case of job 1, its four operations must be developed on machines M6, M7, and M4. Job 2 is scheduled on machines M5, M9, and M8. Job 3 is scheduled on machines M7 and M6. According to the results presented in Fig. 9, the machine that develops the most jobs is M1, with six jobs, followed by M10, M2, M3, M4, M5, M6, and M9, with four jobs and M7 and M8, with three jobs, respectively.

The performance of TLBO-A in the FfJSP environment to minimize the fuzzy Cmax was evaluated by conducting 18 experimental runs for the scenario of Total flexibility with the instances by Lin (2002). The results obtained from these runs are presented in the following table (Table 7):

Table 7 Results and comparisons of the instances by Lin (2002) for the Fuzzy Makespan (FfJSP)
Full size table

The best solution found with the TLBO-A algorithm for the first instance by Lin (2002) is shown in Fig. 10. The optimal solution for the fuzzy makespan for this instance coincides with the best solution. The fuzzy makespan (21-32-45) is the completion time of the operation \({O}_{52}\) assigned to machine M1.

Fig. 10
figure 10

The best solution of instance 1 (Lin (2002)) with the TLBO-A for MOFfJSP

Full size image

The adaptive TLBO-A algorithm shows stability in solving small instances with partial flexibility, as evidenced by the TLBO-A algorithm's evolution in Fig. 11, applied to the first instance by Lin (2002). The figure displays only three out of the 21 points corresponding to the solution space, indicating that the solution remains constant once found. The best solution for this problem is represented by the fuzzy triangular number (21-32-45), with a weight of 32.5 for the fuzzy makespan and a fuzzy average flow of 29.41.

Fig. 11
figure 11

Evolution of the TLBO-A in the best solution for instance 1 (Lin (2002))

Full size image

5.1 Managerial implications

Manufacturing systems must establish strategies that generate agile responses to unexpected orders and product changes in less time. This can be achieved by using optimization algorithms for flexible Job-Shop problems. These algorithms can help manufacturers meet variations in demand and develop products with short cycle times while providing excellent physical and information integration of manufacturing system components.

The practical relevance of modeling the flexible manufacturing systems and the problem of production scheduling is a topic of great interest to researchers and manufacturing industries. By enhancing their production scheduling models, manufacturers can benefit from several advantages, including the following:

  • Visualizing and executing strategies effectively in the production schedule

  • Achieving customer loyalty through faster response times to orders and product changes.

  • Reducing costs through optimized use of resources.

  • Guaranteeing high-quality products through efficient scheduling and production processes.

Optimization algorithms for flexible Job-Shop problems provide a valuable tool for manufacturers to improve their production scheduling models and remain competitive in an ever-changing market.

6 Conclusions

The TLBO-A algorithm outperforms the standard TLBO algorithm on most instances of the FfJSP, except for instances 2 and 5, where it does not outperform the BSHH algorithm. However, when compared to the BSHH algorithm, it was found that the latter produces the best results in all instances for the fuzzy makespan problem. Despite this, the TLBO-A algorithm shows promising results compared to other existing algorithms, with a variation in the best results ranging from 2 to 11% across all instances. The proposed TLBO-A algorithm is a novel solution to optimize non-polynomial problems, such as the Multi-objective Flexible Job Shop Scheduling problem with fuzzy processing times. It incorporates genetic operators and an adaptive strategy for population reconfiguration, which enhances the search process for optimal solutions and complements the fuzzy processing time of the FfJSP, making it suitable for systems with partial or total flexibility within the work routes and available system resources. The TLBO-A is a hybrid improvement metaheuristic that applies the mutation and crossover genetic operators in its exploration strategy to enhance and benefit from its advantages when solving non-polynomial problems such as the P-MOFfJSP. The proposed approach of the TLBO-A algorithm is integrative, where the sequence and assignment subproblems are addressed simultaneously. The multi-criteria optimization technique is used to solve the objective of the FfJSP and P-MOFfJSP, varying the weight percentage of the fuzzy makespan in a percentage range between zero (0) and one (1) to obtain the solutions or decisions of the problem.

In summary, the proposed TLBO-A algorithm presents a novel solution to optimize non-polynomial problems and shows promising results compared to other existing algorithms. It enhances the search process for optimal solutions and complements the fuzzy processing time of the FfJSP, making it suitable for systems with partial or total flexibility within the work routes and available system resources. Finally, one of the limitations of this study is the comparability with other multi-objective studies. It is important to note that the instances used in this study were developed by Lei (2010). To overcome this limitation, future studies could explore new and more challenging instances that better reflect real-world scenarios. This would provide a more comprehensive evaluation of the proposed TLBO-A algorithm's performance and its potential to solve real-world problems.

6.1 Future research

The proposed model for solving the P-MOFfJSP problem has several potential areas for future research. For example, include predictive aspects with machine learning for fuzzy production rescheduling scenarios (Adnan et al. 2018, 2022). The several directions to extending the model and evaluating its behavior with other optimization and hybridization techniques to overcome the limitations of the proposed model are outlines as follows:

Possible extensions:

  • Evaluate the performance of TLBO-A with other multi-objective optimization methods and additional objectives for the P-MOFfJSP problem.

  • Investigate the behavior of TLBO-A with other hybridization techniques and methods to improve its efficiency.

  • Incorporate additional noise factors into the P-MOFfJSP to make it more representative of real-world scenarios, such as delivery and availability times.

  • Study fuzzy environments by including fuzzy processing and delivery times to improve the model's practical applications.

  • Use other crossing strategies for the different phases of the Teaching and Learning phase of the TLBO-A to enhance its results.

  • Analyze the behavior of other criteria, such as a machine with less load, to generate assignments within the Adaptive phase.

  • Incorporate preventive and corrective maintenance periods into the schedule to improve the model's practicality in real-world applications.

  • Combine the TLBO Technique with other metaheuristics that may be different from the evolutionary ones, to identify potentialities in processing capacity.