AHOA: Adaptively Hybrid Optimization Algorithm for Flexible Job-shop Scheduling Problem

Abstract

The Flexible Job-shop Scheduling Problem (FJSP) is a typical scheduling problem in industrial production that is proven to be NP-hard. The Genetic Algorithm (GA) is currently one of the most widely used algorithms to address the FJSP task. The major difficulty of using GA to solve FJSP lies in how to set the key hyperparameters and improve the convergence speed. In this paper, we propose a hybrid optimization method based on Reinforcement Learning (RL) called the Adaptively Hybrid Optimization Algorithm (AHOA) to overcome these difficulties. The proposed algorithm first merges GA and improved Variable Neighborhood Search (VNS), which aims to integrate the advantages of global and local search ability into the optimization process. Then the double Q-learning offers crossover and mutation rates according to the feedback from the hybrid algorithm environment. The innovation of this work lies in that our method can adaptively modify the key hyperparameters in the genetic algorithm. Furthermore, the proposed method can avoid the large overestimations of action values in RL. The experiment is evaluated on the most widely studied FJSP instances and compared with some hybrid and self-learning algorithms including dragonfly algorithm (DA), hybrid gray wolf weed algorithm (GIWO), and self-learning GA (SLGA), etc. The results show that the proposed method outperforms the latest related algorithms by more than 12% on average.

1 Introduction

Production scheduling [15] plays an essential role in the planning and scheduling of the manufacturing system. There are several well-known production scheduling problems including Job shop Scheduling Problem (JSP) and Flexible Job shop Scheduling Problem (FJSP) [15]. JSP is one of the most challenging parts of these kinds of problems and had been proved to be an NP-hard (Non-deterministic Polynomial-time Hard) problem [13]. It can be described as a set of independent jobs to be processed on multiple available machines, and each job contains a series of operations with a specified order. However, each operation must be processed on a specified machine in JSP. It is incapable of meet the flexible scheduling requirements in the real world.

The FJSP is an essential extension of JSP [4] that can address flexible requirements. It allows each operation to be processed on different machines. This means FJSP can be decomposed into two sub-problems including operations sequencing and machines selection [13]. Where, JSP is only composed of the operations sequencing problem to find the best sequence of operations and machines selection problem is a extention of JSP task to assign suitable machines to each operation.

In recent years, a great deal of algorithms have been proposed to address FJSP like Evolutionary Algorithm (EA), Local Search (LS) Algorithm, and Hybrid Optimization Algorithm (HA). For instance, Ding et al. [10] proposed an improved Particle Swarm Optimization (PSO) method based on novel encoding and decoding schemes for the FJSP; Amiri et al. [1] presented a Variable Neighborhood Search(VNS) for the FJSP; Li et al. [26] proposed a HA based on the Genetic Algorithm (GA) and Tabu Search (TS).

These methods are limited by hyperparameters settings. There is evidence [8] showing that hyperparameters like crossover and mutation operator play a crucial role in the evolution of the population. This means that relying on experience to select parameters will affect the efficiency and performance of the algorithm. For instance, the adverse configuration may cause premature convergence to local extreme rather than the globally optimal. To overcome this defect, many researchers often fix or update in a predetermined way [11]. But it still lacks generalization. Moreover, some methods [5] based on RL can also adjust the hyperparameters adaptively. However, the problem of overestimation is not avoided [17].

Based on these motivations, this work proposes an Adaptively Hybrid Optimization Algorithm named AHOA to search the minimum makespan of FJSP. AHOA first utilizes GA to optimize globally and then introduces improved VNS based on the critical path to optimize locally. Finally, the double Q-learning offers crossover and mutation rates according to the feedback from the hybrid algorithm environment. The contributions are as follow:

• 1) Our algorithm can adaptively modify the hyperparameters in the HA based on double Q-learning. It can also avoid the overestimations problem of action values compared to other works based on RL.

• 2) We deploy a hybrid algorithm to solve this problem effectively. It shows an outstanding performance by combining the exploration ability of GA and the exploitation ability of VNS.

The remainder of this work is organized as follows. Section 2 introduces the related work. The problem formulation is presented in Sect. 3, while the proposed algorithm is given in Sect. 4. The experimental result is proposed in Sect. 5. Finally, Sect. 6 describes the conclusion and future work.

2 Related Work

Since Brucker and Schlie [3] first proposed the FJSP in 1990, numerous methods have been suggested to solve the FJSP task in recent years, and most existing algorithms can be classified into two categories: GA based methods and RL based methods. The GA based methods include simple GA and HA. The simple GA is a typically global optimization method [31]. It can scale robustly and easily to complex problems that are difficult to solve by traditional optimization algorithms. For instance, De et al. [7] presented an improved GA for the FJSP, in which a new operator based on LS is combined. Lu et al. [28] proposed a GA embedded with a concise chromosome representation to solve the distributed FJSP. However, the drawbacks of the simple GA are the poor local optimization ability, and its excessively low convergence speed. For solving these problems, HA based on the GA and LS is proposed. This hybrid method can greatly improve the quality of the solution and the efficiency of optimization. Specifically, the GA optimizer always yields an approximate optimal set or population. The best individual of the set is utilized as the starting point for the local search optimizer to run with. So that, the global searching ability of GA and the local searching ability of LS are combined to solve the FJSP effectively. Wang et al. [33] proposed a hybrid algorithm that combines GA and TS. This approach also calls for some improvements, it limited by GA that the hyperparameters cannot be adjusted adaptively during the optimization process.

Therefore, the RL based methods are proposed to overcome this defect. The characteristic of the RL method is self-learning [30]. In other words, it can adaptively adjust the hyperparameters of GA based method. For example, Chen et al. [5] proposed a algorithm combined with the SARSA algorithm and Q-learning algorithm to adjust the hyperparameters. However, the problem of overestimation in RL and sparse Q-table are not avoided.

3 Problem Formulation

3.1 Problem Model

The FJSP can be classified into two types of problems including total FJSP and partial FJSP [18]. The total FJSP means each operation can be processed on every machines and the partial FJSP means each operation can be processed only on one or more machines. In this paper, our major research problem is partial FJSP which is described as follows. There are a set $J=\{J_1,J_2,\cdots ,J_i,\cdots ,J_n\}$ of n jobs and a set $M=\{M_1,M_2,\cdots ,M_k,\cdots ,M_m\}$ of m machines. The total number of operations is defined as $o=\sum _{i=1}^{n} H_{i}$. Each job $J_i$ contains a series of operations $O_i=\{O_{i,1},O_{i,2},\cdots ,O_{i,H_i}\}$ with a specified order. The $j^{th}$ operation $O_{i,j}$ of the $i^{th}$ job $J_i$ can be processed on a machine $M_k$ selected from a set of available machines and $t_{i,j,k}$ is its processing time. The objectives in the FJSP are to find the best sequence of all operations and the most suitable machine for each operation to optimize the makespan, workload, etc. For an intuitive illustration, a specific partial FJSP instance is shown in Table 1. The numbers in the table refers to the processing time $t_{i,j,k}$ and the symbol ‘–’ indicates that operation $O_{i,j}$ can not be processed on a machine $M_k$. The typical assumptions [27] of FJSP are given as follows:

• (1) All jobs can not be processed and all machines are available at the initial time;

• (2) The order of precedence between operations of each job must be obeyed;

• (3) Each machine $M_{k}$ can process only one operation in any time;

• (4) Each operation $O_{i,j}$ owns at least one machine to be processed;

• (5) The processing cannot be interrupted until is finished;

• (6) The transportation time of operations and depreciation of machines are ignored.

Table 1. An instance of 3 $\times$ 3 partial FJSP.

3.2 Optimization Object

In this paper, the optimization object is to obtain a scheduling with the lowest makespan $C_{max}$. The object function can be presented by Eq. (1) and the constraints are listed in Eq. (2)–Eq. (4). Among these equations, $s_{i,j,k}$ represents the work start time of operation $O_{i,j}$ on $M_k$ machine. Equation (2) shows that the processing time of all operations is positive. Equation (3) represents the order of precedence between operations of each job must be performed. Equation (4) represents that each machine $M_{k}$ can process only one operation in any time. Equation (5) shows that each operation $O_{i,j}$ owns at least one machine to be processed.

Object:

$$\begin{aligned} min(C_{\max })=min(max(C_i)) \end{aligned}$$

(1)

Subject to:

$$\begin{aligned} t_{i, j, k}>0 \text { , } i=1,2, \cdots , N ; j=1,2, \cdots , H_i ; k=1,2, \cdots , M \end{aligned}$$

(2)

$$\begin{aligned} s_{i, j, k}+t_{i,j,k}\le s_{i,j+1,k} \text { , }j=1,2, \cdots , (H_i-1) \end{aligned}$$

(3)

$$\begin{aligned} \sum _{i=1}^{N}\sum _{j=1}^{H_i} X_{i, j, k}=1, X_{i, j, k}=\left\{ \begin{array}{lc} 1 &{} \text{ If } O_{i, j} \text{ is } \text{ assigned } \text{ to } k^{th} \text { machine }\\ 0 &{} \text{ Otherwise } \end{array}\right. \end{aligned}$$

(4)

$$\begin{aligned} \sum _{k=1}^{M} X_{i, j, k}\ge 1 \end{aligned}$$

(5)

Fig. 1.

The workflow of the proposed algorithm

4 Proposed Algorithm

4.1 Workflow of the Proposed AHOA

As Fig. 1 shows, AHOA is designed by merging the hybrid algorithm and double Q-learning algorithm. It accepts an instance of the FJSP as the inputs and uses HA that combines GA and VNS to optimize the makespan. To avoid the performance being severely affected by the preset hyperparameters, the double Q-learning algorithm is introduced to intelligently adjust them. The overall workflow of the proposed algorithm is described as Algorithm 1, and the details are described in the following sub-sections.

Fig. 2.

The example of the critical path.

Fig. 3.

The encoding and decoding example based on the Table 1

4.2 Hybrid Algorithm

4.2.1 Neighborhood Structure Based on Critical Path

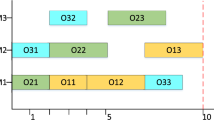
The critical path is the longest path from the start to the end of all the operations in the Gantt chart. There is no interval between any adjacent operations, and the length of the path is equal to the makespan of the current solution. For instance, the combination of the blue blocks including $O_{3,1}\rightarrow O_{2,1}\rightarrow O_{1,1}\rightarrow O_{3,2}\rightarrow O_{3,3}$ is the critical path in Fig. 2. The length of this critical path is 9 which is also the end of the Gantt chart. In the case that the critical path length remains the same, the makespan cannot be reduced [35]. Therefore, the operation based on the critical path is introduced to design a problem-specific neighborhood structure for the VNS and the mutation operators for the GA.

The neighbourhood structure can be decomposed into the following steps. First, all the critical paths in the current Gantt chart are found. Among the critical paths, one path is chosen randomly, and the available machine is selected for each operation on this critical path. For VNS, This neighborhood structure modifies the individuals from the GA to generate new neighborhood solutions. Moreover, this structure is also used as a mutation operator to generate new individuals for the new population in the GA.

4.2.2 Genetic Algorithm

In the proposed algorithm, the encoding method proposed by Gao et al. [12] is adopted. As shown in Fig. 3, the code composes of two strings. One is called OS (Operation Sequence), and the other is called MS (Machine Sequence). As mentioned in Sect. 1, two sub-problems are needed to solve FJSP. The first is to find the best sequence of operations and the second assigns suitable machines to each operation. The two strings correspond to these two sub-problems respectively. For OS string, the number i that appears $j^{th}$ times represents it is the operation $O_{i,j}$ of job $J_i$. For MS string, it presents the selected machines for the corresponding operations of each job. Moreover, the decoding method proposed by Gong et al. [14] is used in this work to minimize the makespan. It can minimize makespan while obeying the constraints during operations and machines.

For selection operators [34], the elitist selection method is performed firstly and the tournament selection method is continuously performed until the size of the new population reaches the Popsize. Each string has its independent crossover and mutation operators. For the OS string, the Precedence Operation crossover (POX) [26] and the Job-Based crossover (JBX) [26] are performed randomly (50%). Moreover, two mutation operators for the OS string have been adopted. The first one is the insertion mutation that selects a random digit to insert before a random position. The second one is the swapping mutation that swaps two random positions. These two mutation operators for the OS string are also performed randomly (50%). For the MS string, the two-point crossover [26] is adopted as the crossover operator. The mutation operator based on the critical path is introduced in this paper. This operator only changes the machine of operation in the critical path which is explicitly described in Sect. 4.2.1.

4.2.3 Variable Neighborhood Search

The LS algorithm is introduced to improve GA in terms of the convergence speed, the quality of individuals, and the local search ability. The VNS is a meta-heuristic LS method proposed by Mladenovi et al. [29]. The core idea is neighborhood transformation which has been successfully applied to numerous combinatorial optimization problems.

The VNS contains two procedures called shaking and local search. These procedures only employ a neighborhood structure based on the critical path. The main structure of the improved VNS is composed of external and internal loops. The external loop performs the shaking procedure, and the internal loop performs a local search. The definition of related symbols is as follows. The symbol $k_{max}$ is the max iterations of the external loop ($k_{max} = 2$), and l is the max iterations of the internal loop ($l_{max} = 2$). The symbol $k_{popsize}$ is delineated as the size of the shaking neighborhood ($k_{popsize} = 3$), and $l_{popsize}$ is the size of the local search neighborhood ($l_{popsize} = 3$). Besides, N(x) is presented as the neighborhood structure related to the critical path which is generated from a solution x.

As shown in Algorithm 2, in the first step, the initial solution x generated from the GA is denoted as the global optimal solution and the $x'$ generated from the neighborhood structure $N_k(x)$ is denoted as the local optimal solution. The shaking procedure firstly selects a random solution $x'$ from the $k^{th}$ neighborhood $N_k(x)$ generated base on x. Then the local search procedure selects a random solution $x''$ from the $l^{th}$ neighborhood $N_l(x')$ generated base on $x'$. If $x''$ is better than $x'$, then set $x'$ to $x''$ and l to 1. The local search procedure continues to be performed until the end of the internal loop iteration. When the end of the local search procedure. If the local optimal solution $x'$ is better than x, then set x to $x'$ and k to 1. Finally, the procedure repeats until the end of the external loop iteration.

4.3 Double Q-learning Procedure

The double Q-learning is a typical reinforcement learning method proposed by Hasselt et al. [17]. It aims to solve the overestimations problem of Q-value defined as Q(s, a). The double Q-learning obtains two intelligent agents $Q^A$ and $Q^B$. The agents interact continuously with the HA environment to find the most cumulative Q-value based on past experience and update the Q-value from the other agent for the next state. Moreover, each agent can obtain a reward or penalty while performing a selected action and learn to maximize the long-term reward after multi iterations.

The agent will take different actions to get crossover and mutation rates combined as the action in the Q-table. Specifically, the crossover rates group $G_c$ is set to $\{0.9,0.8,0.7,0.6,0.5\}$ and the mutation rates group $G_m$ is establish to $\{0.3,0.2,0.1\}$ in the action list $A_{list}$. The $A_{list}$ is the Cartesian product of $G_c$ and $G_m$. Besides, the symbol $\alpha \in [0,1]$ represents the learning rate. The $\gamma \in [0,1]$ represents the attenuation rate for the future reward. The R is defined as the reward shown in Eq. (8).

In the AHOA, we assume that only one static state in the HA environment prevents the sparse Q-table. The specific algorithm is described as Algorithm 3 shows. Firstly, step in the double Q-learning is to initialize agent $Q^A$ and agent $Q^B$ by initializing each Q-table to a zero-value matrix. Then select agent $Q^A$ or agent $Q^B$ to use at random (50%). Assuming that agent $Q^A$ is selected, the $\varepsilon$-greedy strategy as shown in Sect. 4.3.1 is next used to select the action $a^*$ to be performed from the action list $A_{list}$. The HA obtains the crossover rate and mutation rate from $a^*$ and executes to get an evaluation. Finally, the Q-table is updated according to Eq. (6). In Eq. (6), the above equation is used to update if the agent $Q^A$ is selected. Otherwise, the following equation is used to update the table.

$$\begin{aligned} \left\{ \begin{aligned} Q^{A}(s, a) \leftarrow Q^{A}(s, a)+\alpha \times \left( R+\gamma \times Q^{B}\left( s, a^{*}\right) -Q^{A}(s, a)\right)&\text { }\text { }\text { (1)}\\ Q^{B}(s, a) \leftarrow Q^{B}(s, a)+\alpha \times \left( R+\gamma \times Q^{A}\left( s, a^{*}\right) -Q^{B}(s, a)\right)&\text { }\text { }\text { (2)}\\ \end{aligned} \right. \end{aligned}$$

(6)

4.3.1 Selection Strategy

The selection strategy of double Q-learning is the $\varepsilon$-greedy strategy. In this strategy, an action $a^{*}$ will be selected randomly from $A_{list}$ if a random number $rand_{[0-1]}$ is higher than the agreed value $\varepsilon$, otherwise the action with the most Q(s, a) will be selected. The definition is shown in Eq. (7).

$$\begin{aligned} a^*=\left\{ \begin{aligned} \begin{array}{lc} \arg {max}_{a} Q\left( s, a\right) &{}\text { } rand_{[0-1]}<\varepsilon \\ A_{list}[{random}] &{}\text { } rand_{[0-1]} \ge \varepsilon \end{array} \end{aligned} \right. \end{aligned}$$

(7)

4.3.2 Reward Function

The reward function is designed according to the best and the average individual fitness as shown in Eq. (8). In the reward method, $C_{old-ave}$ and $C_{old-best}$ are delineated as the average and the best makespan in the previous population. $C_{new-ave}$ and $C_{new-best}$ are delineated as the average and the best makespan in the current population.

$$\begin{aligned} { R }=\left\{ \begin{aligned} 30&\text{ If } C_{ {new-ave }}<C_{ {old-ave }} \text { and } C_{ {new-best }}<C_{ {old-best }} \\ 15&\text{ If } C_{ {new-ave }}\ge C_{ {old-ave }} \text { and } C_{ {new-best }}<C_{ {old-best }} \\ -0.5&\text{ If } C_{ {new-ave }}<C_{ {old-ave }} \text { and } C_{ {new-best }}\ge C_{ {old-best }} \\ -5&\text{ If } C_{ {new-ave }}\ge C_{ {old-ave }} \text { and } C_{ {new-best }}\ge C_{ {old-best }} \end{aligned} \right. \end{aligned}$$

(8)

4.4 Computation Complexity Analysis

For each generation of the AHOA, the computational complexity can be analyzed as follows. First it is with the computational complexity $\mathcal {O}(P\log P)$ by using quick sorting method to evaluate the population. Then, it is with the computational complexity $\mathcal {O}(P)$ to perform selection operator, with the computational complexity $\mathcal {O}(P\times o)$ to perform crossover operator and with the computational complexity $\mathcal {O}(P\times m\times o)$ to perform mutation operator. Finally, the AHOA applies the VNS based on the critical path with the computational complexity $\mathcal {O}(P\times k_{size}\times k_{pop}\times l_{size}\times l_{pop} \times m^2 \times o)$. Thus, the computational complexity for each generation of the AHOA is $\mathcal {O}[P\times (\log P+o\times k_{size}\times k_{pop}\times l_{size}\times l_{pop} \times m^2)]$.

5 Experiment and Discussions

5.1 Experimental Setup

To demonstrate the performance of the proposed algorithm, ten benchmark instances of the BRdata [2] are tested. The BRdata is a data set consists of 10 test instances (Mk01-Mk10), which are randomly generated using a uniform distribution between given limits. The parameters in the proposed algorithm for these instances are listed in Table 2. The proposed AHOA is implemented in C++ on the AMD Ryzen 5 5600X machine running at 3.7 GHz and the optimization objective of it is makespan. Besides, we select three categories represented algorithms with to compare, including EA based methods, HA based methods, and RL based methods. For instance, Wang et al. [32] proposed a hybrid algorithm named GIWO based on gray wolf and invasive weeds, and Chen et al. [5] and Han et al. [16] both proposed methods based on RL to solve the FJSP.

Table 2. The AHOA parameters.

5.2 Experimental Results

The results of these comparisons are shown in the Table 3. For the EA based methods, the average improving performance of AHOA is 11%, of which the three testing instances Mk02, Mk04, and Mk06 improved by more than 22.8%; for the HA based methods, the average improving performance of AHOA is 6.7%, of which the two testing instances Mk02 and Mk06 improved by more than 16.7%. The most important difference between the AHOA and the above two methods is the ability to adjust the hyperparameters adaptively. The improved PSO [10] proposes some tuning schemes of parameters with exact mathematical methods. However, the accurate mathematical expression of the parameters tuning schemes may be unavailable as the schemes are affected by various factors, such as dynamic conditions. The result shows that the AHOA is more effective in large-scale complex environments. Besides, it can deal with situations in which the mathematical expression of the parameters tuning schemes is not available. These observations align with the findings in [6].

For the RL based methods, the average improving performance of AHOA is 22%, including the three testing instances Mk06, Mk07, and Mk10 increasing by more than 25%. However, the AHOA performs slightly worse than the self-learning GA (SLGA) [5] on Mk05. Because the setting range of the action list in the SLGA is more refined compared with the AHOA. It can find more suitable parameters for complex environments with enough iterations. The SLGA proposes a different way to combine two RL algorithms to enhance the performance of GA. Nevertheless, it still can not avoid the large overestimations of action values in the RL [17]. The result shows that AHOA performs better in terms of solution quality than other RL based methods. Besides, the Gantt chart of the solution obtained by AHOA for the Mk02 and Mk05 instance are presented in Fig. 4 and Fig. 5.

Table 3. The comparison of the makespan in BRdata

Fig. 4.

Gantt chart of the solution of the Mk02 instance

Fig. 5.

Gantt chart of the solution of the Mk05 instance

5.3 Ablation Experiment

As mentioned in Sect. 4, we introduce the critical path and reinforcement learning to solve the FJSP task. In order to illustrate the improvement in the proposed algorithm, we make ablation experiments on these two parts.

5.3.1 The Discussion of the Critical Path

As shown in Table 4, an algorithm with critical path can achieve better performance than an algorithm without critical path. The experiment results show that the makespan of the AHOA is 10.7% more than the method without critical path on the ten instances on average. It indicates that the critical path can effectively improve search quality. As the complexity analysis of AHOA in Sect. 4.4, searching the critical path will increase the time cost of the algorithm, which means that the AHOA will spend more time in a single iteration. However, it can reach convergence with fewer iterations.

Table 4. Experiments observing the influence of the critical path on 10 instances.

Fig. 6.

Histograms reflecting the influence of the different reinforcement learning on 10 instances.

5.3.2 The Discussion of the Reinforcement Learning

We also conduct an ablation experiment on reinforcement learning. It aims to explore the influence of different reinforcement learning methods on HA. As shown in Fig. 6, the makespan of the histogram performs best on the double Q-learning algorithm, which outperforms the HA and the Q-learning algorithm by more than 5.9% and 4.6% respectively. Compared with the HA, the algorithm introduced with reinforcement learning has the characteristics of adaptation which can better adapt to different environments. However, the Q-learning overestimate attempted actions, which will affect the convergence results to a certain extent. The double Q-learning can avoid the positive bias in estimating the action values and achieves better performance. This result shows that the strategy with the double Q-learning has achieved the best results on the ten instances. It indicates that the double Q-learning can improve performance by enhancing generalization and preventing overestimation problems.

6 Conclusion

This paper discusses the FJSP task by proposing a novel algorithm AHOA, combining the hybrid and double Q-learning algorithms. Compared with the widely deployed methods for FJSP, our algorithm can modify the key hyperparameters adaptively in the HA and avoid the overestimations problem of action values compared to other methods based on RL. Moreover, the proposed algorithm is more efficient due to the neighborhood structure based on the critical path. Finally, the experiment results verify that AHOA is suitable for FJSP instances with the high flexibility.

For the future work, we notice that the existing algorithms have achieved remarkable results in static scheduling, but there are few studies on the dynamic scheduling. We would like to investigate the dynamic multi-objective FJSP based on the transfer learning [21, 23,24,25] and domain adaptation learning [20, 22]. Besides, the performance of AHOA in practical applications still needs further testing, our future work will also focus on enhancing the generalization capabilities of the algorithm on the larger FJSP data sets.