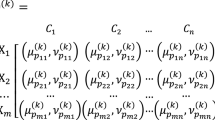Pythagorean fuzzy mathematical programming method for multi-attribute group decision making with Pythagorean fuzzy truth degrees

Abstract

This paper develops a Pythagorean fuzzy (PF) mathematical programming method to solve multi-attribute group decision-making problems under PF environments. The main work is summarized as four aspects: (1) Considering the fuzziness and hesitancy in pairwise comparisons of alternatives, we firstly introduce PF sets to depict the fuzzy truth degrees of alternative comparisons. (2) According to the information entropy, individual subjective attribute weight vectors of decision makers (DMs) are calculated and integrated into a collective one by a cross-entropy optimization model. Then DMs’ weights are objectively derived from the collective subjective attribute weight vector. (3) PF group consistency and inconsistency indices are defined based on PF-positive ideal solution (PFPIS) and PF-negative ideal solution (PFNIS), respectively. To determine comprehensive attribute weights, a biobjective PF mathematical programming model is constructed through minimizing two inconsistency indices based on PFPIS and PFNIS simultaneously. A linear programming method is technically developed to solve this model. (4) Using the cross-entropy again, collective relative closeness degrees of alternatives are explicitly derived to rank the alternatives. Finally, an example of green supplier selection is analyzed to verify the effectiveness of the proposed method.

1 Introduction

Due to the rapid development of economy and the rising public awareness for environment protection, green supply chain management (GSCM) has been a new management mode taking the environment performance into account [4]. As a key of GSCM, green supplier selection (GSS) is important to improve the manufacturer’s benefit and environment protection performance [27]. Since real-life GSS problems usually involve multiple attributes and need several decision makers (DMs) to take part in decision making, the GSS can be regarded as a kind of multi-attribute group decision-making (MAGDM) problems. Owing to the complexity of objective things and fuzziness of human thinking, there exists a great deal of uncertainty and fuzziness inherent in the GSS problems.

Fuzzy set (FS), initiated by Zadeh [51], is a powerful tool to handle the uncertain or fuzzy information in decision making. Atanassov [1] extended FS to propose intuitionistic fuzzy set (IFS). The element of an IFS is expressed by a membership function u and a non-membership function v satisfying the conditions: $u\in [0,1]$, $v\in [0,1]$ and $u+v\le 1$. Thus, IFS can overcome the shortcoming of single membership degree of FS. Atanassov and Gargov [2] further extended IFS to propose interval-valued intuitionistic fuzzy set (IVIFS). In the past few decades, IFS and IVIFS have received increasing attention [8, 17, 34, 36, 37, 40, 43, 48]. They have been widely applied to the fields of multi-attribute decision making (MADM) [11, 15, 30, 46, 47] and MAGDM [31, 33, 45] as well as preference relation research [35, 38, 39, 42].

However, the constraint of $u+v\le 1$ of IFS may bring inconvenience for DM in real-world applications. In some specified circumstances, DM may provide evaluation information with the sum of membership degree u and non-membership degree v being greater than 1. In such case, rather than requiring the DM to change the information to suit the constraints of IFS, Yager [49] introduced the concept of Pythagorean fuzzy (PF) set (PFS) in which the square sum of membership degree u and non-membership degree v is less than or equal to 1. Subsequently, Gou, Xu and Ren [16] developed several PF functions and investigated their fundamental properties such as continuity, derivability, and differentiability, which further enrich the theory of PFS. After reviewing the definitions and basic properties of different types of FSs that have appeared in existing literature, Bustince et al. [3] concluded that IFS is a subset of PFS. Therefore, PFS has stronger ability to characterize uncertainty and fuzziness than IFS. Currently, PFS has gained great popularity in the decision making. Existing achievements on PF MADM and MAGDM can be roughly divided into two classes.

The first class is the theory about aggregation operators, which integrate decision information effectively to deal with MADM and MAGDM in the PF environment. For example, Yager [49], Yager and Abbasov [50] proposed a series of aggregation operators: PF-weighted average operator, PF-weighted geometric operator, PF-weighted power average operator, PF-weighted power geometric operator, and PF-ordered weighted geometric operator to solve the MADM problems. Peng and Yang [24] developed some PF Choquet integral operators and proposed two approaches to tackle MAGDM problems in PF environments. Peng and Yang [25] defined subtraction and division operations and proved some properties of the PF aggregation operators in [49, 50]. Garg [9, 12] proposed several PF averaging and geometric operators using Einstein t-norm and t-conorm, investigated their properties, and then applied them to MADM. Garg [14] developed some PF aggregation operators by incorporating the confidence level factor and applied them to deal with group decision making. Ma and Xu [22] proposed some new operational laws of PFSs and defined symmetric PF-weighted geometric and averaging operators to address MADM problems.

The second class is extensions of some classical decision-making methods which are used to rank alternatives. Zhang and Xu [55] defined novel operational laws of PFSs, proposed a score function based comparison method and extended Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) to MADM with PFSs. Ren, Xu and Gou [28] extended an acronym in Portuguese for Interactive Multi-criteria Decision Making (TODIM) to MAGDM with PF information by the prospect theory. Zhang [53] developed a similarity measure based method to address MAGDM problems under PF environments. Peng and Yang [25] defined an accuracy function and developed a PF superiority and inferiority ranking method to solve MAGDM problems. Garg [10] defined a correlation coefficient between two PFSs to settle decision-making problems. Zhang [54] extended qualitative flexible multiple criteria method (QUALIFLEX) for MADM with interval-valued PFSs (IVPFSs). Subsequently, Garg [7, 13, 16] proposed improved score and accuracy functions for the elements of IVPFSs and applied them to deal with decision-making problems.

The aforementioned methods seem to be effective for solving MADM and MAGDM problems under PF environments. However, there are some defects as follows:

• 1. Methods [9, 22, 52, 55] investigated MADM under PF environments. However, they are only suitable to deal with single-person decision making and are invalid in solving PF MAGDM problems. With the increasing complexity of problems, it is more and more difficult for single DM to evaluate alternatives all round, and thus PF MAGDM is of great importance for scientific research and real applications.

• 2. To rank alternatives, methods [12, 14, 22, 24, 25, 49, 50] proposed some aggregation operators and applied them to obtain the collective values of alternatives. To some extent, using these aggregation operators directly to aggregate PF information may result in loss of information.

• 3. The determination of DMs’ weights is essential and significant in MAGDM. However, DMs’ weights and attribute weights were allocated in advance in methods [24, 25, 28]. It is not easy to avoid subjective randomness to give the weights of DMs and attributes ahead, which may lead to unreasonable decision results. Though method [53] determined the weights of DMs by maximizing the collective similarity degree between the opinions of all individual DMs and the ideal opinion of the decision group, the attribute weights in method [53] were still given a priori.

To overcome the aforesaid defects, this paper proposes a new PF programming method to settle MAGDM problems with PF truth degrees and incomplete attribute weight information and apply to GSS. The main motivations of this paper come from three aspects:

• 1. In a GSS problem, a DM may indicate that his/her support for environmental impact degree of a green supplier is $\frac{1}{2}$ and the support against environmental impact degree is $\frac{\sqrt{3}}{2}$. It can be found easily that $\frac{1}{2}+\frac{\sqrt{3}}{2}>1$, the ordered pair $(\frac{1}{2},\frac{\sqrt{3}}{2})$ is not allowable for an IFS. Hence, it is more suitable and convenient to utilize PFSs to represent the assessment information of green supplier. Moreover, it is very difficult for DM to accurately give the attribute weights because of various subjective and objective reasons. Thus, GSS is a typical PF MAGDM problem with incomplete attribute weight information. This motivates us to develop a new method for PF MAGDM with incomplete attribute weight information.

• 2. Thanks to the background of education, knowledge and experience, different DMs act as diverse roles during the process of decision making. How to obtain the weights of DMs objectively is an important issue for PF MAGDM. For this purpose, this paper utilizes the cross-entropy theory to determine the weights of DMs based on individual decision matrix information.

• 3. As one of classical MADM methods, linear programming technique for multidimensional analysis of preference (LINMAP) [29] has attracted considerable attention and been extended to several fuzzy environments [5, 6, 19,20,21, 31,32,33,34, 52]. Nevertheless, to our best knowledge, there is no research on the extension of LINMAP under the PF environment. The attribute weight is a very crucial factor to decision-making result for MAGDM. Most of existing LINMAP extensions derived the attribute weights only considering positive ideal solution (PIS). However, negative ideal solution (NIS) is also important equally and should not be ignored. Incorporating the NIS into the determination of the attribute weights is more comprehensive and essential to the decision-making results. Hence, this paper constructs a biobjective PF mathematical programming model to derive the comprehensive attribute weights.

In this paper, according to the information entropy, the individual subjective attribute weight vectors of DMs are calculated and integrated into a collective one by a cross-entropy optimization model. Then DMs’ weights are objectively derived from the collective subjective attribute weight vector. Under the framework of LINMAP, PF group consistency and inconsistency indices are defined based on PF-positive ideal solution (PFPIS) and PF-negative ideal solution (PFNIS), respectively. To derive comprehensive attribute weights, a biobjective PF mathematical programming model is constructed by minimizing two group inconsistency indices simultaneously. A linear programming method is technically developed to solve this model. Subsequently, collective relative closeness degrees of alternatives are generated to rank alternatives through integrating individual relative closeness degrees by cross-entropy. Finally, an example of GSS is provided to illustrate the proposed method.

Compared with existing research, the major contributions and features of this paper are summarized below:

• 1. Considering the alternative comparisons with fuzzy truth degrees, it is the first time to adopt PFSs to describe the fuzzy alternative comparisons. Since PFS is the extension of IFS, it is more suitable and flexible to express the fuzzy truth degrees with PFSs.

• 2. Using the cross-entropy theory, the weights of DMs are obtained objectively based on individual PF decision matrices. The determination of DMs’ weights not only makes full use of the original judgment information provided by DMs, but also effectively avoids the subjective randomness of giving DMs’ weights a priori.

• 3. A biobjective PF programming model is constructed to determine the comprehensive attribute weights. A prominent feature of this model is that it takes the inconsistency indices based on PFPIS and PFNIS into consideration simultaneously. Moreover, a linear programming method is technically developed to solve the constructed biobjective PF programming model.

• 4. Collective relative closeness degrees of alternatives are explicitly derived by minimizing the cross-entropy of the collective relative closeness degrees to individual ones. Therefore, the ranking order of alternatives is generated according to the decreasing order of the collective relative closeness degrees.

The remainder of this paper is structured as follows. Section 2 reviews the definitions about IFS and PFS and some operation laws of PFNs. In Sect. 3, PF MAGDM problems with PF truth degrees are described. Section 4 develops a new PF mathematical programming method to solve such MAGDM problems. A GSS example is examined and the comparison analysis is carried out in Sect. 5, followed by conclusions and future works in Sect. 6.

2 Preliminaries

In this section, the concepts of IFS, PFS, and operation laws of PFSs are reviewed to facilitate the discussions. Then, Minkowski distances of PFSs are defined.

2.1 Pythagorean fuzzy sets

Definition 2.1

[1] Let X be a universe of discourse. An IFS I in X is an object having the form

$$\begin{aligned} I=\{<x,u_I (x),v_I (x)>|x\in X\}, \end{aligned}$$

(1)

where the function $u_I :X\rightarrow [0,1]$ and $v_I :X\rightarrow [0,1]$ represent, respectively, the degree of membership and that of non-membership of the element $x\in X$ to I satisfying that $0\le u_I (x)+v_I (x)\le 1$.

For each $x\in X$, $\pi _I (x)=1-u_I (x)-v_I (x)$ is called the degree of indeterminacy of x to I. For simplicity, $\tilde{\alpha }=<u_{\tilde{\alpha }} ,v_{\tilde{\alpha }}>$ is called an intuitionistic fuzzy number (IFN) [47].

Definition 2.2

[50] Let X be a universe of discourse. A PFS P in X is an object having the form

$$\begin{aligned} P=\{{<}x,u_P (x),v_P (x){>}\;|x\in X\}, \end{aligned}$$

(2)

where $u_P :X\rightarrow [0,1]$ denotes the degree of membership and $v_P :X\rightarrow [0,1]$ denotes the degree of non-membership of the element $x\in X$ to P, respectively, with the condition that $0\le u_P^2 (x)+v_P^2 (x)\le 1$. The degree of indeterminacy is $\pi _P (x)=\sqrt{1-u_P^2 (x)-v_P^2 (x)}$.

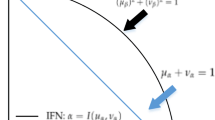
For convenience, $(u_{\tilde{p}} (x),v_{\tilde{p}} (x))$ is called a Pythagorean fuzzy number (PFN) [55] and denoted as $\tilde{p}=(u_{\tilde{p}} ,v_{\tilde{p}} )$. The difference between PFNs and IFNs can be easily shown in Fig. 1.

Fig. 1

Comparison of spaces of PFNs and IFNs

Definition 2.3

[55] Let $\tilde{a}=(u_1 ,v_1 )$, $\tilde{b}=(u_2 ,v_2 )$ and $\tilde{c}=(u,v)$ be three PFNs, $\lambda >0$, then

• 1. $\tilde{a}\oplus \tilde{b}=(\sqrt{u_1^2 +u_2^2 -u_1^2 u_2^2 },v_1 v_2 )$;

• 2. $\tilde{a}\otimes \tilde{b}=(u_1 u_2 ,\sqrt{v_1^2 +v_2^2 -v_1^2 v_2^2 })$;

• 3. $\lambda \tilde{c}=(\sqrt{1-(1-u^{2})^{\lambda }},v^{\lambda })$;

• 4. $\tilde{c}^{\lambda }=(u^{\lambda },\sqrt{1-(1-v^{2})^{\lambda }})$.

Definition 2.4

[49] Let $\tilde{a}=(u_1 ,v_1 )$, $\tilde{b}=(u_2 ,v_2 )$ be two PFNs, a nature quasi-ordering on the PFNs is defined as follows:

$$\begin{aligned} \tilde{a}\succeq \tilde{b}\quad \hbox { if and only if } u_1 \ge u_2\quad \hbox { and }v_1 \le v_2 , \end{aligned}$$

where $\succeq$ means bigger than or indifferent to.

Definition 2.5

[55] For any PFN $\tilde{c}=(u,v)$, the score function of $\tilde{c}$ is defined as follows:

$$\begin{aligned} s(\tilde{c})=u^{2}-v^{2}. \end{aligned}$$

(3)

Proposition 2.1

[55] For any PFN $\tilde{c}=(u,v)$, $s(\tilde{c})\in [-1,1]$.

2.2 Distances of Pythagorean fuzzy sets

Based on the distance of IFSs [46], a Minkowski distance and a weighted Minkowski distance of PFSs are defined below.

Definition 2.6

Let A and B be two PFSs on the domain of discourse $X=\{x_1 ,x_2 ,\ldots ,x_n \}$ and $q\ge 1$. A Minkowski distance between A and B is defined as:

(4)

It can be examined that $d_q (A,B)$ satisfies the axioms of distance:

• 1. Nonnegativity: $d_q (A,B)\ge 0$;

• 2. Symmetry: $d_q (A,B)=d_q (B,A)$;

• 3. Triangle inequality: If $A\subseteq B\subseteq C$, then $d_q (A,B)\le d_q (A,C)$ and $d_q (B,C)\le d_q (A,C)$.

When $q=1$, Eq. (4) is called Hamming distance as follows:

$$\begin{aligned} d_1 (A,B)= & {} \sum _{j=1}^n \frac{1}{2n}(|(u_A (x_j ))^{2}-(u_B (x_j ))^{2}|+|(v_A (x_j ))^{2}-(v_B (x_j ))^{2}|\nonumber \\&+\,|(\pi _A (x_j))^{2}-(\pi _B (x_j ))^{2}|) . \end{aligned}$$

(5)

In particular, if two PFSs A and B reduce to PFNs, Eq. (5) is degenerated to Hamming distance defined in [55].

When $q=2$, Eq. (4) is called Euclidean distance as follows:

(6)

In particular, if two PFSs A and B reduce to PFNs, Eq. (6) is degenerated to Euclidean distance defined in [28].

When $q\rightarrow +\infty$, it follows from Eq. (4) that

$$\begin{aligned} d_{+\infty } (A,B)= & {} \mathop {\max }\limits _{1\le j\le n} \left\{ \frac{1}{2n}|(u_A (x_j ))^{2}-(u_B (x_j ))^{2}|\right. \\&\left. +\,|(v_A (x_j ))^{2}-(v_B (x_j ))^{2}|+|(\pi _A (x_j ))^{2}-(\pi _B (x_j ))^{2}|\right\} , \end{aligned}$$

which is called Chebyshev distance.

Definition 2.7

Let A and B be two PFSs on the domain of discourse $X=\{x_1 ,x_2 ,\ldots ,x_n \}$. A weighted Minkowski distance between A and B is defined as

(7)

where $\omega _j$ is the weight of $x_j$ satisfies the conditions: $\sum _{j=1}^n {\omega _j } =1$ and $\omega _j \ge 0$ $(j=1,2,\ldots ,n)$.

When $q=1$, $q=2$ and $q\rightarrow +\infty$, the corresponding $\bar{{d}}_1 (a,b)$, $\bar{{d}}_2 (a,b)$ and $\bar{{d}}_{+\infty } (a,b)$ are called a weighted Hamming distance, a weighted Euclidean distance and a weighted Chebyshev distance, respectively.

3 Pythagorean fuzzy MAGDM problems with PF truth degrees

In this section, PF MAGDM problems with PF truth degrees and incomplete attribute weight information are described and DMs’ weight vector is derived objectively by the cross-entropy theory.

3.1 Description of problems and normalization method

For simplicity, denote $L=\{1,2,\ldots ,l\}$, $M=\{1,2,\ldots ,m\}$ and $N=\{1,2,\ldots ,n\}$. Suppose that there are l DMs who have to rank m alternatives based on n attributes. Denote an alternative set by $A=\{A_1 ,A_2 ,\ldots ,A_m \}$ and an attribute set by $F=\{f_1 ,f_2 ,\ldots ,f_n \}$. Denote DMs’ weight vector by ${\varvec{w}}=(w_1 ,w_2 ,\ldots ,w_l )^{\hbox {T}}$, where $\mathop {\sum }\limits _{k=1}^l {w_k } =1$ and $w_k \ge 0 \, (k\in L)$. The rating of alternative $A_i$ on attribute $f_j$ given by DM $e_k$ is denoted by a PFN $\tilde{y}_{ij}^k =(u_{ij}^k ,v_{ij}^k ) \, (i\in M,\;j\in N,\;k\in L)$. Hence, a MAGDM problem can be concisely expressed in PF decision matrices ${\varvec{Y}}^{{k}}=(\tilde{y}_{ij}^k )_{m\times n} (k\in L)$.

To eliminate the effect of different dimensions on decision-making results, the values $\tilde{y}_{ij}^k \,(i\in M,\;j\in N,\;k\in L)$ of attributes should be normalized into $\tilde{r}_{ij}^k$ as follows:

$$\begin{aligned} \tilde{r}_{ij}^k =\left\{ {\begin{array}{l} (u_{ij}^k ,v_{ij}^k ),\hbox { if }f_j \in F^{b} \\ (v_{ij}^k ,u_{ij}^k ),\hbox { if }f_j \in F^{c} \\ \end{array}} \right. (i\in M,\;j\in N,\;k\in L) \end{aligned}$$

(8)

where $F^b$ and $F^c$ are the sets of benefit attributes and cost attributes, respectively.

Thus, the PF decision matrices ${\varvec{Y}}^{k}=(\tilde{y}_{ij}^k )_{m\times n} \,(k\in L)$ are transformed into the normalized PF decision matrices ${{\varvec{Y}}'}^{k}=(\tilde{r}_{ij}^k )_{m\times n} \,(k\in L)$.

3.2 Incomplete weight information structure

In decision-making process, the attribute weights should be taken into account. Actually, DM may specify some preference information on attribute weights according to his/her knowledge, experience, and judgment. Such information of attribute weights is incomplete. Denote the comprehensive attribute weight vector by ${{\varvec{\omega }}}=(\omega _1 ,\omega _2 ,\ldots ,\omega _n )^{\mathrm{T}}$, where $\omega _j$ is the attribute weight of $f_j$ satisfying $\sum _{j=1}^n {\omega _j } =1$ and $\omega _j \ge 0 \,(j\in N)$. In this paper, ${{\varvec{\omega }}}$ is incompletely known and need to be determined. Let $\varLambda _0 =\left\{ {\varvec{\omega }}|\sum _{j=1}^n {\omega _j } =1,\;\omega _j \ge \varepsilon \;\;\hbox {for }\;j\in N\right\}$, where $\varepsilon >0$ is a sufficiently small positive number. The constraints $\omega _j \ge \varepsilon \,(j\in N)$ can ensure that each weight of $\varLambda _{0}$ is not equal to zero. The incomplete weight information structures can be expressed in the five basic relations among attribute weights, which are denoted by subsets $\varLambda _s \, (s=1,2,3,4,5)$ of weight vectors in $\varLambda _0$, respectively [18, 32, 44, 45]. In reality, usually the preference information structure $\varLambda$ of attribute importance may consist of several subsets of the above basic subsets $\varLambda _s \,(s=1,2,3,4,5)$.

3.3 Subjective preference relations between alternatives with PF truth degrees

Assume that DM $e_k$ gives the preference relations between alternatives by a PFS of ordered pairs ${\tilde{\Omega }}_k =\{<(g,h),\tilde{a}_k (g,h)>|A_g \underline{\succ }_k A_h \;$ with a PF truth degree $\tilde{a}_k (g,h) \;( g,h\in M)\}$, where (g, h) expresses an ordered pair of alternatives $A_g$ and $A_h$ that DM $e_k$ prefers $A_g$ to $A_h$ (denoted by $A_g \underline{\succ }_k A_h )$ with PF truth degree $\;\tilde{a}_k (g,h)$ and $\;\tilde{a}_k (g,h)=(u_{(g,h)}^k ,v_{(g,h)}^k )$ is a PFN. Define the $(\alpha ,\beta )$-cut set of ${\tilde{\Omega }}_k$ as ${\tilde{\Omega }}_k^{(\alpha ,\beta )} =\{(g,h)|u_{(g,h)}^k \ge \alpha ,\;v_{(g,h)}^k \le \beta \;( g,h\in M)\}$, where $0\le \alpha \le 1$, $0\le \beta \le 1$ and $\alpha ^{2}+\beta ^{2}\le 1$. Then the support of ${\tilde{\Omega }}_k$ is ${\tilde{\Omega }}_k^{(0,1)} =\{(g,h)|u_{(g,h)}^k \ge 0,v_{(g,h)}^k \le 1 ( g,h\in M)\}$ and the symbol $|{\tilde{\Omega }}_k^{(0,1)} |$ indicates the cardinality of ${\tilde{\Omega }}_k^{(0,1)}$, i.e., the number of elements in ${\tilde{\Omega }}_k^{(0,1)}$.

The subjective preference relations ${\tilde{\Omega }}_k^{(0,1)}$ are given through pairwise comparisons between alternatives as a whole rather than every attribute. Generally, not every DM would specify all pairwise comparisons between alternatives, so the number of alternative comparisons is at most equal to $C_m^2 =m(m-1)/2$.

3.4 Determining DMs’ weight vector based on cross-entropy

To derive DMs’ weights, the normalized PF decision matrices ${{\varvec{Y}}'}^{k} \,(k\in L)$ are transformed into the corresponding score matrices ${\varvec{s}}^{k}=(s_{ij}^k )_{m\times n}$ firstly, where $s_{ij}^k$ is the score function of $\tilde{r}_{ij}^k \, (i\in M,\;j\in N,\;k\in L)$ calculated by Eq. (3). It can be found that $s_{ij}^k \in [-1,1]$ by Proposition 2.1. To guarantee the nonnegativity of the elements, all the score functions in ${\varvec{s}}^{k}$ add number 1. Thus the score matrices ${\varvec{s}}^{k} \, (k\in L)$ can be converted into the nonnegative score matrices $\hat{{\varvec{s}}}^{k}=(\hat{{s}}_{ij}^k )_{m\times n}$, where

$$\begin{aligned} \hat{{s}}_{ij}^k =s_{ij}^k +1\quad \hbox {for all } i\in M, j\in N,k\in L. \end{aligned}$$

(9)

Definition 3.1

[26] Let ${\varvec{x}}=(x_1 ,x_2 ,\ldots ,x_n )^{\mathrm{T}}$ and ${\varvec{y}}=(y_1 ,y_2 ,\ldots ,y_n )^{\mathrm{T}}$ be two vectors satisfying $x_j \ge 0$, $y_j \ge 0 (j\in N)$ and $\sum _{j=1}^n {x_j } \le \sum _{j=1}^n {y_j } \le 1$. Then

$$\begin{aligned} D({\varvec{x}},{\varvec{y}})=\sum _{j=1}^n {[x_j \log (x_j /y_j )]} \end{aligned}$$

(10)

is called a cross-entropy of ${\varvec{x}}$ to ${\varvec{y}}$. When $x_j =0$ or $y_j =0$ for any $j\in N$, the cross-entropy of ${\varvec{x}}$ to ${\varvec{y}}$ cannot be calculated by Eq. (10). Thus, in such case, set $D({\varvec{x}},{\varvec{y}})=0$.

The cross-entropy has the following properties:

• 1. $D({\varvec{x}},{\varvec{y}})\ge 0;$ (2) $D({\varvec{x}},{\varvec{y}})=0$ if and only if $x_j =y_j$ for all j.

The cross-entropy $D({\varvec{x}},{\varvec{y}})$ can be viewed as the consistent measurement between ${\varvec{x}}$ and ${\varvec{y}}$. If ${\varvec{x}}={\varvec{y}}$, i.e., ${\varvec{x}}$ is completely consistent with ${\varvec{y}}$, then the cross-entropy is the minimum, i.e., $D({\varvec{x}},{\varvec{y}})=0$.

Let ${{\varvec{\omega }}}^{s(k)}=(\omega _1^{s(k)} ,\omega _2^{s(k)} ,\ldots ,\omega _n^{s(k)} )^{\mathrm{T}}$ be the individual subjective attribute weight vector for DM $e_k$, where $\omega _j^{s(k)}$ means the subjective weight of attribute $f_j$ for DM $e_k$. Then, according to the information entropy theory [41], the individual subjective attribute weights $\omega _j^{s(k)}$ can be obtained as

$$\begin{aligned} \omega _j^{s(k)} =(1-E_j^k )/\sum _{j=1}^n {(1-E_j^k )} \quad \hbox { for all } j\in N, k\in L, \end{aligned}$$

(11)

where $E_j^k =-\frac{1}{\log m}\sum _{i=1}^m {\left[ \left( \hat{{s}}_{ij}^k /\sum _{i=1}^m {\hat{{s}}_{ij}^k } \right) \log \left( \hat{{s}}_{ij}^k /\sum _{i=1}^m {\hat{{s}}_{ij}^k } \right) \right] }$.

Denote the vector of collective subjective attribute weights by ${{\varvec{\omega }} }^{s}=(\omega _1^s ,\omega _2^s ,\ldots ,\omega _n^s )^{\mathrm{T}}$, where $\omega _j^s$ represents the collective subjective weight of attribute $f_j$ for the decision group. As is all known, the more consistent ${{\varvec{\omega }} }^{s}$ and ${{\varvec{\omega }} }^{s(k)}$, the more the cross-entropy of ${{\varvec{\omega }} }^{s}$ to ${{\varvec{\omega }} }^{s(k)}$ is approaching to 0. By minimizing the total cross-entropy of the collective subjective attribute weight vector to each individual one, a cross-entropy optimization model is constructed to derive the vector ${{\varvec{\omega }} }^{s}$ as follows:

$$\begin{aligned} \begin{array}{l} \min \;\;D=\sum \limits _{k=1}^l D ({{\varvec{\omega }}}^{s},{{\varvec{\omega }}}^{s(k)}) \\ \hbox {s.t.}\left\{ {\begin{array}{l} \sum \limits _{j=1}^n {\omega _j^s } =1\hbox { } \\ \omega _j^s \ge 0\;(j\in N)\hbox { } \\ \end{array}} \right. \\ \end{array} \end{aligned}$$

(12)

where $D({{\varvec{\omega }} }^{s},{{\varvec{\omega }} }^{s(k)})\, (k\in L)$ is the cross-entropy of ${{\varvec{\omega }}}^{s}$ to ${{\varvec{\omega }} }^{s(k)}$ calculated by Eq. (10).

Construct the Lagrange function

$$\begin{aligned} \Phi (\omega _j^s ,\lambda )=\sum \limits _{k=1}^l D ({{\varvec{\omega }}}^{s},{{\varvec{\omega }}}^{s(k)})+\lambda \left( \sum \limits _{j=1}^n {\omega _j^s } -1\right) , \end{aligned}$$

where $\lambda$ is a Lagrange multiplier. Set the partial derivatives of $\Phi$ with respect to $\omega _j^s (j\in N)$ and $\lambda$ to be zeros, the following system of equalities is yielded:

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\partial \Phi }{\partial \omega _j^s }=\sum \limits _{k=1}^l {\log \frac{\omega _j^s }{\omega _j^{s(k)} }} +l+\lambda =0\;\;\;\;(j\in N) \\ \frac{\partial \Phi }{\partial \lambda }=\sum \limits _{j=1}^n {\omega _j^s } -1=0 \\ \end{array}} \right. \end{aligned}$$

It can be obtained that $\omega _j^s =\exp (\frac{1}{l}\sum _{k=1}^l {(\log \omega _j^{s(k)} -\lambda -l} )) \, (j\in N)$ and $\lambda =l\cdot \log \left( \sum _{j=1}^n {\exp \left( \frac{1}{l}\sum _{k=1}^l {\log \omega _j^{s(k)} } -1\right) } \right)$. Further, it yields that the collective subjective attribute weight $\omega _j^s$ of attribute $f_j$ is

$$\begin{aligned} \omega _j^s =\frac{\exp \left( \frac{1}{l}\sum _{k=1}^l {\log \omega _j^{s(k)} } \right) }{\sum _{j=1}^n {\exp \left( \frac{1}{l}\sum _{k=1}^l {\log \omega _j^{s(k)} } \right) } } (j\in N). \end{aligned}$$

(13)

Thus, the collective subjective weight vector ${{\varvec{\omega }} }^{s}$ can be obtained. It is apparent that ${{\varvec{\omega }} }^{s(k)} \quad (k\in L)$ and ${{\varvec{\omega }} }^{s}$ are derived according to the individual decision matrices ${\varvec{Y}}^{k}=(\tilde{y}_{ij}^k )_{m\times n} \, (k\in L)$ provided by DMs. Thus, ${{\varvec{\omega }} }^{s(k)}$ and ${{\varvec{\omega }} }^{s}$ are called the individual subjective attribute weight vector for DM $e_k$ and the collective subjective weight vector, respectively. In MAGDM, the more consistent the individual subjective weight vector ${{\varvec{\omega }} }^{s(k)}$ and the collective one ${{\varvec{\omega }} }^{s}$, the bigger the weight of DM $e_k$. Beard this in mind, the weight $w_k$ of DM $e_k$ is defined as

$$\begin{aligned} w_k =\frac{1-D({{\varvec{\omega }}}^{s},{{\varvec{\omega }}}^{s(k)})}{\sum _{k=1}^l {[1-D} ({{\varvec{\omega }}}^{s},{{\varvec{\omega }}}^{s(k)})]} (k\in L). \end{aligned}$$

(14)

It can be easily shown that Eq. (14) satisfies the conditions $w_k \ge 0 \quad (k\in L)$ and $\sum _{k=1}^l {w_k =1}$.

If the attribute weights are known completely in advance, then the distances between alternatives and PFPIS as well as PFNIS can be calculated. The collective relative closeness degrees of alternatives can be used to rank alternatives. Note that in the considered MAGDM problems the attribute weights are incompletely known and need to be determined. To incorporate the incomplete attribute weight information, a biobjective PF programming model is constructed to acquire comprehensive attribute weights in Sect. 4. The process of deriving the weights of attributes and DMs is graphically depicted in Fig. 2.

Fig. 2

Flowchart of deriving the weights of attributes and DMs

4 A PF mathematical programming method to solve the PF MAGDM problems

Under the framework of LINMAP, PFPIS-based group inconsistency, PFPIS-based group consistency, PFNIS-based group inconsistency, and PFNIS-based group consistency are defined. To obtain comprehensive attribute weights, a biobjective PF mathematical programming model is built. Then a collective relative closeness degree vector is calculated to rank alternatives.

4.1 PF consistency and inconsistency based on PFPIS and PFNIS

Suppose that PFPIS is ${\varvec{r}}^{+}=(r_1^+ ,r_2^+ ,\ldots ,r_n^+ )^{\mathrm{T}}$ and PFNIS is ${\varvec{r}}^{-}=(r_1^- ,r_2^- ,\ldots ,r_n^- )^{\mathrm{T}}$, where $r_j^+$ and $r_j^-$ are the best rating and the worst rating on attribute $f_j \,(j\in N)$. Namely, one has

$$\begin{aligned} r_j^+ =(u_j^+ ,v_j^+ ),r_j^- =(u_j^- ,v_j^- ), \end{aligned}$$

(15)

where $u_j^+ =\max _{i\in M,k\in L} \{u_{ij}^k \}$, $v_j^+ =\min _{i\in M,k\in L} \{v_{ij}^k \}$ and $u_j^- =\min _{i\in M,k\in L} \{u_{ij}^k \}$, $v_j^- =\max _{i\in M,k\in L} \{v_{ij}^k \}$.

Using Eq. (7), q power of the weighted Minkowski distances between ${\varvec{r}}_i^k =(\tilde{r}_{i1}^k ,\tilde{r}_{i2}^k ,\ldots ,\tilde{r}_{in}^k )^{\mathrm{T}}$ and ${\varvec{r}}^{+}$ as well as ${\varvec{r}}^{-}$ can be calculated as follows:

$$\begin{aligned} S_i^{k+}= & {} \sum _{j=1}^n {\frac{\omega _j }{2}\left[ \left| \left( u_{ij}^k \right) ^{2}-\left( u_j^+ \right) ^{2}\right| ^{q}+\left| \left( v_{ij}^k \right) ^{2}-\left( v_j^+\right) ^{2}\right| ^{q}+\left| \left( \pi _{ij}^k \right) ^{2}-\left( \pi _j^+ \right) ^{2}\right| ^{q}\right] } \qquad \quad \end{aligned}$$

(16)

$$\begin{aligned} S_i^{k-}= & {} \sum _{j=1}^n {\frac{\omega _j }{2}\left[ \left| \left( u_{ij}^k \right) ^{2}-\left( u_j^-\right) ^{2}\right| ^{q}+\left| \left( v_{ij}^k\right) ^{2}-\left( v_j^- \right) ^{2}\right| ^{q}+\left| \left( \pi _{ij}^k\right) ^{2}-\left( \pi _j^- \right) ^{2}\right| ^{q}\right] }\qquad \quad \end{aligned}$$

(17)

where $(\pi _j^+ )^{2}=1-(u_j^+ )^{2}-(v_j^+ )^{2}$, $(\pi _j^- )^{2}=1-(u_j^- )^{2}-(v_j^- )^{2} \,(j\in N)$ and $\omega =(\omega _1 ,\omega _2 ,\ldots ,\omega _n )^{\mathrm{T}}$ is comprehensive attribute weight vector which needs to be determined.

On the one hand, for each $(g,h)\in {\Omega }_k^{(0,1)}$, if $S_g^{k+} <S_h^{k+}$, then $A_g$ is better than $A_h$. Here the objective ranking order of alternatives $A_g$ and $A_h$ determined by $S_g^{k+}$ and $S_h^{k+}$ is consistent with the subjective preference given by DM $e_k$. Conversely, if $S_g^{k+} \ge S_h^{k+}$, then the objective ranking order of alternatives $A_g$ and $A_h$ determined by $S_g^{k+}$ and $S_h^{k+}$ is inconsistent with the subjective preference given by DM $e_k$.

On the other hand, for each $(g,h)\in {\tilde{\Omega }}_k^{(0,1)}$, if $S_g^{k-} >S_h^{k-}$, then $A_g$ is better than $A_h$. Here the objective ranking order of alternatives $A_g$ and $A_h$ determined by $S_g^{k-}$ and $S_h^{k-}$ is consistent with the subjective preference by DM $e_k$. Conversely, if $S_g^{k-} \le S_h^{k-}$, then the objective ranking order of alternatives $A_g$ and $A_h$ determined by $S_g^{k-}$ and $S_h^{k-}$ is inconsistent with the subjective preference by DM $e_k$.

Therefore, there exist some deviations between the objective ranking orders and the subjective preferences provided by DMs. To measure such deviations, the definitions of inconsistency and consistency based on PFPIS and PFNIS are introduced, respectively.

Definition 4.1

For each $(g,h)\in {\tilde{\Omega }}_k^{(0,1)}$, an index $(S_h^{k+} -S_g^{k+} )^{-}$ is defined as:

$$\begin{aligned} \left( S_h^{k+} -S_g^{k+}\right) ^{-}=\left\{ {{\begin{array}{ll} {\tilde{a}_k (g,h)\left( S_g^{k+} -S_h^{k+}\right) }&{}\quad {\hbox {if }S_g^{k+} \ge S_h^{k+} } \\ 0&{}\quad {\hbox {if }S_g^{k+} <S_h^{k+} } \\ \end{array} }} \right. \end{aligned}$$

(18)

Obviously, $(S_h^{k+} -S_g^{k+})^{-}$ measures inconsistency between the objective ranking order and the subjective preference given by DM $e_k$ based on PFPIS. Then, the inconsistency can be rewritten as $(S_h^{k+} -S_g^{k+} )^{-}=\tilde{a}_k (g,h)\max \{0,S_g^{k+} -S_h^{k+} \}$. Hence, PFPIS-based group inconsistency is defined as follows:

$$\begin{aligned} \tilde{B}^{+}= & {} \sum _{k=1}^l {\left[ w_k \sum _{(g,h)\in \tilde{\Omega }_k^{(0,1)} } {\left( S_h^{k+} -S_g^{k+}\right) ^{-}} \right] }\nonumber \\= & {} \sum _{k=1}^l {\left[ w_k \sum _{(g,h)\in \tilde{\Omega }_k^{(0,1)} } {\tilde{a}_k (g,h)\max \left\{ 0,S_g^{k+} -S_h^{k+} \right\} } \right] } . \end{aligned}$$

(19)

Definition 4.2

For each $(g,h)\in {\tilde{\Omega }}_k^{(0,1)}$, an index $(S_h^{k+} -S_g^{k+})^{+}$ is defined as:

$$\begin{aligned} \left( S_h^{k+} -S_g^{k+}\right) ^{+}=\left\{ {\begin{array}{ll} \tilde{a}_k (g,h)\left( S_h^{k+} -S_g^{k+}\right) ,&{}\quad \hbox {if }S_g^{k+} <S_h^{k+} \\ 0,&{}\quad \,\hbox {if }S_g^{k+} \ge S_h^{k+} \\ \end{array}} \right. \end{aligned}$$

(20)

Similarly, $(S_h^{k+} -S_g^{k+} )^{+}$ measures consistency between the objective ranking order and the subjective preference given by DM $e_k$ based on PFPIS. Furthermore, Eq. (20) is rewritten as $(S_h^{k+} -S_g^{k+} )^{+}=\tilde{a}_k (g,h)\max \{0,S_h^{k+} -S_g^{k+}\}$. Hence, PFPIS-based group consistency is defined as follows:

$$\begin{aligned} \tilde{G}^{+}= & {} \sum _{k=1}^l {\left[ w_k \sum _{(g,h)\in \tilde{\Omega }_k^{(0,1)} } {\left( S_h^{k+} -S_g^{k+}\right) ^{+}} \right] }\nonumber \\= & {} \sum _{k=1}^l {\left[ w_k \sum _{(g,h)\in \tilde{\Omega }_k^{(0,1)} } {\tilde{a}_k (g,h)\max \left\{ 0,S_h^{k+} -S_g^{k+}\right\} } \right] } . \end{aligned}$$

(21)

Definition 4.3

For each $(g,h)\in {\tilde{\Omega }}_k^{(0,1)}$, an index $(S_g^{k-} -S_h^{k-} )^{-}$ is defined as:

$$\begin{aligned} \left( S_g^{k-} -S_h^{k-}\right) ^{-}=\left\{ {\begin{array}{ll} \tilde{a}_k (g,h)\left( S_h^{k-} -S_g^{k-}\right) , &{}\quad \hbox {if }\;S_g^{k-} <S_h^{k-} \\ 0,&{}\,\quad \hbox {if }\;S_g^{k-} \ge S_h^{k-} \; \\ \end{array}} \right. \end{aligned}$$

(22)

Then $(S_g^{k-} -S_h^{k-} )^{-}$ measures inconsistency between the objective ranking order and the subjective preference given by DM $e_k$ based on PFNIS and can be rewritten as $(S_g^{k-} -S_h^{k-} )^{-}=\tilde{a}_k (g,h)\max \{0,S_h^{k-} -S_g^{k-} \}$. Hence, PFNIS-based group inconsistency is defined as follows:

$$\begin{aligned} \tilde{B}^{-}= & {} \sum _{k=1}^l {\left[ w_k \sum _{(g,h)\in \Omega _k^{(0,1)} } {\left( S_g^{k-} -S_h^{k-}\right) ^{-}} \right] }\nonumber \\= & {} \sum _{k=1}^l {\left[ w_k \sum _{(g,h)\in \Omega _k^{(0,1)} } {\tilde{a}_k (g,h)\max \left\{ 0,S_h^{k-} -S_g^{k-}\right\} } \right] } . \end{aligned}$$

(23)

Definition 4.4

For each $(g,h)\in {\tilde{\Omega }}_k^{(0,1)}$, an index $(S_g^{k-} -S_h^{k-} )^{+}$ is defined as:

$$\begin{aligned} \left( S_g^{k-} -S_h^{k-}\right) ^{+}=\left\{ {\begin{array}{ll} \tilde{a}_k (g,h)\left( S_g^{k-} -S_h^{k-}\right) ,&{}\quad \hbox {if }S_g^{k-} >S_h^{k-} \\ 0,&{}\quad \,\hbox {if }S_g^{k-} \le S_h^{k-} \\ \end{array}} \right. \end{aligned}$$

(24)

Then $(S_g^{k-} -S_h^{k-} )^{+}$ measures consistency between the objective ranking order and the subjective preference given by DM $e_k$ based on PFNIS and can be rewritten as $(S_g^{k-} -S_h^{k-} )^{+}=\tilde{a}_k (g,h)\max \{0,S_g^{k-} -S_h^{k-} \}$. Hence, PFNIS-based group consistency is defined as follows:

$$\begin{aligned} \tilde{G}^{-}= & {} \sum _{k=1}^l {\left[ w_k \sum _{(g,h)\in \tilde{\Omega }_k^{(0,1)} } {\left( S_g^{k-} -S_h^{k-}\right) ^{+}} \right] }\nonumber \\= & {} \sum _{k=1}^l {\left[ w_k \sum _{(g,h)\in \tilde{\Omega }_k^{(0,1)} } {\tilde{a}_k (g,h)\max \left\{ 0,S_g^{k-} -S_h^{k-}\right\} } \right] } . \end{aligned}$$

(25)

Remark 1

There exist fuzziness and hesitation for DMs when making pairwise comparisons of alternatives. However, methods [5, 18, 45, 52] overlooked the fuzzy truth degrees of alternative comparisons. Methods [32, 33] described the fuzzy truth degrees of pairwise comparisons of alternatives using IFNs. By contrast, PFN is more flexible and practical to deal with the fuzziness and hesitation than IFN. Therefore, this paper firstly introduces PF truth degrees of alternative comparisons to address PF MAGDM problems.

Remark 2

Methods [5, 6, 18,19,20,21, 31,32,33,34] proposed several mathematical programming models to deal with MADM and MAGDM problems. However, when defining the consistency and inconsistency, methods [18, 19, 32,33,34] only considered the distance between the alternatives and the PIS and neglected the distance between the alternatives and the NIS. Although methods [5, 6, 20, 21, 31] took the PIS and the NIS into consideration simultaneously, they only defined two indices, i.e., inconsistency and consistency, in their models. By contrast, this paper proposes two group inconsistency indices and two group consistency indices. These four indices measure the consistency and inconsistency comprehensively by taking the PIS and NIS into account, which can make full use of decision information provided by DMs.

4.2 A PF mathematical programming model based on PFPIS and PFNIS

In group decision making, the smaller the group inconsistency, the more credible the decision-making result. Thus, the comprehensive attribute weights can be determined by minimizing the group inconsistency as much as possible. Then a biobjective PF mathematical programming model is constructed to derive the comprehensive attribute weight vector ${{\varvec{\omega }}}$ as follows:

$$\begin{aligned} \begin{array}{l} \hbox {min}\{\tilde{B}^{+}\} \\ \hbox {min}\{\tilde{B}^{-}\} \\ \hbox {s.t. }\left\{ {\begin{array}{l} \tilde{G}^{+}-\tilde{B}^{+}\ge \tilde{\xi } \\ \tilde{G}^{-}-\tilde{B}^{-}\ge \tilde{\eta } \\ {{\varvec{\omega }}}\in \hbox { }\varLambda \\ \end{array}} \right. \\ \end{array} \end{aligned}$$

(26)

where $\tilde{\xi }$ and $\tilde{\eta }$ are two PF thresholds given by DMs in advance, denoted by $\tilde{\xi }=(u_\xi ,v_\xi )$ and $\tilde{\eta }=(u_\eta ,v_\eta )$.

From Eqs. (19) and (21), it yields that $\tilde{G}^{+}-\tilde{B}^{+}=\sum _{k=1}^l [w_k \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } [\tilde{a}_k (g,h)(S_h^{k+} -S_g^{k+} )]]$. Similarly, from Eqs. (23) and (25), one has $\tilde{G}^{-}-\tilde{B}=\sum _{k=1}^l {[w_k \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {[\tilde{a}_k (g,h)(S_g^{k-} -S_h^{k-} )]} ]}$. For each $(g,h)\in \tilde{\Omega }_k^{(0,1)}$, denote $\lambda _{gh}^{k+} =\max \{0,S_g^{k+} -S_h^{k+} \}$ and $\lambda _{hg}^{k-} =\max \{0,S_h^{k-} -S_g^{k-} \}$. It can be found that $\lambda _{gh}^{k+} \ge 0$, $\lambda _{hg}^{k-} \ge 0$, $\lambda _{gh}^{k+} \ge S_g^{k+} -S_h^{k+}$ and $\lambda _{hg}^{k-} \ge S_h^{k-} -S_g^{k-}$. Let $t_{hg}^{k+} =S_h^{k+} -S_g^{k+}$ and $t_{gh}^{k-} =S_g^{k-} -S_h^{k-}$. Hence, Eq. (26) can be transformed into a biobjective PF mathematical program:

$$\begin{aligned} \begin{array}{l} \hbox {min}\left\{ \sum \limits _{k=1}^l {\left[ w_k \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left[ \tilde{a}_k (g,h)\lambda _{gh}^{k+} \right] }\right] } \right\} \\ \hbox {min}\left\{ \sum \limits _{k=1}^l {\left[ w_k \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left[ \tilde{a}_k (g,h)\lambda _{hg}^{k-} \right] }\right] }\right\} \\ \hbox {s.t.}\left\{ {\begin{array}{l} \sum _{k=1}^l {\left[ w_k \sum \limits _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left[ \tilde{a}_k (g,h)t_{hg}^{k+} \right] }\right] \ge \tilde{\xi }} \\ \sum _{k=1}^l {\left[ w_k \sum \limits _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left[ \tilde{a}_k (g,h)t_{gh}^{k-} \right] }\right] } \ge \tilde{\eta } \\ t_{hg}^{k+} +\lambda _{gh}^{k+} \ge 0\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ t_{gh}^{k-} +\lambda _{hg}^{k-} \ge 0\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ \lambda _{gh}^{k+} \ge 0,\lambda _{hg}^{k-} \ge 0\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ {{\varvec{\omega }}}\in \hbox { }\varLambda \\ \end{array}} \right. \;\;\hbox { } \\ \end{array} \end{aligned}$$

(27)

4.3 A linear programming method for solving PF mathematical program

According to Definition 2.3 and the nature quasi-ordering on the PFNs in Definition 2.4, Eq. (27) is converted into a four-objective crisp programming model:

$$\begin{aligned}&\begin{array}{l} \min \left\{ {\sqrt{1-\mathop {\prod }\limits _{k=1}^l {\left( \mathop {\prod }\limits _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left( 1-\left( u_{(g,h)}^k \right) ^{2}\right) ^{\lambda _{gh}^{k+} }} \right) ^{w_k }} }} \right\} \\ \max \left\{ {\mathop {\prod }\limits _{k=1}^l {\left( \mathop {\prod }\limits _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left( v_{(g,h)}^k \right) ^{\lambda _{gh}^{k+} }} \right) ^{w_k }} }\right\} \\ \min \left\{ {\sqrt{1-\mathop {\prod }\limits _{k=1}^l {\left( \mathop {\prod }\limits _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left( 1-\left( u_{(g,h)}^k \right) ^{2}\right) ^{\lambda _{hg}^{k-} }} \right) ^{w_k }} }} \right\} \\ \max \left\{ {\mathop {\prod }\limits _{k=1}^l {\left( \mathop {\prod }\limits _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left( v_{(g,h)}^k \right) ^{\lambda _{hg}^{k-} }} \right) ^{w_k }} } \right\} \\ \end{array}\nonumber \\&\hbox {s.t.}\left\{ {\begin{array}{l} \sqrt{1-\prod _{k=1}^l {\left( \prod _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left( 1-\left( u_{(g,h)}^k \right) ^{2}\right) ^{t_{hg}^{k+} }}\right) ^{w_k }} }\ge u_{\tilde{\xi }} \\ \prod _{k=1}^l {\left( \prod _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left( v_{(g,h)}^k\right) ^{t_{hg}^{k+}}}\right) ^{w_k }} \le v_{\tilde{\xi }} \\ \sqrt{1-\prod _{k=1}^l {\left( \prod _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left( 1-\left( u_{(g,h)}^k \right) ^{2}\right) ^{t_{gh}^{k-}}}\right) ^{w_k }} }\ge u_{\tilde{\eta }} \\ \prod _{k=1}^l {\left( \prod _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\left( v_{(g,h)}^k\right) ^{t_{gh}^{k-} }}\right) ^{w_k }} \le v_{\tilde{\eta }} \\ t_{hg}^{k+} +\lambda _{gh}^{k+} \ge 0\;\; \left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ t_{gh}^{k-} +\lambda _{hg}^{k-} \ge 0\;\; \left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ \lambda _{gh}^{k+} \ge 0,\lambda _{hg}^{k-} \ge 0\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ {{\varvec{\omega }}}\in \hbox { }\varLambda \\ \end{array}} \right. \end{aligned}$$

(28)

Using the logarithmic function, Eq. (28) is equivalently transformed into

$$\begin{aligned} \begin{array}{l} \max \left\{ z_1 =\sum \limits _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\lambda _{gh}^{k+} } \log \left( 1-\left( u_{(g,h)}^k \right) ^{2}\right) \right\} \\ \max \left\{ z_2 =\sum \limits _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\lambda _{gh}^{k+} } \log \left( v_{(g,h)}^k\right) \right\} \\ \max \left\{ z_3 =\sum \limits _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\lambda _{hg}^{k-} } \log \left( 1-\left( u_{(g,h)}^k\right) ^{2}\right) \right\} \\ \max \left\{ z_4 =\sum \limits _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {\lambda _{hg}^{k-} } \log \left( v_{(g,h)}^k \right) \right\} \;\;\;\;\hbox { } \\ \hbox {s.t.}\left\{ {\begin{array}{l} \sum _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {t_{hg}^{k+} } \log \left( 1-\left( u_{(g,h)}^k \right) ^{2}\right) \le \log \left( 1-u_{\tilde{\xi }}^2\right) \\ \sum _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {t_{hg}^{k+} } \log \left( v_{(g,h)}^k\right) \le \log v_{\tilde{\xi }} \\ \sum _{k=1}^l {w_k } \sum \limits _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {t_{gh}^{k-} } \log \left( 1-\left( u_{(g,h)}^k\right) ^{2}\right) \le \log \left( 1-u_{\tilde{\eta }}^2 \right) \\ \sum _{k=1}^l {w_k } \sum \limits _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } {t_{gh}^{k-} } \log \left( v_{(g,h)}^k \right) \le \log v_{\tilde{\eta }} \\ t_{hg}^{k+} +\lambda _{gh}^{k+} \ge 0\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ t_{gh}^{k-} +\lambda _{hg}^{k-} \ge 0\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ \lambda _{gh}^{k+} \ge 0,\lambda _{hg}^{k-} \ge 0\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ {{\varvec{\omega }}}\in \hbox { }\varLambda \\ \end{array}} \right. \\ \end{array} \end{aligned}$$

(29)

Plugging Eqs. (16) and (17) into Eq. (29), the multi-objective programming model (i.e., Eq. (29)) can be aggregated into a linear programming model by the equal weighted summation method as follows:

$$\begin{aligned} \begin{array}{l} \max \{z=z_1 +z_2 +z_3 +z_4 \}\;\;\hbox { } \\ \hbox {s.t.}\left\{ {\begin{array}{ll} \sum _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } \left\{ \sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{hj}^k \right) ^{2}-(u_j^+ )^{2}\right| ^{q}+\left| \left( v_{hj}^k \right) ^{2}-(v_j^+ )^{2}\right| ^{q}\right. \right. \\ \quad \left. +\,\left| \left( \pi _{hj}^k \right) ^{2}-(\pi _j^+ )^{2}\right| ^{q}\right] -\sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{gj}^k \right) ^{2}-\left( u_j^+ \right) ^{2}\right| ^{q}+\left| \left( v_{gj}^k\right) ^{2}-\left( v_j^+\right) ^{2}\right| ^{q}\right. \\ \quad \left. \left. +\left| \left( \pi _{gj}^k \right) ^{2}-\left( \pi _j^+ \right) ^{2}\right| ^{q}\right] \right\} \log \left( 1-\left( u_{(g,h)}^k \right) ^{2}\right) \le \log \left( 1-u_{\tilde{\xi }}^2\right) \;\;\; \\ \sum _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } \left\{ \sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{hj}^k \right) ^{2}-\left( u_j^+ \right) ^{2}\right| ^{q}+\left| \left( v_{hj}^k \right) ^{2}-\left( v_j^+\right) ^{2}\right| ^{q}\right. \right. \\ \qquad \left. +\left| \left( \pi _{hj}^k \right) ^{2}-\left( \pi _j^+\right) ^{2}\right| ^{q}\right] \left. \;\;\;-\sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{gj}^k \right) ^{2}-\left( u_j^+ \right) ^{2}\right| ^{q}+\left| \left( v_{gj}^k\right) ^{2}-\left( v_j^+ \right) ^{2}\right| ^{q}\right. \right. \\ \quad \left. \left. +\left| \left( \pi _{gj}^k \right) ^{2}-\left( \pi _j^+ \right) ^{2}\right| ^{q}\right] \right\} \log \left( v_{(g,h)}^k \right) \le \log v_{\tilde{\xi }} \;\;\; \\ \sum _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } \left\{ \sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{gj}^k \right) ^{2}-\left( u_j^- \right) ^{2}\right| ^{q}+\left| \left( v_{gj}^k \right) ^{2}-\left( v_j^- \right) ^{2}\right| ^{q}\right. \right. \\ \qquad \left. +\left| \left( \pi _{gj}^k \right) ^{2}-\left( \pi _j^- \right) ^{2}\right| ^{q}\right] -\sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{hj}^k \right) ^{2}-\left( u_j^- \right) ^{2}\right| ^{q}+\left| \left( v_{hj}^k \right) ^{2}-\left( v_j^-\right) ^{2}\right| ^{q}\right. \\ \left. \left. \;\;\;+\left| \left( \pi _{hj}^k \right) ^{2}-\left( \pi _j^- \right) ^{2}\right| ^{q}\right] \right\} \log \left( 1-\left( u_{(g,h)}^k\right) ^{2}\right) \le \log \left( 1-u_{\tilde{\eta }}^2\right) \;\;\; \\ \sum _{k=1}^l {w_k } \sum _{(g,h)\in {\tilde{\Omega }}_k^{(0,1)} } \left\{ \sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{gj}^k \right) ^{2}-\left( u_j^- \right) ^{2}\right| ^{q}+\left| \left( v_{gj}^k \right) ^{2}-\left( v_j^- \right) ^{2}\right| ^{q}\right. \right. \\ \quad \left. +\left| \left( \pi _{gj}^k \right) ^{2}-\left( \pi _j^- \right) ^{2}\right| ^{q}\right] -\sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{hj}^k \right) ^{2}-\left( u_j^- \right) ^{2}\right| ^{q}+\left| \left( v_{hj}^k \right) ^{2}-\left( v_j^- \right) ^{2}\right| ^{q}\right. \\ \left. \left. \;\;\;+\left| \left( \pi _{hj}^k \right) ^{2}-\left( \pi _j^-\right) ^{2}\right| ^{q}\right] \right\} \log \left( v_{(g,h)}^k\right) \le \log v_{\tilde{\eta }} \;\;\; \\ \sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{hj}^k \right) ^{2}-\left( u_j^+\right) ^{2}\right| ^{q}+\left| \left( v_{hj}^k \right) ^{2}-\left( v_j^+\right) ^{2}\right| ^{q}+\left| \left( \pi _{hj}^k \right) ^{2}-\left( \pi _j^+\right) ^{2}\right| ^{q}\right] \\ \;\;\;-\sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{gj}^k \right) ^{2}-\left( u_j^+ \right) ^{2}\right| ^{q}+\left| \left( v_{gj}^k\right) ^{2}-\left( v_j^+\right) ^{2}\right| ^{q}+\left| \left( \pi _{gj}^k \right) ^{2}-\left( \pi _j^+\right) ^{2}\right| ^{q}\right] \\ \quad +\,\lambda _{gh}^{k+} \ge 0\;\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ \sum _{j=1}^n \frac{\omega _j }{2}\left[ \left| \left( u_{gj}^k \right) ^{2}-\left( u_j^- \right) ^{2}\right| ^{q}+\left| \left( v_{gj}^k\right) ^{2}-\left( v_j^-\right) ^{2}\right| ^{q}+\left| \left( \pi _{gj}^k \right) ^{2}-\left( \pi _j^- \right) ^{2}\right| ^{q}\right] \\ \;\;\;-\sum _{j=1}^n {\frac{\omega _j }{2}\left[ \left| \left( u_{hj}^k \right) ^{2}-\left( u_j^- \right) ^{2}\right| ^{q}+\left| \left( v_{hj}^k \right) ^{2}-\left( v_j^- \right) ^{2}\right| ^{q}+\left| \left( \pi _{hj}^k \right) ^{2}-\left( \pi _j^- \right) ^{2}\right| ^{q}\right] } \\ \quad +\,\lambda _{hg}^{k-} \ge 0\;\;\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \\ {{\varvec{\omega }} }\in \hbox { }\varLambda ,\;\lambda _{gh}^{k+} \ge 0,\lambda _{hg}^{k-} \ge 0\;\left( (g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L\right) \;\; \\ \end{array}} \right. \; \\ \end{array} \end{aligned}$$

(30)

Solving Eq. (30), the comprehensive objective attribute weights ${{\varvec{\omega }} }$ can be determined. Then $S_i^{k+}$ and $S_i^{k-}$ can be calculated by Eqs. (16) and (17), respectively.

Remark 3

In Eq. (30), there are $(2\sum _{k=1}^l {|{\tilde{\Omega }}_k^{(0,1)} |} +n)$ variables need to be determined, including n weights $\omega _j \,(j\in N)$, $2\sum _{k=1}^l {|{\tilde{\Omega }}_k^{(0,1)} |}$ variables $\lambda _{gh}^{k+}$ and $\lambda _{hg}^{k-} \, \;((g,h)\in {\tilde{\Omega }}_k^{(0,1)} ,k\in L)$. There exist $4\sum _{k=1}^l {|{\tilde{\Omega }}_k^{(0,1)} |} +4$ inequalities at least. Generally, the larger the value of $\sum _{k=1}^l {|{\tilde{\Omega }}_k^{(0,1)} |}$ (i.e., the larger the number of pairwise comparisons of alternatives), the more precise and reliable the weight vector derived by Eq. (30). Moreover, since Eq. (30) is a linear programming model, it can be easily solved by the simplex method which needs very little time cost. Hence, the complexity of the developed method is very low.

4.4 Derive collective relative closeness degree by cross-entropy

From the view of DM $e_k$, the smaller the value of $S_i^{k+}$, the better alternative $A_i$. At the same time, the bigger the value of $S_i^{k-}$, the better alternative $A_i$. Hence, the relative closeness degree of alternative $A_i$ given by DM $e_k$ is defined by

$$\begin{aligned} R_i^k =S_i^{k-} /\left( S_i^{k-} +S_i^{k+}\right) . \end{aligned}$$

(31)

It is apparent that $0\le R_i^k \le 1$. Especially, if $S_i^{k-} =0$, then $R_i^k =0$; if $S_i^{k+} =0$, then $R_i^k =1$. Moreover, the bigger the value of $R_i^k$, the better alternative $A_i$ for DM $e_k$.

Denote the individual relative closeness degree vector and the normalized one of DM $e_k$ by ${\varvec{R}}^{k}=(R_1^k ,R_2^k ,\ldots ,R_m^k )^{\mathrm{T}}$ and ${{\varvec{R'}}}^{k}=({R'}_1^k ,{R'}_2^k ,\ldots ,{R'}_m^k )^{\mathrm{T}}$, where ${R'}_i^k =R_i^k /\sum _{i=1}^m {R_i^k }$. Furthermore, different DMs have diversified weights. The ranking order of alternatives should be generated according to the collective relative closeness degrees. Let ${\varvec{R}} = (R_1 ,R_2 ,\ldots ,R_m )^{\mathrm{T}}$ be collective relative closeness degree vector of alternatives, a programming model is built to derive the collective relative closeness degrees:

$$\begin{aligned} \begin{array}{l} \min \;Z=\sum _{k=1}^l {w_k D({\varvec{{R}}},{{\varvec{R}}'}^{k})} \\ \hbox {s.t.}\left\{ {\begin{array}{l} \sum _{i=1}^m {R_i =1} \\ 0\le R_i \le 1\hbox { }\;(i\in M) \\ \end{array}} \right. \\ \end{array} \end{aligned}$$

(32)

where ${\varvec{w}}=(w_1 ,w_2 ,\ldots ,w_l )^{\mathrm{T}}$ is DMs’ weight vector and $D({\varvec{R}},{{\varvec{R}}'}^{k})$ is the cross-entropy of ${\varvec{R}}$ to ${{\varvec{R}}'}^{k}$ calculated by Eq. (10). By Lagrange multiplier method, the collective relative closeness degree $R_i$ of alternative $A_i$ is derived as

$$\begin{aligned} R_i =\frac{\exp \left( \sum _{k=1}^l {w_k \log {R'}_i^k } \right) }{\sum _{i=1}^m {\exp \left( \sum _{k=1}^l {w_k \log {R'}_i^k } \right) } } (i\in M). \end{aligned}$$

(33)

Therefore, the ranking order of alternatives can be determined by the decreasing order of $R_i \,(i\in M)$.

4.5 A PF mathematical programming method to solve the PF MAGDM problems

An algorithm is summarized to solve the PF MAGDM problems with PF truth degrees below.

Step 1::

Identify attribute set F and incomplete attribute weight information structure $\varLambda$.

Step 2::

Elicit PF-ordered pairs for the subjective preference relations between alternatives by ${\tilde{\Omega }}_k$.

Step 3::

Elicit PF decision matrices ${\varvec{Y}}^{k} \, (k\in L)$, obtain normalized decision matrices ${{\varvec{Y}}'}^{k} \, (k\in L)$ by Eq. (8) and then get nonnegative score matrices $\hat{{{\varvec{s}}}}^{k} \,(k\in L)$ by Eqs. (3) and (9).

Step 4::

Derive collective subjective attribute weight vector ${{\varvec{\omega }}}^{s}$ based on cross-entropy via Eqs. (10)–(13).

Step 5::

Calculate DMs’ weight vector ${\varvec{w}}$ by Eq. (14).

Step 6::

Determine PFPIS ${\varvec{r}}^{{+}}$ and PFNIS ${\varvec{r}}^{-}$ according to Eq. (15).

Step 7::

Construct a biobjective PF mathematical programming model (i.e., Eq. (26)) and transform into the corresponding linear programming model (i.e., Eq. (30)).

Step 8::

Derive comprehensive attribute weight vector ${{\varvec{\omega }} }$ through solving Eq. (30).

Step 9::

Calculate individual relative closeness degrees $R_i^k$ of alternatives $A_i$ for DM $e_k \,(i\in M,k\in L)$ using Eq. (31).

Step 10::

Obtain collective relative closeness degrees $R_i (i\in M)$ by Eq. (33) and rank all alternatives according to the decreasing order of $R_i (i\in M)$.

The decision-making process is schematically depicted in Fig. 3.

Fig. 3

Decision-making process of a PF mathematical programming method

5 A GSS example and comparison analysis

In this section, a GSS example is implemented to illustrate the effectiveness of the proposed method in this paper. Further, the advantages of the proposed method are also confirmed by comparing with existing methods [28, 55].

5.1 A GSS example

Jiangxi copper corporation (Jiangxi copper for short), established in 1979, is one of enterprises of the Fortune Top500 in China. For the moment, it has a staff of 24 thousands. With the progress of industrialization, more and more pollution has caused heavy damage for environment and ecology. Green competitiveness has become an important part of the core competitiveness of enterprise, which could affect the sustainable development of enterprise. Under the background of green development, Jiangxi copper always insists on the principle of minimizing environmental costs to create the maximum value of mineral resources. To further expand production, Jiangxi copper plans to purchase a smelting equipment from a green supplier. After a preliminary screening, four green suppliers $A=\{A_1 ,A_2 ,A_3 ,A_4 \}$ are selected as the possible alternatives. To further rank these alternatives, a GSS temporary committee consisting of three experts (or DMs) $E=\{e_1 ,e_2 ,e_3 \}$ is constituted. Three DMs are from materials and equipment department, quality supervision department and engineering department, respectively. These alternatives are evaluated on the basis of five attributes, including resource recovery and utilization $f_1$, green identity $f_2$, environmental impact degree $f_3$, energy consumption $f_4$ and the use of environmental protection funds $f_5$. Among them, $f_1$, $f_2$ and $f_3$ are benefit attributes, whereas $f_4$ and $f_5$ are cost attributes. After data acquisition and statistical treatment, the ratings of alternatives on each attribute provided by DMs are represented by PFNs. The corresponding individual PF decision matrices are given in Table 1.

Table 1 Individual PF decision matrices

According to knowledge and experience, three DMs provide the PF-ordered pairs for the subjective preference relations between alternatives by ${\tilde{\Omega }}_1 =\{{<}(3,2),\tilde{a}_1 (3,2){>},\;{<}(4,2),\tilde{a}_1 (4,2)>\;\}$, ${\tilde{\Omega }}_2 =\{{<}(4,1),\tilde{a}_2 (4,1){>},\;{<}(4,2),\tilde{a}_2 (4,2){>}\;\}$, ${\tilde{\Omega }}_3 =\{{<}(2,1),\tilde{a}_3 (2,1){>},\;{<}(3,4),\tilde{a}_3 (3,4){>}\;\}$, where the corresponding PF truth degrees are $\tilde{a}_1 (3,2)=(0.8,0.2)$, $\tilde{a}_1 (4,2)=(0.7,0.1)$, $\tilde{a}_2 (4,1)=(0.8,0.4)$, $\tilde{a}_2 (4,2)=(0.9,0.3)$, $\tilde{a}_3 (2,1)=(0.8,0.5)$, $\tilde{a}_3 (3,4)=(0.6,0.2)$, respectively.

The incomplete attribute weight information is provided by DMs as follows:

$$\begin{aligned} \varLambda= & {} \{\omega |\omega \in \varLambda _0 ,\omega _2 \ge 2\omega _3 ,\;0.1\le \omega _5 -\omega _1 \le 0.3,\;\omega _2 -\omega _3 \ge \omega _5 \\&-\,\omega _1 ,\;\omega _3 \ge \omega _4 ,\;0.1\le \omega _3 \le 0.15\}. \end{aligned}$$

Using Eq. (8), the normalized matrices ${{\varvec{Y}}'}^{k} \, (k=1,2,3)$ are obtained. Then nonnegative score matrices ${ \hat{{\varvec{s}}}}^{k} \,(k=1,2,3)$ are derived by Eqs. (3) and (9).

According to Eq. (15), the PFPIS ${\varvec{r}}^{{+}}$ and PFNIS ${\varvec{r}}^{-}$ are obtained:

$$\begin{aligned} {\varvec{r}}^{{ +}}= & {} ((0.8,0.2),(0.8,0.1),(0.8,0.1),(0.9,0.1),(0.8,0.2))^{\mathrm{T}},\\ {\varvec{r}}^{-}= & {} ((0.2,0.5),(0.3,0.7),(0.3,0.7),(0.2,0.6),(0.3,0.6))^{\mathrm{T}}. \end{aligned}$$

After calculating the individual and collective subjective attribute weight vectors via Eqs. (10)–(13), the DMs’ weights are derived as $w_1 =0.{313}0$, $w_2 =0.{3367}$, $w_3 =0.{3503}$.

Set $\tilde{\xi }=(0.0001,0.9)$ and $\tilde{\eta }=(0.0001,0.9)$. For simplicity, let $q=2$ in Eq. (30) and then a linear programming model can be constructed (see (M-1) in Appendix). The comprehensive attribute weight vector ${{\varvec{\omega }} }$ is derived through solving the constructed model (M-1) as follows:

$$\begin{aligned} \omega _1 =0.1382, \quad \omega _2 =0.3921, \quad \omega _3 =0.1002, \quad \omega _4 =\hbox {0.0069}, \quad \omega _5 =0.3626. \end{aligned}$$

So, the square of the weighted Euclidean distances between ${\varvec{r}}_i^k$ and ${\varvec{r}}^{+}$ as well as ${\varvec{r}}^{-}$ are calculated as:

$$\begin{aligned} S_1^{1+}= & {} 0.{2186}, \quad S_2^{1+} =0.{1479}, \quad S_3^{1+} =0.{1479}, \quad S_4^{1+} =0.{0756}, \\ S_1^{2+}= & {} 0.{221}0, \quad S_2^{2+} =0.{15}0{6},\quad S_3^{2+} =0.0{997}, \quad S_4^{2+} =0.0{379}, \\ S_1^{3+}= & {} 0.{158}0, \quad S_2^{3+} =0.0{61}0, \quad S_3^{3+} =0.0{2}0{6}, \quad S_4^{3+}=0.0{2}0{6},\\ S_1^{1-}= & {} 0.0{389}, \quad S_2^{1-} =0.0{896}, \quad S_3^{1-} =0.{1638}, \quad S_4^{1-} =0.{115}0, \\ S_1^{2-}= & {} 0.0{862}, \quad S_2^{2-} =0.0{793},\quad S_3^{2-} =0.{1752}, \quad S_4^{2-} =0.{1372},\\ S_1^{3-}= & {} 0.0{311}, \quad S_2^{3-} =0.0{742}, \quad S_3^{3-} =0.{1727}, \quad S_4^{3-} =0.{1727}. \end{aligned}$$

Using Eq. (31), the individual relative closeness degrees $R_i^k \, (i=1,2,3,4;k=1,2,3)$ are calculated. Accordingly, the normalized individual relative closeness degrees are obtained in Table 2.

Table 2 Normalized individual relative closeness degrees

Utilizing Eq. (33), the collective relative closeness degrees $R_i \, (i=1,2,3,4)$ of alternatives are calculated as $R_1 {=0.1163}$, $R_2 {=0.1322}$, $R_3 {=0.3581}$, $R_4 {=0.3934}$. Based on the decreasing order of $R_i \, (i=1,2,3,4)$, the ranking order of alternatives is generated as $A_4 \succ A_3 \succ A_2 \succ A_1$.

5.2 Comparative analyses with PF TOPSIS and PF TODIM methods

In this subsection, the comparative analyses with PF TOPSIS method [55] and PF TODIM method [28] are performed concretely.

5.2.1 Comparison with the PF TOPSIS method

By defining a distance measure for PFNs, Zhang and Xu [55] proposed an extended TOPSIS to deal with the MADM problems. Since there is a single DM in method [55], the individual decision matrix and the group decision matrix (Table 3) aggregated by the individual decision matrices are respectively applied to method [55] to solve the above example. DMs’ weight vector is derived by the proposed method of this paper. Moreover, the attribute weight vector is given in advance. Four cases are taken into account, including ${{\varvec{\omega }} }_{1} =(0.2,0.2,0.2,0.2,0.2)^{\mathrm{T}}$, ${{\varvec{\omega }} }_2 =(0.1,0.2,0.15,0.3,0.25)^{\mathrm{T}}$, ${{\varvec{\omega }} }_3 =(0.1,0.2,0.15,0.25,0.3)^{\mathrm{T}}$ and ${{\varvec{\omega }} }=(0.1382,0.3921,0.1002,{0.0069},0.3626)^{\mathrm{T}}$. Using method [55], the decision results are derived for different cases and are listed in Table 4.

Table 3 Group decision matrix

Table 4 Ranking orders by PF TOPSIS method for different attribute weight vectors

It is easily found that when using the group decision matrix (Table  3), the ranking orders obtained by method [55] are identical to that obtained by the proposed method, which illustrates the proposed method is reliable. However, when applying individual decision matrices to method [55], the ranking orders obtained by method [55] for different attribute weights could be not the same as that obtained by the proposed method. The reasons for this result are concluded as follows:

• 1. Method [55] only focuses on the MADM problems with single DM and cannot be used to solve MAGDM problems. However, the proposed method of this paper can not only deal with MAGDM problems, but also solve MADM problems. Additionally, in this paper, by minimizing the total cross-entropy of the collective subjective attribute weight vector to the individual ones, an optimization program is constructed to determine the collective subjective attribute weight vector which is further applied to derive DMs’ weight vector. Such a method to obtain DMs’ weights is objective and convincing.

• 2. Method [55] provided the attribute weights a priori and ignored the determination of attribute weights. In this paper, by minimizing the PFPIS-based and PFNIS-based group inconsistency simultaneously, a biobjective PF mathematical program is constructed to derive the comprehensive attribute weights. Thus, the determination of the attribute weights is more objective and plausible.

5.2.2 Comparison with the PF TODIM method

Ren, Xu and Gou [28] extended the TODIM to handle MAGDM problems under PF environments. In method [28], the weights of attributes and DMs were given in advance. Thus, set attribute weight vector ${{\varvec{\omega }} }_3 =(0.1,0.2,0.15,0.25,0.3)^{\mathrm{T}}$, DMs’ weights vector ${{\varvec{w}}'}=(\frac{1}{3},\frac{1}{3},\frac{1}{3})^{\mathrm{T}}$ and the attenuation factor of the losses $\theta =2.5$. Using method [28] to solve the above example, the ranking order of alternatives is generated as $A_4 \succ A_3 \succ A_2 \succ A_1$, which is consistent with that obtained by the proposed method of this paper. This observation illustrates the validity of the proposed method of this paper.

Moreover, considering that the weights of attributes and DMs are given a priori in method [28], two special cases are further calculated for different weights of attributes and DMs. (1) When setting attribute weight vector ${{\varvec{\omega }} }_3 =(0.1,0.2,0.15,0.25,0.3)^{\mathrm{T}}$ and DMs’ weight vector ${{\varvec{w}}''}=(0.5,0.2,0.3)^{\mathrm{T}}$, the ranking order obtained by method [28] is $A_3 \succ A_4 \succ A_2 \succ A_1$. (2) When setting attribute weight vector ${{\varvec{\omega }} }_{1} =(0.2,0.2,0.2,0.2,0.2)^{\mathrm{T}}$ and DMs’ weight vector ${{\varvec{w}}''}=(0.5,0.2,0.3)^{\mathrm{T}}$, the ranking order obtained by method [28] is $A_4 \succ A_3 \succ A_2 \succ A_1$. Clearly, the results obtained by method [28] would vary with different weights of attributes and DMs. However, it is somewhat subjective to give attributes weight vector or DMs’ weight vector in advance. On the contrary, this paper determines the DMs’ weights and attribute weights objectively from the individual decision matrices.

Compared with method [28], the proposed method of this paper has several advantages:

• 1. Method [28] allocated DMs’ weights a priori, whereas this paper derives DMs’ weights objectively by a cross-entropy optimization model. The consensus between individual DMs and the decision group is taken into account, which could lead to convincing results that are supported by all group members despite their different opinions.

• 2. Similar to method [55], Ren et al. [28] assigned attribute weights in advance, which is not easy to avoid the subjective randomness. In this paper, four indices are defined to fully measure the consistency and inconsistency of decision group. A biobjective PF mathematical programming model is constructed and transformed into a linear programming model to obtain the comprehensive attribute weights. The method of deriving attribute weights is more comprehensive and accordance with the real-world situations.

5.2.3 Rank-correlation analysis based on Spearman’s rank-correlation coefficient

Based on the above analysis, the ranking orders of alternatives by different methods are not the same. It is apparent that the relations $A_2 \succ A_1$, $A_3 \succ A_2$, $A_3 \succ A_1$, $A_4 \succ A_2$ and $A_4 \succ A_1$ always hold by the proposed method and methods [28, 55]. However, the relation between alternatives $A_3$ and $A_4$ are not the same for different methods.

To further compare these ranking orders, Spearman’s rank-correlation test is utilized to determine whether there is statistical significance of the ranking difference among methods [28, 55] and the proposed method of this paper. In Spearman’s test, the similarity of the rankings can be evaluated by two separate test statistics, $r_{\mathrm{s}}$ and Z, which are calculated by the following formulas [23]:

$$\begin{aligned} r_{\mathrm{s}} =1-6\sum _{\kappa =1}^K {{(d^{\kappa })^{2}}/{K(K^{2}-1)}} , \quad Z=r_{\mathrm{s}} \sqrt{K-1}, \end{aligned}$$

where $d^{\kappa }=x^{\kappa }-y^{\kappa } \,(\kappa =1,2,\ldots ,K)$ denote the ranking difference between two sets of ranking $\{x^{\kappa }\}$ and $\{y^{\kappa }\}$. The rank-correlation coefficient $r_{\mathrm{s}}$ is a relative measure that varies from $+1$, implying a perfect positive relationship between the two sets of rankings, to $-1$, implying a perfect negative relationship between the two sets of rankings. The closer $r_{\mathrm{s}}$ is to $\pm 1$, the stronger the relationship between $\{x^{\kappa }\}$ and $\{y^{\kappa }\}$. In addition, the test statistic Z is compared with a pre-determined level of significance $\alpha$ value. Using a level of significance of $\alpha$ (usually $\alpha =0.05)$, the critical Z value is 1.645 (i.e.,$Z_{0.05} =1.645)$. If the statistic Z exceeds 1.645, it can be concluded that there is evidence of a positive relationship between $\{x^{\kappa }\}$ and $\{y^{\kappa }\}$. Otherwise, the two rankings can be accepted as dissimilar.

Table 5 Comparisons of alternative rankings of PF TOPSIS [55], PF TODIM [28] and the proposed method of this paper

When solving the above GSS example, there are five sets of preference rankings obtained by the proposed method and methods [28, 55], denoted by A, B, C, D, E, respectively. In details, PF TOPSIS (B) and PF TOPSIS (C) denote two ranking orders $A_4 \succ A_3 \succ A_2 \succ A_1$ and $A_3 \succ A_4 \succ A_2 \succ A_1$ generated by method [55] for different attribute weight vectors in Table 4. PF TODIM (D) and PF TODIM (E) denote two ranking orders $A_4 \succ A_3 \succ A_2 \succ A_1$ and $A_3 \succ A_4 \succ A_2 \succ A_1$ derived by method [28] for different attribute weight vectors and different DMs’ weight vectors in Sect. 5.2.2, respectively. To compare these ranking orders, the rank-correlation coefficients and the test statistics are calculated in Table 5.

From Table 5, the result analysis can be summarized as follows:

• 1. Comparing the result obtained by the proposed method of this paper with those obtained by PF TOPSIS [55], the test value $Z=1.7321>1.645$ indicates there is a positive relationship between the ranking (A) in this paper and the ranking (B). However, the ranking (A) in this paper is significantly dissimilar to the ranking (C) because the test value $Z=1.3856$ is smaller than 1.645.

• 2. When comparing the result obtained by the proposed method of this paper with those obtained by PF TODIM [28], the ranking correlation coefficients between A and D, A and E are 1 and 0.8 and the corresponding test values are 1.7321 and 1.3856, respectively. It can be affirmed that the ranking (A) is a positively correlated with the ranking (D), while it is dissimilar to ranking (E).

6 Conclusions

Uncertainty and fuzziness are universal in the actual decision making problems. PFS, as an extension of IFS, can depict such uncertainty and fuzziness effectively and flexibly. This paper proposes a PF mathematical programming method to deal with PF MAGDM with PF truth degrees and incomplete weight information. An example of GSS is demonstrated to verify the proposed method. The main novelties of this paper are outlined below.

• 1. The vector of DMs’ weights is determined objectively through minimizing the cross-entropy of the collective subjective attribute weight vector to the individual ones. To rank orders of alternatives, the collective relative closeness degrees of alternatives are explicitly derived through minimizing the cross-entropy of the collective relative closeness degrees to the individual ones. Using the cross-entropy optimization models twice can greatly improve the objectivity and reasonability of decision making results.

• 2. The PF group consistency and inconsistency indices are respectively defined on the basis of PFPIS and PFNIS. To obtain comprehensive attribute weights, a biobjective PF mathematical programming model is constructed through minimizing two inconsistency indices based on PFPIS and PFNIS simultaneously. This model takes the inconsistency indices based on PIS and NIS into consideration, while the LINMAP and its extensions only consider the consistency index or inconsistency index based on PIS. Thus, this model not only makes up the drawback that the LINMAP and its extensions overlook the NIS during the decision-making process, but also greatly generalizes and promotes the LINMAP method.

• 3. A linear programming method is dexterously developed to solve the constructed biobjective PF mathematical programming model. This method is very easy and simple since the linear programming model can be effectively solved by the Simplex method. Furthermore, the constructed biobjective PF mathematical programming model not only enriches the research contents of fuzzy mathematical programming theory, but also provides a new perspective and means for solving PF decision-making problems.

Nevertheless, the MAGDM problems concerned in this paper only involve single type of attribute values, i.e., PFSs, while MAGDM problems with multiple types of attribute values (i.e., heterogeneous MAGDM) are not considered. In the future, we will extend the proposed method to address heterogeneous MAGDM with PF truth degrees. Additionally, due to the diversification and complication of decision making, several different types of fuzzy truth degrees of alternative comparisons may be coexist in some real-world decision-making problems. How to deal with heterogeneous MAGDM considering several different types of fuzzy truth degrees is a valuable and interesting issue which deserves to be studied for future research.

Appendix