1 Introduction

Many optimization problems in scientific research and industrial applications are intrinsic multi-objective, in which multiple conflicting objectives need to be optimized simultaneously. Thus, it is impossible to achieve the optimality of all problems at the same time. The solution is a Pareto optimal solution set (PS), consisting of multiple compromised solutions among different objectives. Vectors in the objective space that correspond to the PS are Pareto front (PF) (Zhou et al. 2009).

Common approaches to solve multi-objective optimization problems are traditional mathematical analytical algorithms and evolutionary algorithms. Multi-objective evolutionary algorithms (MOEAs) provide a general framework for solving complex problems and have been widely used in dynamic optimization, machine learning, signal processing, adaptive control, and so on. Popular MOEAs are usually based on Pareto dominance, performance indicator, and decomposition (Zhang et al. 2016).

An effective MOEA should make full use of the regularity property of multi-objective optimization problems (Zhang et al. 2016), that is, under certain conditions, the PF and PS of a continuous m-objective optimization problem form an (m-1)-dimensional piecewise continuous manifold in the objective space and the decision space, respectively. Regularity model-based multi-objective estimation of distribution algorithms (Zhang et al. 2008) explicitly uses this property, for modeling the PS (Zhou et al. 2009) and for performing local search (Lara et al. 2010). Cellular multi-objective genetic algorithms (Durillo et al. 2008; Nebro et al. 2009; Zhang et al. 2015), MOEA based on decomposition (MOEAs/D) (Zhang et al. 2008; Li and Zhang 2009; Wang et al. 2016; Zhou and Zhang 2016), and hybrid NSGA-II with self-organizing map (Norouzi and Rakhshandehroo 2011) implicitly use this property.

However, in the evolutionary algorithm, there are uncertainties in the process of population search and the generation of offspring. Fuzzy set theory has inherent advantages in describing uncertain events and inaccurate information. Fuzzy inference system and hybrid methods with other intelligent computations are widely used in the field of evolutionary optimization, and have shown better results than traditional methods. For example, (Melin et al. 2013) used fuzzy logic to dynamically adjust the weight parameters C1 and C2 of the velocity formula in PSO. Olivas et al. (2017) proposed Ant Colony Optimization (ACO) with interval type-2 fuzzy system, which outperformed a rank-based ACO and ACO using type-1 fuzzy system. Santiago et al. (2019) proposed a novel MOEA with fuzzy logic-based adaptive selection of operators. It identifies which mutation operator is more (or less) promising among simulated binary crossover, uniform mutation, polynomial mutation, and DE, for the evolution of the population at each search stage. Also, it uses a fuzzy system to assign the correct application rate to these four operators. (Shen and Ge 2019 proposed a multi-objective particle swarm optimization algorithm based on fuzzy optimization, and the experiment has better performance in terms of solution quality, robustness, and computational complexity. HSMP (Zou et al. 2020) used the current and past continuous PS centers to automatically establish a T–S fuzzy nonlinear regression prediction model that can predict future PS centers to improve the prediction accuracy when environmental changes occur at the inflection point. Korashy et al. (2020)) proposed a method based on multi-objective gray wolf optimization and fuzzy logic decision-making for solving multi-robot coordination problems and a new objective function to minimize the recognition time between the main and backup relays. The feasibility and effectiveness of this method to solve the coordination problem of DOCRs were discussed on two different systems.

In addition, scholars merge fuzzy systems with machine learning and apply them to the field of multi-objective evolution to improve performance. For example, (Chen et al. 2018) proposed a hybrid population prediction strategy based on fuzzy inference and one-step prediction. A fuzzy inference model based on the maximum entropy principle is first extracted automatically from the previously found Pareto optimal solution set, and then the trajectory (position and/or direction) of the new Pareto optimal solution set is inferred. This strategy ensures that the algorithm can respond quickly and effectively when the environment changes. Changing PF, thereby, can be traced. Song et al. (2007) proposed a new fuzzy cognitive map (FCM) learning algorithm based on multi-objective particle swarm optimizations, and experimental results show that the method improves the efficiency and robustness of FCMs. In Yogesh and Ashish (2019), fuzzy logic was used to improve the adaptivity of particle swarm optimization (PSO) by controlling various parameters. Then, the improved PSO was used in K-harmonic means (KHM) for better clustering. Sankhwar et al. (2020) combined improved gray wolf optimization with fuzzy neural classifier for achieving more accurate financial crisis prediction than other methods.

The algorithms mentioned above cannot guarantee the diversity or convergence of the population well or cannot effectively solve functions with complex PF and/or PS shapes. In this paper, a gray wolf optimization-based self-organizing fuzzy multi-objective evolutionary algorithm (GWO-SFMEA) is proposed. Fuzzy system is used to dynamically adjust the weighted parameter F in differential evolution operator, and a new fuzzy differential evolution (FDE) operator is proposed. FDE is used to generate a new initial solution using neighborhood relationship among individuals, followed by polynomial mutation and boundary processing. The new neighborhood relationships of individuals are built by exploiting the peculiarity of the SOM (an unsupervised machine learning method), that is, invariance of the feature distribution, to map the structural information of the current population into Pareto sets. In addition, in this paper, gray wolf optimization is used to optimize the initial neuron weights of SOM.

Based on the above analysis, the main contributions of this paper are as follows:

  1. 1)

    Use GWO to optimize the weights of SOM, enabling individuals to search for their neighbors more efficiently in the global scope.

  2. 2)

    In order to produce high-quality new solutions, and improve the convergence and diversity of the algorithm. We use the fuzzy system to dynamically adjust the weighting parameter F in the process of offspring generation.

  3. 3)

    A gray wolf optimization-based self-organizing fuzzy multi-objective evolution algorithm is proposed to effectively solve multi-objective optimization problems.

Experiments on fifteen test problems with complex PF and/or PS shapes were conducted to verify the effectiveness of our proposed algorithm. Results show that its convergence and diversity are better than several state-of-the-art MOEAs.

The remainder of this paper is organized as follows: Sect. 2 reviews some preliminaries. Section 3 introduces the proposed GWO-SFMEA algorithm in detail. Section 4 presents the test instances and performance metrics. Section 5 describes the parameter settings and experimental results. Section 6 gives additional discussions about GWO-SFMEA. Finally, Sect. 7 draws conclusions.

2 Preliminaries

This paper considers the following form of multi-objective optimization problems (Marler and Arora 2004):

$$\begin{aligned} \min&\quad F(\varvec{x}) =(f_{1}(\varvec{x}),\ f_{2}(\varvec{x}),\ \ldots ,\ f_{m}(\varvec{x}))\\ s.t.&\quad \varvec{x}=(x_{1},\ x_{2},\ \ldots ,\ x_{n}) \in \varOmega \nonumber \end{aligned}$$
(1)

where \(\varOmega \) is the feasible region of the decision space, \(\varvec{x}=(x_{1},x_{2},\ldots ,x_{n}) \in \varOmega \) is the decision variable vector. n is the dimensionality of \(\varvec{x}\), and m is the number of objective functions. \(F:\varOmega \rightarrow {\mathbb {R}}^{m}\) consists of m objective functions \(\{f_{i}(\varvec{x})\}_{i=1}^m\) from the decision space to the objective space.

In this section, we give some knowledge about stochastic operator and gray wolf optimization algorithm.

2.1 Stochastic operator

Most MOEAs are optimized by a set of candidate solutions to the target problems. These candidate solutions are generated by random operators. The main difference between MOEAs lies in the properties and search capabilities of the random operators. DE (Price et al. 2005) is one of the most effective operators to solve both single- and multi-objective continuous optimization problems (Li and Zhang 2009; Zhang et al. 2016; Ming et al. 2017; Bošković and Brest 2018).

Storn (1996), Mendes and Mohais (2005) proposed a variety of differential strategies to implement the mutation operation. Table 1 lists five of them. In \(DE/\varvec{x}/\varvec{y}/\varvec{z}\), \(\varvec{x}\) is a variation vector, which can be a random (rand) vector in the population, or the best (best) vector in the current population; \(\varvec{y}\) is the number of differential vectors; \(\varvec{z}\) represents the mode of crossover, and \(\lambda \) the combination factor.

Table 1 Differential strategies
Full size table

DE/rand/1/bin and DE/best/2/bin are the most popular and successful differential strategies. This paper adopts the former to ensure the diversity of the population, and then integrates a fuzzy inference system into it.

2.2 Gray wolf optimization (GWO)

GWO (Mirjalili et al. 2014; Saremi et al. 2015) is a new population intelligence optimization algorithm with fewer parameters, which is simple, flexible, and scalable. It has been widely used in many fields such as machine learning, image processing, and so on. For example, (Elhariri et al. 2015, 2016) successfully applied a GWO-based support vector machine to image classification and EMG signal classification. Mustaffa et al. (2015) used GWO to optimize the least square support vector machine, and applied it to commodity time series data.

In GWO, gray wolves strictly obey a social dominance hierarchy as shown in Fig. 1, where the \(\alpha \) wolf is the leader of the population. The \(\beta \) wolf is a candidate for the \(\alpha \) wolf, helping the \(\alpha \) wolf make decisions or carry out other wolf group activities. The \(\delta \) wolf complies with \(\alpha \) wolf and \(\beta \) wolf, but dominates \(\omega \) wolf.

Fig. 1
figure 1

Hierarchy of gray wolves

Full size image

In addition to the social hierarchy of wolves, GWO also includes tracking, encircling, attacking prey, etc.

A. Encircling prey

Its mathematical model is:

$$\begin{aligned}&\overrightarrow{D}=|\overrightarrow{C}\cdot \overrightarrow{X_{p}(t)} - \overrightarrow{X}(t)| \end{aligned}$$
(2)
$$\begin{aligned}&\overrightarrow{X}(t+1)=\overrightarrow{X}_{p}(t)-\overrightarrow{A}\cdot \overrightarrow{D} \end{aligned}$$
(3)
$$\begin{aligned}&\overrightarrow{A}=2\overrightarrow{a}\cdot \overrightarrow{r}_{1}-\overrightarrow{a} \end{aligned}$$
(4)
$$\begin{aligned}&\overrightarrow{C}=2\cdot \overrightarrow{r}_{2} \end{aligned}$$
(5)

where t indicates the current iteration, \(\overrightarrow{A}\) and \(\overrightarrow{C}\) are coefficient vectors, \(\overrightarrow{X}_{p}\) is the position vector of the prey, and \(\overrightarrow{X}\) is the position of a gray wolf. In (4), components of \(\overrightarrow{a}\) are linearly decreased from 2 to 0 over the course of iterations, and \(r_{1}\) and \(r_{2}\) are random vectors in \([0,\ 1]\).

B. Hunting

Its mathematical model is:

$$\begin{aligned} \overrightarrow{D}_{\alpha }= & {} |\overrightarrow{C}_{1}\cdot \overrightarrow{X}_{\alpha }-\overrightarrow{X}|,\overrightarrow{D}_{\beta }\nonumber \\= & {} |\overrightarrow{C}_{2}\cdot \overrightarrow{X}_{\beta }-\overrightarrow{X}|,\overrightarrow{D}_{\delta }=|\overrightarrow{C}_{3}\cdot \overrightarrow{X}_{\delta }-\overrightarrow{X}| \end{aligned}$$
(6)
$$\begin{aligned} \overrightarrow{X}_{1}= & {} \overrightarrow{X}_{\alpha }-\overrightarrow{A}_{1}\cdot \overrightarrow{D}_{\alpha },\overrightarrow{X}_{2}\nonumber \\= & {} \overrightarrow{X}_{\beta }-\overrightarrow{A}_{2}\cdot \overrightarrow{D}_{\beta }, \overrightarrow{X}_{3}=\overrightarrow{X}_{\delta }-\overrightarrow{A}_{3}\cdot \overrightarrow{D}_{\delta } \end{aligned}$$
(7)
$$\begin{aligned} \overrightarrow{X}(t+1)= & {} \frac{\overrightarrow{X}_{1}+\overrightarrow{X}_{2}+\overrightarrow{X}_{3}}{3} \end{aligned}$$
(8)

where \(\overrightarrow{X}_{\alpha }\), \(\overrightarrow{X}_{\beta }\) and \(\overrightarrow{X}_{\delta }\) represent the position vectors of \(\alpha \), \(\beta \) and \(\delta \) wolves in the current population, respectively. \(\overrightarrow{D}_{\alpha }\), \(\overrightarrow{D}_{\beta }\) and \(\overrightarrow{D}_{\delta }\) indicate the distance between candidate wolves in the current population and \(\alpha \), \(\beta \), and \(\delta \) wolves, respectively.

C. Attacking prey (exploitation)

When the values of \(\overrightarrow{A}\) are in \([-1,\ 1]\), the next position of the \(\omega \) wolf which prepares for attacking the prey can be between its current position and the position of the prey. Otherwise, the wolves will spread out in search of prey for the sake of a global search and avoiding the local optimum.

3 GWO-based self-organizing fuzzy MOEA (GWO-SFMEA)

This section proposes a new gray wolf optimization-based self-organizing fuzzy multi-objective evolution algorithm. It first uses GWO to optimize the initial network weight vector of the SOM, and then SOM to extract the neighborhood relationship information of the best population individuals. In addition, it uses the fuzzy differential evolution (FDE) operator to generate a new solution.

3.1 GWO initialized SOM

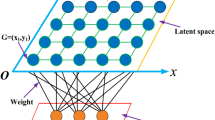
SOM network (Kohonen 1990; Teuvo 1998), proposed by Kohonen et al, is an unsupervised machine learning method. The SOM generally consists of two parts: an input layer and an output layer. The neurons between the two layers are fully connected by a network weight vector. It adaptively adjusts this weight vector by detecting the relationship between the input data and the characteristic of the input data. The common topological structure of SOM is one- or two-dimensional. The topological structure of a two-dimensional SOM is shown in Fig. 2 (Zhang et al. 2016).

Fig. 2
figure 2

An illustration of a two-dimensional SOM

Full size image

To improve the performance of MOEAs, we utilize GWO to optimize the initial weight vector. Its fitness function is:

$$\begin{aligned} g(p_{i})=\frac{100}{F(p_{i})}, \end{aligned}$$
(9)

where \(F(p_{i})=\sum _{n=1}^N \Vert x_{q}-c\Vert ^{2}\) is used to measure the sum of the Euclidean distance between the input vector and the closest weight vector, and \(c=arg \min \limits _{j}\{\Vert x_{q}^{T}-\omega _{j}\Vert ^{2}\}\). Algorithm 1 shows this optimization process.

Algorithm 1 GWO-SOM

1.Input: Population size of the gray wolves, boundary, number of neurons.

2. Set the maximum number of iterations about GWO, initialize gray wolf population (network weight).

3. Calculate the fitness by (9);

4. for \(g=1, 2, ..., maxIter\) do

5.   Boundary processing of the initial population.

6.   Choose \(\alpha \), \(\beta \), \(\delta \) wolves and record the positions.

7.   Update the positions of other gray wolves according to (2)-(8).

8. end

9. Output: Positions of the population, i.e., the initial weight vector of SOM.

3.2 Fuzzy inference system

This paper uses Mamdani-type fuzzy system (Sivanandam et al. 2007) with triangular membership functions and centroid defuzzification to dynamically adjust the value of the mutation parameter F in the process of generating offspring using the DE operator. This mechanism allows different F values to be applied during each iteration so that the operator can generate higher-quality offspring. The exploration and development capabilities of the algorithm, therefore, can be improved.

During the generation of offsprings, the value of the weighted parameter F is generated by a fuzzy system. The fuzzy system first monitors the search process through the number of iterations and utilization, and then updates the value of the weighted parameter F according to the values of these two variables. The initial utilization value is 1. The corresponding utilization is decreased by \(\frac{1}{\mathrm{controlsize}}\) every time the F value is generated. The value of the controlsize must be carefully tuned. It was set to 500 by trial and error.

In Figs. 3 and 4, we show the linguistic variables with the triangular membership functions for the number of iterations and utilization, respectively.

Fig. 3
figure 3

Generation membership function and the representation of linguistic terms

Full size image
Fig. 4
figure 4

Utilization membership function and the representation of linguistic terms

Full size image

After the defuzzification process, we obtain a crisp value F. The specific surface function of fuzzy inference system is shown in Fig. 5, and its membership function as shown in Fig. 6.

Fig. 5
figure 5

Surface function graph of fuzzy inference system

Full size image
Fig. 6
figure 6

The membership function and linguistic terms of output F

Full size image

To model the process with the fuzzy system, we consider 9 rules that help describe the existing relationship between the input and output, as shown in Table 2.

Table 2 Fuzzy inference rules
Full size table
Fig. 7
figure 7

The GWO-SFMEA framework

Full size image
Table 3 The GLT Test Instance Used in the Experiments
Full size table

3.3 GWO-SFMEA framework

Figure 7 shows the specific process of the GWO-SFMEA algorithm.

  1. (1)

    Randomly initialize the population and set parameters of the proposed algorithm;

  2. (2)

    Use Algorithm 1 to initialize the weight vectors of the SOM;

  3. (3)

    Start an iterative loop, use the training data set to update SOM network, i.e., the learning rate, weights, and neighborhood radius. And then extract neighborhood information between the population individuals;

  4. (4)

    Use the tournament selection mechanism to select the parent population from neighbor or current population;

  5. (5)

    Use the fuzzy system to dynamically adjust the weighting parameter F in each iteration.

  6. (6)

    Use the FDE operator and the polynomial mutation operator to generate a new solution;

  7. (7)

    Use the environmental selection mechanism in (Zhang et al. 2016) to update the population and training set. If the termination condition is met, output the optimal solution of the population; otherwise, repeat step (3).

4 Test instances and performance metrics

In this section, six MOPs with complex PF and PS shapes from (Gu et al. 2012; Zhang et al. 2016) are used as test functions. Table 3 introduces the feasible region of the set of test problems, the number of objective functions, and the dimensions of the decision variables.

Table 4 Parameters settings
Full size table

In order to evaluate the convergence and diversity of the approximate PF obtained by the proposed algorithm, this paper adopts two commonly used performance indicators, i.e., \(inverted \ generational \ distance (IGD)\) (Zhou et al. 2005; Zhang et al. 2008; Cai et al. 2020) and hypervolume(HV) (Zitzler and Thiele 1999; Zhang et al. 2016).

Let \(PF^{*}\) and PF be the evenly distributed Pareto optimal solution set in PF and the obtained non-dominated front, respectively. IGD is computed by:

$$\begin{aligned} IGD(PF^{*},PF)=\frac{\sum _{x^{*}\in PF^{*}}d(x^{*},PF)}{|PF^{*}|}, \end{aligned}$$

where \(d(x^{*},PF)\) is the minimal distance between \(x^{*}\) and any point in PF, and \(|PF^{*}|\) is the cardinality of \(PF^{*}\). When using IGD metrics, the true PF value must be known. In the experiments of this section, 1000 uniformly distributed points are selected from PF to form \(|PF^{*}|\).

The calculation of HV is:

$$\begin{aligned}&HV(PF,r^{*})\\&\quad =VOL\left( \bigcup _{x\in PF}[f_{1}(x),r^{*}_{1}]\times \cdots \times [f_{m}(x),r^{*}_{m}]\right) , \end{aligned}$$

where \(r^{*}=(r^{*}_{1},\ldots ,r^{*}_{m})\) is a reference point dominated by any Pareto optimal point in the objective space. \(VOL(\cdot )\) is the Lebesgue measure. In our experiments, we set \(r^{*}=(2,2)\) for GLT1 and GLT3, \(r^{*}=(2,11)\) for GLT2, \(r^{*}=(2,3)\) for GLT4, \(r^{*}=(2,2,2)\) for GLT5 and GLT6. Both the IGD and HV metrics measure the population convergence and diversity. The smaller (larger) the value of IGD(HV) is, the better the performance of an algorithm.

5 Experimental results

In this section, the proposed algorithm GWO-SFMEA compares with SMEA (Zhang et al. 2016), MOEA/D-DE (Li and Zhang 2009), SOM-NSGA-II (Norouzi and Rakhshandehroo 2011), SMPSO (Liang et al. 2019) and FAME (Santiago et al. 2019) in the GLT test instances with regard to IGD value and HV value.

5.1 Parameter setting

The proposed algorithm is implemented on Windows 10, 64-bit, MATLAB2018a. The detailed parameters are set as follows:

  • SOM structures: one-dimensional structure \(1\times 100\) for bi-objective MOPs, two-dimensional \(7\times 15\) for tri-objective MOPs; initial learning rate \(\tau _{0}=0.7\);

  • Size of neighborhood mating pools: \(H=5\);

  • Probability of mating restriction: \(\beta =0.9\);

  • Control parameters for FDE operator: \(CR=1\);

  • Control parameters for PM: \(p_{m}=\frac{1}{n}, \eta _{m}=20\).

The implementation and parameter setting of other algorithms were configured according to the suggestions of the original papers. Table 4 summarizes these parameters.

5.2 Analysis of results

A. Time comparison

Table 5 shows the average time of SMEA and the proposed algorithm on 30 executions of 6 multi-objective test problems. Their time complexity on the bi-objective problem is similar, our proposed algorithm is faster on the tri-objective problem.

Table 5 Average time of SMEA and GWO-SFMEA on the GLT test suite/s
Full size table

B. Comparison of IGD and HV value

The mean and standard deviation of the IGD and HV values of the 30 final populations generated by the six algorithms on the GLT test function are given in Table 6. The bold text indicates the best results (minimum IGD or maximum HV); “\(\S \),” “\(\backslash \)” and “\(\sim \)” in the table indicate that the performance of the algorithm GWO-SFMEA is better than, worse than, and similar to that of the comparison algorithm, respectively. Generally, the performance of GWO-SFMEA was significantly better than other algorithms on all GLT issues.

Table 6 Statistical result (Mean Std [Rank]) of the six algorithms on the GLT test suite of the IGD and HV metrics
Full size table

In terms of IGD, the value achieved by the proposed algorithm was lower than the other five algorithms in both bi-objective and tri-objective problems. The performance of SMPSO on GLT1 and GLT3 was inferior to all algorithms. MOEA/D-DE performed the worst on GLT2, GLT5, and GLT6. The value obtained by FAME on GLT4 was inferior to other algorithms.

Table 7 Average ranking of the algorithms
Full size table

With regard to HV, the proposed algorithm obtained better values than other algorithms on all GLT test instances except GLT1 and GLT3, where FAME and SMPSO ranked first, respectively. However, FAME and MOEA/D-DE performed the worst on bi-objective problems(GLT4 for FAME, GLT2 and GLT3 for MOEA/D-DE). SMPSO had the worst performance on tri-objective problem(GLT5 and GLT6).

Table 7 shows the Friedman ranks of the six algorithms for the two considered indicators, with 95% significance. Regardless of IGD or HV, the average ranking of the proposed algorithm was the first, followed by SMEA. MOEA/D-DE ranked last on all metric values, which means it has the worst performance.

C. Population distribution graph

In order to further compare SMEA, FAME, and GWO-SFMEA, Fig. 8 shows the distribution of the final population implemented independently by three algorithms for 30 times.

Fig. 8
figure 8

The final populations in the objective space obtained by SMEA, FAME, and GWO-SFMEA on GLT1–GLT6 over 30 runs

Full size image

For GLT1, the distribution of the final population achieved by FAME is better than SMEA and GWO-SFMEA, which is consistent with the optimal performance of HV of FAME in Table 6. Besides, the population distribution generated by GWO-SFMEA is better than SMEA. Both FAME and the proposed GWO-SFMEA apply fuzzy systems and outperform SMEA, indicating that the use of fuzzy systems in EAs can make the population distribution more uniform. The population distributions generated by SMEA, FAME, and GWO-SFMEA on GLT2 can cover the whole PFs well and do not show a big difference. SMEA is not much different from GWO-SFMEA on GLT3, but these two algorithms are better than FAME. The distribution of the population achieved by FAME, the right half part is not evenly distributed. Although the FAME guarantees the diversity of the population on GLT4, its distribution is uneven. By contrast, GWO-SFMEA guarantees uniformity. GWO-SFMEA performs better than the SEMA and FAME on tri-objective problems (GLT5 and GLT6).

By analyzing the above experimental results, we can found the SMPSO and MOEA/D-DE performed worst on both complicated PF or PS shapes, which might be because the particles have poor search ability or the set of the weight vectors. FAME works well on MOPs with three objectives, but it performs poorly on the GLT3 might be due to the random selection of the operator. SOM-NSGA-II and SMEA employ SOM to extract neighborhood information from the population, therefore, they can construct better quality parent population. Similarly, the algorithm proposed in this paper uses SOM to construct parent population, and uses the fuzzy system to dynamically adjust the parameters in the generation of its offspring to ensure that each iteration can produce high-quality solutions. Thus, GWO-SFMEA has a significant advantage in dealing with these instances.

6 Discussion

6.1 Test function with complex PF shapes

The WFG (Huband et al. 2005) test instances have a complex PF shape and a simple PS shape. Its characteristics are shown in Table 8.

Through preliminary experiments, the output surface of the fuzzy system with the mutation parameter F in the GWO-SFMEA algorithm is shown in Fig. 9, \(\tau _{0}=0.9\), \(CR=0.8\) and the values of other parameters are the same as in Sect. 5.1.

The five algorithms were run on these instances 30 times. The mean and standard deviation of the IGD and HV values of the final population are shown in Table 9. The reference point for the bi-objective WFG that is used to calculate the HV metric is \(r^{*}=(3,5)\).

As shown in Table 9, the proposed algorithm achieved 8 best values on 18 average metric values. In terms of IGD, the proposed algorithm obtained lower values than other algorithms on WFG2, WFG5, WFG7, and WFG8. FAME performed best on the rest of the problems. MOEA/D-DE and SOM-NSGA-II obtained worst values on WFG1, WFG2, WFG6 and WFG3, WFG5, WFG9, respectively.

With regard to HV , the proposed algorithm was better than the other algorithms on WFG2, WFG5, WFG7-8. It was inferior to FAME and SMEA on WFG1, WFG4, WFG6, WFG9 and WFG3, respectively. However, FAME and SMEA obtain worst value on WFG8 and WFG1, respectively. MOEA /D-DE and SOM-NSGA-II obtained the worst values on WFG5-6 and WFG3, WFG7, WFG9, respectively.

In conclusion, GWO-SFMEA achieved good performance on WFG2, WFG5, WFG7, and WFG8 and ranked second on other problems. It can be seen that the algorithm proposed in this paper is able to tackle MOPs with complex PF shape.

Table 10 shows the Friedman ranks of the five algorithms for the two considered indicators, with 95% significance. The proposed algorithm achieved higher rank than other algorithms.

6.2 Application of fuzzy system

In order to study whether the fuzzy system improves the convergence of the algorithm and the diversity of the population, the GWO-SFMEA was compared with the version without fuzzy inference system by running two algorithms independently on the GLT problems 30 times. The average IGD and HV values after the implementation of two algorithms are shown in Fig. 10. The larger the HV value is or the smaller the IGD value is, the better performance of the algorithm is.

Observe Fig. 10a and compare the values in the figure. We can find that after using the fuzzy system, the IGD values of GLT1–GLT5 have all decreased, only the IGD of GLT6 has increased, but the increased accuracy is not large. Observing Fig. 10b, after using the fuzzy system, the HV values of all problems have increased.

Table 8 The WFG test instance used in the experiments
Full size table
Fig. 9
figure 9

Output surface of fuzzy system with weighted parameter F

Full size image
Table 9 Statistical Result (Mean Std [Rank]) of The Five Algorithms on the GLT Test Suite of the IGD and HV Metrics
Full size table

In summary, the performance of the proposed algorithm on all instances was improved after adopting the fuzzy inference system, which shows that a well-organized fuzzy inference system in the MOEAs can improve the performance of the algorithm and can ensure the diversity of the population and the convergence speed of the population.

6.3 Network structure of SOM

In GWO-SFMEA, the structure of SOM for the bi-objective and tri-objective problems is set to be one-dimensional \((1\times 100)\) and two-dimensional \((7\times 15)\), respectively. In order to study the influence of the SOM structure on the performance metrics IGD and HV of the algorithm, the SOM structure was changed to be two-dimensional \((10\times 10)\) SOM in bi-objective problem and one-dimensional \((1\times 105)\) in tri-objective problem. The two kinds of SOM structures were both run on GLT1–GLT6 for 30 times. The IGD and HV values obtained from each instance are compared with the unmodified ones. The results are shown in Fig. 11.

It can be observed from Fig. 11a that for the bi-objective instances, the IGD value on GLT1-2 is smaller under the one-dimensional SOM structure. However, the IGD value of GLT3-4 is smaller under the two-dimensional structure. For the tri-objective problem, the IGD value is smaller under the two-dimensional structure.

It can be seen from (b) that the change of the SOM structure has little effect on the HV value on all GLT problems. Strictly speaking, the HV value on the bi-objective problem is slightly larger under the one-dimensional structure, and that on the tri-objective problem is a little larger under the two-dimensional structure.

In conclusion, the bi-objective problem has no obvious preference for one-dimensional or two-dimensional SOM, but the tri-objective instance prefers two-dimensional SOM structure.

Table 10 Average rankings of the algorithms
Full size table
Fig. 10
figure 10

The impact of fuzzy system on IGD and HV

Full size image
Fig. 11
figure 11

The Influence of SOM Structure on IGD and HV

Full size image

6.4 Comparison of GWO and other optimization algorithms

In this paper, GWO is used to optimize the initial weight of SOM. In order to further illustrate the advantages of using GWO, we compare GWO with the latest optimization algorithms—bald eagle algorithm(BES)(Alsattar et al. 2020) and slime mold algorithm(SMA)(Li et al. 2020). BES is a new meta-heuristic algorithm proposed by Alsattar in 2020. (Angayarkanni et al. 2021) combined BES algorithm with the gray wolf optimization algorithm to optimize the parameters of support vector regression in the prediction of traffic flow. The experiment shows its effective application in intelligent transportation. Xie et al. (2021) proposed a network public opinion prediction model based on the bald eagle algorithm optimized radial basis function neural network (BES-RBF). This model can better describe the development trend of different network public opinion information. SMA (Li et al. 2020) is another new meta-heuristic algorithm proposed by Li in 2020. Mostafa et al. (2020) used SMA to extract the global optimal values of solar photovoltaic cell parameters, and SMA can handle the nonlinearity and multi-modal properties of photovoltaic cell characteristics.

In this subsection, the above three algorithms are all used to optimize the initial weights of SOM and test on GLT1-6. In order to show the advantages and disadvantages of the three algorithms more directly, no fuzzy system is added in this experimental part. The mean and standard deviation of the IGD and HV values of the 30 final populations generated by the three algorithms on the GLT test function are given in Table 11. The gray background indicates the best results (minimum IGD or maximum HV); “\(\S \),” “\(\backslash \)” and “\(\sim \)” in the table indicate that the performance of the algorithm GWO-SOM is better than, worse than, and similar to that of the comparison algorithm, respectively.

Observing the above table, among the above 12 values, GWO, BES and SMA dominate by 7, 0, and 5, respectively. In terms of IGD, GWO is used to optimize the initial weight of SOM, and the IGD value obtained is the best on GLT1, 5, and 6. Using SMA to optimize the initial weight of SOM is the best on other problems. With regard to HV, the method used in this paper achieves the best value on GLT2, GLT4-6, and SMA-SOM achieves the best value on GLT1 and GLT3. On tri-objective problems, the average values obtained by the three algorithms are the same, but the standard deviation obtained by GWO-SOM is the smallest, indicating that the HV value obtained by GWO-SOM in running 30 times is stable. Therefore, this paper uses GWO to optimize the initial weight of SOM, and compared with BES and SMA, the algorithm has no redundant parameters, does not increase the time complexity of the algorithm, and is easy to operate.

7 Conclusions

In this paper, a new MOEA called gray wolf optimization-based self-organizing fuzzy multi-objective evolution algorithm was proposed. In algorithms which combine SOM with MOEAs, the initial weight of self-organizing map is generated randomly. However, the result depends heavily on the initial weight. Therefore, this paper optimized the initial weights of SOM through gray wolf optimization algorithm. At the same time, SOM can be used to map high-dimensional information to low-dimensional space while maintaining feature distribution invariance and building neighborhood relationships between individuals. In addition, the suboptimal solutions produced in the early optimization process in most MOEAs induce the algorithm to converge prematurely with great probability. To avoid this problem, this paper first utilized FDE operator to generate a new initial solution. Then the PM operator was used to mutate the new solution and boundary processing was performed. FDE dynamically adjusts the weighting parameter F in the difference operator by constructing a fuzzy inference system, which can ensure high-quality new solutions during the generation of offspring and effectively improve the convergence and diversity of the algorithm.

Table 11 Statistical result (Mean Std [Rank]) of the three algorithms on the GLT test suite of the IGD and HV metrics
Full size table

In order to verify the performance of the proposed algorithm, GWO-SFMEA and other state-of-the-art algorithms were tested on the GLT and WFG test functions with complex PF shapes and/or complex PS shapes, respectively. Through experiments, it can be found that the proposed algorithm is significantly better than other algorithms at the 95% confidence level. Through analysis of the sensitivity of GWO-SFMEA to the SOM structure, it can be seen that the SOM structure has no obvious preference for the bi-objective problem, but the tri-objective problem prefers the two-dimensional SOM structure. In addition, the combination of fuzzy systems with EAs can greatly improve the convergence and diversity of evolutionary algorithms.

The fuzzy rules designed in this paper are obtained through repeated trial and error and expert knowledge, which will affect the performance of the algorithm to a certain extent. Therefore, in future research, a fuzzy rule generator will be explored, which can generate fuzzy rules suitable for solving the problem according to the characteristics of the problem to be optimized. Moreover, we will look for different ways to improve the performance of the algorithm so that it can effectively deal with mixed and separable problems.