Keywords

1 Introduction

In last few decades, many researchers have worked on evolutionary computation (EC). Evolutionary computation is a generic population-based meta-heuristic approach which uses the mechanisms inspired by biological evolution such as selection, mutation and recombination. Candidate solutions of the optimization problem play the role of individuals in a population and the fitness function determines the quality of the solutions. Evolution of the population takes place by the repeated application of the above operators. Genetic algorithm (GA) is an evolutionary approach based on natural selection and reproduction.

Real world optimization problems are generally muti-objective in nature having two or more objectives that are conflicting to each other. The main objective of MOGA is to get a diverse set of optimal solutions and converge them to the Pareto front. Diverse solutions are to be distributed uniformly throughout the spectrum of the Pareto front.

In MOGA, initially the set of solutions moves towards the Pareto front quickly, but later the rate of convergence towards the Pareto front gradually decreases making the convergence slow. The reason is that the crossover and mutation in GA are random and they do not consider the neighbours of the current population which are topologically similar to them. It makes GA blind about the neighbours of the current solutions. It does not create any problem when the solutions are far away from the Pareto front, but makes the convergence slow when the set of solutions approach near the Pareto front. Some solutions, existing in the current population, which could lead to global optima may get lost in the successive generations. Conventional MOGA also suffers from the problem of genetic drift [1] due to its stochastic nature. The search process is affected by the genetic drift as the algorithm may get stuck into the local optima and hence the global optimal region may remain unexplored. It may lead to premature convergence of MOGA. To avoid these problems, we have used SOM network in the proposed model to make it more intelligent than conventional MOGA. The objective of the proposed algorithm is to use the knowledge incurred from the previous generations, which in turn improves the local search.

The rest of the paper is organised as follows. In Sect. 2, we have presented a review of some works existing in the literature which are similar to the proposed model. The proposed algorithm is presented and explained, in detail, in Sect. 3. The simulation results and comparisons are provided in Sect. 4. In Sect. 5, we have concluded our work and suggested some future directions of research.

2 Literature Review

The literature on multi-objective optimization problems is rich. In last two decades, many researchers have worked on MOGAs to achieve better convergence towards the optimal front. Some of the MOGAs are NSGA [2], NSGA-II [3], SPEA2 [4], ABYSS [5], MOEA/D [6], ASMiGA [7], PAES [8], etc.

We observe that a new field of hybrid computing, where knowledge obtained through the learning of neural network has been incorporated in MOGA. It can be viewed as an attempt to introduce local search in the exploration of MOGA. In 2005, Arroyo and Armetano introduced an algorithm IM-MOGLS [9]. They have used multi-objective genetic local search technique for intensifying the search in different local regions. Local search methods have been used in MOGA in many works [10, 11] in the literature in order to enhance their performance.

There are some works, where SOM has been used to improve the performance of MOGA. The main reason behind the selection of SOM is its topology and distribution preserving properties. SOM has also the ability to represent high dimensional data into a low dimensional space. In [12] Buche described SOM as a recombination operator for interpolating the parent population. It has increased the possible amount of information to be recombined whereas normal recombination operator uses only two solutions for recombination. An important issue in MOGA is to make a balance between exploration and exploitation. Amour and Rettinger [13] developed an algorithm, Intelligent Exploration for Genetic Algorithm. SOM has been used in it for mining the information from the evolution process which has been used to enhance the search process. Here SOM also helped to control the problem of genetic drift in [13].

Zhang et al. have introduced regularity model-based multiobjective estimation of distribution algorithm (RM-MEDA) [14]. This approach has used local principal component analysis for building the probability model. Local Principal component analysis, a model for feature extraction, has been hybridized in the model for extracting regularity patterns of the Pareto set from the previous search. Yang et al. developed a hybrid multiobjective estimation of distribution algorithm (HMEDA) [15] that uses local linear embedding, which is a manifold learning algorithm and is used in the optimization process. In order to show better convergence than RM-MEDA [14], Cao et al. devised an algorithm named as manifold-learning-based multiobjective evolutionary algorithm via self organizing maps (ML-MOEA/SOM) [16]. In this algorithm, SOM is used to capture and utilize the manifold structure of the Pareto set. In their algorithm, SOM performs reproduction of new solutions and provide it to MOGA in order to get better convergence. Their method has shown the performance similar to that of RM-MEDA [14].

In [1], the authors have devised an algorithm named SOM-Based Multi Objective Genetic Algoritm (SBMOGA). They have used VNS (Variable Neighbourhood Search) [17] as a local search strategy. SOM uses a multi-objective learning rule for its training based on Pareto Dominance. They have implemented a real-world problem and has found better results than that of NSGA-II. Another SOM-based hybrid algorithm is a self-organizing multi-objective evolutionary algorithm [18], developed by Hu Zhang et al. The authors in [18] used SOM to establish neighbourhood relationship between the current solutions. SOM based hybrid method have also been used in [19, 20].

Some of the research works have considered the neighbourhood properties of SOM in the learning algorithm whereas in some other works Pareto dominance property in the learning has been considered. As per our limited survey, we have noticed that no work in the literature has used both of the above mentioned concepts together in the learning of SOM. In the proposed algorithm, we have used both the neighbourhood property and Pareto dominance property for the learning of SOM.

In SBMOGA [1], the SOM neurons get updated when they are dominated by the solutions obtained from MOGA. But, it may not be necessary to update all the dominated neurons, as they all may not be neighbour of any particular solution. In our proposed algorithm, we use a neighbourhood function in SOM that helps to update those neurons that lie within a defined neighbourhood. It is explained later in detail in Sect. 3. In SBMOGA, the SOM neurons remain unaltered when they are not dominated by the solutions obtained from MOGA. Hence, it does not explore the neighbourhood of SOM neurons throughout the execution. As the SOM neurons also provide the optimal solutions, they must explore the search space throughout the execution. Hence, we have incorporated a neighbourhood function in the training of SOM network of the proposed model to continue exploring the local regions. Thus, the neighbourhood property of SOM along with the Pareto dominance property are being utilized to overcome the shortcomings of SBMOGA.

3 The Proposed Methodology

In the proposed algorithm, multi-objective genetic algorithm has been hybridized with self organizing map (SOM) network [21]. SOM has the capability of preserving the topology and distribution of the input dataset, which are the solutions obtained from MOGA. SOM basically performs a local search in the decision space of multi-objective problems. We have used NSGA-II [3] as MOGA in the proposed model.

Implementation starts with the execution of NSGA-II. NSGA-II initializes its population randomly and then creates its off-springs. The current population and the off-spring population are combined and undergo frontification using fast non-dominated sorting algorithm. NSGA-II uses crowding distance operator to maintain the diversity of the solutions.

Fig. 1.
figure 1

Architecture of SOM

Full size image

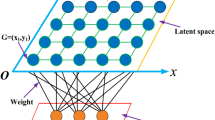
The solutions of the first front generated in each alternate generation of NSGA-II are used as input for the training of the SOM. We use one dimensional SOM output neurons in the proposed model. The number of SOM input neurons is same as the number of decision variables in NSGA-II, denoted by k. The number of SOM output neurons is denoted by M. Weight vectors of SOM, \(\mathbf w _j\), \(\left( j = 1,2,...,M\right) \) are initialized randomly. The decision variables corresponding to the solutions (in objective space) in the first front, generated by NSGA-II, is used to train the SOM. The number of solutions in the first front is denoted by f, which may vary in different generations of NSGA-II. The training of SOM is carried out for T iterations, where T equals to 50 * f in the proposed model. In each iteration, an input vector \(\left( \mathbf v _i\right) \) is chosen randomly from the training dataset of size f. The architecture of SOM is shown in Fig. 1. In the competition among the M output neurons of SOM, the winning neuron \(j^*\) is the Best Match Unit (BMU), where \(j^*\) is defined below in (1). Thus, BMU is an output neuron of SOM from which the Euclidean distance to the input vector is minimum among all the other SOM output neurons.

$$\begin{aligned} j^*=\{j|distance_j = min\{distance(\mathbf v _i(t),\mathbf w _j(t))\}\}, \end{aligned}$$
(1)

where \(j = 1,2,...M\).

After finding the BMU, its neighbourhood radius is computed according to an exponentially decreasing function as defined below in (2).

$$\begin{aligned} \sigma \left( t\right) = \sigma _0 \exp ^{- \frac{t}{\lambda }} \end{aligned}$$
(2)

Here, \(\sigma _0\) = initial value of the neighbourhood radius, \(\textit{t}\) is the current iteration of SOM, \(\lambda = n/{\log \sigma _0}\) and \( \textit{n}\) is the maximum number of generations of NSGA-II.

Then, we perform cooperation among the SOM output neurons. The weight vectors of the SOM neurons, present within the neighbourhood, are updated using (3).

$$\begin{aligned} \mathbf w _j\left( t+1\right) = \mathbf w _j\left( t\right) + L\left( t\right) * \sigma _{j^*}\left( t\right) * \left( \mathbf v _i\left( t\right) - \mathbf w _j\left( t\right) \right) , \end{aligned}$$
(3)

where L(t) represents the learning rate, which is a linearly decreasing function as defined below

$$\begin{aligned} L\left( t\right) = 1 - t/T,\ t = 1,2,...,T \end{aligned}$$

and the neighbourhood function \(\sigma _{j^*}\left( t\right) \) is defined as

$$\begin{aligned} \sigma _{j^*}\left( t\right) = \exp ^{-\frac{d^2}{2\sigma ^2\left( t\right) }}, \end{aligned}$$

where \(\textit{d}\) is the Euclidean distance from the BMU (\(j^*\)) to the current SOM output neuron.

After updating the SOM neurons, we check the dominance between the newly updated weight vector and the previous weight vector. The dominance is based on the concept of Pareto dominance. If \(\mathbf w _j\left( t+1\right) \) dominates \(\mathbf w _j\left( t\right) \), then the final weight vector for the next iteration is set to \(\mathbf w _j\left( t+1\right) \). Otherwise, it is unaltered. Thus if the solutions of the MOGA deviate from its path towards local optima, it will be restricted by SOM as it always checks Pareto dominance before final updation of weights. If in a generation the SOM neuron(s) reach the global optima, it will not change in the next generation(s). The proposed algorithm IMOGA/SOM is presented in Algorithm 1.

figure a

4 Results and Discussions

To test the proposed method, we have used nine standard bi-objective unconstrained test functions, taken from [3]. The summary of the test functions are presented in Table 1. For performance comparison, we have compared the proposed algorithm with two existing algorithms NSGA-II [3] and SBMOGA [1]. We have used jMetal 4.5.2 [22] and MATLAB 8.1 for its simulation.

Table 1. Summary of the test functions
Full size table

4.1 Performance Metrics

Three metrics, used to measure the performance of the algorithms, are defined below.

  1. (i)

    Convergence Metric (\(\varUpsilon \)) [3] measures how much the obtained set of solutions is close to the Pareto front. Smaller value is considered for better convergence.

  2. (ii)

    Diversity Metric (\(\varDelta \)) [1] is used to measure how much the solutions are diverse throughout the spectrum of the Pareto front. The range of the values of diversity metric is [0, 1]. More close is the value to 1, better is the diversity. Diversity metric, used here, is the revised version of that used in [1]. The diversity metric is defined below in (4).

    $$\begin{aligned} \varDelta = \frac{\sum _{Objectives} \sum _{i=1}^{D} count}{No.\ of\ Objectives * \textit{D}}, \end{aligned}$$
    (4)

    where the objective space is divided into D number of divisions for each objective and count will be 1 whenever any point from the obtained set of solutions belongs to \(\textit{i}^{th}\) division for the corresponding objectives.

  3. (iii)

    Inverted Generational Distance (IGD) [16] measures both the convergence and diversity of the obtained set of solutions. It is defined as follows.

    $$\begin{aligned} IGD(F,F^*) = \frac{\sum _{u \in F^*} distance(u,F)}{|F^*|}, \end{aligned}$$
    (5)

    where \(F^*\) represents the Pareto front, F represents the obtained set of solutions and u represents a point in the Pareto front.Lesser the value better is the IGD.

4.2 Parameter Settings

For NSGA-II, population size, maximum number of generations, crossover probability and mutation probability are respectively set to 100, 100, 0.9 and 1/k, where k is the number of decision variables of the test functions. For SOM network, we have considered the number of output neurons M as 100 and initialized the weight vectors randomly in the range of the corresponding decision space. Neighbourhood radius has been initialized to the radius of the decision space. We have used the same parameter values for all of the three algorithms NSGA-II, SBMOGA and proposed IMOGA/SOM. The SOM, used in the proposed algorithm, has been executed for alternate 50 generations, as mentioned earlier in Sect. 3.

Table 2. Simulation results
Full size table
Fig. 2.
figure 2

Poloni’s function (POL)

Full size image

4.3 Experimental Results

The values of the convergence metric (\(\varUpsilon \)), diversity metric (\(\varDelta \)) and the IGD metric for three algorithms: (i) NSGA-II, (ii) SBMOGA and (iii) The proposed IMOGA/SOM are presented in Table 2, where bold entries represent best results. Table 2 shows that for all 9 test functions: SCH, KUR, POL, FON, ZDT1, ZDT2, ZDT3, ZDT4 and ZDT6, the proposed algorithm is better than NSGA-II with respect to all the three metrics: \(\varUpsilon \), \(\varDelta \) and IGD. For the convergence and IGD metrics, results show that the proposed algorithm IMOGA/SOM performs better for 5 functions: KUR, POL, ZDT1, ZDT2 and ZDT4, however SBMOGA shows better results for 2 functions: SCH and ZDT3. The remaining functions FON and ZDT6 have shown competitive results for both the convergence and IGD metrics. SBMOGA has greater diversity than the proposed IMOGA/SOM except for the function ZDT2. The simulation graphs are shown in nine figures, Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10, for nine test functions, where the solutions are plotted in the objective space of the respective function. The figures confirm the convergence of the SOM neurons towards the Pareto front. Though the proposed algorithm IMOGA/SOM gives a diverse set of solutions, SBMOGA has shown better diversity. However, for test function ZDT2, IMOGA/SOM has shown greater diversity.

Fig. 3.
figure 3

Kursawe’s function (KUR)

Full size image
Fig. 4.
figure 4

Schaffer’s function (SCH)

Full size image
Fig. 5.
figure 5

ZDT1 function

Full size image
Fig. 6.
figure 6

ZDT2 function

Full size image
Fig. 7.
figure 7

ZDT3 function

Full size image
Fig. 8.
figure 8

Fonseca and fleming’s function

Full size image
Fig. 9.
figure 9

ZDT4 function

Full size image
Fig. 10.
figure 10

ZDT6 function

Full size image

5 Conclusion

In this study, we have proposed a hybrid model IMOGA/SOM based on SOM and MOGA in order to get better convergence for continuous bi-objective unconstrained optimization problems. SOM is used in the proposed model to perform a local search, which helps the solutions to reach close to the pareto front.

We have compared the results of our algorithm with two existing algorithms NSGA-II and SBMOGA. The proposed algorithm performs better than NSGA-II with respect to all of the three metrics and better than SBMOGA with respect to convergence and IGD metrics.

The proposed method may be improved further in two ways. Firstly, neighbourhood functions for SOM can be improved. Secondly, use of optimum number of SOM output neurons without keeping it fixed may give better results. The proposed algorithm can also be extended for problems having more than two objectives.