Robust decoding strategy of MIMO-STBC using one source Kurtosis based GPSO algorithm

Abstract

Most research papers have referred that the performance of bit error rate (BER) for a Multiple-Input Multipl-Output Space–Time Block Code (MIMO-STBC) decoder fundamentally relies on the number of pilot symbols. This paper proposes a new strategy for decoding a MIMO-STBC using blind source separation (BSS). First, the STBC decoder is modeled as a noisy linear mixing system, which is decomposed using the technique of real-imaginary (Re-Im). Then Kurtosis based BSS algorithm is applied to the decomposition model. The method of one source extraction is also used to reduce decoding time efficiently. Finally, a global particle swarm optimization method (GPSO) is combined with the one source extraction Kurtosis based BSS to obtain a high speed/low complexity MIMO-STBC decoder. The classical PSO algorithm in this paper is modified by innovating a new updating formula, which is the combination of the swarm behavior and BSS algorithm. Although the new decoder is more complicated as compared with the conventional one, it provides superior BER performance using a fewer number of pilot symbols. Computer simulation for QPSK STBC in a quasi-static flat fading MIMO channel was implemented using MATLAB2018. The new decoder algorithm was tested using only two receivers, worst case. The important point denoted through simulation is the BER performance of the proposed decoder was significantly got better when the length of frames gets longer. The proposed strategy was also used in decoding the $8\times 8$ MIMO-STBC system in an extreme noise environment. It was found the BER performance improved nine times as compared with the traditional decoder. Finally, the modified GPSO algorithm made the proposed decoder needs a very small number of iterations, even though the search space dimension is very high.

1 Introduction

A revolutionary technology of a Multiple-Input Multiple-Output (MIMO) system has been recently attacked in diverse ways due to its robust performance and possible gains in transmit diversity, which beats multi-path fading effects and other channel environments. A MIMO communication system provides considerable increase in link range and data throughput without consuming additional bandwidth (Wang et al. 2017). During signals propagation over wireless communication channel, the advantages of MIMO system could be extremely reduced due to the effects not only the small-scale fading but also the large-scale fading (Biguesh and Gershman 2006). The most current diversity technique applied to improve the performance of a MIMO system is Space–Time Block Code (STBC). It has been used in many wireless communication standards such as LTE, WiFi, and WiMAX (Djordjevic 2017). The usefulness behind the STBC system is to maximize spatial diversity as well as decoding probability using linear processing (Li et al. 2001). Recently, the performance of the MIMO‐STBC system has been widely studied with the consideration of different types of fading distribution such as Rayleigh, Weibull, Rician, or generalized-k fading (Maaref 2006; Tarokh et al. 1999; Xue et al. 2012).

For decoding purposes at the receiver side, a major challenge faced in a MIMO communication system is the estimation of instantaneous mixtures channel effects such as distortion delays, attenuations, and phase shifts. Those forms of effects occur to transmitted signals during propagation over wireless channel (Huang et al. 2019). The channel mixtures can be estimated either blindly or using pilot symbols. Typically, more pilot symbols result in better channel estimation, while low transmission efficiencies are obtained (Oyerinde and Mneney 2012). However, blind source separation (BSS) algorithms have been recently developed and employed to directly estimate originally transmitted signals from the statistical properties of received signals without knowing the channel state information (CSI) and without utilizing the pilot symbols. This is done based on exploiting statistical independence of transmitted signals and maximizing the non-Gaussianity of received signals (Hyvarinen 1999). On the other hand, the main snags in all BSS algorithms are order and sign ambiguities of estimated sources. There is no guaranty that estimated sources are of the same order and sign of original sources (Uddin et al. 2017).

In this paper, a new approach to decode a MIMO-STBC using Kurtosis-based BSS algorithm under a quasi-static flat fading channel is proposed. The new robust idea in this approach is employing the technique of Re-Im decomposition to simplify the statistical computation of the BSS algorithm. The proposed decoder doesn’t need for a separate estimator. Pilot symbols are used to initialize the BSS algorithm to remove the problem of sign ambiguities. This minimizes the number of pilot symbols in a data packet so that more information symbols can be transmitted. The decoding strategy is based on modeling a maximum ratio combiner (MRC) matrix as a mixture matrix for the BSS algorithm instead of a channel mixtures matrix. Also, this new model allows applying BSS even that the number of receive antennas of a MIMO channel is less than the number of transmit antennas. Furthermore, the distinctive structure of the MRC matrix offers the capability to extract all sources based on the solution and combination of extracting one source only. This strategy reduces the computational delay since the one-unit BSS algorithm is applied one time only. To accelerate the BSS algorithm, the GPSO algorithm used in which a new update formula is innovated by combining the swarm behavior and GAA algorithm. To verify the proposed decoding strategy, three MIMO-STBC systems are studied with ${G}_{2}$, ${G}_{4}$ and ${G}_{8}$ encoding matrices. For each case, the MRC equation is driven, then decoding complexity is described based on the Re-Im decomposition model.

Motivating by this introduction, the paper is structured as follows: Sect. 2 depicts a conventional decoder for the MIMO-STBC system. In Sect. 3, Kurtosis based blind source separation is presented with some mathematical expressions. The proposed mixing model for the MIMO-STBC system is addressed and presented in Sect. 4, while Sect. 5 illustrates the proposed decoding strategy for the MIMO-STBC using kurtosis based GPSO. In Sect. 6, simulation and analytical outcomes are discussed. Finally, Sect. 7 presents a summary of the paper.

2 Conventional decoder for MIMO-STBC system

The MIMO channel contains simply ${N}_{t}$ antennas at the transmitter side and ${N}_{r}$ antennas at the receiver side. For any ${N}_{t}$ MIMO channel, there is one or more specific STBC encoder with $k$-input symbols: ${S}_{1}, {S}_{2}, \dots , {S}_{k}$. The entries of the $p{\times N}_{t}$ encoding matrix, ${G}_{Nt}$, are a linear combination of the input modulated signals ${S}_{1}, {S}_{2}, \dots , {S}_{k}$ and their conjugates. The key feature of any STBC encoder is that transmitted sequences from any two antennas (rows of ${G}_{Nt}$ matrix) are orthogonal (Bhaskar and Kandpal 2017).

In this paper, three STBCs (${G}_{2}$, ${G}_{4}$ and ${G}_{8}$) are considered to verify the robustness of the proposed algorithm, in which the encoding matrices for those three codes can be expressed as (Andrei 2012; Tarokh et al. 1999; Uddin et al. 2017):

$${G}_{2}=\left(\begin{array}{cc} {S}_{1}& {S}_{2}\\ {-S}_{2}^{*}& {S}_{1}^{*}\end{array} \right) \begin{array}{cc} & \begin{array}{c}k=2\\ p=2\end{array}\end{array}$$

(1)

$${G}_{4}=\left(\begin{array}{c}\begin{array}{c}{ S}_{1}\\ {-S}_{2}\\ -{S}_{3}\end{array}\\ -{S}_{4}\\ {S}_{1}^{*}\\ {-S}_{2}^{*}\\ {-S}_{3}^{*}\\ {-S}_{4}^{*}\end{array} \begin{array}{c}\begin{array}{c}{ S}_{2}\\ {S}_{1}\\ {S}_{4}\end{array}\\ {-S}_{3}\\ { S}_{2}^{*}\\ {S}_{1}^{*}\\ {S}_{4}^{*}\\ {-S}_{3}^{*}\end{array} \begin{array}{c}\begin{array}{c}{ S}_{3}\\ {-S}_{4}\\ { S}_{1}\end{array}\\ { S}_{2}\\ { S}_{3}^{*}\\ {-S}_{4}^{*}\\ { S}_{1}^{*}\\ { S}_{2}^{*}\end{array} \begin{array}{c}\begin{array}{c}{ S}_{4}\\ { S}_{3}\\ {-S}_{2}\end{array}\\ {S}_{1}\\ { S}_{4}^{*}\\ {S}_{3}^{*}\\ {-S}_{2}^{*}\\ {S}_{1}^{*}\end{array}\right)\begin{array}{cc} & \begin{array}{c}k=4\\ p=8\end{array}\end{array}$$

(2)

and,

$${G}_{8}=\left(\begin{array}{c}\begin{array}{c} { S}_{1}\\ -{S}_{2}\\ {-S}_{3}\end{array}\\ {-S}_{4}\\ -{S}_{5}\\ {-S}_{6}\\ {-S}_{7}\\ {-S}_{8}\\ { S}_{1}^{* }\\ { - S}_{2}^{* }\\ { -S}_{3}^{* }\\ { -S}_{4}^{* }\\ { -S}_{5}^{* }\\ { -S}_{6}^{* }\\ { -S}_{7}^{* }\\ { -S}_{8}^{* }\end{array} \begin{array}{c}\begin{array}{c} { S}_{2}\\ { S}_{1}\\ -{S}_{4}\end{array}\\ {S}_{3}\\ {-S}_{6}\\ { S}_{5}\\ { S}_{8}\\ {-S}_{7}\\ { S}_{2}^{* }\\ { S}_{1}^{* }\\ { -S}_{4}^{* }\\ { S}_{3}^{* }\\ { -S}_{6}^{* }\\ { S}_{5}^{* }\\ { S}_{8}^{* }\\ { -S}_{7}^{* }\end{array} \begin{array}{c}\begin{array}{c} { S}_{3}\\ { S}_{4}\\ { S}_{1}\end{array}\\ {-S}_{2}\\ -{S}_{7}\\ -{S}_{8}\\ { S}_{5}\\ { S}_{6}\\ { S}_{3}^{* }\\ { S}_{4}^{* }\\ { S}_{1}^{* }\\ { -S}_{2}^{* }\\ { -S}_{7}^{* }\\ { -S}_{8}^{* }\\ { S}_{5}^{* }\\ { S}_{6}^{* }\end{array} \begin{array}{c}\begin{array}{c} { S}_{4}\\ {-S}_{3}\\ {S}_{2}\end{array}\\ { S}_{1}\\ -{S}_{8}\\ {S}_{7}\\ -{S}_{6}\\ {S}_{5}\\ { S}_{4}^{* }\\ { -S}_{3}^{* }\\ { S}_{2}^{* }\\ { S}_{1}^{* }\\ { -S}_{8}^{* }\\ { S}_{7}^{* }\\ { -S}_{6}^{* }\\ { S}_{5}^{* }\end{array} \begin{array}{c}\begin{array}{c} {S}_{5}\\ { S}_{6}\\ { S}_{7}\end{array}\\ { S}_{8}\\ { S}_{1}\\ {-S}_{2}\\ {-S}_{3}\\ {-S}_{4}\\ { S}_{5}^{* }\\ { S}_{6}^{* }\\ { S}_{7}^{* }\\ { S}_{8}^{* }\\ { S}_{1}^{* }\\ { -S}_{2}^{* }\\ { -S}_{3}^{* }\\ { -S}_{4}^{* }\end{array} \begin{array}{c}\begin{array}{c} { S}_{6}\\ {-S}_{5}\\ {S}_{8}\end{array}\\ {-S}_{7}\\ {S}_{2}\\ { S}_{1}\\ { S}_{4}\\ {-S}_{3}\\ { S}_{6}^{* }\\ {-S}_{5}^{* }\\ { S}_{8}^{* }\\ { -S}_{7}^{* }\\ { S}_{2}^{* }\\ { S}_{1}^{* }\\ { S}_{4}^{* }\\ { -S}_{3}^{* }\end{array} \begin{array}{c}\begin{array}{c} { S}_{7}\\ {-S}_{8}\\ {-S}_{5}\end{array}\\ { S}_{6}\\ { S}_{3}\\ -{S}_{4}\\ { S}_{1}\\ { S}_{2}\\ { S}_{7}^{* }\\ { -S}_{8}^{* }\\ { -S}_{5}^{* }\\ { S}_{6}^{* }\\ { S}_{3}^{* }\\ { -S}_{4}^{* }\\ { S}_{1}^{* }\\ { S}_{2}^{* }\end{array} \begin{array}{c}\begin{array}{c} { S}_{8}\\ { S}_{7}\\ {-S}_{6}\end{array}\\ {-S}_{5}\\ {S}_{4}\\ { S}_{3}\\ {-S}_{2}\\ {S}_{1}\\ { S}_{8}^{* }\\ { S}_{7}^{* }\\ { -S}_{6}^{* }\\ { -S}_{5}^{* }\\ { S}_{4}^{* }\\ { S}_{3}^{* }\\ { -S}_{2}^{* }\\ { S}_{1}^{* }\end{array} \right)\begin{array}{cc} & \begin{array}{c}k= 8\\ p=16\end{array}\end{array}$$

(3)

The mechanism of data transmission through the MIMO system can be modeled using matrix notation as shown in Fig. 1. At time $t$, the transmitted signals can be defined as ${{\varvec{X}}}^{{\varvec{t}}}={\left[\begin{array}{ccc}{x}_{1}^{t}& \dots & {x}_{{N}_{t}}^{t}\end{array}\right]}^{T}$, while the received signals can be defined as ${{\varvec{Y}}}^{{\varvec{t}}}={\left[\begin{array}{ccc}{y}_{1}^{t}& \dots & {y}_{{N}_{r}}^{t}\end{array}\right]}^{T}$, then:

$${{\varvec{Y}}}^{t}= {\varvec{H}}{{\varvec{X}}}^{t}+noise$$

(4)

where ${\varvec{H}}$ is ${N}_{r} \times {N}_{t}$ channel coefficients matrix. Under the quasi-static assumption, the channel response is varied randomly from block to block. However, it is constant within a transmission time, where this time is called a coherence time, ${T}_{coh}$ (Huang et al. 2019; Xue et al. 2012).

Fig. 1

Conventional MRC decoder for MIMO-STBC system

The decoding process shown in Fig. 1 can be achieved using two steps. The channel coefficients must be estimated first using a channel estimator. Then these values will be used to estimate the encoded signals ${S}_{1}, {S}_{2}, \dots , {S}_{k}$ using MRC.

2.1 Least square MIMO channel estimator

In any wireless communication system, known pilot symbols (${X}_{p}$) at a receiver side are used for synchronization, estimation, and equalization. The least square (LS) technique has been quite used to estimate channel coefficients when received pilot symbols (${Y}_{p}={\varvec{H}}{X}_{p}+noise$) are available. Using the solution of the LS technique, the estimated channel matrix can be defined in Eq. (5) (Biguesh and Gershman 2006; Maaref 2006):

$${{\varvec{H}}}_{LS}={Y}_{p}{X}_{p}^{ \dag }$$

(5)

where ${X}_{p}^{\dag}$ is pseudo inverse of ${X}_{P}$ which can be defined as:

$${X}_{p}^{\dag}={{X}_{p}^{H}\left({X}_{p}{X}_{p}^{H}\right)}^{-1}$$

(6)

However, increasing in number of training symbols (${X}_{p})$ improves the quality of channel estimation, but at the same time reduces the transmission efficiency (Uddin et al. 2017).

2.2 STBC decoder using MRC

To illustrate how the MRC decoder works, Alamouti STBC (${G}_{2}$) is used as an example. If the coefficient matrix of the $2\times {N}_{r}$ MIMO channel is denoted as ${\varvec{H}}=\left[\begin{array}{cc}{\hslash }_{1}& {\hslash }_{2}\end{array}\right]$, where ${\hslash }_{i}$ is the ${i}_{th}$ column of ${\varvec{H}}$. Then the received signals can be defined as (Andrei 2012):

$$ Y^{1} = \left[ {\begin{array}{*{20}c} {\hbar_{1} } & {\hbar_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{S}}_{1} } \\ {{\text{S}}_{2} } \\ \end{array} } \right] + noise,\;{\text{at}}\;t = 1 $$

(7)

If the channel coefficients are still constant (quasi-static channel), the received signals can be then expressed as (Andrei 2012):

$$ Y^{2} = \left[ {\begin{array}{*{20}c} {\hbar_{1} } & {\hbar_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - S_{2}^{*} } \\ { S_{1}^{*} } \\ \end{array} } \right] + noise,\;{\text{at}}\;t = 2 $$

(8)

Equation (8) can be rewritten using a simple mathematical modification as (Andrei 2012):

$${\left({Y}^{2}\right)}^{*}=\left[\begin{array}{cc}{\hslash }_{2}^{*}& {-\hslash }_{1}^{*}\end{array}\right]\left[\begin{array}{c}{S}_{1}\\ {S}_{2}\end{array}\right]+noise$$

(9)

The main idea of the MRC is combining Eqs. (7) and (9) together to obtain (Andrei 2012):

$$\left[\begin{array}{c}{Y}^{1}\\ {\left({Y}^{2}\right)}^{*}\end{array}\right]=\left[\begin{array}{c}\begin{array}{cc}{\hslash }_{1}& {\hslash }_{2}\end{array}\\ \begin{array}{cc}{\hslash }_{2}^{*}& -{\hslash }_{1}^{*}\end{array}\end{array}\right]\left[\begin{array}{c}{S}_{1}\\ {S}_{2}\end{array}\right]+noise$$

(10)

In the same manner, the MRC for ${G}_{4}$ and ${G}_{8}$ are driven and defined in Eqs. (11) and (12), respectively,

$$\left[\begin{array}{c}{Y}^{1}\\ {Y}^{2}\\ {Y}^{3}\\ {Y}^{4}\\ {\left({Y}^{5}\right)}^{*}\\ {\left({Y}^{6}\right)}^{*}\\ {\left({Y}^{7}\right)}^{*}\\ {\left({Y}^{8}\right)}^{*}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}{ \hslash }_{1}\\ { \hslash }_{2}\\ { \hslash }_{3}\end{array}\\ { \hslash }_{4}\\ { \hslash }_{1}^{*}\\ { \hslash }_{2}^{*}\\ { \hslash }_{3}^{*}\\ { \hslash }_{4}^{*}\end{array} \begin{array}{c}\begin{array}{c}{ \hslash }_{2}\\ { -\hslash }_{1}\\ { -\hslash }_{4}\end{array}\\ { \hslash }_{3}\\ { \hslash }_{2}^{*}\\ {-\hslash }_{1}^{*}\\ {-\hslash }_{4}^{*}\\ { \hslash }_{3}^{*}\end{array} \begin{array}{c}\begin{array}{c}{ \hslash }_{3}\\ { \hslash }_{4}\\ { -\hslash }_{1}\end{array}\\ { -\hslash }_{2}\\ { \hslash }_{3}^{*}\\ { \hslash }_{4}^{*}\\ {-\hslash }_{1}^{*}\\ {-\hslash }_{2}^{*}\end{array} \begin{array}{c}\begin{array}{c}{ \hslash }_{4}\\ { -\hslash }_{3}\\ { \hslash }_{2}\end{array}\\ { -\hslash }_{1}\\ { \hslash }_{4}^{*}\\ {-\hslash }_{3}^{*}\\ {\hslash }_{2}^{*}\\ {-\hslash }_{1}^{*}\end{array}\right]\left[\begin{array}{c}{S}_{1}\\ {S}_{2}\\ {S}_{3}\\ {S}_{4}\end{array}\right]+noise$$

(11)

and,

$$\left[\begin{array}{c}{Y}^{1}\\ {Y}^{2}\\ {Y}^{3}\\ {Y}^{4}\\ \begin{array}{c}{Y}^{5}\\ {Y}^{6}\\ {Y}^{7}\\ {Y}^{8}\\ {\left({Y}^{9}\right)}^{*}\\ {\left({Y}^{10}\right)}^{*}\\ {\left({Y}^{11}\right)}^{*}\\ {\left({Y}^{12}\right)}^{*}\end{array}\\ {\left({Y}^{13}\right)}^{*}\\ {\left({Y}^{14}\right)}^{*}\\ {\left({Y}^{15}\right)}^{*}\\ {\left({Y}^{16}\right)}^{*}\end{array}\right]=\left[ \begin{array}{c}\begin{array}{c}{\hslash }_{1}\\ {\hslash }_{2}\\ {\hslash }_{3}\end{array}\\ {\hslash }_{4}\\ {\hslash }_{5}\\ {\hslash }_{6}\\ {\hslash }_{7}\\ {\hslash }_{8}\\ {\hslash }_{1}^{* }\\ {\hslash }_{2}^{* }\\ {\hslash }_{3}^{* }\\ {\hslash }_{4}^{* }\\ {\hslash }_{5}^{* }\\ {\hslash }_{6}^{* }\\ {\hslash }_{7}^{* }\\ {\hslash }_{8}^{* }\end{array} \begin{array}{c}\begin{array}{c}{ \hslash }_{2}\\ {-\hslash }_{1}\\ { \hslash }_{4}\end{array}\\ {-\hslash }_{3}\\ { \hslash }_{6}\\ -{\hslash }_{5}\\ {-\hslash }_{8}\\ { \hslash }_{7}\\ {\hslash }_{2}^{* }\\ -{\hslash }_{1}^{* }\\ { \hslash }_{4}^{* }\\ -{\hslash }_{3}^{* }\\ {\hslash }_{6}^{* }\\ {-\hslash }_{5}^{* }\\ -{\hslash }_{8}^{* }\\ {\hslash }_{7}^{* }\end{array} \begin{array}{c}\begin{array}{c} {\hslash }_{3}\\ {-\hslash }_{4}\\ {-\hslash }_{1}\end{array}\\ {\hslash }_{2}\\ { \hslash }_{7}\\ {\hslash }_{8}\\ {-\hslash }_{5}\\ -{\hslash }_{6}\\ {\hslash }_{3}^{* }\\ {-\hslash }_{4}^{* }\\ -{\hslash }_{1}^{* }\\ { \hslash }_{2}^{* }\\ { \hslash }_{7}^{* }\\ { \hslash }_{8}^{* }\\ {-\hslash }_{5}^{* }\\ -{\hslash }_{6}^{* }\end{array} \begin{array}{c}\begin{array}{c} {\hslash }_{4}\\ { \hslash }_{3}\\ {-\hslash }_{2}\end{array}\\ -{\hslash }_{1}\\ { \hslash }_{8}\\ -{\hslash }_{7}\\ {\hslash }_{6}\\ {-\hslash }_{5}\\ {\hslash }_{4}^{* }\\ {\hslash }_{3}^{* }\\ -{\hslash }_{2}^{* }\\ -{\hslash }_{1}^{* }\\ {\hslash }_{8}^{* }\\ -{\hslash }_{7}^{* }\\ {\hslash }_{6}^{* }\\ {-\hslash }_{5}^{* }\end{array} \begin{array}{c}\begin{array}{c} {\hslash }_{5}\\ {-\hslash }_{6}\\ -{\hslash }_{7}\end{array}\\ -{\hslash }_{8}\\ -{\hslash }_{1}\\ { \hslash }_{2}\\ { \hslash }_{3}\\ { \hslash }_{4}\\ { \hslash }_{5}^{* }\\ {-\hslash }_{6}^{* }\\ {-\hslash }_{7}^{* }\\ {-\hslash }_{8}^{* }\\ {-\hslash }_{1}^{* }\\ {\hslash }_{2}^{* }\\ { \hslash }_{3}^{* }\\ { \hslash }_{4}^{* }\end{array} \begin{array}{c}\begin{array}{c}{ \hslash }_{6}\\ {\hslash }_{5}\\ {-\hslash }_{8}\end{array}\\ {\hslash }_{7}\\ -{\hslash }_{2}\\ {-\hslash }_{1}\\ -{\hslash }_{4}\\ {\hslash }_{3}\\ {\hslash }_{6}^{* }\\ {\hslash }_{5}^{* }\\ {-\hslash }_{8}^{* }\\ {\hslash }_{7}^{* }\\ -{\hslash }_{2}^{* }\\ -{\hslash }_{1}^{* }\\ -{\hslash }_{4}^{* }\\ {\hslash }_{3}^{* }\end{array} \begin{array}{c}\begin{array}{c}{ \hslash }_{7}\\ {\hslash }_{8}\\ {\hslash }_{5}\end{array}\\ {-\hslash }_{6}\\ -{\hslash }_{3}\\ {\hslash }_{4}\\ -{\hslash }_{1}\\ {-\hslash }_{2}\\ {\hslash }_{7}^{* }\\ {\hslash }_{8}^{* }\\ { \hslash }_{5}^{* }\\ -{\hslash }_{6}^{* }\\ {-\hslash }_{3}^{* }\\ { \hslash }_{4}^{* }\\ -{\hslash }_{1}^{* }\\ -{\hslash }_{2}^{* }\end{array} \begin{array}{c}\begin{array}{c} {\hslash }_{8}\\ {-\hslash }_{7}\\ { \hslash }_{6}\end{array}\\ {\hslash }_{5}\\ {-\hslash }_{4}\\ {-\hslash }_{3}\\ { \hslash }_{2}\\ {-\hslash }_{1}\\ { \hslash }_{8}^{* }\\ {-\hslash }_{7}^{* }\\ {\hslash }_{6}^{* }\\ { \hslash }_{5}^{* }\\ -{\hslash }_{4}^{* }\\ -{\hslash }_{3}^{* }\\ { \hslash }_{2}^{* }\\ -{\hslash }_{1}^{* }\end{array}\right]\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{S}_{1}\\ {S}_{2}\\ {S}_{3}\end{array}\\ {S}_{4}\end{array}\\ \begin{array}{c}\begin{array}{c}{S}_{5}\\ {S}_{6}\\ {S}_{7}\end{array}\\ {S}_{8}\end{array}\end{array}\right]+noise$$

(12)

In general, for any an orthogonal STBC with the $k$-input samples ${S}_{1}, {S}_{2}, \dots , {S}_{k}$, the MRC equation could be written as (Andrei 2012):

$${Y}_{MRC}={{\varvec{H}}}_{MRC}* \left\lceil \begin{gathered} {\text{S}}_{1} \hfill \\ {\text{S}}_{2} \hfill \\ \vdots \hfill \\ {\text{S}}_{{\text{k}}} \hfill \\ \end{gathered} \right\rceil +noise$$

(13)

It can be noticed from the Eqs. (10), (11) and (12) that for any an orthogonal STBC, the MRC matrix is also orthogonal, which means ${\left({{\varvec{H}}}_{MRC}\right)}^{H}{ {\varvec{H}}}_{MRC}=\Vert { {\varvec{H}}}_{MRC}\Vert {I}_{k}$. The term $I$ stands for the identity matrix, while ${\left(\bullet \right)}^{H}$ stands for the Hermitian operation. Taking advantage of the orthogonality, the decoding process is finally simplified (Andrei 2012; Bhaskar and Kandpal 2017).

$$\left\lceil \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} _{1} \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} _{2} \hfill \\ \vdots \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{S} _{k} \hfill \\ \end{gathered} \right\rceil\cong {\frac{1}{\Vert { {\varvec{H}}}_{MRC}\Vert }\left({{\varvec{H}}}_{MRC}\right)}^{H} {Y}_{MRC}$$

(14)

3 Kurtosis based blind source separation

Blind source separation (BSS) is an advanced signal processing technique, which aims to recover ${n}_{s}$ source signals ${\varvec{U}}$ from ${n}_{r}$ received mixture signals, ${\varvec{R}}={\varvec{M}}{\varvec{U}}$ (${\varvec{M}}$ is ${n}_{r}\times {n}_{s}$ mixing matrix), without any information about the source signals under three conditions. All sources must be mutually independent as well as non-Gaussian. Also, a received mixture ${n}_{r}$ must be greater than or equal to ${n}_{s}$. If ${\varvec{M}}$ is an orthogonal matrix, the one-unit version of BSS (extracting one source only) can be obtained using the following linear transformation (Hyva¨rinen and Oja 2000; Alrufaiaat and Althahab 2019; Luo et al. 2018):

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{u}}={\varvec{w}}{\varvec{R}}$$

(15)

where ${\varvec{w}}$ is a de-mixing vector. The essential notion to estimate the de-mixing vector relies mainly on maximizing a non-Gaussianity measurement of $\varphi ({\varvec{w}}{\varvec{R}})$. The term $\varphi (\bullet )$ is a nonlinear function depending on a criterion used for a non-Gaussianity measurement (Liu and Mandic 2006).

Kurtosis (or its absolute value) is widely used as a measurement of the non-Gaussianity in BSS problems due to its simplicity. Computationally, normalized kurtosis for real random variable u can be defined in Eq. (16). Theoretically, kurtosis is zero for Gaussian random variables (mixture signals ${\varvec{R}}$), but nonzero for non-Gaussian random variables (source signals), absolute value of kurtosis $>0$ (Cichocki and Amari 2002):

$$kurt\left({\varvec{u}}\right)=\frac{E\left\{{{\varvec{u}}}^{4}\right\}}{({E\left\{{{\varvec{u}}}^{2}\right\})}^{2}}-3$$

(16)

The solution of one-unit BSS specified in (15) can be transferred to an optimization problem that searches for an optimum ${n}_{r}$ dimensional vector ${{\varvec{w}}}_{{\varvec{o}}{\varvec{p}}{\varvec{t}}}$, which maximizes the absolute kurtosis value. In other words, the absolute kurtosis is used as a cost function to measure the quality of de-mixing vector ${\varvec{w}}$ (Hyva¨rinen and Oja 2000; Alrufaiaat and Althahab 2019):

$$if {\varvec{w}}= \left\{\begin{array}{ccc}{{\varvec{w}}}_{opt}& \to & \left|kurt\left({\varvec{w}}{\varvec{R}}\right)\right|\approx max\\ else& \to & \left|kurt\left({\varvec{w}}{\varvec{R}}\right)\right|< max\end{array}\right.$$

(17)

Gradient Ascent/Descent Algorithm (GAA) and an evolutionary search algorithm are the two ways to solve this optimization problem. The gradient is a first-order optimization algorithm that seeks maximum/minimum values for the function using the first-order differential of a cost function to recursively update values of ${\varvec{w}}$. First, the value of $\frac{\partial kurt({\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{u}}})}{\partial {\varvec{w}}}$ should be estimated, then ${\varvec{w}}$ can be recursively updated using the following update equation (Cichocki and Amari 2002; Liu and Mandic 2006):

$${{\varvec{w}}}_{{\varvec{i}}t+1}={{\varvec{w}}}_{{\varvec{i}}t}+\mu \boldsymbol{\varphi }\left({\varvec{u}}\right){{\varvec{R}}}^{{\varvec{T}}}$$

(18)

where $\mu$ is the learning rate (step size), and $\boldsymbol{\varphi }\left(\bullet \right)$ is the nonlinear function that can be defined as (Liu and Mandic 2006):

$$\varphi \left({\varvec{u}}\right)=\frac{{\varvec{u}}}{E\left\{{{\varvec{u}}}^{2}\right\}}-\frac{{{\varvec{u}}}^{3}}{E\left\{{{\varvec{u}}}^{4}\right\}}$$

(19)

For each iteration ($it$), the weighted vector must be normalized, i.e., ${{\varvec{w}}}_{it+1}=\frac{{{\varvec{w}}}_{it+1}}{\Vert {{\varvec{w}}}_{it+1}\Vert }$. Finally, the iteration process could be stopped when the vector ${{\varvec{w}}}_{it+1}$ converges to a specific value such that $\left|1-\left|{{\varvec{w}}}_{it}\times {\left({{\varvec{w}}}_{it+1}\right)}^{T}\right|\right|\le Threshold$ (Luo et al. 2018).

4 Proposed mixing model for MIMO-STBC system

To apply the BSS algorithm in decoding a MIMO-STBC system, the MRC decoder must be modeled as a linear mixing system. Then real-imaginary (Re-Im) decomposition is used to eliminate any complex number calculation (Alrufaiaat and Althahab 2019). Assume the ${i}_{th}$ complex source is ${{\varvec{S}}}_{{\varvec{i}}}={{\varvec{u}}}_{{\varvec{i}}}+{\varvec{j}}{{\varvec{u}}}_{{\varvec{k}}+{\varvec{i}}}$, where ${{\varvec{u}}}_{{\varvec{i}}}$ is the real part of ${{\varvec{S}}}_{{\varvec{i}}}$, while ${{\varvec{u}}}_{{\varvec{k}}+{\varvec{i}}}$ is the imaginary part. This decomposition produces ${n}_{s}$ real value sources arranged as:

$$ U = \left[ {\begin{array}{*{20}c} {{\varvec{u}}_{1} } \\ : \\ {{\varvec{u}}_{{\varvec{k}}} } \\ {{\varvec{u}}_{{{\varvec{k}} + 1}} } \\ : \\ {{\varvec{u}}_{{{\varvec{n}}_{{\varvec{s}}} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Re\left\{ {\begin{array}{*{20}c} {{\text{S}}_{1} } \\ {{\text{S}}_{2} } \\ : \\ {{\text{S}}_{{\text{k}}} } \\ \end{array} } \right\}} \\ {Im\left\{ {\begin{array}{*{20}c} {{\text{S}}_{1} } \\ {{\text{S}}_{2} } \\ : \\ {{\text{S}}_{{\text{k}}} } \\ \end{array} } \right\}} \\ \end{array} } \right], n_{s} = 2k $$

(20)

Similarly, ${Y}_{MRC}$ can be decomposed into ${n}_{r}$ real value mixture signals arranged as follows:

$$ R = \left[ {\begin{array}{*{20}c} {Re\left\{ {Y_{MRC} } \right\}} \\ {Im\left\{ {Y_{MRC} } \right\}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{r}}_{1} } \\ {{\varvec{r}}_{2} } \\ : \\ {{\varvec{r}}_{{{\varvec{n}}_{{\varvec{r}}} }} } \\ \end{array} } \right],n_{r} = 2pN_{r} $$

(21)

If there is a linear mixing system with ${n}_{s}$ sources input ${\varvec{U}}$ and ${n}_{r}$ output mixture signals ${\varvec{R}}$, then there is an ${n}_{r}\times {n}_{s}$ mixing matrix ${\varvec{M}}$ that can be represented as:

$${\varvec{M}}=\left[\begin{array}{cc}Re\left\{{H}_{MRC}\right\}& -Im\left\{{H}_{MRC}\right\}\\ Im\left\{{H}_{MRC}\right\}& Re\left\{{H}_{MRC}\right\}\end{array}\right]$$

(22)

Moreover, the overall real values of noisy mixing system can be finally written as:

$${\varvec{R}}={\varvec{M}}{\varvec{U}}+{\varvec{n}}{\varvec{o}}{\varvec{i}}{\varvec{s}}{\varvec{e}}$$

(23)

4.1 Statistical analysis of proposed mixing model

The proposed mixing model with Kurtosis-based BSS is shown in Fig. 2. The first point addressed in this model is that the mixing matrix ${\varvec{M}}$ is orthogonal. Therefore, one-unit kurtosis-based BSS can be applied efficiently (Hyva¨rinen and Oja 2000). Also, the key feature of the proposed model for, ${G}_{2}$, ${G}_{4}$, and ${G}_{8}$ STBC is that the ${n}_{r}$ is always greater than ${n}_{s}$, even though the number of receive antennas is ${N}_{r}\ge 2$. This point will be discussed and proved later in Sect. 6.2. Another important advantage is that the BSS can be implemented efficiently by applying Re-Im decomposition. This decomposition makes the probability distribution of all sources signal non-Gaussian.

Fig. 2

Proposed mixing model and kurtosis-based BSS

In this paper, the quadrature phase shift keying, QPSK, will be used. All sources are represented statistically as discrete random variables with two-level binomial distributions as shown in Fig. 3a. If it is assumed that ${P}_{U}\left(u=-1\right)={P}_{U}\left(u=+1\right)=0.5,$ then the expected statistics of ${\varvec{u}}$ are: mean value $\cong 0$, variance $\cong 0.5$, normalized kurtosis $\cong -2$, and Entropy $\cong 1$. All sources are assumed to be uncorrelated. According to the central limit theory, mixtures received signals ${\varvec{R}}$ can be represented as continues random variables with Gaussian distribution probability density function (Hyva¨rinen and Oja 2000). The expected statistics of ${\varvec{R}}$ are: mean value $\cong 0$, variance $\cong$ noise variance, Entropy of ${\varvec{R}}$ $>$ Entropy of ${\varvec{U}}$, and normalized kurtosis approaches to zero.

Fig. 3

Probability functions of a source signal ${\varvec{u}}$, and b extracted signal $\stackrel{\sim }{{\varvec{u}}}$

Since the de-mixing system separates the mixture signals without affecting the additive noise, the estimated signals can be approximated as $\stackrel{\sim }{{\varvec{u}}}=\alpha {\varvec{u}}+noise$. According to the additive property of two random variables (Cichocki and Amari 2002), the expected probability distribution function ($pdf$) for the estimated signal $\stackrel{\sim }{{\varvec{u}}}$ is

$${P}_{{\varvec{U}}}\left(\stackrel{\sim }{{\varvec{u}}}\right)={P}_{{\varvec{U}}}({\varvec{u}}) \otimes {P}_{noise}$$

(24)

where $\otimes$ is the convolution operation, and ${P}_{noise}$ is a $pdf$ of additive Gaussian noise with the zero mean. The expected $pdf$ of $\stackrel{\sim }{{\varvec{u}}}$ can be represented in Fig. 3b.

4.2 Initialization problem for BSS

Phase and ambiguity have been the most serious problems in BSS. In other words, it cannot specify which one of the sources (moreover its sign) is extracted. It is assumed that there are $2{n}_{s}$ optimum points that maximize/minimize the non-Gaussian measuring of $\varphi ({\varvec{w}}{\varvec{R}})$ (Alrufaiaat and Althahab 2019).

Depending on the initial values of the de-mixing vector ${{\varvec{w}}}_{int}$, the BSS algorithm updates the ${{\varvec{w}}}_{int}$ until the nearest optimum point reached. Therefore, the de-mixing vector ${{\varvec{w}}}_{int}$ should be initialized precisely to specify which source can be extracted. To initialize mixing matrix ${{\varvec{M}}}_{int}$, ${{\varvec{H}}}_{LS}$ can be properly used to obtain a prior knowledge for the MRC matrix, which refers as ${{\varvec{H}}}_{MRC}^{LS}$. Then ${{\varvec{M}}}_{int}$ can be constructed as in Eq. (25) through applying the technique of Re-Im decomposition to the ${{\varvec{H}}}_{MRC}^{LS}$. To extract ${{\varvec{u}}}_{1}$, the initial values of the de-mixing vector should set to be equal to the first column of ${{\varvec{M}}}_{int}$. In the same manner, to extract ${{\varvec{u}}}_{2}$, initial values of the de-mixing vector should set to be equal to the second column of ${{\varvec{M}}}_{int}$, and so on.

$${{\varvec{M}}}_{int}=\left[\begin{array}{cc}Re\left\{{{\varvec{H}}}_{MRC}^{LS}\right\}& -Im\left\{{{\varvec{H}}}_{MRC}^{LS}\right\}\\ Im\left\{{{\varvec{H}}}_{MRC}^{LS}\right\}& Re\left\{{{\varvec{H}}}_{MRC}^{LS}\right\}\end{array}\right]$$

(25)

4.3 Decoding of MIMO-STBC using one source extraction

In this paper, a new technique is used to extract sources ${{\varvec{u}}}_{2},{{\varvec{u}}}_{3},\dots ,{{\varvec{u}}}_{{n}_{s}}$ directly without using the BSS algorithm. This strategy is called one source extraction method. The idea of this strategy is that an optimum de-mixing vector or first source ${{\varvec{w}}}_{1}$ relates to the first column of ${\varvec{M}}$ that made ${{\varvec{w}}}_{2}$ relates to the second column of ${\varvec{M}}$ and so on. Form Eqs. (10), (11), (12), and (22), it can be denoted that if one column of ${\varvec{M}}$ is known, other columns could be evaluated intuitively. This means if the one-unit BSS is used to estimate, let say ${{\varvec{w}}}_{1}$, other de-mixing vectors (${{\varvec{w}}}_{2}, {{\varvec{w}}}_{3},\dots ,{{\varvec{w}}}_{{n}_{s}})$ could be evaluated directly using the structure of ${\varvec{M}}$. This strategy reduces the computational delay into $1/{n}_{s}$ times since the BSS algorithm is applied one time only instead ${n}_{s}$ times. From Eq. (15), the ${i}^{th}$ extracted source is ${ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{{\varvec{u}}}}_{i}={{\varvec{w}}}_{i}{\varvec{R}}$. Then the original complex modulated signal ${{\varvec{S}}}_{i}={{\varvec{u}}}_{i}+{\varvec{j}}{{\varvec{u}}}_{k+i}$ could be directly estimated using:

$${ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{S}}}_{i}=\left({{\varvec{w}}}_{i}+j{{\varvec{w}}}_{k+i}\right){\varvec{R}}\, i=1,2,\ldots,k$$

(26)

5 Kurtosis based GPSO MIMO-STBC decoder

Evolutionary search algorithms such as PSO, IWO, and BFO have been widely used to accelerate the BSS processing (Ali et al. 2018; Chen et al. 2011; Gao and Xie 2004; Li and Xiang-lin 2018). However, there is no specific algorithm that achieves the best solution for BSS problems using a minimum number of iterations, especially when the search space dimension gets increased (Yang 2010). Global particle swarm optimization (GPSO) utilized in this paper is an accelerated version of the classical PSO algorithm. This algorithm can be used for high dimension search problems with a very simple calculation criterion (Clerc and Kennedy 2002).

As mentioned previously in Sect. 3, the kurtosis-based BSS problem can be simplified to an optimization problem that searches for an optimum ${n}_{r}$ dimensional vector ${{\varvec{w}}}_{{\varvec{o}}{\varvec{p}}{\varvec{t}}}$, which maximizes the absolute kurtosis measuring. To adapt the search space of the GPSO algorithm, the position of the ${j}^{th}$ swarm in the ${n}_{r}$ dimensional space can be represented as:

$$ X_{w}^{j} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{w1}^{j} } & {x_{w2}^{j} } \\ \end{array} } & {\begin{array}{*{20}c} {..} & {x_{{wn_{r} }}^{j} } \\ \end{array} } \\ \end{array} } \right]\,j = 1,2, \ldots ,N_{swarm} $$

(27)

where ${N}_{swarm}$ is the number of swarms. The position of any swarm represents a candidate de-mixing vector. In the GPSO algorithm, the position of each swarm must be updated for each iteration using the following standard update formula (Yang 2010):

$${X}_{w}^{j}\left(new\right)={X}_{w}^{j}(old)+\Delta {X}^{j}$$

(28)

In this paper, a new update formula is innovated by combing the accelerated GPSO presented in (Gao and Xie 2004) with the Gradient Ascent/Descent Algorithm (GAA). The optimal weight vector ${{\varvec{w}}}_{{\varvec{o}}{\varvec{p}}{\varvec{t}}}$ in the GAA can be reached if the initial weight is updated by $\mu \boldsymbol{\varphi }\left({\varvec{u}}\right){{\varvec{R}}}^{{\varvec{T}}}$. However, the GPSO is motivated by the simulation of the social behavior (flock of birds) that cooperatives to seek an optimum position by updating their position ${X}_{w}^{j}$ toward the position of global swarm ${X}_{g}$. Combining those two concepts, a new update formula is proposed and given by:

$$\Delta {X}_{w}^{j}=\beta \left({X}_{g}-{X}_{w}^{j}\right)+\vartheta \left(\boldsymbol{\varphi }\left({X}_{w}^{j}{\varvec{R}}\right){{\varvec{R}}}^{{\varvec{T}}}\right)$$

(29)

where $\beta$ is an arbitrary number chosen between 0.1 and 0.5, while $\vartheta$, chosen to be ${0.6}^{it}$, is a random value that decreases monotonically with each iteration (Yang 2010), and ${X}_{g}$ is a global best position that is associated with the maximum absolute kurtosis, in which

$$\left|kurt\left({X}_{g}{\varvec{R}}\right)\right|\ge \left|kurt\left({X}_{w}^{j}{\varvec{R}}\right)\right|\, for\, all\, j$$

(30)

The proposed MIMO-STBC decoder is illustrated in Fig. 4, and the steps of how the decoder works can be summarized as:

• 1. Based on known pilot symbols ${X}_{p}$ and the corresponding received symbols ${Y}_{p}$, ${{\varvec{H}}}_{LS}$ is evaluated using Eq. (5).

• 2. Construct the MRC matrix ${{\varvec{H}}}_{MRC}^{LS}$ from ${{\varvec{H}}}_{LS}$, then apply Re-Im decomposition to obtain ${{\varvec{M}}}_{int}$ using Eq. (25).

• 3. To extract ${{\varvec{u}}}_{1}$, the initial value of the first swarm should be equal to the first column of ${{\varvec{M}}}_{int}$. The other (${N}_{swarm}-1$) swarms are randomly initialized around the first swarm, where the distance does not exceed $\mp 0.1$ from the initial value. This distance is fear enough so that the exploring space does not reach the neighbor maximum points. This step is shown in Fig. 5.

• 4. Construct ${Y}_{MRC}$ by combining the received signals ${Y}^{1},{Y}^{2},\dots ,{Y}^{p}$.

• 5. Apply Re-Im decomposition on ${Y}_{MRC}$ using Eq. (21) to obtain ${n}_{r}$ mixture signals R.

• 6. Evaluate the cost function $\left|kurt\left({X}_{w}^{j}{\varvec{R}}\right)\right|$ for each swarm using the initial position generated in step 3.

• 7. $it=1$ (iteration index).

• 8. Find the position of a global swarm ${X}_{g}$ using Eq. (30).

• 9. Evaluate ($\Delta {X}_{w}^{j}$) for each swarm using Eq. (29).

• 10. To ensure that $\Delta {X}^{j}$ does not exceed the exploring space illustrated in Fig. 5, the hard threshold function is used (Clerc and Kennedy 2002).

  $$\Delta {X}^{j}=sign\left(\Delta {X}^{j}\right)min\left(\begin{array}{cc}\left|\Delta {X}^{j}\right|& {\Delta X}_{max}\end{array}\right)$$

  (31)

  where ${\Delta X}_{max}$ is chosen to be 0.01.

• 11. Find the new position for each swarm using Eq. (28).

• 12. Normalized the new position of each swarm using ${X}_{w}^{j}=\frac{{X}_{w}^{j}}{\Vert {X}_{w}^{j}\Vert }$.

• 13. Evaluate the cost function $\left|kurt\left({X}_{w}^{j}R\right)\right|$ for each swarm according to the new position values.

• 14. The algorithm would be stopped (go to step 15) if

  • a. All swarms converge into a single position (variance of the cost function for all swarms $\le$ $threshold$).

  • b. Number of iterations $\ge$ max. iteration.

    else, $it=it+1$, go to step 8.

• 15. At the end of the iterations, it can be assumed that ${{\varvec{w}}}_{1}={\mathbf{w}}_{opt}={X}_{g}$. The other de-mixing vectors ${{\varvec{w}}}_{2} ,{{\varvec{w}}}_{3},\dots ,{{\varvec{w}}}_{{n}_{s}}$ can be estimated using the criterion of one source extraction. Finally, the transmitted signals ${S}_{1}, {S}_{2}, \dots , {S}_{k}$ are decoded using Eq. (26).

Fig. 4

Proposed MIMO-STBC decoder

Fig. 5

Swarm initialization for GPSO algorithm

6 Simulation and result

In this paper, a MATLAB2018b was utilized to carry out MIMO-STBC systems (${G}_{2}, {G}_{4},$ and ${G}_{8}$) whose encoding and MRC matrices driven in Sect. 2.2. A random generator of data produces digital bits of information, frame-by-frame, in which each frame has $2{N}_{s}$ bits of length. The QPSK modulator is used to modulate each frame and produce ${N}_{s}$ symbols. First, the pilot symbols ${N}_{p}$ that are known at the receiver side are generated, while the remaining ${N}_{s}-{N}_{p}$ will be employed as data symbols and encoded by STBC. Then the encoded symbols are transmitted by ${N}_{t}$ antennas through Rayleigh fading MIMO channel in which a complex AWGN is added to the transmitted signal. The number of receivers ${N}_{r}$ is assumed to be equal $2$, which is the worst case taken into consideration and focused in this paper.

The LS channel estimator uses pilot symbols at the receiver side to estimate the channel coefficients ${{\varvec{H}}}_{LS}$. The received symbols are decoded using the decoding algorithms described in previous sections and then fed to the QPSK demodulator. Finally, the received frame of bits, which is the output of the demodulator, is compared with the original one to obtain the performance of BER corresponding to a given SNR. The total number of frames utilized is ${10}^{4}$.

6.1 Influence of pilot symbols number

The BER performance of MRC decoder for ${G}_{2}, {G}_{4},$ and ${G}_{8}$ STBC is shown in Fig. 6 using the QPSK modulator with 1024 symbols/frame and different numbers of pilot symbols. To obtain an orthogonal pilot sequence, the number of pilot symbols should be an integer and multiples of $p$. As can be shown, an increasing number of pilot symbols provides significant coding for all MIMO-STBC systems.

Fig. 6

Influence of number of pilot symbols on BER performance of ${G}_{2}, {G}_{4}$ and ${G}_{8}$ STBC using conventional MRC and LS estimator

6.2 Performance of proposed decoder

It should be noted here that the quality of the decoder is not specified only on the BER performance. Computational complexity and latency must also be taken into consideration. The number of iterations needed for the GPSO to locate an optimum solution depends mainly on the number of swarms and threshold values. The threshold value is used to check the convergence of the swarms into an optimum position. It provides the quality of estimation. In this paper, the threshold value is set to be ${10}^{-5}$.

If the threshold value decreases, decoder latency reduces, but at the same time, the estimation quality gets worse. A maximum number of allowable iterations is supposed to be 100 even though the swarms don’t converge into a specific location. In the same manner, an increment in the number of swarms reduces the number of iterations, but at the same time, the complexity of the GPSO gets higher. In this paper, the number of swarms used is ${N}_{swarm}=25$.

In case of ${G}_{2}$ STBC: $k=2 , p=2 ;$ there are two complex sources ${S}_{1}$ and ${S}_{2}$ and four ${Y}_{MRC}$ signals. The dimension of ${{\varvec{H}}}_{MRC}$ is $4\times 2$. Based on the proposed mixing model, there are four sources ${u}_{1}, {u}_{2}, {u}_{3}, {u}_{4}$ $\left({n}_{s}=2k\right)$ and eight mixture signals ${r}_{1},{r}_{2},\dots ,{r}_{8}$, (${n}_{r}=2p{N}_{r}$). For each signal, there are ${N}_{s}/2$ samples. The condition of BSS is ${n}_{r}\ge {n}_{s}$ that is fully satisfied in which the size of mixture matrix $M$ is 8 × 4. Now, the GPSO searches for an optimum de-mixing vector in 8 dimensions space. Based on the one source extraction method, it needs to estimate ${{\varvec{w}}}_{1}$ only while other vectors ${{\varvec{w}}}_{2},{{\varvec{w}}}_{3},{{\varvec{w}}}_{4}$ can be estimated intuitively. This process reduces decoding time into$25\%$. Similarly, the decoder complexity for ${G}_{4}$ and ${G}_{8}$ STBC can be summarized in Table 1.

Table 1 Dimension space of signals using the proposed model

6.2.1 BER performance of ${{\varvec{G}}}_{2}$ STBC

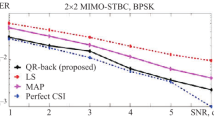
The BER and number of iterations for the proposed decoder in $2\times 2$ MIMO is shown in Fig. 7 using only four pilot symbols. It is not difficult to see excellent BER performance is obtained when the number of symbols/frame ${N}_{s}$ increases. However, there are two drawbacks associated with increasing ${N}_{s}$.

Fig. 7

BER and number of iterations for ${G}_{2}$ STBC in $2\times 2$ MIMO using: ${N}_{p}=4$, threshold = ${10}^{-5}$, ${N}_{swarm}=25$ and a ${N}_{s}=128$, b ${N}_{s}=1024$

The first drawback is that the dimensions of ${\varvec{u}}$ and ${\varvec{r}}$ increase, causing high computational complexity of the decoding process. The second one is that the time of each frame is determined by the so-called coherent time $\left(\left({N}_{s}{T}_{sym}\right)\le {T}_{coh}\right)$. For a fast fading channel, ${N}_{s}$ should be chosen as small as passable.

6.2.2 BER performance of ${{\varvec{G}}}_{4}$ STBC

The BER and number of iterations for the proposed decoder in $4\times 2$ MIMO is illustrated in Fig. 8 using eight pilot symbols. As can be seen and compared with the ${G}_{2}$, the ${G}_{4}$ STBC needs more symbols/frame to obtain excellent BER performance since the length of a mixture signal is ${N}_{s}/4$. On the other hand, the number of iterations required for this case is less than the ${G}_{2}$ case. Also, the relationship between the SNR and no. of iterations cannot be expected since the proposed decoder is based on the probability theory (ICA) and PSO algorithm. Therefore, it could be a linear, an exponential, etc.

Fig. 8

BER and number of iterations for ${G}_{4}$ STBC in $4\times 2$ MIMO using: ${N}_{p}=8$, threshold = ${10}^{-5}$, ${N}_{swarm}=25$ and a ${N}_{s}=128$, b ${N}_{s}=1024$

There is a significant improvement in BER performance when ${N}_{s}$ increases from 128 to 1024 as can be seen in both Figs. 7 and 8. In Fig. 7, coding gain between the proposed decoder and conventional MRC+LS decoder increases from 1 dB (Fig. 7a) to 1.5 dB (Fig. 7b). On the other hand, coding gain between the proposed decoder and conventional MRC+LS decoder increases from 1 dB (Fig. 8a) to 1.8 dB (Fig. 8b).

6.2.3 BER performance of ${{\varvec{G}}}_{8}$ STBC

The performance of BER and number of iterations for the proposed decoder in $8\times 2$ MIMO is depicted in Fig. 9 using 16 pilot symbols. As can be seen that efficient BER performance can be obtained once the number of symbols ${N}_{s}$ increases. In comparison with the ${G}_{2}$, and ${G}_{4}$, the ${G}_{8}$ STBC needs also more symbols/frame to obtain excellent BER performance since the length of a mixture signal is ${N}_{s}/8$. However, the number of iterations required for this case is less than those used in the ${G}_{2}$ and ${G}_{4}$.

Fig. 9

BER and number of iterations for ${G}_{8}$ STBC in $8\times 2$ MIMO using: ${N}_{p}=16$, threshold = ${10}^{-5}$, ${N}_{swarm}=25$ and a ${N}_{s}=502$, b ${N}_{s}=4096$

6.3 Performance of proposed decoder in $8\times 8$ MIMO system

The large-scale MIMO channel, which contains 64 sub-channels, is also considered in this paper due to its significant applications in special modern communication systems. Deep space communication, military communication, communicate between marine and submarine vessels are some application examples utilized massive MIMO channels. The performance of the proposed decoder is evaluated under extreme noise environment using ${G}_{8}$ STBC encoder with QPSK modulation. In this case, there are 256 mixture signals, and each one is ${N}_{s}/8$ samples. Meaning, the GPSO has to search in 256-dimension space to locate an optimum de-mixing vector that maximizes the kurtosis measuring.

The BER and number of iterations for the proposed decoder in $8\times 8$ MIMO is shown in Fig. 10 using ${N}_{p}=16$ and ${N}_{s}=8192$. As compared with the conventional MRC decoder, it can be noticed that the proposed decoder provides 2 dB coding gain at BER = ${10}^{-5}$.

Fig. 10

BER and number of iterations for ${G}_{8}$ STBC in $8\times 8$ MIMO using: ${N}_{p}=16$, threshold = ${10}^{-5}$, ${N}_{swarm}=25$ and ${N}_{s}=8192$

Table 2 illustrates the improvement in BER performance at SNR = $-1$, 0, 1, and 2 dB. In general, the BER performance of $8\times 8$ MIMO-STBC is improved about 8–10 times using the proposed decoder.

Table 2 Improvement in BER for $8\times 8$ MIMO-STBC using proposed decoder

Although the high dimensional search space of the GPSO algorithm (256), the proposed decoder requires a very small number of iterations. It is not difficult to see that the results shown in Table 2 are already taken from Fig. 10.

7 Conclusion

This paper proposes a new technique for direct decoding a MIMO-STBC system based on modeling MRC as a mixing system without the need for a separate estimator. Though the new proposed decoder is highly complicated than conventional MRC, it is found that the new decoder is superior in BER performance using a fewer number of pilot symbols. This decoding strategy is based on modeling a MRC matrix as a mixture matrix for BSS algorithms instead of the channel mixtures matrix. The new model allows applying BSS even that the number of receive antennas of the MIMO channel is less than the number of transmit antennas. The main important point carried out is extracting only one source to decode the overall system. This criterion reduces decoding time into $1/{n}_{s}$. The problem of sign and source ambiguities of BSS is solved using a suitable initialization of the de-mixing vector. In this paper, the classical PSO algorithm is modified by innovating a new update formula, which is the combination of swarm behavior and the GAA algorithm. It is also found that using GPSO with the one source extraction-based kurtosis BSS provides low complexity, high speed, and excellent BER performance. Consequently, the proposed decoder can be implemented with any MIMO-STBC system.