Abstract
The aim of this paper is the study of trapezoidal approximation operators, preserving more indicators of fuzzy numbers, relationships between them and their applications. Initial results lead to achieve three main trapezoidal approximation operators that one of them preserves the core, value and the ambiguity, and another one preserves the core and the expected interval, and third operator preserves the value, ambiguity and expected interval. The related concepts and the important properties of these operators and also, comparisons between them are brought, in details. Finally, a ranking method, an approximation operator preserving the most indicators of fuzzy numbers, and a trapezoidal approximation algorithm with its advantages and comparative examples are given as practical applications of the obtained results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
1.1 Importance and related works
In many science fields, the inaccurate and incomplete information are usually displayed in the form of fuzzy numbers or more generally fuzzy sets (see (Joshi and Kumar 2017, 2018; Vanegasa et al. 2016) as applications of fuzzy sets). In dealing with fuzzy numbers the defuzzification methods cause loss of the some information of fuzziness (see for instance (Bodjanova 2005; Dubois and Prade 1987; Heilpern 1992)). One of these methods is using a notion of an approximation interval (called interval approximation, see (Chanas 2001; Grzegorzewski and Mrowka 1998; Grzegorzewski 2002)) leads to the approximation problem in the fuzzy area is converted into one in the interval arithmetic area, which reduces the information loss. From this perspective, the approximation problem of fuzzy numbers as linear fuzzy number (for example the triangular or trapezoidal fuzzy numbers) is one of important subjects in fuzzy arithmetic. So far, many researchers have tried to find an appropriate triangular or trapezoidal approximation operator (Abbasbandy and Hajjiri 2010; Ban 2008; Ban et al. 2011; Ban 2009b, 2011; Ban et al. 2011; Yeh 2017, 2008b, 2009; Zeng and Li 2007). The major idea in most of the proposed methods is employing a meter defined on the set of fuzzy numbers and minimizing the distance between the initial fuzzy number and its approximation. Many studies are done on the approximation theory of fuzzy numbers based on the Euclidean meter (defined as (13)), that can be browsed as follows. The trapezoidal approximation (Grzegorzewski and Mrowka 2005, 2007) and some notes on it Allahviranloo and Firozja (2007); Yeh (2007), the approximations by interval, triangle and trapezoid by embedding fuzzy numbers into a Hilbert space (Yeh 2009), trapezoidal approximation preserving the expected interval (Ban 2008; Yeh 2008b) with algorithms and properties (Grzegorzewski 2008, 2008), triangular approximation using \(\alpha \)-weighted valuations (Abbasbandy et al. 2010) and remarks and corrections on it Ban (2011), trapezoidal approximation preserving the ambiguity and value (Ban et al. 2011), remarks and corrections to the trapezoidal and triangular approximation (Ban 2009b, 2011), trapezoidal approximation preserving the core and the expected value (Brandas 2011), the nearest parametric approximation of a fuzzy number (Nasibov and Peker 2008) and revisions on it (Ban 2009a), a notion of extended parametric fuzzy number and the metric properties of the nearest extended parametric fuzzy number of a fuzzy number (Ban and Coroianu 2011a), weighted trapezoidal and triangular approximation of fuzzy numbers which is based on assign the Euclidean meter by weighted functions (Ban et al. 2016; Yeh 2009; Zeng and Li 2007), and an improvement of work done in (Zeng and Li 2007), by using the Euclidean meter (Yeh 2008a).
1.2 Objective
Studies cited above in Subsection “Importance and related works” are focused on finding an approximation operator which preserves at most one or two indicators of fuzzy numbers, in general case. Accordingly, the choice of an approximation operator depends on what indicators of fuzzy numbers are important for the decision-maker. Obviously, the decision-maker tends to use an approximation operator which preserves many indicators of fuzzy numbers. Consequently, knowing approximation operators that are preserving most indicators of fuzzy numbers and finding the relationships between them and their applications is an important and necessary subject for the decision-maker which makes up the main objective in this paper.
1.3 Novelties
In this paper, we first point out importance and role of some characteristics related to fuzzy numbers such as the core, value, ambiguity, fuzziness and expected interval in the approximation theory of fuzzy numbers. The preliminary results lead to three important approximation operators. These operators are 1- the approximation operator preserving the core, value and ambiguity, 2- the approximation operator preserving the core and expected interval, and 3- the approximation operator preserving the value, ambiguity and expected interval. In sequel, the concepts related to these operators are introduced and the important properties of them such as scale invariance, identity, translation invariance, nearness criterion, linearity and continuity are investigated and also, some results are found for comparing them. Finally, some applications of the obtained results are proposed such as a ranking method of fuzzy numbers based on the core, value and ambiguity parameters and an approximation algorithm which provides a trapezoidal approximation operator, preserving most indicators of initial fuzzy number such that it has least ambiguity. Further, some advantages of proposed algorithm with respect to previous approximation algorithms and some comparative examples are presented.
2 Preliminaries
In this section, basic concepts of fuzzy set theory and some necessary results and notions are presented.
Definition 2.1
(Dubois and Prade 1987). A fuzzy number A is defined as an ordered pair of functions \(A=\big (A_{L}(\alpha ),A_{U}(\alpha )\big )\), \(\alpha \in [0,1]\), satisfying the following properties:
(i) \(A_{L}(\alpha )\) is a left continuous, bounded and non-decreasing function in (0, 1] and right continuous at 0,
(ii) \(A_{U}(\alpha )\) is a left continuous, bounded and non-increasing function in (0, 1] and right continuous at 0,
(iii) \(A_{L}(\alpha )\le A_{U}(\alpha )\), \(\alpha \in [0,1]\).
The set of all fuzzy numbers defined on real line \({\mathbb {R}}\) is represented by \(F({\mathbb {R}})\). The representation \([A]^{\alpha }=\big [A_{L}(\alpha ),A_{U}(\alpha )\big ]\), \(\alpha \in (0,1]\) is called the \(\alpha \)-cut form of fuzzy number A. Traditionally, \([A]^{\alpha }\) can be denoted as the set \(\big \{x\in {\mathbb {R}}|~A(x)\ge \alpha \big \}\), where A(x) is the degree of membership of x in fuzzy number A. The support of A is defined as the closure of \(\big \{x\in {\mathbb {R}}|~A(x)> 0\big \}\) and it is denoted by \(Supp(A)=[A]^{0}=\big [A_{L}(0),A_{U}(0)\big ]\). The core or \(1-\)cut of A is defined by \(Cor(A)=[A]^{1}=\big [A_{L}(1),A_{U}(1)\big ]\). Diameter or length of \(\alpha -\)cut of A is defined by \(diam [A]^{\alpha }=A_{U}(\alpha )-A_{L}(\alpha )\).
If \(A,B\in F({\mathbb {R}})\) and \(\lambda \in {\mathbb {R}}\), then
and
A fuzzy number A with the membership function below is said to be an LR type fuzzy number, (Bodjanova 2005; Brandas 2011),
where \(a,b,c,d\in {\mathbb {R}}\), \(\ell _{A}:[a,b]\rightarrow [0,1]\) is an increasing and continuous function, \(\ell _{A}(a)=0\), \(\ell _{A}(b)=1\), called the left side of the fuzzy number and \(r_{A}:[c,d]\rightarrow [0,1]\) is a decreasing and continuous function, \(r_{A}(c)=1\), \(r_{A}(d)=0\), called the right side of the fuzzy number. For fuzzy number A, it can be seen easily that \(A_{L}\) and \(A_{U}\) are inverse functions of \(\ell _{A}\) and \(r_{A}\), respectively. In fact, \(\ell _{A}^{-1}:[0,1]\rightarrow [a,b]\) is an increasing and continuous function with \(\ell _{A}^{-1}(0)=a\) and \(\ell _{A}^{-1}(1)=b\) and \(r_{A}^{-1}:[0,1]\rightarrow [c,d]\) is a decreasing and continuous function with \(r_{A}^{-1}(0)=d\) and \(r^{-1}_{A}(1)=c\). So, \([A]^{0}=[a,d]=[\ell _{A}^{-1}(0),r_{A}^{-1}(0)]\) and for \(0<\alpha \le 1\), we have
Let us here consider three important families from LR fuzzy numbers as the following forms:
where n is a positive real number. A fuzzy number A with the membership function A(x), given by one of forms (1), (2) or (3), will be represented by \(A=(a,b,c,d)_{n}\), where \(a\le b\le c\le d\). Let us denote the set of all fuzzy numbers in forms (1), (2) and (3) by,
respectively, and also, \(F_{n}^{T}({\mathbb {R}})=\Omega _{1}\cup \Omega _{2}\cup \Omega _{3}\). It is easy to see that if \(A=(a,b,c,d)_{n}\in F_{n}^{T}({\mathbb {R}})\), then it has the following parametric representation:
In this paper, for simplicity, it is represented by \(F^{T}({\mathbb {R}})\) instead \(F_{1}^{T}({\mathbb {R}})\), and it is said the set of all trapezoidal fuzzy numbers. If \(A\in F^{T}({\mathbb {R}})\), then it is written \(A=(a,b,c,d)\), that is in parametric form \(A=\big (a+(b-a)\alpha ,d-(d-c)\alpha \big )\). If \(A\in F^{T}({\mathbb {R}})\) satisfies one of the cases \(a<b=c<d\), \(a=b<c=d\) or \(a=b=c=d\), then it said that the fuzzy number A is triangular, a real interval or a real number, respectively. Furthermore, the element \(A=(a,b,c,d)_{n}\in F_{n}^{T}({\mathbb {R}})\) is called a quasi-symmetric fuzzy number if \(b-a=d-c\) and also, the quasi-symmetric fuzzy number A is called symmetric if it is a trapezoidal fuzzy number.
Definition 2.2
(Puri and Ralescu 1983). Let \(A,B\in F({\mathbb {R}})\). If there exists \(C\in F({\mathbb {R}})\) such that, \(A=B+C\) then C is called the H-difference of A, B and it is denoted \(A\ominus B\).
The following lemma is useful for some results in the paper.
Lemma 2.3
Suppose that A and B are two trapezoidal fuzzy numbers such that \(Cor(A)=Cor(B)\). In this case, the H-difference \(A\ominus B\) exists if and only if \(Supp(B)\subseteq Supp(A)\).
Proof
Let \(A=(a_{1},a_{2},a_{3},a_{4})\) and \(B=(b_{1},b_{2},b_{3},b_{4})\) be two trapezoidal fuzzy numbers and suppose that the H-difference \(A\ominus B\) exists. So,
But, the hypothesis \(Cor(A)=Cor(B)\) means that \([a_{2},a_{3}]=[b_{2},b_{3}]\), which implies that \(a_{2}=b_{2}\) and \(a_{3}=b_{3}\). So that,
which implies \(a_{1}-b_{1}\le 0\) and \(a_{4}-b_{4}\ge 0\). Therefore \(a_{1}\le b_{1}\le b_{4}\le a_{4}\), that means that \(Supp(B)\subseteq Supp(A)\). Conversely, the condition \(Supp(B)\subseteq Supp(A)\) can be written as \([b_{1},b_{4}]\subseteq [a_{1},a_{4}]\). This provides the triangular fuzzy number \(C=(a_{1}-b_{1},0,0,a_{4}-b_{4})\). It is easy to see that
which means \(B+C=A\), because of \(Cor(A)=Cor(B)\). Thus, \(C=A\ominus B\). \(\square \)
Definition 2.4
(Grzegorzewski and Mrowka 2005). It is said that an approximation operator T fulfills the nearness criterion if for any fuzzy number A its output value T(A) is the nearest trapezoidal fuzzy number to A with respect to metric d, defined in the space of fuzzy numbers. In other words, for any \(A\in F({\mathbb {R}})\) we have
Definition 2.5
(Delgado et al. 1998a; Dubois and Prade 1987). The value, ambiguity and fuzziness of \(A\in F({\mathbb {R}})\) are defined as follows, respectively,
Remark 2.6
It is noteworthy that for each fuzzy number A we have \(Amb(A)\ge 0\) and \(Fuz(A)\ge 0\), because of \(diam [A]^{\alpha }=A_{U}(\alpha )-A_{L}(\alpha )\) is a non-negative and non-increasing function. In special case, for triangular fuzzy number \(A=(a,b,c)\), we easily obtain \(Amb(A)=\frac{c-a}{6}\) and \(Fuz(A)=\frac{c-a}{4}\), that results \(Amb(A)\le Fuz(A)\). This inequality does not hold for an arbitrary fuzzy number. For example, consider two trapezoidal fuzzy numbers \(A=(0,\frac{5}{3},2,3)\) and \(B=(0,1,2,3)\). It is easy to obtain that
while
Definition 2.7
(Delgado et al. 1998a, b). A ranking method with ordering \(\prec \) for two numbers \(A,B\in F({\mathbb {R}})\), based on three parameters value, ambiguity and fuzziness is defined as the following Algorithm:
1. If \(Val(A)=Val(B)\), then go to the next step. Otherwise \(A\prec B\), if \(Val(A)<Val(B)\).
2. If \(Amb(A)=Amb(B)\), then go to the next step. Otherwise \(A\prec B\), if \(Amb(A)<Amb(B)\).
3. If \(Fuz(A)=Fuz(B)\), then it is said that A is equivalent to B. Otherwise \(A\prec B\), if \(Fuz(A)<Fuz(B)\).
Definition 2.8
(Chanas 2001; Dubois and Prade 1987; Heilpern 1992; Wang et al. 2006). The expected interval, the expected value and the width of a fuzzy number \(A=\big (A_{L}(\alpha ),A_{U}(\alpha )\big )\) are defined as follows, respectively
Supposing \(A=(a,b,c,d)_{n}\in F_{n}^{T}({\mathbb {R}})\), the following equalities can be obtained easily
A well-known metric on fuzzy numbers, which is an extension of the Euclidean distance, is defined in (Grzegorzewski and Mrowka 1998), by
where \([A_{L}(\alpha ),A_{U}(\alpha )]\) and \([B_{L}(\alpha ),B_{U}(\alpha )]\) are \(\alpha \)-cut form of fuzzy numbers A and B, respectively.
An another well-known metric between fuzzy numbers is the Hausdorff distance which is defined in (Dubois and Prade 1987), by
where
Moreover, we need to the following families of distances which are based on indicators of fuzzy numbers. The m-source distances between fuzzy numbers are defined in (Amirfakhrian 2010), as follows:
where m is a positive integer number and \(d_{H}\) is given by (14). According to this definition, two fuzzy numbers A and B are equivalent if \(Cor(A)=Cor(B)\), (that means \(d_{H}([A]^{1},[B]^{1})=0\)), \(Val(A)=Val(B)\) and \(Amb(A)=Amb(B)\).
Similarly, we define a family of distances between two fuzzy numbers as follows:
where m is a positive integer number. According to this definition, two fuzzy numbers A and B are equivalent if \(Cor(A)=Cor(B)\) and \(EI(A)=EI(B)\).
Theorem 2.9
If \(T:F({\mathbb {R}})\rightarrow F^{T}({\mathbb {R}})\) is a trapezoidal operator preserving the value or the ambiguity of fuzzy numbers, then T is not a continuous operator with respect to distances \(D_{m}^{C.EI}\).
Proof
Take \(A\in F({\mathbb {R}})\) with \([A]^{\alpha }=[A_{L}(\alpha ),A_{U}(\alpha )],~\alpha \in [0,1]\), satisfying the following conditions
(for example, \([A]^{\alpha }=[3\alpha ^{2}+2\alpha -2,-\alpha ^{2}-\alpha +5]\)). Consider the sequence of fuzzy numbers \(\{A_{n}\}_{n\ge 1}\), given by
It is clear that \(Cor(A_{n})=Cor(A)\). Also, by the conditions (i) and (ii), we get
Therefore, \(D_{m}^{C.EI}(A_{n},A)\rightarrow 0\) as \(n\rightarrow +\infty \), for any positive integer number m. Let T be a continuous trapezoidal operator with respect to \(D_{m}^{C.EI}\). Then, \(D_{m}^{C.EI}(T(A_{n}),T(A))\rightarrow 0\) as \(n\rightarrow +\infty \), where \(T(A_{n})=(t_{1}(n),t_{2}(n),t_{3}(n),t_{4}(n))\) and \(T(A)=(t_{1},t_{2},t_{3},t_{4})\). This follows that
as \(n\rightarrow \infty \) and by (10),
as \(n\rightarrow \infty \). So that, \(lim_{n\rightarrow \infty }t_{i}(n)=t_{i}\), for \(i\in \{1,2,3,4\}\). By Lemma 2 in (Ban and Coroianu 2011b), this confirms that T(A) is a trapezoidal fuzzy number. Now, if T preserves the value of fuzzy numbers, then we get by (7), the following
which is a contradiction to \(\int _{0}^{1}\alpha A_{L}(\alpha )d\alpha \ne 0\).
Similarly, if T preserves the ambiguity of fuzzy numbers, then we will have
Consequently, T does not preserve the value and ambiguity of A. \(\square \)
Theorem 2.10
If \(T:F({\mathbb {R}})\rightarrow F^{T}({\mathbb {R}})\) is a trapezoidal operator preserving the expected value or the width of fuzzy numbers, then T is not a continuous operator with respect to distances \(D_{m}^{C.V.A}\).
Proof
Take \(A\in F({\mathbb {R}})\) with \([A]^{\alpha }=[A_{L}(\alpha ),A_{U}(\alpha )],~\alpha \in [0,1]\), satisfying the following conditions
(for example, \([A]^{\alpha }=[2\alpha ^{2}+3\alpha -3,-\alpha ^{2}-\alpha +4]\)). Consider the fuzzy numbers sequence \(\{A_{n}\}_{n\ge 1}\), given by (17). Since A satisfies the conditions (i) and (iii), it follows that
and similarly,
Therefore, \(D_{m}^{C.V.A}(A_{n},A)\rightarrow 0\) as \(n\rightarrow +\infty \), for any positive integer number m. Let T be a continuous trapezoidal operator with respect to \(D_{m}^{C.V.A}\). So, \(D_{m}^{C.V.A}(T(A_{n}),T(A))\rightarrow 0\) as \(n\rightarrow +\infty \), with \(T(A_{n})=(t_{1}(n),t_{2}(n),t_{3}(n),t_{4}(n))\) and \(T(A)=(t_{1},t_{2},t_{3},t_{4})\). As a result, the factors
and
tend to 0, as \(n\rightarrow \infty \), that result \(lim_{n\rightarrow \infty }t_{i}(n)=t_{i}\), for \(i\in \{1,2,3,4\}\). Now, if T preserves the expected value of fuzzy numbers, then we get by (11), the following
and similarly, if T preserves the width of fuzzy numbers, then it will be obtained
Thus, we arrive at a contradiction because of A satisfies the condition \(\int _{0}^{1}A_{L}(\alpha )d\alpha \ne 0\). \(\square \)
3 Approximations preserving most indicators of fuzzy numbers
In this section, we investigate trapezoidal approximation operators preserving most indicators, such as the value, ambiguity, core, fuzziness and the expected value of fuzzy numbers. Since a trapezoidal approximation operator is characterized by four parameters, so, to ensure uniqueness of the operator it is enough whose parameters satisfy uniquely four linear equations. Therefore, we can search the required operators by producing and solving \(4\times 4\) linear systems with nonsingular matrices. To begin, let us consider three the parameters, value, ambiguity and fuzziness of fuzzy numbers as given in Definition 2.5. An approximation operator, preserving these parameters does not provide a unique trapezoidal approximation for a given fuzzy number, in general. Because, it will be searched between solutions of a linear system with three equations and four unknowns. For example, let \(A=(0,\frac{10}{3},\frac{14}{3},\frac{16}{3})_{\frac{1}{2}}\). Each one of the trapezoidal fuzzy numbers \(B=(1,2,4,7)\) and \(C=(0,\frac{5}{2},\frac{9}{2},6)\) preserves the value, ambiguity and fuzziness parameters of A. Indeed, by using (7)–(9), it is easy to see that \(Val(A)=Val(B)=Val(C)=\frac{10}{3}\), \(Amb(A)=Amb(B)=Amb(C)=\frac{5}{3}\) and \(Fuz(A)=Fuz(B)=Fuz(C)=1\). Accordingly, we must search an approximation operator which preserves the more important indicators containing more information related to fuzzy numbers. Let us to consider the core parameter. Since this parameter is set of points that have the highest degree membership in a fuzzy number, then it is an important parameter for the decision-maker. Therefore, it seems that a suitable approximation operator must preserves the core parameter of fuzzy numbers. Let \(A\in F({\mathbb {R}})\) and consider two the following systems for finding \( B\in F^{T}({\mathbb {R}})\):
or
If \(A\in F^{T}({\mathbb {R}})\) satisfies the case (a) or (b), then by (7)–(9), it is easy to deduce that A and B are identical. Therefore, the trapezoidal fuzzy number, preserving the parameters core, value and ambiguity or the parameters core, value and fuzziness of original fuzzy number is unique (if exists). But, the value parameter is more important than ambiguity parameter and the ambiguity parameter is more important than fuzziness parameter from a fuzzy number (see (Delgado et al. 1998a, b) for more information). Accordingly, a trapezoidal approximation operator satisfying the case (a) includes more information of fuzzy numbers with respect to a trapezoidal approximation operator satisfying the case (b). We thus, abandon the case (b) and consider the case (a). Suppose that \(B=T^{C.V.A}(A)=(t_{1},t_{2},t_{3},t_{4})\) is fuzzy number which satisfies the case (a), for \(A\in F({\mathbb {R}})\), with \(\alpha -\)cut \([A]^{\alpha }=\big [A_{L}(\alpha ),A_{U}(\alpha )\big ],\quad \alpha \in [0,1]\). Under this situation, the system (a) can be written as the following system:
that results
According to monotonicity of two functions \(A_{L}(\alpha )\) and \(A_{U}(\alpha )\) it is easy to deduce that \(t_{1}\le t_{2}\le t_{3}\le t_{4}\).
Now, let us to consider the other important characteristic of fuzzy numbers that is named the expected interval. The following result gives an advantage of the approximation operators which are preserving the expected interval.
Lemma 3.1
Consider an approximation operator \({{\mathcal {T}}}:F({\mathbb {R}})\rightarrow F^{T}({\mathbb {R}})\). This operator preserves expected interval of fuzzy numbers if and only if it preserves two parameters the expected value and the width of fuzzy numbers.
Proof
Take \(A=\big (A_{L}(\alpha ),A_{U}(\alpha )\big )\in F({\mathbb {R}})\) and suppose that \({{\mathcal {T}}}(A)=(a_{1},a_{2},a_{3},a_{4})\). By (4) and (10), the equality \(EI(A)=EI\big ({{\mathcal {T}}}(A)\big )\) implies
These equalities hold if and only if the following equalities hold
that are \(EV(A)=EV\big ({{\mathcal {T}}}(A)\big )\) and \(W(A)=W\big ({{\mathcal {T}}}(A)\big )\), by (5), (6), (11), and (12). \(\square \)
In the event that the decision-maker wants to have an approximation operator which preserves the expected interval of a given fuzzy number A, one of the systems for finding \(B\in F^{T}({\mathbb {R}})\) can be considered as follows:
If we denote \(B=T^{C.EI}(A)=(r_{1},r_{2},r_{3},r_{4})\), then the conditions (c) are as follows:
that result the following unique solution
It is easy to see that \(r_{1}\le r_{2}\le r_{3}\le r_{4}\).
Remark 3.2
For \(A\in F(R)\), the numbers \(T^{C.V.A}(A)\) and \(T^{C.EI}(A)\) can be considered as the best trapezoidal approximations of A. In fact, the numbers \(T^{C.V.A}(A)\) and \(T^{C.EI}(A)\) are the only trapezoidal fuzzy numbers such that \(D^{C.V.A}_{m}\big (T^{C.V.A}(A),A\big )=0\) and \(D^{C.EI}_{m}\big (T^{C.EI}(A),A\big )=0\), (defined by (15) and (16)).
The other system for finding \(B\in F^{T}({\mathbb {R}})\), preserving the expected interval of original fuzzy number A, can be considered as follows:
If we denote \(B=T^{V.A.EI}(A)=(s_{1},s_{2},s_{3},s_{4})\), then system (d) can be written as follows:
that result the following unique solution
This operator was obtained by Grzegorzewski et al. (Grzegorzewski and Mrowka 2005) as the nearest trapezoidal approximation with respect to metric D given in (13), which preserves the expected interval of fuzzy numbers. But, the approximation \(T^{V.A.EI} (A)\) of given fuzzy number A is not always a trapezoidal fuzzy number, as it was proved in (Allahviranloo and Firozja 2007). In fact, it is a trapezoidal fuzzy number, if \(s_{2}\le s_{3}\), that is \(\int _{0}^{1}(1-3\alpha )(A_{U}(\alpha )-A_{L}(\alpha ))d\alpha \le 0 \), (for other more information we propose (Grzegorzewski and Mrowka 2007) and (Grzegorzewski 2008)). In other words, \(A\in S\), where
Furthermore, Ban et al. (Ban et al. 2011) (Theorem 7, (i) or Corollary 8, (i)), have proven that if \(A\in S\), then the approximation \(T^{V.A.EI}(A)\) is the nearest trapezoidal approximation (with respect to metric D), which preserves two the parameters value and ambiguity of A. In fact, the condition (33) from Theorem 7 in (Ban et al. 2011), means that \(A\in S\) and also, equations (39)–(42) in (Ban et al. 2011), are respectively, the same mentioned equations (26)–(29).
We now try to extent the operator \(T^{V.A.EI}\) of S to \(F({\mathbb {R}})\) which is needed to complete some results in the next sections. Let A be an arbitrary fuzzy number and B be a fuzzy number satisfying the condition \(3Amb(B)-W(B)\ge 1\). Consider the fuzzy number
where
We show that \(A^{B}_{s}\) belongs to S. Indeed,
To make \(A^{B}_{s}\) which only depends on k(A), choosing an appropriate fuzzy number B may be useful. It is clear that B can not be a real number. So, in the simplest possible form B is a real interval. Let \(B=[a,b]\) be a real interval. Let us to consider the problem finding the numbers a and b which minimize \(D(A_{s}^{B},A)\) subject to \(a\le b\) and \(3Amb(B)-W(B)=\frac{b-a}{2}\ge 1\). By consideration
it is easy to deduce that this optimization problem has the unique solution \(a=-1\) and \(b=1\).
Consequently, in the rest of paper, we fix \(B=[-1,1]\) and for simplicity, denote the transfer function as follows:
Proposition 3.3
Let A be a fuzzy number. Then
Proof
We have \((A_{s})_{L}(\alpha )=A_{L}(\alpha )-k(A)\) and \((A_{s})_{U}(\alpha )=A_{U}(\alpha )+k(A)\), for all \(\alpha \in [0,1]\), which easily provide the results in (i). Also, we observe that
and
which imply \(d_{H}\big ([A_{s}]^{1},[A]^{1}\big )=k(A)\) and \(d_{H}\big (EI(A_{s}),EI(A)\big )=k(A)\), respectively. Thus, the results in (ii) are readily available.
(iii) Since \(T^{V.A.EI}(A_{s})\) preserves the expected interval of \(A_{s}\), then
By using this equality, we get
By similar reasoning it can be deduced that
The sum of two sides of these equalities leads to the required conclusion. \(\square \)
We now define the operator \(T^{V.A.EI}_{S}:F({\mathbb {R}})\rightarrow F^{T}({\mathbb {R}})\) as an extension of operator \(T^{V.A.EI}\) over all fuzzy numbers by
The following theorem is a completed version of obtained results in (Ban et al. 2011; Ban 2009a; Grzegorzewski and Mrowka 2007; Grzegorzewski 2008).
Theorem 3.4
For each \(A\in F({\mathbb {R}})\) the fuzzy number \(T^{V.A.EI}_{S}(A)\) is the nearest trapezoidal fuzzy number to \(A_{s}\), with respect to metric D. Moreover, \(T^{V.A.EI}_{S}(A)\) is only trapezoidal fuzzy number which preserves the value, ambiguity and expected interval of \(A_{s}\).
Proof
It is enough to prove that
Let \(B=(x_{1},x_{2},x_{3},x_{4})\) be a trapezoidal fuzzy number and consider the problem of finding such real numbers \(x_{1}\le x_{2}\le x_{3}\le x_{4}\) that minimize
Thus, denoting \(f(x_{1},x_{2},x_{3},x_{4})=D^{2}(B,A)\), we have to calculate partial derivatives of f and then to solve
It easily obtained that \(x_{j}=s_{j}\), \(j=1,2,3,4\), described by (26)–(29). Moreover, since the values
are positive, then \(x_{j}=s_{j}\), \(j=1,2,3,4\) given by (25)–(28), actually minimize D(B, A). \(\square \)
For completing, the following linear systems with A as arbitrary fuzzy number and \(B\in F^{T}({\mathbb {R}})\) as unknown fuzzy number, should be considered
It is easy to check that two systems (f) and (g) do not have unique solution. Also, the systems (e) and (h) have unique solution, respectively, as \(B=T^{C.V.W}(A)=(u_{1},u_{2},u_{3},u_{4})\) and \(B=T^{C.A.EV}(A)=(v_{1},v_{2},v_{3},v_{4})\), described by
and
The following example shows that (30)–(33) and (34)-(37) do not always give fuzzy numbers.
Example 3.5
Consider two fuzzy numbers \(A=(0,1,2,20)_{\frac{1}{2}}\) and \(B=(-20,0,1,2)_{2}\). By using (7) and (12), we attain \(Val(A)=\frac{23}{4}\) and \(W(A)=\frac{41}{3}\) and by using (8) and (11), we attain \(Amb(B)=\frac{13}{5}\) and \(EV(B)=-\frac{8}{3}\). Then for fuzzy number A, the equations (30) and (31), imply
and for fuzzy number B the equations (36) and (37), imply
Therefore, \(T^{C.V.W}(A)\) and \(T^{C.A.EV}(B)\) are not fuzzy numbers.
The following theorem provides necessary and sufficient conditions, under which \(T^{C.V.W}(A)\) and \(T^{C.A.EV}(A)\) are trapezoidal fuzzy numbers, for given fuzzy number A.
Theorem 3.6
Let \(A\in F({\mathbb {R}})\), \([A]^{\alpha }=[A_{L}(\alpha ),A_{U}(\alpha )]\), \(\forall \alpha \in [0,1]\). Then
(a) \(T^{C.A.EV}(A)\) is valid as a fuzzy number if and only if
and further
(b) \(T^{C.V.W}(A)\) is valid as a fuzzy number if and only if
and further
Proof
(a) The inequality (38) can be written as
that is \(t_{1}\le r_{1}\), by (18) and (22). Similarly, the inequality (39) is \(r_{4}\le t_{4}\), by (21) and (25). Therefore \(t_{1}\le r_{1}\le r_{4}\le t_{4}\), which is equivalent to
Consequently, by Lemma 2.3, the H-difference \(T^{C.V.A}(A)\ominus T^{C.EI}(A)\) exists if and only if both conditions (38) and (39) hold. Now, let \(T_{1}(A)\) be the trapezoidal fuzzy number in the right-hand side of (40), meaning that
By substituting (18)–(21) and (22)–(25) into this equality, it follows that
that is the same \(T^{C.A.EV}(A)\), described by (34)–(37).
(b) Conditions (41) and (42) are the inverse of conditions (38) and (39). Then, similar to reasoning of case (a), the conditions (41) and (42) are equivalent to that the H-difference \(T^{C.EI}(A)\ominus T^{C.V.A}(A)\) exists. Moreover, similar to case (a), if \(T_{2}(A)\) is trapezoidal fuzzy number given in (43), then it can be obtained that
that is the same \(T^{C.V.W}(A)\), described by (30)–(33). \(\square \)
At the end of this section, let us to consider the operators \(T^{C.V.A}\), \(T^{C.EI}\) and \(T^{V.A.EI}_{S}\) on the set \(F_{n}^{T}({\mathbb {R}})\).
Corollary 3.7
If \(A=(a,b,c,d)_{n}\in F_{n}^{T}({\mathbb {R}})\), then
Proof
Since \(A_{L}(\alpha )=a+(b-a)\root n \of {\alpha }\) and \(A_{U}(\alpha )=d-(d-c)\root n \of {\alpha }\) are the lower and upper functions related to \(\alpha \)-cut of fuzzy number \(A=(a,b,c,d)_{n}\), it is easy to obtain \(A_{L}(1)=b\), \(A_{U}(1)=c\), and
Also, it can be seen that \(A_{s}=\big (a-k(A),b-k(A),c+k(A),d+k(A)\big )\in F_{n}^{T}({\mathbb {R}})\). By substituting these values into (18)–(21), (22)–(25), and (26)–(29), the results are straightforward. \(\square \)
4 Concepts, Common properties and Comparisons
Consider three trapezoidal approximation operators \(T^{C.V.A}\), \(T^{C.EI}\) and \(T^{V.A.EI}\), respectively, described by (18)–(21), (22)–(25), and (26)–(29). In this section, we introduce the new concepts related to these operators and their common important properties, and also comparisons between them.
4.1 Concepts
Carlsson and Fuller (Carlsson and Fuller 2001) defined the lower and upper possible mean values of a fuzzy number A, \([A]^{\alpha }=\big [A_{L}(\alpha ),A_{U}(\alpha )\big ],\quad \forall \alpha \in [0,1]\), as follows:
and
respectively, and introduced the notation
which called the interval-valued possibilistic mean of A. It can be seen \(M_{*}(A)=Val(A)-Amb(A)\) and \(M^{*}(A)=Val(A)+Amb(A)\), then any approximation operator, preserving the value and ambiguity is preserving the lower and upper possible mean values, too. So that, the interval M(A) can be called the interval Value-Ambiguity related to fuzzy number A. In fact, M(A) is only interval that preserves both value and ambiguity of A. In other words,
and
It is noteworthy that the nearest interval, preserving the ambiguity of fuzzy numbers based on metric D is found in (Ban and Coroianu 2012), Theorem 6.
To describe the non-specificity and the spread of the left-hand part and the right-hand part of the core of a fuzzy number, we propose the following definition. Before it, we comment that the concepts of left-hand ambiguity and right-hand ambiguity of a fuzzy number were defined by Grzegorzewski in (Grzegorzewski 2008).
Definition 4.1
For any fuzzy number A, \([A]^{\alpha }=\big [A_{L}(\alpha ),A_{U}(\alpha )\big ],~\alpha \in [0,1]\), we define the concepts the core-left-hand ambiguity, core-right-hand ambiguity, core-left-hand width and core-right-hand width of A as follows:
respectively.
The following property of the approximation operators is immediate.
Proposition 4.2
If A is a fuzzy number then
(i) \(T^{C.V.A}(A)\) preserves the core-left-hand ambiguity and core-right-hand ambiguity of A.
(ii) \(T^{C.EI}(A)\) preserves the core-left-hand width and core-right-hand width of A.
Proof
We have
and similarly, we have \(\Delta _{U}(A)=M^{*}(A)-A_{U}(1)\). Since the operator \(T^{C.V.A}\) preserves \(M_{*}(A),~M^{*}(A)\) and Cor(A), then the statement (i) is true. Analogously, the statement (ii) is resulted, because \(\delta _{L}(A)=E_{*}(A)-A_{L}(1)\) and \(\delta _{U}(A)=E^{*}(A)-A_{U}(1)\). \(\square \)
Remark 4.3
If \(A_{L}(\alpha )\) and \(A_{U}(\alpha )\) are the constant functions on [0, 1], then it is clear that \(\Delta _{L}(A)=\delta _{L}(A)=0\) and \(\Delta _{U}(A)=\delta _{U}(A)=0\), respectively. Also, by Lemma 1 cases (i) and (ii) in (Ban 2008), it is easy to deduce that
for each \(A\in F({\mathbb {R}})\). Furthermore, if we set \(\Delta (A)=\big [\Delta _{L}(A),\Delta _{U}(A)\big ]\) and \(\delta (A)=\big [\delta _{L}(A),\delta _{U}(A)\big ]\), then these intervals separate the core parameter from intervals M(A) and EI(A). In fact, we have \(M(A)=\Delta (A)+Cor(A)\) and \(EI(A)=\delta (A)+Cor(A)\).
Sometimes the \(\alpha -\)cut representation of the present approximation operators might be useful. For fuzzy number A, \([A]^{\alpha }=\big [A_{L}(\alpha ),A_{U}(\alpha )\big ],~\alpha \in [0,1]\) we have, by (18)–(21), the following
that is
Similarly, we obtain, by (22)–(25),
For finding \(\left[ T_{S}^{V.A.EI}(A)\right] ^{\alpha }\), we first obtain
and similarly, we obtain the equalities \(\Delta _{U}(A_{s})=\Delta _{U}(A)\), \(\delta _{L}(A_{s})=\delta _{L}(A)\) and \(\delta _{U}(A_{s})=\delta _{U}(A)\). So that, by employing (26)–(29) for fuzzy number A, we obtain
Easily seen that
and
Please notice that the above representation of \(\alpha -\)cuts of \(T_{S}^{V.A.EI}\) could be useful. In fact, it shows that some important properties of the operators \(T^{C.V.A}\) and \(T^{C.EI}\) such as linearity, can be investigated only on the operator \(T_{S}^{V.A.EI}\). Moreover, the condition \(A\in S\), i.e. \(W(A)\le 3Amb(A)\) can be rewritten as follows:
that is
Theorem 4.4
Let \(A\in F({\mathbb {R}})\). Then
if and only if
and
Proof
For \(A\in F({\mathbb {R}})\), the equality of operators given as (44), (45) and (46), directly concludes the equalities (48) and (49) and that A belongs to S. Conversely, if the equalities (48) and (49) hold for given fuzzy number A, then A clearly satisfies the inequality (47). So that, \(A\in S\) and the consequent is straightforward. \(\square \)
Remark 4.5
It is noteworthy that the conditions (48) and (49) are actually the equality case of inequalities (38) and (39). Therefore, the statement of Theorem 4.4 is true for operators \(T^{C.A.EV}\) in (40) and \(T^{C.V.W}\) in (43), too. But the lower and upper functions of a fuzzy number A are rarely satisfied the conditions (48) and (49). For instance, consider \(A\in F_{n}^{T}({\mathbb {R}})\), according to Corollary 3.7, the conditions (48) and (49) are held for A, only when \(n=1\).
Example 4.6
Let \(\epsilon \in (0,1)\) be fixed and consider the fuzzy number \(A^{\epsilon }\), given by
We have
It is observed that the equality (49) is satisfied but the equality (48) is not satisfied. Indeed,
which, according to Theorem 4.4, implies that whatever \(\epsilon \) is closer to 0, then the approximation operators are closer together. For instance, by substituting the above values into (44) and (45), for \(\epsilon =0.5\), we obtain, for all \(\alpha \in [0,1]\)
It is easy to check that \(A^{0.5}\) satisfies condition (47), so, \(k(A^{0.5})=0\), and we get by (46), the following
4.2 Common properties
Theorem 4.7
Consider three approximation operators \(T^{C.V.A}\), \(T^{C.EI}\) and \(T_{S}^{V.A.EI}\).
(i) These operators are invariant to translation.
(ii) The operators \(T^{C.V.A}\) and \(T^{C.EI}\) are linear on \(F({\mathbb {R}})\) and the operator \(T_{S}^{V.A.EI}\) is linear on S.
(iii) These operators fulfill the identity criterion.
(iv) The operators \(T^{C.V.A}\) and \(T^{C.EI}\) fulfill the nearness criterion on \(F({\mathbb {R}})\) and the operator \(T_{S}^{V.A.EI}\) fulfills the nearness criterion on S.
Proof
(i) The proof of the property (i) for operator \(T_{S}^{V.A.EI}\) simply results that the operators \(T^{C.V.A}\) and \(T^{C.EI}\) have the same property. Suppose that \(A\in F({\mathbb {R}})\) and \(z\in {\mathbb {R}}\). First, by Definition 4.1, we get
Similarly, \(\Delta _{U}(A+z)=\Delta _{U}(A)\). Also, it can be obtained that \(\delta _{L}(A+z)=\delta _{L}(A)\), \(\delta _{U}(A+z)=\delta _{U}(A)\), and \(k(A+z)=k(A)\). Therefore, using the representation of (46), we have
(ii) The linearity of operator \(T_{S}^{V.A.EI}\) on set S, simply results that the operators \(T^{C.V.A}\) and \(T^{C.EI}\) are linear on \(F({\mathbb {R}})\). Let \(A,B\in S\) and \(\lambda \in {\mathbb {R}}\). We have \(A+\lambda B\in S\), because
We get
Similarly, it can be seen that
By substituting these results into (46), it is easy to deduce that
(iii) Since for given fuzzy number A, each one of the approximations \(T^{C.V.A}(A)\), \(T^{C.EI}(A)\) and \(T_{S}^{V.A.EI}(A)\) are uniquely obtained, then, for \(A\in F^{T}({\mathbb {R}})\), we have
(iv) This property is obvious. Because the operators \(T^{C.V.A}\), \(T^{C.EI}\) fulfill the nearness criterion, with respect to distances \(D^{C.V.A}_{m}\), \(D^{C.EI}_{m}\), respectively, and the operator \(T_{S}^{V.A.EI}\) fulfills the nearness criterion, with respect to distance D on set S, by Theorem 3.4. \(\square \)
Theorem 4.8
For each \(A,B\in F({\mathbb {R}})\), if \(A\ominus B\) exists, then
Proof
The following equalities are easy for obtaining
and
Considering (44), (45) and (46) for fuzzy number \(A\ominus B\) and by consideration
the requested properties are straightforward. \(\square \)
The following result gives us the continuity property of the present approximation operators. We note that the operators \(T^{C.V.A}\) and \(T^{C.EI}\) are not continuous with respect to metric D, because they are preserving the core parameter of fuzzy numbers, (see (Ban and Coroianu 2011b), Theorem 4).
Theorem 4.9
The trapezoidal approximation operators \(T^{C.V.A}\), \(T^{C.EI}\) and \(T_{S}^{V.A.EI}\) are continuous with respect to distances \(D^{C.V.A}_{m}\), \(D^{C.EI}_{m}\) and D, respectively.
Proof
Let \(\{A_{n}\}_{n\ge 1}\), be a sequence of fuzzy numbers such that \(A_{n}{\mathop {\longrightarrow }\limits ^{D^{C.V.A}_{m}}}A\), when \(n\rightarrow \infty \), the integer \(m\ge 1\) fixed and A be a fuzzy number. We have, for each \(n\ge 1\),
Similarly, we obtain
if \(A_{n}{\mathop {\longrightarrow }\limits ^{D^{C.EI}_{m}}}A\).
In the event that \(A_{n}{\mathop {\longrightarrow }\limits ^{D}}A\), \(A_{n}=\big (A_{nL}(\alpha ),A_{nU}(\alpha )\big )\) and \(A=\big (A_{L}(\alpha ),A_{U}(\alpha )\big )\in F({\mathbb {R}})\), we get \(A_{nL}(\alpha )\longrightarrow A_{L}(\alpha )\) and \(A_{nU}(\alpha )\longrightarrow A_{U}(\alpha )\), for each \(\alpha \in [0,1]\). Then, using the continuity of integral function, it follows that
and
Applying these equalities and the continuity of the absolute value function, we get
On the other hand, by the proof of Proposition 8 in (Grzegorzewski and Mrowka 2005), we have
We thus obtain
which completes the proof. \(\square \)
Now, let us to consider the present approximation operators on set \(F_{n}({\mathbb {R}})\). The following proposition is obtainable directly from the Corollary 3.7.
Proposition 4.10
If \(A\in \Omega _{i},~i\in \{1,2,3\}\), then the numbers \(T^{C.V.A}(A)\), \(T^{C.EI}(A)\) and \(T_{S}^{V.A.EI}(A)\) are belong to \(\Omega _{i}\), too.
The next result shows that in a special class of \(F_{n}({\mathbb {R}})\), the present approximation operators can have more shared information.
Proposition 4.11
Suppose that \(A\in F_{n}^{T}({\mathbb {R}})\) is a quasi-symmetric fuzzy number. Then, \(T^{C.V.A}(A)\) preserves the expected value, and \(T^{C.EI}(A)\) preserves the value of A.
Proof
Let \(A=(a,b,c,d)_{n}\) with \(T^{C.V.A}(A)=(t_{1},t_{2},t_{3},t_{4})\) and \(T^{C.EI}(A)=(r_{1},r_{2},r_{3},r_{4})\). Because A is quasi-symmetric, then \(b+c=d+a\), we conclude via the equalities (7) and (11),
and
Also, for \(n=1\), we get
and
Using the case (i) of Corollary 3.7, we get
and using the case (ii) of Corollary 3.7, we get
Consequently, \(EV\big (T^{C.V.A}(A)\big )=EV(A)\) and \(Val\big (T^{C.EI}(A)\big )=Val(A)\). \(\square \)
4.3 Comparisons
Since metric D is an extension of the Euclidean distance, then it is an efficient tool to express the distance between two fuzzy numbers. Accordingly, we first compare the present approximation operators under the metric D. For simplicity, let us denote
where \(D_{L}(A,B)=\int _{0}^{1}\big (A_{L}(\alpha )-B_{L}(\alpha )\big )^{2}d\alpha \) and \(D_{U}(A,B)=\int _{0}^{1}\big (A_{U}(\alpha )-B_{U}(\alpha )\big )^{2}d\alpha \).
Theorem 4.12
Let \(A\in F({\mathbb {R}})\). Then
Proof
Suppose that \(A=\big (A_{L}(\alpha ),A_{U}(\alpha )\big )\), \(\forall \alpha \in [0,1]\). Using (44) and (45), we obtain
Similarly, we obtain
We thus conclude that
So that,
To achieve the other required inequality, we first infer
and similarly
which result
By this equality and Theorem 3.4, we obtain
Consequently, the proof is completed. \(\square \)
To express next result we first give the following lemma which can be interesting.
Lemma 4.13
Let \(A\in F({\mathbb {R}})\). Then
Proof
Suppose that \([A]^{\alpha }=\big [A_{L}(\alpha ),A_{U}(\alpha )\big ],~\alpha \in [0,1]\) belongs to the set S. We have
and
and also,
Similarly, we obtain
The above results clearly produce the equalities (50). \(\square \)
Lemma 4.13 shows that for given \(A\in F({\mathbb {R}})\), if \(T^{C.V.A}(A_{s})\) is close to \(T^{C.EI}(A_{s})\), with respect to metric D, then \(T^{C.EI}(A_{s})\) is the same amount close to \(T^{V.A.EI}(A_{s})\), with respect to D.
Theorem 4.14
Let \(A\in F({\mathbb {R}})\). Then
Proof
According to Proposition 1 from (Ban et al. 2011), for any \(A\in S\), we have
and
These equalities with Lemma 4.13 simply produce the equality (51). \(\square \)
Now, we compare the approximation operators via parameter \({\bar{y}}(A)\), called the y-coordinate of centroid point associated with a fuzzy number A, (see (Grzegorzewski 2008; Wang et al. 2006)) which can be written as follows:
It is clear that for each fuzzy number A, we have
Theorem 4.15
Let \(A\in F({\mathbb {R}})\) be a non-real fuzzy number. Then
Proof
By \(\alpha -\)cut forms (44) and (45), it is easy to obtain that
and
Applying (53), we obtain
Similarly, by applying (54), we have
Considering (55) and (56), we obtain
Since
then the inequality (52) is obtained and the proof is completed. \(\square \)
As a consequence of above mentioned theorems, the operator \(T_{S}^{V.A.EI}\) on the set S is preferable rather than the other two operators \(T^{C.V.A}\) and \(T^{C.EI}\). But, considering the representations (44), (45) and (46), the operator \(T_{S}^{V.A.EI}\) requires more computation to be found. Furthermore, as will be shown below, the set S does not contain a broad class of fuzzy numbers.
Corollary 4.16
Let \(A=(a,b,c,d)_{n}\in F_{n}^{T}({\mathbb {R}})\) be a non-real fuzzy number such that \(b=c\) and \(n>1\). Then \(A\notin S\).
Proof
Since \(b=c\), then, according to (47), it must be shown that
Using the proof of Corollary 3.7 and after simplifying, we obtain
which is positive, because \(n>1\) and A is a non-real fuzzy number. \(\square \)
Finally, we compare the two parameters Fuzziness and Ambiguity related to the present approximation operators.
Theorem 4.17
Let \(A\in F({\mathbb {R}})\). The inequalities
\((a)~Fuz\Big (T_{S}^{V.A.EI}(A)\Big )\le Fuz\Big (T^{C.EI}(A)\Big )\le Fuz\Big (T^{C.V.A}(A)\Big ),\)
and
\((b)~Amb\Big (T^{C.EI}(A)\Big )\le Amb(A),\)
hold, if and only if \(\big (2\delta _{U}(A)-3\Delta _{U}(A)\big )-\big (2\delta _{L}(A)-3\Delta _{L}(A)\big )\le 0.\)
Proof
(a) Applying the \(\alpha \)-cut form (46), we calculate
which easily results
Similarly, by applying (44) and (45), we obtain, respectively,
The equalities (57) and (59) give
and the equalities (58) and (59), give
Consequently, the statement of Theorem case (a) is true, by the equalities (60) and (61).
(b) We obtain
that completes the proof. \(\square \)
It is noteworthy that by Proposition 3.3, (i), we have
For observing inequalities in Theorem 4.17, we give the following example.
Example 4.18
Consider two fuzzy numbers \(A=(1,2,3,4)_{\frac{1}{3}}\) and \(B=(1,2,3,4)_{3}\). By applying the results, in the proof of Corollary 3.7, we obtain
Therefore
These values imply that the inequality (47) holds for numbers A and B. So, \(A,B\in S\). By (57)-(59), we get
and
Also, by (9), it can be resulted \(Fuz(A)=0.44\) and \(Fuz(B)=0.31\). About the ambiguity parameter, we get, by (8) and the proof of case (b) of Theorem 4.17,
and
5 Applications
In this section, we suggest some practical applications of obtained results in the previous sections which can be useful in the approximation theory of fuzzy numbers.
5.1 Ranking fuzzy numbers based on the parameters core, value and ambiguity
A ranking method (with ordering \(\prec '\)) of fuzzy numbers can be introduced by the parameters core, value and ambiguity, similar to Definition 2.7, which is considered with ordering \(\prec \) .
Definition 5.1
Consider the ranking method given by Definition 2.7, in which step 3 is replaced by the following step
3’. If \(diam[A]^{1}=diam[B]^{1}\), then they are equivalent (denoted by \(A\sim B\)). Otherwise, \(A\prec ' B\), if \(diam[A]^{1}>diam[B]^{1}\).
Example 5.2
Consider two fuzzy numbers \(A=(1,2,6,7)_{\frac{1}{2}}\) and \(B=(1,\frac{9}{4},\frac{823}{140},\frac{242}{35})_{\frac{1}{3}}\). It is easy to check that \(Val(A)=Val(B)=4\), \(Amb(A)=Amb(B)=\frac{5}{2}\) and \(Fuz(A)=Fuz(B)=\frac{1}{2}\). Then, according to Definition 2.7, the number A is equivalent to B, while according to Definition 5.1, we have \(A\prec ' B\), because \(diam[B]^{1}=\frac{127}{35}<diam[A]^{1}=4\).
Proposition 5.3
Let A, B and C be arbitrary fuzzy numbers. Then, the following hold.
(i) \(A\sim A\).
(ii) If \(A\precsim 'B\) and \(B\precsim 'A\), then \(A\sim B\).
(iii) If \(A\precsim 'B\) and \(B\precsim 'C\), then \(A\precsim 'C\).
(iv) Let \([A]^{\alpha }=[A_{L}(\alpha ),A_{U}(\alpha )]\) and \([B]^{\alpha }=[B_{L}(\alpha ),B_{U}(\alpha )]\), \(\forall \alpha \in [0,1]\). If \(A_{U}(0)<B_{L}(0)\), then \(A\prec 'B\).
(v) Assume that \(S_{1}\) and \(S_{2}\) are two arbitrary finite sets of fuzzy numbers and A and B belong to \(S_{1}\cap S_{2}\), then \(A\prec 'B\) on \(S_{1}\) if and only if \(A\prec 'B\) on \(S_{2}\).
(vi) \(A\prec 'B\) if and only if \(A+C\prec 'B+C\).
(vii) If \(A\ominus C\) and \(B\ominus C\) exist, then \(A\prec ' B\) implies \(A\ominus C\prec 'B\ominus C\).
(viii) If \(A_{U}(0)< 0\) and \(B_{L}(0)> 0\), then \(A\prec 'B\), and if, in addition, \(C_{L}(0)>0\), then \(AC\prec 'BC\).
Proof
An ordering index, based on Definition 5.1, can be designed and employed as follows:
for all \(A,B\in F({\mathbb {R}})\), where \(\chi _{U}(t)=\left\{ \begin{array}{l} 1;~~t\in U\\ 0;~~t\notin U \end{array}\right. \), and U is a subset of real numbers. In fact, it is easy to see that \(A\prec ' B\), if and only if \(M(A,B)<0\) and \(A\sim B\), if and only if \(M(A,B)=0\). Then, the statement (i) is obvious and the statement (ii) is simply resulted from which the inequality \(M(A,B)\le 0\) is equivalent to the inequality \(M(B,A)\ge 0\).
(iii) Since \(A\precsim 'B\), that is, \(M(A,B)\le 0\), then, only one of the following is satisfied:
(a) \(Val(A)<Val(B)\), or
(b) \(Val(A)=Val(B)\) and \(Amb(A)<Amb(B)\), or
(c) \(Val(A)=Val(B)\), \(Amb(A)=Amb(B)\) and \(diam(B)\le diam(A)\).
Similarly, since \(M(B,C)\le 0\), only one of the following is satisfied:
\((a')\) \(Val(B)<Val(C)\), or
\((b')\) \(Val(B)=Val(C)\) and \(Amb(B)<Amb(C)\), or
\((c')\) \(Val(B)=Val(C)\), \(Amb(B)=Amb(C)\) and \(diam(C)\le diam(B)\).
Considering each one of cases (a), (b) and (c) with each one of cases \((a')\), \((b')\) and \((c')\), it is easy to deduce that \(M(A,C)\le 0\).
(iv) Since the lower and upper functions of a fuzzy number are respectively non-decreasing and non-increasing and since \(A_{U}(0)<B_{L}(0)\), we get
which gives
that is \(Val(A)<Val(B)\). Thus, \(A\prec 'B\).
(v) In the ordering approach, by ordering \(\prec '\), ranking order of A and B is solely dependent on the value M(A, B) and has nothing to do with any other fuzzy number in \(S_{1}\) or \(S_{2}\). Therefore, when A and B are ranked on \(S_{1}\) and \(S_{2}\), the same ranking order will be obtained.
(vi) Since \(Val(A+B)=Val(A)+Val(B)\), \(Amb(A+B)=Amb(A)+Amb(B)\) and \(diam(A+B)=diam(A)+diam(B)\) for each \(A,B\in F({\mathbb {R}})\), then, it is easy to obtain that \(M(A+C,B+C)=M(A,B)\), which provides the requirement result.
(vii) There are \(E,F\in F({\mathbb {R}})\) such that \(A=C+E\) and \(B=C+F\). So, \(A\prec 'B\) means \(C+E\prec 'C+F\), which implies \(E\prec 'F\), by (vi).
(viii) It follows that \(A_{L}(\alpha )\le A_{U}(\alpha )<0\) and \(0<B_{L}(\alpha )\le B_{U}(\alpha )\), which clearly give \(Val(A)<0\) and \(Val(B)>0\). So, \(A\prec 'B\). In addition, since \(C_{L}(0)>0\), then \((AC)_{U}(0)=A_{U}(0)C_{L}(0)<0\) and \((BC)_{L}(0)=B_{L}(0)C_{L}(0)>0\), which give the requirement result. \(\square \)
The statements (i) to (vi) of proposition 5.3 are respectively the same as axioms \(A_{1}\) to \(A_{6}\), introduced in (Wang and Kerre 2001), as the reasonable properties for an ordering approach of fuzzy numbers. Then, the statements (i) to (vi) of proposition 5.3 show that ordering \(\prec '\) satisfies the reasonable properties \(A_{1}\) to \(A_{6}\), respectively. Also, the other axiom \(A_{7}\) is introduced in (Wang and Kerre 2001) which can be expressed as follows:
\(A_{7}\): Let M be an ordering method with ordering \({\hat{\prec }}\). Let \(A,B,C\in F({\mathbb {R}})\) and \([C]^{\alpha }\) includes non-negative real numbers for any \(\alpha \in [0,1]\). In this case, the condition \(A{\hat{\prec }} B\) implies \(AC{\hat{\prec }} BC\).
The following example shows the axiom \(A_{7}\) does not hold under ordering \(\prec '\).
Example 5.4
Consider three fuzzy numbers A, B and C with \([A]^{\alpha }=[2\alpha ^{2},4-\alpha ^{2}]\), \([B]^{\alpha }=[2\sqrt{\alpha },4-\sqrt{\alpha }]\) and \([C]^{\alpha }=[2\alpha ,4-\alpha ]\), \(\forall \alpha \in [0,1]\). We get \(Val(A)=\frac{9}{4}\) and \(Val(B)=\frac{12}{5}\), So \(A\prec 'B\). Although \([C]^{\alpha }\) includes non-negative real numbers for any \(\alpha \in [0,1]\), we have \(BC\prec 'AC\), because
Since the operator \(T^{C.V.A}\) preserves the core, value and ambiguity of fuzzy numbers, so it is order invariant under ordering \(\prec '\), means that
The last relationship is an advantage of ordering \(\prec '\) comparing to ordering \(\prec \), as shown in the following example.
Example 5.5
Consider two fuzzy numbers A and B, as given in Example 5.2. By using the case (i) of Corollary 3.7, we obtain
and
By (9), we get
Therefore, \(T^{C.V.A}(A)\prec T^{C.V.A}(B)\), while according to Example 5.2, the number A is equivalent to B, under ordering \(\prec \).
The following result shows that the ordering \(\prec '\) in the space of fuzzy numbers is equivalent to the ordering \(\prec \) in the space of trapezoidal approximations, preserving the core, value and ambiguity.
Theorem 5.6
Let \(A,B\in F({\mathbb {R}})\). Then
Proof
Consider \(A,B\in F({\mathbb {R}})\) and suppose that \(Val(A)=Val(B)\) and \(Amb(A)=Amb(B)\). We thus, get by (58)
which simply completes the proof. \(\square \)
5.2 Trapezoidal approximation operator preserving the most indicators of fuzzy numbers
If the decision-maker is willing to employ an approximation operator which preserves the most indicators of fuzzy numbers, then, based on the results given in the previous section, the operator \(T:F({\mathbb {R}})\rightarrow F^{T}({\mathbb {R}})\) can be proposed as follows:
However, this operator is not a continuous operator with respect to distances \(D_{m}^{C.EI}\), \(D_{m}^{C.V.A}\) and D, as it is shown in Theorem 4 in (Ban and Coroianu 2011b) and Theorems 2.9 and 2.10.
5.3 Trapezoidal approximation algorithm preserving the most indicators of fuzzy numbers with the least ambiguity
Let us point out that the ambiguity parameter may be seen as the global spread which represents the degree of the inaccuracy of a fuzzy number. Based on the extension principle, the use of a fuzzy number with large ambiguity in fuzzy arithmetic leads to the increase of inaccuracy in the results. Therefore, if the ambiguity parameter of a fuzzy number is less than that of its approximation, then employing the approximation is not suitable in fuzzy arithmetic. It is possible that the operator T, defined as (62), provides such an approximate. In fact, for given fuzzy number A, if \(A\notin S\), then by (47), we get
that results \(Amb(T(A))=Amb\big (T^{C.EI}(A)\big )>Amb(A)\), by Theorem 4.17, (b). For overcome this shortcoming, we propose the following approximation algorithm, which gives us a trapezoidal approximation with the least ambiguity, preserving the most indicators of initial fuzzy number.
Algorithm
Take \(A\in F({\mathbb {R}})\)
Step 1: If \(\big (2\delta _{U}(A)-3\Delta _{U}(A)\big )-\big (2\delta _{L}(A)-3\Delta _{L}(A)\big )>A_{U}(1)-A_{L}(1)\), then apply operator \(T^{C.V.A}\) given as \(\alpha -\)cut form (44), else
Step 2: If \(\big (2\delta _{U}(A)-3\Delta _{U}(A)\big )-\big (2\delta _{L}(A)-3\Delta _{L}(A)\big )\le 0\), then apply operator \(T^{C.EI}\) given as \(\alpha -\)cut form (45), else
Step 3: apply operator \(T^{V.A.EI}\) given as \(\alpha -\)cut form (46).
Now, we introduce some advantages of the trapezoidal approximation operator given by the above algorithm with respect to previous proposed approximation operators.
1. The trapezoidal approximation under present algorithm contains more information of the fuzzy number under study. The previous proposed algorithms are at most preserve two characteristics of fuzzy numbers. For instance, the trapezoidal approximation operator, preserving the value and ambiguity dose not preserve the core parameter of any fuzzy number, (see Examples 6 and 9, in (Ban et al. 2011)). Also, the trapezoidal approximation operator, preserving expected interval dose not preserve the value, and the ambiguity, in general case (see Example 14, in (Ban 2008)).
2. The trapezoidal approximation under present algorithm preserves the structure of fuzzy numbers. This means that, if the fuzzy number under study A, is shaped like a trapezoid (triangle) then the present algorithm gives us a trapezoidal (triangular) approximation, too. Approximations such as triangular (Abbasbandy et al. 2010) and semi-trapezoidal (Yeh 2011) do not have this feature (see Example 8.3, in (Abbasbandy et al. 2010) and Example 6.1, in (Yeh 2011)). Also, trapezoidal approximation operator, preserving the ambiguity and the value, and trapezoidal approximation operator, preserving the ambiguity do not preserve the structure of fuzzy numbers (see Example 16, in (Ban et al. 2011) and Example 11, in (Ban and Coroianu 2012)).
Finally, for the sake of better clarify the effect of present approximation operator and algorithm, we give some comparative examples.
Example 5.7
(Brandas 2011). Consider the fuzzy number \(A=(1,100,105,200)_{2}\). The best trapezoidal approximation, preserving the core and the expected value under metric D, introduced by Brandas 2011, is as follows:
We here obtain
Then, the our Algorithm suggests the approximation \(T^{C.V.A}(A)\), which is the same as \(T_{Br}(A)\), by using the case (i) of Corollary 3.7.
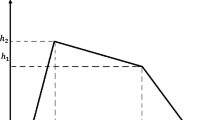
Approximation related to fuzzy number B from Example 5.8
Example 5.8
(Yeh 2008b). Consider the fuzzy number \(B=(-1+\alpha ^{2},1-\sqrt{\alpha }),~~\alpha \in [0,1]\). The nearest fuzzy number, preserving the expected interval of B, which was obtained by Yeh 2008, is as follows:
Since
then the our Algorithm suggests the following approximation
then \(B\prec ' T^{C.EI}(B)\).
See Fig. 1 for the comparison these approximations.
Example 5.9
Consider two fuzzy numbers \(C=(1,2,4,35)_{2}\) and \(D=(3^{\alpha },7-3^{\alpha }),~~\alpha \in [0,1]\). The best trapezoidal approximation, preserving the value and ambiguity of C is found by Ban and et al. (Example 16, in (Ban et al. 2011)), as follows:
Similarly, by using the case (i) of Theorem 7 or Corollary 8 in (Ban et al. 2011), it can be obtained that
But, we have
and
Thus, based on given Algorithm, we should, respectively, consider \(T^{C.V.A}(C)\) and \(T^{C.EI}(D)\) as approximations of C and D, that are
and
by using (18)–(21) and the case (ii) of Corollary 3.7, respectively.
One can notice that based on the ranking method, given by Definition 5.1, the number \(T^{C.V.A}(C)\) is equivalent to C, and since \(diam[C]^{1}=2>diam[T_{Ba}(C)]^{1}=0\), then \(C\prec ' T_{Ba}(C)\). Also, we result that
by the following considerations
\(Val(T^{C.EI}(D))=Val(T_{Ba}(D))=Val(D)=3.5\),
\( Amb(T^{C.EI}(D))=1.29<Amb(T_{Ba}(D))=Amb(D)=1.35,\)
\(diam[D]^{1}=1<diam[T_{Ba}(D)]^{1}=1.4\).
See Figs. 2 and 3 for the comparison these results.
Approximation related to fuzzy number C from Example 5.9
Approximation related to fuzzy number D from Example 5.9
Example 5.10
(Ban and Coroianu 2012). Let \(E=(1,2,3,4)_{2}\). The nearest trapezoidal fuzzy number which preserves the ambiguity of E is given by Ban 2012, as follows:
We have
Thus, the our Algorithm proposes the approximation \(T^{V.A.EI}(E)\), which is the same as \(T_{Ba}(E)\), by using the case (iii) of Corollary 3.7.
6 Conclusion and further research
In this paper we have exposed trapezoidal approximation operators that are preserving the most indicators of fuzzy numbers. It is shown that the obtained approximation operators have the important properties that are attributable to an approximation operator of fuzzy numbers such as scale invariance, identity, translation invariance, and nearness criterion. The results of relationships between these operators and their comparison are found. Moreover, we have presented some applications of obtained results with some comparative examples.
For further research, we propose the study of other approximation operators of fuzzy numbers such as the piecewise linear approximation, symmetric trapezoidal approximation and weighted trapezoidal approximation that are preserving the most indicators of fuzzy numbers. In addition, applying the results of this paper in some scientific issues may be interesting, for example, the fuzzy linear systems, fuzzy linear programming, fuzzy risk analysis, fuzzy error analysis, etc.
Data availability
Enquiries about data availability should be directed to the authors.
References
Abbasbandy S, Ahmady E, Ahmady N (2010) Triangular approximations of fuzzy numbers using \(\alpha \)-weighted valuations. Soft Comput 14:71–79
Abbasbandy S, Hajjiri T (2010) Weighted trapezoidal approximation-preserving core of a fuzzy number. Comput Math Appl 59:3066–3077
Allahviranloo T, Adabitabar FM (2007) Note on “Trapezoidal approximation of fuzzy numbers“. Fuzzy Sets Syst 158:755–756
Amirfakhrian M (2010) Properties of the nearest parametric form approximation operator of fuzzy numbers. An St Univ Ovidius Constanta 18:23–34
Ban AI (2008) Approximation of fuzzy numbers by trapezoidal fuzzy numbers preserving the expected interval. Fuzzy Sets Syst 159:1327–1344
Ban AI, Brandas A, Coroianu L, Negrutiu C, Nica O (2011) Approximations of fuzzy numbers by trapezoidal fuzzy numbers preserving the ambiguity and value. Comput Math Appl 61:1379–1401
Ban AI (2009) On the nearest parametric approximation of a fuzzy number-revisited. Fuzzy Sets Syst 160:3027–3047
Ban AI (2009) Trapezoidal and triangular approximations of fuzzy numbers-inadvertences and corrections. Fuzzy Sets Syst 160:3048–3058
Ban AI (2011) Remarks and corrections to the triangular approximations of fuzzy numbers using \(\alpha \)-weighted valuations. Soft Comput 15:351–361
Ban AI, Coroianu LC, Grzegorzewski P (2011) Trapezoidal approximation and aggregation. Fuzzy Sets Syst 177:45–59
Ban AI, Coroianu LC (2011) Metric properties of the nearest extended parametric fuzzy number and applications. Int J Approx Reason 52:488–500
Ban AI, Coroianu LC (2011) Discontinuity of the trapezoidal fuzzy number-valued operators preserving core. Comput Math Appl 62:3103–3110
Ban AI, Coroianu LC (2012) Nearest interval, triangular and trapezoidal approximation of a fuzzy number preserving ambiguity. Int J Approx Reason 53:805–836
Ban AI, Coroianu LC, Khastan A (2016) Conditioned weighted L-R approximations of fuzzy numbers. Fuzzy Sets Syst 283:56–82
Bodjanova S (2005) Median value interval of a fuzzy number. Inform Sci 172:73–89
Brandas A (2011) Approximation of fuzzy numbers by trapezoidal fuzzy numbers preserving the core and the expected value. Stud Univ Babes-Bolyai Math 56:247–259
Carlsson C, Fuller R (2001) On possibilistic mean value and variance of fuzzy numbers. Fuzzy Sets Syst 122:315–326
Chanas S (2001) On the interval approximation of a fuzzy number. Fuzzy Sets Syst 122:353–356
Delgado M, Vila MA, Voxman W (1998) A fuzziness measure For fuzzy numbers: applications. Fuzzy Sets Syst 94:205–216
Delgado M, Vila MA, Voxman W (1998) On a canonical representation of fuzzy numbers. Fuzzy Sets Syst 93:125–135
Dubois D, Prade H (1987) The mean value of a fuzzy number. Fuzzy Sets Syst 24:279–300
Grzegorzewski P, Mrowka E (1998) Metrics and orders in space of fuzzy numbers. Fuzzy Sets Syst 97:83–94
Grzegorzewski P, Mrowka E (2005) Trapezoidal approximations of fuzzy numbers. Fuzzy Sets Syst 153:115–135
Grzegorzewski P, Mrowka E (2007) Trapezoidal approximations of fuzzy numbers -revisited. Fuzzy Sets Syst 158:757–768
Grzegorzewski P (2008) Trapezoidal approximations of fuzzy numbers preserving the expected interval-Alghoritms and properties. Fuzzy Sets Syst 159:1354–1364
Grzegorzewski P (2002) Nearest interval approximation of fuzzy numbers. Fuzzy Sets Syst 130:321–330
Grzegorzewski P (2008) New algorithms for trapezoidal approximation of fuzzy numbers preserving the expected interval. IPMU 08:117–123
Heilpern S (1992) The expected value of a fuzzy number. Fuzzy Sets Syst 47:81–86
Joshi R, Kumar S (2017) A new exponential fuzzy entropy of order-(\(\alpha \),\(\beta \)) and its application in multiple attribute decision-making problems. Commun Math Stat 5:213–229
Joshi R, Kumar S (2018) An \((R, S)\)-norm fuzzy information measure with its applications in multiple attribute decision making. Comput Appl Math 37:2943–2964
Nasibov EN, Peker S (2008) On the nearest parametric approximation of a fuzzy number. Fuzzy Sets Syst 159:1365–1375
Puri M, Ralescu D (1983) Differentials of fuzzy functions. J Math Anal Appl 91:552–558
Vanegasa MC, Blochb I, Ingladac J (2016) Fuzzy constraint satisfaction problem for model-based image interpretation. Fuzzy Sets Syst 286:1–29
Wang X, Kerre EE (2001) Reasonable properties for the ordering of fuzzy quantities (I). Fuzzy Sets Syst 118:375–385
Wang YM, Yang JB, Xu DL, Chin KS (2006) On the centroids of fuzzy numbers. Fuzzy Sets Syst 157:919–926
Yeh CT (2007) A note on trapezoidal approximation of fuzzy numbers. Fuzzy Sets Syst 158:747–754
Yeh C.T (2009) Approximations by interval, triangular and trapezoidal fuzzy numbers, IFSA-EUSFLAT, 143-148
Yeh CT (2017) Existence of interval, triangular, and trapezoidal approximations of fuzzy numbers under a general condition. Fuzzy Sets Syst 310:1–13
Yeh CT (2008) On improving trapezoidal and triangular approximations of fuzzy numbers. Internat J Approx Reason 48:297–313
Yeh CT (2008) Trapezoidal and triangular approximations preserving the expected interval. Fuzzy Sets Syst 159:1345–1353
Yeh CT (2011) Weighted semi-trapezoidal approximations of fuzzy numbers. Fuzzy Sets Syst 165:61–80
Yeh CT (2009) Weighted trapezoidal and triangular approximations of fuzzy numbers. Fuzzy Sets Syst 160:3059–3079
Zeng W, Li H (2007) Weighted triangular approximation of fuzzy numbers. Int J Approx Reason 46:137–150
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this work.
Ethical approval
The author certifies that this paper consists of original, unpublished work which is not under consideration for publication elsewhere and states that this article does not contain any studies with human participants performed by the author.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chehlabi, M. Trapezoidal approximation operators preserving the most indicators of fuzzy numbers-relationships and applications. Soft Comput 26, 7081–7105 (2022). https://doi.org/10.1007/s00500-022-07172-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-022-07172-y