Approximations of Fuzzy Numbers by General Trapezoidal Fuzzy Numbers

Abstract

Recently, many scholars investigated interval, triangular, trapezoidal, and semi-trapezoidal approximations of fuzzy numbers. These researches can be grouped into two classes: one is to study approximations of fuzzy numbers without any constraint; the other one is to study approximations preserving some attributes. In this paper, we propose two general approximations of fuzzy numbers named general f-trapezoidal approximation and general f-triangular approximation. The two approximations will generalize those approximations of the first class under the Euclidean distance. Finally, we propose an efficient algorithm for computing the proposed approximations and illustrate by an example.

1 Introduction

Fuzzy intervals play important roles in many applications, such as fuzzy control systems, discrete dynamic systems, or intelligence technology. In practice, we often used fuzzy intervals to represent uncertain or incomplete information. For shortening computation time, we usually approximate general fuzzy intervals by interval, triangular, trapezoidal, and/or semi-trapezoidal fuzzy numbers, so as to simplify calculations. In addition, ranking or ordering fuzzy numbers is a fundamental problem of fuzzy optimization or fuzzy decision making. Another application is to make the comparison of fuzzy numbers by using the order relations defined on the approximations of fuzzy numbers. Therefore, how to approximate a fuzzy number is immensely important. In Ma et al. (2000) first studied symmetric triangular approximations of fuzzy numbers. Consequently, in Grzegorzewski (2002) proposed interval approximations, in Abbasbandy and Asady (2004) proposed trapezoidal approximations, in Zeng and Li (2007) proposed weighted triangular approximations which were improved by Yeh (2008, 2009), and in Nasibov and Peker (2008) proposed the nearest parametric approximations which were improved by Ban (2008, 2009) and Yeh (2011), independently. In addition, during the last years, approximations of fuzzy numbers preserving some attributes were studied too. For example, trapezoidal approximations preserving the expected interval were proposed by Grzegorzewski and Mrowka (2005, 2008) and improved by Ban (2008) and Yeh (2007, 2008) independently, trapezoidal approximations preserving cores of fuzzy numbers were proposed by Grzegorzewski and Stefanini in 2009 and further studied by Abbasbandy and Hajjari (2010), and trapezoidal approximations preserving the value and ambiguity were proposed by Ban et al. (2011). In this paper, we study more general approximations without preserving any attribute, named general f-trapezoidal approximations and general f-triangular approximations. In Sect. 2, we present several preliminaries and state our main problem. In Sect. 3, the formulas for computing general f-trapezoidal approximations and general f-triangular approximations are provided. In Sect. 4, we study an efficient algorithm and illustrated by an example. The conclusions are drawn in Sect. 5.

2 Problem Statement

A fuzzy number $\tilde{A}$ is a subset of the real line R with membership function$\mu _{\tilde{A}} :\rightarrow [0,1]$ such that (Dubois and Prade 1978):

• 1. $\tilde{A}$ is normal, i.e., there is an x ₀ ∈ R with $\mu _{\tilde{A}}(x_{0}) = 1.$

• 2. $\tilde{A}$ is fuzzy convex, i.e., $\mu _{\tilde{A}}(rx + (1 - r)y) \leq min\{\mu _{\tilde{A}}(x),\mu _{\tilde{A}}(y)\}$ for all x, y ∈ [0, 1].

• 3. $\tilde{A}$ is upper semicontinuous, i.e., $\mu _{\tilde{A}}^{-1}([\alpha,1])$ is closed for all α ∈ [0, 1].

• 4. The support of $\mu _{\tilde{A}}$ is bounded, i.e., the closure of $\{x \in R :\mu _{\tilde{A}} > 0\}$ is bounded. Recall that $\tilde{A}$ can be also represented by using its α − cuts $[A_{L}(\alpha ),A_{U}(\alpha )],\alpha \in [0,1]$ (an ordered pair of left continuous functions)

which satisfy the following conditions:

• 1. $\tilde{A}_{L}$ is increasing on [0,1].

• 2. $\tilde{A}_{U}$ is decreasing on [0,1].

• 3. $\tilde{A}_{L}(\alpha ) \leq \tilde{ A}_{U}(\alpha )$, for all α ∈ [0, 1].

  Let f : [0, 1] → [0, 1] be a left continuous and decreasing function such that $f(0) = 1,andf(1) = 0$. A fuzzy number $\tilde{A}$ is called general f-trapezoidal if its α-cuts are of the form

  $$\displaystyle{[x_{2} - (x_{2} - x_{1})f(\alpha ),x_{3} + (x_{4} - x_{3})f(\alpha )],\alpha \in [0,1]}$$

where $x_{1} \leq x_{2} \leq x_{3} \leq x_{4}.$ And, when x ₂ = x ₃ additionally, it is called general f-triangular. Recently, the following f-trapezoidal fuzzy numbers had been studied:

• 1. If $f(\alpha ) = 1-\alpha$, they are usually trapezoidal fuzzy numbers.

• 2. Let s > 0 and $f(\alpha ) = {(1-\alpha )}^{s}$ Nasibov and Peker (2008) first studied fuzzy approximations of this type.

• 3. Let n > 0 and $f(\alpha ) = 1 {-\alpha }^{n}$. Bodjanova (2005) first studied trapezoidal fuzzy numbers of this class.

Let F(R), F _T (R), and F _Δ (R) denote the sets of fuzzy numbers, f-trapezoidal fuzzy numbers, and f-triangular fuzzy numbers, respectively, and let λ = λ(t) : [0, 1] → R be a weighted function on [0,1] (i.e., nonnegative function with $\int _{0}^{1}\lambda (t)\mathrm{d}t > 0$). Now, we define a distance on F(R) as follows:

$$\displaystyle{d(\tilde{A},\tilde{B}) = {[\int _{0}^{1}(\vert A_{ L}(\alpha ) - B_{L}(\alpha ){\vert }^{2} + \vert A_{ U}(\alpha ) - B_{U}(\alpha ){\vert }^{2})\lambda (\alpha )\mathrm{d}\alpha ]}^{1/2}}$$

for any fuzzy numbers $\tilde{A} = [A_{L}(\alpha ),A_{U}(\alpha )]$ and $\tilde{B} = [B_{L}(\alpha ),B_{U}(\alpha )]$. For any $\tilde{A} \in F(R)$, a general f-trapezoidal fuzzy number $T_{f}(\tilde{A}) \in F_{T}(R)$ is called the f-trapezoidal approximation of $\tilde{A}$ if it satisfies

$$\displaystyle{d(\tilde{A},T_{f}(\tilde{A})) \leq d(\tilde{A},\tilde{X}),\forall \tilde{X} \in F_{T}(R).}$$

While $f(\alpha ) = 1-\alpha$, it is the trapezoidal approximation of $\tilde{A}$ which had been studied by Abbasbandy and Asady, and while $f(\alpha ) = {(1-\alpha )}^{s}$, it is called the semi-trapezoidal approximation which was first studied by Nasibov and Peker and improved by Ban and Yeh, independently. Similarly, for any $\tilde{A} \in F(R)$, a general f-triangular fuzzy number $\Delta _{f}(\tilde{A}) \in F_{\Delta }(R)$ is called the f-triangular approximation of $\tilde{A}$ if it satisfies

$$\displaystyle{d(\tilde{A},\Delta _{f}(\tilde{A})) \leq d(\tilde{A},\tilde{X}),\forall \tilde{X} \in F_{\Delta }(R).}$$

In this paper, we study the f-trapezoidal approximation and the f-triangular approximation of any fuzzy number which will both generalize and make a survey of the recent approximations.

3 Main Results

Let $\tilde{A} \in F(R)$. For convention, let’s fix the following real numbers:

$$\displaystyle{a =\int _{ 0}^{1}\lambda (t)\mathrm{d}t,\quad b =\int _{ 0}^{1}f(t)\lambda (t)\mathrm{d}t\quad b =\int _{ 0}^{1}f{(t)}^{2}\lambda (t)\mathrm{d}t}$$

and

$$\displaystyle\begin{array}{rcl} l& =& \int _{0}^{1}A_{ L}(t)\lambda (t)\mathrm{d}t,\quad l_{f} =\int _{ 0}^{1}A_{ L}(t)f(t)\lambda (t)\mathrm{d}t {}\\ u& =& \int _{0}^{1}A_{ U}(t)\lambda (t)\mathrm{d}t,\quad u_{f} =\int _{ 0}^{1}A_{ U}(t)f(t)\lambda (t)\mathrm{d}t {}\\ \end{array}$$

Note that a, b, c ≥ 0 and that by applying Cauchy inequality we have ac − b ² ≥ 0. Since f = f(x) is not constant, we have ac − b ² > 0, which implies the matrixes

$$\displaystyle{\phi := \left [\begin{array}{ll} a\ \ \ \ \ b\ \ \ \ 0\ \ \ \ 0\\ b\ \ \ \ c\ \ \ \ 0\ \ \ \ 0 \\ 0\ \ \ \ 0\ \ \ \ a\ \ \ \ b\\ 0\ \ \ \ 0\ \ \ \ b\ \ \ \ c \end{array} \right ],\quad \psi := 4\left [\begin{array}{ll} 2a\ \ \ \ \ b\ \ \ \ b\\ b\ \ \ \ \ \ c\ \ \ \ \ 0 \\ b\ \ \ \ \ \ 0\ \ \ \ \ c \end{array} \right ]}$$

are invertible. It is easy to verify that

$${\displaystyle{\phi }^{-1} = \frac{1} {{(ac - {b}^{2})}^{2}}\left [\begin{array}{lccc} c & - b& 0 & 0 \\ - b& a & 0 & 0 \\ 0 & 0 & c & - b \\ 0 & 0 & - b& c\\ \end{array} \right ],{\quad \psi }^{-1} = \frac{1} {2c(ac - {b}^{2})}\left [\begin{array}{lccc} {c}^{2} & - bc & - bc \\ - bc&2ac - {b}^{2} & {b}^{2} \\ - bc& {b}^{2} & 2ac - {b}^{2} \end{array} \right ]}$$

Also, we define real functions $s_{i} = s_{i}(\tilde{A})$ and $t_{i} = t_{i}(\tilde{A})$ by $(s_{1},s_{2},s_{3},s_{4}) := {(l,l_{f},u,u_{f})\phi }^{-1}$

and $(t_{1},t_{2},t_{3}) := {(l + u,l_{f},u_{f})\psi }^{-1}$.

Now, let’s define four subsets of fuzzy numbers as follows:

Lemma 1.

The four subsets $\Gamma _{i},1 \leq i \leq 4$ , are disjoint and form a partition of fuzzy numbers.

Theorem 2.

Let $T(\tilde{A}) \in F(R)$ and let $T(\tilde{A})$ be its general f-trapezoidal approximation. Then, $T(\tilde{A})$ can be computed in the following cases: If, then

• If $\tilde{A} \in \Gamma _{1}$ , then $T(\tilde{A}) = [s_{1} + s_{2}f(a),s_{3} + s_{4}f(a)]$.

• If $\tilde{A} \in \Gamma _{2}$ , then $T(\tilde{A}) = [t_{1} + t_{2}f(a),t_{1} + t_{3}f(a)]$.

• If $\tilde{A} \in \Gamma _{3}$ , then $T(\tilde{A}) = [x,x + yf(a)]$ , where $(x,y) = (l+u,u_{f}){\left [\begin{array}{ll} 2a\ \ \ \ b\\ b\ \ \ \ c\end{array} \right ]}^{-1}$.

• If $\tilde{A} \in \Gamma _{4}$ , then $T(\tilde{A}) = [x + yf(a),x]$ , where $(x,y) = (l+u,l_{f}){\left [\begin{array}{ll} 2a\ \ \ \ b\\ b\ \ \ \ c\end{array} \right ]}^{-1}$.

Theorem 3.

Let $T(\tilde{A}) \in F(R)$ and let $\Delta (\tilde{A})$ be its general f-triangular approximation. Then, $\Delta (\tilde{A})$ can be computed in the following cases: If $\tilde{A} \in \Gamma _{1}\bigcup \Gamma _{2}$ , then $T(\tilde{A}) = [t_{1} + t_{2}f(a),t_{1} + t_{3}f(a)]$

• If $\tilde{A} \in \Gamma _{3}$ , then $T(\tilde{A}) = [x,x + yf(a)]$ , where $(x,y) = (l+u,u_{f}){\left [\begin{array}{ll} 2a\ \ \ \ b\\ b\ \ \ \ c\end{array} \right ]}^{-1}$.

• If $\tilde{A} \in \Gamma _{4}$ , then $T(\tilde{A}) = [x + yf(a),x]$ , where $(x,y) = (l+u,l_{f}){\left [\begin{array}{ll} 2a\ \ \ \ b\\ b\ \ \ \ c\end{array} \right ]}^{-1}$.

4 Algorithm and Examples

In the previous section, we have presented formulas for computing the general f-trapezoidal approximation $T(\tilde{A})$ and the general f-triangular approximation $\Delta (\tilde{A})$ of any fuzzy number $\tilde{A}$. In the process of applying Theorems 2 and 3, we need to determine which one subset $\Gamma (i),1 \leq i \leq 4$, the given fuzzy number $\tilde{A}$ belongs to. In the following algorithm, we straightforwardly compute $T(\tilde{A})$. It is really more efficient.

4.1 Algorithm 4

Let $\tilde{A} = [A_{L}(\alpha ),A_{U}(\alpha )]$ be a fuzzy number and $T(\tilde{A})$ be general f-trapezoidal approximation of $\tilde{A}$.

• Step 1. Compute the following objectives: a,b,c and $l,l_{f},u,u_{f}$.

• Step 2. Compute ϕ, ϕ ^− 1, and $(s_{1},s_{2},s_{3},s_{4}) = {(l,l_{f},u,u_{f})\phi }^{-1}$. If $s_{1} \leq s_{3}$, then $T(\tilde{A}) = [s_{1} + s_{2}f(a),s_{3} + s_{4}f(a)]$.

• Step 3. Otherwise, compute ψ, ψ ^− 1, and $(t_{1},t_{2},t_{3}) = {(l + u,l_{f},u_{f})\psi }^{-1}$.

• Step 4. If t ₂ ≤ 0 and t ₃ ≥ 0, then $T(\tilde{A}) = [t_{1} + t_{2}f(a),t_{1} + t_{3}f(a)]$.

• Step 5. If t ₂ > 0, then $T(\tilde{A}) = [x,x + yf(a)]$, where $(x,y) = (l+u,u_{f}){\left [\begin{array}{ll} 2a\ \ \ \ b\\ b\ \ \ \ c\end{array} \right ]}^{-1}$.

• Step 6. If t ₃ < 0, then $T(\tilde{A}) = [x + yf(a),x]$, where $(x,y) = (l+u,l_{f}){\left [\begin{array}{ll} 2a\ \ \ \ b\\ b\ \ \ \ c\end{array} \right ]}^{-1}$.

Note that, to obtain an algorithm for computing the general f-triangular approximation $\Delta (\tilde{A})$ of $\tilde{A}$, it only drops Step 2 from the above Algorithm 4.

4.2 Example 5

Let $f(t) = 1 - {t}^{2}$, λ(t) = t, and $\tilde{A} = {[\alpha }^{4},3 -\sqrt{\alpha }]$,0 ≤ α ≤ 1. Find the general f-trapezoidal approximation $T(\tilde{A})$ and the general f-triangular approximation $\Delta (\tilde{A})$ of $\tilde{A}$. First, we apply Algorithm 4 to compute the general f-trapezoidal approximation of $\tilde{A}$, as follows. By Step 1, it is easy to verify that

$$\displaystyle{a = \frac{1} {2},\quad b = \frac{1} {4},\quad c = \frac{1} {6},\quad l = \frac{1} {6},\quad l_{f} = \frac{1} {24},\quad u = \frac{11} {10},\quad u_{f} = \frac{103} {180}.}$$

Therefore, by Step 2 we compute

$$\displaystyle{\phi = \left [\begin{array}{ll} \frac{1} {2}\ \ \ \ \frac{1} {4}\ \ \ \ 0\ \ \ \ 0 \\ \frac{1} {4}\ \ \ \ \frac{1} {6}\ \ \ \ 0\ \ \ \ 0 \\ 0\ \ \ \ 0\ \ \ \ \frac{1} {2}\ \ \ \ \frac{1} {4} \\ 0\ \ \ \ 0\ \ \ \ \frac{1} {4}\ \ \ \frac{1} {6} \end{array} \right ]\ \ \ {\mbox{ and}\ \ \ \phi }^{-1} = 4\left [\begin{array}{ll} 2\ \ \ \ \ \ 3\ \ \ \ 0\ \ \ \ \ \ \ 0\\ - 3\ \ \ \ 6\ \ \ \ 0\ \ \ \ \ \ 0 \\ 0\ \ \ \ \ \ \ 0\ \ \ \ 2\ \ \ \ - 3\\ 0\ \ \ \ \ \ \ 0\ \ \ - 3\ \ \ \ 6 \end{array} \right ].}$$

Hence, we obtain

$$\displaystyle{(s_{1},s_{2},s_{3},s_{4}) = {(l,l_{f},u,u_{f})\phi }^{-1} = (\frac{5} {6},-1, \frac{29} {15}, \frac{8} {15})}$$

Since $s_{1} \leq s_{3}$, the general f-trapezoidal approximation of $\tilde{A}$ is

$$\displaystyle{T(\tilde{A}) = [\frac{5} {6} - (1 {-\alpha }^{2}), \frac{29} {15} + \frac{8} {15}(1 - {a}^{2})]}$$

Now, we compute the general f-triangular approximation of $\tilde{A}$. By Step 3, we compute

$$\displaystyle{\psi = \left [\begin{array}{ll} 1\ \ \ \ \ \frac{1} {4}\ \ \ \ \frac{1} {4} \\ \frac{1} {4}\ \ \ \ \frac{1} {6}\ \ \ \ 0 \\ \frac{1} {4}\ \ \ \ 0\ \ \ \ \frac{1} {6}\\ \end{array} \right ]\ \ \ {\mbox{ and}\ \ \ \psi }^{-1} = 4\left [\begin{array}{ll} 4\ \ \ \ 6\ \ \ \ - 6\\ - 6\ \ \ \ 15\ \ \ \ 9 \\ - 6\ \ \ \ 9\ \ \ \ 15 \end{array} \right ].}$$

Hence, we obtain

$$\displaystyle{(t_{1},t_{2},t_{3} = {(l + u,l_{f},u_{f})\psi }^{-1} = (\frac{83} {60},-\frac{73} {40}, \frac{163} {120})}$$

and the general f-triangular approximation of $\tilde{A}$ is

$$\displaystyle{\Delta (\tilde{A}) = [\frac{83} {60} -\frac{73} {40}(1 {-\alpha }^{2}), \frac{83} {60} + \frac{163} {120}(1 {-\alpha }^{2})]}$$

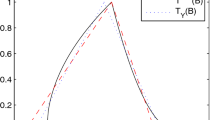
as shown in the following figures:

5 Conclusions

In this paper, we propose two more general approximations of fuzzy numbers, named general f-trapezoidal approximation and general f-triangular approximation. In practices, you can see situation of shape of the given fuzzy number. Then, pick out a suitable function f = f(x), which must be decreasing and left continuous such that f(0) = 1 and f(1) = 0, and pick out a weighted function λ = λ(t) (in general, you can simply choose λ(t) = 1 ). Consequently, apply the proposed Algorithm 4 to compute its general f-trapezoidal approximation and/or f-triangular approximation.