1 Introduction

Clustering is one of the most essential tasks in machine learning [1, 2]. Its main aim is to find a data grouping in such a way that the similarities among data pairs of the same group are as much as possible and the similarities among data pairs of the different groups are as small as possible. It can be used in image processing [3] and image segmentation [4], feature extraction [5] and feature reduction [6], geospatial data clustering [7, 8].

However, applying different clustering algorithms or the same clustering algorithm with different initializations on a same given data-set can result in diverse base clusterings. One of the most challenging issues in clustering task can be to select the best method to cluster a given data-set or at least to find an appropriate clustering algorithm. Strehl and Ghosh [9] proposed a clustering ensemble which combines all clustering results rather than finds the best one. Although clustering ensemble has been applied to many scenarios, not all solutions make positive contribution to the final result. Many existing clustering ensemble algorithms combine all clustering solutions, however, some others find that only merging partial solutions produces better results than combining all solutions [10,11,12,13,14,15,16,17]. Wang et al. [14] regarded selecting solutions as the problem of unsupervised feature selection based on the significance of attribute in rough set theory. Naldi et al. [12] selected solutions based on relative validity indexes. Ni et al. [13] selected solutions based on fractal dimension and projection.

Clustering ensemble is characterized by scalability, high robustness, stability, and parallelism. It combines all results of different clustering algorithms and it can be extended with the increase of clustering algorithms. The experiments in [18] showed that clustering ensemble outperforms single clustering algorithm and it is suitable for more datasets than one single clustering algorithm. Clustering ensemble is robust against noise and it works well on heterogeneous datasets [19, 20]. One of the process in clustering ensemble is combining multiple solutions and this makes clustering ensemble parallel. In addition, clustering ensemble has an advantage in privacy protection and knowledge reuse. It only needs to access clustering solutions rather than original data, so it provides privacy protection for original data [21]. Clustering ensemble produces final partition by using the results of different clustering algorithms. Therefore, clustering ensemble has the characteristics of knowledge reuse [22].

Traditional clustering ensemble contains two main steps: diversity generation and consensus function. The common methods of diversity generation are heterogeneous ensemble, homogeneous ensemble, resampling and projecting data into random subspace [21, 23,24,25,26,27]. The common consensus functions are voting approach, pairwise approach, graph-based approach, feature-based approach, and etc. ([28, 29]; Iam-On andBoongoen 2015; [30, 31]). In addition, the research on clustering ensemble is focused on the selection of solutions. Recently, Yousefnezhad et al. defined selective clustering ensemble in [16]. Selective clustering ensemble selects solutions from solutions library according to some benchmark. Then the consensus function only merges the selected solutions rather than combines all solutions.

Among different aspects to consensus, it is more introduced as a kind of machine learning system consisting of a group of individual and parallel work models. In order to obtain a unique solution to a problem, all inputs of the model are integrated through a decision integration strategy [32]. Based on the above definitions, ensembles methods were initially utilized in the supervised learning. Researchers sought to apply a unique unsupervised learning paradigm due to its successful clustering since the past decade. There are two reasons for application of these methods particularly in clustering problems. First, there is not any knowledge about expected types of specific features and structures or about an expected desired data solution [33, 34].

The clustering ensembles cover the extremely data-dependent performance of a large number of basic clustering algorithms. An appropriate data partition can be provided by a certain clustering algorithm, but it can have a weak performance for other types of data. Clustering algorithms may generally face two serious challenges; first, different types of algorithms may find similar dataset with unequal structures; For instance, k-means is probably the most suitable algorithm for globular clusters. Second, a unit clustering algorithm with a variety of parameters may indicate various structures in the same dataset. Accordingly, it is highly challenging to select the best type of clustering algorithm for a target dataset. A new method based on the integration of some basic partitions is another mechanism solving this challenge. This method is called the cluster ensemble.

A clustering ensemble, called the combined clustering, easily defines a similar clustering method that it in fact combines several clustering partitions in a single consensus partition [9]. A clustering algorithm will be efficient if it provides higher reliability, accuracy and consistency than other individual algorithms of clustering.

Nevertheless, it is impossible to provide a clear conceptual definition for transforming the supervised to unsupervised learning since there are various problems in performing an ensemble clustering. Despite these issues, it is difficult to integrate clusters that are created by clustering partitions (each of these partitions are called a member).

It cannot be done in an ensemble method through a voting straightforward or average-based method because it is feasible in an ensemble classifier; hence, there is a need for complex consensus functions. There are not any efficient and consensus functions in the real world, but it will be possible over time.

The present paper sought to analyze and describe the role of a three-layer aggregator in framework of a clustering ensemble. First, we converted each cluster into a cluster representation, and then we measured the rate of similarity between initial clusters and recombined the highly similar clusters in order to create final k clusters. In the third step, we selected desired clusters for uncertain objects. We created the last partition through successive uncertain objects with the minimum impact on their quality. In summary, the present paper provided an ensemble clustering algorithm on the basis of integrating basic clustering partitions with a three-step process. We then examined this method on numerous datasets and compared it with several methods of the state of the art.

While it has been shown that soft clustering algorithms are capable of producing better clustering results [35], fuzzy clustering ensemble has a little share in clustering ensemble research. Fuzzy clustering ensemble, while being severely ignored, has turned out as a hot topic recently ([19, 23, 36,37,38,39,40,41,42]; Li and Chen, 2018). It has been shown that a clustering ensemble framework with fuzzy clusters can outperform the same clustering ensemble framework with hard clusters [39]. Therefore, we focus on extending the proposed method to be applicable to fuzzy clusters.

The paper can be considered as adescendant of DICLENS. However, it is completely different from DICLENS in terms of the following 3 items: (1) they use different base clustering algorithms, (2) they define clustering similarity different from each other, and finally (3) they use different mechanisms to assign data objects to meta clusters. In fact,this method can be also considered as an advanced version of the method in 2015 [43], and it presents a dual similar clustering ensemble method. DSCE algorithm was developed in terms of three aspects. First, sustainability of the DSCE in generation of the final clustering result was improved through the pre-defined k value even though members had a variety of clusters. Second, the impact of parameters namely,α1 and α2, was decreased on the quality of results through a suitable adaptive strategy for their threshold values. Third, the similarity of adjacent objects was calculated for uncertain objects, and thus no information was removed when an inappropriate cluster was omitted. The proposed method, while taking all advantages of the DSCE algorithm, removes its disadvantages: (1) the parameters namely,α1 and α2, have been removed, and (2) fuzzy clusters can also be used instead of hard clusters. Therefore, the main motivation of the paper is to propose a fuzzy clustering ensemble, while using the cluster clustering idea of DSCE and DICLENS. The proposed method is also better than DSCE because it has no parameter to be tuned and is also applicable to fuzzy clusters. It is also better than DICLENS, because of its flexibility in cluster-cluster similarity definition and its applicability to fuzzy clusters.

Other sections of research were organized as follows. In the Section 2, we introduced the clustering ensemble method as well as a framework for the general clustering ensemble. In the Section 3, we explained the relevant studies; and described details of an appropriate clustering ensemble method and also its different stages in the Section 4. Section 5 presented empirical studies and section 6 provided results of real datasets. Section 7 presented the analyses of parameters and time complexity of our method, and ultimately, the Section 8 presented the conclusion.

2 Clustering ensemble

2.1 Problem definition

Dataset

A dataset is denoted by D and is a set of data points. The ith data point in dataset D is denoted by Di. The size of dataset D is denoted by |D|.

Partition

A dataset partition or a dataset clustering over dataset D is denoted by ϕ(D, c) and is defined as a set of clusters, i.e. ϕ(D, c) = {C(ϕ(D, c), 1), C(ϕ(D, c), 2), C(ϕ(D, c), 3), …, C(ϕ(D, c), c)} where c is number of clusters, and C(ϕ(D, c), i) is the ith cluster in clustering ϕ(D, c).

Fuzzy cluster

A cluster in a dataset partition or a dataset clustering ϕ(D, c)is denoted by C(ϕ(D, c), i) and is defined as a fuzzy set as follows

$$ C\left(\phi \left(D,c\right),i\right)=\left\{\left({D}_1,{\mu}_{C\left(\phi \left(D,c\right),i\right)}\left({D}_1\right)\right),\left({D}_2,{\mu}_{C\left(\phi \left(D,c\right),i\right)}\left({D}_2\right)\right),\dots, \left({D}_{\left|D\right|},{\mu}_{C\left(\phi \left(D,c\right),i\right)}\left({D}_{\left|D\right|}\right)\right)\right\} $$
(1)

where μC(ϕ(D, c), i)(Dj) is membership function indicating how much the jth data point belongs to the ith cluster in clustering ϕ(D, c). It worthy to be mentioned that for all j ∈ {1, 2, …|D|} we have \( \sum \limits_{i=1}^c{\mu}_{C\left(\phi \left(D,c\right),i\right)}\left({D}_j\right)=1 \) and for all j ∈ {1, 2, …|D|} and i ∈ {1, 2, …, c} we have μC(ϕ(D, c), i)(Dj) ≥ 0.

Clustering ensemble

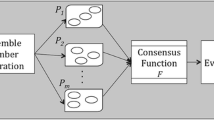
An ensemble is a set of dataset clusterings over a dataset D and it is denoted by Φ(D, b) = {ϕ1(D, c1), ϕ2(D, c2), …, ϕb(D, cb)}where b is ensemble size, ϕj(D, cj) is the jth clustering on the dataset D into cj clusters.

It is worthy to be mentioned that the number of clusters in the members of ensemble may differ from each other and from the real number of clusters; i.e. ci ≠ cj ≠ c.

In the clustering ensemble field, there are two problems. The first one is to find a diverse ensemble;this problem is considered as ensemble generation problem. The second one is to find an aggregated clustering, called a consensus partition,which has the most agreement among the ensemble members;this problem is considered as consensus function problem. The consensus partition is denoted by ϕ∗(D, c). The mentioned two problems in clustering ensemble have been discussed in the next two subsections.

2.2 Ensemble creation problem

The first step for framework of clustering ensemble is the creation of ensemble members. This step aims to generate basic b fuzzy clustering results of {ϕ1(D, c1), ϕ2(D, c2), …, ϕb(D, cb)}. Furthermore, produced members should be different in order to uncover different data structures. These members can increase the performance of consensus clustering, and thus it is essential applying one or more creation methods to access to logical quality with this diversity.

Several researchers applied the problem-based creation method. Strehl and Ghosh [9] utilized some clustering algorithms with numerous data sub-spaces, applied several features, and generated members on them for large-dimension data. They also applied a sub-sampling for objects. Fern and Brodley [44] applied a same approach; for instance, data partitions were obtained for implementing data in a variety of sub-spaces.

Breiman [45] introduced a re-sampling method in machine learning, and it was then developed and improved by Minaei-Bidgoli et al. [46]. Parvin and Minaei-Bidgoli [41] applied an ensemble generation method by the fuzzy clustering. We can generate a different accurate ensemble through the Fuzzy Weighted Locally Adaptive Clustering (FWLAC) algorithm. According to bagging and boosting algorithms in the classification, Minaei-Bidgoli et al. [46] and Parvin et al. [47] also investigated the weighing and non-weighing-based sampling methods for the ensemble generation.

To make the use of a subset of initial members in the ensemble, Alizadeh et al. [23] introduced an ensemble clustering framework instead of applying all previous cases. Accordingly, the qualitative metric, the Normalized Mutual Information (NMI) was utilized to determine the target clustering. However, setting an appropriate NMI threshold depends on data and needs the domain knowledge.

The kmeans clustering algorithm is probably the highly multifaceted clustering algorithm for generating ensemble components due to its simplicity and fastness ([47]; and [46]). For instance, Alizadeh et al. [48] applied the kmeans clustering algorithm consisting of cluster centers with random start or a random c (cluster number) at a target clustering range. Strehl and Ghosh [9] made use of various distance functions for members to take the advantage of a graph clustering algorithm. Furthermore, Topchy et al. [49] applied a weak clustering algorithm with slightly accurate clustering outcomes than the random predictor.

Iam-on et al. [50] used a variety of methods consisting of several kmeans with a fixed number of clusters for all basic partitions as well as selecting a cluster number randomly from a set of \( \left\{2,3,\dots, \sqrt{\left|D\right|}\right\} \). Iam-on et al. [51] also made use of different ensemble creation methods.

Other researchers utilized a variety of basic clustering algorithms for generating ensemble elements. They also applied kmeans and hierarchical clustering algorithms as basic algorithms ([52]; and [53]).

Alizadeh et al. created ensembles based on the concept of the Wisdom of Crowds [48]. This phenomenon, which is established in social sciences, refers to the application of criteria in the group behavior. Group decisions are probably better than individual members due to the fulfilled criteria. Accordingly, the Wisdom of Crowds Cluster Ensemble (WOCCE) was introduced due to its ability to analyze necessary conditions for ensembles in order to indicate their collective wisdom. This process also covered diverse conditions in ensembles, decentralization of generated base clustering, and independence condition among base algorithms.

Akbari et al. [21] proposed the Hierarchical Cluster Ensemble Selection (HCES) method and the diversity measure for determining effects of diversity and quality on final results since there was an uncertain relationship between the diversity and quality. They utilized single, average, and full linkage agglomerative techniques for hierarchical members.

2.3 Consensus function

An consensus function is a function that gives the final consensus partition of ϕ∗(D, c) amd gets the number of desired clusters, i.e. c, and ensembleΦ(D, b) (i.e. base clustering elements) as their inputs. Most researchers consider the consensus function step as the most important components in ensembles.

Alqurashi and Wang [54] analyzed a number of consensus functions. There are generally two groups of consensus functions in the clustering ensembles as follows: (a) heuristic category, and (b) the median clustering category.

The first group seeks to find an extracted consensus partition heuristically, for example from the Co-Association (CA) matrix. This category consists of direct approaches such as the conventional voting method; feature-based approaches such as Bayesian consensus clustering method; graph-based approaches such as the hyper-graph partitioning algorithm; and pairwise similarity-based approaches such as the CA-based method.

Some of the cluster ensemble methods have designed solutions for problem of integrating initial partitions as optimization processes; hence, the information is in bit strings of 0–1 among ensemble members. Similarly, Alizadeth et al. [23] introduced the objective and nonlinear constraint function called the fuzzy string objective function (FSOF) in order to find a median partition by maximizing the agreement between ensemble members and at the same time minimizing the disagreement.

3 Related work

Mapping ensembles into a CA matrix [9] is the most widely used clustering ensemble method. The consensus partition can be then obtained by application of a hierarchical clustering method.

The CA matrix-based clustering ensemble methods prevent the label matching problem by mapping consensus members inside a new representation with computed similarity matrix between a pair of objects as members with the same pair of objects. Fred and Jain [55] obtained the consensus clustering through utilizing average and single-linkage hierarchical clustering algorithms. When there is pairwise information in clustering ensembles, the CA is suitable for clustering as the CA merely considers the relationship of object pairs in consensus members.

Combining boosting and bagging strengths, Yang and Jiang [56] introduced a novel hybrid sampling for cluster ensembles.

Furthermore, Bai et al. [57] introduced a new information-entropy based community description model. They found that the information theory was an appropriate tool for analyzing clusters.

Strehl and Ghosh [9] provided a graph-based consensus function called the Cluster-based Similarity Partitioning Algorithm (CSPA) that considered the CA matrix as a hyper graph. Each row (data point) was considered as a node; and each column as a hyper edge in which the entry matrix value indicated the node membership value to the hyper edge. Afterwards, the hyper graph was partitioned into target numbers of clusters through a graph-partitioning algorithm like HMETIS [58]. They also introduced other hyper-graph partitioning algorithms such as the Meta Clustering Algorithm (MCLA) and the Hyper-Graph Partitioning Algorithm (HGPA) considering each data as a node and each cluster as a hyper-edge.

Fern and Brodley [59] introduced a membership binary matrix for a bipartite graph according to the CSPA, and then applied a graph-partitioning algorithm such as HMETIS for extracting consensus partitions. Their method was called the hybrid bipartite graph formulation (HBGF) algorithm.

Iam-on et al. [28] introduced another advanced CA on the basis of clustering ensemble in order to apply relationships of clusters and redefine the CA matrix. For generation of the final consensus partition, a common clustering algorithm applied this similarity matrix.

Mimaroglu and Aksehirli [67] introduced a new clustering ensemble approach on the basis of a new definition of the similarity. This approach applied a matrix like CA, but each entry determined the similarity of clusters.

This can be measured according to the co-association matrix between two objects in two various clusters indicating the similarity of clusters.

Alqurushi and Wang (2014) introduced a new approach to the clustering ensemble that applied the neighboring relationships of pairs of objects as well as real relationships of pairs in order to measure the similarity matrix. Huang et al. [60] examined and developed the aforementioned approach.

Huang et al. [61] provided an approach to examination of a clustering ensemble problem as a linear binary programming problem for automatic determination of number of clusters.

4 Proposed consensus function

A consensus function is a very important element in clustering ensemble. Indeed, it has a great effect on the efficacy of clustering ensemble. We want to propose a consensus function which is efficient and fast. The proposed consensus function inspires from the co-association based clustering ensemble, but it also bypasses its high computational cost through hierarchical cluster clustering. It first defines a between-cluster similarity measure. Using the mentioned between-cluster similarity measure, a similarity matrix is generated where its columns and rows (in spite of co-association matrix) are base clusters produced in the ensemble generation phase. Then the clusters are merged into new defined clusters. A new cluster-sample similarity measure is also introduced to determine how much a data sample belongs to a newly generated clusters.

Between-Cluster Similarity measure is denoted by \( {Sim}_{P,Q}^{CC} \) where P and Q are two fuzzy base clusters. It is defined based on eq. 2.

$$ {\displaystyle \begin{array}{l} Si{m}_{P,Q}^{CC}=\frac{\sum_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right){\mu}_Q\left({D}_j\right)-\mid D\mid \times \frac{\sum_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right)}{\mid D\mid}\times \frac{\sum_{j=1}^{\mid D\mid }{\mu}_Q\left({D}_j\right)}{\mid D\mid }}{\left(|D|-1\right)\times \sqrt{\frac{\sum_{j=1}^{\mid D\mid }{\left({\mu}_P\left({D}_j\right)-\frac{\sum_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right)}{\mid D\mid}\right)}^2}{\left(|D|-1\right)}\times \frac{\sum_{j=1}^{\mid D\mid }{\left({\mu}_Q\left({D}_j\right)-\frac{\sum_{j=1}^{\mid D\mid }{\mu}_Q\left({D}_j\right)}{\mid D\mid}\right)}^2}{\left(|D|-1\right)}}}=\\ {}\frac{\sum_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right){\mu}_Q\left({D}_j\right)-\frac{\sum_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right)\times {\sum}_{j=1}^{\mid D\mid }{\mu}_Q\left({D}_j\right)}{\mid D\mid }}{\sqrt{\sum_{j=1}^{\mid D\mid }{\left({\mu}_P\left({D}_j\right)-\frac{\sum_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right)}{\mid D\mid}\right)}^2\times {\sum}_{j=1}^{\mid D\mid }{\left({\mu}_Q\left({D}_j\right)-\frac{\sum_{j=1}^{\mid D\mid }{\mu}_Q\left({D}_j\right)}{\mid D\mid}\right)}^2}}=\\ {}\frac{\mid D\mid \times {\sum}_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right){\mu}_Q\left({D}_j\right)-{\sum}_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right)\times {\sum}_{j=1}^{\mid D\mid }{\mu}_Q\left({D}_j\right)}{\mid D\mid \times \sqrt{\sum_{j=1}^{\mid D\mid }{\left({\mu}_P\left({D}_j\right)-\frac{\sum_{j=1}^{\mid D\mid }{\mu}_P\left({D}_j\right)}{\mid D\mid}\right)}^2\times {\sum}_{j=1}^{\mid D\mid }{\left({\mu}_Q\left({D}_j\right)-\frac{\sum_{j=1}^{\mid D\mid }{\mu}_Q\left({D}_j\right)}{\mid D\mid}\right)}^2}}\end{array}} $$
(2)

The mentioned similarity measure computes the correlation between two clusters [62]. The mentioned similarity measure returns a real number in the interval [−1, 1]. The mentioned similarity measure returns 0 for two completely different clusters, 1 for two similar clusters, −1 for two complementary clusters [63].

Assume the number of all clusters is denoted by a, therefore, it is defined based on eq. 3.

$$ a=\sum \limits_{i=1}^b{c}_i $$
(3)

A similarity matrix of size a × a, where a is the number of clusters and it is computed based on equation 3, denoted by Sij is defined based on equation 4.

$$ {S}_{ij}^{CC}={Sim}_{C\left({\phi}_p\left(D,{c}_p\right),r\right),C\left({\phi}_q\left(D,{c}_q\right),t\right)}^{CC} $$
(4)

where p andr are positive integers and computed based on equation 5.

$$ {\displaystyle \begin{array}{l}i={\sum}_{i=1}^{p-1}{c}_i+r\\ {}\mathrm{s}.\mathrm{t}.r\le {c}_p\end{array}} $$
(5)

and q and t are positive integers and they are computed based on equation 6.

$$ {\displaystyle \begin{array}{l}j={\sum}_{i=1}^{q-1}{c}_i+t\\ {}\mathrm{s}.\mathrm{t}.t\le {c}_q\end{array}} $$
(6)

An example has been presented here for more clarification.

The similarity matrix \( {S}_{ij}^{CC} \) is transformed into a distance matrix in the next step. The distance matrix is denoted by \( {\dot{S}}_{ij}^{CC} \) and is computed based on equation 7.

$$ {\dot{S}}_{ij}^{CC}=1-\frac{S_{ij}^{CC}+1}{2} $$
(7)

After obtaining the distance matrix, a partition is extracted on the base fuzzy clusters by applying a hierarchical average linkage clustering algorithm on the mentioned matrix; indeed, each of the base fuzzy clusters in the ensemble is considered as a data point. Each cluster of the base fuzzy clusters is denoted by ωi. The number of clusters in this step is equal to the real number of clusters in the ground truth labels. After obtaining the clusters of the base fuzzy clusters, the step one is completed.

Example I

Assume an assumptive dataset of size 13. Assume also we have run fuzzy kmeans on the mentioned assumptive dataset 5 times and the number of clusters requested from the clustering algorithm is 2, 2, 3, 3, and 3 consecutively. Assume the toy fuzzy ensemble on the mentioned assumptive dataset is the one which is depicted in Table 1. The similarity matrix computed between the fuzzy clusters of the ensemble presented in Table 1 is depicted in Table 2. The distance matrix has been computed based on similarity matrix and it is depicted in Table 3. Then the output dendrogram and clusters of the average-linkage hierarchical clustering algorithm on the distance matrix depicted in Table 3 have been represented in Fig. 1. According to the output clustering, three clusters have been emerged among the fuzzy base clusters.

Table 1 A representative assumptive ensemble with the size of five base clustering members
Full size table
Table 2 The similarity matrix computed between the fuzzy clusters of the ensemble presented in Table 1
Full size table
Table 3 The distance (or dissimilarity) matrix of the base fuzzyclusters presented in Table 1
Full size table
Fig. 1
figure 1

The output dendrogram and clusters of the average-linkage hierarchical clustering algorithm on the distance matrix depicted in Table 3

Full size image

The next step is to assign each data point to exactly one of the clusters defined on the base fuzzy clusters. We define an object-cluster membership matrix as follows.

$$ {S}_{ij}^{OC}=\frac{Sim_{D_i,{\omega}_j}^{OC}}{\sum \limits_{k=1}^c{Sim}_{D_i,{\omega}_k}^{OC}} $$
(8)

where \( {Sim}_{D_i,{\omega}_j}^{OC} \) is asimilarity measure between an object and a cluster and is defined based on equation 9.

$$ {Sim}_{D_i,{\omega}_j}^{OC}=\frac{\sum \limits_{P\in {\omega}_j}{\mu}_P\left({D}_j\right)}{\sum \limits_{P\in {\omega}_j}1} $$
(9)

Example II

Consider the previous example. The new clusters of ω1, ω2 and ω3 of the base fuzzy clusters are depicted in Table 4. The similarity measure and the object-cluster membership matrix have been also depicted in the Table 4. In the last row of the Table 4, the consensus partition has been depicted.

Table 4 The similarity measure, the object-cluster membership matrix and consensus partition of the fuzzy ensemble presented in Table 1
Full size table

To sum up the proposed method, it first produces a number of fuzzy clusterings. Then, it transforms them into a number of fuzzy clusters. After that, it makes a cluster-cluster similarity matrix whose entries indicates how much two fuzzy clusters are similar. This similarity has been estimated by fuzzy correlation. In the next step, the fuzzy clusters have been clustered into a predefined number of meta clusters according to a hierarchical clustering algorithm. In the last step, each data is assigned to exactly one meta cluster according to mean aggregation.

5 Experimental study

5.1 Datasets

The proposed method, i.e. RCESCC, has been evaluated on a set of real and artificial datasets. The real datasets,except USPS dataset which is from [64], are from the UCI machine learning repository [65]. The detailed specifications of the employed datasets are presented in Table 5. All of the artificial datasets include 2 features and 3 classes. The artificial datasets have been plotted in Fig. 2. The artificial datasets Gaussian datasets. All datasets are standardized. It means that any feature in any datasets is transformed into a new feature which comes from N(0, 1) distribution. Features with missing values are also removed from the datasets.

Table 5 Detailed specifications of the employed datasets
Full size table
Fig. 2
figure 2

Artificialdatasets

Full size image

5.2 Parameter setting

Like the approach employed by Ren et al. [66],an ensemble of size 200, i.e. b = 200, is produced. A set of 100 subsets is prepared, each of them is extracted by a bootstrapped subsampling out of the given dataset. Each of them contains 80% of all data points in the dataset. A fuzzy cmeans algorithm is run on each of bag, and then for the missing data points in the bag, according to distance of the data point to the representators of fuzzy clusters,the membership values of the data point to all fuzzy clusters are computed. Therefore, it means that a fuzzy partition is obtained for each bag on all of data points. An additional set of 100 base fuzzy clusterings on the given dataset are created through applying fuzzy cmeans on 100 subspaces of the given dataset. Each subspace includes half of randomly selected features.

The recent works which have been used as baseline methods include HBPGF [59], CO-AL [55], SRS (Iam-On et al., 2008), WCT [28], DICLENS [67], ONCE-AL[54], CSEAC [68], DSCE [43], WCE [48], WEAC [69], GPMGLA [69], TME [29], ECSEAC [41], DSCE [43], FSCEOGA1 [23] and CLWEAC [39]. All reported results in the paper are averaged over 100 independent runs. All methods use their default values mentioned in their corresponding papers for their parameters. Ensemble size is 200 throughout all the paper experiments.

5.3 Evaluation metrics

Four different metrics are used in the experimental results: Adjust Rand Index (ARI), Normalized Mutual Information (NMI), Accuracy (ACC) and F-Measure (FM). ARI is defined based on equation 10.

$$ ARI\left({P}^{\ast },{L}^t\right)=\frac{\sum \limits_{i=1}^c\sum \limits_{j=1}^c\left(\begin{array}{c}{n}_{ij}\\ {}2\end{array}\right)-\frac{\sum \limits_{i=1}^k\left(\begin{array}{c}{n}_i^{\ast}\\ {}2\end{array}\right)\times \sum \limits_{j=1}^k\left(\begin{array}{c}{n}_j^t\\ {}2\end{array}\right)}{\left(\begin{array}{c}n\\ {}2\end{array}\right)}}{\frac{\sum \limits_{i=1}^c\left(\begin{array}{c}{n}_j^{\ast}\\ {}2\end{array}\right)+\sum \limits_{j=1}^c\left(\begin{array}{c}{n}_j^t\\ {}2\end{array}\right)}{2}-\frac{\sum \limits_{i=1}^c\left(\begin{array}{c}{n}_i^{\ast}\\ {}2\end{array}\right)\times \sum \limits_{j=1}^c\left(\begin{array}{c}{n}_j^t\\ {}2\end{array}\right)}{\left(\begin{array}{c}n\\ {}2\end{array}\right)}} $$
(10)

where P∗ is the consensus partition, Lt is the ground-truth labels of the given dataset, n is the total number of objects in given dataset X, nij is the number of objects in the intersection of the ith clusterof P∗ and the jth cluster of Lt, \( {n}_i^{\ast } \) and \( {n}_j^t \)are the number of objects in the ith cluster in P∗and the number of objects in the jth cluster in Ltrespectively. The expression \( \left(\genfrac{}{}{0pt}{}{n}{2}\right) \)stands for the binomial coefficient.

NMI is defined as follows:

$$ NMI\left({P}^{\ast },{L}^t\right)=\frac{\sum \limits_{i=1}^c\sum \limits_{j=1}^c{n}_{ij}{\log}_2\left(\frac{n{n}_{ij}}{n_i^{\ast }{n}_j^t}\right)}{\sqrt{\sum \limits_{i=1}^c{n}_i^{\ast }{\log}_2\left(\frac{n_i^{\ast }}{n}\right)\times \sum \limits_{i=1}^c{n}_j^t{\log}_2\left(\frac{n_j^t}{n}\right)}} $$
(11)

ACC is another metric based on that to evaluate quality of the different partitions. But to compute this metric, the partitions should be relabeled in order to match maximally with the ground-truth labels. This problem is handled by the Hungarian algorithm [70]. FM is the last criterion employed in this paper to assess quality of a partition and is defined based on equation 12.

$$ FM\left({P}^{\ast },{L}^t\right)=\underset{\sigma }{\max}\sum \limits_{j=1}^c\frac{2{n}_{\sigma (j)}^{\ast}\frac{n_{\sigma (j)j}}{n_j^t}\times \frac{n_{\sigma (j)j}}{n_{\sigma (j)}^{\ast }}}{n\left(\frac{n_{\sigma (j)j}}{n_j^t}+\frac{n_{\sigma (j)j}}{n_{\sigma (j)}^{\ast }}\right)} $$
(12)

where σ is a permutation of {1, 2, …, c} and σ(i) is the ith value in the permutation σ, i.e. ∀i ∈ {1, 2, …, c} : σ(i) ∈ {1, 2, …, c} and ∀i, j ∈ {1, 2, …, c} : (σ(i) = σ(j)) → (i = j).

Each of the mentioned criteria (ARI, NMI, FM, and ACC) is bounded in [0, 1]. While the values near to zero indicate the two input partitions are the independent clusterings,the values near to one indicate the two input partitions are the identical clusterings.

5.4 Experiments

Figure 3 depicts the performance of proposed method comparing with the state of the art methods in terms of NMI. The numbers of times that the proposed method wins/draws with/loses to other methods validated by paired t-test are summarized in Table 6. It is notable that we have separated the clustering ensemble methods which use fuzzy clustering from those which use hard clustering in Table 6. Therefore, we have used both fuzzy clustering ensemble and hard clustering ensemble as baseline methods in the experimental results.

Fig. 3
figure 3

The performances of different methods in terms of NMI

Full size image
Table 6 Performances of different state of the art methods comparing with performance of the proposed method, i.e. RCESCC, in terms of NMI. A triple W-D-L indicates the numbers of that the proposed method wins/draws with/loses to other methods validated by paired t-test
Full size table

Figures 4, 5 and 6 represent the performances of different methods respectively in terms of ARI, ACC, and FM.

Fig. 4
figure 4

The performances of different methods in terms of ARI

Full size image
Fig. 5
figure 5

The performances of different methods in terms of accuracy

Full size image
Fig. 6
figure 6

The performances of different methods in terms of F-measure

Full size image

Although in 6 datasets (i.e. Glass, Wine, Iris, Half-Ring, Artificial2, ISOLET) the proposed method has not shown the best results, it overshadows all other methods. Indeed, there is not a method overshadowing others, i.e. while a method may have the best result on a special dataset, it has not the best in others.

Considering the performances of the state-of-the-art methods in terms of accuracy, presented in Fig. 6, we notice several interesting outcomes. First, the performance of the proposed method is considerably better than all other methods in eight datasets, while its performance on other datasets is very close to the best. Second, the performance of the proposed method is considerably worse than some of the state-of-the-art methods only in three datasets, while its performance is still among the top three best methods. On the other datasets, the performance of the proposed method is either very close to the best, or the best with slight margin.

5.5 Time complexity

The proposed method time complexity of the worst case is member of O(c2b2 log(cb))where the approximate number of clusters by c × b (c is the real number of clusters and b is the ensemble size).

5.6 Parameter analysis

Noise effect has been examined in this subsection. For robustness analysis, we have selected the three best methods according to Table 6, i.e. RCESCC, ECSEAC and CLWEAC. We have added Gaussian noise with different energy levels and then applied these three methods. The results for Iris and Wine datasets have been depicted in Fig. 7.

Fig. 7
figure 7

The NMI results for Iris and Wine datasets in the presence of different levels of noise

Full size image

6 Conclusions and future work

Clustering ensemble has been recently a hot topic in computer science communities. It makes it possible to overcome the instability of basic clustering algorithms and therefore it can boost the clustering efficacy. There are two sub-problems in clustering ensemble: ensemble generation problem, and ensemble aggregation problem. The paper works on the second problem by presenting an ensemble clustering framework to combine the ensemble members by a fast and robust two-phase clustering method. Indeed, it uses an ensemble of fuzzy clusterings generated by the fuzzy cmeans clustering algorithm. To produce the necessary diversity in the ensemble, the subsampling has been used. The experimental results on standard UCI datasets have shown that our algorithm which uses a fast and robust two-phase clustering method performs well on almost all datasets and outperforms all the state of the art clustering ensemble algorithms.