1 Introduction

Owing to the progress and extension of technologies, science, and industries, the hazardous wastes’ volume produced by human activities have increased rapidly, and consequently associated risks included in treatment, recycling, disposing, and transportation of these dangerous wastes and especially environmental issues, have become the more attractive subject for the researchers. Hazardous waste can be characterized as flammable, irritant, poisonous, carcinogenic, toxic, infectious, and reactive (Nema and Gupta 1999). There are various ranges of industries producing hazardous waste like chemical manufacturing, oil refining, iron production, and hospitals (Samanlioglu 2013). Hazardous waste could have undesirable impacts on human health (Vrijheid 2000), and it can also influence the environment directly or indirectly (Ardjmand et al. 2016). Considering these conditions, many governments employ hazardous waste management (HWM) systems to organize collection, transportation, treatment, recycling, and disposal of these hazardous materials (Samanlioglu 2013). The main goal of using HWM systems is doing all the aforementioned processes with the minimum of cost and environmental and human bad effects (Nema and Gupta 1999). Simply say, there is a trade-off between cost and risk; for instance, from the transportation firms’ point of view, the shortest way is the optimal route; on the other hand, for the governments, the reliable path is the optimal route according to several risk factors. Moreover, hazardous wastes pass through various processes based on their type; therefore, preparation and operating costs of these processes are imposed on the HWM system (Alumur and Kara 2007).

Generally, optimization studies investigating HWMs are divided into three main categories. The first category relates to location planning due to its importance in HWM systems. Routes planning is the second category of HWM studies which emerges as the vehicle routing problem (VRP) in the HWM models. Finally, the third category is the combination of two mentioned models which is known as location routing problem (LRP). Due to the supreme importance of economic and environmental aspects of HWM, the LRP could properly formulate the concepts of HWM problems in both theoretical and practical situations and the integration of these concepts is recognized as hazardous waste location routing problem (HWLRP) (Ardjmand et al. 2016; Rabbani et al. 2018a).

In addition, job satisfaction is a new topic attracting researchers’ attention in recent years. If one organization seeks long-term success, it will consider its employee’s satisfaction level to increase productivity, responsibility, and efficiency. Therefore, employee satisfaction or dissatisfaction plays a critical role in organizational performance. One essential factor that influences on job satisfaction level is the workload. In order to increase employee satisfaction, it is necessary to balance the workload among the employees as much as possible (Matl et al. 2019; Velarde Cantú et al. 2017). Given the importance of workload balancing to increase productivity, we need to consider it as one of the study goals that has so far been ignored in previous HWM studies.

One fundamental part of the HWM systems is the scheduling of activities such as collection of wastes and other processes. To clarify the importance of this issue, imagine a facility producing explosive waste; the more scheduling of collection is irregular, the more risk is imposed to facility because of the variable amount of collected wastes in the storage; therefore, not only does time window consideration increase customer satisfaction but also it reduces the risk and the cost. Consequently, we append time windows constraints to the previous models to fill this gap.

This paper proposes a new multi-objective mathematical model for hazardous waste management, considering three objective functions including two systematic goals (cost and risk) and one social goal (workload balancing). Given the NP-hard nature of LRP problems, the proposed model is solved first by the exact method to verify model performance and then three multi-objective evolutionary algorithms, NSGA-II, PESA-II, and SPEA-II, are employed; meanwhile, an adaptive penalty function is proposed to facilitate reaching the feasible region for evolutionary algorithms. We also improved PESA-II function by removing duplicated solutions from its archive. Finally, several multi-objective evolutionary algorithm metrics including Quality Metric (QM), Mean Ideal Distance (MID), Spacing Metric (SM), Diversity Metric (DM), Hypervolume (HV), and Inverted Generational Distance (IGD) are employed to discuss the efficiency of these algorithms in HWLRP problems.

The rest of the paper is organized as follows: In Sect. 2, we review the relevant literature. In Sect. 3, the mathematical model and problem description are presented. In Sect. 4, the proposed algorithms are presented. In Sect. 5, numerical experiments and results are discussed. Finally, in Sect. 6 remarks of conclusion and future research directions are presented.

2 Literature review

The literature review is investigated in three main parts. The first part of the literature investigates hazardous waste location-routing problems. The second part focuses on the workload balancing, and the third part is assigned to the time windows and customer satisfaction. Finally, the literature gap recognition is presented at the end of this section.

2.1 Hazardous waste location routing problem

Initially, Zografos and Samara (1989) formulated HWLRP with a single type of waste. They used a goal programming method and considered travel time, transportation risk, and disposal facilities’ risk as the main criteria to locate disposal nodes and determine the optimal routes between demanding nodes. For the first time, Alumur and Kara (2007) considered some constraints which have been ignored by then such as treatment technology of each treatment center, and compatibility between treatment technology and waste in order to increase the efficiency of the model. Finally, they solved the proposed model considering a multi-type of hazardous waste and using multi-objective LRP. A new model for satisfying the air pollution standards was proposed by Emek and Kara (2007). They concentrated on incinerators’ establishment in a hazardous waste LRP and incorporated recycling and treatment facilities. In addition, they used an integer programming model considering the transportation cost and air pollution policies. The work of Samanlioglu (2013) is an example of an HWM network considering a mathematical model with three objectives. In the model, three criteria were considered: minimizing total cost, total transportation risk, and the total risk of the population around waste management sites and the author used a lexicographic weighted Tchebycheff formulation for obtaining efficient solutions from the Pareto frontier and then the model was implemented in a region of Turkey. Martínez-Salazar et al. (2014) addressed a location-routing model considering inventory risks for explosive waste management (EWM) and utilize three types of vehicle routes, direct route, and tour and a return trip in their proposed model. Ghezavati and Morakabatchian (2015) improved previous work by appending fuzzy satisfaction concepts, and human feeling factors to the previous model and also increased the flexibility of model by considering some nodes as warehouse nodes to collect the wastes. Zhao and Verter (2015) focused on hazardous material of used oil and proposed a bi-objective model for LRP in order to minimize the environmental risk and total cost. They used a modified Goal Programming (GP) approach for transforming the bi-objective model into a single objective, and then they tested the application of the proposed analytical framework in China. In addition to this study, the routes were supposed to be a tour, or in other words, the vehicle ends its tour at the starting point. Yu and Solvang (2016) presented an HWLRP model that was filling the literature gap by considering the risk level based on the type of waste and treatment technology on HWM system planning. They also used a ε-constraint method to solve the proposed model. Farrokhi-Asl et al. (2017) presented a model included heterogeneous fleet, which has multi-separated compartments and vehicles had different capacity, different travel time and distance limitation and different fixed and variable costs. Finally, the model was solved with two MOEAs [NSGA-II and Multi-Objective Particle Swarm Optimization (MOPSO)], and the results were compared with each other. The work of Rabbani et al. (2018a) is an example for HWLRP which considers constraints about the incompatibility between some kinds of wastes and incorporates routing into the model. They considered three objectives, including cost, transportation risk, and risk of hazardous waste sites. The researchers used two multi-objective evolutionary algorithms and compared their results. Aydemir-Karadag (2018) developed a profit-oriented mixed-integer mathematical model for the HWLRP considering energy recovery from waste and the application of the polluter pays principle. The auteur addressed the location and number of hazardous waste centers and waste residue flow among these centers. A rolling horizon basis through the objective function of net present value (NPV) is considered in the study, and the profitability of the HMW system was analyzed. The results verified the applicability and effectiveness of the suggested model for large-scale HWM problems. Rabbani et al. (2019) proposed a multi-objective stochastic mixed-integer nonlinear programming (MINLP) model to integrate decisions of location, routing, and inventory. The auteurs alleged that their work is novel in considering the stochastic environment, multi-period planning horizon, and inventory control decisions. They also introduced a simheuristic method which is an integration of NSGA-II and Mont Carlo simulation. The study result confirmed the efficiency of the approach to finding a high-quality solution within a reasonable time.

2.2 Workload balancing

Martínez-Salazar et al. (2014) presented a mathematical formulation, for Transportation Location Routing Problem (TLRP) with two objectives. The first objective is reducing distribution costs, and the other is balancing the workload for drivers in the routing stage. They also proposed a new representation of the model, which reduces the computation time. Cantú et al. (2017) developed a VRP network based on a mixed integer programming (MIP) model for hazardous material transportation. They integrated the design of territory and distribution routing in order to minimize routes travelled by each vehicle. They also considered hazardous material pickup and delivery costs and solved the model with an exact algorithm, and they could improve workload balancing in each territory with a central depot and tour-routes by their proposed model. Rabbani et al. (2018b) considered workload balance in a sustainable TLRP with soft time windows. The objectives of the problem are as follows: distribution cost, fuel consumption, and carbon dioxide emission minimizing and balancing the workload for city drivers. Sivaramkumar et al. (2018) considered a vehicle routing problem with time windows and they applied two balancing strategies, route balancing and total time balancing, on their study. They asserted that time balancing is superior to route balancing because in time balancing service time is considered. Finally, they solved their model under three strategies by Fitness Aggregated Genetic Algorithm (FAGA) and Fitness Aggregated Differential Evolution (FADE) and they concluded that FAGA acts better than FADE in their study.

2.3 Time window and customer satisfaction

Generally, the time windows are in two forms, hard time windows (no violation of the interval is allowed) and soft time windows (violation is allowed by paying penalties). In this study, the soft time windows are used, and consequently, our problem is converted to a Location Routing Problem Time Window (LRPTW). Zarandi et al. (2011) developed a Multi-depot Capacitated Location Routing Problem (MDCLRP) in which several parameters such as traveling time were assumed fuzzy, and they considered a time window for each node. Dotoli and Epicoco (2017) presented a method to address the VRP and scheduling problem for HWM collection and disposal. Their model allows traveling by limitations on the time window and fleet availability. They benchmark the proposed model with a real case. A simulated algorithm was used for solving the proposed model, and they concluded that their model is robust and it is suitable for practical situations. Fazayeli et al. (2018) combined multimodal routing and LRP for a product distribution problem and appended time window to their model seeking to increase customer satisfaction. They assumed that the products should be delivered at a determined time interval. Moreover, the products demands were assumed a fuzzy number and finally, a mix integer programming was developed to solve the problem. Wang et al. (2018) introduced a two-echelon time window LRP problem in which the customers were clustered based on location and purchasing behavior. They considered two objectives, minimizing costs and maximizing customers’ satisfaction affected by delivery time and also fuzzy time windows were considered in their proposed model. A modified NSGA-II was presented for problem-solving, and then, the authors demonstrated the better performance of modified NSGA-II than a multi-objective genetic algorithm (MOGA) and MOPSO regarding quality metric and computation time.

2.4 Recognizing the literature gap and contributions

According to reviewed studies and the best of our knowledge, it can be concluded that some of the momentous topics that have been overlooked in previous studies are workload balances and time windows constraints. Table 1 summarizes related literature and shows the novelty of the presented work in this paper.

Table 1 Summary of the HWLRP literature review
Full size table

Given the mentioned gaps, the contributions of our study are summarized as follows:

  • Considering workload balancing in HWLRP by minimizing the difference between each fleet crew workload and overall workload average.

  • Taking into account customer satisfaction in HWLRP by meeting customers’ time window.

  • Taking into account simultaneously waste to waste compatibility and waste to technology compatibility which are rarely addressed in the relevant literature.

  • Using three multi-objective evolutionary algorithms, NSGA-II, PESA-II and, SPEA-II for solving the problem with innovation in the structure of algorithms and developing an adaptive penalty function.

3 Problem description

3.1 Problem definition

In this study, an LRP is addressed in the case of hazardous waste management systems in which several social objectives such as customer satisfaction (as cost) and workload balance are added to previous researches. Waste to waste (waste-waste) and waste to technology (waste-technology) compatibilities are also considered in the problem. Therefore, several new constraints are appended to previous models to formulate the aforementioned contributions into the model.

In the realist scenario, there may be several heterogeneous or homogeneous containers in the fleet but, as mentioned before, waste–waste compatibility is considered in this study so, a heterogeneous fleet is assumed in order to avoid combination and interaction between incompatible wastes such as toxic waste and explosive waste. This fleet of vehicles is also different in waste capacity and route length based on the waste type.

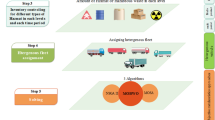
In our model, each collection vehicle starts its route at a central depot and finally ends in the same depot. After a collection vehicle visits a set of demanding nodes (based on waste compatibility) and collects their wastes, it has two different options. First, it can move to a treatment facility that is compatible with its load, and the second option is it can move to recycle centers and transposes their processed waste to the other facilities. The treatment processes produce two kinds of waste that can be categorized as recyclable and non-recyclable waste. Therefore, the recyclable part is transported to the recycling centers and the residue is transported to the disposal centers. Like the treatment centers, the recycling centers also have useless parts in their outputs which should be carried by the fleet to the disposal centers. A conceptual framework of the research model is presented in Fig. 1.

Fig. 1
figure 1

Conceptual framework of the proposed structure

Full size image

3.2 Assumptions and notations

Besides the economic goals, we should go over environmental and social risks to achieve an acceptable and proper solution for the HWM problems. As such, the three main objective functions are developed. The first one addresses economic aspects including transportation costs, facilities establishment costs, and customer time window penalties; the second objective function handles the risk aspects including transportation risk and site risk. In addition, the third objective function takes workload balance into account to increase staff satisfaction and social justice. Other assumptions are as follows:

  • We assume four types of wastes

    • Recyclable waste.

    • Non-recyclable waste which is compatible with incineration technology.

    • Non-recyclable waste which is compatible with the chemical technology.

    • Non-recyclable waste which is compatible with both technologies.

  • All of the waste types could be produced at each demanding node.

  • A time window constraint is assumed for each customer; that is, if the service time deviates from the allowed interval, a penalty cost affiliated with the amount of deviation will be imposed on the system.

  • The length of service time is zero.

  • The amount of waste in any type generated in the source node cannot surpass the collection vehicle capacity.

  • The partial waste collection is not allowed.

  • Vehicles related to any type of waste are homogeneous regarding capacity and maximum tour length.

  • Facilities in the problem have a limited capacity for processing waste.

  • Two types of treatment technologies are available, but just one of them can be applied to any treatment center.

  • A symmetric distance matrix, where the distance of the nodes is calculated from each other, is used to estimate distances in this study and transportation cost and traveling time between nodes are calculated based on the travelled distance.

  • In some of the equations presented in the proposed model, there are operators such as multiplication and absolute value that make the model nonlinear. Hence, auxiliary equations and variables are used to linearize the proposed model.

The notations of this study are represented in Table 2.

Table 2 Notations of the study
Full size table

3.3 Mathematical model

Considering the mentioned assumptions, we formulate a new multi-objective MIP model to address HWLRP which develops the model proposed by Rabbani et al. (2018a). The goals we are following for this model are as follows:

$$ \hbox{min} f_{1} \left( x \right) = \mathop \sum \limits_{i \in G} \mathop \sum \limits_{j \in G \cup T \cup R} \mathop \sum \limits_{k \in K} c_{ij} x_{ijk} l_{ik} $$
(1.1)
$$ + \mathop \sum \limits_{i \in T} \mathop \sum \limits_{j \in R} c_{ij} xtr_{ij} $$
(1.2)
$$ + \mathop \sum \limits_{i \in T} \mathop \sum \limits_{j \in F} c_{ij} xtf_{ij} $$
(1.3)
$$ + \mathop \sum \limits_{i \in R} \mathop \sum \limits_{j \in F} c_{ij} xrf_{ij} $$
(1.4)
$$ + \mathop \sum \limits_{q \in Q} \mathop \sum \limits_{i \in T - T'} ft_{qi} t_{qi} $$
(1.5)
$$ + \mathop \sum \limits_{i \in R - R'} fr_{i} r_{i} $$
(1.6)
$$ + \mathop \sum \limits_{i \in F - F'} ff_{i} f_{i} $$
(1.7)
$$ + \mathop \sum \limits_{i \in g} (p_{e} ve_{i} + p_{l} vl_{i} ) $$
(1.8)
$$ \hbox{min}\, f_{2} \left( x \right) = \mathop \sum \limits_{i \in T} \mathop \sum \limits_{w \in W} PA_{i} xt_{wi} $$
(2.1)
$$ + \mathop \sum \limits_{i \in F} PA_{i} xf_{i} $$
(2.2)
$$ + \mathop \sum \limits_{i \in G} \mathop \sum \limits_{j \in G \cup T} \mathop \sum \limits_{k \in K} pop_{ij} x_{ijk} l_{ik} $$
(2.3)
$$ + \mathop \sum \limits_{i \in T} \mathop \sum \limits_{j \in F} pop_{ij} xtf_{ij} $$
(2.4)
$$ \begin{aligned} & \hbox{min}\, f_{3} \left( x \right) = \mathop \sum \limits_{k \in K} \left| {LR_{k} - \mathop \sum \limits_{k \in K} \frac{1}{\left| K \right|}LR_{k} } \right| \\ & s.t. \\ \end{aligned} $$
(3)
$$ \mathop \sum \limits_{i \in D} \mathop \sum \limits_{j \in G} x_{ijk} = 1 \forall k \in K $$
(4)
$$ \mathop \sum \limits_{i \in D \cup G} x_{ijk} - \mathop \sum \limits_{{i^{\prime} \in G \cup R \cup T}} x_{{ji^{'} k}} = 0\quad \forall j \in G,k \in K $$
(5)
$$ \mathop \sum \limits_{j \in G \cup R \cup T} \mathop \sum \limits_{k \in K} x_{ijk} v_{wk} = 1\quad \forall i \in G,w \in W $$
(6)
$$ \mathop \sum \limits_{i \in G} x_{ijk} - \mathop \sum \limits_{{i^{\prime} \in D}} x_{{ji^{'} k}} = 0\quad \forall j \in R \cup T,k \in K $$
(7)
$$ x_{ijk} \le \mathop \sum \limits_{w \in W} \mathop \sum \limits_{q \in Q} v_{wk} com_{wq} t_{qj} \quad \forall i \in G,j \in T,k \in K $$
(8)
$$ x_{ijk} \le \mathop \sum \limits_{w \in W} v_{wk} \frac{{\left( {\left( {2 - \mathop \sum \nolimits_{q \in Q} com_{wq} } \right)r_{j} } \right)}}{2}\quad \forall i \in G,j \in R,k \in K $$
(9)
$$ e_{ik} - e_{jk} + \mathop \sum \limits_{w \in W} v_{wk} \left( {\left( {\gamma_{w} + dis_{ij} } \right)x_{ijk} + \left( {\gamma_{w} - dis_{ij} } \right)x_{jik} } \right) \le \mathop \sum \limits_{w \in W} v_{wk} \gamma_{w} \forall i,j \in G \cup R \cup T,k \in K $$
(10.1)
$$ \mathop \sum \limits_{i \in D} dis_{ijk} x_{ijk} \le e_{jk} \le \mathop \sum \limits_{w \in W} v_{wk} \left( {\gamma_{w} + \mathop \sum \limits_{i \in D} (dis_{ij} - \gamma_{w} )x_{ijk} } \right)\quad \forall i \in G,k \in K $$
(10.2)
$$ e_{ik} \le \mathop \sum \limits_{w \in W} v_{wk} \gamma_{w} - \mathop \sum \limits_{j \in D} dis_{ij} x_{ijk} \forall i \in R \cup T,k \in K $$
(10.3)
$$ LR_{k} = \mathop \sum \limits_{i \in D \cup G \cup T \cup R } \mathop \sum \limits_{j \in D \cup G \cup T \cup R} dis_{ij} x_{ijk} \quad k \in K $$
(11)
$$ s_{iw} + M\left( {\left( {1 - x_{ijk} } \right) + \left( {1 - v_{wk} } \right)} \right) \ge {\text{time}}_{ij} \quad \forall i \in D,j \in G,k \in K,w \in W $$
(12.1)
$$ s_{jw} + M\left( {\left( {1 - x_{ijk} } \right) + \left( {1 - v_{wk} } \right)} \right) \ge s_{iw} + {\text{time}}_{ij} \quad \forall i,j \in G,k \in K,w \in W $$
(12.2)
$$ ve_{iw} \ge er_{iw} - s_{iw} \quad \forall i \in G,w \in W $$
(13.1)
$$ vl_{iw} \ge s_{iw} - la_{iw} \quad \forall i \in G,w \in W $$
(13.2)
$$ l_{ik} - l_{jk} + \mathop \sum \limits_{w \in W} v_{wk} \delta_{w} x_{ijk} \le \mathop \sum \limits_{w \in W} v_{wk} \left( {\delta_{w} - d_{jw} } \right)\quad \forall i,j \in G,k \in K $$
(14.1)
$$ \mathop \sum \limits_{w \in W} d_{wi} v_{wk} \le l_{ik} \le \mathop \sum \limits_{w \in W} v_{wk} \delta_{w} \quad \forall i \in G,k \in K $$
(14.2)
$$ \mathop \sum \limits_{i \in D} \mathop \sum \limits_{w \in W} x_{ijk} d_{wj} v_{wk} \le l_{jk} \quad \forall j \in G,k \in K $$
(14.3)
$$ l_{jk} \le \mathop \sum \limits_{w \in W} v_{wk} \left( {\delta_{w} + \mathop \sum \limits_{i \in D} v_{wk} \left( {d_{jw} - \delta_{w} } \right)x_{ijk} } \right)\quad \forall j \in G,k \in K $$
(14.4)
$$ xt_{wj} = \mathop \sum \limits_{k \in K} \mathop \sum \limits_{i \in G} x_{ijk} l_{ik} v_{wk} \quad \forall j \in T,w \in W $$
(15)
$$ \mathop \sum \limits_{w \in W} xt_{wj} \le tc_{j} \mathop \sum \limits_{q \in Q} t_{qj} \quad \forall j \in T $$
(16.1)
$$ \mathop \sum \limits_{w \in W} xt_{wj} \ge tc_{j}^{m} \mathop \sum \limits_{q \in Q} t_{qj} \quad \forall j \in T $$
(16.2)
$$ \mathop \sum \limits_{w \in W} \mathop \sum \limits_{q \in Q} xt_{wi} t_{qi} \left( {1 - r_{wq} } \right)\beta_{wq} = \mathop \sum \limits_{j \in R} xtr_{ij} \quad \forall i \in T $$
(16.3)
$$ xr_{j} = \mathop \sum \limits_{w \in W} \mathop \sum \limits_{k \in K} \mathop \sum \limits_{i \in G} x_{ijk} l_{ik} v_{wk} + \mathop \sum \limits_{i \in T} xtr_{{i^{\prime}j}} \quad \forall j \in R $$
(17.1)
$$ xr_{j} \le rc_{j} r_{j} \quad \forall j \in R $$
(17.2)
$$ xr_{j} \ge rc_{j}^{m} r_{j} \quad \forall j \in R $$
(17.3)
$$ \mathop \sum \limits_{w \in W} \mathop \sum \limits_{q \in Q} xt_{wi} t_{qi} \left( {1 - r_{wq} } \right)\left( {1 - \beta_{wq} } \right) = \mathop \sum \limits_{j \in F} xtf_{ij} \quad \forall i \in T $$
(18.1)
$$ xr_{j} \left( {1 - w_{i} } \right) = \mathop \sum \limits_{j \in F} xrf_{ij} \quad \forall i \in R $$
(18.2)
$$ xf_{i} = \mathop \sum \limits_{j \in T} xtf_{ji} + \mathop \sum \limits_{{j^{\prime} \in R}} xrf_{{j^{\prime}i}} \quad \forall i \in F $$
(19.1)
$$ xf_{i} \le fc_{i} f_{j} \quad \forall i \in F $$
(19.2)
$$ xf_{i} \ge fc_{i}^{m} f_{j} \quad \forall i \in F $$
(19.3)
$$ \mathop \sum \limits_{w \in W} \mathop \sum \limits_{i \in G} d_{wi} = \mathop \sum \limits_{w \in W} \mathop \sum \limits_{j \in T} xt_{wt} + \mathop \sum \limits_{j \in R} xr_{j} $$
(20)
$$ \mathop \sum \limits_{q \in Q} t_{qi} \le 1\quad \forall i \in T $$
(21)
$$ t_{qi} = a_{qi} \quad \forall q \in Q,i \in T' $$
(22.1)
$$ r_{i} = 1\quad \forall i \in R' $$
(22.2)
$$ f_{i} = 1\quad \forall i \in F^{\prime} $$
(22.3)
$$ \begin{aligned} & xtf_{ij} \ge 0,xf_{i} \ge 0\quad \forall i \in T,j \in F \\ & xtr_{ij} \ge 0,xt_{wi} \ge 0 \quad \forall i \in T,j \in R,w \in W \\ & xtf_{ij} \ge 0,xr_{i} \ge 0\quad \forall i \in R,j \in F \\ & e_{ik} \ge 0\quad \forall i \in \left( {D \cup G} \right),k \in K \\ & l_{ik} \ge 0\quad \forall i \in G,k \in K \\ & s_{iw} \ge 0\quad \forall i \in G,k \in K \\ & LR_{k} \ge 0\quad \forall k \in K \\ \end{aligned} $$
(22.4)
$$ \begin{aligned} & x_{ijk} \in \left\{ {0,1} \right\}\quad \forall i \in \left( {D \cup G} \right),j \in \left( {G \cup T \cup R} \right),k \in K \\ & t_{qi} \in \left\{ {0,1} \right\}\quad \forall q \in Q,i \in T \\ & r_{i} \in \left\{ {0,1} \right\}\quad \forall i \in R \\ & f_{i} \in \left\{ {0,1} \right\}\quad \forall i \in F \\ \end{aligned} $$
(22.5)

The first objective function is dedicated to the system’s costs calculation. Equation (1.1) specifies the waste transportation costs related to the waste collection stage, including carrying wastes from demanding nodes to the treatment centers and recycling centers. The transportation costs associated with conveying wastes between facilities are formulated by Eqs. (1.2–1.4). Equations (1.5–1.7) determine new facilities establishment costs and Eq. (1.8) addresses the customers’ time window penalties.

The second objective function takes risk parameters into account. Risks involve treatment and disposal sites risk knowing the crowd around them by Eqs. (2.1) and (2.2). Equations (2.3) and (2.4) try to minimize the transportation risk for both the waste collection stage and conveying between the facilities’ stage.

Finally, the last objective function, which has a social origin, ensures that the workload between collecting fleet is divided equitably. It calculates the deviation of each vehicle’s travelled distance from the total travelled distance of the fleet. As this objective function is a nonlinear equation, a linear form is represented in the following.

Equation (4) sets the depot as the starting point for each servicing vehicle. Equation (5) guarantees that each collection vehicle will leave the nodes after service servicing. Equation (6) is formulated to guarantee that for each type of waste, all demanding nodes are visited exactly once. Equation (7) sets the depot as the final destination for vehicles after they have delivered their load to the treatment and recycling sites. Equation (8) enforces the collection vehicles to unload their shipment to a suitable site considering the type of waste and its compatibility with the technology. Equation (9) ensures that the collection vehicles unload their recyclable waste at the recycling sites before returning to the depot. In order to calculate the travelled distance and to ensure that the route length does not exceed the allowable distance, which each vehicle could travel, Eqs. (10.1–10.3) are formulated based on Desrochers and Laporte (1991). Equation 11 determines the travelled distance of each vehicle in order to be used in the workload balancing objective function. Collecting waste start time at first customer is formulated by Eq. (12.1), and starting time at the other customers, located on the route, is formulated by Eq. (12.2). Equations (13.1) and (13.2) calculate the violation from the customer’s time windows. Equations (14.1)–(14.4) are utilized in order to remove sub-tours and also ensure the load of the waste does not exceed the vehicle capacity (Desrochers and Laporte 1991). Equation (15) computes the amount of waste that is processed by each treatment center. The set of Eqs. (16.1–16.3) check capacity limitations and calculate the amount of the imported wastes to the treatment facilities, and investigate new treatment facility establishment. In addition, Eq. (16.3) formulates the flow from treatment facilities to recycling facilities. Similar to the previous equation set, Eqs. (17.1–17.3) consider the aforementioned aspects of recycling sites. The waste flow from the treatment facilities to the disposal facilities is addressed by Eq. (18.1), and the waste flow from the recycling facilities to the disposal sites is considered by Eq. (18.2). The amount of the wastes, which are disposed at the disposal centers, is calculated by Eq. (19.1) and the capacity limitation of each active disposal site is considered by Eq. (19.2). The minimum amount of limitation required to establish a new disposal facility is investigated by Eq. (19.3). Equation (20) guarantees that the total demand at each generation node is met. As mentioned before, each treatment center could utilize maximum one technology. Therefore, this constraint is formulated as Eq. (21). Finally, the set of Eqs. (22.1–22.5) specify the type of the variables and determine the amount of several coefficients considering conditions governing the problem.

As mentioned before, there are three nonlinear Eqs. (2.3, 3, and 16.3) that make the model nonlinear. The following equations are used to linearize the proposed model. We have used the following equations for eliminating variables product, considering an auxiliary variable and subsisting it with variables’ product.

$$ xl_{ijk} \le M x_{ijk} \quad \forall i \in G,j \in G \cup R \cup T,k \in K $$
(23)
$$ xl_{ijk} \le l_{ik} \quad \forall i \in G,j \in G \cup R \cup T,k \in K $$
(24)
$$ xl_{ijk} \ge l_{ik} - \left( {1 - x_{ijk} } \right)M\quad \forall i \in G,j \in G \cup R \cup T,k \in K $$
(25)
$$ xl_{ijk} \ge 0, M > \infty \quad \forall i \in G,j \in G \cup R \cup T,k \in K $$
(26)

We also use the following equations in order to remove the absolute value from the formula by using two auxiliary variables as follows and substituting Eq. (27) with absolute value expression:

$$ LR_{\text{mean}}^{'} + LR_{k}^{'} \quad \forall k \in K $$
(27)
$$ LR_{\text{mean}} = \mathop \sum \limits_{k \in K} \frac{1}{\left| K \right|}LR_{k} $$
(28)
$$ LR_{\text{mean}} - LR_{k} = LR_{\text{mean}}^{'} - LR_{k}^{'} \quad \forall k \in K $$
(29)
$$ LR_{\text{mean}}^{'} \ge 0, LR_{k}^{'} \ge 0\quad \forall k \in K $$
(30)

4 Methodology

In HWM problems, we are usually facing with different goals; therefore, HWM problems usually are classified into multi-objective problems, and it is required to utilize multi-objective decision making (MODM) techniques. The researchers who have worked on HWM usually use the weighted sum method (WSM) to solve their proposed multi-objective models (Alumur and Kara 2007; Nema and Gupta 1999; Samanlioglu 2013). Since the LRP problems are classified into NP-hard problems (Rabbani et al. 2019), and solving them in a reasonable time is impossible, we should use metaheuristic algorithms to solve these problems. We apply three well-known metaheuristic algorithms for multi-objective problems, NSGA-II, PESA-II, and SPEA-II for tackling the presented problem.

4.1 Model validation

In order to validate the performance of the proposed model, a small-scaled problem is solved using GAMS software. Assuming identical weights for the objective functions, WSM is employed to address this multi-objective problem, and the WSM results are shown in Table 3 in which D, T, R, F represent depot, treatment facility, recycling facility, and disposal facility, respectively. In addition, numbers represent the generation node. To prove the confliction among the objectives, we use the Epsilon-constraint method, and the Pareto frontier of the three-objective problem is shown in Fig. 2. We also investigate the conflict between each pair of two objectives and the results are shown in Fig. 3.

Table 3 Results of the WSM solution
Full size table
Fig. 2
figure 2

Pareto frontier of epsilon-constraint with three objectives functions

Full size image
Fig. 3
figure 3

Pairwise comparison of objective functions by Epsilon-constraint

Full size image

4.2 Solution representation

To represent the solution in the algorithm, matrixes, called chromosomes in the genetic algorithm, are used. In this study, we consider each chromosome as a matrix with W + N rows and G columns, where W, N, and G represent the number of waste types, the number of different kinds of facilities, and the number of generating nodes, respectively. To determine the sequence of generating nodes for each kind of waste, W strings consisting of permutation numbers from 1 to G are generated and are put in the top W rows of the chromosome. We also create N strings, including permutation numbers from 1 to M, in which M denotes the total number of facilities depending on its type, and the strings are placed from the (W + 1)-th to (W + N)-th rows of the chromosome in order to determine allocation order of facilities to the tours. Figure 4 represents the conceptual structure of the chromosome.

Fig. 4
figure 4

Chromosome structure

Full size image

We use a complex chromosome structure in this study according to Rabbani et al. (2018a); this shape of chromosome provides a wide range of mutations and crossover operators which leads to generating a more diverse population faster. To examine this hypothesis, a medium-sized problem was solved by NSGA-II for 30 times with 100 maximum iterations using the proposed string-shaped chromosome suggested by Farrokhi-Asl et al. (2017). We solved that test problem in the same conditions using our proposed chromosome structure. The results indicated that there is a significant difference between CPU time of two algorithms at the significant level of 5% and the string-shaped chromosome acts 19% faster than matrix-shaped but our proposed chromosome structure could generate 23% more feasible solution and it can be attributed to the use of various crossover and mutation operators. Therefore, it can be inferred that our proposed chromosome structure is more productive.

The chromosome decoding procedure includes two stages. The former is the routing stage and wastes’ collection from generating nodes; the latter is the shipment of processed wastes between facilities. We briefly called “Routing” and “Shipment” stages. Figure 5 illustrates the decoding flowchart of the routing and shipment stages. For a better understanding of these two stages, an example with two types of waste and two types of treatment methods is explained. Consider a hazardous waste management system consists of six generation nodes, four treatment nodes (two nodes with technology 1 and two nodes with technology 2), two recycling nodes, and two disposal nodes. Each of these nodes has a unique location and we use a distance matrix for calculation of the passed distance in this study. This system uses four vehicles to collect and transfer wastes to the treatment nodes that vehicles 1 and 2, shown in blue, are compatible with type 1 waste and vehicles 3 and 4, shown in red, are compatible with type 2 waste. According to the decoding procedure, in the first step, vehicle one moves to generating node 3 to collect type 1 waste of the node and then visits generating nodes 1 and 2, respectively. After serving generating node 2, due to the limitation of the load route of vehicle one, vehicle two will collect the rest of the first-row nodes of the chromosome. After this step, the vehicle moves to one of the treatment nodes that are compatible with its load considering chromosome cells sequence and residual capacity of the treatment nodes. The decoding for type 2 waste is similar to the above procedure. For the sake of simplicity, this section omits to explain the return of vehicles to the depot. After the end of the “Routing” stage, the “Shipment” stage starts with transporting processed wastes in the treatment nodes to the recycling or disposal nodes according to their sequence in the chromosome and residual capacity. In the present example, waste processed at treatment 1 with technology 1 is sent to disposal node 1 without recycling (it is assumed that this kind of waste is non-recyclable). In the next step, wastes of treatment node 1 with technology 2 are transported to the recycling node 1 and treatment node 2 with technology 2 also transports its processed waste to recycling node 1, assuming the residual capacity of recycling node is greater than processed waste at the treatment node. In the final step, the waste recycled at recycling node 1 is moved to disposal node 2 because it exceeds the free capacity of disposal node 1. Treatment node 2 with technology 1 and recycling node 2 are non-operational in this example. A conceptual vision of the decoding example is depicted in Fig. 6.

Fig. 5
figure 5

Decoding flowchart of the routing and shipment stages

Full size image
Fig. 6
figure 6

Decoding example

Full size image

4.3 NSGA-II

In this study, we utilize three metaheuristic algorithms for our multi-objective problem that one of them is Non-Dominated Sorting Genetic Algorithm- II; NSGA-II is one of the most well-known evolutionary algorithms which is population-based and its working infrastructure is based on genetic algorithm (GA) with the difference that GA obtains a single solution for single-objective problems, but NSGA-II obtains a set of solutions called Pareto frontier. This algorithm starts its work by generating a random population and then calculates objective functions for each individual, and it calculates rank and crowding distance of each individual to rank the present population. Similar to GA, NSGA-II applies crossover and mutation to create new individuals, and then it merges the old and new populations and recalculates the rank and crowding distance of the population. As the new population is larger than the initial population, the algorithm truncates the extra individuals considering their ranks and crowding distances. This procedure continues until the completion of the termination conditions. Pseudocode of the proposed NSGA-II is represented in Fig. 7.

Fig. 7
figure 7

Pseudocode of the proposed NSGA-II

Full size image

4.4 PESA-II

Pareto envelope-based selection algorithm is known as a multi-objective evolutionary algorithm, and it works based on region selection which is the main difference between this algorithm and the other algorithms which are based on individual selection. This algorithm tries to arrange Pareto instead of individuals. The main advantage of this method becomes evident when the number of archive population exceeds the allowed amount. In this situation, the algorithm attempts to remove extra individuals from the Pareto cell which are more crowded to keep Pareto frontier diversity, whereas the other algorithms do not investigate the Pareto and eliminate individuals based on their ranks. Similar to NSGA-II, PESA-II is a population-based algorithm, and it starts its work with an initial population and manipulates its population with GA crossover and mutation operators. As mentioned before, PESA-II tries to improve Pareto quality by making a uniform frontier. Therefore, it eliminates the extra individuals from the crowded Pareto cells and also chooses parents for mutation and crossover from low-population Pareto cells to increase the probability of offspring generation in these cells.

In this study, we improve the PESA-II by removing analogous chromosomes from the archive that causes generating sparse Pareto; therefore, the quality of the modified PESA-II is improved. Additional descriptions are presented in the following, and Fig. 8 represents pseudocode of the proposed modified PESA-II as follows:

Fig. 8
figure 8

Pseudocode of the proposed modified PESA-II

Full size image

4.5 SPEA-II

Strength Pareto Evolutionary Algorithm-II was introduced as a modified version of the SPEA. This algorithm considers two sets of the population that one of them is formed from a regular population, keeping individuals generated in each loop of algorithm and the other is an archive of the best individuals generated during algorithm runtime. The algorithm uses the Pareto dominance concept and fitness value for selection process. In the first step, this algorithm generates a population of random individuals and calculates their objective functions, dominance, and fitness. Then, the algorithm merges two sets of population and calculates dominance and fitness. According to the number of archive individuals, the algorithm may truncate the archive using the truncate operator or fill the archive using dominated individuals. At each iteration and so long as the stop condition is not reached, GA mutation and crossover operators, which use binary tournament for selecting parents, generate new regular population and then fitness values of individuals in both populations are calculated and superior individuals stay in the archive. Pseudocode of the proposed SPEA-II is represented in Fig. 9.

Fig. 9
figure 9

Pseudocode of the proposed SPEA-II

Full size image

4.6 Crossover operator

Three kinds of crossover operators are defined for this problem: two one-point crossovers and a double-point crossover. The conceptual framework of the crossover operators is shown in Fig. 10.

Fig. 10
figure 10

Crossover operators

Full size image

In the one-point crossover, a number between one to G is generated randomly, and it will be used as the crossover point. It is clear from Fig. 10 that the first chromosome’s columns from beginning to selected column by the crossover point and second chromosome’s columns from the column after the crossover point to the end are generating the first offspring. The second offspring is also created in the same way, with the difference that the first and second chromosomes are replaced. It is worth to notice that since routing and shipment stages are independent, their crossover should not affect each other so that only one of the two sections of the chromosome goes under crossover at a time; the constant part is specified by gray color in Fig. 10. In the one-point crossover maybe some elements are removed or are duplicated in a row, so several corrective actions are applied to prevent generating non-feasible children. The cells on which corrective actions are applied are indicated in yellow in Fig. 10.

In the double-point crossover, two numbers that the minimum of them is between one to W + N − 1, we call it C1, and the maximum of them is between two to W + N, we call it C2, are selected randomly. As it is recognizable from Fig. 10, we generate the first offspring from the beginning to C1-th and C2-th to last rows of the first chromosome and (C1 + 1)-th to C2-th rows of the second chromosome. The second offspring will be generated by replacing the first and second chromosomes. Unlike the one-point crossover, double point crossover does not require corrective actions and its children are always feasible.

4.7 Mutation operator

Generally, there are three kinds of mutation operators for the problem with permutation solutions, namely, Swap, reversion, and insertion. These operators are usually applied on chromosomes which have strain structure. In this study, our chromosomes are shaped like a matrix, therefore, it is required to manipulate the operators to create new high-quality off-springs. For this purpose, six mutation operators are designed which are shown in Fig. 11. As mentioned before, each chromosome contains 4 rows for the routing stage and 4 rows for system facilities allocation. In order to utilize permutation mutation operators, we assume each row of the chromosome as a string. Because the members of the chromosome’s rows are not equal, two categories of the operators are designed, one category specific to the generation points and the other specific to the system facilities. The rows are selected randomly so that a random number between one to W or N based on the operators’ category is generated called S, to determine how many row(s) should be mutated. After this step, a random sample with S members will be chosen from a 1 to W or N to determine which row(s) should be mutated.

Fig. 11
figure 11

Mutation operator

Full size image

4.8 Parameter tuning

There are several parameters for each evolutionary algorithm that should be tuned to optimize the algorithm performance. For this purpose, several experiences with different values of parameters are designed and the performance of each algorithm is investigated. In this study, Taguchi-based method is employed for designing experiences, which is a prevalent method of parameter tuning and it produces reasonable results from a low amount of information. For NSGA-II, we set the Number of Function Evaluation (NFE), population size (NPop), mutation percentage (PMutation), and crossover percentage parameters (PCrossover). For PESA-II, NFE, population size (NPop), archive size (NArchive), crossover percentage (PCrossover), selection pressure (BetaS), and removing pressure (BetaR) parameters are tuned and for SPEA-II, NFE, population size (NPop), archive size (NArchive), and crossover percentage (PCrossover) are tuned. It is worth to notice that the percentage of mutation in PESA-II and SPEA-II is equal to one minus the crossover percentage (PCrossover), therefore we just have tuned crossover percentage and mutation percentage (PMutation) is calculated based on it.

Minitab 17 software is employed for designing experiments by a three-level Taguchi method, and the normalized amounts of the objective functions are considered as the response for the Taguchi method. The output of the Minitab for parameter tuning for SPEA-II, PESA-II, and NSGA-II is shown in Fig. 12, and the parameter tuning result is presented in Table 4.

Fig. 12
figure 12

Parameter tuning for SPEA-II, PESA-II, and NSGA-II

Full size image
Table 4 Parameter tuning results
Full size table

4.9 Constraints handling and penalty function

There are several ways to handle system constraints in the metaheuristic algorithms, such as eliminating non-feasible solutions and imposing penalty function to non-feasible points. In this study, it has been attempted as far as possible to prevent generating non-feasible solutions in the population generation stage. However, several constraints, most related to capacity, could not be handled in the generation stage, and they should be handled by a penalty function.

The penalty function is a popular method for researchers to handle constraints; there are several types of penalty function methods such as static penalties, dynamic penalties, adaptive penalties, etc. In this study, an adaptive penalty function that respects the feasible solution numbers created on the Pareto frontier is presented and is compared with static penalty function. The proposed function increases penalty coefficient, if the number of feasible points on the Pareto frontier is relatively low in order to force the algorithm to reach feasible areas, but when the algorithm found a significant number of feasible solutions, it diminishes the penalty coefficient gradually to reduce the pressure on the algorithm for finding feasible points, and the algorithm can explore the solution space better by investigating non-feasible solutions and consequently, the probability of staying at local optimums decreases; Eq. (31) and Fig. 13 represents the adaptive penalty function amounts assuming NPop = 100. P(x) represents penalty function value, and x represents the number of feasible solutions achieved on the Pareto frontier. To prove the superiority of the proposed adaptive penalty function, a problem includes 25 generation nodes, 12 treatment facilities, 10 recycling facilities, and 14 disposal facilities is solved under different types of penalty function for 30 times for each kind of penalty function and finally a comparison in quality metric, which will be further explained in the next section, is presented. The summary results of comparison between adaptive and static penalty functions are represented in Table 5.

$$ P\left( x \right) = 100^{{\log \left( {\left( {NPop + 1) - x} \right)} \right)}} $$
(31)
Fig. 13
figure 13

Adaptive penalty function

Full size image
Table 5 Comparison between adaptive and static penalty functions
Full size table

5 Results and discussion

In this section, we make two different comparisons between the algorithms. At first, classic PESA-II and modified PESA-II are compared, and then, the superior method in the first comparison is compared with proposed NSGA-II and SPEA-II. For numerical examples, we use 30 problems in three different sizes (small, medium, large) generated randomly in which the parameters are established appropriately. Table 6 shows the test problems’ characteristics.

Table 6 Test problems and their characteristics
Full size table

5.1 Comparison metrics

There are several comparison metrics, such as Quality Metric (QM), Mean Ideal Distance (MID) Diversification Metric (DM), Spacing Metric (SM), CPU time (CPU), hypervolume (HV), number of explored feasible solution (NF), and Inverted Generational Distance (IGD). These metrics will be described in the following considering each comparison requirement.

  • Quality metric (QM)

Quality metric is one of the most common metrics which computes the domination percentage of two or more algorithms on each other. In other word, it combines non-dominated points of two or more multi-objective algorithms and recalculates domination criteria and reports the percentage of remaining non-dominated points after recalculation. It is clear that a higher amount of this parameter expresses a better performance of the algorithm (Tavakkoli-Moghaddam et al. 2011). In this study, we use a pairwise comparison for evaluating algorithms’ performance.

  • Mean ideal distance (MID)

    $$ {\text{MID}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \sqrt {\mathop \sum \limits_{j = 1}^{3} \left( {\frac{{f_{ij} - f_{j}^{\text{best}} }}{{f_{j}^{\hbox{max} } - f_{j}^{\hbox{min} } }}} \right)^{2} } $$
    (32)

MID calculates the distance between the best solution founded on the Pareto and the other Pareto points. MID can be calculated as follows (Farrokhi-Asl et al. 2018):

Where n represents the number of non-dominated points, respectively \( f_{j}^{\hbox{max} } , f_{j}^{\hbox{min} } , f_{j}^{\text{best}} \) represent the maximum, the minimum, and the best solutions of j-th objective function among all non-dominated points. It is clear that lower values of MID, expresses the lower distance between the ideal solution and the other solutions, therefore algorithms with lower MID have better performance.

  • Spacing metric (SM)

Spacing metric is usually used for evaluating the uniformity of attained Pareto frontier, and it is calculated by Eqs. (33) and (34) in which \( n, d_{i} , \bar{d} \), respectively, denote the number of non-dominated points on the Pareto frontier, minimum distance from the i-th point to the other points on the Pareto frontier, and the average of \( d_{i} \). Similar to MID, lower values of this parameter are desirable, because it indicates more uniformity in the Pareto frontier (Rabbani et al. 2019).

$$ d_{i} = \mathop {\hbox{min} }\limits_{j} \mathop \sum \limits_{k = 1}^{3} \left| {f_{k}^{j} - f_{k}^{i} } \right|;\quad \forall i,j\,\epsilon \left\{ {1, 2, 3, \ldots , n} \right\} $$
(33)
$$ {\text{SM}} = \sqrt {\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\bar{d} - d_{i} } \right)^{2} }}{n - 1}} $$
(34)

  • Diversity metric (DM)

This parameter determinates the Pareto frontier spread, and it is calculated by Eqs. (35) and (36). Similar to QM, higher values of DM indicate a better algorithm’s performance.

$$ d_{i} = \mathop {\hbox{max} }\limits_{j} \left\{ {\mathop \sum \limits_{k = 1}^{3} \left( {f_{k}^{j} - f_{k}^{i} } \right)^{2} } \right\};\quad \forall i,j\,\epsilon \left\{ {1, 2, 3, \ldots , n} \right\} $$
(35)
$$ {\text{DM}} = \sqrt {\mathop \sum \limits_{i = 1}^{n} d_{i} } $$
(36)

  • Hypervolume (HV)

Hypervolume or S-metric is a well-known and prevalent metric in assessing multi-objective algorithms. HV uses the covered space dominate by an obtained Pareto front as a quality parameter. It usually considers the worst values of the objective functions as the reference point for the calculation. A higher value of HV indicates higher diversity and convergence of the Pareto front; therefore, it is desirable that this metric value be as high as possible (Lwin et al. 2014; Moraes et al. 2019).

  • Inverted generational distance (IGD)

IGD is a performance metric for evaluating the obtained Pareto front quality. It considers a true Pareto front as a reference and calculates the distance of each its solutions from the true Pareto front. IGD measures both the diversity and the convergence of the solution set. The lower value of IGD indicates a closer front to the true Pareto front. In highly constraint models like the proposed model in this study, the true Pareto front is unknown, therefore, best-obtained values for each objective function is used for reference points. The IGD formula is as follows where n is the number of solutions in the obtained Pareto front and d is the Euclidean distance between each solution in the true Pareto and the nearest solution in the Pareto front (Hu et al. 2019; Lwin et al. 2014).

$$ IGD = \frac{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} d_{i}^{2} } }}{n} $$
(37)

5.2 Modified PESA-II and classic PESA-II comparison

We employ multi-objective metaheuristics algorithms to recognize the preferable method for solving HWM problems. A modified PESA-II is presented, and its results are compared with the classic PESA-II which is commonly used by other researchers (Anagnostopoulos and Mamanis 2011; Montoya et al. 2014). The results demonstrate that modified PESA-II not only improves the Pareto frontier but also reduces the computation time. It can be inferred that by removing replicated chromosomes from the archive, some unnecessary computations are eradicated and consequently, the time can be saved, so there is no replicated solution in the archive, the empty space in the archive can be assigned to new solutions, therefore, less memory will be used. Since it was proven that modified PESA-II is more efficient than classic PESA-II, we use our proposed modified PESA-II as PESA-II method in the rest of the paper and other algorithms will be compared with this novel method. The summary of modified PESA-II and classic PESA-II comparison results is represented in Table 7.

Table 7 Modified PESA-II and classic PESA-II comparison results
Full size table

5.3 Comparison metrics’ results and discussion

In this section we investigate three algorithms, NSGA-II, PESA-II, and SPEA-II based on summery results of comparison metrics which is represented in Table 8; The result of Algorithm-1 ↔ Algorithm-2 is shown as “+”, “−”, or “∼” when Algorithm-1 is significantly better than, significantly worse than, or statistically equivalent to Algorithm-2, respectively; the detailed results are also presented in “Appendix”. According to the results, PESA-II acts significantly better than NSGA-II in the exploration of the feasible solutions, spacing metric, quality metric, and IGD in any dimension of the test problems. It also overcame NSGA-II in MID in small and medium test problems, but in CPU time in medium and large test problems NSGA-II had a better performance. On the other hand, like PESA-II, SPEA-II acts better than NSGA-II in QM, SM, and IGD in all dimensions of the test problems. It also performed significantly better than NSGA-II in finding the feasible solutions in medium-size test problems but in CPU time in small and large problems NSGA-II had a better performance. NSGA-II also performed better than PESA-II and SPEA-II in DM in all kind of test problems or in other words it was able to search a wider area of the problem space. The performance of PESA-II and SPEA-II did not differ significantly in most cases; however, PESA-II acted better than SPEA-II in the small test problems in obtaining more feasible solutions, QM in the large-size test problems, and CPU time in small and medium test problems. On the other hand, SPEA-II dominated PESA-II in SM in all kind of test problems. In the case of the hypervolume metric, no significant difference was found between the algorithms’ performance. In general, it can be concluded that given the results of algorithms’ comparison, the performance of proposed modified PESA-II is more suitable than the other two algorithms, and the use of this algorithm in HWM Problems can lead to the production of a more efficient set of answers. For better conceptual understanding, boxplots of comparison metrics, convergence IGD graph, and Pareto front of several test problems are represented in Figs. 14, 15 and 16, respectively.

Table 8 Summary of comparison results of algorithms
Full size table
Fig. 14
figure 14figure 14

Boxplot of comparison metrics

Full size image
Fig. 15
figure 15

IGD convergence plot

Full size image
Fig. 16
figure 16

Pareto approximation of six test problems

Full size image

6 Conclusion

In this study, we proposed a new model for HWLRP. The service time windows and workload balancing were appended to the previous models, and three objective functions including two systematic goals (cost and risk) and one social goal (workload balancing) were considered for the new model. We also considered waste–waste compatibility and heterogeneous fleet, which have been rarely investigated in the literature. Since our model was classified into multi-objective models, two exact methods including the weighted sum method and Epsilon-constraint method were used to validate the model structure. In addition, since the model nature was NP-hard, three multi-objective evolutionary algorithms, NSGA-II, PESA-II, and SPEA-II have been employed to solve large-scale problems. Moreover, an adaptive penalty function that was more applicable in Pareto frontier improvement has been developed in this paper. In the next step, the presented PESA-II was modified by removing replicated solutions from its archive and then was compared with classic PESA-II, NSGA-II, and SPEA-II. We used different MOEA comparison metrics including the number of feasible solutions, quality metric, spacing metric, CPU time, mean ideal distance, diversity metric, hypervolume, and inverted generational distance to evaluate the algorithms’ performance in HWLRP.

Modified PESA-II could prevail over PESA-II in CPU time and QM. It also acted better than NSGA-II in most cases; however, it had a weak performance in DM against NSGA-II. As shown in Fig. 14, with increasing problem dimensions, SM and DM increase faster for the NSGA-II algorithm than two others. As such, PESA-II and SPEA-II are more reasonable algorithms for large size problems because of the power of the NSGA-II decreases more rapidly with increasing dimensions of the problem in finding feasible solutions. Although NSGA-II performed weaker than PESA-II and SPEA-II in creating efficient Pareto, it could generate wider Pareto frontier compared to PESA-II and SPEA-II, which is appropriate for the situation that the decision-maker prefers to distinguish all options instead of knowing a limited number of best options. Finally, the Pareto approximation of each algorithm in several test problems is represented in Fig. 16.

In addition to the conclusions above, this study demonstrates the application of the PESA-II method in routing problems which is scarce in the literature, and it can be a new subject for interested researchers.

For future researches, the following contributions are suggested. As mentioned in the previous sections, social and systematical decisions are complimentary which, without considering them simultaneously, cannot expect a reasonable answer in a problem. Therefore, it seems that is essential to append more social objectives in the HWM problems to enrich the efficiency and comprehensiveness of the results. Considering green objectives and clustering approaches can be other suggestions for future researchers.