Evidential model for intuitionistic fuzzy multi-attribute group decision making

Abstract

Due to the uncertainty existing in real-world, intuitionistic fuzzy sets (IFSs) are used to model uncertain information in multi-attribute group decision making (MAGDM). The intuitionistic fuzzy MAGDM problems have gained great popularity recently. But, most of the current methods depend on various aggregation operators that may provide unreasonable collective intuitionistic fuzzy values of alternatives to be ranked. To solve such problem, a new method is developed based on evidence theory and IFSs. First, the mathematical relation between IFSs and evidence theory is analyzed, followed by the transformation from intuitionistic fuzzy evaluation information to basic belief assignment in evidence theory. Then, a new intuitionistic fuzzy weighted evidential (IFWE) average operator is introduced based on the operation of evidence discounting and evidence combination rule. We also develop a possibility-based ranking method for intuitionistic fuzzy values (IFVs) to obtain the linear ordering of IFVs. The proposed evidential model uses the IFWE average operator to aggregate the decision matrix and the attribute weight that is given by each decision maker, based on which each decision maker’s aggregated decision matrix can be obtained. Based on the decision matrices of all decision makers and the weights of the decision makers, the aggregated intuitionistic fuzzy value of each alternative can be obtained by the IFWE average operator. Finally, the preference order of all alternatives can be obtained by the possibility-based ranking method. Comparative analysis based on several application examples of MAGDM demonstrates that the proposed method can overcome the drawbacks of existing methods for MAGDM in intuitionistic fuzzy environments.

1 Introduction

Based on fuzzy set theory initiated by Zadeh (1965), Atanassov (1986, 1999) presented the concept of intuitionistic fuzzy sets (IFSs) for a more meticulous depiction on uncertainty. For a fuzzy set, its membership and non-membership grades are summed to one. Nevertheless, for an IFS, such constraint is relaxed and the hesitancy grade is introduced to measure the gap between 1 and the sum of membership and non-membership grades. Vague sets, which were proposed by Gau and Buehrer (1993), were regarded as another extension of fuzzy sets. Bustince and Burillo (1996) have pointed out that the concept of IFSs and that of vague sets coincide with each other. Due to its agility and flexibility in describing uncertainty and vagueness, intuitionistic fuzzy set theory has been broadly applied in lots of fields, such as uncertainty reasoning (Fan et al. 2018b; Song et al. 2018), pattern recognition (Song et al. 2015, 2019) and decision making in uncertain environments (Fan et al. 2018a; Memari et al. 2019).

As an important research area of decision making, multi-attribute group decision making (MAGDM) problems have attracted much interest. Since information from the real world is usually incomplete, the attributes in decision making problems may not be expressed by crisp numbers. It is more suitable to represent some of them in an uncertain way. Fuzzy sets and their extensions including intuitionistic fuzzy sets, valued–valued fuzzy sets and interval-valued intuitionistic fuzzy sets have been used to model uncertainty in MAGDM problems (Liu and Wang 2018a, b; Liu 2014, 2018; Liu et al. 2018; Liu and Zhang 2018; Liu and Tang 2018; Liu and Liu 2018). Hence, increasing attention has been focused on the problem of multi-attribute group decision making in intuitionistic fuzzy environments.

In recent years, intuitionistic fuzzy sets have been applied to the problem of MAGDM under uncertainty. Some methods (Boran 2009; Chai and Liu 2010; Chen et al. 2015, 2016; Li 2009; Ouyang and Pedrycz 2016; Szmidt and Kacprzyk 2002; Tan et al. 2009; Wang and Song 2018; Wang et al. 2009; Wei 2010; Wen 2010; Xu 2007a, 2010, 2011; Xu and Yager 2008; Yue 2014; Zeng and Su 2011) have been proposed for uncertain multi-attribute group decision making based on intuitionistic fuzzy sets. Based on the intuitionistic fuzzy Technique for Order Performance by Similarity to an Ideal Solution (TOPSIS) method, a fuzzy MAGDM method was presented by Boran (2009) for solving supplier selection problems. Chai and Liu (2010) proposed an approach for MAGDM to address the problem of selecting supply chain partners in an environment with uncertainty. In Chai and Liu (2010), the Intuitionistic Fuzzy Superiority and Inferiority Ranking (IF-SIR) method is applied for decision making. Using intuitionistic fuzzy sets to express ratings of alternatives with respect to attributes and weights of attributes, Li (2009) proposed a methodology for solving MAGDM problems, where the fractional programming model was utilized to rank all alternatives. Szmidt and Kacprzyk (2002) developed solution concepts that are related to group decision making problems under intuitionistic (individual and social) fuzzy preference relations. An intuitionistic fuzzy geometric aggregation (IFGA) operator was defined by Tan et al. (2009) on the basis of a fuzzy measure. The IFGA operator was used to aggregate decision matrices, which are represented by intuitionistic fuzzy values, in fuzzy group decision making problems. On the basis of the projection method, Wang and Song (2018) presented an approach for MAGDM in intuitionistic fuzzy environments. Wei (2010) proposed an induced intuitionistic fuzzy ordered weighted geometric operator for aggregating intuitionistic information in group decision making. Aiming at the practical scenario of information collaboration partner selection, Wen (2010) proposed a method for solving fuzzy multi-criteria group decision making problems based on intuitionistic fuzzy sets.

In the MAGDM models that were proposed by Xu (2007a) for intuitionistic fuzzy conditions, the intuitionistic fuzzy hybrid geometric operator is applied to aggregate individual intuitionistic fuzzy decision matrices and score functions are used to rank all alternatives. In Xu (2010), a deviation-based fuzzy MAGDM model is constructed based on the deviation measure between two intuitionistic fuzzy values (IFVs), with the help of intuitionistic fuzzy hybrid geometric operator, score functions and accuracy functions. In Xu (2011), a series of intuitionistic fuzzy aggregation operators were proposed by Xu and their properties were described. He then used these operators to propose MAGDM approaches in intuitionistic fuzzy condition (Xu 2011). Xu and Yager (2008) investigated the multi-attribute decision making (MADM) problems in dynamic conditions with intuitionistic fuzzy information. They defined a dynamic weighted averaging operator and an uncertain dynamic weighted averaging operator for IFVs (Xu and Yager 2008). Taking the time factor into consideration, they applied these operators to propose a procedure for handling fuzzy MAGDM problems, where all intuitionistic fuzzy decision information was collected sequentially.

Yue (2014) put forward a new group decision making methodology for solving these problems under intuitionistic fuzzy environments. In the model that was proposed in Yue (2014), the weight of each decision maker was determined by an extended TOPSIS technique. The weighted average operator for intuitionistic fuzzy values is used to aggregate the individual decision matrix of each decision maker into a group decision. The alternatives are ranked by using an extended TOPSIS technique.

Zeng and Su (2011) proposed an intuitionistic fuzzy ordered weighted distance (IFOWD) operator. A wide scope of aggregation operators and distance measures is included in the IFOWD operator. Based on the proposed IFOWD operator, they proposed a new approach for solving group decision making problems in intuitionistic fuzzy conditions.

Chen et al. (2016) put forward a new approach for fuzzy MAGDM problems based on IFSs and evidential reasoning methodology (Xu and Yager 2006; Yang et al. 2006). Ouyang and Pedrycz (2016) proposed a new approach for intuitionistic fuzzy MADM problems based on a new intuitionistic fuzzy weighted arithmetic (IFWA) average operator. In this IFWA average operator, two weight vectors are considered to describe the uncertainty more accurately.

However, since the methods that were proposed in Xu (2010) and Yue (2014) both use intuitionistic fuzzy weighted average operators to aggregate intuitionistic fuzzy information, they may rank all alternatives in an unreasonable way and counterintuitive preference orders may be obtained in some situations. Moreover, the method proposed by Zeng and Su (2011) can only address cases in which the attribute weights assigned by all decision makers are equal to each other. In the aggregation stage, the method proposed in Zeng and Su (2011) may lead to unreasonable ranking order for all alternatives in some situations because of the limitations of the intuitionistic fuzzy weighted average operator. In the method that was proposed by Chen et al. (2016), transformations from IFV to belief degree and from belief degree to basic probability mass are needed. Additional transformations, together with the reasoning process, will increase the computational burden. Moreover, in Chen et al. (2016), alternatives are ranked based on their distance from the ideal positive alternative. The choice of distance measure will influence the preference order. In Ouyang and Pedrycz (2016), the model is constructed based on two weight vectors, which are not always available. To overcome the limitations of these methods, we need to develop an effective method for solving intuitionistic fuzzy MAGDM problems.

To provide a new perspective of solving MAGDM problems with intuitionistic fuzzy information, and avoid unreasoning results obtained by current methods, MAGDM problems will be addressed in this paper in the framework of IFSs and evidence theory. We will construct a new model to solve intuitionistic fuzzy MAGDM problems with the help of evidence theory (Dempster 1967; Shafer 1976). In an MAGDM problem, all attributes are mutually independent. Each alternative’s evaluation results with respect to each attribute can be considered as the evaluation result that is provided by this attribute. Hence, in the decision matrix that is proposed by a decision maker, all alternatives are evaluated for every attribute. Thus, we can aggregate all attributes into the framework of evidence theory. In the stage of group decision making, all decision makers are independent. Their decisions on each alternative can be fused by evidence theory. First, the evaluation results that are expressed by IFVs are transformed into basic belief assignments (BBAs). The original BBAs are modified according to the weighting factors of the attributes and the evidence discounting operation. Then, the assessments of each alternative under all attributes are aggregated by Dempster’s combination rule. Based on the comprehensive view of all decision makers, a decision matrix can be constructed for group decision making. Similarly, the IFVs in the group decision matrix are transformed to BBAs, which are discounted according to the importance weights of each decision maker. In the decision making stage, we propose a possibility-based ranking method for IFVs. Illustrative examples show that the proposed evidential model outperforms the methods that were proposed in Xu (2010), Yue (2014) and Zeng and Su (2011) by overcoming their drawbacks for fuzzy MAGDM problems under intuitionistic fuzzy condition. Moreover, it is demonstrated that the proposed model is more convenient and much easier to implement than the method that was proposed by Chen et al. (2016).

We note that evidential reasoning method and IFSs have been used to develop a decision making method for fuzzy MAGM problems in Chen et al. (2016). In the method proposed in Chen et al. (2016), an evidential reasoning method is applied to aggregate the decision matrices of all decision makers and their provided attribute weights to generate an aggregated decision matrix that corresponds to each decision maker. Then, they used the evidential reasoning method to integrate the obtained aggregated all decision makers’ decision matrices and the weight of each decision maker to get the aggregated evaluation results of all alternatives, which are expressed by IFVs. Finally, decisions can be made according to the value that is transformed from the obtained intuitionistic fuzzy value that corresponds to each alternative. The difference between our method and the method that was presented in Chen et al. (2016) is that our method is based on original evidence theory and Dempster’s (1967) combination rule, whereas the method that was presented in Chen et al. (2016) is based on the evidence reasoning methodology that was proposed by Yang (Xu and Yager 2006; Yang et al. 2006). In our proposed method, preference orders are ranked by the possibility-based ranking method, which also differs from the method that was presented in (Chen et al. 2016).

The rest of this paper starts by a brief review on the basic concepts of IFSs, intuitionistic fuzzy aggregation operators and some information about evidence theory. In Sect. 3, we analyze several existing methods for MAGDM problems and discuss their main drawbacks. In Sect. 4, the intuitionistic fuzzy weighted evidential average operator and possibility-based ranking method for IFVs are presented. Then, we propose a procedure for solving MAGDM problems based on intuitionistic fuzzy sets and evidence theory. In Sect. 5, some application examples are used to facilitate the comparison between the proposed method and the methods that were presented in Chen et al. (2016; Xu 2010; Yue 2014; Zeng and Su 2011). Some conclusions of this paper and future research directions are presented in Sect. 6.

2 Preliminaries

2.1 Intuitionistic fuzzy sets

The concept of IFS is developed from Zadeh’s fuzzy set. Hence, the definition of a fuzzy set proposed by Zadeh (1965) will be firstly reviewed. Then, we present some basic concepts related to the theory of IFS.

Definition 2.1

(Zadeh 1965). Let a non-empty set $X$ be the universe of discourse. A is a fuzzy set defined in $X$. Then, A can be expressed as:

$$ A = \left\{ {\left\langle {x,\mu_{A} (x)} \right\rangle \left| {x \in X} \right.} \right\} $$

(1)

where $\mu_{A} (x):X \to [0,1]$ is the membership degree.

Definition 2.2

(Atanassov 1986, 1999) An intuitionistic fuzzy set $A$ in $X$ described by Atanassov can be written as:

$$ A = \left\{ {\left\langle {x,\mu_{A} (x),v_{A} (x)} \right\rangle \left| {x \in X} \right.} \right\} $$

(2)

where $\mu_{A} (x):X \to [0,1]$ and $v_{A} (x):X \to [0,1]$ are the membership degree and non-membership degree, respectively.

For any $x \in X$, the sum of $\mu_{A} (x)$ and $v_{A} (x)$ is no more than 1, such that:

$$ 0 \le \mu_{A} (x) + v_{A} (x) \le 1 $$

(3)

For an IFS A in X, $\forall x \in X$, the difference between 1 and the sum of the membership degree and non-membership degree is called as the hesitancy degree, which is denoted by $\pi_{A} (x)$. It can be expressed by:

$$ \pi_{A} (x) = 1 - \mu_{A} (x) - v_{A} (x) $$

(4)

It is indicated that $\pi_{A} (x) \in [0,1]$, $\forall x \in X$.

For an IFS A in X and $x \in X$, $\pi_{A} (x)$ is also considered as the intuitionistic index of $x$ with respect to $A$. Greater $\pi_{A} (x)$ indicates higher uncertainty in $x$ with respect to A. If $\forall x \in X$, $\pi_{A} (x) = 0$, the IFS A reduces to Zadeh’s classical fuzzy set. Furthermore, for a fuzzy set $B$ defined in $X$, since $v_{B} (x) = 1 - \mu_{B} (x)$, $\forall x \in X$, the hesitancy degree of $x$ with respect to $B$ is 0. Thus, Zadeh’s classical fuzzy set can be regarded as a special case of the intuitionistic fuzzy set.

Besides Definition 2.2, there are also other possible expressions of IFSs. It was proposed by Hong and Kim (1999) that the interval $\left[ {\mu_{A} (x),1 - v_{A} (x)} \right]$ can be used to represent the membership degree of x in intuitionistic fuzzy set $A$ defined in X, $x \in X$. This interval expression is identical to that of interval-valued fuzzy set (IVFS), where $\mu_{A} (x)$ is the lower bound of membership degree, and $1 - v_{A} (x)$ is the upper bound of the membership degree of x. Since $\mu_{A} (x) + v_{A} (x) \le 1$ always implies $\mu_{A} (x) \le 1 - v_{A} (x)$, the interval $\left[ {\mu_{A} (x),1 - v_{A} (x)} \right]$ is valid. This also indicates the equivalence relation between IFSs and IVFSs from a mathematical perspective.

For clarity, we use $\text{IFSs}(X)$ to denote the set of all IFSs defined in X. In the case where only one element x is contained in the universe of discourse $X$, the IFS $A$ defined in $X$ can be written as $A = \left\langle {\mu_{A} ,v_{A} } \right\rangle$ for short. $A = \left\langle {\mu_{A} ,v_{A} } \right\rangle$ is also called an IFV. For an IFV $A = \left\langle {\mu_{A} ,v_{A} } \right\rangle$, its hesitancy degree is also denoted as $\pi_{A} = 1 - \mu_{A} - v_{A}$. Furthermore, considering the equivalence relation between IVFSs and IFSs, we can get an interval value $\left[ {\mu_{A} ,1 - v_{A} } \right]$ from the IFV $A = \left\langle {\mu_{A} ,v_{A} } \right\rangle$. There is a one-to-one correspondence between IFV and interval value. For an IFV $A = \left\langle {\mu_{A} ,v_{A} } \right\rangle$, it degrades to a real number when $\mu_{A} = 1 - v_{A}$. The space constituted by all intuitionistic fuzzy values can be denoted as $L^{*}$ (Li and He 2013).

From the perspective of application, IFSs also have specific practical meanings, i.e., we can interpret an IFS from a physical point of view. For example, an IFS defined in X = {x} is given as $A = \left\langle {\mu_{A} (x),v_{A} (x)} \right\rangle = \left\langle {0.2,0.3} \right\rangle$, and its hesitancy degree $\pi_{A} (x)$ can be derived as 0.5. This situation can be interpreted as “the degree of $x$ belonging to $A$ is 0.2, the degree of $x$ not belonging to $A$ is 0.3, and the degree of element $x$ belonging indeterminately to $A$ is 0.5.” In the model of voting, this result can be further interpreted as “the vote for the resolution is two in favor and three against, with five abstentions” (Gau and Buehrer 1993).

Definition 2.3

(Atanassov 1986) For $A \in (X)$ and $B \in (X)$, these relations between them can be defined:

(R1):

$A \subseteq B \Leftrightarrow \mu_{A} (x) \le \mu_{B} (x),v_{A} (x) \ge v_{B} (x),\forall x \in X$;

(R2):

$A = B \Leftrightarrow \mu_{A} (x) = \mu_{B} (x),v_{A} (x) = v_{B} (x),\forall x \in X$;

(R3):

$A^{C} = \left\{ {\left\langle {x,v_{A} (x),\mu_{A} (x)} \right\rangle \left| {x \in X} \right.} \right\}$, where $A^{C}$ is the complement of $A$

Definition 2.4

(Atanassov 1986, 1999). For two IFVs $\alpha = \left\langle {\mu_{1} ,v_{1} } \right\rangle$ and $\beta = \left\langle {\mu_{2} ,v_{2} } \right\rangle$, the following expressions are defined to depict the partial order relation between them:$\alpha \le_{A} \beta$$\Leftrightarrow$$\mu_{1} \le \mu_{2} ,v_{1} \ge v_{2}$. Based on above partial order relation, it can be inferred that IFV $\left\langle {0,1} \right\rangle$ is the smallest one in the space $L^{*}$, and the largest one is $\left\langle {1,0} \right\rangle$.

Definition 2.5

(Atanassov 1986, 1999; Xu and Yager 2006)For $A \in (X)$ and $B \in (X)$, some operational laws between them are defined as following:

$$ \begin{aligned} A \cap B &= \left\{ {\left\langle {x,\hbox{min} \left( {\mu_{A} (x),\mu_{B} (x)} \right),\hbox{max} \left( {v_{A} (x),v_{B} (x)} \right)} \right\rangle \left| {x \in X} \right.} \right\},\\ A \cup B &= \left\{ {\left\langle {x,\hbox{max} \left( {\mu_{A} (x),\mu_{B} (x)} \right),\hbox{min} \left( {v_{A} (x),v_{B} (x)} \right)} \right\rangle \left| {x \in X} \right.} \right\},\\A + B &= \left\{ {\left\langle {x,\mu_{A} (x) + \mu_{B} (x) - \mu_{A} (x) \cdot \mu_{B} (x),v_{A} (x) \cdot v_{B} (x)} \right\rangle \left| {x \in X} \right.} \right\}, \\A \cdot B &= \left\{ {\left\langle {x,\mu_{A} (x) \cdot \mu_{B} (x),v_{A} (x) + v_{B} (x) - v_{A} (x) \cdot v_{B} (x)} \right\rangle \left| {x \in X} \right.} \right\}, \\ \gamma \cdot A &= \left\{ {\left\langle {x,1 - \left( {1 - \mu_{A} (x)} \right)^{\gamma } ,\left( {v_{A} (x)} \right)^{\gamma } } \right\rangle \left| {x \in X} \right.} \right\},\\ A^{\gamma } &= \left\{ {\left\langle {x,\left( {\mu_{A} (x)} \right)^{\gamma } ,1 - \left( {1 - v_{A} (x)} \right)^{\gamma } } \right\rangle \left| {x \in X} \right.} \right\}.\end{aligned} $$

Similarly, for two IFVs $\alpha = \left\langle {\mu_{\alpha } ,v_{\alpha } } \right\rangle$ and $\beta = \left\langle {\mu_{\beta } ,v_{\beta } } \right\rangle$, the following operational laws between them can be obtained:

$$ \alpha + \beta = \left\langle {\mu_{\alpha } + \mu_{\beta } - \mu_{\alpha } \cdot \mu_{\beta } ,v_{\alpha } \cdot v_{\beta } } \right\rangle ,\,\alpha \beta = \left\langle {\mu_{\alpha } \cdot \mu_{\beta } ,v_{\alpha } + v_{\beta } - v_{\alpha } \cdot v_{\beta } } \right\rangle , $$

$$ \gamma \alpha = \left\langle {1 - (1 - \mu_{\alpha } )^{\gamma } ,(v_{\alpha } )^{\gamma } } \right\rangle ,\,\alpha^{\gamma } = \left\langle {(\mu_{\alpha } )^{\gamma } ,1 - (1 - v_{\alpha } )^{\gamma } } \right\rangle . $$

2.2 Intuitionistic fuzzy aggregation operators

Based on these intuitionistic fuzzy operational laws, Xu (2007b) and Xu and Yager 2006 have developed the weighted arithmetic average operator and weighted geometric average operator for IFVs to aggregate intuitionistic fuzzy information.

Definition 2.6

(Xu 2007b; Xu and Yager 2006) For IFVs $\alpha_{i} = < \mu_{i} ,v_{i} >$ with $i = 1,2, \ldots ,n$ and the weighting vector $\varvec{w = }(w_{1} ,w_{2} , \ldots ,w_{n} )^{\rm T}$, $0 \le w_{i} \le 1$, $\sum\nolimits_{i = 1}^{n} {w_{i} } = 1$, the intuitionistic fuzzy weighted arithmetic (IFWA) average operator and the intuitionistic fuzzy weighted geometric (IFWG) averaging operator are, respectively, defined by:

$$ {\text{IFWA}}_{w} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \sum\limits_{i = 1}^{n} {w_{i} \alpha_{i} } $$

(5)

$$ {\text{IFWG}}_{w} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \prod\limits_{i = 1}^{n} {\alpha_{i}^{{w_{i} }} } $$

(6)

Based on the operational laws between IFVs which are mentioned above, we can further get:

$$ {\text{IFWA}}_{w} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \mu_{i} } \right)^{{w_{i} }} } ,\prod\limits_{i = 1}^{n} {v_{i}^{{w_{i} }} } } \right\rangle $$

(7)

$$ {\text{IFWG}}_{w} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {\prod\limits_{i = 1}^{n} {\mu_{i}^{{w_{i} }} } ,1 - \prod\limits_{i = 1}^{n} {\left( {1 - v_{i} } \right)^{{w_{i} }} } } \right\rangle $$

(8)

The IFWA and IFWG operators have been widely applied to solve MAGDM problems with intuitionistic fuzzy information (Li 2011; Yang and Chen 2012). However, they are troubled by some difficulties in application, since the IFWA and IFWG operators are not competent in some extreme situations. We will use the following example to show that we may obtain totally different results when, respectively, applying the IFWA and the IFWG operators in the same case (Beliakov et al. 2011).

Example 2.1

Let $\{ A_{1} ,A_{2} , \ldots ,A_{m} \}$ be the set of all alternatives and $X = \{ x_{1} ,x_{2} , \ldots ,x_{n} \}$ be the set of all considered attributes. Suppose A₁ is described by {α₁,α₂,$\ldots$,α_n}, which satisfy α₁ = <0,1 > and α₂ = < 1, 0 > , and $\varvec{w = }(w_{1} ,w_{2} , \ldots ,w_{n} )^{\rm T}$ is an arbitrary weighting vector with $0 \le w_{i} \le 1$ and $\sum\nolimits_{i = 1}^{n} {w_{i} } = 1$.

If we use the IFWA operator to aggregate the evaluation values of A₁ with regard to all attributes, then we obtain IFWA_w(α₁,α₂,$\ldots$,α_n) = <1,0 > , which indicates that A₁ is the best choice. This result is independent of other values. However, if the IFWG operator is used, we obtain IFWG_w(α₁,α₂,$\ldots$,α_n) = <0,1 > , which indicates that A₁ is the worst choice.

These observations demonstrate that the IFWA operator is easily influenced by extremely large intuitionistic fuzzy values, while the IFWG operator is easily influenced by extremely low intuitionistic fuzzy values. To overcome this deficiency, Beliakov et al. (2011) and Xia et al. (2012) introduced new averaging operators for IFVs by applying a continuous Archimedean t-norm and its dual t-conorm, which is defined as:

$$ {\text{IFWA}}_{w}^{M} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {h^{ - 1} \left( {\sum\limits_{i = 1}^{n} {w_{i} h(\mu_{i} )} } \right),g^{ - 1} \left( {\sum\limits_{i = 1}^{n} {w_{i} g(v_{i} )} } \right)} \right\rangle $$

(9)

where g and h are the additive generator of a continuous Archimedean t-norm and its dual t-conorm, respectively. Beliakov et al. (2011) pointed out that (9) is identical to the operation which is defined on classical fuzzy sets if the t-norm is Łukasiewiczone. In such case, (9) can be written as:

$$ {\text{IFWA}}_{{^{w} }}^{{M_{2} }} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {\sum\limits_{i = 1}^{n} {w_{i} \mu_{i} } ,\sum\limits_{i = 1}^{n} {w_{i} v_{i} } } \right\rangle $$

(10)

The operator shown in (10) was also analyzed in Chen and Tan (1994) and Xu and Yager (2009). The operator ${\text{IFWA}}_{{^{w} }}^{{M_{2} }}$ can reduce computation complexity since it is easy to implement by calculating the weighted arithmetic averages of membership and non-membership grades.

Following this way, Ouyang and Pedrycz (2016) introduced the following intuitionistic fuzzy operator named intuitionistic fuzzy pseudo-weighted geometric (IFPWG) average operator. It is expressed as:

$$ {\text{IFPWG}}_{w} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) = \left\langle {\sum\limits_{i = 1}^{n} {\mu_{i}^{{w_{i} }} } ,\sum\limits_{i = 1}^{n} {v_{i}^{{w_{i} }} } } \right\rangle $$

(11)

We can see that this operator is carried out by geometrically weighted averaging the membership and non-membership grades. The IFPWG operator is monotonic with respect to the partial order relation that was introduced in Definition 2.4. That is, if $\alpha_{i} = < \mu_{i} ,v_{i} >$ and $\alpha_{i}^{*} = < \mu_{i}^{*} ,v_{i}^{*} >$, for $i = 1,2, \ldots ,n$, are IFVs such that both $\mu_{i} \le \mu_{i}^{*}$ and $v_{i} \ge v_{i}^{*}$ for any i, then ${\text{IFPWG}}_{w} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \le {\text{IFPWG}}_{w} (\alpha_{1}^{*} ,\alpha_{2}^{*} , \ldots ,\alpha_{n}^{*} )$ for any weight vector w. Due to the idempotency of the weighted geometric average, we conclude that ${\text{IFPWG}}_{w} (\alpha ,\alpha , \ldots ,\alpha ) = \alpha$ for any IFV α. Moreover, from the monotonicity and the idempotency of the IFPWG operator, we know that IFPWG is bounded, that is, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } \le {\text{IFPWG}}_{w} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \le \bar{\alpha }$, where $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } = \cap_{i = 1}^{n} \alpha_{i} = \left\langle {\mathop {\hbox{min} }\limits_{i} \{ \mu_{i} \} ,\mathop {\hbox{max} }\limits_{i} \{ v_{i} \} } \right\rangle$ and $\bar{\alpha } = \cup_{i = 1}^{n} \alpha_{i} = \left\langle {\mathop {\hbox{max} }\limits_{i} \{ \mu_{i} \} ,\mathop {\hbox{min} }\limits_{i} \{ v_{i} \} } \right\rangle$.

Note that the IFPWG operator cannot be inferred from (9). Moreover, the IFPWG operator is also sensitive to extreme data.

2.3 D-S evidence theory

Dempster–Shafer evidence theory (Dempster 1967; Shafer 1976), which is usually shortened as D–S evidence theory or evidence theory, is a popular approach for uncertainty modeling and reasoning. We can use evidence theory to combine uncertain information from different evidence sources and obtain an aggregated belief degree. Since its inception, evidence theory has developed into an important tool for information fusion (Fan et al. 2018b; Wang and Song 2018). For convenience of discussion, basic concepts that are related to evidence theory, evidence combination rule and counterintuitive issues that may be encountered are first briefly reviewed in this subsection. Then, we introduce the strategy of discounting unreliable evidence sources.

D-S evidence theory was theoretically modeled in the framework of a finite set whose elements are mutually exclusive. This finite set is called the discernment frame and expressed by $\varOmega$. Its power set, which is denoted as $2^{\varOmega }$, contains all subsets of $\varOmega$ including $\varOmega$ itself. Subsets of $\varOmega$ which contains only one element are called as atomic sets since they contain no non-empty subsets. If one set in the power set of $\varOmega$ is believed to be true in some degree, we can assign some belief masses to this set. Based on above analysis, the following significant definitions in evidence theory can be developed.

Definition 2.7

(Dempster 1967) Let $\varOmega = \{ A_{1} , \ldots ,A_{n} \}$ be the frame of discernment. A basic belief assignment (BBA) is a function $m:2^{\varOmega } \to [0,1]$ that satisfies (1) $m(\emptyset ) = 0$ and (2) $\sum\nolimits_{A \subseteq \varOmega } {m(A)} = 1$, where $\emptyset$ denotes the empty set.

The BBA function is also named the belief structure or basic mass assignment (BMA). For any set $A \subseteq \varOmega$, the value that the BBA function takes on $A$ is named as the basic belief mass of $A$, which is written as $m(A)$. This definition indicates that the belief mass on the empty set is 0 and the masses on all subsets of $\varOmega$ are summed to 1. The 0 belief mass indicates total nonsupport a hypothesis, while the belief mass of 1 indicates total support. The mass of $\varOmega$, which is denoted as $m(\varOmega )$, indicates the amount of uncertainty, which is called ignorance.

Definition 2.8

(Dempster 1967). For any subset $A \subseteq \varOmega$ and a BBA m defined in $\varOmega$, if $m(A) > 0$, then $A$ is the focal element of m.

In addition to BBA, two belief measures are associated with the evidence theory. They play important roles in information fusion. One is the belief function, which is expressed by Bel. The belief function is a mapping ${\rm Bel}:2^{\varOmega } \to [0,1]$ that measures the total belief mass that will be distributed, according to a certain rule, among all elements of the subset of $\varOmega$. The belief function is defined as follows:

Definition 2.9

(Shafer 1976) Given a BBA $m$ on $\varOmega$, the belief function corresponding to $m$ is expressed by:

$$ {\text{Bel}}(A) = \sum\limits_{B \subseteq A} {m(B)} $$

(12)

Particularly, the belief function with respect to $A$ can be interpreted as the sum of the probability masses on all proportions that involve $A$.

The plausibility function, which is denoted as Pl, is another important measure in evidence theory. This measure is a mapping ${\text{Pl}}:2^{\varOmega } \to [0,1]$. For a BBA, the plausibility function quantifies the maximal belief mass that may be distributed to each element in a certain subset of $\varOmega$. The plausibility function that corresponds to a belief structure is defined as follows:

Definition 2.10

(Shafer 1976) Given a BBA $m$ defined on $\varOmega$, the value of the plausibility function on the subset $A$ is:

$$ {\text{Pl}}(A) = \sum\limits_{B \cap A \ne \emptyset } {m(B)} $$

(13)

The values of ${\text{Bel}}(A)$ and ${\text{Pl}}(A)$ can be regarded as the lower bound and upper bound, respectively, of the belief level for hypothesis $A$. The belief function of hypothesis $A$ is regarded as the minimal uncertainty regarding $A$, and its plausibility function is regarded as the maximal uncertainty regarding $A$. The relation between them is:

$$ {\text{Pl}}(A) = 1 - {\text{Bel}}(\bar{A}) $$

(14)

$$ {\text{Pl}}(A) \ge {\text{Bel}}(A) $$

(15)

where $\bar{A}$ is the classical complement of hypothesis $A$.

Interval value $[{\text{Bel}}(A),{\text{Pl}}(A)]$ constitutes the confidence interval that describes the uncertainty regarding $A$ and ${\text{Pl}}(A) - {\text{Bel}}(A)$ represents the ignorance level of $A$. If the difference between ${\text{Bel}}(A)$ and ${\text{Pl}}(A)$ increases, the available information for fusion decreases or becomes unreliable. The difference between ${\text{Bel}}(A)$ and ${\text{Pl}}(A)$ also provides an uncertainty measure for the belief level in decision making.

The range of belief degree delimits the upper bound and lower bound for the belief degree in hypothesis $A$. Some special belief ranges with specific meanings are given as follows:

• (i) belief range [1, 1] indicates that hypothesis $A$ is definitely true;

• (ii) belief range [0, 0] indicates that hypothesis $A$ is definitely false;

• (iii) belief range [0, 1] indicates that hypothesis $A$ is completely unknown.

To facilitate decision making based on evidence theory, it is necessary to transform the BBA into a probability distribution on the discernment frame. One of the most widely used probability transformations is the pignistic transformation, which was proposed by Smets 35. The pignistic transformation maps the BBA $m$ to a pignistic probability function on the elements that of all focal sets. The pignistic transformation is defined by Smets 35 as follows:

Definition 2.11

(Smets 2005). A BPA $m$ that is defined on $\varOmega = \{ A_{1} , \ldots ,A_{n} \}$ can be transformed into the pignistic probability according to the following expression:

$$ {\rm Bet}P(A) = \sum\limits_{B \subseteq \varOmega } {\frac{{\left| {A \cap B} \right|}}{\left| B \right|}\frac{m(B)}{1 - m(\emptyset )}} ,\forall A \subseteq \varOmega $$

(16)

where $| \cdot |$ represents the cardinality of a set.

Particularly, when $m(\emptyset ) = 0$, for $A_{i} \in \varOmega$, $i = 1,2, \ldots ,n$, we can obtain the pignistic probability of $\{A_{i}\}$ as:

$$ {\rm Bet} P(\{A_{i}\} ) = \sum\limits_{A \in B} {\frac{m(B)}{\left| B \right|}} ,i = 1,2, \ldots ,n,B \subseteq \varOmega $$

(17)

Definition 2.12

(Dempster 1967). If two independent belief structures $m_{1}$ and $m_{2}$ defined on $\varOmega$ are available, the belief structure that results from the application of Dempster’s combination rule, which is denoted as $m_{1} \odot m_{2}$, or $m_{12}$ for short, is given by:

$$ m_{12} (A) = \left\{ \begin{aligned} &\frac{{\sum\nolimits_{B \cap C = A} {m_{1} (B)m_{2} (C)} }}{{1 - \sum\nolimits_{B \cap C = \emptyset } {m_{1} (B)m_{2} (C)} }},\forall A \subseteq \varOmega ,A \ne \emptyset \hfill \\ &0{\kern 1pt} ,A = \emptyset \hfill \\ \end{aligned} \right. $$

(18)

If multiple independent belief structures are available, they can be combined following Dempster’s combination rule as:

$$ m(A) = \left\{ \begin{aligned}& \frac{{\sum\nolimits_{{ \cap A_{i} = A}} {\prod\nolimits_{i = 1}^{n} {m_{i} (A_{i} )} } }}{{1 - \sum\nolimits_{{ \cap A_{i} = \emptyset }} {\prod\nolimits_{i = 1}^{n} {m_{i} (A_{i} )} } }},\forall A \subseteq \varOmega ,A \ne \emptyset \hfill \\ &0{\kern 1pt} {\kern 1pt} ,A = \emptyset \hfill \\ \end{aligned} \right. $$

(19)

Here, $n$ is the number of belief structures in the combination process, $i$ denotes the $i$th piece of BPA, and $m_{i} (A_{i} )$ is the basic belief mass of hypothesis $A_{i}$ that is supported by evidence $m_{i}$. The value of $m(A)$ reflects the integrated support degree, which is equal to the joint mass, from $n$ mutually independent evidence sources, which correspond to $m_{1} ,m_{2} , \ldots ,m_{n}$. The quantity $k$, which is defined in (20), is the conflict degree among $n$ mutually independent evidence sources. The conflict degree is equal to the belief mass that is assigned to the empty set by the conjunctive combination without the normalization step.

$$ k = \sum\limits_{{ \cap A_{i} = \emptyset }} {\prod\limits_{i = 1}^{n} {m_{i} (A_{i} )} } $$

(20)

The value $k = 0$ implies that there is no contradiction among the information provided by different evidence sources, while $k = 1$ corresponds to complete conflict among these evidence sources. Indeed, $k = 0$ indicates that combining all BBAs creates no empty set, and $k = 1$ means that the sets generated by the combination process are all empty sets.

Despite its convenience in evidence combination, Dempster’s combination rule has an innate drawback: when $k = 1$, i.e., the information that is provided by all evidence sources is completely contradictory, Dempster’s combination rule is undefined. Thus, it cannot be used to combine uncertain information. If evidence sources are highly in conflict, i.e., $k \to 1$, Dempster’s combination rule may generate unsatisfactory results that do not accord with the actual situation. Worse still, some results may be counterintuitive. We will quote the example in Zadeh (1986) to demonstrate this.

Example 2.2

Assume that the discernment frame is $\varOmega = \{ A,B,C\}$. Two BBAs, namely, $m_{1}$ and $m_{2}$, in discernment frame $\varOmega$ are considered, which are given as follows:

$$ m_{1} :m_{1} (A) = 0.9,m_{1} (B) = 0.1,\,m_{2} :m_{2} (B) = 0.1,m_{2} (C) = 0.9. $$

If we use Dempster’s combination rule to combine these BBAs, we will obtain $m(A) = 0$, $m(B) = 1$ and $m(C) = 0$. We notice that both $m_{1}$ and $m_{2}$ assign low levels of support to hypothesis B. However, the combination result completely supports hypothesis B. In contrast, $m_{1}$ and $m_{2}$ have high support levels for hypotheses A and C, respectively; however, A and C are completely refuted by the combination result, which is counterintuitive.

This counterintuitive result shows that Dempster’s combination rule is not suitable for evidence sources with high conflict. This problem can be solved from two aspects.

If it is believed that unreliable evidence sources lead to the counterintuitive phenomenon, the evidence sources should be modified. However, if such a counterintuitive result is caused by the combination rule itself, modification of the combination process is necessary, as proposed in existing studies (Florea et al. 2009; Yang et al. 2013).

When an evidence source is considered partially reliable and is assigned a reliability factor $\lambda \in [0,1]$, the discounting operation can be implemented on the BBA that corresponds to the unreliable evidence source (Florea et al. 2009). One widely used discounting rule is the operation that was proposed by Shafer (1976). This discounting operation is defined as follows:

$$ \left\{ \begin{aligned} &m^{\prime}(A) = \lambda m(A),A \subset \varOmega \hfill \\ &m^{\prime}(\varOmega ) = 1 - \lambda + \lambda m(\varOmega ) \hfill \\ \end{aligned} \right. $$

(21)

where $\lambda$ is interpreted as the reliability degree of the evidence source. $\lambda = 1$ indicates that the evidence source is totally reliable. In this case, the associated BBA will remain unchanged after discounting. $\lambda = 0$ indicates that the evidence source is entirely unreliable. In this case, the original BBA will be changed to $m(\varOmega ) = 1$ after discounting, which indicates that this evidence source provides no information that supports decision making.

3 Review of existing methods for MAGDM

Xu’s method (Xu 2010) is defined based on the IFWA operator, as is expressed in (7). In Xu (2010), $R = (r_{ij} )_{m \times n}$ denotes the collective decision matrix with intuitionistic fuzzy values of all individual decision makers’ evaluations on alternative x_i with respect to attribute a_j. It is defined as:

$$ R = (r_{ij} )_{m \times n} = \left( {\left\langle {1 - \prod\limits_{k = 1}^{t} {\left( {1 - \mu_{{\dot{r}_{ij}^{{\left( {\sigma (k)} \right)}} }} } \right)^{{\varpi_{k} }} ,\prod\limits_{k = 1}^{t} {\left( {v_{{\dot{r}_{ij}^{{\left( {\sigma (k)} \right)}} }} } \right)^{{\varpi_{k} }} } } } \right\rangle } \right)_{m \times n} $$

(22)

where $\varpi_{1} ,\varpi_{2} , \ldots ,\varpi_{t}$ are the weights of the intuitionistic fuzzy evaluation values $\left\langle {\mu_{ij}^{1} ,v_{ij}^{1} } \right\rangle ,\left\langle {\mu_{ij}^{2} ,v_{ij}^{2} } \right\rangle , \ldots ,\left\langle {\mu_{ij}^{t} ,v_{ij}^{t} } \right\rangle$, respectively. The weights $\varpi_{1} ,\varpi_{2} , \ldots ,\varpi_{t}$ satisfy $0 \le \varpi_{p} \le 1$, $p = 1,2, \ldots ,t$. $\left\langle {\mu_{ij}^{k} ,v_{ij}^{k} } \right\rangle$ is the intuitionistic fuzzy value that is given by decision maker E_k to denote the evaluation value of alternative x_i with respect to attribute a_j. $\sigma_{1} ,\sigma_{2} , \ldots ,\sigma_{t}$ is a descending permutation of $1,2, \ldots ,t$, where $t$ is the number of decision makers. Hence, the intuitionistic fuzzy value $\dot{r}_{ij}^{{\left( {\sigma (k)} \right)}} = \left\langle {\mu_{{\dot{r}_{ij}^{{\left( {\sigma (k)} \right)}} }} ,v_{{\dot{r}_{ij}^{{\left( {\sigma (k)} \right)}} }} } \right\rangle$ is the kth largest value among all intuitionistic fuzzy values $\dot{r}_{ij}^{1} ,\dot{r}_{ij}^{2} , \ldots ,\dot{r}_{ij}^{t}$. $\dot{r}_{ij}^{k} = \left\langle {1 - \left( {1 - \mu_{ij}^{k} } \right)^{{t\omega_{k} }} \left( {v_{ij}^{k} } \right)^{{t\omega_{k} }} } \right\rangle$ is an intuitionistic fuzzy value and $\omega_{k}$ denotes the weighting factor of decision maker E_k. All parameters satisfy the following relations: $\mu_{{\dot{r}_{ij}^{{\left( {\sigma (k - 1)} \right)}} }} - v_{{\dot{r}_{ij}^{{\left( {\sigma (k - 1)} \right)}} }} > \mu_{{\dot{r}_{ij}^{{\left( {\sigma (k)} \right)}} }} - v_{{\dot{r}_{ij}^{{\left( {\sigma (k)} \right)}} }}$, $0 \le \mu_{ij}^{k} \le 1$, $0 \le v_{ij}^{k} \le 1$, $0 \le \mu_{ij}^{k} + v_{ij}^{k} \le 1$, $1 \le i \le m$, $1 \le j \le n$, and $1 \le k \le t$. If $v_{ij}^{k} = 0$ for some $1 \le i \le m$, $1 \le j \le n$ and $1 \le k \le t$, then $\prod\limits_{k = 1}^{t} {\left( {v_{{\dot{r}_{ij}^{{\left( {\sigma (k)} \right)}} }} } \right)^{{\varpi_{k} }} }$ in (22) is 0 and we will obtain an incorrect collective decision matrix R, which ranks all alternatives in an unreasonable preference order.

Thus, the method that was proposed by Xu (2010) has the limitation that an improper preference order for all alternatives will be obtained if there is at least one intuitionistic fuzzy evaluation value with zero non-membership degree. This is caused by the aggregation operator that it uses.

In Yue’s method (2014), the positive ideal decision matrix $Y^{*}$ of alternative x_i, which represents the opinions of completely independent decision makers and corresponds to attribute a_j, is defined as

$$ Y^{*} = \left( {\left\langle {1 - \prod\limits_{k = 1}^{t} {\left( {1 - \mu_{ij}^{k} } \right)^{{w_{j}^{k} \times \frac{1}{t}}} } ,\prod\nolimits_{k = 1}^{t} {\left( {v_{ij}^{k} } \right)^{{w_{j}^{k} \times \frac{1}{t}}} } } \right\rangle } \right)_{m \times n} $$

(23)

$\left\langle {\mu_{ij}^{k} ,v_{ij}^{k} } \right\rangle$ is an intuitionistic fuzzy value that is proposed by decision maker E_k for evaluating alternative x_i with respect to attribute a_j, with $0 \le \mu_{ij}^{k} \le 1$, $0 \le v_{ij}^{k} \le 1$, $0 \le \mu_{ij}^{k} + v_{ij}^{k} \le 1$. $w_{j}^{k}$ is the weight factor of attribute a_j that is assigned by decision maker E_k with $0 \le w_{j}^{k} \le 1$, $1 \le j \le n$, and $\sum\nolimits_{j = 1}^{n} {w_{j}^{k} } = 1$. n is the total number of considered attributes. $1 \le i \le m$, where m is the total number of alternatives. $1 \le k \le t$, where t is the number of decision makers.

Equation (23) is also defined based on the IFWA operator, which is expressed in (7). If $v_{ij}^{k} = 0$ for some $1 \le i \le m$, $1 \le j \le n$ and $1 \le k \le t$, then $\prod\nolimits_{k = 1}^{t} {\left( {v_{ij}^{k} } \right)^{{w_{j}^{k} \times \frac{1}{t}}} }$ in (23) is 0, which leads to an unreasonable positive ideal decision matrix Y* and an incorrect preference order for all alternatives. Moreover, if $\mu_{ij}^{k} = 1$ for some $1 \le i \le m$, $1 \le j \le n$ and $1 \le k \le t$, then $1 - \prod\nolimits_{k = 1}^{t} {\left( {1 - \mu_{ij}^{k} } \right)^{{w_{j}^{k} \times \frac{1}{t}}} }$ in (23) is 1. In this case, the obtained positive ideal decision matrix Y* will also be incorrect, which will result in a fallacious preference order of all alternatives.

The method that was proposed by Zeng and Su (2011) can only address MAGDM problems in which the attribute weights given by all decision makers are equal. Zeng and Su’s fuzzy MAGDM method also applies the IFWA operator, which is defined in (7), to aggregate the intuitionistic fuzzy evaluation values from all decision makers to obtain the general payoff decision matrix D:

$$ D = \left( {\left\langle {\mu_{ij} ,v_{ij} } \right\rangle } \right)_{m \times n} = \left( {\left\langle {1 - \prod\limits_{k = 1}^{t} {\left( {1 - \mu_{ij}^{k} } \right)^{{\omega_{k} }} } ,\prod\limits_{k = 1}^{t} {\left( {v_{ij}^{k} } \right)^{{\omega_{k} }} } } \right\rangle } \right)_{m \times n} $$

(24)

where $\left\langle {\mu_{ij} ,v_{ij} } \right\rangle$ represents an intuitionistic fuzzy value that denotes the general payoff intuitionistic fuzzy evaluation value of alternative x_j given by all the decision makers, which corresponds to attribute a_i, where $0 \le \mu_{ij} \le 1$, $0 \le v_{ij} \le 1$, $0 \le \mu_{ij} + v_{ij} \le 1$, $1 \le i \le m$, m is the number of alternatives, $1 \le j \le n$, n is the number of attributes, $\omega_{k}$ is the weight factor of decision maker E_k, $0 \le \omega_{k} \le 1$, $1 \le k \le t$, t is the number of decision makers, and $\sum\nolimits_{k = 1}^{t} {\omega_{k} } = 1$.

Because of the drawbacks of the IFWA operator, Zeng and Su’s method will also obtain an unsatisfactory preference order for all alternatives when we have an intuitionistic fuzzy evaluation value whose non-membership degree is equal to 0. Therefore, the IFWA operator that is shown in (24) cannot address cases with extreme data. The expression in (24) will result in unreasonable decisions in some MAGDM problems.

To avoid the drawbacks of the methods that were presented in Xu (2010), Yue (2014) and Zeng and Su (2011), a new method for fuzzy MAGDM problems was proposed in Chen et al. (2016). The method in Chen et al. (2016) was developed based on the evidential reasoning method and intuitionistic fuzzy sets. The evidential reasoning method was used to aggregate the evaluation result of each alternative with respect to all attributes from each decision maker. The attribute weights were taken into consideration in constructing basic belief masses based on the decision matrix. The integrated evaluation results of all alternatives from each decision maker were obtained by combining these basic belief masses. The aggregated intuitionistic fuzzy value of each alternative was obtained by aggregating the evaluation results of all decision makers and the decision makers’ weights based on the evidential reasoning method. Although the method in Chen et al. (2016) can solve fuzzy MAGDM problems under intuitionistic fuzzy condition by avoiding the drawbacks of the methods that were proposed in Xu (2010), Yue (2014) and Zeng and Su (2011), the calculation process may bring large computational burden, which is not helpful for quick decision making.

In the next section, we will present a new model for fuzzy multi-attribute group decision making to overcome the drawbacks of the methods that were presented in Xu (2010), Yue 2014 and Zeng and Su 2011) and reduce the computational burden of the method that was proposed in Chen et al. (2016).

4 Evidential model for IF-MADM

4.1 New IFWE operator

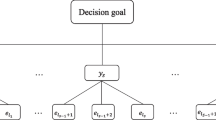
In this section, we take advantage of evidence theory and the powerful representation capability of intuitionistic fuzzy sets to propose a new multi-attribute decision making method. This method overcomes the drawbacks of the methods that were proposed by Xu (2010), Yue (2014) and Zeng and Su (2011). Let $E$ be the set of decision makers, where $E = \{ E_{1,} E_{2} , \ldots ,E_{t} \}$; let $X$ be the set of alternatives, where $X = \{ x_{1,} x_{2} , \ldots ,x_{p} \}$; and let $A$ be the set of attributes, where $A = \{ a_{1,} a_{2} , \ldots ,a_{q} \}$. Let $D_{k}$ be a decision matrix that is given by decision maker $E_{k}$:

$$ \varvec{D}_{k} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{q} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \\ x_{p} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} { < \mu_{11}^{k} ,v_{11}^{k} > } & { < \mu_{12}^{k} ,v_{12}^{k} > } & \ldots & { < \mu_{1q}^{k} ,v_{1q}^{k} > } \\ { < \mu_{21}^{k} ,v_{21}^{k} > } & { < \mu_{22}^{k} ,v_{22}^{k} > } & \ldots & { < \mu_{2q}^{k} ,v_{2q}^{k} > } \\ \vdots & \vdots & \ddots & \vdots \\ { < \mu_{p1}^{k} ,v_{p1}^{k} > } & { < \mu_{p2}^{k} ,v_{p2}^{k} > } & \ldots & { < \mu_{pq}^{k} ,v_{pq}^{k} > } \\ \end{array} } \right)} \\ \end{array} $$

(25)

In decision matrix $D_{k}$, each alternative is evaluated according to a principle that is based on all attributes. If we consider the attribute as an evaluation subject, similar to an evaluator, each alternative is evaluated by all evaluation subjects. The evaluation result $< \mu_{11}^{k} ,v_{11}^{k} >$ for alternative $x_{1}$ that is given by subject $a_{1}$ can be translated to a BBA in evidence theory. The IFV $< \mu_{11}^{k} ,v_{11}^{k} >$ can be regarded as the answer to the question, “Does $x_{1}$ satisfy the standard of excellence according to $a_{1}$ ?” The discernment frame of this problem is $\varTheta = \{ H_{1} ,H_{2} \}$, where $H_{1}$ represents completely satisfying the concept of ‘‘excellence’’ and $H_{2}$ represents not satisfying the concept of “excellence.” Accordingly, we can obtain a BBA, namely, $m_{11}^{k}$, based on the evaluation result $< \mu_{11}^{k} ,v_{11}^{k} >$. The derived BBA can be written as:

$$ \left\{ \begin{aligned} &m_{11}^{k} (\{ H_{1} \} ) = \mu_{11}^{k} \hfill \\ &m_{11}^{k} (\{ H_{2} \} ) = v_{11}^{k} \hfill \\ &m_{11}^{k} (\varTheta ) = 1 - \mu_{11}^{k} - v_{11}^{k} \hfill \\ \end{aligned} \right. $$

(26)

Similarly, the evaluation results that are derived based on other attributes can be used to obtain corresponding BBAs. Since all attributes are mutually independent, all evaluation subjects assess each alternative independently. This satisfies the assumption that all BBAs are independent in evidence theory. Thus, we can obtain the comprehensive evaluation result of alternative $x_{1}$ by combining all BBAs. Considering the excellent properties of Dempster’s combination rule, we use it to fuse the evaluation results.

Given two IFVs, namely, $V_{1} = < \mu_{1} ,v_{1} >$ and $V_{2} = < \mu_{2} ,v_{2} >$, which represent the assessment results of alternative $x$ under attributes $a_{1}$ and $a_{2}$, respectively, two BBAs that correspond to them can be obtained as:

$$ \left\{ \begin{aligned} &m_{1} (\{ H_{1} \} ) = \mu_{1} \hfill \\ &m_{1} (\{ H_{2} \} ) = v_{1} \hfill \\ &m_{1} (\varTheta ) = 1 - \mu_{1} - v_{1} \hfill \\ \end{aligned} \right.,\;\left\{ \begin{aligned} &m_{2} (\{ H_{1} \} ) = \mu_{2} \hfill \\ &m_{2} (\{ H_{2} \} ) = v_{2} \hfill \\ &m_{2} (\varTheta ) = 1 - \mu_{2} - v_{2} \hfill \\ \end{aligned} \right. $$

Then, we can obtain their aggregation as $V_{1} \oplus V_{2} = m_{1} \oplus m_{2}$. If we denote $V = < \mu ,v > = V_{1} \oplus V_{2}$, where $m = m_{1} \oplus m_{2}$, then we can obtain:

$$ \left\{ \begin{aligned} &m(\{ H_{1} \} ) = \frac{{\mu_{1} (1 - v_{2} ) + \mu_{2} (1 - \mu_{1} - v_{1} )}}{{1 - \mu_{1} v_{2} - \mu_{2} v_{1} }} \hfill \\ &m(\{ H_{2} \} ) = \frac{{v_{1} (1 - \mu_{2} ) + v_{2} (1 - \mu_{1} - v_{1} )}}{{1 - \mu_{1} v_{2} - \mu_{2} v_{1} }} \hfill \\ &m(\varTheta ) = \frac{{(1 - \mu_{1} - v_{1} )(1 - \mu_{2} - v_{2} )}}{{1 - \mu_{1} v_{2} - \mu_{2} v_{1} }} \hfill \\ \end{aligned} \right. $$

(27)

In (27), the undefined situation in which $1 - \mu_{1} v_{2} - \mu_{2} v_{1} \ne 0$ is not included. Since $1 - \mu_{1} v_{2} - \mu_{2} v_{1} = 0$ indicates that $V_{1}$ and $V_{2}$ are real numbers 0 and 1, this special situation is outside of the scope of this operation.

According to the correspondence relationship between IFV and BBA, we can obtain:

$$ V = \left\langle {\frac{{\mu_{1} (1 - v_{2} ) + \mu_{2} (1 - \mu_{1} - v_{1} )}}{{1 - \mu_{1} v_{2} - \mu_{2} v_{1} }},\frac{{v_{1} (1 - \mu_{2} ) + v_{2} (1 - \mu_{1} - v_{1} )}}{{1 - \mu_{1} v_{2} - \mu_{2} v_{1} }}} \right\rangle $$

(28)

Then, we can develop a new operation on intuitionistic fuzzy values as follows:

Definition 4.1

Given two IFVs, namely, $V_{1} = < \mu_{1} ,v_{1} >$ and $V_{2} = < \mu_{2} ,v_{2} >$, the orthogonal sum operation on these IFVs can be defined as:

$$ V_{1} \oplus V_{2} { = }\left\langle {\frac{{\mu_{1} (1 - v_{2} ) + \mu_{2} (1 - \mu_{1} - v_{1} )}}{{1 - \mu_{1} v_{2} - \mu_{2} v_{1} }},\frac{{v_{1} (1 - \mu_{2} ) + v_{2} (1 - \mu_{1} - v_{1} )}}{{1 - \mu_{1} v_{2} - \mu_{2} v_{1} }}} \right\rangle $$

(29)

This operation can be easily extended to calculate the orthogonal sum of more than two IFVs. By virtue of the commutative and associative properties of Dempster’s combination rule, we have:

• (i) $V_{1} \oplus V_{2} { = }V_{2} \oplus V_{1}$

• (ii) $V_{1} \oplus V_{2} \oplus V_{3} { = }V_{1} \oplus \left( {V_{2} \oplus V_{3} } \right)$

Thus, the orthogonal summation result of multiple IFVs is independent of their calculation order. This also provides us with the freedom to perform parallel computation when many IFVs are available.

Suppose that the weighting factors of IFVs $V_{1} = < \mu_{1} ,v_{1} >$ and $V_{2} = < \mu_{2} ,v_{2} >$ are w₁ and w₂, respectively. Based on the evidence discounting operation, we can obtain the discounted BBAs that correspond to them as follows:

$$ \left\{ \begin{aligned} &m_{1}^{{w_{1} }} (\{ H_{1} \} ) = w_{1} \mu_{1} \hfill \\ &m_{1}^{{w_{1} }} (\{ H_{2} \} ) = w_{1} v_{1} \hfill \\ &m_{1}^{{w_{1} }} (\varTheta ) = 1 - w_{1} \mu_{1} - w_{1} v_{1} \hfill \\ \end{aligned} \right.,\;\left\{ \begin{aligned}& m_{2}^{{w_{2} }} (\{ H_{1} \} ) = w_{2} \mu_{2} \hfill \\ &m_{2}^{{w_{2} }} (\{ H_{2} \} ) = w_{2} v_{2} \hfill \\ &m_{2}^{{w_{2} }} (\varTheta ) = 1 - w_{2} \mu_{2} - w_{2} v_{2} \hfill \\ \end{aligned} \right. $$

Considering the relation between BBAs and IFVs, we propose a new multiplication operation on intuitionistic fuzzy values.

Definition 4.2

Given an IFV $V = < \mu ,v >$ and a real number $w$, where $0 \le w \le 1$, the multiplication operation between $V = < \mu ,v >$ and $w$ is defined as:

$$ w \circ V = \left\langle {w\mu ,wv} \right\rangle $$

(30)

Following the above two definitions, we can construct a new intuitionistic fuzzy weighted evidential (IFWE) average operator.

Definition 4.3

Given IFVs $\alpha_{i} = < \mu_{i} ,v_{i} >$ with $i = 1,2, \ldots ,n$ and the weighting vector $\varvec{w = }(w_{1} ,w_{2} , \ldots ,w_{n} )^{\rm T}$ with $0 \le w_{i} \le 1$ and $\sum\nolimits_{i = 1}^{n} {w_{i} } = 1$, the intuitionistic fuzzy weighted evidential average operator (IFWE) with respect to the weight vector $\varvec{w}$ can be defined as:

$$ \begin{aligned} &{\rm IFWE}_{w} (\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \hfill \\ &= \oplus_{i = 1}^{n} (w_{i} \circ \alpha_{i} ) \hfill \\& = (w_{1} \circ \alpha_{1} ) \oplus (w_{2} \circ \alpha_{2} ) \oplus \ldots \oplus (w_{n} \circ \alpha_{n} ) \hfill \\ \end{aligned} $$

(31)

4.2 Possibility-based ranking method for IFVs

When solving MAGDM problems, it is necessary to get the preference order of all alternatives by comparing their evaluation information. If intuitionistic fuzzy information is involved, the ranking method of IFVs must be discussed.

The order $\le_{A}$ has been proposed by Atanassov (1999) to compare IFVs, as defined in Definition 2.4. But this is a partial orderable relation because it is not suitable for all IFVs. Notice that for the situation of $\mu_{A} \ge \mu_{B} ,v_{A} \ge v_{B}$, we cannot rank them according to the partial order. Such partial orderable relation cannot be used to make a decision. So a linear order for IFVs is desirable. Several linear orders for IFVs have been discussed in Liu and Wang (2007). Next, we will review the most widely used linear order relation which was developed based on score function and the accuracy function of IFVs (Chen and Tan 1994; Hong and Choi 2000).

Definition 4.4

(Chen and Tan 1994; Hong and Choi 2000). For an IFV $\alpha = \left\langle {\mu ,v} \right\rangle$, its score function $s$ and accuracy function $h$ can be expressed as $s(\alpha ) = \mu - v$ and $h(\alpha ) = \mu + v$, respectively.

From Definition 4.4, we can easily get that $s(\alpha ) \in [ - 1,1]$ and $h(\alpha ) \in [0,1]$ for IFV $\alpha$. Based on the score function and the accuracy function, IFVs can be ranked into a linear order.

Definition 4.5

(Hong and Choi 2000) For two IFVs $\alpha = \left\langle {\mu_{1} ,v_{1} } \right\rangle$ and $\beta = \left\langle {\mu_{2} ,v_{2} } \right\rangle$, their score functions are denoted as s(α) and s(β), respectively. And their accuracy functions are written as h(α) and h(β), respectively. Then, α and β can be ranked following these rules:

• (i) If $s(\alpha ) > s(\beta )$, then $\alpha$ is bigger than $\beta$, expressed by $\alpha > \beta$;

• (ii) If $s(\alpha ) < s(\beta )$, then $\alpha$ is smaller than $\beta$, expressed as by $\alpha < \beta$;

• (iii) If $s(\alpha ) = s(\beta )$, then

  • a) If $h(\alpha ) = h(\beta )$, then $\alpha$ is equal to $\beta$, expressed by $\alpha = \beta$;

  • b) If $h(\alpha ) > h(\beta )$, then $\alpha$ is bigger than $\beta$, expressed by $\alpha > \beta$.

  • c) If $h(\alpha ) < h(\beta )$, then $\alpha$ is smaller than $\beta$, expressed by $\alpha < \beta$.

Example 4.1

Three IFVs are given as $\alpha_{1} = \left\langle {0.5,0.1} \right\rangle$, $\alpha_{2} = \left\langle {0.55,0.2} \right\rangle$, and $\alpha_{3} = \left\langle {0.6,0.25} \right\rangle$. According to Definition 4.4, we can get the score functions of IFVs $\alpha_{1}$, $\alpha_{2}$ and $\alpha_{3}$ as following:

$$ s(\alpha_{1} ) = 0.5 - 0.1 = 0.4,\,s(\alpha_{2} ) = 0.55 - 0.2 = 0.35,\,s(\alpha_{3} ) = 0.6 - 0.25 = 0.35. $$

Then, we can get $\alpha_{1} > \alpha_{2}$ and $\alpha_{1} > \alpha_{3}$ when their score functions are merely considered. To rank $\alpha_{2}$ and $\alpha_{3}$, their accuracy functions should be accounted. The accuracy functions of $\alpha_{2}$ and $\alpha_{3}$ can be calculated as follows:

$$ h(\alpha_{2} ) = 0.55 + 0.2 = 0.75,\,h(\alpha_{3} ) = 0.6 + 0.25 = 0.85. $$

Then, following the ranking rule presented in Definition 4.5, we can get the linear order $\alpha_{1} > \alpha_{3} > \alpha_{2}$.

Although the order for IFVs based on the score function and accuracy function is regarded as admissible, this may not be an ideal rule for choosing the best alternative. Since the score function and accuracy function are considered separately, and in most cases only the score functions are taken into consideration, this ranking method will produce counterintuitive results in some situation. Therefore, a more reasonable linear order for IFVs is desirable. Next, we will propose a new linear order for IFVs based on possibility to address the decision making problem in our evidential model for MAGDM.

We have claimed that there is equivalence relation between IFVs and interval values. Hence, based on such equivalence relation, we can rank IFVs by using the possibility-based ranking method for interval values.

Definition 4.6

(Nakahara 1998; Nakahara et al. 1992). Suppose that $\alpha = [a^{L} ,a^{U} ]$ and $\beta = [b^{L} ,b^{U} ]$ are two interval values with $a^{L} < a^{U}$ and $b^{L} < b^{U}$. The possibility degree of interval value $\alpha$ preceding interval value $\beta$, which is denoted as $P_{(\alpha \ge \beta )}$, can be defined as:

$$ P_{(\alpha \ge \beta )} = \hbox{min} \left\{ {1,\hbox{max} \left\{ {\frac{{a^{U} - b^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}},0} \right\}} \right\} $$

(32)

It is worth mentioning that if $\alpha$ and $\beta$ both reduce to precise values, i.e., $a^{L} = a^{U} = a$ and $b^{L} = b^{U} = b$, (32) will be undefined since $(a^{U} - a^{L} ) + (b^{U} - b^{L} ) = 0$. In this special case, we take $P_{(\alpha \ge \beta )} = 1$ for $a > b$. Particularly, we assume $P_{(\alpha \ge \beta )} = 0.5$ for $a = b$.

Theorem 4.1

(Facchinetti et al. 1998; Nakahara 1998). Suppose two interval values are given as$\alpha = [a^{L} ,a^{U} ]$and$\beta = [b^{L} ,b^{U} ]$. The possibility degree$P_{(\alpha \ge \beta )}$has the following properties:

(i) $0 \le P_{(\alpha \ge \beta )} \le 1$, (ii) $P_{(\alpha \ge \alpha )} = 0.5$, (iii) $P_{(\alpha \ge \beta )} = 1 \Leftrightarrow a^{L} \ge b^{U}$, and (iv) $P_{(\alpha \ge \beta )} + P_{(\beta \ge \alpha )} = 1$.

Proof

Based on the definition of $P_{(\alpha \ge \beta )}$, proving properties (i) and (ii) is straightforward. (iii) We can obtain the following relation effortlessly:

$$ P_{(\alpha \ge \beta )} = 1 \Rightarrow \hbox{max} \left\{ {\frac{{a^{U} - b^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}},0} \right\} \ge 1 \Rightarrow \frac{{a^{U} - b^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}} \ge 1 $$

Since the denominator $(a^{U} - a^{L} ) + (b^{U} - b^{L} )$ is positive, we can obtain $a^{U} - b^{L} > 0$. It follows that $a^{U} - b^{L} \ge (a^{U} - a^{L} ) + (b^{U} - b^{L} ) = a^{U} - b^{L} - (a^{L} - b^{U} )$, which indicates that $a^{L} - b^{U} \ge 0$, i.e., $a^{L} \ge b^{U}$.

This proof process is reversible, so $P_{(\alpha \ge \beta )} = 1 \Leftrightarrow a^{L} \ge b^{U}$.

iv) We need to consider three cases, as listed in Fig. 1.

Fig. 1

Cases of interval relations. a Separation case; b overlapping case; and c inclusion case

(a) In the separation case, which is shown in Fig. 1a, we obtain $a^{L} \ge b^{U}$, $P_{(\alpha \ge \beta )} = 1$ and $P_{(\beta \ge \alpha )} = 0$. Thus, $P_{(\alpha \ge \beta )} + P_{(\beta \ge \alpha )} = 1$.

(b) For the overlapping case, which is shown in Fig. 1b, $b^{L} \le a^{L} \le b^{U} \le a^{U}$, so we have:

$$ P_{(\alpha \ge \beta )} = \frac{{a^{U} - b^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}},\,P_{(\beta \ge \alpha )} = \frac{{b^{U} - a^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}}. $$

Thus,

$$ \begin{aligned} P_{(\alpha \ge \beta )} + P_{(\beta \ge \alpha )} \hfill \\ = \frac{{a^{U} - b^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}} + \frac{{b^{U} - a^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}} \hfill \\ = 1. \hfill \\ \end{aligned} $$

(c) The inclusion case is shown in Fig. 1c, $b^{L} \ge a^{L} ,b^{U} \le a^{U}$. Then, we obtain:

$$ P_{(\alpha \ge \beta )} = \frac{{a^{U} - b^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}},\,P_{(\beta \ge \alpha )} = \frac{{b^{U} - a^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}}. $$

Therefore,

$$ \begin{aligned} P_{(\alpha \ge \beta )} + P_{(\beta \ge \alpha )} \hfill \\ = \frac{{a^{U} - b^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}} + \frac{{b^{U} - a^{L} }}{{(a^{U} - a^{L} ) + (b^{U} - b^{L} )}} \hfill \\ = 1 \hfill \\ \end{aligned} . $$

Hence, all properties in Theorem 4.1 hold. □

Since intuitionistic fuzzy values $A = \left\langle {\mu_{A} ,v_{A} } \right\rangle$ and $B = \left\langle {\mu_{B} ,v_{B} } \right\rangle$ can be expressed by interval values $A = \left[ {\mu_{A} ,1 - v_{A} } \right]$ and $B = \left[ {\mu_{B} ,1 - v_{B} } \right]$, respectively, we can also define the possibility of $A \ge B$ from Definition 4.6.

Definition 4.7

Suppose that $A = \left\langle {\mu_{A} ,v_{A} } \right\rangle {\kern 1pt} {\kern 1pt}$ and ${\kern 1pt} {\kern 1pt} B = \left\langle {\mu_{B} ,v_{B} } \right\rangle$ are two intuitionistic fuzzy values with $\pi_{A} \cdot \pi_{B} \ne 0$. The possibility degree of $A \ge B$ can be defined as:

$$ P_{(A \ge B)} = \hbox{min} \left\{ {1,\hbox{max} \left\{ {\frac{{1 - v_{A} - \mu_{B} }}{{\pi_{A} + \pi_{B} }},0} \right\}} \right\} $$

(33)

In the case of $\pi_{A} + \pi_{B} = 0$, $A$ and $B$ are both associated with crisp real numbers. Then, $P_{(A \ge B)} = 1$ if $\mu_{A} > \mu_{B}$ and $P_{(A \ge B)} = 0.5$ if $\mu_{A} = \mu_{B}$.

Theorem 4.2

Given two intuitionistic fuzzy values$A = \left\langle {\mu_{A} ,v_{A} } \right\rangle$and${\kern 1pt} {\kern 1pt} B = \left\langle {\mu_{B} ,v_{B} } \right\rangle$, we have:

• 1. $0 \le P_{(A \ge B)} \le 1$;

• 2. $P_{(A \ge A)} = 0.5$;

• 3. $P_{(A \ge B)} = 1 \Leftrightarrow \mu_{A} \ge 1 - v_{B}$;

• 4. $P_{(A \ge B)} + P_{(B \ge A)} = 1$.

Proof

All four properties follow directly from Theorem 4.1 and Definition 4.7. □

From the third property in Theorem 4.2, it follows that $P_{(A \ge B)} = 1 \Rightarrow 1 - v_{A} \ge \mu_{A} \ge 1 - v_{B} \ge \mu_{B} \Rightarrow \mu_{A} \ge \mu_{B} ,v_{A} \le v_{B}$. However, this is not reversible, i.e., $\mu_{A} \ge \mu_{B} ,v_{A} \le v_{B} \Rightarrow P_{(A \ge B)} = 1$ does not hold. This differs from the ordinary partial order relation that was presented in Definition 2.4. Thus, the relation $A \ge B$ defined in Definition 4.7 is much more stringent than the ordinary partial order relation in Definition 2.4.

We suppose that IFVs $A_{1} ,A_{2} , \ldots ,A_{n}$ are given as $A_{i} = \left\langle {\mu_{{A_{i} }} ,v_{{A_{i} }} } \right\rangle$, $i = 1,2, \ldots ,n$. To rank all of these intuitionistic fuzzy values, we first compare each intuitionistic fuzzy value $A_{i}$ with all intuitionistic fuzzy values $A_{1} ,A_{2} , \ldots ,A_{n}$, $i = 1,2, \ldots ,n$. By Definition 4.7, we have:

$$ P_{{(A_{i} \ge A_{j} )}} = \hbox{min} \left\{ {1,\hbox{max} \left\{ {\frac{{1 - v_{{A_{i} }} - \mu_{{A_{j} }} }}{{\pi_{{A_{i} }} + \pi_{{A_{j} }} }},0} \right\}} \right\},\,i,j = 1,2, \ldots ,n $$

(34)

For simplicity, we let $P_{ij} = P_{{(A_{i} \ge A_{j} )}}$. Then, we can construct a complementary comparison matrix as follows:

$$ \varvec{P} = \left( {\begin{array}{*{20}c} {P_{11} } & {P_{12} } & \ldots & {P_{1n} } \\ {P_{21} } & {P_{22} } & \ldots & {P_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {P_{n1} } & {P_{n2} } & \ldots & {P_{nn} } \\ \end{array} } \right) $$

(35)

$\forall i,j \in \{ 1,2, \ldots ,n\}$, we have the following relations: $0 \le P_{ij} \le 1$, $P_{ij} + P_{ji} = 1$, and $P_{ii} = 0.5$.

Calculating the column sum of matrix $\varvec{P}$, we obtain:

$$ P_{i} = \sum\limits_{j = 1}^{n} {P_{ij} } $$

(36)

Then, we can rank these intuitionistic fuzzy values $A_{1} ,A_{2} , \ldots ,A_{n}$ according to the value of $P_{i}$, $i \in \{ 1,2, \ldots ,n\}$.

4.3 New method for MAGDM

The new method for MAGDM is proposed based on intuitionistic fuzzy sets and evidence theory. It is now presented as follows.

Let $D_{k}$ be the decision matrix that is given by decision maker $E_{k}$:

$$ \varvec{D}_{k} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{q} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \\ x_{p} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} { < \mu_{11}^{k} ,v_{11}^{k} > } & { < \mu_{12}^{k} ,v_{12}^{k} > } & \ldots & { < \mu_{1q}^{k} ,v_{1q}^{k} > } \\ { < \mu_{21}^{k} ,v_{21}^{k} > } & { < \mu_{22}^{k} ,v_{22}^{k} > } & \ldots & { < \mu_{2q}^{k} ,v_{2q}^{k} > } \\ \vdots & \vdots & \ddots & \vdots \\ { < \mu_{p1}^{k} ,v_{p1}^{k} > } & { < \mu_{p2}^{k} ,v_{p2}^{k} > } & \ldots & { < \mu_{pq}^{k} ,v_{pq}^{k} > } \\ \end{array} } \right)} \\ \end{array} $$

where $0 \le \mu_{ij}^{k} \le 1$, $0 \le v_{ij}^{k} \le 1$,$\mu_{ij}^{k} + v_{ij}^{k} \le 1$, $1 \le k \le t$, $1 \le i \le p$, and $1 \le j \le q$.

The weight of each attribute is assigned as $w_{j}^{k}$ by decision maker $E_{k}$. Then, based on the IFWE average operator, the evaluation result of alternative $x_{i}$, for $1 \le i \le p$, with respect to all attitudes, can be aggregated as:

$$ \begin{aligned} < \mu_{i}^{k} ,v_{i}^{k} >& \hfill \\ &= IFWE_{{w^{k} }} ( < \mu_{i1}^{k} ,v_{i1}^{k} > , < \mu_{i2}^{k} ,v_{i2}^{k} > , \ldots , < \mu_{iq}^{k} ,v_{iq}^{k} > ) \hfill \\ &{\kern 1pt} = \oplus_{j = 1}^{q} (w_{j}^{k} \circ < \mu_{ij}^{k} ,v_{ij}^{k} > ) \hfill \\ &{\kern 1pt} = < w_{1}^{k} \mu_{i1}^{k} ,w_{1}^{k} v_{i1}^{k} > \oplus < w_{2}^{k} \mu_{i2}^{k} ,w_{2}^{k} v_{i2}^{k} > \oplus \ldots \oplus < w_{q}^{k} \mu_{iq}^{k} ,w_{q}^{k} v_{iq}^{k} > \hfill \\ \end{aligned} $$

(37)

Based on the aggregated decisions of all decision makers, we can obtain the overall decision making matrix as:

$$ \varvec{D} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {E_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{k} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \\ x_{p} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} { < \mu_{1}^{1} ,v_{1}^{1} > } & { < \mu_{1}^{2} ,v_{1}^{2} > } & \ldots & { < \mu_{1}^{k} ,v_{1}^{k} > } \\ { < \mu_{2}^{1} ,v_{2}^{1} > } & { < \mu_{2}^{2} ,v_{2}^{2} > } & \ldots & { < \mu_{2}^{k} ,v_{2}^{k} > } \\ \vdots & \vdots & \ddots & \vdots \\ { < \mu_{p}^{1} ,v_{p}^{1} > } & { < \mu_{p}^{2} ,v_{p}^{2} > } & \ldots & { < \mu_{p}^{k} ,v_{p}^{k} > } \\ \end{array} } \right)} \\ \end{array} $$

(38)

Since all decision makers are in mutual independence, the IFWE average operator can be used to aggregate the information that is proposed by all decision makers. Suppose that the weighting factor of decision maker $E_{k}$ is $\lambda^{k}$, $1 \le k \le t$. We can aggregate the evaluation values of the decision makers with respect to alternative x_i to obtain the final assessment of x_i.

$$ \begin{aligned} &< \mu_{i} ,v_{i} > = IFWE_{{\lambda^{k} }} ( < \mu_{i}^{1} ,v_{i}^{1} > , < \mu_{i}^{2} ,v_{i}^{2} > , \ldots , < \mu_{i}^{t} ,v_{i}^{t} > ) \hfill \\ &{\kern 1pt} {\kern 1pt} = \oplus_{k = 1}^{t} (\lambda^{k} \circ < \mu_{i}^{k} ,v_{i}^{k} > ){\kern 1pt} = < \lambda^{1} \mu_{i}^{1} ,\lambda^{1} v_{i}^{1} > \oplus < \lambda^{2} \mu_{i}^{2} ,\lambda^{2} v_{i}^{2} > \oplus \cdots \oplus < \lambda^{t} \mu_{i}^{t} ,\lambda^{t} v_{i}^{t} > \hfill \\ \end{aligned} $$

(39)

After obtaining the final assessment of each alternative, we can order them by the possibility-based ranking method for IFVs.

Given two alternatives x_i and x_j with intuitionistic fuzzy assessments $< \mu_{i} ,v_{i} >$ and $< \mu_{j} ,v_{j} >$, respectively, we can calculate the possibility of $x_{i} \succ x_{j}$($x_{i}$ is better than $x_{j}$):

$$ P_{{(x_{i} \succ x_{j} )}} = \hbox{min} \left\{ {1,\hbox{max} \left\{ {\frac{{1 - v_{i} - \mu_{j} }}{{2 - \mu_{i} - v_{i} - \mu_{j} - v_{j} }},0} \right\}} \right\} $$

(40)

For alternatives $x_{1,} x_{2} , \ldots ,x_{p}$, the comparison matrix can be constructed as:

$$ \varvec{P} = \left( {\begin{array}{*{20}c} {P_{{(x_{1} \succ x_{1} )}} } & {P_{{(x_{1} \succ x_{2} )}} } & \ldots & {P_{{(x_{1} \succ x_{p} )}} } \\ {P_{{(x_{2} \succ x_{1} )}} } & {P_{{(x_{2} \succ x_{2} )}} } & \ldots & {P_{{(x_{2} \succ x_{p} )}} } \\ \vdots & \vdots & \ddots & \vdots \\ {P_{{(x_{p} \succ x_{1} )}} } & {P_{{(x_{p} \succ x_{2} )}} } & \ldots & {P_{{(x_{p} \succ x_{p} )}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {P_{11} } & {P_{12} } & \ldots & {P_{1n} } \\ {P_{21} } & {P_{22} } & \ldots & {P_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {P_{n1} } & {P_{n2} } & \ldots & {P_{nn} } \\ \end{array} } \right) $$

(41)

It follows that $\forall i,j \in \{ 1,2, \ldots ,p\}$, $0 \le P_{ij} \le 1$, $P_{ij} + P_{ji} = 1$, and $P_{ii} = 0.5$.

In the matrix P, the values of the ith row reflect the possibility that $x_{i}$ is better than other alternatives. Therefore, the column sum can be used to rank all alternatives. Summing all elements in each row of matrix $\varvec{P}$, we have:

$$ P_{i} = \sum\limits_{j = 1}^{p} {P_{ij} } $$

(42)

Then, we can order the alternatives $x_{1,} x_{2} , \ldots ,x_{p}$ by the value of $P_{i}$, $i \in \{ 1,2, \ldots ,p\}$. The larger the value of $P_{i}$, the better the preference order of alternative x_i, where $i \in \{ 1,2, \ldots ,p\}$.

5 Application examples and comparative analysis

In this section, we will present some illustrative examples from MAGDM application to analyze the effectiveness and rationality of our proposed method for solving MAGDM problems. Comparative analysis will be presented based on the results obtained based on our proposed method and other methods proposed in Chen et al. (2016), Xu (2010), Yue (2014) and Zeng and Su (2011).

Example 5.1

(Yue 2014): The leading group of a college needs to be assessed in the year-end report. The index of satisfaction is important to the evaluation. So the satisfaction degree with the members in the leading group will be evaluated by consulting masses from each level. One president and three vice presidents of the college will be assessed. For clarity, these four members to be assessed are regarded as four alternatives denoted by x₁, x₂, x₃ and x₄, where x₁ represents the president and x₂, x₃ and x₄ represent the vice presidents, respectively. The masses are constituted by three teams: teachers {E₁}, researchers {E₂} and undergraduate students {E₃}. They are considered as three decision makers (reviewers) for the assess work. Three attributes, including working performance, academic performance and personal reputation, are considered by decision makers E₁, E₂ and E₃ to evaluate the alternatives x₁, x₂, x₃ and x₄. Three attributes to be considered are denoted as following:

• 1. a₁: working performance,

• 2. a₂: academic performance,

• 3. a₃: personal reputation.

Decision makers E₁, E₂ and E₃ provide decision matrices D₁, D₂ and D₃, respectively. Due to the limit of expertise, uncertain information expressed by IFVs is involved in the evaluation. These decision matrices with intuitionistic fuzzy information are listed as follows:

$$ \varvec{D}_{1} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ x_{4} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.36,0.27} \right\rangle } & {\left\langle {0.53,0.28} \right\rangle } & {\left\langle {0.57,0.22} \right\rangle } \\ {\left\langle {0.72,0.28} \right\rangle } & {\left\langle {0.91,0.07} \right\rangle } & {\left\langle {0.80,0.10} \right\rangle } \\ {\left\langle {0.63,0.19} \right\rangle } & {\left\langle {0.88,0.12} \right\rangle } & {\left\langle {0.86,0.14} \right\rangle } \\ {\left\langle {0.65,0.33} \right\rangle } & {\left\langle {0.72,0.23} \right\rangle } & {\left\langle {0.77,0.23} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

$$ \varvec{D}_{2} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ x_{4} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.53,0.26} \right\rangle } & {\left\langle {0.54,0.35} \right\rangle } & {\left\langle {0.68,0.32} \right\rangle } \\ {\left\langle {0.85,0.15} \right\rangle } & {\left\langle {0.86,0.13} \right\rangle } & {\left\langle {0.69,0.30} \right\rangle } \\ {\left\langle {0.83,0.16} \right\rangle } & {\left\langle {0.76,0.24} \right\rangle } & {\left\langle {0.73,0.13} \right\rangle } \\ {\left\langle {0.90,0.07} \right\rangle } & {\left\langle {0.91,0.03} \right\rangle } & {\left\langle {0.66,0.12} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

$$ \varvec{D}_{3} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ x_{4} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.81,0.18} \right\rangle } & {\left\langle {0.76,0.24} \right\rangle } & {\left\langle {0.74,0.19} \right\rangle } \\ {\left\langle {0.75,0.16} \right\rangle } & {\left\langle {0.84,0.16} \right\rangle } & {\left\langle {0.97,0.03} \right\rangle } \\ {\left\langle {0.89,0.11} \right\rangle } & {\left\langle {0.78,0.21} \right\rangle } & {\left\langle {0.74,0.11} \right\rangle } \\ {\left\langle {0.66,0.18} \right\rangle } & {\left\langle {0.63,0.27} \right\rangle } & {\left\langle {0.71,0.29} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

The weighting factors of three decision makers E₁, E₂ and E₃ are assigned as 0.33, 0.34 and 0.33, respectively, i.e., $\lambda^{1} = 0.33$, $\lambda^{2} = 0.34$, and $\lambda^{3} = 0.33$. The weighting factors of attributes a₁, a₂ and a₃ assigned by E₁ are 0.4, 0.2 and 0.4, respectively, i.e., $w_{1}^{1} = 0.4$, $w_{2}^{1} = 0.2$, $w_{3}^{1} = 0.4$. The weighting factors of attributes a₁, a₂ and a₃ that are given by decision maker E₂ are 0.3, 0.3 and 0.4, respectively, i.e., $w_{1}^{2} = 0.3$, $w_{2}^{2} = 0.3$, $w_{3}^{2} = 0.4$. The weighting factors of attributes a₁, a₂ and a₃ that are given by decision maker E₃ are 0.4, 0.4 and 0.2, respectively, i.e., $w_{1}^{3} = 0.4$, $w_{2}^{3} = 0.4$, and $w_{3}^{3} = 0.2$.

According to the relationship between IFV and BBA, we can obtain BBAs in the discernment frame $\varTheta = \{ H_{1} ,H_{2} \}$, where $H_{1}$ represents complete satisfaction of the concept of ‘‘excellence’’ with respect to the attitude and $H_{2}$ represents non-satisfaction of the concept of ‘‘excellence’’ with respect to the attitude. The BBAs are listed in the following Tables (1, 2 and 3).

Table 1 BBAs generated from D₁

Table 2 BBAs generated from D₂

Table 3 BBAs generated from D₃

By the IFWE average operator, we can get the comprehensive decision matrix that is proposed by all decision makers.

$$ \varvec{D} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{3} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ x_{4} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.3647,0.1742} \right\rangle } & {\left\langle {0.4281,0.1979} \right\rangle } & {\left\langle {0.5609,0.1160} \right\rangle } \\ {\left\langle {0.5732,0.0941} \right\rangle } & {\left\langle {0.5605,0.1131} \right\rangle } & {\left\langle {0.6015,0.0738} \right\rangle } \\ {\left\langle {0.5667,0.0876} \right\rangle } & {\left\langle {0.5563,0.0948} \right\rangle } & {\left\langle {0.5780,0.0753} \right\rangle } \\ {\left\langle {0.5183,0.1356} \right\rangle } & {\left\langle {0.5948,0.0419} \right\rangle } & {\left\langle {0.4822,0.1451} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

The final assessments of the four leaders can be obtained by (39):

$$ \begin{aligned} V_{{x_{1} }} = \left\langle {0.3589,0.1150} \right\rangle ,V_{{x_{2} }} = \left\langle {0.4565,0.0608} \right\rangle , \hfill \\ V_{{x_{3} }} = \left\langle {0.4506,0.0562} \right\rangle ,V_{{x_{4} }} = \left\langle {0.4240,0.0713} \right\rangle . \hfill \\ \end{aligned} $$

By (40) and (41), we can obtain the comparison matrix of these four final assessment IFVs:

$$ \varvec{P} = \left( {\begin{array}{*{20}c} {0.5} & {0.4247} & {0.4261} & {0.4472} \\ {0.5753} & {0.5} & {0.5007} & {0.5218} \\ {0.5739} & {0.4993} & {0.5} & {0.5209} \\ {0.5528} & {0.4782} & {0.4791} & {0.5} \\ \end{array} } \right) $$

The column sums of matrix P can be obtain as $P_{1} = 1.7981,P_{2} = 2.0977,P_{3} = 2.0941,P_{4} = 2.0101$.

Thus, all alternatives can be ranked as preference order: $x_{2} \succ x_{3} \succ x_{4} \succ x_{1}$.

The ranking orders of all alternatives can also be obtained by the method introduced in Chen et al. (2016), Xu (2010) and Yue (2014). Since the attribute weights proposed by different decision makers are different, the method proposed in Zeng and Su (2011) cannot solve this problem. For comparison, ranking orders from different methods are presented in Table 4. We note that the methods proposed in Chen et al. (2016), Xu (2010) and Yue 2014) and our proposed method can get the same ranking order $x_{2} \succ x_{3} \succ x_{4} \succ x_{1}$. This indicates that the proposed method is competent to solving MAGDM problems where the attribute weights from different decision makers are different.

Table 4 The ranking orders of lead group in Example 5.1

Example 5.2

(Zeng and Su 2011): A venture investment company plans to invest a sum of money in one of six candidate projects, namely, a chemical industry, an artificial intelligence company, a food factory, a super market, a car factory and a pharmaceutical factory. To achieve the best option, three experts are consulted. These experts will assess six factories with respect to six attributes: short-term benefits, midterm benefits, long-term benefits, investment venture, investment difficulty and influence on environment.

For clarity, we use six alternatives x₁, x₂, x₃, x₄, x₅ and x₆ to denote six candidate projects. They are listed as following:

• 1. x₁: a chemical industry,

• 2. x₂: an artificial intelligence company,

• 3. x₃: a food factory,

• 4. x₄: a super market,

• 5. x₅: a car factory,

• 6. x₆: a pharmaceutical factory.

Six evaluation indexes are regarded as six attributes, namely, a₁, a₂, a₃, a₄, a₅ and a₆, as follows:

• 1. a₁: short-term benefits,

• 2. a₂: midterm benefits,

• 3. a₃: long-term benefits,

• 4. a₄: investment venture,

• 5. a₅: investment difficulty,

• 6. a₆: influence on environment.

Three consultant experts are denoted as E₁, E₂ and E₃ to evaluate the alternatives x₁, x₂, x₃, x₄, x₅ and x₆ with respect to six attributes a₁, a₂, a₃, a₄, a₅ and a₆.

Assume that decision matrices provided by three experts contain intuitionistic fuzzy information which is expressed by IFVs. Three decision matrices corresponding to E₁, E₂ and E₃ are, respectively, shown as:

$$ \varvec{D}_{1} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{4} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{5} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{6} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ x_{4} \hfill \\ x_{5} \hfill \\ x_{6} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.5,0.4} \right\rangle } & {\left\langle {0.5,0.3} \right\rangle } & {\left\langle {0.2,0.6} \right\rangle } & {\left\langle {0.4,0.4} \right\rangle } & {\left\langle {0.5,0.4} \right\rangle } & {\left\langle {0.3,0.5} \right\rangle } \\ {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.4,0.5} \right\rangle } \\ {\left\langle {0.5,0.4} \right\rangle } & {\left\langle {0.6,0.4} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.5,0.3} \right\rangle } & {\left\langle {0.6,0.3} \right\rangle } & {\left\langle {0.4,0.4} \right\rangle } \\ {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.4,0.2} \right\rangle } & {\left\langle {0.5,0.2} \right\rangle } & {\left\langle {0.4,0.4} \right\rangle } & {\left\langle {0.6,0.3} \right\rangle } \\ {\left\langle {0.4,0.3} \right\rangle } & {\left\langle {0.5,0.2} \right\rangle } & {\left\langle {0.4,0.5} \right\rangle } & {\left\langle {0.4,0.6} \right\rangle } & {\left\langle {0.3,0.4} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } \\ {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.4,0.3} \right\rangle } & {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.6,0.3} \right\rangle } & {\left\langle {0.5,0.4} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

$$ \varvec{D}_{2} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{4} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{5} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{6} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ x_{4} \hfill \\ x_{5} \hfill \\ x_{6} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.5,0.5} \right\rangle } & {\left\langle {0.8,0.2} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.6,0.3} \right\rangle } & {\left\langle {0.5,0.4} \right\rangle } \\ {\left\langle {0.4,0.5} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.3,0.4} \right\rangle } & {\left\langle {0.7,0.1} \right\rangle } & {\left\langle {0.8,0.2} \right\rangle } \\ {\left\langle {0.5,0.2} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.8,0.1} \right\rangle } & {\left\langle {0.7,0.1} \right\rangle } & {\left\langle {0.3,0.4} \right\rangle } & {\left\langle {0.6,0.3} \right\rangle } \\ {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.3,0.4} \right\rangle } & {\left\langle {0.5,0.5} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.4,0.5} \right\rangle } & {\left\langle {0.5,0.2} \right\rangle } \\ {\left\langle {0.7,0.1} \right\rangle } & {\left\langle {0.5,0.1} \right\rangle } & {\left\langle {0.3,0.2} \right\rangle } & {\left\langle {0.4,0.3} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.4,0.3} \right\rangle } \\ {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.8,0.2} \right\rangle } & {\left\langle {0.6,0.3} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.5,0.3} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

$$ \varvec{D}_{3} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{4} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{5} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{6} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ x_{4} \hfill \\ x_{5} \hfill \\ x_{6} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.5,0.3} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.5,0.3} \right\rangle } & {\left\langle {0.5,0.4} \right\rangle } & {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.4,0.3} \right\rangle } \\ {\left\langle {0.6,0.3} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.8,0.1} \right\rangle } & {\left\langle {0.5,0.4} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } \\ {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.4,0.4} \right\rangle } & {\left\langle {0.6,0.3} \right\rangle } & {\left\langle {0.4,0.2} \right\rangle } & {\left\langle {0.6,0.3} \right\rangle } & {\left\langle {0.4,0.4} \right\rangle } \\ {\left\langle {0.4,0.4} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.4,0.2} \right\rangle } & {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.5,0.3} \right\rangle } \\ {\left\langle {0.7,0.2} \right\rangle } & {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.6,0.1} \right\rangle } & {\left\langle {0.7,0.3} \right\rangle } & {\left\langle {0.5,0.3} \right\rangle } & {\left\langle {0.3,0.4} \right\rangle } \\ {\left\langle {0.5,0.2} \right\rangle } & {\left\langle {0.5,0.3} \right\rangle } & {\left\langle {0.8,0.2} \right\rangle } & {\left\langle {0.6,0.1} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } & {\left\langle {0.6,0.2} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

The weights of experts E₁, E₂ and E₃ are assigned as 0.3, 0.3 and 0.4, respectively. Hence, $\lambda^{1} = 0.3$, $\lambda^{2} = 0.3$, and $\lambda^{3} = 0.4$. The attribute weights given by three experts are identical. The weighting factors of a₁, a₂, a₃, a₄, a₅ and a₆ are 0.09, 0.17, 0.24, 0.24, 0.17 and 0.09, respectively. So, we have:$w_{1}^{1} = w_{1}^{2} = w_{1}^{3} = 0.09$, $w_{2}^{1} = w_{2}^{2} = w_{2}^{3} = 0.17$, $w_{3}^{1} = w_{3}^{2} = w_{3}^{3} = 0.24$, $w_{4}^{1} = w_{4}^{2} = w_{4}^{3} = 0.24$, $w_{5}^{1} = w_{5}^{2} = w_{5}^{3} = 0.17$, and $w_{6}^{1} = w_{6}^{2} = w_{6}^{3} = 0.09$.

Based on the proposed IFWE average operator, we can yield each expert’s aggregated assessment results of all alternatives based on his own decision matrix. These results are presented as:

$$ \begin{aligned} V_{{x_{1} }}^{1} = \left\langle { 0. 2 4 9 5 , 0. 2 9 3 7} \right\rangle ,V_{{x_{2} }}^{1} = \left\langle { 0. 4 3 0 4 , 0. 1 4 4 0} \right\rangle ,V_{{x_{3} }}^{1} = \left\langle { 0. 3 7 4 4 , 0. 1 8 7 7} \right\rangle , \hfill \\ V_{{x_{4} }}^{1} = \left\langle { 0. 3 6 9 6 , 0. 1 5 1 1} \right\rangle ,V_{{x_{5} }}^{1} = \left\langle { 0. 2 8 0 4 , 0. 2 7 2 5} \right\rangle ,V_{{x_{6} }}^{1} = \left\langle { 0. 3 9 2 8 , 0. 1 7 9 4} \right\rangle . \hfill \\ \end{aligned} $$

$$ \begin{aligned} V_{{x_{1} }}^{2} = \left\langle { 0. 4 3 7 8 , 0. 1 4 6 7} \right\rangle ,V_{{x_{2} }}^{2} = \left\langle { 0. 3 9 2 0 , 0. 1 6 8 8} \right\rangle ,V_{{x_{3} }}^{2} = \left\langle { 0. 4 4 8 2 , 0. 1 0 9 5} \right\rangle , \hfill \\ V_{{x_{4} }}^{2} = \left\langle { 0. 3 2 5 5 , 0. 2 2 8 0} \right\rangle ,V_{{x_{5} }}^{2} = \left\langle { 0. 3 4 7 1 , 0. 1 3 5 3} \right\rangle ,V_{{x_{6} }}^{2} = \left\langle { 0. 4 3 6 5 , 0. 1 4 2 6} \right\rangle . \hfill \\ \end{aligned} $$

$$ \begin{aligned} V_{{x_{1} }}^{3} = \left\langle { 0. 3 8 1 2 , 0. 1 8 5 8} \right\rangle ,V_{{x_{2} }}^{3} = \left\langle { 0. 4 5 6 8 , 0. 1 2 1 7} \right\rangle ,V_{{x_{3} }}^{3} = \left\langle { 0. 3 5 2 3 , 0. 1 8 8 5} \right\rangle , \hfill \\ V_{{x_{4} }}^{3} = \left\langle { 0. 3 9 3 2 , 0. 1 3 7 9} \right\rangle ,V_{{x_{5} }}^{3} = \left\langle { 0. 4 2 1 7 , 0. 1 4 6 9} \right\rangle ,V_{{x_{6} }}^{3} = \left\langle { 0. 4 4 4 6 , 0. 1 1 1 4} \right\rangle . \hfill \\ \end{aligned} $$

Then, the decision matrix for group decision making can be constructed as follows:

$$ \varvec{D} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ x_{4} \hfill \\ x_{5} \hfill \\ x_{6} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle { 0. 2 4 9 5 , 0. 2 9 3 7} \right\rangle } & {\left\langle { 0. 4 3 7 8 , 0. 1 4 6 7} \right\rangle } & {\left\langle { 0. 3 8 1 2 , 0. 1 8 5 8} \right\rangle } \\ {\left\langle { 0. 4 3 0 4 , 0. 1 4 4 0} \right\rangle } & {\left\langle { 0. 3 9 2 0 , 0. 1 6 8 8} \right\rangle } & {\left\langle { 0. 4 5 6 8 , 0. 1 2 1 7} \right\rangle } \\ {\left\langle { 0. 3 7 4 4 , 0. 1 8 7 7} \right\rangle } & {\left\langle { 0. 4 4 8 2 , 0. 1 0 9 5} \right\rangle } & {\left\langle { 0. 3 5 2 3 , 0. 1 8 8 5} \right\rangle } \\ {\left\langle { 0. 3 6 9 6 , 0. 1 5 1 1} \right\rangle } & {\left\langle { 0. 3 2 5 5 , 0. 2 2 8 0} \right\rangle } & {\left\langle { 0. 3 9 3 2 , 0. 1 3 7 9} \right\rangle } \\ {\left\langle { 0. 2 8 0 4 , 0. 2 7 2 5} \right\rangle } & {\left\langle { 0. 3 4 7 1 , 0. 1 3 5 3} \right\rangle } & {\left\langle { 0. 4 2 1 7 , 0. 1 4 6 9} \right\rangle } \\ {\left\langle { 0. 3 9 2 8 , 0. 1 7 9 4} \right\rangle } & {\left\langle { 0. 4 3 6 5 , 0. 1 4 2 6} \right\rangle } & {\left\langle { 0. 4 4 4 6 , 0. 1 1 1 4} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

Considering the independence of each decision maker, we can aggregate all experts’ assessment on each alternative by using the IFWE average operator. Aggregating the IFVs in each row of decision matrix D, we can get the final evaluation result of each alternative as:

$$ \begin{aligned} V_{{x_{1} }} = \left\langle { 0. 2 8 6 3 , 0. 1 5 4 4} \right\rangle ,V_{{x_{2} }} = \left\langle { 0. 3 4 7 9 , 0. 1 0 2 7} \right\rangle , \hfill \\ V_{{x_{3} }} = \left\langle { 0. 3 1 3 4 , 0. 1 2 2 2} \right\rangle ,V_{{x_{4} }} = \left\langle { 0. 2 9 7 4 , 0. 1 2 6 7} \right\rangle , \hfill \\ V_{{x_{5} }} = \left\langle { 0. 2 8 9 6 , 0. 1 3 6 4} \right\rangle ,V_{{x_{6} }} = \left\langle { 0. 3 4 5 8 , 0. 1 0 1 8} \right\rangle . \hfill \\ \end{aligned} $$

The comparison matrix of these six alternatives is shown as follows:

$$ \varvec{P} = \left( {\begin{array}{*{20}c} {0.5} & {0.4489} & {0.4736} & {0.4829} & {0.4906} & {0.4496} \\ {0.5511} & {0.5} & {0.5242} & {0.5331} & {0.5409} & {0.5005} \\ {0.5264} & {0.4758} & {0.5} & {0.5090} & {0.5167} & {0.4764} \\ {0.5171} & {0.4669} & {0.4910} & {0.5} & {0.5076} & {0.4675} \\ {0.5094} & {0.4591} & {0.4833} & {0.4294} & {0.5} & {0.4597} \\ {0.5504} & {0.4995} & {0.5236} & {0.5325} & {0.5403} & {0.5} \\ \end{array} } \right) $$

The column sum of each row can be calculated as:

$$ P_{ 1} = 2. 8 4 5 7,P_{ 2} = 3. 1 4 9 9,P_{ 3} = 3.00 4 3,P_{ 4} = 2. 9 500,P_{ 5} = 2. 90 3 9,P_{ 6} = 3. 1 4 6 2. $$

Since $P_{2} > P_{6} > P_{3} > P_{4} > P_{5} > P_{1}$, we can rank the six alternatives as preference order $x_{2} \succ x_{6} \succ x_{3} \succ x_{4} \succ x_{5} \succ x_{1}$.

We note that the attribute weights provided by each expert are identical. So, the method proposed in Zeng and Su (2011) can be used to solve the MAGDM problem in this example. Different operators are combined with the method in Zeng and Su (2011) to solve this problem. The ranking preference orders of six projects are presented in Table 5. It is shown that these methods introduced in Chen et al. (2016), Xu (2010) and Yue (2014) and the proposed method can obtain the same ranking order $x_{2} \succ x_{6} \succ x_{3} \succ x_{4} \succ x_{5} \succ x_{1}$. From Table 5, we can see that the results obtained by the combination of different operators and the method in Zeng and Su (2011) are slightly different. But the most recommended alternatives derived by five operators (the Min operator and IFOWED operator are excluded) are the same as other methods. This example shows that the proposed method can get reasonable results as most other methods. The method proposed in Zeng and Su (2011) is easy to be affected by the aggregated operator it uses.

Table 5 The ranking orders of six projects in Example 5.2

Example 5.3

(Chen et al. 2016) A venture investment company plans to invest a sum of money in the best factory. Three factories being considered are: a car factory, a TV factory and a food factory. Three top decision makers in this investment company will assess these factories from three attributes. These three top decision makers are: the chief director (E₁), the general manager (E₂) and the director assistant (E₃). Three attributes are taken into account are: the venture index, the growth rate and the social impact index.

For clarity, the following assumptions are put forward:

Three factories are expressed by alternatives x₁, x₂ and x₃:

• 1. x₁: a car factory,

• 2. x₂: a TV factory,

• 3. x₃: a food factory.

Three attributes used in the assessment are denoted by a₁, a₂ and a₃:

• 1. a₁: the venture index,

• 2. a₂: the growth rate,

• 3. a₃: the social impact index.

Three decision makers, namely, E₁, E₂ and E₃ evaluate these companies by intuitionistic fuzzy values. They propose three decision matrices: D₁, D₂ and D₃, respectively. These decision matrices are shown as follows:In the decision matrices given by decision makers E₁, E₂ and E₃, uncertain information is represented by IFVs. The decision matrices associated with E₁, E₂ and E₃ are, respectively, shown as following:

$$ \varvec{D}_{1} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.80,0} \right\rangle } & {\left\langle {0.50,030} \right\rangle } & {\left\langle {0.50,0.20} \right\rangle } \\ {\left\langle {0.85,0.01} \right\rangle } & {\left\langle {0.85,0.15} \right\rangle } & {\left\langle {0.80,0.10} \right\rangle } \\ {\left\langle {0.99,0.01} \right\rangle } & {\left\langle {0.90,0.05} \right\rangle } & {\left\langle {0.85,0.05} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

$$ \varvec{D}_{2} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.10,0.90} \right\rangle } & {\left\langle {0.15,070} \right\rangle } & {\left\langle {0.20,0.60} \right\rangle } \\ {\left\langle {0.20,0.65} \right\rangle } & {\left\langle {0.35,0.60} \right\rangle } & {\left\langle {0.30,0.50} \right\rangle } \\ {\left\langle {0.25,0.01} \right\rangle } & {\left\langle {0.50,0.40} \right\rangle } & {\left\langle {0.40,0.40} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

$$ \varvec{D}_{3} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.05,0.95} \right\rangle } & {\left\langle {0.20,075} \right\rangle } & {\left\langle {0.15,0.65} \right\rangle } \\ {\left\langle {0.15,0.80} \right\rangle } & {\left\langle {0.40,0.60} \right\rangle } & {\left\langle {0.30,0.60} \right\rangle } \\ {\left\langle {0.35,0.60} \right\rangle } & {\left\langle {0.50,0.40} \right\rangle } & {\left\langle {0.35,0.50} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

The importance weights $\lambda^{1}$, $\lambda^{2}$ and $\lambda^{3}$ of decision makers E₁, E₂ and E₃ are 0.36, 0.32 and 0.32, respectively. The weights of attributes a₁, a₂ and a₃ that are given by decision maker E₁ are 0.01, 0.49 and 0.50, respectively, i.e., $w_{1}^{1} = 0.01$, $w_{2}^{1} = 0.49$, and $w_{3}^{1} = 0.50$. The weights of attributes a₁, a₂ and a₃ that are given by decision maker E₂ are 0.01, 0.49 and 0.50, respectively, i.e., $w_{1}^{2} = 0.01$, $w_{2}^{2} = 0.49$, and $w_{3}^{2} = 0.50$. The weights of attributes a₁, a₂ and a₃ that are given by decision maker E₃ are 0.01, 0.49 and 0.50, respectively, i.e., $w_{1}^{3} = 0.01$, $w_{2}^{3} = 0.49$, and $w_{3}^{3} = 0.50$.

Based on the decision matrix from each decision maker, we can obtain each decision maker’s preferences on these alternatives. They are shown as follows:

$$ V_{{x_{1} }}^{1} = \left\langle { 0. 4 0 0 8 , 0. 1 8 1 0} \right\rangle ,V_{{x_{2} }}^{1} = \left\langle { 0. 6 3 4 3 , 0. 0 7 2 7} \right\rangle ,V_{{x_{3} }}^{1} = \left\langle { 0. 6 7 4 7 , 0. 0 2 7 8} \right\rangle . $$

$$ V_{{x_{1} }}^{2} = \left\langle { 0. 1 1 5 9 , 0. 5 1 6 3} \right\rangle ,V_{{x_{2} }}^{2} = \left\langle { 0. 2 2 8 4 , 0. 4 2 2 5} \right\rangle ,V_{{x_{3} }}^{2} = \left\langle { 0. 3 3 8 7 , 0. 2 9 4 1} \right\rangle . $$

$$ V_{{x_{1} }}^{3} = \left\langle { 0. 1 1 2 2 , 0. 5 4 9 8} \right\rangle ,V_{{x_{2} }}^{3} = \left\langle { 0. 2 3 7 0 , 0. 4 5 4 1} \right\rangle ,V_{{x_{3} }}^{3} = \left\langle { 0. 3 3 8 7 , 0. 2 9 4 1} \right\rangle . $$

Then, the decision matrix for group decision making can be constructed as:

$$ \varvec{D} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{3} {\kern 1pt} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.4008,0.1810} \right\rangle } & {\left\langle {0.1159,0.5163} \right\rangle } & {\left\langle {0.1122,0.5498} \right\rangle } \\ {\left\langle {0.6343,0.0727} \right\rangle } & {\left\langle {0.2284,0.4225} \right\rangle } & {\left\langle {0.2370,0.4541} \right\rangle } \\ {\left\langle {0.6747,0.0278} \right\rangle } & {\left\langle {0.3387,0.2941} \right\rangle } & {\left\langle {0.3387,0.2941} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

By the proposed IFWE average operator, we can obtain the final assessment results of all alternatives:

$$ V_{{x_{1} }} = \left\langle { 0. 1 5 5 3 , 0. 3 1 6 2} \right\rangle ,V_{{x_{2} }} = \left\langle { 0. 2 8 2 4 , 0. 2 1 8 6} \right\rangle ,V_{{x_{3} }} = \left\langle { 0. 3 5 9 1 , 0. 1 3 4 9} \right\rangle . $$

The comparison matrix of these IFVs can be obtained based on the possibility-based ranking method:

$$ \varvec{P} = \left( {\begin{array}{*{20}c} {0.5} & {0.3907} & {0.3139} \\ {0.6093} & {0.5} & {0.4202} \\ {0.6861} & {0.5798} & {0.5} \\ \end{array} } \right). $$

The column sums of matrix P can be calculated as:

$$ P_{ 1} = 1.2045,P_{ 2} = 1.5296,P_{ 3} = 1.7659. $$

Therefore, the preference order of the three companies can be obtained according to the values of the column sums: $x_{3} \succ x_{2} \succ x_{1}$.

We can get the ranking orders of three alternatives by the methods in Chen et al. (2016), Xu (2010), Yue (2014) and Zeng and Su (2011). For comparison, we present the results derived by different methods in Table 6. It is shown that the method in Chen et al. (2016) and Zeng and Su (2011) ranks three factories in the same order $x_{3} \succ x_{2} \succ x_{1}$, which is identical to the order obtained by our proposed method. The ranking preference orders derived by the methods in Xu (2010) and Yue (2014) are unreasonable because of the extreme IFV < 0.8, 0 > , where the non-membership degree is 0.

Table 6 The ranking orders of three factories in Example 5.3

For Xu’s method (2010), we can obtain the collective intuitionistic fuzzy decision matrix as:

$$ \varvec{R} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.385,0} \right\rangle } & {\left\langle {0.270,0.572} \right\rangle } & {\left\langle {0.281,0.461} \right\rangle } \\ {\left\langle {0.476,0.229} \right\rangle } & {\left\langle {0.573,0.419} \right\rangle } & {\left\langle {0.494,0.345} \right\rangle } \\ {\left\langle {0.766,0.027} \right\rangle } & {\left\langle {0.670,0.234} \right\rangle } & {\left\langle {0.573,0.246} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

The aggregated IFV of alternative x₁ with regard to attribute a₁ is < 0.385, 0 > , which is obtained by aggregating the assessment values < 0.8, 0 > , < 0.1, 0.9 > and < 0.05, 0.95 > , given by decision makers E₁, E₂ and E₃, respectively, for attribute a₁. This is caused by the calculation process of Xu’s method (2010). In Xu’s method (2010), the aggregated non-membership degree is the power product of all non-membership degrees with their weighting factors. Therefore, the non-membership degree of the aggregated result will be 0 when there exists a zero non-membership degree in the original data. Other values with higher non-membership degrees are not considered. Thus, the method proposed by Xu (2010) obtains the incorrect integrated intuitionistic fuzzy decision matrix R and an unreasonable ranking preference order of alternatives x₁, x₂ and x₃, as shown in Table 6.

For the method in Yue (2014) which is proposed based on (12), we can obtain the positive ideal decision matrix ${\varvec{Y}}^{*}$ as:

$$ {\varvec{Y}}^{*} = \begin{array}{*{20}c} {} & {\begin{array}{*{20}l} {{\kern 1pt} {\kern 1pt} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{3} {\kern 1pt} } \hfill \\ \end{array} } \\ \begin{aligned} x_{1} \hfill \\ x_{2} \hfill \\ x_{3} \hfill \\ \end{aligned} & {\left( {\begin{array}{*{20}c} {\left\langle {0.006,0} \right\rangle } & {\left\langle {0.162,0.739} \right\rangle } & {\left\langle {0.165,0.654} \right\rangle } \\ {\left\langle {0.008,0.983} \right\rangle } & {\left\langle {0.371,0.621} \right\rangle } & {\left\langle {0.321,0.557} \right\rangle } \\ {\left\langle {0.018,0.968} \right\rangle } & {\left\langle {0.453,0.454} \right\rangle } & {\left\langle {0.377,0.464} \right\rangle } \\ \end{array} } \right)} \\ \end{array} $$

The obtained positive ideal intuitionistic fuzzy value for alternative x₁ with respect to attribute a₁ is < 0.006, 0 > . The non-membership degree is 0. This is also caused by the power product operation in Yue’s method (2014). The existence of only one zero non-membership value can make irrelevant high non-membership degrees, such as 0.9 and 0.95. Therefore, the ideal positive value < 0.006, 0 > is incorrect. Thus, the method in Yue (2014) obtains an unreasonable positive ideal decision matrix ${\varvec{Y}}^{*}$ in the case where there is an IFV with 0 non-membership degree in a decision matrix. This will lead to an unreasonable ranking preference order of the alternatives x₁, x₂ and x₃, as shown in Table 6.

This example indicates that the proposed method is robust enough to extreme IFVs in the decision matrices.

6 Conclusions

Using the relation between IFSs and evidence theory, we propose an evidential model for solving the problem of MAGDM in intuitionistic fuzzy environment. The proposed evidential model is developed based on two new methods as following. The first one is the IFWE average operator, which is developed based on the evidence discounting operation and Dempster’s combination rule. Another one is the possibility-based ranking method for IFVs. According to the weights of attributes and decision makers, all decision makers’ evaluation information can be aggregated by the IFWE average operator. Finally, the aggregated IFV of each alternative is ordered by our proposed possibility-based ranking method for IFVs. Comparative analysis based on application examples of MAGDM shows that the proposed model can overcome the deficiencies in existing methods and obtain reasonable results. The applicability, availability and superiority of the proposed method are well illustrated.

The study also has several limitations, which may serve as avenues for future research. First, information loss is not considered in the transformation from intuitionistic fuzzy information to basic belief assignments. We have noted that IFV and BBA are not in one-to-one correspondence. The deep relation between intuitionistic fuzzy sets and evidence theory is left for us to explore in future work. Second, the decision makers’ preferences are not considered in the proposed approach. The subjective factors from decision makers can affect the final result. It is of interest to examine the influence of decision makers’ preferences and compare the decision making results under different preference perspectives. Therefore, the description and quantification of decision makers’ preferences are desirable in future research. Last, the proposed approach could be extended to some practical scenarios such as site selection in airport construction and project selection for venture investment. Tailored decision making procedures, corresponding attributes and reasonable proposals could be developed for those scenarios.