Abstract
In multi-attribute group decision making methods, team often needs to deal with both quantitative data and qualitative information with uncertainty. It is essential to properly represent and use uncertain information to conduct rational decision analysis. Having regarded this fact many approaches have been proposed for solving group decision-making problems, especially in fuzzy environments, but due to their drawbacks they get an unreasonable preference order of the alternatives in some situation. Thus in this paper based on interval-valued intuitionistic fuzzy sets and evidential reasoning methodology, a new approach has been proposed for supporting such decision situation. The experimental results are examined using the proposed approach. Computation steps and analysis results are provided to demonstrate its implementation process. The proposed method can overcome the drawbacks of the existing methods for fuzzy multi-attribute group decision making in intuitionistic fuzzy environments.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
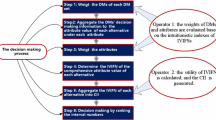
Decision making is extremely intuitive when considering single criterion problems, since we only need to choose the alternative with the highest preference rating. However, when decision makers evaluate alternatives with multiple criteria, many problems, such as weights of criteria, preference dependence and conflicts among criteria, seem to complicate the problems and need to be overcome by more sophisticated methods (Tzeng and Huang 2011). To facilitate systematic research in the field of multi-criteria decision making (MCDM), Hwang and Yoon (1981) suggested that MCDM problems can be classified into two main categories: multiple attribute decision making (MADM) and multiple objective decision making (MODM), based on the different purposes and different data types. The former is applied in the evaluation facet, which is usually associated with a limited number of predetermined alternatives and discrete preference ratings. The latter is especially suitable for the design/planning facet, which aims to achieve the optimal or aspired goals by considering the various interactions within the given constraints. It is worth noting that in this study our focus will be on the MADM’s topic. However, conventional MADM only considers the crisp decision problems and lacks a general paradigm for specific real-world problems, such as group decisions and uncertain preferences. Therefore, most MADM problems in the real world should naturally be regarded as fuzzy MADM problems (Bellman and Zadeh 1970).
Consequently, the fuzzy sets defined by Zadeh (1965) are used with the ability of covering the variety set of ambiguity, imprecise and incomplete problems. Then the interval-valued fuzzy sets (IVFSs) defined by Zadeh (1975) are shown by the membership function within a closed subinterval of [0, 1], but sometimes, due to knowledge limitation and time pressure, the decision making process confronts with hesitancy. In order to consider this matter, Atanassov (1986) introduced the intuitionistic fuzzy sets (IFSs), which are characterized by the membership function, non-membership function and hesitancy function. The IVFSs and the IFSs are regarded as flexible and practical tools for dealing with fuzziness and uncertainty. Atanassov and Gargov (1989) later introduced the interval-valued intuitionistic fuzzy sets (IVIFSs), as a generalization of the IVFSs and the IFSs that provides the membership function and non-membership function with intervals rather than exact numbers. Hence, Zhang et al. (2008) suggested that it is more suitable to represent an individual’s opinion based on IVIFSs. Therefore, intuitionistic fuzzy numbers (IFNs) and interval-valued intuitionistic fuzzy numbers (IVIFNs) were increasingly used in different studies.
In recent years, some methods have been presented for fuzzy multi-attribute group decision making based on IVIFSs. Joshi and Kumar (2016) presented a fuzzy multi-criteria group decision making method by using the interval-valued intuitionistic fuzzy Technique for Order Performance by Similarity to an Ideal Solution (TOPSIS). Xu and Shen (2014) presented a new outranking choice method for group decision making under interval-valued intuitionistic fuzzy environment. Wan and Dong (2015) developed a mathematical programming methodology for hybrid fuzzy multi-criteria group decision making considering alternative comparisons with hesitancy degrees, where the subjective preference relations between alternatives given by each decision maker are formulated as an IVIFS. Liu et al. (2014) presented an interval-valued intuitionistic fuzzy principal component analysis (IVIF-PCA) model to solve multi-attribute large-group decision making problems where attribute values are IVIFNs, the number of decision attributes is often large and their correlation degrees are high. Meng and Chen (2014) presented an interval-valued intuitionistic fuzzy multi-criteria group decision making approach based on cross entropy and 2-additive measures. Hashemi et al. (2016) presented an interval-valued intuitionistic fuzzy multi-criteria group decision making approach based on the ELECTRE III method. Li et al. (2014) presented an improved method on group decision making based on interval-valued intuitionistic fuzzy prioritized operators. İntepe et al. (2013) presented an interval-valued intuitionistic fuzzy multi-criteria group decision making method for selection of technology forecasting method. Xu (2007) presented some interval-valued intuitionistic fuzzy arithmetic aggregation operator based on a fuzzy measure for aggregating intuitionistic fuzzy information for fuzzy group decision making. Meanwhile, Xu and Chen (2007); Wei and Wang 2007) presented some aggregation operators in terms of geometrics. Makui et al. (2015b) presented a fuzzy multi-criteria group decision making approach based on the interval-valued intuitionistic fuzzy preference relation and the interval-valued intuitionistic fuzzy decision matrix, while their main focus was to contribute the risk attitude of each decision makers in the decision making process. Jin et al. (2014) presented an interval-valued intuitionistic fuzzy continuous weighted entropy which generalizes intuitionistic fuzzy entropy measures defined by Szmidt and Kacprzyk (2001) on the basis of the continuous ordered weighted averaging (COWA) operator. However, Makui et al.’s method (Makui et al. 2015b) and Jin et al.’s method (Jin et al. 2014) have the drawbacks that they get unreasonable preference orders of alternatives in some situations. Therefore, to overcome the drawbacks of Makui et al.’s method (Makui et al. 2015b) and Jin et al.’s method (Jin et al. 2014), we need to develop a new method for fuzzy multi-attribute group decision making.
Then, in this paper, we propose a new fuzzy multi-attribute group decision making method based on IVIFSs (Atanassov and Gargov 1989) and the evidential reasoning methodology (ERM) (Yang 2001; Yang et al. 2006a; Yang and Singh 1994; Yang et al. 2006b; Yang and Xu 2002). Yang and Singh (1994) presented an evidential reasoning approach for multi-attribute decision making with uncertainty. Yang (2001) presented a rule- and utility-based evidential reasoning approach for multi-attribute decision analysis under uncertainty. Yang et al. (2006a) presented a belief rule-based inference methodology using the evidential reasoning approach. Yang and Xu (2002) presented an evidential reasoning algorithm for multi-attribute decision analysis under uncertainty. Yang et al. (2006b) presented an evidential reasoning approach for multi-attribute decision analysis under both probabilistic and fuzzy uncertainties. From Yang (2001), Yang et al. (2006a), Yang and Singh (1994), Yang et al. (2006b) and Yang and Xu (2002), we can see that the ERM has successfully been applied to deal with multiple attribute decision analysis and multi-attribute decision making problems. Therefore, in this paper, we take the advantage of the ERM and the powerful representation capability of the IVIFSs to propose a new fuzzy multi-attribute group decision making method. First, the proposed method uses the ERM to aggregate each decision maker’s decision matrix and the weights of the attributes given by decision makers to get the aggregated decision matrix of each decision maker. Then, it uses the obtained aggregated decision matrices of the experts, the weights of the experts and the ERM to get the aggregated intuitionistic fuzzy value in form of interval for each alternative. Finally, it uses a combined approach based on Grey Relational Analysis (GRA) and TOPSIS method for ranking the alternatives. The proposed method can overcome the drawbacks of Makui et al.’s method (Makui et al. 2015b) and Jin et al.’s method (Jin et al. 2014) for fuzzy multi-attribute group decision making problems in intuitionistic fuzzy environments.
The rest of this paper is organized as follows: In Sect. 2, we briefly review basic concepts of the IVIFSs, the combined approach based on GRA and TOPSIS method for ranking the alternatives and the ERM. In Sect. 3, we analyse the drawbacks of the fuzzy multi-attribute group decision making methods presented in Makui et al. (2015b) and Jin et al. (2014). In Sect. 4, we propose a new fuzzy multi-attribute group decision making method based on the IVIFSs and the ERM. In Sect. 5, we use some examples to compare the experimental results of the proposed method with the ones of the methods presented in Makui et al. (2015b) and Jin et al. (2014). The conclusions are discussed in Sect. 6.
2 Preliminaries
As a preparation for introducing our new approach, some relevant concepts are illustrated in this section.
2.1 Interval-valued intuitionistic fuzzy sets (IVIFSs)
Definition
(Atanassov and Gargov 1989). Let D[0, 1] be the set of all closed subintervals of the interval [0, 1]. Let \(X\ne \Phi \) be a given set. An interval-valued intuitionistic fuzzy set A in X is given by \(A=\left\{ {(x,\mu _A ( x),v_A ( x)):x\in X} \right\} \), where\(\mu _A ( x)\in [0,1]\), \(v_A ( x)\in [0,1]\) and \(0\le \sup _x \mu _A (x)+\sup _x v_A (x)\le 1\).
The intervals \(\mu _A (x)\) and \(v_A (x)\) denote, respectively, the degree of belongingness and the degree of non-belongingness of the element x to the set A. Thus, for each \(x\in X\), \(\mu _A (x)\) and \(v_A (x)\) are closed intervals whose lower and upper end points are, respectively, denoted by \(\mu _{AL} (x)\), \(\mu _{AU} (x)\), \(v_{AL} (x)\) and \(v_{AU} (x)\). A can be denoted by
where \(0\le \mu _{AU} (x)+v_{AU} ( x)\le 1\), \(\mu _{AL} ( x)\ge 0\) and \(v_{AL} (x)\ge 0\). In addition the set of all the IVIFS in X is shown by IVIFS(X). For each element x the unknown degree (uncertainty degree) in A can be defined as follows:
An IVIFS is denoted by \(A=([a,b],[c,d])\) for convenience.
Definition
(Szmidt and Kacprzyk 2000) For two IVIFSs A and B in \(X=\{ {x_1 ,x_2 ,\ldots ,x_m } \}\), the normalized Hamming distance is defined as follows:
Clearly this distance satisfies the conditions of the metric.
2.2 Combined approach based on GRA and TOPSIS method for ranking the alternatives
Makui et al. (2015a) presented a combined approach based on GRA and TOPSIS method for MCDM problems with interval-valued intuitionistic fuzzy information that can accurately reflect the relationship between alternative’s data and ideal solutions. The introduced method involves the following steps:
-
Step 1: Determine the positive ideal solution (PIS) and the negative ideal solution (NIS) with interval-valued intuitionistic fuzzy information.
$$\begin{aligned} \widetilde{r}^{+}= & {} ( [ {a_1 ^{+},b_1 ^{+}} ],[ {c_1 ^{+},d_1 ^{+}} ],[ {a_2 ^{+},b_2 ^{+}} ],[ {c_2 ^{+},d_2 ^{+}} ],\nonumber \\&\ldots ,[ {a_n ^{+},b_n ^{+}} ],[ {c_n ^{+},d_n ^{+}} ]), \end{aligned}$$(4)$$\begin{aligned} \widetilde{r}^{-}= & {} ([ {a_1 ^{-},b_1 ^{-}} ],[ {c_1 ^{-},d_1 ^{-}} ],[ {a_2 ^{-},b_2 ^{-}} ],[ {c_2 ^{-},d_2 ^{-}} ],\nonumber \\&\ldots ,[ {a_n ^{-},b_n ^{-}} ],[ {c_n ^{-},d_n ^{-}} ]), \end{aligned}$$(5)where:
$$\begin{aligned} {\tilde{r}}_{j}^{+}= & {} ( {[ {a_j ^{+},b_j ^{+}} ],[ {c_j ^{+},d_j ^{+}} ]})=([ {\mathop {\max }\limits _i a_{ij} ,\mathop {\max }\limits _i b_{ij} } ],\\&[ {\mathop {\min }\limits _i c_{ij} ,\mathop {\min }\limits _i d_{ij} } ]),\quad j\in 1,2,\ldots ,n. \end{aligned}$$$$\begin{aligned} {\tilde{r}}_{j}^{-}= & {} ( {[ {a_j ^{-},b_j ^{-}} ],[ {c_j ^{-},d_j ^{-}} ]})=( [ {\mathop {\min }\limits _i a_{ij} ,\mathop {\min }\limits _i b_{ij} } ],\\&[ {\mathop {\max }\limits _i c_{ij} ,\mathop {\max }\limits _i d_{ij} } ]),\quad j\in 1,2,\ldots ,n. \end{aligned}$$ -
Step 2: Calculate the grey relational coefficients of each alternative from PIS and NIS, respectively, by using the following equations:
$$\begin{aligned} \xi _{ij}^{+}= & {} \frac{\mathop {\min }\nolimits _{1\le i\le m} \mathop {\min }\nolimits _{1\le j\le n} d( {{\tilde{r}}_{ij} ,{\tilde{r}}_{ij}^{+} }){+}\rho \mathop {\max }\nolimits _{1\le i\le m} \mathop {\max }\nolimits _{1\le j\le n} d( {{\tilde{r}}_{ij} ,{\tilde{r}}_{ij}^{+} })}{d( {{\tilde{r}}_{ij} ,{\tilde{r}}_{ij}^{+} }){+}\rho \mathop {\max }\nolimits _{1\le i\le m} \mathop {\max }\nolimits _{1\le j\le n} d( {{\tilde{r}}_{ij} ,{\tilde{r}}_{ij}^{+} })},\nonumber \\&\quad \quad i=1,2,\ldots ,m,\quad j=1,2,\ldots ,n. \end{aligned}$$(6)$$\begin{aligned} \xi _{ij}^{-}= & {} \frac{\mathop {\min }\nolimits _{1\le i\le m} \mathop {\min }\nolimits _{1\le j\le n} d( {{\tilde{r}}_{ij} ,{\tilde{r}}_{ij}^{-} }){+}\rho \mathop {\max }\nolimits _{1\le i\le m} \mathop {\max }\nolimits _{1\le j\le n} d( {{\tilde{r}}_{ij} ,{\tilde{r}}_{ij}^{-} })}{d( {{\tilde{r}}_{ij} ,{\tilde{r}}_{ij}^{-} }){+}\rho \mathop {\max }\nolimits _{1\le i\le m} \mathop {\max }\nolimits _{1\le j\le n} d( {{\tilde{r}}_{ij} ,{\tilde{r}}_{ij}^{-} })},\nonumber \\&\quad \quad i=1,2,\ldots ,m,\quad j=1,2,\ldots ,n. \end{aligned}$$(7)where the identification coefficient \(\rho =0.5\). And the normalized Hamming distance has been used.
-
Step 3: Calculating the degree of gray relational coefficients of each alternative from PIS and NIS by using, respectively:the following equations:
$$\begin{aligned}&\xi _i^{+} =\mathop \sum \limits _{j=1}^n w_j \xi _{ij}^{+}, \quad i=1,2,\ldots ,m. \end{aligned}$$(8)$$\begin{aligned}&\xi _i^{-} =\mathop \sum \limits _{j=1}^n w_j \xi _{ij}^{-} , \quad i=1,2,\ldots ,m. \end{aligned}$$(9)The basic principle of the combined method is that the chosen alternative should have the “largest degree of grey relation” from the PIS and the “smallest degree of grey relation” from the NIS.
-
Step 4: Calculate the relative grey relational degree of each alternative from the PIS using the following equation:
$$\begin{aligned} \xi _i =\frac{\xi _i^{+} }{\xi _i^{+} +\xi _i^{-}},\quad i=1,2,\ldots ,m. \end{aligned}$$(10) -
Step 5: Rank all the alternatives \(X_i \quad (i=1,2,\ldots ,m)\) and select the best one(s) in accordance with \(\xi _i (i=1,2,\ldots ,m)\). If any alternative has the highest \(\xi _i\) value, then, it is the most important alternative.
2.3 Evidential reasoning methodology (ERM)
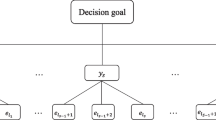
In the following, we briefly review the ERM for multi-attribute decision analysis under uncertain environments (Yang and Xu 2002). Let X be a set of alternatives, where \(X=\left\{ {x_1 ,x_2 ,\ldots ,x_m } \right\} \), and let A be a set of attributes, where \(A=\left\{ {a_1 ,a_2 ,\ldots ,a_n } \right\} \). Let W be a set of weights, where \(W=\left\{ {w_1 ,w_2 ,\ldots ,w_n } \right\} \), \(w_j\) is the weight of attribute \(a_j\), \(0\le w_j \le 1\), \(1\le j\le n\) and \(\mathop \sum \nolimits _{j=1}^n w_j =1\). Assume that there are pevaluation grades \(H_1 ,H_2 , \ldots ,H_p \) for assessing the attributes of alternatives. Let \(\beta _{q,j} (x_i)\) denote the degree of belief that attribute \(a_j\) of alternative \(x_i\) is assessed to the evaluation grade \(H_q\), where \(0\le \beta _{q,j} (x_i )\le 1\) and \(\mathop \sum \nolimits _{q=1}^p \beta _{q,j} (x_i )\le 1\). Let \(S(a_j (x_i))\) denote the evaluation value of attribute \(a_j \) of alternative \(x_i\), defined as follows:
where \(H_q\) is an evaluation grade, \(1\le q\le p\), \(1\le i\le m\) and \(1\le j\le n\). The assessments of the attributes of the alternatives are represented by a decision matrix D, shown as follows:
where \(1\le i\le m\) and \(1\le j\le n\). Based on the decision matrix D, we can aggregate the evaluating values of the attributes of each alternative \(x_i\), where \(1\le i\le m\), described as follows (Yang and Xu 2002):
First, the degree of belief \(\beta _{q,j} (x_i)\) of the evaluation grade \(H_q\) of attribute \(a_j\) for alternatives \(x_i\) is transformed into the basic probability mass \(m_{q,j} (x_i)\), where
\(1\le q\le p, 1\le i\le m\) and \(1\le j\le n\). Let \(m_{H,j} (x_i\)) be the remaining probability mass of attribute \(a_j \) for alternative \(x_i \), shown as follows:
where \(1\le q\le p\), \(1\le i\le m\) and \(1\le j\le n\). The remaining probability mass initially unassigned to any individual evaluation grades will be treated separately in terms of the relative weights of attributes and the incompleteness in an assessment.
\({\overline{m}}_{H,j} ({x_i})\) is the first part of the remaining probability mass that is not yet assigned to individual grades. Due to the fact that attribute j (denoted by \(a_j\)) only plays one part in the assessment relative to its weight. \({\overline{m}} _{H,j} ( {x_i })\) is a linear decreasing function of \(w_j \). \({\overline{m}} _{H,j} ({x_i })\) will be one if the weight of \(a_j\) is zero or \(w_j =0\); \({\overline{m}}_{H,j} ({x_i})\) will be zero if \(a_j\) dominates the assessment or \(w_j =1\). In other words, \({\overline{m}}_{H,j} ({x_i})\) represents the degree to which other attributes can play a role in the assessment. \({\overline{m}}_{H,j} ({x_i})\) should eventually be assigned to individual grades in a way that is dependent upon how all attributes are weighted and assessed.
\({\tilde{m}}_{H,j} ({x_i })\) is the second part of the remaining probability mass unassigned to individual grades, which is caused due to the incompleteness in the assessment \(S(a_j (x_i ))\). \({\tilde{m}}_{H,j} ({x_i })\) will be zero if \(S(a_j (x_i ))\) is complete, or \(\mathop \sum \nolimits _{q=1}^p \beta _{q,j} (x_i )=1\); otherwise, \({\tilde{m}} _{H,j} ({x_i})\) will be positive. \({\tilde{m}}_{H,j} ({x_i})\) is proportional to \(w_j\) and will cause the subsequent assessments to be incomplete.
Next, define \(G_{I(l)}\) as the subset of the first l attributed as follows:
Let \(m_{q,I(l)} ({x_i})\) be a probability mass defined as the degree to which all the l attributes in \(G_{I(l)}\) support the hypothesis that \(x_i\) is assessed to the grade \(H_q\). \(m_{H,I(l)} ({x_i })\) is the remaining probability mass unassigned to individual grades after all the attributes in \(G_{I(l)}\) have been assessed. \(m_{q,I(l)}({x_i})\) and \(m_{H,I(l)} ({x_i})\) can be generated by combining the basic probability masses \(m_{q,j} ({x_i})\) and \(m_{H,j} ({x_i})\) for all \(q=1,2,\ldots ,p\) and \(j=1,2,\ldots ,l\).
Given the above definitions and discussions, the recursive evidential reasoning algorithm can be summarized as follows:
where \(K_{I(l+1)}\) is a normalizing factor so that \(\mathop \sum \nolimits _{q=1}^p m_{q,I(l+1)} ( {x_i })+m_{H,I(l+1)} ( {x_i })=1\). Note that \(m_{q,I(1)} ( {x_i })=m_{q,1} ( {x_i })(q=1,2,\ldots ,p)\) and \(m_{H,I(1)} ( {x_i })=m_{H,1} ( {x_i })\). Also note that the attributes in G are numbered arbitrarily. This means that the results \(m_{q,I(l)} ({x_i})\), \((q=1,2,\ldots ,p)\) and \(m_{H,I(l)} ({x_i })\) do not depend on the order in which the attributes are aggregated.
In the evidential reasoning approach, after all n assessments have been aggregated, the combined degree of belief \(\beta _{q}\) is directly given by
where \(\beta _H \) is the degree of belief unassigned to any individual evaluation grade after all the n attributes have been assessed. It denotes the degree of incompleteness that generated in the assessment. And \(\mathop \sum \nolimits _{q=1}^p \beta _q ( {x_i })+\beta _H ( {x_i })=1\).
3 Analysing the drawbacks of the existing fuzzy multi-attribute group decision making methods
In this paper, we find that the Makui et al.’s method (Makui et al. 2015b) has the drawback that it will get an unreasonable preference order of the alternatives when there is an evaluating intuitionistic fuzzy value whose membership degree is equal to 1 and/or non-membership degree is equal to 0 due to the fact that the collective intuitionistic fuzzy decision matrix \(\dot{\tilde{D}} =\left( {\dot{\tilde{d}}_{ij}}\right) _{m\times n}\) presented in Makui et al. (2015b) is not well defined, where
where \(w=(w_1 ,w_2 ,\ldots ,w_t )^\mathrm{T}\) is the weight vector of the interval-valued intuitionistic fuzzy ordered weighted aggregation (IIFOWA) operator, \(w_k \in [0,1]\) and \(\mathop \sum \nolimits _{k=1}^t w_k =1\) . The weight vector of the IIFOWA operator can be determined by the Xu’s method presented in Xu (2005). \(( {[ {a_{ij} ,b_{ij} } ]^{(k)},[ {c_{ij} ,d_{ij} } ]^{(k)}})\) is an IVIFN denoting the evaluating value of decision maker \(e_k \) with respect to attribute \(a_j\) of alternative \(x_i \), \(( {\dot{\tilde{d}}_{{ij}_{\sigma (1)}} ,\dot{\tilde{d}}_{{ij}_{\sigma (2)}} ,\ldots ,\dot{\tilde{d}}_{{ij}_{\sigma (t)}}})\) be a permutation of \(( {\dot{\tilde{d}}_{ij} ^{(1)},\dot{\tilde{d}}_{ij} ^{(2)},\ldots ,\dot{\tilde{d}}_{ij} ^{(t)}})\), such that \(\dot{\tilde{d}}_{{ij}_{\sigma ({k-1})}} \ge \dot{\tilde{d}}_{{ij}_{\sigma (k)}}\) for all k, and let \(\dot{\tilde{d}}_{{ij} _{\sigma (k)}} =( {[ {a_{{ij}_{\sigma (k)}} ,b_{{ij} _{\sigma (k)}} } ],[ {c_{{ij}_{\sigma (k)}} ,d_{{ij} _{\sigma (k)}} } ]})\); t is the number of decision makers. If \(a_{{ij}_{\sigma (k)}} =1\) and/or \(b_{{ij} _{\sigma (k)}} =1\) exist, where \(1\le i\le m\), \(1\le j\le n\), \(1\le k\le t\). Then \(1-\mathop \prod \nolimits _{k=1}^t ( {1-a_{{ij}_{\sigma (k)}} })^{w_k}\) and/or \(1-\mathop \prod \nolimits _{k=1}^t ( {1-b_{{ij}_{\sigma (k)}} })^{w_k}\) in Eq. (24) become 1 and it gets an incorrect collective intuitionistic fuzzy decision matrix \(\dot{\tilde{D}}\) and gets an unreasonable preference order of the alternatives. In addition if \(c_{{ij}_{\sigma (k)}} =0\) and/or \(d_{{ij}_{\sigma (k)}} =0\) exist, where \(1\le i\le m\), \(1\le j\le n\), \(1\le k\le t.\) Then \(\mathop \prod \nolimits _{k=1}^t c_{{ij}_{\sigma (k)}} ^{w_k}\) and/or \(\mathop \prod \nolimits _{k=1}^t d_{{ij}_{\sigma (k)}} ^{w_k}\) in Eq. (24) become 0 and it gets an incorrect collective intuitionistic fuzzy decision matrix \(\dot{\tilde{D}}\) and gets an unreasonable preference order of the alternatives.
For example, for any value of \(w_k \), where \(0\le w_k \le 1\), if \(a_{{ij}_{\sigma (1)}} =1\), \(a_{{ij} _{\sigma (2)}} =0, {\ldots }, a_{{ij} _{\sigma (t)}} =0,\) then \(1-\mathop \prod \nolimits _{k=1}^t ( {1-a_{{ij}_{\sigma (k)}} })^{w_k }\) in Eq.(24) becomes 1, which is incorrect due to the fact that if only \(a_{{ij} _{\sigma (1)}} =1\) exists, then it causes \(1-\mathop \prod \nolimits _{k=1}^t ( {1-a_{{ij}_{\sigma (k)}} })^{w_k }\) in Eq. (24) to become 1 without considering the values of \(a_{{ij} _{\sigma (2)}} =0\), \(a_{{ij} _{\sigma (3)}} =0, {\ldots }\) and \(a_{{ij} _{\sigma (t)}} =0\). Therefore, the IIFOWA operator shown in Eq. (24) is not well defined. Because the fuzzy multi-attribute group decision making method presented in Makui et al. (2015b) uses the ill-defined IIFOWA operator shown in Eq. (24) to aggregate the evaluating intuitionistic fuzzy values of the decision makers to get the unified payoff decision matrix \(\dot{\tilde{D}}\), it will get an unreasonable preference order of the alternatives in some situations.
In this paper, we also find that the Jin et al.’s method (Jin et al. 2014) has the following drawbacks:
-
(1)
It will get an unreasonable preference order of the alternatives when there is an evaluating intuitionistic fuzzy value whose membership degree is equal to 1 and/or non-membership degree is equal to 0 due to the fact that the collective intuitionistic fuzzy decision matrix \(D=( {{\tilde{\alpha }} _{ij} })_{m\times n}\) presented in Jin et al. (2014) is not well defined, where
$$\begin{aligned}&D=\left( {{\tilde{\alpha }} _{ij} }\right) _{m\times n} =\left( \left[ 1-\mathop \prod \limits _{k=1}^t ( {1-a_{ij} ^{(k)}})^{w_k },1\right. \right. \nonumber \\&\left. \left. -\mathop \prod \limits _{k=1}^t ( {1-b_{ij} ^{(k)}})^{w_k } \right] ,\left[ {\mathop \prod \limits _{k=1}^t c_{ij} ^{{(k)}^{w_k }},\mathop \prod \limits _{k=1}^t d_{ij} ^{{(k)}^{w_k }}} \right] \right) _{m\times n} ,\nonumber \\ \end{aligned}$$(25)where \(w=(w_1 ,w_2 ,\ldots ,w_t )^\mathrm{T}\) is the weight vector of the interval-valued intuitionistic fuzzy weighted arithmetic aggregation (IIFWA) operator, \(w_k \in [0,1]\), and \(\mathop \sum \nolimits _{k=1}^t w_k =1\). \(( {[ {a_{ij} ,b_{ij} } ]^{(k)},[ {c_{ij} ,d_{ij} } ]^{(k)}})\) is an IVIFN denoting the evaluating value of decision maker \(e_k \) with respect to attribute \(a_j \) of alternative \(x_i \), such that \(1\le i\le m\), \(1\le j\le n\), \(1\le k\le t\). If \(a_{ij} ^{(k)}=1\) and/or \(b_{ij} ^{(k)}=1\) exist, then \(1-\mathop \prod \nolimits _{k=1}^t ( {1-a_{ij} ^{(k)}})^{w_k }\) and/or \(1-\mathop \prod \nolimits _{k=1}^t ( {1-b_{ij} ^{(k)}})^{w_k }\) in Eq. (25) become 1 and it gets an incorrect collective intuitionistic fuzzy decision matrix D and gets an unreasonable preference order of the alternatives. And also, if \(c_{ij} ^{(k)}=0\) and/or \(d_{ij} ^{(k)}=0\) exists, then \(\mathop \prod \nolimits _{k=1}^t c_{ij} ^{{(k)}^{w_k}}\) and/or \(\mathop \prod \nolimits _{k=1}^t d_{ij} ^{{(k)}^{w_k}}\) in Eq. (25) become 0 and it gets an incorrect collective intuitionistic fuzzy decision matrix D and gets an unreasonable preference order of the alternatives.
-
(2)
In addition to above drawback, the proposed method in Jin et al. (2014) has another disadvantage that it cannot allow the attributes to have different weights assigned by different experts. In the next session, we will propose a new method for fuzzy multi-attribute group decision making to overcome the drawbacks of the methods presented in Makui et al. (2015b) and Jin et al. (2014).
4 A new method for fuzzy multi-attribute group decision making based on the IVIFSs and the ERM
In this section, we take the advantage of the ERM and the powerful representation capability of the IVIFSs to propose a new fuzzy multi-attribute group decision making method to overcome the drawbacks of Makui et al.’s method (Makui et al. 2015b) and Jin et al.’s method (Jin et al. 2014). Let E be a set of decision makers, where \(E=\left\{ {e_1 ,e_2 ,\ldots ,e_t } \right\} \), let X be a set of alternatives, where \(X=\left\{ {x_1 ,x_2 ,\ldots ,x_m } \right\} \) and let A be a set of attributes, where \(A=\left\{ {a_1 ,a_2 ,\ldots ,a_n } \right\} \). Let \(D_k \) be a decision matrix given by decision maker \(e_k \), shown as follows:
where \(( {[ {a_{ij} ,b_{ij} } ]^{(k)},[ {c_{ij} ,d_{ij} } ]^{(k)}})\) is an IVIFN denoting the evaluating value of decision maker \(e_k\) with respect to attribute \(a_j\) of alternative \(x_i\); \(0\le a_{ij} ^k\le 1\), \(0\le b_{ij} ^k\le 1\), \(0\le c_{ij} ^k\le 1\), \(0\le d_{ij} ^k\le 1\), \(0\le b_{ij} ^k+d_{ij} ^k\le 1\), \(1\le i\le m\), m is the number of alternatives, \(1\le j\le n\), n is the number of attributes, \(1\le k\le t\), and t is the number of decision makers. Let \(W_k \) be a set of weights given by decision maker \(e_k \), where \(W_k =\{ {w_1 ^k,w_2 ^k,\ldots ,w_n ^k} \}\), \(w_j ^k\) is the weight of attribute \(a_j \) given by decision maker \(e_k \), \(0\le w_j ^k\le 1\), \(1\le j\le n\) and \(\mathop \sum \nolimits _{j=1}^n w_j ^k=1\). Let \(\omega \) be a set of weights, where \(\omega =\{ {\omega _1 ,\omega _2 ,\ldots ,\omega _t } \}\) is the weight of decision maker \(e_k \), \(0\le \omega _k \le 1\), \(1\le k\le t\) and \(\mathop \sum \nolimits _{k=1}^t \omega _k =1\). Assume that \(H_1 \), \(H_2 \) and H are the evaluation grades to be used for assessing the attributes of alternatives, where \(H_1 \) represents completely satisfying the fuzzy concept “excellence”, \(H_2 \) represents not satisfying the fuzzy concept “excellence”, and H represents the evaluation grade of indeterminacy. The proposed method for fuzzy multi-attribute group decision making based on the IVIFSs and the ERM is now presented as follows:
-
Step 1: Let
 (26)
(26)where \(( [ {\beta _{1,j_L } (x_i ),\beta _{1,j_U } (x_i )} ]^{(k)},[ \beta _{2,j_L } (x_i ),\beta _{2,j_U } (x_i ) ]^{(k)})=( {[ {a_{ij} ,b_{ij} } ]^{( k)},[ {c_{ij} ,d_{ij} } ]^{( k)}})\), \([ \beta _{1,j_L } (x_i ),\beta _{1,j_U } (x_i ) ]^{(k)}\) and \([ {\beta _{2,j_L } (x_i ),\beta _{2,j_U } (x_i )} ]^{(k)}\) denote the degrees of belief of decision maker \(e_k \) with respect to attribute \(a_j \) of alternative \(x_i \) regarding the evaluation grades \(H_1 \) and \(H_2 \), respectively, \(0\le \beta _{1,j_L } (x_i )^k\le 1\), \(0\le \beta _{1,j_U } (x_i )^k\le 1\), \(0\le \beta _{2,j_L } (x_i )^k\le 1\), \(0\le \beta _{2,j_U } (x_i )^k\le 1\), \(0\le \beta _{1,j_U } (x_i )^k+\beta _{2,j_U } (x_i )^k\le 1\), \(1\le i\le m\), \(1\le j\le n\) and \(1\le k\le t\). Based on the decision matrix \(D_k =( {( {[ {\beta _{1,j_L } (x_i ),\beta _{1,j_U } (x_i )} ]^{(k)},[ {\beta _{2,j_L } (x_i ),\beta _{2,j_U } (x_i )} ]^{(k)}})})_{m\times n} \) and the weights \(w_1 ^k,w_2 ^k\),...,\(w_n ^k\)of the attributes \(a_1,a_2 \),...,\(a_n \), respectively, where \(w_j ^k\) is the weight of attributes \(a_j \) is given by decision maker \(e_k \), \(1\le i\le m\), \(1\le j\le n\) and \(1\le k\le t\), do the following sub-steps:
-
Step 1.1: Transform the degree of belief \([ \beta _{q,j_L } (x_i ),\beta _{q,j_U } (x_i ) ]^{(k)}\) of decision maker \(e_k \) with respect to attribute \(a_j \) of alternative \(x_i \) regarding the evaluation grade \(H_q \) into the basic probability mass \([ {m_{q,j_L } (x_i ),m_{q,j_U } (x_i )} ]^{(k)}\) and the remaining probability mass \([ {m_{H,j_L } (x_i ),m_{H,j_U } (x_i )} ]^{(k)}\) of decision maker \(e_k \) with respect to attribute \(a_j \) of alternative \(x_i \) regarding the evaluation grades \(H_q \) and H, respectively, shown as follows:
$$\begin{aligned}&\left[ {m_{q,j_L } (x_i ),m_{q,j_U } (x_i )}\right] ^{(k)}{=}w_j ^k{\times } \left[ {\beta _{q,j_L } (x_i ),\beta _{q,j_U }(x_i )}\right] ^{(k)},\nonumber \\ \end{aligned}$$(27)$$\begin{aligned}&\left[ {m_{H,j_L } (x_i ),m_{H,j_U } (x_i )} \right] ^{(k)} {=}\bigg [ ( {1-w_j ^k})+w_j ^k\nonumber \\&\bigg (1{-}\mathop \sum \limits _{q=1}^2 \beta _{q,j_U } (x_i )\bigg ),( {1{-}w_j ^k}){+}w_j ^k\bigg (1{-}\mathop \sum \limits _{q=1}^2 \beta _{q,j_L } (x_i )\bigg )\bigg ]^{(k)},\nonumber \\ \end{aligned}$$(28)where \(w_j ^k\)is the weight of attribute \(a_j \) given by decision maker \(e_k \), \(w_j ^k\in \left[ {0,1} \right] \), \(\mathop \sum \nolimits _{j=1}^n w_j ^k=1\),\(1\le i\le m\), \(1\le j\le n\), \(1\le q\le 2\) and \(1\le k\le t\). Based on Eq. (27), get the basic probability mass matrix \(P_k \) of the decision maker \(e_k \), shown as follows:
$$\begin{aligned}&P_k =\left( \left( \left[ {m_{1,j_L } (x_i ),m_{1,j_U } (x_i )} \right] ^{(k)},\right. \right. \nonumber \\&\left. \left. \quad \left[ {m_{2,j_L } (x_i ),m_{2,j_U } (x_i )} \right] ^{(k)}\right) \right) _{m\times n} , \end{aligned}$$(29)where \(0\le m_{1,j_L } (x_i )^k\le 1\), \(0\le m_{1,j_U } (x_i )^k\le 1\), \(0\le m_{2,j_L } (x_i )^k\le 1\), \(0\le m_{2,j_U } (x_i )^k\le 1\), \(0\le m_{1,j_U } (x_i )^k+m_{2,j_U } (x_i )^k\le 1\), \(1\le i\le m\), \(1\le j\le n\) and \(1\le k\le t\).
-
Step 1.2: Define \(G_{I(n)} \) as the set of the all n attributed as follows:
$$\begin{aligned} G_{I(n)} =\left\{ {a_1 ,a_2 ,\ldots ,a_n } \right\} , \end{aligned}$$(30)Let \([ {m_{q,I( n)_L } (x_i ),m_{q,I( n)_U } (x_i )}]^{(k)}\) be a probability mass defined as the degree to which all the n attributes in \(G_{I(n)} \) support the hypothesis that \(x_i \) is assessed to the grade \(H_q \). \([ {m_{H,I( n)_L } (x_i ),m_{H,I( n)_U } (x_i )} ]^{(k)}\) is the remaining probability mass unassigned to individual grades after all the attributes in \(G_{I(n)} \) have been assessed. \([ {m_{q,I( n)_L } (x_i ),m_{q,I( n)_U } (x_i )} ]^{(k)}\) and \([ m_{H,I( n)_L } (x_i ),m_{H,I( n)_U } (x_i ) ]^{(k)}\) can be generated by combining the basic probability masses \([ {m_{q,j_L } (x_i ),m_{q,j_U } (x_i )} ]^{(k)}\) and \([ {m_{H,j_L } (x_i ),m_{H,j_U } (x_i )} ]^{(k)}\) for all \(q=1,2, j=1,2,\ldots ,n\), as described in Eq.(17) to Eq.(21). Note that \([ {m_{q,I( 1)_L } (x_i ),m_{q,I( 1)_U } (x_i )} ]^{(k)}{=}[ {m_{q,1_L } (x_i ),m_{q,1_U } (x_i )} ]^{(k)}\) \((q=1,2)\) and \([ {m_{H,I( 1)_L } (x_i ),m_{H,I( 1)_U } (x_i )} ]^{(k)}=[ {m_{H,1_L } (x_i ),m_{H,1_U } (x_i )} ]^{(k)}\).
$$\begin{aligned}&K_{I(l+1)_L } ^{(k)}=\left[ {1{-}\mathop \sum \limits _{u=1}^p \mathop \sum \limits _{{\begin{array}{ccc} {f{=}1} \\ {f{\ne }u} \\ \end{array} }}^p m_{u,I(l)_L } ( {x_i })m_{f,l+1_L } ( {x_i })} \right] ^{-1},\nonumber \\ \end{aligned}$$(31)$$\begin{aligned}&K_{I(l+1)_U } ^{(k)}{=}\left[ {1{-}\mathop \sum \limits _{u=1}^p \mathop \sum \limits _{{\begin{array}{ccc} {f{=}1} \\ {f{\ne }u} \\ \end{array} }}^pm_{u,I(l)_U } ( {x_i })m_{f,l+1_U } ( {x_i })} \right] ^{-1},\nonumber \\ \end{aligned}$$(32)$$\begin{aligned}&\left[ {m_{H,I(l+1)_L } ( {x_i }),m_{H,I(l+1)_U } ( {x_i })} \right] ^{(k)}{=}\left[ {\overline{m}} _{H,I(l+1)_L } ( {x_i })\right. \nonumber \\&\quad +\,{\tilde{m}} _{H,I(l+1)_L } (x_i ),\left. {\overline{m}} _{H,I(l+1)_U } ( {x_i })\right. \nonumber \\&\quad \left. +\,{\tilde{m}} _{H,I(l+1)_U } (x_i ) \right] ^{(k)}, \end{aligned}$$(33)$$\begin{aligned}&\left[ {m_{q,I( {l+1})_L } ( {x_i }),m_{q,I( {l+1})_U } (x_i )} \right] ^{(k)}\nonumber \\&\quad =[ K_{I(l+1)_L } ^{(k)}\left[ m_{q,I(l)_L } ( {x_i })m_{q,l+1_L } ( {x_i })\right. \nonumber \\&\qquad \left. +\,m_{H,I(l)_U } ( {x_i })m_{q,l+1_L } ( {x_i })\right. \nonumber \\&\qquad +\,m_{q,I(l)_L } ( {x_i })m_{H,l+1_U } ( {x_i }) ],K_{I(l+1)_U } ^{(k)}\nonumber \\&\quad \left[ m_{q,I(l)_U } ( {x_i })m_{q,l+1_U } ( {x_i })+m_{H,I(l)_L } ( {x_i })m_{q,l+1_U } ( {x_i })\right. \nonumber \\&\qquad \left. \left. +\,m_{q,I(l)_U } ( {x_i })m_{H,l+1_L } ( {x_i }) \right] \right] ^{(k)}, \end{aligned}$$(34) -
Step 1.3: Aggregate the evaluating values of the attributes of alternative \(x_i \) to get the degree of belief \([ \beta _{q_L } (x_i ),\beta _{q_U } (x_i ) ]^{(k)}\) of decision maker \(e_k \) with respect to alternative \(x_i \) regarding the evaluation grade \(H_q \) and the degree of belief \([ {\beta _{H_L } (x_i ),\beta _{H_U } (x_i )} ]^{(k)}\) produced by unknown information, respectively, shown as follows:
$$\begin{aligned}&\left\{ {H_q } \right\} :\left[ {\beta _{q_L } (x_i ),\beta _{q_U } (x_i )} \right] ^{(k)}\nonumber \\&\quad =\left[ {\frac{m_{q,I( n)_L } (x_i )}{1-{\overline{m}} _{H,I( n)_L } (x_i )},\frac{m_{q,I( n)_U } (x_i )}{1-{\overline{m}} _{H,I( n)_U } (x_i )}} \right] ^{(k)}, \end{aligned}$$(35)$$\begin{aligned}&\left\{ H \right\} :\left[ {\beta _{H_L } (x_i ),\beta _{H_U } (x_i )} \right] ^{(k)}\nonumber \\&\quad =\left[ {\frac{{\tilde{m}} _{H,I( n)_L } (x_i )}{1-{\overline{m}} _{H,I( n)_L } (x_i )},\frac{{\tilde{m}} _{H,I( n)_U } (x_i )}{1-{\overline{m}} _{H,I( n)_U } (x_i )}} \right] ^{(k)}, \end{aligned}$$(36)where \(\mathop \sum \nolimits _{q=1}^2 [ {\beta _{q_L } (x_i ),\beta _{q_U } (x_i )} ]^{(k)}\!+\![ {\beta _{H_L } (x_i ),\beta _{H_U } (x_i )} ]^{(k)}=1\), \(1\le i\le m\), \(1\le q\le 2\) and \(1\le k\le t\). Let the obtained aggregated values \([ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ]^{(k)}\) and \([ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]^{(k)}\) form an IVIFN \(( [ \beta _{1_L } (x_i ),\beta _{1_U } (x_i ) ]^{(k)}\), \([ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]^{(k)})\), where \([ \beta _{1_L } (x_i ),\beta _{1_U } (x_i ) ]^{(k)}\) and \([ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]^{(k)}\) are the degrees of belief of decision maker \(e_k \) with respect to alternative \(x_i \) to the evaluation grades \(H_1 \) and \(H_2 \), respectively, \(1\le i\le m\) and \(1\le k\le t\).
-
Step 2: Based on the obtained IVIFNs \(( [ \beta _{1_L } (x_i ),\beta _{1_U } (x_i ) ]^{(k)}\),\([ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]^{(k)})\), \(1\le i\le m\) and \(1\le k\le t\), construct the aggregated decision matrix Y, shown as follows:
 (37)
(37)where \(( {[ {\beta _{1,k_L } (x_i ),\beta _{1,k_U } (x_i )} ],[ {\beta _{2,k_L } (x_i ),\beta _{2,k_U } (x_i )} ]})\) \(=( [ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ]^{(k)},[ \beta _{2_L } (x_i ),\beta _{2_U } (x_i ) ]^{(k)})\), \(( [ {\beta _{1,k_L } (x_i ),\beta _{1,k_U } (x_i )} ]\), \([ \beta _{2,k_L } (x_i ),\beta _{2,k_U } (x_i ) ])\) is an IVIFN denoting the evaluating value of decision maker \(e_k \) with respect to alternative \(x_i \), \([ \beta _{1,k_L } (x_i ),\beta _{1,k_U } (x_i ) ]\) and \([ {\beta _{2,k_L } (x_i ),\beta _{2,k_U } (x_i )} ]\) denote the degrees of belief of decision maker \(e_k \) with respect to alternative \(x_i \) regarding the evaluation grades \(H_1 \) and \(H_2 \), respectively, \(0\le \beta _{1,k_L } (x_i )\le 1\), \(0\le \beta _{1,k_U } (x_i )\le 1\), \(0\le \beta _{2,k_L } (x_i )\le 1\), \(0\le \beta _{2,k_U } (x_i )\le 1\), \(0\le \beta _{1,k_U } (x_i )+\beta _{2,k_U } (x_i )\le 1\), \(1\le i\le m\) and \(1\le k\le t\).
-
Step 3: Based on the aggregated decision matrix \(Y=( {( {[ {\beta _{1,k_L } (x_i ),\beta _{1,k_U } (x_i )} ],[ {\beta _{2,k_L } (x_i ),\beta _{2,k_U } (x_i )} ]})})_{m\times t} \) and the weights \(\omega _1 ,\omega _2 \), ..., and \(\omega _t \) of decision makers \(e_1 ,e_2 \), ..., and \(e_t \), respectively, do the following sub-steps:
-
Step 3.1: Transform the degree of belief \([ \beta _{q,k_L } (x_i ),\beta _{q,k_U } (x_i ) ]\) of decision maker \(e_k \) with respect to alternative \(x_i \) regarding the evaluation grade \(H_q \) into the basic probability mass \([ {m_{q,k_L } (x_i ),m_{q,k_U } (x_i )} ]\) and the remaining probability mass \([ {m_{H,k_L } (x_i ),m_{H,k_U } (x_i )} ]\) of decision maker \(e_k \) with respect to alternative \(x_i \) regarding the evaluation grades \(H_q \) and H, respectively, shown as follows:
$$\begin{aligned} \left[ {m_{q,k_L } (x_i ),m_{q,k_U } (x_i )} \right] \!=\!\omega _k \times \left[ {\beta _{q,k_L } (x_i ),\beta _{q,k_U } (x_i )} \right] ,\nonumber \\ \end{aligned}$$(38)$$\begin{aligned}&\left[ {m_{H,k_L } (x_i ),m_{H,k_U } (x_i )} \right] \nonumber \\&\qquad \qquad =\left[ ( {1-\omega _k })+\omega _k \left( 1-\mathop \sum \limits _{q=1}^2 \beta _{q,k_U } (x_i )\right) ,\right. \nonumber \\&\qquad \qquad \times \left. ( {1-\omega _k })+\,\omega _k (1-\mathop \sum \limits _{q=1}^2 \beta _{q,k_L } (x_i )) \right] , \end{aligned}$$(39)where \(\omega _k \) is the weight of decision maker \(e_k \), \(\omega _k \in \left[ {0,1} \right] \), \(\mathop \sum \nolimits _{k=1}^t \omega _k =1\),\(1\le i\le m\), \(1\le q\le 2\) and \(1\le k\le t\). Based on Eq. (38), get the basic probability mass matrix P, shown as follows:
$$\begin{aligned} P=\left( {\left( {\left[ {m_{1,k_L } (x_i ),m_{1,k_U } (x_i )} \right] ,\left[ {m_{2,k_L } (x_i ),m_{2,k_U } (x_i )} \right] }\right) }\right) _{m\times t},\nonumber \\ \end{aligned}$$(40)where \(0\le m_{1,k_L } (x_i )\le 1\), \(0\le m_{1,k_U } (x_i )\le 1, \quad 0\le m_{2,k_L } (x_i )\le 1\), \(0\le m_{2,k_U } (x_i )\le 1\), \(0\le m_{1,k_U } (x_i )+m_{2,k_U } (x_i )\le 1\), \(1\le i\le m\) and \(1\le k\le t\).
-
Step 3.2: Define \(G_{I(t)} \) as the set of the all t decision maker as follows:
$$\begin{aligned} G_{I(t)} =\left\{ {e_1 ,e_2 ,\ldots ,e_t } \right\} , \end{aligned}$$(41)Let \([ {m_{q,I( t)_L } (x_i ),m_{q,I( t)_U } (x_i )} ]\) be a probability mass defined as the degree to which all the t decision makers in \(G_{I(t)} \) support the hypothesis that \(x_i \) is assessed to the grade \(H_q \). \([ {m_{H,I( t)_L } (x_i ),m_{H,I( t)_U } (x_i )} ]\) is the remaining probability mass unassigned to individual grades after all the decision makers in \(G_{I(t)} \) have been assessed. \([ {m_{q,I( t)_L } (x_i ),m_{q,I( t)_U } (x_i )} ]\) and \([ m_{H,I( t)_L } (x_i ),m_{H,I( t)_U } (x_i ) ]\) can be generated by combining the basic probability masses \([ {m_{q,k_L } (x_i ),m_{q,k_U } (x_i )} ]\) and \([ m_{H,k_L } (x_i ),m_{H,k_U } (x_i ) ]\) for all \(q=1,2\), \(k=1,2,\ldots ,t\), as described in Eq. (31) to Eq. (34). Note that \([ {m_{q,I( 1)_L } (x_i ),m_{q,I( 1)_U } (x_i )} ]=[ {m_{q,1_L } (x_i ),m_{q,1_U } (x_i )} ] (q=1,2)\) and \([ m_{H,I( 1)_L } (x_i ),m_{H,I( 1)_U } (x_i ) ]=[ {m_{H,1_L } (x_i ),m_{H,1_U } (x_i )} ]\).
-
Step 3.3: Aggregate the evaluating values of the decision makers with respect to alternative \(x_i \) to get the degree of belief \([ {\beta _{q_L } (x_i ),\beta _{q_U } (x_i )} ]\) of alternative \(x_i \) regarding the evaluation grade \(H_q \) and the degree of belief \([ {\beta _{H_L } (x_i ),\beta _{H_U } (x_i )} ]\) produced by unknown information, respectively, shown as follows:
$$\begin{aligned}&\left\{ {H_q } \right\} :\left[ {\beta _{q_L } (x_i ),\beta _{q_U } (x_i )} \right] \nonumber \\&=\left[ {\frac{m_{q,I( t)_L } (x_i )}{1-{\overline{m}} _{H,I( t)_L } (x_i )},\frac{m_{q,I( t)_U } (x_i )}{1-{\overline{m}} _{H,I( t)_U } (x_i )}} \right] , \end{aligned}$$(42)$$\begin{aligned}&\left\{ H \right\} :\left[ {\beta _{H_L } (x_i ),\beta _{H_U } (x_i )} \right] \nonumber \\&=\left[ {\frac{{\tilde{m}} _{H,I( t)_L } (x_i )}{1-{\overline{m}} _{H,I( t)_L } (x_i )},\frac{{\tilde{m}} _{H,I( t)_U } (x_i )}{1-{\overline{m}} _{H,I( t)_U } (x_i )}} \right] , \end{aligned}$$(43)where \(\mathop \sum \nolimits _{q=1}^2 [ {\beta _{q_L } (x_i ),\beta _{q_U } (x_i )} ]+[ {\beta _{H_L } (x_i ),\beta _{H_U } (x_i )} ]=1\), \(1\le i\le m\) and \(1\le q\le 2\). Let the obtained aggregated values \([ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ]\) and \([ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]\) form an IVIFN \(( {[ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]})\), where \([ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ]\) and \([ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]\) are the degrees of belief of alternative \(x_i \) to the evaluation grades \(H_1 \) and \(H_2 \), respectively, and \(1\le i\le m\).
-
Step 4: Based on Eqs. (4) and (5), determine the PIS and the NIS with interval-valued intuitionistic fuzzy information, \({\tilde{r}} ^{+}\) and \({\tilde{r}} ^{-}\), where: \({\tilde{r}} ^{+}=( [ {\beta _{1_L } ^{+},\beta _{1_U } ^{+}} ],[ {\beta _{2_L } ^{+},\beta _{2_U } ^{+}} ])\) \(=( [ {\max \beta _{1_L } (x_i ),\max \beta _{1_U } (x_i )} ]\), \([ \min \beta _{2_L } (x_i ),\min \beta _{2_U } (x_i ) ])\) and \({\tilde{r}} ^{-}=( {[ {\beta _{1_L } ^{-},\beta _{1_U } ^{-}} ],[ {\beta _{2_L } ^{-},\beta _{2_U } ^{-}} ]})=( {[ {\min \beta _{1_L } (x_i ),\min \beta _{1_U } (x_i )} ],[ {\max \beta _{2_L } (x_i ),\max \beta _{2_U } (x_i )} ]})\), \(i=1,2,\ldots ,m\). Then calculate the gray relational coefficients of each alternative from PIS and NIS using, respectively, the following equations:
$$\begin{aligned}&\xi _i^{+} =\frac{\mathop {\min }\limits _{1\le i\le m} d( {{\tilde{r}} _i ,{\tilde{r}} ^{+}})+\rho \mathop {\max }\limits _{1\le i\le m} d( {{\tilde{r}} _i ,{\tilde{r}} ^{+}})}{d( {{\tilde{r}} _i ,{\tilde{r}} ^{+}})+\rho \mathop {\max }\limits _{1\le i\le m} d( {{\tilde{r}} _i ,{\tilde{r}} ^{+}})},\quad i=1,2,\ldots ,m \end{aligned}$$(44)$$\begin{aligned}&\xi _i^{-} =\frac{\mathop {\min }\limits _{1\le i\le m} d( {{\tilde{r}} _i ,{\tilde{r}} ^{-}})+\rho \mathop {\max }\limits _{1\le i\le m} d( {{\tilde{r}} _i ,{\tilde{r}} ^{-}})}{d( {{\tilde{r}} _i ,{\tilde{r}} ^{-}})+\rho \mathop {\max }\limits _{1\le i\le m} d( {{\tilde{r}} _i ,{\tilde{r}} ^{-}})},\quad i=1,2,\ldots ,m \end{aligned}$$(45)where the identification coefficient \(\rho =0.5\). And the normalized Hamming distance has been used. Based on Eq. (10), calculate the relative grey relational degree of each alternative from the PIS by using the following equation:
$$\begin{aligned} \xi _i =\frac{\xi _i^{+} }{\xi _i^{+} +\xi _i^{-}},\quad i=1,2,\ldots ,m. \end{aligned}$$(46)Rank all the alternatives \(X_i (i=1,2,\ldots ,m)\) and select the best one(s) in accordance with \(\xi _i (i=1,2,\ldots ,m)\). If any alternative has the highest \(\xi _i \) value, then, it is the most important alternative.
5 Experimental results
In this section, we use some examples to compare the experimental results of the proposed method with the ones of the methods presented in Makui et al. (2015b) and Jin et al. (2014).
Example 5.1
(Makui et al. 2015b). In order to increase market share over the long-term planning Tajhiz Tunnel Engineering (T.T.E) company wants to select the best supplier for establishing an effective supply chain management. Four suppliers were identified (\(x_1 ,x_2 ,x_3 \mathrm{and} x_4 )\) and five experts (\(e_1 ,e_2 ,e_3 ,e_4 \mathrm{and} e_5\)), who were technically competent and experienced, participated in their study. The expert weight vector was given by \(\omega =(0.30,0.25,0.15,0.15,0.15)^\mathrm{T}\). The criteria considered in the selection process were as follows: producing ability (\(a_1\)), financial issues (\(a_2\)), delivery time (\(a_3\)) and services (\(a_4\)). The decision matrices \(D_1 \), \(D_2 \), \(D_3 \), \(D_4 \) and \(D_5 \) represented by IVIFNs given by the decision makers \(e_1 \), \(e_2 \), \(e_3 \), \(e_4 \) and \(e_5 \), respectively, are shown as follows:
Assume that the weights of the attributes \(a_1 \), \(a_2 \), \(a_3 \) and \(a_4 \) given by the decision maker \(e_1 \) are 0.4, 0.3, 0.2and 0.1, respectively, i.e., \(w_1^1 =0.4\), \(w_2^1 =0.3\), \(w_3^1 =0.2\) and \(w_4^1 =0.1\). Assume that the weights of the attributes \(a_1 \), \(a_2 \), \(a_3 \) and \(a_4 \) given by the decision maker \(e_2 \) are 0.4, 0.4, 0.1 and 0.1, respectively, i.e., \(w_1^2 =0.4\), \(w_2^2 =0.4\), \(w_3^2 =0.1\) and \(w_4^2 =0.1\). Assume that the weights of the attributes \(a_1 \), \(a_2 \), \(a_3 \) and \(a_4 \) given by the decision maker \(e_3 \) are 0.3, 0.4, 0.2and 0.1, respectively, i.e., \(w_1^3 =0.3\), \(w_2^3 =0.4\), \(w_3^3 =0.2\) and \(w_4^3 =0.1\). Assume that the weights of the attributes \(a_1 \), \(a_2 \), \(a_3 \) and \(a_4 \) given by the decision maker \(e_4 \) are 0.4, 0.4, 0.1 and 0.1, respectively, i.e., \(w_1^4 =0.4\), \(w_2^4 =0.4\), \(w_3^4 =0.1\) and \(w_4^4 =0.1\). Assume that the weights of the attributes \(a_1 \), \(a_2 \), \(a_3 \) and \(a_4 \) given by the decision maker \(e_5 \) are 0.3, 0.3, 0.2 and 0.2, respectively, i.e., \(w_1^5 =0.3\), \(w_2^5 =0.3\), \(w_3^5 =0.2\) and \(w_4^5 =0.2\).
-
[Step 1]: Based on the decision matrices \(D_1 \), \(D_2 \), \(D_3 \), \(D_4 \) and \(D_5 \) and the weights of the attributes given by the decision makers, we can get
-
[Step 1.1]: Based on Eqs. (27) and (29), we can get the basic probability mass matrices \(P_1 \), \(P_2 \), \(P_3 \), \(P_4 \) and \(P_5 \) of the decision makers \(e_1 ,e_2 ,e_3 ,e_4 \text{ and } e_5 \), respectively, shown as follows:
$$\begin{aligned} P_1 =\left[ {{\begin{array}{ccc} {( {\left[ {0.12,0.20} \right] ,\left[ {0.16,0.20} \right] })} &{} {( {\left[ {0.18,0.21} \right] ,\left[ {0.03,0.06} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.10,0.12} \right] ,\left[ {0.04,0.06} \right] })} &{} {( {\left[ {0.04,0.07} \right] ,\left[ {0.00,0.01} \right] })} \\ \end{array} }} \\ {( {\left[ {0.24,0.32} \right] ,\left[ {0.04,0.08} \right] })} &{} {( {\left[ {0.18,0.21} \right] ,\left[ {0.06,0.09} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.12,0.16} \right] ,\left[ {0.02,0.04} \right] })} &{} {( {\left[ {0.05,0.07} \right] ,\left[ {0.01,0.03} \right] })} \\ \end{array} }} \\ {{\begin{array}{ccc} {( {\left[ {0.28,0.32} \right] ,\left[ {0.04,0.08} \right] })} \\ {( {\left[ {0.08,0.12} \right] ,\left[ {0.16,0.20} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.21,0.24} \right] ,\left[ {0.00,0.03} \right] })} \\ {( {\left[ {0.15,0.21} \right] ,\left[ {0.03,0.09} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.10,0.14} \right] ,\left[ {0.04,0.06} \right] })} \\ {( {\left[ {0.08,0.12} \right] ,\left[ {0.06,0.08} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.06,0.08} \right] ,\left[ {0.01,0.02} \right] })} \\ {( {\left[ {0.04,0.05} \right] ,\left[ {0.01,0.03} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$$$\begin{aligned} P_2 =\left[ {{\begin{array}{ccc} {( {\left[ {0.20,0.24} \right] ,\left[ {0.12,0.16} \right] })} &{} {( {\left[ {0.16,0.24} \right] ,\left[ {0.04,0.08} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.06,0.07} \right] ,\left[ {0.02,0.03} \right] })} &{} {( {\left[ {0.05,0.06} \right] ,\left[ {0.01,0.02} \right] })} \\ \end{array} }} \\ {( {\left[ {0.24,0.28} \right] ,\left[ {0.04,0.08} \right] })} &{} {( {\left[ {0.20,0.24} \right] ,\left[ {0.12,0.16} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.04,0.05} \right] ,\left[ {0.03,0.04} \right] })} &{} {( {\left[ {0.05,0.07} \right] ,\left[ {0.01,0.02} \right] })} \\ \end{array} }} \\ {{\begin{array}{ccc} {( {\left[ {0.24,0.32} \right] ,\left[ {0.04,0.08} \right] })} \\ {( {\left[ {0.16,0.24} \right] ,\left[ {0.12,0.16} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.24,0.28} \right] ,\left[ {0.04,0.08} \right] })} \\ {( {\left[ {0.16,0.20} \right] ,\left[ {0.00,0.04} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.05,0.06} \right] ,\left[ {0.03,0.04} \right] })} \\ {( {\left[ {0.04,0.05} \right] ,\left[ {0.02,0.04} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.07,0.09} \right] ,\left[ {0.00,0.01} \right] })} \\ {( {\left[ {0.04,0.06} \right] ,\left[ {0.01,0.02} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$$$\begin{aligned} P_3 =\left[ {{\begin{array}{ccc} {( {\left[ {0.15,0.21} \right] ,\left[ {0.06,0.09} \right] })} &{} {( {\left[ {0.20,0.24} \right] ,\left[ {0.04,0.08} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.10,0.12} \right] ,\left[ {0.04,0.08} \right] })} &{} {( {\left[ {0.04,0.06} \right] ,\left[ {0.01,0.03} \right] })} \\ \end{array} }} \\ {( {\left[ {0.15,0.18} \right] ,\left[ {0.03,0.06} \right] })} &{} {( {\left[ {0.20,0.28} \right] ,\left[ {0.08,0.12} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.06,0.12} \right] ,\left[ {0.04,0.08} \right] })} &{} {( {\left[ {0.06,0.08} \right] ,\left[ {0.00,0.01} \right] })} \\ \end{array} }} \\ {{\begin{array}{ccc} {( {\left[ {0.15,0.24} \right] ,\left[ {0.03,0.06} \right] })} \\ {( {\left[ {0.12,0.18} \right] ,\left[ {0.03,0.09} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.20,0.32} \right] ,\left[ {0.04,0.08} \right] })} \\ {( {\left[ {0.16,0.24} \right] ,\left[ {0.00,0.04} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.08,0.14} \right] ,\left[ {0.04,0.06} \right] })} \\ {( {\left[ {0.06,0.10} \right] ,\left[ {0.04,0.08} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.05,0.08} \right] ,\left[ {0.00,0.02} \right] })} \\ {( {\left[ {0.04,0.06} \right] ,\left[ {0.02,0.03} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$$$\begin{aligned} P_4 =\left[ {{\begin{array}{ccc} {( {\left[ {0.12,0.16} \right] ,\left[ {0.16,0.24} \right] })} &{} {( {\left[ {0.24,0.28} \right] ,\left[ {0.04,0.08} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.07,0.08} \right] ,\left[ {0.01,0.02} \right] })} &{} {( {\left[ {0.05,0.06} \right] ,\left[ {0.00,0.01} \right] })} \\ \end{array} }} \\ {( {\left[ {0.20,0.32} \right] ,\left[ {0.04,0.08} \right] })} &{} {( {\left[ {0.24,0.28} \right] ,\left[ {0.08,0.12} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.04,0.06} \right] ,\left[ {0.01,0.04} \right] })} &{} {( {\left[ {0.05,0.06} \right] ,\left[ {0.01,0.03} \right] })} \\ \end{array} }} \\ {{\begin{array}{ccc} {( {\left[ {0.28,0.32} \right] ,\left[ {0.04,0.08} \right] })} \\ {( {\left[ {0.08,0.12} \right] ,\left[ {0.16,0.20} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.28,0.32} \right] ,\left[ {0.00,0.04} \right] })} \\ {( {\left[ {0.20,0.28} \right] ,\left[ {0.04,0.12} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.05,0.07} \right] ,\left[ {0.02,0.03} \right] })} \\ {( {\left[ {0.05,0.06} \right] ,\left[ {0.01,0.03} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.06,0.07} \right] ,\left[ {0.01,0.02} \right] })} \\ {( {\left[ {0.04,0.05} \right] ,\left[ {0.01,0.03} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$$$\begin{aligned} P_5 =\left[ {{\begin{array}{ccc} {( {\left[ {0.09,0.12} \right] ,\left[ {0.12,0.18} \right] })} &{} {( {\left[ {0.18,0.21} \right] ,\left[ {0.06,0.09} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.12,0.14} \right] ,\left[ {0.40,0.06} \right] })} &{} {( {\left[ {0.10,0.14} \right] ,\left[ {0.00,0.02} \right] })} \\ \end{array} }} \\ {( {\left[ {0.12,0.18} \right] ,\left[ {0.06,0.12} \right] })} &{} {( {\left[ {0.18,0.24} \right] ,\left[ {0.03,0.06} \right] })} &{} {{\begin{array}{ccc} {( {\left[ {0.10,0.12} \right] ,\left[ {0.60,0.08} \right] })} &{} {( {\left[ {0.14,0.16} \right] ,\left[ {0.02,0.04} \right] })} \\ \end{array} }} \\ {{\begin{array}{ccc} {( {\left[ {0.15,0.21} \right] ,\left[ {0.03,0.09} \right] })} \\ {( {\left[ {0.06,0.09} \right] ,\left[ {0.15,0.18} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.21,0.27} \right] ,\left[ {0.00,0.03} \right] })} \\ {( {\left[ {0.15,0.21} \right] ,\left[ {0.03,0.09} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.10,0.12} \right] ,\left[ {0.40,0.08} \right] })} \\ {( {\left[ {0.08,0.12} \right] ,\left[ {0.20,0.04} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.12,0.18} \right] ,\left[ {0.00,0.02} \right] })} \\ {( {\left[ {0.08,0.12} \right] ,\left[ {0.02,0.06} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$where \([ {m_{1,j_L } (x_i ),m_{1,j_U } (x_i )} ]^{(k)}\)and \([ m_{2,j_L } (x_i ),m_{2,j_U } (x_i ) ]^{(k)}\) are the basic probability masses of decision maker \(e_k \) with respect to attribute \(a_j \) of alternative \(x_i \) regarding the evaluation grades \(H_1 \) and \(H_2 \), respectively, \(1\le i\le 4\), \(1\le j\le 4\) and \(1\le k\le 5\).
-
[Step 1.2]: Define \(G_{I(4)} \) as the set of the all 4 attributed as follows:
$$\begin{aligned} G_{I(4)} =\left\{ {a_1 ,a_2 ,a_3 ,a_4 } \right\} , \end{aligned}$$We can now use the recursive Eqs. (31)–(34) to calculate the combined probability masses as follows. Let \([ {m_{q,I( 1)_L } (x_i ),m_{q,I( 1)_U } (x_i )} ]^{(k)}=[ m_{q,1_L } (x_i ),m_{q,1_U } (x_i ) ]^{(k)}\) and \([ {m_{H,I( 1)_L } (x_i ),m_{H,I( 1)_U } (x_i )} ]^{(k)}=[ m_{H,1_L } (x_i ),m_{H,1_U } (x_i ) ]^{(k)}\) for \((q=1,2)\). Therefore,
$$\begin{aligned}&\left[ {m_{1,I( 4)_L } ( {x_1 }),m_{1,I( 4)_U } (x_1 )} \right] ^{(1)}=\left[ {0.3362,0.4141} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_2 }),m_{1,I( 4)_U } (x_2 )} \right] ^{(1)}=\left[ {0.4654,0.5354} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_3 }),m_{1,I( 4)_U } (x_3 )} \right] ^{(1)}=\left[ {0.5182,0.5686} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_4 }),m_{1,I( 4)_U } (x_4 )} \right] ^{(1)}=\left[ {0.2683,0.3353} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_1 }),m_{2,I( 4)_U } (x_1 )} \right] ^{(1)}=\left[ {0.1649,0.2099} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_2 }),m_{2,I( 4)_U } (x_2 )} \right] ^{(1)}=\left[ {0.0844,0.1313} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_3 }),m_{2,I( 4)_U } (x_3 )} \right] ^{(1)}=\left[ {0.0557,0.1045} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_4 }),m_{2,I( 4)_U } (x_4 )} \right] ^{(1)}=\left[ {0.1950,0.2589} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_1 }),m_{1,I( 4)_U } (x_1 )} \right] ^{(2)}=\left[ {0.3700,0.4380} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_2 }),m_{1,I( 4)_U } (x_2 )} \right] ^{(2)}=\left[ {0.4054,0.4518} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_3 }),m_{1,I( 4)_U } (x_3 )} \right] ^{(2)}=\left[ {0.4768,0.5449} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_4 }),m_{1,I( 4)_U } (x_4 )} \right] ^{(2)}=\left[ {0.3323,0.4160} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_1 }),m_{2,I( 4)_U } (x_1 )} \right] ^{(2)}=\left[ {0.1371,0.1845} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_2 }),m_{2,I( 4)_U } (x_2 )} \right] ^{(2)}=\left[ {0.1339,0.1826} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_3 }),m_{2,I( 4)_U } (x_3 )} \right] ^{(2)}=\left[ {0.0708,0.1188} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_4 }),m_{2,I( 4)_U } (x_4 )} \right] ^{(2)}=\left[ {0.1167,0.1777} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_1 }),m_{1,I( 4)_U } (x_1 )} \right] ^{(3)}=\left[ {0.3869,0.4439} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_2 }),m_{1,I( 4)_U } (x_2 )} \right] ^{(3)}=\left[ {0.3766,0.4669} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_3 }),m_{1,I( 4)_U } (x_3 )} \right] ^{(3)}=\left[ {0.3931,0.5481} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_4 }),m_{1,I( 4)_U } (x_4 )} \right] ^{(3)}=\left[ {0.3254,0.4292} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_1 }),m_{2,I( 4)_U } (x_1 )} \right] ^{(3)}=\left[ {0.1023,0.1658} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_2 }),m_{2,I( 4)_U } (x_2 )} \right] ^{(3)}=\left[ {0.1066,0.1617} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_3 }),m_{2,I( 4)_U } (x_3 )} \right] ^{(3)}=\left[ {0.0773,0.1178} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_4 }),m_{2,I( 4)_U } (x_4 )} \right] ^{(3)}=\left[ {0.0672,0.1489} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_1 }),m_{1,I( 4)_U } (x_1 )} \right] ^{(4)}=\left[ {0.3717,0.4031} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_2 }),m_{1,I( 4)_U } (x_2 )} \right] ^{(4)}=\left[ {0.4339,0.5196} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_3 }),m_{1,I( 4)_U } (x_3 )} \right] ^{(4)}=\left[ {0.5451,0.5941} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_4 }),m_{1,I( 4)_U } (x_4 )} \right] ^{(4)}=\left[ {0.2957,0.3624} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_1 }),m_{2,I( 4)_U } (x_1 )} \right] ^{(4)}=\left[ {0.1474,0.2286} \right] ,\\ \end{aligned}$$$$\begin{aligned}&\left[ {m_{2,I( 4)_L } ( {x_2 }),m_{2,I( 4)_U } (x_2 )} \right] ^{(4)}=\left[ {0.0998,0.1554} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_3 }),m_{2,I( 4)_U } (x_3 )} \right] ^{(4)}=\left[ {0.0428,0.0962} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_4 }),m_{2,I( 4)_U } (x_4 )} \right] ^{(4)}=\left[ {0.1665,0.2536} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_1 }),m_{1,I( 4)_U } (x_1 )} \right] ^{(5)}=\left[ {0.3694,0.4061} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_2 }),m_{1,I( 4)_U } (x_2 )} \right] ^{(5)}=\left[ {0.4162,0.4735} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_3 }),m_{1,I( 4)_U } (x_3 )} \right] ^{(5)}=\left[ {0.4782,0.5479} \right] ,\\&\left[ {m_{1,I( 4)_L } ( {x_4 }),m_{1,I( 4)_U } (x_4 )} \right] ^{(5)}=\left[ {0.2902,0.3644} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_1 }),m_{2,I( 4)_U } (x_1 )} \right] ^{(5)}=\left[ {0.1477,0.2109} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_2 }),m_{2,I( 4)_U } (x_2 )} \right] ^{(5)}=\left[ {0.1102,0.1670} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_3 }),m_{2,I( 4)_U } (x_3 )} \right] ^{(5)}=\left[ {0.0452,0.1163} \right] ,\\&\left[ {m_{2,I( 4)_L } ( {x_4 }),m_{2,I( 4)_U } (x_4 )} \right] ^{(5)}=\left[ {0.1635,0.2330} \right] . \end{aligned}$$Based on Eq. (33), we can get the remaining combined probability masses, shown as follows:
$$\begin{aligned}&\left[ {m_{H,I( 4)_L } ( {x_1 }),m_{H,I( 4)_U } (x_1 )} \right] ^{(1)}=\left[ {0.3760,0.4989} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_2 }),m_{H,I( 4)_U } (x_2 )} \right] ^{(1)}=\left[ {0.3333,0.4502} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_3 }),m_{H,I( 4)_U } (x_3 )} \right] ^{(1)}=\left[ {0.3269,0.4261} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_4 }),m_{H,I( 4)_U } (x_4 )} \right] ^{(1)}=\left[ {0.4058,0.5367} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_1 }),m_{H,I( 4)_U } (x_1 )} \right] ^{(2)}=\left[ {0.3775,0.4929} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_2 }),m_{H,I( 4)_U } (x_2 )} \right] ^{(2)}=\left[ {0.3656,0.4607} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_3 }),m_{H,I( 4)_U } (x_3 )} \right] ^{(2)}=\left[ {0.3363,0.4524} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_4 }),m_{H,I( 4)_U } (x_4 )} \right] ^{(2)}=\left[ {0.4063,0.5510} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_1 }),m_{H,I( 4)_U } (x_1 )} \right] ^{(3)}=\left[ {0.3903,0.5108} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_2 }),m_{H,I( 4)_U } (x_2 )} \right] ^{(3)}=\left[ {0.3714,0.5168} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_3 }),m_{H,I( 4)_U } (x_3 )} \right] ^{(3)}=\left[ {0.3341,0.5296} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_4 }),m_{H,I( 4)_U } (x_4 )} \right] ^{(3)}=\left[ {0.4219,0.6074} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_1 }),m_{H,I( 4)_U } (x_1 )} \right] ^{(4)}=\left[ {0.3683,0.4809} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_2 }),m_{H,I( 4)_U } (x_2 )} \right] ^{(4)}=\left[ {0.3250,0.4663} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_3 }),m_{H,I( 4)_U } (x_3 )} \right] ^{(4)}=\left[ {0.3097,0.4121} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_4 }),m_{H,I( 4)_U } (x_4 )} \right] ^{(4)}=\left[ {0.3840,0.5378} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_1 }),m_{H,I( 4)_U } (x_1 )} \right] ^{(5)}=\left[ {0.3830,0.4829} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_2 }),m_{H,I( 4)_U } (x_2 )} \right] ^{(5)}=\left[ {0.3595,0.4736} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_3 }),m_{H,I( 4)_U } (x_3 )} \right] ^{(5)}=\left[ {0.3358,0.4766} \right] ,\\&\left[ {m_{H,I( 4)_L } ( {x_4 }),m_{H,I( 4)_U } (x_4 )} \right] ^{(5)}=\left[ {0.4026,0.5463} \right] ,\\ \end{aligned}$$ -
[Step 1.3]: Based on Eq. (35), we can get
$$\begin{aligned}&\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ^{(1)}=\left[ {0.4967,0.6284} \right] ,\\&\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] ^{(1)}=\left[ {0.2436,0.3185} \right] ,\\&\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ^{(1)}=\left[ {0.6875,0.8126} \right] ,\\&\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] ^{(1)}=\left[ {0.1247,0.1993} \right] ,\\&\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ^{(1)}=\left[ {0.7656,0.8630} \right] ,\\&\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] ^{(1)}=\left[ {0.0823,0.1586} \right] ,\\&\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ^{(1)}=\left[ {0.3963,0.5088} \right] ,\\&\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] ^{(1)}=\left[ {0.2881,0.3929} \right] ,\\&\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ^{(2)}=\left[ {0.5341,0.6473} \right] ,\\&\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] ^{(2)}=\left[ {0.1979,0.2727} \right] ,\\&\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ^{(2)}=\left[ {0.5852,0.6677} \right] ,\\&\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] ^{(2)}=\left[ {0.1933,0.2699} \right] ,\\&\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ^{(2)}=\left[ {0.6883,0.8053} \right] ,\\&\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] ^{(2)}=\left[ {0.1022,0.1756} \right] ,\\&\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ^{(2)}=\left[ {0.4796,0.6148} \right] ,\\&\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] ^{(2)}=\left[ {0.1685,0.2627} \right] ,\\&\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ^{(3)}=\left[ {0.5663,0.6696} \right] ,\\&\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] ^{(3)}=\left[ {0.1498,0.2502} \right] ,\\ \end{aligned}$$$$\begin{aligned}&\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ^{(3)}=\left[ {0.5512,0.7042} \right] ,\\&\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] ^{(3)}=\left[ {0.1561,0.2439} \right] ,\\&\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ^{(3)}=\left[ {0.5754,0.8267} \right] ,\\&\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] ^{(3)}=\left[ {0.1132,0.1776} \right] ,\\&\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ^{(3)}=\left[ {0.4763,0.6474} \right] ,\\&\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] ^{(3)}=\left[ {0.0984,0.2245} \right] ,\\&\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ^{(4)}=\left[ {0.5398,0.6028} \right] ,\\&\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] ^{(4)}=\left[ {0.2141,0.3418} \right] ,\\&\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ^{(4)}=\left[ {0.6302,0.7771} \right] ,\\&\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] ^{(4)}=\left[ {0.1449,0.2324} \right] ,\\&\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ^{(4)}=\left[ {0.7918,0.8885} \right] ,\\&\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] ^{(4)}=\left[ {0.0621,0.1439} \right] ,\\&\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ^{(4)}=\left[ {0.4295,0.5420} \right] ,\\ \end{aligned}$$$$\begin{aligned}&\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] ^{(4)}=\left[ {0.2419,0.3793} \right] ,\\&\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ^{(5)}=\left[ {0.5570,0.6341} \right] ,\\&\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] ^{(5)}=\left[ {0.2227,0.3292} \right] ,\\&\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ^{(5)}=\left[ {0.6276,0.7393} \right] ,\\&\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] ^{(5)}=\left[ {0.1662,0.2607} \right] ,\\&\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ^{(5)}=\left[ {0.7210,0.8554} \right] ,\\&\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] ^{(5)}=\left[ {0.0681,0.1816} \right] ,\\&\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ^{(5)}=\left[ {0.4376,0.5690} \right] ,\\&\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] ^{(5)}=\left[ {0.2466,0.3637} \right] ,\\ \end{aligned}$$Therefore, we can get the aggregated IVIFNs \(\left( \left[ \beta _{1_L } (x_i ),\right. \right. \left. \left. \beta _{1_U } (x_i ) \right] \right. \) ,\(\left. \left[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} \right] \right) ^{(k)}\) of the evaluating value of the attributes of decision maker \(e_k \) with respect to alternative \(x_i \), where \(1\le i\le 4\)and \(1\le k\le 5\).
-
[Step 2]: Based on the obtained aggregated IVIFNs \(( {[ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]})^{(k)}\), where \(1\le i\le 4\) and \(1\le k\le 5\), we can get the aggregated decision matrix Y, shown as follows:
$$\begin{aligned}&Y=\left[ {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.4967,0.6284} \right] ,\left[ {0.2436,0.3185} \right] })} \\ {( {\left[ {0.6875,0.8126} \right] ,\left[ {0.1248,0.1993} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.7656,0.8630} \right] ,\left[ {0.0824,0.1586} \right] })} \\ {( {\left[ {0.3963,0.5088} \right] ,\left[ {0.2881,0.3929} \right] })} \\ \end{array} }} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.5341,0.6473} \right] ,\left[ {0.1979,0.2727} \right] })} \\ {( {\left[ {0.5852,0.6677} \right] ,\left[ {0.1933,0.2699} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.6883,0.8053} \right] ,\left[ {0.1022,0.1756} \right] })} \\ {( {\left[ {0.4796,0.6148} \right] ,\left[ {0.1685,0.2627} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right. \end{aligned}$$$$\begin{aligned}&\left. {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.5663,0.6696} \right] ,\left[ {0.1498,0.2502} \right] })} \\ {( {\left[ {0.5512,0.7042} \right] ,\left[ {0.1561,0.2439} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.5754,0.8267} \right] ,\left[ {0.1132,0.1776} \right] })} \\ {( {\left[ {0.4763,0.6474} \right] ,\left[ {0.0984,0.2245} \right] })} \\ \end{array} }} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.5398,0.6028} \right] ,\left[ {0.2141,0.3418} \right] })} \\ {( {\left[ {0.6302,0.7771} \right] ,\left[ {0.1449,0.2324} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.7918,0.8885} \right] ,\left[ {0.0621,0.1439} \right] })} \\ {( {\left[ {0.4295,0.5420} \right] ,\left[ {0.2419,0.3793} \right] })} \\ \end{array} }} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.5570,0.6341} \right] ,\left[ {0.2227,0.3292} \right] })} \\ {( {\left[ {0.6276,0.7393} \right] ,\left[ {0.1662,0.2607} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.7210,0.8554} \right] ,\left[ {0.0681,0.1816} \right] })} \\ {( {\left[ {0.4376,0.5690} \right] ,\left[ {0.2466,0.3637} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$ -
[Step 3]: Based on the obtained aggregated decision matrix Y and the weights \(\omega _1 \), \(\omega _2 \), \(\omega _3 \), \(\omega _4 \) and \(\omega _5 \) of the decision makers \(e_1 \), \(e_2 \), \(e_3 \), \(e_4 \) and \(e_5 \), respectively, we can get
-
[Step 3.1]: Based on Eqs. (38) and (40), we can get the basic probability mass matrix P, shown as follows:
$$\begin{aligned}&P=\left[ {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.1490,0.1885} \right] ,\left[ {0.0730,0.0955} \right] })} \\ {( {\left[ {0.2062,0.2437} \right] ,\left[ {0.0374,0.0598} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.2296,0.2589} \right] ,\left[ {0.0247,0.0476} \right] })} \\ {( {\left[ {0.1189,0.1526} \right] ,\left[ {0.0864,0.1178} \right] })} \\ \end{array} }} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.1335,0.1618} \right] ,\left[ {0.0494,0.0681} \right] })} \\ {( {\left[ {0.1463,0.1669} \right] ,\left[ {0.0483,0.0674} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.1720,0.2013} \right] ,\left[ {0.0255,0.0439} \right] })} \\ {( {\left[ {0.1199,0.1537} \right] ,\left[ {0.0421,0.0656} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right. \end{aligned}$$$$\begin{aligned} \left. {{\begin{array}{ccc} {{\begin{array}{ccc} {( {\left[ {0.0849,0.1004} \right] ,\left[ {0.0224,0.0375} \right] })} \\ {( {\left[ {0.0826,0.1056} \right] ,\left[ {0.0234,0.0365} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.0863,0.1240} \right] ,\left[ {0.0169,0.0266} \right] })} \\ {( {\left[ {0.0714,0.0971} \right] ,\left[ {0.0147,0.0336} \right] })} \\ \end{array} }} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.0809,0.0904} \right] ,\left[ {0.0321,0.0512} \right] })} \\ {( {\left[ {0.0945,0.1165} \right] ,\left[ {0.0217,0.0348} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.1187,0.1332} \right] ,\left[ {0.0093,0.0215} \right] })} \\ {( {\left[ {0.0644,0.0813} \right] ,\left[ {0.0362,0.0569} \right] })} \\ \end{array} }} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.0835,0.0951} \right] ,\left[ {0.0334,0.0493} \right] })} \\ {( {\left[ {0.0941,0.1108} \right] ,\left[ {0.0249,0.0391} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.1081,0.1283} \right] ,\left[ {0.0102,0.0272} \right] })} \\ {( {\left[ {0.0656,0.0853} \right] ,\left[ {0.0370,0.0545} \right] })} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$where \([ {m_{1,k_L } (x_i ),m_{1,k_U } (x_i )} ]\) and \([ {m_{2,k_L } (x_i ),m_{2,k_U } (x_i )} ]\) are the basic probability masses of decision maker \(e_k \) of alternative \(x_i \) regarding the evaluation grades \(H_1 \) and \(H_2 \), respectively, \(1\le i\le 4\), and \(1\le k\le 5\).
-
[Step 3.2]: Define \(G_{I(5)} \) as the set of the all 5 attributed as follows:
$$\begin{aligned} G_{I(5)} =\left\{ {e_1 ,e_2 ,e_3 ,e_4 ,e_5 } \right\} , \end{aligned}$$We can now use the recursive Eqs. (31)–(34) to calculate the combined probability masses as follows: Let \([ {m_{q,I( 1)_L } (x_i ),m_{q,I( 1)_U } (x_i )} ]=[ {m_{q,1_L } (x_i ),m_{q,1_U } (x_i )} ]\) and \([ m_{H,I( 1)_L } (x_i ),m_{H,I( 1)_U } (x_i ) ]=[m_{H,1_L } (x_i ),m_{H,1_U } (x_i ) ]\) for \((q=1,2)\). Therefore,
$$\begin{aligned}&\left[ {m_{1,I( 5)_L } ( {x_1 }),m_{1,I( 5)_U } (x_1 )} \right] =\left[ {0.3921,0.4285} \right] ,\\&\left[ {m_{1,I( 5)_L } ( {x_2 }),m_{1,I( 5)_U } (x_2 )} \right] =\left[ {0.4654,0.5080} \right] ,\\&\left[ {m_{1,I( 5)_L } ( {x_3 }),m_{1,I( 5)_U } (x_3 )} \right] =\left[ {0.5458,0.5896} \right] ,\\&\left[ {m_{1,I( 5)_L } ( {x_4 }),m_{1,I( 5)_U } (x_4 )} \right] =\left[ {0.3353,0.3843} \right] ,\\&\left[ {m_{2,I( 5)_L } ( {x_1 }),m_{2,I( 5)_U } (x_1 )} \right] =\left[ {0.1345,0.1729} \right] ,\\&\left[ {m_{2,I( 5)_L } ( {x_2 }),m_{2,I( 5)_U } (x_2 )} \right] =\left[ {0.0933,0.1260} \right] ,\\&\left[ {m_{2,I( 5)_L } ( {x_3 }),m_{2,I( 5)_U } (x_3 )} \right] =\left[ {0.0494,0.0832} \right] ,\\&\left[ {m_{2,I( 5)_L } ( {x_4 }),m_{2,I( 5)_U } (x_4 )} \right] =\left[ {0.1502,0.1981} \right] ,\\ \end{aligned}$$Based on Eq. (33), we can get the remaining combined probability masses, shown as follows:
$$\begin{aligned}&\left[ {m_{H,I( 5)_L } ( {x_1 }),m_{H,I( 5)_U } (x_1 )} \right] =\left[ {0.3986,0.4734} \right] ,\\&\left[ {m_{H,I( 5)_L } ( {x_2 }),m_{H,I( 5)_U } (x_2 )} \right] =\left[ {0.3660,0.4413} \right] ,\\&\left[ {m_{H,I( 5)_L } ( {x_3 }),m_{H,I( 5)_U } (x_3 )} \right] =\left[ {0.3272,0.4048} \right] ,\\&\left[ {m_{H,I( 5)_L } ( {x_4 }),m_{H,I( 5)_U } (x_4 )} \right] =\left[ {0.4176,0.5145} \right] , \end{aligned}$$ -
[Step 3.3]: Based on Eq. (42), we can get

Therefore, we can get the aggregated IVIFN \(( [ \beta _{1_L } (x_i ),\beta _{1_U } (x_i ) ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ])\) of alternative \(x_i \) with respect to all the decision makers \(e_1 \), \(e_2 \), \(e_3 \), \(e_4 \) and \(e_5 \), where \(1\le i\le 4\). shown as follows:




-
[Step 4]: Obtain the PIS and the NIS with interval-valued intuitionistic fuzzy information by utilizing Eqs. (4) and (5), respectively.

Calculate the separation measures, using the normalized Hamming distance.
$$\begin{aligned} d_i ^{+}=\left[ {{\begin{array}{ccc} {0.2243} \\ {0.1222} \\ {{\begin{array}{ccc} {0.0000} \\ {0.3026} \\ \end{array} }} \\ \end{array} }} \right] ,\quad d_i ^{-}=\left[ {{\begin{array}{ccc} {0.0782} \\ {0.1968} \\ {{\begin{array}{ccc} {0.3026} \\ {0.0000} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$Calculate the grey relational coefficients of each alternative from PIS and NIS.
$$\begin{aligned} \xi _i^{+} =\left[ {{\begin{array}{ccc} {0.4027} \\ {0.5531} \\ {{\begin{array}{ccc} {1.0000} \\ {0.3333} \\ \end{array} }} \\ \end{array} }} \right] ,\quad \xi _i^{-} =\left[ {{\begin{array}{ccc} {0.6591} \\ {0.4345} \\ {{\begin{array}{ccc} {0.3333} \\ {1.0000} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$Calculate the relative grey relational degree of each alternative from PIS.
$$\begin{aligned} \xi _1 =0.3792,\quad \xi _2 =0.5600,\quad \xi _3 =0.750,\quad \xi _4 =0.2500. \end{aligned}$$Because \(\xi _3 > \xi _2 >\xi _1 >\xi _4 \), the preference order of the alternatives \(x_1 \), \(x_2 \), \(x_3 \) and \(x_4 \) is \(x_3 > x_2 >\) \(x_1 > x_4 \) . This result coincides with the one presented in Makui et al. (2015b).
Table 1 shows a comparison of the preference order of the alternatives for different methods, where the proposed method and Makui et al.’s method (Makui et al. 2015b) get the same preference order of the alternatives, i.e., \(x_3 >x_2 >x_1 > x_4 \), whereas Jin et al.’s method (Jin et al. 2014) cannot deal with Example 5.1 due to the fact that it cannot allow the attributes to have different weights assigned by different experts.
Example 5.2
(Jin et al. 2014). There are five emergency operating centers (EOCs) (\(x_1 ,x_2 ,x_3 ,x_4 \text{ and } x_5\)) to be evaluated by three evaluators (\(e_1 ,e_2 \text{ and } e_3\)). We suppose that the emergency management evaluation task has the following features:
-
(1)
There are eight criteria to evaluate five EOCs, including energy (\(a_1 )\), food (\(a_2\)), health and medical services (\(a_3\)), communication equipment (\(a_4\)), emergency medical personnel (\(a_5\)), human resource coordinator (\(a_6\)), cars (\(a_7\)) and generators (\(a_8\)).
-
(2)
There are three evaluators \(e_1 ,e_2 \text{ and } e_3 \) associated with weighting vector \(\omega =(0.35,0.40,0.25)^\mathrm{T}\).
The decision matrices \(D_1 \), \(D_2 \) and \(D_3 \) represented by IVIFNs given by the decision makers \(e_1 \), \(e_2 \) and \(e_3 \), respectively, are shown as follows:
Assume that the weights of the attributes \(a_1 \), \(a_2 \), \(a_3 \), \(a_4 \), \(a_5 \), \(a_6 \), \(a_7 \) and \(a_8 \) given by the decision maker \(e_1 \) are 0.1537, 0.1052, 0.0933, 0.1646, 0.1170, 0.1458, 0.1337 and 0.0867, respectively, i.e., \(w_1^1 =0.1537\), \(w_2^1 =0.1052\), \(w_3^1 =0.0933\), \(w_4^1 =0.1646 \), \(w_5^1 =0.1170 \), \(w_6^1 =0.1458 \), \(w_7^1 =0.1337\) and \(w_8^1 =0.0867\). Assume that the weights of the attributes \(a_1 \), \(a_2 \), \(a_3 \), \(a_4 \), \(a_5 \), \(a_6 \), \(a_7 \) and \(a_8 \) given by the decision maker \(e_2 \) are 0.1537, 0.1052, 0.0933, 0.1646, 0.1170, 0.1458, 0.1337 and 0.0867, respectively, i.e., \(w_1^2 =0.1537\), \(w_2^2 =0.1052\), \(w_3^2 =0.0933\), \(w_4^2 =0.1646 \), \(w_5^2 =0.1170 \), \(w_6^2 =0.1458 \), \(w_7^2 =0.1337\)and \(w_8^2 =0.0867\). Assume that the weights of the attributes \(a_1 \), \(a_2 \), \(a_3 \), \(a_4 \),, \(a_5 \), \(a_6 \), \(a_7 \) and \(a_8 \) given by the decision maker \(e_3 \) are 0.1537, 0.1052, 0.0933, 0.1646, 0.1170, 0.1458, 0.1337 and 0.0867, respectively, i.e., \(w_1^3 =0.1537\), \(w_2^3 =0.1052\), \(w_3^3 =0.0933\), \(w_4^3 =0.1646\), \(w_5^3 =0.1170\), \(w_6^3 =0.1458\), \(w_7^3 =0.1337\) and \(w_8^3 = 0.0867\).
-
[Step 1]: Based on the decision matrices \(D_1 \), \(D_2 \) and \(D_3 \) and the weights of the attributes given by the decision makers \(e_1 \), \(e_2 \) and \(e_3 \), we can get the aggregated IVIFNs \(( {[ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]})^{(k)}\) of the evaluating value of the attributes of decision maker \(e_k \) with respect to alternative \(x_i \), where \(1\le i\le 5\) and \(1\le k\le 3\), shown as follows:
$$\begin{aligned}&( {\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ,\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] })^{(1)}\\&\quad =( {\left[ {0.5563,0.7050} \right] ,\left[ {0.1943,0.2590} \right] }), \\&( {\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ,\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] })^{(1)}\\&\quad =( {\left[ {0.3603,0.4606} \right] ,\left[ {0.3434,0.4387} \right] }), \\&( {\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ,\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] })^{(1)}\\&\quad =( {\left[ {0.5432,0.6530} \right] ,\left[ {0.2144,0.2870} \right] }), \\&( {\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ,\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] })^{(1)}\\&\quad =( {\left[ {0.4862,0.5691} \right] ,\left[ {0.2444,0.3559} \right] }), \\&( {\left[ {\beta _{1_L } (x_5 ),\beta _{1_U } (x_5 )} \right] ,\left[ {\beta _{2_L } (x_5 ),\beta _{2_U } (x_5 )} \right] })^{(1)}\\&\quad =( {\left[ {0.5236,0.5804} \right] ,\left[ {0.2126,0.3254} \right] }), \\&( {\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ,\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] })^{(2)}\\&\quad =( {\left[ {0.4341,0.5750} \right] ,\left[ {0.2816,0.3360} \right] }), \\&( {\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ,\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] })^{(2)}\\&\quad =( {\left[ {0.4426,0.5446} \right] ,\left[ {0.2550,0.3243} \right] }), \\&( {\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ,\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] })^{(2)}\\&\quad =( {\left[ {0.4654,0.5979} \right] ,\left[ {0.2699,0.3188} \right] }), \\&( {\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ,\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] })^{(2)}\\&\quad =( {\left[ {0.3743,0.4578} \right] ,\left[ {0.3312,0.4414} \right] }), \\&( {\left[ {\beta _{1_L } (x_5 ),\beta _{1_U } (x_5 )} \right] ,\left[ {\beta _{2_L } (x_5 ),\beta _{2_U } (x_5 )} \right] })^{(2)}\\&\quad =( {\left[ {0.4252,0.5161} \right] ,\left[ {0.2970,0.3970} \right] }), \\&( {\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ,\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] })^{(3)}\\&\quad =( {\left[ {0.5153,0.6065} \right] ,\left[ {0.2826,0.3535} \right] }), \\&( {\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ,\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] })^{(3)}\\&\quad =( {\left[ {0.5143,0.6304} \right] ,\left[ {0.2764,0.3230} \right] }), \\&( {\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ,\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] })^{(3)}\\&\quad =( {\left[ {0.6295,0.6823} \right] ,\left[ {0.2106,0.2900} \right] }), \\&( {\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ,\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] })^{(3)}\\&\quad =( {\left[ {0.4010,0.5521} \right] ,\left[ {0.2977,0.3915} \right] }), \\&( {\left[ {\beta _{1_L } (x_5 ),\beta _{1_U } (x_5 )} \right] ,\left[ {\beta _{2_L } (x_5 ),\beta _{2_U } (x_5 )} \right] })^{(3)}\\&\quad =( {\left[ {0.5994,0.7537} \right] ,\left[ {0.1746,0.2406} \right] }). \end{aligned}$$ -
[Step 2]: Based on the obtained aggregated IVIFNs \(( {[ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]})^{(k)}\), where \(1\le i\le 5\) and \(1\le k\le 3\), we can get the aggregated decision matrix Y, shown as follows:
$$\begin{aligned} Y=\left[ {{\begin{array}{ccc} {( {\left[ {0.5563,0.7050} \right] ,\left[ {0.1943,0.2590} \right] })} &{} {( {\left[ {0.4341,0.5750} \right] ,\left[ {0.2816,0.3360} \right] })} &{} {( {\left[ {0.5153,0.6065} \right] ,\left[ {0.2826,0.3535} \right] })} \\ {( {\left[ {0.3603,0.4606} \right] ,\left[ {0.3434,0.4387} \right] })} &{} {( {\left[ {0.4426,0.5446} \right] ,\left[ {0.2550,0.3243} \right] })} &{} {( {\left[ {0.5143,0.6304} \right] ,\left[ {0.2764,0.3230} \right] })} \\ {{\begin{array}{ccc} {( {\left[ {0.5432,0.6530} \right] ,\left[ {0.2144,0.2870} \right] })} \\ {( {\left[ {0.4862,0.5691} \right] ,\left[ {0.2444,0.3559} \right] })} \\ {( {\left[ {0.5236,0.5804} \right] ,\left[ {0.2126,0.3254} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.4654,0.5979} \right] ,\left[ {0.2699,0.3188} \right] })} \\ {( {\left[ {0.3743,0.4578} \right] ,\left[ {0.3312,0.4414} \right] })} \\ {( {\left[ {0.4252,0.5161} \right] ,\left[ {0.2970,0.3970} \right] })} \\ \end{array} }} &{} {{\begin{array}{ccc} {( {\left[ {0.6295,0.6823} \right] ,\left[ {0.2106,0.2900} \right] })} \\ {( {\left[ {0.4010,0.5521} \right] ,\left[ {0.2977,0.3915} \right] })} \\ {( {\left[ {0.5994,0.7537} \right] ,\left[ {0.1746,0.2406} \right] })} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$ -
[Step 3]: Based on the aggregated decision matrix Y and the weights \(\omega _1 \), \(\omega _2 \) and \(\omega _3 \) of the decision makers \(e_1 \), \(e_2 \) and \(e_3 \), respectively, we can get the aggregated IVIFNs \(( {[ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]})\) of alternative \(x_i \) with respect to the decision makers \(e_1 \), \(e_2 \) and \(e_3 \), where \(1\le i\le 5\), shown as follows:
$$\begin{aligned}&( {\left[ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} \right] ,\left[ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} \right] })\\&\quad =( {\left[ {0.5496,0.6635} \right] ,\left[ {0.2510,0.2867} \right] }), \\&( {\left[ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} \right] ,\left[ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} \right] })\\&\quad =( {\left[ {0.4104,0.5214} \right] ,\left[ {0.3019,0.3540} \right] }), \\&( {\left[ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} \right] ,\left[ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} \right] })\\&\quad =( {\left[ {0.5888,0.6779} \right] ,\left[ {0.2304,0.2755} \right] }), \\&( {\left[ {\beta _{1_L } (x_4 ),\beta _{1_U } (x_4 )} \right] ,\left[ {\beta _{2_L } (x_4 ),\beta _{2_U } (x_4 )} \right] })\\&\quad =( {\left[ {0.4038,0.4927} \right] ,\left[ {0.3269,0.3888} \right] }), \\&( {\left[ {\beta _{1_L } (x_5 ),\beta _{1_U } (x_5 )} \right] ,\left[ {\beta _{2_L } (x_5 ),\beta _{2_U } (x_5 )} \right] })\\&\quad =( {\left[ {0.5294,0.6333} \right] ,\left[ {0.2755,0.2997} \right] }). \\ \end{aligned}$$ -
[Step 4]: Obtain the PIS and the NIS with interval-valued intuitionistic fuzzy information, respectively, shown as follows:
$$\begin{aligned} \begin{array}{c} A^{+}=( {\left[ {0.5888,0.6779} \right] ,\left[ {0.2304,0.2755} \right] ,\left[ {0.0466,0.1808} \right] }), \\ A^{-}=( {\left[ {0.4038,0.4927} \right] ,\left[ {0.3269,0.3888} \right] ,\left[ {0.1185,0.2693} \right] }), \\ \end{array} \end{aligned}$$Calculate the separation measures, using the normalized Hamming distance.
$$\begin{aligned} d_i ^{+}=\left[ {{\begin{array}{ccc} {0.0268} \\ {0.1674} \\ {{\begin{array}{ccc} {0.0000} \\ {{\begin{array}{ccc} {0.1851} \\ {0.0520} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] ,\quad d_i ^{-}=\left[ {{\begin{array}{ccc} {0.1583} \\ {0.0299} \\ {{\begin{array}{ccc} {0.1851} \\ {{\begin{array}{ccc} {0.0000} \\ {0.1331} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$Calculate the grey relational coefficients of each alternative from PIS and NIS.
$$\begin{aligned} \xi _i^{+} =\left[ {{\begin{array}{ccc} {0.7745} \\ {0.3559} \\ {{\begin{array}{ccc} {1.0000} \\ {{\begin{array}{ccc} {0.3333} \\ {0.6402} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] ,\quad \xi _i^{-} =\left[ {{\begin{array}{ccc} {0.3689} \\ {0.7558} \\ {{\begin{array}{ccc} {0.3333} \\ {{\begin{array}{ccc} {1.0000} \\ {0.4101} \\ \end{array} }} \\ \end{array} }} \\ \end{array} }} \right] , \end{aligned}$$Calculate the relative grey relational degree of each alternative from PIS.
$$\begin{aligned}&\xi _1 =0.6776,\quad \xi _2 =0.3201,\quad \xi _3 =0.7500,\\&\xi _4 =0.2500,\quad \xi _5 =0.6095. \end{aligned}$$Because \(\xi _3 >\xi _1 >\xi _5 >\xi _2 >\xi _4 \), the preference order of the alternatives \(x_1 \), \(x_2 \), \(x_3 \), \(x_4 \) and \(x_5 \) is \(x_3 > x_1 >x_5 > x_2 > x_4 \). This result coincides with the ones presented in Makui et al. (2015b) and Jin et al. (2014).
Table 2 shows a comparison of the preference order of the alternatives for different methods, where the proposed method and Makui et al.’s method (Makui et al. 2015b) get the same preference order of the alternatives, i.e., \(x_3 >x_1 >x_5 >x_2 >x_4 \), whereas Jin et al.’s method (Jin et al. 2014) gets the same preference order of the alternatives, but with a small difference in the preference order of the alternatives \(x_3 \) and \(x_5 \).
Example 5.3
A commercial holding company wants to invest amount of money in the best business areas. There are three alternatives: a pharmaceutical company (\(x_1\)), a petroleum company (\(x_2\)) and a software company (\(x_3\)) to be assessed. Also there are three attributes: growth index (\(a_1\)), risk index (\(a_2\)) and capital return rate (\(a_3\)) to be used to evaluate the three alternatives \(x_1 ,x_2\, \text{ and }\, x_3 \) by the three decision makers, i.e., the manager (\(e_1\)), the financial director (\(e_2\)) and the assistant manager (\(e_3\)).
Assume that the decision matrices \(D_1 \), \(D_2 \) and \(D_3 \) represented by IVIFNs given by the decision makers \(e_1 \), \(e_2 \) and \(e_3 \), respectively, are shown as follows:
Assume that the weights \(\omega _1 \), \(\omega _2 \) and \(\omega _3 \) of the decision makers \(e_1 \), \(e_2 \) and \(e_3 \) are 0.36, 0.32 and 0.32, respectively. Assume that the weights of the attributes \(a_1 \), \(a_2 \) and \(a_3 \) given by the decision maker \(e_1 \) are 0.01, 0.49 and 0.50, respectively, i.e., \(w_1^1 =0.01\), \(w_2^1 =0.49\) and \(w_3^1 =0.50\). Assume that the weights of the attributes \(a_1 \), \(a_2 \) and \(a_3 \) given by the decision maker \(e_2 \) are 0.01, 0.49 and 0.50, respectively, i.e., \(w_1^2 =0.01\), \(w_2^2 =0.49\) and \(w_3^2 =0.50\). Assume that the weights of the attributes \(a_1 \), \(a_2 \) and \(a_3 \) given by the decision maker \(e_3 \) are 0.01, 0.49 and 0.50, respectively, i.e., \(w_1^3 =0.01\), \(w_2^3 =0.49\) and \(w_3^3 =0.50\).
-
[Step 1]: Based on the decision matrices \(D_1 \), \(D_2 \) and \(D_3 \) and the weights of the attributes given by the decision makers \(e_1 \), \(e_2 \) and \(e_3 \), we can get the aggregated IVIFNs \(( {[ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]})^{(k)}\) of the evaluating values of the attributes of decision maker \(e_k \) with respect to alternative \(x_i \), where \(1\le i\le 3\) and \(1\le k\le 3\), shown as follows:
$$\begin{aligned}&( { [ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} ], [ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} ]})^{(1)}\\&\quad =( { [ {0.4616,0.5483} ], [ {0.1574,0.2476} ]}), \\&( { [ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} ], [ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} ]})^{(1)}\\&\quad =( { [ {0.8001,0.8784} ], [ {0.0431,0.1009} ]}), \\&( { [ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} ], [ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} ]})^{(1)}\\&\quad =( { [ {0.8636,0.9632} ], [ {0.0084,0.0397} ]}), \\&( { [ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} ], [ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} ]})^{(2)}\\&\quad =( { [ {0.0720,0.1582} ], [ {0.6244,0.7050} ]}), \\&( { [ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} ], [ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} ]})^{(2)}\\&\quad =( { [ {0.2215,0.3016} ], [ {0.4809,0.5578} ]}), \\&( { [ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} ], [ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} ]})^{(2)}\\&\quad =( { [ {0.3661,0.4471} ], [ {0.3075,0.3885} ]}), \\&( { [ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} ], [ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} ]})^{(3)}\\&\quad =( { [ {0.0702,0.1533} ], [ {0.6729,0.7517} ]}), \\&( { [ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} ], [ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} ]})^{(3)}\\&\quad =( { [ {0.2344,0.3091} ], [ {0.5170,0.5888} ]}), \\&( { [ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} ], [ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} ]})^{(3)}\\&\quad =( { [ {0.3292,0.4090} ], [ {0.3606,0.4400} ]}), \end{aligned}$$ -
[Step 2]: Based on the obtained aggregated IVIFNs \(( {[ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]})^{(k)}\), where \(1\le i\le 3\) and \(1\le k\le 3\), we can get the aggregated decision matrix Y, shown as follows:
$$\begin{aligned} Y=\left[ {{\begin{array}{ccc} {( {\left[ {0.4616,0.5483} \right] ,\left[ {0.1574,0.2476} \right] })} &{} {( {\left[ {0.0720,0.1582} \right] ,\left[ {0.6244,0.7050} \right] })} &{} {( {\left[ {0.0702,0.1533} \right] ,\left[ {0.6729,0.7517} \right] })} \\ {( {\left[ {0.8001,0.8784} \right] ,\left[ {0.0431,0.1009} \right] })} &{} {( {\left[ {0.2215,0.3016} \right] ,\left[ {0.4809,0.5578} \right] })} &{} {( {\left[ {0.2344,0.3091} \right] ,\left[ {0.5170,0.5888} \right] })} \\ {( {\left[ {0.8636,0.9632} \right] ,\left[ {0.0084,0.0397} \right] })} &{} {( {\left[ {0.3661,0.4471} \right] ,\left[ {0.3075,0.3885} \right] })} &{} {( {\left[ {0.3292,0.4090} \right] ,\left[ {0.3606,0.4400} \right] })} \\ \end{array} }} \right] , \end{aligned}$$ -
[Step 3]: Based on the aggregated decision matrix Y and the weights \(\omega _1 \), \(\omega _2 \) and \(\omega _3 \) of the decision makers \(e_1 \), \(e_2 \) and \(e_3 \), respectively, we can get the aggregated IVIFNs \(( {[ {\beta _{1_L } (x_i ),\beta _{1_U } (x_i )} ],[ {\beta _{2_L } (x_i ),\beta _{2_U } (x_i )} ]})\) of alternative \(x_i \) with respect to the decision makers \(e_1 \), \(e_2 \) and \(e_3 \), where \(1\le i\le 3\), shown as follows:
$$\begin{aligned}&( { [ {\beta _{1_L } (x_1 ),\beta _{1_U } (x_1 )} ], [ {\beta _{2_L } (x_1 ),\beta _{2_U } (x_1 )} ]})=( { [ {0.2090,0.2820} ], [ {0.5344,0.5956} ]}), \\&( { [ {\beta _{1_L } (x_2 ),\beta _{1_U } (x_2 )} ], [ {\beta _{2_L } (x_2 ),\beta _{2_U } (x_2 )} ]})=( { [ {0.4518,0.5142} ], [ {0.3213,0.3695} ]}), \\&( { [ {\beta _{1_L } (x_3 ),\beta _{1_U } (x_3 )} ], [ {\beta _{2_L } (x_3 ),\beta _{2_U } (x_3 )} ]})=( { [ {0.5956,0.6691} ], [ {0.1990,0.2420} ]}), \\ \end{aligned}$$ -
[Step 4]: Obtain the PIS and the NIS with interval-valued intuitionistic fuzzy information, respectively, shown as follows:
$$\begin{aligned} \begin{array}{l} A^{+}=( {\left[ {0.5956,0.6691} \right] ,\left[ {0.1990,0.2420} \right] ,\left[ {0.0889,0.2054} \right] }), \\ A^{-}=( {\left[ {0.2090,0.2820} \right] ,\left[ {0.5344,0.5956} \right] ,\left[ {0.1224,0.2566} \right] }), \\ \end{array} \end{aligned}$$Calculate the separation measures, using the normalized Hamming distance.
$$\begin{aligned} d_i ^{+}=\left[ {{\begin{array}{ccc} {0.3868} \\ {0.1493} \\ {0.0000} \\ \end{array} }} \right] ,\quad d_i ^{-}=\left[ {{\begin{array}{ccc} {0.0000} \\ {0.2375} \\ {0.3868} \\ \end{array} }} \right] , \end{aligned}$$Calculate the grey relational coefficients of each alternative from PIS and NIS.
$$\begin{aligned} \xi _i^{+} =\left[ {{\begin{array}{ccc} {0.3333} \\ {0.5642} \\ {1.0000} \\ \end{array} }} \right] ,\quad \xi _i^{-} =\left[ {{\begin{array}{ccc} {1.0000} \\ {0.4488} \\ {0.3333} \\ \end{array} }} \right] , \end{aligned}$$Calculate the relative grey relational degree of each alternative from PIS.
$$\begin{aligned} \xi _1 =0.2500,\quad \xi _2 =0.5569,\quad \xi _3 =0.7500. \end{aligned}$$Because \(\xi _3 >\xi _2 >\xi _1 \), the preference order of the alternatives \(x_1 \), \(x_2 \) and \(x_3 \) is \(x_3 >x_2 >x_1 \).
Table 3 shows a comparison of the preference order of the alternatives for different methods, where the proposed method gets the preference order of the alternatives, i.e., \(x_3 >x_2 >x_1 \), whereas Makui et al.’s method (Makui et al. 2015b) and Jin et al.’s method (Jin et al. 2014) get an unreasonable preference order of the alternatives because there is an evaluating intuitionistic fuzzy value whose non-membership degree is equal to 0.
In the following, we analyse the drawbacks of the methods that presented in Makui et al. (2015b) and Jin et al. (2014). Therefore, consider the information that presented, in Example 5.3 then: Where there is an IVIFN \(( {\left[ {0.70,0.80} \right] ,\left[ {0.00,0.00} \right] })\) in the first row and the first column of the decision matrix \(D_1 \) whose non-membership degree is equal to 0. Because the weights \(\omega _1 \), \(\omega _2 \) and \(\omega _3 \) of the decision makers \(e_1 \), \(e_2 \) and \(e_3 \) are 0.36, 0.32 and 0.32, respectively, because the weights of the attributes \(a_1 \), \(a_2 \) and \(a_3 \) given by the decision maker \(e_1 \) are 0.01, 0.49 and 0.50, respectively, i.e., \(w_1^1 =0.01\), \(w_2^1 =0.49\) and \(w_3^1 =0.50\), because the weights of the attributes \(a_1 \), \(a_2 \) and \(a_3 \) given by the decision maker \(e_2 \) are 0.01, 0.49 and 0.50, respectively, i.e., \(w_1^2 =0.01\), \(w_2^2 =0.49\) and \(w_3^2 =0.50\) and because the weights of the attributes \(a_1 \), \(a_2 \) and \(a_3 \) given by the decision maker \(e_3 \) are 0.01, 0.49 and 0.50, respectively, i.e., \(w_1^3 =0.01\), \(w_2^3 =0.49\) and \(w_3^3 =0.50\).
-
(1)
The drawback of Makui et al.’s method (Makui et al. 2015b): Based on Eq. (24), we can get the collective intuitionistic fuzzy decision matrix \(\dot{\tilde{D}} =( {\dot{\tilde{d}}_{ij}})_{3\times 3} \), where

For example, we can see that the aggregated IVIFN in the first row and the first column of the collective intuitionistic fuzzy decision matrix \(\dot{\tilde{D}} \) is \(( \left[ {0.2908,0.3851} \right] ,\left[ {0.0000,0.0000} \right] )\), which is obtained by aggregating the IVIFNs \(({\left[ {0.70,0.80} \right] ,\left[ {0.00,0.00} \right] })\), \((\left[ {0.05,0.10} \right] ,\left[ {0.80,0.90} \right] )\) and \(( {\left[ {0.01,0.05} \right] ,\left[ {0.85,0.95} \right] })\) in the first row and the first column of the decision matrices \(D_1 \), \(D_2 \) and \(D_3 \), respectively, based on Eq. (24), where
$$\begin{aligned}&( { [ {a_{{11} _{(1)}} ,b_{{11} _{(1)}} } ], [ {c_{{11} _{(1)}} ,d_{{11} _{(1)}} } ]} )\\&= ( [{1{-}(1{-}0.70)^{3\times 0.36},1{-}(1{-}0.80)^{3\times 0.36}} ], [ (0.00)^{3\times 0.36},\\&\quad (0.00)^{3\times 0.36} ] )= ( { [ {0.7275,0.8241}], [ {0.00,0.00} ]} ), \end{aligned}$$$$\begin{aligned}&( { [ {a_{{11} _{(2)}} ,b_{{11} _{(2)}} }], [ {c_{{11} _{(2)}} ,d_{{11} _{(2)}} } ]} )\\&= ( [{1-(1-0.05)^{3\times 0.32},1-(1-0.10)^{3\times 0.32}} ],\\&\quad [ {(0.80)^{3\times 0.32},(0.90)^{3\times 0.32}} ] )= ( [ {0.0408,0.0961} ], \\&\quad [ {0.8071,0.9038} ] ) \end{aligned}$$And
$$\begin{aligned}&( { [ {a_{{11} _{(3)}} ,b_{{11} _{(3)}} } ], [ {c_{{11} _{(3)}} ,d_{{11} _{(3)}}} ]} )= ( [1{-}(1{-}0.01)^{3\times 0.32},\\&\quad 1-(1-0.05)^{3\times 0.32} ], [ {(0.85)^{3\times 0.32},(0.95)^{3\times 0.32}} ] )\\&\quad = ( { [ {0.0096,0.0480} ], [ {0.8555,0.9519} ]} ), \end{aligned}$$shown as follows:
$$\begin{aligned}&{\dot{\tilde{d}}_{11}}= \left( \left[ {1{-}\mathop \prod \limits _{k=1}^3 ( {1{-}a_{{11}_{\sigma (k)}} })^{w_k },1{-}\mathop \prod \limits _{k=1}^3 ( {1-b_{{11}_{\sigma (k)}} })^{w_k }} \right] ,\right. \nonumber \\&\left. \quad \left[ {\mathop \prod \limits _{k=1}^3 c_{{11}_{\sigma (k)}} ^{w_k },\mathop \prod \limits _{k=1}^3 d_{{11}_{\sigma (k)}} ^{w_k }} \right] \right) \\&=\Bigg ( [ 1-( {1-0.7275})^{0.243}\times ( {1-0.0480})^{0.514}\\&\quad \times ( {1-0.0096})^{0.243},1-( {1-0.8241})^{0.243}\\&\quad \times ( {1-0.0961})^{0.514}\times ( {1-0.0480})^{0.243} ],\\&\big [ ( {0.0000})^{0.243}\times ( {0.8071})^{0.514}\times ( {0.8555})^{0.243},\\&\quad ({0.0000})^{0.243}\times ( {0.9038})^{0.514}\times ( {0.9519})^{0.243} \big ]\Bigg ) \\&=( {\left[ {0.2908,0.3851} \right] ,\left[ {0.0000,0.0000} \right] }), \end{aligned}$$where the aggregating result \((\left[ {0.2908,0.3851} \right] ,\left[ {0.0000,0.0000} \right] )\) is incorrect due to the fact that there only exists \([ {c_{{11}_{(1)}} ,d_{{11}_{(1)}} } ]=\left[ {0.00,0.00} \right] \), which causes \(\mathop \prod \nolimits _{k=1}^3 c_{{11}_{\sigma (k)}} ^{w_k }=0\) and/or \(\mathop \prod \nolimits _{k=1}^3 d_{{11}_{\sigma (k)}} ^{w_k }=0\) without considering the other values of \([ {c_{{11} _{(2)}} ,d_{{11}_{(2)}} } ]=\left[ {0.80,0.90} \right] \) and \([ {c_{{11} _{(3)}} ,d_{{11} _{(3)}} } ]=\left[ {0.85,0.95} \right] \), where \(w_1 =0.243\), \(w_2 =0.514\) and \(w_3 =0.243\). Thus, the presented method in Makui et al. (2015b) gets the incorrect collective intuitionistic fuzzy decision matrix \(\dot{\tilde{D}} \) and gets an unreasonable preference order of the alternatives \(x_1 \), \(x_2 \) and \(x_3 \).
-
(2)
The drawback of Jin et al.’s method (Jin et al. 2014): Based on Eq. (25), we can get the collective intuitionistic fuzzy decision matrix \(D=( {{\tilde{\alpha }} _{ij} })_{3\times 3} \), where
$$\begin{aligned} D=\left[ {{\begin{array}{ccc} {( {\left[ {0.0399,0.0550} \right] ,\left[ {0.0000,0.0000} \right] })} &{} {( {\left[ {0.6437,0.8069} \right] ,\left[ {0.0205,0.0595} \right] })} &{} {( {\left[ {0.6511,0.8113} \right] ,\left[ {0.0037,0.0190} \right] })} \\ {( {\left[ {0.0482,0.0700} \right] ,\left[ {0.8380,0.8905} \right] })} &{} {( {\left[ {0.9554,0.9869} \right] ,\left[ {0.0012,0.0116} \right] })} &{} {( {\left[ {0.9252,0.9736} \right] ,\left[ {0.0007,0.0040} \right] })} \\ {( {\left[ {0.0784,0.1370} \right] ,\left[ {0.7394,0.7963} \right] })} &{} {( {\left[ {0.9816,0.9963} \right] ,\left[ {0.0002,0.0006} \right] })} &{} {( {\left[ {0.6528,0.7715} \right] ,\left[ {0.0002,0.0007} \right] })} \\ \end{array} }} \right] , \end{aligned}$$For example, we can see that the aggregated IVIFN in the first row and the first column of the collective intuitionistic fuzzy decision matrix D is \(( \left[ {0.0399,0.0550} \right] ,\left[ {0.0000,0.0000} \right] )\), which is obtained by aggregating the IVIFNs \(( {\left[ {0.70,0.80} \right] ,\left[ {0.00,0.00} \right] })\), \(( \left[ {0.05,0.10} \right] ,\left[ {0.80,0.90} \right] )\) and \(( {\left[ {0.01,0.05} \right] ,\left[ {0.85,0.95} \right] })\) in the first row and the first column of the decision matrices \(D_1 \), \(D_2 \) and \(D_3 \), respectively, based on Eq. (25), where
$$\begin{aligned}&( [ {a_{{11} _{(1)}} ,b_{{11} _{(1)}} } ], [ {c_{{11} _{(1)}} ,d_{{11} _{(1)}} } ] )= ( [1{-}(1{-}0.70)^{3\times 0.01},\\&\quad 1{-}(1{-}0.80)^{3\times 0.01} ], [ (0.00)^{3\times 0.01},\\&\quad (0.00)^{3\times 0.01} ] )= ( { [ {0.1026,0.1348} ], [ {0.00,0.00} ]} ), \end{aligned}$$$$\begin{aligned}&( { [ {a_{{11} _{(2)}} ,b_{{11} _{(2)}} } ], [ {c_{{11} _{(2)}} ,d_{{11} _{(2)}} } ]} )\\&= ( [{1-(1-0.05)^{3\times 0.01},1-(1-0.10)^{3\times 0.01}} ],\\&\quad [ {(0.80)^{3\times 0.01},(0.90)^{3\times 0.01}} ] )= ( [ {0.0046,0.0094} ],\\&\quad [ {0.9801,0.9905} ] ) \end{aligned}$$And
$$\begin{aligned}&( { [ {a_{{11} _{(3)}} ,b_{{11} _{(3)}} } ], [ {c_{{11} _{(3)}} ,d_{{11} _{(3)}} } ]} )\\&= ( [{1-(1-0.01)^{3\times 0.01},1-(1-0.05)^{3\times 0.01}} ],\\&\quad [ {(0.85)^{3\times 0.01},(0.95)^{3\times 0.01} ]} )= ( [ {0.0009,0.0046} ],\\&\qquad [ {0.9854,0.9953} ] ), \end{aligned}$$shown as follows:
$$\begin{aligned}&d_{11} =\left( \left[ {1{-}\mathop \prod \limits _{k=1}^3 ( {1{-}a_{{11} _{(k)}} })^{w_k },1{-}\mathop \prod \limits _{k=1}^3 ( {1{-}b_{{11} _{(k)}} })^{w_k }} \right] ,\right. \\&\left. \quad \left[ {\mathop \prod \limits _{k=1}^3 c_{{11} _{(k)}} ^{w_k },\mathop \prod \limits _{k=1}^3 d_{{11} _{(k)}} ^{w_k }} \right] \right) \\&\quad =\Bigg ( [1-( {1-0.1026})^{0.36}\times ( {1-0.0046})^{0.32}\\&\qquad \times ( {1-0.0009})^{0.32},1-( {1-0.1348})^{0.36}\\&\qquad \times ( {1-0.0094})^{0.32}\times ( {1-0.0046})^{0.32} ],\\&\qquad \big [ ( {0.0000})^{0.36}\times ( {0.9801})^{0.32}\times ( {0.9854})^{0.32},\\&\qquad ( {0.0000})^{0.36}\times ( {0.9905})^{0.32}\times ( {0.9953})^{0.32} \big ]\Bigg ) \\&\quad =( {\left[ {0.0399,0.0550} \right] ,\left[ {0.0000,0.0000} \right] }), \end{aligned}$$where the aggregating result \(( \left[ {0.0399,0.0550} \right] ,\left[ {0.0000,0.0000} \right] )\) is incorrect due to the fact that there only exists \([ {c_{{11} _{(1)}} ,d_{{11} _{(1)}} } ]=\left[ {0.00,0.00} \right] \), it causes \(\mathop \prod \nolimits _{k=1}^3 c_{{11} _{(k)}} ^{w_k }=0\) and/or \(\mathop \prod \nolimits _{k=1}^3 d_{{11} _{(k)}} ^{w_k }=0\) without considering the other values of \([ {c_{{11} _{(2)}} ,d_{{11} _{(2)}} } ]=\left[ {0.80,0.90} \right] \) and \([ {c_{{11} _{(3)}},d_{{11} _{(3)}} } ]=\left[ {0.85,0.95} \right] \). Thus, presented method in Jin et al. (2014) gets the incorrect collective intuitionistic fuzzy decision matrix D and gets an unreasonable preference order of the alternatives \(x_1 \), \(x_2 \) and \(x_3 \), as shown in Table 3.
6 Conclusions
In this paper, we have proposed a new fuzzy multi-attribute group decision making method based on the IVIFSs and the ERM. From the experimental results shown in Tables 1, 2 and 3, we can extract that the proposed method can overcome the drawbacks of Makui et al.’s method (Makui et al. 2015b) and Jin et al.’s method (Jin et al. 2014) for fuzzy multi-attribute group decision making. The proposed method moves us one step closer to the usage of multi-attribute group decision making in real-world situations and provides us with a useful way for group decision making problems in intuitionistic fuzzy environments. Therefore, in future, this method can be used for dealing with uncertainty in MADM problems such as project selection, manufacturing systems, pattern recognition, medical diagnosis and many other areas of management decision problems.
References
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Atanassov K, Gargov G (1989) Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31:343–349
Bellman RE, Zadeh LA (1970) Decision-making in a fuzzy environment. Manag Sci 17:B-141–B-164
Hashemi SS, Hajiagha SHR, Zavadskas EK, Mahdiraji HA (2016) Multicriteria group decision making with ELECTRE III method based on interval-valued intuitionistic fuzzy information. Appl Math Model 40(2):1554–1564
Hwang C-L, Yoon K (1981) Lecture notes in economics and mathematical systems: multiple attribute decision making: methods and application. Springer, New York
İntepe G, Bozdag E, Koc T (2013) The selection of technology forecasting method using a multi-criteria interval-valued intuitionistic fuzzy group decision making approach. Comput Ind Eng 65:277–285
Jin F, Pei L, Chen H, Zhou L (2014) Interval-valued intuitionistic fuzzy continuous weighted entropy and its application to multi-criteria fuzzy group decision making. Knowl Based Syst 59:132–141
Joshi D, Kumar S (2016) Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. Eur J Oper Res 248:183–191
Li Y, Deng Y, Chan FT, Liu J, Deng X (2014) An improved method on group decision making based on interval-valued intuitionistic fuzzy prioritized operators. Appl Math Model 38:2689–2694
Liu B, Chen Y, Shen Y, Sun H, Xu X (2014) A complex multi-attribute large-group decision making method based on the interval-valued intuitionistic fuzzy principal component analysis model. Soft Comput 18:2149–2160
Makui A, Gholamian MR, Mohammadi SE (2015a) A hybrid intuitionistic fuzzy multi-criteria group decision making approach for supplier selection. J Optim Ind Eng (in press)
Makui A, Gholamian MR, Mohammadi SE (2015b) Supplier selection with multi-criteria group decision making based on interval-valued intuitionistic fuzzy sets (case study on a project-based company). J Ind Syst Eng 8(4):19–38
Meng F, Chen X (2014) Interval-valued intuitionistic fuzzy multi-criteria group decision making based on cross entropy and 2-additive measures. Soft Comput 1–12
Szmidt E, Kacprzyk J (2000) Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst 114:505–518
Szmidt E, Kacprzyk J (2001) Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst 118:467–477
Tzeng G-H, Huang J-J (2011) Multiple attribute decision making: methods and applications. CRC Press, New York
Wan S-P, Dong J-Y (2015) Interval-valued intuitionistic fuzzy mathematical programming method for hybrid multi-criteria group decision making with interval-valued intuitionistic fuzzy truth degrees. Inf Fusion 26:49–65
Wei GW, Wang XR (2007) Some geometric aggregation operators based on interval-valued intuitionistic fuzzy sets and their application to group decision making. In: Proceedings of the international conference on computational intelligence and security. IEEE Computer Society Press, Washington, DC, pp 495–499
Xu ZS (2005) An overview of methods for determining OWA weights. Int J Intell Syst 20:843–865
Xu ZS (2007) Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis 22:215–219
Xu ZS, Chen J (2007) On geometric aggregation over interval-valued intuitionistic fuzzy information. In: Proceedings of the fourth international conference on fuzzy systems and knowledge discovery. IEEE Computer Society Press, Washington, DC, pp 466–471
Xu J, Shen F (2014) A new outranking choice method for group decision making under Atanassov’s interval-valued intuitionistic fuzzy environment. Knowl Based Syst 70:177–188
Yang J-B (2001) Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties. Eur J Oper Res 131:31–61
Yang J-B, Singh MG (1994) An evidential reasoning approach for multiple-attribute decision making with uncertainty. IEEE Trans Syst Man Cybern 24:1–18
Yang J-B, Xu D-L (2002) On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty. IEEE Trans Syst Man Cybern Part A Syst Hum 32:289–304
Yang J-B, Liu J, Wang J, Sii H-S, Wang H-W (2006) Belief rule-base inference methodology using the evidential reasoning approach—RIMER. IEEE Trans Syst Man Cybern Part A Syst Hum 36:266–285
Yang J-B, Wang Y-M, Xu D-L, Chin K-S (2006) The evidential reasoning approach for MADA under both probabilistic and fuzzy uncertainties. Eur J Oper Res 171:309–343
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning-I. Inf Sci 8:199–249
Zhang X, Liu J, Lei J, Yang BA (2008) The weak consistency of an interval-valued intuitionistic fuzzy matrix. In: IEEE international conference on fuzzy systems, FUZZ-IEEE 2008. IEEE world congress on computational intelligence, pp 1124–1127
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors whose names are listed in the publication certify that they have no affiliation with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this publication.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Mohammadi, S.E., Makui, A. Multi-attribute group decision making approach based on interval-valued intuitionistic fuzzy sets and evidential reasoning methodology. Soft Comput 21, 5061–5080 (2017). https://doi.org/10.1007/s00500-016-2101-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-016-2101-6