Valuation of European option under uncertain volatility model

Abstract

Valuation of an option plays an important role in modern finance. As the financial market for derivatives continues to grow, the progress and the power of option pricing models at predicting the value of option premium are under investigations. In this paper, we assume that the volatility of the stock price follows an uncertain differential equation and propose an uncertain counterpart of the Heston model. This study also focuses on deriving a numerical method for pricing a European option under uncertain volatility model, and some numerical experiments are presented. Numerical experiments confirm that the developed methods are very efficient.

1 Introduction

In 1931, Nobert Wiener presented a continuous stochastic process and after that the use of this process has made adorable changes in asset pricing.

This was the beginning of the way that guided Ito in 1943 to find stochastic calculus. In 1973, Black and Scholes (1973) provided a formula to price a specific derivative called option.

Derivatives are financial instruments that their values depend on the value of something else. Options are a type of financial derivatives. The value of an option is determined by the likelihood of change in price of underlying asset. Actually, it is a contract that gives its holder the right to buy or sell a prescribed asset (e.g., stock) for a specific price at a specific time. The prescribed price and the specific time are called strike price and maturity date, respectively. Options have two classifications, call option and put option. Finding the fair value of options is a problem that forces many researchers to discuss about it. Black–Scholes model is widely used in the asset pricing. But in this model, the volatility is assumed to be constant. To overcome this difficulty, several stochastic volatility models had been proposed in financial mathematics such as Hull and White model (1987), Stein and Stein model (1991), Heston model (1993) and SABR model. In these models, both stock price and volatility have stochastic dynamics. The Heston model as one of the most important stochastic volatility models could make a progress in the Black–Scholes–Merton model.

We have to notice that, in real life we need a large amount of historical data to estimate a probability distribution and it is a really tough job to get a large number of samples. Besides, in many cases there is no sample to determine a probability distribution. On the other hand, empirical studies showed that phenomena like stock price does not act like randomness or fuzziness. In these cases, we have to invite some domain experts to estimate the belief degree for each event. Degrees of belief formally represent the strength with which we believe the truth of various propositions (Huber and Schmidt-Petri 2009). Kahneman and Tversky (1979) showed that the belief degrees have much greater variances than frequency. So, the human’s belief degrees do not behave like probability distribution. In order to deal with uncertainty caused by human, Liu (2007) founded an uncertainty theory. Nowadays, uncertainty theory is a branch of mathematics. This theory is based on normality, duality, subadditivity and product axioms. In 2008, Liu (2008) proposed uncertain process and after that in 2009, he presented a canonical Liu process. Liu process is an uncertain counterpart of Wiener process. To describe an uncertain variable and an uncertain process, Liu introduced the concept of uncertainty distribution and inverse uncertainty distribution in 2014. Uncertain differential equation was proposed by Liu (2008) and used to model the stock price in 2009. Based on it, Chen and Liu (2010), Liu (2012), Yao (2013) and Yao and Chen (2013) designed some methods to solve the uncertain differential equations. Besides, Yao (2013b) proposed some numerical methods to estimate the integral of the solution. The existence and uniqueness theorem of solution of uncertain differential equation was proved by Chen and Liu (2010) and also, Liu (2009) presented stability of uncertain differential equation. In 2009, Liu (2009) introduced an uncertain stock model and obtained some option pricing formulas based on the model. Later, Peng and Yao (2011), Yu (2012), Chen et al. (2013), Yao (2015) and Ji and Zhou (2015) investigated widely in uncertain stock models. In 2011, Chen (2011) derived a formula for pricing American option.

In this paper, we propose a new stock model based on an assumption that the volatility of the stock follows an uncertain dynamic. Indeed, our model is an uncertain counterpart of Heston model. The volatility is a measure for variation of value of a stock model overall time of its performance in financial markets. Uncertain volatility is defined as an uncertain process in which the return variation dynamic includes an unpredictable shock in stock prices. Based on this model, some theorems are proved and we derive a numerical method for value of European option.

We organize the rest of our article as follows: In Sect. 2, we provide some definitions and theorems to introduce uncertainty theory. Uncertain calculus is briefly presented in Sect. 3, whereas in Sect. 4, uncertain differential equation is introduced. Some useful stock models are shown in Sect. 5. We present our stock model in Sect. 6. In Sect. 7, European call and put option pricing formulas are discussed. Finally, some algorithms and numerical results are provided in Sect. 8.

2 Preliminaries

In this section, we introduce some concepts about uncertainty theory by providing the following definitions and theorems.

Definition 1

(Liu 2007) Let L be a $\sigma$-algebra on a nonempty set ${\Gamma }$. Each element ${\Lambda }\in \mathcal{L}$ is called an event. A set function $\mathcal{M}:\mathcal{L}\rightarrow \left[ {0,1} \right]$ is called an uncertain measure if it satisfies the following axioms:

Axiom 1

(Normality Axiom) $\mathcal{M}\left\{ {\Gamma } \right\} =1$ for the universal set ${\Gamma }$.

Axiom 2

(Duality Axiom) $\mathcal{M}\left\{ {\Lambda } \right\} +\mathcal{M}\left\{ {{\Lambda }^{c}} \right\} =1$ for any event ${\Lambda }$.

Axiom 3

(Subadditivity Axiom) For every countable sequence of events ${\Lambda }_1 ,{\Lambda }_2 ,\ldots ,$ we have

$$\begin{aligned} \mathcal{M}\left\{ {\mathop \bigcup \limits _{i=1}^\infty {\Lambda }_i } \right\} \le \mathop \sum \limits _{i=1}^\infty \mathcal{M}\left\{ {{\Lambda }_i } \right\} . \end{aligned}$$

The triple $\left( {{\Gamma },\mathcal{L},\mathcal{M}} \right)$ is called an uncertainty space. A product uncertain measure was defined by Liu (2009), hence the fourth axiom of uncertainty theory released as following

Axiom 4

(Product Axiom) Let $\left( {{\Gamma }_k ,\mathcal{L}_k ,\mathcal{M}_k } \right)$ be uncertainty spaces for $k=1,2,\ldots ,n$. Then, the product uncertain measure $\mathcal{M}$ is an uncertain measure on product $\sigma$-algebra $\mathcal{L}_1 \times \mathcal{L}_2 \times \cdots \times \mathcal{L}_n$ satisfying

$$\begin{aligned} \mathcal{M}\left\{ {\mathop \prod \limits _{k=1}^n {\Lambda }_k } \right\} =\mathop {\min }\limits _{1\le k\le n} \mathcal{M}_k \left\{ {{\Lambda }_k } \right\} \end{aligned}$$

where ${\Lambda }_k$ are arbitrarily chosen events from $\mathcal{L}_k$ for $k=1,2,\ldots ,$ respectively.

Definition 2

(Liu 2007) An uncertain variable is a function X from an uncertainty space $\left( {{\Gamma },\mathcal{L},\mathcal{M}} \right)$ to the set of real numbers such that $\left\{ {X\in B} \right\}$ is an event for any Borel set B of real numbers.

Definition 3

(Liu 2007) An uncertainty distribution ${\Phi }$ of an uncertain variable is defined by

$$\begin{aligned} {\Phi }\left( x \right) =\mathcal{M}\left\{ {X\le x} \right\} \end{aligned}$$

for any real number x.

Definition 4

(Liu 2015) An uncertain variable X is called normal if it has a normal uncertainty distribution

$$\begin{aligned} {\Phi }\left( x \right) =\left( {1+\exp \left( {\frac{\pi \left( {\mu -x} \right) }{\sqrt{3}\sigma }} \right) } \right) ^{-1},\quad x\in {\mathbb {R}} \end{aligned}$$

denoted by $\mathcal{N}\left( {\mu ,\sigma } \right)$ where $\mu$ and $\sigma$ are real numbers with $\sigma >0$.

Definition 5

(Liu 2015) An uncertain variable is called lognormal if $\ln X$ is a normal uncertain variable $\mathcal{N}\left( {\mu ,\sigma } \right)$. In other words, a lognormal uncertain variable has an uncertainty distribution

$$\begin{aligned} {\Phi }\left( x \right) =\left( {1+\exp \left( {\frac{\pi \left( {\mu -\ln x} \right) }{\sqrt{3}\sigma }} \right) } \right) ^{-1},\quad x\ge 0 \end{aligned}$$

denoted by $L\mathcal{O}\mathcal{G}\mathcal{N}\left( {\mu ,\sigma } \right)$, where $\mu$ and $\sigma$ are real numbers with $\sigma >0$.

Definition 6

(Liu 2010) An uncertainty distribution ${\Phi }\left( x \right)$ is said to be regular if it is a continuous and strictly increasing function with respect to x at which $0<{\Phi }\left( x \right) <1$, and

$$\begin{aligned} {\lim }_{x\rightarrow -\infty } {\Phi }\left( x \right) =0, {\lim }_{x\rightarrow +\infty } {\Phi }\left( x \right) =1. \end{aligned}$$

Definition 7

(Liu 2007) Let X be an uncertain variable with regular uncertainty distribution ${\Phi }\left( x \right)$. Then, the inverse function ${\Phi }^{-1}\left( \alpha \right)$ is called the inverse uncertainty distribution of X.

Definition 8

(Liu 2010) The uncertain variables $X_1 ,X_2 ,\ldots ,X_n$ are said to be independent if

$$\begin{aligned} \mathcal{M}\left\{ {\mathop \bigcap \limits _{i=1}^n \left( {X_i \in B_i } \right) } \right\} =\mathop {\min }\limits _{1\le i\le n} \mathcal{M}\left\{ {X_i \in B_i } \right\} \end{aligned}$$

for any Borel sets $B_1 ,B_2 ,\ldots ,B_n$ of real numbers.

Theorem 1

(Liu 2010) Let $X_1 ,X_2 ,\ldots ,X_n$ be independent uncertain variables with regular uncertainty distributions ${\Phi }_1 ,{\Phi }_2 ,\ldots ,{\Phi }_n$, respectively. If $f\left( {X_1 ,X_2 ,\ldots ,X_n } \right)$ is strictly increasing with respect to $X_1 ,X_2 ,\ldots ,X_m$ and strictly decreasing with respect to $X_{m+1} ,X_{m+2} ,\ldots ,X_n$, then

$$\begin{aligned} X=f\left( {X_1 ,X_2 ,\ldots ,X_n } \right) \end{aligned}$$

has an inverse uncertainty distribution

$$\begin{aligned}&{\Psi }^{-1}\left( \alpha \right) =f\left( {\Phi }_1^{-1} \left( \alpha \right) ,\ldots ,{\Phi }_m^{-1} \left( \alpha \right) ,\right. \\&\left. {\Phi }_{m+1}^{-1} \left( {1-\alpha } \right) ,\ldots ,{\Phi }_n^{-1} \left( {1-\alpha } \right) \right) . \end{aligned}$$

Definition 9

(Liu 2007) Let X be an uncertain variable. Then, the expected value of X is defined by

$$\begin{aligned} E\left[ X \right] =\int \nolimits _0^{+\infty } \mathcal{M}\left\{ {X\ge x} \right\} dx-\int \nolimits _{-\infty }^0 \mathcal{M}\left\{ {X\le x} \right\} dx \end{aligned}$$

provided that at least one of the two integrals is finite.

Theorem 2

(Liu 2007) Let X be an uncertain variable with uncertainty distribution ${\Phi }$. Then

$$\begin{aligned} E\left[ X \right] =\mathop {\int }\nolimits _0^{+\infty } \left( {1-{\Phi }\left( x \right) } \right) dx-\mathop {\int }\nolimits _{-\infty }^0 {\Phi }\left( x \right) dx. \end{aligned}$$

Theorem 3

(Liu 2010) Let X be an uncertain variable with regular uncertainty distribution ${\Phi }$. Then, we have

$$\begin{aligned} E\left[ X \right] =\mathop {\smallint }\nolimits _0^1 {\Phi }^{-1}\left( \alpha \right) d\alpha . \end{aligned}$$

Theorem 4

(Liu and Ha 2010) Assume $X_1 ,X_2 ,\ldots ,X_n$ are independent uncertain variables with regular uncertainty distributions ${\Phi }_1 ,{\Phi }_2 ,\ldots ,{\Phi }_n$, respectively. If $f( X_1 ,X_2 ,\ldots ,X_n )$ is strictly increasing with respect to $X_1 ,X_2 ,\ldots ,X_m$ and strictly decreasing with respect to $X_{m+1} ,X_{m+2} ,\ldots ,X_n$, then $X=f\left( {X_1 ,X_2 ,\ldots ,X_n } \right)$

has an expected value below

$$\begin{aligned}&E\left[ X \right] =\mathop {\smallint }\nolimits _0^1 f\left( {\Phi }_1^{-1} \left( \alpha \right) ,\ldots ,{\Phi }_m^{-1} \left( \alpha \right) ,\right. \\&\left. {\Phi }_{m+1}^{-1} \left( {1-\alpha } \right) ,\ldots ,{\Phi }_n^{-1} \left( {1-\alpha } \right) \right) . \end{aligned}$$

3 Uncertain Process

This section presents the concept of uncertain process and stationary increment process.

Definition 10

(Liu 2008) Let $\left( {{\Gamma },\mathcal{L},\mathcal{M}} \right)$ be an uncertainty space and let T be a totally ordered set (e.g., time). An uncertain process is a function $X_t \left( \gamma \right)$ from $T\times \left( {{\Gamma },\mathcal{L},\mathcal{M}} \right)$ to the set of real numbers such that $\left\{ {X_t \in B} \right\}$ is an event for any Borel set B of real numbers at each $t\in T$.

Definition 11

(Liu 2014) An uncertain process $X_t$ is said to have an uncertainty distribution ${\Phi }_t \left( x \right)$ if at each time t, the uncertain variable $X_t$ has the uncertainty distribution ${\Phi }_t \left( x \right)$.

Definition 12

(Liu 2008) An uncertain process $X_t$ is said to have independent increments if

$$\begin{aligned} X_{t_1 } ,X_{t_2 } -X_{t_1 } ,\ldots ,X_{t_k } -X_{t_{k-1} } \end{aligned}$$

are independent uncertain variables where $t_1 ,t_2 ,\ldots ,t_k$ are any times with $t_1<t_2<\cdots <t_k$.

Definition 13

(Liu 2015) An uncertain process is said to have stationary increments if its increments are identically distributed uncertain variables whenever the time intervals have the same length. Also, it is said to be a stationary independent increment process if it has not only stationary increments but also independent increments.

Definition 14

(Liu 2009) Let $X_t$ be an uncertain process. For any partition of closed interval $\left[ {a,b} \right]$ with $a=t_1<t_2<\cdots <t_{k+1} =b$, the mesh written as

$$\begin{aligned} {\Delta }={\max }_{1\le i\le k} \left| {t_{i+1} -t_i } \right| . \end{aligned}$$

Then, the time integral of $X_t$ with respect to t is

$$\begin{aligned} \mathop {\smallint }\nolimits _a^b X_t dt={\lim }_{{\Delta }\rightarrow 0} \sum \limits _{i=1}^k X_{t_i } .\left( {t_{i+1} -t_i } \right) \end{aligned}$$

provided that the limit exists almost surely and is finite. $X_t$ is said to be time integrable.

4 Uncertain differential equation

Definition 15

(Liu 2009) An uncertain process $C_t$ is said to be a canonical Liu process if

(i):

$C_0 =0$ and almost all sample paths are Lipschitz continuous,

(ii):

$C_t$ has stationary and independent increments,

(iii):

every increment $C_{s+t} -C_s$ is a normal uncertain variable with expected value 0 and variance $t^{2}$. The uncertainty distribution of $C_t$ is

$$\begin{aligned} {\Phi }_t \left( x \right) =\left( {1+\exp \left( {-\frac{\pi x}{\sqrt{3}t}} \right) } \right) ^{-1}, x\in {\mathbb {R}} \end{aligned}$$

and its inverse uncertainty distribution is as follows

$$\begin{aligned} {\Phi }_t^{-1} \left( \alpha \right) =\frac{t\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }. \end{aligned}$$

Definition 16

(Liu 2015) Let $C_t$ be a canonical Liu Process. Then for any real numbers $\mu _1$ and $\sigma _1 >0$, the uncertain process

$$\begin{aligned} A_t =\mu _1 t+\sigma _1 C_t \end{aligned}$$

is called an arithmetic Liu process, where $\mu _1$ is the drift and $\sigma _1$ is the diffusion. Besides, the uncertain process

$$\begin{aligned} G_t =\hbox {exp}\left( {\mu _2 t+\sigma _2 C_t } \right) \end{aligned}$$

is called a geometric Liu process, where $\mu _2$ is the log-drift and $\sigma _2$ is the log-diffusion.

Definition 17

(Liu 2009) Let $X_t$ be an uncertain process and let $C_t$ be a canonical Liu process. For any partition of closed interval $\left[ {a,b} \right]$ with $a=t_1<t_2<\cdots <t_{k+1} =b$, the mesh written as

$$\begin{aligned} {\Delta }={\max }_{1\le i\le k} \left| {t_{i+1} -t_i } \right| . \end{aligned}$$

Then, Liu integral of $X_t$ with respect to $C_t$ is defined as

$$\begin{aligned} \mathop {\smallint }\nolimits _a^b X_t dC_t ={\lim }_{{\Delta }\rightarrow 0} \sum \limits _{i=1}^k X_{t_i } \cdot \left( {C_{t_{i+1} } -C_{t_i } } \right) \end{aligned}$$

provided that the limit exists almost surely and is finite. By this definition, the uncertain process $X_t$ is said to be integrable.

Definition 18

(Chen and Ralescu 2013) Let $C_t$ be a canonical Liu process and let $V_t$ be an uncertain process. If there exist uncertain processes $\mu _t$ and $\sigma _t$ such that

$$\begin{aligned} V_t =V_0 +\mathop {\smallint }\nolimits _0^t \mu _s ds+\mathop {\smallint }\nolimits _0^t \sigma _s dC_s \end{aligned}$$

for any $t\ge 0$, then $V_t$ is called a Liu process with drift $\mu _t$ and diffusion $\sigma _t$. Furthermore, $V_t$ has an uncertain differential

$$\begin{aligned} dV_t =\mu _t dt+\sigma _t dC_t . \end{aligned}$$

Definition 19

(Liu 2008) Suppose $C_t$ is a canonical Liu process, and f and g are two functions. Then,

$$\begin{aligned} dX_t =f\left( {t,X_t } \right) dt+g\left( {t,X_t } \right) dC_t \end{aligned}$$

(1)

is called an uncertain differential equation. A solution is a Liu process $X_t$ that satisfies (1) identically in t.

Theorem 5

(Wang 2012) Let f be a function of two variables, and $\sigma _t$ be an integrable process. Then, the uncertain differential equation

$$\begin{aligned} dX_t =f\left( {t,X_t } \right) dt+\sigma _t X_t^p dC_t , p\ne 1 \end{aligned}$$

has an analytic solution

$$\begin{aligned} X_t =\left( {Y_t +Z_t } \right) ^{\frac{1}{1-p}} \end{aligned}$$

where

$$\begin{aligned} Y_t =\left( {1-p} \right) \mathop {\smallint }\nolimits _0^t \sigma _s dC_s \end{aligned}$$

and $Z_t$ solves the uncertain differential equation

$$\begin{aligned} dZ_t =\left( {1-p} \right) \left( {Y_t +Z_t } \right) ^{-\frac{p}{1+p}}f\left( {t,\left( {Y_t +Z_t } \right) ^{\frac{1}{1-p}}} \right) dt \end{aligned}$$

with initial value $Z_0 =X_0^{1-p}$.

Theorem 6

(Existence and Uniqueness Theorem) (Chen and Liu 2010) The uncertain differential equation

$$\begin{aligned} dX_t =f\left( {t,X_t } \right) dt+g\left( {t,X_t } \right) dC_t \end{aligned}$$

has a unique solution if the coefficients $f\left( {t,x} \right)$ and $g\left( {t,x} \right)$ satisfy the linear growth condition

$$\begin{aligned} \left| {f\left( {t,x} \right) } \right| +\left| {g\left( {t,x} \right) } \right| \le L\left( {1+\left| x \right| } \right) , \quad \forall x\in {\mathbb {R}}, t\ge 0 \end{aligned}$$

and Lipschitz condition

$$\begin{aligned}&| {f({t,x})-f ({t,y})} |+|(g ({t,x})-g({t,y})| \\&\quad \le L |x-y|, \forall x,y\in {\mathbb {R}}, t\ge 0 \end{aligned}$$

for some constant L. Moreover, the solution is sample-continuous.

Definition 20

(Yao and Chen 2013) Let $\alpha$ be a number with $0<\alpha <1$. An uncertain differential equation

$$\begin{aligned} dX_t =f\left( {t,X_t } \right) dt+g\left( {t,X_t } \right) dC_t \end{aligned}$$

is said to have an $\alpha$-path $X_t^\alpha$ if it solves the corresponding ordinary differential equation

$$\begin{aligned} dX_t^\alpha =f\left( {t,X_t^\alpha } \right) dt+\left| {g\left( {t,X_t^\alpha } \right) } \right| {\Phi }^{-1}\left( \alpha \right) dt \end{aligned}$$

where ${\Phi }^{-1}\left( \alpha \right)$ is the inverse standard normal uncertainty distribution, i.e.,

$$\begin{aligned} {\Phi }^{-1}\left( \alpha \right) =\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }. \end{aligned}$$

In this case, $X_t$ is called a contour process.

Theorem 7

(Yao and Chen 2013) Let $X_t$ and $X_t^\alpha$ be the solution and $\alpha$-path of the uncertain differential equation

$$\begin{aligned} dX_t =f\left( {t,X_t } \right) dt+g\left( {t,X_t } \right) dC_t \end{aligned}$$

respectively. Then

$$\begin{aligned}&\mathcal{M}\left\{ {X_t \le X_t^\alpha , \forall t} \right\} =\alpha ,\\&\mathcal{M}\left\{ {X_t >X_t^\alpha , \forall t} \right\} =1-\alpha . \end{aligned}$$

Theorem 8

(Yao and Chen 2013) Let $X_t$ and $X_t^\alpha$ be the solution and $\alpha$-path of the uncertain differential equation

$$\begin{aligned} dX_t =f\left( {t,X_t } \right) dt+g\left( {t,X_t } \right) dC_t \end{aligned}$$

respectively. Then, the solution $X_t$ has an inverse uncertainty distribution ${\Psi }_t^{-1} \left( \alpha \right) =X_t^\alpha$.

Theorem 9

(Yao and Chen 2013) Let $X_t$ and $X_t^\alpha$ be the solution and $\alpha$-path of the uncertain differential equation

$$\begin{aligned} dX_t =f\left( {t,X_t } \right) dt+g\left( {t,X_t } \right) dC_t \end{aligned}$$

respectively. Then, for any monotone function J, we have

$$\begin{aligned} E\left[ {J\left( {X_t } \right) } \right] ={\mathop {\smallint }\nolimits } _0^1 J\left( {X_t^\alpha } \right) d\alpha . \end{aligned}$$

5 Some stock models in uncertain markets

In 2009, Liu (2009) presented a stock model based on an assumption that the stock price follows uncertain differential equation and proposed an uncertain stock model as follows

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{dB_t }{B_t }=rdt } \\ {\frac{dS_t }{S_t }=\mu dt+\sigma dC_t } \\ \end{array} }} \right. \end{aligned}$$

where $B_t$ is the bond price, $S_t$ denotes stock price, r is the riskless interest rate, $\mu$ is the log-drift, $\sigma$ is the log-diffusion and $C_t$ is a canonical Liu process.

Also, Peng and Yao (2011) proposed a stock model as an uncertain counterpart of Black–Karasinski’s model in 2011. This model is as follows

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{dB_t }{B_t }=rdt } \\ {dS_t =\left( {m-\alpha S_t } \right) dt+\sigma S_t dC_t } \\ \end{array} }} \right. \end{aligned}$$

where $r,m,\alpha ,$ and $\sigma$ are some constants and $C_t$ is a canonical Liu process.

In both models, the interest rate is constant. But in 2015, Yao (2015) assumed that both interest rate and the stock price follow uncertain differential equation and gave an uncertain stock model as follows

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{dr_t }{r_t }=\mu _1 dt+\sigma _1 dC_{1t} } \\ {\frac{dS_t }{S_t }=\mu _2 dt+\sigma _2 dC_2 } \\ \end{array} }} \right. \end{aligned}$$

where $\mu _1$ and $\sigma _1$ are the log-drift and log-diffusion of the interest rate $r_t$, respectively, and $\mu _2$ and $\sigma _2$ are the log-drift and log-diffusion of the stock price $S_t$, respectively. In this model, $C_{1t}$ and $C_{2t}$ are independent canonical Liu processes.

In 2016, Sun and Su (2016) proposed a mean-reverting stock model with floating interest rate. They released this stock model based on the presumption that the stock model fluctuates periodically around a certain price in the long term. The Sun-Su’s model is as follows

$$\begin{aligned} \left\{ {{\begin{array}{l} {dr_t =\left( {m_1 -a_1 r_t } \right) dt+\sigma _1 dC_{1t} } \\ {dS_t =\left( {m_2 -a_2 S_t } \right) dt+\sigma _2 dC_{2t} } \\ \end{array} }} \right. \end{aligned}$$

where $m_1 ,m_2 ,a_1 ,a_2 ,\sigma _1$ and $\sigma _2$ are some real numbers with $a_1 ,a_2 \ne 0$.

6 The stock model with an uncertain volatility

There is one point that can be seen in all mentioned models which is the constant volatility. In this section, we present a new stock model as an uncertain counterpart of Heston model. Uncertain volatility is described as an uncertain process which lets the volatility follows canonical Liu process and makes the value of the option much better adapted to the realities of the market.

We consider that a stock price can be described by an uncertain model if the behavior of the stock price satisfies uncertain differential equation and present the stock model with uncertain volatility as follows

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\begin{array}{l} {dB_t =rB_t dt } \\ {dS_t =S_t \left( {\mu dt+\sqrt{\sigma _t }dC_{1t} } \right) } \\ \end{array} }} \\ {d\sigma _t =\kappa \left( {\theta -\sigma _t } \right) dt+\sigma \sqrt{\sigma _t }dC_{2t} } \\ \end{array} }} \right. \end{aligned}$$

(2)

where $C_{1t}$ and $C_{2t}$ are two independent canonical Liu processes. Other uncertain variables of the model are defined as follows

• $S_t :$ the stock price at time t

• $B_t :$ the bond price at time t

• $\sigma _t :$ volatility of the stock price

• r :  risk-free interest rate

• $\mu :$ the log-drift of the stock price

• $\kappa :$ rate of reversion to the long-term price variance

• $\theta :$ long-term price variance

• $\sigma :$ volatility of the volatility.

We assume that $\theta >0$ and $\kappa >0$. Indeed, the volatility dynamic is just same as Chen and Gao’s model (2013) for an uncertain interest rate model.

The matrix form of Eq. (2) is given by

$$\begin{aligned} \left( {{\begin{array}{c} {dB_t } \\ {dS_t } \\ {d\sigma _t } \\ \end{array} }} \right) =\left( {{\begin{array}{c} {rB_t } \\ {\mu S_t } \\ {\kappa \left( {\theta -\sigma _t } \right) } \\ \end{array} }} \right) dt+\left( {{\begin{array}{c} 0 \\ {\sqrt{\sigma _t }S_t } \\ {\sigma \sqrt{\sigma _t }} \\ \end{array} }} \right) \left( {{\begin{array}{c} 0 \\ {dC_{1t} } \\ {dC_{2t} } \\ \end{array} }} \right) \end{aligned}$$

(3)

where $C_t =\left( {C_0 ,C_{1t} ,C_{2t} } \right) ^{T}$.

Three-compartment model Eq. (3) would be expressed as follows

$$\begin{aligned} dX_t =F\left( {t,X_t } \right) dt+G\left( {t,X_t } \right) dC_t \end{aligned}$$

(4)

where

$$\begin{aligned} F=\left( {f_1 ,f_2 ,f_3 } \right) ^{T}\hbox { and }G=\left( {g_1 ,g_2 ,g_3 } \right) ^{T}. \end{aligned}$$

Besides, we have

$$\begin{aligned}&dX_t =\left( {dB_t ,dS_t ,d\sigma _t } \right) ^{T},\\&F\left( {t,X_t } \right) =\left( {rB_t ,\mu S_t ,\kappa \left( {\theta -\sigma _t } \right) } \right) \hbox { and}\\&G\left( {t,X_t } \right) =\left( {0,\sqrt{\sigma _t }S_t ,\sigma \sqrt{\sigma _t }} \right) . \end{aligned}$$

Eq. (4) now appears like one-dimensional uncertain differential equation.

There is no analytic solution for model (2). In order to overcome this problem, we provide the following theorem for applying the $\alpha$-path method as a numerical method.

Theorem 10

Suppose that $Y_t$ and $Y_t^\alpha$ be the solution and $\alpha$-path of an uncertain differential equation

$$\begin{aligned} dY_t =f_1 \left( {t,Y_t } \right) dt+g_1 \left( {t,Y_t } \right) dC_{1t} \end{aligned}$$

respectively. Let $\left| {h\left( {t,y} \right) } \right|$ be a continuous increasing function. Then, the solution $X_t$ of an uncertain differential equation

$$\begin{aligned} dX_t =f_2 \left( {t,X_t } \right) dt+h\left( {t,Y_t } \right) g_2 \left( {t,X_t } \right) dC_{2t} \end{aligned}$$

is a contour process with an $\alpha$-path $X_t^\alpha$ that solves the corresponding ordinary differential equation

$$\begin{aligned} dX_t^\alpha =f_2 \left( {t,X_t^\alpha } \right) dt+\left| {h\left( {t,Y_t^\alpha } \right) g_2 \left( {t,X_t^\alpha } \right) } \right| {\Phi }^{-1}\left( \alpha \right) dt \end{aligned}$$

where

$$\begin{aligned} {\Phi }^{-1}\left( \alpha \right) =\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }, \quad \alpha \in \left( {0,1} \right) \end{aligned}$$

and $C_{1t}$ and $C_{2t}$ are independent canonical Liu processes. In other words

$$\begin{aligned} \mathcal{M}\left\{ {X_t \le X_t^\alpha , \forall t} \right\}= & {} \alpha \\ \mathcal{M}\left\{ {X_t >X_t^\alpha , \forall t} \right\}= & {} 1-\alpha . \end{aligned}$$

Proof

Given $\alpha \in \left( {0,1} \right)$. We define the following sets

$$\begin{aligned} P= & {} \left\{ {t\in \left[ {0,T} \right] | h\left( {t,Y_t } \right) g_2 \left( {t,X_t } \right) \ge 0} \right\} \\ N= & {} \left\{ {t\in \left[ {0,T} \right] | h\left( {t,Y_t } \right) g_2 \left( {t,X_t } \right) <0} \right\} \end{aligned}$$

Then $P\cup N=\left[ {0,T} \right]$. Also, write

$$\begin{aligned} {\Sigma }_1^+= & {} \left\{ \gamma \big |\frac{dC_{2t} }{dt}\le {\Phi }^{-1}\left( \alpha \right) , \forall t\in \left( {0,s} \right] \right\} ,\\ {\Sigma }_1^-= & {} \left\{ \gamma \big |\frac{dC_{2t} \left( \gamma \right) }{dt}\ge {\Phi }^{-1}\left( {1-\alpha } \right) , \forall t\in \left( {0,s} \right] \right\} ,\\ {\Lambda }_1^+= & {} \left\{ \lambda \big |\frac{dC_{1t} \left( \lambda \right) }{dt}\le {\Phi }^{-1}\left( \alpha \right) , \forall t\in \left( {0,c} \right] \right\} \end{aligned}$$

and

$$\begin{aligned} {\Lambda }_1^+ =\left\{ \lambda |\frac{dC_{1t} \left( \lambda \right) }{dt}\ge {\Phi }^{-1}\left( {1-\alpha } \right) , \forall t\in \left( {0,c} \right] \right\} . \end{aligned}$$

Notice that $s, c\in \left[ {0,T} \right]$. P and N are disjoint sets, and $C_{1t}$ and $C_{2t}$ are independent increment processes, and by assumption, we have

$$\begin{aligned}&\mathcal{M}\left\{ {{\Sigma }_1^+ } \right\} =\alpha ,\\&\mathcal{M}\left\{ {{\Sigma }_1^- } \right\} =\alpha ,\\&\mathcal{M}\left\{ {{\Sigma }_1^+ \cap {\Sigma }_1^- } \right\} =\alpha ,\\&\mathcal{M}\left\{ {{\Lambda }_1^+ } \right\} =\alpha ,\\&\mathcal{M}\left\{ {{\Lambda }_1^- } \right\} =\alpha ,\\&\mathcal{M}\left\{ {{\Lambda }_1^+ \cap {\Lambda }_1^- } \right\} =\alpha \end{aligned}$$

and

$$\begin{aligned} \mathcal{M}\left\{ {{\Sigma }_1^+ \cap {\Lambda }_1^+ } \right\}= & {} \min \left\{ {\mathcal{M}\left\{ {\varSigma _1^+ } \right\} ,\mathcal{M}\left\{ {\varLambda _1^+ } \right\} } \right\} =\alpha ,\\ \mathcal{M}\left\{ {{\Sigma }_1^- \cap {\Lambda }_1^- } \right\}= & {} \min \left\{ {\mathcal{M}\left\{ {\varSigma _1^- } \right\} ,\mathcal{M}\left\{ {\varLambda _1^- } \right\} } \right\} =\alpha \end{aligned}$$

and

$$\begin{aligned} \mathcal{M}\left\{ {\left( {{\Sigma }_1^+ \cap {\Lambda }_1^+ } \right) \cap \left( {{\Sigma }_1^- \cap {\Lambda }_1^- } \right) } \right\} =\alpha . \end{aligned}$$

For any $\beta \in \left( {{\Sigma }_1^+ \cap {\Lambda }_1^+ } \right) \cap \left( {{\Sigma }_1^- \cap {\Lambda }_1^- } \right)$, we have

$$\begin{aligned}&h\left( {t,Y_t \left( \beta \right) } \right) g_2 \left( {t,X_t \left( \beta \right) } \right) \frac{dC_{2t} }{dt}\\&\quad \le \left| {h\left( {t,Y_t^\alpha } \right) g\left( {t,X_t^\alpha } \right) } \right| {\Phi }^{-1}\left( \alpha \right) dt, \forall t\in \left[ {0,T} \right] . \end{aligned}$$

Then

$$\begin{aligned} X_t \left( \beta \right) \le X_t , \forall t\in \left[ {0,T} \right] . \end{aligned}$$

Hence, we can write

$$\begin{aligned}&\mathcal{M}\left\{ {X_t \le X_t^\alpha , \forall t\in \left[ {0,T} \right] } \right\} \nonumber \\&\quad \ge \mathcal{M}\left\{ {\left( {{\Sigma }_1^+ \cap {\Lambda }_1^+ } \right) \cap \left( {{\Sigma }_1^- \cap {\Lambda }_1^- } \right) } \right\} =\alpha . \end{aligned}$$

(5)

Besides, define

$$\begin{aligned} {\Sigma }_2^+= & {} \left\{ \gamma |\frac{dC_{2t} }{dt}>{\Phi }^{-1}\left( \alpha \right) , \forall t\in \left( {0,s} \right] \right\} ,\\ {\Sigma }_2^-= & {} \left\{ \gamma |\frac{dC_{2t} \left( \gamma \right) }{dt}<{\Phi }^{-1}\left( {1-\alpha } \right) , \forall t\in \left( {0,s} \right] \right\} ,\\ {\Lambda }_2^+= & {} \left\{ \lambda |\frac{dC_{1t} \left( \lambda \right) }{dt}>{\Phi }^{-1}\left( \alpha \right) , \forall t\in \left( {0,c} \right] \right\} \end{aligned}$$

and

$$\begin{aligned} {\Lambda }_2^+ =\left\{ \lambda |\frac{dC_{1t} \left( \lambda \right) }{dt}<{\Phi }^{-1}\left( {1-\alpha } \right) , \forall t\in \left( {0,c} \right] \right\} . \end{aligned}$$

Notice that $s, c\in \left[ {0,T} \right]$. P and N are disjoint sets and $C_{1t}$ and $C_{2t}$ are independent increment processes and by assumption, we have

$$\begin{aligned}&\mathcal{M}\left\{ {{\Sigma }_2^+ } \right\} =1-\alpha ,\\&\mathcal{M}\left\{ {{\Sigma }_2^- } \right\} =1-\alpha .,\\&\mathcal{M}\left\{ {{\Sigma }_2^+ \cap {\Sigma }_2^- } \right\} =1-\alpha ,\\&\mathcal{M}\left\{ {{\Lambda }_2^+ } \right\} =1-\alpha ,\\&\mathcal{M}\left\{ {{\Lambda }_2^- } \right\} =1-\alpha ,\\&\mathcal{M}\left\{ {{\Lambda }_2^+ \cap {\Lambda }_2^- } \right\} =1-\alpha \end{aligned}$$

and

$$\begin{aligned} \mathcal{M}\left\{ {{\Sigma }_2^+ \cap {\Lambda }_2^+ } \right\}= & {} \min \left\{ {\mathcal{M}\left\{ {\varSigma _2^+ } \right\} ,\mathcal{M}\left\{ {\varLambda _2^+ } \right\} } \right\} =1-\alpha ,\\ \mathcal{M}\left\{ {{\Sigma }_2^- \cap {\Lambda }_2^- } \right\}= & {} \min \left\{ {\mathcal{M}\left\{ {\varSigma _2^- } \right\} ,\mathcal{M}\left\{ {\varLambda _2^- } \right\} } \right\} =1-\alpha \end{aligned}$$

and

$$\begin{aligned} \mathcal{M}\left\{ {\left( {{\Sigma }_2^+ \cap {\Lambda }_2^+ } \right) \cap \left( {{\Sigma }_2^- \cap {\Lambda }_2^- } \right) } \right\} =1-\alpha . \end{aligned}$$

For any $\beta \in \left( {{\Sigma }_2^+ \cap {\Lambda }_2^+ } \right) \cap \left( {{\Sigma }_2^- \cap {\Lambda }_2^- } \right)$, since

$$\begin{aligned}&h\left( {t,Y_t \left( \beta \right) } \right) g_2 \left( {t,X_t \left( \beta \right) } \right) \frac{dC_{2t} }{dt}\\&\quad >\left| {h\left( {t,Y_t^\alpha } \right) g\left( {t,X_t^\alpha } \right) } \right| {\Phi }^{-1}\left( \alpha \right) dt, \forall t\in \left[ {0,T} \right] , \end{aligned}$$

we have

$$\begin{aligned} X_t \left( \beta \right) >X_t^\alpha , \forall t\in \left[ {0,T} \right] . \end{aligned}$$

Hence, we can write

$$\begin{aligned}&\mathcal{M}\left\{ {X_t >X_t^\alpha , \forall t\in \left[ {0,T} \right] } \right\} \nonumber \\&\quad \ge \mathcal{M}\left\{ {\left( {{\Sigma }_2^+ \cap {\Lambda }_2^+ } \right) \cap \left( {{\Sigma }_2^- \cap {\Lambda }_2^- } \right) } \right\} =1-\alpha . \end{aligned}$$

(6)

Since

$$\begin{aligned}&\mathcal{M}\left\{ {X_t \le X_t^\alpha , \forall t\in \left[ {0,T} \right] } \right\} \\&\quad +\mathcal{M}\left\{ {X_t >X_t^\alpha , \forall t\in \left[ {0,T} \right] } \right\} \le 1, \end{aligned}$$

From inequalities (5) and (6), we have

$$\begin{aligned} \mathcal{M}\left\{ {X_t \le X_t^\alpha , \forall t\in \left[ {0,T} \right] } \right\}= & {} \alpha ,\\ \mathcal{M}\left\{ {X_t >X_t^\alpha , \forall t\in \left[ {0,T} \right] } \right\}= & {} 1-\alpha . \end{aligned}$$

$\square$

7 European option pricing

In this section, we consider a European option and propose a numerical method to price this type of option based on our proposed stock model (2).

In order to value a European option price, we define this type of contract.

We recall that a European call option is a contract that gives its holder the right but not the obligation to buy a prescribed stock for a certain price at a determined time in future.

We now consider a European call option with a strike price K and maturity date T. Then, its valuation is as follows

$$\begin{aligned} C=e^{-rT}E\left[ {\left( {S_T -K} \right) ^{+}} \right] \end{aligned}$$

where $S_T$ is the stock price at time T.

Theorem 11

The valuation of a European call option of the stock price (2) with expiration date T and strike price K is as follows

$$\begin{aligned} C=e^{-rT}\int \nolimits _0^1 \left( {S_T^\alpha -K} \right) ^{+}d\alpha \end{aligned}$$

where

$$\begin{aligned} S_T^\alpha =S_0 \exp \left( {\mu T+\mathop {\smallint }\nolimits _0^T \frac{\sqrt{\sigma _t^\alpha }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }dt} \right) \end{aligned}$$

and $\sigma _t^\alpha$ is the solution of the following ordinary differential equation

$$\begin{aligned} d\sigma _t^\alpha =\kappa \left( {\theta -\sigma _t^\alpha } \right) dt+\frac{\sigma \sqrt{\sigma _t^\alpha }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }dt, \end{aligned}$$

$\kappa , \theta$ and $\sigma$ are some constants.

Proof

According to Theorem 10, $S_t$ is a contour process and its $\alpha$-path is the solution of the following ordinary differential equation

$$\begin{aligned} dS_t^\alpha =S_t^\alpha \left( \mu +\frac{\sqrt{\sigma _t^\alpha }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) dt \end{aligned}$$

and $\sigma _t^\alpha$ is the solution of the following ordinary differential equation

$$\begin{aligned} d\sigma _t^\alpha =\kappa \left( {\theta -\sigma _t^\alpha } \right) dt+\frac{\sigma \sqrt{\sigma _t^\alpha }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }dt. \end{aligned}$$

Besides, the price of a European call option is

$$\begin{aligned} C=e^{-rT}E\left[ {\left( {S_T -K} \right) ^{+}} \right] . \end{aligned}$$

Then, by Theorems 3 and 9, the theorem is proved. $\square$

Another classification of a European option is a put option. Indeed, a European put option is a contract that gives its holder the right but not the obligation to sell a prescribed stock for a certain price at a determined time in future.

Consider a European put option with a strike price K and maturity date T. Then, its valuation is

$$\begin{aligned} P=e^{-rT}E\left[ {\left( {K-S_T } \right) ^{+}} \right] \end{aligned}$$

where $S_T$ is the stock price at time T.

Theorem 12

The valuation of a European put option of the stock price (2) with expiration date T and strike price K is as follows

$$\begin{aligned} P=e^{-rT}\int \nolimits _0^1 \left( {K-S_T^\alpha } \right) ^{+}d\alpha \end{aligned}$$

where

$$\begin{aligned} S_T^\alpha =S_0 \exp \left( {\mu T+\int \nolimits _0^T \frac{\sqrt{\sigma _t^\alpha }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }dt} \right) \end{aligned}$$

and $\sigma _t^\alpha$ is the solution of the following ordinary differential equation

$$\begin{aligned} d\sigma _t^\alpha =\kappa \left( {\theta -\sigma _t^\alpha } \right) dt+\frac{\sigma \sqrt{\sigma _t^\alpha }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }dt, \end{aligned}$$

$\kappa , \theta$ and $\sigma$ are some constants.

Proof

Based on Theorem 10, $S_t$ is a contour process and its $\alpha$-path is the solution of the following ordinary differential equation

$$\begin{aligned} dS_t^\alpha =S_t^\alpha \left( \mu +\frac{\sqrt{\sigma _t^\alpha }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }\right) dt \end{aligned}$$

and $\sigma _t^\alpha$ is the solution of the following ordinary differential equation

$$\begin{aligned} d\sigma _t^\alpha =\kappa \left( {\theta -\sigma _t^\alpha } \right) dt+\frac{\sigma \sqrt{\sigma _t^\alpha }\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }dt. \end{aligned}$$

Besides, the price of a European put option is

$$\begin{aligned} P=e^{-rT}E\left[ {\left( {K-S_T } \right) ^{+}} \right] . \end{aligned}$$

Then, by Theorems 3 and 9, the theorem is proved. $\square$

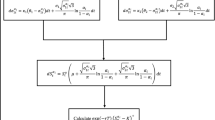
8 Numerical results

In this section, we propose an algorithm to calculate the price of European option under the stock model (2). Some numerical examples are provided which their parameters are given by Dunn et al. (2014)

The following algorithm calculates the European call option under the stock price model (2).

Step 0: Fix the exercise date at time T, fix the volatility at time zero $\sigma _0^\alpha =\sigma _0$ and choose $N=100$ and set $i=1,2,\ldots ,N-1$.

Step 1: Set $\alpha \leftarrow \frac{i}{N}$.

Step 2: set $i\leftarrow i+1$.

Step 3: Solve the corresponding ordinary differential equation via Runge–Kutta scheme (Shen and Yang 2015),

$$\begin{aligned} d\sigma _t^{\alpha _i } =\kappa \left( {\theta -\sigma _t^{\alpha _i } } \right) dt+\frac{\sigma \sqrt{\sigma _t^{\alpha _i } }\sqrt{3}}{\pi }\ln \frac{\alpha _i }{1-\alpha _i }dt \end{aligned}$$

and

$$\begin{aligned} dS_t^{\alpha _i } =S_t^\alpha \left( \mu +\frac{\sqrt{\sigma _t^{\alpha _i } }\sqrt{3}}{\pi }\ln \frac{\alpha _i }{1-\alpha _i }\right) dt, \end{aligned}$$

respectively. Then obtain $\sigma _T^{\alpha _i }$ and $S_T^{\alpha _i }$ for $i=1,2,\ldots ,99$.

Step 4: Calculate the positive deviation between the stock price and strike price at time T

$$\begin{aligned} \left( {S_T^{\alpha _i } -K} \right) ^{+}=\hbox {max}\left( {0,S_T^{\alpha _i } -K}\right) . \end{aligned}$$

Step 5: Calculate

$$\begin{aligned} \exp \left( {-rT} \right) \left( {S_T^{\alpha _i } -K} \right) ^{+}. \end{aligned}$$

If $i<N-1$, return to step 2.

Step 6: Calculate the value of the European call option

$$\begin{aligned} C\leftarrow \frac{1}{N-1}\exp \left( {-rT} \right) \sum \nolimits _{i=1}^{N-1} \left( {S_T^{\alpha _i } -K} \right) ^{+}. \end{aligned}$$

Consider a European put option under the stock model (2). According to Theorem 12, the following algorithm is designed to price a mentioned option.

Step 0: Fix the exercise date at time T, fix the volatility at time zero $\sigma _0^\alpha =\sigma _0$ and choose $N=100$ and set $i=1,2,\ldots ,N-1$.

Step 1: Set $\alpha \leftarrow \frac{i}{N}$.

Step 2: set $i\leftarrow i+1$.

Step 3: Solve the corresponding ordinary differential equation via Runge–Kutta scheme proposed by Shen and Yang (2015),

$$\begin{aligned} d\sigma _t^{\alpha _i } =\kappa \left( {\theta -\sigma _t^{\alpha _i } } \right) dt+\frac{\sigma \sqrt{\sigma _t^{\alpha _i } }\sqrt{3}}{\pi }\ln \frac{\alpha _i }{1-\alpha _i }dt \end{aligned}$$

and

$$\begin{aligned} dS_t^{\alpha _i } =S_t^\alpha \left( \mu +\frac{\sqrt{\sigma _t^{\alpha _i } }\sqrt{3}}{\pi }\ln \frac{\alpha _i }{1-\alpha _i }\right) dt, \end{aligned}$$

respectively. Then obtain $\sigma _T^{\alpha _i }$ and $S_T^{\alpha _i }$ for $i=1,2,\ldots ,99$.

Step 4: Calculate the positive deviation between the stock price and strike price K at time T

$$\begin{aligned} \left( {K-S_T^{\alpha _i } } \right) ^{+}=\hbox {max}\left( {0,K-S_T^{\alpha _i } } \right) . \end{aligned}$$

Step 5: Calculate

$$\begin{aligned} \exp \left( {-rT} \right) \left( {K-S_T^{\alpha _i } } \right) ^{+}. \end{aligned}$$

If $i<N-1$, return to step 2.

Step 6: Calculate the value of the European put option

$$\begin{aligned} P\leftarrow \frac{1}{N-1}\exp \left( {-rT} \right) \sum \limits _{i=1}^{N-1} \left( {K-S_T^{\alpha _i } } \right) ^{+}. \end{aligned}$$

Example 1

Assume that spot price is 425.73, maturity date is 24 days, the risk-free interest rate and the log-drift are $6.50 \times 10^{-4}$ and strike price is 395. Let $\kappa =2$, $\theta =5.16\times 10^{-5}$, $\sigma _0 =0.001$ and $\sigma =2.38\times 10^{-3}$. Then, the price of a European call option is $C=30.75$.

Table 1 summarizes the parameter that we used for comparison between uncertain stock model and stochastic stock model. The option price via the Heston model in stochastic form is estimated by Monte Carlo simulation method.

Table 1 Parameters

The European call option prices on uncertain stock model and stochastic stock model are outlined in Table 2.

Table 2 European call option valuation comparison

Table 3 European put option valuation comparison

Fig. 1

Price of European call option via stochastic and uncertain approaches for a 24-day period

Fig. 2

Price of European put option via stochastic and uncertain approaches for a 24-day period

Next, we provide an example for a European put option and compare the value of put options in two approaches, stochastic and uncertain approaches.

Example 2

Assume that spot price is 425.73, maturity date is 24 days, the risk-free interest rate and the log-drift are $6.50\times 10^{-4}$ and strike price is 470. Let $\kappa =2$, $\theta =5.16\times 10^{-5}$, $\sigma _0 =0.001$ and $\sigma =2.38\times 10^{-3}$. Then, the price of a European put option is $P=44.25$.

According to Tables 2, 3, Figs. 1, and 2, we can see that the European option prices under uncertain approach is close enough to the stochastic approach. Based on the data given by Dunn et al. (2014), the uncertain approach performs much better than the classical stochastic approach; see Dunn et al. (2014). Actually, it is so close to the actual price.

9 Remarks and conclusions

In this paper, we assumed that the volatility of the stock price follows an uncertain differential equation instead of being constant and proposed a new stock model which is an uncertain counterpart of the Heston model. Furthermore, we present a numerical method for obtaining a European option price under the proposed uncertain model. The numerical results indicate our model has high pricing accuracy and efficiency. In the future, it could be interesting to continue the investigation of the effect uncertain interest rate models have on the option prices.