Abstract
Uncertain finance is an application of uncertainty theory in the field of finance. This paper investigates the uncertain financial market based on the exponential Ornstein–Uhlenbeck model. European option pricing formulas and American option pricing formulas are derived via the \(\alpha \)-path method. Finally, some mathematical properties of the uncertain option pricing formulas are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Black and Shocles (1973) and Merton (1973) used the geometric Brownian motion to construct a theory for pricing the options. From then on, Black–Scholes formula has been pivotal to the growth and success of financial engineering.
As we all know, when using probability theory, a fundamental premise is that the estimated probability distribution is close enough to the long-run cumulative frequency. Otherwise, the law of large numbers is no longer valid and probability theory is no longer applicable. However, in many situations, there are not enough (or even no) historical data. Then we have to invite some domain experts to evaluate their belief degree that each event will occur. In order to model human belief degrees, uncertainty theory was established by Liu (2007) and refined by Liu (2010a). Nowadays, uncertainty theory has become a branch of axiomatic mathematics with diverse applications such as uncertain logic (Li and Liu 2009), uncertain risk analysis (Liu 2010c), uncertain set (Liu 2010b, 2013a) and uncertain game (Yang and Gao 2013, 2014). In order to describe dynamic uncertain systems, (Liu 2008) introduced uncertain process. Besides, Liu (2009) designed canonical Liu process which could be seen as a counterpart of Brownian motion. Based on canonical Liu process, Liu introduced uncertain calculus (Liu 2009) and uncertain differential equations (Liu 2008). After that, Chen and Liu (2010) proved the existence and uniqueness theorem of solution of uncertain differential equation. The concept of stability of uncertain differential equation was presented by Liu (2009). Later on Yao et al. (2013) proved some stability theorems of uncertain differential equation. Chen and Liu (2010), Liu (2012) and Yao (2013a) developed many methods to solve the uncertain differential equations. Furthermore, Yao and Chen (2013) designed the \(\alpha \)-path method, which produced an inverse uncertainty distribution of the solution. Based on \(\alpha \)-path, Yao (2013b) presented some formulas to calculate the extreme value, first hitting time, and time integral of solution of uncertain differential equation.
As a different doctrine, based on the assumption that stock price follows a geometric canonical process, uncertainty theory was first introduced into finance by Liu (2009) in 2009. And Liu (2009) also proposed an uncertain stock model and derived its European option price formulas. Later on, Chen (2011) studied American option pricing formulas for uncertain stock market, Sun and Chen (2013) derived Asian option price formulas, and Yao (2015) proved a no-arbitrage theorem for this type of uncertain stock model. In addition, Peng and Yao (2010) proposed a different uncertain stock model and derived some option price formulas. Liu et al. (2012) proposed an uncertain currency model and explored some mathematical properties of it. Under the assumption of short interest rate following uncertain processes, Chen and Gao (2013) derived the term-structure equation to value the zero-coupon bond. Besides, Jiao and Yao (2015) investigated another type of uncertain interest rate model. For exploring the recent developments of uncertain finance, the readers may consult (Liu 2013b) and the book by Liu (2015).
Peng–Yao stock model (Peng and Yao 2010) incorporated a general economic behavior: mean reversion. That is, when the stock price is too high, the price tends to fall more likely; when the stock price is too low, the price tends to rise more likely. However, this model is linear mean reversion. In this paper, we shall use a nonlinear mean reversion, assuming that the stock price follows uncertain counterpart of the exponential Ornstein–Uhlenbeck model. European option pricing formulas and American option pricing formulas are derived, respectively. Furthermore, some mathematical properties are discussed.
The rest of the paper is organized as follows. Some preliminary concepts of uncertain process are recalled in “Preliminaries” section. The exponential Ornstein–Uhlenbeck model for uncertain markets is formulated in “Exponential Ornstein–Uhlenbeck model” section. “European option price” section gives European option pricing formulas and discusses some properties of the formulas. “American opition price” section gives American option pricing formulas and discusses some properties of the formulas. Finally, a brief summary is given in “Conclusion ” section.
Preliminaries
Uncertainty theory was established by Liu (2007) and refined by Liu (2010a). Nowadays, uncertainty theory has become a branch of axiomatic mathematics for modelling human belief degrees. In this section, we will introduce some basic results in uncertainty theory. For more detailed expositions of uncertainty theory with applications (Gao 2013; Liu 2013a, b, 2014), the readers may consult Liu’s recent book (Liu 2015).
Definition 1
(Liu 2007) Let \({\mathcal {L}}\) be a \(\sigma \)-algebra on a nonempty set \(\varGamma \). A set function \({\mathcal {M}}: {\mathcal {L}}\rightarrow [0,1]\) is called an uncertain measure if it satisfies the following axioms:
-
Axiom 1. (Normality Axiom) \({\mathcal {M}}\{\varGamma \}=1\) for the universal set \(\varGamma \).
-
Axiom 2. (Duality Axiom) \({\mathcal {M}}\{\varLambda \}+{\mathcal {M}}\{\varLambda ^{c}\}=1\) for any event \(\varLambda \).
-
Axiom 3. (Subadditivity Axiom) For every countable sequence of events \(\varLambda _1,\varLambda _2,\ldots ,\) we have
$$\begin{aligned}&{\mathcal {M}}\left\{ \bigcup _{i=1}^{\infty }\varLambda _i\right\} \le \sum _{i=1}^{\infty }{\mathcal {M}}\{\varLambda _i\}. \end{aligned}$$
Besides, in order to provide the operational law, (Liu 2009) defined the product uncertain measure on the product \(\sigma \)-algebre \({\mathcal {L}}\) as follows.
-
Axiom 4. (Product Axiom) Let \((\varGamma _k,{\mathcal {L}}_k,{\mathcal {M}}_k)\) be uncertainty spaces for \(k=1, 2, \ldots \) The product uncertain measure \({\mathcal {M}}\) is an uncertain measure satisfying
$$\begin{aligned}&\displaystyle {\mathcal {M}}\left\{ \prod _{k=1}^\infty \varLambda _k\right\} =\bigwedge _{k=1}^\infty {\mathcal {M}}_k\{\varLambda _k\} \end{aligned}$$
where \(\varLambda _k\) are arbitrarily chosen events from \({\mathcal {L}}_k\) for \(k=1, 2, \ldots \), respectively.
Definition 2
(Liu 2007) An uncertain variable is a function from an uncertainty space \((\varGamma ,{\mathcal {L}},{\mathcal {M}})\) to the set of real numbers, such that, for any Borel set B of real numbers, the set
is an event.
In order to describe uncertain variables in practice, the concept of uncertainty distribution was introduced.
Definition 3
(Liu 2007) The uncertainty distribution of an uncertain variable \(\xi \) is defined as
for any real number \(x\).
An uncertainty distribution \(\varPhi (x)\) is said to be regular if its inverse function \(\varPhi ^{-1}(\alpha )\) exists and is unique for each \(\alpha \in (0,1)\). And \(\varPhi ^{-1}(\alpha )\) is called the inverse uncertainty distribution of \(\xi \). In this paper, we assume that all the payoffs are characterized by regular uncertain variables.
Definition 4
(Liu 2009) The uncertain variables \(\xi _1,\xi _2,\ldots ,\xi _m\) are said to be independent if
for any Borel sets \(B_1,B_2,\ldots ,B_m\) of real numbers.
The operational law of uncertain variables was proposed by Liu (2010c) to calculate the inverse uncertainty distribution of strictly monotonous function.
Theorem 1
(Liu 2010c) Let \(\xi _1,\xi _2,\ldots ,\xi _n\) be independent uncertain variables with uncertainty distributions \(\varPhi _1,\varPhi _2,\ldots ,\varPhi _n\), respectively. If the function \(f(x_1,x_2,\ldots , x_n)\) is strictly increasing with respect to \(x_1,x_2,\ldots ,x_m\) and strictly decreasing with \(x_{m+1},x_{m+2},\ldots ,x_n\), then
is an uncertain variable with inverse uncertainty distribution
Definition 5
(Liu 2007) Let \(\xi \) be an uncertain variable. Then the expected value of \(\xi \) is defined as
provided that at least one of the two integral is finite.
If \(\xi \) is a regular uncertain variable with uncertainty distribution \(\varPhi \), then its expected value can be briefed as
Definition 6
(Liu 2008) Let \(T\) be an index set and let \((\varGamma ,{\mathcal {L}},{\mathcal {M}})\) be an uncertainty space. An uncertain process is a measurable function from \(T\times (\varGamma ,{\mathcal {L}},{\mathcal {M}})\) to the set of real numbers, i.e., for each \(t\in T\) and any Borel set \(B\),
is an event.
Definition 7
(Liu 2008) An uncertain process \(X_t\) is said to have independent increments if
are independent uncertain variables where \(t_0\) is the initial time and \(t_1,t_2,\ldots ,t_k\) are any time with \(t_0<t_1 < \cdots < t_k\).
Definition 8
(Liu 2008) An uncertain process \(X_t\) is said to have stationary increments if, for any given \(t>0\), the increments \(X_{s+t}-X_{s}\) are identically distributed uncertain variables for all \(s>0\).
Definition 9
(Liu 2009) An uncertain process \(C_t\) is said to be a canonical process if
-
(i)
\(C_0=0\) and almost all sample paths are Lipschitz continuous,
-
(ii)
\(C_t\) has stationary and independent increments,
-
(iii)
every increment \(C_{s+t}-C_s\) is a normal uncertain variable with expected value 0 and variance \(t^2\), whose uncertainty distribution is
$$\begin{aligned} \varPhi (x)=\left( 1+\exp \left( \frac{-\pi x}{\sqrt{3}t}\right) \right) ^{-1},\ x\in \mathfrak {R}. \end{aligned}$$
Definition 10
(Liu 2009) Let \(X_t\) be an uncertain process and let \(C_t\) be a canonical Liu process. For any partition of closed interval \([a,b]\) with \(a=t_1<t_2< \cdots < t_{k+1}=b\), the mesh is written as
Then Liu integral of \(X_t\) with respect to \(C_t\) is defined as
provided that the limit exists almost surely and is finite. In this case, the uncertain process \(X_t\) is said to be integrable.
Definition 11
(Liu 2008) Suppose \(C_t\) is a canonical Liu process, and \(f\) and \(g\) are two functions. Then
is called an uncertain differential equation. A solution is a Liu process \(X_t\) that satisfies the equation identically in \(t\).
Definition 12
(Yao and Chen 2013) Let \(\alpha \) be a number with \(0<\alpha <1\). An uncertain differential equation
is said to have an \(\alpha \)-path \(X_t^{\alpha }\) if it solves the corresponding ordinary differential equation
where \(\varPhi ^{-1}(\alpha )\) is the inverse uncertainty distribution of standard normal uncertain variable, i.e.,
Theorem 2
(Yao and Chen 2013) Let \(X_t\) and \(X_t^{\alpha }\) be the solution and \(\alpha \)-path of the uncertain differential equation
respectively. Then the solution \(X_t\) has an inverse uncertainty distribution
Theorem 3
(Yao and Chen 2013) Let \(X_t\) and \(X_t^{\alpha }\) be the solution and \(\alpha \)-path of the uncertain differential equation
respectively. Then for any monotone function \(J\), we have
Theorem 4
(Yao 2013b) Let \(X_t\) and \(X_t^{\alpha }\) be the solution and \(\alpha \)-path of the uncertain differential equation
respectively. Then for any time \(s>0\) and strictly increasing function \(J(x)\), the supremum
has an inverse uncertainty distribution
Theorem 5
(Yao 2013b) Let \(X_t\) and \(X_t^{\alpha }\) be the solution and \(\alpha \)-path of the uncertain differential equation
respectively. Then for any time \(s>0\) and strictly decreasing function \(J(x)\), the supremum
has an inverse uncertainty distribution
Exponential Ornstein–Uhlenbeck model
In this section, we give the exponential Ornstein–Uhlenbeck model for uncertain markets.
Let \(X_t\) be the stock price and \(Y_t\) be the bond price. Suppose that the stock price \(X_t\) follows a geometric canonical process. Then Liu’s stock model (Liu 2008) is written as follows,
where \(r\) is the riskless interest rate, \(\mu \) is the stock drift, \(\sigma \) is the stock diffusion, and \(C_t\) is a canonical process. This model represents that the stocks have constant expected rate of return.
Besides, Peng–Yao’s stock model (Peng and Yao 2010) has the following form
where \(r>0, m>0, \alpha >0\) and \(\sigma >0\) are constants. This model incorporates a general economic behavior: mean reversion. That is, when the stock price is too high, the price tends to fall more likely; when the stock price is too low, the price tends to rise more likely. However, this model is linear mean reversion. In the sequel, we shall give the following nolinear model
where \(r>0, c>0, \sigma >0\) and \(\mu \) are constants. For \(c=0\), it is clearly Liu’s stock model (1). This model is the exponential Ornstein–Uhlenbeck model.
Now, we use the \(\alpha \)-path’s method to discuss the exponent OU model under the uncertain environment.
Theorem 6
Suppose that the stock price follows the model
where \(X_t\) represents the stock price at the moment \(t\). Then the \(\alpha \)-path of \(X_t\) is
Proof
By Definition 12, we have
So
The above ordinary differential equation has a solution
Then
The \(\alpha \)-path’s formula of \(X_t\) is verified.
European option price
A European option gives one the right, but not the obligation, to buy or sell a stock at a specified time for a specified price. Suppose that a European call option has a strike price \(K\) and an expiration time \(T\). If \(X_T\) is the final price of the underlying stock, then the payoff from buying a European call option is \((X_T-K)^{+}\). Considering the time value of money resulted from the bond, the present value of this payoff is \(\exp (-rT)(X_T-K)^{+}\) . Hence the European call option should be the expected present value of the payoff. Then this option has a price
Theorem 7
(European call option pricing formula) Suppose a European call option for the stock model (3) has a strike price \(K\) and an expiration time \(T\). Then the European call option pricing formula is
where
Proof
By Theorem 3, we have
Letting
we have
where
Then
The European call option pricing formula is verified.
Theorem 8
(Monotonicity of European call option pricing model) Suppose the stock price follows the stock model (3), which has a strike price \(K\) and an expiration time \(T\). Then \(f_c\) has the following properties:
-
1.
\(f_c\) is a decreasing function of \(K\);
-
2.
\(f_c\) is a decreasing function of \(r\);
-
3.
\(f_c\) is an increasing function of \(X_0\).
Proof
-
1.
By equation (4) we get assertion clearly.
-
2.
Since \(\exp (-rt)\) is a decreasing function of \(r\), the result is obvious.
-
3.
Let
$$\begin{aligned} G&= \exp \left( \exp (-\mu cT)\ln X_0+(1-\exp (-\mu cT))\right. \\&\left. \left( \frac{1}{c}+\frac{\sigma \sqrt{3}}{\mu c\pi }\ln \frac{\alpha }{1-\alpha }\right) \right) . \end{aligned}$$Then
$$\begin{aligned} f_c=\exp (-rT)\int _0^1 (G-K)^+ \mathrm{d}\alpha . \end{aligned}$$Since
$$\begin{aligned} \frac{\mathrm{d}G}{\mathrm{d}X_0}&= \exp \left( \!(1\!-\!\exp (\!-\!\mu cT))\left( \frac{1}{c}\!+\!\frac{\sigma \sqrt{3}}{\mu c\pi }\ln \frac{\alpha }{1\!-\!\alpha }\right) \right) \\&\quad \frac{\mathrm{d}\exp (\exp (-\mu cT)\ln X_0)}{\mathrm{d}X_0}\\&= \exp \left( (1-\exp (-\mu cT))\left( \frac{1}{c}+\frac{\sigma \sqrt{3}}{\mu c\pi }\ln \frac{\alpha }{1-\alpha }\right) \right. \\&\left. -\,\mu cT+(\exp (-\mu cT)-1)\ln X_0\frac{}{}\!\right) \\&> 0. \end{aligned}$$It is obvious that \(f_c\) is an increasing function of \(X_0\) since \(G\) is an increasing function of \(X_0\). The Monotonicity of European call option pricing formula is verified.
Suppose that a European put option has a strike price \(K\) and an expiration time \(T\). If \(X_T\) is the final price of the underlying stock, then the payoff from buying a European put option is \((K-X_T)^+\). Considering the time value of money resulted from the bond, the present value of this payoff is \(\exp (-rT)(K-X_T)^+\). Hence the European call option should be the expected present value of the payoff. Then this option has a price
Theorem 9
(European put option pricing formula) Suppose a European call option for the stock model (3) has a strike price \(K\) and an expiration time \(T\). Then the European put option pricing formula is
where
Proof
By Theorem 3, we have
Let
we have
where
So
The European put option pricing formula is verified.
Theorem 10
(Monotonicity of European put option pricing model) Suppose the stock price follows the stock model (3), which has a strike price \(K\) and an expiration time \(T\). Then \(f_p\) has the following properties:
-
1.
\(f_p\) is a decreasing function of \(K\);
-
2.
\(f_p\) is a decreasing function of \(r\);
-
3.
\(f_p\) is a decreasing function of \(X_0\).
Proof
The proof is omitted here for it is similar to that of Theorem 8.
American opition price
An American option gives one the right, but not the obligation, to buy or sell a stock before a specified time for a specified price. Suppose that an American call option has a strike price \(K\) and an expiration time \(T\). If \(X_T\) is the final price of the underlying stock, then the payoff from buying an American call option is the supremum of \((X_t-K)^+\) over the time interval \([0,T]\). Considering the time value of money resulted from the bond, the present value of this payoff is the supremum of \(\exp (-rt)(X_t-K)^+\). Hence an American call option should be the expected present value of the payoff. Then this option has a price
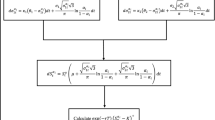
Theorem 11
(American call option pricing formula) Suppose an American call option for the stock model (3) has a strike price \(K\) and an expiration time \(T\). Then the American call option pricing formula is
Proof
We note that \(\exp (-rt)(X_t-K)^{+}\) is an increasing function of \(X_t\). According to Theorem 4, we get that the inverse distribution function of \(\sup \nolimits _{0\le t\le T}\exp (-rt)(X_t-K)^{+}\) is
From Theorem 6, we have
Thus we get
So
The American call option pricing formula is verified.
Theorem 12
(Monotonicity of American call option pricing model) Suppose the stock price follows the stock model (3), which has a strike price \(K\) and an expiration time \(T\). Then \(F_c\) has the following properties:
-
1.
\(F_c\) is a decreasing function of \(K\);
-
2.
\(F_c\) is a decreasing function of \(r\);
-
3.
\(F_c\) is an increasing function of \(T\);
-
4.
\(F_c\) is an increasing function of \(X_0\).
Proof
The proof is omitted here for it is similar to that of Theorem 8.
Suppose that an American put option has a strike price \(K\) and an expiration time \(T\). If \(X_T\) is the final price of the underlying stock, then the payoff from buying an American put option is the supremum of \((K-X_t)^+\) over the time interval \([0,T]\). Considering the time value of money resulted from the bond, the present value of this payoff is the supremum of \(\exp (-rt)(K-X_t)^+\). Hence an American call option should be the expected present value of the payoff. Then this option has a price
Theorem 13
(American put option pricing formula) Suppose an American put option for the stock model (3) has a strike price \(K\) and an expiration time \(T\). Then the American put option pricing formula is
Proof
We note that \(\exp (-rt)(K-X_t)^{+}\) is an decreasing function of \(X_t\). According to Theorem 5, we get that the inverse distribution function of \(\sup \limits _{0\le t\le T}\exp (-rt)(X_t-K)^{+}\) is
From Theorem 6, we have
Thus we get
So
The American put option pricing formula is verified.
Theorem 14
(Monotonicity of American put option pricing model) Suppose the stock price follows the stock model (3), which has a strike price \(K\) and an expiration time \(T\). Then \(F_p\) has the following properties:
-
1.
\(F_p\) is an increasing function of \(K\);
-
2.
\(F_p\) is a decreasing function of \(r\);
-
3.
\(F_p\) is an increasing function of \(T\);
-
4.
\(F_p\) is a decreasing function of \(X_0\).
Proof
The proof is omitted here for it is similar to that of Theorem 8.
Conclusion
In this paper, we investigated the option pricing problems for uncertain financial market. European option price formulas and American option price formulas are calculated by the \(\alpha \)-path method for the exponential Ornstein–Uhlenbeck model. At the same time, some properties of these formulas are discussed.
References
Black, F., & Shocles, M. (1973). The pricing of option and corporate liabilities. Journal of Political Economy, 81, 637–654.
Chen, X. (2011). American option pricing formula for uncertain financial market. International Journal of Operations Research, 8(2), 32–37.
Chen, X., & Liu, B. (2010). Existence and uniqueness theorem for uncertain differential equations. Fuzzy Optimization and Decision Making, 9(1), 69–81.
Chen, X., & Gao, J. (2013). Uncertain term structure model of interest rate. Soft Computing, 17(4), 597–604.
Gao, J. (2013). Uncertain bimatrix game with applications. Fuzzy Optimization and Decision Making. doi:10.1007/s10700-012-9145-6.
Jiao, D., & Yao, K. (2015). An interest rate model in uncertain environment. Soft Computing. doi:10.1007/s00500-014-1301-1.
Li, X., & Liu, B. (2009). Hybrid logic and uncertain logic. Journal of Uncertain Systems, 3(2), 83–94.
Liu, B. (2007). Uncertainty theory (2nd ed.). Berlin: Springer.
Liu, B. (2008). Fuzzy process, hybrid process and uncertain process. Journal of Uncertain Systems, 2(1), 3–16.
Liu, B. (2009). Some research problems in uncertainty theory. Journal of Uncertain Systems, 3(1), 3–10.
Liu, B. (2010a). Uncertainty theory: A branch of mathematics for modeling human uncertainty. Berlin: Springer.
Liu, B. (2010b). Uncertain set theory and uncertain inference rule with application to uncertain control. Journal of Uncertain Systems, 4(2), 83–98.
Liu, B. (2010c). Uncertain risk analysis and uncertain reliability analysis. Journal of Uncertain Systems, 4(3), 163–170.
Liu, B. (2013a). A new definition of independence of uncertain sets. Fuzzy Optimization and Decision Making, 12(4), 451–461.
Liu, B. (2013b). Toward uncertain finance theory. Journal of Uncertainty Analysis and Applications, 1. Article 1.
Liu, B. (2014). Uncertain random graph and uncertain random network. Journal of Uncertain Systems, 8(2), 3–12.
Liu, B. (2015). Uncertainty theory (4th ed.). Berlin: Springer.
Liu, Y. (2012). An analytic method for solving uncertain differential equations. Journal of Uncertain Systems, 6(3), 181–186.
Liu, Y., Chen, X., & Ralescu, D. A. (2012). Uncertain currency model and currency option pricing. International Journal of Intelligent Systems (published).
Merton, R. (1973). Theory of rational option pricing. Bell Journal Economics & Management Science, 4(1), 141–183.
Peng, J., & Yao, K. (2010). A new option pricing model for stocks in uncertainty markets. International Journal of Operations Research, 7(4), 213–224.
Sun, J., & Chen, X. (2013). Asian option pricing formula for uncertain financial market. http://orsc.edu.cn/online/130511.
Yang, X., & Gao, J. (2013). Uncertain differential games with application to capitalism. Journal of Uncertainty Analysis and Applications, 1. Aticle 17.
Yang, X., & Gao, J. (2014). Uncertain core for coalitional game with uncertain payoffs. Journal of Uncertain Systems, 8(2), 13–21.
Yao, K., & Chen, X. (2013). A numerical method for solving uncertain differential equations. Journal of Intelligent and Fuzzy Systems, 25(3), 825–832.
Yao, K., Gao, J., & Gao, Y. (2013). Some stability theorems of uncertain differential equation. Fuzzy Optimization and Decision Making, 12(1), 3–13.
Yao, K. (2013a). A type of uncertain differential equations with analytic solution. Journal of Uncertainty Analysis and Applications, 1. Article 8.
Yao, K. (2013b). Extreme value and integral of solution of uncertain differential equation. Journal of Uncertainty Analysis and Applications, 1. Article 2.
Yao, K. (2015). A no-arbitrage theorem for uncertain stock model. Fuzzy Optimization and Decision Making. doi:10.1007/s10700-014-9198-9.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by National Natural Science Foundation of China (Grant No. 61074193 and 61374082).
Rights and permissions
About this article
Cite this article
Dai, L., Fu, Z. & Huang, Z. Option pricing formulas for uncertain financial market based on the exponential Ornstein–Uhlenbeck model. J Intell Manuf 28, 597–604 (2017). https://doi.org/10.1007/s10845-014-1017-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-014-1017-1