A quantum-inspired version of the nearest mean classifier

Abstract

We introduce a framework suitable for describing standard classification problems using the mathematical language of quantum states. In particular, we provide a one-to-one correspondence between real objects and pure density operators. This correspondence enables us: (1) to represent the nearest mean classifier (NMC) in terms of quantum objects, (2) to introduce a quantum-inspired version of the NMC called quantum classifier (QC). By comparing the QC with the NMC on different datasets, we show how the first classifier is able to provide additional information that can be beneficial on a classical computer with respect to the second classifier.

1 Introduction

Quantum machine learning aims at merging the methods from quantum information processing and pattern recognition to provide new solutions for problems in the areas of pattern recognition and image understanding (Schuld et al. 2014a; Wittek 2014; Wiebe et al. 2015). In the first aspect, the research in this area is focused on the application of the methods of quantum information processing (Miszczak 2012) for solving problems related to classification and clustering Trugenberger (2002), Caraiman and Manta (2012). One of the possible directions in this field is to provide a representation of computational models using quantum mechanical concepts. From the other perspective, the methods for classification developed in computer engineering are used to find solutions for problems such as quantum-state discrimination (Helstrom 1976; Chefles 2000; Hayashi et al. 2005; Lu and Braunstein 2014), which are tightly connected with the recent developments in quantum cryptography.

Using quantum states for the purpose of representing patterns is naturally motivated by the possibility of exploiting quantum algorithms to boost the computational intensive parts of the classification process. In particular, it has been demonstrated that quantum algorithms can be used to improve the time complexity of the k-nearest neighbor (kNN) method. Using the algorithms presented in Wiebe et al. (2015), it is possible to obtain polynomial reductions in query complexity in comparison with the corresponding classical algorithm. Such an approach has been exploited by various authors. In Tanaka and Tsuda (2008), the authors propose an extension of Gaussian mixture models by using the statistical mechanics point of view. In their approach, the probability density functions of conventional Gaussian mixture models are expressed by density matrix representations. On the other hand, in Ostaszewski et al. (2015), the authors utilize the quantum representation of images to construct measurements used for classification. Such approach might be particularly useful for the physical implementation of the classification procedure on quantum machines.

In the last few years, many efforts have been made to apply the quantum formalism to non-microscopic contexts (Aerts and D’Hooghe 2009; Aerts et al. 2013; Chiang et al. 2013; Eisert et al. 1999; Nagel 1963; Nagy and Nagy 2016; Ohya and Volovich 2011; Schwartz et al. 2005; Sozzo 2015; Stapp 1993) and to signal processing (Eldar and Oppenheim 2002). Moreover, some attempts to connect quantum information to pattern recognition can be found in Schuld et al. (2014a), Schuld et al. (2014b), Schuld et al. (2014c). An exhaustive survey and bibliography of the developments concerning the applications of quantum computing in computational intelligence are provided in Manju and Nigam (2014), Wittek (2014). Even if these results seem to suggest some possible computational advantages of an approach of this sort, an extensive and universally recognized treatment of the topic is still missing (Schuld et al. 2014a; Lloyd et al. 2014, 2013).

Also, this paper is motivated by the idea of using quantum formalism in a non-standard domain that consists in solving classification problems on datasets of classical objects. The main contribution of our work is the introduction of a new framework to encode the classification process by means of the mathematical language of density matrices (Beltrametti et al. 2014b, a). We show that this representation leads to two different developments: (i) It enables us to provide a representation of the nearest mean classifier (NMC) in terms of quantum objects; (ii) it can be used to introduce a quantum-inspired version of the NMC, that we call quantum classifier (QC), which can be considered (similarly as the NMC) to be a minimum distance classifier. This allows us a detailed comparison between NMC and QC. In particular, we will show that QC provides additional information about the data distribution and, in different cases, an improvement in the performance on a classical computer.

The paper is organized as follows. In Sect. 2, the basic notions of quantum information and pattern recognition are introduced. In Sect. 3, we formalize a correspondence between arbitrary two-feature patterns and pure density operators and we define the notion of density pattern. In Sect. 4, we provide a representation of NMC by using density patterns and by the introduction of an ad hoc definition of the distance between quantum states. Section 5 is devoted to the description of a new quantum classifier QC that does not have a classical counterpart in the standard classification process. Numerical simulations for both QC and NMC are presented, and particular benefits in favor of the first classifier are exploited. In Sect. 6, a geometrical idea to generalize the model to arbitrary n-feature patterns is proposed. Finally, Sect. 7 presents concluding remarks and suggests further developments.

2 Representing classical and quantum information quantities

In the standard quantum information theory (Bennett and Shor 1998; Shannon 1948), the states of physical systems are described by unit vectors and their evolution is expressed in terms of unitary matrices (i.e., quantum gates). However, this representation can be applied for an ideal case only, because it does not take into account some unavoidable physical phenomena, such as interactions with the environment and irreversible transformations. In the modern quantum information theory (Jaeger 2007, 2009; Wilde 2013), another approach is adopted. The states of physical systems are described by density operators—also called mixed states (Aharonov et al. 1998; Chiara et al. 2004; Freytes et al. 2010)—and their evolution is described by quantum operations. The space $\varOmega _n$ of density operators for n-dimensional system consists of positive semidefinite matrices with unit trace.

A quantum state can be pure or mixed. We say that a state of a physical system is pure if it represents “maximal” information about the system, i.e., information that cannot be improved by further observations. A probabilistic mixture of pure states is said to be a mixed state. Generally, both pure and mixed states are represented by density operators that are positive and Hermitian operators (with unitary trace) living in a n-dimensional complex Hilbert space $\mathcal {H}$. Formally, a density operator $\rho$ is pure iff $\text {tr}(\rho ^2)=1$ and it is mixed iff $\text {tr}(\rho ^2)<1$.

If we confine ourselves to the two-dimensional Hilbert space $\mathcal {H}$, a suitable representation of an arbitrary density operator $\rho \in \varOmega _2$ is provided by

$$\begin{aligned} \begin{aligned} \rho&=\frac{1}{2}(I+r_1\sigma _1+r_2\sigma _2+r_3\sigma _3)\\&=\frac{1}{2} \begin{pmatrix}1+r_3 &{} r_1-ir_2 \\ r_1+ir_2 &{} 1-r_3 \end{pmatrix}, \end{aligned} \end{aligned}$$

(1)

where $\sigma _i$ are the Pauli matrices. This expression is useful when providing a geometrical representation of $\rho$. Indeed, each density operator $\rho \in \varOmega _2$ can be geometrically represented as a point of a radius-one sphere centered in the origin (the so-called Bloch sphere), whose coordinates (i.e., Pauli components) are $r_i$ (with $\sum _ir_i^2\le 1$). By using the generalized Pauli matrices (Bertlmann and Krammer 2008; Kimura 2003), it is also possible to provide a geometrical representation for an arbitrary n-dimensional density operator, as it will be showed in Sect. 6. Again, by restricting to a two-dimensional Hilbert space, points on the surface of the Bloch sphere represent pure states, while inner points represent mixed states.

Quantum formalism turns out to be very useful not only in the microscopic scenario but also to encode classical data. This has naturally suggested several attempts to represent the standard framework of machine learning through the quantum formalism (Lloyd et al. 2013; Schuld et al. 2014a). In particular, pattern recognition (Webb and Copsey 2011; Duda et al. 2000) is the scientific discipline which deals with theories and methodologies for designing algorithms and machines capable of automatically recognizing “objects” (i.e., patterns) in noisy environments. Some typical applications are multimedia document classification, remote-sensing image classification, and people identification using biometrics traits such as fingerprints.

A pattern is a representation of an object. The object can be a concrete one (i.e., an animal), and the pattern recognition task could be to identify the kind of animal or an abstract one (i.e., a facial expression), and the task could be to identify the emotion expressed by the facial expression. The pattern is characterized via a set of measurements called features.¹ Features can assume the forms of categories, structures, names, graphs, or, most commonly, a vector of real numbers (feature vector) ${\mathbf {x}} = (x_1, x_2, \dots , x_d)\ \in \mathbb {R}^d$. Intuitively, a class is the set of all similar patterns. For the sake of simplicity, and without loss of generality, we assume that each object belongs to one and only one class, and we will limit our attention to two-class problems. For example, in the domain of “cats and dogs,” we can consider the classes $C_\mathrm{cats}$ (the class of all cats) and $C_\mathrm{dogs}$ (the class of all dogs). The pattern at hand is either a cat or a dog, and a possible representation of the pattern could consist of the height of the pet and the length of its tail. In this way, the feature vector $\mathbf{x}_{\mathbf{1}} = (x_{11},x_{12})$ is the pattern representing a pet whose height and length of the tail are $x_{11}$ and $x_{12},$ respectively.

Now, let us consider an object ${\mathbf {x}}_t$ whose membership class is unknown. The basic aim of the classification process is to establish which class ${\mathbf {x}}_t$ belongs to. To achieve this goal, standard pattern recognition designs a classifier that, given the feature vector ${\mathbf {x}}_t$, has to determine the true class of the pattern. The classifier should take into account all available information about the task at hand (i.e., information about the statistical distributions of the patterns and information obtained from a set of patterns whose true class is known). This set of patterns is called “training set,” and it will be used to define the behavior of the classifier.

If no information about the statistical distributions of the patterns is available, an easy classification algorithm that could be used is the nearest mean classifier (NMC) (Manning et al. 2008; Hastie et al. 2001) or minimum distance classifier. The NMC

• computes the centroids of each class, using the patterns on the training set $\mu ^*_i = \frac{1}{n_i}\sum _{ {\mathbf {x}} \in C_i} {\mathbf {x}}$, where $n_i$ is the number of patterns of the training set belonging to the class $C_i$;

• assigns the unknown pattern ${\mathbf {x}}_t$ to the class with the closest centroid.

In the next section, we provide a representation of arbitrary 2D patterns by means of density matrices, while in Sect. 4, we introduce a representation of NMC in terms of quantum objects.

3 Representation of two-dimensional patterns

Let $\mathbf{x}_{\mathbf{i}}=(x_{i1},\ldots ,x_{ik})$ be a generic pattern, i.e., a point in $\mathbb {R}^k$. By means of this representation, we consider all the k features of $\mathbf{x}_{\mathbf{i}}$ as perfectly known. Therefore, $\mathbf{x}_{\mathbf{i}}$ represents a maximal kind of information, and its natural quantum counterpart is provided by a pure state. For the sake of simplicity, we will confine ourselves to an arbitary two-feature pattern indicated by ${\mathbf {x}}=(x,y)$.² In this section, a particular one-to-one correspondence between each pattern and its corresponding pure density operator is provided.

The pattern ${\mathbf {x}}$ can be represented as a point in $\mathbb {R}^2$. The stereographic projection (Coxeter 1969) allows to unequivocally map any point $r=(r_1,r_2,r_3)$ on the surface of a radius-one sphere $\mathbb {S}^2$ (except for the north pole) onto a point ${\mathbf {x}}=(x,y)$ of $\mathbb {R}^2$ as

$$\begin{aligned} SP:(r_1,r_2,r_3) \mapsto \left( \frac{r_1}{1-r_3},\frac{r_2}{1-r_3}\right) . \end{aligned}$$

(2)

The inverse of the stereographic projection is given by

$$\begin{aligned} SP^{-1}:(x,y) \mapsto \left( \frac{2x}{x^2+y^2+1},\frac{2y}{x^2+y^2+1},\frac{x^2+y^2-1}{x^2+y^2+1}\right) . \end{aligned}$$

(3)

Therefore, by using the Bloch representation given by Eq. (1) and placing

$$\begin{aligned} r_1= & {} \frac{2x}{x^2+y^2+1},\quad r_2=\frac{2y}{x^2+y^2+1},\nonumber \\ r_3= & {} \frac{x^2+y^2-1}{x^2+y^2+1}, \end{aligned}$$

(4)

we obtain the following definition.

Definition 1

(Density pattern) Given an arbitrary pattern ${\mathbf {x}}=(x,y)$, the density pattern (DP) $\rho _{\mathbf {x}}$ associated with ${\mathbf {x}}$ is the following pure density operator

$$\begin{aligned} \rho _{\mathbf {x}}= & {} \frac{1}{2}\begin{pmatrix}1+r_3 &{} r_1-ir_2 \\ r_1+ir_2 &{} 1-r_3 \end{pmatrix}\nonumber \\= & {} \frac{1}{x^2+y^2+1} \begin{pmatrix} x^2+y^2 &{} x-iy \\ x+iy &{} 1 \end{pmatrix}. \end{aligned}$$

(5)

It is easy to check that $\text {tr}(\rho ^2_{\mathbf {x}})=1$. Hence, $\rho _{\mathbf {x}}$ always represents a pure state for any value of the features x and y.

Following the standard definition of the Bloch sphere, it can be verified that $r_i=\text {tr}{(\rho _{\mathbf {x}}\cdot \sigma _i)},$ with $i\in \{1,2,3\}$ and $\sigma _i$ are Pauli matrices.

Example 1

Let us consider the pattern ${\mathbf {x}}=(1,3)$. The corresponding $\rho _{\mathbf {x}}$ reads

$$\begin{aligned} \rho _{\mathbf {x}}=\frac{1}{11} \begin{pmatrix}10 &{} 1-3i \\ 1+3i &{} 1 \end{pmatrix}.\end{aligned}$$

One of the advantages of this encoding is based on the fact that it allows an easy visualization of an arbitrary two-feature dataset on the Bloch sphere, as it will be showed in the next section. The manner to encode a real pattern onto the space of the density operators is not unique and there is a risk of losing some information during the encoding. Taking into account the recent debates (Schuld et al. 2014a; Lloyd et al. 2013; Rebentrost et al. 2014), in order to encode a real vector to a quantum states without losing information, it is necessary to normalize the vector but maintain some information about the norm of the same vector at the same time. By following this procedure, we briefly show that it is alternatively possible to recover the stereographic encoding proposed in Eq. (5) also by simple analytical considerations.

Let ${{\mathbf {x}}}=(x,y)$ be an arbitrary real vector.

• 1. First, we map ${{\mathbf {x}}}$ onto a vector ${{\mathbf {x}}}'$ whose first component is given by $x+iy$ and the second component is given by the norm of ${{\mathbf {x}}}$ ($|{{\mathbf {x}}}| = \sqrt{x^2 + y^2}$); i.e., ${\mathbf {x}}=(x,y)\mapsto {\mathbf {x}}' = (x+iy,\sqrt{x^2 + y^2}).$

• 2. Now, we consider a second map: ${\mathbf {x}}'\mapsto {\mathbf {x}}'' = \Big (\frac{x+iy}{\sqrt{x^2 + y^2}},\sqrt{x^2 + y^2}\Big )$, obtained by normalizing the first component of ${\mathbf {x}}'.$

• 3. Then, we consider the norm of ${\mathbf {x}}''$, i.e., $|{\mathbf {x}}''|=\sqrt{x^2 + y^2 + 1}$ and we normalize the vector ${\mathbf {x}}''$, i.e., ${\mathbf {x}}''\mapsto {\mathbf {x}}''' = \frac{{\mathbf {x}}''}{|{\mathbf {x}}''|} = \Big (\frac{x+iy}{\sqrt{(x^2 + y^2)(x^2 + y^2 + 1)}},\sqrt{\frac{x^2 + y^2}{x^2 + y^2 + 1}}\Big ).$

• 4. Now, we consider the projector: $\mathbb {P}= {\mathbf {x}}'''\cdot ({\mathbf {x}}''')^\dagger =\frac{1}{x^2 + y^2 + 1} \begin{pmatrix}1 &{} x + iy \\ x - iy &{} x^2 + y^2 \end{pmatrix}.$

• 5. Finally, we apply the operator $Not=\begin{pmatrix}0 &{} 1 \\ 1 &{} 0 \end{pmatrix}$ to $\mathbb {P}$ and we recover: $Not(\mathbb {P})=\frac{1}{x^2 + y^2 + 1} \begin{pmatrix}x^2+y^2 &{} x - iy \\ x + iy &{} 1 \end{pmatrix}$, that is the same expression of the density pattern $\rho _x$ introduced in Eq (5).

The introduction of the density pattern leads to two different developments. The first one is shown in the next section and consists of the representation of the NMC in quantum terms. Moreover, in Sect. 5, starting from the framework of density patterns, it will be possible to introduce a quantum classifier that exhibits an improvement in the performance (in terms of decreasing of the error in the classification process) with respect to the NMC.

4 Classification process for density patterns

As introduced in Sect. 2, the NMC is based on the computation of the minimum Euclidean distance between the pattern to classify and the centroids of each class. In the previous section, a quantum counterpart of an arbitrary (two feature) “classical” pattern was provided. In order to obtain a quantum counterpart of the standard classification process, we need to provide a suitable definition of distance d between DPs. In addition to satisfy the standard conditions of metric, the distance d also needs to satisfy the preservation of the order: Given three arbitrary patterns a, b, c such that $d_E(a,b)\le d_E(b,c)$, if $\rho _a,\rho _b,\rho _c$ are the DPs related to a, b, c, respectively, then $d(\rho _a,\rho _b)\le d(\rho _b,\rho _c).$ In order to fulfill all the previous conditions, we obtain the following definition.

Definition 2

(Normalized trace distance) The normalized trace distance $\overline{d}_{\text {tr}}$ between two arbitrary density patterns $\rho _a$ and $\rho _b$ is given by formula

$$\begin{aligned} \overline{d}_{\text {tr}}(\rho _a,\rho _b) = K_{a,b}d_{\text {tr}}(\rho _a,\rho _b), \end{aligned}$$

(6)

where $d_{\text {tr}}(\rho _a,\rho _b)$ is the standard trace distance, $d_{\text {tr}}(\rho _a,\rho _b) = \frac{1}{2}\sum _i|\lambda _i|$, with $\lambda _i$ representing the eigenvalues of $\rho _a-\rho _b$ (Barnett 2009; Nielsen and Chuang 2000), and $K_{a,b}$ is a normalization factor given by $K_{a,b}=\frac{2}{\sqrt{(1-r_{a_3})(1-r_{b_3})}}$, with $r_{a_3}$ and $r_{b_3}$ representing the third Pauli components of $\rho _a$ and $\rho _b$, respectively.

Proposition 1

Given two arbitrary patterns $a=(x_a,y_a)$ and $b=(x_b,y_b)$ and their respective density patterns, $\rho _a$ and $\rho _b$, we have that

$$\begin{aligned} \overline{d}_{\text {tr}}(\rho _a,\rho _b)=d_{E}(a,b). \end{aligned}$$

(7)

Proof

It can be verified that the eigenvalues of the matrix $\rho _a-\rho _b$ are given by

$$\begin{aligned} \mathrm{Eig}(\rho _a-\rho _b)=\pm \frac{d_{E}(a,b)}{\sqrt{(1+x_a^2+y_a^2)(1+x_b^2+y_b^2)}}. \end{aligned}$$

(8)

Using the definition of trace distance, we have

$$\begin{aligned} \text {tr}\sqrt{(\rho _a-\rho _b)^2}=\frac{d_{E}(a,b)}{\sqrt{(1+x_a^2+y_a^2)(1+x_b^2+y_b^2)}}. \end{aligned}$$

(9)

By applying formula (4) to both $r_{a_3}$ and $r_{b_3}$, we obtain that

$$\begin{aligned} K_{a,b}=\frac{2}{\sqrt{(1-r_{a_3})(1-r_{b_3})}}=\sqrt{(1+x_a^2+y_a^2)(1+x_b^2+y_b^2)}. \end{aligned}$$

(10)

$\square$

Using Proposition 1, one can see that the normalized trace distance $\overline{d}_{\text {tr}}$ satisfies the standard metric conditions and the preservation of the order.

Due to the computational advantage of a quantum algorithm able to faster calculate the Euclidean distance (Wiebe et al. 2015), the equivalence between the normalized trace distance and the Euclidean distance turns out to be potentially beneficial for the classification process we are going to introduce.

Let us now consider two classes, $C_A$ and $C_B$ and the respective centroids³ $a^*=(x_a,y_a)$ and $b^*=(x_b,y_b).$ The classification process based on NMC consists of finding the space regions given by the points closest to the first centroid $a^*$ or to the second centroid $b^*$. The patterns belonging to the first region are assigned to the class $C_A$, while patterns belonging to the second region are assigned to the class $C_B$. The points equidistant from both the centroids represent the discriminant function (DF), given by

$$\begin{aligned} f_\mathrm {DF}(x,y) = 2(x_a - x_b)x + 2(y_a - y_b)y + (|b^*|^2 - |a^*|^2)=0. \end{aligned}$$

(11)

Thus, an arbitrary pattern $c=(x,y)$ is assigned to the class $C_A$ (or $C_B$) if $f_\mathrm {DF}(x,y) > 0$ (or $f_\mathrm {DF}(x,y) < 0$).

Let us notice that the Eq. (11) is obtained by imposing the equality between the Euclidean distances $d_{E}(c,a^*)$ and $d_{E}(c, b^*)$. Similarly, we obtain the quantum counterpart of the classical discriminant function.

Proposition 2

Let $\rho _{a^*}$ and $\rho _{b^*}$ be the DPs related to the centroids $a^*$ and $b^*$, respectively. Then, the quantum discriminant function (QDF) is defined as

$$\begin{aligned} f_\mathrm {QDF}(r_1,r_2,r_3) = \mathbf {F}(r_{a^*},r_{b^*})^T\cdot \mathbf {r} + \tilde{K}^2 - 1 = 0 \end{aligned}$$

(12)

where $\mathbf {r} = (r_1, r_2, r_3)$, $\{r_{a^*_i}\}$, $\{r_{b^*_i}\}$ are Pauli components of $\rho _{a^*}$ and $\rho _{b^*}$, respectively, $\tilde{K} = \tilde{K}(r_{a^*_3}, r_{b^*_3}) = \frac{K_{c,a^*}}{K_{c,b^*}} = \sqrt{\frac{1 - r_{a^*_3}}{1 - r_{b^*_3}}}$, $\mathbf {F}(r_{a^*},r_{b^*}) = (r_{a^*_1} - \tilde{K}^2r_{b^*_1}, r_{a^*_2} - \tilde{K}^2r_{b^*_2}, r_{a^*_3} - \tilde{K}^2r_{b^*_3}).$

Proof

In order to find the QDF, we use the equality between the normalized trace distances $K_{c,a^*}d_{\text {tr}}(\rho _c,\rho _{a^*})$ and $K_{c,b^*}d_{\text {tr}}(\rho _c,\rho _{b^*})$, where $\rho _c$ is a generic DP with Pauli components $r_1$, $r_2$, $r_3$. We have

$$\begin{aligned} \begin{aligned} K_{c,a^*}d_{\text {tr}}(\rho _c,\rho _{a^*})&= \sqrt{\frac{(r_1 - r_{a^*_1})^2 + (r_2 - r_{a^*_2})^2 + (r_3 - r_{a^*_3})^2}{(1 - r_{a^*_3})(1 - r_3)}}, \\ K_{c,b^*}d_{\text {tr}}(\rho _c,\rho _{b^*})&= \sqrt{\frac{(r_1 - r_{b^*_1})^2 + (r_2 - r_{b^*_2})^2 + (r_3 - r_{b^*_3})^2}{(1 - r_{b^*_3})(1 - r_3)}}. \end{aligned} \end{aligned}$$

(13)

The equality $K_{c,a^*}d_{\text {tr}}(\rho _c,\rho _{a^*}) = K_{c,b^*}d_{\text {tr}}(\rho _c,\rho _{b^*})$ reads

$$\begin{aligned}&\sum _{i=1}^3 r_i^2 + \sum _{i=1}^3 r_{a^*_i}^2 - 2\sum _{i=1}^3 r_i r_{a^*_i} \nonumber \\&\quad = \frac{1-r_{a^*_3}}{1 - r_{b^*_3}}\left( \sum _{i=1}^3 r_i^2 + \sum _{i=1}^3 r_{b^*_i}^2 - 2\sum _{i=1}^3 r_i r_{b^*_i}\right) . \end{aligned}$$

(14)

In view of the fact that $\rho _{a^*}$, $\rho _{b^*}$ and $\rho _{c}$ are pure states, we use the conditions $\sum _{i=1}^3 r^2_{a^*_i} = \sum _{i=1}^3 r^2_{b^*_i} = \sum _{i=1}^3 r^2_i = 1$ and we get

$$\begin{aligned} \sum _{i=1}^3 \left( r_{a^*_i} - \frac{1-r_{a^*_3}}{1 - r_{b^*_3}}r_{b^*_i}\right) r_i + \frac{1-r_{a^*_3}}{1 - r_{b^*_3}} - 1 = 0. \end{aligned}$$

(15)

$\square$

This completes the proof.

Similarly to the classical case, we assign the DP $\rho _c$ to the class $C_A$ (or $C_B$) if $f_\mathrm {QDF}(r_1,r_2,r_3) > 0$ (or $f_\mathrm {QDF}(r_1,r_2,r_3) < 0$). Geometrically, Eq. (12) represents the surface equidistant from the DPs $\rho _{a^*}$ and $\rho _{b^*}$.

Let us remark that, if we express the Pauli components $\{r_{a^*_i}\}$, $\{r_{b^*_i}\}$ and $\{r_i\}$ in terms of classical features by Eq. (4), then Eq. (12) exactly corresponds to Eq. (11). As a consequence, given an arbitrary pattern $c=(x,y)$, if $f_\mathrm {DF}(c)>0$ (or $f_\mathrm {DF}(c)<0$), then its relative DP $\rho _c$ will satisfy $f_\mathrm {QDF}(\rho _c)>0$ (or $f_\mathrm {QDF}(\rho _c)<0$, respectively).

As an example, the comparison between the classical and quantum discrimination functions for the Moon dataset (composed of 200 patterns equally allocated in two classes) is made in Fig. 1. Plots in Fig. 1a, b present the classical and quantum discrimination, respectively.

Fig. 1

Comparison between the discrimination procedures for the Moon dataset in $\mathbb {R}^2$ (a) and in the Bloch sphere $\mathbb {S}^2$ (Banana). Green and blue points represent the two classes in the real space and in the Bloch sphere, respectively. The straight line in b represents the classical discriminant function given by (11); on the other hand, the plane that intersects the Bloch sphere in b represents the quantum discriminant function given by (12)

It is worth noting that the correspondence between the pattern expressed as a feature vector (according to the standard pattern recognition approach) and the pattern expressed as a density operator is quite general. Indeed, it is not related to a particular classification algorithm (NMC, in the previous case) nor to the specific metric at hand (the Euclidean one). Therefore, it is possible to develop a similar correspondence by using other kinds of metrics and/or classification algorithms, different from NMC, adopting exactly the same approach.

This result suggests potential developments which consist of finding a quantum algorithm able to implement the normalized trace distance between density patterns. So, it would correspond to implement the NMC on a quantum computer with the consequent well-known advantages (Wiebe et al. 2015). The next section is devoted to the exploration of another development that consists of using the framework of density patterns in order to introduce a “purely” quantum classification process (having no direct classical correspondence) called QC. It can be considered as a quantum-inspired version of the classical NMC because it substantially is a minimum distance classifier among quantum objects. The main difference between them, as we will show by numerical simulations, is that the NMC is a linear classifier which does not take into account the data dispersion, while the QC is not linear, and conversely, it seems sensitive to the data dispersion. As it will be showed in the next section by involving some datasets, this fact seems to be particularly beneficial (with respect to the NMC) mostly in the cases where the classes are quite mixed, and hence, the NMC generates a considerable error.

5 Quantum classification procedure

In Sect. 4, we have shown that the NMC can be expressed by means of quantum formalism, where each pattern is replaced by a corresponding density pattern and the Euclidean distance is replaced by the normalized trace distance. Representing classical data in terms of quantum objects seems to be particularly promising in quantum machine learning. Quoting Lloyd et al. (2013) “Estimating distances between vectors in N-dimensional vector spaces takes time O(logN) on a quantum computer. Sampling and estimating distances between vectors on a classical computer is apparently exponentially hard”. This convenience has already been exploited in machine learning for similar tasks (Wiebe et al. 2015; Giovannetti et al. 2008). Hence, finding a quantum algorithm for pattern classification using the proposed encoding could be particularly beneficial to speed up the classification process and it can suggest interesting developments. However, they are beyond the scope of this paper.

What we propose in this section is to exhibit some explicative examples to show how, on a classical computer, our classification procedure, based on the minimum distance, gives additional information with respect to the standard NMC.

5.1 Description of the quantum classifier (QC)

In order to get a real advantage in the classification process, we need to be not confined in a pure representation of the classical procedure in quantum terms. For this reason, we introduce a purely quantum representation where we consider a new definition of centroid. The basic idea is to define a quantum centroid not as the stereographic projection of the classical centroid, but as a convex combination of density patterns.

Trivially, given two real points x and y, the point $z=\frac{1}{2}(x+y)$ has the property to minimize the quantity $d_E(x,z) + d_E(z,y)$. In this case, $d_E(x,z) = d_E(z,y) = \frac{1}{2}d_E(x,y)$. Similarly, let us consider two density operators $\rho$ and $\sigma$ and let $\tau =\frac{1}{2}(\rho +\sigma )$. It is straightforward to show that $d_{\text {tr}}(\rho ,\tau )=d_{\text {tr}}(\tau ,\sigma )=\frac{1}{2}d_{\text {tr}}(\rho ,\sigma ).$ In fact, $d_{\text {tr}}(\rho ,\tau )=d_{\text {tr}}(\rho ,\frac{1}{2}(\rho +\sigma ))=\frac{1}{2}\sum |{\text {Eigenvalues}}(\rho -\frac{1}{2}\rho -\frac{1}{2}\sigma )|=\frac{1}{2}\sum |{\text {Eigenvalues}}(\frac{1}{2}(\rho -\sigma ))|=\frac{1}{2}\cdot \frac{1}{2}\sum |{\text {Eigenvalues}}(\rho -\sigma )|=\frac{1}{2}d_{\text {tr}}(\rho ,\sigma ).$ Analogously, we prove that $d_{\text {tr}}(\sigma ,\tau )=\frac{1}{2}d_{\text {tr}}(\rho ,\sigma ).$

Following this argument, we reasonably introduce the following definition.

Definition 3

(Quantum centroid) Given a dataset $\{P_1,\ldots ,P_n\}$ with $P_i=(x_i,y_i)$, let us consider the respective set of density patterns $\{\rho _1,\ldots ,\rho _n\}.$ The Quantum centroid is defined as:

$$\begin{aligned} \rho _{QC}=\frac{1}{n}\sum _{i=1}^n\rho _i. \end{aligned}$$

Obviously, the reasonable ways to define a quantum version of the classical centroid are not unique. We accord with this definition because, as we show in the rest of the section, it turns out to be beneficial in the reduction of the error during some typical classification process. The reasons of this convenience are intuitively contained in the following argument. Let us notice that $\rho _{QC}$ is a mixed state that does not have any counterpart in the standard pattern recognition. Indeed, the quantum centroid may include some further information that the classical centroid generally discards (Kolossa and Haeb-Umbach 2011; Sause and Horn 2013). In fact, the classical centroid does not involve all the information about the dispersion of a given dataset, i.e., the classical centroid is invariant under uniform scaling transformations of the data. Consequently, the classical centroid does not take into account any dispersion phenomena. Standard pattern recognition compensates for this lack by involving the covariance matrix (Duda et al. 2000).

On the other hand, the quantum centroid is not invariant under uniform scaling. In what follows, we show how the general expression of the quantum centroid is dependent on an arbitrary rescaling of a given dataset.

Let us consider the set of n points $\{P_1,\ldots ,P_n\}$, where $P_i=(x_i,y_i)$ and let $C=(c_x,c_y)=(\frac{1}{n}\sum _{j=1}^n x_j, \frac{1}{n}\sum _{j=1}^n y_j)$ be the respective classical centroid. A uniform rescaling of n points of the dataset corresponds to move each point $P_i$ along the line joining itself with C, whose generic expression is given by: $y_{x_i}=\frac{x-c_x}{x_i-c_x}(y_i-c_y)+c_y.$ Let $\tilde{P}_i=(\tilde{x}_i,y_{\tilde{x}_i})$ be a generic point on this line. Obviously, a uniform rescaling of $P_i$ by a real factor $\alpha$ is represented by the map: ${\tilde{P}}_i=(\tilde{x}_i,y_{\tilde{x}_i})\mapsto \alpha {\tilde{P}}_i=(\alpha {\tilde{x}}_i,y_{\alpha \tilde{x}_i}).$ Even if the classical centroid is not dependent on the rescaling factor $\alpha$, on the other hand the expression of the quantum centroid is:

$$\begin{aligned} \rho _{QC}=\frac{1}{n}\begin{pmatrix} \sum _{i=1}^n\frac{(\alpha \tilde{x}_i)^2+(y_{\alpha \tilde{x}_i})^2}{(\alpha \tilde{x}_i)^2+(y_{\alpha \tilde{x}_i})^2+1} &{} \sum _{i=1}^n\frac{\alpha \tilde{x}_i-iy_{\alpha \tilde{x}_i}}{(\alpha \tilde{x}_i)^2+(y_{\alpha \tilde{x}_i})^2+1}\\ \sum _{i=1}^n\frac{\alpha \tilde{x}_i+iy_{\alpha \tilde{x}_i}}{(\alpha \tilde{x}_i)^2+(y_{\alpha \tilde{x}_i})^2+1} &{}\sum _{i=1}^n\frac{1}{(\alpha \tilde{x}_i)^2+(y_{\alpha \tilde{x}_i})^2+1} \end{pmatrix} \end{aligned}$$

that, clearly, is dependent on $\alpha .$

According to the same framework used in Sect. 4, given two classes $C_A$ and $C_B$ of real data, let $\rho _{QCa}$ and $\rho _{QCb}$ be the respective quantum centroids. Given a pattern P and its respective density pattern, $\rho _P$, P is assigned to the class $C_A$ (or $C_B$) if $d_{tr}(\rho _P,\rho _{QCa})<d_{tr}(\rho _P,\rho _{QCb})$ (or $d_{tr}(\rho _P,\rho _{QCa})>d_{tr}(\rho _P,\rho _{QCb})$, respectively). Let us remark that we no longer need any normalization parameter to be added to the trace distance $d_{tr}$, because the exact correspondence with the Euclidean distance is no more a necessary requirement in this framework. From now on, we refer to the classification process based on density patterns, quantum centroids, and trace distances as the Quantum Classifier (QC).

We have shown that the quantum centroid is not independent from the dispersion of the patterns and it could contain some additional information with respect to the classical centroid. Consequently, it is reasonable to expect that in different cases QC could provide some better performance than the NMC. The next subsection will be devoted to the exploitation of the difference between the classification procedures by means of numerical simulations on different datasets.

Before presenting the experimental results, let us briefly introduce the main statistical indices widely used to evaluate the performance of a supervised learning algorithm.

In particular, for each class, it is typical to refer to the respective confusion matrix (Fawcet 2006). It is based on four possible kinds of outcome after the classification of a certain pattern:

• True positive (TP): pattern correctly assigned to its class;

• True negative (TN): pattern correctly assigned to another class;

• False positive (FP): pattern uncorrectly assigned to its class;

• False negative (FN): pattern uncorrectly assigned to another class.

According to above, it is possible to recall the following definitions use to evaluate the performance of an algorithm.⁴

True positive rate (TPR), or sensitivity or recall: $\mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}$; false positive rate (FPR): $\mathrm{FPR}=\frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN}}$; true negative rate (TNR): $\mathrm{TNR}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}$; false negative rate (FNR): $\mathrm{FNR}=\frac{\mathrm{FN}}{\mathrm{FN}+\mathrm{TP}}$.

Let us consider a dataset of C elements allocated in m different classes. We also recall the following basic statistical notions:

• Error: $E=1-\frac{\mathrm{TP} + \mathrm{TN}}{C};$

• Precision: $\mathrm{Pr}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}.$

Moreover, another statistical index that is very useful to indicate the reliability of a classification process is given by the Cohen’s k, that is $k=\frac{\mathrm{Pr}(a)-\mathrm{Pr}(e)}{1-\mathrm{Pr}(e)}$, where $\mathrm{Pr}(a)=\frac{\mathrm{TP}+\mathrm{TN}}{C}$ and $\mathrm{Pr}(e)=\frac{(\mathrm{TP}+\mathrm{FP})(\mathrm{TP}+\mathrm{FN}) + (\mathrm{FP}+\mathrm{TN})(\mathrm{TN}+\mathrm{FN})}{C^2}$. The value of k is such that $-1\le k \le 1$, where the case $k=1$ corresponds to a perfect classification procedure and the case $k=-1$ corresponds to the worst classification procedure.

5.2 Implementing the quantum classifier

In this subsection, we implement the QC on different datasets and show the difference between QC and NMC in terms of the values of error, accuracy, precision, and other probabilistic indices summarized above.

We will show how our quantum classification procedure exhibits partial or significant convenience with respect to the NMC on a classical computer.

In particular, we consider four datasets: Two of them (following Gaussian distributions) called Gaussian and 3ClassGaussian, where the first one is composed of 200 patterns allocated in two classes and the second one is composed of 450 patterns allocated in three classes, and the other two, called Moon and Banana, composed of 200 and 5300 patterns (respectively) allocated in two different classes.

The experiments have been conducted by randomly subdividing each dataset into a training set made up of $80\%$ of instances and a test set containing the remaining instances. The results are reported in terms of averages of the computed statistical indices over 100 runs of the experiments.

We denote the variables listed in the tables as follows: E = Error; $E_i$ = Error on the class i; Pr = Precision; k = Cohen’s k; TPR = True positive rate; FPR = False positive rate; TNR = True negative rate; FNR = False negative rate. Let us remark that i) the values listed in the table are referred to the mean values over the classes; ii) in the case where the number of the classes is equal to two, a pattern that is correctly classified as belonging to a class corresponds to a pattern that is correctly classified as not belonging to the other class; on this basis, the mean value of TPR is equal to the mean value of TNR, and similarly, the mean value of FPR is equal to the mean value of FNR.

In order to provide a complete visualization of the difference between the two classification procedures, we also represent in the figures below the results of both classifications by considering the whole dataset for both training and test dataset.⁵

We stress that for some of the following datasets, the NMC is clearly not the optimal classifier and there exist classifiers that overcome it in terms of accuracy and performance. However, our aim in this context is confined the comparison of two minimum distance classifiers (classical and quantum-inspired version) trying to capture the main differences.

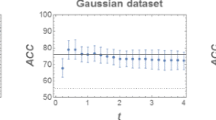
5.2.1 Gaussian dataset

This dataset consists of 200 patterns allocated in two classes (of equal size), following Gaussian distributions whose means are $\mu _1 = (1,1)$, $\mu _2 = (2,2)$ and covariance matrices are $\varSigma _1 = \mathrm{diag}(20,50)$, $\varSigma _2 = \mathrm{diag}(5,5)$, respectively.

As depicted in Fig. 2, the classes appear particularly overlapped and the QC is able to classify a number of true positive patterns that is significantly larger than the NMC. Hence, see Table 1, the error of the QC is (about $20\%$) smaller than the error of the NMC. In particular, the QC turns out to be strongly beneficial in the classification of the patterns of the second class. Moreover, the values related to accuracy, precision, and the other statistical indices also exhibit relevant improvements with respect to the NMC.⁶

Fig. 2

Experimental results obtained for the Gaussian dataset: a dataset used in the experiments, b classification obtained using NMC, c classification obtained using QC

Table 1 Gaussian dataset

5.2.2 The 3ClassGaussian dataset

In this example, we consider an equally distributed three-class dataset, consisting of 450 patterns. The classes are distributed as Gaussian random variables whose means are $\mu _1 = (-3,-3)$, $\mu _2 = (5,5)$, $\mu _3 = (7,7)$ and covariance matrices are $\varSigma _1 = \mathrm{diag}(50,100)$, $\varSigma _2 = \mathrm{diag}(10,5)$, and $\varSigma _3 = \mathrm{diag}(30,70)$, respectively.

As for the two-class Gaussian dataset, the three classes appear quite overlapped, and once again, the computation of the error and the other statistical indices evaluated for both QC and NMC shows that the first one is more convenient especially for the classification of the first- and second-class patterns (Table 2).⁷

Table 2 3ClassGaussian Dataset

5.2.3 The Moon dataset

This dataset consists of 200 patterns equally distributed in two classes. In this case, we observe a mean error reduction of about $4\%$. In particular, the classification error related to the second class is very similar for both NMC and QC, while we can note that the QC turns out to be particularly beneficial in the classification of the first-class patterns (for which the error decreases by about $10\%$).

5.2.4 The Banana dataset

The Banana dataset presents a particularly complex distribution that is very hard to deal with the NMC. Indeed, the classification error we get by using the NMC is high and we would not use it in practice. Anyway, as we have already explained, we consider this particular dataset in order to show the substantial difference between two approaches (i.e., minimum distance classifiers) having the same nature (Fig. 3; Table 3).

This dataset consists of 5300 patterns unequally distributed between the two classes (2376 patterns belonging to the first class and 2924 belonging to the second one). In this case, the QC turns out to be beneficial in terms of all statistical indices and for both classes⁸ it exhibits a mean error reduction of about 3% (Figs. 4, 5; Table 4).

Fig. 3

Experimental results obtained for the 3ClassGaussian dataset: a dataset used in the experiments, b classification obtained using NMC, c classification obtained using QC

Fig. 4

Experimental results obtained for the Moon dataset: a dataset used in the experiments, b classification obtained using NMC, c classification obtained using QC

Table 3 Moon dataset

Fig. 5

Experimental results obtained for the Banana dataset: a dataset used in the experiments, b classification obtained using NMC, c classification obtained using QC

Table 4 Banana dataset

Let us notice that, in accordance with the well known No Free Lunch Theorem (Duda et al. 2000), even if the previous examples exhibit a (particular or partial) benefit of the QC with respect to the NMC, in general there is no classifier whose performance is better than all the others for any dataset. This paper is focused on the comparison between the NMC and the QC because these methods are exclusively based on the pattern-centroid distance. Anyway, a wide comparison among the QC and other commonly used classifiers (such as the LDA—Linear Discriminant Analysis—and the QDA—Quadratic Discriminant Analysis) will be proposed for future works, where also other quantum metrics (such as the Fidelity, the Bures distance etc) instead of the trace distance and alternative definitions of quantum centroids will be considered to provide an adaptive version of the quantum classifier.

6 Geometrical generalization of the model

In Sect. 3, we provided a representation of an arbitrary two-feature pattern ${\mathbf {x}}$ in terms of a point on the surface of the Bloch sphere $\mathbb {S}^2$, i.e., a density operator $\rho _{\mathbf {x}}$. A geometrical extension of this model to the case of n-feature patterns inspired by quantum framework is possible.

In this section, by generalizing the encoding proposed in Sect. 2, we introduce a method for representing an arbitrary n-dimensional real pattern as a point in the radius-one hypersphere $\mathbb {S}^n$, centered in the origin.

A quantum system described by a density operator $\rho$ in an n-dimensional Hilbert space $\mathcal {H}$ can be represented by a linear combination of the n-dimensional identity I and $n^2 - 1$ ($n\times n$)-square matrices $\{\sigma _i\}$ [i.e., generalized Pauli matrices (Bertlmann and Krammer 2008; Kimura 2003)]:

$$\begin{aligned} \rho =\frac{1}{n}I+\frac{1}{2}\sum _{i=1}^{n^2-1}r_i\sigma _i, \end{aligned}$$

(16)

where the real numbers $\{r_i\}$ are the Pauli components of $\rho$. Hence, by Eq. (16), a density operator $\rho$ acting on an n-dimensional Hilbert space can be geometrically represented as a $(n^2-1)$-dimensional point $P=(r_1,r_2,\ldots ,r_{\tilde{n}})$ in the Bloch hypersphere $\mathbb {S}^{\tilde{n}-1}$, with $\tilde{n}=n^2-1$. Therefore, by using the generalization of the stereographic projection (Karlıǧa 1996), we obtain the vector ${\mathbf {x}}=(x_1,x_2,\ldots ,x_{\tilde{n}-1})$ that is the correspondent of P in $\mathbb {R}^{n^2-2}.$ In fact, the generalization of Eqs. (2–3) is given by

$$\begin{aligned}&SP_{(\tilde{n})}:(r_1,r_2,\ldots ,r_{\tilde{n}})\mapsto \left( \frac{r_1}{1-r_{\tilde{n}}},\frac{r_2}{1-r_{\tilde{n}}},\ldots ,\frac{r_{\tilde{n}-1}}{1-r_{\tilde{n}}}\right) \nonumber \\&\quad =(x_1,x_2,\ldots ,x_{\tilde{n}-1}) \end{aligned}$$

(17)

$$\begin{aligned}&SP^{-1}_{(\tilde{n})}:(x_1,x_2,\ldots ,x_{\tilde{n}-1})\nonumber \\&\quad \mapsto \left( \frac{2x_1}{\sum _{i=1}^{\tilde{n}}x_i^2+1},\dots ,\frac{2x_{\tilde{n}-1}}{\sum _{i=1}^{\tilde{n}}x_i^2+1},\frac{\sum _{i=1}^{\tilde{n}}x_i^2-1}{\sum _{i=1}^{\tilde{n}}x_i^2+1}\right) \nonumber \\&\quad =(r_1,r_2,\ldots ,r_{\tilde{n}}). \end{aligned}$$

(18)

Hence, by Eq. (17), a two-dimensional density matrix is determined by three Pauli components and it can be mapped onto a two-dimensional real vector. Analogously, a three-dimensional density matrix is determined by eight Pauli components and it can be mapped onto a seven-dimensional real vector. Generally, an n-dimensional density matrix is determined by $n^2-1$ Pauli components and it can be mapped onto an $n^2-2$-dimensional real vector.

Now, let consider an arbitrary vector ${\mathbf {x}}=(x_1, x_2,\ldots ,x_{m})$ with $(n-1)^2-1<m<n^2-2$. In this case, Eq. (18) cannot be applied because $m\ne n^2-2.$ In order to represent a in an n-dimensional Hilbert space, it is sufficient to involve only $m+1$ Pauli components (instead of all the $n^2-1$ Pauli components of the n-dimensional space). Hence, we need to project the Bloch hypersphere $\mathbb {S}^{n^2-2}$ onto the hypersphere $\mathbb {S}^m$. We perform this projection by using Eq. (18) and by assigning some fixed values to a number of Pauli components equal to $n^2-m-2$. In this way, we obtain a representation in $\mathbb {S}^m$ that involves $m+1$ Pauli components and it finally allows the representation of an m-dimensional real vector.

Example 2

Let us consider a vector ${\mathbf {x}}=(x_1,x_2,x_3).$ By Eq. (18), we can map ${\mathbf {x}}$ onto a vector $r_{\mathbf {x}}=(r_1,r_2,r_3,r_4)\in \mathbb {S}^3.$ Hence, we need to consider a three-dimensional Hilbert space $\mathcal {H}$. Then, an arbitrary density operator $\rho \in \varOmega _3$ can be written as

$$\begin{aligned} \rho =\frac{1}{3}\left( I+\sqrt{3}\sum _{i=1}^8r_i\sigma _i\right) \end{aligned}$$

(19)

with $\{r_i\}$ Pauli components such that $\sum _{i=1}^8 r_i^2\le 1$ and $\{\sigma _i\}$ generalized Pauli matrices. In this case, $\{\sigma _i\}$ is the set of eight $3\times 3$ matrices also known as Gell-Mann matrices, namely

$$\begin{aligned} \begin{aligned} \sigma _1&=\begin{pmatrix} 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{pmatrix}, \quad \sigma _2=\begin{pmatrix} 0 &{} -i &{} 0\\ i &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{pmatrix}, \quad \sigma _3=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} -1 &{} 0\\ 0 &{} 0 &{} 0\\ \end{pmatrix}, \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} \sigma _4&=\begin{pmatrix} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 \end{pmatrix}, \quad \sigma _5=\begin{pmatrix} 0 &{} 0 &{} -i\\ 0 &{} 0 &{} 0\\ i &{} 0 &{} 0 \end{pmatrix}, \quad \sigma _6=\begin{pmatrix} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 0 \end{pmatrix},\\ \quad \sigma _7&=\begin{pmatrix} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -i\\ 0 &{} i &{} 0 \end{pmatrix}, \quad \sigma _8=\frac{1}{\sqrt{3}}\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} -2 \end{pmatrix}. \end{aligned} \end{aligned}$$

(20)

Consequently, the generic form of a density operator $\rho$ in the three-dimensional Hilbert space is given by

$$\begin{aligned} \rho =\frac{1}{3} \begin{pmatrix} \sqrt{3}r_3+r_8+1 &{} \sqrt{3}(r_1-ir_2) &{} \sqrt{3}(r_4-ir_5)\\ \sqrt{3}(r_1+ir_2) &{} -\sqrt{3}r_3+r_8+1 &{} \sqrt{3}(r_6-ir_7)\\ \sqrt{3}(r_4+ir_5) &{} \sqrt{3}(r_6+ir_7) &{} 1-2r_8 \end{pmatrix}. \end{aligned}$$

(21)

Then, for any $\rho$, it is possible to associate an eight-dimensional Bloch vector $r=(r_1,\ldots ,r_8)\in \mathbb {S}^7$. However, by taking $r_j=0$ for $j=5,\ldots ,8$, we obtain

$$\begin{aligned} \rho _{\mathbf{x}}=\frac{1}{3}\begin{pmatrix} \sqrt{3}r_3+1 &{} \sqrt{3}(r_1-ir_2) &{} \sqrt{3} r_4\\ \sqrt{3}(r_1+ir_2) &{} -\sqrt{3}r_3+1 &{} 0\\ \sqrt{3} r_4 &{} 0 &{} 1 \end{pmatrix} \end{aligned}$$

(22)

that, by Eq. (18), can be seen as a point projected in $\mathbb {S}^3,$ where

$$\begin{aligned}&SP^{-1}_{(4)}(\mathbf{x})=r_{\mathbf{x}}\nonumber \\&\quad =\left( \frac{2x_1}{\sum _{i=1}^3x_i^2+1},\frac{2x_2}{\sum _{i=1}^3x_i^2+1},\frac{2x_3}{\sum _{i=1}^3x_i^2+1},\frac{\sum _{i=1}^3x_i^2-1}{\sum _{i=1}^3x_i^2+1}\right) .\nonumber \\ \end{aligned}$$

(23)

The generalization introduced above allows the representation of arbitrary patterns ${\mathbf {x}}\in \mathbb {R}^n$ as points $\rho _{\mathbf {x}}\in \mathbb {S}^n$ as a natural extension of the encoding proposed in Sect. 2. Also, the classification procedure introduced in Sect. 4 can be naturally extended for an arbitrary n-feature pattern where the normalized trace distance between two DPs $\rho _a$ and $\rho _b$ can be expressed using Eq. (17) in terms of the respective Pauli components as

$$\begin{aligned} \overline{d}_{\text {tr}}(\rho _a,\rho _b)=\frac{\sqrt{\sum _{i=1}^n[(r_{a_i}-r_{b_i})-(r_{a_i}r_{a_{n+1}}-r_{b_i}r_{a_{n+1}})]^2}}{(1-r_{a_{n+1}})(1-r_{b_{n+1}})}.\nonumber \\ \end{aligned}$$

(24)

Analogously, also the QC could be naturally extended to a n-dimensional problem (without loss of generality) by introducing a n-dimensional quantum centroid.

7 Conclusions and further developments

In this work, we have proposed a quantum-inspired version (QC) of the nearest mean classifier (NMC) and we have shown some convenience of the QC by comparing them on different datasets. Firstly, we have introduced a one-to-one correspondence between two-feature patterns and pure density operators by using the concept of density patterns. Starting from this representation, firstly we have described the NMC in terms of quantum objects by introducing an ad hoc definition of normalized trace distance. We have found a quantum version of the discrimination function by means of Pauli components. The equation of this surface was obtained by using the normalized trace distance between density patterns. Geometrically, it corresponds to a surface that intersects the Bloch sphere. This result could be potentially useful because it suggests to find an appropriate quantum algorithm able to provide a quantum version of the NMC in a quantum computer, with a consequent significative reduction in the computational complexity of the process (Lloyd et al. 2013; Wiebe et al. 2015).

Secondly, a suitable definition of a quantum centroid that does not have a classical direct correspondence permits to introduce a quantum classifier, which can be considered as a quantum-inspired version of the NMC, i.e., a minimum distance classifier.

The main implementative result of the paper consists of comparing the performance of NMC and QC on datasets with different properties. In particular, we found out that the QC may exhibit some better performance sensitive to the data dispersion. Then, the QC seems to be promising for classifying datasets whose classes have mixed distributions more difficult to treat by using the NMC. This also suggests to compare the QC with other standard classifiers as a further development. Further developments will be devoted to compare the QC with other commonly used classical classifiers.

Finally, we have presented a generalization of our model that allows to express arbitrary n-feature patterns as points on the hypersphere $S^n$, obtained by using the generalized stereographic projection. However, even if it is possible to associate the points of a n-hypersphere to n-feature patterns, these points do not generally represent density operators. In Kimura (2003), Jakóbczyk and Siennicki (2001), Kimura and Kossakowski (2005), the authors found some conditions that guarantee the one-to-one correspondence between the points on particular regions of the hypersphere and density matrices. A full development of our work is therefore intimately connected to the study of the geometrical properties of the generalized Bloch sphere.