Quantum decision tree classifier

Abstract

We study the quantum version of a decision tree classifier to fill the gap between quantum computation and machine learning. The quantum entropy impurity criterion which is used to determine which node should be split is presented in the paper. By using the quantum fidelity measure between two quantum states, we cluster the training data into subclasses so that the quantum decision tree can manipulate quantum states. We also propose algorithms constructing the quantum decision tree and searching for a target class over the tree for a new quantum object.

1 Introduction

Machine learning (ML) and pattern recognition aim to generate classifying expressions simple enough to be understood easily by a human. The problem of searching for patterns in data is a fundamental one and has a long and successful history [1, 2]. Most research in pattern recognition is about methods for supervised learning or unsupervised learning [3]. Classic decision tree classification belongs to supervised learning methods. On the other hand, quantum information processing (QIP) has been achieving much progress in recent years [4]. Quantum information is a natural generalization of classical information. It is based on quantum mechanics, the most accurate and complete description of the world. However, it is quite different from its classical counterpart since the quantum version of classical algorithms presents different characteristics. This paper concerns quantum classification.

In classical machine learning, statistical classification is a supervised learning procedure in which individual objects are assigned into groups based on quantitative information on one or more characteristics inherent in the objects and based on a training set of previously labeled objects. Top-down induction of a decision tree is a powerful and simple method of pattern classification. Formally, the problem can be stated as follows: given a set of classes containing $m$ values: $C=\{c_1,c_2,\ldots c_m\}$, a set of training data containing $n$ objects is described as $\{(x_1,y_1),(x_2,y_2),\ldots ,(x_i,y_i),\ldots ,(x_n,y_n)\}$, where $x_i$ is a vector of $d$ attributes and $y_i\in C$ is the class label corresponding to the object $x_i$. The attributes set of the input objects can be denoted by $A=\{a_1,a_2,\ldots ,a_i,\ldots ,a_d\}$. For each attribute $a_i \in A$, its domain values set is described by $V_{a_i}=\{v_{i,1},v_{i,2},\ldots ,v_{i,m_i}\}$, where $m_i$ is the cardinality of $V_{a_i}$. The goal of classification is to develop an optimal classification rule that can determine the class of any object from its values of the attributes. According to the classifier, we can find the class $y\in C$ for a new object $x$.

Decision tree classifiers are used successfully in many diverse areas such as data mining, radar signal classification, character recognition, remote sensing, medical diagnosis, expert systems, and speech recognition. A classical decision tree classifier is a learning method for approximating discrete-valued target functions. Decision trees can also be re-represented as sets of if-then rules easily [5]. The problem of decision tree classification can be decomposed into two subproblems: (1) generate an optimal decision tree classifier with minimum generalization error and (2) determine the class of the unseen objects with as high of an accuracy as possible. Since the second problem is trivial for classical decision tree classifiers, most researchers focused on the first problem. The key task of the first problem is the selection of a node splitting rule. The most common splitting criteria includes information gain, GINI index, chi-squared statistic, and distance measure.

QIP promises to perform parallel information processing and rapid search over the data potentially yielding significant advances to the whole field of computer science. It will be very exciting to combine quantum computation with machine learning or artificial intelligence (AI). The area of quantum machine learning, which investigates its classical counterpart in quantum systems, has been of recent interest [6–11]. Several papers have already reported how QIP could be used to construct a quantum classifier. Ezhov [12] and Ventura [13] represented each of the labeled objects in the training data as a basis state, say $|\psi \rangle$, in a superposition with some coefficient. They take the basis state $|\psi \rangle$ as an initial state and iterate it using Grover’s algorithm [14]. The classification result was obtained by measuring the system after an appropriate number of iterations. Reference [13] had a poor ability at generalization due to the uncertainty in the number of iterations required. The classification pattern was limited to binary classification in [12] and [13]. Schützhold [15] presented a quantum pattern recognition algorithm which was more abstract than statistical classification. In Ref. [16], an algorithm for quantum data classification was developed which referred to quantum state distinction or detection rather than pattern classification. Furthermore, it only coped with labeled items. In Ref. [17], the problem of the classification of two arbitrary unknown mixed qubit states is researched. To the best of our knowledge, however, not much progress has been made in quantum classification up to now.

The aim of this paper is to consider the quantum version of a decision tree classifier, which can also deal with multiclass situations. The remainder of the paper is organized as follows: Sect. 2 devises a quantum decision tree classifier. There von Neumann entropy is used for splitting the object space. To discretize the quantum attribute states, a quantum clustering method is proposed. Section 3 presents the algorithm for searching over the quantum decision tree. According to the quantum fidelity metric, the unseen quantum data can be classified to a certain class. This is also useful for predicting quantum states. A brief conclusion is drawn in Sect. 4.

2 Quantum decision tree classifier model

2.1 Problem statement

A decision tree classifier learns from a training dataset which contains observations about objets, which are either obtained empirically or acquired from experts. In a quantum world, the training data consist of quantum objects instead of classical observations on classical data.

A quantum training dataset with $n$ quantum data pairs can be described as $D = \{(|x_1\rangle , |y_1\rangle ), (|x_2\rangle , |y_2\rangle ), \ldots , (|x_n\rangle , |y_n\rangle )\}$, where $|x_i\rangle$ is the $i$th quantum object of the training dataset and $|y_i\rangle$ is the known class state corresponding to the quantum state $|x_i\rangle$. We call the set of all example quantum states $X = \{|x_1\rangle ,|x_2\rangle ,\ldots ,|x_i\rangle ,\ldots ,|x_n\rangle \}$ the sample set, and the set of all quantum class states $Y = \{|y_1\rangle ,|y_2\rangle ,\ldots ,|y_i\rangle ,\ldots ,|y_n\rangle \}$ is called the class sample set. We also call a class state $|y_i\rangle$ the target attribute state.

A quantum state, $|x_i\rangle$, is represented by a $d$-dimensional attribute vector (or $attribute\ state), \,|x_i\rangle \ = (|x_{1,i}\rangle , |x_{2,i}\rangle , \ldots , |x_{d,i}\rangle )$, depicting $d$ measurements made on the tuple from $d$ attributes, respectively, $a_1, a_2, \ldots , a_d$. For attribute $a_i$, where $i = 1, 2, \ldots , d$, its domain value set $V_{a_i}$ is described as $\{|v_{i,1}\rangle ,|v_{i,2}\rangle ,\ldots ,|v_{i,m_i}\rangle \}$, where $|v_{i,j}\rangle$ is the $j$th basis state and $m_i$ stands for its cardinality. These basis states span a Hilbert space ${S_i}$. Any quantum state $|\phi \rangle$ belongs to the space ${S_i}$ and can be described by a superposition of the basis states:

$$\begin{aligned} \phi \rangle \ =\sum _{j=1}^{m_i}\alpha _{i,j}|v_{i,j}\rangle \end{aligned}$$

(1)

The coefficients $\alpha _{i,j}$ may be complex with $\sum _j|\alpha _{i,j}|^2=1$. The set of all possible input objects is called the instance space, which is defined as a tensor product of all input attributes’ quantum systems: ${S} = {S_1}\otimes {S_2} \otimes \ldots \otimes {S_d}$.

We assume that $C_b = \{|c_{b1}\rangle ,|c_{b2}\rangle ,\ldots |c_{bm}\rangle \}$ is the set of $m$ basis states which describe the class state. $|c_{bi}\rangle$ is called class basis state, where $i = 1, 2, \ldots , m$. These class basis states which span a Hilbert space ${S_c}$ (called class space). A class state $|y_j\rangle$ can be described by a superposition of these class basis states : $|y_j\rangle \ =\sum _{i = 1}^{m}\alpha _{i}|c_{bi}\rangle$, where $\sum _i|\alpha _i|^2=1$. Provided the universal set of distinct class states is described as $C = \{|c_1\rangle ,|c_2\rangle ,\ldots ,|c_i\rangle ,\ldots ,|c_M\rangle \}$, where $|c_i\rangle \ \in {S_c}$. For arbitrary class state $|c_i\rangle \ \in C$ and $|c_j\rangle \ \in C$, we have $|c_i\rangle \ \ne |c_j\rangle$ if $i \ne j$.

Obviously, the sample set belongs to the instance space, i.e., $X \subset {S}$. We also have $Y \subset {S_c}$. In this paper, we restrict arbitrary attribute state $|x_{i,j}\rangle$ and class state $|y_k\rangle$ to pure states.

Given a training dataset $D$ with attribute set $A=\{a_1,a_2,\ldots ,a_i,\ldots ,a_d\}$, for each attribute $a_i \in A$, we denote the set of its attribute states by $D_i$, where $D_i = \{|x_{i,1}\rangle , |x_{i,2}\rangle , \ldots , |x_{i,n}\rangle \}$. And then, the training dataset $D$ can be rewritten as: $D = \{D_1^T, D_2^T,\ldots ,D_d^T, Y^T \}$.

The goal is to form a decision tree classifier that can be used to predict a previously unseen object by explicitly assigning it to a specific class state. More accurately, using the training quantum states and the corresponding class states, a decision tree classifier $t$ is designed. Provided we are given a finite copies of a new pure state $|x_{new}\rangle \in {S}$. By searching over the quantum decision tree $t$, we can obtain a precise class state $|y_{new}\rangle \in C$ corresponding to the quantum state $|x_{new}\rangle$.

In a quantum world, learning is more difficult for a classification algorithm than in a classical world. The reason is that the quantum mechanics forbids us to obtain two or more identical copies of unknown quantum state. In this paper, the constraint can be relaxed by considering the case of multiple copies of the state either to be learn or to be classified (see the quantum template matching problem of [18]). So, in the remainder of the paper, both the training state $|x_{i,j}\rangle$ and the state to be classified $|x_{new}\rangle$ have multiple copies.

2.2 Quantum decision trees

Sometimes, the term quantum decision tree is used while actually referring to a quantum query algorithm or quantum black-box algorithm (for instance, Grover’s algorithm [14]), which calculates the function $f:\{0,1\}^n \rightarrow \{0,1\}$ with the help of quantum superpositions [19, 20]. Such quantum algorithms are in fact not trees. In this context, our quantum decision tree is a real tree like the classical version.

In classical trees, attributes may be either discrete, having values drawn from a known set of possible values, or they may be continuous with values that are real numbers. The outcomes of the test nodes can simply be the values for discrete attributes or the intervals for continuous attributes in the classical setting. However, the above-mentioned method is invalid for quantum decision trees since the values of an attribute can be in superposition states which result in too much distinct data. Overtrained classifier and larger tree would be generated if we split the training dataset according to these distinct discrete values simply. For each attribute, in this paper, we partition or cluster the attribute states into several subclasses according to the fidelity between quantum states. For each subclass of an attribute, we calculate its centroid which can represent the subclass.

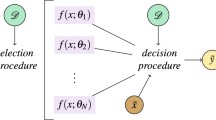
Similar to the classical decision tree, a quantum counterpart $R$ consists of nodes that from a rooted tree, meaning it is a directed tree with a node called root that has no incoming edges. All other nodes have exactly one incoming edge. A node with outgoing edges is called an internal or test node which represents an attribute $a_i \in A$. All other nodes are called leaves or decision nodes which belong to $C$ (the set of class states). In a quantum decision tree, each internal node splits the training dataset into two or more subsets according to a certain discrete function of the input attribute states. In this paper, each test considers a single attribute, such that the training dataset is partitioned according to the subclasses of the attribute. Each leaf is assigned to one class representing the most appropriate target attribute state. A quantum decision tree classifies objects by sorting them down the tree from the root to some leaf node, which provides the classification of the object. An object is classified by starting at the root node of the tree, testing the attribute specified by this node, and then moving down the tree branch corresponding to the subclass of the attribute in the given object. This decision is then repeated for the subtree rooted at the new node.

Given a quantum decision tree $R$ deriving from the training dataset $D = \{(|x_1\rangle ,\,|y_1\rangle ),\,(|x_2\rangle ,\,|y_2\rangle )$, ..., $(|x_n\rangle , |y_n\rangle )\} = \{D_1^T, D_2^T,\ldots ,D_d^T, Y^T \}$. Each node in $R$ is also a tree. Any node $t$ in $R$ is described as $t = \{D^{(t)}, a_i, \{t_{c1}, t_{c2}, \ldots , t_{ct_i}\}\}$, where $D^{(t)}$ is the set of training data in the node $t,\,a_i \in A$, and $\{t_{c1}, t_{c2}, \ldots , t_{ct_i}\}$ is the set of its $t_i$ subnodes. The tree $t$ is split into $t_i$ subtrees according to the attribute $a_i$. Let $t.attribute$ denote the attribute of the node $t$, then $t.attribute = a_i$. For the root $R,\,D^{(R)} = D$.

For a node $t,\,D^{(t)} = \{D_1^{(t)}, D_2^{(t)},\ldots ,D_d^{(t)}, Y^{(t)} \}$. Suppose $t.attribute = a_i$, we divide $D_i^{(t)}$ into $t_i$ clusters: $D_{i,1}^{(t)}, D_{i,2}^{(t)}, \ldots , D_{i,t_i}^{(t)}$, where $D_{i,j}^{(t)} \subseteq D_i^{(t)}$. Each cluster $D_{i,j}^{(t)}$ has a centroid denoted by $|xc_{i,j}^{(t)}\rangle$, then the set of centroids for attribute $a_i$ at node $t$ is described by $XC_i^{(t)} = \{|xc_{i,1}^{(t)}\rangle , |xc_{i,2}^{(t)}\rangle , \ldots , |xc_{i,t_i}^{(t)}\rangle \}$.

Then, for each item $D_j^{(t)} \in D^{(t)}$, it is divided into $t_i$ clusters: $D_{j,1}^{(t)}, D_{j,2}^{(t)}, \ldots , D_{j,t_i}^{(t)}$, where $j \ne i$. The partitioning method is described as below. If a state $|x_{i,k}\rangle \in D_i^{(t)}$ is divided into the set $D_{i,l}^{(t)}$, then we assign the state $|x_{j,k}\rangle \in D_j^{(t)}$ into the cluster $D_{j,l}^{(t)}$, where $1 \le l \le t_i$. The training dataset $D^{(t)}$ then is partitioned into $t_i$ subsets according to the set of centroids, $XC_i^{(t)}$. That is to say, the node $t$ is split into $t_i$ descendant node: $t_{c1}, t_{c2}, \ldots , t_{cj}, \ldots , t_{ct_i}$. In the meantime, the set of target attribute states, $Y^{(t)}$, is also partitioned into $t_i$ subsets described by $Y^{(t)} = \{Y_1^{(t)}, Y_2^{(t)}, \ldots , Y_{t_i}^{(t)}\}$, where $t$ and $i$ mean that the class states is partitioned by attribute $a_i$ at node $t$. For a descendant node $t_{cj}$, we generate an edge with a label $|xc_{i,t_i}^{(t)}\rangle$ by linking node $t$ to node $t_{cj}$. This process is then repeated for each subtree of $t$.

To construct a quantum decision tree, we need to (1) decide which attribute to test at each node in the tree. We would like to select the attribute that is most useful for classifying objects. We discuss the detail of node splitting criterion in Sect. 2.3. (2) clustering the attribute states of expected attribute into appropriate clusters. The problem is discussed in Sect. 2.4.

2.3 Node splitting criterion

Much of research in designing decision trees focuses on assigning which attribute test should be performed at each node. The fundamental principle underlying tree creation is that of simplicity: We prefer decisions that lead to a simple, compact tree with few nodes. According to the principle of Occam’s razor, the simplest model that explains data is the one to be preferred. To this end, we look for an attribute test at each node that makes the subsidiary decision trees to be as simple as possible. In classical algorithms, the most popular criterion is the entropy impurity: $Entropy(t) = \sum _{i=1}^{m_t}-p_ilog_2p_i$, where $p_i$ is the proportion of node $t$ belonging to class $i,\,m_t$ is the total number of classes of node $t$.

Classical node splitting criteria are not working in quantum world since the classes can be in superposition states. We present a new criterion quantum entropy impurity to measure the attributes. Given a quantum decision tree or subtree $t$ and the set of class states $Y^{(t)} = \{|y_1^{(t)}\rangle ,|y_2^{(t)}\rangle , \ldots , |y_{n_t}^{(t)}\rangle \}$ which belongs to $t$, where $Y^{(t)} \subseteq Y$, and $n_t$ is the cardinality of $Y^{(t)}$. Let $Y^{(\mathrm{d}t)} = \{|y_1^{(\mathrm{d}t)}\rangle ,|y_2^{(\mathrm{d}t)}\rangle , \ldots , |y_{n_{\mathrm{d}t}}^{(\mathrm{d}t)}\rangle \}$ denote the set of distinct class states of $Y^{(t)}$, where $n_{\mathrm{d}t}$ is the cardinality of $Y^{(\mathrm{d}t)}$, then $Y^{(\mathrm{d}t)} \subseteq Y^{(t)}, Y^{(\mathrm{d}t)} \subseteq C$, and $n_t \ge n_{\mathrm{d}t}$. For any class states $|y_i^{(\mathrm{d}t)}\rangle \ \in Y^{(\mathrm{d}t)}$ and $|y_j^{(\mathrm{d}t)}\rangle \ \in Y^{(\mathrm{d}t)}$, we have $|y_i^{(\mathrm{d}t)}\rangle \ \ne |y_j^{(\mathrm{d}t)}\rangle$ if $i \ne j$. The quantum entropy impurity of node $t$ can be defined by the following:

$$\begin{aligned} {} S(\rho ) = -tr(\rho \log \rho ) \end{aligned}$$

(2)

where $\rho = \sum _{i=1}^{n_{\mathrm{d}t}}p_i^{(\mathrm{d}t)}|y_i^{(\mathrm{d}t)}\rangle \langle y_i^{(\mathrm{d}t)}|$ is the average state of $Y^{(t)}$ or density operator of $Y^{(t)}$, where $p_i^{(\mathrm{d}t)}$ is the fraction of states $|y_i^{(\mathrm{d}t)}\rangle$ at node $t$ that are in $Y^{(t)}$.

Equation (2) defines quantum entropy or von Neumann entropy of quantum state $\rho$. When the target attribute states in $Y^{(\mathrm{d}t)}$ are all orthogonal, the definition coincides with the classical case.

Given a partial quantum tree down to node $t$ with the set of class states $Y^{(t)} = \{|y_1^{(t)}\rangle ,|y_2^{(t)}\rangle , \ldots , |y_{n_t}^{(t)}\rangle \}$, the key problem is what attribute value we should choose for the attributes test. If the expected splitting attribute is $a_i$ at node $t$, and then, the attribute states belonging to set $D_i^{(t)}$ are partitioned into $t_i$ subsets $D_{i,1}^{(t)}, D_{i,2}^{(t)}, \ldots , D_{i,t_i}^{(t)}$ , the set of class states $Y^{(t)}$ will then be partitioned into $Y_i^{(t)} = \{Y_{i,1}^{(t)}, Y_{i,2}^{(t)}, \ldots , Y_{i,j}^{(t)}, \ldots , Y_{i,t_i}^{(t)}\}$, where $Y_i^{(t)} = Y^{(t)},\,Y_{i,j}^{(t)}$ contains those target attribute states in $Y^{(t)}$ that have attribute states belonging to $D_{i,j}^{(t)}$. The quantum entropy of $Y_{i,j}^{(t)}$ is denoted by $S(\rho _{i,j}^{(t)})$. Then, the expected quantum entropy of the system after node $t$ is split using attribute $a_i$ is

$$\begin{aligned} {} S_e(\rho _i^{(t)}) = \sum _{j=1}^{t_i}p_jS(\rho _{i,j}^{(t)}) \end{aligned}$$

(3)

where $\rho _{i,j}^{(t)}$ is the density operator of $Y_{i,j}^{(t)}$, which represents the set of class states of the $j$th expected subnode $t_{ci_j}$ of attribute $a_i$ in node $t$, and $p_j = |Y_{i,j}^{(t)}|/n_t$ is the probability of state $\rho _{i,j}^{(t)}$. The sum of the probability is equal to 1, i.e., $\sum _{j=1}^{t_i} = 1$.

Quantum entropy specifies the minimum number of qubits of information needed to encode the classification of an arbitrary member of $Y^{(t)}$. The smaller the value of quantum entropy is, the fewer number of qubits is required, and then, the smaller or simpler the quantum decision tree is. For each attribute, we calculate its expected quantum entropy for node $t$, and then, we get $d$ expected quantum entropies for node $t:\, S_e(\rho _1^{(t)}),S_e(\rho _2^{(t)}), \ldots , S_e(\rho _i^{(t)}), \ldots , S_e(\rho _d^{(t)})$. We choose the attribute $a_i$ whose expected quantum entropy $S_e(\rho _i^{(t)})$ is the minimum among above values of quantum entropies as the splitting attribute for node $t$.

We modify the algorithm proposed in [21] to find the splitting attribute with the minimum expected quantum entropy. We call the algorithm finding the splitting node Select_Splitting_Node, and the outline of the algorithm is as follows:

First, the algorithm chooses randomly an index $i$ and then calculates the expected quantum entropy of attribute $a_i$, i.e., $S_e(\rho _i^{(t)})$ which is set to the initially minimum value. Second, Grover’s algorithm is used to find a new index $j$ such that the expected quantum entropy of attribute $a_j$ is smaller than the previous minimum value $S_{e_{min}}$. If the index $j$ is found, we update the minimum value and the index $i$ by $S_e(\rho _j^{(t)})$ and $j$, respectively, and then run Grover’s algorithm repeatedly; otherwise, we get the splitting attribute $a_i$ of node $t$.

In the algorithm, the expected quantum entropy $S_e(\rho _i^{(t)})$ of attribute $a_i$ will be calculated. To obtain the expected quantum entropy, we need to design quantum circuits computing the sum of variables and the von Neumann entropy of a quantum state. Based on quantum mechanics, we can easily build these quantum circuits.

2.4 Attributes data partition

In a quantum decision tree, each decision outcome at a node is called a partition, since it corresponds to splitting a subset of the training data. The root node splits the full training dataset, and each successive decision splits a proper subset of the data. The number of splits at a node is closely related to the type of the attribute and could vary throughout the tree. For a discrete attribute, the classical algorithms create a descendant of current node for each possible value of current attribute, and then, the training objects are sorted to the appropriate descendant node.

Each attribute can be considered as discrete in a quantum decision tree since its values are vectors of a Hilbert space spanned by the attribute’s basis states and can be regarded as a member of an unordered set. An attribute value in the tree can be any linear combinations of the attribute’s basis states; thus, the dataset of the attribute value holds an infinite cardinality. Infinite set will invalidate the classical discrete attribute method. Alternatively, we can extract the distinct values from the training objets for an attribute and then generate a descendant of current node for each distinct attribute value. However, the prerequisite of the manner is the distribution of the attribute values is not too sparse; namely, the number of the distinct attribute values cannot be too large. Otherwise, the generalization of quantum classifier will be worse. An extreme example is that the number of distinct attribute values is equal to the cardinality of the training dataset.

A new attributes data partition method is proposed in this paper. Suppose we are given the training dataset $D^{(t)}$ at node $t$ and the set of attribute states for attribute $a_i \in A: D_i^{(t)} = \{|x_{i,1}^{(t)}\rangle , |x_{i,2}^{(t)}\rangle , \ldots , |x_{i,n_t}^{(t)}\rangle \}$, where $n_t$ is the number of attribute states for tree $t$. We have $D^{(t)} = \{(D_1^{(t)})^T,\,(D_2^{(t)})^T,\ldots ,(D_d^{(t)})^T,\,(Y^{(t)})^T \}$. Let $D_i^{(\mathrm{d}t)} = \{|x_{i,1}^{(\mathrm{d}t)}\rangle , |x_{i,2}^{(\mathrm{d}t)}\rangle , \ldots , |x_{i,n_{\mathrm{d}t}}^{(\mathrm{d}t)}\rangle \}$ denotes the set of distinct attribute states of $D_i^{(t)}$, where $n_{\mathrm{d}t}$ is the cardinality of $D_i^{(\mathrm{d}t)}$, then $D_i^{(\mathrm{d}t)} \subseteq D_i^{(t)}, D_i^{(\mathrm{d}t)} \subseteq D_i$. For any attribute state $|x_{i,j}^{(\mathrm{d}t)}\rangle \ \in D_i^{(\mathrm{d}t)}$ and $|x_{i,k}^{(\mathrm{d}t)}\rangle \ \in D_i^{(\mathrm{d}t)}$, we have $|x_{i,j}^{(\mathrm{d}t)}\rangle \ \ne |x_{i,k}^{(\mathrm{d}t)}\rangle$ if $j \ne k$. We partition the set $D_i^{(t)}$ into $t_i$ subclasses: $D_{i,1}^{(t)}, D_{i,2}^{(t)}, \ldots , D_{i,j}^{(t)}, \ldots , D_{i,t_i}^{(t)}$, where $D_{i,j}^{(t)} \subseteq D_i^{(t)},\,\bigcap _{k = 1}^{t_i}D_{i,k}^{(t)} = D_i^{(t)}$. For any $D_{i,j}^{(t)} \subseteq D_i^{(t)}$ and $D_{i,k}^{(t)} \subseteq D_i^{(t)},\,D_{i,j}^{(t)} \bigcap D_{i,k}^{(t)} = \emptyset$ if $j \ne k$. For each $|x_{i,j}^{(t)}\rangle \ \in D_i^{(t)}$, we can find one and only one subclass $D_{i,k}^{(t)}$ which contains $|x_{i,j}^{(t)}\rangle , i.e., |x_{i,j}^{(t)}\rangle \ \in D_{i,k}^{(t)}$, where $D_{i,k}^{(t)} \subseteq D_i^{(t)}$. For each subclass $D_{i,j}^{(t)}$, we calculate its centroid $|xc_{i,j}^{(t)}\rangle$ which represents the subclass, and the set of the centroids is described by $XC_i^{(t)} = \{|xc_{i,1}^{(t)}\rangle , |xc_{i,2}^{(t)}\rangle , \ldots , |xc_{i,t_i}^{(t)}\rangle \}$. In the meantime, the class states set $Y^{(t)}$ is also split into $t_i$ subset $Y_i^{(t)} = \{Y_{i,1}^{(t)}, Y_{i,2}^{(t)}, \ldots , Y_{i,t_i}^{(t)}\}$, where $Y_i^{(t)} = Y^{(t)}$. For each $|y_j^{(t)}\rangle \ \in Y^{(t)}$, we can find one and only one subset $Y_{i,k}^{(t)}$ which contains $|y_j^{(t)}\rangle , i.e., |y_{o,j}\rangle \ \in Y_{i,k}^{(t)}$, where $Y_{i,k}^{(t)} \in Y_i^{(t)}$. And then, the training dataset $D^{(t)}$ is also partitioned $t_i$ subsets: $D^{(t_{c1})}, D^{(t_{c2})}, \ldots , D^{(t_{cj})}, \ldots , D^{(t_{ct_i})}$, and the $j$th partition is described by $D^{(t_{cj})} = \{(D_{1,j}^{(t)})^T, (D_{2,j}^{(t)})^T, \ldots , (D_{d,j}^{(t)})^T, (Y_{i,j}^{(t)})^T\}$.

Before partitioning an attribute, the data distribution pattern of the attribute is discriminated in advance. Given the attribute $a_i \in A$ and its attribute states set $D_i^{(t)}$ at node $t$, for an attribute state $|x_{i,j}^{(t)}\rangle$, we call the multiplicity of the state to the cardinality of the set multiplicity ratio, denoted by $mr_{i,j}^{(t)} = m_{i,j}^{(t)}/t_i$, where $m_{i,j}^{(t)}$ is the multiplicity of $|x_{i,j}^{(t)}\rangle$ in set $D_i^{(t)}$. We say that an attribute state $|x_{i,j}^{(t)}\rangle$ large state if its multiplicity ratio is not smaller than the user-specified minimum multiplicity ratio (called $minmr$). The number of large states to the number of distinct attribute states in the set is called simple pattern ratio of the attribute $a_i$ at node $t$, defined by $spr_i^{(t)}$. The data pattern of an attribute at a node is simple pattern if its simple pattern ratio is equal or greater than the user specified minimum simple pattern ratio (called $minspr$); otherwise, it is called complex pattern.

In order to determine the data distribution of an attribute, we need to look over all distinct variables in the training data of the given attribute. To achieve this, a quantum search algorithm needs $(1 + \sqrt{2} + \sqrt{3} + \cdots + \sqrt{n}) \approx \frac{2}{3}n^{\frac{3}{2}}$ times Grover’s oracle computing, where $n$ is the number of the values. On the other hand, sorting the states and then counting them is an alternative method which generally makes $cn\log n$ comparisons to sort $n$ items in a classical world, where $c$ is a constant. For the above reason, we just use a classical sorting algorithm, like Quicksort, sorts the attribute states of a node and then counts the large states from the beginning to the end. At last, we determine the data pattern by using simple computing. The algorithm is called Calculating_Pattern. We omit its description due to its triviality.

For an attribute with simple pattern, we just assign each distinct attribute states into an unique subset. When an attribute $a_i$ is characterized by complex pattern, we then group the attribute states into $t_i$ clusters so that states in the same cluster are similar in some sense, and the dissimilar states are in different clusters. An important task in a clustering is to select a similarity measure. Fidelity is a static distance measure of the close degree between two quantum states. Given two quantum states $|x_i\rangle$ and $|x_j\rangle$, their fidelity is denoted by the following:

$$\begin{aligned} F(\rho ,\sigma ) = tr\sqrt{\rho ^{\frac{1}{2}}\sigma \rho ^{\frac{1}{2}}} \end{aligned}$$

(4)

where $\rho = |x_i\rangle \langle x_i|$ and $\sigma = |x_j\rangle \langle x_j|$. The fidelity of two quantum states has the properties of the metric property, contractivity, and strong concavity, and the fidelity is bounded between 0 and 1, i.e., $0 \le F(\rho ,\sigma ) \le 1$. The more similar two states are the greater fidelity between them is, in contrast, the more dissimilar two states are the smaller fidelity between them is. In this paper, we take the fidelity distance as the clustering criterion of quantum states.

Given $n_t$ attribute states set $D_i^{(t)}$ of attribute $a_i$ at node $t$. The clustering process consists of two steps. During the first step, all pairs of states with the largest similarity are searched; then, we create a cluster for each state of the found states, and mark the state as the centroid of each cluster. During the second step, each noncentroid state is assigned to its most similar cluster. The description of the algorithm is as follows:

In the algorithm of Clustering_Attribute, $F_\mathrm{max}$ denotes the variable of the largest fidelity, $\rho _{i,j}^{(\mathrm{d}t)} = |x_{i,j}^{(\mathrm{d}t)}\rangle \langle x_{i,j}^{(\mathrm{d}t)}|$ and $\rho _{i,j_k}^{(\mathrm{d}t)} = |x_{i,j_k}^{(\mathrm{d}t)}\rangle \langle x_{i,j_k}^{(\mathrm{d}t)}|$ are the density operators of the attribute states $|x_{i,j}^{(\mathrm{d}t)}\rangle$ and $|x_{i,j_k}^{(\mathrm{d}t)}\rangle$, respectively, where $|x_{i,j_k}^{(\mathrm{d}t)}\rangle \ \in D_i^{(\mathrm{d}t)}$. During the process of computing the subroutine Calculating_Pattern, the distinct stateset $D_i^{(\mathrm{d}t)}$ is calculated in advance: $D_i^{(\mathrm{d}t)} = \{\mathrm{distinct}\ x| x \in D_i^{(t)}\}$. To a simple pattern, every class member in the same cluster is the same and the centroid of a cluster is just its member. To a complex pattern, we first search the farthest state to each state in set $D_i^{(\mathrm{d}t)}$, and we then obtain the all pairs of centroid. And then, we assign each state into an appropriate group by computing the fidelity between it and each centroid belonging to the set $XC_i^{(t)}$.

Let $DC_i^{(t)} = \{D_{i,1}^{(t)}, D_{i,2}^{(t)}, \ldots , D_{i,j}^{(t)}, \ldots , D_{i,t_i}^{(t)}\}$ to be the set of clusters which are obtained by assigning attribute states for simple pattern or clustering items of an attribute for complex pattern, where $DC_i^{(t)} = D_i^{(t)}$, and $D_{i,j}^{(t)}$ is the $j$th clusters of the attribute $a_i$ at node $t$ of a quantum decision tree. We then partition the training data of attribute $a_i$ at node $t$ into $t_i$ subspaces. The attribute states in a cluster $D_{i,j}^{(t)}$ are all equal or similar. The centroid of a cluster $D_{i,j}^{(t)}$ is denoted by $|xc_{i,j}^{(t)}\rangle$ which is a real state belonging to $D_{i,j}^{(t)}$. For a simple pattern attribute, the centroid of a cluster is the member of the cluster. For a complex pattern, the centroid of an attribute subpartition $D_{i,j}^{(t)}$ is the state which belongs to the intersection of the subpartition $D_{i,j}^{(t)}$ and the set of centroids, $XC_i^{(t)}$, i.e., $|xc_{i,j}^{(t)}\rangle \ = D_{i,j}^{(t)}\cap XC_i^{(t)}$.

2.5 Constructing quantum decision tree

We now construct the quantum decision tree $t$. At first, for each attribute $a_i$, we cluster the data into $t_i$ clusters $D_{i,1}^{(t)}, D_{i,2}^{(t)}, \ldots , D_{i,t_i}^{(t)}$, and these clusters have mutually exclusive centroids $|xc_{i,1}^{(t)}\rangle , |xc_{i,2}^{(t)}\rangle , \ldots , |xc_{i,t_i}^{(t)}\rangle$ which represent the $t_i$ clusters, respectively. The set of the clusters is denoted by $D_i^{(t)}$; we then have $d$ clusters set: $D_1^{(t)},\,D_2^{(t)}$, ..., $D_d^{(t)}$. Second, according to Eq. (3), we calculate the expected quantum entropy after $t$ is split for each attribute, and then, we choose the attribute with the smallest expected quantum entropy as the splitting node. Suppose the splitting attribute is $a_i$, we then split $t$ into $t_i$ descendant nodes and label the edges from node $t$ to each descendant node $|xc_{i,1}^{(t)}\rangle , |xc_{i,2}^{(t)}\rangle , \ldots , |xc_{i,t_i}^{(t)}\rangle$, respectively.

The process of choosing a new attribute and dividing the training data is then repeated for each internal child node. In the process, only the attribute states associated with the child node is used. This process continues until any of two stopping criteria is met: (1) Every attribute has already been included along this path through the tree, or (2) the attribute states associated with the current node all have the same target attribute state (i.e., their quantum entropy is zero).

We then come to a leaf node. A class label is assigned to the node; this is the simplest step in tree construction. The process for constructing a quantum decision tree is described as follows:

In the algorithm, $j$ means that $a_j$ is chosen as a splitting attribute at node $t,\,t_{ci}$ is the $i$th childtree of $t,\,D^{(t_{ci})}$ is the $i$th subset of training dataset $D$. According the ideal stoping criteria, each training object will be classified perfectly and each leaf node corresponds to the lowest quantum entropy impurity. While this is sometimes a reasonable strategy, in fact it can lead to difficulties when there is noise in the data. In this case, the training data will typically be overfit. Conversely, if splitting is stopped too early, then the error on the training data is not sufficiently low and hence performance may suffer. We then set a small threshold value in the reduction in quantum entropy, and splitting is stopped if the best candidate split at a node reduces the impurity by less than that preset amount. Thus, when a quantum tree down to a leaf node, there will be more than one class in the set of target classes, and then, the function Selecting_Class chooses a class state with the most number in the set of class states at the node $t$, the input parameter $D.Y$ of the function means the set of class states of a training dataset $D$.

Besides the quantum entropy impurity threshold, minimum multiplicity ratio, and minimum simple pattern ratio are also used in the subfunction of the algorithm Quantum_Decision_Tree_Classifier. To select better values of these thresholds, we need train them in advance.

2.6 Running time analysis

For the sake of simplicity, we just analyze one case of the algorithm constructing a quantum decision tree. We have the following restrictions:

• (1) The tree is a full quantum decision $k$-$tree$ with $n$ training data.

• (2) All attribute states for each attribute are mutually exclusive.

• (3) The bound errors of the algorithm are not considered.

We first analyze the running time of the sub-algorithms Select_Splitting_Node and Clustering_Attribute.

For the algorithm Select_Splitting_Node, the expected quantum entropy calculation is $k$ times. The running time of the algorithm is $T_1 = c_1k\sqrt{d}$ because that it needs $c_1\sqrt{d}$ queries for finding the most appropriate splitting node, where $c_1$ is a constant.

For the algorithm Clustering_Attribute, to compute the data pattern, we need to sort the training data and then count them in order, so $c_2nlogn + c_3n$ times is required, where $c_2$ and $c_3$ are constant. Let $|x_{i,1}^{(\mathrm{d}t)}\rangle$ be the member of $D_i^{(\mathrm{d}t)}$ at the beginning of clustering process, it requires $\sqrt{n}$ queries for searching an attribute state $|x_{i,j}^{(\mathrm{d}t)}\rangle$. For the second member, we need $\sqrt{n - 1}$ queries since we dot not need to examine the state $|x_{i,j}^{(\mathrm{d}t)}\rangle$ at this time. Similarly, for the third state, we query $\sqrt{n - 2}$ times, and then, we need query $(\sqrt{n} + \sqrt{n-1}+ \cdots + \sqrt{2}) \le \frac{2}{3}n^{\frac{3}{2}}$ times for the first step of clustering. At the second step, the quantum algorithm takes a time in $c_4(n-k)\sqrt{k}$, where $c_4$ is a constant. The running time is then $T_2 = c_2nlogn + c_3n + \frac{2}{3}n^{\frac{3}{2}} + c_4(n-k)\sqrt{k}$.

Now, we calculate the running time of the whole algorithm. At the root node (level 0) of the tree, for each attribute the query time is $T_1 + T_2$. Thus for level 0, the running time is $d(T_1 + T_2)$. For the full $k-tree$, each of the $k$ branches contains $1/k$ training objects. Accordingly, we need $\frac{1}{\sqrt{k}}d(T_1 + T_2)$ queries in level 1. For the level 2, the query times is $\frac{1}{k}d(T_1 + T_2)$, and so on. The total running time of the algorithm is $\frac{(\sqrt{n}-1)\sqrt{k}d}{\sqrt{n}(\sqrt{k}-1)}(T_1 + T_2)$ for the $log_kn$ levels in the tree.

3 Searching over decision tree

Provided we are given a new object $|x_{new}\rangle \ = |x_{1,new}\rangle \otimes |x_{2,new}\rangle \otimes \cdots \otimes |x_{d,new}\rangle$, the classification begins the root node $t$ of a quantum decision tree. Let attribute of the root node be $a_i$, we calculate $t_i$ fidelities between $|x_{i,new}\rangle$ and the centroids of $t_i$ branches of the root node: $F(\rho _{i,new}, \rho _{i,1}^{(t)}),\,F(\rho _{i,new}, \rho _{i,2}^{(t)}), \ldots , F(\rho _{i,new}, \rho _{i,j}^{(t)}), \ldots , F(\rho _{i,new}, \rho _{i,t_i}^{(t)})$, where $\rho _{i,new} = |x_{i,new}\rangle \langle x_{i,new}|$ and $\rho _{i,j}^{(t)} = |xc_{i,j}^{(t)}\rangle \langle xc_{i,j}^{(t)}|$. Suppose the $j$th branch with the largest fidelity is selected, we then follow the $j$th branch to a descendant node $t_{cj}$. The second step is to make the decision at the childnode $t_{cj}$, which can be considered the root of a sub-tree. We continue this way until we reach a leaf node, which has no further test. The new object is then assigned the class of the leaf node reached.

Quantum decision tree is an ordered list. Theoretically, a tree with arbitrary branching factor at different nodes can always be represented by a functionally equivalent binary tree. However, multibranch decision tree is still very popular since the rulers from them are more human readability and understandability in many occasions. We now describe the algorithm for searching over the decision tree:

In the algorithm Searching_Quantum_Tree, $t_{cj}$ denotes the $j$th subtree of $t$, and $XC_i^{(t)} = \{|xc_{i,1}^{(t)}\rangle , |xc_{i,2}^{(t)}\rangle , \ldots , |xc_{i,t_i}^{(t)}\rangle \}$ represents the set of centroids of all subbranches of tree $t$.

Supposing that the quantum decision tree is a full $k-tree$ with $n$ training data, the tree contains $(kn - 1)/(k - 1)$ nodes with a height $h = log_kn + 1$. For algorithm Searching_Quantum_Tree, since we use Grover’s algorithm to search the most possible branch in each node, thus for each node, we need $c_5\sqrt{k}$ queries, and then, the algorithm would have a running time $c_5\sqrt{k}log_kn$ if there is no errors, where $c_5$ is a constant.

4 Conclusion

In this paper, we have investigated the quantum decision tree classification, and then, we described a new simple learning model which could grow a quantum decision tree used for classifying the quantum objects. To construct a quantum tree, we used von Neumann entropy instead of classical shannon entropy as the splitting criterion to determine which attribute should be split. We introduced a quantum clustering algorithm to discretize the quantum training data.

The study of machine learning in the quantum world is still at the budding stage. Many research topics related to decision trees were not involved in this paper. These open problems include the following: (1) how to analyze the error bound of a quantum decision tree; (2) the pruning strategies to stop splitting; (3) how to construct quantum decision trees if some attributes samples are missed; (4) the problem of attributes with differing costs; (5) the problem of training data with quantum noise; and (6) how to generate the quantum classifier if the training data are composed of mixed states instead of pure states. In addition, as a supervised learning method, it is important that the performance of an algorithm is demonstrated experimentally. In classical world, the experiments can be carried out conveniently since there are plenty of repositories of data are publicly available online. On the contrary, it is still uncultivated land for a quantum field.