A preference-based multi-objective evolutionary algorithm using preference selection radius

Abstract

In traditional preference-based multi-objective optimization, the reference points in different regions often impact the performance of the algorithms so that the region of interest (ROI) cannot easily be obtained by the decision maker (DM). In dealing with many-objective optimization problems, the objective space is filled with non-dominated solutions in terms of the Pareto dominance relationship, since the dominance relationship cannot differentiate the mutual relationship between the solutions. To solve the above problems, this paper proposes a new selection mechanism with two main steps. First, we construct a preference radius to divide the whole population into two distinct parts: a dispreferred solution set and a preferred solution set. Second, the algorithm selects the optimal solutions in the preferred solution set by means of the Pareto dominance relationship. If the number of the obtained solutions does not satisfy the quantity’s upper limit, it selects those dispreferred solutions which have smaller distances to the reference direction until the number matches the size of the population. Experimental results show that the algorithm applying the mechanism is able to adapt to different reference points in varying regions in objective space. Moreover, it assists the DM in obtaining different sizes of ROI by adjusting the length of the radius of ROI. In dealing with many-objective problems, the mechanism can dramatically contribute to the convergence of an algorithm proposed in this paper, in comparison with other two state-of-the-art algorithms: g-dominance and r-dominance. Thus, this paper provides a new way to deal with user preference-based multi-objective optimization problems.

1 Introduction

Multi-objective evolutionary algorithms (MOEAs) are one kind of global searching algorithm, and they simulate the biological evolutionary mechanisms to solve multi-objective optimization problems (MOPs) (Deb 2001; Cui and Lin 2005). The objectives in MOPs are often conflicting, wherein an improvement in one objective cannot be achieved without detriment to another objective. Thus, MOEAs often try to search a set of trade-off solutions in the optimization such as NSGA-II (Deb et al. 2002b), SPEA2 (Laumanns 2001), MOEA/D (Zhang and Li 2007), IBEA (Zitzler and Künzli 2004), and so forth. Currently, MOEAs mainly focus on the distribution of Pareto optimal solutions (Deb et al. 2003), the allocation strategies of the fitness value (Davarynejad et al. 2012) and the improvement of the convergence performance (Sindhya et al. 2011).

Fig. 1

Illustration of the ROI

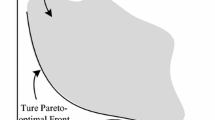
In real life, in most cases, the DM is not interested in searching for the entire Pareto optimal front, but only the region of interest (ROI) (Adra et al. 2007). As shown in Fig. 1, the ROI is defined as the preferred region close to or on the true Pareto front on the basis of the DM’s interests. In the optimization, the preference information specified by the DM could guide a more focused searching to the ROI, so that it could greatly save computing resource. Thus, numerical research has been conducted on the preference-based MOEAs (Chugh et al. 2015; Aittokoski and Tarkkanen 2011; Yu et al. 2015; Deb et al. 2010; Cheng et al. 2015).

According to when the DM provides his or her preference information into the optimization, multiple criteria decision making (MCDM) and evolutionary multi-criterion optimization (EMO) can be divided into three classes—a priori, interactive and a posteriori, respectively (Wang et al. 2015a; Purshouse et al. 2014; Jin and Sendhoff 2002).

• (1) In an a priori decision-making approach, the DMs present their preference information before MOEAs search for ROI. However, it seems to be difficult for the DMs to express their preferences.

• (2) In an interactive decision-making approach, the DM can interfere in the whole process of the optimization. Hence, the DM can learn progressively about the MOPs and then express their preferences interactively. The main drawback of this approach is that the DM may need to be involved intensively during the searching process.

• (3) In an a posteriori decision-making approach, the DM can select the preferred solutions from the final supplied set of compromise solutions. This approach can be effective for MOPs with two or three objectives, because a good approximation of the Pareto optimal front can be relatively easily obtained, and the DM can easily select the preferred solutions from the whole optimal solutions. On the contrary, an a posteriori approach becomes less effective on many-objective optimization problems.

With the progress of preference-based optimization, more and more representative preference-based MOEAs have been proposed. For example, Fonseca and Fleming (1995) firstly applied preference information of the DM in evolutionary optimization and defined the relational operator called “preferability”. Molina et al. (2009) proposed a strengthened relationship called g-dominance to obtain ROI skillfully. Ben Said et al. (2010) proposed a strict partial ordering relationship called r-dominance which could achieve good performance on many-objective evolution problems.

Although many classical evolutionary algorithms have been combined with preference information to solve MOPs, there are still some problems in the optimization. Fonseca and Fleming (1993) firstly attempted to incorporate preference information in EMO. In this approach, the DM should specify aspiration points and reservation points. Additionally, the preference threshold vector and parameter $\varepsilon$ are provided to control the range of ROI. But the main issue of this approach is that it requires the DM to know the ranges of objective values so as to initialize coherent aspiration levels. Another representative approach is the Necessary-preference-enhanced Evolutionary Multi-objective Optimizer (NEMO) proposed by Branke et al. (2015). In this approach, the DM needs to either compare some pairs of solutions which are preferred or to compare intensities of preference between pairs of solutions. Some value functions (Greco et al. 2008) are constructed by the above results to guide the searching process towards ROI. NEMO performs well on bi-objective problems. However, in addressing many-objective problems, its performance scalability has not been examined. Looking into the former research, there are three important issues to be concerned with as follows:

• The locations of the reference points may seriously affect the performance of those user-preference based algorithms. For example, when a specific reference point is close to or on the true Pareto front, g-NSGA-II (Molina et al. 2009) fails to obtain optimal solutions with good convergence and stability.

• Some preference-based MOEAs cannot satisfy the DM to get different sizes of ROI. The size of the obtained region is extremely unstable when the given reference point is located in different regions in the objective space. For instance, the size of the desired region obtained by g-NSGA-II cannot be controlled by the DM.

• On many-objective problems, the traditional preference-based MOEAs commonly apply the Pareto dominance relationship to select solutions, which gives rise to bad convergence, because with the increase of the number of objectives, the number of non-dominated solutions will dramatically increase.

To solve the above problems, this paper proposes a preference-based MOEA based on a new selection mechanism of introducing a preference radius. The preference radius here has two characteristics. First, it can clearly divide the whole population into two parts (a dispreferred solution set and a preferred solution set). Second, it can promote the selection pressure to guide the population approximating to the ROI. About the selection mechanism, it can express and satisfy the DM’s preference information effectively and efficiently without extra settings. Furthermore, the selection mechanism can enhance the convergence as well and exempt the impact from the reference point.

By introducing the selection mechanism and preference radius, the approach proposed in this paper has the following advantages:

• The algorithm is competitive when the specific reference point is in different regions as shown in Fig. 2.

• The proposed model can assist the algorithm in obtaining different sizes of ROI in terms of the DM’s preference information.

• By integrating the selection mechanism proposed in this paper into the NSGA-II (denoted by “p-NSGA-II”), p-NSGA-II has good convergence and stability on two- and three-objective problems.

• The selection mechanism can be applied to deal with many-objective problems with good convergence.

The remainder of this paper is structured as follows. Section 2 gives the basic concepts and related works. Section 3 is devoted to describing our proposed approach and introducing a model of the selection mechanism. Section 4 presents the frame of the approach in this paper, while Sect. 5 validates the new approach by means of comparative experiments. Finally, we conclude in Sect. 6.

Fig. 2

Illustration of the objective space

2 Basic concepts and related works

2.1 Basic concepts

In this section, we present some basic concepts. Without loss of generality, we consider minimization problems, since maximization could be easily transformed to minimization. An MOP can be defined as follows:

$$\begin{aligned} \text {Minimize}: f(x)=(f_1 (x),\cdots , f_m (x))^\mathrm{T} \end{aligned}$$

(1)

such that

$$\begin{aligned}&g_i (x)\le 0\;\;\;\;\;i=1,\ldots , P\end{aligned}$$

(2)

$$\begin{aligned}&h_j (x)=0\;\;\;\;j=1,\ldots , Q \end{aligned}$$

(3)

where $f_i (x)$ is the objective function; m is the number of objectives; $g_i (x)$ and $h_j (x)$ are the constraints of the problem.

Fig. 3

Illustration of the preference model

Definition 1

(Pareto dominance relation) Xand Y are any two individuals in the population. X is said to dominate Y(denoted by$X\prec Y)$ if and only if: $f_i (X)\le f_j (Y)\,\forall i\in \{1,\ldots ,m\}{} \mathrm{and}\;\exists {}j\in \{1,\ldots ,m\}$, where$f_j (X)<f_j (Y)$.

Definition 2

(Pareto optimal set) The Pareto optimal set $P^*$ is defined by: $P^*=\{X\in F;F\;\mathrm{is}\;\mathrm{the}\;\mathrm{feasible}\;\mathrm{space},\;\mathrm{and}X\;\mathrm{is}\;\mathrm{Pareto}\;\mathrm{optimal}\;\}$.

Definition 3

(Pareto front) The Pareto front $PF^*$ is defined by: $PF^*=\{\;f(x)=(f_1 (X),f_2 (X),\ldots ,f_m (X))\vert X\in \{X^*\}\}$, where $f_i (x)$ is the objective function, and $X^*$ is the Pareto optimal set.

Fig. 4

Illustration of g-dominance when the reference point is specified in different regions. The red region is the ROI

2.2 Related works

2.2.1 Preference model

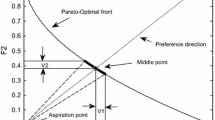
Jaszkiewicz and Słowiński (1999) proposed a model of complex partial preference relations as shown in Fig. 3. The reference point is specified by the DM. In this model, ROI is the region approximating to the optimal Pareto front and the reference direction, which is from the aspiration point to the reference point. This model could save many computational resources, because the reference point allows algorithms to have a much more focused searching. Therefore, applying this model could effectively and efficiently address preference-based MOPs such as Ruiz et al. (2012), Thiele et al. (2009), and Deb et al. (2006).

2.2.2 The g-dominance

On the basis of the Pareto dominance relationship, Molina et al. (2009) proposed a g-dominance relationship combining the traditional Pareto efficiency with the use of reference points. In the g-dominance relationship, the reference point becomes a carrier of preference information, and it redefines the Pareto dominance relation into a simple, flexible dominance relation. The g-dominance can be defined as follows:

Definition 4

(g-Dominance) Given two solutions X and Y , X is said to g-dominate Y if and only if the two solutions satisfy one of the following conditions:

• (1) $\mathrm{Flag}_\mathrm{g} (X)>\mathrm{Flag}_\mathrm{g} (Y).$

• (2) If $X_i \le Y_i$, $\forall i=1,2,\ldots ,m$ and $\mathrm{Flag}_\mathrm{g} (X)=\mathrm{Flag}_\mathrm{g} (Y),$ then $X_j <Y_j \;\;\exists j=1,\;2,\;\ldots ,\;m$.

$\mathrm{Flag}_\mathrm{v} (w)$ can be defined as follows:

$$\begin{aligned} \mathrm{Flag}_\mathrm{v} (w)=\left\{ {{\begin{array}{*{20}c} {1,} \\ {1,} \\ {0,} \\ \end{array} }{\begin{array}{*{20}c} &{} {w_i \le v_i ,} &{} \quad {\forall i=1,\;2,\;\ldots ,m} \\ &{} {v_i \le w_i ,} &{} \quad {\forall i=1,\;2,\;\ldots ,m} \\ &{} {\mathrm{otherwise}} &{} \\ \end{array} }} \right. , \end{aligned}$$

(4)

where v is the reference point, and w is the goal of any point in space.

In Fig. 4, the objective space will be divided into two parts (regions with Flag $=$ 0 and Flag $=$ 1) in terms of the above definition. The solutions in the white regions with Flag $=$ 0 are dominated by the solutions in the blue regions with Flag $=$ 1. Thus, the g-dominance-based algorithm can perform well when the reference point is in the infeasible region or feasible region.

However, when the reference point is close to or on the true Pareto front, the performance of the g-dominance-based algorithm denoted by g-NSGA-II will be degraded and may not converge into the true PF on DTLZ1 (Beume et al. 2009) as shown in Fig. 5.

Fig. 5

Solutions obtained by the g-NSGA-II on DTLZ1

2.2.3 The r-dominance

Ben Said et al. (2010) proposed an r-dominance relationship based on a weighted Euclidean distance to strengthen the Pareto dominance relations. This method enhances the selection pressure and assists the r-dominance relation-based algorithm in finding the preferred solutions. The r-dominance can be defined as follows:

Definition 5

(r-Dominance) Given two solutions $X\;\text{ and }\;Y$, X is said to r-dominate Y if and only if the two solutions satisfy one of the following conditions:

• (1) X dominates Y in the Pareto sense;

• (2) X and Y are Pareto-equivalent and $D(X,Y,g)<-\delta$, where$\delta \in [0,1]$ is termed the non-r-dominance threshold and

$$\begin{aligned} D(X,Y,g)=\frac{\mathrm{Dist}(X,g)-\mathrm{Dist}(Y,g)}{\mathrm{Dist}_{\max } -\mathrm{Dist}_{\min } }, \end{aligned}$$

(5)

$$\begin{aligned}&\mathrm{Dist}_{\max } =\mathrm{Max}_{Z\in P} \mathrm{Dist}(Z,g), \end{aligned}$$

(6)

$$\begin{aligned}&\mathrm{Dist}_{\min } =\mathrm{Min}_{Z\in P} \mathrm{Dist}(Z,g). \end{aligned}$$

(7)

The weighted Euclidean distance is defined as follows:

$$\begin{aligned} \begin{array}{l} \mathrm{Dist}(X,g)=\sqrt{\displaystyle \sum \limits _{i=1}^M {w_i \left( \frac{f_i (X)-f_i (g)}{f_i^{\max } -f_i^{\min } }\right) ^2} } \\ w_i \in [0,1],\quad \displaystyle \sum \limits _{i=1}^M {w_i =1}, \\ \end{array} \end{aligned}$$

(8)

where X is the considered solution; g is the user-specified reference point; $f_i^{\max }$is the upper bound of the $i\mathrm{th}$ objective value;$f_i^{\min }$is the lower bound of the $i\mathrm{th}$ objective value; and $w_i$is the weight associated with the $i\mathrm{th}$ objective.

However, when the reference point is in the feasible region, the r-dominance relation-based algorithm denoted by r-NSGA-II fails to converge into the true Pareto front on DTLZ5 (Deb et al. 2002a) as shown in Fig. 6. The reason is that Eq. (8) tries to guide the solutions to the reference point, so that it may lead the solutions away from the true Pareto front when the reference point is in the feasible region.

Fig. 6

Solutions obtained by the r-NSGA-II on DTLZ5

3 The proposed approach

In this section, we detail the proposed approach. Firstly, some basic relevant concepts are described. Secondly, a simple preference-based model of the proposed approach is illustrated. Finally, we improve the model to satisfy the DM to obtain different sizes of ROI by adjusting the size of the preference radius.

Fig. 7

Illustration of the preference radius

3.1 Basic definition of the proposed approach

Definition 6

(Reference direction) The direction vector from a starting point to the reference point is referred to as reference direction.

Definition 7

(Radius of ROI) The radius of the preferred region (denoted by $\bar{d})$ is defined as the radius of the region of interest (ROI). The parameter $\bar{d}$ is given by the DM and $0\le \bar{d}\le 1$.

Definition 8

(Preference radius) The preference radius (denoted by $d_{p^j}$in Fig. 7) can be defined as follows:

$$\begin{aligned} {{d_{p^j} =\sum \limits _i^N {d_{P_i^j } } }} \! /N, \end{aligned}$$

(9)

where $d_{P_i^j } =\sqrt{\vert \overrightarrow{OB} -\overrightarrow{Oi} \vert ^2}$ (shown in Fig. 7) and $d_{P_i^j }$ is the distance from solution i to the reference direction in the jth generation; N is the population size; thus, $d_{P_i^j }$ is the average value in terms of Definition 8.

$$\begin{aligned}&\overrightarrow{OB} =(\overrightarrow{Oi} \bullet \overrightarrow{E} )\bullet \overrightarrow{E} =\left( \frac{\overrightarrow{Oi} \bullet \overrightarrow{E} }{\vert \overrightarrow{E} \vert }\right) *\overrightarrow{E} =\mathrm{COS}\theta *\vert \overrightarrow{Oi} \vert *\overrightarrow{E},\nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned}&\overrightarrow{E} =\frac{\overrightarrow{OR} }{\vert \overrightarrow{OR} \vert }, \end{aligned}$$

(11)

where B is the pedal; R is a reference point; $\vec {E}$ is a unit vector; $\overrightarrow{OR}$ is the reference direction; and $\theta$ is the angle between vector $\overrightarrow{Oi}$ and $\vec {E}$ as shown in Fig. 7.

At the beginning of the algorithm, we set preference radius $d_{p^0} =\infty$, then calculated the preference radius for each generation by Eq. (9). During the optimization, if $d_{P^j}$ is less than or equal to $\bar{d}$, we set the parameter $d_{P^j} =\bar{d}$, else if $d_{P^{j}}$ is greater than $d_{P^{j-1}}$, we set $d_{P^j} =d_{P^{j-1}}$; otherwise, we set $d_{P^j} =d_{P^j}$.

Definition 9

(Preference region) The preference region is the region surrounding the reference direction, and its radius is defined as in Definition 8. Figure 8 shows that the $d_{p}^{j}$ is the radius of the preference region.

Definition 10

(Non-preference region) The regions excluding the preference region are defined to be the non-preference region.

Fig. 8

Illustration of the two-objective model

Fig. 9

Relation between the number of objectives and non-dominated solutions

3.2 The model of a new selection mechanism

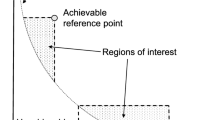
With the increase of the number of objectives, the number of non-dominated solutions dramatically increases (Purshouse and Fleming 2003) as shown in Fig. 9. Although the traditional algorithms using the Pareto dominance relationship have good convergence in addressing two- and three-objective MOPs (Hughes 2005; Zitzler and Thiele 1998), their performance is degraded in many-objective problems (Adra and Fleming 2009; Wagner et al. 2007). Furthermore, the size of the ROI may not be controlled by the DM (Adra et al. 2007).

To illustrate the model of the new selection mechanism, Fig. 8 presents the two-dimensional model, in which the reference direction starts from the origin to the reference point, and the current preference radius $(d_{P^j})$ is calculated from the parent preference radius and the radius of ROI ($\overline{d})$. The details of the mechanism are as follows:

First, we use a preference radius to divide the population into two parts. One of them is a preferred solution set and the other a dispreferred solution set. Then, we calculate the number of solutions in the preferred solution set. After that, if the number is bigger than the population size, then the superfluous solutions by Pareto dominance relationship are removed, or if the number is smaller than the size, those solutions which have smaller distances to the reference direction in the dispreferred solution set are selected until the number matches the population size. Particularly, if all the preferred solutions are non-dominated, we calculate the crowding distance of each solution, and the solution with the smallest crowding distance will be eliminated until the number of preferred solutions matches the population size.

Fig. 10

Effect of varying radius of ROI by setting $\bar{d}=0.0,\;{}\bar{d}=0.1,\;{}\bar{d}=0.5,\;{}\bar{d}=1.0$ on the DTLZ5

The new selection mechanism tries to separate the solutions into two different sets and guide the solutions to the ROI, so that the algorithm based on this mechanism is able to obtain the preferred solutions satisfying the DM. Compared with representative preference-based MOEAs such as g-NSGA-II and r-NSGA-II, the algorithms applying this mechanism not only reduce consumption of resources, but also have better performance.

It is important to mention that the preference region is a rectangular area in the two-objective case and is a cylinder in the three-dimension case. In the model, the location information of the reference point is converted into reference direction and preference radius, and the algorithm based on this mechanism can adjust to the reference points specified in different regions.

Furthermore, in terms of the mechanism, it is obvious that the key issue is to construct the preference radius which is closely linked to the acquisition of stable ROI. So in the next section, we analyze the relation between a preference radius and ROI.

3.3 The effect of the radius of ROI

In dealing with preference-based MOPs, the DM always has requirements for the size of ROI, while some of the traditional preference-based MOEAs cannot satisfy these requirements. To test the effect of the radius of ROI, this paper conducts an experiment by setting different lengths of radii of ROI.

In this experiment, we operate four different sets of radii of ROI on problem DTLZ5 (Deb et al. 2002a) with $\bar{d}=0.0,\;{}\bar{d}=0.1,\;{}\bar{d}=0.5,\;{}\bar{d}=1.0$ , and the reference point is specified as (0.7, 0.7, 0.8) and shown with a red star.

In Fig. 10, there are four different charts which show the effect of varying lengths of radius of ROI. When the radius of ROI is set to be $\bar{d}=0.0$, the solutions converge to one point as shown in Fig. 10a. The range of the obtained ROI covers or approximates the whole true Pareto optimal front by setting $\bar{d}=1.0$ as shown in Fig. 10d. It is apparent that the range of the ROI increases with the increase of the value of radius of ROI. Therefore, it can be concluded that the DM is able to control the spread of the obtained ROI by adjusting the radius of ROI.

4 The frame of the selection mechanism-based approach

In this section, we first introduce the main frame of the approach. Then instructions on how to apply the selection mechanism into the EnvironmentSelection are given. Finally, we analyze the complexity.

Algorithm 1 is the main frame of this paper. The radius of ROI in the input items is given by the DM. At the beginning of the algorithm, the solution set P is randomly generated and evaluated. Then, the offspring population Q is obtained from P after the evolutionary operations such as MatingSelection, Crossover and Mutation. After that, the set P and Q are combined into a mixed population R that is $R=P\cup Q$. The environment selection elicits the new generation P from the mixed population R. This process is repeated to update the population set P until termination. The population set (P) is exported finally.

Algorithm 2 presents the environment selection in detail. Firstly, two empty Population P and L must be created. Then the jth preference radius $d_{p^j}$ is achieved in line 2, which is described in Algorithm 3. For each solution $x_i$, if its preference radius $d_{P_i^j }$ is smaller than $d_{p^j}$, the solution is added into P like $P=P\cup \{x_i \}$. Otherwise, it is added into L as shown in line 7. After that, to maintain the solution size (n), two main steps must be executed. Firstly, when the size of P is smaller than the specified population size (n), line 12 is executed; otherwise, line 15 Elimination (P) is executed. Line 12 selects the candidate solutions from the set L by sorting their preference radii, and the solution with a minimum preference radius will be selected. In conclusion, Algorithm 2 selects optimal solutions from population R.

Algorithm 3 introduces how to obtain the average preference radius of population R. First, the preference radius of each solution is calculated in the set R in terms of Definition 8, and the average preference radius of the population is acquired. Next, the preference radius of the current population is determined by comparing the father preference radius $(\,d_{p^{j-1}})$, the radius of ROI $(\overline{d})$ provided by the DM and $d_{p}^{j}$.

Algorithm 4 chooses elite solutions in the solution set R by fast-non-dominated-sort (Deb et al. 2002b) and crowding_distance_assignment (Deb et al. 2002b). The fast-non-dominated-sort aims to sort the whole population into different layers {L1, L2, ...}. In terms of the size of each layer, when the sum of the size of the current population and the selected Li is smaller than n, then the solutions in this layer are added into the current population as shown in line 5. Otherwise, line 7 is executed. Line 7 selects optimal solutions in the final layer Li in terms of their crowding distances. Notably, crowding_distance_assignment promotes the diversity of the population, because the adjacent solutions are eliminated with smaller crowding distances.

In conclusion, the main complexity of Algorithm 1 lies in the EnvironmentSelection. In Algorithm 4, in the worst case, the complexity of fast-non-dominated-sort is $O(mN^2)$ and that of crowding distance assignment is $O(mN\mathrm{log}N)$, where m is the number of objectives and N is the population size. In Algorithm 3, the first iteration requires O(mN) computations. Thus, the total complexity of this algorithm is O(mN). The complexity of Algorithm 2 mainly focuses on the computation of the preference radius (which costs O(mN) computations) and the elimination selection (which costs O(mN) computations). Therefore, the overall complexity of the algorithm is $O(mN^2)$.

5 Experimental study

This section presents the experimental study of this paper. The first subsection presents the parameters setting. The second subsection introduces the experimental evaluation indicator. The third subsection analyzes and compares the experimental results obtained by our proposed approach and other state-of-the-art algorithms.

5.1 Parameter setting

In problems of comparison, the two sets of ZDT (Zitzler et al. 2000) and DTLZ (Deb et al. 2002a) problems are considered. The ZDT1–ZDT4 and ZDT6 are chosen to be the two-objective test instances. The DTLZ1–DTLZ6 are chosen to be the three-objective test instances. The 5-, 8-, 10- and 15-objective DTLZ2 and DTLZ3 are chosen to be the many-objective test instances.

For each test instance, we present the mean and variance of GD values of the obtained results over 30 independent simulation runs. In all simulations, we use the simulations binary crossover operation with a distribution index of 10 and polynomial mutation with a distribution index of 20 (Deb 2002). The crossover probability and mutation probability are set to $P_\mathrm{c} =0.9$ and $P_\mathrm{m} =0.03,$ respectively, on the set of ZDT test instances. The parameters $P_\mathrm{c}$ and $P_\mathrm{m}$ are set to be 0.9 and 0.08, respectively, on the set of DTLZ test instances. The size of the population is 100 on two- or three-objective test problems. The size of the population is 200 on other test problems. The maximum number of the generation is 299 on two- and three-objective test instances. Especially, the maximum number of the generations is set to be 599 on ZDT4, and 999 on DTLZ3 and DTLZ6, because the ZDT4, DTLZ3 and DTLZ6 test instances are designed to make it difficult to approximate the true PF. For all test instance experiments, the parameter $\bar{d}$ in p-NSGA-II is set to be 0.1 and the parameter $\delta$ in r-NSGA-II is set to be 0.3.

In this paper, to inspect the effect of the locations of the reference point on the algorithms, three scenarios are considered. The first one is to specify the reference points in the infeasible region (far away from the true Pareto front). The second one is that the reference points are very close to or on the true Pareto front. The third one is that the reference points are given in the feasible region. Finally, some special reference points: (0.0, 0.0, 0.6), (0.0, 0.6, 0.0) and (0.6, 0.0, 0.0) are specified to test the robustness of the algorithms. The settings of the reference points are presented in Table 1.

Table 1 Reference points setting in the infeasible region, on/close to PF, and in the feasible region on two- and three-objective instances

5.2 Evaluation indicator

In this subsection, we will present the evaluation indicator. In our experiments, the following performance index is adopted to measure the closeness of a solution front (PF$_{\mathrm{solution}}$) to the Pareto optimal front ($\mathrm{PF}_{\mathrm{true}})$.

Generational distance (GD) (Van Veldhuizen and Lamont 1998): the GD is defined as follows:

$$\begin{aligned} \mathrm{GD}=\frac{\sqrt{\sum \nolimits _{i=1}^n {\mathrm{dist}_i^2 } } }{n}, \end{aligned}$$

(12)

where n is the number of solutions and dist$_i$ is the Euclidean distance between each solution in PF$_{\mathrm{solution}}$ and the nearest member in the Pareto optimal front. The smaller the value of GD, the better is the convergence of the algorithm.

5.3 Comparative experiments

In this subsection, firstly, the p-NSGA-II is compared with two state-of-the-art reference-based evolutionary multi-objective optimization approaches: (1) the g-dominance (Molina et al. 2009) and (2) the r-dominance (Ben Said et al. 2010). We experimentally demonstrate the positive effect of managing varying locations of the reference points and achieving varying sizes of the desired region. Secondly, we demonstrate the selection mechanism’s positive effect on convergence; and especially on addressing many-objective problems, the p-NSGA-II and the p-non-NSGA-II are compared to g-dominance and r-dominance.

Table 2 The GD values of the solutions obtained by the p-NSGA-II, g-NSGA-II on the set of ZDT and DTLZ

5.3.1 The p-NSGA-II versus g-dominance on two- and three-objective problems

In this subsection, we compare the p-NSGA-II to the g-dominance relation on two- and three-objective optimization problems. Here, the NSGA-II version incorporating the g-dominance relation is denoted by the g-NSGA-II. We conducted experiments with the sets of ZDT and DTLZ test instances on three scenarios with the reference point in the feasible region, on/close to the true PF, and in the infeasible region. The settings of the reference points are listed in Table 1. Moreover, we also conducted experiments by using some special reference points to test the stability of p-NSGA-II.

Table 2 shows the mean and variance of GD values of the obtained results over 30 independent simulation runs on the sets of ZDT and DTLZ test instances. The best mean and variance of the GD values are shown in bold type.

From Table 2, it is obvious that the GD values obtained by p-NSGA-II are smaller than 0.01, which means that p-NSGA-II has converged into the Pareto optimal front. Moreover, most of them are smaller than that of g-NSGA-II. Notably, the mean and variance of the GD values of solutions obtained by the p-NSGA-II are remarkably less than the solutions obtained by the g-NSGA-II on ZDT1, ZDT2, ZDT3 and on the whole set of DTLZ test instances in these three scenarios, which denotes that p-NSGA-II has better convergence than g-NSGA-II on those instances, and the locations of the reference points have little effect on the performance relatively. However, on ZDT1 when the reference point is close to the true PF, the values obtained by g-NSGA-II are smaller than that of p-NSGA-II. Solutions obtained by g-NSGA-II converge into one point shown in Fig. 11b, which indicates that g-NSGA-II cannot meet the DM’s needs to get a relatively stable ROI.

Fig. 11

Optimal solutions on ZDT1 with the reference point in the infeasible region (0.1, 0.2): a g-NSGA-II, b p-NSGA-II; on/close to true PF (0.5, 0.3): c g-NSGA-II, d p-NSGA-II; and in the feasible region (0.5, 0.6): e g-NSGA-II, f p-NSGA-II

Fig. 12

Optimal solutions on DTLZ2 with the reference point in the infeasible region (0.2, 0.3, 0.4): a g-NSGA-II, b p-NSGA-II; on/close to true PF (0.5, 0.7, 0.5): c g-NSGA-II, d p-NSGA-II; and in the feasible region (0.7, 0.8, 0.8): e g-NSGA-II, f p-NSGA-II

Fig. 13

Optimal solutions on DTLZ3 with the reference point in the infeasible region (0.3, 0.4, 0.5): a g-NSGA-II, b p-NSGA-II; on/close to true PF (0.4, 0.8, 0.45): c g-NSGA-II, d p-NSGA-II; and in the feasible region (0.8, 0.8, 0.8): e g-NSGA-II, f p-NSGA-II

Fig. 14

Optimal solutions on DTLZ2 with the reference point in special regions (0.6, 0.0, 0.0): a g-NSGA-II, b p-NSGA-II, (0.0, 0.6, 0.0): c g-NSGA-II, d p-NSGA-II and (0.0, 0.0, 0.6): e g-NSGA-II, f p-NSGA-II

Especially, on DTLZ2 with the reference points in the infeasible region and on the true PF as shown in Fig. 12, there are still some solutions obtained by g-NSGA-II not converging into the true PF, and it can be explained by the fact that some solutions are Pareto-equivalent to the reference point and discouraged to remain in the race. From the figure, when the reference points are in the feasible region, the p-NSGA-II also outperforms the g-NSGA-II. Also, on DTLZ3 in Fig. 13, solutions obtained by g-NSGA-II cannot converge into the true PF on three scenarios, but p-NSGA-II has good convergence and stability. It can be validated that although the preference point varies, the DM can still control the spread of the obtained ROI by setting the parameter $\bar{d}$ in terms of p-NSGA-II. Another experiment also demonstrates p-NSGA-II has better performance as shown in Fig. 14. The experiment was conducted by setting some special reference points: (0.6, 0.0, 0.0), (0.0, 0.6, 0.0), (0.0, 0.0, 0.6) on DTLZ2. From the experiment, we can see that p-NSGA-II could acquire the ROI under these special conditions, which means that p-NSGA-II has better stability.

In summary, the p-NSGA-II has better convergence than the g-NSGA-II. Moreover, it can control the spread of the ROI. Thus, the selection mechanism can promote the convergence of p-NSGA-II and stabilize ROI.

5.3.2 The p-NSGA-II versus r-dominance on two- and three-objective problems

In this subsection, we compare the p-NSGA-II with the r-dominance relation-based NSGA-II (r-NSGA-II) on two- and three-objective optimization problems. The r-NSGA-II can enhance the pressure of convergence by creating a strict partial order among Pareto-equivalent solutions. The relevant settings are shown in Table 1.

Table 3 presents the mean and variance of GD values of the obtained solutions of r-NSGA-II and p-NSGA-II. It can be seen that in most of the test instances, the mean and variance of GD values of the solutions obtained by p-NSGA-II are smaller than those by r-NSGA-II, which demonstrates that p-NSGA-II has better stability and convergence than r-NSGA-II when the reference points are in three regions (in the feasible region, on or close to the true Pareto front, and in the infeasible region). Specifically, on ZDT1 in Fig. 15c, the solutions obtained by r-NSGA-II converge to a small region, which fails to satisfy the DM when the reference point is on/close to the true Pareto front. Additionally, in Fig. 16e, r-NSGA-II performs worse than the p-NSGA-II on DTLZ5 when the reference point is in the feasible region. Specially, the p-NSGA-II has better stability than r-NSGA-II with some special reference points: (0.6, 0.0, 0.0), (0.0, 0.6, 0.0), and (0.0, 0.0, 0.6) as shown in Fig. 17. The conclusion to draw from all these observations is that the selection mechanism could increase the pressure of convergence and assist p-NSGA-II to obtain the desired regions.

However, about ZDT6, the r-NSGA-II has better performance than the p-NSGA-II when the reference points are in the feasible and on or close to the true Pareto front. This phenomenon can be explained by the fact that there are not many solutions in the preference region when the reference radius is small. Thus, more solutions are selected from dispreferred solution set, which gives rise to bad performance of p-NSGA-II. On DTLZ3, the solutions obtained by r-NSGA-II have converged, but they cover the whole Pareto front as shown in Fig. 18a, c, and e, when the reference point is under the three scenarios. This phenomenon indicates that the r-NSGA-II may fall into the optimum and perform badly. On the contrary, p-NSGA-II can not only converge to the true Pareto front, but also acquire a stable ROI as shown in Fig. 18b, d, and f.

In summary, the selection mechanism is able to contribute to p-NSGA-II increasing the pressure of convergence and obtaining stable ROI.

Table 3 The GD values of the solutions obtained by the p-NSGA-II, g-NSGA-II on the sets of ZDT and DTLZ

Fig. 15

Optimal solutions on ZDT1 with the reference point in the infeasible region (0.1, 0.2): a r-NSGA-II, b p-NSGA-II; on/close to true PF (0.5, 0.3): c r-NSGA-II, d p-NSGA-II; and in the feasible region (0.5, 0.6): e r-NSGA-II, f p-NSGA-II

Fig. 16

Optimal solutions on DTLZ5 with the reference point in the infeasible region (0.3, 0.3, 0.4): a r-NSGA-II, b p-NSGA-II; on/close to true PF (0.4, 0.4, 0.82): c r-NSGA-II, d p-NSGA-II; and in the feasible region (0.7, 0.7, 0.8): e r-NSGA-II, f p-NSGA-II

Fig. 17

Optimal solutions on DTLZ2 with the reference point in special regions (0.6, 0.0, 0.0): a r-NSGA-II, b p-NSGA-II, (0.0, 0.6, 0.0): c r-NSGA-II, d p-NSGA-II, and (0.0, 0.0, 0.6): e r-NSGA-II, f p-NSGA-II

Fig. 18

Optimal solutions on DTLZ3 with the reference point in the infeasible region (0.3, 0.4, 0.5): a r-NSGA-II, b p-NSGA-II; on/close to true PF (0.4, 0.8, 0.45): c r-NSGA-II, d p-NSGA-II; and in the feasible region (0.8, 0.8, 0.8): e r-NSGA-II, f p-NSGA-II

Table 4 The GD values of the solutions obtained by the p-NSGA-II, p-non-NSGA-II, r-NSGA-II, g-NSGA-II on 5-, 8-, 10-, and 15-objective DTLZ2

Fig. 19

Optimal solutions on five-objective DTLZ2 with the reference point (0.1, 0.3, 0.2, 0.4, 0.2). a g-NSGA-II, b r-NSGA-II, c p-non-NSGA-II, d p-NSGA-II

5.3.3 Comparative experiments on the many-objective problems

To demonstrate that the selection mechanism could be applied to deal with many-objective problems, we conduct comparative experiments with four algorithms: p-NSGA-II, p-non-NSGA-II, g-NSGA-II and r-NSGA-II. The p-non-NSGA-II only changes the elimination selection (in Algorithm 4) into the random selection on DTLZ2 and DTLZ3 with 5, 8, 10, and 15 objectives. The population size is set to be 200, and the reference points are (0.10, 0.30, 0.20, 0.40, 0.20) on 5-objective instances, (0.30, 0.30, 0.30, 0.10, 0.30, 0.55, 0.35, 0.35) on 8-objective instances, (0.30, 0.30, 0.30, 0.10, 0.30, 0.55, 0.35, 0.35, 0.25, 0.45) on 10-objective instances, and (0.30, 0.30, 0.30, 0.10, 0.30, 0.55, 0.35, 0.35, 0.25, 0.45, 0.10, 0.40, 0.20, 0.30, 0.10) on 15-objective instances.

Fig. 20

Optimal solutions on ten-objective DTLZ2 with the reference point (0.3, 0.3, 0.3, 0.1, 0.3, 0.55, 0.35, 0.35, 0.25, 0.45). a g-NSGA-II, b r-NSGA-II, c p-non-NSGA-II, d p-NSGA-II

Fig. 21

Optimal solutions on 15-objective DTLZ2 with the reference point (0.3, 0.3, 0.3, 0.1, 0.3, 0.55, 0.35, 0.35, 0.25, 0.45, 0.1, 0.4, 0.2, 0.3, 0.1). a g-NSGA-II, b r-NSGA-II, c p-non-NSGA-II, d p-NSGA-II

Table 5 The GD values of the solutions obtained by the p-NSGA-II, p-non-NSGA-II, r-NSGA-II and g-NSGA-II on 5-, 8-, 10- and 15-objective DTLZ3

Firstly, DTLZ2 is designed to investigate the scalability of algorithms. Table 4 presents the GD values of the solutions obtained by four algorithms. In Table 4, the solutions obtained by p-NSGA-II and r-NSGA-II both converge to the true Pareto optimal region. The mean of GD values of the solutions obtained by r-NSGA-II is smaller than that obtained by p-NSGA-II on 5- and 8-objective DTLZ2, but the result is inverse on 10- and 15-objective DTLZ2. The main reason is that the number of non-dominated solutions increases when the problem dimensions increase. In comparison with p-NSGA-II, p-non-NSGA-II could still converge to five-, eight-, ten- and fifteen-objective DTLZ2 without applying the Pareto dominance relationship, which means that the selection mechanism has dominated promotion to the convergence of p-NSGA-II rather than the Pareto dominance relationship.

Figures 19, 20, and 21 present the obtained solutions by the algorithms, and each line stands for a solution. From those figures, the solutions obtained by p-NSGA-II and the r-NSGA-II are able to converge to the true Pareto optimal region on 5-, 8-, 10-, and 15-objective DTLZ2 except g-NSGA-II. The reason why g-NSGA-II cannot obtain ROI on many-objective problems is that the number of non-dominated solutions dramatically increases when the problem dimension increases. Importantly, p-non-NSGA-II performs better than the g-NSGA-II on those many-objective problems; in other words, the selection mechanism could increase the pressure of convergence and allow a much more focused searching. Notably, the p-non-NSGA-II is able to converge to the PF on five-, eight-, and ten-objective DTLZ2, but its mean and variance of GD values are bigger than that of p-NSGA-II and r-NSGA-II. This phenomenon is probably caused by the random selection, which cannot ensure that the solutions selected by the p-non-NSGA-II are close to the Pareto optimal region. However, by applying the selection mechanism, p-NSGA-II can perform better than r-NSGA-II on 10- and 15-objective problems.

Fig. 22

Optimal solutions on five-objective DTLZ3 with the reference point (0.1, 0.3, 0.2, 0.4, 0.2). a g-NSGA-II. b r-NSGA-II. c p-non-NSGA-II. d p-NSGA-II

Fig. 23

Optimal solutions on ten-objective DTLZ3 with the reference point (0.3, 0.3, 0.3, 0.1, 0.3, 0.55, 0.35, 0.35, 0.25, 0.45). a g-NSGA-II. b r-NSGA-II. c p-non-NSGA-II. d p-NSGA-II

Fig. 24

Optimal solutions on 15-objective DTLZ3 with the reference point (0.3, 0.3, 0.3, 0.1, 0.3, 0.55, 0.35, 0.35, 0.25, 0.45, 0.1, 0.4, 0.2, 0.3, 0.1). a g-NSGA-II. b r-NSGA-II. c p-non-NSGA-II. d p-NSGA-II

Secondly, DTLZ3 is applied to investigate the ability to converge to the global Pareto front. In Table 5, the mean and variance of the GD values of solutions obtained by p-NSGA-II are the smallest than those of all the algorithms, which means that p-NSGA-II outperforms the other algorithms, and it also can be seen in Figs. 22, 23 and 24. Specifically, g-NSGA-II and r-NSGA-II cannot converge to the true Pareto front on all many-objective DZLZ3, as g-NSGA-II and r-NSGA-II are easy to trap into the local optima. While p-non-NSGA-II could also converge into the global Pareto front and perform better than the g-NSGA-II and the r-NSGA-II, both the preference radius and the selection mechanism could promote the convergence.

From the above experiments, the proposed approach (p-NSGA-II) benefits from the mechanism and the preference radius avoids falling into the local optimum. Furthermore, the performance of p-NSGA-II is much better than that of p-non-NSGA-II. Therefore, integrating the selection mechanism using a preference radius with the Pareto dominance relationship could assist the algorithm in converging and obtaining better optimal solutions.

6 Conclusion

In this paper, we proposed a new selection mechanism based on the preference radius. This new approach has the following characteristics:

• The p-NSGA-II can obtain the ROI with the reference points in three scenarios (the reference point in the feasible region, on/close to the Pareto front and in the infeasible region).

• The spread of the obtained ROI can be controlled by adjusting the size of the radius of interest.

• The p-NSGA-II has better performance compared with g-NSGA-II and r-NSGA-II on most two- and three-objective problems.

• The new selection mechanism of introducing the preference radius could prompt the convergence of the algorithm, especially on many-objective problems.

On some problems, we could extend this approach. The new selection mechanism could also be applied to different classes of multi-objective evolutionary algorithms such as SPEA2 Laumanns (2001), MOEA/D Zhang and Li (2007), Hype Bader and Zitzler (2011), PICEAs Wang et al. (2013), Wang et al. (2015b), MSPSO Santana-Quintero et al. (2006), and so on. Furthermore, we will research how to apply p-NSGA-II to deal with the MOPs based on multiple reference points.