Decomposing the user-preference in multiobjective optimization

Abstract

Preference information (such as the reference point) of the decision maker (DM) is often used in multiobjective optimization; however, the location of the specified reference point has a detrimental effect on the performance of multiobjective evolutionary algorithms (MOEAs). Inspired by multiobjective evolutionary algorithm-based decomposition (MOEA/D), this paper proposes an MOEA to decompose the preference information of the reference point specified by the DM into a number of scalar optimization subproblems and deals with them simultaneously (called MOEA/D-PRE). This paper presents an approach of iterative weight to map the desired region of the DM, which makes the algorithm easily obtain the desired region. Experimental results have demonstrated that the proposed algorithm outperforms two popular preference-based approaches, g-dominance and r-dominance, on continuous multiobjective optimization problems (MOPs), especially on many-objective optimization problems. Moreover, this study develops distinct models to satisfy different needs of the DM, thus providing a new way to deal with preference-based multiobjective optimization. Additionally, in terms of the shortcoming of MOEA/D-PRE, an improved MOEA/D-PRE that dynamically adjusts the size of the preferred region is proposed and has better performance on some problems.

1 Introduction

In real life, most complex problems are optimization problems. Because of this, may state-of-the-art optimization algorithms (Bastos-Filho et al. 2011; Precup et al. 2011; Serdio et al. 2014; El-Hefnawy 2014) have been developed to solve these problems. However, there are still a number of problems that are hard to solve, most of which are multiobjective optimization problems (MOPs). A multiobjective optimization problem can be defined mathematically as follows:

$$\begin{aligned} \text {minimize: } F(x) = (f_{1}(x),\ldots ,f_{m}(x))^T \text {subject to: } x\in {\Omega },\nonumber \\ \end{aligned}$$

(1)

where $\Omega$ is the decision (variable) space, $F: \Omega \rightarrow {R}^{m}$ consists of m real-valued objective functions and ${R}^{m}$ denotes the objective space. The attainable objective set is defined as the set $\{F(x)\mid x \in {\Omega }\}$.

If $x \in {R}^{m}$, all the objectives are continuous, and $\Omega$ is described by $\Omega = \{x \in R^{m}\mid h_{j}(x)\le 0,j=1,\ldots ,m\}$, where $h_{j}(x)$ is the jth continuous function. Therefore, Eq. (1) is defined as a continuous MOP.

Let $x,y \in R^m$; x is said to dominate y if and only if $x_{i}\le y_{i}$ for $\forall i \in \{1,\ldots ,m \}$ and $\exists j\in \{1,\ldots ,m \}$ st $x_{j}< y_{j}$. A non-dominated set is a set of solutions where all of its members are not dominated by each other. The non-dominated set mapping in the objective space is commonly referred to as Pareto-optimal front (PF).

Evolutionary multiobjective optimization (EMO) methodologies (Deb 2008; Coello and Lamont 2004) have been devoted to finding a representative set of the Pareto-optimal solutions over the past decades. EMO techniques have been successfully applied to real-world applications like optimal control (Scruggs et al. 2012), data mining (Corne et al. 2012), robot path planning (Ahmed et al. 2013), job scheduling (Fard et al. 2012), etc. These techniques often pursue a balance between convergence and diversity of the obtained solutions (Deb et al. 2002a, b; Li et al. 2013, 2014a, b; Zitzler et al. 2002).

Recently, much research has been done on the design of fitness assignment (Li et al. 2012; Metaxiotis and Liagkouras 2012), and diversity maintenance (Davarynejad et al. 2012; Sindhya et al. 2011) of the algorithms. However, the performance of the evolutionary multiobjective approaches degrades rapidly as the number of objectives increases (Ishibuchi et al. 2008). Moreover, in real-world application, the DM is interested in one or several specific solutions rather than the overall PF. Lately, an increasing emphasis on adding the decision-making task to the searching process has been promoted, so that the user-preference-based multiobjective evolutionary algorithms (MOEAs) have become a hot issue (Deb et al. 2006). For instance, the reference point-based MOEAs can satisfy the DM more effectively than the traditional MOEAs, for the reason that they only need to search the desired region.

Therefore, many classical algorithms combine preference information with MOEAs to solve MOPs. Fonseca and Fleming (1995) have defined the relational operator called preferability; Cvetkovic and Parmee (1999, 2002) have used a fuzzy matrix to change the preference information into weights of the objectives quantitatively and established Pareto relation based on the weights. Molina et al. (2009) have proposed a relaxed relationship called g-dominance, which performs well in MOEAs based on the reference point. Ben Said et al. (2010) have come up with a strict partial order relationship called r-dominance, which can obtain good performance on many-objective problems.

However, there are still some underlying disadvantages in preference-based MOEAs.

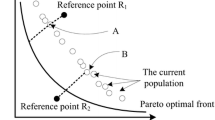
First, the performance of some classical algorithms are unstable when the reference point is close to the PF or in the feasible objective region. The entire population will be misled by the reference point and trapped in the local optimum, and fluctuate between the reference point and the PF. Experimental results show that when the reference point is located on the PF, g-dominance has bad convergence, so does r-dominance when the reference point is in the feasible region.

Second, some algorithms cannot satisfy the DM to get different sizes of the desired region, and the size of the obtained region is extremely unstable when the reference point is located in different positions in the objective space. Experiments have shown that the size of the desired region of r-dominance is not stable.

Third, on dealing with the many-objective optimization problems, the performance of the algorithms deteriorates significantly with the increase of the number of objectives (Wagner et al. 2007; Ishibuchi et al. 2008). So when working on many-objective problems, how to achieve good performance is the key challenge of the MOEAs based on preference information.

In this paper, inspired by the multiobjective evolutionary algorithm based on decomposition (MOEA/D) (Zhang and Li 2007), we decompose the preference information (the reference point) into a number of scalar optimization problems and optimize them simultaneously for both multi- and many-objective problems. In particular, the proposed algorithm has the following major advantages:

• The framework of the algorithm is easy to implement, and the idea is also simple.

• The performance of the algorithm is stable wherever the reference point is.

• The algorithm has good convergence to the Pareto-optimal front.

• The size of the desired region can be controlled by the DM.

• The algorithm provides a flexible framework of MOEA/D for preference-based evolutionary multiobjective optimization.

The organization of the rest of this paper is as follows. In Sect. 2, we introduce the model of the preference relation, and give a brief description of the g-dominance and r-dominance relations. Section 3 contains the related works on MOEA/D. The proposed algorithm is described in Sect. 4. The experimental results are presented and analyzed in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Background

2.1 Preference relation model

In this section, we firstly illustrate the objective space. All the objectives are minimized. Apparently, the feasible objective region is above the PF, and the unfeasible objective region is below the PF, as shown in Fig. 1.

Fig. 1

Illustration of the objective space

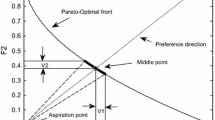
Considering the perspective of the decision makers, they have different interests in different objectives. Thus, there is no need to sort all of the Pareto solutions, but only a desired region of the Pareto-optimal region based on the DM’s preference. In terms of the need of DM, Jaszkiewicz and Slowinski (1999) gave a general overview of the light beam search (LBS) methodology and application. In this model, the DM should give the aspiration point, reservation point, indifference threshold, preference threshold and veto threshold.

This paper adopts the simplification model (Deb and Kumar 2007) shown in Fig. 2. This model allows the DMs to specify their desired region through a reference point. What’s more, a multitude of computational resources can be saved as the reference point possesses a wealth of information on evolution direction as well as allows for much more focused searching. These inherent advantages motivate the researchers to apply preference-based approaches to the field of evolution multiobjective optimization (Deb 2008; Coello and Lamont 2004).

Fig. 2

Illustration of the preference relation model

2.2 The g-dominance relation

Molina et al. (2009) proposed the reference point-based dominance relation (g-dominance relation) for multiobjective metaheuristic algorithm. The g-dominance relation relaxes Pareto dominance relation via the reference point, which is easy to display the preference information and acquire the desired region.

Given two points $A,B \in R^m$, A g-dominance B if:

• 1. $\mathrm{Flag}_g(A)>\mathrm{Flag}_g(B)$

• 2. Being $\mathrm{Flag}_g(A)\!=\!\mathrm{Flag}_g(B)$, $A_i\!\le \! B_i$,    $\forall i\!=\!1,2,\ldots ,m$

with at least one j such that $A_j<B_j$. Where

$$\begin{aligned} \mathrm{Flag}_g(w)=\left\{ \begin{array}{lll} 1 &{}&{} w_i\le g_i, \forall i=1,2,\ldots ,m \\ 1 &{}&{} g_i\le w_i, \forall i=1,2,\ldots ,m \\ 0 &{}&{} \text {otherwise} \end{array} \right. \end{aligned}$$

(2)

g is the reference point, and m is the number of objectives.

From Fig. 3, there are four regions divided by the dotted lines in the objective space. The figure illustrates how to relax the Pareto dominance relation according to expression (2), and the regions with Flag $= 1$ dominates the regions with Flag $=0$. Considering the definition, the g-dominance relation based g-NSGA-II has good convergence when the reference point is in the unfeasible objective region or in the feasible objective region.

Fig. 3

Illustration of the g-dominance relation when the reference point is located in the infeasible region and feasible region

However, the g-NSGA-II does not perform well when the reference point is on the PF or close to the PF, and displays poorly on a problem with many objectives. Under this circumstance, the entire population will easily fall into local optimal region, especially, on the problems in which it is difficult to gain the PF.

2.3 The r-dominance relation

A new dominance relation (r-dominance relation) (Ben Said et al. 2010) has been proposed for interactive evolutionary multicriteria decision-making. The relation is capable of obtaining a strict partial order among Pareto-equivalent individuals and increasing the pressure of selection. These inherent factors make such a relation guide the search process to the desired region of the Pareto-optimal region based on the DM’s preferences.

Given two points $A,B \in R^m$, A r-dominance B, if one of the following statements holds:

• 1. A dominates B in the Pareto sense, $A\prec B$

• 2. A and B are Pareto-equivalent and $D(A,B,g)<-\delta$, where $\delta \in [0,1]$ and

$$\begin{aligned}&D(A,B,g)= \frac{\mathrm{Dist}(A,g) - \mathrm{Dist}(B,g)}{\mathrm{Dist}_\mathrm{max} - \mathrm{Dist}_\mathrm{min}}\end{aligned}$$

(3)

$$\begin{aligned}&\mathrm{Dist}_\mathrm{max}= \mathrm{Max}_{x\in P}\mathrm{Dist}(x,P)\end{aligned}$$

(4)

$$\begin{aligned}&\mathrm{Dist}_\mathrm{min}= \mathrm{min}_{x\in P}\mathrm{Dist}(x,P) \end{aligned}$$

(5)

where $\delta$ is termed the non-r-dominance threshold, and g is the reference point. The distance formula uses the weighted Euclidean distance (Deb et al. 2006):

$$\begin{aligned} \mathrm{Dist}(y,g)= \sqrt{\displaystyle \sum _{i=1}^mw_i\left( \frac{f_i(y)-f_i(g)}{f_i^\mathrm{max}-f_i^\mathrm{min}}\right) ^2} \end{aligned}$$

(6)

where $w_i\in [0,1]$, $\sum _{i=1}^mw_i=1$.

Considering the definition of r-dominance relation, the relation is said to be Pareto dominance compliant. Moreover, the relation not only expresses the DM’preferences (the reference point) exactly but also preserves the Pareto dominance appropriately. Therefore, the r-dominance relation based r-NSGA-II has good convergence when the reference point is in the unfeasible objective region or on the PF.

However, r-dominance’s performance will deteriorate when the reference point is in the feasible objective region. Equations (3) and (6) show that the desired region obtained by r-NSGA-II depends on the location of the reference point. The entire population will be guided by the reference point to approximate the region close to the reference point as much as possible.

3 Related works

3.1 A decomposition-based multiobjective evolutionary algorithm (MOEA/D)

The idea of MOEA/D (Zhang and Li 2007) originates from the traditional methods of the mathematical optimization. The MOEA/D depends on a decomposition strategy to decompose a multiobjective optimization problem into a number of scalar optimization subproblems and to optimize them simultaneously. MOEA/D needs a uniform spread of N weight vectors $\lambda ^1,\lambda ^2,\ldots ,\lambda ^N$, and each $\lambda ^j=(\lambda _1^j,\lambda _2^j,\ldots ,\lambda _m^j)$ satisfies $\sum _{k=1}^m\lambda _k^i=1$ and $\forall \lambda _k^j\ge 0$, where m is the number of objectives. In addition, several approaches have been proposed to convert the problem into a number of scalar optimization problems.

3.1.1 Weighted sum approach (Miettinen 1999)

The weighted sum approach is a well-known strategy to convert a MOP into a set of single-objective problems. The objective function of the jth minimization subproblem is:

$$\begin{aligned} \begin{array}{ll} \text {minimize } g^{ws}(\overrightarrow{x}\mid \overline{\lambda })= \sum _{i=1}^m \lambda _i f_i(\overrightarrow{x}) \\ \quad \text {subject to } x \in \Omega \end{array} \end{aligned}$$

(7)

where $i\in \{1,\ldots ,m\}$, and m is the number of objectives.

However, a drawback of this approach is that it is only suitable to the MOPs whose PFs’ shape is convex because the entire population will be dominated by the terminal vertexes as Fig. 4a shows. In Fig. 4a, the red arc (PF) is above the contour line $\overline{AB}$, which indicates the whole PF dominated by the terminal vertexes (A and B). This figure and the expression (7) show that the weighted vector $\overrightarrow{\lambda }$ and the evolutionary direction vector $\overrightarrow{v}$ are collinear.

Fig. 4

Illustration of the relationship between weight vector and the gradient vector of Weighted Sum approach, Tchebycheff approach, PBI approach

3.1.2 Tchebycheff approach (Miettinen 1999)

The scalar optimization problem in this approach adopts the following equation:

$$\begin{aligned} \begin{array}{ll} \displaystyle \text {minimize } g^{tche}(\overrightarrow{x}\mid \overline{\lambda },z_i^{*})= \max _{1\le i \le m}{\lambda _i\mid f_i(\overrightarrow{x})-z_i^{*} \mid } \\ \displaystyle \quad \text {subject to } x \in \Omega \end{array} \end{aligned}$$

(8)

where $i\in \{1,\ldots ,m\}$, $z^*=(z_1^*,\ldots ,z_m^*)^T$ is the ideal point, i.e., $z_i^*= \mathrm{min}\{f_i(x)\mid x\in \Omega \}$, and m is the number of objectives.

The major advantage of the Tchebycheff approach is that it can deal with the problems with any shape of the PF. However, the weight vector $\overrightarrow{\lambda }$ and the gradient vector $\overrightarrow{v}$ are not collinear. As shown In Fig. 4b, the best individual A will be obtained in the evolution direction $\overrightarrow{v}$ instead of the desired individual B by adopting the weight vector $\overrightarrow{\lambda }$.

3.1.3 Penalty-based boundary intersection (PBI) (Zhang and Li 2007)

In this approach, the scalar optimization problem of PBI is

$$\begin{aligned} \begin{array}{ll} \displaystyle \text {minimize } g^\mathrm{pbi}(\overrightarrow{x}\mid \overline{\lambda },z_i^{*})= d_1+\theta d_2 \\ \quad \text {subject to } x \in \Omega \\ \end{array} \end{aligned}$$

(9)

where

$$\begin{aligned} d_1&=\frac{\Vert (z^*-F(\overrightarrow{x}))^T\lambda \Vert }{\Vert \overrightarrow{\lambda }\Vert }\\ d_2&=\Vert F(\overrightarrow{x})-(z^*-d_1\overrightarrow{\lambda })\Vert , \end{aligned}$$

and $\theta >0$ is a preset penalty parameter.

In Fig. 4c, the PBI method can be used to deal with the MOPs with different shapes of PF as well as obtain uniformly distributed optimal solutions. Moreover, Fig. 4c shows that the weight vector $\overrightarrow{\lambda }$ and the evolution direction vector $\overrightarrow{v}$ are collinear. But, these benefits come with a price that it has to set the value of the penalty factor to $\theta$.

3.2 The frame of MOEA/D

MOEA/D (Zhang and Li 2007) decomposes a multiobjective optimization problem into a number of scalar optimization subproblems and optimizes them simultaneously. Each subproblem is optimized by only using the information from its neighboring subproblems. The procedure of MOEA/D is presented as follows:

Input:

• MOP: the multiobjective optimization problem;

• $z(z_1,z_2,\ldots ,z_m)$ : $z_i$ is the best value found so far for $f_i$;

• N: the size of population;

• A uniform spread of N weight vectors: $\lambda ^1,\ldots ,\lambda ^N$;

• T: the size of the neighborhood of each weight vector.

Output EP: the elite population.

Step (1) Initialization.

• Step (1.1) Set $EP=\emptyset$.

• Step (1.2) Calculate the T closest weight vectors of each weight vector, For each $i=1,2,\ldots ,N$, set $NS_i=\{i_1,\ldots ,i_T\}$, where $\lambda ^{i_1},\ldots ,\lambda ^{i_T}$ are T closest weight vectors to $\lambda ^i$.

• Step (1.3) Generate an initial population $x^1,\ldots ,x^N$ by specific method, then calculate the fitness of each individual like $fitness(x^i)$.

• Step (1.3) Initialize the $z(z_1,z_2,\ldots ,z_m)$.

Step (2) Update.

For i = 1 to N do

• Step (2.1) Gene recombination (in neighbor set, randomly choose two individuals which will generate a new individual x by using genetic operators)

• Step (2.2) Apply a problem-specific repair heuristic on x to produce $x^{\prime }$.

• Step (2.3) Update Neighboring Solutions

  For each index $j\in NS_i$, If $g^{te}(x^{'}\mid \lambda ^{j},z)\le g^{te}(y^{j}\mid \lambda ^{j},z)$

  then set $y^{j}=x^{'}$

  end For

• Step (2.4) Update EP.

  end For

Step (3) Stopping Criteria.

If Terminal condition is satisfied then output EP

else go to Step 2

end If

where in the frame, $g^{te}(x^{'}\mid \lambda ^{j},z)$ is one kind of decomposition method like Weighted Sum Approach, Tchebycheff Approach, or PBI, like $g^\mathrm{PBI}(x^{'}\mid \lambda ^{j},z)$.

In terms of the frame of MOEA/D, the algorithm decomposes the MOP into a number of single-objective optimization problems (SOPs), then optimizes each subproblem and obtains the optimal solutions of each subproblem by means of the information from its neighboring subproblems generation by generation. Thus, the convergence can be maintained by this strategy. Moreover, the spread of weight vectors can ensure the diversity of the obtained solutions.

4 Proposed approach

According to the preference relation model (Deb and Kumar 2007), the preference-based searching algorithms are to obtain a region on or approximating to the PF. Inspired by the Light Beam Search (LBS) methodology and applications (Jaszkiewicz and Slowinski 1999) and MOEA/D (Zhang and Li 2007), in this section, we construct a user-preference-based model to decompose the MOP into a number of single optimization problems. How to construct the model combining the user-preference and the frame of MOEA/D is crucial, moreover, how to obtain the weight vectors in MOEA/D is a key challenge. Therefore, this paper proposes a preference information-based MOEA/D (MOEA/D-PRE) to realize them.

In terms of MOEA/D-PRE, we illustrate the idea as Fig. 5 shows: we construct a set of light beams (from the original point to the mapping region, in which the reference point is enclosed, so that the intersection between these light beams and the Pareto front is the desired region. Specifically, the size of the desired region is controlled by the boundary of the mapping region, and the key issue of this model is how to decompose the preference information of the reference point.

Fig. 5

Illustration of the idea of MOEA/D-PRE

In this section, we give the model of obtaining weighted vectors. Then, we illustrate the model of alterable size of the desired region. Finally, we present the frame of MOEA/D-PRE and the improved version in detail.

4.1 The model for obtaining weighted vectors

• Step 1: We seek the mapping point of the reference point. Given the reference point $A^{*}=(f_1^{*},\ldots ,f_m^{*})$, the corresponding mapping point $A^{'}(f_1^{'},\ldots ,f_m^{'})$ can be obtained by the Eq. (10):

  $$\begin{aligned} {\left\{ \begin{array}{ll} \frac{f_1^{*}}{f_1^{'}}=\frac{f_2^{*}}{f_2^{'}}=\cdots =\frac{f_m^{*}}{f_m^{'}}\\ f_1^{'}+f_2^{'}+\cdots +f_m^{'}=1 \end{array}\right. } \end{aligned}$$

  (10)
  $$\begin{aligned} f_i^{'}=\frac{f_i^{*}}{\sum _{i=1}^m f_i^{*}} , i=(1,2,\ldots ,m) \end{aligned}$$

  where $\forall i,f_i^{'}>0$, and m is the number of objectives.

• Step 2: We determine the boundary of the mapping region. Firstly, we obtain the intersection points between the surface: $f_1+\cdots +f_m =1$ and the number axes. Then, we acquire the boundary points to determine the boundary of the mapping region by adjusting parameter $\varepsilon$. In Figs. 6, 7a, the boundary points ($B^{'}, C^{'}, D^{'}$) can be calculated by the following equation:

  $$\begin{aligned} {\left\{ \begin{array}{ll} \overrightarrow{A^{'}B^{'}}=\varepsilon _1\cdot \overrightarrow{A^{'}B} \\ \overrightarrow{A^{'}C^{'}}=\varepsilon _2\cdot \overrightarrow{A^{'}C}\\ \overrightarrow{A^{'}D^{'}}=\varepsilon _3\cdot \overrightarrow{A^{'}D},\\ \end{array}\right. } \end{aligned}$$

  (11)

  where $\varepsilon =(\varepsilon _1,\varepsilon _2,\varepsilon _3)$ is to limit the magnitude of the vectors.

  Fig. 6

  

  Illustration of the two- and three-dimensional models

• Step 3: We obtain weight vectors from the original point to the mapping region. Referring to the Normal Boundary Intersection (Das and Dennis 1998) to obtain weight vectors, we propose the iterative weight approach via the three-dimensional models like Fig. 7a.

  • 1. Obtain the mapping point $A'$ by the Eq. (10).

  • 2. Obtain the boundary points (the intersection points between $S: f_1+f_2+f_3=1$ and the number axis) such as B(1, 0, 0), C(0, 1, 0) and D(0, 0, 1).

  • 3. Obtain the boundary points of the mapping region like $B',C',D'$ by Eqs. (10) and (11).

  • 4. Add the mapping boundary points and the mapping point $A'$ to the set Q, so the point set $Q=\{A',B',C',D'\}$. Then, obtain the midpoint set P through computing the intermediate points of any two points in the set Q, like the points 1–6 in Fig. 7a, so the obtained point set $P=\{1,2,3,4,5,6\}$.

  • 5. Obtain midpoint set $P'$ through computing all of the intermediate points between every point in set P and everyone in the set Q.

  • 6. $Q=Q\cup P$, use the same way to obtain the midpoint set P from $P'$ and Q.

  • 7. Iterate the steps 5, 6 till $\mid Q \mid =population$ size.

  The point set Q is the weighted vector set, and each $\lambda ^j=(\lambda _1^j,\lambda _2^j,\ldots ,\lambda _m^j)$ satisfies $\sum _{k=1}^m\lambda _k^i=1$ and $\forall \lambda _k^j\ge 0$. Figure 8 gives the two-dimensional and three-dimensional examples obtained by using the iterative weight approach.

Fig. 7

Illustration of the three-dimensional iterative weight approach in a, and the alterable size of the desired region in b

Fig. 8

The weight vectors obtained by the iterative weight approach in two-dimensional and three-dimensional spaces. The reference point is set to (0.5, 0.5) in the left plot and (0.2, 0.2, 0.25) in the right plot

4.2 The model of alterable size of the desired region

The DM has special requirements regarding the size of the desired region. With the location of the reference point varying, the size of the desired region obtained by some algorithms is occasionally not stable. Thus, how to get a stable and controllable size of the desired region is an essential and necessary area of research. This paper gives a model that the size of desired region can be altered depending on the DM’s preference.

Determining the boundary of the mapping region is essential because the desired region will be limited by the mapping region as Fig. 5 shows. In order to illustrate the alterable size model, according to Eq. (11), one of the boundary points $B'$ in Fig. 7b is obtained as follows:

$$\begin{aligned} \overrightarrow{OB^{'}}= \overrightarrow{OA^{'}}+\overrightarrow{A^{'}B^{'}}=\overrightarrow{OA^{'}}+\frac{\varepsilon ^{'}}{\mid \overrightarrow{A^{'}B} \mid }\cdot \overrightarrow{A^{'}B} \end{aligned}$$

(12)

Given a mapping relation: $\varepsilon \sim \frac{\varepsilon ^{'}}{\overrightarrow{A^{'}B}}$, Eq. (12) will be changed into Eq. (13) as follows:

$$\begin{aligned} \begin{array}{ll} \overrightarrow{OB^{'}}= \overrightarrow{OA^{'}}+\overrightarrow{A^{'}B^{'}}=\overrightarrow{OA^{'}}+\varepsilon \cdot \overrightarrow{A^{'}B}\\ \text {where } \varepsilon \in [0,1] \end{array} \end{aligned}$$

(13)

By using this model, the DM can obtain different sizes of the desired region by setting the parameter $\varepsilon$, as shown in Fig. 10. Provided that all of the elements in $\varepsilon =(\varepsilon _1,\varepsilon _2,\ldots ,\varepsilon _m)$ are set the same like $\varepsilon =(0.1,0.1,\ldots ,0.1)$, the DM will just adjust one parameter $\varepsilon$ to take control of the size of the desired region like $\varepsilon =0.1$, which is applied in this paper. The bigger the value of $\varepsilon$ is, the larger the size of the obtained desired region.

4.3 The frame of MOEA/D-PRE

MOEA/D-PRE decomposes the preference information (the reference point) into a number of scalar optimization subproblems and optimizes them simultaneously to obtain the desired region. The algorithm proposed in this paper needs a set of uniform weight vectors from the original point to the mapping region, and any deterministic weight approach can be added to the framework. The procedure of MOEA/D-PRE is presented as follows:

Input:

• MOP: the multiobjective optimization problem;

• $A(f_1,f_2,\ldots ,f_m)$: the reference point;

• $\varepsilon ^{\prime }$: the size of the desired region;

• N: the size of population;

• T: the size of the neighborhood of each weight vector.

Output: EP: the elite population.

Step (1) Initialization.

• Step (1.1) Set $EP=\emptyset$ and get the mapping point $A^{'}$.

• Step (1.2) Obtain a number of the weight vectors $\{\lambda ^1,\ldots ,\lambda ^N\}$ by using the iterative weight approach then compute the neighborhood index set (NS) (it is to compute the Euclidean distances between any two weight vectors; next we calculate the T closest weight vectors of each weight vector, then add the indexes of the T weight vectors into set NS)

Step (2) Update.

For $i=1$ to N do

$\varepsilon = \varepsilon ^{,}$

• Step (2.1) Gene recombination (in neighbor set, randomly choose two individuals which will generate a new individual x by using genetic operators)

• Step (2.2) Apply a problem-specific repair heuristic on x to produce $x^{'}$.

• Step (2.3) Update Neighboring Solutions

  For each index $j\in NS_i$, If $g^{pbi}(x^{'}\mid \lambda ^{j},A)\le g^{pbi}(y^{j}\mid \lambda ^{j},A)$

  then set $y^{j}=x^{'}$

  end For

• Step (2.4) Update EP.

  end For

Step (3) Stopping Criteria.

If Terminal condition is satisfied then output EP

else go to Step 2

end If

In the frame, $NS_i$ is the jth index in NS of the ith subproblem, and the reference point A is given by DM. The $\varepsilon$ is the size of the preferred region. Especially, the reason why we adopt the PBI approach to be the scalar optimization problem instead of the Weighted Sum approach and Tchebycheff approach is because the evolution direction of PBI and the weight vector are collinear. Referring to the Weighted Sum approach, the approach cannot deal with the MOP when the shape of its PF is convex. Moreover, as for the Tchebycheff approach, the evolution direction and the weight vector are not collinear. Thus, the PBI approach is the most appropriate for the model of MOEA/D-PRE.

In terms of the frame, MOEA/D-PRE has fixed search directions and may trap in local optimum in dealing with difficult problems. Thus, we propose an improved version of MOEA/D-PRE (IMOEA/D-PRE). If necessary, the DM can adjust the weight vectors and the $\varepsilon$ to dynamically control the preferred region, as in step 2, update $\varepsilon = 1-(1-\varepsilon ^{,})\frac{\mathrm{gen}}{\mathrm{Maxgen}}$ and weight vectors, where gen is the present generation and Maxgen is the maximum number of generation.

5 Experimental study

This section demonstrates simulation results on multiobjective test problems using the MOEA/D-PRE algorithm. First, we demonstrate experimentally the positive effect of managing reference points with various locations and regions with various sizes. Second, the MOEA/D-PRE is compared to two other recently proposed preference-based EMO approaches: (1) the g-dominance (Molina et al. 2009), (2) the r-dominance (Ben Said et al. 2010).

5.1 Result of varying the location of the reference points and the size of the desired region

First, we apply the 3-objective 12-variable DTLZ2 (Deb et al. 2002b) test problem with a concave Pareto-optimal front. Figure 9 shows the effect of different locations of reference points on the distribution of the obtained solutions after performing 500 generations (i.e., 10,0000 evaluations since MOEA/D-PRE evaluates 200 individuals per generation). We choose three reference points: (0.9, 0.1, 0.2), (0.1, 0.9, 0.2), (0.1, 0.2, 0.9) which are designated by a star. The $\varepsilon =(0.2,0.1,0.3)$ is to control the size of the desired region.

Fig. 9

Effect of varying locations of reference points with $\varepsilon =(0.2,0.1,0.3)$, and the corresponding reference points are: (0.9, 0.1, 0.2), (0.1, 0.9, 0.2), (0.1, 0.2, 0.9)

In Fig. 9, solutions (red points) with different locations of reference points are shown on the Pareto-optimal front. The reference points are close to the edge of the Pareto-optimal front. It is obvious that the desired regions can be obtained by MOEA/D-PRE. Thus, we conclude that if the DM would like to attain different desired regions, different reference points can be chosen.

Second, we investigate the effect of changing different values of $\varepsilon$. We consider the 2-objective 30-variable ZDT1 (Zitzler et al. 2000) and the 3-objective 12-variable DTLZ2 (Deb et al. 2002b) test problems. Figure 10 shows the effect of different sizes of desired regions obtained by MOEA/D-PRE by setting different values of $\varepsilon$ after 500 generations (i.e., 5,0000 evaluations for ZDT1 with 100 individuals and 10,0000 for DTLZ2 with 200 individuals). For the purpose of comparison, the elements of each $\varepsilon$ are set the same with 1.0, 0.5, 0.1, 0.0. For example, (1.0, 1.0) is for the first plot of ZDT1 on the first row. We use the reference points (0.3, 0.45) and (0.4, 0.8, 0.45) for ZDT1 and DTLZ2, respectively.

Fig. 10

Different sizes of the desired regions obtained by MOEA/D-PRE by setting different parameters $\varepsilon$ ($\varepsilon =1.0, 0.5, 0.1, 0.0$)

In Fig. 10, for $\varepsilon =(1.0,1.0)$, all population individuals have converged to the closest real PF. Solutions with other $\varepsilon$ values are shown in Fig. 10. It is obvious that the range of the obtained desired regions decreases with the decrease of the values of $\varepsilon$. Thus, if the DM would like to obtain a large neighborhood of solutions near the desired region, a large value of $\varepsilon$ should be chosen. We conclude that the DM could control the spread of the desired regions by means of $\varepsilon$.

5.2 Comparative experiments

To investigate the performance of the MOEA/D-PRE and IMOEA/D-PRE, first of all, we give the corresponding parameter settings and test instances. Then, we describe the performance metrics used in the experiments. Finally, we confront MOEA/D-PRE, IMOEA/D-PRE with the other two preference-based EMO algorithms: g-NSGA-II (Molina et al. 2009) and r-NSGA-II (Ben Said et al. 2010) on 2-, 3- and many-objective problems.

5.2.1 Parameter setting

As a basis of comparison, the sets of ZDT (Deb et al. 2002b) and DTLZ (Zitzler et al. 2000) are considered. The ZDT1, ZDT2, ZDT3, ZDT4, and ZDT6 are chosen to be the 2-objective test instances. DTLZ1, DTLZ2, DTLZ3, DTLZ4, DTLZ5 and DTLZ6 are chosen to be the 3-objective test instances, and the 5-objective, 8-objective, 10-objective and 15-objective of DTLZ2 are chosen to be the many-objective test problems.

In all simulations, we use the simulated binary crossover operator with a distribution index of 10 and polynomial mutation with a distribution index of 20. The crossover probability and mutation probability are set to $P_c = 0.99$ and $P_m = 0.1$, respectively. The maximum number of the generation is 500 on 2-objective and 3-objective instances. Especially, the maximum number of the generation is 1500 on ZDT4 and 1200 on ZDT6 (ZDT4 and ZDT6 are designed to be hard to approximate their real PFs). The number of the population is 100 on 2-objective problems and 200 on 3-objectives problems. The setting of the reference point is in the Table 1. About MOEA/D-PRE and IMOEA/D-PRE, T is 10, and the preset penalty parameter $\theta$ in PBI approach is set to be 5. Considering the r-dominance relation, $\delta$ is set to be 0.2.

Table 1 Reference points setting in the infeasible region, on true PF, and in the feasible region on the 2-objective and 3-objective instances

On many-objective instances, the setting of reference points and the correlative factors are presented in Table 2 in detail. Especially, the termination criterion is referred to as the result which is calculated by multiplying the maximum number of the generation by the population-size. About MOEA/D-PRE and IMOEA/D-PRE, T is 10, and the sizes of the desired region are set to be 0.1 on 2-objective and 3-objective problems, namely, $\varepsilon =(0.1,0.1)$ and $\varepsilon =(0.1,0.1,0.1)$ respectively. By this analogy, the sizes of desired region are set to be 0.05 for 5-, 8-, and 10-objective DTLZ2, and 0.01 for 15-objective DTLZ2.

Table 2 Parameter setting of the many-objective DTLZ2 and the correlated variables

Concerning Table 2, it should be stated that the value of $\sum _{i=1}^{m}f_i^2$ of the reference point indicates the closeness between the reference point and the true PF (since the Pareto-optimal solutions of DTLZ2 satisfy $\sum _{i=1}^{m}f_i^2=1$). In other words, under the condition of expression of (1), if the value is smaller than 1.0, the reference point will be in the infeasible region and below the true PF. Otherwise, the reference point will be in the feasible region and above the true PF.

5.2.2 Evaluation indicators

Due to the nature of the MOPs, a host of performance indexes should be applied for evaluating the performances of different algorithms (Zitzler et al. 2003). In our experiments, the following performance indexes are adopted to measure the closeness of a solution front ($PF_{sol}$) to the Pareto-optimal front ($PF_{true}$).

• Generational distance (GD) (Van Veldhuizen and Lamont 1998): The GD is defined as:

  $$\begin{aligned} GD= \frac{\sqrt{\sum _{i=1}^{n}d_i^2}}{n}, \end{aligned}$$

  (14)

  where n is the size of $|PF_\mathrm{sol}|$, and $d_i$ is the Euclidean distance (measured in the objective space) between each solution in $PF_\mathrm{sol}$ and the nearest member in $PF_\mathrm{true}$. The smaller the value of GD is, the better the convergence of an algorithm.

• Another GD: The equation is:

  $$\begin{aligned} F_\mathrm{indicator}= \sum _{i=1}^{m}f_i^2 \end{aligned}$$

  (15)

  Equation (15) is used to evaluate the solutions obtained by algorithms on the test instances DTLZ2 because the Pareto-optimal solutions of DTLZ2 satisfy $\sum _{i=1}^{m}f_i^2=1$. Thus, the $F_\mathrm{indicator}$ of the solutions obtained by an algorithm is closer to 1.0, and the convergence of the algorithm will be better.

5.2.3 Experiments analysis

The algorithms have been independently run 30 times at each instance on an identical-computer (Core(TM) i3-3220 3.30 GHz, 4GB). jMetal (Durillo and Nebro 2011) has been employed to develop the MOEA/D-PRE and IMOEA/D-PRE.

In this subsection, two sets of comparative experiments are discussed. In the first set, we confront the MOEA/D-PRE to IMOEA/D-PRE g-NSGA-II (Molina et al. 2009) and r-NSGA-II (Ben Said et al. 2010) on 2-objective and 3-objective problems, and set different locations of the reference point on different test instances to investigate the stability and the searching ability of the algorithms. In the second set, we confront the three algorithms to test the scalability of dealing with many-objective optimization problems.

5.2.4 Performance comparison on 2-objective problems

Experiments were conducted with the set of ZDT on three scenarios with the reference point in the infeasible region, very close to the true PF, and in the feasible region. The setting of the reference points is listed in Table 1.

Table 3 shows the GD values of the obtained solutions over 30 runs by the four algorithms on ZDT1, ZDT2, ZDT3, ZDT4, and ZDT6, where the best mean and variance are shown in bold type. As can be seen in Table 3, the average GD values obtained by MOEA/D-PRE are smaller than that of IMOEA/D-PRE, g-NSGA-II and r-NSGA-II on ZDT1, ZDT2, ZDT3 on three scenarios where the reference points are in the infeasible region, on true PF and in the feasible region. Moreover, the solutions obtained by MOEA/D-PRE converged into the true PF on all of the test problems because all of the average values of GD are smaller than 0.01.

Table 3 The GD values of the solutions obtained by g-NSGA-II, r-NSGA-II, IMOEA/D-PRE and MOEA/D-PRE on the set of ZDT

About ZDT4 and ZDT6 designed to be hard to search their true PFs, g-NSGA-II and r-NSGA-II failed to converge into the true PF on ZDT4 as shown in Table 3 and Fig. 11. However, IMOEA/D-PRE performs better than all the others except for ZDT6 with the reference point in the infeasible region as shown in Table 3 and Fig. 11. In this respect, IMOEA/D-PRE can obtain desired regions with better convergence because IMOEA/D-PRE can adjust the weight vectors to avoid the traps of the problems. Furthermore, it indicates that adjusting the weight vectors can contribute to the promotion of searching ability and dealing with some difficult problems.

Fig. 11

Comparative experiments on ZDT4 and ZDT6 on three scenarios with the reference point in the infeasible region, close to the true PF, and in the feasible region

Specifically, about ZDT6 in Table 3, we can see that MOEA/D-PRE does not perform better than r-NSGA-II when the reference points are on the true PF and in the feasible region. The main reason is that the beforehand fixed weight vectors may decrease the pressure of convergence. In other words, if we make sure that all the solutions are in the preferred directions, MOEA/D-PRE will be better. Thus, the solutions obtained by IMOEA/D-PRE will be better than r-NSGA-II.

In summary, MOEA/D-PRE has better convergence and stability on ZDT1, ZDT2 and ZDT3, and IMOEA/D-PRE performs better on ZDT4 and ZDT6.

5.2.5 Performance comparison on 3-objective problems

To investigate the stability and convergence of the algorithms on 3-objective problems, the set of DTLZ is applied to three scenarios with the reference point in the infeasible region, very close to the true PF and in the feasible region as shown in Table 1. Table 4 shows the average GD values of the obtained solutions over 30 runs by the four algorithms on DTLZ1, DTLZ2, DTLZ3, DTLZ4, DTLZ5, and DTLZ6, in which the best mean and variance are in bold type.

Table 4 The GD values of the solutions obtained by g-NSGA-II, r-NSGA-II, IMOEA/D-PRE and MOEA/D-PRE on the set of DTLZ

Table 4 shows that in terms of GD, the final solutions obtained by MOEA/D-PRE are better than those gotten by g-NSGA-II and r-NSGA-II on most of the test instances of the set of DTLZ on three scenarios, which indicates that the MOEA/D-PRE has better stability and convergence.

For DTLZ1 and DTLZ3, both of which are difficult to search their true PFs, Table 4 shows that the solutions obtained by g-NSGA-II do not converge into the true PF in the three scenarios. Moreover, Fig. 12 shows that the g-NSGA-II does not obtain the desired region on DTLZ3 and DTLZ6 as well. As to r-NSGA-II, although r-NSGA-II has converged on DLTZ3 when the reference points are in these three scenarios, the obtained solutions of r-NSGA-II cannot satisfy the DM on account of the obtained solutions covering the whole optimal PF. Furthermore, in Fig. 12, the obtained solutions r-NSGA-II do not converge into the true PF on the DTLZ6 test problem. Therefore, the performance of g-NSGA-II and r-NSGA-II are not stable, especially on DTLZ1, DTLZ3 and DTLZ6 which creates some obstacles for algorithms to converge into the PF (Deb et al. 2008).

Fig. 12

Comparative experiments on DTLZ1, DTLZ3 and DTLZ6 on three scenarios with the reference point in the infeasible region, very close to the true PF, and in the feasible region

Referring to the instances with the reference point in the infeasible region, IMOEA/D-PRE performs better than the other three algorithms on DTLZ1, DTLZ3, DTLZ5 and DTLZ6. Moreover, it has balanced performances in other instances. Thus, the performance of IMOEA/D-PRE surpasses MOEA/D-PRE to some extent. In this respect, MOEA/D-PRE still needs improvement and investigation.

From the variance value of GD in Table 4, MOEA/D-PRE can obtain a relatively stable solution set compared with the other three algorithms. Moreover, as shown in Fig. 12, MOEA/D-PRE has converged into the true PF on DTLZ3 and DTLZ6. Moreover, the obtained region for the DM varies little in these three scenarios. Therefore, the solutions obtained by MOEA/D-PRE are more stable. It is noteworthy that MOEA/D-PRE can not only obtain the desired region with good convergence, but can also adjust the size of the desired region as the DM desires.

5.2.6 Performance comparison on the many-objective problem

To investigate the scalability needed to deal with many-objective optimization problems, we use the typical continuous instance DTLZ2 with 5, 8, 10, and 15 objectives, which are always used to test the algorithms’ ability to tackle many-objective problems.

Tables 5 and 6 present the average $F_\mathrm{indicator}$ values of the solutions obtained by g-NSGA-II, r-NSGA-II, IMOEA/D-PRE and MOEA/D-PRE over 30 runs over 5-, 8-, 10- and 15-objective DTLZ2, and the best values are in bold type.

In these two tables, it is obvious that $F_\mathrm{indicator}$ values of the solutions obtained by MOEA/D-PRE are smaller than that of other algorithms. The $F_\mathrm{indicator}$ values of MOEA/D-PRE are the closest to 1.0, which indicates that MOEA/D-PRE performs better than g-NSGA-II, r-NSGA-II and IMOEA/D-PRE.

According to Eq. 15, a smaller value of $F_{indicator}$ to 1.0 means a better convergence. On 5-objective DTLZ2, all of the algorithms have converged into the true PF. Nevertheless, on 8-, 10- and 15-objective DTLZ2, the average $F_\mathrm{indicator}$ values of g-NSGA-II are over 7.0, and the ability of g-NSGA-II to deal with many-objective optimization problem deteriorates rapidly with the increase of the number of objectives. Consistent with these two tables, Figs. 13 and 14 indicate that the solutions obtained by g-NSGA-II have not converged.

Table 5 The $F_\mathrm{indicator}$ values of the solutions obtained by the g-NSGA-II, r-NSGA-II, IMOEA/D-PRE and MOEA/D-PRE on 5-Objective and 8-Objective DTLZ2

Table 6 The $F_\mathrm{indicator}$ values of the solutions obtained by the g-NSGA-II, r-NSGA-II, IMOEA/D-PRE and MOEA/D-PRE on 10-objective and 15-objective DTLZ2

In Table 5, the r-NSGA-II has good performance on 5- and 8-objective DTLZ2. However,in Table 6, on 10- and 15-objective DTLZ2, the average values of $F_\mathrm{indicator}$ obtained by r-NSGA-II are bigger than 1.12, which means that some solutions do not converge, as shown in Figs. 13 and 14. The reference points on 10- and 15-objective DTLZ2 are located in the feasible region. Nevertheless, about r-NSGA-II, some red lines (individuals) in Figs. 13 and 14 are quite close to the blue line (reference point), which means that the individuals are crowded to the reference point. In other words, some solutions do not converge to the true PF.

Fig. 13

Plot of the experiments of g-NSGA-II, r-NSGA-II, IMOEA/D-PRE and MOEA/D-PRE on 5-objective, 8-objective, and 10-objective DTLZ2, respectively

Fig. 14

Plot of the experiments of g-NSGA-II, r-NSGA-II, IMOEA/D-PRE and MOEA/D-PRE on 15-objective DTLZ2, respectively

In comparison with r-NSGA-II and g-NSGA-II, the average $F_\mathrm{indicator}$ values on many-objective instances by MOEA/D-PRE and IMOEA/D-PRE are smaller than 1.002 as shown in Tables 5 and 6. Moreover, as shown in Figs. 13 and 14, MOEA/D-PRE and IMOEA/D-PRE performs good on 5-, 8-, 10- and 15-objective DTLZ2. Specifically, on 5-,8-objective DTLZ2, Figs. 13 and14 show that the distributions of the solutions obtained by MOEA/D-PRE and IMOEA/D-PRE are better than r-NSGA-II. As for 15-objective DTLZ2, it is notable that solutions (red lines) obtained by both MOEA/D-PRE and IMOEA/D-PRE are beneath the blue line (the reference point), which means that solutions obtained by MOEA/D-PRE and IMOEA/D-PRE have better convergence.

6 Conclusion

The key issue of the preference-based MOEAs is to accurately express the DM’s preference information and obtain the optimal solutions in the desired region. This paper has focused on the above issue and has demonstrated:

• Inspired by MOEA/D, this study has decomposed the DM’s preference information (the reference point) into a number of scalar optimization subproblems.

• MOEA/D-PRE has adopted iterative weight approach to the search process, making the algorithm avoid falling to the local optimum as well as having good diversity.

• This paper has given a model based on the varying size of the desired region, which is easy to obtain and satisfy the demands of the DM.

• Combined with MOEA/D, MOEA/D-PRE can escape from the influence of the reference point’s location, which results in good convergence.

• The algorithm has been shown to have good scalability in high-dimensional objective space.

Especially, it is worth mentioning that the framework of MOEA/D-PRE is flexible. Any approaches for obtaining weight can be added to the framework which provides a new way to solve multiobjective optimization problems. In addition, if the DM has requirements for the size or shape of the desired region, it can be easily satisfied by adjusting the weights in the framework.

One line of future work is to extend the proposed algorithm to adapt more than one reference point provided, although it will surely increase the difficulty of assigning the weight vectors for the algorithm. Moreover, investigating MOEA/D-PRE on more MOPs, such as a problem with complicated Pareto set shape, is needed to further verify the algorithm’s performance.