1 Introduction

It is well known that groundwater exists in complex strata below the surface. In addition, the flow of underground water is extremely slow, and these characteristics of groundwater systems make it difficult to detect and control groundwater contamination in a timely manner (Atmadja and Bagtzoglou 2001; Sun et al. 2006; Zhao et al. 2016; Hou and Lu 2018). The contamination of groundwater poses a huge threat to the ecological environment, human life, and economic development. Therefore, the timely detection and treatment of contaminated groundwater is crucial (Chang et al. 2021, 2022a, b). The treatment of contaminated groundwater requires understanding the characteristics of groundwater contamination sources (GCSs) (Yeh, et al. 2007; Datta et al. 2011; Zhang et al. 2016). Therefore, research into IGCSs is particularly important.

In recent years, many studies have investigated the problem of IGCSs and various methods have been applied, including optimization approaches (Mahinthakumar and Sayeed 2005; Ayvaz 2010; Zhao et al. 2020, Li et al. 2020), probabilistic and geostatistical simulation approaches (Michalak and Kitanidis 2004; Butera, et al. 2013; Zanini, and Woodbury 2016; Chen et al. 2018), analytical solution and regression approaches (Sidauruk et al. 1998), and direct approaches (Milnes and Perrochet 2007).

Among the commonly used methods for IGCSs, the analytical and direct methods are only applicable to scenarios with simple hydrogeological conditions, and they are often difficult to apply to complex IGCSs problems (Sidauruk et al. 1998; Neupauer et al. 2000; Milnes and Perrochet 2007). The simulation optimization method has been used widely but "equivalent effect of different parameters" readily occurs when the dimensions of variables increase (Xing et al. 2020; Chang et al. 2022a, b). Despite the effectiveness of using stochastic theory and geostatistics methods in IGCSs, those methods are affected by challenges related to their substantial computational cost and slow convergence, particularly when applied to high-dimensional problems. These limitations may hinder their widespread application in such scenarios (Zhang et al. 2016, 2020). Various methods can be applied to identify GCSs, and each method has its own advantages and disadvantages. Therefore, different methods often have different identification effects when applied to the same case. For example, Wang et al. (2022) applied the ensemble Kalman filter (EnKF) and simulation optimization method to the same case, and they found that the identification accuracy of EnKF was lower compared with the simulation optimization method. Therefore, more methods for IGCSs need to be investigated to provide decision makers with greater choice.

The Kalman filter (KF) is a data assimilation method that is typically applicable to linear systems (Kalman 1960; Huang et al. 2012). Due to the KF only being applicable to linear systems, it usually cannot directly identify variables (such as the release history of GCSs) that have complex nonlinear mapping relationships with contaminant concentrations. Therefore, if KF is directly applied to IGCSs problem with complex nonlinear characteristics, the identification results may not be ideal due to the requirement for the linear approximation of nonlinear systems. Therefore, in recent years, some researchers have combined KF with fuzzy set methods and simulation optimization methods (Jiang et al. 2013; Gu et al. 2017; Li et al., 2017) to identify the information for GCSs. KF is usually suitable for solving data assimilation problems in linear systems, but its variant EnKF has the ability to solve data assimilation problems in nonlinear systems. The EnKF data assimilation method was proposed by Evensen (2003). In previous studies, EnKF was often combined with other methods (such as normal score transformation) to identify non-uniform and non-Gaussian hydraulic conductivity or porosity data (Franssen and Kinzelbach 2009; Li et al. 2012; Xu et al. 2013a, b; Crestani et al. 2013; Xu and Gomez-Hernandez 2015). The application areas of EnKF subsequently expanded further to identifying GCSs (Xu and Gomez-Hernandez 2016, 2018; Butera et al. 2021). Xu and Gomez-Hernandez (2018) extended their work to jointly identifying the information of GCSs and the hydraulic conductivity field in a synthetic aquifer and in a tank experiment (Chen et al. 2018). Previous studies have shown that EnKF can solve nonlinear problems with good results. However, Wang et al (2022) noted that when the inverse problem has strong nonlinearity, the identification accuracy still needs improvement.

The ensemble smoother (ES) first proposed by Van Leeuwen and Evensen (1996), is a variant of EnKF (Xu and Gomez-Hernandez 2016, 2021). ES updates the model parameters and states with all observed data in all time steps, which avoids restarting the simulation at each time step, thereby making ES faster and easier to implement than EnKF (Emerick and Reynolds 2013; Xu et al. 2021). However, there is only one update process with conventional ES and it is sometimes ineffective at dealing with nonlinear problems (Xu et al. 2021). Subsequently, Emerick and Reynolds (2013) proposed ES combined with multiple data assimilation (ES-MDA), and Chang et al. (2022a, b) proposed a multiple update process for ES to alleviate this problem. However, when conducting IGCSs using ES, the selection of the initial ensemble parameters and number of parameter groups in the ensemble can affect the accuracy and stability of the identification results. The application of ES based approaches to IGCSs has increased the number of methods available for identifying GCSs (Todaro et al. 2021; Chang et al. 2022a, b; Xia et al. 2023), but given its problems and considering that different KF methods are suitable under different conditions, more methods based on the KF should still be studied, explored, and compared. This will make it convenient for researchers to choose the most appropriate methods to identify GCSs according to the specific site conditions, as well as to minimize the calculation load and time required, while also ensuring that stable and accurate identification results are obtained.

The unscented Kalman filter (UKF) is also a data assimilation method developed based on KF. The UKF uses the KF framework but unscented transformation is introduced to solve the nonlinear transfer problem for the variables (Julier and Uhlmann, 2004; Sun et al. 2014). Thus, UKF is suitable for estimating some state variables for linear systems, but it is also applicable to estimating some state variables for nonlinear systems (Lu et al. 2018a, b; Knudsen and Leth 2019). The UKF is widely used in the fields of navigation and tracking fields (Park and D'Amico 2023), such as missile reentry problems (Ristic et al. 2003), ground vehicle navigation (Julier and Uhlmann 2002), mechanical diagnosis (Lu et al. 2018a, b) and predicting the remaining useful life of batteries (Xue et al. 2020). The UKF is suitable for nonlinear systems but it also has the potential to identify the information for GCSs, and the iterative process readily converges (Giannitrapani et al. 2011).

However, in the same manner as EnKF, UKF is a real-time data assimilation method. When performing IGCSs, UKF also requires complex operational steps like EnKF, and the accuracy of identification results are poor sometimes. Thus, inspired by the development of ES based on EnKF, an UKF-based unscented Kalman smoother (UKS) has been developed and applied to handle nonlinear problems. The UKF-based unscented Kalman smoother (UKS) is currently applied in fields such as flight path reconstruction (Teixeira et al. 2011), extracting stock prices and options volatility (Li 2013), kernel nonlinear dynamic system identification (Zhu and Príncipe 2022), and tracking subatomic particles in high energy physics experiments (Akhtar et al. 2023) with good research results. Due to the good performance of UKS in handling nonlinear problems, and inspired by the application of ES in IGCSs (Emerick and Reynolds 2013; Chang et al. 2022a, b), an UKS was developed for the first time in the present study to identify the hydraulic conductivity and GCSs. In the same manner as ES (Xu et al. 2021), UKS uses data observed in all time steps during the update process. ES and UKS belong to the same kind of methods and both are suitable for handling nonlinear problems. Moreover, ES has also achieved good results in IGCSs (Chang et al. 2022a, b). Therefore, to analyze the performance of UKS in IGCSs, ES was also applied for comparison in this study. In addition, unlike the previous applications of ES in IGCSs, to obtain better assimilation results, a stop iteration condition was set for ES and UKS in the present study, thereby allowing UKS and ES to perform multiple iteration calculations instead of only performing one update process. UKS with multiple update processes and ES with multiple update processes were applied to identify the hydraulic conductivity and GCSs, and the identification results obtained by the two methods were compared. The suitability of the two methods for identifying the hydraulic conductivity and GCSs was analyzed and compared based on the effectiveness and speed of identification.

Numerical simulation models are called repeatedly in processes when using ES and UKS to identify the hydraulic conductivity and GCSs, which generates a high computational load and wastes a lot of computational time (Zhao et al. 2016). Surrogate models are effective tools for reducing the computational load and time (Asher et al. 2015). The kriging method is widely used in surrogate modeling for IGCSs because of its rapid training speed, simple calling, and low time consumption when establishing a surrogate model for the simulation model (Guo et al. 2019; Jiang et al. 2021). Therefore, to alleviate computational problems as well as ensuring a certain degree of computational accuracy, the kriging method was applied to establish surrogate models of simulation models for iterative calculations in this study.

2 Methodology and applications

A flow diagram illustrating the method for identifying the hydraulic conductivity and GCSs based on UKS is shown in Fig. 1.

Fig. 1
figure 1

Flow diagram showing the method for identifying the hydraulic conductivity and GCSs based on UKS

Full size image

2.1 Groundwater flow and contaminant transport

To identify the hydraulic conductivity and GCSs, it is necessary to establish a numerical simulation model of the groundwater flow and contaminant transport (Datta et al. 2011). The numerical models for the groundwater flow and contaminant transport are typically presented in the form of governing partial differential equations (Singh and Datta 2006).

The governing partial differential equation for the groundwater flow is defined as follows (Sanayei et al. 2021):

$$\frac{\partial }{{\partial x_{i} }}(K_{ij} \frac{\partial H}{{\partial x_{j} }}) + Q = S_{s} \frac{\partial H}{{\partial t}}\;\;\;\;i,j = 1,2\;\;t \ge 0.$$
(1)

where \(x_{i}\) and \(x_{j}\) are the positional differences in the horizontal and longitudinal directions, respectively, \(K_{ij}\) is the hydraulic conductivity [LT−1], \(H\) is the hydraulic head [L], \(Q\) is the volumetric flux per unit volume [T−1], \(S_{s}\) is the specific storage [L−1], and \(t\) is the time [T].

After establishing the numerical simulation model of the groundwater flow, it was necessary to establish the numerical simulation model of contaminant transport. The governing partial differential equation for contaminant transport is defined as follows (Karatzas 2017, Xing et al. 2019):

$$\frac{\partial (\theta c)}{{\partial t}} = \frac{\partial }{{\partial x_{i} }}(\theta D_{ij} \frac{\partial c}{{\partial x_{j} }}) - \frac{\partial }{{\partial x_{i} }}(u_{i} c) + q_{s} c_{s} + \sum {f_{n} } \;\;\;\;i,j = 1,2\;\;t \ge 0.$$
(2)
$$\sum {f_{n} = - \rho_{b} \frac{{\partial \tilde{c}}}{\partial t}} - \lambda_{1} \theta c - \lambda_{2} \rho_{b} \tilde{c}$$
(3)
$$\tilde{c} = K_{d} c$$
(4)
$$u_{i} = \frac{{K_{ij} }}{\theta }\frac{\partial H}{{\partial x_{i} }}\;\;\;i,j = 1,2.$$
(5)

where \(\theta\) is the effective porosity, dimensionless, \(c\) is the contaminant concentration [ML−3], is the hydrodynamic dispersion tensor [L2T−1], \(u_{i}\) is the average linear velocity [LT−1], \(q_{s}\) is the volumetric flow rate per unit volume of aquifer representing fluid sources (positive) or sinks (negative) [T−1], \(c_{s}\) is the concentration of the fluid source or sink [ML−3], \(f_{n}\) is the chemical reaction term, \(\rho_{b}\) is the bulk density of the groundwater medium [ML−3], \(\tilde{c}\) is the sorbed concentration [MM−1], \(K_{d}\) is the distribution coefficient of the linear sorption isotherm [L3M−1] \(\lambda_{1}\) and \(\lambda_{2}\) are the first reaction rate for the dissolved phase [T−1] and sorbed phases [T−1] respectively.

2.2 Kriging surrogate model

The kriging method is widely used to establish surrogate models when performing IGCSs. The function for the kriging method can be described as follows (Sacks et al. 1989; Zeng et al. 2016; Wang et al. 2022; Chang et al. 2021):

$$y({\mathbf{x}}) = f^{{\text{T}}} ({\mathbf{x}})\beta + z({\mathbf{x}})$$
(6)

where \({\mathbf{x}}{ = [}{\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \cdots ,{\mathbf{x}}_{m} {]}\) is the input, \(y({\mathbf{x}})\) is the output, \(f({\mathbf{x}})\) is the regression function, \(\beta\) is the regression parameter, \(z({\mathbf{x}})\) is the random function, and it satisfies Eq. (7):

$$\left\{ {\begin{array}{*{20}l} {E[z({\mathbf{x}})] = 0} \hfill \\ {D[z({\mathbf{x}})] = \sigma^{2} } \hfill \\ \begin{gathered} {\text{cov}} [z({\mathbf{x}}_{i} ),z({\mathbf{x}}_{j} )] = \sigma^{2} \cdot R({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} ) \hfill \\ R({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} ) = \exp ( - \sum\limits_{k = 1}^{n} {\theta_{k} \left| {x_{i}^{k} - x_{j}^{k} } \right|^{2} } ) \hfill \\ \end{gathered} \hfill \\ \end{array} } \right.$$
(7)

where \(E( \cdot )\) and \(D( \cdot )\) are operators representing the expectation and variance, respectively, \(\sigma\) is the standard deviation, and \(R({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} )\) represents the correlation function between \({\mathbf{x}}_{i}\) and \({\mathbf{x}}_{j}\), n is the dimension of \({\mathbf{x}}_{i}\) or \({\mathbf{x}}_{j}\), \(\theta_{k}\) is the undetermined coefficient, and \(x_{i}^{k}\) is the k-th dimension’s value of \({\mathbf{x}}_{i}\).

For any input \({\mathbf{x}}\), the predicted input of the kriging model is as follows:

$$\hat{y}\left( {\mathbf{x}} \right) = f^{{\text{T}}} ({\mathbf{x}}){{\varvec{\upbeta}}} + {\mathbf{r}}({\mathbf{x}})^{{\text{T}}} {\mathbf{R}}^{ - 1} ({\mathbf{y}} - {\mathbf{F\beta }})$$
(8)
$$\left\{ {\begin{array}{*{20}l} {{\mathbf{r}}^{{\text{T}}} ({\mathbf{x}}) = [R({\mathbf{x}},{\mathbf{x}}_{1} ),R({\mathbf{x}},{\mathbf{x}}_{2} ), \cdots ,R({\mathbf{x}},{\mathbf{x}}_{m} )]} \hfill \\ {{\mathbf{R}} = \left[ {\begin{array}{*{20}c} {R({\mathbf{x}}_{1} ,{\mathbf{x}}_{1} )} & \cdots & {R({\mathbf{x}}_{1} ,{\mathbf{x}}_{1} )} \\ \vdots & \ddots & \vdots \\ {R({\mathbf{x}}_{m} ,{\mathbf{x}}_{1} )} & \cdots & {R({\mathbf{x}}_{m} ,{\mathbf{x}}_{m} )} \\ \end{array} } \right]} \hfill \\ {{{\varvec{\upbeta}}} = ({\mathbf{F}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{F}})^{ - 1} {\mathbf{F}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{y}}} \hfill \\ \end{array} } \right.$$
(9)

where \({\mathbf{r}}({\mathbf{x}})\) is the correlation vector, \({\mathbf{R}}\) is the correlation matrix, and \({\mathbf{F}}\) is the design matrix. According to the principles given above, all of the parameter matrices for the kriging model can be calculated after \(\theta_{k}\) is calculated, and \(\theta_{k}\) can be obtained by solving the following optimization problem:

$$\mathop {\max }\limits_{{\theta_{k} > 0}} \left\{ { - \frac{1}{2}\left[ {m\ln (\sigma^{2} ) + \ln (\left| {\mathbf{R}} \right|)} \right]} \right\}$$
(10)
$$\sigma^{2} = \frac{1}{m}({\mathbf{y}}{ - }{\mathbf{F\beta }})^{{\text{T}}} {\mathbf{R}}^{ - 1} ({\mathbf{y}}{ - }{\mathbf{F\beta }})$$
(11)

After establishing surrogate models, the coefficient of determination (R2) and mean relative error (MRE) were used to evaluate the accuracy of the kriging surrogate models in this study:

$$R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {(y_{ij} - \hat{y}_{ij} )^{2} } } }}{{\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {(y_{ij} - \overline{y})^{2} } } }}$$
(12)
$$MRE = \frac{{\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {{{\left| {y_{ij} - \hat{y}_{ij} } \right|} \mathord{\left/ {\vphantom {{\left| {y_{ij} - \hat{y}_{ij} } \right|} {y_{ij} }}} \right. \kern-0pt} {y_{ij} }}} } }}{m * n}$$
(13)

where m represents the total number of test samples, n is the dimension of the concentrations vector output by the simulation model (surrogate model), \(y_{ij}\) is the j-th concentration of the i-th test sample output by the simulation model, \(\hat{y}_{ij}\) is the j-th concentration of the i-th test sample output by the surrogate model, and \(\overline{y}\) is the mean concentration of the simulation model output. An R2 value closer to 1 and smaller MRE value indicate that a surrogate model has higher accuracy.

2.3 Ensemble smoother

When ES is applied to IGCSs, the main steps comprise the initial parameter ensemble generation process, forecast process, and update process.

  1. (1).

    Initial parameter ensemble generation process. At the beginning of the iteration calculation, N parameter vectors are randomly generated according to the prior information for the parameters (for ease of operation, it is assumed that all parameters in this study follow a uniform distribution) to form the parameter ensemble at the initial time. In this study, the unifrnd function (generate uniform random number) in MATLAB was used to generate the initial parameter ensemble for ES. The sampling command is X0 = unifrnd (ones(N,1)*lb,ones(N,1)*up,N,d), d is the parameter vector dimension, and lb and up are the lower and upper limits of the prior sampling range, respectively:

    $$X_{0} = [x_{0}^{1} ,x_{0}^{2} , \cdots ,x_{0}^{{\text{N}}} ]$$
    (14)

    where \(x_{0}^{{\text{k}}}\) is the parameter vector, the superscript (k = 1, …, N) denotes the sequence number of the parameter vector in the ensemble and the subscript denotes the initial time.

  2. (2).

    Forecast process. The prior parameter vector \(x_{{\text{m}}}^{{\text{k}}}\) (when m = 0 denotes the initial time) is input into the numerical simulation model to obtain the simulated concentrations in the observation wells:

    $$\left\{ \begin{gathered} c_{{\text{m}}}^{{\text{k}}} = {\text{h}}(x_{{\text{m}}}^{{\text{k}}} )\;\;\;\;{\text{k = }}0{,}\;1\;{,}\;...\;{,}\;{\text{N}} \hfill \\ \overline{c}_{{\text{m}}} = \sum\limits_{{{\text{k = }}1}}^{{\text{N}}} {c_{{\text{m}}}^{{\text{k}}} /{\text{N}}} \hfill \\ \end{gathered} \right.\;\;\;\;\;$$
    (15)

    where \(c_{{\text{m}}}^{{\text{k}}}\) is the simulated concentrations at all time steps in the observation well at iteration \(m\), \({\text{h}}( \cdot )\) is the simulation model, which is replaced by a surrogate model during the forecast process and \(\overline{c}_{{\text{m}}}\) is the mean simulated concentration.

  3. (3).

    Update process. The update process is conducted, before using the Kalman filter gain matrix and observed data to correct and update the prior parameters in the iteration process.

    $$\left\{ \begin{gathered} {\mathbf{K}}_{{\text{m}}} = {\mathbf{P}}_{{{\mathbf{X}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }} {\mathbf{P}}_{{{\mathbf{C}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}^{{{ - }1}} \hfill \\ x_{{{\text{m + }}1}}^{{\text{k}}} { = }x_{{\text{m}}}^{{\text{k}}} { + }{\mathbf{K}}_{{\text{m}}} (c_{{{\text{obs}}}}^{{}} - c_{{\text{m}}}^{{\text{k}}} ) \hfill \\ \end{gathered} \right.\;\;\;\;\;$$
    (16)

The auto-covariance matrix \({\mathbf{P}}_{{{\mathbf{C}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}\) and cross-covariance matrix \({\mathbf{P}}_{{{\mathbf{X}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}\) in Eq. (16) are calculated as:

$$\left\{ \begin{gathered} {\mathbf{P}}_{{{\mathbf{C}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }} = \frac{1}{{{\text{N}} - 1}}\sum\limits_{{{\text{k = }}1}}^{{\text{N}}} {[c_{{\text{m}}}^{{\text{k}}} - \overline{c}_{{\text{m}}}^{{}} ][c_{{\text{m}}}^{{\text{k}}} - \overline{c}_{{\text{m}}}^{{}} ]^{{\mathbf{T}}} } + {\mathbf{R}} \hfill \\ {\mathbf{P}}_{{{\mathbf{X}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }} = \frac{1}{{{\text{N}} - 1}}\sum\limits_{{{\text{k = }}1}}^{{\text{N}}} {[x_{{\text{m}}}^{{\text{k}}} - \overline{x}_{{\text{m}}}^{{}} ][c_{{\text{m}}}^{{\text{k}}} - \overline{c}_{{\text{m}}}^{{}} ]^{{\mathbf{T}}} } \hfill \\ \end{gathered} \right.\;\;\;\;\;$$
(17)

where \({\mathbf{R}}\) is the observation noise, \({\mathbf{P}}_{{{\mathbf{C}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}\) is the auto-covariance matrix of \({\mathbf{C}}_{{\text{m}}} = [c_{{\text{m}}}^{1} ,c_{{\text{m}}}^{2} , \cdots ,c_{{\text{m}}}^{{2{\text{n}} + 1}} ]\), and \({\mathbf{P}}_{{{\mathbf{X}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}\) is the cross-covariance matrix of \({\mathbf{C}}_{{\text{m}}} = [c_{{\text{m}}}^{1} ,c_{{\text{m}}}^{2} , \cdots ,c_{{\text{m}}}^{{2{\text{n}} + 1}} ]\) and \({\mathbf{X}}_{{\text{m}}} = [x_{{\text{m}}}^{1} ,x_{{\text{m}}}^{2} , \cdots ,x_{{\text{m}}}^{{\text{N}}} ]\).

UKS and ES have the same stop conditions. Processes 2 to 3 are repeated in a cyclic manner until the stop condition is satisfied, and the final identification results are then obtained.

$${\text{S}}({\mathbf{X}}_{{\text{m}}} ) = \sum\limits_{{{\text{k = }}1}}^{{\text{N}}} {[c_{{{\text{obs}}}} { - }c_{{\text{m}}}^{{\text{k}}} ]} [c_{{{\text{obs}}}} { - }c_{{\text{m}}}^{{\text{k}}} ]^{{\mathbf{T}}}$$
(18)
$${\text{S}}({\mathbf{X}}_{{{\text{m + }}1}} ) - {\text{S}}({\mathbf{X}}_{{\text{m}}} ) \le \xi$$
(19)

where \(\xi\) equal to 0.0001.

2.4 Unscented Kalman smoother

When the UKS is applied to IGCSs, the main steps comprise the unscented transformation process, forecast process, and update process for the variables that needed to be identified. In this study, the unifrnd function (generate uniform random number) in MATLAB was used to generate the initial parameter of UKS. The sampling command is x0 = unifrnd (ones(1,1)*lb,ones(1,1)*up,1,d), d is the parameter vector dimension, and lb and up are the lower and upper limits of the prior sampling range, respectively.

  1. (1).

    Unscented transformation process. The prior parameter vector \(x_{{\text{m}}}^{{}}\) undergoes unscented transformation to generate a prior parameters ensemble. It should be noted that when m = 0, \(x_{0}^{{}}\) represents the initial prior parameter vector:

    $$\left\{\begin{array}{c}\begin{array}{cc}{{\varvec{x}}}_{m}^{i}={{\varvec{x}}}_{m}+\sqrt{\left(n+\lambda \right){\mathbf{P}}_{m}}& i=\text{1,2},\cdots ,n\end{array}\\ \begin{array}{cc}{{\varvec{x}}}_{m}^{i}={{\varvec{x}}}_{m}-\sqrt{\left(n+\lambda \right){\mathbf{P}}_{m}}& i=n+1,n+2,\cdots ,2n\end{array}\\ {\mathbf{X}}_{m}=\left[{{\varvec{x}}}_{m},{{\varvec{x}}}_{m}+\sqrt{n+\lambda {\mathbf{P}}_{m}},{x}_{m}-\sqrt{\left(n+\right){\mathbf{P}}_{m}}\right]=\left[{{\varvec{x}}}_{m}^{1},{{\varvec{x}}}_{m}^{2},\cdots ,{{\varvec{x}}}_{m}^{2n+1}\right]\end{array}\right.$$
    (20)

    where \(x_{{\text{m}}}^{{}}\) is the prior parameter vector at iteration \(m\;(m > 0)\), \(x_{{\text{m}}}^{{\text{i}}}\) is the parameter vector after unscented transformation at iteration \(m\), \({\text{i}}\) denotes the sequence number of the parameter vector in the parameter ensemble \({\mathbf{X}}_{{\text{m}}} = [x_{{\text{m}}}^{1} ,x_{{\text{m}}}^{2} , \cdots ,x_{{\text{m}}}^{{2{\text{n + }}1}} ]\), \(n\) is the dimension of \(x_{{\text{m}}}^{{\text{i}}}\), \(\lambda\) is the scaling parameter, \({\mathbf{X}}_{{\text{m}}}\) is the prior parameter matrix at iteration \(m\), and \({\mathbf{P}}_{{\text{m}}}\) is the prior covariance matrix at iteration \(m\). It is difficult to guarantee the positive definiteness of \({\mathbf{P}}_{{\text{m}}}\) in the untraced transformation process, so the unit matrix was used to conduct untraced transformation in this study.

  2. (2).

    Forecast process. \(x_{{\text{m}}}^{{\text{i}}}\) is entered into the numerical simulation model (nonlinear system) to obtain the simulated concentrations in the observation wells:

    $$\left\{ \begin{gathered} c_{{\text{m}}}^{{\text{i}}} = {\text{h}}(x_{{\text{m}}}^{{\text{i}}} )\;\;\;\;{\text{i = }}\;1\;{,}\;2{,}\;...\;{,}\;2{\text{n + }}1 \hfill \\ \overline{c}_{{\text{m}}} = \sum\limits_{{{\text{i = }}1}}^{{2{\text{n + }}1}} {{\upomega }_{{\text{m}}}^{{\text{i}}} c_{{\text{m}}}^{{\text{i}}} } \hfill \\ \end{gathered} \right.\;\;\;\;\;$$
    (21)

    where \(c_{{\text{m}}}^{{\text{i}}}\) is the simulated concentrations at all time steps in the observation well at iteration \(m\), \({\text{h}}( \cdot )\) is the simulation model, which is replaced by a surrogate model during the forecast process, \({\upomega }_{{\text{m}}}^{{\text{i}}}\) is the weight used to calculate the mean.

  3. (3).

    Update process. The dynamic observed concentrations are used to correct and update the prior parameter \(x_{{\text{m}}}^{{\text{i}}}\):

    $$\left\{ \begin{gathered} {\mathbf{K}}_{{\text{m}}} = {\mathbf{P}}_{{{\mathbf{X}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }} {\mathbf{P}}_{{{\mathbf{C}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}^{{{ - }1}} \hfill \\ x_{{{\text{m + }}1}}^{{\text{i}}} { = }x_{{\text{m}}}^{{\text{i}}} { + }{\mathbf{K}}_{{\text{m}}} (c_{{{\text{obs}}}} - c_{{\text{m}}}^{{\text{i}}} ) \hfill \\ x_{{{\text{m + }}1}}^{{}} = \sum\limits_{{{\text{i = }}1}}^{{2{\text{n + }}1}} {{\upomega }_{{\text{m}}}^{{\text{i}}} x_{{{\text{m + }}1}}^{{\text{i}}} } \hfill \\ \end{gathered} \right.\;\;\;\;\;$$
    (22)

    where \({\mathbf{K}}_{{\text{m}}}\) is the Kalman gain matrix at iteration \(m\), \(c_{{{\text{obs}}}}\) denotes the observed concentrations at all time steps in the observation well, and \(x_{{{\text{m}} + 1}}\) is the mean vector of the posterior parameter ensemble \({\mathbf{X}}_{{{\text{m + }}1}} = [x_{{{\text{m + }}1}}^{1} ,x_{{{\text{m + }}1}}^{2} , \cdots ,x_{{{\text{m + }}1}}^{{2{\text{n + }}1}} ]\), Eq. (19) is the condition for the stopping calculation.

The auto-covariance matrix \({\mathbf{P}}_{{{\mathbf{C}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}\) and the cross-covariance matrix \({\mathbf{P}}_{{{\mathbf{X}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}\) in Eq. (22) are calculated as:

$$\left\{ \begin{gathered} {\mathbf{P}}_{{{\mathbf{C}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }} = \sum\limits_{{{\text{i = }}1}}^{{2{\text{n}} + 1}} {\omega_{{\text{c}}}^{{\text{i}}} (c_{{\text{m}}}^{{\text{i}}} - \overline{c}_{{\text{m}}} )(c_{{\text{m}}}^{{\text{i}}} - \overline{c}_{{\text{m}}} )^{{\mathbf{T}}} } + {\mathbf{R}} \hfill \\ {\mathbf{P}}_{{{\mathbf{X}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }} = \sum\limits_{{{\text{i = }}1}}^{{2{\text{n}} + 1}} {\omega_{{\text{c}}}^{{\text{i}}} (x_{{\text{m}}}^{{\text{i}}} - \overline{x}_{{\text{m}}}^{{}} )(c_{{\text{m}}}^{{\text{i}}} - \overline{c}_{{\text{m}}}^{{}} )^{{\mathbf{T}}} } \hfill \\ \end{gathered} \right.\;\;\;\;\;$$
(23)

where \({\upomega }_{{\text{c}}}^{{\text{i}}}\) is the weight used to calculate the covariance, \({\mathbf{P}}_{{{\mathbf{C}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}\) and \({\mathbf{P}}_{{{\mathbf{X}}_{{\text{m}}} {\mathbf{C}}_{{\text{m}}} }}\) have already explained above.

Processes 1 to 3 are repeated in a cyclic manner until the stop condition is satisfied, and the final identification results are then obtained.

2.5 Overview of case study

The study area considered was a modified version of the cases utilized by many well-known researchers (Ayvaz 2010; Xing, et al. 2019; Secci et al. 2022; Todaro et al. 2022). The study area was divided into five parameter zones and the hydraulic conductivity in each zone was unknown. Figure 2 shows a plan view for the study area, with two GCSs, one pumping well (the pumping volume is shown in Fig. 3) and seven observation wells. The total simulation time was 3,600 days, which was divided into 60 equal simulation periods. The GCSs were assumed to release contaminant during the first four simulation periods. Thus, 13 unknown variables had to be identified (eight release intensities for two sources × four stress periods and five hydraulic conductivities). The study area is a confined aquifer and had specified head boundary conditions on sides AB and CD, with no flow on the other sides. The head values for sides AB and CD in scenario two were 100.0 m and 80.0 m, respectively. There is chemical reaction in the study area, and the type of chemical reaction was first-order irreversible kinetic reaction.

Fig. 2
figure 2

Hypothetical aquifer for study area

Full size image
Fig. 3
figure 3

Pumping volume in each time period

Full size image

Table 1 lists the basic parameters for the aquifer in study area. Table 2 lists the parameters for the chemical reaction. The hydraulic conductivities in the five zones and the designed values for the source fluxes in different release periods are shown in Tables 1 and 3, respectively.

Table 1 Basic parameters for the aquifer in the study area
Full size table
Table 2 Chemical reaction parameters for the case study
Full size table
Table 3 Designed source fluxes in different release periods
Full size table

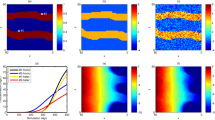
The hypothetical application case was considered to verify the effectiveness of IGCSs. As no actual observed contaminant concentration was available, therefore, it was necessary to enter the information designed for the hydraulic conductivity and GCSs into the numerical simulation model and run it to obtain the observed contaminant concentration (using MODFLOW and MT3DMS in GMS). The simulated contaminant concentrations corresponding to the information designed for the hydraulic conductivity and GCSs were then used as the observed data for the subsequent IGCSs. Figure 4 shows the contamination fields (concentration plume) in the study area for 1200 days, 2400 days, and 3600 days. Figure 5 shows the simulated contaminant concentrations (regarded as observed data) for each observation well in different time periods.

Fig. 4
figure 4

Contamination plume distributions

Full size image
Fig. 5
figure 5

Contaminant concentration curves

Full size image

The MODFLOW and MT3DMS modules in GMS (Version: GMS 7.1) software were used to solve the groundwater flow and contaminant transport numerical simulation models.

During the inverse process, the prior ranges of the parameter value of each parameter to be identified are shown in Table 4.

Table 4 Range of parameter value
Full size table

3 Results

3.1 Accuracy analysis of surrogate model

Due to the advantages of the kriging method, a surrogate model was established for the simulation models using the method described in this study, and the Latin hypercube sampling method was used for sampling. Further details of the principles of the Latin hypercube sampling method were described by Helton and Davis (2003), and Hossain, et al., (2006).

First, the Latin hypercube sampling method was used to sample 280 sets of parameters within the ranges of the required identification variables. The sampling results were entered into the simulation model. The simulation model was used to obtain the contaminant concentrations corresponding to each sampling group, which were used as the training data. The test data were obtained by using the same process applied to generate training data, except the test data comprised 80 sets of input and output data.

The training data were then used to train the surrogate model. After establishing the surrogate model, the training data and test data were used to evaluate the accuracy of the surrogate model. The R2 and MRE values for the output results for each observation well obtained by the surrogate model are shown in Table 4. The fitting degrees for the output results from the surrogate model and simulation model are shown in Fig. 6. For the training data, the R2 value of each observation well reached 1. The MRE value of each observation well was close to 0 (based on the retention of four decimal places). For the test data, the R2 value of each observation well were more than 0.99. The MRE value of each observation well less than 2.02%. According to the evaluation results based on the training data and test data, the accuracy of the surrogate model at approximating the simulation model was very high, and it could replace the simulation model in the iterative calculation. Invoking the surrogate model to participate in iterative calculations could reduce the calculation load and time required by about 99%.

Fig. 6
figure 6figure 6

Fitting degrees between simulation model and surrogate model: (a) training data (b) test data

Full size image

3.2 Comparison of identification performance between UKS and ES

UKS and ES were applied to identify the hydraulic conductivities and GCSs. It is difficult to ensure the accuracy of the results if they are calculated only once, so to test the stability of the identification methods and further verify their accuracy at identification, UKS and ES were applied to identify the hydraulic conductivities and GCSs 20 times (20 experiments).

UKS and ES apply different sampling methods for the initial parameter ensemble, so in order to comprehensively compare the identification effects for the two methods, the following four situations were considered in this study. (1) UKS sampling according to its own principles by first randomly selecting the initial values, and then conducting unscented transformation to obtain the initial parameter ensemble with 27 parameter groups. (2) ES based on its own sampling principle, where the initial parameter ensemble with 27 parameter groups for ES was obtained through random sampling (designated as ensemble smoother-27 (ES-27)). (3) The initial parameter ensembles for ES and UKS were exactly the same, and the sampling method followed the sampling principle for UKS (designated as ensemble smoother same ensemble (ES-SE)). (4) The parameter groups in the initial parameter ensemble for ES were adjusted to 270, which was 10 times the original ensemble for situation (2) (designated as ensemble smoother-270 (ES-270)). It should be noted that in 20 experiments to test the dependence of the two methods on the initial parameter ensemble, the initial parameter ensemble was different for each experiment (the sampling details can be found in Sections 2.3 and 2.4).

The effectiveness at identification was then analyzed for UKS, ES-27, ES-SE, and ES-270 in terms of the identification performance (accuracy and stability) and time required.

  1. (1)

    Identification performance

Figure 7 shows boxplots of the identification results obtained with UKS, ES-27, ES-SE and ES-270. The identification results obtained by UKS exhibited almost no fluctuations, where the hydraulic conductivities or source fluxes of the GCSs were not affected by the initial values selected. However, the identification results obtained based on ES-27 exhibited dramatic fluctuations, where the fluctuation amplitudes for hydraulic conductivity comprised K1 = 1.87 m/d, K2 = 0.29 m/d, K3 = 0.25 m/d, K4 = 1.45 m/d, K5 = 10.43 m/d. Thus, the maximum fluctuation amplitude was for K5. The fluctuation amplitudes of the source fluxes (mg/d × 105) in the four release periods for S1 were 52.86, 79.51, 41.83 and 11.58, respectively. The fluctuation amplitudes of the source fluxes (mg/d × 105) in the four release periods for S2 were 4.19, 12.50, 6.28 and 6.92, respectively. The fluctuation amplitudes of the source fluxes (mg/d × 105) for S2 were possibly smaller than those for S1 because S2 was closer to the observation wells and more readily constrained by the concentrations in each observation well. Therefore, the fluctuation amplitude was still smaller even when the ES method with poor effectiveness at identification was used. These results indicate that compared with ES-27, the identification results obtained using UKS were more stable and not affected by the initial parameters selected.

Fig. 7
figure 7

Boxplots of the identification results

Full size image

The identification results obtained based on ES-SE exhibited more drastic fluctuations than those using ES-27. The fluctuation amplitudes of the hydraulic conductivity using ES-SE were 1–8 times those with ES-27. The maximum fluctuation amplitude for K5 was 11.87 m/d. The fluctuation amplitudes of the source fluxes in the four release periods for S1 were 1.2 to 2.5 times those with ES-27. The fluctuation amplitudes of the source fluxes in the four release periods for S2 were 1.1 to 3.1 times higher using ES-SE than those with ES-27. These results indicate that the identification results based on ES-SE tended to exhibit worse variation compared with ES-27 and the identification results for the hydraulic conductivity and GCSs depended completely on the selected initial parameter ensemble, where the identification results were extremely unstable with low reliability.In the fourth situation, the stability of the identification results obtained with ES-270 improved significantly. The fluctuation amplitudes of the hydraulic conductivity and fluctuation amplitudes of the source fluxes in the four release periods were only 0.114–0.46 times those with ES-27. There were still fluctuations in the identification results but compared with ES-27 and ES-SE, the stability of their identification results was significantly improved, although they were not as stable as those with UKS.

Figure 8 shows the relative error (RE) values for the identification results using UKS, ES-27, ES-SE and ES-270. The RE ranges for each variable for identification using UKS, ES-27, ES-SE and ES-270 were 0.01–19.74%, 0.01–77.94%, 0.04–98.18% and 0.01–40.33%, respectively. According to the results based on 20 experiments, the MRE values for all the identification results was 5.05% using UKS, between 5.23% and 17.94% using ES, between 5.15% and 24.94% using ES-SE, and between 5.29% and 7.92% using ES-270. The MRE values for the identification results in each experiment were all lower using UKS than ES-27, ES-SE, and ES-270. Compared with ES and ES-SE, ES-270 had the smallest MRE value, followed by ES and ES-SE.

Fig. 8
figure 8figure 8figure 8

Relative error of hydraulic conductivity and GCSs identification results: (a) UKS compared with ES-27 (b) UKS compared with ES-SE (c) UKS compared with ES-270

Full size image

These results indicate that the identification results obtained with UKS were unaffected by the initial value selection but they were the most stable, and the accuracy of the identification results was the highest.

After conducting 20 experiments to identify the hydraulic conductivity and GCSs based on UKS and ES, we sequentially input the identification results for the hydraulic conductivity and GCSs obtained with UKS and ES into the simulation model. The simulation model was used to obtain the contaminant concentrations for all observation wells in different observation periods. The MREs between the contaminant concentrations obtained with UKS and ES in each experiment and the observed concentrations were calculated separately, and the MREs are shown in Fig. 9. The results indicated that the contaminant concentrations corresponding to the identification results obtained using UKS were closer to the observed concentrations, with smaller MREs below 1%. The MREs with the other methods increased from ES-270 to ES-27 and ES-SE. In some cases, the MREs with ES-270, ES-27, and ES- SE were similar to those with UKS, but the overall experimental results showed that this was a random phenomenon that depended entirely on the selection of the initial parameter ensemble. This was a serious drawback because it was difficult for us to select an appropriate initial parameter ensemble before the forecast process and update process.

Fig. 9
figure 9

Comparison of MREs between contaminant concentrations corresponding to the identification results and observed concentrations

Full size image

For the case study, the 20 identification results showed that compared with various situations using ES, UKS obtained the most stable identification results with the highest identification accuracy. The fitting effect between the contaminant concentrations and observed concentrations was the best with UKS.

  1. (2).

    Time required

A computer equipped with an Intel Xeon W-2295 CPU @ 3.00 GHz processor, 64 GB RAM, and RTX 3090 GPU was used to perform the iterative calculations.

Figure 10 shows boxplots of the required iterations and computational time. The fluctuation ranges for iterations were 6–45 for UKS, 131–1927 for ES-27, 51–2499 for ES-SE and 32–392 for ES-270. The fluctuation ranges for the computational time were 0.26–1.76 s for UKS, and 77.47–1099.67 s for ES-27, 26.56–1388.67 s for ES-SE and 25.71–312.12 s for ES-270. Overall, a positive correlation was found between the number of iterations and the computational time. The fluctuations in the iterations and computational time were the smallest with UKS, followed by ES-270, and ES-27, but the largest using ES-SE, thereby indicating that the number of iterations and computational time required by UKS, ES-27, ES-SE and ES-270 were all influenced by the initial parameters selected, but UKS was less affected compared with ES in various sampling situations, and the differences were almost negligible.

Fig. 10
figure 10

Boxplot of the number of iteration and calculated time

Full size image

Figure 10 shows that the mean numbers of iterations were 15 for UKS, 726 for ES-27, 1170 for ES-SE and 127 for ES-270. Table 5 shows the mean computational time required using the different methods. The mean computational time required by ES-27, ES-SE and ES-270 was hundreds or even thousands of times that by UKS because ES-27, ES-SE and ES-270 required far more iterative calculation than UKS. Although the number of iterations and computation time required by ES-270 improved significantly compared with ES-27, it still required much more computational time and number of iterations than UKS in most experiments. Furthermore, it should be noted that the iteration calculation time was shorter for ES-270 than ES-27 because ES-270 required fewer iterations.

Table 5 R2 and MRE values for the surrogate model in each observation well
Full size table

Thus, the results showed that UKS was advantageous for reducing the computational time and calculation load when applied to the identification of hydraulic conductivity and GCSs, as well as improving the accuracy and stability of the identification results.

In addition, if want to further improve the identification accuracy and use the simulation model instead of the surrogate model to participate in the iterative calculations, UKS would be highly advantageous in terms of reducing the computational time and calculation load. For this study case, UKS would require 1.35 h (27 h would be required for 20 calculations), ES-27 would require 2.72 d (54.4 d would be required for 20 calculations), ES-SE would require 4.38 d (87.6 d would be required for 20 calculations), and ES-270 would require 4.76 d (95.2 d would be required for 20 calculations). However, in terms of the identification accuracy, using ES-SE is unnecessary (Table 6)(add q).

Table 6 The average computational time required using different methods
Full size table

Figures 11 show the convergence curve for each parameter for the study case (one group of identification results were randomly selected from 20 groups of identification results). UKS generally started to converge in the fifth iteration step and the rate of convergence was very fast. The fast convergence of the iterative process was responsible for the rapid computation using UKS. However, some parameters of the identification results based on ES-27 and ES-SE still did not converge after even hundreds of calculations. Comparing with UKS, ES-270 converged in a relatively stable and rapid manner but it often required more iterations and computational time under the same stopping iteration calculation conditions. Therefore, UKS was still comparatively more advantageous. Figure 12 shows the final identification results for the hydraulic conductivity and GCSs.

Fig. 11
figure 11figure 11

Convergence curve for each parameter of the study case: (a) UKS (b) ES-27 (c) ES-ES (d) ES-270

Full size image
Fig. 12
figure 12

Identification results for hydraulic conductivity and information for GCSs

Full size image

In summary, higher identification accuracy, more stable identification results, and faster identification speed were obtained using UKS in this study case compared with ES.

4 Discussion

  1. (1).

    Errors were found between the identification results and the values designed for the case study. These errors may have been caused by the identification process or by errors in the output results from the surrogate model and simulation model. Errors occurred between the outputs from the surrogate model and the simulation model, and using the output concentrations from the surrogate model to identify the hydraulic conductivity and GCSs was equivalent to using the observed data containing errors for hydraulic conductivity and GCSs identification. The identification results showed that UKS, ES-27, ES-SE and ES-270 were all sensitive to errors. Therefore, future research should consider mixing other errors into the observed concentrations, and studying how to mitigate the effects of errors on UKS and ES.

  2. (2).

    When using UKS to identify the hydraulic conductivity and GCSs, the positive definiteness of the covariance matrix was difficult to fully guarantee in the update process for the variables for identification, so the unit matrix was used to replace the covariance matrix for iterative calculation in this study. However, there may be a more suitable matrix (such as an adaptive matrix) than the unit matrix for the correct and update process for the variables to be identified, which could further improve the accuracy of the hydraulic conductivity and GCSs, and thus this should also be addressed in future research.

  3. (3).

    When identifying common solute GCSs, the identification results obtained in the present study demonstrated the advantages of UKS, where the identification speed was faster, with greater stability, and relatively high identification accuracy. However, for more complex contamination situations, such as multiphase flow contamination, the advantage and disadvantage of using UKS and ES need to be studied further. Thus, application scenarios for UKS and ES need to be explored further to facilitate the selection of the most suitable methods for improving the accuracy of GCS identification under variable contamination site conditions.

  4. (4).

    UKS needs relatively fewer iterations compared with ES, and thus the computational time would be reduced in the identification process. In addition, UKS is more advantageous in terms of reducing the computational time if the establishment of surrogate models is not required and simulation models can be used instead to participate in iterative calculations.

  5. (5).

    During the research process, we found that the layout of the observation wells could greatly affect the accuracy of the identification results for different GCSs. Therefore, further studies should be conducted in the future by combining the optimized layout of the monitoring wells with the IGCSs to improve the accuracy of the identification results.

  6. (6).

    In this study, the variables that needed to be identified were the hydraulic conductivity of different zones and the release intensity of GCSs at different time periods, and the dimensions of the variables that needed to be identified were not considered high. Therefore, further research should investigate the differences, advantages, and disadvantages of the application of UKS and ES methods in IGGCs with high-dimensional mapping relationships (such as the need to simultaneously identify hydraulic conductivity field and information of GCSs, where the number of variables that need to be identified may exceed hundreds). In addition, when solving the problem of IGCSs with high-dimensional mapping relationships, more than a hundred variables often need to be identified. Under these conditions, if the kriging method is still used to establish a surrogate model for the simulation model, the accuracy of the surrogate model may not be ideal. Therefore, when applying UKS and ES to solve the problem of IGCSs with high-dimensional mapping relationships, it is still necessary to explore other surrogate modeling methods to establish surrogate models for simulation models for iterative calculations. For example, the current impressive deep learning methods aim to improve the approximation accuracy of surrogate models compared with simulation models with high-dimensional mapping relationships, thereby improving the accuracy of data assimilation and identification.

5 Conclusion

In this study, UKS, ES-27, ES-SE and ES-270 were used to simultaneously identify the hydraulic conductivity and GCSs. The following conclusions can be made based on the results obtained in this study.

Based on the analysis of 20 groups of identification results, regardless of the initial values selected, compared with ES-27, ES-SE, and ES-270, UKS achieved almost no fluctuations in the identification results for the hydraulic conductivity and GCSs, with greater stability and identification accuracy (MRE = 5.05%), and it was more likely to converge during the iteration process. The accuracy and stability of the identification results obtained with ES-27, ES-SE, and ES-270 all depended on the selection of the initial parameter ensemble. If the selection of the initial parameter ensemble was unreasonable, significant decreases occurred in the identification accuracy and significant increases in the time consumption, especially with ES-27 and ES-SE. The identification results obtained by ES-SE had the largest fluctuation range, lowest stability, and worst accuracy, followed by those using ES-27 and ES-270. Compared with ES-27, ES-SE and ES-270, the accuracies of the identifications results were 4.08%, 5.14%, and 1.54% higher, respectively, using UKS.

In 20 experiments, compared with S2, the fluctuation amplitude of the source fluxes was greater for S1, possibly because S1 was further away from the observation wells and less constrained, so it was more susceptible to the effects of the initial parameter ensemble selection.

The number of iterations and computational times required using UKS, ES-27, ES- SE, and ES-270 were all affected by the initial values selected. However, compared with ES-27, ES-SE, and ES-270, the number of iterations and computational time were affected less by the initial values selected when using UKS, which had a smaller fluctuation range. Compared with ES-27, ES-SE, and ES-270, UKS greatly reduced the computational time because UKS required far less iterations.

Increasing the parameter groups in the initial parameter ensemble for ES increased the stability and accuracy of the identification results to some extent, but its performance was still lower than that of UKS in terms of the number of iterations required, time consumption, and the accuracy and stability of the identification results.

The results obtained in this study demonstrated that compared with ES-27, ES-SE and ES-270, the hydraulic conductivity and GCSs identification results obtained with UKS exhibited greater stability and higher accuracy, while this method also greatly reduced the computational time required and computational load.