1 Introduction

Joint inversion of physical and geochemical parameters in groundwater reactive transport models is critical for reliable contaminant plume prediction, remediation and management, but it is still a great challenge due to the intrinsic heterogeneities of natural porous media and the scarcity of observation data. The subsurface environment is highly variable in its physical and chemical composition. Heterogeneity of physical parameters (e.g., hydraulic conductivity) has been shown to exert a key control on the mixing and spreading of conservative solutes (Dagan 1984; Rubin 1991; Sudicky 1986). For reactive solutes, their transport and reactions are simultaneously influenced by geochemical parameters (Atchley et al. 2014; Li et al. 2010; Scheibe et al. 2006). Similar to physical heterogeneity, the heterogeneity of geochemical parameters exists as well, which may be caused, for example, by spatial variability in the activity of bacteria related to biodegradation (Fennell et al. 2001; Sandrin et al. 2004). Therefore, it is important to jointly estimate the spatial distribution of physical and geochemical parameters in groundwater reactive transport models.

Inverse methods are often used by conditioning on observation data to characterize the spatial variation of parameters, which has been extensively investigated in the literature (e.g., Carrera et al. 2005; Dagan 1985; Doherty 2004; Gómez-Hernández et al. 2003; Hendricks Franssen et al. 2009; Neuman 1973; Oliver et al. 1997; Zhou et al. 2014). The ensemble Kalman filter (EnKF, Evensen 2003, 2009) is one of the most popular inverse methods over the last decade (Aanonsen et al. 2009; Oliver and Chen 2011; Zhou et al. 2014), recently used in parameter estimation and state prediction (Chen and Zhang 2006; Huang et al. 2009; Tong et al. 2010). It is a variant of the Kalman Filter (KF, Kalman 1960) based on the Monte Carlo method. Unlike the KF, the EnKF was developed for nonlinear problems (Evensen 2003, 2009), its efficiency and effectiveness in nonlinear problems with high dimensionality have been illustrated (Chen and Zhang 2006; Hendricks Franssen and Kinzelbach 2008; Moradkhani et al. 2005; Sorensen et al. 2004). In addition to the EnKF, the Ensemble Smoother (ES, Van Leeuwen and Evensen 1996) and its iterative variants, like the Ensemble Smoother with multiple data assimilation (ES-MDA, Emerick and Reynolds 2013), are popular as well. Unlike the EnKF, the ES and the ES-MDA perform global update rather than sequential update during the data assimilation, avoiding restarting models again and again, so they are of more simplicity and computational efficiency than the EnKF.

Much research has focused on developing better methods based on the EnKF to broaden its implementation scale and improve its accuracy (Chen and Oliver 2010; Emerick and Reynolds 2011; Gu and Oliver 2007; Li and Reynolds 2009), with the sampling locations fixed during the data assimilation (called the conventional strategy in the following discussion). However, it is intuitive that the data worth of measurements is dramatically influenced by sampling locations, and the parameter estimation result can be improved if the measurements are more informative even though the number of sampling locations is the same. There has been much research revealed the effect of sampling strategies on the parameter uncertainty and predictive uncertainty in groundwater models (Carrera and Neuman 1986; Cleveland and Yeh 1990; Knopman and Voss 1987; Nowak et al. 2010; Sun and Yeh 2007; Ushijima and Yeh 2015; Zhang et al. 2015). In view of these two aspects, Man et al. (2016) integrated a sequential optimal design and the information theory into the EnKF framework seamlessly to provide the most informative measurements for more accurate parameter estimation, and proposed a sequential ensemble-based optimal design (SEOD) method. Man et al. (2016) demonstrated the effectiveness of this method by estimating only physical parameters in unsaturated flow models, assimilating only piezometric head data. However, the SEOD method developed by Man et al. (2016) invokes the optimization algorithm (the genetic algorithm) at each assimilation step, so its computational efficiency is not very satisfying. Furthermore, to the best of our knowledge, few studies have focused on joint inversion of physical and geochemical parameters by assimilating multiple kinds of data.

The objective of this study is to estimate both physical and geochemical parameters accurately in groundwater models by using the recent proposed SEOD method, and to enhance the computational efficiency of the SEOD method by replacing the EnKF with the ES-MDA. The rest of the paper is organized as follows. In Sect. 2, the groundwater reactive transport model and the SEOD method are described. In Sect. 3, synthetic one-dimensional and two-dimensional groundwater reactive transport model cases are constructed to jointly estimate the physical and geochemical parameters by using the SEOD method. In Sect. 4, the comparison between the sequential optimization strategy and the conventional strategy, and the effects of the ensemble size and the number of optimal sampling locations are discussed. Furthermore, we improve the SEOD method by replacing the EnKF with the ES-MDA to enhance its computational efficiency, and make a comparison of the original and the improved SEOD method in Sect. 4.4. Conclusions are summarized in Sect. 5.

2 Methodologies

2.1 Groundwater reactive transport model

In this work, transient flow is assumed, as the following governing equation (Bear 1972),

$$\nabla \cdot ({\bf K}\nabla H) + W = \mu_{s} \frac{\partial H}{\partial t}$$
(1)

where \(\nabla \cdot\) is the divergence operator; \(\nabla\) is the gradient operator; K is the hydraulic conductivity (LT−1); H is the hydraulic head (L); W is the volumetric injection (pumping) flow rate per unit volume of the aquifer (T−1); μ s is the specific storage of the aquifer (L−1); t is the time (T).

The governing equation for the transport and reactions of aqueous species is defined as (Zheng 2006; Prommer and Post 2010):

$$\frac{{\partial C_{n} }}{\partial t} = \nabla \cdot \left( {{\bf D} \cdot \nabla C_{n} } \right) - \nabla \cdot \left( {vC_{n} } \right) + r_{{{\text{re}}ac,n}} + \frac{{q_{s} }}{\theta }C_{n}^{s}$$
(2)

where C n is the aqueous concentration of the nth component (ML−3); t is the time (T); D is the diffusion coefficient (L2T−1); \(v = ( - K\nabla H)/\theta\) (LT−1); r reac,n is the concentration change of the nth component caused by reactions (ML−3); q s is the volumetric flow rate per unit volume of the aquifer (T−1); θ is the effective porosity; and C s n is the concentration of the source or sink flux of the nth component (ML−3).

Equation (1) is solved by the numerical code MODFLOW-2000 (Harbaugh et al. 2000), and Eq. (2) is solved by the numerical code MT3DMS (Zheng 2006).

2.2 Sequential ensemble-based optimal design (SEOD) method

The sequential ensemble-based optimal design (SEOD) method is a new recently proposed optimal method based on the EnKF (Man et al. 2016). At each recursive step, the SEOD method provides an optimal sampling strategy, giving the maximum value of information metric. Then, the analysis equation of the EnKF is used to update estimated parameters by assimilating the most informative measurements, obtained based on the optimal sampling strategy.

In this work, relative entropy (RE), also known as the Kullback–Leibler divergence (Kullback 1997), is used to measure the information content of the posterior probability density function (pdf) relative to the prior pdf. If these two distributions are both n-dimensional Gaussian, RE between these two distributions is defined as:

$$RE = J_{b} + [{ \ln }\;{ \det }({\mathbf{BA}}^{ - 1} ) + {\text{Tr}}({\mathbf{AB}}^{ - 1} ) - n]/2$$
(3)

where \(J_{b} = ({\mathbf{a}} - {\mathbf{b}})^{\text{T}} {\mathbf{B}}^{ - 1} ({\mathbf{a}} - {\mathbf{b}})/2\) is the signal part of RE; \({ \det }( \cdot )\) denotes the determinant; \({\text{Tr}}( \cdot )\) denotes the trace; a and A denote the mean and covariance matrix of prior statistics respectively; b and B denote the mean and covariance matrix of posterior statistics respectively.

The loop of the SEOD method for parameter estimation is briefly recalled. More details can be found in Man et al. (2016). In the EnKF, all the parameters of interest p are augmented with state variables h into a joint state vector \({\mathbf{x}}\,{ = [}{\mathbf{p}} \, {\mathbf{h}} ]^{\text{T}}\). Before the forecast step, an ensemble of N e realizations of parameters is generated.

  1. I.

    Forecast step

Rerun the forward model G from time 0 to time step j + 1 with parameters updated at time step j [Eq. (4)].

$${\mathbf{X}}_{i,j + 1}^{f} = G\left( {{\mathbf{x}}_{i,j}^{a} } \right),\quad i = 1,2, \ldots ,N_{e}$$
(4)

In the above equation, i is the ensemble member index, j is the time step index, superscripts f and a denote forecast and analysis, respectively.

  1. II.

    Optimal design

Given a specific sampling strategy \({\mathbf{H}}^{{\prime }}\), the possible realizations of measurements can then be expressed as \({\mathbf{d}}_{i}^{{\prime }} = {\mathbf{H}}^{{\prime }} {\mathbf{x}}_{i}^{f} + {\varvec{\upxi}}_{i}\). With the realizations of measurements, the updated ensemble can be obtained from the Eq. (6). According to the prior and posterior statistics (mean and covariance), the information metrics RE of each candidate sampling strategies can be calculated. By comparing the RE values of different candidate sampling strategies, the optimal sampling design \({\mathbf{H}}_{\text{opt}}\) can be determined by solving the following optimization problem [Eq. (5)] with the help of the genetic algorithm (GA, Whitley 1994).

$${\mathbf{H}}_{\text{opt}} = \arg \hbox{max} \,RE({\mathbf{H}})$$
(5)
  1. III.

    Analysis step

After obtaining the optimal sampling strategy, the actual measurements \({\mathbf{d}}\) can be obtained and used in the analysis step [Eq. (6)].

$${\mathbf{x}}_{i,j + 1}^{a} = {\mathbf{x}}_{i,j + 1}^{f} + {\mathbf{C}}_{\text{YD}} ({\mathbf{C}}_{\text{DD}} + {\mathbf{C}}_{\text{D}} )^{ - 1} ({\mathbf{d}}_{{obs_{i,j + 1} }} - {\mathbf{d}}_{i,j + 1} ),\quad i = 1,2, \ldots ,N_{e}$$
(6)

In the above equation, \({\mathbf{C}}_{\text{YD}}\) is the cross-covariance matrix between the forecast state and the predicted data, \({\mathbf{C}}_{\text{DD}}\) is the covariance matrix of the predicted data, \({\mathbf{C}}_{\text{D}}\) is the covariance matrix of the measurements error, \({\mathbf{d}}_{obs}\) is the perturbed observations with noise of covariance \({\mathbf{C}}_{\text{D}}\), and \({\mathbf{d}}\) is the predicted data.

After the analysis step, the updated ensemble Xa is obtained. Then, go back to step (I), the updated ensemble obtained this step is implemented for the next step.

To evaluate the performance of parameter estimation, two commonly used indicators, the RMSE and the Ensemble Spread, are defined as:

$$RMSE = \sqrt {\frac{1}{{N_{m} }}\sum\limits_{i = 1}^{{N_{e} }} ( \overline{{Y_{i} }} - Y_{i} )^{2} }$$
(7)
$$Ensemble\,Spread\; = \sqrt {\frac{1}{{N_{m} }}\sum\limits_{i = 1}^{{N_{e} }} {var(Y_{i} )} }$$
(8)

where \(\overline{Y}\) and \(Y\) are the estimated and the reference field respectively; \(\text{var} (Y)\) is the ensemble variance of the field; N m is the total number of nodes in the study domain; N e is the ensemble size; i is the node index. The RMSE measures the accuracy of the estimation, while the Ensemble Spread measures the uncertainty of the estimation.

3 Case studies

3.1 Case 1: One-dimensional synthetic case

In this case, a one-dimensional confined aquifer with a starting head of 100 m is constructed, in which saturated transient flow is assumed. As shown in Fig. 1a, we choose the horizontal aquifer to be 5 m × 150 m and the grid space to be 5 m both in horizontal x and y direction. Then, a Trichloroethylene (TCE) leaking area with an initial concentration of 1000 mg/L is introduced into the aquifer, and the degradation of TCE is assumed to follow first-order kinetic reaction. Furthermore, an injection well and a pumping well are set upstream and downstream respectively, and all boundaries of the aquifer are assumed to be impermeable. In this case, the spatial distribution of the hydraulic conductivity (K) and the first-order rate constant (kTCE) (Fig. 1b, c) are jointly estimated. At every assimilation step 2 optimal sampling locations are selected from 30 candidate locations to provide the most informative measurements. More details are given in Tables 1 and 2.

Fig. 1
figure 1

The conceptual model (a), the reference fields of the hydraulic conductivity (b) and the first-order rate constant (c) for Case 1

Full size image
Table 1 Flow and transport parameters used in Case 1
Full size table
Table 2 Data assimilation related parameters used in different cases
Full size table

The log saturated hydraulic conductivity Y1 = ln(K) and the first-order rate constant Y2 = kTCE are assumed to be Gaussian distributed, with mean \(\mu_{{Y_{1} }} = 1\) and \(\mu_{{Y_{2} }} = 0.17\) and variance \(\sigma_{{Y_{1} }} = 1\) and \(\sigma_{{Y_{2} }} = 0.47\) respectively. Two arbitrary locations (x1, y1) and (x2, y2) in the random field are assumed to be correlated in the following form:

$$C_{Y} (x_{1} ,x_{2} ) = C_{Y} (x_{1} ,y_{1} ;x_{2} ,y_{2} ) = \sigma^{2} \exp \left[ - \frac{{|x_{1} - x_{2} |}}{{\lambda_{x} }} - \frac{{|y_{1} - y_{2} |}}{{\lambda_{y} }}\right]$$
(9)

where the horizontal correlation length λ x  = 5 m, and the vertical correlation length λ y  = 30 m. Here we use the Karhunen–Loeve (K–L) expansion (Zhang and Lu 2004) to parameterize the random field so as to achieve the reference fields and initial ensemble members. The measurement errors of the head and concentration data are assumed to follow the standard normal distribution with the standard deviation of 0.01 m and 10−6 mg/L respectively. Since the SEOD method is sequential, the uncertainty changes as real-time measurements are assimilated, which leads to the optimal sampling locations changing with time. The optimal sampling locations at 10 assimilation steps are shown in Fig. 2. It shows that the optimal sampling locations change with the flow and concentration fields so as to obtain the most informative measurements. It is interesting to note that the most optimal sampling locations are located at the front of the contaminant plume, which means that these locations can provide the most informative measurements.

Fig. 2
figure 2

The calculated flow field (a) and concentration field (b) in Case 1. The circles denote the optimal sampling locations proposed by the SEOD method

Full size image

In Fig. 3, we plot the curves of the ensemble mean and the standard deviation at different assimilation steps. It shows that, for both Y1 and Y2, the ensemble mean at the final assimilation step is very close to the reference field. Furthermore, the ensemble standard deviation is high at the early steps; however, it reduces dramatically after assimilating the most informative measurements from the optimal sampling locations. As shown in Fig. 4, the RMSE and the Ensemble Spread of Y1 and Y2 decrease as the assimilation step increases, which also suggests that estimated fields are close to their reference fields and of low uncertainty.

Fig. 3
figure 3

The ensemble mean and the standard deviation of field Y1 and Y2 in Case 1. (a) and (b) are the ensemble mean and the standard deviation of field Y1 respectively, while (c) and (d) are the ensemble mean and the standard deviation of field Y2 respectively

Full size image
Fig. 4
figure 4

The performance indicators (the RMSE and the Ensemble Spread) at each assimilation step for field Y1 and Y2 in Case 1

Full size image

To further illustrate the accuracy and uncertainty of the estimation, we also evaluate the performance of data match and model prediction. Considering the limitation of space, two wells (marked with black circles in Fig. 1a) are selected randomly to show the following evaluation results.

The initial and final ensembles of Y1 and Y2 are taken into the synthetic model respectively to calculate the head and concentration data, which are then compared with the real observations. After data assimilation, the data calculated by the final ensemble become closer to the real observations, as shown in Figs. 5 and 6. Overall, model uncertainty is significantly reduced after assimilating the most informative measurements from the optimal sampling locations.

Fig. 5
figure 5

The performance of data match. (a), (c) show the data match of the head of two selected wells respectively, while (b), (d) show the data match of the TCE concentration data of two selected wells respectively

Full size image
Fig. 6
figure 6

The performance of model prediction. (a), (c) show the prediction of the head of two selected wells respectively, while (b), (d) show the prediction of the TCE concentration data of two selected wells respectively

Full size image

3.2 Case 2: Two-dimensional synthetic case

In this case, saturated transient flow is assumed in a two-dimensional confined aquifer with a starting head of 50 m. As shown in Fig. 7, we choose the horizontal aquifer to be 105 m × 65 m and the grid space to be 5 m both in horizontal x and y direction. Three TCE leaking sources with the constant injection flow of 80 m3/day and the constant concentration of 50 mg/L per well are set upstream in the aquifer. Furthermore, the liner sorption reaction of the TCE is considered in this case. Besides three injection wells, two pumping wells with the constant pumping flow of 120 m3/day per well are set downstream (Fig. 7). In addition, all boundaries of the aquifer are assumed to be impermeable. In this case, the hydraulic conductivity (K) and the liner sorption constant (k d ) are assumed to be spatially heterogeneous (Fig. 9). At every assimilation step, 2 optimal sampling locations are selected from 77 candidate locations (Fig. 7) to provide the most informative measurements. More details are given in Tables 2 and 3.

Fig. 7
figure 7

The schematic of the two-dimensional conceptual model

Full size image
Table 3 Flow and transport parameters used in Case 2
Full size table

The log saturated hydraulic conductivity Y1 = ln(K) is assumed to be Gaussian distributed with mean \(\mu_{{Y_{1} }} = 1\) and variance \(\sigma_{{Y_{1} }} = 1\). The horizontal and vertical correlation lengths of Y1 are 40 and 20 m respectively. With these statistics, the reference field and initial ensemble members of Y1 can be generated by the K–L decomposition based on Eq. (9). For field Y2, it is assumed that there is a positive correlation between Y2 = ln(k d ) and Y1, i.e. Y2 = 0.5 × Y1 − 15.95, on which the generation of reference field Y2 and its initial ensemble members are based. In addition, the measurement errors of the head and concentration data are assumed to follow the standard normal distribution with the standard deviation of 0.01 m and 10−6 mg/L respectively.

In Fig. 8, we plot the optimal sampling locations at each assimilation step. It shows the tendency that locations of large gradient are more likely to be selected as the optimal sampling locations. Overall, it shows that the choice of the optimal sampling locations at each assimilation step changes with the flow and concentration fields to obtain the most informative measurements.

Fig. 8
figure 8

The optimal sampling locations (red stars) at every assimilation step of Case 2. (a) and (b) are the contour maps of the flow field and the concentration field, respectively

Full size image

The contour maps of the ensemble mean and the standard deviation at different assimilation steps are plotted in Fig. 9. It shows that, for both Y1 and Y2, the contour maps of the ensemble mean exhibit a pattern very similar to the reference fields. Even just after 4 assimilation steps, the contour maps of the ensemble mean recover the major features of the reference fields of Y1 and Y2. Furthermore, the ensemble standard deviations reduce dramatically after assimilating the most informative measurements from the optimal sampling locations, indicating that the optimal sampling strategy does play a crucial role in the model inversion though only 2 sampling locations are selected at every assimilation step.

Fig. 9
figure 9

The ensemble mean and the standard deviation of field Y1 and Y2 in Case 2. I for Field Y1, II for Field Y2

Full size image

The RMSE and the Ensemble Spread of Y1 and Y2 are plotted in Fig. 10. It shows that, these two indicators gradually decrease as assimilation step increases and finally reach a low value, suggesting that the estimations of Y1 and Y2 in this case are accurate and effective. Meanwhile, the difference between the RMSE and the Ensemble Spread is small, indicating that the SEOD method estimates the uncertainty properly.

Fig. 10
figure 10

The performance indicators (the RMSE and the Ensemble Spread) at each assimilation step for field Y1 and Y2 in Case 2

Full size image

To evaluate the performance of data match and model prediction, the initial and final ensembles of Y1 and Y2 are taken into the synthetic model respectively to calculate the head and concentration data, which are then compared with the real observations. It should be noted that only three wells (black circles in Fig. 7) are selected randomly from the study domain to show the evaluation results due to the space limitation. As shown in Figs. 11 and 12, the data calculated by the final ensemble are very close to the real observations, performing much better than those calculated by the initial ensemble. It indicates that the estimated fields of Y1 and Y2 are both of low uncertainty after assimilating the most informative measurements from the optimal sampling locations.

Fig. 11
figure 11

The performance of data match. (a), (c), (e) show the data match of the head of three selected wells respectively, while (b), (d), (f) show the data match of the TCE concentration data of three selected wells respectively

Full size image
Fig. 12
figure 12

The performance of model prediction. (a), (b), (c), (e) show the prediction of the head of three selected wells respectively, while (b), (d), (f) show the prediction of the TCE concentration data of three selected wells respectively

Full size image

4 Discussion

4.1 Comparison of sequential optimization strategy and conventional strategy

In order to illustrate and demonstrate the effectiveness and efficiency of the SEOD method for jointly estimating physical and geochemical parameters, the sequential optimization strategy is compared with the conventional strategy in this subsection. For the convenience of comparison, several synthetic cases (Case 11, 12 13) are constructed based on Case 2 by replacing the sequential optimization strategy with the conventional strategy (different fixed sampling locations numbers for different cases). Except this, the other model parameters of cases constructed here are the same as those of Case 2. More details are given in Table 2.

Figure 13 shows the RMSE and the Ensemble Spread for different cases. It illustrates that the sequential optimization strategy obtains better performance of the parameter estimation when the number of sampling locations is the same. Even more, the sequential optimization strategy with 2 optimal sampling locations (Case 2) performs better than the conventional strategy with 10 fixed sampling locations (Case 12). Besides, the conventional strategy with a large number of fixed sampling locations could result in the Ensemble Spread becoming very small at the first few assimilation steps, which could prevent assimilating further measurements.

Fig. 13
figure 13

The performance indicators (the RMSE and the Ensemble Spread) at each assimilation step for different sampling strategies

Full size image

4.2 Effect of ensemble size

All results shown so far of Case 2 are based on an ensemble of 100 realizations. To evaluate the impact of the ensemble size on the parameter estimation, an analysis with an ensemble of 50, 300, 500, 1000 realizations (Table 2) is performed here.

The RMSE and the Ensemble Spread of different cases are shown in Fig. 14 below. It shows that an appropriate ensemble size is important for the parameter estimation. If the ensemble size is too small (Case 3), ensemble collapse, a phenomenon in which the Ensemble Spread is artificially small relative to its RMSE, could happen. If the ensemble size is too large (Case 5, 6), it could lead to more computational burden and introduce more observation errors into the model as the SEOD method is based on the Monte Carlo method. It shows that the RMSE and the Ensemble Spread of Y1 and Y2 are small and close to each other when the ensemble size is 100, suggesting that the estimations of Y1 and Y2 are accurate and the model uncertainty is estimated properly. Accordingly, the ensemble size is set to 100 in the cases discussed below.

Fig. 14
figure 14

The performance indicators (the RMSE and the Ensemble Spread) at each assimilation step for different ensemble sizes

Full size image

4.3 Effect of the number of optimal sampling locations

Optimizing too many sampling locations could bring a heavy computational burden. Here, to explore the impact of the number of optimal sampling locations on the parameter estimation, several synthetic cases with different numbers of optimal sampling locations are constructed. More details are given in Table 2.

As shown in Fig. 15 below, the RMSE is no longer sensitive to the number of optimal sampling locations when the number of optimal sampling locations is large enough, suggesting that there could be a threshold value of the number of optimal sampling locations in this synthetic model. On the one hand, if the number of optimal sampling locations is too large, the Ensemble Spread becomes extremely small at the first few assimilation steps, which could prevent assimilating further measurements into the model. On the other hand, too many optimal sampling locations could lead to high economic cost and heavy computational burden. Therefore, 2–5 optimal sampling locations are enough and appropriate in this model.

Fig. 15
figure 15

The performance indicators (the RMSE and the Ensemble Spread) at each assimilation step for different numbers of optimal sampling locations

Full size image

4.4 Improvement of the SEOD method

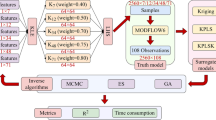
In the original SEOD method, since the EnKF is a sequential history matching method, the optimization algorithm part (GA) needs to be invoked N s times to obtain the optimal sampling design at each assimilation step, which is time-consuming. To enhance its computational efficiency, we improve the original SEOD method by replacing the EnKF with the ES-MDA. The loop of the improved SEOD method is shown in Fig. 16.

Fig. 16
figure 16

The loop diagram of the improved SEOD method

Full size image

Figure 16 shows that the loop of the improved SEOD method is divided into outer loop and inner loop. The outer loop is similar to the original SEOD method, which consists of a forecast step, an optimal design step and an analysis step. The inner loop of the improved SEOD method is part of the ES-MDA. Unlike the EnKF, the ES-MDA performs N a times global update so as to assimilate the same data (all available data) multiple times without restarting the forward model, which helps enhance the computational efficiency. In the improved SEOD method, we divide all N s assimilation steps in the original SEOD method into N g groups, the following loop is performed for each group in chronological order (from 1 to N g ). Note that N a of all cases in this subsection (Case 14, 15, 16, 17) is set to 4 (Emerick and Reynolds 2013). More details are given in Table 2.

  1. 1.

    Forecast step

Run the forward model G from beginning time step of the group j + 1 to the end time step of the group j + 1 with updated parameters from the group j [Eq. (10)].

$${\text{x}}_{i,j + 1}^{f} = G\left( {{\text{x}}_{i,j}^{a} } \right),\quad i = 1,2, \ldots ,N_{e}$$
(10)

In the above equation, i is the ensemble member index, j is the group index (from 1 to N g ), superscripts f and a denote forecast and analysis, respectively.

  1. II.

    Optimal design

This step is similar with the original SEOD method, using the GA to solve an optimization problem to obtain the most informative measurements from the optimal sampling design.

  1. III.

    Analysis step

The following update equation [Eq. (11)] of the ES-MDA is different from that of the EnKF.

$${\mathbf{x}}_{i,j + 1}^{a} = {\mathbf{x}}_{i,j + 1}^{f} + {\mathbf{C}}_{\text{YD}} ({\mathbf{C}}_{\text{DD}} + \alpha_{l} {\mathbf{C}}_{\text{D}} )^{ - 1} ({\mathbf{d}}_{{obs_{i,j + 1} }} - {\mathbf{d}}_{i,j + 1} ),\quad i = 1,2, \ldots ,N_{e}$$
(11)

In the above equation, l is the times index of the ES-MDA, \(l = 1,2, \ldots ,N_{a}\); \({\mathbf{d}}_{obs}\) is the perturbed observations with noise of covariance \(\alpha_{l} {\mathbf{C}}_{\text{D}}\) (α1 = 9.333, α2 = 7.0, α3 = 4.0 and α4 = 2.0, Emerick and Reynolds 2013). Other letters in this equation have the same meaning as those in Eq. (6).

After N a times global update, the updated ensemble Xa of the group j + 1 is obtained here. Then, go back to step (I), the updated ensemble is implemented for the next group. Through this improvement, the times of invoking the GA decrease from N s to N g , which helps enhance the computational efficiency.

To compare the improved SEOD method with the original one and discuss the influence factors of the improved one, several cases are constructed with all model parameters the same as those in Case 2. More details can be found in Table 2. The results of these cases are shown in Fig. 17.

Fig. 17
figure 17

The performance indicators (the RMSE and the Ensemble Spread) at each assimilation step for different cases using the improved SEOD method

Full size image

Figure 17 shows that the number of optimal sampling locations dominantly affects the results of the improved SEOD method. In Case 2, two optimal sampling locations are chosen at each assimilation step. During the whole data assimilation, total 20 sampling locations are used to obtain measurements at most (2 × 10, if the optimal sampling locations are different at each step). Therefore, if the number of optimal sampling locations in the improved SEOD method is too small, the improved SEOD method can’t estimate the parameters of the entire study domain well just through a few sampling locations (e.g., Case 14 with total 4 optimal sampling locations at most). When the number of sampling locations is enough, the result of the improved SEOD method is acceptable (e.g., Case 15 with total 10 optimal sampling locations at most). The result of Case 15 is comparable with the result of Case 2, but the computer cost of Case 15 is much less than that of Case 2 because that Case 15 just invokes the GA only twice while Case 2 invokes the GA 10 times. Therefore, if the number of optimal sampling locations is not set to a very small value, the computational efficiency will be enhanced by using the improved SEOD method (Table 4).

Table 4 Computational costs
Full size table

Furthermore, the way of dividing the observation time (assimilation steps in the original SEOD method) into several groups (called the group division strategy in the following context) affects the results of the improved method as well. From the comparison of Cases 15, 16 and 17, it is obvious that Case 16, whose observation time in each divided groups is progressively increasing, has a better data assimilation result than the other two cases, whose observation time in each divided groups is equivalent or progressively decreasing. It is an interesting phenomenon, which is worth further research. For now, we think it is probably because more and more precise measurements in the early stage of the data assimilation would lead to excessive update of estimated parameters (Burgers et al. 1998; Evensen 2009). Therefore, future studies should focus on optimizing the group division strategy to obtain a more accurate estimation of model parameters.

5 Conclusions

In this study, we make use of a sequential ensemble-based optimal design (SEOD) method to jointly estimate physical and geochemical parameters of groundwater models.

Both physical and geochemical parameters are estimated accurately in the one-dimensional and two-dimensional synthetic cases by using the SEOD method. Uncertainties of both physical and geochemical parameters decrease after assimilating the most informative measurements at the optimal sampling locations, and the accuracy of model prediction increases meanwhile. Furthermore, several comparison cases are tested and analyzed, results illustrate and demonstrate the effectiveness and efficiency of the SEOD method on jointly estimating high-dimensional physical and geochemical parameters in groundwater models.

The ensemble size and the number of optimal sampling locations have impacts on the parameter estimation based on the SEOD method. A too small ensemble size would lead to the ensemble collapse. Furthermore, when the number of optimal sampling locations is too large, heavier computational burden and more observation errors would be caused, and the RMSE is no longer sensitive to the number of optimal sampling locations. How to determine the optimal ensemble size and sampling locations number for different scenarios is worth further investigation.

The original SEOD method has a heavy computational burden because it invokes the GA too many times. To enhance its computational efficiency, we proposed an improved SEOD method in this study by replacing the EnKF with the ES-MDA. The results of comparison cases show that the improved SEOD method is advantageous than the original one, which makes the SEOD framework more promising for the parameter estimation and the optimal sampling strategy design. The number of optimal sampling locations and the strategy of dividing groups would affect the results of the improved SEOD method.

It is noted that only two kinds of measurements (head and concentration) are assimilated in this work. More kinds of measurements (e.g., hydraulic conductivity, porosity, temperatures and hydrogeophysical data) can be assimilated simultaneously so as to make use of more hard and soft data to improve the accuracy of parameter estimation in further study.