1 Introduction

Short or incomplete historical records, either in their length or spatial coverage, can limit hydrological analyses and consequently make water engineering designs more difficult (Loucks et al. 1981). A large number of environmental and hydrological applications where hydro-ecological variables are simulated to evaluate alternative designs and policies (Brocca et al. 2013) cannot be satisfactorily carried out with sufficient observed hydro-climatic records. Instead, modellers resort to stochastic weather generators to generate long and gap-free time series of atmospheric variables using available historical climate data. The synthetically generated outputs ideally have the same characteristics as observations (e.g., mean or variance) and used to assess the impacts of climate variability (Ailliot et al. 2015; Guo et al. 2017). The implications of using such outputs as inputs to a hydrological model are investigated in this paper.

A large number of weather generators since the 1980s has been presented with different structure and mathematical algorithms to address climate-related, and hydrological problems (e.g., Richardson 1981; Kavvas and Herd 1985; Govindaraju and Kavvas 1991). More recently, they have been also used to study climate change impacts (e.g., Kim et al. 2007; Hashmi et al. 2011; Forsythe et al. 2014; Camera et al. 2016). Interestingly, Let-It-Rain (Kim et al. 2017), for example, is a new stochastic weather generator that provides end user with high temporal resolution synthetic rainfall time series easily online. Weather generators are computationally inexpensive tools, typically utilized to produce precipitation (PCP), minimum temperature (Tmin) and maximum temperature (Tmax), as well as solar radiation data (Brissette et al. 2007) based on a calibration data set for a particular location. Weather generators are classified, according to Baigorria and Jones (2010), to three main groups: (1) parametric based on random sampling from parametric distributions (e.g., Wilks 1998; Brissette et al. 2007), (2) non-parametric based on resampling from observations (e.g., Rajagopalan et al. 1997; Wilby et al. 2003), and (3) hybrid approaches (e.g., Palutikof et al. 2002; Shao et al. 2016).

Weather generators performance, however, has been repeatedly criticized. Their drawbacks include their poor performance when simulating inter-annual variability of monthly precipitation means (Ailliot et al. 2015), although some recent rainfall generation models (e.g., Kim et al. 2013) were presumably able to overcome this issue by incorporating more information about the observed precipitation. They also suffer notoriously from their strictly site-specific nature (Fowler et al. 2007), which limits the usefulness of their results and makes them difficult to transferable to other locations and climates. Nevertheless, weather generators are useful means for areas lacking adequate climate data and hydrological applications particularly in developing countries (Wilby and Fowler 2011). In the face of the recent advances in weather generators, the accuracy of generated weather data has not always been satisfactorily justified. Precise meteorological data cannot be expected from weather generators considering the stochastic uncertainties involved, making any decision for or against the use of a certain weather generator in a decision or design framework particularly challenging. Therefore, the credibility of a given weather generator should be deliberated by quantifying their suitability for a specific field or climate zone.

The present paper proposes a new avenue to build a framework for assessing weather generators realizations by comparing the mapping between observed and generated climate states, and describing statistics that are relevant to the problem at hand.

A time series \({\text{X}}_{\text{t}}\), representing a climatic or hydrologic variable, is substituted with a set of statistics \({\mathcal{V}}_{\text{T}}\), that are related to investigated problem (e.g., annual precipitation, and monthly flow), computed for a desired period, T (41 years in the present case) as introduced by Brown et al. (2012). This process is executed for two time series: observed and stochastically generated sequences. The stochastic hydrologic variable, represented by relevant indicators, is obtained through an impact model fed with synthetically generated climate information (\({\text{X}}_{\text{t}}\)). This was accomplished by using five weather generation models to create plausible daily data series of precipitation and temperatures. Each one of the generated time series (i.e., realization of climate data) was then used as an input to a rainfall-runoff model to explore their realism in risk and performance indicators for an explicit accounting of streamflow.

With the multitude of numerous available approaches, this paper focuses on weather generators that adopt diverse methodologies, namely: WeaGETS, MulGETS, and \(k\)-nn, where the first two models are products by École de Technologie Supérieure (ETS). Since the selection of weather generators is not exhaustive but to showcase a proposed framework to evaluate weather generators, the choice is made to work on a selected ensemble of schemes. The WeaGETS model (Chen et al. 2012) is an updated form of the WGEN model (Richardson and Wright 1984). Unlike WGEN, however, WeaGETS provides a spectral correction approach for a better estimation of low-frequency component and consequently improved simulation of monthly and interannual variability. Yet, WeaGETS is rather more suited to smaller in size watersheds where a representative station could be used (Chen et al. 2012), and is thus of limited use for modelling multi-site watersheds within large basins (Mehrotra et al. 2006). The so-called MulGETS has been put forward as an extension of WeaGETS by Chen et al. (2014) with the capability to account for the spatial attributes of climate data. Beside WeaGETS and MulGETS, the K-nearest neighbor scheme (\(k\)-nn) is used for precipitation sequences following the model of Goyal et al. (2013) while the method by Sharif and Burn (2007) was implemented for the generation of temperature sequences. \(k\)-nn is a broadly used non-parametric procedure to simulate daily weather variables with no assumptions of the probability distributions. Its principal concept is to stochastically reshuffle the values from the observed records by looking for a similar pattern to the day of interest (Yates et al. 2003).

The hydrological response to the synthetic climate series is a key component for impact assessments. This was evaluated in the Soil and Water Assessment Tool (SWAT-2012). The semi-distributed, basin-scale SWAT model has been widely used by hydrologists to tackle complex water-induced issues and provide information used for appropriate decisions on water resource management (Srinivasan and Arnold 1994; Arnold et al. 1998; White and Chaubey 2005; Neitsch et al. 2011; Tuppad et al. 2011; Arnold et al. 2012a, b; Santhi et al. 2001). Weather information, precipitation in particular, is the main physically-based input in SWAT that governs streamflow simulation (Arnold et al. 2012a, b). The spatial variations in a watershed is dealt with in SWAT by creating sufficient hydrologic response units (HRUs), each has its own physical characteristics (Neitsch et al. 2011).

2 Study area, and hydroclimatic data

2.1 Study area

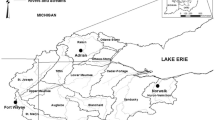
An example case study was conducted on the South Nation Watershed (Fig. 1), in Eastern Ontario, Canada, covering an area about 4000 km2. The South Nation River, which drains the watershed, runs for 175 km with relatively flat topography from Brockville, its headwaters, towards Plantagenet where it meets Ottawa River. Given a low topographic gradient, the watershed is hardly drained and flood risk poses a real threat especially to heavy agricultural activities in the region.

Fig. 1
figure 1

The South Nation watershed and the meteorological gages

Full size image

2.2 Hydroclimatic data

Observed climate time series were obtained from four stations that have complete data series for the period of 1971–2011. The locations of these stations, namely; Russell, Morrisburg, St. Albert and South Mountains, were chosen to be representative of the entire South Nation watershed (cf., Fig. 1 and Table 1). On average, the watershed receives annual precipitation of around 985 mm, with 11.5 and 1.2 °C annual mean maximum and minimum temperatures, respectively (Environment Canada 2012). For the simulations with the weather generators, days with a minimum precipitation of 1 mm are considered wet as defined by earlier studies (e.g., Frich et al. 2002; Sun et al. 2006; Klein Tank et al. 2009; Polade et al. 2014) to neglect small traces of moisture present in the air (i.e., by dew, or fog) (Benestad et al. 2012). The length of the generated data set is chosen to match the length of the observed time series.

Table 1 Meteorological stations details
Full size table

3 Methodology

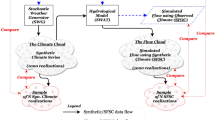
The main components of the methodology are illustrated in Fig. 2. A number of weather generators are first used to generate 1000 realizations of precipitation and temperature time series. Each realization of the generated climate time series is used afterwards individually as an input to a calibrated SWAT model to obtain streamflow time series. The number of realization was set to 1000 in order to insure that the confidence intervals of statistics in the Climate Statistics Space (CSS) and Risk and Performance Indicators Space (RPIS) are calculated with precision. Guo et al. (2017) looked into the numbers of realizations that can satisfactorily capture a number of statistical characteristics of precipitation, and minimum and maximum temperature generated by CLIGEN, LARSWG and WeaGETS. They analyzed increasing numbers of realizations (1, 25, 50, and 100) and concluded that a weather generator would well reproduce essential statistical characteristics with 25 realizations. However, the statistics considered in their papers only belong to the CSS. Given that the calculation of statistics in the RPIS involves highly nonlinear rainfall-runoff transformation, it is speculated that a higher number of realizations would be needed. It was therefore decided to use a number of realizations which is two orders of magnitude compared to the one recommended by Guo et al. (2017). A number of statistics (i.e., moments) of the simulated climate as well as Simulated Flow using Synthetic data (SFSD) time series are juxtaposed to those of observed climate as well as Simulated Flow using Observed data (SFOD) time series to assess how good the weather generators are. Further, the autocovariance structure of streamflow is analyzed as well. Autocorrelation function measures the stochastic component in a time series by reflecting on the relationship between the observations to each other. Flow autocorrelation is important factor also for reservoir operation studies.

Fig. 2
figure 2

A schematic diagram illustrating the methodology

Full size image

The different algorithms and submodels applied in the methodology are delineated in the next sections.

3.1 Stochastic weather generators

The present approach is examined in, but not limited to, several weather generators that apply different methodologies and schemes to generate climatic series. The generation of temperatures in weather generators is relatively simple as it takes a continuous range of values and can be described by a normal distribution (Chen and Brissette 2014) whereas simulation of precipitation may be an intricate challenge. The stochastic nature of precipitation is typically reproduced in a two-step process for occurrences and amounts. It is a common practice to use Markov chain (Markov 1906) models for precipitation states (i.e., wet or dry, of a given day based on the previous state) for daily precipitation occurrence while some weather generators use the alternative renewal process such as LARS-WG (Semenov and Barrow 2002). The basic input data to tested weather generators in this study include observed precipitation as well as minimum and maximum temperatures data.

In WeaGETS (version 1.6), three orders of Markov chains (two-state Markov chain with first-, second- and third-order models) can be used to estimate wet and dry spells and four distributions for precipitation amounts (gamma, exponential, mixed exponential and skewed normal distributions) based on a bi-weekly time scale. In this study, daily precipitation sequences are simulated using a third-order Markov model without parameter smoothing coupled with exponential (herein called ‘WE’) and gamma (herein called ‘WG’) distributions with a minimum precipitation threshold of 0.1 mm. A higher-order Markov model, which requires more parameters, is chosen to adequately predict lengths of consecutive dry/wet days (Bastola et al. 2012). This selection was adopted routinely by earlier works (e.g., Wilks 1998; Lennartsson et al. 2008; Chen et al. 2012; Ailliot et al. 2015). WeaGETS is temperature variables are generated conditional to each other using a normal distribution. For the purpose of generating maximum and minimum temperatures, the model uses first-order linear auto-regression coupled with constant lag-1 auto correlation and cross correlation. WeaGETS implements Finite Fourier series with two harmonics to model seasonal cycles.

MulGETS (version 1.2) is a multisite, multivariate weather model initiated by Chen et al. (2014) to model daily precipitation (based on Brissette et al. 2007) and temperature. However, unlike WeaGETS, MulGETS constructs random values taking into account the spatial correlation between scattered climate stations. This is achieved following a non-parametric approach, described by Iman and Conover 1982, coupled with an optimization algorithm described by Brissette et al. (2007). For precipitation occurrence process, a first-order Markov chain with Cholesky factorization is applied. Wet-day precipitation sequences were reproduced from MulGETS using a combination of several gamma distributions (herein called ‘MG’) and a combination of several Exponential distribution configuration (herein called ‘ME’). In terms of generating temperature variables, MulGETS is WeaGETS-like, yet the generation of spatially correlated temperature variables (Tmin and Tmax) is achieved following a non-parametric approach and implementing a first-order linear autoregressive model.

A simple \(k\)-nearest neighbor resampling model as proposed by Goyal et al. (2013) is used to generate precipitation sequences. The later seemingly allows producing of unprecedented values in the calibration data set. The procedure involves taking into account the spatial correlation by computing the regional means of the precipitation. Some \(k\)-nn models that use gamma kernel approaches can prevent producing unrealistic values of less than zero but consequently affect the mean value overall. However, Goyal et al. (2013) approach implements gamma kernel perturbation following Salas and Lee (2010) wherein a random value, for a certain day, is perturbed from the kernel density after placing one of the \(k\) nearest neighbors to the current value \(X\) at the center of a gamma kernel. For precipitation, the temporal window \(w\) and the number of nearest neighbors \(k\) are chosen to be 7 days and 13 neighbors. The method by Sharif and Burn (2007) was implemented for the generation of temperature sequences, with no underlying probability distribution assumptions. This approach is based on a traditional autoregressive model but a random component is added to the individual resampled data points in order to reproduce values that are not in the historical records. For temperature variables, the temporal window and the number of nearest neighbors \(k\) are arbitrarily chosen to be 14 days and 7 neighbors. Since Tmax and Tmin were modeled independently from the precipitation status while they are coextensive with each other in real-world cases, this could affect their efficiency (i.e., by not preserving the correlations between precipitation and temperature). Yet, this should not constrain their individual ability to simulate univariate interannual variability accurately.

For generation of precipitation amounts, there is an extensive literature on the goodness of fit of a wide range of probability distribution function. Wet-day precipitation sequences were reproduced from WeaGETS and WeaGETS using Gamma and Exponential set-up. The probability density distribution (pdf) of gamma is given by:

$$f(x) = \frac{{\left( {x/\beta } \right)^{\alpha - 1} exp\left[ { - x/\beta } \right]}}{\beta \varGamma \left( \alpha \right)}$$
(1)

where α and β are the shape and scale parameters, and are directly linked to the mean (\(\mu\)) and the standard deviation (\(\sigma\)) as follows:

$$\mu = \alpha /\beta$$
(2)
$$\sigma = \sqrt \alpha /\beta$$
(3)

The probability density function (pdf) of exponential distribution is relatively simpler and given by:

$$f(x) = \lambda \;e^{ - \lambda x}$$
(4)

where x is the daily precipitation intensities and its parameter λ equals 1/mean.

3.2 Hydrological modelling

The SWAT-2012 is used to evaluate the hydrological response of the watershed to the synthetically generated climate series. In order to preserve the spatial distribution of hydrological processes, the South Nation watershed was divided into 31 distinct reach. Calibration based on local conditions was done with SWAT-CUP (Abbaspour et al. 2007) using the SUFI-2 optimization algorithm to reduce the prediction uncertainty.

A set of statistical metrics was used to examine the accuracy of the calibrated model comprise: the Nash–Sutcliffe coefficient, the RMSE-observations standard deviation ratio, and the percent bias. The criteria adopted herein to evaluate the SWAT model goodness of fit are suggested by Liew et al. (2007) and Moriasi et al. (2007). The Nash–Sutcliffe coefficient (NS) (Nash and Sutcliffe 1970), is vastly used as an efficiency indicator of the hydrological model, which can range from − ∞ to 1. The closer NS is to 1, the better the agreement between observations and simulations. The NS can be computed as:

$${\text{NS = 1 }}-\left[ {\frac{{\mathop \sum \nolimits_{\text{i = 1}}^{\text{n}} ( {\text{O}}_{\text{i}} - {\text{P}}_{\text{i}} )^{ 2} }}{{ \mathop \sum \nolimits_{\text{i = 1}}^{\text{n}} ( {\text{O}}_{\text{i}}- {\bar{\text{O})}}^{ 2} }}} \right]$$
(5)

where O stands for observed and P for predicted values.

The RMSE-observations standard deviation ratio (RSR) was used whenever root-mean-square error (RMSE) values were less than half the standard deviation of the observed data (Singh et al. 2005). RSR can be calculated as:

$${\text{RSR = }}\frac{\text{RMSE}}{{{\text{SRDEV}}_{\text{obs}} }}{ = }\frac{{\left[ {\sqrt {\mathop \sum \nolimits_{\text{i = 1}}^{\text{n}} ( {\text{O}}_{\text{i}} - {\text{P}}_{\text{i}} )^{ 2} } } \right]}}{{\left[ {\sqrt {\mathop \sum \nolimits_{\text{i = 1}}^{\text{n}} ( {\text{O}}_{\text{i}} - {\bar{ \text{O})}}^{ 2} } } \right]}}$$
(6)

The percentage of bias (PBIAS) compares the simulated discharge to observed values, yielding positive/negative values for over-/underestimations, respectively, but ideally a percentage close to zero (Gupta et al. 1999). PBIAS percentages are computed as:

$${\text{PBIAS = }}\frac{{\mathop \sum \nolimits_{\text{i = 1}}^{\text{n}} ( {\text{O}}_{\text{i}} - {\text{P}}_{\text{i}} ) * 1 0 0}}{{ \mathop \sum \nolimits_{\text{i = 1}}^{\text{n}} ( {\text{O}}_{\text{i}} )}}$$
(7)

3.3 Performance spaces (CSS and RPIS)

In the present approach, the abovementioned stochastic models have been run one thousand times (i.e., realizations) for reasonable capturing of basic statistical characteristics of the climate (Hansen and Ines 2005; Guo et al. 2017). Similar to observations in length, 41-year synthetic observed-like weather series were generated for each station. Each realization was represented by its statistics (\({\mathcal{V}}_{\text{T}}\)) in the confidence interval plots. The goal is to find out whether an observation point is close by or far away from the mean of cloud of points representing the stochastically generated sequences in the performance space. Simply, a point representing observed time series is tested against the normal pattern of synthetic weather generator data (i.e., cluster of experiments), based on an acceptance threshold. Synthetic climate and streamflow data of a well-behaved weather generator should preserve the observed climate and streamflow statistical moments, namely the mean (\(\mu\)), standard deviation (\(\sigma\)), skewness (\(\alpha_{3}\)), and kurtosis (\(\alpha_{4}\)). Nonetheless, the proposed approach is not limited to these statistics and further investigation may be necessary to address other characteristics that are relevant to the problem at hand. For example, more analysis based on cross-correlation or log-odd ratios between all stations is suggested to explore the usefulness of multisite modeling of weather generators.

Furthermore, we investigate whether proximity with observations in the CSS translates into proximity in the RPIS. The calibrated SWAT model was forced with each one of the thousand synthetically-generated climate realizations for each weather generator, each realization comprises precipitation, maximum and minimum temperatures data. Other meteorological inputs, such as relative humidity, solar radiation and wind speed data, were kept constant using observational data. We then compared a set of one thousand simulated streamflow ensemble to simulated streamflow using observed climate data, in order to examine the model performance and their realism in RPIS. The streamflow moments were used to evaluate the degree to which a weather generator could reproduce the measured streamflow distributions.

Given the stochastic nature of streamflow, it is often in the interest of hydrologists to examine flow extremes using statistical models (probability distribution based) in order to assess risk associated with the extreme hydrological events. Two sets of hydrologic risk indicators were used to compare the performance of each weather generator in the RPIS including the traditional case of annual maxima (AM series) and the low flows frequency. The AM series was fitted to the three-parameter Generalized Extreme Value (GEV) distribution (Cunnane 1989), while the three-parameter Gumbel Type III distribution, or Weibull (WBL), (Pilon 1990), was applied to the annual 7-day minima flow (7Q), implementing the maximum likelihood estimates (MLE) for parameter distributions. The 7-day minima flow, computed on an annual basis over the smallest flow of 7-consecutive days. The 7Q10, for example, is the single most commonly employed drought index with a 10-year recurrence interval, and has a non-exceedance probability of 10%.

3.4 Assessing similarity in the CSS and RPIS

As stated by Kovalchuk et al. (2017), the quality of ensemble-based simulations can be estimated using the relative distance of a group of simulation outputs to its corresponding observations. Kovalchuk et al. (2017) listed several potential distance-based metrics such as the Euclidian distance or the Mahalanobis distance. Given the multitude of competitive techniques, the Mahalanobis distance (MD), also known as the generalized squared distance, is the selected probabilistic metric in order to compare observed-to-ensemble of realizations in the CSS and RPIS because of its less sensitive to the differences of magnitudes of the statistics. MD is a metric often applied for detecting of anomalous. It is used for a discriminant analysis to find the probability of a certain sample belonging to a certain group (Huber and Ronchetti 2009; Fritsch et al. 2012; Wang and Zwilling 2015). In statistics, Mahalanobis 1936 is a scale-invariant quadratic distance of a pre-selected point \(x_{i} \in {\mathbb{R}}^{\text{P}}\)(an event representing observations) from the origin \(\mu\) (the centre of a cloud representing ensemble realizations), governed by a covariance matrix \(\Sigma\) (a shape parameter), given by:

$$MD (\overrightarrow {{x_{i} }} ,\overrightarrow {\mu } ) = \left( {\overrightarrow {{x_{i} }} - \overrightarrow {\mu } } \right)^{ T} \varSigma^{ - 1} (\overrightarrow {{x_{i} }} - \overrightarrow {\mu } )$$
(8)

Moreover, the problem of possible inter-correlation between the original variables is solved through components analysis, which reduces the number of variables to the most relevant.

For a bivariate space, the group of points that shared invariant Mahalanobis distances will form an ellipse about the mean vector, \(\mu\). The orthogonal axes of the formed ellipse is determined by the eigenvectors (Φ) of the covariance vector (Σ), with the lengths are governed the eigenvalues (Λ). A smaller MD is desired as it indicates a closer position to the focus of the ellipse while outliers can be identified as having large MD values. The definition of a particular threshold distance to identify outliers should therefore be performed with caution, as it depends on the particular application and type of sample. In theory, the Mahalanobis squared distance delineates how far a point in units of standard deviation from the group mean; thus, as dictated by the three-sigma rule, a point with an MD value of < 3 is located within 99% boundary of all data. Therefore, a weather generator is labeled as good-fit candidate if the reference point of observations (summarized by two of its probability moments) falls within a reasonably adopted threshold distance.

The joint density function of two random variables x (\(\mu_{x}\) and \(\sigma_{x}\)) and y (\(\mu_{y}\) and \(\sigma_{y}\)) that hypothetically have a bivariate normal distribution as:

$$f \left( {x,y,\rho } \right) = \frac{1}{{ 2\pi \sigma_{x} \sigma_{y} \sqrt { 1 - \rho^{2} } }} exp\left\{ {\frac{ - 1}{{2(1 - \rho^{2} )}}\left[ {\left( {\frac{{x - \mu_{x} }}{{\sigma_{x} }}} \right)^{2} - 2\rho \left( {\frac{{x - \mu_{x} }}{{\sigma_{x} }}} \right)\left( {\frac{{y - \mu_{y} }}{{\sigma_{y} }}} \right) + \left( {\frac{{y - \mu_{y} }}{{\sigma_{y} }}} \right)^{2} } \right] } \right\}$$
(9)

where \(\uprho\) is correlation coefficient of x and y (= \(\frac{{\sigma_{xy} }}{{\sigma_{x} \sigma_{y} }}\)). An ellipse is formed, centred on the means (\(\mu_{x}\) and \(\mu_{y}\)), representing a plane of density surface, parallel to the x and y coordinates at a certain height K. If the data is dependent (\(\rho \ne 0\)), the resulting error ellipse will not be axis aligned. The integral over an ellipse with centre at (\(\mu_{x}\), \(\mu_{y}\)) is:

$$\iint\limits_{A} {\left( {\sigma_{x} \sigma_{y} } \right)^{ - 1} }f\left( {\frac{{x - \mu_{x} }}{{\sigma_{x} }},\frac{{y - \mu_{y} }}{{\sigma_{y} }}, \rho } \right)dxdy = 1 - e^{{ - \alpha^{2} /2}}$$
(10)

where the equation that describes its area (A) can be parameterized with \(\sigma_{x}\), \(\sigma_{y}\) and \(\rho\) as follows (Abramowitz and Stegun 1972):

$$\left( {\frac{{x - \mu_{x} }}{{\sigma_{x} }}} \right)^{2} - 2\rho \left( {\frac{{x - \mu_{x} }}{{\sigma_{x} }}} \right)\left( {\frac{{y - \mu_{y} }}{{\sigma_{y} }}} \right) + \left( {\frac{{y - \mu_{y} }}{{\sigma_{y} }}} \right)^{2} = \left( {1 - \rho^{2} } \right)\alpha^{2}$$
(11)

where

$$\alpha^{2} = ln\left[ {4 \pi^{2} K^{2}\upsigma_{\text{y}}^{2}\upsigma_{\text{x}}^{2} \left( {1 - \rho^{2} } \right)} \right]^{ - 1}$$
(12)

is constant.

The resulting ellipses of constant density (i.e., constant Mahalanobis distance) will not be axis aligned and the rotated new coordinate system is following the principal axes of the ellipse, which are the eigenvectors of the data’s covariance matrix. The first principal component lies in the direction of the highest variance in the data. The data projected onto the principal axes (\(\grave{x}\) and \(\grave{y}\)) of the ellipse-shaped cloud are now independent (when \(\rho\) is zero), and a point of observations \(\bar{X}\) and \(\bar{Y}\) is within a constant probability ellipse if,

$$\left( {\frac{{\bar{X}}}{{\upsigma_{\text{x}} }}} \right)^{ 2} { + }\left( {\frac{{\bar{Y}}}{{\upsigma_{\text{y}} }}} \right)^{ 2} \le \alpha^{2}$$
(13)

The random variable U = \(\left( {\frac{{\bar{X}}}{{\upsigma_{\text{x}} }}} \right)^{ 2} { + }\left( {\frac{{\bar{Y}}}{{\upsigma_{\text{y}} }}} \right)^{ 2}\) follows a Chi square (\(\upchi^{2}\)) distribution with the number of degrees of freedom (\(df\)) equivalent to the number of independent variables (Hardin and Rocke 2005). Therefore, its probability to lie within a certain ellipse is:

$$P\left[ {U \le c^{2} } \right] = \mathop \smallint \limits_{0}^{{c^{2} }} \frac{{e^{ - u/2} }}{2}du = 1 - e^{{ - c^{2} /2}}$$
(14)

\(\alpha\) value. For example, 50% and 99% of samples in a bivariate normal distribution (\(df\) = 2) lie within ellipses that have critical values of the \(\upchi^{2}\) distribution of 1.386 and 9.210, respectively. In the current approach, a weather generator is considered a good candidate if the observed data falls within its 99% Confidence ellipse. Caution is advised as certain intervals tend to be larger than others if their variability are large (Helsel and Hirsch 1992). Graphical representations in combination with a visual examination may therefore be useful to obtain a better grasp of the data.

3.5 Flow autocovariance

Storage-related statistics are particularly important for water resources reservoir simulation, and these are largely functions of the variance and autocovariance structure of the generated time series (Sveinsson et al. 2007). Flow autocorrelation is important for reservoir operation studies. Reservoirs are less sensitive to instantaneous extremes such as low and high flow, but their simulation is sensitive to persistence of low or high values, hence to correlations in flow time series.

For a time series \(y_{1}\), \(y_{2}\)…, \(y_{T}\) and a sample mean \(\bar{y}\), the lag-h correlation between \(y_{t}\) and \(y_{t + 1 }\) is given by

$$\hat{\rho }_{h} = \frac{{\mathop \sum \nolimits_{t = h + 1}^{T} \left( {y_{t} - \bar{y}} \right)\left( {y_{t + 1} - \bar{y}} \right)}}{{\mathop \sum \nolimits_{t = 1}^{T} \left( {y_{t} - \bar{y}} \right)^{2} }}$$
(15)

where h = 1,2,…,N − 1,

The standard error \({\text{SE}}_{\uprho}\) and the approximate 95% confidence intervals \({\text{CI}}_{95}\) are estimated as

$$SE_{\rho } = \sqrt {\left( {1 + 2 \mathop \sum \limits_{i = 1}^{h - 1} \hat{\rho }_{i}^{2} } \right)/N}$$
(16)
$$CI_{95} = \hat{\rho }_{h} \pm 1.96 SE_{\rho }$$
(17)

In this paper, a visual comparison of the autocorrelation functions were drawn at of observed and simulated monthly flows will be used to assess the performance of the weather generators under investigation. A good weather generator is expected to have most of its autocorrelations estimates within the 95% confidence interval bounds.

3.6 Dimensions of the CSS and RPIS

Ideally the CSS and RPIS will have a dimension for each statistic that is of interest to the analysis. Obviously, the number of potential dimensions is potentially unlimited and it is not obvious to draw a line between meaningful statistics and the others for a particular problem. Furthermore, visual comparison and interpretation of results in a space with more than three dimensions is tricky. For the sake of simplicity and ease of interpretation, only two-dimensional CSS and RPIS are discussed in this paper. We also restricted ourselves to the mean, standard deviation, skewness and kurtosis in the two spaces. The mean controls the magnitude of the variable and is particularly important in hydrological analyses where water volumes are used for reservoir design. The standard deviation is a quantification of the spread about the mean and describes the predictability of a particular variable. The skewness and kurtosis play a crucial role in the distribution of extreme values and impacts the design of flood and drought control structures. Additional dimensions can be added to the CSS and RPIS is the problem at hand warrants it, but the interpretation of the results becomes more difficult with spaces of higher dimensions.

4 Results and discussion

The comparisons between observed and weather generator-driven data, in the CSS and RPIS, allow for quantifying the performances of these weather generators. The relative positions of the mean, standard deviation, skewness, and kurtosis of simulated annual precipitation, maximum and minimum temperature were compared to the ones estimated using observations in the CSS. A similar comparison was carried out for streamflow data in the RPIS space. All statistics were found to be stable in the CSS earlier than those in the RPIS. As an example, the plot of the mean annual precipitation and mean monthly streamflow is shown in Fig. 3 as function of the number of realization. It shows that 25 realizations, as recommended by Guo et al. (2017), seem shorter than desired, particularly in the RPIS, to construct robust confidence intervals. These results comforted us in the choice of 1000 for the number of realisations for each weather generators, despite the high computational demand.

Fig. 3
figure 3

The number of realizations needed to calculate statistics in the CSS and RPIS

Full size image

4.1 Climate Statistics Space (CSS)

The analysis of the stochastically generated climatic daily sequences, compared to the reference data, is demonstrated here using lumped approach by averaging the climate data over all locations. The statistics of observed precipitation are shown along with elliptically-shaped confidence intervals from each weather generator dataset, representing 99% and 50% of the data (Fig. 4). Despite the recommendation of Chen et al. (2012) to reproduce precipitation amounts using the Gamma distribution rather than Exponential, yet Figs. 4 and 5a suggest that the two distributions are comparable in the CSS. The generated precipitation amounts, using the exponential distribution in MulGETS, are slightly better than those produced with the gamma distribution, in terms of retaining observed attributes in the CSS with MD of observed point of 0.45 and located within 9% confident interval of \(\sigma\) and \(\alpha_{3}\) and located acceptably in 59% of \(\alpha_{4}\). These findings are partially consistent with the work by Wilks (1998) where the exponential distribution was a better fit than the gamma distribution. The MulGETS no matter the distribution used for precipitation outperformed the WeaGETS where MD of standard deviations of ME, MG, WE and WG, were found to be 0.45, 1.03, 8.4 and 7.2, respectively (Fig. 6). That possibly indicates the importance of preserving the cross-correlation structure between all stations. Nevertheless, the skewness and kurtosis of both models were within 99% confidence interval.

Fig. 4
figure 4

Statistics comparison of observed precipitation data (OBS) with 1000 realizations from each weather model, represented as ellipsoidally-shaped clouds around their centers with isolines of the 50% and 99% confidence intervals

Full size image
Fig. 5
figure 5figure 5

Visual inspection of the five weather generators for a precipitation, b maximum temperature, c minimum temperature and d streamflow

Full size image
Fig. 6
figure 6

Level of adequacy of weather generators using Mahalanobis distance from the observed statistics to the cloud’s center of the generated PCP, Tmax, Tmin and SFSD (compared to SFOD) statistics

Full size image

Compared to other weather generators considered in this study, the \(k\)-nn approach was noticeably the least efficient model in reproducing precipitation attributes, where all precipitation statistics were way above the MD threshold of three. In terms of temperature variables, \(k\)-nn appears superior to the other four models in generating synthetic temperatures time series while precisely preserving the statistical moments of observed data (Figs. 5b, c, 6). These differences in the obtained results can be explained, in part, by differences in the underlying numerical data assimilation algorithms for the land–ocean–atmosphere relations (Warner 2010). An additional factor may be an inherent limitation of certain weather generators for certain climatic or topographic conditions. Fowler et al. (2007) also criticized weather generators for being strictly location-based, which implies that they may not be suitable to any region or climate. Also, further investigation of weather generators’ ability of estimating extreme values of climate variables, as done for rainfall extremes by Ramesh et al. (2018), is warranted.

4.2 Risk and performance indicator space

As reflected in the high NS value (0.79), coupled with the low values obtained for PBIAS (3%) and RSR (0.45), the SWAT model fed with observed meteorological information was very capable in simulating monthly streamflow according to the Liew et al. (2007) and Moriasi et al. (2007) criteria. The initial range for the most sensitive parameters, together with the best fit values from within the prediction uncertainty band, that were then adopted during the subsequent analyses, are provided in Table 2.

Table 2 Description of SWAT2012 most sensitive parameters calibrated for the South Nation watershed
Full size table

A central goal of the current work, from a practical point of view, was to determine how the simulated flow using observed climate data (SFOD) comes to lie within the modelled data cluster obtained by feeding SWAT with synthetic data (SFSD). There is an infinite number of potential indicators (such as annual, seasonal, and daily indicators) that can be studied, but obviously only a few can be presented herein and annual data is considered in the analysis. The MulGETS-Gamma set-up appears to be the best weather generator for our study area, in that it preserves the basic SFOD statistics (Figs. 5d, 6), followed by the MulGETS-Exponential configuration. Streamflow driven by the MulGETS-Gamma configuration appears to be satisfactorily consistence with the SFOD with MD values of 0.85, 0.3 and 0.32 respectively for \(\sigma\), \(\alpha_{3}\) and \(\alpha_{4}\), respectively. The MulGETS-Exponential configuration performed less efficiently, yet within the adopted threshold of 3 MD. However, the WeaGETS, implementing both distributions for precipitation generation, as well as the \(k\)-nn models were poorly preserving SFOD statistics, especially the higher moments (\(\alpha_{3}\) and \(\alpha_{4}\)) (Fig. 6).

The performances of the weather models in terms of reproducing extreme flow are presented in Fig. 7. Besides the 7-day dry spells (2-, 5-, 10- and 20-year for 7Q2, 7Q5, 7Q10 and 7Q20, respectively), high return period floods (2-, 5-, 10- and 50-year) from the annual maximum series (AM2, AM5, AM10 and AM50, respectively) were achieved. No apparent differences were found in the low-flow frequency results, as all tested weather generators performed quite well except for 7Q2 of \(k\)-nn (Fig. 7). The high-flow frequency results, on the other hand, were indicative of a convincing performance by the MulGETS models, where all tested recurrence intervals were satisfactorily reproduced with less than two units of standard deviation, as defined by MD. That indicates that they are interesting weather generation models where proximity with observations in the CSS translates very well into proximity in the RPIS. Such results were mainly driven by the accurate generation of streamflow statistics, especially the skewness and kurtosis as indicated previously. The outperformance of the MulGETS models is not surprising as they are the only ones with account for spatial dependence between climate variables at different stations. It is well known that the reproduction of hydrologic extremes is dependent of such spatial dependence (e.g., a flood is generally the result of simultaneous high precipitation at various locations; low flow events are more likely to be triggered by low precipitation at several locations).

Fig. 7
figure 7

The performance of the low and high streamflow indicators of the SFSD compared to the SFOD based on Mahalanobis distance

Full size image

The auto-covariance structures of SFOD and SFSD streamflow are shown in Fig. 8. All weather generators had their autocorrelation within the 95% confidence interval. The reproduction is reasonable but not perfect as the observed autocorrelation is in the interquartile range of the simulated time series only for lags 0–3. Visual inspection did not show clear differences in performance in reproducing the autocorrelation function between weather generators.

Fig. 8
figure 8

Flow autocorrelation of the five weather generators

Full size image

The above results show that the choice of a particular weather generator for water resources assessment can have an impact on key statistics of the simulated time series, hence on the estimated level of risk and the selection of management strategies. It is also shown that a given weather generator will perform differently on different variables. In the five weather generators, k-nn would be the recommended weather generator for risks related to temperature (e.g. heat and cold waves, changes growing season, etc.) while MulGETS would be the best for precipitation and streamflow, presumably because of its multisite features. This study is not exhaustive as there are a large number of other weather generators available to the modellers, as well as an infinite number of potential risk indicators. Our recommendation is that for each particular risk assessment problem, once the indicators are selected, the modellers should assess the performance of the weather generators available to them, or at least assess the performance of the one they intends to use.

5 Conclusions

In this study, the comparisons between observed and weather generator-driven data, in the CSS and RPIS, allowed for quantifying the performances of these weather generators. The delineated approach was developed to provide a statistical baseline to examine how the observational data come to lie within the modelled data cluster. An explicit accounting of risk and performance indicators was considered to assess uncertainties associated with stochastically generated weather data. Weather generator-derived sequences were compared with the observed climate by training both data series through a calibrated SWAT model. The high NS coefficient, coupled with low values obtained for PBIAS and RSR, implied that the SWAT forced with observed meteorological information was able to predict observed streamflow very satisfactorily. Apart from the k-nn approach, we utilized MulGETS and WeaGETS to reproduce temperature variables, and precipitation amounts and occurrences implementing two distributions, Exponential and Gamma, for the South Nation watershed. In total, the present study has analyzed five weather generators, coupled with an impact model for the hydrological response, while involving more models would lead emphatically to a better comprehensive decision.

A large number of sequence samples (1000 stochastic sequences) was vetted in the CSS and RPIS spaces. Generally, the CSS results demonstrated that MulGETS-models were generally the better-performing weather generators for the South Nation area but was outperformed by the k-nn approach in case of temperature. The statistics of SFSD were found to lie mostly outside 99% confidence intervals ellepes for the WeaGETS and k-nn models. The MulGETS model is thus considered the preferred choice candidates for risk analysis and discovery, mainly due this models’ ability to incorporate covariance for several stations. Low and high flow frequency analyses were conducted on each dataset to examine risk indices. The observed differences between examined weather generators in terms of low flow index results were not statistically significant, and further studies with a particular focus on how low flow indices reproduced by weather generators data are recommended.

While there cannot be a binary black-and-white classification of weather generators, it is possible to quantify their suitability for a specific field or geographical area, based on their individual strengths and weaknesses. The current work should appeal to end users of climate products, to facilitate the appropriate pick of the right weather generators, conditioned on the relevant CSS and RPIS information. It would also be worth investigating to verify these findings by versatile applications, such as economical, ecological, electricity demand, or crop-yield models.