1 Introduction

Stochastic rainfall generators are widely used in hydrologic analysis because they can provide precipitation input to models in situations where data are not available. In general, stochastic rainfall generators are classified into the three following categories: (1) the multi-scaling models, which are based on the observation that rainfall patterns have “self-similarity” at a given range of timescales (Lovejoy and Schertzer 1990 among many), (2) the non-parametric resampling models, which forms the new rainfall time series by borrowing the fragments from the instrumental data with similar statistical properties (Lall and Sharma 1996; Tarboton et al. 1998; Westra et al. 2012), (3) the Poisson cluster rainfall models, which is being considered in this study. The Poisson cluster rainfall models (Rodriguez-Iturbe et al. 1987, 1988), a type of stochastic rainfall models, represent rainfall as a sequence of storms composed of rain cell clusters (Kavvas and Delleur 1975). According to Olsson and Burlando (2002), “the representation of storm occurrence as a point process and the internal storm intensity structure as a cluster of rectangular pulses mimicking rain cells has proven to be (…) a physically realistic way to describe temporal rainfall”. The applicability of the Poisson cluster rainfall models has been validated over various geographic locations with different rainfall characteristics (Isham et al. 1990; Bo et al. 1994; Onof and Wheater 1994; Glasbey et al. 1995; Khaliq and Cunnane 1996; Onof et al. 1996; Cowpertwait et al. 1996; Verhoest et al. 1997) and these models have been used in a wide range of studies dealing with flooding (e.g. Wheater et al. 2005), drought (e.g. Yoo et al. 2008), contaminant transport (e.g. Botter et al. 2006), and ecosystem behavior (e.g. Laio et al. 2009), among others. A more thorough explanation about the developments, applications, and limitations to overcome of the Poisson cluster rainfall models can be found in Onof et al. (2000).

In Poisson cluster models, model parameters are typically calculated for each month of the year based on the multi-annual rainfall statistics of the corresponding months to account for the seasonal variability of rainfall (i.e., month-to-month variability), resulting in twelve parameter sets instead of one (Burton et al. 2008 among others). However, to our knowledge, the inter-annual variability of the precipitation statistics has not been incorporated in the estimation of the model parameters, and its effect on stochastically generated rainfall time series has not been studied.

In this study, it is hypothesized that overlooking the inter-annual variability of the statistics when generating stochastic rainfall causes errors and biases that might affect the overall rainfall depth variability and frequency of extreme values. To validate the proposed approach, a rainfall generator that can account for inter-annual variability is developed. Then, the rainfall time series generated based on this model was compared to the observed ones and also to the time series generated without accounting for inter-annual variability.

Section 2 describes the modified Bartlett-Lewis rectangular pulse (MBLRP) model, the stochastic rainfall model used in this study. Section 3 describes inter-annual variability of precipitation in detail. Section 4 describes how the new method of rainfall generation called “the hybrid model” (THM) is developed. Section 5 presents its results and discussion. Finally, Sect. 6 concludes this study.

2 The modified Bartlett-Lewis rectangular pulse (MBLRP) model

The MBLRP model, rainfall time series are represented as sequences of storms comprised of cluster of rain cells (see Fig. 1). In the model, X1 [T] is a random variable that represents the storm arrival time, which is governed by a Poisson process with parameter λ [1/T]; X2[T] is a random variable that represents the duration of storm activity (i.e., the time window after the beginning of the storm within which rain cells can arrive), which varies according to an exponential distribution with parameter γ [1/T]; X3 [T] is a random variable that represents the rain cell arrival time within the duration of storm activity, which is governed by a Poisson process with parameter β [1/T]; X4 [T] is a random variable that represents the duration of the rain cells, which varies according to an exponential distribution with parameter η [1/T] that, in turn, has a gamma distribution with parameters ν [T] and α (dimensionless); and X5 [L/T] is a random variable that represents the rain cell intensity, which varies according to an exponential distribution with parameter 1/μ [T/L]. From the physical viewpoint, λ is the expected number of storms that arrive in a given period, 1/γ is the expected duration of storm activity, β is the expected number of rain cells that arrive within the duration of storm activity, 1/η is the expected duration of the rain cells, and μ is the expected rain cell intensity. Parameters ν and α do not have a clear physical meaning, but the expected value and variance of η can be expressed as α/ν and α/ν2. Therefore, the model has six parameters: λ, γ, β, ν, α and μ; however, it is customary to use dimensionless ratios φ = γ/η and κ = β/η as parameters instead of γ and β. Based on these model assumptions, Rodriguez-Iturbe et al. (1988) derived the equations for the statistics of the simulated rainfall time series at an accumulation interval T as follow:

$$ {\text{E}}[{\text{Y}}_{\text{t}}^{{({\text{t}})}} ]\; = \;\lambda \;{{\upmu}}\;{{\upmu}}_{\text{c}} \;\frac{\upnu }{\upalpha - 1}\;{\text{T}} $$
(1)
$$ \begin{aligned} {\text{Var}}[{\text{Y}}_{\text{t}}^{{({\text{T}})}} ] = &\frac{{2\;{\text{v}}^{2 - \upalpha } {\text{T}}}}{\upalpha - 2}\left( {{\text{k}}_{1} - \frac{{{\text{k}}_{2} }}{\upphi }} \right) - \frac{{2\;{\text{v}}^{3 - \upalpha } }}{(\upalpha - 2)(\upalpha - 3)}\left( {{\text{k}}_{1} - \frac{{{\text{k}}_{2} }}{{\upphi^{2} }}} \right) \\ &\quad + \frac{2}{(\upalpha - 2)(\upalpha - 3)}\left[ {{\text{k}}_{1} ({\text{T}} + {{\upnu}})^{3 - \upalpha } - \frac{{{\text{k}}_{2} }}{{\upphi^{2} }}(\upphi {\text{T}} + {{\upnu}})^{3 - \upalpha } } \right] \\ \end{aligned} $$
(2)
$$ \begin{aligned} {\text{Cov}}[{\text{Y}}_{\text{t}}^{{({\text{T}})}} ,{\text{Y}}_{{{\text{t}} + {\text{s}}}}^{{({\text{T}})}} ] & = & \frac{{{\text{k}}_{1} }}{(\upalpha - 2)(\upalpha - 3)}\left\{ {\;[{\text{T}}\;({\text{s}} - 1) + {{\upnu}}]^{3 - \upalpha } + [{\text{T}}\;({\text{s}} + 1) + {{\upnu}}]^{3 - \upalpha } - 2({\text{T s}} + {{\upnu}})^{3 - \upalpha } } \right\} \\ & \quad + \frac{{{\text{k}}_{2} }}{{\upphi^{2} (\upalpha - 2)(\upalpha - 3)}}\left\{ {\;2(\upphi \;{\text{T}}\;{\text{s}} + {{\upnu}})^{3 - \upalpha } - [\upphi \;{\text{T}}\;({\text{s}} - 1) + {{\upnu}}]^{3 - \upalpha } - [\upphi \;{\text{T}}\;({\text{s}} + 1) + {{\upnu}}]^{3 - \upalpha } } \right\} \\ \end{aligned} $$
(3)
$$ \begin{aligned} {\text{P(Zero rainfall)}} = & { \exp }\left\{ { - \lambda {\text{T}} - \frac{\lambda \upnu }{\upphi (\upalpha - 1)}} \right.\left[ {1 + \upphi (\kappa + \upphi ) - \frac{1}{4}\upphi (\kappa + \upphi )(\kappa + 4\upphi )} \right. \\ \quad \left. { + \frac{{\upphi (\kappa + \upphi)(4\kappa^{2} + 27\kappa \upphi+ 72\upphi^{2} )}}{72}} \right] + \frac{\lambda \upnu }{(\upalpha - 1)(\kappa + 4\upphi)}\left( {1 - \kappa - \upphi+ \frac{3}{2}\kappa \upphi+ \upphi^{2} + \frac{{\kappa^{2} }}{2}} \right) \\ \left. {\quad + \frac{\lambda \upnu }{(\upalpha - 1)(\kappa + \upphi)}\left[ {\frac{\upnu }{{\upnu + (\kappa + \upphi){\text{T}}}}} \right]^{\upalpha - 1} \frac{\kappa }{\upphi}\left( {1 - \kappa - \upphi+ \frac{3}{2}\kappa \upphi+ \upphi^{2} + \frac{{\kappa^{2} }}{2}} \right)} \right\} \\ \end{aligned} $$
(4)

where

$$ {\text{k}}_{1} = \left( {2\lambda \mu_{\text{c}} \mu^{2} + \frac{{\lambda \mu_{\text{c}} \kappa \upphi \mu^{2} }}{{\upphi^{2} - 1}}} \right)\left( {\frac{{\upnu^{\upalpha } }}{\upalpha - 1}} \right) $$
(5)
$$ {\text{k}}_{2} \; = \;\left( {\frac{{\lambda \;\mu_{\text{c}} \;\kappa \;\upphi \;\mu^{2} }}{{\upphi^{2} - 1}}} \right)\left( {\frac{{\upnu^{\upalpha } }}{\upalpha - 1}} \right) $$
(6)
$$ \mu_{\text{c}} \; = \;1 + \frac{\kappa }{\upphi }, $$
(7)

where s is the lag time in number of accumulation intervals, and Yt(T) is the rainfall time series at an accumulation interval T.

Fig. 1
figure 1

Schematic of the MBLRP model. The white and gray circles represent the arrival time of storms and rain cells, respectively. Each rain cell is represented by a rectangle whose width and height represent its duration and rainfall intensity, respectively

Full size image

Estimation of MBLRP model parameters is accomplished by minimizing the discrepancy between the statistics of simulated and observed rainfall time series. Some statistics commonly used are the mean, variance and lag-s covariance of the precipitation depth, and the probability of zero rainfall at various accumulation levels (Khaliq and Cunnane 1996). Bo et al. (1994) suggested the following equation as an objective function in calibration:

$$ \sum\limits_{{{\text{k}} = 1}}^{\text{n}} {{\text{w}}_{\text{k}} } \left[ {1 - \frac{{{\text{F}}_{\text{k}} (\vec{\theta })}}{{{\text{f}}_{\text{k}} }}} \right]^{2} $$
(8)

where \( \vec{\theta } \) is a vector of the model parameters, n is the number of rainfall statistics being matched at various temporal accumulation level, Fk is the kth statistic of the synthetic rainfall time series (Eqs. 1 to 4), fk is the kth statistic of the observed rainfall time series, and wk is the weight factor for the kth statistic (Kim and Olivera 2012).

3 Rainfall inter-annual variability

Figure 2 shows the seasonality and inter-annual variability of the statistics of the rainfall time series observed in the NCDC (2011) gage FL-9148 (star mark in Fig. 3). In the figure, the hollow circles connected by solid lines represent the statistics calculated for the entire period of record; while the solid dots show the statistics of individual months that vary with years (e.g. January of 1985, January of 1986). The wide range of the vertical distribution of the solid dots in each plot suggest that the monthly statistics vary significantly from year to year and that lumping them into a single value could be an oversimplification. Here, it is noteworthy that the conventional approaches of Poisson cluster rainfall modeling (Burton et al. 2008 among others) generates the rainfall time series based on this “lumped” rainfall statistics. This study proposes a noble approach that can incorporate the inter-annual variability of rainfall statistics and shows how it enhances the properties of the generated rainfall time series. We name this approach THM and explain it in the following section.

Fig. 2
figure 2

Monthly variations of the rainfall statistics observed at gage FL-9148. The statistics referring to the month of the entire length of rainfall time series are shown as the hollow circles along with the lines and the ones referring to the month of a specific year are shown as the solid dots

Full size image
Fig. 3
figure 3

Gage FL-9148 (star) and the 11 gages used for model validation (circles)

Full size image

4 The hybrid model (THM)

4.1 Overview

The model presented in this study incorporates the inter-annual variability of rainfall statistics by simulating short-term rainfall statistics (that is, rainfall statistics of individual months) based on the correlation between observed rainfall statistics. Then, the model generates rainfall time series using the MBLRP model based on the simulated short-term rainfall statistics. This model is named “THM” because it combines the process of generating rainfall statistics and the process of generating rainfall time series. The development of the model is explained in detail using the precipitation data observed at gage FL-9148 (star mark in Fig. 3). Finally, the model is validated using the rainfall data observed at 11 rain gages (total of 11 × 12 months = 132 gage-months) located across the United States (Fig. 3).

4.2 Generation of rainfall statistics

The first step of THM is to stochastically generate rainfall statistics of individual months that is to be used for parameter calibration of the MBLRP model. The model generates the following monthly rainfall statistics based on the correlation between them; mean at an hourly accumulation level (MEAN1), variances at hourly, 3-, 12-, and 24-hourly accumulation levels (VAR1, VAR3, VAR12, and VAR24); probability of zero rainfall at hourly, 3-, 12-, and 24-hourly accumulation levels (PROB0-1, PROB0-3, PROB0-12, and PROB0-24); lag-1 autocorrelation at hourly, 3-, 12-, and 24-hourly accumulation levels (AC1, AC3, AC12, and AC24).

Figure 4 shows the scatter plots of the STD1 (\( { = }\sqrt {\text{VAR1}} \)), PROB0-1 and AC1 versus MEAN1 of the rainfall time series observed at gage FL-9148 for the month of June. Each point in the plots represents the monthly statistic of the rainfall time series (e.g. June 1981, June 1995, etc.). Consequently, there are 61 points in each plot because the gage has 61 years of records. Linear regression analysis was performed to identify the relationship between the variables. Table 1 shows the regression coefficients between the variables. VAR1 and PROB0-1 showed a clear correlation with MEAN1 while AC1 did not. THM randomly generates MEAN1 first, and then VAR1(\( {\text{ = STD1}}^{2} \)) and PROB0-1 based on the generated MEAN1 according to the relationship identified through these regression analyses. AC1 was generated independently since it did not show a considerable correlation with the other statistics.

Fig. 4
figure 4

Correlations between MEAN1 and STD1, MEAN1 and PROB0-1, and MEAN1 and AC1 at rainfall gage FL-9148 for the month of June

Full size image
Table 1 Results of the regression analysis between the rainfall statistics of the month of June at gage NCDC-FL9148
Full size table

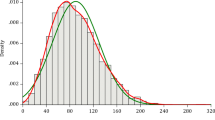
The histogram of MEAN1 for the month of June for gage FL-9148 and its corresponding fitted gamma distribution are shown in Fig. 5. The gamma distribution was used to model MEAN1 as suggested by Ozturk (1981). The two parameters of the distribution were estimated using the method of maximum likelihood. Then, MEAN1 was randomly drawn from the gamma distribution with the estimated parameters. The histogram of AC1 observed at gage FL-9148 during the month of June is also shown in Fig. 5. Because of its near-symmetrical shape, a normal distribution was adopted to fit the distribution, from which AC1 is randomly drawn.

Fig. 5
figure 5

Histogram of MEAN1 and AC1. The fitted curve of a gamma distribution for MEAN1 is shown along with the histogram (left side)

Full size image

Because STD1(\( = \sqrt {\text{VAR1}} \)) and PROB0-1 are highly correlated with MEAN1 (Fig. 4), VAR1 and PROB0-1 are generated based on MEAN1 using the result of the regression analysis in Table 1. For example, the following two equations specifically address the relationships between these variables for gage FL-9148 for the month of June:

$$ {\text{STD1 }} = { 4}. 7 20 3 {\text{ Mean1 }} + \, 0.0 4 9 7 3 { } + \, \varepsilon_{ 1} $$
(9)
$$ {\text{PROB}}\,0 - 1 { } = \,-0.9718 {\text{ Mean1 }} + \, 0. 9 5 8 3 { } + \, \varepsilon_{ 2} $$
(10)

where ε1 and ε2 represent residual errors expected when using the regression equation.

ε1 and ε2 in Eqs. (9) and (10) were randomly drawn from a normal distribution with mean 0 and variance equal to the error variance of the regression equation (Column “Var(Error)” in Table 1).

A strong linear correlation was identified between the rainfall statistics at different temporal accumulation levels with the correlation coefficient ranging between 0.41 and 0.99. The result of the linear regression analysis is summarized in Table 1. The same methodology that was used for the generation of VAR1 and PROB0-1 from MEAN1 was used to generate the rainfall VAR, AC, and PROB0 at 3-, 12-, and 24-hourly accumulation levels: VAR1 is used for the generation of VAR3, which is, in turn, used for the generation of VAR12. VAR12, then again, is used as the basis of the generation of VAR24. The same principle was applied for the generation of PROB0-3, PROB0-12, and PROB0-24 from PROB0-1; and AC3, AC6, AC12, and AC24 from AC1. The generated statistics values were perturbed by the amount specified by the variance of error according to the regression analysis (Column “Var(Error)” in Table 1)

The described process is repeated for the number of months for which rainfall time series is generated. For example, if the model is to generate 50 years of rainfall time series, THM generates rainfall statistics sets for the 600 months (50 years × 12 months/year). This is the key concept of THM to integrate inter-annual variability of rainfall statistics, and it contrasts to the traditional approach which uses 12 sets (1 per each month regardless of the number of years being simulated) of observed rainfall statistics.

4.3 Generation of rainfall time series using the MBLRP model

Once the rainfall statistics is generated as described in Sect. 4.2, the next step is to obtain the 6 parameters (\( \overrightarrow {{{\uptheta}}} \)) of the MBLRP model, which were calibrated using ISPSO (Cho et al. 2011) based on the rainfall statistics generated for the individual months using Eq. 8 as objective function. This procedure is repeated for the number of individual months to be used for simulation. For example, if 50 years of rainfall time series is to be simulated, the parameter calibration is repeated for 600 (=50 × 12) times, which yields 600 model parameter set. Once the parameters are obtained, THM generates synthetic rainfall time series of each individual month using the MBLRP model based on the estimated parameter sets.

Because the generated rainfall time series for each of the months has the length of only one month, the statistics of it does not usually match the targeting rainfall statistics. To reduce these residuals in statistics, the process of rainfall generation is repeated for 20 times using a given parameter set, which yields 20 rainfall time series with the length of one month. Then, the rainfall time series with the lowest statistics residual is chosen as the finalist. The difference between the statistics of the simulated rainfall time series of the jth month and the target statistics is calculated as follow:

$$ {\text{R}}_{\text{j}} = \sum\limits_{{{\text{i}} = 1}}^{\text{n}} {\left[ {({\text{Z}}_{\text{i}}^{\text{simul}} - {\text{Z}}_{\text{i}}^{\text{target}} )^{2} } \right]} $$
(11)

,where \( {\text{Z}}_{\text{i}}^{\text{simul}} \) is the Z-score (departure of a given statistics from its global mean normalized by global standard deviation) of the ith statistics of the simulated rainfall time series and \( {\text{Z}}_{\text{i}}^{\text{target}} \) is the Z-score of the ith target statistics. Z-score was calculated based on the mean and standard deviation of the rainfall statistics that were estimated using the rainfall time series observed at 1,099 rain gages across the United States (Table 1 in Kim and Olivera 2011). This study used MEAN1, VAR1, AC1, and PROB0-1 to calculate Rj (n = 4). Then, the synthetic rainfall time series for the jth month with the lowest value of Rj is chosen as the finalist among the 20 months of generated rainfall time series.

4.4 Model validation

The performance of THM was tested based on its ability to reproduce the distribution of the monthly maximum rainfall depths and extreme precipitation depth. A total of 132 months of precipitation data observed at 11 NCDC precipitation gages (12 months per one gage) across the coterminous United States (Fig. 3) were used for this validation procedure. All chosen gages have at least 50 years of records. For each of the 132 gage-months, 100 months of synthetic rainfall time series were generated using both THM and the conventional MBLRP modeling approach. Subsequently, each of the gage-months has three different types of rainfall time series including observed one. Then, monthly maximum rainfall depths with the duration of 1, 3, and 6 h were calculated. As a result, each gage-month is associated with 300 simulated monthly maximum rainfall depths accounting for statistic variability (i.e., 3 rainfall durations × 100 years of simulation) (\( {\text{P}}_{\text{THM}}^{ 1} ,\,{\text{P}}_{\text{THM}}^{ 3} ,\,{\text{P}}_{\text{THM}}^{ 6} \)), 300 simulated monthly maximum rainfall depths not accounting for statistic variability (i.e., 3 rainfall durations × 100 years of simulation) (\( {\text{P}}_{\text{Trad}}^{ 1} ,\,{\text{P}}_{\text{Trad}}^{ 3} ,\,{\text{P}}_{\text{Trad}}^{ 6} \)); and a number of monthly maximum observed rainfall depths (i.e., 3 rainfall durations × years of record) (\( {\text{P}}_{\text{Obs}}^{ 1} ,\,{\text{P}}_{\text{Obs}}^{ 3} ,\,{\text{P}}_{\text{Obs}}^{ 6} \)).

The two-sample Kolmogorov–Smirnov test (K–S test) was used to compare the distributions of the variables calculated from the observed rainfall time series and those calculated from the synthetic rainfall time series. The test statistic of the two-sample Kolmogorov–Smirnov test, which compares the distributions of data sets x1 and x2, is as follows:

$$ \hbox{max} \left| {{\text{F}}{}_{1}({\text{x}}) - {\text{F}}_{2} ({\text{x}})} \right| $$
(12)

where \( {\text{F}}{}_{ 1} ( {\text{x)}} \) is the proportion of data set x1 less than or equal to x. The null hypothesis of the test is that data sets x1 and x2 are from the same continuous distribution. Therefore, if the result of the test indicates that the null hypothesis is not rejected, one can say that data sets x1 and x2 are from the same continuous distribution with a given significance level that is specified in the test. In this study, a significance level of 5 % was used.

A set of two tests should be performed to tell if THM outperforms the traditional approach. For example, if a test comparing \( {\text{P}}_{\text{Obs}}^{ 1} \) and \( {\text{P}}_{\text{THM}}^{ 1} \) indicates that both variables are from the same continuous distributions and another test comparing \( {\text{P}}_{\text{Obs}}^{ 1} \) and \( {\text{P}}_{\text{Trad}}^{ 1} \)indicates that they are from different distributions, the advantage of using THM over the traditional approach to predict the maximum precipitation depth at an hourly duration is justified. This set of tests was repeated for the three testing variables (\( {\text{P}}_{{}}^{1} ,\,{\text{P}}_{{}}^{ 3} ,\,{\text{P}}_{{}}^{6} \)) to see how the performance of THM compares to that of the traditional approach.

In addition to this rather qualitative approach to compare the models’ performance, each model’s performance to reproduce the extreme rainfall depth was quantitatively estimated. Frequency analysis was performed on \( {\text{P}}^{1} , {\text{ P}}^{3} \), and \( {\text{P}}^{6} \) to estimate extreme rainfall depth with 100-, 50-, and 30-months of recurrence interval. Here, it is noteworthy that the extreme rainfall depth has the frequency unit of month instead of year. For example, 100-month rainfall represents the rainfall depth that has the exceedance probability of 1 % of a given month. Another approach of estimating the rainfall depth with the frequency unit of year was considered, but such approach was not adopted because it disturbs the direct comparison between the variables by filtering out the maximum rainfall depths of the remaining 11 months.

Generalized logistic distribution (Asquith 1998) was used to model the distribution of the monthly maximum rainfall, and the method of L-moment (Hosking 1990) was used to estimate the parameters of the distribution. Then, the normalized residual of each model’s design precipitation estimate was calculated as follow:

$$ {\text{RP}}_{\text{trad}}^{\text{RI}} = \frac{{{\text{DP}}_{\text{trad}}^{\text{RI}} - {\text{DP}}_{\text{obs}}^{\text{RI}} }}{{{\text{DP}}_{\text{obs}}^{\text{RI}} }} $$
(13)
$$ {\text{RP}}_{\text{THM}}^{\text{RI}} = \frac{{{\text{DP}}_{\text{THM}}^{\text{RI}} - {\text{DP}}_{\text{obs}}^{\text{RI}} }}{{{\text{DP}}_{\text{obs}}^{\text{RI}} }} $$
(14)

,where RP represents the normalized residual of the extreme precipitation; DP represents the depth of the extreme precipitation; and superscript and subscript represent recurrence interval and the type of time series on which the calculation is based, respectively. If the distribution of these residuals is concentrated to 0, the advantage of using one model over the other can be justified.

5 Results and discussion

5.1 Reproduction of monthly maximum rainfall depth

Table 2 shows the performance of each model in reproducing the distribution of the observed monthly maximum rainfall depths. THM outperformed in reproducing the distributions of 3- and 6-hour duration monthly maximum precipitations while the traditional approach outperformed THM in reproducing the one with 1-hour duration. The success ratio of both approaches ranged between 45 and 81 %. Even though the values presented in Table 2 do not explicitly prove the superiority of THM over the traditional modeling approach, they provide a general idea on the performance of both models in reproducing the distribution of the maximum rainfall depth. It also has to be noted that the result of the K–S test tends to be more sensitive near the center of the distribution than it is at the tails. This result suggests that considering inter-annual variability does not necessarily enhance the rainfall model’s performance to reproduce the overall distribution of the maximum rainfall depth.

Table 2 Performance of THM and the traditional MBLRP approach in reproducing the distribution of extreme rainfall depths
Full size table

5.2 Reproduction of extreme rainfall depth

The result of the analysis on extreme precipitation depth reproduction enlightens the perspective of THM that could not be caught by the K–S test. Figure 6 shows the histograms of the normalized residual (Eqs 13 and 14) of 1-hour duration design precipitation with 100-, 50-, and 30-month recurrence interval for THM (upper row) and traditional MBLRP model (lower row). In the plots of Fig. 6, sharper shape of the distribution means higher model’s consistency. Also, model’s unbiasedness increases as the center of the distribution gets closer to 0. In general, it is observed that the distributions of \( {\text{RP}}_{\text{Trad}} \) for all three recurrence intervals are systematically biased to the left side of 0. This means that the traditional MBLRP approach systematically and significantly underestimates the extreme rainfall of the observed data. On the contrary, the level of biasedness of the distribution of \( {\text{RP}}_{\text{THM}} \) is significantly less than that of \( {\text{RP}}_{\text{Trad}} \). The consistency of the model’s performance was similar for both of the approaches showing similar peakedness of the distribution. For some cases, THM had slightly less performance consistency compared to the traditional approach. However, the fact that the traditional approach has lower standard deviation than the suggested approach does not mean that it outperforms THM because it means the traditional approach underestimates the extreme rainfall values more consistently compared to THM. Another way to compare the model’s performance is to see the proportion that the estimated extreme rainfall depth (RP) falls within a given percentage (20 %) of the observed counterpart, which is shown in the 4th, 7th, and 10th row of Table 3. These values are significantly greater for THM. Table 3 also summarizes the mean, standard deviation of the distribution of RP. Similar result was obtained for all other comparison cases (extreme rainfall depth with 3 h and 6 h duration). The mean of \( {\text{RP}}_{\text{THM}} \) is notably closer to 0 compared to \( {\text{RP}}_{\text{Trad}} \) while the standard deviation is slightly greater for THM (again, this does not leads to the conclusion that the traditional approach outperforms THM). Also, the probability that the estimated RP values falls within ±20 % of the observed counterpart was significantly greater for \( {\text{RP}}_{\text{THM}} \).

Fig. 6
figure 6

Histograms of the normalized residual of the extreme precipitation depths reproduced by THM and the traditional approach of MBLRP rainfall modeling. From top to bottom, then left to right are shown the histograms of \( {\text{RP}}_{\text{THM}}^{ 1 0 0} \), \( {\text{RP}}_{\text{THM}}^{50} \), \( {\text{RP}}_{\text{THM}}^{30} \) \( {\text{RP}}_{\text{Trad}}^{ 1 0 0} \), \( {\text{RP}}_{\text{Trad}}^{50} \), and \( {\text{RP}}_{\text{Trad}}^{30} \)

Full size image
Table 3 Performance comparison between THM and the traditional approach on reproduction of design rainfall values
Full size table

In Fig. 6, the histograms of \( {\text{RP}}_{\text{THM}} \) have stronger positive skew than those corresponding to \( {\text{RP}}_{\text{Trad}} \), which also causes the greater variability of the \( {\text{RP}}_{\text{THM}} \) values. This means that the extreme precipitation simulated by THM is more likely to be greater than the observed one compared to the one estimated using the traditional method. The most probable cause of this problem is that the Gamma distribution adopted to model the mean rainfall for all gages and months. The distribution of the mean rainfall can follow other distributions especially because the gages used for the model validation are physically distant thus can have different climatic properties. Considering that mean monthly rainfall is used as the basis of the generation of the other statistics and the MBLRP model parameter calibration, choosing the right distribution type of the mean rainfall can greatly affect the accuracy of the model. This problem may be resolved if the correct type of distribution is customized for each of the gage-months based on the result of the statistical tests such as Kolmogorov–Smirnov test.

It also has to be noted that some recent developments in non-parametric stochastic rainfall generation has been successful in reproducing the extreme rainfall depths more closely (e.g., Westra et al. 2012). In this broader context of the stochastic rainfall generation, the contribution of this study in improving the ability of stochastic rainfall generation model in reproducing extreme rainfall values should be considered limited.

6 Conclusions

We proposed a novel approach of stochastic rainfall generation based on MBLRP model that can account for the inter-annual variability of rainfall statistics. While the newly proposed approach did not show apparent advantage over the traditional approach in reproducing the distribution of the maximum rainfall depth, it clearly outperformed the conventional one in reproducing extreme precipitation depths by reducing the systematic bias. This result indicates that the inter-annual variability of rainfall contains the important information about extreme values of precipitations that the lumped long-term monthly statistics could easily miss.

Numerous previous studies regarding Poisson cluster rainfall models have tried to enhance the model’s ability to capture extreme rainfall. Cowpertwait (1998) modified the model such that it can explicitly count for the 3rd order moment of the observed rainfall time series. Evin and Favre (2012) refined the model structure by introducing the concept of transient storm arrival rate. These studies tried to refine the model structure to enhance the performance. In this context, the result of this study suggests that the performance of the rainfall generation model can be improved not only by altering or refining model structure but also by incorporating more information about the observed rainfall time series, especially its internal variability. We expect the same principle be applicable in other types of stochastic rainfall generators to enhance the performance.