Introduction

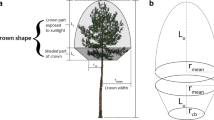
Crown width (CW) is defined as an average of two crown diameters at two cardinal directions: east–west and south–north, obtained from measurements of four crown radii (crown components), namely east crown radius (CRE), west crown radius (CRW), south crown radius (CRS), and north crown radius (CRN) (Bragg 2001). It is a useful measure of tree vigor (Assman 1970; Hasenauer and Monserud 1997; Hynynen et al. 2002), mortality (Monserud and Sterba 1996), and above-ground biomass (Carvalho and Parresol 2003; Fu et al. 2016). CW can be also used in ecological modeling to predict light interception in tree canopy (Oker-Blom et al. 1989; Pukkala et al. 1991). However, despite its numerous benefits, measuring the CW of every sampled tree is costly and time-consuming (Bragg 2001; Sönmez 2009; Fu et al. 2013; Sharma et al. 2016). Thus, accurate CW models are required for accurate predictions of CW.

CW estimates obtained from measurements of stand and tree characteristics serve as input information to deterministic or stochastic CW models (Biging and Wensel 1990; Baldwin and Peterson 1997; Bragg 2001; Sönmez 2009; Fu et al. 2013; Hao et al. 2015; Sharma et al. 2016). Methods of developing CW models have evolved from simple ordinary least squares (OLS) regression to linear mixed-effects (LME) modeling, and then to nonlinear mixed-effects (NLME) modeling (Sánchez-González et al. 2007; Fu et al. 2013; Hao et al. 2015; Sharma et al. 2016; Fu et al. 2017a). All existing CW models have been developed using the average of two crown diameters as a function of tree variables (e.g., diameter at breast height, total tree height, height to crown base, and the height–diameter ratio) and stand variables (e.g., dominant height, site index, and stand density measures) using OLS regression or an LME/NLME modeling approach.

For each tree in a specific stand, especially for natural forests, the differences among the crown components (CRE, CRW, CRS, and CRN) are usually very large because of vigorous competition with neighboring trees (Power et al. 2012). The CW and crown components are also strongly correlated with each other (Power et al. 2012). However, none of the CW models that were developed using existing methods have accounted for the differences among the relationships between each of four crown components and predictor variables of the CW models. In addition, correlations among the crown components have also been ignored. Thus, these CW models are not estimated efficiently, and they do not account for additivity among the crown components (Parresol 1999). The lack of additivity in existing modeling methods results in an inconsistency, as the sum of the predicted values from the crown components models does not equal the predicted value from the CW models (Kozak 1970). In addition, these CW models also have fallen short of statistical efficiency in terms of parameter estimation. These limitations might result in low prediction accuracies of the CW models (Tang et al. 2015).

A potential solution to the problem is the use of nonlinear simultaneous equations (NSEs) that not only ensure the additivity of nonlinear CW and crown components models, but also account for the correlations among the crown components (Fuller 1987; Kangas 1998; Tang and Zhang 1998; Tang et al. 2001, 2015; Carroll et al. 2006). For example, Tang et al. (2000) proposed a disaggregation model structure using an NSE, namely a one-step, proportional weighting system, in which an above-ground biomass model is first developed, and then the estimated above-ground biomass is disaggregated into tree components (e.g., wood, bark, branch, and foliage) based on their proportions in the above-ground biomass. Furthermore, if subtotal biomass estimates are also desirable, the estimated above-ground biomass is first disaggregated into subtotals (e.g., stem and crown) based on their proportions in the above-ground biomass. Then, the estimated stem biomass is divided into wood and bark based on their proportions in the stem biomass, and the estimated crown biomass is divided into branch and foliage based on their proportions in the crown biomass. This constitutes a two-step, proportional weighting system (Tang et al. 2000). Tang et al. (2000) found that the system of biomass equations developed using this method effectively ensured additivity, and had high prediction accuracy.

In recent years, NSE has been increasingly used in forestry to develop various additive models, especially additive biomass equations (Parresol 1999; Bi et al. 2004; Dong et al. 2015, 2016; Fu et al. 2016, 2017b). It has been found that NSE ensures high additivity efficiencies of the forest models, and strong abilities of accounting for correlations among the components. NSE increases the prediction accuracy of the models, compared with other non-additive methods, such as OLS methods (Lindstrom and Bates 1990; Vonesh and Chinchilli 1997). To our knowledge, however, no study has used NSE to ensure the additivity of crown components during the estimation of CW.

In addition to NSE, two other methods, adjustment in proportion (AP) and an OLS with separating regression (OLSSR), are commonly used for forcing the additivity of a set of nonlinear models (Parresol 1999, 2001; Tang et al. 2001, 2015; Tang and Wang 2002; Fu et al. 2016). AP directly partitions the total CW of a tree into its four basic crown components (CRE, CRW, CRS, and CRN) by weighting, whereas for OLSSR, a total CW regression function is defined as the half sum of the separately calculated regression functions of the crown components. However, neither the AP nor OLSSR models account for inherent correlations among the components. Regarding the NSE, no study has used these two methods to develop a system of nonlinear CW models.

The objectives of this study were: (1) to develop nonlinear CW models using NSE under two disaggregation procedures (a one-step, proportional weighting system and a two-step, proportional weighting system) for Prince Rupprecht larch (Larix principis-rupprechtii Mayr.) in natural stands in northern China, and (2) to compare the AP and OLSSR procedures with respect to their abilities to predict CW and estimate crown components.

Materials and methods

Data

We used data from 116 permanent sample plots (PSPs) that were established in natural stands of Prince Rupprecht larch in the state-owned Guandi mountain forest (67 PSPs) and the state-owned Boqiang forest (49 PSPs) of northern China (Fig. 1). Each PSP was a 0.04 ha square. The PSPs were selected in such a way that they provided representative information for a variety of stand structures and densities, tree heights and ages, and site productivity.

Fig. 1
figure 1

Location of the study area consisting of the Guandi mountain forest and the Boqiang forest in northern China (lower left and right), and the spatial distribution of permanent sample plots (upper left)

Full size image

Within each PSP, for all standing and living trees with diameter at breast height (D) ≥5 cm, we measured total tree height (H), height to crown base (height above ground to crown base, HCB), and the four crown radii (CRE, CRW, CRS, and CRN). Tree HCB was defined as the height from the ground to the base of the first normal green branch as a part of the crown; this excluded the secondary branches (epicormics and adventitious) (Hasenauer and Monserud 1996). Furthermore, a single green branch was not the base of tree crown if there were at least three whorls above it (Hasenauer and Monserud 1996). The forked trees with the forks below 1.3 m were treated as separate trees and otherwise, as a single tree. The positions of four crown radii of each tree were determined by two cardinal directions (Bragg 2001). The first cardinal direction was defined as the direction from south to north (the corresponding crown width was defined as the south–north crown width, CWSN), and the second cardinal direction was perpendicular to the first, namely the direction from east to west (the corresponding crown width is defined as the east–west crown width, CWEW) (Fig. 2). The crown radii were measured as the horizontal distances between the center of a tree bole and the greatest extent of the crown from the bole (Fig. 2). The branch tip was located by vertical sighting with a clinometer (Marshall et al. 2003). CW was computed by (CRS + CRN + CRE + CRW)/2. Four dominant or codominant trees were identified and measured in each PSP (the proportion of the 100 thickest trees per ha) (Raulier et al. 2003). The ages of the selected dominant or codominant trees were recorded by counting the growth rings based on increment cores taken from the stem at a height of 0.1 m (above ground) (Rozas 2003). For each PSP, plot dominant tree diameter at breast height DD, plot dominant tree height DH, and dominant mean age DA were obtained from the averages of these attributes (Du et al. 2000). The relationships among CW, CRE, CRW, CWEW, CRS, CRN, and CWSN and the five tree variables, including D, H, HCB, DH, and DD, are shown in Fig. 3.

Fig. 2
figure 2

The positions of the east crown radius (CRE), west crown radius (CRW), south crown radius (CRS), north crown radius (CRN), south–north crown width (CWSN), and east–west crown width (CWEW) of a sample tree, E, W, S and N represent the east, west, south and north, respectively

Full size image
Fig. 3
figure 3

The relationships among east crown radius (CRE), west crown radius(CRW), south crown radius (CRS), north crown radius (CRN), east–west crown width (CWEW), south–north crown width (CWSN), and crown width (CW) with five tree variables, including diameter at breast height (D), total tree height (H), height to crown base (HCB), total height of the dominant tree (DH), and D of the dominant tree (DD) for two forests: the Guandi mountain forest denoted with black circles and the Boqiang forest denoted with gray circles

Full size image

The PSPs were randomly divided into two groups: model-fitting and model-validation groups. The model-fitting group contained 2250 trees from 69 PSPs, while the model-validation group consisted of 1119 trees from 37 plots. The statistics and relevant stand characteristics of the measurements are summarized in Table 1.

Table 1 Summary of the statistics for the model-fitting and model-validation datasets
Full size table

Base model

Fu et al. (2013) developed a logistic model for Chinese fir (Cunninghamia lanceolata) CW estimation based on D, H, HCB, and DH. They reported that their CW model provided higher predictive accuracy than other tested CW models. To account for the differences between the Guandi mountain and Boqiang forests, one additional dummy variable, \(P\), was created; \(P = 0\) denotes the Guandi mountain forest, and \(P = 1\) denotes the Boqiang forest. After imposing the \(P\) on \(\beta_{1}\) and \(\beta_{2}\), the modified Fu’s CW model took the following form:

$${\text{CW}} =\; f({\mathbf{x}},P,{\varvec{\upbeta}}) = [\beta_{1} + k_{1} P + (\beta_{2} + k_{2} P){\text{DH}}]/\left[ {1 + (\beta_{3} + \beta_{4} {\text{HCB}})\exp ( - (\beta_{5} + \beta_{6} H)D)} \right] + \varepsilon$$
(1)

where \({\mathbf{x}}\) is the covariate vector, including D, H, HCB, and DH, \({\varvec{\upbeta}} = (\beta_{1} ,\beta_{2} ,\beta_{3} ,\beta_{4} ,\beta_{5} ,\beta_{6} ,k_{1} ,k_{2} )\) is an eight-dimensional parameter vector, and \(\varepsilon\) is an error term. Model (1) was used as the base function to develop the nonlinear CW models.

NSE

Following Tang et al. (2001), a general NSE can be formulated as follows:

$$\left\{ \begin{array}{ll} {\mathbf{f}}({\mathbf{y}}_{i} ,{\mathbf{x}}_{i} ,{\varvec{\upbeta}}) = 0,&\quad i = 1, \ldots ,n \hfill \\ {\mathbf{Y}}_{i} = {\mathbf{y}}_{i} + {\mathbf{e}}_{i} &\hfill \\ E({\mathbf{e}}_{i} ) = 0,&\quad Var({\mathbf{e}}_{i} ) = {\varvec{\Sigma}} \hfill \\ \end{array} \right.$$
(2)

where \(n\) is the total number of observations; \({\mathbf{x}}_{i}\) is the observed value of a q-dimensional, error-free variable (exogenous variable); \({\mathbf{Y}}_{i}\) is the observed value of a p-dimensional, endogenous variable with error; \({\mathbf{y}}_{i}\) is the true value of \({\mathbf{Y}}_{i}\); \({\varvec{\Sigma}}\) is the \(p \times p\) dimensional, positive definite variance–covariance matrix of the error term \({\mathbf{e}}_{i}\), and the general expression of the matrix is given by \({\varvec{\Sigma}} = \sigma^{2} {\varvec{\uppsi}}\); \(\sigma^{2}\) is the scaling factor for the error dispersion, which is given by the residual variance of the model; \({\varvec{\uppsi}}\) is the \(p \times p\) dimensional error structure matrix; and \({\varvec{\upbeta}}\) is the \(n_{par} \times 1\) dimensional parameter vector. \({\mathbf{f}} = (f_{1} ,f_{2} , \ldots ,f_{P} )^{T}\), with T indicating the transpose of a matrix or vector, is a \(p\)-dimensional vector function, and in this study, it was composed of the CW and crown radii equations that were used in the base model (1) for the components.

Model (2) intrinsically ensures the compatibility of parameters for any data structure, and it does not require the specification of dependent and independent variables, as is required by the OLS model. Model (2) can be solved by a two-stage, errors-in-variables model (TSEM) algorithm (Tang and Li 2002; Fu et al. 2016). The details of NSE, TSEM estimation algorithm, and their computer implementation can be found in the studies of Tang et al. (2001, 2015).

Within the aforementioned NSE framework, there are two alternative procedures for ensuring additivity: one directly partitions the total CW of a tree into its four basic components, including CRE, CRW, CRS, and CRN, which is called a one-step, proportional weighting system; and the other, which is called a two-step, proportional weighting system, first divides the total tree biomass into subtotals, CWEW and CWSN, and then it partitions the subtotals into four basic components.

One-step, proportional weighting system

The one-step, proportional weighting system ensures that the summation of the crown radii values from all the components is equal to twice the total CW. For \(i = 1, \ldots ,n\), \({\text{CW}}_{i}\), \({\text{CR}}_{\text{Ei}}\), \({\text{CR}}_{\text{Wi}}\), \({\text{CR}}_{\text{Si}}\), and \({\text{CR}}_{\text{Ni}}\) represent the observed biomass values of CW, CRE, CRW, CRS, and CRN for the ith tree, respectively, and their values contain random errors. \({\text{cw}}_{i}\), \({\text{cw}}_{\text{Ei}}\), \({\text{cw}}_{\text{Wi}}\), \({\text{cw}}_{\text{Si}}\), and \({\text{cw}}_{\text{Ni}}\) are the true values of \({\text{CW}}_{i}\), \({\text{CR}}_{\text{Ei}}\), \({\text{CR}}_{\text{Wi}}\), \({\text{CR}}_{\text{Si}}\), and \({\text{CR}}_{\text{Ni}}\), respectively. Their expressions in the NSE are given by

$$\left\{ \begin{array}{l} {\text{cw}}_{\text{Ei}} = \frac{{f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} )}}{{f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} ) + f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} ) + f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} ) + f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )}}cw_{i} \hfill \\ {\text{cw}}_{\text{Wi}} = \frac{{f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} )}}{{f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} ) + f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} ) + f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} ) + f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )}}cw_{i} \hfill \\ {\text{cw}}_{\text{Si}} = \frac{{f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} )}}{{f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} ) + f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} ) + f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} ) + f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )}}{\text{cw}}_{i} \hfill \\ {\text{cw}}_{\text{Ni}} = \frac{{f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )}}{{f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} ) + f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} ) + f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} ) + f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )}}{\text{cw}}_{i} \hfill \\ {\text{cw}} = f_{T} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{T} ) \hfill \\ {\mathbf{Y}}_{i} = {\mathbf{y}}_{i} + {\mathbf{e}}_{i} ,{\mathbf{Y}}_{i} = (\text{CW}_{\text{Ei}} , \text{CW}_{\text{Wi}} , \text{CW}_{\text{Si}} , \text{CW}_{\text{Ni}} , \text{CW)}^\text{{T}} ,{\mathbf{y}}_{i} = ({\text{cw}}_{\text{Ei}} , {\text{cw}}_{\text{Wi}} , {\text{cw}}_{\text{Si}} , {\text{cw}}_{\text{Ni}} , {\text{cw}})^{T} , \hfill \\ E({\mathbf{e}}_{i} ) = 0,\text{var} ({\mathbf{e}}_{i} ) = \sigma^{2} {\varvec{\uppsi}},i = 1, \ldots ,n \hfill \\ \end{array} \right.$$
(3)

where the functions \(f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} )\), \(f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} )\), \(f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} )\), \(f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )\), and \(f_{T} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{T} )\) are obtained from the base model (1) for CRE, CRW, CRS, CRN, and CW, respectively; \({\varvec{\upbeta}}_{E}\), \({\varvec{\upbeta}}_{W}\), \({\varvec{\upbeta}}_{S}\), \({\varvec{\upbeta}}_{N}\), and \({\varvec{\upbeta}}_{T}\) are the parameter vectors for CRE, CRW, CRS, CRN, and CW, respectively; and \(P_{i}\) is the value of the dummy variable for the ith tree. The structure matrix, \({\varvec{\uppsi}}\), with a size of \(5 \times 5\), is used to account for the inherent correlations among the total CW and crown components (Tang et al. 2015, 2008).

Two-step, proportional weighting system

The two-step, proportional weighting system not only ensures that the sum of the crown radii values is equal to twice the total CW, but it also guarantees that the values of the basic components for CWEW and CWSN are summed and that the summations are equal to the corresponding subtotals. The expressions of the NSE for this procedure are given by

$$\left\{ \begin{array}{l} {\text{cw}}_{\text{Ei}} = \frac{{f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} )}}{{f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} ) + f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} )}}\frac{{f_{EW} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{EW} )}}{{f_{EW} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{EW} ) + f_{SN} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{SN} )}}cw \hfill \\ {\text{cw}}_{\text{Wi}} = \frac{{f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} )}}{{f_{E} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{E} ) + f_{W} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{W} )}}\frac{{f_{EW} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{EW} )}}{{f_{EW} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{EW} ) + f_{SN} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{SN} )}}cw \hfill \\ {\text{cw}}_{\text{Si}} = \frac{{f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} )}}{{f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} ) + f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )}}\frac{{f_{SN} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{SN} )}}{{f_{EW} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{EW} ) + f_{SN} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{SN} )}}{\text{cw}} \hfill \\ {\text{cw}}_{\text{Ni}} = \frac{{f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )}}{{f_{S} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{S} ) + f_{N} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{N} )}}\frac{{f_{SN} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{SN} )}}{{f_{EW} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{EW} ) + f_{SN} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{SN} )}}{\text{cw}} \hfill \\ {\text{cw}} = f_{T} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{T} ) \hfill \\ {\mathbf{Y}}_{i} = {\mathbf{y}}_{i} + {\mathbf{e}}_{i} ,{\mathbf{Y}}_{i} = (\text{CW}_{\text{Ei}} , \text{CW}_{\text{Wi}} , \text{CW}_{\text{Si}} , \text{CW}_{\text{Ni}} , \text{CW)}^\text{{T}} ,{\mathbf{y}}_{i} = ({\text{cw}}_{\text{Ei}} , {\text{cw}}_{\text{Wi}} , {\text{cw}}_{\text{Si}} , {\text{cw}}_{\text{Ni}} , {\text{cw}})^{T} \hfill \\ E(e_{i} ) = 0,\text{var} (e_{i} ) = \sigma^{2} {\varvec{\uppsi}},i = 1, \ldots ,n \hfill \\ \end{array} \right.$$
(4)

where the functions \(f_{\text{EW}} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{\text{EW}} )\) and \(f_{\text{SN}} ({\mathbf{x}}_{i} ,P_{i} ,{\varvec{\upbeta}}_{\text{SN}} )\) are obtained from the base model (1) for CWEW and CWSN, respectively. The inherent correlations among the total CW and crown components in this case are accounted for by the structure matrix \({\varvec{\uppsi}}\) with a size of \(5 \times 5\). All other variables, parameters, and variance–covariance structures in this model were as defined in the nonlinear CW model (3).

AP

The AP approach ensures that the sum of the values of all the crown components is equal to twice the total CW. The total CW of a tree is divided into four basic crown components, including CRE, CRW, CRS, and CRN, by proportional weights. In this approach, the base model (1) was separately fitted by nonlinear OLSs for CW, CRE, CRW, CRS, and CRN. The estimates of CW, CRE, CRW, CRS, and CRN were calculated by

$$\begin{array}{l} {\mathop {\text{CR}}\limits^{ \wedge }}_{\text{E}} = \frac{{2f_{E} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{E} )}}{{f_{\text{E}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{E}} ) + f_{\text{W}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{W}} ) + f_{\text{S}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{S}} ) + f_{\text{N}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{N}} )}}\mathop {CW}\limits^{ \wedge } + \varepsilon_{E} \hfill \\ {\mathop {\text{CR}}\limits^{ \wedge }}_{\text{W}} = \frac{{2f_{\text{W}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{W}} )}}{{f_{\text{E}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{E}} ) + f_{\text{W}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{W}} ) + f_{\text{S}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{S}} ) + f_{\text{N}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{N}} )}}\mathop {\text{CW}}\limits^{ \wedge } + \varepsilon_{\text{W}} \hfill \\ {\mathop {\text{CR}}\limits^{ \wedge }}_{\text{S}} = \frac{{2f_{S} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{S} )}}{{f_{\text{E}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{E}} ) + f_{\text{W}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{W}} ) + f_{\text{S}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{S}} ) + f_{\text{N}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{N}} )}}\mathop {\text{CW}}\limits^{ \wedge } + \varepsilon_{\text{S}} \hfill \\ {\mathop {\text{CR}}\limits^{ \wedge }}_{\text{N}} = \frac{{2f_{N} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{N} )}}{{f_{\text{E}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{E}} ) + f_{\text{W}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{W}} ) + f_{\text{S}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{S}} ) + f_{\text{N}} ({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}_{\text{N}} )}}\mathop {\text{CW}}\limits^{ \wedge } + \varepsilon_{\text{N}} \hfill \\ \mathop {\text{CW}}\limits^{ \wedge } = f({\mathbf{x}},P,{\hat{\varvec{\upbeta}}}) + \varepsilon \hfill \\ \end{array}$$
(5)

where \(\mathop {\text{CW}}\limits^{ \wedge }\), \({\mathop {\text{CR}}\limits^{ \wedge }}_{\text{E}}\), \({\mathop {\text{CR}}\limits^{ \wedge }}_{\text{W}}\), \({\mathop {\text{CR}}\limits^{ \wedge }}_{\text{S}}\), and \({\mathop {\text{CR}}\limits^{ \wedge }}_{\text{N}}\) are estimates of CW, CRE, CRW, CRS, and CRN, respectively. \({\hat{\varvec{\upbeta}}}\), \({\hat{\varvec{\upbeta}}}_{\text{E}}\),\({\hat{\varvec{\upbeta}}}_{W}\),\({\hat{\varvec{\upbeta}}}_{S}\), and \({\hat{\varvec{\upbeta}}}_{N}\) are estimates of the parameters obtained by fitting the base model (1) separately for CW, CRE, CRW, CRS, and CRN, respectively.

OLSSR

The base model (1) was separately fitted by nonlinear OLSs for CRE, CRW, CRS, and CRN, and the CW estimate was obtained by obtaining the half sum of the four crown components:

$$\mathop {\text{CW}}\limits^{ \wedge } = {(\mathop {\text{CR}}\limits^{ \wedge }}_{\text{E}} + {\mathop {\text{CR}}\limits^{ \wedge }}_{\text{W}} + {\mathop {\text{CR}}\limits^{ \wedge }}_{\text{S}} + {\mathop {\text{CR}}\limits^{ \wedge}}_{\text{N}} )/2$$
(6)

where \({\mathop {\text{CR}}\limits^{ \wedge }}_{\text{E}}\), \({\mathop {\text{CR}}\limits^{ \wedge }}_{\text{W}}\), \({\mathop {\text{CR}}\limits^{ \wedge }}_{\text{S}}\), and \({\mathop {\text{CR}}\limits^{ \wedge }}_{\text{N}}\) are obtained from the base model (1) with known parameter values.

Model evaluation

We first assessed the accuracy of the base model for CRE, CRW, CWEW, CRS, CRN, CWSN, and CW based on the mean bias (\(\bar{e}\)), the variance of the residuals (\(\delta\)), the root mean square error (\({\text{RMSE}}\)), the total relative error (\({\text{TRE}}\)), and the adjusted coefficient of determination (\(R_{\alpha }^{2}\)), using both the model-fitting and model-validation datasets. Then, the fitting and predictive ability of the systems of CW models (3) and (4) and the two additive models (AP and OLSSR) were evaluated by the statistics \(\bar{e}\), \(\delta\), \({\text{RMSE}}\), and \({\text{TRE}}\), using both the model-fitting and model-validation datasets. These evaluation statistics were defined as:

$$\bar{e} = \sum {(Y_{i} - \hat{Y}_{i} )/n}$$
(7)
$$\delta = \sum {(Y_{i} - \hat{Y}_{i} )^{2} } /(n - 1)$$
(8)
$${\text{RMSE}} = \sqrt {\bar{e}^{2} + \delta }$$
(9)
$${\text{TRE}} = 100\sum\nolimits_{i = 1}^{n} {(Y_{i} - \hat{Y}_{i} )^{2} } /\sum\nolimits_{i = 1}^{n} {\hat{Y}_{i} }$$
(10)
$$R_{\alpha }^{2} = 1 - \frac{{(n - 1)\sum\nolimits_{i = 1}^{n} {(Y_{i} - \hat{Y}_{i} )^{2} } }}{{(n - P)\sum\nolimits_{i = 1}^{n} {(Y_{i} - \bar{Y})^{2} } }}$$
(11)

where \(Y_{i}\) and \(\hat{Y}_{i}\) are the observed and predicted CW or crown radius values, respectively, for the ith observation; \({\text{RMSE}}\), which combines the mean bias and the variation of the residuals, was used as the primary criterion for the CW model evaluations. All the calculations were carried out using ForStat 2.2 software (Tang et al. 2008).

Results

Base model

The parameter estimates of the base model (1) that was separately fitted by nonlinear OLSs for CRE, CRW, CWEW, CRS, CRN, CWSN, and CW are listed in Table 2. Except for \(\beta_{6}\), all the other parameter estimates in the base model (1) for each crown component and CW were significantly different from 0 (p < 0.05). The fit and prediction statistics of the base model (1) for each crown component and CW are provided in Table 3.

Table 2 Parameter estimates of the base model (1) obtained by separately fitting using nonlinear ordinary least squares for east crown radius (CRE), west crown radius (CRW), south crown radius (CRS), north crown radius (CRN), east–west crown width (CWEW), south–north crown width (CWSN), and total crown width (CW)
Full size table
Table 3 Evaluation indices of the base model (1) for east crown radius (CRE), west crown radius (CRW), south crown radius (CRS), north crown radius (CRN), east–west crown width (CWEW), south–north crown width (CWSN), and total crown width (CW)
Full size table

A Student’s t test indicated that the \(\bar{e}\) statistics for the base model (1) for CRE, CRW, CRS, CRN, CWEW, CWSN, and CW were not significantly different from 0 (p < 0.05). Table 3 shows that the differences of the fit and prediction accuracies among the different crown components and CW were significant (p < 0.05). The base model (1) showed the best overall performance for CW prediction.

Comparison between the different CW models

The fit statistics of CW models (3) and (4) and the AP and OLSSR models are presented in Table 4. All the models guaranteed that the sum of CRE, CRW, CRS, and CRN was equal to twice the total CW. A Student’s t test indicated that the mean biases (\(\bar{e}\)) for all the models for CRE, CRW, CRS, CRN, and CW were not significantly different from 0 (p > 0.05). Except for the fact that the OLSSR under-predicted CRE, CRS, and CW in the model fitting, all the other predictions for each model—in terms of both model fitting and validation—showed over-predictions.

Table 4 Evaluation indices for the system of nonlinear simultaneous equation (NSE) with both one- and two-step procedures, and the adjustment in proportion (AP) and the ordinary least squares with separating regression (OLSSR) models
Full size table

CW model (4) had the better statistics for the crown components and CW, compared with CW model (3) and the AP and OLSSR models. For example, based on the fitting results, the statistics \(\delta\), \({\text{RMSE}}\), \({\text{TRE}}\), and \(R_{\alpha }^{2}\) of CW model (4) were 29.28, 15.91 and 9.20% smaller, and 10.39% larger, respectively, than those of CW model (3); 20.42, 10.78 and 25.02% smaller, and 4.70% larger, respectively, than those of the AP model; and 45.96, 26.48 and 25.09% smaller, and 26.04% larger, respectively, than those of the OLSSR model. Based on the validation results, the values of \(\delta\), \({\text{RMSE}}\), and \({\text{TRE}}\) from CW model (4) for CW were 20.39, 10.67 and 4.70% smaller, respectively, than those of CW model (3); 42.70, 25.02 and 34.36% smaller, respectively, than those of the AP model; and 42.74, 25.02 and 34.39% smaller, respectively, than those of the OLSSR model.

The parameter estimates for CW model (4) are listed in Table 5. The estimates of \(k_{1}\) and \(k_{ 2}\) in CW model (4) were significant (p < 0.05), indicating that there was a pronounced difference between the values of CRs from the Guandi mountain forest and the Boqiang forest. All the other parameter estimates of CW model (4) were also highly significant (p < 0.05), and their magnitudes and signs were also biologically plausible. Based on the validation data, the plots in Fig. 4 show that there was no serious trend in the residuals when the CW components were predicted with CW model (4); the model-fitting dataset resulted in similar patterns of the residuals. Therefore, CW model (4) is ultimately recommended for predicting the crown components and CW of Prince Rupprecht larch.

Table 5 Parameter estimates of crown width (CW) model (4)
Full size table
Fig. 4
figure 4

Residuals graphed against predicted responses of crown width (CW) model (7) based on the model-fitting data for east crown radius (CRE), west crown radius (CRW), south crown radius (CRS), north crown radius (CRN), and total crown width (CW)

Full size image

Discussion

Additivity of crown radii is a desirable characteristic for CW models used to predict CW. Moreover, if CW models can account for the inherent correlations among the crown components and CW, they will possess a great statistical efficiency (Parresol 1999, 2001). In this study, NSE was first time applied to develop CW models and also compared with other two additive models (the AP and OLSSR models) that are widely used to develop CW models. These methods effectively ensured that the sum of CRE, CRW, CRS, and CRN was equal to twice the total CW. For the NSE, the correlations among the components were effectively accounted for by the covariance matrix of random errors. In the AP and OLSSR models, however, the crown component models because of the assumption of homogeneous random error variances were fitted separately. Thus, both AP and OLSSR models could not account for the correlations.

Based on the results of Table 4, both the one- and two-step procedures maintained the property of additivity for the CW models. The prediction accuracies of each crown component and CW using the two-step procedure were much higher than those for the corresponding components using the one-step procedure. Model specification for a two-step procedure is more complicated than that for a one-step procedure (Zeng and Tang 2010; Fu et al. 2016). Therefore, in practice, researchers prefer the use of a one-step procedure to develop a system of additive biomass equations (Zeng and Tang 2010; Fu et al. 2014, 2016). However, in this study, because the prediction accuracies of the developed CW models were not very high overall (Table 4), the model with the most powerful predictive ability with the same predictors is of greater interest to us. Thus, CW model (4) was selected to predict the crown components and CW.

In some studies that developed additive biomass equations using one- and two-step procedures, e.g., Zeng and Tang (2010), Dong et al. (2015), and Fu et al. (2016), the biomass equation of the total tree was not included, and estimated separately using OLS. These models also resulted in high prediction accuracies. In this study, we developed CW models, without including the total CW model, using one- and two-step procedures. The results showed that although the previously developed models were simpler than the CW models (3) and (4), their prediction accuracies were much lower than those of the CW models (3) and (4). In addition, the prediction accuracies of the previously developed models were similar to that of the base model (1) in this case, which is meaningless for applying one- and two-step procedures to improve the accuracy of CW prediction.

The results in Table 4 showed that the NSE more accurately predicted the crown components and the total CW, compared with the AP and OLSSR models. Particularly, when NSE was used, the prediction accuracies of the crown components and the total CW were the highest. These results indicated that CW model (4) was a more effective additive model for crown components and total CW predictions. For the AP model, the total CW was estimated from a separately fitted model (model (1), and therefore, the prediction accuracy of the total CW was equal to that of the CW from the base model (1) (see Table 3). Similarly, in the OLSSR model, CRE, CRW, CRS, and CRN were estimated by the separately fitted base model (1), and therefore, the prediction accuracies of the crown components of the OLSSR were equal to those of the base model (1) (see Table 3). Relative to the base model (1), the prediction accuracy of the total CW obtained from the OLSSR was reduced. Over-predictions took place for all the estimations using the AP and NSE from both model-fitting and model-validation datasets and using the OLSSR from the model-validation dataset, and for the estimations of the CRW and CRN using the OLSSR from the model fitting dataset. This may be because the base model (1) used in this study has a characteristics of over-prediction for the total CW and crown components for trees with the corresponding large CW or crown components (Fig. 3). Therefore, this model needs to be further improved in future study. The numbers of the PSPs allocated in both the state-owned Guandi mountain forest and Boqiang forest (Fig. 1) were approximately proportional to their contributions and total stock volumes of the natural stands of Prince Rupprecht larch in the entire northern China. The trees in the PSPs had a range of diameters from 5 to 60.5 cm. For Prince Rupprecht larch, the trees with diameter greater than 50 cm belong to super large diameter class group in the forest management (Zhang, 2008). Thus, the developed models in this study were also validated for the trees with diameter greater than 50 cm.

Measuring tree crown components (CRE, CRW, CRS, and CRN) may be subject to errors, even though stand and tree variables are commonly assumed to be measured without errors (Omule 1980; Gertner 1990). Measurement errors made by field crews or faulty instruments, or both, can be substantial (Omule 1980). For example, HCB is generally measured with a standard height measurement instrument, but when a crown is uneven, one often visually rearranges crown branches to obtain a value for HCB. There is ample evidence in the literature about the ambiguity of the visual estimation of tree variables. Nicholas et al. (1991) and Ghosh et al. (1995) highlighted the variations that could arise from the subjective measurements of tree and stand variables. In all existing CW models (Sánchez-González et al. 2007; Fu et al. 2013; Sharma et al. 2016), including those developed in this study, it is assumed that (i) CW and crown components (crown radii) are random variables, and (ii) other independent variables are fixed and measured without errors. It is well known that violations of the second assumption may lead to biased parameter estimates and standard errors, which consequently misleads the hypothesis test (Fuller 1987; Rencher and Schaalje 2008). When the covariate predictors in CW model (4) are likely to have significant errors, a new modeling approach, such as a nonlinear error-in-variable model (Fu et al. 2016), needs to be developed. We are in the process of developing CW models to solve such problems.

Conclusion

In this study, NSE, AP, and OLSSR approaches were used to develop CW models based on the CW datasets of Prince Rupprecht larch that were collected in northern China. One- and two-step procedures were applied to ensure the additivity for the NSE. We found that the model (1) proposed by Fu et al. (2013) could be used as a base model for effectively developing CW models. CW model (4) with a two-step proportional weighting system performed better than with a one-step proportional weighting system for predictions of crown components and total CW. NSE accounted for the inherent correlations among the crown components and CW, whereas the AP and OLSSR models did not. The prediction accuracy of CW model (4) was the highest among these methods. In summary, this study developed a system of nonlinear, additive CW models in which the correlations among the crown components and CW were accounted for during the modeling and prediction of the CW of the individual trees and their crown components. The obtained results can be generalized. Thus, it is expected that this methodology can be applied to any model system in which a quantity can be partitioned into additive components.

Author contribution statement

LF and ST conceived the study. LF and KH performed the analysis and wrote the initial draft of the manuscript. WX drew the figures and GW revised the MS and checked the grammatical errors in English. All authors contributed in interpreting the results and improving the manuscript.