1 Introduction

There are hardly any perfectly homogeneous materials at macroscale, and this is the case for both materials from nature as well as synthetic materials. At macroscale, continuum solids have complex microstructure, which determines their overall material properties. Commonly, we categorize microstructure of inhomogeneous materials into two types: materials with periodic microstructure and materials with randomly distributed microstructure. There are two classes of most common microstructure that are often seen in various composite materials:

(1) the deterministic microstructure with periodicity, and (2) the statistical microstructure with random distributions.

With the developments of micromechanics and homogenization theories, many homogenization methods for finding effective material properties of composite materials have been developed over the past half century, e.g. [1,2,3,4,5]. In particular, since 1980s, there is a rapid development in computational homogenization methods e.g. [6, 7]. The computational homogenization method for composite materials also may be divided into two main categories: (1) Computational asymptotic homogenization method or multiscale computational homogenization, which is aimed for composite materials with periodic microstructure, e.g. [8, 9], and (2) Computational micromechanics method, which is mainly aimed for composite materials with random microstructure, even though it may also be applied to materials with periodic microstructure e.g. [10, 11].

In computational micromechanics methods, a main approach is to use the variational principle of composite continua to develop the homogenization procedure. Today, computational variational homogenization has become an important approach to find the effective properties of composites.

In his pioneer work [12], Eshelby first proposed an effective eigenstrain method to estimate fluctuation strain in a heterogeneous solid due to an ellipsoid inclusion, which can then be utilized to find the close-form expression of effective material properties of composites at macroscale. The equations as well as the solution of the eigenstrain method are beautiful from mathematics perspective, but they are severely limited because of the associated simplifications, idealization, and assumptions made in the theory. For example, in theoretical micromechanics, we have to assume that the representative volume element (RVE) is infinitely large, and the inhomogeneities insider RVE must be ellipsoid in shape, and the elastic composite must be linear elastic and under small deformation, etc. among others. Due to these restrictions in theoretical micromechanics, many researchers have been focusing on developing various micromechanics methods that are capable of predicting effective material properties for finite representative volume element (RVE) with inclusions or second phases in arbitrary shape and for nonlinear composite materials e.g. [5, 13]. It turns out that the computational micromechanics may be the best approach to solve such complex realistic homogenization problem, because it provides precise homogenization solutions for engineering problems, and the overall material property predictions can converge to real material properties in the framework of general micromechanics modeling, as the numerical model is refined.

From the perspective of modeling and simulation, in their seminal works, Suquet and his collaborators [14, 15] have set the foundation for computational micromechanics. Later, Miehe and his co-workers have systematically developed the finite element method based computational variational homogenization approach to solve various homogenization problems for hyperelastic and elastoc-plastic composite materials e.g. [10, 11, 16]. Their results represent the state-of-the-art computational homogenization technology in computational micromechanics as well as computational composite materials.

In micromechanics homogenization theory, usually we impose two types of boundary conditions (BCs) to a given RVE: (1) the prescribed strains or displacements on the boundary of an RVE, and (2) the prescribed stress or traction on the boundary of an RVE. The two boundary conditions correspond two types of the Hill-Mandel lemmas (see [5]). In computational homogenization theory, we usually refer the homogenization with the prescribed strain BC as the strain-driven homogenization and refer the homogenization of the prescribed stress BC as stress-driven homogenization. In general, the strain-driven computational homogenization is based on the minimum potential energy principle, and the stress-driven homogenization should be based on the complementary potential energy principle. In analytical micromechanics, these correspond to two well-known overall material property estimates: the Vogit bound and the Reuss bound (see [5] for details). However, in computational homogenization, since stress is the primary variable in the complementary potential principle, and in practice most of finite element methods are based on displacement formulation, thus, to the best of authors’ knowledge, there has been no rigorous or purely stress-driven computational homogenization.

In fact, most work done by Miehe and his co-workers are the strain-driven homogenization for elastic and inelastic composites based on the variational formulation of the minimum potential energy principle. In [11], they conducted a computational two-scale analysis for the treatment of a homogenized macro-continuum with locally attached micro-structure of inelastic constituents. The key contribution of the work is the development of a direct incremental variational formulation that can determine the fine-scale displacement-fluctuation field in inelastic micro-structures. In [16], Miehe developed computational algorithms to compute the homogenized stresses and overall material tangent moduli of the composite material undergoing finite strain deformation, and they constructed a family of algorithms and matrix representations of overall properties of discretized micro-structures which are motivated by a minimization of the average incremental energy. Indeed, in [16], Miehe also proposed a stress-driven computational formulation by using an approach of Lagrangian multiplier, and however, it appears to us that he did not do implement it. The formulation was later implemented by van Dijk [17] and Javili et al. [18]. In particular, Javili et al. found a way to eliminate the possible rigid-body motions induced by the traction-only boundary condition. The main shortcoming of the Lagrangian multiplier approach is that it is not a minimum or extreme variational principle, and it is only a stationary variational principle. Even though, one may find the valid results for a given computational homogenization problem, that result may not provide a lower bound estimate for the overall material properties, like the lower bound estimate such as the Reuss bound in theoretical micromechanics. In the applications of composite materials, the lower bound estimate is much important than the upper bound estimate, because it provides a criterion for safety and reliability in material designs.

Different from Miehe’s Lagrangian multiplier approach, in the present work, we develop a novel stress-driven variational homogenization method based on the complementary strain energy of a composite material system; on the other hand, the primary variable of the complementary variational principle is still the displacement field. To make it clear, the main novelty of the present work is that we have developed a stress-driven homogenization method based the minimum complementary variational principle whose primary unknown is still displacement field.

The highlights of this work are the development of a family of displacement-based complementary variational homogenization algorithms and the discretized finite element formulations for finding effective elastic material properties for both linear elastic and hyperelastic composites under both small deformation and finite deformation. In particular, by comparing the homogenization results obtained by the present method with the results of the strain-driven homogenization, we have shown that the present stress-driven computational method provides a lower bound for the effective material properties of the composites.

The paper is organized as follows: In Sect. 2, we shall present several stress-driven complementary variational homogenization formulations and their finite element formulations. In Sect. 3, we shall demonstrate finite element implementation and computational results, and we conclude the study in the last Section of the paper.

2 Stress-driven complementary variational homogenization method and its finite element formulation

Different from Miehe and his collaborators’ work, we developed a stress-driven homogenization method to compute the effective material properties based on an incremental variational formulation. We are able to implement the corresponding variational formulation and compute homogenized material properties based on finite element method (FEM).

2.1 Some basic concepts of micromechanics homogenization theory

Before starting the derivation of stress-driven complementary potential energy, we first introduce basic continuum kinematic relations, microscopic and macroscopic quantities and average field in an RVE.

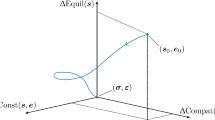
Figure 1 shows that the material configuration \(\varvec{\mathcal {B}}_0\) corresponds to a RVE which is mapped to its spatial configuration through the non-linear deformation \(\varvec{\varphi }\). The local macroscopic response is determined through homogenizing the response of the corresponding micro-structure obtained from solving the associated boundary value problem.

In the reference configuration, the position of an arbitrary material node is denoted as \(\varvec{X}\). The surface normal vector on boundary \(\partial \varvec{\mathcal {B}}_0\) in reference coordinate is denoted as \(\varvec{N}\). In the current configuration, the position of an arbitrary material node is denoted as \(\varvec{x}\). The surface normal vector on boundary \(\partial \varvec{\mathcal {B}}_t\) in current coordinate is denoted as \(\varvec{n}\).

The deformation between these two configurations can be characterized by deformation gradient \(\varvec{F}\), which is defined as

$$\begin{aligned} \varvec{F} = \frac{\partial \varvec{x}}{\partial \varvec{X}} \end{aligned}$$
(1)

To associate a microlevel tensor field with a tensorial quantity at macrolevel, we first define the average operator \(<\cdot>\). The average value of a microlevel tensor field \(\varvec{T}(\varvec{x})\) of a material point ensemble is defined as:

$$\begin{aligned} \varvec{T}^M = <\varvec{T}>_{\varvec{x}} = \frac{1}{V} \int _V \varvec{T}(\varvec{x}) d V_{\varvec{x}} ~. \end{aligned}$$
(2)

in which the integration is over the volume of the RVE, V, with respect to \(\varvec{x}\).

Accordingly, we can have relations between microscale quantities and macroscale quantities, for example,

$$\begin{aligned} \begin{aligned} \varvec{P}^M = \frac{1}{V_0} \int _{V_0} \varvec{P} d V_{\varvec{x}}, \quad \varvec{F}^M = \frac{1}{V_0} \int _{V_0} \varvec{F} d V_{\varvec{x}} \\ \varvec{\sigma }^M = \frac{1}{V} \int _V \varvec{\sigma } d V_{\varvec{x}}, \quad \mathrm{and}~~ \varvec{\epsilon }^M = \frac{1}{V} \int _V \varvec{\epsilon } d V_{\varvec{x}} ~, \end{aligned} \end{aligned}$$
(3)

where \(\varvec{P}^M\) is the macroscopic 1st Piola-Kirchhoff (PK-I) stress, \(\varvec{P}\) is microscopic PK-I stress, \(\varvec{F}^M\) is macroscopic deformation gradient, \(\varvec{F}\) is microscopic deformation gradient, \(\varvec{\sigma }^M\) is macroscopic Cauchy stress, \(\varvec{\sigma }\) is microscopic Cauchy stress, and \(\varvec{\epsilon }^M\) is macroscopic strain. Note that \(\varvec{\epsilon }\) is microscopic strain, \(V_0\) is the undeformed volume in reference configuration, and V is deformed volume in current configuration.

Fig. 1
figure 1

Graphical summary of computational homogenization

Full size image

2.2 Stress-driven homogenization for linear elastic composites

To start, we first introduce the Hill-Mandel complementary virtual work theorem:

Assume that the condition that the density of macroscale complementary virtual work at a heterogeneous material point equals the average complementary virtual work inside the corresponding RVE holds,

$$\begin{aligned} \delta \varvec{\sigma }^M : \varvec{\epsilon }^M = \frac{1}{V} \int _{V} \delta \varvec{\sigma } : \varvec{\epsilon } dV, \end{aligned}$$
(4)

it will lead to:

$$\begin{aligned} \delta W_c^M = \delta \bar{W}_c \Rightarrow W_c^M(\varvec{\sigma }^M) = \bar{W}_c(\varvec{\sigma }^*)~, \end{aligned}$$
(5)

if the RVE is subjected to the following boundary condition:

$$\begin{aligned} \bar{\varvec{t}} = \varvec{\sigma }^M \cdot \varvec{n}, \qquad \forall \varvec{x} \in \partial V~. \end{aligned}$$
(6)

where \(\varvec{\sigma }^M\) and \(\varvec{\epsilon }^M\) are macroscopic Cauchy stress and strain, \(\varvec{\sigma }\) and \(\varvec{\epsilon }\) are microscopic stress and strain, \(\varvec{\sigma }^{*}\) is true solution of stress distribution, \(W_c^M\) is macroscopic complementary potential energy, \(\bar{W}_c\) is averaged microscopic complementary potential energy. For the detailed proof of the above Hill-Mandel theorem, interested readers can consult [5].

Based on the Hill-Mandel Complementary Virtual Work Theorem and the Legendre-Fenchel transformation, we propose the following complementary variational principle,

$$\begin{aligned} \bar{W}_c(\varvec{\sigma }^*)= & {} \sup \limits _{\varvec{\sigma }\in S({\varvec{\sigma }^*})} \left\{ \varvec{\sigma }^M : \varvec{\epsilon }^M - \frac{1}{V} \int _{V} W(\varvec{\epsilon }) dV_{\varvec{x}} \right\} \nonumber \\= & {} \sup \limits _{\varvec{\sigma }\in S({\varvec{\sigma }^*})} \left\{ \sigma ^M_{ij} \frac{1}{V}\int _{V} \epsilon _{ij} dV_{\varvec{x}} - \frac{1}{2V}\int _{V} \sigma _{ij} \epsilon _{ij} dV_{\varvec{x}}\right\} \nonumber \\= & {} \sup \limits _{\varvec{\sigma }\in S({\varvec{\sigma }^*})} \left\{ \frac{1}{V}\int _{V}\left\{ \varvec{\epsilon }\right\} ^T dV \left\{ \varvec{\sigma }^M\right\} \right. \nonumber \\&\left. - \frac{1}{2V}\int _{V}\left\{ \varvec{\epsilon }\right\} ^T \left[ \varvec{D}\right] \left\{ \varvec{\epsilon }\right\} dV_{\varvec{x}} \right\} , \end{aligned}$$
(7)

where \(S(\varvec{\sigma }^*)\) is all possible Cauchy stress fields, i.e.

$$\begin{aligned} S:= \big \{ \varvec{\sigma } | \varvec{\sigma } \in L_2, \varvec{\sigma } \cdot \varvec{n} = \varvec{t} = \varvec{\sigma }^M \cdot \varvec{n} ~\mathrm{on} ~\partial V ~ \big \} \end{aligned}$$

where \({\varvec{\epsilon }}= \mathbf{C}:{\varvec{\sigma }}\) and \(\mathbf{C}=\mathbf{D}^{-1}\) is the elastic compliance tensor. In above equation, \(\bar{W}_c\) is the averaged complementary potential energy, which is equal to macro-complementary potential energy; W is the micro-complementary potential energy, \(\varvec{\sigma }^M\) is the macro-stress, and V is the total volume of RVE.

We can slightly change Eq. (7) into the following form,

$$\begin{aligned} \bar{W}_c (\mathbf {u}^*)\le & {} \sup \limits _{ \mathbf {u} \in \mathcal {U}} \left\{ \varvec{\sigma }^M : \varvec{\epsilon }^M - \frac{1}{V} \int _{V} W(\varvec{\epsilon }) dV_{\varvec{x}} \right\} \nonumber \\= & {} \sup \limits _\mathbf{{u} \in \mathcal {U}} \left\{ \frac{1}{V}\int _{V}\left\{ \varvec{\epsilon }\right\} ^T dV \left\{ \varvec{\sigma }^M\right\} \right. \nonumber \\&\left. - \frac{1}{2V}\int _{V}\left\{ \varvec{\epsilon }\right\} ^T \left[ \varvec{D}\right] \left\{ \varvec{\epsilon }\right\} dV_{\varvec{x}} \right\} \nonumber \\\le & {} \sup \limits _\mathbf{{u}^h \in \mathcal {U}} \left\{ \frac{1}{V} (\sum ^{N_e}_{e=1} \left\{ \varvec{\epsilon }\right\} ^T V_e) \left\{ \varvec{\sigma }^M\right\} \right. \nonumber \\&\left. - \frac{1}{2V} \sum \limits ^{N_e}_{e=1}(\left\{ \varvec{\epsilon }\right\} ^T\left[ \varvec{D}\right] \left\{ \varvec{\epsilon }\right\} V_e) \right\} \end{aligned}$$
(8)

where \(\varvec{\epsilon } = {1 \over 2} (\nabla \otimes \mathbf{u}^{h} + (\nabla \otimes \mathbf{u}^{h})^T)\) and \(\mathcal {U}\) is the space for all the admissible displacement fields,

$$\begin{aligned} \mathcal {U}= & {} \big \{ \mathbf{u} \Bigm | \mathbf{u} \in H^1, \mathbf{u} = {\varvec{\epsilon }}^M \cdot \mathbf{x} ~\mathrm{on}~ \partial V ~\mathrm{and}~\varvec{\epsilon }^M =\mathbf{C}: \varvec{\sigma }^M,\\&\mathbf{C}=\mathbf{D}^{-1} \big \}~. \end{aligned}$$

In Eq. (8), \(\mathbf{u}^h\) is a finite element displacement interpolation field; \(V_e\) is the elementary volume in FEM discretization, \(N_e\) is number of elements and \(\left\{ \cdot \right\} \) is the vectorial form and \(\left[ \varvec{D}\right] \) is the matrix form of elastic tensor.

To obtain the effective elastic tensor that can characterize the constitutive response of the linear elastic composite material, we first derive the matrix formulation of the effective material elastic tensor based on FEM discretization.

First, we introduce a FEM discretization to the RVE, and discretized displacement field, and then find the expression for FEM nodal strains,

$$\begin{aligned} \left\{ \varvec{\epsilon }\right\} = \left[ \varvec{B}\right] \left\{ \varvec{d}\right\} \end{aligned}$$

where \(\varvec{d}\) is the total nodal displacement, which can be decomposed into two parts: \(\varvec{d} = \varvec{\epsilon }^M \cdot \varvec{x} + \varvec{w}^d\). The first term \(\varvec{\epsilon }^M \cdot \varvec{x}\) represents the averaged nodal displacement or macro nodal displacement field; the second term \(\varvec{w}^d\) represents the fine-scale nodal fluctuation displacement field, such that \(\mathbf{w}^d =0, \mathrm{on} ~\partial V\).

Substituting it into Eq. (7), we have the following equation for discrete representation of the complementary potential energy,

$$\begin{aligned} \begin{aligned} \bar{W}_c(\varvec{d}^{*})&\le \sup \limits _{\varvec{d}\in \mathcal {V}}\left\{ \left\{ \varvec{d}\right\} ^T \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \left\{ \varvec{\sigma }^M\right\} \right. \\&\left. \quad - \frac{1}{2V} \sum ^{N_e}_{e=1} (\left[ \varvec{B}^e\right] \left\{ \varvec{d}^e\right\} )^T \left[ \varvec{D}\right] \left[ \varvec{B}^e\right] \left\{ \varvec{d}^e\right\} \cdot V_e \right\} \\&= \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \left\{ \varvec{d}\right\} ^T \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \left\{ \varvec{\sigma }^M\right\} \right. \\&\left. \quad - \frac{1}{2V} \left\{ \varvec{d}\right\} ^T \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T \left[ \varvec{D}\right] \left[ \varvec{B}^e\right] V_e) \cdot \left\{ \varvec{d}\right\} \right\} \\&= \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \left\{ \varvec{d}\right\} ^T \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \left\{ \varvec{\sigma }^M\right\} \right. \\&\left. \quad - \frac{1}{2V} \left\{ \varvec{d}\right\} ^T \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{K}^e\right] \left\{ \varvec{d}\right\} \right\} \\&= \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \left\{ \varvec{d}\right\} ^T \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \left\{ \varvec{\sigma }^M\right\} \right. \\&\left. \quad - \frac{1}{2V} \left\{ \varvec{d}\right\} ^T \left[ \varvec{K}\right] \left\{ \varvec{d}\right\} \right\} \end{aligned} \end{aligned}$$
(9)

where \(\mathcal {V}\) is a finite dimensional linear space, such that \(\mathcal {V}:= \big \{\varvec{d} | \varvec{d} \in \mathbb {R}^n, \varvec{d} = \varvec{d}_0 ~\mathrm{on} ~\partial V \big \}\); \(\varvec{K}\) is the global stiffness matrix, \(\varvec{K}^e\) is element stiffness matrix, \(\varvec{d}^*\) is the true nodal displacement field, \(\varvec{d}\) is the possible nodal displacement field, and \(\left[ \varvec{B}^e\right] \) is element stress–strain matrix, \(\varvec{\mathcal {A}}^{N_e}\) is element assembly symbol.

To find the true nodal displacements, we need to take variation of \(\bar{W}_c(\varvec{d})\):

$$\begin{aligned} \delta \bar{W}_c(\varvec{d}) = \frac{\partial \bar{W}_c}{\partial \varvec{d}} \delta \varvec{d} = \varvec{0} \end{aligned}$$

Therefore, the necessary condition for solution existence of the supremum \(\bar{W}_c\) is:

$$\begin{aligned} \frac{\partial \bar{W}_c}{\partial \varvec{d}} = \varvec{0} \end{aligned}$$
(10)

Substituting the finite element displacement interpolation field into Eq. (10), we can derive the total nodal displacements as follows,

$$\begin{aligned} \begin{aligned} \frac{\partial \bar{W}_c}{\partial \varvec{d}}&= \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \cdot \left\{ \varvec{\sigma }^M \right\} \\&\quad - \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{K}^e\right] ) \left\{ \varvec{d}\right\} = \varvec{0}\\ \Rightarrow \left\{ \varvec{d}\right\}&= \left[ \varvec{K}\right] ^{-1} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \cdot \left\{ \varvec{\sigma }^M\right\} ~. \end{aligned} \end{aligned}$$
(11)

Based on Eq. (11), the effective compliance tensor for linear elastic composite materials is derived as,

$$\begin{aligned} \begin{aligned} \varvec{D}^M&:= \bar{\varvec{D}} = \frac{\partial \varvec{\epsilon }^M }{\partial \varvec{\sigma }^M}\\&= \frac{1}{V} \int _{V} \frac{\partial \varvec{\epsilon }}{\partial \varvec{\sigma }^M} dV_{\varvec{x}} = \frac{1}{V} \sum _{e=1}^{N_e} \frac{\partial \varvec{\epsilon }}{\partial \varvec{\sigma }^M} V_e \\&=\frac{1}{V} \sum _{e=1}^{N_e} \left[ \varvec{B}^e\right] \left\{ \varvec{d}_{,\varvec{\sigma }^M}\right\} ^e V_e \\&= \frac{1}{V} \varvec{\mathcal {A}}_{e=1}^{N_e} (\left[ \varvec{B}^e\right] V_e) \cdot \left\{ \varvec{d}_{,\varvec{\sigma }^M}\right\} \end{aligned} \end{aligned}$$
(12)

where \(N^e\) is the total number of elements.

Based on Eq. (11), we have obtained \(\varvec{d}_{,\varvec{\sigma }^M}\) given as below,

$$\begin{aligned} \left\{ \varvec{d}_{,\varvec{\sigma }^M}\right\} = \left[ \varvec{K}\right] ^{-1} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \end{aligned}$$
(13)

Substituting Eq. (13) into Eq. (12), we can obtain the effective macro-compliance tensor as follows,

$$\begin{aligned} \varvec{D}^M= & {} \bar{\varvec{D}}\nonumber \\= & {} \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} ( \left[ \varvec{B}^e\right] V_e ) \left[ \varvec{K}\right] ^{-1} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e ), \end{aligned}$$
(14)

where \(\varvec{D}^M\) is called the macro-compliance tensor, which is the inverse of effective elastic tensor. \(\varvec{K}\) is the global stiffness matrix. Therefore, the effective elastic tensor \(\varvec{C}^M\) can be derived as,

$$\begin{aligned} \varvec{C}^M = \bar{\varvec{C}} = \varvec{D}^{M,-1}~. \end{aligned}$$

2.3 Stress-driven homogenization for hyper-elastic material

To beginning with, we first prove the existence of a solution to the stress-driven homogenization for nonlinear elastic solids under small deformation.

Proof

Similar to the linear elastic case, the Hill-Mandel Complementary Virtual Work Theorem is applied on nonlinear case in terms of nonlinear constitutive relation. Again, we assume that the RVE is prescribed with traction boundary condition,

$$\begin{aligned} \bar{\varvec{t}} = \varvec{\sigma }^M \cdot \varvec{n}, \qquad \forall \varvec{x} \in \partial \varOmega _t \end{aligned}$$
(15)

where \(\bar{\varvec{t}}\) is applied traction force on the boundary \(\partial \varOmega _t\).

The total potential energy of the system is shown:

$$\begin{aligned} \varPi= & {} \int _{\varOmega } W(\varvec{\epsilon }) dV - \int _{\partial \varOmega _t} \bar{\varvec{t}}\cdot \varvec{u} dA \nonumber \\= & {} \int _{\varOmega } W(\epsilon _{ij}) dV - \int _{\partial \varOmega _t} \bar{t}_i u_i dA \end{aligned}$$
(16)

where \(\varPi \) is the total potential energy of the continuum, \(W(\varvec{\epsilon })\) is the strain energy density, \(\varvec{u}\) is the displacement field on the continuum, \(\varOmega \) is the continuum domain, \(\partial \varOmega _t\) is traction boundary of the continuum domain.

Due to the relation of traction and macro-stress shown below:

$$\begin{aligned} \int _{\partial \varOmega _t} \bar{t}_i u_i dA = \int _{\partial \varOmega _t} \sigma ^M_{ij} n_j u_i dA = \sigma ^M_{ij} \int _{\varOmega } \epsilon _{ij} dV \end{aligned}$$

Eq. (16) can be transformed into:

$$\begin{aligned} \varPi = \int _{\varOmega } W(\varvec{\epsilon })dV - \varvec{\sigma }^M \int _{\varOmega } \varvec{\epsilon } dV \end{aligned}$$
(17)

The true strain \(\varvec{\epsilon }^*\) is inserted into the total energy of system equation and based on following derivation:

$$\begin{aligned} \begin{aligned} \int _{\varOmega } \varvec{\sigma } :\varvec{\epsilon ^*} dV&= \int _{\varOmega } \varvec{\sigma } : \nabla \varvec{u^*} dV \\&= \int _{\varOmega } \nabla \cdot (\varvec{\sigma }^T \cdot \varvec{u^*}) - div\varvec{\sigma } \cdot \varvec{u^*} dV \\&= \int _{\partial \varOmega } \varvec{\sigma }\cdot \varvec{u^*}\cdot \varvec{n} dA = \varvec{\sigma }^M : \int _{\varOmega } \varvec{\epsilon ^*} dV \end{aligned} \end{aligned}$$
(18)

The infimum inequality is shown as below:

$$\begin{aligned} \varPi (\varvec{\epsilon ^{*}})= & {} \int _{\varOmega } W(\varvec{\epsilon ^{*}}) - \varvec{\sigma }: \varvec{\epsilon ^{*}} dV \nonumber \\= & {} \int _{\varOmega } -W_c(\varvec{\epsilon ^{*}}) dV \le \varPi (\varvec{\epsilon }) \end{aligned}$$
(19)

Therefore, we have the inequality:

$$\begin{aligned}&\int _{\varOmega } W_c(\varvec{\epsilon ^{*}}) dV \ge - \varPi (\varvec{\epsilon })\nonumber \\&\Rightarrow \int _{\varOmega } W_c(\varvec{\epsilon ^{*}}) dV = \sup \limits _{\varvec{d} \in \mathcal {V}} (-\varPi (\varvec{\epsilon })) \end{aligned}$$
(20)

It then proves that the existence of a extreme solution to the following optimization problem,

$$\begin{aligned} \begin{aligned} \bar{W}_c&= \frac{1}{V} \int _{\varOmega } W_c(\varvec{\epsilon ^{*}}) dV = \frac{1}{V} \sup \limits _{\varvec{d} \in \mathcal {V}} (-\varPi (\varvec{\epsilon }))\\&= \frac{1}{V} \sup \limits _{\varvec{d} \in \mathcal {V}} \left[ -\int _{\varOmega } W(\varvec{\epsilon }) dV + \varvec{\sigma }^M : \int _{\varOmega } \varvec{\epsilon } dV\right] \\&= \frac{1}{V} \sup \limits _{\varvec{\sigma } \in S(\varvec{\sigma }^*)} \left[ \int _{\varOmega } W_c(\varvec{\sigma }) dV \right] . \end{aligned} \end{aligned}$$
(21)

\(\square \)

Since the existence of extreme solution of complementary potential has been proved, the necessary condition of the variational principle of complementary potential energy can be stated as follows,

$$\begin{aligned} \delta \bar{W}_c = \frac{\partial \bar{W}_c}{\partial \varvec{d}} \delta \varvec{d} = \varvec{0} \Rightarrow \frac{\partial \bar{W}_c}{\partial \varvec{d}} = \varvec{0} \end{aligned}$$
(22)

It may be noted that the complementary potential energy has been modified in terms of displacement variables,

$$\begin{aligned} \begin{aligned} \bar{W}_c(\varvec{d}^*)&= \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \varvec{\sigma }^M : \varvec{\epsilon }^M - \frac{1}{V} \int _{\varOmega } W(\varvec{\epsilon }) dV \right\} \\&= \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \frac{1}{V}\int _{\varOmega }\left\{ \varvec{\epsilon }\right\} ^T dV \left\{ \varvec{\sigma }^M\right\} \right. \\&\left. \quad - \frac{1}{V} \int _{\varOmega } W(\varvec{\epsilon }) dV \right\} \\&\le \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \frac{1}{V} \sum ^{N_e}_{e=1}(\left\{ \varvec{\epsilon }\right\} ^T V_e) \left\{ \varvec{\sigma }^M \right\} \right. \\&\left. \quad - \frac{1}{V} \sum ^{N_e}_{e=1} W(\varvec{\epsilon })V_e \right\} \end{aligned} \end{aligned}$$
(23)

By using finite element discretized strain field representation \(\left\{ \varvec{\epsilon }\right\} = \left[ \varvec{B}\right] \left\{ \varvec{d}\right\} \), the necessary condition for existence a maximizer \(\mathbf{d}^{\star }\) is \(\frac{\partial \bar{W}_c}{\partial \varvec{d}} = \varvec{0}\), which can be expressed as,

$$\begin{aligned} \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \cdot \left\{ \varvec{\sigma }^M\right\} - \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} \left( \frac{\partial W}{\partial \left\{ \varvec{d}\right\} } V_{e}\right) =\varvec{0} \end{aligned}$$
(24)

Due to the nonlinearity of \(\frac{\partial \bar{W}_c}{\partial \varvec{d}}\), one is to linearize the necessary condition \(\frac{\partial \bar{W}_c}{\partial \varvec{d}} = \varvec{0}\). Based on first order Taylor expansion, the linearized necessary condition is:

$$\begin{aligned} \begin{aligned}&\bar{W}^c_{,\varvec{d}}(\varvec{d}) + \bar{W}^c_{,\varvec{d} \varvec{d}}(\varvec{d}) \varDelta \varvec{d} = 0\\&\Rightarrow \varDelta \varvec{d} = - \left[ \bar{W}^c_{,\varvec{d} \varvec{d}}(\varvec{d})\right] ^{-1} \bar{W}^c_{,\varvec{d}}(\varvec{d}) \end{aligned} \end{aligned}$$
(25)

Therefore, the total nodal displacement field can be solved by the Newton-Raphson iteration algorithm,

$$\begin{aligned} \varvec{d}^{i+1}= & {} \varvec{d}^i + \varDelta \varvec{d}^i\nonumber \\= & {} \varvec{d}^i - \left[ \bar{W}^c_{,\varvec{d}\varvec{d}}\right] ^{-1} \bar{W}^c_{,\varvec{d}} \qquad \text {until} \qquad \Vert \bar{W}^c_{,\varvec{d}}(\varvec{d}^i)\Vert < tol\nonumber \\ \end{aligned}$$
(26)

Remark

The displacement field solution \(\varvec{d}\) is unique, if we apply suitable displacement boundary condition that can eliminate rigid body motion.

The discretized formulation for \(\frac{\partial \bar{W}_c}{\partial \left\{ \varvec{d}\right\} }\) is given as follows,

$$\begin{aligned} \frac{\partial \bar{W}_c}{\partial \left\{ \varvec{d}\right\} }= & {} \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \left\{ \varvec{\sigma }\right\} ^M \nonumber \\&- \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} \left( \left[ \varvec{B}^e\right] ^T \left\{ \frac{\partial W}{\partial \varvec{\epsilon }}\right\} ^T V_{e}\right) \end{aligned}$$
(27)

The discretized formulation of \(\frac{\partial ^2 \bar{W}_c}{\partial \varvec{d}^2}\) can be shown as:

$$\begin{aligned} \frac{\partial ^2 \bar{W}_c}{\partial \varvec{d}^2} = -\frac{1}{V}\varvec{\mathcal {A}}^{N_e}_{e=1}\left( \left[ \varvec{B}^e\right] ^T \left\{ \frac{\partial ^2 W}{\partial \varvec{\epsilon }^2}\right\} ^T \left[ \varvec{B}^e\right] V_{e}\right) \end{aligned}$$
(28)

Based on above equation, the true total nodal displacement \(\varvec{d}^*\), which is a maximizer of the averaged complementary potential energy \(\bar{W}_c\), can be found. We can then derive the FEM formulations for macro-strain \(\varvec{\epsilon }^M\) and the effective compliance tensor of composites \(\varvec{D}^M(\bar{\varvec{D}})\) as follows,

$$\begin{aligned} \varvec{\epsilon }^M= & {} \frac{\partial \bar{W}_c}{\partial \varvec{\sigma }^M}\nonumber \\= & {} \frac{1}{V} \sum ^{N_e}_{e=1} \left\{ \varvec{\epsilon }\right\} ^T V_e \end{aligned}$$
(29)
$$\begin{aligned} \varvec{D}^M= & {} \bar{\varvec{D}}\nonumber \\= & {} \frac{\partial \bar{W}^c_{,\varvec{\sigma }^M}}{\partial \varvec{\sigma }^M} = \bar{W}^c_{,\varvec{\sigma }^M\varvec{d}} \varvec{d}_{,\varvec{\sigma }^M} \end{aligned}$$
(30)

in which

$$\begin{aligned} \bar{W}^c_{,\varvec{\sigma }^M\varvec{d}} = \frac{1}{V} \frac{\partial \sum \limits ^{N_e}_{e=1} \left\{ \varvec{\epsilon } \right\} V_e}{\partial \varvec{d}} = \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] V_e \end{aligned}$$
(31)

and

$$\begin{aligned} \varvec{d}_{,\varvec{\sigma }^M}= & {} \left( \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] ^T \left\{ \frac{\partial ^2 W}{\partial \varvec{\epsilon }^2} \right\} \left[ \varvec{B}^e\right] V_e \right) ^{-1}\nonumber \\&\left( \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] ^T V_e \right) \end{aligned}$$
(32)

Therefore the discretized formulation for the effective compliance tensor is:

$$\begin{aligned} \varvec{D}^M= & {} \bar{\varvec{D}}\nonumber \\= & {} \left( \frac{1}{V}\varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] V_e \right) \left( \frac{1}{V}\varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] ^T \left\{ \frac{\partial ^2 W}{\partial \varvec{\epsilon }^2}\right\} \right. \nonumber \\&\left. \cdot \left[ \varvec{B}^e\right] V_e\right) ^{-1} \left( \frac{1}{V} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] ^T V_e\right) \end{aligned}$$
(33)

The computational procedure of the proposed homogenization method is summarized in the Box 1.

figure a

2.4 Stress-driven homogenization for finite deformation

In this section, the stress-driven homogenization based on incremental variational method is extended from small deformation to finite deformation.

Consider a finite motion of a continuum composites \(\varphi (\varvec{X},t):\quad \varOmega _0 \rightarrow \varOmega _t\). Thus the deformation gradient of the motion can be defined as:

$$\begin{aligned} \varvec{F} = \frac{\partial \varvec{x}}{\partial \varvec{X}} = \nabla \varphi \end{aligned}$$
(34)

We first assume that composite material is quasi-convex with respect to \(\varvec{F}\). A function W is said to be quasi-convex with respect to \(\varvec{F}\) if

$$\begin{aligned}&W(\varvec{F}) \le \frac{1}{V_0} \int _{\varOmega _0} W(\varvec{F}+\nabla _{\varvec{X}}\varvec{\chi })d\varvec{X},\nonumber \\&\quad \forall \varvec{F} \in \mathbb {R}^{3\times 3}, \quad \varvec{\chi } \in W^{1,\infty }_0(V;\mathbb {R}^3) \end{aligned}$$
(35)

in which, \(\varvec{\chi }\) is a perturbation of \(\varphi (\varvec{X},t)\). The quasi-convexity of functional W implies that

$$\begin{aligned} (\varvec{n}\otimes \varvec{N}) : \partial ^2_{\varvec{F}\varvec{F}}W : (\varvec{n}\otimes \varvec{N}) \ge 0 \end{aligned}$$
(36)

where \(\varvec{n},\varvec{N} \in \mathbb {R}^3\). This condition is called the Legendre-Hadamard or strong ellipticity condition.

We now prove the existence of an extremum solution to the complementary potential energy under finite deformation.

Proof

For finite deformation, we may have the following minimum potential energy principle:

$$\begin{aligned} \varPi (\varvec{u}^*) = \inf _{\varvec{u} \in \mathcal {V}} \pi (\varvec{u}), \quad \forall \varvec{u} \in \mathcal {V} \end{aligned}$$
(37)

where \(\mathcal {V}\) is the function space for all admissible displacement fields.

$$\begin{aligned} \varPi = \int _{\varOmega _0} W(\varvec{F}) dV - \int _{\partial \varOmega _t} \bar{\varvec{p}} \cdot \varvec{u} dA \end{aligned}$$
(38)

where \(\bar{\varvec{p}}\) is applied traction in the reference coordinate.

Such transformation relation is introduced:

$$\begin{aligned} \int _{\partial \varOmega _t} \bar{\varvec{p}} \cdot \varvec{u} dA = \int _{\partial \varOmega _t} \varvec{P}^M \varvec{N} \cdot \varvec{u} dA = \varvec{P}^M \int _{\partial \varOmega _t} \nabla _{\varvec{X}} \varvec{u} dV \end{aligned}$$

where \(\varvec{P}^M\) is the macroscale 1st Piola-Kirchhoff stress.

The potential energy of the system can be given as follows,

$$\begin{aligned} \varPi = \int _{\varOmega _0}W(\varvec{F}) dV - \varvec{P}^M \int _{\varOmega _0} \nabla _{\varvec{X}} \varvec{u} dV \end{aligned}$$
(39)

The principle of minimum potential energy will lead to such equation:

$$\begin{aligned} \varPi (\varvec{u}^*) = \int _{\varOmega _0} W(\varvec{F}^*) dV - \varvec{P}^M \int _{\varOmega _0} \frac{\partial \varvec{u}^{*}}{\partial \varvec{X}} dV \end{aligned}$$
(40)

where \(\varvec{F}^*\) is deformation gradient due to true displacement \(\varvec{u}^*\).

Considering such transformation relation shown below

$$\begin{aligned} \begin{aligned} \int _{\varOmega _0} \varvec{P} : \nabla _{\varvec{X}}\varvec{u}^* dV&= \int _{\varOmega _0} \nabla _{\varvec{X}} \cdot (\varvec{P}^T\varvec{u}^*) - Div\varvec{P} \cdot \varvec{u}^* dV\\&= \int _{\partial \varOmega _t} \varvec{P}\varvec{N} \cdot \varvec{u}^* dA - \int _{\varOmega _0} Div\varvec{P} \cdot \varvec{u}^* dV\\&= \int _{\partial \varOmega _t} \varvec{P}\varvec{N} \cdot \varvec{u}^* dA \\&=\varvec{P}^M \int _{\partial \varOmega _t} \varvec{u}^* \otimes \varvec{N} dA \\&= \varvec{P}^M : \int _{\varOmega _0} \nabla _{\varvec{X}} \varvec{u}^* dV, \end{aligned} \end{aligned}$$

we have found that

$$\begin{aligned} \int _{\varOmega _0} \varvec{P} : \nabla _{\varvec{X}} \varvec{u}^* dV = \varvec{P}^M : \int _{\varOmega _0} \nabla _{\varvec{X}} \varvec{u}^* dV~. \end{aligned}$$
(41)

Substituting it into Eq. (40), we have following relations,

$$\begin{aligned} \begin{aligned} \varPi (\varvec{F}^*)&= \int _{\varOmega _0} W(\varvec{F}^*) dV - \varvec{P}^M :\int _{\varOmega _0} \nabla _{\varvec{X}}\varvec{u}^* dV \\&= \int _{\varOmega _0} W(\varvec{F}^*) dV - \int _{\varOmega _0} \varvec{P} : \nabla _{\varvec{X}}\varvec{u}^* dV \\&= \int _{\varOmega _0} - W_c(\varvec{F}^*) dV \le \varPi (\varvec{F})~. \end{aligned} \end{aligned}$$
(42)

Therefore, one can find the following inequality,

$$\begin{aligned}&\int _{\varOmega _0} W_c(\varvec{F}^*) dV \ge - \varPi (\varvec{F})\nonumber \\&\Rightarrow \int _{\varOmega _0} W_c(\varvec{F}^*) dV = \sup \limits _{\varvec{d}\in \mathcal {V}} (-\varPi (\varvec{F}))~. \end{aligned}$$
(43)

Based on above equation, the averaged complementary potential energy can be found as,

$$\begin{aligned} \begin{aligned} \bar{W}_c&= \frac{1}{V_0} \int _{\varOmega _0} W_c(\varvec{F}^*) dV = \frac{1}{V_0} \sup \limits _{\varvec{d}\in \mathcal {V}} (-\varPi (\varvec{F})) \\&= \sup \limits _{\varvec{d}\in \mathcal {V}} \frac{1}{V_0}\left[ -\int _{\varOmega _0} W(\varvec{F}) dV + \varvec{P}^M : \int _{\varOmega _0} \nabla _{\varvec{X}} \varvec{u} dV \right] \\&= \sup \limits _{\varvec{P}\in S(\varvec{P}^*)}\frac{1}{V_0} \int _{\varOmega _0} W_c(\varvec{P}) dV \end{aligned} \end{aligned}$$
(44)

where \(S(\varvec{P}^*)\) is the space for all admissible 1st Piola-Kirchhoff stress tensors. \(\square \)

Since that the existence of extremal solution of complementary potential energy is proved, one can derive the corresponding FEM discretization formulation, which can be expressed as,

$$\begin{aligned} \bar{W}_c(\varvec{P}^*)&\le \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \varvec{P}^M : \frac{1}{V_0}\int _{\varOmega _0}\nabla _{\varvec{X}} \varvec{u} dV\right. \nonumber \\&\left. \quad - \frac{1}{V_0} \int _{\varOmega _0} W(\varvec{F})dV \right\} \nonumber \\&= \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \frac{1}{V_0} \int _{\varOmega _0} \left\{ \frac{\partial \varvec{u}}{\partial \varvec{X}}\right\} ^T dV \left\{ \varvec{P}^M \right\} \right. \nonumber \\&\left. \quad - \frac{1}{V_0} \int _{\varOmega _0} W(\varvec{F}) dV \right\} \nonumber \\&\le \sup \limits _{\varvec{d} \in \mathcal {V}} \left\{ \frac{1}{V_0}\left( \sum ^{N_e}_{e=1} \left\{ \frac{\partial \varvec{u}}{\partial \varvec{X}}\right\} ^T V_e\right) \left\{ \varvec{P}^M\right\} \right. \nonumber \\&\left. \quad - \frac{1}{V_0} \sum ^{N_e}_{e=1} W(\varvec{F}) V_e \right\} ~. \end{aligned}$$
(45)

The FEM discretization of displacement \(\varvec{u}\) is shown as:

$$\begin{aligned} \left\{ \frac{\partial \varvec{u}}{\partial \varvec{X}}\right\} = \left[ \varvec{B}\right] \left\{ \varvec{d}\right\} \end{aligned}$$
(46)

where \(\varvec{d}\) represents the total nodal displacement which can be decomposed as \(\varvec{d} = (\varvec{F}^M-\mathbb {1}) {\cdot } \varvec{X} + \varvec{w}^d\). The first term, \((\varvec{F}^M-\mathbb {1}){\cdot } \varvec{X}\), represents the averaged nodal displacement field or the prescribed boundary displacement field, and the second term, \(\varvec{w}^d\), represents the fine-scale nodal fluctuation displacement.

To find the extremal nodal displacement solution to the macro-complementary potential energy, we take a variation on the averaged complementary potential energy \(\bar{W}_c\) shown as follows,

$$\begin{aligned} \delta \bar{W}_c = \frac{\partial \bar{W}_c}{\partial \varvec{d}} \delta \varvec{d} = \varvec{0}~. \end{aligned}$$
(47)

It then leads to the necessary condition of incremental variational problem:

$$\begin{aligned} \frac{\partial \bar{W}_c}{\partial \varvec{d}} = \varvec{0} \end{aligned}$$
(48)

The FEM discretization formulation of necessary condition is shown as,

$$\begin{aligned} \frac{\partial \bar{W}_c}{\partial \varvec{d}}= & {} \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \cdot \left\{ \varvec{P}^M\right\} \nonumber \\&- \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} \left( \frac{\partial W}{\partial \varvec{d}} V_{e}\right) \nonumber \\= & {} \varvec{0} \end{aligned}$$
(49)

Because of the nonlinearity of above formulation of \(\bar{W}^c_{,\varvec{d}}\), we need to linearize it to obtain an iterative solution of the total nodal displacement solution to the extreme complementary potential energy of system.

The first order Taylor expansion is used to have linearized formulation of \(\bar{W}^c_{,\varvec{d}}\)

$$\begin{aligned} \begin{aligned} \bar{W}^c_{,\varvec{d}} = \bar{W}^c_{,\varvec{d}}(\varvec{d}^i) + \bar{W}^c_{,\varvec{d} \varvec{d}}(\varvec{d}^i) \varDelta \varvec{d}^i = 0 \\ \Rightarrow \varDelta \varvec{d}^i = -\left[ \bar{W}^c_{\varvec{d}\varvec{d}}(\varvec{d}^i)\right] ^{-1} \bar{W}^c_{,\varvec{d}}(\varvec{d}^i) \end{aligned} \end{aligned}$$
(50)

Therefore, the Newton-Raphson iterative algorithm for solving total nodal displacement is,

$$\begin{aligned}&\varvec{d}^{i+1} = \varvec{d}^i + \varDelta \varvec{d}^i = \varvec{d}^i - \left[ \bar{W}^c_{,\varvec{d}\varvec{d}}\right] ^{-1}\bar{W}^c_{,\varvec{d}} \qquad \text {until}\nonumber \\&\quad \Vert \bar{W}^c_{,\varvec{d}}(\varvec{d}^{i})\Vert \le tol \end{aligned}$$
(51)

Remark

The displacement field solution, \(\varvec{d}\), is unique if we apply the displacement boundary condition that eliminates the rigid body motion.

The FEM discretization formulation of \(\frac{\partial \bar{W}_c}{\partial \varvec{d}}\) is given as follows,

$$\begin{aligned} \frac{\partial \bar{W}^c}{\partial \varvec{d}}= & {} \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] ^T V_e) \left\{ \varvec{P}^M\right\} \nonumber \\&- \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} \left( \left[ \varvec{B}^e\right] ^T \left\{ \frac{\partial W}{\partial \varvec{F}}\right\} ^T V_{e}\right) \end{aligned}$$
(52)

The discretized formulation of \(\frac{\partial ^2 \bar{W}^c}{\partial \varvec{d}^2}\) is shown below,

$$\begin{aligned} \frac{\partial ^2 \bar{W}_c}{\partial \varvec{d}^2} = -\frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} \left( \left[ \varvec{B}^e\right] ^T \left\{ \frac{\partial ^2 W}{\partial \varvec{F}^2}\right\} ^T \left[ \varvec{B}^e\right] V_{e}\right) ~. \end{aligned}$$
(53)

Based on these formulations, we can solve the total nodal displacement \(\varvec{d}\), the average displacement gradient \(\bar{\frac{\partial \varvec{u}}{\partial \varvec{X}}}\), as well as the effective compliance tensor \(\bar{\varvec{D}}(\varvec{D}^M)\) of composites,

$$\begin{aligned} \overline{\frac{\partial \varvec{u}}{\partial \varvec{X}}}= & {} \frac{\partial \bar{W}^c}{\partial \varvec{P}^M}\nonumber \\= & {} \frac{1}{V_0} \sum ^{N_e}_{e=1} \left\{ \frac{\partial \varvec{u}}{\partial \varvec{X}}\right\} ^T V_e \end{aligned}$$
(54)
$$\begin{aligned} \varvec{D}^M= & {} \bar{\varvec{D}}\nonumber \\= & {} \frac{\partial \bar{W}^c_{,\varvec{P}^M}}{\partial \varvec{P}^M} = \bar{W}^c_{,\varvec{P}^M\varvec{d}} \varvec{d}_{,\varvec{P}^M} \end{aligned}$$
(55)

in which the discretized formulations of \(\bar{W}^c_{,\varvec{P}^M\varvec{d}}\) and \(\varvec{d}_{,\varvec{P}^M}\) are shown as follows,

$$\begin{aligned} \bar{W}^c_{,\varvec{P}^M\varvec{d}}= & {} \frac{1}{V_0} \frac{\partial }{\partial \varvec{d}} (\sum \limits ^{N_e}_{e=1} \left\{ \frac{\partial \varvec{u}}{\partial \varvec{X}} \right\} V_e)\nonumber \\= & {} \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} (\left[ \varvec{B}^e\right] V_e) \end{aligned}$$
(56)
$$\begin{aligned} \varvec{d}_{,\varvec{P}^M}= & {} \left[ \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] ^T \left\{ \frac{\partial ^2 W}{\partial \varvec{F}^2}\right\} \left[ \varvec{B}^e\right] V_e \right] ^{-1} \nonumber \\&\left( \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] ^T V_e\right) \nonumber \\= & {} \left( \left[ -\bar{W}^c_{,\varvec{d}\varvec{d}}\right] ^T\right) ^{-1} \bar{W}^c_{,\varvec{d}\varvec{P}^M} \end{aligned}$$
(57)

Therefore, we have the discretization formulation of \(\bar{\varvec{D}}(\varvec{D}^M)\) as follows,

$$\begin{aligned} \varvec{D}^M= & {} \bar{\varvec{D}}\nonumber \\= & {} \left( \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] V_e\right) \nonumber \\&\left( \left[ \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] ^T \left\{ \frac{\partial ^2 W}{\partial \varvec{F}^2}\right\} \left[ \varvec{B}^e\right] V_e \right] ^{-1} \right) \nonumber \\&\cdot \left( \frac{1}{V_0} \varvec{\mathcal {A}}^{N_e}_{e=1} \left[ \varvec{B}^e\right] ^T V_e\right) ~. \end{aligned}$$
(58)

The main computation steps of the proposed computational homogenization procedure are summarized in the Box 2.

figure b

3 Numerical examples

In this Section, we shall present several benchmark homogenization examples for both linear elastic material and hyper-elastic material under both small deformation and finite deformation. Furthermore, we shall make a comparison of the numerical results obtained by using the present method with that obtained from the strain-driven homogenization variational method, which offers an upper bound for the effective material properties.

3.1 Linear elastic composite material

We first consider an RVE of a linear elastic composite, and the cubic shaped RVE with edge size is 4.0 and an ellipsoid inclusion with semi-axis radius \(a=0.5,\ b=0.4,\ c=0.3\) is set up (Tables 1, 2). The inclusion material is \(G_1=80,000,\ K_1=23,000\) and the matrix is \(G_2 = 40,000,\ K_2 = 11500\). The ellipsoid configuration and matrix configuration are shown in Fig. 2.

The effective elastic tensors based on strain-driven and stress-driven are shown in Tables 1, 2.

Table 1 Effective elastic tensor of strain-driven homogenization
Full size table
Table 2 Effective elastic tensor of stress-driven homogenization
Full size table

From the tables shown above, one may find that stress-driven homogenization method is able to estimate the effective elastic tensor, which can be approximated from the homogenized stress–strain relation.

For the computational homogenization method we are not restricted by geometry of inclusion, therefore one can also consider matrix as a hollow sphere and the inclusion as a concentric sphere as shown in Fig. 3.

Fig. 2
figure 2

a Undeformed ellipsoid inclusion; b undeformed rectangular cuboid

Full size image
Fig. 3
figure 3

a Undeformed spherical inclusion; b undeformed hollow spherical matrix

Full size image

For the matrix material, \(G_1 = 25,000\), \(K_1 = 23,000\), the inclusion sphere \(G_2 = G_1z_1\), \(K_2 = K_1z_2\). \(z_1\) and \(z_2\) are ratios that control the bulk modulus and shear modulus of inclusion material. Due to the arbitrary shape of inclusion of computational homogenization, we can have the effective bulk modulus \(\bar{\kappa }\) and effective shear modulus \(\bar{\mu }\) with different volume fraction of inclusion. The results are shown in Fig. 4.

Fig. 4
figure 4

a \( \frac{\kappa _{inclusion}}{\kappa _{matrix}} = 10\); b \( \frac{\kappa _{inclusion}}{\kappa _{matrix}} = 100\); c \( \frac{\mu _{inclusion}}{\mu _{matrix}} = 4\); d \( \frac{\mu _{inclusion}}{\mu _{matrix}} = 50\)

Full size image

From the numerical results presented above we may conclude that the stress-driven estimate is inside the domain of the Hashin-Shtrikman bounds. It proves the validity of stress-driven computational homogenization theory. Generally speaking, effective \(\bar{\kappa }\), \(\bar{\mu }\) from stress-driven are lower than that from strain-driven homogenization. It means that stress-driven homogenization offers a lower bound solution for material constants of composites. This observation is coincident with our previous derivation of supreme extremal solution of stress-driven homogenization. Besides, when volume fraction is below 0.8 the stress-driven curve tends to approximate to the lower bound of Hashin-Shtrikman while when volume fraction exceeds 0.8 the stress-driven curve tends to approach to the Hashin-Shtrikman upper bound. Furthermore, the strain-driven homogenization has the similar tendency and it even exceeds the domain of Hashin-Shtrikman bounds (Fig. 4).

3.2 Homogenization of hyperelastic composite material under small deformation

For the hyper-elastic material, an ellipsoid with semi-axis \(a=0.8\), \(b=0.96\), \(c=1.12\) and a matrix with edges \(2.0 \times 2.0 \times 3.0\) are set up. The ellipsoid inclusion and cubic matrix are shown in Fig. 5.

We now consider a special class of nonlinear composite materials, in which both the inclusion and matrix are isotropic and homogeneous, and they have the same form of nonlinear constitutive relation as shown below,

$$\begin{aligned} W = \frac{1}{2}\kappa I_1^2(\varvec{\epsilon }) + \mu I_2^2(\varvec{\epsilon }) \end{aligned}$$
(59)

in which, \(I_1(\varvec{\epsilon }) = trace(\varvec{\epsilon })\) and \(I_2(\varvec{\epsilon }) = \frac{1}{2} (trace(\varvec{\epsilon })^2 - trace(\varvec{\epsilon }^2))\).

For this type of nonlinear materials, the micro-stress can be found as,

$$\begin{aligned} \frac{\partial W}{\partial \varvec{\epsilon }} = \kappa I_1(\varvec{\epsilon }) \mathbb {1} + 2\mu I_2(\varvec{\epsilon }) \big (I_1(\varvec{\epsilon })\mathbb {1} - \varvec{\epsilon }\big ), \end{aligned}$$
(60)

and the corresponding fine-scale elastic tensor can be derived as,

$$\begin{aligned} \frac{\partial ^2 W}{\partial \varvec{\epsilon }^2}= & {} \kappa \mathbb {1} \otimes \mathbb {1} + 2\mu \left[ (I_1^2+I_2)\mathbb {1}\otimes \mathbb {1}\right. \nonumber \\&\left. - I_1 (\mathbb {1}\otimes \varvec{\epsilon } + \varvec{\epsilon } \otimes \mathbb {1}) - I_2 \mathbb {1}^{4s} + \varvec{\epsilon }\otimes \varvec{\epsilon }\right] \end{aligned}$$
(61)

where \(\mathbb {1}\) is the second order identity, \(\mathbb {1}^{4s}\) is the fourth order identity and \(\mathbb {1} \otimes \varvec{\epsilon }\) and \(\varvec{\epsilon } \otimes \mathbb {1}\) are respectively the tensor product of micro-strain and second order identity.

Fig. 5
figure 5

Hyperelastic material RVE: a Undeformed ellipsoid inclusion; b undeformed matrix

Full size image

Assume that the matrix material parameters are \(\kappa _1 = 120\), \(\mu _1 = 30\) and the inclusion material parameters are \(\kappa _2 = 90\), \(\mu _2 = 20\).

Due to the nonlinearity of material constitutive relation, the material properties constants are variables depending on deformation (See: Fig. 6, Tables 3, 4). Therefore, we plot the stress–strain curve to show its constitutive response:

Fig. 6
figure 6

stress–strain curves

Full size image

In the following example, we compare the effective elastic tensor obtained from the stress-driven homogenization with that obtained from the strain-driven homogenization.

Table 3 Effective elastic tensor of stress-driven homogenization
Full size table
Table 4 Effective elastic tensor of strain-driven homogenization
Full size table

From the calculated stress–strain curves and effective elastic tensors, it is found that the constitutive relation of stress-driven is within the domain of matrix and inclusion bounds and the stress-driven homogenization offers a lower bound while strain-driven homogenization offers an upper bound. This is consistent with the supremum and infimum extremal solutions of stress-driven and strain-driven variational derivation. Based on these tables, we can find that the effective elastic tensor of strain-driven has a good agreement with stress-driven homogenization result. Accordingly, based on the microscale material property, the macroscale material properties have been shown in two effective elastic tensor tables.

3.3 Hyper-elastic material under finite deformation

In engineering applications, it is very rare to have a hyperelastic material whose constitutive relation is quasi-convex. Therefore, a polyconvex stress potential in [16] is chosen in this numerical example.

We assume the constitutive response of the micro-structural constituents to be isotropic and governed by this form:

$$\begin{aligned} W(\varvec{F};\varvec{X}) = \frac{\mu }{2}\left[ \left\| \varvec{F}\right\| ^2-3\right] + \frac{\mu }{\beta }\left[ (det\varvec{F})^{-\beta }-1\right] \end{aligned}$$
(62)

which satisfies the material stability condition:

$$\begin{aligned}&W(\varvec{F}) \le \frac{1}{V} \int _V W(\varvec{F}+\nabla _{\varvec{X}}\varvec{\chi })d\varvec{x},\nonumber \\&\quad \forall \varvec{F} \in \mathbb {R}^{3\times 3}, \varvec{\chi } \in W_0^{1,\infty }(V;\mathbb {R}^3) \end{aligned}$$
(63)

The constitutive response is governed by two material variables \(\mu \) and \(\beta := \kappa / \mu - 2/3\), where \(\kappa \in \mathbb {R}_+\) denotes the bulk modulus and \(\mu \in \mathbb {R}_+\) the shear modulus.

Our theory is validated by setting up such a model: a two-phase composites with stiff inclusions embedded into a soft matrix and \(\kappa _{\mathscr {M}} = 17.5\), \(\mu _{\mathscr {M}}=8.0\) for the matrix and \(\kappa _{\mathscr {I}}=100\kappa _{\mathscr {M}}\), \(\mu _{\mathscr {I}}=100\mu _{\mathscr {M}}\) for the inclusion. To make a comparison with strain-driven homogenization [16], we also have a composite with a circular inclusion embedded into the center of a soft matrix. The side length of the matrix \(h=1.0\), the diameter of the inclusion \(d=0.4\).

Fig. 7
figure 7

a Deformed mesh of extension mode based on stress-driven homogenization; b Deformed mesh of shear mode based on stress-driven homogenization

Full size image

In our method, a macroscopic plane-stress extension mode is applied:

\(\varvec{P}^M = \left[ P^M_{11}; P^M_{22}; P^M_{12}; P^M_{21}\right] = \left[ 8.4; 2.0; 0.0; 0.0\right] \) and a shear mode:

\(\varvec{P} = \left[ P^M_{11}; P^M_{22}; P^M_{12}; P^M_{21}\right] = \left[ 0.0; 0.0; 4.0; 4.0\right] \).

Comparing with strain-driven method, from Tables 3 and 4, we find that our method offers a lower bound of material response. And the deformed mesh of extension mode and shear mode for different mico-to-macro transition based on stress-driven homogenization are shown in Fig. 7, where the red circle represents inclusion part (Tables 5, 6).

4 Conclusions and discussions

In this work, we present a stress-driven computational homogenization procedure to find the effective material properties of both linear elastic and hyperelastic composite materials with arbitrary microstructure. A consistent variational framework for construction computational homogenization formulations for linear elastic and hyperelastic composite solids under both small and finite deformation has been developed. For the broad class of generalized composite media, an incremental variational formulation for general material responses is set up. The existence of a quasi-hyperelastic stress potential energy allowed the computation homogenization approach to be applied to a fair large class of hyperelastic materials. Under the macro stress-driven condition, we have developed an incremental variational formulation for the global homogenization problem where a quasi-hyperelastic macro-stress potential is obtained from a global minimization problem with respect to the fine scale displacement filed.

Table 5 The stress-driven method for \(\varvec{P}\) and \(\varvec{F}\)
Full size table
Table 6 The strain-driven method for \(\varvec{P}\) and \(\varvec{F}\) [16]
Full size table

The main novelty of this work are three: (1) The unknown variable in the proposed stress-driven homogenization formulation is not stress but displacement, which circumvents the main difficulty in stress-driven complementary variational principle formulation. This is the main reason why we succeeded; (2) We have shown that the stress-driven computational homogenization approach proposed in this work indeed provides a lower bound for effective material properties, and (3) We are able to apply the stress-driven homogenization method to find the effective material properties of nonlinear hyperelastic composite materials under finite deformations. This is the case that even the strain-driven homogenization method has difficulty to do.

Finally based on the analysis of the numerical simulation results obtained in this work, we have reached to the following conclusions:

  1. (1)

    The numerical results obtained by using the proposed stress-driven homogenization method are shown that they are in a good agreement with the results of the Hashin-Shtrikman lower and upper bounds [19, 20] for linear elastic composite materials (see Fig. 4).

  2. (2)

    The stress-driven homogenization method provides the lower bound estimate of the effective material properties of linear elastic composites, whereas the strain-driven homogenization offers the upper bound estimate of effective elastic material properties of linear elastic composites, and the combination of them can give a more accurate numerical estimate of effective material properties than the Hashin-Shtrikman’s analytical predictions;

  3. (3)

    Based on the numerical results obtained in nonlinear homogenization, we find that the effective material properties are bounded within the certain range between the material properties of the inclusion and matrix materials, which suggests that the variational principle based stress-driven homogenization formulation can predict the nonlinear effective material properties;

  4. (4)

    The stress-driven homogenization based on the incremental variational formulation offers the lower bound estimate of effective material properties for nonlinear hyperelastic composites, while the strain-driven homogenization offers the upper bound estimate of effective material properties of nonlinear hyperelastic materials, and,

  5. (5)

    By using the polyconvex potential function, the stress-driven homogenization method under finite deformation also offers a lower bound estimate of the material response comparing to the results obtained from the strain-driven homogenization. To close the presentation, we would like to emphasize that the computational procedure developed in this work can be applied to any shaped RVEs with arbitrary of inclusions of any shape and any number. However, it is noteworthy that irregular shape of domain (both RVE as well as inclusions) will require finer mesh and therefore it may require more computational costs. Furthermore, we believe that this method is also applicable to the homogenization of fiber-reinforced composite problems under elastic range with finite deformation. Moreover, this method may be able to extended to some inelastic cases because it is an incremental formulation. However for the case of the composites with fiber/matrix debonding, it may need additional numerical techniques.