Aspects of implementing constant traction boundary conditions in computational homogenization via semi-Dirichlet boundary conditions

Abstract

In the past decades computational homogenization has proven to be a powerful strategy to compute the overall response of continua. Central to computational homogenization is the Hill–Mandel condition. The Hill–Mandel condition is fulfilled via imposing displacement boundary conditions (DBC), periodic boundary conditions (PBC) or traction boundary conditions (TBC) collectively referred to as canonical boundary conditions. While DBC and PBC are widely implemented, TBC remains poorly understood, with a few exceptions. The main issue with TBC is the singularity of the stiffness matrix due to rigid body motions. The objective of this manuscript is to propose a generic strategy to implement TBC in the context of computational homogenization at finite strains. To eliminate rigid body motions, we introduce the concept of semi-Dirichlet boundary conditions. Semi-Dirichlet boundary conditions are non-homogeneous Dirichlet-type constraints that simultaneously satisfy the Neumann-type conditions. A key feature of the proposed methodology is its applicability for both strain-driven as well as stress-driven homogenization. The performance of the proposed scheme is demonstrated via a series of numerical examples.

1 Introduction

Almost all materials in nature possess a heterogeneous micro-structure at a certain length scale. Furthermore, composites consisting of two or more constituents show more interesting properties compared to homogeneous materials and are often particularly tailored for specific purposes. Therefore, it is extremely important to predict the overall material response based on the constitutive behavior of its underlying micro-structure. In doing so, several multi-scale techniques have been developed in the past. Multi-scale models are traditionally categorized into the homogenization method [1, 2] and the concurrent method [3–5]. This contribution details on the homogenization method where the length scales of micro- and macro-problems are sufficiently separate.

The main objective of the homogenization method is to estimate the effective macroscopic properties of a heterogeneous material from the response of its underlying micro-structure thereby allowing to substitute the heterogeneous material with an equivalent homogeneous one. Homogenization techniques are commonly classified into two general categories of analytical homogenization and computational homogenization. Preliminary steps in analytical homogenization were made in the pioneering works of [6–11] further developed in [12–15] among others; see [16–19] for an overview on analytical homogenization models. Although the analytical homogenization method renders useful information and is computationally favorable, it is generally not suitable for complex geometries where the shape, size, distribution pattern and volume fraction of the inclusions greatly influence the final characteristic of composites. In order to deal with such complexities, the computational homogenization method has been established in the past two decades [20–50] and thoroughly reviewed in [51–55]. The most popular technique among computational homogenization models is the direct micro-to-macro transition method which evaluates the stress-strain relationship at each quadrature point of the macro-scale through solving the associated boundary value problem at the micro-scale. It is commonly assumed that the behavior of the material at the micro-scale is known and defined through an energy density function. Alternatively, it is possible to develop physically interpretable and micro-mechanically motivated material models as discussed in [56–58]. In the literature, the “appropriate” micro-scale sample is referred to as the representative volume element (RVE); see for instance [59–62] for detailed discussions about the definition and the size of the RVE.

Central to the homogenization method is the Hill–Mandel condition that enforces an incremental energy equivalence between the micro-scale and the macro-scale. The boundary conditions of the micro-problem are chosen such that the Hill–Mandel condition is a priori satisfied. Among numerous boundary conditions satisfying the Hill–Mandel condition, linear displacement (DBC), periodic displacement and anti-periodic traction (PBC) and constant traction (TBC) are more recognized and are collectively referred to as canonical boundary conditions. It is relatively well-established that in purely mechanical problems and for a finite size of the RVE, the effective behavior obtained under PBC is bounded by DBC from above and TBC from below [63–66]. Therefore, PBC has become the most commonly used boundary condition in homogenization problems. However, it has been discussed [22, 67, 68] that PBC provides the most precise results only for periodic micro-structures and not necessarily for micro-structures with random distributions of inclusions. Moreover, Drago and Pindera [69] have shown that the overall transverse Poisson’s ratio obtained via PBC is not necessarily bounded between TBC and DBC in contrast to what is commonly expected.

The computational algorithms to implement DBC and PBC have been widely discussed and are well-established. Nevertheless, the implementation of TBC have been rarely detailed mainly due to the associated problems arising from the singularity of the stiffness matrix caused by prescribing a purely Neumann-type boundary condition on the RVE. Various techniques proposed to treat this problem include using the Lagrange multiplier method and mass-type diagonal perturbation to regularize the stiffness matrix [70] or construction of a free-flexibility matrix to preserve the rigid body modes [71]. In this contribution, we propose a novel algorithm to implement TBC for the finite deformation setting. The robustness of the proposed strategy is illustrated through a series of numerical examples. Although throughout this paper we mainly devote our attention to strain-driven computational homogenization, the proposed algorithm is particularly attractive since it is suitable for stress-driven homogenization, too.

The remainder of this manuscript is organized as follows. The finite deformation formulations governing the response of the micro-structure, admissible boundary conditions and the connection between the scales are briefly discussed in Sect 2. Section 3 furnishes the finite element formulation of the micro-problem and elaborates on the proposed methodology to implement TBC. The utility of the proposed algorithm is elucidated through various numerical examples. Section 4 concludes this work and provides further outlook.

Fig. 1

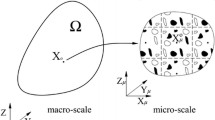
Graphical summary of computational homogenization. The material configuration $\mathcal {B}_\text {0}$ corresponds to a RVE which is mapped to its spatial configuration through the non-linear deformation ${\varvec{\varphi }}$. The local macroscopic response is determined through homogenizing the response of the corresponding micro-structure obtained from solving the associated boundary value problem

2 Theory

This section details on theoretical aspects of modeling the micro-structure of a heterogeneous material undergoing large deformations. This work is based on first-order strain-driven homogenization in the sense that the macroscopic deformation gradient is the input of the micro-problem and the macroscopic Piola stress is sought.

The configuration $\mathcal {B}_\text {0}$ defines the RVE in the material configuration whose boundary is denoted $\partial {\mathcal {B}_\text {0}}$ with the outward unit normal $\varvec{N}$, see Fig. 1. The spatial configuration of the RVE is defined analogously. Let $\varvec{X}$ be the position vector of a point in $\mathcal {B}_\text {0}$. The non-linear deformation ${\varvec{\varphi }}$ maps $\varvec{X}$ to its spatial counterpart $\varvec{x}$ via $\varvec{x}=\varvec{\varphi }(\varvec{X})$. A material line element $\text{ d }\varvec{X}$ is mapped to its counterpart $\text{ d }\varvec{x}$ in the spatial configuration as $\text{ d }{\varvec{x}} = \varvec{F} \cdot \text{ d }{\varvec{X}}$ with $\varvec{F}=\text{ Grad }\varvec{\varphi }$ being the deformation gradient. The governing equations of the micro-problem are the balances of linear and angular momentum. The local form of the balance of linear momentum reads

$$\begin{aligned} \hbox {Div}\varvec{P}&= \varvec{0}\quad \text {in} \; \mathcal {B}_\text {0}\quad \text {subject to} \quad \varvec{P} \cdot \varvec{N} = {\varvec{t}}_\text {0}\quad \text {on}\; \partial \mathcal {B}_\text {0}\qquad \text {and} \qquad \nonumber \\ {\varvec{t}}_\text {0}&= {\varvec{t}}{}^{\text {p}}_\text {0}\quad \text {on}\; \partial \mathcal {B}_\text {0,N}\,, \end{aligned}$$

(1)

in which ${\varvec{t}}_\text {0}$ denotes the traction on the boundary $\partial \mathcal {B}_\text {0}$ and $\varvec{P}$ is the Piola stress.¹ The prescribed traction on the Neumann part of the boundary $\partial \mathcal {B}_\text {0,N}\subset \partial \mathcal {B}_\text {0}$ is denoted ${\varvec{t}}{}^{\text {p}}_\text {0}$. The volume and inertia forces at the micro-scale are neglected due to the assumption of scale separation. The local form of the balance of angular momentum in the material configuration $\varvec{P}\cdot \varvec{F}{}^{\mathrm {t}}=\varvec{F}\cdot \varvec{P}{}^{\mathrm {t}}$ is essentially equivalent to the symmetry of Cauchy stresses.

In contrast to the micro-scale, the material response at the macro-scale is unknown. Nevertheless, the macro Piola stress ${}^\text {{M}}\!{\varvec{P}}$ is related to the macro deformation gradient ${}^\text {{M}}\!{\varvec{F}}$ through homogenization. Motivated by the average strain and stress theorems, the macroscopic deformation gradient and the macroscopic Piola stress are defined as the volume average of their microscopic counterparts as

$$\begin{aligned} {}^\text {{M}}\!{\varvec{F}}:= & {} \langle {\varvec{F}} \rangle = \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\mathcal {B}_\text {0}} \varvec{F} \, \text{ d }V = \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\partial \mathcal {B}_\text {0}} \varvec{\varphi } \otimes \varvec{N} \, \text{ d }A,\nonumber \\ {}^\text {{M}}\!\varvec{P}:= & {} \langle {\varvec{P}} \rangle = \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\mathcal {B}_\text {0}} \varvec{P} \, \text{ d }V = \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\partial \mathcal {B}_\text {0}} \varvec{t}_\text {0}\otimes \varvec{X} \, \text{ d }A \,, \end{aligned}$$

(2)

with $\mathscr {V}_\text {0}$ the volume of the RVE. The averaging relations (2) relate the deformation gradients and the stresses between the two scales. The next task is to enforce the incremental energy equivalence between the two scales, referred to as the Hill–Mandel condition

$$\begin{aligned} \langle { \varvec{P}:\delta \varvec{F} } \rangle - {}^\text {{M}}\!\varvec{P} : \delta {}^\text {{M}}\!\varvec{F} \mathop {=}\limits ^{!} 0 \,. \end{aligned}$$

(3)

With the aid of the Hill’s lemma, the Hill–Mandel condition can be converted into the surface integral

$$\begin{aligned}&\langle { \varvec{P}:\delta \varvec{F} } \rangle - {}^\text {{M}}\!\varvec{P} : \delta {}^\text {{M}}\!\varvec{F}\nonumber \\&\quad = \int _{\partial \mathcal {B}_\text {0}} [\delta \varvec{\varphi } - \delta {}^\text {{M}}\!\varvec{F} \cdot \varvec{X}] \cdot [\varvec{t}_\text {0}- {}^\text {{M}}\!\varvec{P}\cdot \varvec{N}] \ \text{ d }A \, , \end{aligned}$$

(4)

from which the admissible boundary conditions to be imposed on the micro-sample are determined. Among numerous choices satisfying the Hill–Mandel condition (3), linear displacement boundary conditions (DBC), periodic displacement and anti-periodic traction boundary conditions (PBC) and constant traction boundary conditions (TBC) are more recognized. These conditions guarantee the conservation of the incremental energy in the transition from the micro-scale to the macro-scale. In the current contribution, we only detail on computational aspects of TBC and refer the interested readers to [55, 60, 70, 73–75] for further details about computational implementations of DBC and PBC. We emphasize that the purpose of the current manuscript is to render a generalized framework to implement TBC and not to introduce a generalized type of boundary condition such as [74, 75] or for material layers [41, 76, 77].

3 Computational aspects

The main objective of this section is to detail on the computational aspects of TBC. First, the finite element formulation of the problem is briefly discussed. It is then followed by elaborating on the computational algorithms to implement TBC for two- and three-dimensional problems in the context of strain- and stress-driven homogenization frameworks.

Derivation of the weak formulation as well as the discretization are straightforward and well-established and, hence are not presented here for the sake of conciseness, see for instance [55] for details. The discretized weak form of the balance of linear momentum (1) reads

$$\begin{aligned} \varvec{R}^I := \underbrace{\overset{{\#}\text {be}}{\underset{\beta = 1}{\large {\varvec{\mathsf {A}}}}} \int _{\mathcal {B}_\text {0}^{\beta }} \varvec{P} \cdot \text{ Grad }\textit{N}^i \,\text{ d }\textit{V}}_{\varvec{R}^{I}_{\text {int}}} - \underbrace{\overset{{\#}\text {se}}{\underset{\gamma = 1}{\large {\varvec{\mathsf {A}}}}}\int _{\partial \mathcal {B}_\text {0,N}^{\gamma }} \, \varvec{{t{}^{\text {p}}_\text {0}}} \cdot {\textit{N}^i} \,\text{ d }\textit{A}}_{\varvec{R}^{I}_{\text {ext}}} \overset{!}{=} \varvec{0}\,, \end{aligned}$$

(5)

where #be and #se represent the number of bulk and surface elements, respectively. The domain of the bulk element $\beta$ is denoted $\mathcal {B}_\text {0}^{\beta }$, and $\partial \mathcal {B}_\text {0,N}^{\gamma }$ denotes the domain of the surface element $\gamma$ upon which traction is prescribed. Moreover, the shape functions are denoted N and i is the local equivalent of the global node I. Next, the nodal residuals $\varvec{R}^I$ are arranged in a global residual vector $\mathbf {R}$ and the fully-discrete non-linear system of equations becomes

$$\begin{aligned} \mathbf {R} = \mathbf {R}\left( {\mathbf {d}} \right) \overset{!}{=} \varvec{0}, \quad \mathbf {R} = \mathbf {R}_{\text {int}} + \mathbf {R}_{\text {ext}}\,, \end{aligned}$$

(6)

where $\mathbf {d}$ is the unknown global vector of deformations and $\mathbf {R}_{\text {int}}$ and $\mathbf {R}_{\text {ext}}$ are the assembled vectors of $\varvec{R}^{I}_{\text {int}}$ and $\varvec{R}^{I}_{\text {ext}}$, corresponding to internal and external residuals, respectively. The Newton–Raphson scheme is employed to find the solution of the system of Eq. (6). The consistent linearization of the resulting system of equations yields

$$\begin{aligned} \mathbf {R} \left( {\varvec{\mathbf {d}}_{i+1}} \right)= & {} \mathbf {R} \left( {\varvec{\mathbf {d}}_{i}} \right) + \mathbf {K} \cdot \, \Delta \mathbf {d}_{i} \overset{!}{=} \varvec{0} \qquad \text {with} \quad \mathbf {K} = \displaystyle \frac{\partial {\mathbf {R}}}{\partial {\mathbf {d}}}\mid _{i},\nonumber \\ \mathbf {d}_{i+1}= & {} \mathbf {d}_{i} + \Delta \mathbf {d}_{i}\,, \end{aligned}$$

(7)

where i is the iteration step and $\mathbf {K}$ is the assembled tangent stiffness matrix of nodal stiffness. Solving the system of Eq. (7) yields the iterative increment $\Delta \mathbf {d}_{i}$ and consequently $\mathbf {d}_{i+1}$.

The micro-scale boundary value problem requires the boundary conditions to be imposed on the system of Eq. (7) and the boundary condition of interest here is TBC. That is, the boundary of the micro-sample undergoes uniform distribution of ${}^\text {{M}}\!{\varvec{P}}\cdot \varvec{N}$. Recall in the context of the strain-driven homogenization, the input of the problem is ${}^\text {{M}}\!{\varvec{F}}$ and the output is ${}^\text {{M}}\!{\varvec{P}}$. Hence, at the beginning of the algorithm, ${}^\text {{M}}\!{\varvec{P}}$ is not known and an initial guess is required. We initiate ${}^\text {{M}}\!{\varvec{P}}$ with zero. This guess is then updated iteratively until $\langle {\varvec{F}} \rangle = {}^\text {{M}}\!{\varvec{F}}$ is achieved.

Obviously, the solution of the micro-problem is unique only up to rigid body motions. Therefore, sufficient constraints should be added on the boundary of the RVE to completely remove the rigid body motions. In doing so, we introduce and employ the concept of semi-Dirichlet boundary conditions. That is, we assign Dirichlet boundary conditions to three degrees of freedoms in two-dimensional problems and six degrees of freedoms in three-dimensional problems. Simultaneously we guarantee that the generated tractions at the Dirichlet parts are identical to the hypothetically prescribed tractions by updating the locations of the semi-Dirichlet constraints until they entirely accommodate the TBC. This procedure is further elaborated in what follows.

Assume the micro-sample is a square spanning the domain $[0,1]^{\text {2}}$, as shown in Fig. 2, whose boundary is subject to a uniform distribution of ${}^\text {{M}}\!{\varvec{P}}\cdot \varvec{N}$. In order to remove translational rigid body motions, a Dirichlet boundary condition is assigned to an arbitrary point A on the boundary in both directions. Assigning Dirichlet boundary condition to any other point (e.g. point B with ${X}_{x}^{\text {B}} \ne {X}_x^{\text {A}}$) in y direction eliminates the rotational rigid body motions. If the solution of TBC, illustrated using the dashed line, necessitates the point B to move in the direction that it is fixed, extra tractions (in addition to the contributions from ${}^\text {{M}}\!{\varvec{P}}\cdot \varvec{N}$) would develop on the Dirichlet constraints. Existence of such extra tractions disturbs the uniform distribution of the tractions over the boundary of the RVE, hence, violating TBC. We refer to these extra tractions as spurious tractions, denoted $\varvec{\zeta }$, in the sense that they do not comply with TBC.

Fig. 2

The entire boundary $\partial \mathcal {B}_\text {0}$ except point A in both directions and point B in y direction is prescribed with ${}^\text {{M}}\!\varvec{P} \cdot \varvec{N}$. Point A is fixed in both directions and point B is fixed in y direction so as to remove rigid body motions. Fixing these points can lead to spurious tractions $\varvec{\zeta }$ on the Dirichlet part of the boundary. The dashed line and the solid black line indicate the deformation of the micro-structure in the absence and presence of the spurious forces, respectively

The total nodal tractions on points A and B read $\varvec{t}^{\text {A}} = {}^\text {{M}}\!\varvec{P}\cdot \varvec{N}^{\text {A}}+\varvec{\zeta }^{\text {A}}$ and $\varvec{t}^{\text {B}} = {}^\text {{M}}\!\varvec{P}\cdot \varvec{N}^{\text {B}}+\varvec{\zeta }^{\text {B}}$ with $\zeta _{x}^{\text {A}}=0$ and $\zeta _{y}^{\text{ A }}=-\zeta _{y}^{\text {B}}$ following the balance of forces. Accordingly, the volume average of the Piola stress reads

$$\begin{aligned} \langle {\varvec{P}} \rangle&= \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\partial \mathcal {B}_\text {0}} \varvec{t}{}^{\text {p}}_\text {0}\otimes \varvec{X} \, \text{ d }A = \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\partial \mathcal {B}_\text {0}} [{}^\text {{M}}\!\varvec{P} \cdot \varvec{N}] \otimes \varvec{X} \, \text{ d }A \nonumber \\&\quad \, + \displaystyle \frac{1}{\mathscr {V}_\text {0}} \sum _{i=\text {A},\text {B}} \varvec{\zeta }^{i} \otimes \varvec{X}^{i} \, \delta A^{i} \nonumber \\&= {}^\text {{M}}\!\varvec{P} +\displaystyle \frac{1}{\mathscr {V}_\text {0}}\Bigg \{ \begin{bmatrix} 0 \\ \zeta ^{\text {A}}_{y} \end{bmatrix} \otimes \begin{bmatrix} {X}_x^{\text {A}} \\ {X}_y^{\text {A}} \end{bmatrix} + \begin{bmatrix} 0 \\ \zeta ^{\text {B}}_{\text {y}} \end{bmatrix} \otimes \begin{bmatrix} {X}_x^{\text {B}} \\ {X}_y^{\text {B}} \end{bmatrix} \Bigg \} \, \delta A \nonumber \\&= {}^\text {{M}}\!\varvec{P} + \displaystyle \frac{1}{\mathscr {V}_\text {0}} \begin{bmatrix} 0&0 \\ \zeta _{y}^{\text {A}} {X}_x^{\text {A}} + \zeta _{y}^{\text {B}} {X}_x^{\text {B}}&\zeta _{y}^{\text {A}} {X}_y^{\text {A}} + \zeta _{y}^{\text {B}} {X}_y^{\text {B}} \end{bmatrix} \, \delta A \, , \end{aligned}$$

(8)

assuming that the effective nodal areas of A and B are identical and equal to $\delta A$. As we will see shortly, this assumption does not restrict the applicability of the presented framework and is made here only for the sake of brevity. In order to ensure that the Dirichlet part is under the same traction as prescribed on the Neumann part, both $\zeta _{y}^{\text {A}}$ and $\zeta _{y}^{\text {B}}$ must always vanish. The positions of A and B on the material configuration are arbitrary. A simple concrete setting is to assign point A to [0,0] and point B to [1,0], as illustrated in Fig. 3. Inserting these coordinates into the relation (8) yields

$$\begin{aligned} \langle {\varvec{P}} \rangle = {}^\text {{M}}\!\varvec{P} + \displaystyle \frac{1}{\mathscr {V}_\text {0}} \begin{bmatrix} 0&0 \\ \zeta _{y}^{\text {B}}&0 \end{bmatrix} \, \delta A \, , \end{aligned}$$

(9)

from which the required condition to suppress the spurious traction component $\zeta _{y}^{\text {B}}$ is derived as

$$\begin{aligned} \zeta _{y}^{\text {B}} \overset{!}{=} 0 \quad \Leftrightarrow \quad \langle {P_{yx}} \rangle - {}^\text {{M}}\!P_{yx} \overset{!}{=} 0\,. \end{aligned}$$

(10)

Note that the effective nodal area $\delta A$ is solely introduced to relate the tractions to the forces and consequently, their balance. More importantly, the effective nodal area $\delta A$ vanishes from the condition (10) which is crucial from a numerical implementation viewpoint. One can show that the effective nodal areas of A and B do not have to be identical and thus, the proposed methodology holds for non-regular meshes, as well. Satisfying (10), ensures the uniform distribution of traction ${}^\text {{M}}\!{\varvec{P}}\cdot \varvec{N}$ over the entire boundary of the RVE. In order to fulfill (10), we successively update the current position of B in the y direction, denoted $\eta$, until it no longer introduces a spurious traction.

Fig. 3

Graphical illustration of the TBC implementation setting. We prescribe and update ${}^\text {{M}}\!{\varvec{P}} \cdot \varvec{N}$ and $\eta$ iteratively until $\langle {\varvec{F}} \rangle -\varvec{{}^\text {{M}}\!{F}} \overset{!}{=} \varvec{0}$ and $\zeta _{y}^{\text {B}} \overset{!}{=} 0$ are satisfied

In addition to the condition (10), the condition $\langle {\varvec{F}} \rangle -{}^\text {{M}}\!{\varvec{F}} \overset{!}{=} \varvec{0}$ must be satisfied at the same time. These conditions are inserted into an error vector denoted $\varvec{\Omega }$ which is a non-linear function of ${}^\text {{M}}\!\varvec{P}$ and $\eta$

$$\begin{aligned} \varvec{\Omega }({}^\text {{M}}\!\varvec{P},\eta ) = [\langle {\varvec{F}} \rangle - {}^\text {{M}}\!\varvec{F}, \zeta _{y}^{\text {B}}]{}^{\mathrm {t}}\overset{!}{=} \varvec{0}\, . \end{aligned}$$

(11)

The consistent linearization of this non-linear vector function reads

$$\begin{aligned} \varvec{\Omega }({}^\text {{M}}\!\varvec{P}_{i+1}, \eta _{i+1})= & {} \varvec{\Omega }({}^\text {{M}}\!\varvec{P}_{i}, \eta _{i}) + \displaystyle \frac{\partial \varvec{\Omega }}{\partial {}^\text {{M}}\!\varvec{P}}\mid _{i} \, : \Delta {}^\text {{M}}\!\varvec{P}_{i} \nonumber \\&+ \displaystyle \frac{\partial \varvec{\Omega }}{\partial \eta }\mid _{i}\Delta \eta _{i} \overset{!}{=}\varvec{0}\, , \end{aligned}$$

(12)

from which the increments $\Delta {}^\text {{M}}\!\varvec{P}_{i}$ and $\Delta \eta _{i}$ are obtained and the state is updated according to ${}^\text {{M}}\!\varvec{P}_{i+1} = {}^\text {{M}}\!\varvec{P}_{i} + \Delta {}^\text {{M}}\!\varvec{P}_{i}$ and $\eta _{i+1} = \eta _{i} + \Delta \eta _{i}$ where i is the iteration step. The system of Eq. (12) can be presented in matrix format as

The algorithm to implement TBC is given in Algorithm 1.

Positions of A and B are arbitrary Changing the initial positions of the points A and B would lead essentially to the same condition as (10). For example, assume the configuration in which point A is assigned to [1,1] and point B is assigned to [0.5,0], as shown in Fig. 4. Based on this setting and using the relation (8), the volume average of the Piola stress reads

$$\begin{aligned} \begin{aligned} \langle {\varvec{P}} \rangle&= {}^\text {{M}}\!\varvec{P} + \displaystyle \frac{1}{\mathscr {V}_\text {0}} \left[ \begin{array}{lc} 0 &{}\quad 0 \\ \zeta _{y}^{\text {A}}+0.5\zeta _{y}^{\text {B}} &{} \zeta _{y}^{\text {A}} \end{array}\right] \delta A\\&= {}^\text {{M}}\!\varvec{P} + \displaystyle \frac{1}{\mathscr {V}_\text {0}} \left[ \begin{array}{lc} 0 &{}\quad 0 \\ -0.5\zeta _{y}^{\text {B}} &{} -\zeta _{y}^{\text {B}} \end{array}\right] \, \delta A \, , \end{aligned} \end{aligned}$$

in which the equality $\zeta _{y}^{\text {A}}=-\zeta _{y}^{\text {B}}$ is considered. In order to ensure uniform distribution of the traction over the entire boundary of the RVE, the condition

$$\begin{aligned} \zeta _{y}^{\text {B}} \overset{!}{=} 0 \quad \Leftrightarrow \quad \langle {P_{yx}} \rangle - {}^\text {{M}}\!P_{yx} \overset{!}{=} 0 \quad \text {or} \quad \langle {P_{yy}} \rangle - {}^\text {{M}}\!P_{yy} \overset{!}{=} 0\,, \end{aligned}$$

must be met which clearly shows that the condition $\zeta _{y}^{\text {B}} \overset{!}{=} 0$ is independent of the choice of the constraints A and B.

Fig. 4

Another example of TBC implementation setting. Positions of the constraints are arbitrary. All different choices of A and B would essentially lead to the same condition to be satisfied to guarantee uniform distribution of tractions over the boundary of the micro-structure

The proposed framework extends readily to 3D Six degrees of freedoms need be fixed to prevent rigid body motions in three dimensions. Figure 5 illustrates how to implement TBC for three-dimensional problems. Similar to the two-dimensional case, we assign homogeneous Dirichlet boundary condition to point A in x, y and z directions to eliminate translational rigid body motions and semi-Dirichlet boundary conditions to B in x direction, C in y direction and D in z direction to remove rotational rigid body motions. We update the locations of B, C and D successively until a uniform distribution of traction over the boundary of the RVE is achieved. As long as B, C and D have not reached their final positions, spurious forces on the Dirichlet parts of the boundary are observed. The nodal tractions on points A, B, C and D are $\varvec{t}^{i} = {}^\text {{M}}\!\varvec{P}\cdot \varvec{N}^{i}+\varvec{\zeta }^{i}$ for $i=\text {A, B, C, D}$. Accordingly, the volume average of the Piola stress reads

$$\begin{aligned} \begin{aligned} \langle {\varvec{P}} \rangle&= \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\partial \mathcal {B}_\text {0}} \varvec{t}{}^{\text {p}}_\text {0}\otimes \varvec{X} \, \text{ d }A = \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\partial \mathcal {B}_\text {0}} [{}^\text {{M}}\!\varvec{P} \cdot \varvec{N}] \otimes \varvec{X} \, \text{ d }A\\&\quad + \displaystyle \frac{1}{\mathscr {V}_\text {0}} \sum _{i=\text {A},\text {B},\text {C},\text {D}} \varvec{\zeta }^{i} \otimes \varvec{X}^{i} \, \delta A^{i} \,, \end{aligned} \end{aligned}$$

which can be expanded as

$$\begin{aligned} \begin{aligned} \langle {\varvec{P}} \rangle&= {}^\text {{M}}\!\varvec{P} +\displaystyle \frac{1}{\mathscr {V}_\text {0}}\Bigg \{ \begin{bmatrix} \zeta ^{\text {A}}_{x} \\ \zeta ^{\text {A}}_{y} \\ \zeta ^{\text {A}}_{z} \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} \zeta ^{\text {B}}_{x} \\ 0 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} + \begin{bmatrix} 0 \\ \zeta ^{\text {C}}_{y} \\ 0 \end{bmatrix}\\&\quad \,\otimes \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0 \\ \zeta ^{\text {D}}_{z} \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} \Bigg \} \, \delta A = {}^\text {{M}}\!\varvec{P} + \displaystyle \frac{1}{\mathscr {V}_\text {0}} \begin{bmatrix} 0&0&\zeta ^{\text {B}}_{x}\\ \zeta ^{\text {C}}_{y}&0&0\\ 0&\zeta ^{\text {D}}_{z}&0 \end{bmatrix} \, \delta A \, , \end{aligned} \end{aligned}$$

from which the required conditions to suppress the spurious forces are obtained as

$$\begin{aligned} \begin{aligned}&\zeta _{x}^{\text {B}} \overset{!}{=} 0 \quad \Leftrightarrow \quad \langle {P_{xz}} \rangle - {}^\text {{M}}\!P_{xz} \overset{!}{=} 0 \quad ,\\&\zeta _{y}^{\text {C}} \overset{!}{=} 0 \quad \Leftrightarrow \quad \langle {P_{yx}} \rangle - {}^\text {{M}}\!P_{yx} \overset{!}{=} 0\quad , \\&\zeta _{z}^{\text {D}} \overset{!}{=} 0 \quad \Leftrightarrow \quad \langle {P_{zy}} \rangle - {}^\text {{M}}\!P_{zy} \overset{!}{=} 0 \, . \end{aligned} \end{aligned}$$

Fig. 5

Graphical illustration of the TBC implementation setting in three-dimensional problems. We prescribe and update ${}^\text {{M}}\!{\varvec{P}} \cdot \varvec{N}$, $\eta ^{\text {B}}$, $\eta ^{\text {C}}$ and $\eta ^{\text {D}}$ iteratively until $\langle {\varvec{F}} \rangle -\varvec{{}^\text {{M}}\!{F}} \overset{!}{=} \varvec{0}$, $\zeta _{x}^{\text {B}} \overset{!}{=} 0$, $\zeta _{y}^{\text {C}} \overset{!}{=} 0$ and $\zeta _{z}^{\text {D}} \overset{!}{=} 0$ are satisfied. Note, point D is free to move in x and y directions

In order to satisfy these conditions, we prescribe and successively update the positions of the points B, C and D in x, y and z directions, respectively. Hence, the error vector reads $\varvec{\Omega }({}^\text {{M}}\!\varvec{P},\eta ^{\text {B}},\eta ^{\text {C}},\eta ^{\text {D}}) = [\langle {\varvec{F}} \rangle - {}^\text {{M}}\!\varvec{F}, \zeta ^{\text {B}}_{x},\zeta ^{\text {C}}_{y},\zeta ^{\text {D}}_{z}]{}^{\mathrm {t}}\overset{!}{=} \varvec{0}$ with $\eta ^{\text {B}}, \eta ^{\text {C}} \text { and } \eta ^{\text {D}}$ being the prescribed displacements on points B, C and D. The consistent linearization of the error function at iteration step i reads

$$\begin{aligned}&\varvec{\Omega }({}^\text {{M}}\!\varvec{P}_{i+1},\eta ^{\text {B}}_{i+1},\eta ^{\text {C}}_{i+1},\eta ^{\text {D}}_{i+1}) = \varvec{\Omega }({}^\text {{M}}\!\varvec{P}_{i}, \eta _{i}^{\text {B}},\eta _{i}^{\text {C}},\eta _{i}^{\text {D}})\\&\quad +\, \displaystyle \frac{\partial \varvec{\Omega }}{\partial {}^\text {{M}}\!\varvec{P}}\mid _{i}\, :\Delta {}^\text {{M}}\!\varvec{P}_{i} + \displaystyle \frac{\partial \varvec{\Omega }}{\partial \eta ^{\text {B}}}\mid _{i}\Delta \eta _{i}^{\text {B}}\\&\quad +\, \displaystyle \frac{\partial \varvec{\Omega }}{\partial \eta ^{\text {C}}}\mid _{i}\Delta \eta _{i}^{\text {C}} + \displaystyle \frac{\partial \varvec{\Omega }}{\partial \eta ^{\text {D}}}\mid _{i}\Delta \eta _{i}^{\text {D}} \overset{!}{=}\varvec{0}\,, \end{aligned}$$

which furnishes the iterative increments $\Delta {}^\text {{M}}\!\varvec{P}_{i}$, $\Delta \eta _{i}^{\text {B}}$, $\Delta \eta _{i}^{\text {C}}$, $\Delta \eta _{i}^{\text {D}}$ that are used to update the state according to ${}^\text {{M}}\!\varvec{P}_{i+1} = {}^\text {{M}}\!\varvec{P}_{i} + \Delta {}^\text {{M}}\!\varvec{P}_{i}$, $\eta _{i+1}^{\text {B}} = \eta _{i}^{\text {B}} + \Delta \eta _{i}^{\text {B}}$, $\eta _{i+1}^{\text {C}} = \eta _{i}^{\text {C}} + \Delta \eta _{i}^{\text {C}}$ and $\eta _{i+1}^{\text {D}} = \eta _{i}^{\text {D}} + \Delta \eta _{i}^{\text {D}}$.

The proposed strategy reduces to the Lagrange multiplier algorithm A commonly accepted strategy to implement TBC is based on imposing the prescribed macro deformation gradient via a Lagrange multiplier [70] briefly formulated in Appendix A, see also [78–80]. Firstly, note that our proposed methodology would become identical to the Lagrange multiplier algorithm if we insert the condition (11) into the residual vector and update the displacements, macro Piola stress and $\eta$ simultaneously. Roughly speaking, we regard the residual and the condition (11) in a staggered manner while the Lagrange multiplier algorithm [70] solves both systems of equations in a monolithic sense. Secondly and more importantly, the applicability of our proposed approach is not limited to the strain-driven computational homogenization but, it is also capable of efficiently dealing with stress-driven homogenization. The Lagrange multiplier algorithm is intrinsically developed for strain-driven homogenization. We have implemented the approach in [70], too and both methods obviously lead to identical results.

Stress-driven homogenization follows naturally In the context of the stress-driven homogenization, the macro Piola stress is the input of the problem. Therefore, no iteration for updating the macro Piola stress is required. However, the displacement to be prescribed on the semi-Displacement constraints has to be updated until uniform distribution of the traction over the boundary of the RVE is guaranteed. Hence, condition (11) and the system of Eq. (12) reduce to one single condition

$$\begin{aligned} \Omega (\eta ) = \zeta _{y}^{\text {B}} \overset{!}{=} 0 \,, \end{aligned}$$

that is satisfied iteratively as

$$\begin{aligned} \Omega (\eta _{i+1}) = \Omega (\eta _{i}) + \displaystyle \frac{\partial \Omega }{\partial \eta }\mid _{i}\Delta \eta _{i} \overset{!}{=}0 \quad , \quad \eta _{i+1} = \eta _{i} + \Delta \eta _{i}\,, \end{aligned}$$

The algorithm to implement TBC in a stress-driven computational homogenization is given in Alg. 2. Here, we have only considered two-dimensional problems and the setting illustrated in Fig. 3. However, the given algorithm remains formally identical for two-dimensional problems with different settings and three-dimensional problems.

Semi-Dirichlet boundary conditions do not update in small-strain setting Macroscopic balance of angular momentum manifests itself in vanishing spurious forces $\varvec{\zeta }$. In a finite deformation setting, the macroscopic balance of angular momentum reads ${}^\text {{M}}\!{\varvec{P}}\cdot {}^\text {{M}}\!{\varvec{F}}{}^{\mathrm {t}}={}^\text {{M}}\!{\varvec{F}}\cdot {}^\text {{M}}\!{\varvec{P}}{}^{\mathrm {t}}$ and carries geometrical information via ${}^\text {{M}}\!{\varvec{F}} = \langle {\varvec{F}} \rangle$. This interpretation is particularly important to explain an analogous strategy to prescribe TBC for strain-driven homogenization in a small strains. For a small-strain setting, the macroscopic balance of angular momentum reads ${}^\text {{M}}\!{\varvec{\sigma }} = {}^\text {{M}}\!{\varvec{\sigma }}{}^{\mathrm {t}}$ with $\varvec{\sigma }$ being the linearized symmetric stress at the material configuration often referred to as Cauchy stress. At small strains, the spurious forces must vanish to guarantee the symmetry of Cauchy stresses and equivalently, or rather consequently in this case, to satisfy the balance of angular momentum. More precisely, in contrast to the finite deformation setting, the balance of angular momentum at small strains does not contain any geometrical quantity. Thus, vanishing spurious forces do not furnish any information regarding the update of the semi-Dirichlet boundary condition nor it is required to update the semi-Dirichlet boundary condition, at all, since the macroscopic balance of angular momentum is satisfied a priori.

Semi-Dirichlet boundary conditions intrinsically utilize the uniqueness of the solution It is clear that the proposed strategy heavily relies on the uniqueness of the solution to the problem. For instance, if non-uniqueness arises due to bifurcation instabilities, this methodology captures only one of the possible solutions. It is however possible to perturb the current position of the semi-Dirichlet constraints to obtain all the possible solutions or to employ the eigenvalue analysis to track the solution of interest or the one associated to the lowest energy mode [81, 82].

The proposed methodology is fully compatible with $\textit{FE}^2$ methods The current manuscript elaborates on the implementation of semi-Dirichlet constraints in a computational homogenization setting and avoids the discussion on computing the consistent tangents within a full $\hbox {FE}^2$ framework. This is simply due to the fact that the associated $\hbox {FE}^2$ framework is not influenced by our proposed methodology. In our recent review article [55], we have shown how Semi-Dirichlet boundary condition compares to other canonical boundary conditions in a complete $\hbox {FE}^2$ context via numerical examples.

Fig. 6

Mesh set-ups of the two- and three-dimensional samples

4 Numerical examples

This section demonstrates the performance of the proposed algorithm to implement TBC via a series of numerical examples. We conduct our numerical analysis on both two-dimensional numerical examples corresponding to fiber reinforced composites as well as a three-dimensional micro-structure representing particle reinforced composites. In particular, we study the evolution of $\eta$ for different macro deformation gradients. More specifically, the settings illustrated in Figs. 3 and 5 are employed and the value of $\eta$ for two-dimensional micro-structures and the values of $\eta ^{\text {B}}$, $\eta ^{\text {C}}$ and $\eta ^{\text {D}}$ for the three-dimensional micro-structure are investigated. Moreover, we investigate the evolution of $f:=\langle {P_{yx}} \rangle -{}^\text {{M}}\!{P}_{yx}$ according to Eq. (9) with respect to the macro deformation gradient for the case that Dirichlet boundary condition is used to eliminate rotational rigid body motions instead of semi-Dirichlet boundary conditions. The existence of a non-zero f clearly demonstrates the importance of semi-Dirichlet boundary conditions as compared to the classical Dirichlet boundary conditions. Obviously, f vanishes iteratively when semi-Dirichlet boundary conditions are utilized. The prescribed macroscopic deformation gradient of interest corresponds to simple-shear in the xy-plane of the form ${}^\text {{M}}\!\varvec{F} = \varvec{I} + {}^\text {{M}}\!{F}_{xy} \, \varvec{e}_x \otimes \varvec{e}_y$ with ${}^\text {{M}}\!{F}_{xy}$ representing the shear. In addition, the convergence rate of the residual vector (6) and the error vector (11) are detailed. The inclusion volume fraction is assumed to be 25 % for all the examples. The samples are discretized for simplicity using bilinear and trilinear finite elements in 2D and 3D problems, respectively. The samples and the associated finite element discretizations are shown in Fig. 6.

The energy density and the associated constitutive response of the micro-samples are assumed to be known. For the sake of presentation, both the inclusion and the matrix are assumed to behave according to a hyperelastic model with the free energy density function $\psi$ per unit volume in the material configuration of the form

$$\begin{aligned}&\psi = \psi (\varvec{F}) = \tfrac{1}{2} \, \mu \, [ \varvec{F}:\varvec{F} - 3 - 2 \, \log J ]+\tfrac{1}{2} \, \lambda \, \log ^{2} J \quad \text {with}\nonumber \\&J = \det \varvec{F} \,, \end{aligned}$$

(13)

and the associated Piola stress

$$\begin{aligned} \varvec{P} := \displaystyle \frac{\partial \psi }{\partial \varvec{F}} = \varvec{P} (\varvec{F}) = \mu \, [ \varvec{F} - \varvec{F}{}^{ -\text {t}}] + \lambda \, \log J \, \varvec{F}{}^{ -\text {t}}\,, \end{aligned}$$

(14)

with $\mu$ and $\lambda$ denoting the Lamé parameters. The material parameters of the matrix are assumed the shear modulus $\mu ^{\text {m}}$ = 8.0 and the Poisson’s ratio $\nu ^{\text {m}}$ = 0.3. The same Poisson’s ratio is chosen for the inclusion material. Both the inclusion and the matrix are assumed to behave according to the free energy density (13). The inclusion to matrix stiffness ratio is denoted r. That is, r=10 for micro-structures with inclusions 10 times stiffer than the matrix and r=0.1 for the ones containing inclusions 10 times more compliant to the matrix. Perfect bonding between the matrix and the inclusion is assumed. All the examples are solved using our in-house finite element code in C++ syntax. The solution procedure is robust and for all examples shows the asymptotic quadratic rate of convergence associated with the Newton–Raphson scheme.

Fig. 7

Evolution of $\eta$ (solid line) and f (dashed line) for three different two-dimensional micro-structures undergoing 0 up to 250 % simple-shear deformation. The parameter $\eta$ is the required displacement at the semi-Dirichlet boundary condition so that the spurious forces vanish. The parameter f manifests the force that would have been generated if a classical Dirichlet boundary condition was used instead of the newly proposed semi-Dirichlet boundary condition. Both cases of more compliant inclusion (left) and stiffer inclusion (right) are considered. The deformation modes depicted below the plots, from left to right, correspond to the results of the TBC for ${}^\text {{M}}\!{F}_{xy}=$ 0.625, ${}^\text {{M}}\!{F}_{xy}=$ 1.3 and ${}^\text {{M}}\!{F}_{xy}=$ 1.875, respectively

4.1 Two-dimensional micro-structures

Figure 7 illustrates the evolution of $\eta$ and f for two-dimensional micro-samples undergoing 0 up to 250 % simple-shear deformation in the xy-plane for $r=0.1$ and $r=10$. Three different micro-samples (a), (b) and (c) in Fig. 6, are considered. The numerical results show that the evolution of $\eta$ is non-uniform and very complex, in general. The value $\eta$ depends on the amount of the macroscopic deformation, position of the inclusion as well as the inclusion to matrix stiffness ratio. In particular, it is observed that when $r=0.1$, irrespective of the prescribed deformation value, $\eta$ remains always positive for the micro-sample (a). In contrast, the values of $\eta$ obtained for the micro-sample (c) are always negative for all the prescribed deformations. An opposite behavior is observed for $r=10$. For both cases of $r=0.1$ and $r=10$ and for all the deformation values, $\eta$ is greater for micro-sample (c) compared to the micro-sample (a). In particular, when 250 % of deformation is prescribed on micro-sample (c), the value of $\eta$ approaches $-0.28$ for $r=0.1$ and 0.35 for $r=10$. Another interesting point is that $\eta$ can vanish even for nonzero deformations. Furthermore, the evolution of $f:=\langle {P_{yx}} \rangle -{}^\text {{M}}\!{P}_{yx}$ is illustrated. The parameter f manifests the force that would have been generated if a classical Dirichlet boundary condition was used instead of the newly proposed semi-Dirichlet boundary condition. As expected, f evolves oppositely to $\eta$ and f reaches zero when $\eta$ vanishes.

Fig. 8

Evolution of xy-component of macro Piola stress and $\eta$ for the three-dimensional micro-structure containing a spherical inclusion at its center and undergoing 0 up to 250 % simple-shear deformation. Both cases of more compliant inclusion (top) and stiffer inclusion (bottom) are considered. The depicted deformation modes, from left to right, correspond to the results of the TBC for ${}^\text {{M}}\!{F}_{xy}=$ 0.625, ${}^\text {{M}}\!{F}_{xy}=$ 1.3, ${}^\text {{M}}\!{F}_{xy}=$ 1.875 and ${}^\text {{M}}\!{F}_{xy}=$ 2.5, respectively

4.2 Three-dimensional micro-structures

The main objective of this section is to demonstrate the performance of the proposed scheme for three-dimensional problems using a micro-sample with a spherical inclusion in the center. The evolution of both ${}^\text {{M}}\!{P}_{xy}$ and $\eta$ versus the prescribed shear value ${}^\text {{M}}\!{F}_{xy} \in [0,2.5]$ are investigated. Figure 8 illustrates that the overall response of the material is nearly linear for both cases of $r=0.1$ and r = 10. Moreover, the displacement to be prescribed at point B in x direction is always vanishing for this particular load case. However, a very wide range of values of $\eta$ are required to be prescribed at semi-Displacement constraints D and C.

Table 1 Convergence behavior of the residual vector (6) and the error vector (11) for two different values of simple-shear macro deformation gradient with ${}^\text {{M}}\!{F}_{xy}=$ 0.1 and ${}^\text {{M}}\!{F}_{xy}=$ 0.5. Both cases of $r=0.1$ and $r=10$ are considered

4.3 Convergence behavior

Finally, in order to demonstrate the detailed performance of our proposed algorithm, we study the convergence behavior of both residual vector (6) and the error vector (11) when a two-dimensional micro-structure undergoes 10 % and 50 % of simple-shear deformation. Similar to the previous sections, both cases of $r=0.1$ and $r=10$ are considered. Here, the two-dimensional micro-sample containing a circular inclusion at its center is chosen.

As reported in Table 1, the convergence rate of both the residual vector and the error vector are asymptotically quadratic. When 50 % of simple-shear deformation is prescribed, the macro Piola stress, which is initially zero, is updated 4 times until it reaches the correct solution. Moreover, after the first update of the macro Piola stress, 9 iterations for $r=10$ and 8 iterations for $r=0.1$ are required for the residual vector to be converged. When 10 % simple-shear deformation is prescribed, a better convergence trend is observed. In this case, 3 updates of the initial guess of the macro Piola stress is sufficient for the problem to converge. We emphasize that for all the cases reported in Table 1, the problem is solved in a single load increment and convergence is achieved in less than 1 second on an average laptop. Obviously, the convergence trend improves significantly for a larger number of load steps.

5 Concluding remarks

In this manuscript, we have presented a novel approach to implement TBC in a computational homogenization framework at finite strains. The main issue with the implementation of TBC is to deal with the singularity of the stiffness matrix due to rigid body motions. Our proposed algorithm is based on employing semi-Dirichlet boundary conditions to eliminate the rigid body motions. Semi-Dirichlet boundary conditions are non-homogeneous Dirichlet-type constraints that simultaneously satisfy the Neumann-type conditions.

The commonly accepted strategy to implement TBC in a strain-driven homogenization framework is given by Miehe [70]. This approach is essentially based on employing a variational formulation and imposing the prescribed macro deformation gradient via a Lagrange multiplier. While this methodology is suitable for strain-driven computational homogenization, it cannot be readily extended to stress-driven computational homogenization. This lack of uniformity has been the primary motivation of the present contribution. Our main objective is to provide a computational algorithm for constant traction boundary conditions suitable for both strain-driven as well as stress-driven homogenization. The performance of the proposed scheme is demonstrated via a series of numerical examples.

In summary, this manuscript presents an attempt to shed light on the micro-to-macro transition for both stress-driven as well as strain-driven homogenization frameworks. This allows us to predict the overall material response via computational homogenization using TBC. We believe that this generic framework is broadly applicable to enhance our understanding of the behavior of continua with a large variety of applications.

Appendix: Implementation of TBC via the Lagrange multiplier method

This methodology is essentially based on solving the incremental minimization problem of homogenization

$$\begin{aligned} {}^\text {{M}}\!{W}({}^\text {{M}}\!{\varvec{F}})= & {} \inf _{\mathbf {d}} {}^\text {{M}}\!{W}(\mathbf {d}) \qquad \text {with} \nonumber \\ {}^\text {{M}}\!{W}(\mathbf {d})= & {} \displaystyle \frac{1}{\mathscr {V}_\text {0}}\int _{\mathcal {B}_\text {0}} W(\varvec{F};\varvec{X}) \, \text{ d }V\, , \end{aligned}$$

(15)

with $\mathbf {d}$ being the unknown global vector of deformations which minimizes the average incremental energy of the micro-structure for a given macro deformation gradient. In order to impose the constraint $\langle {\varvec{F}} \rangle - {}^\text {{M}}\!{\varvec{F}} \overset{!}{=} \varvec{0}$, the Lagrange multiplier method is used which yields the Lagrangian

$$\begin{aligned} {{L}}(\mathbf {d}, \varvec{\lambda }; {}^\text {{M}}\!{\varvec{F}}) = {}^\text {{M}}\!{W}(\mathbf {d}) - \varvec{\lambda }: [\langle {\varvec{F}} \rangle - {}^\text {{M}}\!{\varvec{F}}]\, , \end{aligned}$$

(16)

with $\varvec{\lambda }$ being the Lagrange multiplier. It can be readily verified that

$$\begin{aligned} \displaystyle \frac{\partial {{{L}}(\mathbf {d}, \varvec{\lambda }; {}^\text {{M}}\!{\varvec{F}})}}{\partial {}^\text {{M}}\!{\varvec{F}}} = {}^\text {{M}}\!{\varvec{P}} \qquad \text {with} \qquad {}^\text {{M}}\!{\varvec{P}} = \varvec{\lambda }\,. \end{aligned}$$

(17)

Next, the derivatives of the Lagrangian functional with respect to its variables are set to zero and the following system of equations is obtained.

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial {{{L}}(\mathbf {d}, {}^\text {{M}}\!{\varvec{P}};{}^\text {{M}}\!{\varvec{F}})}}{\partial \mathbf {d}} = \varvec{0}~~ \Rightarrow ~~ \underbrace{\displaystyle \frac{\partial {{}^\text {{M}}\!{W}(\mathbf {d})}}{\partial {\mathbf {d}}}}_{\mathbf {R}_{\varvec{\text {int}}}} - \underbrace{{}^\text {{M}}\!{\varvec{P}}: \displaystyle \frac{\partial {\langle {\varvec{F}} \rangle }}{\partial {{\mathbf {d}}}}}_{\mathbf {R}_{\varvec{\text {ext}}}} = \varvec{0}\,, \\ \displaystyle \frac{\partial {{{L}}(\varvec{\mathbf {d}}, {}^\text {{M}}\!{\varvec{P}}; {}^\text {{M}}\!{\varvec{F}})}}{\partial {}^\text {{M}}\!{\varvec{P}}} = \varvec{0}~~ \Rightarrow ~~ {}^\text {{M}}\!{\varvec{F}}-\langle {\varvec{F}} \rangle = \varvec{0}\,. \end{array}\right. } \end{aligned}$$

(18)

Linearization of this system of equations yields

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbf {R}_{\varvec{int}}}(\mathbf {d}_{i+1}) - {\mathbf {R}_{\varvec{ext}}}({}^\text {{M}}\!{\varvec{P}}_{i+1}) = {\mathbf {R}_{\varvec{int}}}(\mathbf {d}_{i}) - {\mathbf {R}_{\varvec{ext}}}({}^\text {{M}}\!{\varvec{P}}_{i}) \\ \quad +\displaystyle \frac{\partial {\mathbf {R}_{\varvec{int}}}}{\partial {\mathbf {d}}}\mid _{i} \cdot \, \Delta \mathbf {d}_{i} - \displaystyle \frac{\partial \mathbf {R}_{\varvec{ext}}}{\partial {}^\text {{M}}\!{\varvec{P}}}\mid _{i} \, : \Delta {}^\text {{M}}\!{\varvec{P}}_{i} \overset{!}{=} \varvec{0}\,, \\ {}^\text {{M}}\!{\varvec{F}}-\langle {\varvec{F}} \rangle (\mathbf {d}_{i+1}) = {}^\text {{M}}\!{\varvec{F}}-\langle {\varvec{F}} \rangle (\mathbf {d}_{i}) -\displaystyle \frac{\partial \langle {\varvec{F}} \rangle }{\partial {\mathbf {d}}}\mid _{i} \cdot \, \Delta \mathbf {d}_{i} \overset{!}{=} \varvec{0}\,. \end{array}\right. } \end{aligned}$$

(19)

where $\mathbf {K} = \partial {\mathbf {R}_{\varvec{\text {int}}}}/\partial {\mathbf {d}}$ is the assembled tangent stiffness matrix. In order to represent the system of Eq. (19) in matrix format, all tensor products should be reformulates as matrix multiplications. To do so, we first derive the nodal equivalents of the global matrices $\partial \mathbf {R}_{\varvec{\text {ext}}}/\partial {}^\text {{M}}\!{\varvec{P}}$ and $\partial \langle {\varvec{F}} \rangle /\partial {\mathbf {d}}$ as

$$\begin{aligned}&\displaystyle \frac{\partial }{\partial {}^\text {{M}}\!{\varvec{P}}}({}^\text {{M}}\!{\varvec{P}}:\displaystyle \frac{\partial \langle {\varvec{F}} \rangle }{\partial {\varvec{\varphi }^{J}}}) = \varvec{I} \otimes \langle {\text{ Grad }{N^{J}}} \rangle \qquad \text {and} \nonumber \\&\displaystyle \frac{\partial \langle {\varvec{F}} \rangle }{\partial {\varvec{\varphi }^{J}}} = \varvec{I} \, \overline{\otimes }\,\langle {\text{ Grad }{N^{J}}} \rangle \, , \end{aligned}$$

(20)

respectively. The non-standard tensor product $\overline{\otimes }$ of a second-order tensor $\varvec{A}$ and a vector $\varvec{b}$ is the third-order tensor $\mathbbm {D} = \varvec{A} \, \overline{\otimes }\, \varvec{b}$ with components ${D}_{ijk} = {A}_{ik} {b}_{j}$. Next, the double contraction of the third-order tensor (20)$_{1}$ with $\Delta {}^\text {{M}}\!{\varvec{P}}$ and the dot product of the third-order tensor (20)$_{2}$ with nodal $\Delta \varphi ^{J}$ in matrix format are derived as

$$\begin{aligned}&\varvec{I} \otimes \langle {\text{ Grad }{N^{J}}} \rangle : \Delta {}^\text {{M}}\!{\varvec{P}} = \Delta {}^\text {{M}}\!{\varvec{P}} \cdot \langle {\text{ Grad }N^{J}} \rangle \nonumber \\&\quad \equiv \left[ \begin{array}{llll} \langle {\text{ Grad }N^{J}} \rangle _{x} &{} \langle {\text{ Grad }N^{J}} \rangle _{y} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \langle {\text{ Grad }N^{J}} \rangle _{x} &{}\quad \langle {\text{ Grad }N^{J}} \rangle _{y} \\ \end{array}\right] \nonumber \\&\qquad \qquad \begin{bmatrix} {}^\text {{M}}\!{P}_{xx}\\ {}^\text {{M}}\!{P}_{xy}\\ {}^\text {{M}}\!{P}_{yx}\\ {}^\text {{M}}\!{P}_{yy} \end{bmatrix}\, , \end{aligned}$$

(21)

$$\begin{aligned}&\varvec{I} \, \overline{\otimes }\, \langle {\text{ Grad }{N^{J}}} \rangle \cdot \Delta \varvec{\varphi }^{J} = \Delta \varvec{\varphi }^{J} \otimes \langle {\text{ Grad }N^{J}} \rangle \nonumber \\&\quad \equiv \left[ \begin{array}{ll} \langle {\text{ Grad }N^{J}} \rangle _{x} &{}\quad 0 \\ \langle {\text{ Grad }N^{J}} \rangle _{y} &{}\quad 0 \\ 0 &{}\quad \langle {\text{ Grad }N^{J}} \rangle _{x} \\ 0 &{}\quad \langle {\text{ Grad }N^{J}} \rangle _{y} \end{array}\right] \begin{bmatrix} \Delta \varphi ^{J}_{x} \\ \Delta \varphi ^{J}_{y} \end{bmatrix}, \end{aligned}$$

(22)

respectively. Hence, the final matrix format representation of the system of Eq. (19) the reads

where n denotes the total number of nodes and $\text{ Grad }N$ is represented as $\nabla N$ for the sake of space. This system turns out to be not singular and can be solved without further modifications.