1 Introduction

Due to the complexity of the crack pattern in engineering applications, numerical methods play a crucial role in fracture analyses. In particular, finite element methods (FEMs) are used extensively in conjunction with Griffiths-type linear elastic fracture mechanics models. Among the most commonly used finite element models are the virtual crack closure technique (VCCT) [1], cohesive zone model [2] and, in more recent years, the extended finite element method (XFEM) [3, 4]. These methods explicitly represent cracks as discontinuities. Such methods usually have one or more of the following limitations: (1) They need to adjust the mesh in traditional FEMs [5]. (2) They need to introduce extra degrees of freedom (DOFs) like XFEM [6]. (3) They need the artificial introduction of criteria for crack initiation, branching and coalescence [7]. The counterpart method is to describe the crack by dispersion. In these methods, cracks are usually not tracked explicitly but locate the location or region of the crack surface according to the values of some field variables, such as phase field method [8, 9], peridynamics (PD) [10] and cracking-particle method (CPM) [11].

Phase-field method, as a widely concerned method in recent years, can simulate arbitrary propagation, branching and convergence of cracks based on the basic theory of Griffith elastic fracture mechanics [12,13,14,15]. In the phase field method, no additional discontinuity is required in the model. Instead, the distribution of cracks is approximated by a phase field variable which smoothes the crack boundary in a small area [16,17,18]. The main advantage of using phase field variable is that the evolution of fracture surface follows the solution of coupled partial differential equations (PDEs). Thus, no additional tracking of the crack surface is required. This description method of the crack surface is in sharp contrast to the complexity of many discrete fracture models and is especially beneficial to the 3D complex fracture network.

The origin of the phase field method is due to the phased phase field implementation by Francfort and Marigo [19], and Bourdin et al. [20]. Mumford and Shah [21] have derived variational formulas and energy functional for quasi-static brittle fracture. Ambrosio and Tortorelli [22] proposed the phase field approximation of Mumford-Shah potential based on C-convergence theory. Verhoosel and Borst [23] developed a phase-field model for cohesive fracture. Waisman et al. developed phase field models that are capable of capturing the ductile-brittle transition for shear band problem [24] and modeling fracture propagation of viscoelastic solids [25]. Borden et al. [26] introduced several contributions such as stress triaxiality effects to further develop phase-field models for ductile fracture. In recent years, the phase field method has been comprehensively expounded by Miehe et al. [27,28,29], and applied to complex fracture problems such as multi-field coupling and large deformation. A great deal of research work on the phase-field method to simulate crack propagation mainly focuses on quasi-static crack propagation, and mainly based on implicit time integration algorithm. Recently, dynamic crack growth has attracted more and more attention [30]. Many studies have successfully introduced dynamic crack growth into phase field models in implicit algorithms, such as the work by Spatschek et al. [31] and Hofacker et al. [32]. In terms of explicit algorithms, Ziaei-Rad and Shen [33] developed a massively explicit parallel algorithm on the graphical processing unit (GPU) to solve the problem of high computational cost in the phase field method with two-dimensional (2D) cases. Borden et al. [34] used fully parallel explicit and implicit algorithms to implement field models and combined isogeometric analysis to solve complex crack propagation problems. In this paper, we developed a 3D explicit parallel phase field model to study dynamic and quasi-static problems, and focused on the failure behavior of rock-like materials.

As typical engineering materials, rock-like materials have very complex fracture modes [35]. Cajuhi et al. [36] proposed a phase-field model to describe the coupling of pore mechanics and cracks in porous media with variable saturation, such as soil and concrete. Zhang et al. [37] introduced a modified phase field model to simulate mixed mode crack propagation in rock-like materials. Bryant and Sun [38] proposed a mixed-mode phase field fracture model in anisotropic rocks. Choo and Sun [39] coupled a pressure-sensitive plasticity model with a phase-field approach and simulated shear slip zone of the rock. As we known, the Mohr–Coulomb criterion is a very widely used criterion to describe rock-like materials failure [40]. However, up to now, there has been no research on the combination of the Mohr–Coulomb criterion and phase field method. Based on the 3D explicit phase field method, the Mohr–Coulomb failure criterion is introduced to successfully simulate the compression process of rock-like materials in this paper. The failure mode of compression-shear is captured. To improve computational efficiency, we take advantage of the ease of parallel computing with explicit time integration. The solution domain is divided into several parts, and multiple central processing units (CPUs) is used for time integration.

This paper is organized as follows: In Sect. 2, we review the basic principle and the governing equation of the phase field method and introduce the Mohr–Coulomb failure criterion for rock-like materials. In Sect. 3, we discretize the governing equations in space and time, and discuss the stable time increment of the explicit integration algorithm. In Sect. 4, three typical dynamic and quasi-static numerical examples are presented to verify the correctness and efficiency of the numerical implementation. As applications, we studied the compression-shear failure of rock-like materials in Sect. 5. The concluding remarks are given in Sect. 6.

2 Phase-field description of diffuse crack

2.1 Geometric description of phase field crack

Compared to the discrete description of the geometry of the crack, such as XFEM [3], interface element method [41], etc., the phase field method avoids artificially tracking the crack path by introducing a diffuse crack geometry. Considering the displacement field and crack phase field

$$\begin{aligned} {{\varvec{u}}}{:}\left\{ {\begin{array}{l} {{{{{\mathcal {B}}}}_0} \times {{{\mathcal {T}}}} \rightarrow \;{{{{\mathcal {B}}}}_t} \subset {{\mathbb {R}}^\delta }}\\ {\left( {{\varvec{X}},t} \right) \mapsto {{\varvec{u}}}\left( {{\varvec{X}},t} \right) } \end{array}} \right. \quad \mathrm{{and}}\quad d:\left\{ \begin{array}{l} {{{{\mathcal {B}}}}_0} \times {{{\mathcal {T}}}} \rightarrow \;\left[ {0,1} \right] \\ \left( {{{\varvec{X}}},t} \right) \mapsto d\left( {{{\varvec{X}}},t} \right) \end{array} \right. \nonumber \\ \end{aligned}$$
(1)

where \({{{{\mathcal {B}}}}_0} \subset {{{\mathbb {R}}}^\delta }\) and \({{{{\mathcal {B}}}}_t} \subset {{{\mathbb {R}}}^\delta }\) are the reference and current configurations of a material body with dimension \(\delta \in \left[ {1,2,3} \right] \) in space and \(\partial {{{{\mathcal {B}}}}_0} \subset {{{\mathbb {R}}}^{\delta - 1}}\) is its boundary, \({{{\mathcal {T}}}} \subset {{{\mathbb {R}}}^1 }\) is the time domain. The phase field d is similar to a scalar damage variable and its evolution process determines the failure of local material points. If \(d=0\), the material is unbroken; if \(d=1\), it is fully broken.

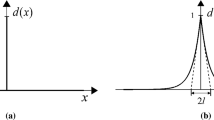
Following the idea that the crack is not a discrete phenomenon, but initiates with micro-cracks and voids, an exponential function for approximating the diffuse crack topology in one-dimensional (1D) case is introduced by Miehe et al. [42]

$$\begin{aligned} d(x) = {\mathrm{{exp}}\left( - \frac{ \left| x \right| }{l_c}\right) } \end{aligned}$$
(2)
Fig. 1
figure 1

Description of cracks in a one-dimensional bar: a diffuse crack and b sharp crack

Full size image

where \(l_c\) is a characteristic scale parameter representing the width of diffuse crack. Eq. (2) has the property \(d(0) = 1\) and \(d( \pm \infty ) = 0\) (i.e. Dirichlet-type boundary condition). The value of \(l_c\) controls the rate at which d decreases from 1 to 0 as x moves from 0 to \(\pm \infty \). When \({l_c} \rightarrow 0\), the above equation degenerates into a sharp crack, as shown in Fig. 1.

The function d(x) in Eq. (2) is the solution of a homogeneous differential equation, which is

$$\begin{aligned} d\left( x \right) - l_c^2{d''}\left( x \right) = 0 \end{aligned}$$
(3)

The weak form corresponding to the strong form in Eq. (3) can be obtained by variational principle

$$\begin{aligned} d = \mathrm{{Arg}}\left\{ {\mathop {\inf }\limits _{d \in W} I\left( d \right) } \right\} \end{aligned}$$
(4)

where \({\varGamma }_d=\{d|d(0) = 1, d( \pm \infty ) = 0\}\) is the Dirichlet-type boundary condition and

$$\begin{aligned} I\left( d \right) = \int _{{{{{\mathcal {B}}}}_0}} {\frac{1}{2}\left( {{{d}^2} + l_c^2{d'}^2} \right) \mathrm{{d}}V} \end{aligned}$$
(5)

For the case of one dimension, we have \(\mathrm{{d}}V = {\varGamma }_l \cdot \mathrm{{d}}x\). Substituting Eq. (2) into Eq. (5) leads to \(I\left( {d = {e^{ - \left| x \right| /{l_c}}}} \right) = {l_c}{\varGamma }_l\). Therefore, the crack surface density function can be introduced to assist the phase field description

$$\begin{aligned} {\varGamma }_l= & {} \frac{1}{{{l_c}}}I\left( d \right) \nonumber \\= & {} \int _{{{{{\mathcal {B}}}}_0}} {\left( \frac{1}{2l_c}{{{d}^2} + \frac{l_c}{2}{d'}^2} \right) \mathrm{{d}}V} = \int _{{{{{\mathcal {B}}}}_0}} {\gamma _l(d,d')\mathrm{{d}}V} \end{aligned}$$
(6)

where \(\gamma _l(d,d')=\frac{1}{2l_c}{{{d}^2} + \frac{l_c}{2}{{d'}^2}}\) is the crack surface density function in 1D case and can be extended to multi-dimensional case

$$\begin{aligned} {\varGamma }_l(d) = \int _{{{{{\mathcal {B}}}}_0}} {\gamma _l(d,\nabla d)\mathrm{{d}}V} \end{aligned}$$
(7)

where \(\gamma _l \left( {d,\nabla d} \right) \) is the crack surface density function in multi-dimensions

$$\begin{aligned} \gamma _l \left( {d,\nabla d} \right) = \frac{1}{{2{l_c}}}{d^2} + \frac{{{l_c}}}{2}{\left| {\nabla d} \right| ^2} \end{aligned}$$
(8)

The Euler equations of the variational principle Eq. (4) with \(I(d) = l_c {\varGamma }_l(d)\) are

$$\begin{aligned} d - l_c^2{\nabla ^2}d = 0\quad \mathrm{{in}}\;{{{{{\mathcal {B}}}}}_0}\quad \mathrm{{and}}\quad \nabla d \cdot {{\varvec{n}}_0} = 0\quad \mathrm{{on}}\;\partial {{{{\mathcal {B}}}}_0} \end{aligned}$$
(9)

where \({\varvec{n}}_0\) is the unit outer normal of the boundary \(\partial {{{{\mathcal {B}}}}_0}\).

2.2 Governing equations of phase field evolution

A generalized formulation for the evolution of the phase field \(d({{\varvec{X}}}, t)\) for different constitutive models of energetic and non-energetic driving forces is used here. We assume that the evolution of the crack surface function is driven by the constitutive crack driving function \(S(d,\dot{d}, {{{\mathcal {H}}}})\), which depends on the crack phase field d, its rate \(\dot{d}\) and the local crack driving force field \({{{\mathcal {H}}}}\). The force field \(\mathcal{H}\) depends on the full history of the considered local bulk response, such as the energy state or stress state of the solid.

$$\begin{aligned} \frac{\mathrm{{d}}}{{\mathrm{{d}}t}}{{\varGamma }_l}\left( d \right) = S\left( {d,\dot{d},{{{\mathcal {H}}}}} \right) \end{aligned}$$
(10)

The Eq. (10) can be viewed as a balance of crack surface, that equalizes the rate of the crack generation with the power of crack driving force.

2.2.1 Geometric resistance of phase field

By deriving Eq. (7) with respect to time, the geometric resistance of the phase field evolution can be obtained

$$\begin{aligned} \frac{\mathrm{{d}}}{{\mathrm{{d}}t}}{{\varGamma }_l}\left( d \right) = \frac{1}{{{l_c}}}\int _{{{{{\mathcal {B}}}}_0}} { \left[ {D_c}\dot{d} \right] \mathrm{{d}}V + } \int _{\partial {{{{\mathcal {B}}}}_0}} { \left[ \left( {{\partial _{\nabla d}}{\gamma _l} \cdot {n_0}} \right) \dot{d} \right] \mathrm{{d}}A}\nonumber \\ \end{aligned}$$
(11)

The function \(D_c\) is a dimensionless geometric resistance of phase field evolution. It is related to the variational derivative of the crack density function \(\gamma _l\) introduced in Eq. (8) by

$$\begin{aligned} {D_c}: = {l_c}{\delta _d}{\gamma _l} = d - l_c^2{\nabla ^2}d \end{aligned}$$
(12)

2.2.2 Constitutive driving function of phase field

Similar to the first term in the right side of Eq. (11), the driving source of crack propagation in Eq. (10) can be written as the power expression [42]

$$\begin{aligned} S = \frac{1}{{{l_c}}}\int _{{{{{\mathcal {B}}}}_0}} { \left\{ \left[ {\left( {1 - d} \right) {{{\mathcal {H}}}} - {{{\mathcal {R}}}}} \right] \dot{d} \right\} \mathrm{{d}}V} \end{aligned}$$
(13)

where, \({{{\mathcal {H}}}}\) is the local crack driving force and \({{{\mathcal {R}}}}\) is the local viscous crack evolution dissipation. It is assumed that both fields are governed by constitutive expressions. For the local crack driving force \({{{\mathcal {H}}}}\), we assume that it’s a function of the history of state variables \(\phi \left( {{{\varvec{X}}},s} \right) \) associated with the solids bulk response, such as stress state, energetic state or selected internal variables. For the local viscous crack evolution dissipation item \({{{\mathcal {R}}}}\), we assume that it has a simple one-to-one dependency on \(\dot{d}\)

$$\begin{aligned} {{{\mathcal {R}}}}\left( {{{\varvec{X}}},t} \right)= & {} \tilde{\mathcal{R}}\left( {\dot{d}\left( {{{\varvec{X}}},t} \right) } \right) \quad \mathrm{{and}}\quad {{{\mathcal {H}}}}\left( {{{\varvec{X}}},t} \right) = \tilde{\mathcal{H}}\left( \left( \phi \left( {{{\varvec{X}}},s} \right) ,\right. \right. \nonumber \\&\left. \left. s \in \left[ {0,t} \right] \right) \right) \end{aligned}$$
(14)

Further, we assume a linear viscous dissipation process. That is, the viscous dissipation term of crack evolution is proportional to the time derivative of phase field variable d

$$\begin{aligned} \tilde{{{\mathcal {R}}}}\left( {\dot{d}\left( {{{\varvec{X}}},t} \right) } \right) = {\tilde{\eta }} \dot{d} \end{aligned}$$
(15)

where \({\tilde{\eta }}\) is a parameter that characterizes the viscous dissipation of phase field evolution.

2.2.3 Evolution equation of crack phase field

By combining Eqs. (11–15), the strong form and boundary conditions of the governing equation for the evolution of crack phase field at a local material point can be obtained

$$\begin{aligned}&\underbrace{{\tilde{\eta }} \dot{d}}_{\mathrm{{evolution}}} = \underbrace{\left( {1 - d} \right) \tilde{{{\mathcal {H}}}}}_{\mathrm{{driving}}\;\mathrm{{force}}} - \underbrace{\left[ {d - l_c^2{\nabla ^2}d} \right] }_{\mathrm{{geometric}}\;\mathrm{{resistance}}} \quad \mathrm{{in}}\;{{{{{\mathcal {B}}}}}_0}\quad \mathrm{{and}}\quad \nabla d \nonumber \\&\quad \cdot {{\mathbf {n}}_0} = 0\quad \mathrm{{on}}\;\partial {{{{\mathcal {B}}}}_0} \end{aligned}$$
(16)

The Eq. (16) controls the evolution of time-dependent crack phase field, that is, the evolution of crack phase field depends on the difference between effective driving force \((1-d) \tilde{\mathcal{H}}\) and geometric crack resistance \(D_c\).

2.2.4 Irreversible phase field evolution conditions

The initiation and propagation of cracks is an irreversible process. Therefore, there are the following phase field evolution constraints

$$\begin{aligned} \frac{\mathrm{{d}}}{{\mathrm{{d}}t}}{{\varGamma }_l}\left( d \right) = S\left( {d,\dot{d},{{{\mathcal {H}}}}} \right) \ge 0 \end{aligned}$$
(17)

In other words, the constitutive crack driving functional is always positive. Combined with the general expression of the constitutive crack driving functional Eq. (13), the following constraints can be obtained

$$\begin{aligned} d\left( {{{\varvec{X}}},t} \right) \in [0,1], \quad \dot{d}\left( {{{\varvec{X}}},t} \right) \ge 0, \quad {{{\mathcal {H}}}}\left( {{{\varvec{X}}},t} \right) \ge 0 \end{aligned}$$
(18)

The above constraints ensure that the phase field variables can evolve in the right way within a reasonable range. To further understand the constitutive definition of the driving force \(\mathcal{H}\), considering a time-independent phase field evolution with \({\tilde{\eta }} = 0\) for a homogeneous solid with \(\Delta d = 0\). Then Eq. (16) gives a one-to-one relationship between the crack phase field d and the nominal driving force \({{{\mathcal {H}}}}\). As a consequence, conditions Eq. (18) can be recast into the following constraints

$$\begin{aligned} d = \frac{{{{\mathcal {H}}}}}{{1 + {{{\mathcal {H}}}}}} \in \left[ {0,1} \right] ,\quad \dot{d} = \frac{{\dot{{{\mathcal {H}}}}}}{{{{\left( {1 + {{{\mathcal {H}}}}} \right) }^2}}} \ge 0,\quad {{{\mathcal {H}}}} \ge 0 \end{aligned}$$
(19)

Through the above constraints, we can get the value of \({{{\mathcal {H}}}}\) corresponding to \(d=0\) (unbroken state) and \(d=1\) (fully broken state)

$$\begin{aligned} \left\{ \begin{array}{l} d = 0\quad \Leftrightarrow \quad {{{\mathcal {H}}}} = 0 \quad \;\; \Leftrightarrow \quad \tilde{{{\mathcal {H}}}}\left| {_{\mathrm{{state}}}^{\mathrm{{unbroken}}} = 0} \right. \\ d = 1\quad \Leftrightarrow \quad {{{\mathcal {H}}}} \rightarrow \infty \quad \Leftrightarrow \quad \tilde{{{\mathcal {H}}}}\left| {_{\mathrm{{state}}}^{\mathrm{{broken}}} = \infty } \right. \\ \dot{d} \ge 0\quad \Leftrightarrow \quad \dot{{{\mathcal {H}}}} \ge 0 \quad \;\; \Leftrightarrow \quad {\dot{\tilde{{{\mathcal {H}}}} }} \ge 0 \end{array} \right. \end{aligned}$$
(20)

Arbitrary evolution of the state variable \(\phi ({{\varvec{X}}}, t)\) associated with the time-bulk response is considered to be related to the loading and unloading of the solid under consideration. The monotonic growth condition of \({{{\mathcal {H}}}}\) in Eq. (20) is satisfied by assuming the relationship between \({{{\mathcal {H}}}}\) and the constitutive crack driving force as follows.

$$\begin{aligned} {\tilde{{{\mathcal {H}}}}}\left( {X,t} \right) = \mathop {\max }\limits _{s \in [0,t]} \left\{ {\tilde{{{\mathcal {D}}}}\left( {\phi \left( {{{\varvec{X}}},s} \right) } \right) } \right\} \end{aligned}$$
(21)

Then the constraint for the constitutive crack driving force \(\mathcal{H}\) can be transformed to the constraint on the crack state function \(\tilde{{{\mathcal {D}}}}\)

$$\begin{aligned} \tilde{{{\mathcal {D}}}}\left| {_{\mathrm{{state}}}^{\mathrm{{unbroken}}} = 0}\right. , \quad \tilde{{{\mathcal {D}}}}\left| {_{\mathrm{{state}}}^{\mathrm{{broken}}} = \infty }\right. \end{aligned}$$
(22)

2.3 Driving forces for brittle failure

The only point that remains to make the phase field Eqs. (16) and (20) concrete is the definition of the crack state function \(\tilde{{{\mathcal {D}}}}\). This makes the formulation very flexible with regard to the incorporation of alternative crack driving criteria. In the following, we outline some of the evolutionary criteria for brittle failure.

2.3.1 Governing equations in gradient damage mechanics

A class of gradient damage approaches for the modeling of brittle fracture assumes a total pseudo-energy density W per unit volume, which contains the sum of a degrading elastic bulk energy \(W_{\mathrm{{bulk}}}\) and a contribution due to fracture \(W_{\mathrm{{frac}}}\) that contains the accumulated dissipative energy

$$\begin{aligned} W\left( {{{\varvec{\varepsilon }}},d,\nabla d} \right) = {W_{\mathrm{{bulk}}}}\left( {{{\varvec{\varepsilon }}};d} \right) + {W_{\mathrm{{frac}}}}\left( {d,\nabla d} \right) \end{aligned}$$
(23)

where \({\varvec{\varepsilon }}\) is the strain tensor. We calculate it using small strain theory: \({{\varvec{\varepsilon }}} = \frac{1}{2}\left[ {{{\left( {\nabla {{\varvec{u}}}} \right) }^T} + \nabla {{\varvec{u}}}} \right] \). In this paper, we assume the bulk contribution as the simple form

$$\begin{aligned} {W_{\mathrm{{bulk}}}}\left( {{{\varvec{\varepsilon }}};d} \right) = g\left( d \right) {{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) = {\left( {1 - d} \right) ^2}{{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) \end{aligned}$$
(24)

where \({{{\tilde{\psi }}}} \left( {{\varvec{\varepsilon }}} \right) = \frac{1}{2} {\varvec{\varepsilon }} : {\varvec{C}} : {\varvec{\varepsilon }}\) is the effective elastic energy stored in the undamaged material, \({\varvec{C}}\) is the material stiffness matrix and \(g(d) = (1-d)^2\) is a degradation function that satisfies the properties: \(W_{\mathrm{{bulk}}}({{\varvec{\varepsilon }}}; 0) = {{{\tilde{\psi }}}} \left( {{\varvec{\varepsilon }}} \right) \), \(W_{\mathrm{{bulk}}}({{\varvec{\varepsilon }}}; 1) = 0\), \({\partial _d}{W_{\mathrm{{bulk}}}}\left( {{{\varvec{\varepsilon }}};d} \right) < 0\) and \({\partial _d}{W_{\mathrm{{bulk}}}}\left( {{{\varvec{\varepsilon }}};1} \right) = 0\).

Due to damage, the elastic energy is degraded with function g(d). By calculating its first derivative with respect to the strain tensor, we can get the expression of stress (Cauchy stress)

$$\begin{aligned} {{\varvec{\sigma }}} = g\left( d \right) \frac{{\partial {{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) }}{{\partial {{\varvec{\varepsilon }}}}} = {\left( {1 - d} \right) ^2}\frac{{\partial {{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) }}{{\partial {{\varvec{\varepsilon }}}}} \end{aligned}$$
(25)

Also, the stress needs to satisfy the momentum balance equation and the traction boundary condition

$$\begin{aligned} \nabla \cdot {{\varvec{\sigma }}} + \rho {{\varvec{b}}} = \rho {{\varvec{\ddot{u}}}} \quad \mathrm{{in}}\;{{{{{\mathcal {B}}}}}_t}\quad \mathrm{{and}}\quad {\varvec{\sigma }} \cdot {{\mathbf {n}}} = {\varvec{t}}_N \quad \mathrm{{on}}\;\partial {{{{\mathcal {B}}}}_t} \end{aligned}$$
(26)

where \({\varvec{\ddot{u}}}\) means the second derivative of displacement vector with respect to t, \(\rho \) is the density of the solid, \({\varvec{b}}\) is the body force per unit mass exerted to the solid, \({\varvec{n}}\) is the unit outer normal to \(\partial {{{{\mathcal {B}}}}_t}\) and \({\varvec{t}}_N\) is the prescribed traction boundary conditions on \(\partial {{{{\mathcal {B}}}}_t}\).

2.3.2 Strain criteria with and without threshold

An energetic criterion without threshold used by Miehe et al. [42] is based on the fracture contribution to the total pseudo-energy

$$\begin{aligned} {W_{\mathrm{{frac}}}}\left( {d,\nabla d} \right) = {g_c}{\gamma _l}\left( {d,\nabla d} \right) = \frac{{{g_c}}}{{2{l_c}}}\left[ {{d^2} + l_c^2{{\left| {\nabla d} \right| }^2}} \right] \end{aligned}$$
(27)

where, \(g_c\) is Griffiths critical energy release rate. Hence, a fracture surface energy per unit volume is obtained by multiplying Griffiths critical energy release rate \(g_c\) with the crack surface density function \(\gamma _l\). The total pseudo-energy potential takes the form

$$\begin{aligned} W\left( {{{\varvec{\varepsilon }}},d,\nabla d} \right) = {\left( {1 - d} \right) ^2}{{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) + {g_c}{\gamma _l}\left( {d,\nabla d} \right) \end{aligned}$$
(28)

According to the variational principle

$$\begin{aligned} - {\delta _d}W\left( {{{\varvec{\varepsilon }}},d,\nabla d} \right)= & {} 2\left( {1 - d} \right) {{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) \nonumber \\&- \frac{{{g_c}}}{{{l_c}}}\left[ {d - l_c^2{\nabla ^2}d} \right] \end{aligned}$$
(29)

Compared with the previous equations, Eq. (16) can be rewritten into the following form

$$\begin{aligned} \underbrace{\eta \dot{d}}_{\mathrm{{evolution}}}= & {} \underbrace{2 \left( {1 - d} \right) \mathop {\max }\limits _{s \in [0,t]} \left\{ {{\tilde{\psi }}\left( {{\varvec{\varepsilon }} \left( {{{\varvec{X}}},s} \right) } \right) } \right\} }_{\mathrm{{driving}}\;\mathrm{{force}}} \nonumber \\&- \underbrace{\frac{{{g_c}}}{{{l_c}}} \left[ {d - l_c^2{\nabla ^2}d} \right] }_{\mathrm{{geometric}}\;\mathrm{{resistance}}} \quad \mathrm{{in}}\;{{{{{\mathcal {B}}}}}_0} \end{aligned}$$
(30)

where \(\eta = {{\tilde{\eta }}} \left( {{g_c}/{l_c}} \right) \) is the viscous parameter that controls phase field evolution. Hence, The crack driving state function is

$$\begin{aligned} \tilde{{{\mathcal {D}}}} = \frac{{2{{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) }}{{{g_c}/{l_c}}} \end{aligned}$$
(31)

Note that this criterion does not distinguish between tension and compression modes. Miehe et al. [42] considered a formulation based on the decomposition of free energy into tensile and compressive parts.

Criterion in Eq. (31) is a monotonically increasing function of the strain, which results in damage degradation of the material at lower stress levels. To avoid this effect, an energy criterion with a threshold can be constructed based on the contribution of the crack to the “total” pseudo energy [27], i.e.

$$\begin{aligned} \tilde{{{\mathcal {D}}}} = \left\langle {\frac{{{{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) }}{{{\psi _c}}} - 1} \right\rangle _ + \end{aligned}$$
(32)

where \(\psi _c\) is a specific fracture energy per unit volume and \({\left\langle a \right\rangle _ \pm }: = \left( {a \pm \left| a \right| } \right) /2\) for all \(a \in {\mathbb {R}}\).

2.3.3 Stress criteria with and without threshold

To obtain a simple stress-based criterion for brittle fracture and to take into account the decomposition of the tensile and compressive forces, Miehe et al. [42] derived the stress criterion. To this end, consider converting the effective energy \({{\tilde{\psi }}}\) to its conjugate residual energy \({{{{\tilde{\psi }}} }^ * }\) by the Legendre-Fenchel transformation.

$$\begin{aligned} {{{{\tilde{\psi }}} }^ * }\left( {{{\varvec{{{\tilde{\sigma }}} }}}} \right) = \mathop {\sup }\limits _{{\varvec{\varepsilon }}} \left[ {{{\varvec{{{\tilde{\sigma }}} }}}:{{\varvec{\varepsilon }}} - {{\tilde{\psi }}} \left( {{\varvec{\varepsilon }}} \right) } \right] \end{aligned}$$
(33)

where \({{\varvec{{{\tilde{\sigma }}} }}} := {{\varvec{ \sigma }}}/(1-d)^2\) is effective Cauchy stresses. According to the theory of linear elastic mechanics

$$\begin{aligned} {{{{\tilde{\psi }}} }^ * }\left( {{{\varvec{{{\tilde{\sigma }}} }}}} \right) = \tilde{\psi }\left( {{\varvec{\varepsilon }}} \right) = \frac{1}{2}{{\varvec{\tilde{\sigma }}}}:{{\varvec{\varepsilon }}} \end{aligned}$$
(34)

Similar to the previous strain criteria with and without threshold in Sect. 2.3.2, we can get the stress criteria with and without threshold

$$\begin{aligned} \tilde{{{\mathcal {D}}}} = \frac{{2{{{{\tilde{\psi }}} }^ * }\left( {{{\varvec{\tilde{\sigma }}}}} \right) }}{{{g_c}/{l_c}}}\quad \mathrm{{and}}\quad \tilde{{{\mathcal {D}}}} = {\left\langle {\frac{{{{{{\tilde{\psi }}} }^*}\left( {{{\varvec{{{\tilde{\sigma }}} }}}} \right) }}{{{\psi _c}}} - 1} \right\rangle _ + } \end{aligned}$$
(35)

2.3.4 Mohr–Coulomb criterion

The Mohr–Coulomb criterion is primarily used to describe the response of brittle materials (such as concrete and rock) to shear and normal stresses. Most classical engineering materials follow this rule in at least a portion of their shear failure envelope. Generally, this criterion applies to materials with compressive strengths far exceeding tensile strength.

The Mohr–Coulomb failure criterion represents a linear envelope obtained from a plot of the shear strength of the material versus the applied normal stress. This relationship is expressed as

$$\begin{aligned} \left| \tau \right| = \sigma \cdot \tan \left( \phi \right) + c \end{aligned}$$
(36)

where \(\tau \) is the shear stress, \(\sigma \) is the normal stress and compression is positive, c is the intercept of the failure envelope with the \(\tau \) axis, and \(\tan (\phi )\) is the slope of the failure envelope. The quantity c is often called the cohesion and \(\phi \) is called the angle of internal friction. The Mohr–Coulomb criterion in three dimensions is often expressed as

$$\begin{aligned} \pm \frac{{{\sigma _1} - {\sigma _2}}}{2}&= \left[ {\frac{{{\sigma _1} + {\sigma _2}}}{2}} \right] \sin \phi + c \cdot \cos \phi \end{aligned}$$
(37a)
$$\begin{aligned} \pm \frac{{{\sigma _2} - {\sigma _3}}}{2}&= \left[ {\frac{{{\sigma _2} + {\sigma _3}}}{2}} \right] \sin \phi + c \cdot \cos \phi \end{aligned}$$
(37b)
$$\begin{aligned} \pm \frac{{{\sigma _3} - {\sigma _1}}}{2}&= \left[ {\frac{{{\sigma _3} + {\sigma _1}}}{2}} \right] \sin \phi + c \cdot \cos \phi \end{aligned}$$
(37c)

where \(\sigma _1\), \(\sigma _2\) and \(\sigma _3\) are the principal stress in three directions. The Mohr–Coulomb failure surface is a cone with hexagonal cross section in deviating stress space.

In order to obtain the phase field evolution conditions based on the Mohr–Coulomb criterion, we first define an over shear stress

$$\begin{aligned} {\tau _d} = {\left\langle {\left| \tau \right| - \left( {\sigma \cdot \tan \left( \phi \right) + c} \right) } \right\rangle _ + } \end{aligned}$$
(38)

For 3D cases, it can be written as

$$\begin{aligned} {\tau _d} = \max \left\{ {{{\left\langle {\tau _d^1} \right\rangle }_ + },{{\left\langle {\tau _d^2} \right\rangle }_ + },{{\left\langle {\tau _d^3} \right\rangle }_ + }} \right\} \end{aligned}$$
(39)

where \(\tau _d^1\), \(\tau _d^2\) and \(\tau _d^3\) are the over shear stress, which are defined as follows

$$\begin{aligned} \tau _d^1&= \left| {\frac{{{\sigma _1} - {\sigma _2}}}{2}} \right| - \left[ {\frac{{{\sigma _1} + {\sigma _2}}}{2}} \right] \sin \phi - c \cdot \cos \phi \end{aligned}$$
(40a)
$$\begin{aligned} \tau _d^2&= \left| {\frac{{{\sigma _2} - {\sigma _3}}}{2}} \right| - \left[ {\frac{{{\sigma _2} + {\sigma _3}}}{2}} \right] \sin \phi - c \cdot \cos \phi \end{aligned}$$
(40b)
$$\begin{aligned} \tau _d^3&= \left| {\frac{{{\sigma _3} - {\sigma _1}}}{2}} \right| - \left[ {\frac{{{\sigma _3} + {\sigma _1}}}{2}} \right] \sin \phi - c \cdot \cos \phi \end{aligned}$$
(40c)

In the second step, the quadratic over shear stress function is defined for the definition of the fracture driving force

$$\begin{aligned} {{\tilde{\psi }}} _{\mathrm{{d}}}^*\left( {{\tau _d}} \right) = \frac{1}{{2G}}{\tau _d}^2 \end{aligned}$$
(41)

where \(G = E/2\left( {1 - \nu } \right) \) is the shear modulus, E is Young’s modulus, and \(\nu \) is Poisson’s ratio. Similarly, we can get the crack driving state function for the Mohr–Coulomb criterion

$$\begin{aligned} \tilde{{{\mathcal {D}}}} = \frac{{2{{{\tilde{\psi }}} _{\mathrm{{d}}}^* }\left( {{ \tau _d }} \right) }}{{{g_c}/{l_c}}} \end{aligned}$$
(42)

Note that this is a threshold criterion that the phase field will evolve only when the state of the material exceeds the envelope of the Mohr–Coulomb failure surface, as shown in Fig. 2. When the stress state is in the gray area of the figure, the material is intact and no damage is generated; otherwise, the damage will rapidly evolve to produce cracks.

Fig. 2
figure 2

Failure surface for Mohr–Coulomb failure criterion in Eq. (42). Stress states above the failure surface, determined by the cohesion c and internal friction angle \(\phi \), raise the driving force function \(\tilde{{{\mathcal {D}}}}\) in Eq. (42)

Full size image

3 Numerical strategy

In the previous section, we deduced the governing equations of the phase field method and introduced the Mohr–Coulomb failure criterion. Next, we will discretize them numerically. In space, the standard finite element method is used to discretize the displacement field and the phase field. In time, the explicit central difference scheme and the forward difference scheme are adopted to discretize the displacement field and the phase field. These time integration methods have good robustness and are easy to be implemented in parallel. Through this we can solve the problem of the high computational cost of the phase field method to a certain extent.

3.1 Spatial-discrete Galerkin scheme

The domain \({{\mathcal {B}}}\) is discretized using a mesh family \(\{\mathcal{T}_h\}\), which has a feature element size of h. We can approximate \(({\varvec{u}},d)\) with the standard first-order finite element shape function

$$\begin{aligned} {{\varvec{u}}^e}\left( {{{\varvec{x}}},t} \right)&= {\sum \limits _{I = 1}^n {{{{N}}{{_{{\varvec{u}}}^e}_I}}\left( {{\varvec{x}}} \right) {{\varvec{u}}_I^e}\left( t \right) } } \end{aligned}$$
(43a)
$$\begin{aligned} d^e \left( {{{\varvec{x}}},t} \right)&= \sum \limits _{I = 1}^n {{{N}_d^e}_I \left( {{\varvec{x}}} \right) {d_I^e}\left( t \right) } \end{aligned}$$
(43b)

where \({\varvec{u}}^e\) and \(d^e\) are the displacement and phase fields of the element e, n is the number of nodes in the element, \({{N}}{{_{{\varvec{u}}}^e}_I}\) and \({{N}}{{_{d}^e}_I}\) are the standard finite element shape functions [43].

Then the spatial discrete equations of the problem are obtained by standard Galerkin approximation

$$\begin{aligned} {{\varvec{M\ddot{u}}}}&= {{{\varvec{F}}}^{\mathrm{{ext}}}}\left( {{\varvec{u}}} \right) - {{{\varvec{F}}}^{{\mathrm{int}} }}\left( {{{\varvec{u}}},{{\varvec{d}}}} \right) \end{aligned}$$
(44a)
$$\begin{aligned} {{\varvec{C\dot{d}}}}&= {\left\langle {{{\varvec{Y}}}\left( {{{\varvec{u}}},{{\varvec{d}}}} \right) } \right\rangle _ + } \end{aligned}$$
(44b)

where \({\varvec{u}} = \{{\varvec{u}}^e\}\) and \({\varvec{d}} = \{d^e\}\) are displacement and phase field vectors that contain the time-dependent nodal DOFs of \({\varvec{u}}\) and d, respectively, and the explicit expressions of the matrices involved in Eq. (44) are as follows

(45a)
(45b)
(45c)
(45d)
(45e)

where the operator represents the element-to-global assembly in classic finite element method, \(N_e\) is the total number of elements, \({{\varvec{N}}}{{_{{\varvec{u}}}^e}}\) and \({{\varvec{N}}}{{_{d}^e}}\) are the vectors of the finite element shape functions: \({{\varvec{N}}}{{_{{\varvec{u}}}^e}} ={{\varvec{N}}}{{_{d}^e}}= [N_1, \cdots ,N_b]\) (where \(b=4\) for 2D and \(b=8\) for 3D), \({{\varvec{B}}}{{_{{\varvec{u}}}^e}}\) and \({{\varvec{B}}}{{_{d}^e}}\) are the shape functions’ spacial derivatives [43]. The local gradient of d reads similarly as: \({\nabla d} = {{\varvec{B}}}{{_{d}^e}} {{\varvec{d}}}\).

3.2 Temporal-discrete scheme

In order to integrate over time, we first discretize the time interval \([0,t_f]\) into a number of small time intervals \(0=t_0< t_1< \cdots < t_N = t_f\) and define \(\Delta t_k = t_k - t_{k-1}\). In addition, we define the middle time of each time interval \(t_{k+\frac{1}{2}} =\frac{1}{2} (t_k + t_{k+1})\) for calculating the velocity vector at that time.

In this paper, the displacement field is integrated using the explicit central-difference integration rule and the phase field is integrated using the explicit forward-difference time integration rule with the use of diagonal or lumped element mass/capacity matrices. The approximate solutions of \({\varvec{u}}(t_k)\), \({\varvec{\dot{u}}}(t_{k+\frac{1}{2}})\), \({\varvec{\ddot{u}}}(t_k)\), \({\varvec{d}}(t_k)\), and \({\varvec{\dot{d}}}(t_k)\) are denoted as \({\varvec{u}}_k\), \({\varvec{v}}_{k+\frac{1}{2}}\), \({\varvec{a}}_k\), \({\varvec{d}}_k\), and \({\varvec{r}}_k\), respectively.

(1) Central difference method for displacement phase integration. The central difference method is used to compute \({\varvec{u}}_{k+1}\), \({\varvec{v}}_{k+\frac{1}{2}}\), \({\varvec{a}}_{k+1}\) from \({\varvec{u}}_{k}\), \({\varvec{v}}_{k-\frac{1}{2}}\), \({\varvec{a}}_{k}\) and \({\varvec{d}}_k\) according to

$$\begin{aligned}&{\varvec{a}}_{k} = {\varvec{M}}^{-1}( {{{\varvec{F}}}^{\mathrm{{ext}}}}\left( {{\varvec{u}}_k} \right) - {{{\varvec{F}}}^{{\mathrm{int}} }}\left( {{{\varvec{u}}_k},{{\varvec{d}}_k}} \right) ) \end{aligned}$$
(46a)
$$\begin{aligned}&{\varvec{v}}_{k+\frac{1}{2}} = {\varvec{v}}_{k-\frac{1}{2}} + \frac{\Delta t_{k+1} + \Delta t_{k}}{2} {\varvec{a}}_k \end{aligned}$$
(46b)
$$\begin{aligned}&{\varvec{u}}_{k+1} = {\varvec{u}}_{k} + \Delta t_{k+1} {\varvec{v}}_{k+\frac{1}{2}} \end{aligned}$$
(46c)

The central difference operator is not self-starting, because the value of velocity \({\varvec{v}}_{-\frac{1}{2}}\) needs to be defined. For this purpose, we use the following two equations to deal with the initial condition of velocity.

$$\begin{aligned} {\varvec{v}}_{+\frac{1}{2}}&= {\varvec{v}}_{0} + \frac{\Delta t_1}{2} {\varvec{a}}_0 \end{aligned}$$
(47a)
$$\begin{aligned} {\varvec{v}}_{-\frac{1}{2}}&= {\varvec{v}}_{0} - \frac{\Delta t_0}{2} {\varvec{a}}_0 \end{aligned}$$
(47b)

(2) Forward-difference method for phase field integration. The forward-difference method is used to compute \({\varvec{d}}_{k+1}\), \({\varvec{r}}_{k+1}\) from \({\varvec{d}}_{k}\), \({\varvec{u}}_{k}\) and \({\varvec{r}}_{k}\) according to

$$\begin{aligned}&{\varvec{r}}_{k} = {\varvec{C}}^{-1}({\left\langle {{{\varvec{Y}}}\left( {{{\varvec{u}}_k},{{\varvec{d}}_k}} \right) } \right\rangle _ + }) \end{aligned}$$
(48a)
$$\begin{aligned}&{\varvec{d}}_{k+1} = {\varvec{d}}_{k} + {\Delta t_{k+1}} {\varvec{r}}_k \end{aligned}$$
(48b)

Because both forward and central differential integrals are explicit, the solutions of displacement and phase fields can be obtained simultaneously by explicit coupling. Therefore, there is no need for iterative solution or tangent stiffness matrix, and the solution process in each incremental step is very efficient. Moreover, explicit integrals are independently integrated at each node. The model can be divided into several regions, and each region can be computed by an independent CPU, so that parallel computing can be implemented and computing efficiency can be improved. A detailed study of parallel performance is provided in “Appendix A”.

3.3 Stable time increment

Explicit time integration uses many small time intervals to integrate over time. The central difference operator and the forward difference operator are conditionally stable. The stable time increments of two explicit integral operators can be obtained under the following conditions

$$\begin{aligned} \Delta t \le \min \{\Delta {t_{{\varvec{u}}}}, \Delta {t_d}\} = \min \left\{ \frac{2}{\omega _{\max }}, \; \frac{2}{\lambda _{\max }}\right\} \end{aligned}$$
(49)

where \(\omega _{\max }\) is the highest frequency in the system of equations of the displacement field solution response and \(\lambda _{\max }\) is the largest eigenvalue in the system of equations of the phase field solution response.

An approximation to the stability limit for the central difference operator in the displacement field solution response and the forward-difference operator in the phase field solution response are given by

$$\begin{aligned} \Delta {t_{{\varvec{u}}}}&\approx \frac{{{L_{\min }}}}{{{c_d}}} \end{aligned}$$
(50a)
$$\begin{aligned} \Delta {t_d}&\approx \frac{{L_{\min }^2}}{{2\alpha }} \end{aligned}$$
(50b)

where \({L_{\min }}\) is the smallest element size in the mesh, \(c_d\) is the dilatational wave speed and \(\alpha = \left( {{g_c}{l_c}} \right) /\eta \) is the phase field diffusivity.

To reduce the possibility of solution instability, we introduce a scale factor \( \zeta =0.5 \) to adjust the stable time increment. Thus the final stable time increment is determined by

$$\begin{aligned} \Delta {t_c} = \zeta \cdot \min \left\{ \frac{{{L_{\min }}}}{{{c_d}}}, \; \frac{{L_{\min }^2}}{{2\alpha }} \right\} \end{aligned}$$
(51)

Note that the time increment for each incremental step is dynamically adjusted to achieve the highest computational efficiency.

4 Verification examples

In this section, we demonstrate the correctness and efficiency of the numerical implementation through three examples of typical 2D and 3D dynamic crack propagation and branching. Energy-based criteria are used in all three examples. For dynamic crack branching problems, crack propagation velocity is an important indicator. We give the crack propagation velocity and compare it with the wave speed of shear and Rayleigh waves, which are two typical elastic waves in solid materials.

Fig. 3
figure 3

Experiment set-up for edge-cracked plate under impact loading reported by Kalthoff and Winkler [44], The crack is modeled by an actual discontinuity in the mesh with a sharp crack tip

Full size image

4.1 Kalthoff test verification

The simulation of the edge-cracked plate under impact loading is carried out to verify the accuracy of the method. The experiment data are reported by Kalthoff and Winkler [44]. A plate with two initial symmetry cracks are subjected to impact by an object, as shown in Fig. 3. The experiment demonstrates two different failure modes with different impact speeds: at a higher speed, a shear band is observed to propagate from the notch tip at a negative angle about \(-10^{\circ }\); at a lower impact speed, a brittle fracture mode is observed with a propagation angle about \(70^\circ \). The 2D and 3D analysis of this problem is carried out by Belytschko et al. [45] with XFEM, Remmers et al. [41] with cohesive segments and Borden et al. [34] with phase field method.

Table 1 The material properties and viscosity parameter used in Sect. 4.1
Full size table
Fig. 4
figure 4

Evolution of the phase field through time in original configuration with characteristic element size \(h=0.05 \; \mathrm {mm}\) and \(l_c=2h\) for the simulation of Kalthoff experiment. The resulting crack propagation angle is nearly \(70^\circ \) and in agreement with the experimentally observed angle reported by Kalthoff and Winkler [44] : a\(t=25 \; \mathrm {us}\), b\(t=50 \; \mathrm {us}\), c\(t=75 \; \mathrm {us}\) and d\(t=100 \; \mathrm {us}\)

Full size image
Fig. 5
figure 5

Comparison of phase field distribution at \(t=100 \; \mathrm {us}\) in the original configuration under different feature element size h and feature crack width \(l_c\) : a\(h = 0.1 \; \mathrm{{mm}},\; {l_c} = 2h\), b\(h = 0.1 \; \mathrm{{mm}},\; {l_c} = 4h\) and c\(h = 0.05 \; \mathrm{{mm}},\; {l_c} = 2h\)

Full size image

Owing to the symmetry, only the upper part of the plate is simulated. The boundary conditions are given as: the symmetry condition is applied on the bottom edge; a velocity \(v_0 = 20.0 \; \mathrm {m}/\mathrm {s}\) is applied at the initial time increment and held constant throughout the simulation on the left edge for \(0 \le y \le 25 \; \mathrm {mm}\); other edges are traction-free, as shown in Fig. 3. The material properties and viscosity parameter used here are listed in Table 1. The corresponding material shear and Rayleigh wave speeds are \(v_s = 3022 \; \mathrm {m/s}\) and \(v_R = 2803 \; \mathrm {m/s}\). The plate is discretized with 4,000,000 eight-node hexahedron elements (\(h=0.05 \; \mathrm {mm}\)).

Fig. 6
figure 6

A post-processed plot of deformation at \(t = 75 \; \mathrm {us}\). The displacements have been scaled by a factor of 5 and areas of model where \(d > 0.99\) have been removed from the plot to show cracks. The contour of strain component \(\varepsilon _{11}\) is shown

Full size image

The simulating results for the evolution of the phase field through time with feature element size \(h=0.05 \; \mathrm {mm}\) and \(l_c=2h\) are shown in Fig. 4. The resulting crack propagation angle is nearly \(70^\circ \) and in good agreement with the experimentally observed angle reported by Kalthoff and Winkler [44]. The crack propagation paths under different element feature size h and crack characteristic width parameter \(l_c\) are shown in Fig. 5. It can be found from the figure that the crack propagation paths under different element feature size h and crack characteristic width parameters \(l_c\) are in good agreement, which shows that the simulation results are mesh convergent.

Fig. 7
figure 7

The geometric dimensions and boundary conditions of a plate under transient tensile loading

Full size image
Table 2 The material properties and viscosity parameter used in Sect. 4.2
Full size table
Fig. 8
figure 8

Evolution of the phase field through time in original configuration with characteristic element size \(h=0.1 \; \mathrm {mm}\) and \(l_c=2h\) for the dynamic crack branching problem: a\(t=14 \; \mathrm {us}\), b\(t=36 \; \mathrm {us}\), c\(t=50 \; \mathrm {us}\) and d\(t=80 \; \mathrm {us}\)

Full size image

In Fig. 6 we show the deformation of the cracked plate at time \(t = 75 \; \mathrm {us}\). The displacements have been scaled by a factor of 5 and areas of the model where \(d > 0.99\) have been removed from the plot for visualization.

4.2 Dynamic crack branching

The second example concerns a dynamic crack branching process of a central crack in a plate under transient tensile loading, as shown in Fig. 7. The dimension of the specimen is \(100 \times 40 \; \mathrm {mm}\), and the length of the initial crack is \(50 \; \mathrm {mm}\). The tensile stress of 1.0 MPa is applied instantaneously on the top and bottom surfaces of the plate. The material properties and viscosity parameter used here are listed in Table 2. The corresponding shear and Rayleigh wave speeds are \(v_s = 2333 \; \mathrm {m/s}\) and \(v_R = 2125 \; \mathrm {m/s}\). The plate is discretized with 400,000 eight-node hexahedron elements (\(h=0.1 \; \mathrm {mm}\)).

This problem has been experimentally investigated by Sharon et al. [46] and Fliss et al. [47] and numerically studied by Belytschko et al. [45] and Xu et al. [48] by XFEM and Borden et al. [34] by phase field method. These experimental and numerical studies have shown that the crack will branch in the process of rapid propagation.

The propagation paths and phase fields under different time obtained from the simulation with characteristic element size \(h=0.1 \; \mathrm {mm}\) and \(l_c=2h\) are shown in Fig. 8. The crack starts to propagate as a typical mode I crack. The initial crack grows along the original direction for a certain distance and then branching occurs at about 36 us. After that time, the two branches continue to propagate separately. Figure 9 shows the curve of crack propagation velocity with time. It can be seen from the figure that the crack velocity increases with time, and when a certain value is reached, the crack begins to branch.

Fig. 9
figure 9

The crack propagation velocity over time during the entire analysis under different element size h for dynamic crack branching problem

Full size image
Fig. 10
figure 10

Geometric dimensions and boundary conditions of a pressured cylinder model with initial crack

Full size image
Fig. 11
figure 11

Evolution of the phase field for pressured cylinder example through time in original configuration with characteristic element size \(h=1.5 \; \mathrm {mm}\) and \(l_c = 2h\): a\(t=1.2 \; \mathrm {ms}\), b\(t=1.4 \; \mathrm {ms}\), c\(t=1.8 \; \mathrm {ms}\) and d\(t=2.0 \; \mathrm {ms}\)

Full size image

4.3 Multiple branching of crack in a pressurized cylinder

In this example, we show a 3D computation of a multiple branching of crack in a pressurized cylinder with a spherical end cap. The geometric dimensions and boundary conditions of a pressured cylinder are shown in Fig. 10, where symmetry is used to reduce the computational cost. A hydrostatic pressure load linearly increase to \(10 \; {\mathrm{MPa}}\) within \(2.0 \; \mathrm {ms}\) is applied to the inner surface. The material properties and viscosity parameter are the same as that in Sect. 4.1 (i.e., in Table 1). The corresponding shear and Rayleigh wave speeds are \(v_s = 3022 \; \mathrm {m/s}\), \(v_R = 2803 \; \mathrm {m/s}\). The cylinder is discretized with 589,032 eight-node hexahedron elements (\(h=2.0 \; \mathrm {mm}\)).

The Evolution of the phase field for pressured cylinder example through time in original configuration with characteristic element size \(h=1.5 \; \mathrm {mm}\) and \(l_c = 2h\) is shown in Fig. 11. It can be seen that there are two branches in the process of crack propagation, and a complex crack mode is formed. We also compare the results of crack propagation paths under different mesh sizes, as shown in Fig. 12. It can be found that the crack propagation paths under three mesh sizes are in good agreement. This shows that the algorithm in this paper can still get accurate crack propagation path under the coarse mesh.

A post-processed plot of deformation at \(t = 2.0 \; \mathrm {ms}\) is shown in Fig. 13 with the displacements scaled by a factor of 2 and the areas of the model where \(d > 0.99\) have been removed from the plot to show cracks.

Fig. 12
figure 12

Comparison of phase field distribution at \(t=2.0 \; \mathrm {ms}\) in the original configuration under different feature element size h: a\(h=1.5 \; \mathrm {mm}\), b\(h=2.0 \; \mathrm {mm}\) and c\(h=4.0 \; \mathrm {mm}\)

Full size image

The crack propagation speed over time during the entire analysis under different element size h is shown in Fig. 14. The first branching occurs at \(t=1.34 \; \mathrm {ms}\), and the second branching occurs at \(t=1.78 \; \mathrm {ms}\), corresponds to the two gray bands in Fig. 14. It can be seen from the figure that the crack propagation speed under different element size h has a good consistency. Also, when the crack branching occurs, the crack propagation speed is slightly increased. At the same time, we also notice that the crack propagation speed is not very fast when it branches, which is less than 0.2 times of the Rayleigh wave speed. It is also lower than that of the dynamic crack branching in Sect. 4.2. This may be due to the local stress field of the cylindrical structure.

To understand the multiple branching behavior of a crack from another perspective, we first took out the semicircular path along the circumference of the cylinder near the crack tip before the two branchings began, as shown in Figs. 15a and 16a. Then we drew the distribution of the maximum principal stress along the path at different time before branching occurs, as shown in Figs. 15b and 16b. It can be found from the figures that when the crack is about to branch, the maximum principal stress near the crack tip will be converted from one peak to two peaks, which directly leads to the branching of the crack.

Fig. 13
figure 13

A post-processed plot of deformation at \(t = 2.0 \; \mathrm {ms}\). The displacements have been scaled by a factor of 2 and areas of the model where \(d > 0.99\) have been removed from the plot to show cracks. The contour of displacement component \(u_{1}\) is shown

Full size image
Fig. 14
figure 14

The crack propagation speed over time during the entire analysis under different element size h

Full size image

5 Compression-shear failure of rock-like materials

Rock is a typical engineering material that can withstand compression. Normally, its compressive strength is higher than its tensile and shear strength. And it often works under compressive loads, at which point the compression-shear failure is its main failure mode. By introducing the Mohr–Coulomb criterion in the phase field method, we can well capture the compression-shear failure process of rock-like materials. In this section, we illustrate the applicability of the model to rock-like materials by studying the compression-shear failure process of rock slabs and rock pillars, respectively.

Fig. 15
figure 15

Maximum principal stress along an annular path when the crack begins to branch for the first time: a annular path for extracting stress, b maximum principal stress along an annular path

Full size image
Fig. 16
figure 16

Maximum principal stress along an annular path when the crack begins to branch for the second time: a annular path for extracting stress, b maximum principal stress along an annular path

Full size image

5.1 Quasi-static compression-shear failure of rock slabs

In this example, we simulated the compression process and failure mode of rock slab under quasi-static loading. The geometric dimensions, loading and boundary conditions of the model are shown in Fig. 17a. The Mohr–Coulomb failure criterion of the crack driving state function is used. The material properties used here are listed in Table 3. To simulate quasi-static loading, we linearly load the axial displacement slowly so that the kinetic energy during the simulation is much smaller than the internal energy and external work of the system. The rock slab is discretized with 250,000 eight-node hexahedron elements (\(H = 100 \; \mathrm {mm}\), \(h=0.2 \; \mathrm {mm}\)). As reinforcement, a displacement constraint is applied in the z-direction of the plate (perpendicular to the direction of the paper). Unless the effect of \(\eta \) on the results is studied, \(\eta \) in all simulations in this section is set to \(1.0 \times 10^{-8} \; \mathrm {kN}*\mathrm {s}/\mathrm {mm^2}\).

The phase field evolution for compression of 3D rock slab (\(H = 100 \; \mathrm {mm}\)) through axial displacement in original configuration with characteristic element size \(h=0.2 \; \mathrm {mm}\) and \(l_c = 2h\) is shown in Fig. 18. As can be seen from the figure, there are two sets of typical slip zones near the upper and lower parts of the rock slab. Each set of slip zones has two main cracks at an angle of approximately 45 degrees to the loading direction, which are the main failure modes of rock slab when they are compressed.

For comparison, we simulated another case of rock slabs with a height of 50 mm. The simulation results of the phase field evolution for compression of 3D rock slab (\(H = 50 \; \mathrm {mm}\)) through axial displacement in original configuration with characteristic element size \(h=0.2 \; \mathrm {mm}\) and \(l_c = 2h\) are shown in Fig. 19. It can be seen that when the height of the rock slab is reduced by half, only a pair of mutually perpendicular main cracks are formed. The failure mode is still the same as the previous result, that is, shear friction damage is dominant. To more clearly observe the final shape of the crack in the rock slabs, we plot the crack distribution of the two slabs in three dimensions in Fig. 20.

Fig. 17
figure 17

Geometric dimensions and boundary conditions of uniaxial compression model of rock slab and pillar: a rock slab and b rock pillar

Full size image
Table 3 The material properties used in Sect. 5.1
Full size table
Fig. 18
figure 18

Evolution of the phase field for compression of 3D rock slab (\(H = 100 \; \mathrm {mm}\)) through axial displacement in original configuration with characteristic element size \(h=0.2 \; \mathrm {mm}\) and \(l_c = 2h\): a\(u_z=1.94 \; \mathrm {mm}\), b\(u_z=1.96 \; \mathrm {mm}\) and c\(u_z=2.0 \; \mathrm {mm}\)

Full size image

The load-displacement curves of two rock plates with different heights under different length scaling parameters are shown in Fig. 21. It can be found that the calculation results under different length scale parameters are consistent, which shows the mesh convergence of the numerical method. In the initial stage, the material is intact without failure damage, and the load increases linearly. When the load increases to a certain value, the material begins to locally damage and the load increment begins to decrease. As the damage accumulates, a set of macroscopic main cracks is generated. At this point, the load suddenly drops to zero and the rock slab cannot continue to withstand the load. Besides, we also found that the ultimate load of different height slabs is consistent. In this example, it is \(227.0 \pm 0.3 \; \mathrm {kN}\).

Fig. 19
figure 19

Evolution of the phase field for compression of 3D rock slab (\(H = 50 \; \mathrm {mm}\)) through axial displacement in original configuration with characteristic element size \(h=0.2 \; \mathrm {mm}\) and \(l_c = 2h\): a\(u_z=0.96 \; \mathrm {mm}\), b\(u_z=1.02 \; \mathrm {mm}\) and c\(u_z=1.08 \; \mathrm {mm}\)

Full size image

To study the influence of viscous parameter \(\eta \) on the results, we compressed rock slabs with a height of 50 mm under different values of \(\eta \) (\(\eta =2.0 \times 10^{-8} \; \mathrm {kN}\,\mathrm {s}/\mathrm {mm^2}\), \(\eta =1.0 \times 10^{-8} \; \mathrm {kN}\,\mathrm {s}/\mathrm {mm^2}\) and \(\eta =0.5 \times 10^{-8} \; \mathrm {kN}\,\mathrm {s}/\mathrm {mm^2}\) ), and extracted their compression reaction force-displacement curves, as shown in Fig. 22. From the figure, it can be seen that the calculated results under different values of \(\eta \) are in good agreement at the load rising stage. Since the material is elastic before phase field damage initiation, the viscous dissipation parameter \(\eta \) used to characterize the damage process has little effect on the results. With the accumulation and evolution of damage, the viscous dissipation of damage has a certain impact on the results, but because the viscous parameters we take are very small, the effect of \(\eta \) on the results is still very small. We also found that as \(\eta \) decreases, the results gradually converge to the case of non-viscous damage dissipation.

Fig. 20
figure 20

The final crack path of rock slabs with different heights (\(H=100 \; \mathrm {mm}\) and \(H=50 \; \mathrm {mm}\)) under compressive loading (3D view)

Full size image
Fig. 21
figure 21

Reaction force versus displacement at different rock slab heights (\(H=100 \; \mathrm {mm}\) and \(H=50 \; \mathrm {mm}\)) and different length scale parameters (\(l_c=0.4 \; \mathrm {mm}\) and \(l_c=0.2 \; \mathrm {mm}\)) for rock slabs compression

Full size image
Fig. 22
figure 22

Reaction force vs. displacement at different values of viscous parameter \(\eta \) ( \(\eta =2.0\times 10^{-8} \; \mathrm {kN}\,\mathrm {s}/\mathrm {mm^2}\), \(\eta =1.0 \times 10^{-8} \; \mathrm {kN}\,\mathrm {s}/\mathrm {mm^2}\) and \(\eta =0.5 \times 10^{-8} \; \mathrm {kN}\,\mathrm {s}/\mathrm {mm^2}\) ) for rock slabs ( \(H=50 \; \mathrm {mm}\) ) compression

Full size image

5.2 Compression-shear failure of 3D rock pillars

In this example, we simulate the quasi-static compression process of a rock pillar. This is a typical rock experiment, which usually results in very complex 3D crack morphology. The geometric dimensions, loading and boundary conditions of the model are shown in Fig. 17. The Mohr–Coulomb failure criterion of the crack driving state function is used. The material parameters are the same as that in Sect. 5.1 (i.e., in Table 3). The rock pillar is discretized with 1,943,200 eight-node hexahedron elements (\(H = 100 \; \mathrm {mm}\), \(h=0.2 \; \mathrm {mm}\)).

Similar to the previous section, we studied the compression failure process of two heights of rock pillars (\(H=100 \; \mathrm {mm}\) and \(H=50 \; \mathrm {mm}\) ). The morphology of the cracks and the failure modes of the rock pillars at the two heights are shown in Fig. 23 (\(H=100 \; \mathrm {mm}\)) and Fig. 24 (\(H=50 \; \mathrm {mm}\)), respectively. As the displacement is loaded, two 3D fan-shaped main crack surfaces are formed. The angle of the fan-shaped surface and the loading direction is about 45 degrees.

Fig. 23
figure 23

Evolution of the phase field for compression of 3D rock pillars (\(H=100 \; \mathrm {mm}\)) through axial displacement in original configuration with characteristic element size \(h=0.2 \; \mathrm {mm}\) and \(l_c = 2h\) (a quarter of the model is cut off to show internal cracks): a\(u_z=0.48 \; \mathrm {mm}\), b\(u_z=0.485 \; \mathrm {mm}\)c\(u_z=0.49 \; \mathrm {mm}\) and d\(u_z=0.50 \; \mathrm {mm}\)

Full size image
Fig. 24
figure 24

Evolution of the phase field for compression of 3D rock pillars (\(H=50 \; \mathrm {mm}\)) through axial displacement in original configuration with characteristic element size \(h=0.2 \; \mathrm {mm}\) and \(l_c = 2h\) (a quarter of the model is cut off to show internal cracks): a\(u_z=0.24 \; \mathrm {mm}\), b\(u_z=0.2425 \; \mathrm {mm}\) and c\(u_z=0.245 \; \mathrm {mm}\)

Full size image

The reaction force-displacement curves at two different heights of the rock pillars (\(H=100 \; \mathrm {mm}\) and \(H=50 \; \mathrm {mm}\)) are shown in Fig. 25. The compression-shear failure process of rock pillar is similar to that of rock slab. In the initial stage, the material is intact without damage, and the load increases linearly. When the load increases to a certain value, the material begins to locally damage and the load increment begins to decrease. As the damage accumulates, a set of macroscopic main crack clusters is generated. The number of main crack clusters depends on the height of the rock pillars. Finally, the load suddenly drops to zero and the rock pillars cannot continue to withstand the load. In addition, we also found that the ultimate load of different height pillars is consistent. In this example, it is \(205.8 \pm 1.6 \; \mathrm {kN}\).

At the same time, we also noticed that the compression of the rock pillars and the rock slabs is different. After the reaction force-displacement curve of the rock pillars’ compression reaches the highest point, there is a descending section (as shown in Fig. 25). On the contrary, after the compression load of the rock slab reaches the highest point, it is quickly reduced to 0 (almost instantaneously, as shown in Fig. 21). This may be because the compression process of the rock slab is an approximate 2D crack evolution process, while the rock pillar is 3D.

Fig. 25
figure 25

Reaction force versus displacement at different pillar heights (\(H=100 \; \mathrm {mm}\) and \(H=50 \; \mathrm {mm}\)) for rock pillars compression

Full size image
Fig. 26
figure 26

Reaction force vs. displacement at different cohesion strength c and internal friction angle \(\phi \) for compression of 3D rock pillars (\(H=50 \; \mathrm {mm}\)): a initial damage line of phase field for different c, b initial damage line of phase field for different \(\phi \), c reaction force vs. displacement for different c and d reaction force vs. displacement for different \(\phi \)

Full size image

The Reaction force-displacement curves of the compression of the rock pillars (\(H=50 \; \mathrm {mm}\)) under different rock cohesive strength c and internal friction angle \(\phi \) are shown Fig. 26. It can be seen that the ultimate load of the rock pillars and the load at the beginning of the damage of the pillars will increase with the increase of c and \(\phi \).

6 Concluding remarks

In this paper, we review the basic idea of the phase field method, derive the governing equations of an explicit phase field model with compression-shear failure mode, and numerically discretize them. The main conclusions of this paper are as follows.

  1. (1)

    The 3D explicit parallel phase field method is numerically implemented to simulate a large-scale complex dynamic and quasi-static crack network. The explicit central difference scheme and the forward difference scheme are used to discretize the displacement field and the phase field respectively.

  2. (2)

    The Mohr–Coulomb failure criterion is introduced into the framework of the phase field method and numerically implemented, which is suitable for shear friction damage of rocks and other brittle materials.

  3. (3)

    Some typical 2D and 3D dynamic crack propagation and branching examples are simulated to illustrate the correctness and effectiveness of the algorithm.

  4. (4)

    The quasi-static compression-shear failure processes of 3D rock slabs and pillars are simulated. The results show that the rock will produce a set of shear crack surfaces with an angle of about 45 degrees in the loading direction during compression.

In summary, the model proposed in this paper can be used to simulate complex dynamic and quasi-static crack growth problems of brittle materials, especially the rock-like materials with compressive-shear failure behavior.