Keywords

1 Introduction

The development of an adequate scheme for the numerical simulation of crack initiation and propagation is still a significant challenge for the Computational Mechanics community. Huge efforts have already been made to develop novel and accurate models for fracture and an enormous progress has been achieved. A particularly successful approach is provided by the Linear Elastic Fracture Mechanics (LEFM) theory based on Griffith’s theory for brittle fracture, which relates crack nucleation and propagation to a critical value of the energy release rate.

The efforts to model brittle fracture focus essentially on two broad approaches: (i) the discrete methods, such as the element deletion method [2], the embedded finite element method [13] or the extended finite element method [23, 27], which use the finite element method in conjunction with Griffith’s-type LEFM models to incorporate discontinuities into the displacement field, and (ii) the continuum-damage (CD) methods [12], which incorporate a damage parameter into the model that describes the material’s deterioration and controls its strength. Some of these methods are already available in commercial CAE software packages and can be used for various design applications. However, it has long been recognized that, while discrete methods are well suited mostly for static fracture and for a moderate number of cracks, CD methods are not effective when modelling large dominant cracks, since the damage zone tends to widen in a direction normal to the crack initiation as the simulation proceeds. Another shortcoming of the CD methods is that regularization algorithms are needed to overcome mesh dependency. Additionally, current methods for predicting crack propagation, in particular for dynamic loading conditions and 3D problems, still lack accuracy and robustness, even when applied to relatively simple benchmark tests [26]. Due to these reasons, several efforts were made in the last decade for the development of alternative schemes. Recently, a new method for the numerical simulation of fracture has emerged—the Variational Phase-Field Method [14, 21].

Variational methods are a relatively new development in the field of Fracture Mechanics. The underlying theory was introduced in [14] for quasi-static brittle fracture, and is based on the idea that cracks should propagate along a path of least energy. The goal of variational methods is to circumvent several weaknesses of the classical LEFM theory of Griffith. As pointed out in [14], the inverse proportionality of the critical stress to the square root of the initial crack length indicates that the classical LEFM theory is unable to predict crack initiation. Indeed, for a solid without an initial crack, the stress required for crack propagation becomes infinite. Other important weaknesses of this theory are the inadequacy for predicting the direction of crack propagation and its inability to handle crack jumps.

Later, Bourdin et al. [5, 6] carried out numerical tests based on this method, and introduced a phase-field approximation of the energy functional in order to facilitate the determination of the numerical solution of the variational method. The phase-field was included in the energy functional in addition to the primary displacement field in order to regularize the jumps of the displacement field representing the cracks. The phase-field parameter models the continuous change in stiffness between broken and undamaged parts of the material on a small lengthscale controlled by a regularization parameter. This regularization allows for the treatment of the global energy minimization as a standard variational problem, for which classical finite element methods are adequate. In the variational phase-field approach, the evolution of fracture surfaces follows from the solution of a coupled system of partial differential equations. Due to this—and contrarily to many discrete methods—its implementation does not require fracture surfaces to be tracked algorithmically.

The variational phase-field approach has been recently applied in a dynamic setting by Bourdin et al. [7] and Larsen et al. [19, 20].

Alternative phase-field models of fracture were proposed by Miehe et al. [21, 22]. An important addition to the existing theory was the modelling of anisotropic degradation, which allows the analysis of tensile fracture, thus resolving the issue of interpenetration encountered in [7] for crack branching simulations. This model has been extended by Borden et al. [4] to the dynamic case.

In the phase-field approach to fracture, a crack is a small region in which damage accumulates, as quantified by the order parameter. This description is conceptually similar to the ones employed within the framework of continuum gradient theories for damage [25], wherein the damage gradient is considered as an independent constitutive variable. The phase-field approach to fracture may be viewed as a continuum gradient theory for damage with an alternative derivation for the equation governing damage evolution.

The goal of this paper is to give an overview of current numerical methods proposed for analysis of brittle fracture problems and to present a finite element phase-field model to deal with such problems. Additionally, some numerical experiments are presented, which demonstrate that, unlike many of the current numerical methods based on the classical theory of Griffith, the presented phase-field fracture model is able to reproduce various complex phenomena, such as deflection or branching of pre-existing cracks, as well as the nucleation of new cracks in originally undamaged domains.

2 Literature Review

2.1 General Considerations

The prevention of fracture-induced failure is a major constraint in engineering designs, and the numerical simulation of fracture processes often plays a key role in design decisions. A successful model is provided by the LEFM theory based on Griffith’s theory for brittle fracture. A general concept in this theory is that, upon the attainment of a critical energy release rate, a fully opened crack is nucleated or propagated. As a result, the process zone, i.e., the zone in which the material changes from an undamaged state to a damaged one, is lumped into a single point at the crack tip. In the dynamic setting, crack growth velocity is selected based on the balance between the mechanical energy that flows within the process zone per unit time and the dissipated energy within the process zone over the same period. Although LEFM predictions agree well with observations for a sufficiently slow crack growth, large discrepancies may be found at high loading speeds.

Due to the complexity of fracture processes in engineering applications, numerical methods play a crucial role in fracture analyses. Efforts to model crack propagation were focused mainly on two broad approaches: (i) discrete methods, which use the FEM in conjunction with Griffith’s-type LEFM models in order to incorporate discontinuities into the displacement field, and (ii) continuum-damage methods, which incorporate a damage parameter into the model that controls the strength of the material.

Among the most commonly used methods in the first category are: the Element Deletion Method (EDM) [2], the Interelement Separation Method (ISM) [9], the Embedded Element Method (EFEM) [13], the Cohesive Zone Method (CZM) [24], and the Extended Finite Element Method (XFEM) [23, 27]. All of these approaches represent cracks as discrete discontinuities, either by inserting discontinuity lines by means of remeshing strategies, or by enriching the displacement field with discontinuities using the partition of unity method. Continuum-Damage methods were particularly adopted to model diffusive fracture processes [12].

Some of the aforementioned methods are already available in commercial CAE software packages and can be used for various applications. However, it has long been recognized that discrete methods are only well suited for static fracture, and when a moderate number of cracks occurs. The EDM, for instance, suffers from extreme mesh dependency and is not well suited for dynamics. In the case of the ISM, cracks are only allowed to develop along existing interelement edges, which also leads to strong mesh dependency. Also, the EFEM may be sensitive to the orientation of the discontinuity surface. As for the XFEM, it requires an algorithm to ensure crack path continuity, which is particularly challenging in 3D. Additionally, and unlike the EFEM, the enrichment parameters used in the XFEM cannot be condensed at the element level, yielding computationally demanding algorithms, mostly when dealing with an increasing number of cracks and crack branches. Another important shortcoming of XFEM is that numerical integration requires special attention, particularly around the crack tip when employing non-polynomial enrichment functions, where several thousand Gauss-points may be needed to reduce the integration error. These shortcomings, together with those for CD methods mentioned in Sect. 1, resulted in many efforts, in particular in the last decade, to develop novel, efficient, and accurate computational methods for brittle dynamic fracture.

2.2 Extended Finite Element Method

Simulating the propagation of cracks using traditional finite element methods is challenging since the topology of the domain changes continuously. XFEM has been very successfully employed to model cracks, since the finite element mesh can be created independently from the crack geometry, and, in particular, since the domain does not have to be remeshed as the crack propagates. Remeshing is particularly cumbersome in dynamic crack propagation problems. Indeed, as the crack advances over a large part of the mesh, remeshing needs to be performed many times, leading unavoidably to computationally expensive simulations.

The basic idea behind the XFEM is to decompose the displacement field into continuous and discontinuous parts. The continuous part is the standard finite element interpolation, while the discontinuous, or enrichment, part is introduced into the finite element interpolation by means of the local partition of unity method. This enrichment is carried out with additional degrees of freedom introduced into the discretization of the test and trial functions, which are multiplied by the so-called enrichment shape functions incorporating the near tip asymptotic solutions and allowing displacements to be discontinuous across the crack face.

Application of the XFEM to cracks began with Belytschko and Black in [1]. In [23], the XFEM was used to create a technique for simulating crack propagation in two dimensions without the need to remesh the domain. The extension to three dimensions was initiated in [27].

However, the XFEM approach carries technical challenges: assembling the stiffness matrix requires integration of singular/discontinuous functions, and implementing enrichment requires resolving material connectivity (often using a level set representation). As for the integration issue, as noted in [11], the use of Gauss quadrature or Monte Carlo integration techniques is unstable. Indeed, since the crack path through a given triangle is a priori unknown, the singularities can move very close to quadrature points. Regarding the material connectivity issue, in a region unambiguously separated into two pieces (i.e., away from the crack tip), the enrichment is provided by a Heaviside function, defined to be 1 on one side of the crack and −1 on the other side. This is easy for the case of a single straight crack, but more challenging for more complex crack geometries.

The XFEM was mainly applied to problems involving the growth of a single crack or a few cracks; there are only a few contributions dealing with fracture problems that involve the growth of numerous (several hundreds of) cracks [8, 30]. The case of complex crack patterns such as branching and merging cracks was dealt with in [11], with separate enrichments used for each crack, and an additional enrichment function used to represent the junction itself. However, the formulation becomes cumbersome with increasing number of cracks and crack branches. Moreover, those methods suffer (in practice) from the absence of a reliable crack branching criteria.

In the last few years, several implementations of the XFEM have been presented in the literature. Bordas et al. in [3] developed object-oriented libraries for the XFEM. The implementation of the XFEM within a general-purpose Fortran finite element code was discussed in [28]. Wyart et al. in [29] proposed a substructuring approach to decompose a cracked domain into a safe subdomain and a cracked subdomain analyzed separately by FEM and XFEM codes, respectively. An alternative approach was pursued in [15], where the XFEM was implemented in the commercial finite element software Abaqus. Although Abaqus is a very general and well known finite element software tool, its XFEM package can handle only static analyses. Another important limitation of the XFEM in Abaqus is that only linear continuum elements are allowed.

2.3 Variational Approach: Phase-Field Models

Macroscopic continuum models for fracture can be classified into two main groups: (i) sharp-crack models, where crack surfaces are zero-traction boundaries extending to a sharp tip, and (ii) smeared-crack approaches, where the change in stiffness between broken and undamaged parts of an elastic material is modelled continuously with a damage parameter. The classical Griffith theory, as well as the variational approach to brittle fracture, belongs to the first group. In both theories the evolution of cracks results from a competition between a release of elastic energy and an increase of the surface energy. Thus, the energy release rate plays an important role in the determination of crack propagation. A numerical treatment of sharp-crack models is always faced with the difficulty of dealing with discontinuous displacement fields across the cracks. Phase-field models avoid these difficulties by introducing a continuous scalar field—the phase-field parameter—which smoothly interpolates between undamaged and failed states.

The reasons for introduction of variational approaches as a means to overcome limitations of LEFM were presented in Sect. 1 together with some models.

Standard approaches for dynamic crack propagation represent cracks as discrete discontinuities, either by inserting discontinuity lines, by means of remeshing techniques, or by enriching the displacement field with discontinuities using the partition of unity method. Tracing the evolution of complex fracture surfaces has, however, proven to be a tedious task, particularly in 3D. Contrarily, within the framework of a variational approach, discontinuities are not introduced into the solid. Instead, the fracture surface is approximated by a phase-field, which smoothens the boundary of the crack over a small region. The evolution of fracture surfaces follows from the solution of a coupled system of partial differential equations. From an implementation point of view, it does not require the fracture surfaces to be tracked algorithmically, which is particularly advantageous when multiple branching and merging cracks are considered in 3D. The numerical solution of the strong form of the equations of motion requires both spatial and temporal discretizations. The spatial discretization was carried out by means of the Galerkin method, either using the standard C 0-continuous finite elements [21], or, more recently, Non-Uniform Rational Basis Splines (NURBS) and T-Spline basis functions used within the framework of the Isogeometric Analysis [4]. For the temporal discretization, two different schemes were adopted: the monolithic scheme, which requires to solve the coupled system of equations simultaneously, and the staggered scheme, in which the displacements and the phase-field are solved for separately [19, 20].

A challenge that emerges with the use of phase-field models for fracture is their computational cost associated with mesh size requirements. Indeed, the use of a mesh with a characteristic length that is not small enough compared to the crack regularization parameter yields erroneous results with regard to the energy.

The variational approach is a robust technique for dealing with dynamic crack propagation problems. Still, it might be anticipated that, combining the advantages of partition of discrete methods (such as XFEM) and the variational approach will not be an easy task, although it could lead to a new efficient and reliable pathway to model complex fracture patterns.

One of the simplest two-dimensional isoparametric C 0-continuous finite elements is the four-node quadrilateral element, with three degrees of freedom per node, i.e. two displacement degrees of freedom and one phase-field degree of freedom per node. The discretization of arbitrarily shaped structures also requires an approximation of the geometry. The isoparametric concept makes use of the same shape functions to represent both the element geometries and the unknown displacement fields.

The presence of the transient term in the phase-field evolution equation requires the application of a time integration scheme in addition to the spatial discretization. For the temporal discretization, two different schemes can be adopted: (i) the monolithic scheme, based on the generalized-alpha method introduced in [10], which requires to solve the coupled system of equations simultaneously using a Newton-Raphson method, and (ii) the staggered scheme, in which the displacements and the phase-field are solved for separately [19, 20]. In the staggered time integration scheme, the momentum equation is solved first, at a given time step, in order to get the updated displacements. Using these updated displacements, the phase-field equation is solved subsequently. In addition to reducing the problem of solving two (possibly linear) systems, this scheme also allows greater flexibility in terms of how the momentum equation is solved, i.e., either implicit or explicit schemes can be used. This scheme can also be generalized to a predictor/multi-corrector format where additional Newton-Raphson iterations can be performed within a time step.

To be physically consistent, phase-field fracture models have to enforce irreversibility of the fracture process. In other words, all cracks must only grow with time. Different approaches were proposed in the literature to enforce irreversibility. The approach suggested in [6] constrains a subset of the discrete phase-field control variables that meet a minimum threshold value. This approach is easy to solve numerically but it requires the selection of an additional numerical parameter. An alternative approach, based on a strain-history functional was introduced in [21]. One advantage of this approach is its computational efficiency. The only computational cost is a floating point comparison, and it only requires storing one history variable per integration point. Another advantage of this approach is that an initial strain-history functional can be used to model initial cracks. Furthermore, the initial cracks can be located anywhere in the domain without reference to the mesh, which may prove highly advantageous in specifying complex surface cracks, in particular in three-dimensional bodies.

The width of the transition zone, where the phase-field interpolates between 1 and 0, is controlled by a length scale parameter. In order to obtain reasonable results, without overestimating the influence of the fractured zone, this length parameter should be chosen sufficiently small compared to the global dimensions of the considered sample. The mesh size has to be chosen sufficiently small in order to accurately resolve steep gradients and high curvatures of the crack field in the transition zones between cracked and uncracked areas. The accurate approximation of the crack field is important to capture the surface energy and, thus, the thresholds and dynamics of crack propagation correctly. However, small values of the length parameter require a high level of mesh refinement, which is numerically demanding in terms of computation time and required memory. Several approaches were proposed in the literature in order to meet the requirements for a sufficiently fine resolution, on the one hand, and to keep the computation time within bounds, on the other hand. In an effort to accomplish this, Kuhn and Muller [17, 18] introduced specially engineered finite element shape functions of an exponential nature to discretize the phase-field. These shape functions are parametrized by the ratio between the element size and the phase-field regularization parameter. Their results showed that, with these special shape functions, an accurate prediction of the surface energy associated with the phase-field is possible with a much lower level of refinement when compared to the standard finite element shape functions. The drawback of this approach is that some information regarding crack orientation is necessary for the proper construction of the exponential shape functions. Also, the choice of a good quadrature method is crucial for the performance of this approach.

3 Griffith’s Theory of Brittle Fracture

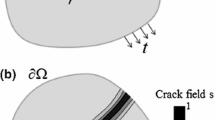
Consider an arbitrary body \(\Upomega \in {\mathcal{R}}^{2}\) with external boundary \(\partial \Upomega\) and an internal discontinuity boundary Γ. Let \({\partial \Upomega } = {\partial \Upomega }_{N} \cup {\partial \Upomega }_{D}\), with \({\partial \Upomega }_{N}\) and \({\partial \Upomega }_{D}\) being the Neumann and Dirichlet boundaries, respectively, such that \({\partial \Upomega }_{N} \cap {\partial \Upomega }_{D} = \emptyset\). The displacement of a point \(\varvec{x} \in\Upomega\) at time t is denoted by u(x, t). u may be a result of either the applied body forces b, tractions \(\bar{\varvec{t}}\), prescribed boundary displacements \(\bar{\varvec{u}}\), or a combination of these actions. The body is assumed linear elastic, homogeneous, and isotropic with Young’s modulus E, Poisson’s ratio ν and mass density ρ.

According to the Griffith’s theory of brittle fracture, the energy required to create a unit area of fracture surface is equal to the critical energy release rate \({\mathcal{G}}_{c}\).

The Lagrangian for the discrete fracture problem is

$$L(\varvec{u},\dot{\varvec{u}},\Gamma ) =\Pi _{k} (\dot{\varvec{u}}) -\Pi _{p} (\varvec{u},\Gamma )$$
(1)

where

$$\Pi _{k} = \int\limits_{\Upomega } \left( {\frac{1}{2}\rho \dot{\varvec{u}} \cdot \dot{\varvec{u}}} \right)d\Upomega$$
(2)

is the kinetic energy functional, and

$$\Pi _{p} = \int\limits_{\Upomega } W(\varvec{\varepsilon})\;d\Upomega + \int\limits_{\varGamma } {\mathcal{G}}_{c} \;d\Gamma$$
(3)

is the potential energy functional, with

$$\varvec{\varepsilon}= \varvec{Du}$$
(4a)
$$W(\varvec{\varepsilon}) = \frac{1}{2}\varvec{\varepsilon}^{T} \varvec{C\varepsilon }$$
(4b)
$$\varvec{\sigma}= \frac{\partial W}{{\partial\varvec{\varepsilon}}} = \varvec{C\varepsilon }$$
(4c)

Here, W represents the strain energy density. ε and σ are the infinitesimal strain vector and the Cauchy stress vector, respectively, represented in Voigt’s notation as follows

$$\varvec{\sigma}= \left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right],\varvec{\varepsilon}= \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {2\varepsilon_{xy} } \\ \end{array} } \right]$$
(5)

In (4a, 4b, 4c), D is the compatibilty operator and C is the constitutive matrix, defined as

$$\varvec{D} = \left[ {\begin{array}{*{20}l} {\frac{\partial }{{\partial x_{1} }}} \hfill & 0 \hfill \\ 0 \hfill & {\frac{\partial }{{\partial x_{2} }}} \hfill \\ {\frac{\partial }{{\partial x_{2} }}} \hfill & {\frac{\partial }{{\partial x_{1} }}} \hfill \\ \end{array} } \right]\quad {\text{and}}\quad \varvec{C} = \frac{1}{{E^{\prime}}}\left[ {\begin{array}{*{20}c} 1 & { - \nu^{\prime}} & 0 \\ { - \nu^{\prime}} & 1 & 0 \\ 0 & 0 & {2(1 + \nu^{\prime})} \\ \end{array} } \right]$$

where \(E^{\prime} = E,\;\nu^{\prime} = \nu\) for plane-stress problems, and \(E^{\prime} = E/(1 - \nu^{2} ),\;\nu^{\prime} = \nu /(1 - \nu )\) for plane-strain problems.

The Euler-Lagrange equations of this functional determine the motion of the body.

3.1 Phase-Field Approximation

In this approach, the fracture energy is approximated as

$$\int\limits_{\Gamma } {\mathcal{G}}_{c} \;d\Gamma \approx \int\limits_{\Omega} {\mathcal{G}}_{c} \left(\frac{{(1 - c)^{2} }}{4\varepsilon } + {\varepsilon} {\boldsymbol{\nabla }}c\right)\;d {\Omega}$$
(6)

where c is the phase-field, taking values from 0 to 1. c = 0 inside the crack and c = 1 away from the crack. ε is the regularization parameter that controls the width of the smooth approximation of the crack.

To model the loss of material stiffness in the failure zone, the strain energy density is redefined as

$$W(\varvec{\varepsilon},c) = \frac{1}{2}(c^{2} + \eta )\varvec{\varepsilon}^{T} \varvec{C\varepsilon }$$
(7)

where η is the small dimensionless parameter \(0\,<\, \eta \,{ \ll }\,1\) introduced to avoid numerical difficulties where the material is broken (i.e., where \(c = 0\)). The degradation of stiffness in the broken phase is modelled by the factor \((c^{2} + \eta )\).

Substitution of the phase-field approximation for the fracture energy (6) and the elastic energy density (7) into the Lagrange energy functional (1) yields

$$L(\varvec{u},\dot{\varvec{u}},c) = \int\limits_{\Upomega } \left(\frac{1}{2}\rho \dot{\varvec{u}} \cdot \dot{\varvec{u}} - \frac{1}{2}(c^{2} + \eta )\varvec{\varepsilon}^{T} \varvec{C\varepsilon }\right)\;d\Upomega - \int\limits_{\Upomega } {\mathcal{G}}_{c} \left(\frac{{(1 - c)^{2} }}{4 \epsilon} + \epsilon {\boldsymbol{\nabla }}c\right)\;d\Upomega$$
(8)

Note that, in order to conserve mass, the kinetic energy term is unaffected by the phase-field approximation.

The Euler-Lagrange equations of the problem can be used to arrive at the following strong form of the equations of motion in a Cartesian reference system \((x_{1} ,x_{2} )\) to be solved in Ω

$$\varvec{D}^{T}\varvec{\sigma}+ \varvec{b} = \rho {\varvec{\mathop {u}\limits^{..}}}$$
(9a)
$$\dot{c} = - M\left(c\varvec{\varepsilon}^{T} \varvec{C\varepsilon } - {\mathcal{G}}_{c} \left(2 \epsilon\Delta c + \frac{1 - c}{2\epsilon}\right)\right)$$
(9b)

with

$$\varvec{\sigma}= (c^{2} + \eta )\varvec{C\varepsilon }$$

Here, M is the mobility parameter, taken as constant and positive (classical Ginzburg-Landau equation).

The equations of motion are coupled with the phase-field c. Since c varies continuously, the singularity at the crack tip is replaced with a smooth region where c varies rapidly from 1 to 0.

It should also be emphasized that, within the framework of this model, the irreversibility condition \(\Gamma (t) \subseteq\Gamma (t +\Delta t)\) needs to be enforced.

Additionally, the following sets of boundary conditions

$$\begin{aligned} \varvec{u} & = \bar{\varvec{u}},\;{\text{on}}\;\partial \Upomega_{D} \\ {\mathbf{N}}\varvec{\sigma}& = \bar{\varvec{t}},\;{\text{on}}\;\partial \Upomega_{N} \\ \end{aligned}$$

with

$${\mathbf{N}} = \left[ {\begin{array}{*{20}l} {n_{1} } \hfill & 0 \hfill & {n_{2} } \hfill \\ 0 \hfill & {n_{2} } \hfill & {n_{1} } \hfill \\ \end{array} } \right]$$

where \(n_{j}\) are the components of the external unit normal n of \(\partial \Upomega_{N}\), and initial conditions

$$\begin{aligned} \varvec{u}(\varvec{x},0) & = \varvec{u}_{0} (\varvec{x}),\;\varvec{x} \in\Upomega \\ \dot{\varvec{u}}(\varvec{x},0) & = \varvec{v}_{0} (\varvec{x}),\;\varvec{x} \in\Upomega \\ \end{aligned}$$

must hold, where u 0 and v 0 are the initial displacements and velocities, respectively.

4 Finite Element Formulation

An implementation of the initial boundary-value problem into a finite element scheme is given in this section. The numerical solution of the initial boundary-value problem requires both a spatial and temporal discretization. In this work, the spatial discretization is formulated by means of the Galerkin method, whereas an implicit Euler method is adopted for the temporal discretization. In particular, for the discretization in space, four-node quadrilateral (bilinear Lagrangian) elements with three degrees of freedom per node, i.e., two displacement and one phase-field degrees of freedom per node, and a 2 × 2 Gauss quadrature rule are adopted in this work. The nonlinear coupled system of equations is solved using a Newton-Raphson algorithm.

4.1 Weak Form of the BVP

The trial solution spaces are defined as

$${\mathcal{U}}_{u} = \{ \varvec{u}(t) \in ({\mathcal{H}}^{1} (\Upomega ))^{d} |\varvec{u} = \bar{\varvec{u}}\;{\text{on}}\;\partial\Upomega _{D} \}$$
(10a)
$${\mathcal{U}}_{c} = \{ c(t) \in {\mathcal{H}}^{1} (\Upomega )\}$$
(10b)

Similarly, the weighting function spaces are defined as

$${\mathcal{V}}_{u} = \{ \varvec{w} \in ({\mathcal{H}}^{1} (\Upomega ))^{d} |\varvec{w} = 0\;{\text{on}}\;\partial \Upomega_{D} \}$$
(11a)
$${\mathcal{V}}_{c} = \{ q \in {\mathcal{H}}^{1} (\Upomega )\}$$
(11b)

Multiplying Eqs. 9a, 9b by the appropriate weighting functions and applying integration by parts leads to the following weak formulation: given \(\bar{\varvec{u}}\), \(\bar{\varvec{t}}\), b, \(\varvec{u}_{0}\), \(\varvec{v}_{0}\) and \(c_{0}\) find \(\varvec{u}(t) \in {\mathcal{U}}_{u}\) and \(c(t) \in {\mathcal{U}}_{c} ,\;t \in [0,T]\), such that for all \(\varvec{w} \in {\mathcal{V}}_{u}\) and \(q \in {\mathcal{V}}_{c}\), the following conditions hold

$$\int\limits_{\Upomega } (\sigma^{T} \varvec{Dw} + \rho {\varvec{\mathop {u}\limits^{..}}}^{T} \varvec{w})\;d\Upomega - \int\limits_{\Upomega } \varvec{b}^{T} \varvec{w}\;d\Upomega - \int\limits_{{\partial \Upomega_{N} }} \varvec{t}^{ - T} \varvec{w}\;d\partial \Upomega = 0$$
(12a)
$$\int\limits_{\Upomega } \left(\left(c\varvec{\varepsilon}^{T} \varvec{C\varepsilon } - \frac{{{\mathcal{G}}_{c} }}{\epsilon}(1 - c)\right)q - \frac{{\dot{c}}}{M}q +\varvec{\xi}^{T} {\mathbf{\nabla }}q\right)\;d\Upomega = 0$$
(12b)
$$\int\limits_{\Upomega } \rho (\varvec{u}^{T} (0) - \varvec{u}_{0}^{T} )\varvec{w}\;d\Upomega = 0$$
(12c)
$$\int\limits_{\Upomega } \rho (\varvec{v}^{T} (0) - \varvec{v}_{0}^{T} )\varvec{w}\;d\Upomega = 0$$
(12d)
$$\int\limits_{\Upomega } \rho (\varvec{c}(0) - \varvec{c}_{0} )q\;d\Upomega = 0$$
(12e)

4.2 Discrete Weak Form

Following the Galerkin method, the finite-dimensional approximations to the function spaces are assumed as \({\mathcal{U}}_{u}^{h} \in {\mathcal{U}}_{u} ,\;{\mathcal{U}}_{c}^{h} \in {\mathcal{U}}_{c} ,\;{\mathcal{V}}_{u}^{h} \in {\mathcal{V}}_{u}\) and \({\mathcal{V}}_{c}^{h} \in {\mathcal{V}}_{c}\), leading to the discrete form of the problem as: given \(\bar{\varvec{u}}\), \(\bar{\varvec{t}}\), b, \(\varvec{u}_{0}\), \(\varvec{v}_{0}\) and \(c_{0}\) find \(\varvec{u}^{h} (t) \in {\mathcal{U}}_{u}^{h}\) and \(c^{h} (t) \in {\mathcal{U}}_{c}^{h} ,\;t \in [0,T]\), such that for all \(\varvec{w}^{h} \in {\mathcal{V}}_{u}^{h}\) and \(q^{h} \in {\mathcal{V}}_{c}^{h}\), the following conditions hold

$$\int\limits_{\Upomega } (\varvec{\sigma}^{{h^{T} }} \varvec{Dw}^{h} + \rho {\varvec{\mathop {u}\limits^{..}}}^{{h^{T} }} \varvec{w}^{h} )\;d\Upomega - \int\limits_{\Upomega } \varvec{b}^{T} \varvec{w}^{h} \;d\Upomega - \int\limits_{{\partial \Upomega_{N} }} \varvec{t}^{ - T} \varvec{w}^{h} \;d\partial \Upomega = 0$$
(13a)
$$\int\limits_{\Upomega }\left (\left(c\varvec{\varepsilon}^{{h^{T} }} \varvec{C\varepsilon }^{h} - \frac{{{\mathcal{G}}_{c} }}{\epsilon}(1 - c^{h} )\right)q^{h} - \frac{{\dot{c}^{h} }}{M}q^{h} +\varvec{\xi}^{{h^{T} }} {\boldsymbol{\nabla }}q^{h}\right )\;d\Upomega = 0$$
(13b)
$$\int\limits_{\Upomega } \rho (\varvec{u}^{{h^{T} }} (0) - \varvec{u}_{0}^{T} )\varvec{w}^{h} \;d\Upomega = 0$$
(13c)
$$\int\limits_{\Upomega } \rho (\varvec{v}^{{h^{T} }} (0) - \varvec{v}_{0}^{T} )\varvec{w}^{h} \;d\Upomega = 0$$
(13d)
$$\int\limits_{\Upomega } \rho (\varvec{c}^{h} (0) - \varvec{c}_{0} )q^{h} \;d\Upomega = 0$$
(13e)

The explicit representations of the approximations for the displacement and phase-field variables in terms of the basis functions and nodal variables are

$$\varvec{u}^{h} = \sum\limits_{I} N_{I} \varvec{u}_{I}$$
(14a)
$$c^{h} = \sum\limits_{I} N_{I} c_{I}$$
(14b)

with \(I = 1,2,3,4\). Similarly, assuming that both the finite-dimensional trial solution and weighting function spaces are defined by the same set of basis functions, the approximations for the weighting functions are defined as

$$\varvec{w}^{h} = \sum\limits_{I} N_{I} \varvec{w}_{I}$$
(15a)
$$q^{h} = \sum\limits_{I} N_{I} q_{I}$$
(15b)

where the \(N_{I}\) are the global basis functions and u I , c I , w I and \(q_{I}\) are the nodal degrees of freedom.

Making use of these approximations, \(\varvec{\varepsilon}^{h}\) and \({\boldsymbol{\nabla }}c^{h}\) can be written as

$$\varvec{\varepsilon}^{h} = \sum\limits_{I} \varvec{B}_{I}^{u} \varvec{u}_{I}$$
(16a)
$${\boldsymbol{\nabla }}c^{h} = \sum\limits_{I} \varvec{B}_{I}^{c} c_{I}$$
(16b)

with

$$\varvec{B}_{I}^{u} = \left[ {\begin{array}{*{20}c} {N_{I,x} } & 0 \\ 0 & {N_{I,y} } \\ {N_{I,y} } & {N_{I,x} } \\ \end{array} } \right]\quad {\text{and}}\quad \varvec{B}_{I}^{c} = \left[ {\begin{array}{*{20}c} {N_{I,x} } \\ {N_{I,y} } \\ \end{array} } \right]$$

4.3 Element Residuals and Their Derivatives

To solve the resulting coupled nonlinear system of equations, an incremental iterative Newton-Raphson solution strategy based on a consistent linearization of the governing equations is used. The element residuals can be written as

$$\varvec{R}_{I}^{u} = - \varvec{F}_{int,I}^{u} + \varvec{F}_{ext,I}^{u}$$
(17a)
$$\varvec{R}_{I}^{c} = - \varvec{F}_{int,I}^{c}$$
(17b)

with

$$\varvec{F}_{{int} ,I}^{u} = \int\limits_{\Upomega } (\rho N_{I} {\varvec{\mathop {u}\limits^{..}}}^{h} + \varvec{B}_{I}^{{u^{T} }}\varvec{\sigma}^{h} )\;d\Upomega$$
(18a)
$$\varvec{F}_{ext,I}^{u} = \int\limits_{\Upomega } N_{I} \varvec{b}^{h} \;d\Upomega + \int\limits_{\Gamma } N_{I} \varvec{t}^{ - h} \;d\Upomega$$
(18b)
$$\varvec{F}_{{int} ,I}^{c} = \int\limits_{\Upomega } \left(N_{I} \frac{{\dot{c}^{h} }}{M} + \varvec{B}_{I}^{{c^{T} }}\varvec{\xi}^{h} + N_{I} \left(c^{h}\varvec{\varepsilon}^{{h^{T} }} \varvec{C\varepsilon }^{h} - \frac{{{\mathcal{G}}_{c} }}{2\epsilon}(1 - c^{h} )\right)\right)\;d\Upomega$$
(18c)

where \({\boldsymbol{\it{\xi}}}^{h} = 2{\mathcal{G}}_{c} \epsilon {\mathbf{\nabla }}c^{h}\).

The derivatives of the element residuals with respect to the nodal degrees of freedom come out as

$$\varvec{K}_{IJ}^{uu} = \frac{{\partial \varvec{R}_{I}^{u} }}{{\partial \varvec{u}_{J} }} = \int\limits_{\Upomega } \varvec{B}_{I}^{{u^{T} }} (c^{2} + \eta )\varvec{CB}_{J}^{u} \;d\Upomega$$
(19a)
$$\varvec{K}_{IJ}^{uc} = \frac{{\partial \varvec{R}_{I}^{u} }}{{\partial c_{J} }} = 2\int\limits_{\Upomega } \varvec{B}_{I}^{{u^{T} }} c\varvec{C\varepsilon }N_{J} \;d\Upomega$$
(19b)
$$\varvec{K}_{IJ}^{cc} = \frac{{\partial \varvec{R}_{I}^{c} }}{{\partial c_{J} }} = \int\limits_{\Upomega } \left(2\varvec{B}_{I}^{{c^{T} }} {\mathcal{G}}_{c} \varvec{\epsilon B}_{J}^{c} + N_{I} (\varvec{\varepsilon}^{T} \varvec{C\varepsilon } + \frac{{{\mathcal{G}}_{c} }}{2\epsilon})N_{J} \right)\;d\Upomega$$
(19c)
$$D_{IJ}^{cc} = \frac{{\partial \varvec{R}_{I}^{c} }}{{\partial \dot{c}_{J} }} = \int\limits_{\Upomega } N_{I} \frac{1}{M}N_{J} \;d\Upomega$$
(19d)
$$M_{IJ}^{uu} = \frac{{\partial \varvec{R}_{I}^{u} }}{{\partial {\varvec{\mathop {u}\limits^{..}}}_{J} }} = \int\limits_{\Upomega } N_{I} \rho N_{J} \;d\Upomega$$
(19e)

4.4 Time Discretization: Quasi-static Regime—Implicit Euler Method

The global residual vector that results from the assembly of the element residuals is defined as

$$\varvec{R}(\varvec{d},\dot{\varvec{d}}) = \varvec{F}_{ext} - \varvec{F}_{int} (\varvec{d},\dot{\varvec{d}}): = 0$$
(20)

Let d n and \(\dot{\varvec{d}}_{n}\) denote the global vector of degrees of freedom for time step n and its time derivative, respectively, defined as follows

$$\varvec{d} = \left[ {\begin{array}{*{20}c} {\varvec{d}_{1} } \\ {\varvec{d}_{2} } \\ \vdots \\ \end{array} } \right],\;\dot{\varvec{d}} = \left[ {\begin{array}{*{20}c} {\dot{\varvec{d}}_{1} } \\ {\dot{\varvec{d}}_{2} } \\ \vdots \\ \end{array} } \right]$$
(21)

with

$$\varvec{d}_{I} = \left[ {\begin{array}{*{20}c} {\varvec{u}_{I} } \\ {\varvec{c}_{I} } \\ \end{array} } \right],\;\dot{\varvec{d}}_{I} = \left[ {\begin{array}{*{20}c} {\dot{\varvec{u}}_{I} } \\ {\dot{\varvec{c}}_{I} } \\ \end{array} } \right]$$
(22)

The implicit (or backward) Euler method is stated as follows: given \((\varvec{d}_{n} ,\dot{\varvec{d}}_{n} )\), find \((\varvec{d}_{n + 1} ,\dot{\varvec{d}}_{n + 1} )\) such that

$$\varvec{R}(\varvec{d}_{n + 1} ,\dot{\varvec{d}}_{n + 1} ) = 0$$
(23)

with

$$\dot{\varvec{d}}_{n + 1} = \frac{{\varvec{d}_{n + 1} - \varvec{d}_{n} }}{{\Delta t}}$$
(24)

where \(\Delta t\) is the time step. This problem can be redefined as

$$\varvec{R}(\varvec{d}_{n} ,\varvec{d}_{n + 1} ) = 0$$
(25)

At each time step, the solution to this problem is obtained using a Newton-Raphson method to solve the non-linear system of equations. Letting k be the k-th Newton iteration step, the linearized system of equations that needs to be solved is

$$\varvec{R}_{n + 1}^{(k)} - \varvec{T}_{n + 1}^{(k)}\Delta \varvec{d}_{n + 1}^{(k)} = 0$$
(26)

with T the global tangent matrix, formed by assembly of the element matrices given by

$$\varvec{T}_{IJ} = \varvec{K}_{IJ} + \frac{1}{{\Delta t_{n} }}\varvec{D}_{IJ}$$
(27)

with

$$\varvec{K}_{IJ} = \left[ {\begin{array}{*{20}c} {\varvec{K}_{IJ}^{uu} } & {\varvec{K}_{IJ}^{uc} } \\ {\varvec{K}_{IJ}^{{uc^{T} }} } & {\varvec{K}_{IJ}^{cc} } \\ \end{array} } \right]$$
(28)

and

$$\varvec{D}_{IJ} = \left[ {\begin{array}{*{20}c} \varvec{O} & \varvec{O} \\ \varvec{O} & {D_{IJ}^{cc} } \\ \end{array} } \right]$$
(29)

being the element stiffness and damping matrices, respectively.

The problem is initialized with

$$\varvec{d}_{n + 1}^{(0)} = \varvec{d}_{n}$$
(30)

and the solution is computed iteratively using the update formula given by

$$\varvec{d}_{n + 1}^{(k + 1)} = \varvec{d}_{n + 1}^{(k)} +\Delta \varvec{d}_{n + 1}^{(k)}$$
(31)

where the increment \(\Delta \varvec{d}_{n + 1}^{(k)}\) is determined from the linearized system of Eq. 26. The iteration procedure continues until convergence of the residual vector is achieved.

4.5 Irreversibility of Cracking

Perhaps the most significant drawback of variational phase-field models is that they typically allow for crack healing. To rule out such unphysical behavior, Hakim and Karma proposed constraining the time-rate of the phase field to be less than or equal to zero at all points and times [16]. In simulations of quasi-static fracture processes in anti-plane shear and plane strain, they observed that, while slightly larger loads appear to be required when their irreversibility criterion is imposed, crack paths were essentially unaffected. Alternatively, following the approach proposed in [5], the irreversibility of cracking can be guaranteed by imposing homogeneous Dirichlet boundary conditions on the phase-field once a crack as been detected. The latter formulation is adopted in this work.

5 Numerical Results

5.1 Square Plate Under Quasi-static Prescribed Displacement

The square plate under quasi-static prescribed displacement depicted in Fig. 1 was considered. A uniform 64 × 64 mesh was adopted. The material parameters (assumed to be dimensionally consistent) were set to \(E = 10^{6} ,\;\nu = 0.3\) and \({\mathcal{G}}_{c} = 0.01\), and plane stress was assumed. The regularization, viscosity and mobility parameters were chosen to be \(\epsilon = 0.02,\;\eta = 10^{- 5}\) and \(M = 10^{9}\), respectively. The prescribed displacement was set to \(\bar{u} = 4.5 \times 10^{ - 4}\). The problem was solved in an incremental-iterative fashion by resorting to the Newton-Raphson method. An adaptive time-stepping scheme was used, for which the convergence tolerance was set to \(1.0 \times 10^{ - 9}\) and the optimal number of iterations to 4. For a larger number of iterations, the adaptive scheme automatically decreases the time step size, whereas for a smaller number of iterations the adaptive scheme increases it.

Fig. 1
figure 1

Square plate under quasi-static tensile load: problem definition

Full size image

The obtained distributions of stresses and phase-field are shown in Fig. 2. Two cracks initiate from the corners of the built-in edge at a displacement of \(\bar{u} = 2.9 \times 10^{ - 4}\). At \(\bar{u} = 4.1 \times 10^{ - 4}\) the cracks start deviating from the vertical edge. As expected, high stress gradients can be observed at the crack tips.

Fig. 2
figure 2

Square plate under quasi-static prescribed displacement: stresses and phase-field obtained on a 64 × 64 mesh for \(\bar{u} = 4.5 \times 10^{ - 4}\)

Full size image

The undeformed and deformed configurations of the plate are plotted in Fig. 3.

Fig. 3
figure 3

Square plate under quasi-static prescribed displacement: deformed (scaled) and undeformed configurations of the plate obtained for \(\bar{u} = 4.5 \times 10^{ - 4}\)

Full size image

5.2 Pre-notched Square Plate Under Quasi-static Prescribed Displacement

The pre-notched square plate under quasi-static prescribed displacement depicted in Fig. 4 is considered in this section. The same 64 × 64 mesh and material parameters were employed. The regularization, viscosity and mobility parameters remained at the same level. The prescribed displacement in this case was set to \(\bar{u} = 1.5 \times 10^{ - 4}\). The problem was solved in an incremental-iterative fashion similar to the previous example.

Fig. 4
figure 4

Pre-notched square plate under quasi-static prescribed displacement: problem definition

Full size image

The obtained distributions of stresses and phase-field are shown in Fig. 5.

Fig. 5
figure 5

Pre-notched square plate under quasi-static prescribed displacement: stresses and phase-field obtained on a 64 × 64 mesh for \(\bar{u} = 1.5 \times 10^{ - 4}\)

Full size image

The obtained results indicate that the proposed phase-field fracture model is capable to reproduce various complex phenomena, such as deflection or branching of pre-existing cracks, as well as the nucleation of new cracks in originally undamaged domains. However, a high resolution of the crack is needed, leading to computationally expensive simulations.

6 Conclusions

The numerical simulation of brittle fracture is still a significant challenge for the Computational Mechanics community. An overview of the main current numerical methods available in the literature for the analysis of brittle fracture problems was given. It can be concluded that discrete methods are well suited only for static fracture and a moderate number of cracks. On the other hand, continuum damage methods are not effective when modelling large dominant cracks. The recently introduced variational approach circumvents the implementation of complex crack-tracking algorithms and the need to describe the topology of the crack surface.

A finite element phase-field scheme relying on the variational approach to model brittle fracture problems was presented and some numerical experiments were implemented with this scheme. It was demonstrated that the presented model is capable to reproduce various complex phenomena, although it requires a high resolution of the crack, which may lead to computationally expensive simulations.