J-integral evaluation for 2D mixed-mode crack problems employing a meshfree stabilized conforming nodal integration method

Abstract

Two-dimensional (2D) in-plane mixed-mode fracture mechanics problems are analyzed employing an efficient meshfree Galerkin method based on stabilized conforming nodal integration (SCNI). In this setting, the reproducing kernel function as meshfree interpolant is taken, while employing the SCNI for numerical integration of stiffness matrix in the Galerkin formulation. The strain components are smoothed and stabilized employing Gauss divergence theorem. The path-independent integral (J-integral) is solved based on the nodal integration by summing the smoothed physical quantities and the segments of the contour integrals. In addition, mixed-mode stress intensity factors (SIFs) are extracted from the J-integral by decomposing the displacement and stress fields into symmetric and antisymmetric parts. The advantages and features of the present formulation and discretization in evaluation of the J-integral of in-plane 2D fracture problems are demonstrated through several representative numerical examples. The mixed-mode SIFs are evaluated and compared with reference solutions. The obtained results reveal high accuracy and good performance of the proposed meshfree method in the analysis of 2D fracture problems.

1 Introduction

Faithfully reproducing the displacement discontinuity across the crack faces and the stress singularity at the crack tip when solving linear fracture mechanics problems often requires effective numerical methods. The same requirement is also mandatory in modeling fast cracking problems. Meshfree/Meshless methods, e.g., the element free Galerkin method [1], the reproducing kernel (RK) particle method [2] and the meshless local Petrov-Galerkin method [3] provide advantages in analyzing crack problems. A cracked body is discretized using distributed nodes, and the deformation is approximated by meshfree interpolation functions based upon the nodes. It offers a flexible means in modeling cracks by using meshfree methods. Alternatively, the extended finite element method (X-FEM) was also introduced in [4] to effectively model cracks by adding appropriate enrichment functions into the standard finite element approximation space in terms of the partition of unity concept [5]. Researchers have employed and developed several other numerical methods for crack problems, e.g., see [6–13]. Tanaka et al. [14–16] analyzed two-dimensional (2D) fracture mechanics problems by combining X-FEM and a spline-based wavelet Galerkin method [17].

The present paper describes an effective meshfree Galerkin formulation for analyzing 2D in-plane mixed-mode fracture mechanics problems. In the Galerkin formulation, the RK function serving as basis functions is employed. With the RK approximation, the continuous stress and strain components can be obtained over the entire analysis domain. In addition, the stabilized conforming nodal integration (SCNI) [18] is applied to numerically integrate the stiffness matrix. The strain components are smoothed by a divergence theorem, and a linear exactness can be satisfied by imposing an integration constraint in the meshfree formulation. High accuracy and stabilized solutions are obtained without taking derivatives of the RKs. To date, the meshfree discretization has been adopted for a large deformation problems by Chen et al. [19]; Wang and Chen [20, 21] analyzed beam and plate bending problems. Wang and Sun [22] and Sadamoto et al. [23] solved geometrical nonlinear problems of a shear deformable plate based on the meshfree formulation. In the present formulation, a diffraction method and a visibility criterion [24, 25] are included to represent the displacement discontinuity along the crack segments. An enriched basis [26] is also introduced in the RKs to effectively represent the stress singularity around the crack tip.

A nodal integration technique is applied here to evaluate the path-independent integral (J-integral). Previously, the J-integral was often analyzed in domain-integral form, and an interaction integral technique was used to extract the 2D in-plane mixed-mode stress intensity factors (SIFs) from the J-integral, e.g., Fleming et al. [6], Rao and Rahman [27], and Tanaka et al. [14]. In the proposed technique, a contour integral is numerically analyzed based on the nodal integration. The J-value is calculated by summing the smoothed physical quantities and segments of the contour. To enhance the accuracy of the crack analysis and J-integral evaluation, sub-domain stabilized conforming integration (SSCI) [28–31] is thus adopted. In addition, mixed-mode SIFs are extracted from the J-integral by decomposing the displacement and stress fields into symmetric and antisymmetric parts [32, 33]. The J-integral evaluation is simple. The SIFs can be calculated by employing smoothed physical values and segments of the contour in post-processing of the meshfree analysis. Gauss quadrature is not required. In our previous study [34], we showed that the moment intensity factor and path-independent property obtained for a cracked shear deformable plate are highly accurate. In this paper, the accuracy of the mixed-mode SIFs and the path-independent nature are examined through several numerical examples for 2D in-plane crack problems. Because we developed a flat shell formulation in [23], a cracked shell problems can be analyzed when the in-plane fracture analysis is coupled with a plate bending formulation.

This paper is organized as follows. A 2D fracture mechanics analysis employing the proposed meshfree formulation and the discretization is described in Sect. 2. The J-integral evaluation and a mode splitting technique of the J-integral are presented in Sect. 3. Numerical examples for several 2D mixed-mode crack problems are considered and the obtained results are then presented in Sect. 4. Concluding remarks are presented in Sect. 5.

2 Meshfree Galerkin formulation

2.1 Boundary value problem for 2D cracked elastic solids

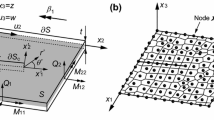
Let us consider a 2D cracked solid as schematically depicted in Fig. 1a. The material being considered is assumed to be elastic and small strain. The analysis domain is denoted by $\varOmega$, and its boundary by $\varGamma$. $\varGamma _{c}$ represents a crack segment. A traction force $\bar{\varvec{t}}$ is applied on the traction boundary $\varGamma _{t}$, while a prescribed displacement $\bar{\varvec{u}}$ is imposed on the displacement boundary $\varGamma _{u}$.

Fig. 1

Boundary value problem and the meshfree discretization: $\mathbf{a}$ A 2D cracked elastic body with a hole, $\mathbf{b}$ A meshfree discretization with Voronoi cell diagram

The principle of virtual work for the elastostatic body with zero body force can be written as:

$$\begin{aligned}&\int _{\varOmega } \varvec{\varepsilon } (\delta \varvec{u}) : \varvec{D} : \varvec{\varepsilon } (\varvec{u}) d\varOmega -\delta W=0, \nonumber \\&\delta W=\int _{\varGamma _{u}} \delta \varvec{u} \cdot \bar{\varvec{t}}\;d\varGamma , \nonumber \\&u_{i}({\varvec{x}})=\bar{u}_i\;\;\;on\;\;\;\varGamma _u, \end{aligned}$$

(1)

where $\varvec{u}$ is a displacement vector and $\delta \varvec{u}$ is the variation. $\delta W$ is the external virtual work. The symmetric part of the strain components $\varvec{\varepsilon } (\varvec{u})(=\varepsilon _{ij}$) are written as,

$$\begin{aligned} \varepsilon _{ij}=\frac{1}{2} \left( \frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}} \right) . \end{aligned}$$

(2)

The elastic constant matrix $\varvec{D}$ for the plane stress condition is

$$\begin{aligned} \varvec{D}= \frac{E}{1-\nu ^2} \left[ \begin{array}{ccc} 1 &{} \nu &{} 0 \\ \nu &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{1-\nu }{2} \end{array} \right] , \end{aligned}$$

(3)

and for plane strain condition

$$\begin{aligned} \varvec{D}= \frac{(1-\nu )E}{(1+\nu )(1-2\nu )} \left[ \begin{array}{ccc} 1 &{} \frac{\nu }{(1-\nu )} &{} 0 \\ \frac{\nu }{(1-\nu )} &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{1-2\nu }{2(1-\nu )} \end{array} \right] , \end{aligned}$$

(4)

with E and $\nu$ being the Young’s modulus and the Poisson’s ratio, respectively.

2.2 Meshfree discretization

A meshfree discretization for the cracked elastic body including a hole is schematically depicted in Fig. 1b. The nodes (${\varvec{x}}_{1}, \ldots , {\varvec{x}}_{I}, \ldots , {\varvec{x}}_{\mathrm{NP}}$) are distributed across the entire analysis domain, and Voronoi cells are used to establish subdomains ($\varOmega _1, \ldots , \varOmega _I, \ldots , \varOmega _{\mathrm{NP}}$) around each node. $\mathrm{NP}$ is the total number of nodes. The external and hole boundaries are represented by nodes and Voronoi cells. The crack tip is located on a node, and the crack segment is defined by an assembly of nodes. RK is adopted as the meshfree interpolant.

The RKs are defined at each node, and a physical value within the function support is approximated as shown in Fig. 1b. There are two degrees of freedom per node. A physical value at point ${\varvec{x}}$ is approximated using the RKs, and is written

$$\begin{aligned} \varvec{d}^h({\varvec{x}})=\sum _{I=1}^{\mathrm{NP}}\varPsi _{I}({\varvec{x}})\varvec{d}_{I}, \end{aligned}$$

(5)

where $\varvec{d}^{h}({\varvec{x}})=\{d_{1}^{h}({\varvec{x}}) \; d_{2}^{h}({\varvec{x}})\}^{T}$ ($I=1$, $\ldots$, $\mathrm{NP}$) is a vector of the approximated value. $\varPsi _{I}({\varvec{x}})$ is the RK of the I-th node and $\varvec{d}_{I}=\{d_{I1} \; d_{I2}\}^{T}$ is their coefficient vector. The RKs are constructed using the sum of the original kernels by imposing a so-called consistency condition

$$\begin{aligned} \varPsi _{I}({\varvec{x}})=\varvec{H}^{T}({\varvec{x}}_{I}-{\varvec{x}})\varvec{b}({\varvec{x}})\phi _{aI}({\varvec{x}}_{I}-{\varvec{x}}), \end{aligned}$$

(6)

where $\varvec{H}({\varvec{x}}_{I}-{\varvec{x}})$ is a basis vector, and $\varvec{b}({\varvec{x}})$ is the coefficient vector required to construct the RKs. When employing a linear basis vector, it is expressed as

$$\begin{aligned} \varvec{H}({\varvec{x}})=\{1 \;\; x_{1} \;\; x_{2} \}, \end{aligned}$$

(7)

whereas for the quadratic basis vector

$$\begin{aligned} \varvec{H}({\varvec{x}})=\{ 1 \;\; x_{1} \;\; x_{2} \;\; x_{1}^{2} \;\; x_{1}x_{2} \;\; x_{2}^{2} \}. \end{aligned}$$

(8)

$\phi _{aI}({\varvec{x}})$ in Eq. (6) is an original kernel. Cubic spline function is employed, as:

$$\begin{aligned} \phi _{aI}({\varvec{x}}_{I}-{\varvec{x}},h)=\frac{10}{7 \pi h^{2}} \left\{ \begin{array}{ll} 1-\frac{3}{2}s^{2}+\frac{3}{4}s^{3}&{}(0 \le s \le 1) \\ \frac{1}{4}(2-s)^{3}&{}(1 \le s \le 2)\;\;\;, \\ 0&{}(2 \le s) \end{array} \right. \end{aligned}$$

(9)

where $s= (||{\varvec{x}}_{I}-{\varvec{x}}||/h$) is a normalized distance from the center of the kernel, and h is a parameter that determines the function support. The RKs are modified so as to generate the crack effectively. Meshfree crack modeling is presented in Sect. 2.3.

The deformation $\varvec{u}({\varvec{x}})$ of the elastic body is approximated by the RKs, and it is written using the vector $\varvec{d}_{I}$ in matrix form

$$\begin{aligned} \varvec{u}^h({\varvec{x}})=\sum _{I=1}^{\mathrm{NP}}\varvec{N}_I\varvec{d}_I,\;\;\; \varvec{N}_I&= \left[ \begin{array}{cc} \varPsi _{I} &{} 0 \\ 0 &{} \varPsi _{I} \end{array} \right] , \end{aligned}$$

(10)

where $\varvec{u}^h({\varvec{x}})=\{u_{1}^h({\varvec{x}}) \; u_{2}^h({\varvec{x}}) \}^T$ denotes the approximate values of the displacements in the $x_i$ ($i=1,2$) direction and $\varvec{N}_I$ is a matrix of the RKs. The strain is thus expressed as

$$\begin{aligned} \varvec{\varepsilon }^h({\varvec{x}})=\sum _{I=1}^{\mathrm{NP}}\varvec{B}_I\varvec{d}_I,\;\;\; \varvec{B}_I&=\left[ \begin{array}{cc} \varPsi _{I,1} &{} 0 \\ 0 &{} \varPsi _{I,2} \\ \varPsi _{I,2} &{} \varPsi _{I,1} \end{array}\right] , \end{aligned}$$

(11)

where $\varvec{\varepsilon }^h({\varvec{x}})=\{\varepsilon _{11}^h({\varvec{x}}) \; \varepsilon _{22}^h({\varvec{x}}) \; 2\varepsilon _{12}^h({\varvec{x}}) \}^{T}$ is the approximated strain vector. $\varPsi _{I,i}$ is the partial derivative of the RKs, and $\varvec{B}_I$ is the displacement-strain matrix.

When analyzing the weak form in Eq. (1), SCNI [18] is introduced as the numerical integration technique for the stiffness matrix. The SCNI satisfies the integration constraint, which is a necessary condition for a linear exactness in the meshfree Galerkin methods. Numerical instabilities due to a spurious mode of the stiffness matrix can be excluded by a direct nodal integration.

Fig. 2

Schematic outlining nodal integration of a Voronoi cell with SCNI [18]

Fig. 3

Crack modeling by the meshfree method: $\mathbf{a}$ diffraction method, $\mathbf{b}$ visibility criterion and polar coordinate system around the crack tip, $\mathbf{c}$ SSCI [28]

An illustration of SCNI for a Voronoi cell is presented in Fig. 2. The strain components are evaluated by a line integration of the RKs, and are smoothed by employing the Gauss divergence theorem. Equation (11) can be rewritten

$$\begin{aligned}&\tilde{\varvec{\varepsilon }}^h({\varvec{x}})=\sum _{I=1}^{\mathrm{NP}}\tilde{\varvec{B}_I}\varvec{d}_I,\;\;\; \tilde{\varvec{B}_I}=\left[ \begin{array}{cc} \tilde{b}_{I1} &{} 0 \\ 0 &{} \tilde{b}_{I2} \\ \tilde{b}_{I2} &{} \tilde{b}_{I1} \end{array} \right] ,\end{aligned}$$

(12)

$$\begin{aligned}&\tilde{b}_{Ij}({\varvec{x}}_{K})=\frac{1}{A_{K}}\int _{\varGamma _{K}} \varPsi _{I}n_{j} d\varGamma _{K}, \end{aligned}$$

(13)

where $n_j$ ($j=1,2$) denotes the $x_{j}$-component of the normal vector $\varvec{n}$ and $A_{K}$ is the area of domain $\varOmega _K$. A line integration in Eq. (13) is employed along the Voronoi cell boundary $\varGamma _{K}$ shown in Fig. 2. The smoothed strain $\tilde{{\varvec{\varepsilon }}}({\varvec{x}})$ is evaluated for each node of the Voronoi cell. Five Gauss quadrature points are applied for the numerical integration of each segment.

A penalty formulation is introduced to impose the essential boundary conditions. The principle of virtual work can be written as

$$\begin{aligned}&\int _{\varOmega } \varvec{\varepsilon } (\delta \varvec{u}) : \varvec{D} : \varvec{\varepsilon } (\varvec{u})d\varOmega \nonumber \\&\quad +\alpha \int _{\varGamma _{u}} \delta \varvec{u} \cdot (\varvec{u}-\bar{\varvec{u}}) d\varGamma =\int _{\varGamma _t} \delta \varvec{u} \cdot \bar{\varvec{t}}\; d\varGamma , \end{aligned}$$

(14)

where $\alpha$ is a penalty parameter and $\bar{\varvec{u}}$ is an enforced value vector along the essential boundaries $\varGamma _u$. Displacements, smoothed strains and elastic constant matrix are introduced in Eq. (14), and a set of linear simultaneous equations derived. There are no derivative of the RKs in the meshfree discretization.

2.3 Crack modeling

To analyze 2D in-plane fracture mechanics problems in the meshfree formulation, a diffraction method and a visibility criterion [24, 25] are adopted to represent displacement discontinuities across the crack segment. Also, an enriched basis [26] is introduced to effectively represent strong stress concentration around the crack tip. Crack modeling is employed to analyze a bending cracked plate as well in [34]. The adaptation to the 2D in-plane crack problems is briefly reviewed.

A diffraction method is introduced to represent a displacement discontinuity when a crack tip partially cut the meshfree functions. A schematic illustration is presented in Fig. 3a. When a crack tip is located in the function support of a RK, the support is modified so as to wrap around the crack tip. The normalized distance in Eq. (9) is then corrected

$$\begin{aligned} s=\left( \frac{s_{1}+s_{2}({\varvec{x}})}{s_{0}({\varvec{x}})}\right) ^{\lambda } \frac{s_{0}({\varvec{x}})}{h}, \end{aligned}$$

(15)

where $s_{0}({\varvec{x}})=||{\varvec{x}}-{\varvec{x}}_{I}||$, $s_{1}=||{\varvec{x}}_{c}-{\varvec{x}}_{I}||$ and $s_{2}({\varvec{x}})=||{\varvec{x}}-{\varvec{x}}_{c}||$. The shape factor $\lambda$ is chosen as unity. The modifications of the meshfree functions are employed for the displacement matrix $\varvec{N}_I$ in Eq. (10).

The visibility criterion is employed to represent a displacement discontinuity of the crack segment. When a meshfree function crosses the segment, double nodes are made on the segment. The numerical integration of the stiffness matrix is partially performed for either one or the other sides of the RKs (see Fig. 3b). In addition, an enriched term is introduced in the basis vector $\varvec{H}({\varvec{x}})$ in Eqs. (7) and (8) to effectively represent a strong stress concentration near the crack tip. For the linear basis,

$$\begin{aligned} \varvec{H}({\varvec{x}})=\{ 1 \;\;\; x_{1} \;\;\; x_{2} \;\;\; \sqrt{r'}\sin (\theta '/2) \}, \end{aligned}$$

(16)

and for the quadratic basis,

$$\begin{aligned} \varvec{H}({\varvec{x}})=\{ 1 \;\;\; x_{1} \;\;\; x_{2} \;\;\; x_{1}^{2} \;\;\; x_{1}x_{2} \;\;\; x_{2}^{2} \;\;\; \sqrt{r'}\sin (\theta '/2) \}, \end{aligned}$$

(17)

where $r'$ and $\theta '$ are local polar coordinates at the crack tip (Fig. 3b). The enriched basis is adopted around the crack tip. This is an effective and convenient way to capture the $1/\sqrt{r'}$ stress-singularity around the crack tip in the meshfree discretization.

To accurately integrate the stiffness matrix including a visibility criterion, a diffraction method and an enriched basis vector, SSCI [28] is introduced. In crack modeling, a Voronoi cell is partially/completely cut by a segment (Fig. 3b). A Voronoi cell is further divided into a number of triangles, and SCNI is adopted on each triangle. An illustration of SSCI is sketched in Fig. 3c. A Voronoi cell $\varOmega _{K}$ is composed of a number of triangles, and the components of the smoothed B-matrix $\tilde{\varvec{B}_I}$ in Eq. (13) is defined on each triangle $\varOmega _{K_i}$, and is written as

$$\begin{aligned}&\tilde{b}_{Ij}({\varvec{x}}_{K_i})=\frac{1}{A_{K_i}}\int _{\varGamma _{K_i}} \varPsi _{I}n_{j} d\varGamma _{K_i}, \end{aligned}$$

(18)

where $\varGamma _{K_i}$ is the boundary of a surface $\varOmega _{K_i}$, and $n_{j}$ ($j=1,2$) denotes the $x_{j}$ component of the normal vector to the boundary $\varGamma _{K_i}$ in Fig. 3c. The strain and stress components are stabilized in the triangles $\varOmega _{K_i}$. The smoothed strain $\tilde{{\varvec{\varepsilon }}}({\varvec{x}})$ in Eq. (12) is evaluated at the center of gravity of each triangle.

3 SIFs evaluation

A path-independent integral is adopted to calculate SIFs in the meshfree method. An energetic contour integral is analyzed. When evaluating fracture mechanics parameters in 2D in-plane mixed-mode crack problems, it is necessary to separate the J-value into crack opening and in-plane shear modes. A method of decomposition [32, 33, 35] is introduced to evaluate the mixed-mode SIFs $K_I$ and $K_{II}$ by splitting the displacement and stress fields into symmetric and antisymmetric parts. The contour integral is evaluated by the smoothed values in post-processing of the meshfree analysis. A special subroutine for the Gauss quadrature is not required in the discretization.

3.1 J-integral review

A schematic illustration of a crack tip region, and the J-integral evaluation is shown in Fig. 4a. A surface traction on the crack face is not considered. $\varGamma _\mathrm{Jint}$ denotes the contour surrounding the crack tip and $\varvec{n}'$ denotes the normal vector to the $\varGamma _\mathrm{Jint}$. $x_1$ and $x_2$ are global coordinates, while $x'_1$ and $x'_2$ are local coordinates at the crack tip. The $x'_1$ direction is defined as being parallel to the crack segment. $\theta '$ and $r'$ are the local polar coordinates with origin centered on the crack tip. Proposed by Rice [36], the J-integral is written as

$$\begin{aligned} J=\int _{\varGamma _\mathrm{Jint}} \left( Wn_{1}'-\sigma _{ij}'\frac{\partial u_{i}'}{\partial x_{1}'}n_{j}' \right) d\varGamma _\mathrm{Jint}, \end{aligned}$$

(19)

where $n_{j}'$ ($j=1,2$) are the components of the normal vector and W is the strain energy density, which is given by

$$\begin{aligned} W=\int \sigma _{ij}' d\varepsilon _{ij}'. \end{aligned}$$

(20)

When a linear elastic solid is considered, the J-value corresponds to the energy release rate G. It is noted that the J-value is path-independent.

Fig. 4

J-integral and the separation of the deformation modes in 2D in-plane mixed-mode crack problems: $\mathbf{a}$ J-integral evaluation, $\mathbf{b}$ Symmetric and antisymmetric displacement/stress components are evaluated at points $P(x_{1}', x_{2}^{\prime })$ and $Q(x_{1}^{\prime }, -x_{2}^{\prime })$

3.2 A decomposition method for J-integral mode separation

In mixed-mode crack problems, it is necessary to separate the energy release rate G into opening mode $G_{I}$ and shear mode $G_{II}$ components to evaluate the mixed-mode SIFs $K_{I}$ and $K_{II}$, i.e., $G=G_{I}$+$G_{II}$. A method of decomposition is chosen in the contour integral discretization. The SIFs can be evaluated in the line integral also by separating the displacement/stress components into symmetric and antisymmetric parts.

A close-up view of the crack tip region is depicted in Fig. 4b. The point $Q(x_{1}', -x_{2}')$ is line symmetric to point $P(x_{1}', x_{2}')$ across the crack segment. The components of displacement $\varvec{u}'$ and stress $\varvec{\sigma }'$ are then decomposed using points $P(x_{1}', x_{2}')$ and $Q(x_{1}', -x_{2}')$, respectively. For example, the displacements $\varvec{u}'_{P}$ and stress components $\varvec{\sigma }'_{P}$ at $P(x_{1}', x_{2}')$ are represented as

$$\begin{aligned} {\varvec{u}'_{P}}&={ (\varvec{u}'_{P})^{I} } + { (\varvec{u}'_{P})^{II} } \nonumber \\&= \frac{1}{2}\left\{ \begin{array}{c} u_{1P}'+u_{1Q}'\\ u_{2P}'-u_{2Q}' \end{array} \right\} + \frac{1}{2}\left\{ \begin{array}{c} u_{1P}'-u_{1Q}'\\ u_{2P}'+u_{2Q}' \end{array} \right\} , \end{aligned}$$

(21)

$$\begin{aligned} {\varvec{\sigma }'_{P}}&={(\varvec{\sigma }'_{P})^{I}}+{(\varvec{\sigma }'_{P})^{II}}\nonumber \\&= \frac{1}{2}\left\{ \begin{array}{c} \sigma _{11P}'+\sigma _{11Q}'\\ \sigma _{22P}'+\sigma _{22Q}'\\ \sigma _{12P}'-\sigma _{12Q}' \end{array} \right\} + \frac{1}{2}\left\{ \begin{array}{c} \sigma _{11P}'-\sigma _{11Q}'\\ \sigma _{22P}'-\sigma _{22Q}'\\ \sigma _{12P}'+\sigma _{12Q}' \end{array} \right\} , \end{aligned}$$

(22)

where ${(\varvec{u}')^{k}}$ and ${(\varvec{\sigma }')^{k}}$ ($k=I, II$) are the displacement and stress components for mode-I and -II, respectively. $(\;\;)_{P}$ and $(\;\;)_{Q}$ are the components at points $P(x_{1}', x_{2}')$ and $Q(x_{1}', -x_{2}')$, respectively.

Fig. 5

Schematic of a contour integral discretization for Gauss quadrature using a rectangular contour

Employing the displacement ${(\varvec{u}')^{k}}$ and stress components ${(\varvec{\sigma }')^{k}}$ for mode-I and -II in Eqs. (21) and (22), the mixed-mode energy release rates $G_{k}$ are evaluated as

$$\begin{aligned} G_{k}=\int _{\varGamma _\mathrm{Jint}} \left( W_{k}n_{1}'-{(\sigma _{ij}')^{k}}\frac{\partial {(u_{i}')^{k}}}{\partial x_{1}'}n'_{j} \right) d\varGamma _\mathrm{Jint}, \end{aligned}$$

(23)

where $W_{k}$ ($k=I,II$) is the strain energy density of mode-k, which is calculated by the separated strain ${(\varvec{\varepsilon }')^{k}}$ and stress ${(\varvec{\sigma }')^{k}}$ components employing Eq. (20). The separated energy release rates $G_{k}$ also have a path-independent nature.

To decompose the displacement/stress components in separating the J-integral into the mixed-mode SIFs, a symmetric contour across the crack segment is required. A rectangular contour is chosen as shown in Fig. 5. The contour $\varGamma _\mathrm{Jint}$ is divided into a number of segments, and the unit length is $ds_{m}$ ($m=1, \ldots , N_\mathrm{Seg}$). $N_\mathrm{Seg}$ is the total number of the segments. Equation (19) is discretized by adopting the Gauss quadrature rule, as:

$$\begin{aligned} G_{k}=\sum _{m=1}^{N_\mathrm{Seg}}\left\{ \sum _{l=1}^{N_\mathrm{Gauss}}\left( {W}_{k} n_{1}'-{{(\sigma }_{ij}')^{k}}\frac{\partial {({u}_{i}')^{k}}}{\partial x_{1}'}n_{j}' \right) \omega _l \right\} _{m} ds_{m}, \end{aligned}$$

(24)

where $N_\mathrm{Gauss}$ is the number of Gauss points per a segment. and $\omega _l$ the weight of the Gauss quadrature.

Employing the energy release rates $G_{k}$, the SIFs can be evaluated giving

$$\begin{aligned} K_{I}=\sqrt{E'G_{I}},\;\;\;K_{II}=\sqrt{E'G_{II}}, \end{aligned}$$

(25)

where $E'=E$ for plane stress condition, and $E'=E/(1-\nu ^{2})$ for plane strain condition, respectively.

3.3 J-integral evaluation employing the nodal integration techniques

In the present formulation, nodal integration techniques SCNI/SSCI are employed to integrate the stiffness matrix numerically. The SCNI/SSCI are also adopted for the J-integral evaluation. In our previous study, a moment intensity factor was calculated by employing the SCNI/SSCI in [34]. The nodal integration techniques are adopted and examined for the 2D in-plane mixed-mode crack problems.

Rectangular contours are also adopted in nodal integrations as shown in Fig. 5. In the meshfree discretization, the contour integral in Eq. (24) includes a number of Voronoi cells and triangular domains for SCNI/SSCI. The discretization of the contour integral with SCNI and SSCI are shown in Fig. 6a and b, respectively. The energy release rates are smoothed $\tilde{G}_{k}$, and are evaluated using smoothed physical quantities,

$$\begin{aligned} \tilde{G}_{k}&= \sum _{m=1}^{N_\mathrm{SCNI}} \left( \tilde{W}_{k}n_{1}'-{(\tilde{\sigma }_{ij}')^{k}}\frac{\partial {(\tilde{u}_{i}')^{k}}}{\partial x_{1}'}n_{j}' \right) _{m} ds_{m} \nonumber \\&\quad \, + \sum _{m=1}^{N_\mathrm{SSCI}} \left( \tilde{W}_{k}n_{1}'-{(\tilde{\sigma }_{ij}')^{k}}\frac{\partial {(\tilde{u}_{i}')^{k}}}{\partial x_{1}'}n_{j}' \right) _{m} ds_{m}, \end{aligned}$$

(26)

where $(\;\tilde{\;}\;)$ represents the smoothed physical values calculated by SCNI/SSCI, and $ds_m$ is the segment divided by a Voronoi cell and a triangular domain for SCNI and SSCI, as shown in Fig. 6a and b. $N_\mathrm{SCNI}$ and $N_\mathrm{SSCI}$ are the number of segments for SCNI/SSCI used for the contour integral evaluation. The physical quantities of SCNI are determined based on nodes, and the values of SSCI are calculated at the center of gravity for each triangle.

The physical values in the nodal integration form of the J-integral is evaluated by the post-process of the meshfree analysis. The smoothed displacements $\tilde{\varvec{u}}$ can be calculated by SCNI, as

$$\begin{aligned} {\tilde{\varvec{u}}({\varvec{x}}_{K})=\sum _{I=1}^{\mathrm{NP}}\frac{1}{A_{K}}\int _{\varOmega _{K}} \varPsi _{I}\varvec{d}_{I} d\varOmega _{K},} \end{aligned}$$

(27)

and for SSCI, as

$$\begin{aligned} {\tilde{\varvec{u}}({\varvec{x}}_{K_i})=\sum _{I=1}^{\mathrm{NP}}\frac{1}{A_{K_i}}\int _{\varOmega _{K_i}} \varPsi _{I}\varvec{d}_{I} d\varOmega _{K_i},} \end{aligned}$$

(28)

where $\varvec{d}_{I}$ is a solution vector evaluated by a linear simultaneous equation. Smoothed strain $\tilde{\varvec{\varepsilon }}$ and stress $\tilde{\varvec{\sigma }}$ ($=\!\varvec{D}\tilde{\varvec{\varepsilon }}$) calculated by SCNI/SSCI are given by Eq. (12). The strain energy density in Eq. (26) can de evaluated, as:

$$\begin{aligned} {\tilde{W}_k=\frac{1}{2}(\tilde{\sigma }_{ij}')^k(\tilde{\varepsilon }_{ij}')^k.} \end{aligned}$$

(29)

Fig. 6

Meshfree discretization of a contour integral employing nodal integration techniques: $\mathbf{a}$ SCNI, $\mathbf{b}$ SSCI

Fig. 7

Three kinds of numerical integration domains with SCNI/SSCI for a cracked plate: $\mathbf{a}$ A meshfree model for a cracked plate, $\mathbf{b}$ Type A, $\mathbf{c}$ Type B, $\mathbf{d}$ Type C

Although a special subroutine for the Gauss quadrature is needed for calculating $G_{k}$ in Eq. (24), they can be evaluated using the superposition of the physical quantities and segments of the contour employing Eq. (26). The accuracy and the path-independence of the nodal integration techniques for the SIFs are explored through several 2D mixed-mode fracture problems.

4 Numerical examples

Several numerical examples for 2D in-plane fracture mechanics problems are considered to examine the meshfree discretization and the J-integral evaluation. A plane stress condition is assumed. Young’s modulus is $E=206$ GPa, and Poisson’s ratio is $\nu =0.3$. According to our numerical test, an acceptable solution can be obtained when the penalty parameter in Eq. (14) is chosen as $\alpha =1.0\,\times \,10^7$, in all the numerical examples. In adopting the enriched basis vectors of Eqs. (16) and (17), an enriched term $\sqrt{r'}\sin (\theta '/2)$ is introduced on the nodes when the function support includes the crack tip.

A meshfree model of a cracked plate is illustrated in Fig. 7a. $r_d$ is a parameter determining the size of the rectangular contour. To verify the accuracy and effectiveness of modeling the crack, three kinds of numerical integration domains with SCNI/SSCI, which are labeled as Types A, B and C, respectively, are examined (Fig. 7b–d). In Type A, the Voronoi cells are generated over the entire rectangular domain for SCNI. Additionally, the Voronoi cells spanning the crack segment are divided into triangular domains for SSCI, in preparing for the diffraction method and visibility criterion. In Type B, the entire domain is divided into triangular domains for SSCI. Type C has hybrid domains of SCNI/SSCI. A Voronoi cell is chosen for the entire the domain, and the triangular domains are partially employed when the function support spans a crack segment and/or contour. If a rectangular contour $2r_d\,\,\times \,\,2r_d$ is used for the J-integral evaluation as shown in Fig. 7a, the shaded regions in Fig. 7b–d are taken as the nodal integration domain.

The accuracy in the mixed-mode SIFs for the numerical and reference solutions is examined. The error $\eta$ $\%$ is defined as

$$\begin{aligned} \eta =\frac{| K_k^{\mathrm{Num.}}-K_k^\mathrm{Ref.} |}{K_k^{\mathrm{Ref.}}} \,\,\times \,\, 100\;\;[\%], \end{aligned}$$

(30)

where $K_{k}^{\mathrm{Num.}}$ and $K_{k}^{\mathrm{Ref.}}$ ($k=I, II$) are the numerical and reference solutions, respectively.

4.1 An edge crack under uniform tensile loads

A rectangular plate with an edge crack of $a=5.0$ mm as depicted in Fig. 8a is considered. The plate width is $b=10.0$ mm, and the height is $c=10.0$ mm. A uniform pressure $\sigma _{22}=1.0$ MPa is applied to the top and bottom edges of the plate. To verify the accuracy of the meshfree analysis, 21$\,\,\times \,\,$21, 41$\,\times \,$41, 81$\,\,\times \,\,$81 and 161$\,\,\times \,\,$161 nodes models are chosen. The function support of the RKs is set to be $h=1.2h^{p}$, with $h^{p}$ being a characteristic length between the nodes as shown in Fig. 7a. Three kinds of nodal integration domains of Types A, B and C as defined above are examined. For example, a computational model of 21$\,\,\times \,\,$21 scattered nodes (Type A) is sketched in Fig. 8b. The standard linear, enriched linear, and enriched quadratic basis vectors $\varvec{H}({\varvec{x}})$ of Eqs. (7), (16), and (17) are employed to examine the performance of the enriched basis vectors. $K_{I}^{\mathrm{Ref.}}=11.93~\hbox {MPa}$ mm$^{1/2}$ [37] is presented as our reference solution.

Fig. 8

Edge crack in a rectangular plate, and meshfree modeling: $\mathbf{a}$ Model to be analyzed, $\mathbf{b}$ 21$\,\,\times \,\,$21 nodes meshfree model (Type A)

Fig. 9

Comparison of SIF $K_{I}$ for different paths (A standard linear basis vector): $\mathbf{a}$ Type A, $\mathbf{b}$ Type B

The numerical results $K_{I}^{\mathrm{Num.}}$ of Type A are presented in Fig. 9a. The horizontal axis is a parameter $r_d$. The $K_{I}^{\mathrm{Num.}}$ is evaluated by varying the size of the rectangular contour. A standard linear basis vector $\varvec{H}({\varvec{x}})$ in Eq. (7) is applied. The solid line is the reference solution $K_{I}^{\mathrm{Ref.}}$. As the density of the nodes increases, the accuracy in SIF $K_{I}$ is improved. In contrast, an oscillation in $K_{I}^{\mathrm{Num.}}$ can be observed dependent on the size of the rectangular contour.

To further examine the accuracy of the meshfree discretization, Type B is employed as the nodal integration domain. The standard linear basis vector is employed, as in Fig. 9a. The results are presented in Fig. 9b. Although the convergence rate of $K_{I}^{\mathrm{Num.}}$ in Type B is similar to that of Type A, path-independency is found. Therefore, the SSCI is effective for evaluating the J-integral in the meshfree crack modeling.

It is found that $K_{I}^{\mathrm{Num.}}$ uniformly converges in Type B, as the density of the nodes increases (Fig. 9b). There is still a difference between the numerical results and the reference solutions even when a model with a set of 81$\,\,\times \,\,$81 scattered node is used. The standard linear, enriched linear, and enriched quadratic basis vectors of Eqs. (7), (16), and (17) are adopted. The error $\eta$ $\%$ is evaluated using Eq. (30). Type B is employed for the nodal integration domain. The size of the contour is $r_d=2.5$ mm. The convergence rates for each of the basis vectors are presented in Fig. 10a. All numerical results uniformly converge. Additionally, it is confirmed that a high accuracy solution can be obtained in adopting the enriched linear and quadratic basis vectors.

Although the use of Type B is effective for the nodal integration domain, it takes considerable computation time because the meshfree modeling uses only triangular domain for the nodal integration. A hybrid nodal integration domain of SCNI/SSCI (Type C) is taken to reduce the computational time, while retaining the accuracy of the meshfree analysis. The accuracy in SIF $K_{I}^{\mathrm{Num.}}$ is presented in Fig. 11. An enriched quadratic basis vector is employed. From the numerical results, a high accuracy of the SIF and a path-independent behavior are obtained for the SCNI/SSCI hybrid nodal integration domain.

Fig. 10

Convergence for the edge crack problem with standard and enriched basis vectors (Type B, $r_d=2.5$ mm)

Fig. 11

Comparison of SIF $K_{I}$ for different paths (Type C, an enriched quadratic basis vector)

In addition, accuracy in SIF $K_{I}$ is examined when the diffraction method or visibility criterion is adopted at the crack tip. The numerical results are presented in Fig. 12. The quadratic basis vector is employed. From the convergence study, the accuracy is improved when diffraction method is employed. We thus employ the diffraction method at the crack tip.

Fig. 12

Comparison of SIF $K_{I}$ for diffraction method and visibility criterion at the crack tip (Type C, an enriched quadratic basis vector)

Fig. 13

Rectangular plate with an edge crack under shear loads: $\mathbf{a}$ Model for analysis, $\mathbf{b}$ 15$\,\,\times \,\,$33 nodes meshfree model (Type A)

Fig. 14

Convergence results for the mixed-mode SIFs employing the enriched linear and quadratic basis vectors (Type C, $r_d=1.75$ mm): $\mathbf{a}$ $K_{I}$, $\mathbf{b}$ $K_{II}$

A meshfree analysis for cracked plate bending problems was analyzed in [34] employing the crack modeling and the J-integral evaluation. A similar trend in accuracy and path-independency nature was found for a pure-$K_I$ problem. This thus confirms that meshfree modeling is effective for both the 2D in-plane and plate bending problems.

Fig. 15

SIFs for different rectangular paths (An enriched quadratic basis vector): $\mathbf{a}$ $K_{I}$ (Type A), $\mathbf{b}$ $K_{II}$ (Type A), $\mathbf{c}$ $K_{I}$ (Type C), $\mathbf{d}$ $K_{II}$ (Type C)

4.2 An edge crack under shear loads

A cracked rectangular plate under shear loads is analyzed to check the accuracy and the path-independent nature of the mixed-mode crack problem. The model is presented in Fig. 13a. The parameter settings for the cracked rectangular plate are $a/b=1/2$ and $c/b=16/7$ to the plate breadth $b=7.0$ mm. A uniform shear stress $\tau =1.0$ MPa is applied to the top of the plate, whereas the bottom of the plate is fully clamped. Different sets of 15$\,\,\times \,\,$33, 29$\,\times \,$65, 43$\,\,\times \,\,$97 and 71$\,\,\times \,\,$161 nodes meshfree models are successively employed. A meshfree model with a set of 15$\,\,\times \,\,$33 discretized nodes (Type A) is visualized in Fig. 13b. As reference SIFs, $K_{I}^{\mathrm{Ref.}}=34.0$ MPa mm$^{1/2}$ and $K_{II}^{\mathrm{Ref.}}=4.55$ MPa mm$^{1/2}$ are available in the literature [39]. The function support of the RKs is set to $h=1.2h^{p}$.

A convergence study was performed to examine the accuracy of the enriched basis vectors for the mixed-mode crack problem. The linear and quadratic basis vectors of Eqs. (16) and (17), respectively, are used. Type C is employed as a nodal integration domain. The convergence of $K_{I}^{\mathrm{Num.}}$ and $K_{II}^{\mathrm{Num.}}$ are then depicted in Fig. 14a and b. The size of the contour $r_d=1.75$ mm is taken. It is interesting to see that all the numerical results are uniformly converged. The accuracy in $K_I$ and $K_{II}$ is improved using the enriched basis vectors. Also, the accuracy of the quadratic basis vector is superior in the mixed-mode crack problem.

To further examine the mixed-mode crack problem, path-independency in $K_{I}$ and $K_{II}$ is investigated. Also, Types A and C are adopted for the nodal integration domains. The obtained numerical of Type A are presented in Fig. 15a and b, for $K_{I}$ and $K_{II}$ respectively, and the results of Type C are in Fig. 15c and d. As well as the pure-$K_I$ problem in Sect. 4.1, path-independency can be seen when Type C is employed for the nodal integration domain. It can also be confirmed that the evaluation of the energy release rates using SCNI/SSCI of Eq. (26), and Type C for the nodal integration domain are effective in the mixed-mode crack problems in separating the J-value into $K_I$ and $K_{II}$. In the following numerical examples, the quadratic basis vector and Type C are used in the meshfree modeling.

To effectively analyze several 2D in-plane mixed-mode crack problems, we derived an equation relating the crack length a and the characteristic length between the nodes $h^{p}$ in the uniform refinement models. From the results of convergence studies plotted in Fig. 14a and b for $K_I$ and $K_{II}$, we infer that the solutions of SIFs have converged sufficiently and possessed a path-independency if $a/h^{p}>$15 is adopted.

4.3 A slanted edge crack under uniform tensile loads

A rectangular plate with a slanted edge crack as schematically shown in Fig. 16a is analyzed. The dimensions of the model are $b=10.0$ mm and $c_{1}=c_{2}=10.0$ mm. The crack length is varied $a=2.0, 3.0, 4.0$, and 5.0 mm, respectively, and crack angles $\theta =30$ and 45 deg. are chosen. A meshfree model with a set of 41$\,\,\times \,\,$101 scattered nodes is used. Fig. 16b shows a close-up view near the crack tip. Notice that, unlike the two previous examples, an irregular nodal discretization is applied to this domain, showing the capability of the method in dealing with irregular distribution of the nodes. The function support of the RKs is set to $h=1.2h^{p}$. For the inclined crack problem, nodes on uniform grid are placed around the crack tip to separate the mixed-mode SIFs. The region is smoothly connected to the external area using meshfree modeling. Additionally, $\tilde{G}_{k}$ of Eq. (26) is evaluated for a rectangular contour within the grid (Fig. 16b). The SIFs were normalized, and the computed numerical results compared with reference solutions given in [37]. The results are also compared with those obtained by using a commercial FEM software [38] with a very fine mesh.

The results obtained for SIFs with $\theta =30$ and 45 deg. are presented in Tables 1 and 2 for different ratios of a / b; $r_d=a$/3 mm is adopted. The $F_{k}^{\mathrm{Num.}}$, $F_{k}^{\mathrm{FEM}}$ and $F_{k}^{\mathrm{Ref.}}$ ($k=I, II$) are results of the meshfree, FEM and reference solutions, respectively. As expected, they are in good agreement between each other. Additionally, differences in the SIFs between the meshfree and FEM results are less than 1 %.

Fig. 16

Rectangular plate with a slant edge crack problem: $\mathbf{a}$ the model analyzed, $\mathbf{b}$ close-up view of the crack tip region in 41$\,\,\times \,\,$101 nodes meshfree model (Type A)

Table 1 Normalized SIFs $F_{I}$ and $F_{II}$ for $\theta =30{^\circ }$

Table 2 Normalized SIFs $F_{I}$ and $F_{II}$ for $\theta =45{^\circ }$

4.4 A semi-circular specimen with a slant crack

The final numerical example deals with a slanted edge crack in a semi-circular specimen. The model configuration is presented in Fig. 17a. The radius of the semi-circular plate is $R=100$ mm, the crack length $a=50$ mm, and the plate thickness $t=1.0$ mm. The specimen is fixed by pins, and a point load P is applied on top of the specimen. The width between the supports is s. Three ratios $s/R=0.5$, 0.61, and 0.67 are chosen in the meshfree modeling, by changing the crack angle $\theta$ from 0 to $60{^\circ }$. The meshfree model is generated so that the characteristic length $h^{p}$ is 2.5 mm. For example, a meshfree model with $s/R=0.5$ and $\theta =30$ deg. is given in Fig. 17b. The function support of RKs is set to $h=1.25h^{p}$. The SIFs are normalized by

$$\begin{aligned} F_{k}=\frac{2Rt K_{k}}{P \sqrt{\pi a}},\;\;\;(k=I, II) \end{aligned}$$

(31)

where $F_{k}$ denotes the normalized SIFs. As reference solutions, the SIFs in [40] is digitized and employed. Also, a very fine FEM model as shown in Fig. 17c is used for our comparison purpose [38].

Fig. 17

Edge crack in a semi-circular specimen: $\mathbf{a}$ Analysis model, $\mathbf{b}$ Meshfree modeling for $\theta =30$ deg. and $s/R=0.5$ (Type A), $\mathbf{c}$ FEM model

The numerical results of the normalized SIFs $F_{k}^{\mathrm{Num.}}$ ($k=I$, II) are respectively presented in Fig. 18a–c, for $s/R=0.5$, 0.61, and 0.67. In the meshfree modeling, $r_d=10.0$ mm is chosen. $F_{k}^{\mathrm{FEM}}$ and $F_{k}^{\mathrm{Ref.}}$ are also presented. In all cases, the results are in good agreement with each other, thereby confirming that the meshfee modeling is effective in analyzing the 2D in-plane mixed-mode crack problems.

Fig. 18

Comparison of normalized SIFs $F_{I}$ and $F_{II}$ (An enriched quadratic basis vector, Type C): $\mathbf{a}$ $s/R=0.5$. $\mathbf{b}$ $s/R=0.61$. $\mathbf{c}$ $s/R=0.67$

5 Conclusion

We have presented an effective meshfree Galerkin formulation based on SCNI for modeling 2D in-plane mixed-mode crack problems. The J-integral is discretized in terms of the SCNI/SSCI, and a special technique to separate the mixed-mode SIFs is described. The accuracy, performance and the path-independency of the proposed meshfree method are analyzed and demonstrated through a series of representative numerical examples. The computed numerical results are verified rigorously by comparing the obtained results with respect to the reference solutions. The comparison reveals one important thing that, as expected, high accuracy on the SIFs derived from the proposed formulation is obtained. It is also found from our numerical investigations that the present formulation is very effective in modeling crack problems.