The complex variable reproducing kernel particle method for the analysis of Kirchhoff plates

Abstract

In this paper, the complex variable reproducing kernel particle method (CVRKPM) for the bending problem of arbitrary Kirchhoff plates is presented. The advantage of the CVRKPM is that the shape function of a two-dimensional problem is obtained one-dimensional basis function. The CVRKPM is used to form the approximation function of the deflection of a Kirchhoff plate, the Galerkin weak form of the bending problem of Kirchhoff plates is adopted to obtain the discretized system equations, and the penalty method is employed to enforce the essential boundary conditions, then the corresponding formulae of the CVRKPM for the bending problem of Kirchhoff plates are presented in detail. Several numerical examples of Kirchhoff plates with different geometry and loads are given to demonstrate that the CVRKPM in this paper has higher computational precision and efficiency than the reproducing kernel particle method under the same node distribution. And the influences of the basis function, weight function, scaling factor, node distribution and penalty factor on the computational precision of the CVRKPM in this paper are discussed.

1 Introduction

The bending problem of Kirchhoff plates is one of the important research topics in solid mechanics. An overview of the existing literature reveals that most of the previous exact analyses were developed using the semi-inverse method for Levy-type plates. It is rather difficult to obtain trial functions satisfying the non-simply supported boundary conditions and natural boundary conditions. Then many researchers have put in considerable efforts to develop efficient numerical methods to solve this problem.

In classical thin plate theory introduced by Kirchhoff, the governing equation about the deflection $w$ is a fourth order elliptic partial differential equation. Due to the complicated equation, the finite element method (FEM) for solving the bending problem of Kirchhoff plates was developed with some challenges [1]. The boundary element method (BEM) was presented to solve the problems of the static bending of thin and thick plates [2, 3]. In the BEM, the high-order singularity of the kernel functions requires the corresponding algorithms of numerical integrations with high precision [4].

Beyond the traditional FEM and BEM, meshless (or meshfree) methods have been developed to solve a lot of problems in the past decades. The shape functions in meshless methods depend on the nodes in the problem domain, and can solve many complicated problems with high precision without the remeshing technique [5, 6]. Many meshless methods, such as smooth particle hydrodynamics (SPH) method [7], diffuse element method (DEM) [8], element-free Galerkin (EFG) method [9], improved element-free Galerkin (IEFG) method [10–14], interpolating element-free Galerkin method [15–17], meshless local Petrov–Galerkin (MLPG) method [18], reproducing kernel particle method (RKPM) [19], reproducing kernel element method (RKEM) [20–23], local Petrov–Galerkin approach with moving Kriging interpolation [24–27], element-free kp-Ritz method [28], complex variable meshless method [29–37], and meshless with boundary integral equation methods [38–44], have been developed.

The moving least-squares (MLS) approximation is widely used to form the shape function in many meshless methods, but the MLS approximation is the approximations of the scalar functions, and thus the meshless methods that is derived from it require a lot of nodes in the domain. The complex variable moving least-squares (CVMLS) approximation was developed for the approximation of a vector function [45, 46]. Under similar computational precision, the meshless methods based on the CVMLS approximation can distribute fewer nodes in the domain than the ones based on the MLS approximation. Combining the CVMLS approximation with the Galerkin weak form, the complex variable element-free Galerkin (CVEFG) method was presented for two-dimensional elasticity, fracture, elastodynamics, elastoplasticity and viscoelasticity problems [47–52].

The RKPM is another one of important meshless methods [53, 54]. It has been used to analyze structural dynamics [55, 56], large deformation [57, 58], and fluid mechanics problems [59]. Similar to the MLS approximation, the RKPM is the approximation for scalar functions. Then the RKPM requires a lot of nodes in the domain, and the shape functions and their derivatives must be obtained at every node, which leads to a great computational cost. Hence, the complex variable reproducing kernel particle method (CVRKPM) for the approximation of a vector function was developed by the authors of this paper, and was then applied to some problems [29–36]. The advantage of the CVRKPM is that the correction function of a 2D problem is formed with 1D basis function when the shape functions are obtained. Then the number of unknown coefficients of the correction function in the CVRKPM is fewer than the one in the RKPM, then for an arbitrary point in the domain we need fewer nodes which support domains cover the point. And in the CVRKPM the dimension of the matrices used to form the shape functions and their derivatives is reduced, which improves greatly the computational efficiency without loss of the computational accuracy. In addition, the fewer unknown coefficients are also lead to the fewer nodes required in the entire domain of a problem, then under the same node distribution, the CVRKPM has greater precision than the RKPM.

In recent years, some meshless methods have been applied to plate problems. Belytschko et al. have used the EFG method to solve thin plate problems [60]. Liu et al. presented the meshfree method for static and free vibration problems of thin plates [61, 62]. Liu et al. [63] and Sladek et al. [64] proposed meshfree methods for numerical simulations of large deflection of plates. Long et al. applied respectively the MLPG method and meshless local boundary integral equation method for the analysis of thin plates [65–67]. Atluri et al. presented the MLPG method to analyze thick plate problems [68]. Li et al. applied the RKEM to solve Kirchhoff plate problems [22, 23]. Tinh et al. proposed a moving Kriging interpolation-based meshfree method for numerical simulation of Kirchhoff plates problems [69, 70]. And Yan et al. presented the dual reciprocity hybrid radial boundary node method to solve Kirchhoff plates [71].

In this paper, the CVRKPM for solving the bending problem of Kirchhoff plates is presented. The Galerkin weak form is used to obtain the discretized system equations, and the penalty method is employed to apply the essential boundary conditions, then the corresponding formulations of the CVRKPM for the analysis of thin plates are obtained in detail. Several numerical examples are presented to verify the accuracy of the CVRKPM, and the corresponding numerical results are compared with the ones of the RKPM and the analytical solutions to show the advantages of the present method.

2 Governing equations and some definitions of the Kirchhoff plate

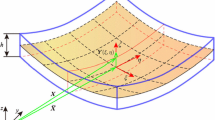
A Kirchhoff plate, defined on the plate domain $\Omega$ enclosed by the boundary $\Gamma$, is considered, and a Cartesian reference system $Ox_1 x_2 x_3$ located on its middle plane is used (see Fig. 1). The thin plate with uniform thickness $h$ is subjected to a transversal distributed load $q(x_1,x_2 )$ per unit area.

Fig. 1

Thin plate subjected to transverse distributed load

In Kirchhoff plate theory, the displacements $u$ and $v$, which parallel to the undeformed middle plane, can be expressed as

$$\begin{aligned} u&= -x_3 \frac{\partial w}{\partial x_1 },\end{aligned}$$

(1)

$$\begin{aligned} v&= -x_3 \frac{\partial w}{\partial x_2 }, \end{aligned}$$

(2)

where $w$ is the transversal displacement of the middle plane, which is also called the deflection of the middle plane of the thin plate in the $x_3$ direction. It is clearly shown that the deflection $w$ of the thin plate can be regarded as the field variable of the bending problem of thin plates.

For the homogeneous and isotropic Kirchhoff plate, the governing equation for the deflection can be written as

$$\begin{aligned} D_0 \nabla ^{4}w(x_1,x_2 )=q(x_1,x_2 ), \quad \left( {(x_1,x_2 )\in \Omega } \right) , \end{aligned}$$

(3)

where $\nabla ^{4}( \cdot )$ is a biharmonic operator,

$$\begin{aligned} \nabla ^{4}( \cdot )=\frac{\partial ^{4}( \cdot )}{\partial x_1^4 }+2\frac{\partial ^{4}( \cdot )}{\partial x_1^2 \partial x_2^2 }+\frac{\partial ^{4}( \cdot )}{\partial x_2^4 }, \end{aligned}$$

(4)

$D_0$ is the flexural stiffness of Kirchhoff plate,

$$\begin{aligned} D_0 =\frac{Eh^{3}}{12\left( 1-\nu ^{2}\right) }, \end{aligned}$$

(5)

$E$ is Young’s modulus, $\nu$ is Poisson’s ratio, and $h$ is the thickness of the thin plate.

The essential boundary conditions are

$$\begin{aligned}&w=\bar{{w}}, \quad \left( {(x_1,x_2 )\in \Gamma _{u_1 }} \right) ,\end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial w}{\partial {\mathbf {n}}}=\bar{{\theta }}_n, \quad \left( {(x_1 ,x_2 )\in \Gamma _{u_2 } } \right) ; \end{aligned}$$

(7)

and the natural boundary conditions are

$$\begin{aligned}&M_n =\bar{{M}}_n, \quad \left( {(x_1,x_2 )\in \Gamma _{t_1 } } \right) ,\end{aligned}$$

(8)

$$\begin{aligned}&V_n =\bar{{V}}_n, \quad \left( {(x_1,x_2 )\in \Gamma _{t_2 } } \right) , \end{aligned}$$

(9)

where $M_n$ and $V_n$ are the bending moment and the effective shear force, respectively; $\bar{{w}}$, $\bar{{\theta }}_n$, $\bar{{M}}_n$ and $\bar{{V}}_n$ are the prescribed deflection on the essential boundary $\Gamma _{u_1 }$, the rotation angle about the tangent to the essential boundary $\Gamma _{u_2 }$, the bending moment on the natural boundary $\Gamma _{t_1 }$, and the effective shear force on the natural boundary $\Gamma _{t_2 }$, respectively; ${\mathbf {n}}$ denotes the outward normal direction to the natural boundary $\Gamma$.

3 The approximation of the CVRKPM

Suppose that the problem domain $\Omega$ is discretized by a set of nodes $\{z_1,z_2,\ldots ,z_n \}$, and $n$ is the total number of nodes. Using the CVRKPM, the approximation $w^{h}(z)$ of a function $w(z)$ at an arbitrary point $z, z=x_1 +\hbox {i}x_2$, is defined as

$$\begin{aligned} w^{h}(z)=\sum _{I=1}^N {\tilde{\varPhi }_I (z)\cdot w_I } =\tilde{\varvec{\varPhi } }(z)\cdot {\mathbf {w}}, \end{aligned}$$

(10)

where

$$\begin{aligned}&\tilde{\varPhi }_I (z)=\hbox {Re}[\varPhi _I (z)],\end{aligned}$$

(11)

$$\begin{aligned}&\tilde{\varvec{\varPhi }}(z)=\left( \tilde{\varPhi }_1 (z),\tilde{\varPhi }_2 (z), \ldots ,\tilde{\varPhi }_N (z)\right) ,\end{aligned}$$

(12)

$$\begin{aligned}&{\mathbf {w}}=(w_1,w_2, \ldots , w_N )^\mathrm{T}, \end{aligned}$$

(13)

$N$ is the number of nodes which support domains cover the point $z$, $w_I$ is the node deflection at the node $z_I$ in the middle plane of the thin plate; $\varPhi _I (z)$ is the shape function of the CVRKPM,

$$\begin{aligned} \varPhi _I (z)=C(z;z-z_I )w_h (z-z_I )\Delta V_I, \end{aligned}$$

(14)

$\Delta V_I$ is the volume of node $z_I$, $w_h (z-z_I )$ is the weight function, $C(z;z-z_I )$ is the correction function, which is expressed as

$$\begin{aligned}&C(z;z-z_I )=\sum _{i=0}^m {p_i (z-z_I )\cdot b_i (z)} = {\mathbf {p}}^{\mathrm{T}}(z-z_I ){\mathbf {b}}(z),\end{aligned}$$

(15)

$$\begin{aligned}&{\mathbf {b}}^{\mathrm{T}}(z)=(b_0 (z), b_1 (z), \ldots , b_m (z)), \end{aligned}$$

(16)

$m$ is the highest order of polynomial basis functions, and $p_i (z-z_I )$ are the basis functions, which can be chosen as

• Quadratic basis:

  $$\begin{aligned} {\mathbf {p}}^{\mathrm{T}}(z-z_I )=(1, (z-z_I ), (z-z_I )^{2}), \;\;\hbox {and}\;\; m=2;\nonumber \\ \end{aligned}$$

  (17)

• Cubic basis:

  $$\begin{aligned} {\mathbf {p}}^{\mathrm{T}}\!=\!(1, (z-z_I ), (z-z_I )^{2}, (z-z_I )^{3}), \;\;\hbox {and}\;\; m\!=\!3;\nonumber \\ \end{aligned}$$

  (18)

• Quartic basis:

  $$\begin{aligned}&{\mathbf {p}}^{\mathrm{T}}=(1, (z-z_I ), (z-z_I )^{2}, (z-z_I )^{3}, (z-z_I )^{4}),\nonumber \\&\quad \hbox {and}\;\; m=4. \end{aligned}$$

  (19)

The quintic spline weight function is defined as

$$\begin{aligned} w_h (r)=\left\{ {{\begin{array}{l@{\quad }l} 1-10r^{2}+20r^{3}-15r^{4}+4r^{5}, \quad &{}0\le r\le 1, \\ 0, \quad &{}{r>1}\\ \end{array}}}\right. \nonumber \\ \end{aligned}$$

(20)

where $r=\frac{d_I }{\rho _I }, \,d_I =\left| {z-z_I } \right| , \,\rho _I =d_{\mathrm{max}} \cdot c_I$ is the size of the support domain of the weight function at node $z_I$, $d_{\mathrm{max}}$ is the scaling factor of the support domain of the weight function, and $c_I$ is the least distance between node $z_I$ and other nodes.

The coefficients $b_i (z)$ in Eq. (16) are obtained via the reproducing conditions, i.e.

$$\begin{aligned} {\mathbf {G}}(z)\cdot {\mathbf {b}}(z)={\mathbf {H}}, \end{aligned}$$

(21)

where

$$\begin{aligned} {\mathbf {G}}(z)=\sum _{I=1}^m {{\mathbf {p}}(z-z_I )\cdot {\mathbf {p}}^{\mathrm{T}}(z-z_I )} \cdot w_h (z-z_I )\cdot \Delta V_I,\nonumber \\ \end{aligned}$$

(22)

and

$$\begin{aligned} {\mathbf {H}}=(1, 0, \ldots , 0)^{\mathrm{T}}. \end{aligned}$$

(23)

Then we have

$$\begin{aligned} {\mathbf {b}}(z)={\mathbf {G}}^{-1}(z)\cdot {\mathbf {H}}. \end{aligned}$$

(24)

The advantage of the CVRKPM is that the correction function of a two-dimensional problem is obtained using one-dimensional basis function, which leads to the fewer unknown coefficients in the CVRKPM than those in the RKPM. Especially for the bending problem of thin plates, the second derivatives of the shape functions are involved, then the highest order of polynomial basis functions is at least quadratic. For the quadratic basis, the basis function in the RKPM is ${\mathbf {p}}^{\mathrm{T}}=\left( 1, x_1 -{x}'_1 , x_2 -{x}'_2 , (x_1 -{x}'_1 )^{2}, (x_1 -{x}'_1 )(x_2 -{x}'_2 ), (x_2 -{x}'_2 )^{2}\right)$, and six unknown coefficients are needed, however the basis function in the CVRKPM is ${\mathbf {p}}^{\mathrm{T}}=\left( 1, z-{z}', (z-{z}')^{2}\right)$, and only three unknown coefficients are needed. Accordingly, for the cubic basis, ten unknown coefficients are needed in the RKPM, but only four unknown coefficients are needed in the CVRKPM. Because the fewer unknown coefficients will result in fewer dimension of the matrix ${\mathbf {G}}$, the inversion of the matrix ${\mathbf {G}}$ and the product of matrices can be obtained simply and rapidly. Then the CVRKPM has greater computational efficiency than the RKPM.

In addition, because the unknown coefficients are fewer, we need fewer nodes which support domains cover the point $z$. Then we also require fewer nodes in the entire domain of a problem. Accordingly, under the same node distribution in the problem domain, the CVRKPM has greater precision than the RKPM [29, 30].

4 The CVRKPM for the analysis of Kirchhoff plates

In this section, the formulae of the CVRKPM for the analysis of Kirchhoff plates are obtained in detail.

We define respectively pseudo-strain and pseudo-stress as

$$\begin{aligned} {\varvec{\varepsilon }_{p}} =\left[ {{\begin{array}{c} {-\frac{\partial ^{2}w}{\partial x_1^2 }} \\ {-\frac{\partial ^{2}w}{\partial x_2^2 }} \\ {-2\frac{\partial ^{2}w}{\partial x_1 \partial x_2 }} \\ \end{array} }} \right] ={\mathbf {L}}w \end{aligned}$$

(25)

and

$$\begin{aligned} {\varvec{\sigma }_{p}} =\left[ {{\begin{array}{c} {M_{11} } \\ {M_{22} } \\ {M_{12} } \\ \end{array} }} \right] ={{\mathbf {D}}\varvec{\varepsilon }_{p}}, \end{aligned}$$

(26)

where ${\mathbf {L}}$ is the differential operator matrix,

$$\begin{aligned} {\mathbf {L}}(\cdot )=\left[ {{\begin{array}{c} {-\frac{\partial ^{2}}{\partial x_1^2 }} \\ {-\frac{\partial ^{2}}{\partial x_2^2 }} \\ {-2\frac{\partial ^{2}}{\partial x_1 \partial x_2 }} \\ \end{array} }} \right] ( \cdot ), \end{aligned}$$

(27)

$M_{ii} , \quad i=1, 2,$ is the bending moment at $x_i$ direction, $M_{12}$ is the twisting moment; ${\mathbf {D}}$ is a matrix of constants related to the material property and the thickness of the plate, and for homogeneous plates,

$$\begin{aligned} {\mathbf {D}}=D_0 \left[ {{\begin{array}{c@{\quad }c@{\quad }c} 1&{} \quad \nu &{} \quad 0 \\ \nu &{} \quad 1&{} \quad 0 \\ 0&{} \quad 0&{} \quad {\frac{1-\nu }{2}} \\ \end{array} }} \right] . \end{aligned}$$

(28)

The Galerkin weak form is employed to discretize the governing equation. Because the shape functions of the CVRKPM do not satisfy the property of Kronecker $\delta$ function, the essential boundary conditions can not be applied directly. In this paper, penalty method is used to impose the essential boundary conditions. The corresponding constrained Galerkin weak form can be given as [62, 65]

$$\begin{aligned}&\int _{\Omega } \delta \varvec{\varepsilon }_{p}^{\mathrm{T}} \cdot \varvec{\sigma }_{p} \hbox {d}{\Omega } - \int _{\Omega } {\delta w \cdot q\hbox {d}\Omega } - \int _{{\Gamma }_{{t_{1}}}} \delta \left( {\frac{\partial w}{\partial {\mathbf {n}}}}\right) \bar{M}_{n} \hbox {d}\Gamma \nonumber \\&\quad - \int _{\Gamma _{t_{2}}} {\delta w\bar{V}_{n} \hbox {d}\Gamma }+ \int _{\Gamma _{u_{1}}} \delta \left( {w - \bar{w}} \right) \cdot \alpha _{1} \cdot \left( {w - \bar{w}} \right) \hbox {d}\Gamma \nonumber \\&\quad + \int _{\Gamma _{u_{2}}} \delta \left( {\frac{{\partial w}}{{\partial {\mathbf {n}}}}} - \bar{\theta } \right) ^{\mathrm{T}} \cdot \alpha _{2} \cdot \left( {\frac{{\partial w}}{{\partial {\mathbf {n}}}}} - \bar{\theta } \right) \hbox {d}\Gamma = 0, \end{aligned}$$

(29)

where $\alpha _{1}$ and $\alpha _{2}$ are penalty factors which are used to apply the essential boundary conditions. In this paper, when

$$\begin{aligned} \alpha _{1} = \alpha _{2} = (1.0\sim 1.0 \times 10^{1} )E, \end{aligned}$$

(30)

we can obtain the solutions with high precision.

By using the stress–strain relationship Eq. (26) and the strain–displacement relationship Eqs. (25), (29) can be explicitly expressed as

$$\begin{aligned}&\int _{\Omega } \delta ({\mathbf {L}}w)^{\mathrm{T}} \cdot {\mathbf {D}} \cdot ({\mathbf {L}}w)\hbox {d}\Omega - \int _{\Omega } \delta w \cdot q\hbox {d}\Omega \nonumber \\&\quad + \int _{\Gamma _{t_{1}}} \delta \left( {\frac{{\partial w}}{{\partial {\mathbf {n}}}}} \right) \cdot \bar{M}_{n} \hbox {d}\Gamma - \int _{\Gamma _{t_{2}}} \delta w \cdot \bar{V}_{n} \hbox {d}\Gamma \nonumber \\&\quad + \int _{\Gamma _{u_{1}}} \delta (w - \bar{w}) \cdot \alpha _{1} \cdot (w - \bar{w})\hbox {d}\Gamma \nonumber \\&\quad + \int _{\Gamma _{u_{2}}} \delta \left( {\frac{{\partial w}}{{\partial {\mathbf {n}}}} - \bar{\theta }} \right) ^{\mathrm{T}} \cdot \alpha _{2} \cdot \left( {\frac{{\partial w}}{{\partial {\mathbf {n}}}} - \bar{\theta }} \right) \hbox {d}\Gamma = 0. \end{aligned}$$

(31)

From Eq. (10), we have

$$\begin{aligned} {\mathbf {L}}w&= {\mathbf {L}}\left( \sum _{I=1}^{N} \tilde{\varPhi }_I w_I \right) =\sum _{I=1}^N {\mathbf {L}}(\tilde{\varPhi }_I w_I)\nonumber \\&= \sum _{I=1}^N {\left[ {{\begin{array}{c} {-\frac{\partial ^{2}}{\partial x_1^2 }} \\ {-\frac{\partial ^{2}}{\partial x_2^2 }} \\ {-2\frac{\partial ^{2}}{\partial x_1 \partial x_2 }} \\ \end{array} }} \right] (\hbox {Re}[\varPhi _I (z)]\cdot w_I )}\nonumber \\&= \sum _{I=1}^N {\left[ {{\begin{array}{c} {-\hbox {Re}[\varPhi _{I,11} ]} \\ {-\hbox {Re}[\varPhi _{I,22} ]} \\ {-2\hbox {Re}[\varPhi _{I,12} ]} \\ \end{array} }} \right] } \cdot w_I =\sum _{I=1}^N {{\mathbf {B}}_I w_I } ={\mathbf {B}}\cdot {\mathbf {w}},\nonumber \\ \end{aligned}$$

(32)

where $\varPhi _{I, ij}$, $i,j=1,2$, represents the second derivative of the CVRKPM shape function,

$$\begin{aligned}&{\mathbf {B}}(z)=({\mathbf {B}}_1 (z), {\mathbf {B}}_2 (z), \ldots , {\mathbf {B}}_N (z)),\end{aligned}$$

(33)

$$\begin{aligned}&{\mathbf {B}}_I =\left[ {{\begin{array}{c} {-\hbox {Re}[\varPhi _{I,11} ]} \\ {-\hbox {Re}[\varPhi _{I,22} ]} \\ {-2\hbox {Re}[\varPhi _{I,12} ]} \\ \end{array} }} \right] . \end{aligned}$$

(34)

Substituting Eqs. (10) and (32) into Eq. (31) yields

$$\begin{aligned}&\delta {\mathbf {w}}^{\mathrm{T}}\cdot \left( {\int _\Omega {{\mathbf {B}}^{\mathrm{T}}{\mathbf {DB}}\hbox {d}\Omega } } \right) \cdot {\mathbf {w}}-\delta {\mathbf {w}}^{\mathrm{T}}\cdot \left( {\int _\Omega {\tilde{\varvec{\varPhi } }^{\mathrm{T}}q\hbox {d}\Omega } } \right) \nonumber \\&\quad -\,\delta {\mathbf {w}}^{\mathrm{T}}\cdot \left( {\int _{\Gamma _{t_1 } } {\left( {\frac{\partial \tilde{\varvec{\varPhi }}}{\partial {\mathbf {n}}}} \right) ^{\mathrm{T}}\bar{{M}}_n \hbox {d}\Gamma } } \right) \nonumber \\&\quad -\,\delta {\mathbf {w}}^{\mathrm{T}}\cdot \left( {\int _{\Gamma _{t_2 } } {\tilde{\varvec{\varPhi }}^{\mathrm{T}}\cdot \bar{{V}}_n \hbox {d}\Gamma } } \right) \nonumber \\&\quad +\,\delta {\mathbf {w}}^{\mathrm{T}}\cdot \left( {\int _{\Gamma _{u_1 } } {\tilde{\varvec{\varPhi }}^{\mathrm{T}}\cdot \alpha _1 \cdot \tilde{\varvec{\varPhi }}\hbox {d}\Gamma } } \right) \cdot {\mathbf {w}}\nonumber \\&\quad -\,\delta {\mathbf {w}}^{\mathrm{T}}\cdot \left( {\int _{\Gamma _{u_1 } } {\tilde{\varvec{\varPhi }}^{\mathrm{T}}\cdot \alpha _1 \cdot \bar{{w}}\hbox {d}\Gamma } } \right) \nonumber \\&\quad +\,\delta {\mathbf {w}}^{\mathrm{T}}\cdot \left( {\int _{\Gamma _{u_2 } } {\left( {\frac{\partial \tilde{\varvec{\varPhi }}}{\partial {\mathbf {n}}}} \right) ^{\mathrm{T}}\cdot \alpha _2 \cdot \left( {\frac{\partial \tilde{\varvec{\varPhi }}}{\partial {\mathbf {n}}}} \right) \hbox {d}\Gamma } } \right) \cdot {\mathbf {w}}\nonumber \\&\quad -\,\delta {\mathbf {w}}^{\mathrm{T}}\int _{\Gamma _{u_2 } } {\left( {\frac{\partial \tilde{\varvec{\varPhi }}}{\partial {\mathbf {n}}}} \right) ^{\mathrm{T}}\cdot \alpha _2 \cdot \bar{{\theta }}\hbox {d}\Gamma } =0. \end{aligned}$$

(35)

Because $\delta {\mathbf {w}}^{\mathrm{T}}$ is arbitrary, from Eq. (35) we have the final discrete equation as

$$\begin{aligned} \bar{{{\mathbf {K}}}}{\mathbf {w}}=\bar{{{\mathbf {F}}}}, \end{aligned}$$

(36)

where

$$\begin{aligned} \bar{{{\mathbf {K}}}}&= {\mathbf {K}}+{\mathbf {K}}^{\alpha },\end{aligned}$$

(37)

$$\begin{aligned} \bar{{{\mathbf {F}}}}&= {\mathbf {F}}+{\mathbf {F}}^{\alpha }, \end{aligned}$$

(38)

${\mathbf {K}}$ is the global stiffness matrix,

$$\begin{aligned} {\mathbf {K}}=\int _\Omega {{\mathbf {B}}^{\mathrm{T}}\cdot {\mathbf {D}}\cdot {\mathbf {B}}\hbox {d}\Omega } ; \end{aligned}$$

(39)

${\mathbf {K}}^{\alpha }$ is the global penalty matrix,

$$\begin{aligned} {\mathbf {K}}^{\alpha }\!=\!\int _{\Gamma _{u_1 } } {\tilde{\varvec{\varPhi }}^{\mathrm{T}}\cdot \alpha _1 \cdot \tilde{\varvec{\varPhi }}\hbox {d}\Gamma } \!+\!\int _{\Gamma _{u_2 } } {\left( {\frac{\partial \tilde{\varvec{\varPhi }}}{\partial {\mathbf {n}}}} \right) ^{\mathrm{T}}\cdot \alpha _2 \cdot \left( {\frac{\partial \tilde{\varvec{\varPhi } }}{\partial {\mathbf {n}}}} \right) \hbox {d}\Gamma };\nonumber \\ \end{aligned}$$

(40)

${\mathbf {F}}$ is the global external force vector,

$$\begin{aligned} {\mathbf {F}}=\int _\Omega {\tilde{\varvec{\varPhi }}^{\mathrm{T}}q\hbox {d}\Omega } +\int _{\Gamma _{t_1 } } {\left( {\frac{\partial \tilde{\varvec{\varPhi }}}{\partial {\mathbf {n}}}} \right) ^{\mathrm{T}}\bar{{M}}_n \hbox {d}\Gamma } +\int _{\Gamma _{t_2 } } {\tilde{\varvec{\varPhi } }^{\mathrm{T}}\bar{{V}}_n \hbox {d}\Gamma },\nonumber \\ \end{aligned}$$

(41)

and the vector ${\mathbf {F}}^{\alpha }$ is caused by the essential boundary condition,

$$\begin{aligned} {\mathbf {F}}^{\alpha }\!=\!\int _{\Gamma _{u_1 } } {\tilde{\varvec{\varPhi }}^{\mathrm{T}}\cdot \alpha _1 \cdot \bar{{w}}\hbox {d}\Gamma } \!+\!\int _{\Gamma _{u_2 } } {\left( {\frac{\partial \tilde{\varvec{\varPhi } }}{\partial {\mathbf {n}}}} \right) ^{\mathrm{T}}\cdot \alpha _2 \cdot \bar{{\theta }}\hbox {d}\Gamma }. \end{aligned}$$

(42)

5 Numerical examples

In this section, several numerical results for selected plate problems with boundary conditions are presented to illustrate the implementation of the CVRKPM for the bending problem of arbitrary Kirchhoff plates in this paper.

In the numerical examples presented in this section, the material properties are given as follows: Young’s modulus $E=2.1\times 10^{11}\,\hbox {N/m}^{2}$, Poisson’s ratio $\nu =0.3$ and the thickness of the plate $h=0.01\,\hbox {m}$. A regular node distribution and the background mesh for quadrature are used to obtain the final system equation. $4\times 4$ Gaussian quadrature is used for numerical integrations on each cell of the background mesh.

5.1 A square plate for convergence analysis

The convergence of the present CVRKPM for the bending problem of thin plates is studied by analyzing the node deflections and strain energy. And the influences of the basis function, weight function, scaling factor, node distribution and penalty factor on the computational precision of the CVRKPM in this paper are discussed.

The deflection norm $\left\| w \right\|$ and strain energy norm $\left\| e \right\|$ are defined as

$$\begin{aligned}&\left\| w \right\| =\left( {\int _\Omega {w^{2}\hbox {d}\Omega } } \right) ^{\frac{1}{2}};\end{aligned}$$

(43)

$$\begin{aligned}&\left\| e \right\| =\left[ {\frac{D_0 }{2}\int _\Omega {(\nabla ^{2}w)^{2}\hbox {d}\Omega } } \right] ^{\frac{1}{2}}. \end{aligned}$$

(44)

The relative errors of $\left\| w \right\|$ and $\left\| e \right\|$ are defined as

$$\begin{aligned} r_w =\frac{\left\| {w^{n}-w^{e}} \right\| }{\left\| {w^{e}} \right\| } \end{aligned}$$

(45)

and

$$\begin{aligned} r_e =\frac{\left\| {e^{n}-e^{e}} \right\| }{\left\| {e^{e}} \right\| }, \end{aligned}$$

(46)

respectively. Here $w^{n}$ and $e^{n}$ are the numerical results of the deflection and the strain energy obtained by the present method, respectively; $w^{e}$ and $e^{e}$ are the analytical ones of the deflection and the strain energy, respectively.

In this example, a square plate subjected a uniformly distributed load with all edges simply supported (see Fig. 2) is considered to illustrate the convergence of the CVRKPM in this paper. The analytical solution of the problem is

$$\begin{aligned} w=\frac{16q_0 }{\uppi ^{6}D_0 }\sum _{m=1,3,\ldots }^\infty {\sum _{n=1,3,\ldots }^\infty {\frac{\sin \frac{m{\uppi }{x}_1 }{a}\cdot \sin \frac{n{\uppi }x_2 }{a}}{mn\left( {\frac{m^{2}}{a^{2}}+\frac{n^{2}}{a^{2}}} \right) }} } , \end{aligned}$$

(47)

where $D_0$ is the flexural rigidity in Eq. (5), $q_0$ is the uniformly distributed load, and $a$ is the side length of the square plate. In this example, $q_0 =1,000\,\hbox {N/m}^{2}$ and $a=1.0$.

Fig. 2

A square plate subjected to a uniformly distributed load

Regular node distributions of $7\times 7, 11\times 11$ and $21\times 21$ are used to study the relative errors of the numerical solutions of the present CVRKPM. The size $h$ in the Figs. 3, 4, 5, 6 is defined as the distance in the $x_1$ direction between two neighboring nodes. The quadratic, cubic and quartic basis functions and the quintic spline weight function are employed. The relative errors of the deflection norm $\left\| w \right\|$ and strain energy norm $\left\| e \right\|$ are shown in Figs. 3 and 4, respectively. It can be seen that cubic basis function can give better results than quadratic basis function. In addition, quartic basis function can also give similar good results as the cubic basis function, but it spends more CPU time.

Fig. 3

Relative errors of the deflection norm $\left\| w \right\|$

Fig. 4

Relative errors of the strain energy norm $\left\| e \right\|$

Fig. 5

Relative errors of the deflection norm $\left\| w \right\|$

The CVRKPM is flexible with respect to the construction of the shape functions. It is possible to optimize the accuracy of the present method by using a proper weight function because the approximation results are governed by the continuity of the weight function. Therefore, in this paper, we compare the relative errors of the CVRKPM when using different spline weight functions. Figs. 5 and 6 show the relative errors of the norms $\left\| w \right\|$ and $\left\| e \right\|$ using the cubic, the quartic and quintic spline weight function, respectively, while the cubic basis function is employed. It can be seen that the quintic spline weight function can obtain the solution with higher accuracy. In fact, the quintic spline function possesses $C^{2}$ continuity within the support domain, as well as on its boundary, then $C^{3}$ shape functions can be obtained due to the properties of the quintic spline weight function.

Fig. 6

Relative errors of the strain energy norm $\left\| e \right\|$

All of these figures also show that the present CVRKPM has high precision for the norms $\left\| w \right\|$ and $\left\| e \right\|$, and gives reasonable numerical results for the unknown variable and its derivatives. At the same time, because the continuity of the approximation is in connection with the continuity of the weight function, if the order of the weight function is higher than the order of the basis function, the order of the continuity of the numerical approximation will be similar to that of the weight function. Then in this case we can only require the basis function with lower order. It is a good choice to use cubic basis function as well as the quintic spline weight function in our numerical analyses. Then in the following examples, the cubic basis and quintic spline weight function are used in the CVRKPM for Kirchhoff plates.

The influences of scaling factor $d_{\mathrm{max}}$ on the numerical results are investigated under different regular node distributions. The relationship between the relative error of the deflection norm $\left\| w \right\|$ and the scaling factors $d_{\mathrm{max}}$ is shown in Fig. 7. From the numerical results, we can see that the best solutions are obtained when $d_{\mathrm{max}} =4.1$. In the following examples in this paper, we let $d_{\mathrm{max}} =4.1$.

Fig. 7

Influence of $d_{\mathrm{max}}$ on the relative errors of the deflection norm $\left\| w \right\|$

The study of the influence of penalty factor $\alpha$ on the solutions of the CVRKPM is considered here. The relative errors of the norm $\left\| w \right\|$ for different penalty factor $\alpha$ under different node distributions of $7\times 7, 9\times 9, 11\times 11, 13\times 13, 15\times 15, 17\times 17$ and $19\times 19$ are shown in Fig. 8. It is shown that the good solutions of the thin plate can be obtained when $\alpha =(1.0\sim 10)\times E$. The large errors appear when $\alpha >(10^{3}\times E)$. On the other hand, $\alpha$ should be a large number. It is difficult to obtain a good result when $\alpha <(10^{-2}\times E)$. In the following examples in this paper, we let $\alpha =1.0\times E$.

Fig. 8

The relative errors of the norm $\left\| w \right\|$ for different penalty factor $\alpha$

The numerical errors of the present CVRKPM at different node distributions are compared with those of the RKPM, as shown in Fig. 9. It can be seen that the computational accuracy of the CVRKPM is higher than the one of the RKPM under the same node distribution. Moreover, the numerical results obtained by the present CVRKPM become more accurate when the number of nodes increases.

Fig. 9

The relative errors of the norm $\left\| w \right\|$ under various node distributions

Under the same node distribution, the CVRKPM takes less CPU time than the RKPM. Table 1 shows the comparison of the corresponding CPU time of the CVRKPM and RKPM under various node distributions. It is shown that the CVRKPM has greater computational efficiency than the RKPM under the same node distribution.

5.2 Simply supported rectangular plate

As the second example, we consider a simply supported rectangular plate with uniformly distributed bending moment on two opposite edges (see Fig. 10).

Fig. 10

Simply supported rectangular plate

The analytical solution of the deflection when $x_2 =0$ is

$$\begin{aligned} (w)_{x_2 =0} =\frac{2M_0 a^{2}}{\uppi ^{3}D_0 }\sum _{m=1}^\infty {\frac{1}{m^{3}}\frac{\alpha _m \hbox {th}\alpha _m }{\hbox {ch}\alpha _m}\sin \frac{m{\uppi }{x}_1}{a}}, \end{aligned}$$

(48)

where

$$\begin{aligned} \alpha _m =\frac{m\uppi b}{2a},\quad (m=1, 3, 5, \ldots ). \end{aligned}$$

(49)

Table 1 Comparison of CPU time under various node distributions

In this example, the parameters used for the numerical simulation are $a=2$, $b=1$ and $M_0 =1,000\,\hbox {N}\hbox {m/m}$. Based on the results of the first numerical example, we take the scaling factor $d_{\mathrm{max}} =4.1$ and the penalty factor $\alpha _1 =2.1\times 10^{11}$. The numerical results of the RKPM, the present CVRKPM and the analytical solution along $x_1$ axis are shown in Fig. 11. It can be seen that the present CVRKPM and the RKPM have similar numerical precision, but the present CVRKPM takes less CPU time than the RKPM.

Fig. 11

The deflection $w$ when $x_2 =0$

5.3 Simply supported square plate under hydrostatic pressure

The third example considered is a square plate subjected to the linearly distributed hydrostatic pressure with all edges simply-supported, as shown in Fig. 12. The analytical solution is

$$\begin{aligned}&w=\frac{8q_0 a^{4}}{D_0 \uppi ^{6}}\sum _{m=1}^\infty {\sum _{n=1}^\infty {\frac{(-1)^{m+1}}{mn(m^{2}+n^{2})^{2}}\sin \frac{m{\uppi }{x}_1}{a}\sin \frac{n{\uppi }x_2}{a}}},\nonumber \\&\quad (n=1, 3, 5, \ldots ), \end{aligned}$$

(50)

where $q_0$ is the maximum numerical value of distributed hydrostatic pressure.

Fig. 12

Simply supported square plate with linearly hydrostatic pressure

In this study, $q_0 =1,000\,\hbox {N/m}^{2}, a=1.0, d_{\max } =4.1$ and $\alpha _1 =2.1\times 10^{11}$. And the regular node distribution of $11\times 11$ are used. The material properties are the same as those in the previous examples.

The analytical solution and the numerical results of the present method at $(x_1 , 0.5)$ and $(0.5, x_2 )$ are shown in Figs. 13 and 14. It can be seen that there is very good agreement between the numerical results and the analytical solution given by Eq. (50).

Fig. 13

The deflection $w$ at points $(x_1 , 0.5)$

Fig. 14

The deflection $w$ at points $(0.5, x_2 )$

5.4 Clamped circular plate with uniform load

A clamped circular plate, as shown in Fig. 15, subjected to the uniform transverse pressure $q$ is considered to further investigate the applicability of the CVRKPM of the bending problems of Kirchhoff plate with curved boundary.

Fig. 15

Clamped circular plate. a Clamped circular plate. b A quarter of the plate

The analytical solution of the problem is

$$\begin{aligned} w=\frac{qR^{4}}{64D_0 }\left( {1-\frac{r^{2}}{R^{2}}} \right) ^{2}, \end{aligned}$$

(51)

where $R$ is the radius of the plate, and $r$ is the distance from the center of the middle plane of the thin plate.

In this example, the parameters selected for the present CVRKPM are $d_{\max } =4.1, \alpha _1 =\alpha _2 =2.1\times 10^{11}, R=1.0$ and $q=1,000\,\hbox {N/m}^{2}$. Due to symmetry, only a quarter of the plate is considered (see Fig. 15b). Figure 16 shows the node distribution on the quarter of the plate. The numerical results of the deflection $w$ at the points with different distances from the center are shown in Fig. 17. It can be seen that the present CVRKPM gives the numerical solution with high precision.

Fig. 16

Node distribution

Fig. 17

The deflection $w$ at $r$-direction

6 Conclusions

The CVRKPM for solving the bending problems of Kirchhoff plates is proposed in this paper. The advantage of the CVRKPM is that the correction function of a 2D problem is formed with 1D basis function when the shape functions are formed. Then the unknown coefficients of correction function in the CVRKPM are fewer than in the RKPM. Therefore, we need fewer nodes with support domains that cover an arbitrary point in the problem domain. At the same time, the fewer unknown coefficients will reduce the dimension of matrices, then we can obtain the inversion of matrices, as well as the product of matrices, simply and rapidly, which will lead to the greater computational efficiency.

Convergence studies in the first numerical example show that the present method possesses an excellent convergence rate for the deflection and the strain energy. Numerical results show that using the cubic basis and the quintic spline weight function can get quite accurate numerical results. Moreover, the scaling factor is examined numerically. It is evident that good computational results can be achieved if appropriate scaling factor is selected. Several numerical examples have been given and the numerical results show that the present method is accurate and in agreement with the theoretical analysis.

Although isotropic material law and uniform plate thickness were assumed for simplicity, the formulae in this paper can be applied directly to the bending problems of Kirchhoff plates with any material law and any thickness variation. Besides, the current formulation possesses flexibility in adapting the density of the nodes at any place of the problem domain such that the precision of the solution can be improved easily. This is especially useful in developing intelligent, adaptive algorithms based on error indicators for engineering applications.