1 Introduction

The beams, plates and shells, widely used in engineering, are often affected by vibration and impact. The finite element method depends on the mesh division to deal with such problems [1, 2]. When the mesh is distorted, the accuracy of the results obtained by the finite element method decreases. The meshless method adopts point-based approximation and can ignore the influence of mesh distortion when dealing with numerical problems [3]. The meshless method has the advantages of saving analysis time and ensuring calculation accuracy, which at present is the hot spot and development direction of scientific and engineering calculation methods [4].

In the calculation process, only node information is needed, which overcomes the limitation of connecting nodes to elements between nodes [5]. The meshless method can easily deal with the problems of large deformation [6], crack-growth processes [7], convection heat transfer [8], fluid-structure interaction [9], and elastodynamics [10, 11].

With the rapid development of computer technology and calculation method, various numerical methods have become important means to solve scientific and engineering problems [12–17]. As an important scientific problem, structural dynamic analysis has been paid more attention in various fields [18–21]. In this case, the finite element method (FEM), as the most general numerical method, becomes the main method for dynamic analysis and nonlinear analysis [22, 23]. The FEM for solving structural dynamic problems depends on the division and refinement of elements [24]. In the case of complex geometry, stress singularities and concentration occur unless a high-quality finite element mesh is generated at a very time consuming and tedious cost [25]. The output result of the quadratic approximation will be distorted when the discontinuity stress related to the elements is in the area of the stress concentration [26]. The meshless methods were first used to simulate celestial phenomena without boundaries [27, 28]. The meshless method uses the approximation of the point, and the displacement trial function of the calculation point is only associated with the shape function of the discrete point in the influence domain. Without the dependence of the grids, the output displacement, strain, and stress are continuous in the whole analysis domain, and the error of the quadratic approximation is avoided [29, 30]. Two mainstream meshless methods are the element-free Galerkin methods [31–35] and the reproducing kernel particle methods [36–39]. However, the meshless method based on the Galerkin discretization scheme is not easy to apply the boundary conditions.

Dynamic analysis is an important step in the evaluation of elastic structures. Meshless methods take particles as basic computing units, and there is no need to establish fixed topological relations between particles, so they are suitable for solving elastic dynamic problems [40, 41]. Several authors have attempted to apply meshless methods to elastodynamics problems. Selecting an appropriate form function can reduce the computational cost [42]. A meshless local integral method for two-dimensional elastodynamic fracture problems by the Laplace transform technique is proposed [43]. The Newmark method is generally selected as an approximation scheme to deal with time-dependent cases [44–46].

In this paper, combining the IRKPM with the integral weak form governing equation of elastodynamics, we establish a high-order smooth interpolated reproducing kernel particle method for two-dimensional elastodynamics problems. We derive the corresponding discrete equations and adopt the time domain integration the Newmark constant average acceleration method. This method adopts point-based approximation, which can ignore the influence of grid distortion in the dynamic analysis, save the analysis time, and ensure the calculation accuracy. This method can easily apply boundary conditions like the finite element method and can avoid the difficulties in dealing with the boundary condition. Compared with other meshless methods, this method has the character of directly applying boundary conditions, a small amount of calculation, and high accuracy. The correctness and effectiveness of this method are proved by some numerical examples.

2 The basic equation of elastic mechanics

Let Ω be the domain of problem with boundary Γ. For linear elastic problem, b is the body force, \(\bar{\boldsymbol{t}}\) is the known surface force on the natural boundary, \(\bar{\boldsymbol{u}}\) is the known displacement on essential boundary, and n is the directional cosine matrix at the point x on the natural boundary. The basic equations of two-dimensional elastic mechanics are

$$\begin{aligned}& \boldsymbol{L}^{\mathrm{T}}\boldsymbol{\sigma} + \boldsymbol{b} - \rho \ddot{ \boldsymbol{u}} - \mu \dot{\boldsymbol{u}} = \boldsymbol{0}\quad \text{in } \varOmega , \end{aligned}$$
(1)
$$\begin{aligned}& \boldsymbol{\varepsilon} = \boldsymbol{Lu}\quad \text{in } \varOmega , \end{aligned}$$
(2)
$$\begin{aligned}& \boldsymbol{\sigma} = \boldsymbol{D}\boldsymbol{\varepsilon}\quad \text{in } \varOmega , \end{aligned}$$
(3)
$$\begin{aligned}& \boldsymbol{\sigma} \boldsymbol{n} = \bar{\boldsymbol{t}}\quad \text{on } \varGamma _{u}, \end{aligned}$$
(4)
$$\begin{aligned}& \boldsymbol{u} = \bar{\boldsymbol{u}}\quad \text{on } \varGamma _{t}, \end{aligned}$$
(5)
$$\begin{aligned}& \boldsymbol{u}(\boldsymbol{x},t_{0}) = u_{0}( \boldsymbol{x}),\quad \boldsymbol{x} \in \boldsymbol{\varOmega}, \end{aligned}$$
(6)
$$\begin{aligned}& \dot{\boldsymbol{u}}(\boldsymbol{x},t_{0}) = \boldsymbol{v}_{0}( \boldsymbol{x}),\quad \boldsymbol{x} \in \boldsymbol{\varOmega}, \end{aligned}$$
(7)

where L is the differential operator matrix

$$ \boldsymbol{L} = \begin{bmatrix} \frac{\partial}{\partial x_{1}} & 0 & \frac{\partial}{\partial x_{2}} \\ 0 & \frac{\partial}{\partial x_{2}} & \frac{\partial}{\partial x_{1}} \end{bmatrix}^{\mathrm{T}}, $$
(8)

ρ is the density, μ is the damping coefficient, \(- \mu \dot{\boldsymbol{u}}\) is the damping force, \(- \rho \ddot{\boldsymbol{u}}\) is the inertia force;

$$\begin{aligned}& \boldsymbol{\sigma} = \begin{bmatrix} \sigma _{11}(t) & \sigma _{22}(t) & \sigma _{12}(t) \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(9)
$$\begin{aligned}& \boldsymbol{b} = \begin{bmatrix} b_{1}(t) & b_{2}(t) \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(10)
$$\begin{aligned}& \boldsymbol{\varepsilon} = \begin{bmatrix} \varepsilon _{11}(t) & \varepsilon _{22}(t) & \varepsilon _{12}(t) \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(11)
$$\begin{aligned}& \boldsymbol{u} = \begin{bmatrix} u(t) & v(t) \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(12)

where σ, b, ε, and u are the stress vector, body force vector, strain matrix, and displacement matrix at any point on the domain, respectively;

$$\begin{aligned}& \dot{\boldsymbol{u}}^{\mathrm{T}} = \bigl(\dot{u}(t),\dot{v}(t) \bigr), \end{aligned}$$
(13)
$$\begin{aligned}& \ddot{\boldsymbol{u}}^{\mathrm{T}} = \bigl(\ddot{u}(t),\ddot{v}(t) \bigr), \end{aligned}$$
(14)

where \(\dot{\boldsymbol{u}}\) and \(\ddot{\boldsymbol{u}}\) are the first and second derivatives of the displacement matrix u, respectively.

Let D be the elasticity matrix. The plane stress matrix can be expressed as

$$ \boldsymbol{D} = \frac{E}{1 - \mu ^{2}} \begin{bmatrix} 1 & \mu & 0 \\ \mu & 1 & 0 \\ 0 & 0 & \frac{1 - \mu}{2} \end{bmatrix}, $$
(15)

where E is Young’s modulus, and μ is Poisson’s ratio.

3 Interpolated reproducing kernel particle method for elastodynamics problems

3.1 Shape function of the interpolated reproducing kernel particle method

When the number of nodes in the compact support domain is greater than the number of the basis function monomials, we construct the interpolating shape function of the improved reproducing kernel particle method.

The cubic spline function is adopted as a weight function, that ism

$$ \hat{\varPhi}_{\hat{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I}) = \varPhi ( d ) = \textstyle\begin{cases} \frac{2}{3} - 4d^{2} + 4d^{3},& d \le \frac{1}{2}, \\ \frac{4}{3} - 4d + 4d^{2} - \frac{4}{3}d^{3},& \frac{1}{2} < d \le 1, \\ 0,& d > 1. \end{cases} $$
(16)

Let the improved interpolating nuclear particle of \(u(x)\) be approximately

$$ u^{a}(\boldsymbol{x}) = \sum_{I = 1}^{NP} \varPsi _{I}(\boldsymbol{x}) u_{I}, $$
(17)

where the shape function of the improved interpolating kernel particle is

$$ \varPsi _{I}(\boldsymbol{x}) = \hat{\varPsi}_{I}( \boldsymbol{x}) + \bar{\varPsi}_{I}(\boldsymbol{x}), $$
(18)

with a function \(\hat{\varPsi}_{I}(\boldsymbol{x})\) that possesses the Kronecker delta property and an enhanced function \(\bar{\varPsi}_{I}(\boldsymbol{x})\) in the form of IRKPM. Therefore the constructed shape function has the property of interpolating on any point and a higher-order smoothness not less than that of the kernel function.

The improved second-order interpolating condition of the interpolating kernel particle shape function \(\varPsi _{I}(\boldsymbol{x})\) can be given as

$$ \sum_{I = 1}^{NP} \bigl[\hat{ \varPsi}_{I}(\boldsymbol{x}) + \bar{\varPsi}_{I}( \boldsymbol{x}) \bigr] x_{I}^{\alpha} = x^{\alpha}, \quad \vert \alpha \vert \le 2. $$
(19)

If the simple function \(\hat{\varPsi}_{I}(\boldsymbol{x})\) satisfies the Kronecker delta property, that is, \(\hat{\varPsi}_{I}(\boldsymbol{x}_{J}) = \delta _{I J}\), and Eq. (19) holds, then the enhancement function vector is as follows:

$$ \bar{\boldsymbol{\varPsi}} (\boldsymbol{x}) = \bigl\{ \bar{\varPsi}_{1}( \boldsymbol{x}),\bar{\varPsi}_{2}(\boldsymbol{x}), \ldots ,\bar{ \varPsi}_{NP}(\boldsymbol{x}) \bigr\} . $$
(20)

The basis vectors made up of moving monomials, which are orthogonal, can be written as

$$\begin{aligned}& \boldsymbol{h}_{i}(\boldsymbol{x}) = \bigl\{ h_{i}( \boldsymbol{x} - \boldsymbol{x}_{1}),h_{i}( \boldsymbol{x} - \boldsymbol{x}_{2}),\ldots,h_{i}( \boldsymbol{x} - \boldsymbol{x}_{NP}) \bigr\} , \end{aligned}$$
(21)
$$\begin{aligned}& \boldsymbol{H} ( \boldsymbol{x} - \boldsymbol{x}_{I} ) = \bigl[1,x_{1} - x_{I1},\ldots,x_{d} - x_{Id},(x_{1} - x_{I 1})^{2}, \ldots,(x_{d} - x_{Id})^{n} \bigr]^{\mathrm{T}}, \end{aligned}$$
(22)

where the ith element of \(\boldsymbol{H} ( \boldsymbol{x} - \boldsymbol{x}_{I} )\), for example, for all discrete points \(\{ \boldsymbol{x}_{J} \}_{J = 1}^{NP}\), is

$$ \bar{\boldsymbol{\varPsi}} (\boldsymbol{x}_{J})^{\mathrm{T}} \boldsymbol{h}_{i}(\boldsymbol{x}_{J}) = 0 \quad \forall J . $$
(23)

In view of Eq. (19), Eq. (23) can be rewritten as

$$ \sum_{I = 1}^{NP} \bigl[\hat{ \varPsi}_{I}(\boldsymbol{x}) + \bar{\varPsi}_{I}( \boldsymbol{x}) \bigr] \boldsymbol{H}(\boldsymbol{x} - \boldsymbol{x}_{I}) = \boldsymbol{H}(\boldsymbol{0}). $$
(24)

For \(\boldsymbol{x}_{J}\), we have

$$ \sum_{I = 1}^{NP} \bigl[\hat{ \varPsi}_{I}(\boldsymbol{x}_{J}) + \bar{ \varPsi}_{I}(\boldsymbol{x}_{J}) \bigr] \boldsymbol{H}( \boldsymbol{x}_{J} - \boldsymbol{x}_{I}) = \boldsymbol{H}(\boldsymbol{0}). $$
(25)

If \(\hat{\varPsi}_{I}(\boldsymbol{x}_{J}) = \delta _{I J}\) and any J point satisfies \(\sum_{I = 1}^{NP} \delta _{I J} \boldsymbol{H}(\boldsymbol{x}_{J} - \boldsymbol{x}_{I}) = \boldsymbol{H}(\boldsymbol{0})\), then based on the last equation, we have

$$ \sum_{I = 1}^{NP} \bar{ \varPsi}_{I}(\boldsymbol{x}_{J}) \boldsymbol{H}( \boldsymbol{x}_{J} - \boldsymbol{x}_{I}) = \boldsymbol{0}. $$
(26)

We can obtain the equivalent equation

$$ \sum_{I = 1}^{NP} \bar{ \varPsi}_{I}(\boldsymbol{x}_{J})h_{i}( \boldsymbol{x}_{J} - \boldsymbol{x}_{I}) = 0. $$
(27)

Thus we obtained Eq. (23).

Let

$$ \bar{\varPsi}_{I}(\boldsymbol{x}) = \boldsymbol{G}^{\mathrm{T}}( \boldsymbol{x} - \boldsymbol{x}_{I})\boldsymbol{b}( \boldsymbol{x}), $$
(28)

where \(\boldsymbol{G}(\boldsymbol{x} - \boldsymbol{x}_{I})\) is the vector of basis functions that has the same dimension as \(\boldsymbol{H}(\boldsymbol{x}_{J} - \boldsymbol{x}_{I})\), and \(\boldsymbol{b}(\boldsymbol{x})\) is the corresponding coefficient vector. Substituting Eq. (28) into Eq. (26) we have

$$ \boldsymbol{Q}(\boldsymbol{x}_{J})\boldsymbol{b}( \boldsymbol{x}_{J}) = \boldsymbol{0}, $$
(29)

where

$$ \boldsymbol{Q}(\boldsymbol{x}) = \sum_{I} \boldsymbol{H}(\boldsymbol{x} - \boldsymbol{x}_{I}) \boldsymbol{G}^{\mathrm{T}}(\boldsymbol{x} - \boldsymbol{x}_{I}). $$
(30)

If \(\boldsymbol{Q}(\boldsymbol{x}_{J})\) is nonsingular, then from Eq. (29) we obtain \(\boldsymbol{b}(\boldsymbol{x}_{J}) = \boldsymbol{0}\). Since \(\bar{\varPsi}_{I}(\boldsymbol{x}_{J}) = 0\) by Eq. (28), we get

$$ \varPsi _{I}(\boldsymbol{x}_{J}) = \bar{ \varPsi}_{I}(\boldsymbol{x}_{J}) + \stackrel{\frown}{ \varPsi}_{I}(\boldsymbol{x}_{J}) = \delta _{I J}. $$
(31)

To make \(\boldsymbol{Q}(\boldsymbol{x})\) nonsingular, an obvious choice for \(\boldsymbol{G}(\boldsymbol{x} - \boldsymbol{x}_{I})\) is

$$ \boldsymbol{G}(\boldsymbol{x} - \boldsymbol{x}_{I}) = \boldsymbol{H}(\boldsymbol{x} - \boldsymbol{x}_{I})\bar{ \varPhi}_{\bar{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I}), $$
(32)

where \(\bar{\varPhi}_{\bar{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I}) \ge 0\) is a weight function with compact support. So

$$ \bar{\varPsi}_{I}(\boldsymbol{x}) = \boldsymbol{H}^{\mathrm{T}}( \boldsymbol{x} - \boldsymbol{x}_{I})\boldsymbol{b}(\boldsymbol{x}) \bar{\varPhi}_{\bar{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I}). $$
(33)

As we can see from the above, if the enhancement function is of the form (28) and the simple function has the Kronecker delta property, then the interpolation function \(\varPsi _{I}(\boldsymbol{x})\) will be generated if Eq. (19) is satisfied.

The coefficient \(\boldsymbol{b}(\boldsymbol{x})\) of \(\bar{\varPsi}_{I}(\boldsymbol{x})\) can be obtained by the condition of reproducing, and \(\hat{\varPsi}_{I}(\boldsymbol{x})\) can be expressed as

$$ \hat{\varPsi}_{I}(\boldsymbol{x}) = \frac{\hat{\varPhi}_{\hat{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I})}{\hat{\varPhi}_{\hat{a}_{I}}(\boldsymbol{0})},\quad \hat{a}_{I} < \min \bigl\{ \Vert \boldsymbol{x}_{I} - \boldsymbol{x}_{J} \Vert \ \forall J \ne I \bigr\} , $$
(34)

where \(\hat{\varPsi}_{I}(\boldsymbol{x})\) satisfies the Kronecker delta condition.

Substituting Eqs. (33) and (34) into Eq. (18) yields

$$ \sum_{I = 1}^{NP} \bigl[\hat{ \varPsi}_{I}(\boldsymbol{x}) + \boldsymbol{H}^{\mathrm{T}}( \boldsymbol{x} - \boldsymbol{x}_{I})\boldsymbol{b}(\boldsymbol{x}) \hat{\varPhi}_{\hat{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I}) \bigr] \boldsymbol{x}_{I}^{\alpha} = \boldsymbol{x}^{\alpha}, \quad \vert \alpha \vert \le n. $$
(35)

From Eq. (35) we have

$$ \sum_{I = 1}^{NP} \boldsymbol{H}( \boldsymbol{x} - \boldsymbol{x}_{I}) \bigl[\hat{\varPsi}_{I}( \boldsymbol{x}) + \boldsymbol{H}^{\mathrm{T}}(\boldsymbol{x} - \boldsymbol{x}_{I})\boldsymbol{b}(\boldsymbol{x})\hat{ \varPhi}_{\hat{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I}) \bigr] = \boldsymbol{H}(\boldsymbol{0}). $$
(36)

The coefficient vector \(\boldsymbol{b}(\boldsymbol{x})\) can be obtained as

$$ \boldsymbol{b}(\boldsymbol{x}) = \boldsymbol{Q}^{ - 1}(\boldsymbol{x}) \bigl[\boldsymbol{H}(\boldsymbol{0}) - \hat{\boldsymbol{H}}(\boldsymbol{x}) \bigr], $$
(37)

where

$$ \hat{\boldsymbol{H}}(\boldsymbol{x}) = \sum_{I = 1}^{NP} \boldsymbol{H}(\boldsymbol{x} - \boldsymbol{x}_{I}) \hat{ \varPsi}_{I}(\boldsymbol{x}). $$
(38)

Finally, we obtain the interpolation shape function of the improved reproducing kernel particle as follows:

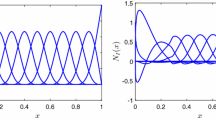
$$ \varPsi _{I}(\boldsymbol{x}) = \hat{\varPsi}_{I}( \boldsymbol{x}) + \boldsymbol{H}^{\mathrm{T}}(\boldsymbol{x} - \boldsymbol{x}_{I})Q^{ - 1}(x) \bigl[\boldsymbol{H}( \boldsymbol{0}) - \hat{\boldsymbol{H}}(\boldsymbol{x}) \bigr]\bar{ \varPhi}_{\bar{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I}). $$
(39)

As Fig. 1 shows, 121 particles are nonuniformly put on the 2D domain \((x,y) \in [0,10] \times [0,10]\), the cubic spline functions are taken as the weight functions of \(\hat{\varPhi}_{\hat{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I})\) and \(\bar{\varPhi}_{\bar{a}_{I}}(\boldsymbol{x} - \boldsymbol{x}_{I})\), \(\hat{a}_{1} = 0.48d_{c}\), \(\bar{a} = 3.0d_{c}\), and \(\hat{\varPsi}_{I}(\boldsymbol{x})\) is the minimum particle spacing. Then the shape functions of the asterisk particle are shown in Fig. 1.

Figure 1
figure 1

Shape functions of 2D IRKPM with nonuniform particles

Full size image

Figure 1 illustrates that the shape function has an excellent characteristic of node interpolation. The displacement, stress, and strain obtained by this method have smooth continuity on the whole domain and avoid the calculation error from the finite element method.

We analyze the reproducing kernel shape function and its interpolation properties in particular cases and study the construction process of the interpolation shape function of the improved reproducing kernel particle. We can see from these figures that the improved reproducing kernel shape function has good interpolation characteristics. Theoretically, the smoothness of the shape function of the improved reproducing kernel particle is guaranteed to be no less than that of the weight function.

The interpolation form function of the improved reproducing kernel particle is based on the coupling of a simple function with the Kronecker delta property and an enhanced function of IRKPM shape function format. When the original simple function is used to introduce the discrete Kronecker delta property and the enhancement function is used to construct the reproducing condition, if the enhancement function vector of the discrete point and the basis function vector of the moving monomial satisfy the orthogonality condition, then the shape function of the improved reproducing kernel particle with the Kronecker delta property is obtained. This makes it convenient to directly apply displacement boundary conditions.

3.2 Numerical equations of elastodynamics problems

In the domain Ω the displacement \(\boldsymbol{u} = [ u \enskip v ]^{\mathrm{T}}\) of any point x at any time t can be written as

$$ \boldsymbol{u} = \boldsymbol{\psi} \boldsymbol{u}^{n}, $$
(40)

where \(n = NP \le m\), m is the total number of discrete notes in elasticity domain Ω, and

$$\begin{aligned}& \boldsymbol{\psi} = \begin{bmatrix} \boldsymbol{\psi}_{1} & \boldsymbol{\psi}_{2} & \cdots & \boldsymbol{\psi}_{n} \end{bmatrix}, \end{aligned}$$
(41)
$$\begin{aligned}& \boldsymbol{u}^{n} = \begin{bmatrix} \boldsymbol{u}_{1}^{\mathrm{T}} & \boldsymbol{u}_{2}^{\mathrm{T}} & \cdots & \boldsymbol{u}_{n}^{\mathrm{T}} \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(42)

where ψ is the shape function, and \(\boldsymbol{u}^{n}\) is the displacement vector of n discrete points on compact support domain of the point x.

Setting \(I = 1,2,\ldots,n\), \(\boldsymbol{\varPsi}_{I}\) is the shape function submatrix of any particle \(\boldsymbol{x}_{I}\), \(\boldsymbol{u}_{I}\) is the displacement vector of any particle \(\boldsymbol{x}_{I}\), and we have

$$\begin{aligned}& \boldsymbol{\psi}_{I} = \begin{bmatrix} \varPsi _{I} & 0 \\ 0 & \varPsi _{I} \end{bmatrix}, \end{aligned}$$
(43)
$$\begin{aligned}& \boldsymbol{u}_{I} = \begin{bmatrix} u_{I} & v_{I} \end{bmatrix}^{\mathrm{T}}. \end{aligned}$$
(44)

3.3 High-order smooth elastodynamic algorithm

Based on the meshless shape function of any discrete point with smooth interpolation property, a higher-order smooth displacement function can be constructed as follows.

The speed and acceleration at any time t at any point x on the domain can be written as

$$\begin{aligned}& \dot{\boldsymbol{u}} = \sum_{I}^{n} \boldsymbol{\psi}_{I}\dot{\boldsymbol{u}}_{I}, \end{aligned}$$
(45)
$$\begin{aligned}& \ddot{\boldsymbol{u}} = \sum_{I}^{n} \boldsymbol{\psi}_{I}\ddot{\boldsymbol{u}}_{I}, \end{aligned}$$
(46)

where \(\dot{\boldsymbol{u}}_{I}\) and \(\ddot{\boldsymbol{u}}_{I}\) are the speed and acceleration of the point x at time t, respectively, and they can be written as

$$\begin{aligned}& \dot{\boldsymbol{u}}_{I} = \begin{bmatrix} \dot{u}_{I} & \dot{v}_{I} \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(47)
$$\begin{aligned}& \ddot{\boldsymbol{u}}_{I} = \begin{bmatrix} \ddot{u}_{I} & \ddot{v}_{I} \end{bmatrix}^{\mathrm{T}}. \end{aligned}$$
(48)

The strain of a point x can be obtained from Eqs. (2) and (40):

$$\begin{aligned}& \boldsymbol{\varepsilon} = \boldsymbol{Lu} = \boldsymbol{Bu}^{n}, \end{aligned}$$
(49)
$$\begin{aligned}& \boldsymbol{B} = \begin{bmatrix} \boldsymbol{B}_{1} & \boldsymbol{B}_{2} & \cdots & \boldsymbol{B}_{n} \end{bmatrix}, \end{aligned}$$
(50)

where B is the strain matrix, and the submatrix \(\boldsymbol{B}_{I}\) of the strain matrix at a particle \(\boldsymbol{x}_{I}\) is

$$ \boldsymbol{B}_{I} = \begin{bmatrix} \frac{\partial \varPsi _{I}}{\partial x_{1}} & 0 \\ 0 & \frac{\partial \varPsi _{I}}{\partial x_{2}} \\ \frac{\partial \varPsi _{I}}{\partial x_{2}} & \frac{\partial \varPsi _{I}}{\partial x_{1}} \end{bmatrix}. $$
(51)

By the virtual work principle of elastic mechanics we have

$$ \delta \varPi = - \int _{\varOmega} (\boldsymbol{\sigma} - \rho \ddot{\boldsymbol{u}} - \mu \dot{\boldsymbol{u}} + \boldsymbol{b})\delta \boldsymbol{u}\,\mathrm{d} \varOmega + \int _{\varGamma _{t}} (\boldsymbol{\sigma} \boldsymbol{n} - \bar{ \boldsymbol{t}})\delta \boldsymbol{u}\,\mathrm{d}\varGamma = 0, $$
(52)

i.e.,

$$ \int _{\varOmega} (\boldsymbol{D}\varepsilon \delta \varepsilon + \rho \ddot{\boldsymbol{u}}\delta \boldsymbol{u} - \mu \dot{\boldsymbol{u}}\delta \boldsymbol{u})\,\mathrm{d}\varOmega - \biggl( \int _{\varOmega} \boldsymbol{b}\delta \boldsymbol{u}\,\mathrm{d} \varOmega - \int _{\varGamma _{t}} \bar{\boldsymbol{t}}\delta \boldsymbol{u} \, \mathrm{d}\varGamma \biggr) = 0. $$
(53)

By Eqs. (40), (45), (46), and (49) we can obtain the following equation:

$$ \begin{aligned} & \int _{\varOmega} \delta \Biggl(\sum_{I}^{n} \boldsymbol{\psi}_{I}\boldsymbol{u}_{I} \Biggr)^{\mathrm{T}}\rho \Biggl(\sum_{J}^{n} \boldsymbol{\psi}_{J}\ddot{\boldsymbol{u}}_{J} \Biggr) \,\mathrm{d}\varOmega + \int _{\varOmega} \delta \Biggl(\sum_{I}^{n} \boldsymbol{\psi}_{I}\boldsymbol{u}_{I} \Biggr)^{\mathrm{T}}\mu \Biggl(\sum_{J}^{n} \boldsymbol{\psi}_{J}\dot{\boldsymbol{u}}_{J} \Biggr)\, \mathrm{d}\varOmega \\ &\quad {}+ \int _{\varOmega} \delta \Biggl(\sum_{I}^{n} \boldsymbol{B}_{I}\boldsymbol{u}_{I} \Biggr)^{\mathrm{T}}\boldsymbol{D}\Biggl(\sum_{J}^{n} \boldsymbol{B}_{J}\boldsymbol{u}_{J} \Biggr)\, \mathrm{d}\varOmega - \int _{\varOmega} \delta \Biggl(\sum_{I}^{n} \boldsymbol{\psi}_{I}\boldsymbol{u}_{I} \Biggr)^{\mathrm{T}}\boldsymbol{b}\,\mathrm{d}\varOmega \\ &\quad {}- \int _{\varGamma _{t}} \delta \Biggl(\sum_{I}^{n} \boldsymbol{\psi}_{I}\boldsymbol{u}_{I} \Biggr)^{\mathrm{T}}\bar{\boldsymbol{t}}\,\mathrm{d}\varGamma = 0. \end{aligned} $$
(54)

Because of the arbitrariness of δu, we can write the discrete system equation

$$ \boldsymbol{M}\ddot{\boldsymbol{u}} + \boldsymbol{C}\dot{\boldsymbol{u}} + \boldsymbol{Ku} = \boldsymbol{f}. $$
(55)

If the damping is ignored, Eq. (55) can be simplified as

$$ \boldsymbol{M}\ddot{\boldsymbol{u}} + \boldsymbol{Ku} = \boldsymbol{f}. $$
(56)

If the right-hand item is zero, then this formula is a free vibration equation of the system. u, \(\dot{\boldsymbol{u}}\), and \(\ddot{\boldsymbol{u}}\) are the displacement, speed, and acceleration vectors of the particle, respectively. M, C, K, and f are the quality, damping, stiffness, and particle load matrices, respectively. They can be written as

$$\begin{aligned}& \boldsymbol{u} = \begin{bmatrix} \boldsymbol{u}_{1}^{\mathrm{T}} & \boldsymbol{u}_{2}^{\mathrm{T}} & \cdots & \boldsymbol{u}_{m}^{\mathrm{T}} \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(57)
$$\begin{aligned}& \dot{\boldsymbol{u}} = \begin{bmatrix} \dot{\boldsymbol{u}}_{1}^{\mathrm{T}} & \dot{\boldsymbol{u}}_{2}^{\mathrm{T}} & \cdots & \dot{\boldsymbol{u}}_{m}^{\mathrm{T}} \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(58)
$$\begin{aligned}& \ddot{\boldsymbol{u}} = \begin{bmatrix} \ddot{\boldsymbol{u}}_{1}^{\mathrm{T}} & \ddot{\boldsymbol{u}}_{2}^{\mathrm{T}} & \cdots & \ddot{\boldsymbol{u}}_{m}^{\mathrm{T}} \end{bmatrix}^{\mathrm{T}}, \end{aligned}$$
(59)
$$\begin{aligned}& \boldsymbol{M}_{IJ} = \int _{\varOmega} \boldsymbol{\psi}_{{I}}^{\mathrm{T}} \rho \boldsymbol{\psi}_{{J}}^{\mathrm{T}}\,\mathrm{d}\varOmega \quad (I,J = 1,\ldots,m), \end{aligned}$$
(60)
$$\begin{aligned}& \boldsymbol{C}_{IJ} = \int _{\varOmega} \boldsymbol{\psi}_{{I}}^{\mathrm{T}} \mu \boldsymbol{\psi}_{{J}}^{\mathrm{T}}\,\mathrm{d}\varOmega , \end{aligned}$$
(61)
$$\begin{aligned}& \boldsymbol{K}_{IJ} = \int _{\varOmega} \boldsymbol{B}_{I}^{\mathrm{T}} \boldsymbol{DB}_{J}\,\mathrm{d}\varOmega , \end{aligned}$$
(62)
$$\begin{aligned}& \boldsymbol{f}_{I} = \int _{\varOmega} \boldsymbol{\psi}_{{I}}^{\mathrm{T}} \boldsymbol{b}\,\mathrm{d}\varOmega + \int _{\varGamma _{t}} \boldsymbol{\psi}_{{I}}^{\mathrm{T}} \bar{\boldsymbol{t}}\,\mathrm{d}\varGamma , \end{aligned}$$
(63)

where \(I,J = 1,2,\ldots,m\), and \(\boldsymbol{K}_{IJ}\), \(\boldsymbol{C}_{IJ}\), and \(\boldsymbol{f}_{I}\) are the elements of K, C, and f.

The shape functions of the interpolated reproducing kernel particle all have the characteristics of the Kronecker delta function in a discrete particle, so that the essential boundary can be directly applied.

3.4 Implicit time integration

The time domain is discretized by n time increments. The Newmark method is adopted for the time discretization of the equations of motion. The relationship between the displacement and speed from time \(t_{n}\) to time \(t_{n + 1}\) can be written as

$$\begin{aligned}& \boldsymbol{u}_{n + 1} = \boldsymbol{u}_{n} + \Delta t\dot{ \boldsymbol{u}}_{n} + \frac{1}{2}(1 - \beta _{2})\Delta t^{2}\ddot{\boldsymbol{u}}_{n} + \frac{1}{2}\beta _{2}\Delta t^{2}\ddot{ \boldsymbol{u}}_{n + 1}, \end{aligned}$$
(64)
$$\begin{aligned}& \dot{\boldsymbol{u}}_{n + 1} = \dot{\boldsymbol{u}}_{n} + (1 - \beta _{1})\Delta t\ddot{\boldsymbol{u}}_{n} + \beta _{1}\Delta t\ddot{\boldsymbol{u}}_{n + 1}, \end{aligned}$$
(65)

where \(\beta _{1}\) and \(\beta _{2}\) affect the stability and accuracy of the calculation result. Different parameter selections correspond to different integration methods:

$$\begin{aligned} \mbox{(i)}&\quad \beta _{1} = \frac{1}{2},\qquad \beta _{2} = \frac{1}{3}\quad \mbox{(linear acceleration method)}; \\ \mbox{(ii)}&\quad \beta _{1} = \frac{1}{2},\qquad \beta _{2} = \frac{1}{2}\quad \mbox{(average acceleration method)}; \\ \mbox{(iii)} &\quad \beta _{1} = \frac{1}{2},\qquad \beta _{2} = 0\quad \mbox{(uniform acceleration method)}; \\ \mbox{(iv)}&\quad \beta _{1} = \frac{3}{2}, \qquad \beta _{2} = \frac{8}{5}\quad \mbox{(Galerkin method)}; \\ \mbox{(v)}&\quad \beta _{1} = \frac{3}{2},\qquad \beta _{2} = 4 \quad \mbox{(backward difference method)}. \end{aligned}$$

From Eq. (64) we have

$$ \ddot{\boldsymbol{u}}_{n + 1} = \frac{2}{\beta _{2}\Delta t^{2}}( \boldsymbol{u}_{n + 1} - \boldsymbol{u}_{n}) - \frac{2}{\beta _{2}\Delta t}\dot{\boldsymbol{u}}_{n} - \biggl( \frac{1}{\beta _{2}} - 1 \biggr)\ddot{\boldsymbol{u}}_{n}. $$
(66)

Let

$$\begin{aligned}& \alpha _{1} = \frac{2}{\beta _{2}\Delta t^{2}}, \end{aligned}$$
(67)
$$\begin{aligned}& \alpha _{2} = \frac{2}{\beta _{2}\Delta t}, \end{aligned}$$
(68)
$$\begin{aligned}& \alpha _{3} = \frac{1}{\beta _{2}} - 1. \end{aligned}$$
(69)

Considering Eqs. (67), (68), and (69), Eq. (66) can be written as

$$ \ddot{\boldsymbol{u}}_{n + 1} = \alpha _{1}( \boldsymbol{u}_{n + 1} - \boldsymbol{u}_{n}) - \alpha _{2}\dot{\boldsymbol{u}}_{n} - \alpha _{3} \ddot{\boldsymbol{u}}_{n}. $$
(70)

Substituting Eq. (70) into Eq. (65), we obtain

$$ \dot{\boldsymbol{u}}_{n + 1} = \beta _{1}\alpha _{2}(\boldsymbol{u}_{n + 1} - \boldsymbol{u}_{n}) + \biggl(1 - \frac{2\beta _{1}}{\beta _{2}} \biggr)\dot{\boldsymbol{u}}_{n} + \biggl(1 - \frac{\beta _{1}}{\beta _{2}} \biggr)\Delta t\ddot{\boldsymbol{u}}_{n}. $$
(71)

In the Newmark method the displacement solution \(\boldsymbol{u}_{n + 1}\) is obtained by Eq. (56). Then

$$ \boldsymbol{M}\ddot{\boldsymbol{u}}_{{n} + 1} + \boldsymbol{Ku}_{n + 1} = \boldsymbol{f}_{n + 1}. $$
(72)

Substituting Eqs. (70) and (71) into Eq. (72), we obtain

$$ (\boldsymbol{K}_{n + 1} + \alpha _{1}\boldsymbol{M}_{n + 1}) \boldsymbol{u}_{n + 1} = \boldsymbol{f}_{n + 1} + \boldsymbol{M}_{n + 1}(\alpha _{1}\boldsymbol{u}_{n} + \alpha _{2}\dot{\boldsymbol{u}}_{n} + \alpha _{3}\ddot{\boldsymbol{u}}_{n}). $$
(73)

When \(\boldsymbol{u}_{n + 1}\) is calculated, \(\dot{\boldsymbol{u}}_{n + 1}\) and \(\ddot{\boldsymbol{u}}_{n + 1}\) are determined by Eqs. (70) and (71), respectively.

3.5 Numerical algorithm flow

Firstly, the initial calculation is performed as follows:

Step 1. From Eqs. (60) to (62), M, C, K, and f are determined;

Step 2. Essential boundary condition is applied;

Step 3. u, \(\dot{\boldsymbol{u}}\), and \(\ddot{\boldsymbol{u}}\) are set;

Step 4. Δt, \(\beta _{1}\), and \(\beta _{2}\) are set, and \(\alpha _{1}\), \(\alpha _{2}\), and \(\alpha _{3}\) are obtained.

Secondly, the time step is looped. For every time step,

Step 1. The payload is calculated at time \(t + \Delta t\);

Step 2. According to Eq. (56), the displacement \(\boldsymbol{u}_{t + \Delta t}\) at time \(t + \Delta t\) is obtained;

Step 3. The velocity \(\dot{\boldsymbol{u}}_{t + \Delta t}\) at time \(t + \Delta t\) is found;

Step 4. The acceleration \(\ddot{\boldsymbol{u}}_{t + \Delta t}\) at time \(t + \Delta t\) is found;

Step 5. After the particle displacement vector \(\boldsymbol{u}_{t + \Delta t}\) is obtained, the stress and strain of the particle are obtained according to Eqs. (2) and (3).

Finally, the time step cycle ends, and the particle displacement response, velocity, and stress are output. In this paper, the average acceleration method is adopted, which is an unconditionally stable integral scheme. Thus the new meshless method is formed.

4 Numerical examples

4.1 Vibration analysis of cantilever beam

As shown in Fig. 2, the cantilever beam subjected to a dynamic sudden load at the free end. The length and height of the cantilever beam are \({l} = 0.4~\text{m}\) and \(h = 0.05~\text{m}\), respectively. The material constants are Young’s modulus \(E = 200~\text{GPa}\), Poisson’s ratio \(\nu = 0.3\), and the density \(\rho = 7850~\text{kg}/\text{m}^{3}\). The effect of damping is ignored. The sudden uniform tangential load \(p(t) = 1000~\text{Pa}\) is applied on the free end of the beam at time \(t = 0\). As shown in Fig. 3, ignoring the static load, the plane stress method is adopted to calculate. The displacement along the \(x_{1}\) direction is u. The displacement along the \(x_{2}\) direction is v. The initial conditions are \(\boldsymbol{u}_{0} = \dot{\boldsymbol{u}}_{0} = 0\).

Figure 2
figure 2

The cantilever beam subjected to a dynamic sudden load

Full size image
Figure 3
figure 3

The dynamic load

Full size image

Analytic solution of deflection at the midpoint of the free end of the beam is

$$ w(t) = \frac{1}{2} \biggl[1 - \cos \biggl(\frac{2\pi t}{T} \biggr) \biggr]w_{\max}, $$
(74)

where T and \(w_{\max} \) are the natural vibration frequency of the cantilever beam and maximum deflection of the free end of the beam, respectively,

$$\begin{aligned}& T = \frac{2\pi}{1.875^{2}}\sqrt{\frac{12\rho l^{4}}{Eh^{2}}}, \end{aligned}$$
(75)
$$\begin{aligned}& w_{\max} = \frac{2phl^{3}}{3EI}. \end{aligned}$$
(76)

\(21 \times 6\) particles are used in the domain, as shown in Fig. 4. The cubic spline function is used as a weight function. The linear basis function is used as a base function. The time step chosen for the time integration is \(\Delta t = 2 \times 10^{ - 6}\text{ s}\).

Figure 4
figure 4

The node distribution of the cantilever beam

Full size image

The solutions of the displacement at the free end midpoint of the beam obtained by IRKPM and analytical method are shown in Fig. 5. The comparison of the results calculated by IRKPM and analytical method is shown in Table 1, where R is the relative error, and the maximum relative error is 3.8%. Combining Fig. 5 and Table 1, we can see that IRKPM has a great precision and stability.

Figure 5
figure 5

The time-dependent deflection of the midpoint of the free end

Full size image
Table 1 The deflection of the midpoint of the free end
Full size table

4.2 The dynamic response of cantilever beam under the axial sudden load

As shown in Fig. 6, the cantilever beam is under the sudden load in the axial direction. The geometric and physical parameters are as in Sect. 4.1. The effect of damping is ignored, and the sudden axial load \(p(t) = 1~\text{GPa}\) is applied on the free end of the beam at time \(t = 0\). The sudden load remains the same.

Figure 6
figure 6

The cantilever beam under axial linear sudden load

Full size image

\(21 \times 6\) particles are used in the domain. The cubic spline function is used as a weight function. The linear basis function is used as a base function. The mesh of the finite element method corresponds to the density of the particles.

Figure 7 shows the time-dependent displacements u at the point A calculated by IRKPM and finite element method. Figure 8 shows the time-dependent displacements v at the point A calculated by IRKPM and finite element method.

Figure 7
figure 7

The time-dependent displacement u at the point A

Full size image
Figure 8
figure 8

The time-dependent displacement v at the point A

Full size image

Table 2 shows the displacements of point A at different times calculated by the IRKPM and the finite element method, where R is the relative error. The maximum relative error of time-dependent displacement u is 2.6%. The maximum relative error of time-dependent displacement v is 2.6%. Figure 9 shows the time-dependent stress \(\sigma _{11}\) at point B.

Figure 9
figure 9

The time-dependent stress \(\sigma _{11}\) at the point B

Full size image
Table 2 The displacement v of the point A
Full size table

5 Conclusions

The high-order smooth IRKPM for two-dimensional problems has been formed by combining the shape function of interpolated reproducing kernel particle method and the principle of virtual displacement of elastodynamics. The discrete form of the algorithm has been deduced subsequently.

This method has the advantage of applying the boundary conditions directly like the finite element method and improves the computational efficiency. The new method can be directly used in engineering more easily. Several examples show that the proposed method has higher accuracy and stability as dealing with two-dimensional elastokinetic problems.