1 Introduction

In one of their seminal articles on allowable sequences [28] Goodman and Pollack gave combinatorial generalizations (left as conjectures) for the following three problems in discrete geometry:

  • \({\textbf {A}}\): the Erdős–Szekeres conjecture that any \(2^{n-2}+1\) points in general position in the plane contains n points in convex position,

  • \({\textbf {B}}\): the Dirac conjecture that any set of n noncollinear points in the plane contains a point incident to at least cn connecting lines determined by the set, for some constant \(c>0\),

  • \({\textbf {C}}\): the problem of finding the minimum number of directions determined by n noncollinear points in the plane.

The notion of allowable sequences of permutations provides a natural combinatorial setting independent from geometry for analyzing these problems and making them more transparent. Within this formalism, the conjectured generalizations for the three statements above read as follows:

  • \({\textbf {A}}\varvec{'}\): [28] Let \(\Sigma \) be an allowable \((2^{n-2}+1)\)-sequence in which only strings of length two are reversed. Then there are n indices such that each occurs as the first or as the last in this subset—in some term of \(\Sigma \).

  • \({\textbf {B}}\varvec{'}\): [28] Any nontrivial allowable n-sequence \(\Sigma \) has a local sequence \(\Lambda _i\) whose half-period is at least cn, for some constant \(c>0\).

  • \({\textbf {C}}\varvec{'}\): [28] If \(\Sigma \) is a nontrivial allowable n-sequence, the half-period of \(\Sigma \) is at least \(2 \lfloor n/2 \rfloor \).

The formalism will be made precise in Sect. 2, at the end of which we state our results and review the status of the three problems and their generalizations. It will be evident at that point that \(\mathrm {A'}\,{\Rightarrow }\,\textrm{A}\), \(\mathrm {B'} \,{\Rightarrow }\, \textrm{B}\), and \(\mathrm {C'} \,{\Rightarrow }\, \textrm{C}\), though not conversely. Our goal in this paper is the proof of statement \(\mathrm {B'}\).

Connecting lines and a theorem of de Bruijn and Erdős. Before discussing Dirac’s conjecture, it is natural to mention how this question appeared in the broader context of estimating the total number of connecting lines determined by a noncollinear point set (clearly the answer is 1 for collinear sets). Theorem 2 below provides the answer.

Historically, the study of point sets and their connecting lines draws from a question asked by Sylvester [54] about 50 years earlier: For a finite set of points, not all on a line, does there always exist a line that contains exactly two of the points? If the answer is positive, the corresponding equivalent statement would read: if for every pair of points in the set, the line determined by these points contains a third one, then all the points are collinear. Given a point set S, a connecting line (i.e., a line determined by the set) is called ordinary if it contains precisely two points of S; see also [7]. Sylvester problem got forgotten over time but was rediscovered by Erdős [18] in 1943.

The first proof of existence of an ordinary line dates back to those times and it is now commonly referred to as the Sylvester–Gallai Theorem (solutions were found by several researchers). Its colorful history is recounted by Chvátal in his recent monograph [11]. Earlier accounts on its development can be found in [8, 12, 20, 35, 47].

Theorem 1

(Sylvester–Gallai) Every set of n noncollinear points in the plane admits an ordinary line.

Motzkin [41] was the first to show that the number of ordinary lines tends to infinity with n. Further, Kelly and Moser [34] proved that there are at least 3n/7 ordinary lines, and Csima and Sawyer [13] raised this bound to 6n/13 for \(n\ge 8\). Finally, Green and Tao [30] proved that if n is sufficiently large then there are at least n/2 ordinary lines, thereby settling the so called strong Dirac–Motzkin conjecture for large n (even though neither of the authors seem to have conjectured this in print, see [30]). On the other hand, there are arbitrarily large points sets with no more than n/2 ordinary lines: for even n, take a regular (n/2)-gon, which determines n/2 directions, and the n/2 projective points corresponding to these directions; see [8, Chap. 7.2].

Erdős [18] deduced the following interesting corollary of Theorem 1. Here the term near-pencil describes a point set that is almost collinear, in the sense that all but of one the points are collinear.

Theorem 2

For a set of n noncollinear points in the plane, the number of connecting lines is always at least n; and it is equal to n if and only if the points form a near-pencil.

In fact every other configuration determines more lines as quantified in the following result of Kelly and Moser [34].

Theorem 3

Let S be a set of n points and let \(\lambda =\lambda (S)\) denote the number of connecting lines. If at most \(n-k\) points of S are collinear and \(n >\{3(3k-2)^2 + 3k-1 \}/2\) then \(\lambda \ge kn - (3k+2)(k-1)/2\).

In particular (\(k=2\)), if at most \(n-2\) points are collinear and \(n \ge 27\), the number of connecting lines is always at least \(2n-4\); the lower bound actually holds for \(n \ge 10\), see [35, Chap. 6].

Perhaps even more interesting than Theorem 2 is the following result of de Bruijn and Erdős [9] from about the same time—which provides the same answer under more general circumstances that distill the essential features present in the theorem. See also [38, Chap. 19] and [45].

Theorem 4

(de Bruijn and Erdős [9])   Let (V, E), \(|V|=n\), \(|E|=m\), be a hypergraph, where every pair of elements in V is contained in precisely one edge in E and where V itself is not an edge. Then \(m \ge n\), with equality if and only if (i) one of the sets contains all but one elements of V and the others are two-element sets containing the remaining element; or (ii) E is the system of lines of a finite projective plane defined on V.

A result of Motzkin [42], Rabin, and Chakerian [10] states that any set of n two-colored (say, by red or blue) noncollinear points in the plane determines a monochromatic line; see also [2, Chap. 13].

Dirac’s conjecture. For a noncollinear set S of n points in the plane, let t(S) be the maximum number of lines spanned by S that are incident to a point in S. In a dual setting, for a set \({\mathcal {L}}\) of n lines in the plane, no two of which are parallel, let \(r({\mathcal {L}})\) be the maximum number of crossing points (vertices of the line arrangement) on a line in \({\mathcal {L}}\).

Dirac [14] and Motzkin [41], independently of each other and at the same time proposed the following problem: Does every noncollinear set of points contain some point that is incident to at least n/2 lines determined by the set? Initially Dirac proved that there are at least \(\sqrt{n+1}\) lines incident to one of the points and conjectured the existence of a point incident to at least \(\lfloor n/2 \rfloor \) connecting lines, namely that \(t(S) \ge \lfloor n/2 \rfloor \) for every noncollinear set S. Several counterexamples were found by Grünbaum (for \(n=9, 15,19,25,31,37\)), see [31] and [12, F12], and so the conjecture has been modified [19] to read as follows:

Conjecture 1

(Dirac)   Given a set S of n noncolllinear points in the plane, there exists a point in S incident to cn lines determined by S, for some constant \(c>0\).

From the other direction, Akiyama et al. [4] considered the problem of finding noncollinear point sets S with \(t(S) \le \lfloor n/2 \rfloor \). They showed that for every \(n \ge 8\) of the form \(n=12k + r\), \(r \ne 11\), there exists a set S of n noncollinear points satisfying \(t(S) \le \lfloor n/2 \rfloor \). An infinite family of counterexamples to the original Dirac conjecture was found by Felsner [8, p. 313]. In the dual setting it consists of \(6k+7\) lines in the real projective plane (r.p.p.) where no line is incident to more than \(3k+2\) points of intersection. In a stronger form—the so called strong Dirac conjecture—the bound is replaced by \(n/2 -c\), where \(c>0\) is a constant [43]; see also [8, Chap. 7.3].

In 1983 Beck [5] proved the following result and further observed that Conjecture 1 immediately follows from it.

Theorem 5

Let S be a set of n points in the plane. If at most \(\ell \) points of S are collinear, then S determines at least \(\Omega (n(n-\ell ))\) distinct lines.

At about the same time Szemerédi and Trotter [56] obtained their classic result on the number of point-lines incidences in the plane: Theorem 6 or 7 below. Their result also implies Conjecture 1. Interestingly enough, as remarked by Székely [55], Beck obtained his result on connecting lines from a result weaker than the Szemerédi–Trotter theorem.

Here we give two equivalent formulations of the Szemerédi and Trotter result. Given a point set S in \(\mathbb {R}^2\), for any integer \(k\ge 2\), a line is called k-rich if it is incident to at least k points of S.

Theorem 6

(Szemerédi–Trotter [56])   The number of point-line incidences among n points and \(\ell \) lines in \(\mathbb {R}^2\) is

$$\begin{aligned} I(n,\ell )={\mathcal {O}}(n^{2/3}\ell ^{2/3}+n+\ell ). \end{aligned}$$

Theorem 7

(Szemerédi–Trotter [56])   Given n points in \(\mathbb {R}^2\), the number of k-rich lines, \(k\ge 2\), is

$$\begin{aligned} {\mathcal {O}}\biggl (\frac{n^2}{k^3}+\frac{n}{k}\biggr ). \end{aligned}$$

The resulting constants, however, in the above proofs for Conjecture 1 are quite small; for instance, the constant obtained in [56] is \(10^{-1087}\); see also [35, Chap. 6]. New developments in the theory of geometric graphs have lead over time to better constants in Dirac’s conjecture. One such tool is the classic crossing lemma proved in the early 1980s by Ajtai et al. [3] and Leighton [37]. The sharper constant appearing at the end of the lemma was established recently by Ackerman [1] who improved an earlier bound by Pach et al. [46]; see also [47, Chap. 4].

Lemma 1

(Ajtai et al. [3], Leighton [37], Ackerman [1])   Let \(G=(V,E)\), where \(|V|=n\), \(|E|=e\), be a simple graph with with n vertices and \(e \ge 4n\) edges. Then \(\textrm{cr}(G) \ge c e^3/n^2\), for a suitable constant \(c>0\). In particular, one may take \(c=1/64\); and if \(e \ge 6.95n\), then one may take \(c=1/29\).

Another key development is due to Székely [55], whose groundbreaking approach of constructing suitable graphs and running the crossing lemma machinery led to new bounds and improved constants in relation to Dirac’s conjecture, but in many other problems as well. For instance, using this approach, Payne [48] showed in his thesis that Conjecture 1 holds with \(c=2^{-15}\); see also [49]. Further, Payne and Wood [49] raised the bound to \(c=1/37\); notably, Hirzebruch’s inequality is used in their proof; see also [8, Chap. 7]. Another approach for improving the constant in Conjecture 1 was proposed around the same time by Pinchasi [51]. Subsequently, Pham and Phi refined the argument of Payne and Wood and improved the bound to \(c=1/26\) [50]. Recently, Han [32] established the current best result in Dirac’s conjecture, showing that there is a point incident to \(\lceil n/3\rceil +1\) connecting lines; notably, the Bojanowski–Pokora inequality is used in their proof. His result answers a question of Klee and Wagon [35, Chap. 6]; the same question was reposed 20 years later by Akiyama et al. [4].

In regard to the proof techniques, it is worth mentioning that neither the Hirzebruch’s inequality nor the Bojanowski–Pokora inequality are known to hold in a pseudoline setting (discussed in Sect. 2).

Outline of the paper. Sect. 2 gives an overview of pseudoline arrangements and allowable sequences and lists our results. The main results are the lower bounds in Theorems 8 and 9 in relation to Conjecture 2 in Sect. 2 (i.e., statement \(\mathrm {B'}\) at the beginning of Sect. 1). The upper bound in Theorem 10 gives a partial answer to a question of Lund et al. [40]. Section 3 contains the proofs of Theorems 8 and 9. Section 4 contains the proof of Theorem 10.

2 Pseudolines, Allowable Sequences, and Wiring Diagrams

Pseudoline arrangements. A family (collection) of two-way infinite x-monotone curves in the plane is called an (Euclidean) arrangement of pseudolines if any two curves have precisely one point in common, at which they properly cross [23, Chap. 6]. An arrangement is simple if no three pseudolines have a common point of intersection, see Fig. 1 (left). An arrangement is nontrivial if not all pseudolines cross at a single point.

Fig. 1
figure 1

Left: A simple arrangement \({\mathcal {A}}\). Center: Wiring diagram of \({\mathcal {A}}\). Right: An arrangement \({\mathcal {A}}'\) that is not isomorphic to the arrangement \({\mathcal {A}}\) on the left

Full size image

A family \({\mathcal {P}}\) of pseudolines is stretchable if there exists a family of lines \({\mathcal {L}}\) such that the cell decompositions induced by \({\mathcal {P}}\) and \({\mathcal {L}}\) are topologically isomorphic. Two arrangements are isomorphic, i.e., considered the same, if they can be mapped onto each other by a homeomorphism of the plane [25]; see Fig. 1 (right). Equivalently, two arrangements are isomorphic if there is an isomorphism between the induced cell decompositions [23, Chap. 6]. Two classic representations of pseudoline arrangements are allowable sequences [27, 29] and wiring diagrams [24].

Allowable sequences. Let P be a set of n points in the plane and assume that no two points have the same x-coordinate. Label the points of P by \(1,2,\ldots ,n\) in increasing order of their x-coordinate. Take a horizontal line \(\ell \) and start rotating it counterclockwise about a fixed point; In each position, the order of the orthogonal projections of the elements of P onto \(\ell \) makes a permutation of \(1,2,\ldots ,n\). As the line \(\ell \) rotates counterclockwise about a fixed point, we obtain a periodic sequence of permutations which is called the circular sequence of the configuration [28]; see also [16, Chap. 2], [23, Chap. 6], [24, 47, Chap. 1]. The first half-period of this sequence starts with the identity permutation \(1,2,\ldots ,n\) and ends with its reversal, \(n,n-1,\ldots ,1\); this corresponds to a rotation of \(\ell \) by \(180^\circ \). During this half-period the following rule is in effect:

  1. 1.

    Every permutation is obtained from the previous one by reversing one or more nonoverlapping increasing subsequences of adjacent elements.

If the rotation of \(\ell \) continues, we obtain the same sequence of permutations as before, except that now each of them is reversed. After a complete rotation of \(360^\circ \), we get back \(1,2,\ldots ,n\), the permutation we started with. And so one is usually interested only in the sequence for the first half-period.

Goodman and Pollack [28] generalized this process associated with a point set to an abstract setting. Any sequence of permutations that starts with \(1,2,\ldots ,n\), ends in \(n,n-1,\ldots ,1\), and satisfies the above rule is called an allowable sequence (or n-sequence). The half-period of this sequence is one less than the number of permutations in the sequence, i.e., the number of steps (or moves) in the process.Footnote 1 An allowable sequence \(\Sigma \) is simple if any two consecutive permutations in \(\Sigma \) differ by the reversal of an adjacent pair ij, where \(i<j\). An allowable sequence is nontrivial if it has more than two permutations; equivalently \(1,2,\ldots ,n\) is not reversed in one step. Throughout this paper, we only consider nontrivial sequences.

One can extract an allowable sequence of permutations from any given arrangement of pseudolines by sweeping a vertical line from left to right and recording the switches that occur in that order. Even though not every allowable sequence is geometrically realizable as the circular sequence generated by a set of points (or lines), it is however true that every allowable sequence is realizable as the n-sequence generated by an arrangement of pseudolines [29]. Write each permutation in the sequence as a vertical column of n numbers and put the columns one after the other. The ith pseudoline is the piecewise linear x-monotone curve obtained by connecting all occurrences of number i, for \(i=1,2,\ldots ,n\) and extended both ways to infinity. By construction, this family of curves is a pseudoline arrangement whose sweep-sequence is the given allowable sequence. By this equivalence, in our arguments we may use language that applies to one setting (allowable sequences) or the other one (pseudolines) as convenient.

Let \(\Sigma \) be an allowable n-sequence. For each \(i \in [n]\), its local sequence \(\Lambda _i(\Sigma )\) is the sequence of reversals involving the index i. Obviously such reversals appear in succession, i.e., no two are simultaneous. The half-period (or length) of a local sequence is the number of reversals in the sequence.

Fig. 2
figure 2

Wiring diagrams of a simple arrangement (left) and a non-simple one (right)

Full size image

Wiring diagrams. A wiring diagram is an Euclidean arrangement of pseudolines consisting of piece-wise linear ‘wires’, each horizontal except for shorter slanted segments where it crosses other wires. Each pair of wires cross exactly once; see Fig. 1 (center). Wiring diagrams are also known as reflection networks, i.e., networks that bring n wires labeled from 1 to n into their reflection by means of performing switches of (two or more) adjacent wires [36, p. 35]. For example, the 5-sequence for the wiring diagram in Fig. 2 (right) is

$$\begin{aligned} 12345 \xrightarrow {12,45} 21354\xrightarrow {135} 25314 \xrightarrow {25,14} 52341\xrightarrow {34} 52431 \xrightarrow {24} 54231 \xrightarrow {23} 54321. \end{aligned}$$

Its half-period is 6. Its five local sequences are the following. \(\Lambda _1 = 12, 135, 14\); \(\Lambda _2 = 12, 25, 24, 23\); \(\Lambda _3 = 135, 34, 23\); \(\Lambda _4 = 45, 14, 34, 24\); and \(\Lambda _5 = 45, 135, 25\). The half-period of \(\Lambda _5\) is 3.

Applications of allowable sequences. A classic example is the result of Ungar mentioned in the introduction on the minimum number of directions determined by n noncollinear points in the plane. If D(n) denotes this number, Ungar [57] showed that \(D(n)= 2\lfloor n/2\rfloor \), which is tight for the near-pencil configuration. His proof via allowable sequences concentrates on the subsequence of switches crossing the midline that separates the first n/2 elements from the last n/2 elements (assuming that n is even). Another key result is one obtained by Edelsbrunner and Welzl [17] in the study of k-sets; they showed that the number of k-sets in a set of n points is \({\mathcal {O}}(n k^{1/2})\); see also [16, Chap. 2]. More recent applications can be found in [15] and [44]. In the latter article, Nilakantan obtained an alternative proof of Theorem 1 via allowable sequences by arguing the existence of a simple switch, namely one that involves only two elements.

Dirac–Goodman–Pollack conjecture for pseudolines. For an arrangement \({\mathcal {L}}\) of pseudolines let \(r({\mathcal {L}})\) be the maximum number of crossing points (vertices of the line arrangement) on a pseudoline in \({\mathcal {L}}\). The conjecture can be formulated in terms of allowable sequences (as mentioned in Sect. 1) or in terms of systems of pseudolines. The latter formulation is as follows.

Conjecture 2

[14, 28] Let \({\mathcal {L}}\) be a nontrivial arrangement of n pseudolines. Then \(r({\mathcal {L}}) \ge c n\), for some constant \(c>0\).

Lund et al. [40] claimed that such a bound holds, but did not provide any proof. From the other direction, they constructed arrangements with \(r({\mathcal {L}}) \le 4n/9 \). Regardless, here we obtain the first concrete lower bound (Theorem 8) and an extension for many pseudolines (Theorem 9).

Theorem 8

Let \({\mathcal {L}}\) be a nontrivial arrangement of n pseudolines. Then there is a pseudoline in \({\mathcal {L}}\) that is incident to at least cn crossing points. In particular, one may take \(c=1/845\) for large n.

Theorem 9

\(Let ~0<\delta <1\) be any constant. Consider an arrangement of pseudolines in which every crossing involves at most \(\delta n\) elements. Then there exist \(\Omega (n)\) pseudolines whose local sequences have length (i.e., half-period) \(\Omega (n)\).

From the other direction, an old construction studied by Rigby [52] shows the following.

Theorem 10

There is an infinite family of arrangements of n lines (as a system of pseudolines), such that

  • each vertex is incident to at most three lines, and

  • no line is incident to more than \(n/2 + {\mathcal {O}}(1) \) vertices.

We end this section with a brief review of the status of the three problems and their generalizations (from Sect. 1). Statement \(\mathrm {C'}\) has been settled by Ungar in 1982 [57]. Statement \(\mathrm {B'}\) is proved in Theorem 8 with a bound of n/845 (for n sufficiently large). Statement \(\mathrm {A'}\) remains open, however, recent results are closing in on this problem. Let f(n) denote the minimum number of points in general position that determine a convex n-gon. For the geometric variant \(\textrm{A}\), Erdős and Szekeres [21, 22] proved many years ago that \(2^{n-2}+1 \le f(n) \le 4^{n(1-o(1))}\); after several constant-factor improvements by other researchers that we skip here, Suk [53] managed to bring the upper bound to same base as the lower bound, i.e., \(f(n) \le 2^{n+ {\mathcal {O}}(n^{2/3} \log {n})}\). Holmsen et al. [33] generalized Suk’s result to pseudoline arrangements and improved the error term. The improvement carries over to the geometric variant and implies \(f(n) \le 2^{n+ {\mathcal {O}}(\sqrt{n \log {n}})}\).

3 Proofs of the Main Results

In this section we prove Theorems 8 and 9. The key component in the proof is a dual extension of the Szemerédi–Trotter theorem for point-line incidences to arrangements of x-monotone pseudolines. We employ Székely’s method [55]. Let \(2\le k\le n\). A crossing point is k-rich if it is incident to at least k pseudolines.

Lemma 2

Let \(5 \le k \le n-1\). For an arrangement of n pseudolines, the number of k-rich crossing points is at most

$$\begin{aligned} c_1 \frac{n}{k} + c_2 \frac{n^2}{k^3}, \end{aligned}$$
(1)

for a suitable constants \(c_1,c_2>0\). In particular, one may take \(c_1=5\) and \(c_2=125/2\); and if \(k \ge 8\) one may take \(c_1=14\) and \(c_2=18.12\).

Fig. 3
figure 3

The graph G; here \(n=9\), \(k=3\), \(m=9\), and \(|E|=19\)

Full size image

Proof

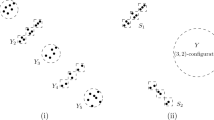
Construct a graph \(G=(V,E)\) drawn in the plane, where V is the set of k-rich crossing points in \({\mathcal {A}}\) and edges connect vertices along the pseudolines in \({\mathcal {A}}\). Let \(|V|=m\). Refer to Fig. 3 for an example.

The graph G is simple since every pair of pseudolines cross exactly once. Since \({\mathcal {A}}\) is an arrangement of n pseudolines, \(\textrm{cr}(G) \le {n \atopwithdelims ()2}\). We have \(|V| =m\) and \(|E| \ge km -n\) by easy counting. We distinguish two cases.

  • Case 1: \(km \le 5n\). Then \(m \le 5n/k\), as required.

  • Case 2: \(km \ge 5n\). Then \(|E| \ge km - km/5 = 4\,km/5 \ge 4m\) by the assumption \(k \ge 5\). The former setting of the crossing lemma (Lemma 1) can be applied and it gives

    $$\begin{aligned} {n\atopwithdelims ()2} \ge \textrm{cr}(G) \ge \frac{|E|^3}{64|V|^2},\quad \text { or }\quad n^2 \ge \frac{2}{64} \cdot \frac{4^3}{5^3} \cdot \frac{k^3 m^3}{m^2}. \end{aligned}$$

    It follows that \(m \le 62.5\cdot n^2/k^3\), as required.

Assume now that \(k \ge 8\). We distinguish two cases.

  • Case 1: \(km \le 14n\). Then \(m \le 14n/k\), as required.

  • Case 2: \(km \ge 14n\). Then \(|E| \ge km - km/14 = 13km/14 \ge 7m\) by the assumption \(k \ge 8\). The latter setting of the crossing lemma can be applied and it gives

    $$\begin{aligned} \left( {\begin{array}{c}n\\ 2\end{array}}\right) \ge \textrm{cr}(G) \ge \frac{|E|^3}{29|V|^2}, \quad \text { or }\quad n^2 \ge \frac{2}{29} \cdot \frac{13^3}{14^3} \cdot \frac{k^3 m^3}{m^2}. \end{aligned}$$

    It follows that \(m \le 18.12\cdot n^2/k^3\), as required. \(\square \)

Showing that \(\Sigma \) has a local sequence \(\Lambda _i\) whose half-period is \(\Omega (n)\) is equivalent to showing that at least one pseudoline is incident to \(\Omega (n)\) crossing points (these may be vertices of G or edge crossings with the respective pseudoline).

Observation 1

Let \({\mathcal {L}}' \subset {\mathcal {L}}\) be the subset of pseudolines participating in a crossing \(\xi \) and \(\ell \in {\mathcal {L}}\setminus {\mathcal {L}}'\) be any other pseudoline. Then \(\ell \) must cross every pseudoline in \({\mathcal {L}}'\) at a different crossing point.

Proof

Let \({\mathcal {L}}'' \subset {\mathcal {L}}\) be the subset of pseudolines participating in a fixed crossing other than \(\xi \). Then \(|{\mathcal {L}}' \cap {\mathcal {L}}''| \le 1\), since every pair of pseudolines cross exactly once. Since \(\ell \) must cross every other pseudoline, in particular, every pseudoline in \({\mathcal {L}}'\), \(\ell \) must have at least \(|{\mathcal {L}}'|\) different crossing points. \(\square \)

Note that the condition on the uniqueness of any pairwise intersection (as above) is essentially the same as that appearing in Theorem 4; see also [38, Chap. 19].

Proof of Theorem 8

First assume that there exists a k-rich crossing point \(\xi \) for \(k=n/845\). Consider the subset of pseudolines \({\mathcal {L}}' \subset {\mathcal {L}}\) involved in this crossing. We have \(|{\mathcal {L}}'| \ge n/845\); recall that \(|{\mathcal {L}}'| \le n-1\). Pick any pseudoline \(\ell \in {\mathcal {L}}\setminus {\mathcal {L}}'\). By Observation 1, \(\ell \) must intersect every element in \({\mathcal {L}}'\) at a different crossing point. In other words, the length of \(\ell \)’s local sequence is at least \(|{\mathcal {L}}'| \ge n/845\), as required.

We may now assume for the remainder of the proof that there are no k-rich crossing points for \(k=n/845\). Since every pair of pseudolines intersect exactly once, the total number of pair switches is \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) \). We next compute an upper bound on the number of pair switches at the k-rich crossing points for \(256 \le k < n/845\). Since \(k \ge 8\), we can use the latter setting of Lemma 2, with \(c_1=14\) and \(c_2=18.12\). Once this bound is obtained, we deduce from it (and the total count) a lower bound on the total number of switches at k-rich crossing points for \(2 \le k \le 255\). Finally we obtain a lower bound on the maximum number of crossings on some pseudoline in \({\mathcal {L}}\).

For \(i \ge 1\), let \(V_i \subset V\) denote the subset of vertices incident to at least \(2^i\) and at most \(2^{i+1}-1\) pseudolines. Observe that a vertex in \(V_i\) contributes fewer than \(\left( {\begin{array}{c}2^{i+1}\\ 2\end{array}}\right) \le 2 \cdot 4^i\) switches (out of \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) \)).

Let \(N_1\) denote the number of switches at k-rich vertices for \(256 \le k < n/845\) contributed by the first term (linear in n) in (1). Let x be the minimum integer such that \(2^{x+1} \ge n/845\). Then \(2^x < n/845\), whence we have

$$\begin{aligned} N_1\le c_1 n \sum _{i=8}^x \frac{1}{2^i}\left( {\begin{array}{c}2^{i+1}\\ 2\end{array}}\right) \le 2 c_1 n \sum _{i=8}^x 2^i\le 4c_1 n\cdot 2^x \le 4 c_1 n \cdot \frac{n}{845}\le \frac{4.242}{64}n^2. \end{aligned}$$

Let \(N_2\) denote the number of switches at k-rich vertices for \(256 \le k < n/845\) contributed by the second term (quadratic in n) in (1). We have

$$\begin{aligned} N_2 \le \sum _{i=8}^\infty c_2 \frac{n^2}{2^{3i}}\left( {\begin{array}{c}2^{i+1}\\ 2\end{array}}\right) \le 2 c_2 n^2\sum _{i=8}^\infty \frac{1}{2^i}= 2 c_2 \frac{n^2}{128} =\frac{18.12}{64}n^2. \end{aligned}$$

Adding up the two contributions yields

$$\begin{aligned} N_1 + N_2 \le \frac{22.362}{64}n^2. \end{aligned}$$

Hence at least

$$\begin{aligned} \left( {\begin{array}{c}n\\ 2\end{array}}\right) - \frac{22.362}{64}n^2 \ge \frac{9.637}{64}n^2 \end{aligned}$$
(2)

switches occur at crossing points that involve at most 255 pseudolines. In the last inequality we used the fact that n is large enough. A crossing of j pseudolines, where \(2 \le j \le 255\), distributes j credits to the respective lines and uses \(\left( {\begin{array}{c}j\\ 2\end{array}}\right) \) switches from the pool in (2). One credit received by a pseudoline counts for one crossing point on the respective pseudoline. The ratio of credits to switches in such a crossing,

$$\begin{aligned} \frac{j}{\left( {\begin{array}{c}j\\ 2\end{array}}\right) }= \frac{2}{j-1}, \end{aligned}$$

is minimized at \(j=255\), when the ratio is 1/127. Consequently, by the pigeonhole principle, there is a pseudoline that receives at least

$$\begin{aligned} \frac{9.637}{64}n^2 \cdot \frac{1}{127} \cdot \frac{1}{n} \ge \frac{n}{845} \end{aligned}$$

credits, i.e., has at least this number of crossing points, as required.\(\square \)

The resemblance of the argument in the proof of Theorem 8 with the following result of Beck [5] is worth noting.

Theorem 11

There is constant \(c>0\) such that for any set S of n points in the plane, either

(\(\alpha \)):

some line contains at least cn points of S, or

(\(\beta \)):

the number of distinct lines determined by S is at least \(c n^2\).

In general, one cannot guarantee the existence of more pseudolines with the property in Theorem 8. Indeed, consider the n-sequence of permutations:

$$\begin{aligned} 1,2,\ldots ,n-1,n{} & {} \xrightarrow {1,2,\ldots ,n-1} n-1,n-2,\ldots ,2,1,n\\{} & {} \xrightarrow {1,n} n-1,n-2,\ldots ,2,n,1\xrightarrow {} \cdots \xrightarrow {} n,n-1,\ldots ,2,1. \end{aligned}$$

The only pseudoline whose local sequence is of length \(\Omega (n)\) is the nth one. However, under very mild conditions, the stronger statement in Theorem 9 is in effect. Its proof is analogous to that of Theorem 8.

Proof of Theorem 9 (sketch)

Assume first that there exists a k-rich crossing point \(\xi \) for \(k=c n\), for some positive constant \(c \le \delta \). Consider the subset of pseudolines \({\mathcal {L}}' \subset {\mathcal {L}}\) involved in this crossing. We have \(c n \le |{\mathcal {L}}'| \le \delta n\). By Observation 1, for every pseudoline \(\ell \in {\mathcal {L}}{\setminus } {\mathcal {L}}'\), the length of \(\ell \)’s local sequence is at least cn. Moreover, \(|{\mathcal {L}}{\setminus } {\mathcal {L}}'| \ge (1-\delta )n\), as required. If there is no k-rich crossing point for \(k= c n\), for a sufficiently small \(c>0\), the proof is finished as before, by obtaining an \(\Omega (n^2)\) lower bound analogous to (2). We omit the details. \(\square \)

It should be noted that Theorem 9 is a dual extension of Beck’s result mentioned above.

4 Upper Bound Questions and Concluding Remarks

In this section we prove Theorem 10. In 2014, Lund et al. [40] demonstrated an infinite family of (nontrivial) pseudoline arrangements, in which an arrangement of n pseudolines has no member incident to more than 4n/9 points of intersection (i.e., vertices of the arrangement), and thereby showed that the strong Dirac conjecture does not hold for pseudolines. One feature of the respective family of arrangements is that they contain vertices with high incidence, in particular, about n/3 pseudolines are incident to a single vertex. The authors asked the following.

Question 1

Is there an infinite family of arrangements of n pseudolines, such that

  • no vertex is incident to \(\Omega (n)\) pseudolines, and

  • no pseudoline is incident to more than \((1-\varepsilon )n/2\) vertices, for some constant \(\varepsilon >0\)?

The authors further relaxed the second requirement by replacing \((1-\varepsilon )n/2\) with cn, where \(c<1\) is a constant, and asked for such an arrangement. Here we give a positive answer to the latter question, while we show that the first requirement can be substantially strengthened in that case. Interestingly enough, the best construction we found uses straight lines as we were not able to exploit the power of curved pseudolines. The features of the construction are described in Theorem 10. It is worth noting, however, that this construction falls short of answering Question 1.

The deltoid construction. The construction can be traced back to Rigby [52] who provided an analysis, and even further back; for instance, an illustration can be found in [39, Chap. 8]. This line arrangement has been also used in [6, 26], where descriptions and useful properties can be found. Let \(\ell (\theta )\) denote the line connecting \(e^{i\theta }\) and \(e^{i(\pi -2\theta )}\) on the unit circle, with the understanding that \(\ell (\theta )\) is the tangent line when the two points coincide. We take the freedom to denote the construction in this way based on the fact that \(\ell (\theta )\) envelops a deltoid as \(\theta \) varies. Its key property stems from the following.

Lemma 3

(Rigby [52], Füredi and Palásti [26])   The lines \(\ell (\alpha )\), \(\ell (\beta )\), and \(\ell (\gamma )\) are concurrent if and only if \(\alpha + \beta + \gamma \equiv 0\ (mod \;2\pi )\).

Fig. 4
figure 4

The deltoid construction for \(n=18\) lines

Full size image

Consider a regular n-gon inscribed in the unit circle centered at the origin, where n is even, and refer to Fig. 4. Let \(p_0,p_1,\dots ,p_{n-1}\) denote its vertices labeled counterclockwise starting from \(p_0=(1,0)\). For \(i=0,1,\dots ,n-1\), draw the lines connecting \(p_i\) with \(p_{n/2-2i}\), where indices are considered modulo n. If the points \(p_i\) and \(p_{n/2-2i}\) coincide, draw the tangent line to the circle at \(p_i\). The resulting arrangement has n lines, \(1+\lceil {n(n-3)}/{6}\rceil \) triple points (i.e., vertices incident to three lines), and \(n-3+\delta (n)\) double points (i.e., ordinary vertices), where \(\delta (n)=0\) if \(n \equiv 0\ (mod \;3)\) and \(\delta (n)=2\) otherwise; see, e.g., [6]. Moreover, double points may only appear on the outer envelope, whence each line is incident to at most three double points, and Theorem 10 follows. Obviously, the constant 1/2 in the theorem is the best possible (for lines or pseudolines) under the first constraint.

Determining the right constant in Conjecture 2 remains an interesting open problem. It is easy to obtain small improvements in the lower bound by slightly adjusting the parameters in the proof of Theorem 8. Since we suspect that the answer is much closer to the best known upper bound of Lund, Purdy, and Smith, we did not insist in that direction.