An Improved Upper Bound for the Erdős–Szekeres Conjecture

Abstract

Let ES(n) denote the minimum natural number such that every set of ES(n) points in general position in the plane contains n points in convex position. In 1935, Erdős and Szekeres proved that ES$(n) \le {2n-4 \atopwithdelims ()n-2}+1$. In 1961, they obtained the lower bound $2^{n-2}+1 \le \mathrm{ES}(n)$, which they conjectured to be optimal. In this paper, we prove that

$$\begin{aligned} \mathrm{ES}(n) \le \Big (\begin{array}{c}{2n-5} \\ {n-2}\end{array}\Big ) -\Big (\begin{array}{c}{2n-8} \\ {n-3}+2\end{array}\Big ) \approx \frac{7}{16} \Big (\begin{array}{c}{2n-4}\\ {n-2}\end{array}\Big ). \end{aligned}$$

1 Introduction

In 1933, Esther Klein asked about the existence of the least natural number ES(n) such that every set of ES(n) points in general position in the plane contains n points in convex position. Erdős and Szekeres [3] gave a positive answer in 1935, by proving that ES$(n) \le {2n-4 \atopwithdelims ()n-2}+1$. In 1961, they gave a construction in [4] and proved that $2^{n-2}+1 \le \mathrm{ES}(n)$. The lower bound is conjectured to be tight.

In 1998, Chung and Graham [2] improved the upper bound by 1. In the same year, Kleitman and Pachter [5] proved that ES$(n) \le {2n-4 \atopwithdelims ()n-2}-2n+7$. Shortly after that, Tóth and Valtr [7] improved the bound roughly by a factor of 2 by showing that ES$(n) \le {2n-5 \atopwithdelims ()n-2}+2$. In [8], they combined the ideas from [2, 7] to improve this bound by another 1. We refer the reader to [1] for other questions and results related to the Erdős–Szekeres theorem.

In his recent paper [9], Vlachos further improved the bound and showed that

$$\begin{aligned} \mathrm{ES}(n) \le \Big (\begin{array}{c}{2n-5} \\ {n-2} \end{array}\Big )-\Big (\begin{array}{c}{2n-8} \\ {n-3}\end{array}\Big )+\Big (\begin{array}{c}{2n-10} \\ {n-3}\end{array}\Big )+2, \end{aligned}$$

(1)

which implies

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty } \tfrac{\mathrm{ES}(n)}{\Big (\begin{array}{c}{2n-5} \\ {n-2}\end{array}\Big )} \le \frac{29}{32}. \end{aligned}$$

(2)

Vlachos’ manuscript [9] has revitalized the subject and has led to further improvements. Using slightly different techniques, Norin and Yuditsky [6] showed that

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty } \tfrac{\mathrm{ES}(n)}{{2n-5 \atopwithdelims ()n-2}} \le \frac{7}{8}. \end{aligned}$$

(2′)

On the other hand, during the refereeing process of [9], each of the two current authors independently fine-tuned the original arguments of [9] to get rid of the term ${2n-10 \atopwithdelims ()n-3}$ in (1).

Our main result is the following.

Theorem 1.1

Let ES(n) be the minimum natural number such that every set of ES(n) points in the plane contains n points in convex position. For any natural number $n \ge 6$, we have

$$\begin{aligned} \mathrm{ES}(n) \le \Big (\begin{array}{c}{2n-5} \\ {n-2}\end{array}\Big )-\Big (\begin{array}{c}{2n-8} \\ {n-3}\end{array}\Big )+2. \end{aligned}$$

Note that this result is slightly stronger than that in [6], but it yields the same asymptotic upper bound ($2^{\prime }$).

In Sect. 2 of the paper, a partitioning of any point set, with some nice applications is introduced. We use this partitioning to give an alternative proof of the first upper bound for ES(n), which was obtained by Erdős and Szekeres [3]. In Sect. 3, we introduce an auxiliary function called the convexification function h(m, l), and establish some of its most important properties. Among them, Lemma 3.3 and Theorem 3.4 are taken from [9]. We prove another property of h(m, l) in Theorem 3.5. Combining this result with the other two will give us an improved upper bound on the convexification function. By using this bound and applying a projective transformation taken from [7], we prove Theorem 1.1 in the last section, and deduce the asymptotic bound ($2^{\prime }$) from it.

2 Preliminary Results

First, we define a few properties of the point sets in the plane.

Definition 2.1

A set is said to be in general position, if it does not contain any three collinear points.

A set is non-vertical, if any vertical line in the plane contains at most one point of the set. In other words, no line spanned by the points of the set is vertical.

Unless otherwise stated, all sets we consider in this paper (even when considering the union of two sets) are assumed to be finite, non-vertical and in general position.

Definition 2.2

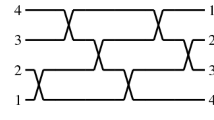
(Cups and Caps) Let $m \ge 3$ be a natural number. We say that the points $(x_1,y_1),(x_2,y_2),\dots ,(x_m,y_m)$ form an m-cup (Fig. 1) if they satisfy the following properties:

• 1. $x_1< x_2< \dots < x_m$;

• 2. $\frac{y_2-y_1}{x_2-x_1}< \frac{y_3-y_2}{x_3-x_2}< \dots < \frac{y_m-y_{m-1}}{x_m-x_{m-1}}$.

In a similar way, they form an m-cap (Fig. 1) if we have

• 1. $x_1< x_2< \dots < x_m$;

• 2. $\frac{y_2-y_1}{x_2-x_1}> \frac{y_3-y_2}{x_3-x_2}> \dots > \frac{y_m-y_{m-1}}{x_m-x_{m-1}}$.

Fig. 1

A 5-cup and a 5-cap

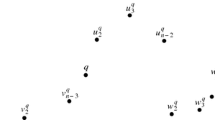
The following definition introduces a partitioning of any point set in the plane with some nice applications (Lemma 2.5). For any point p, let $(p_x,p_y)$ denote its coordinates.

Definition 2.3

(Upper and Lower subsets) Consider the point set S in the plane. Pick an arbitrary $s=(s_x,s_y) \in S$ and let

$$\begin{aligned} S_s^-=\{s' \in S : s'_x < s_x\}, \quad S_s^+=S{\setminus } (S_s^-\cup \{s\}). \end{aligned}$$

For any $s' \in S{\setminus }\{s\}$, define the angle between s and $s'$, $\angle (s,s')$, in the following way.

• 1. If $s' \in S_s^-$: $\angle (s,s')=\angle (s',s,(s_x,s_y+1))$;

• 2. If $s' \in S_s^+$: $\angle (s,s')=\angle ((s_x,s_y-1),s,s')$.

Let $\angle (s,p_s)=\min \{\angle (s,s'): s' \in S{\setminus }\{s\}\}$. Note that since S is in general position, $p_s$ is the unique point of $S{\setminus }\{s\}$ with that property. Now if $p_s \in S_s^+$, then we call s an upper point for S; otherwise we call it a lower point. See Fig. 2. We denote the upper and lower subsets of S by $U_S$ and $L_S$, which consist of the upper and lower points of S, respectively.

Fig. 2

Upper and lower points

Lemma 2.4

For any point set S, $\{U_S,L_S\}$ gives a nontrivial partition of S.

Proof

According to Definition 2.3, it is easy to see that $S=U_S \cup L_S$ and $U_S\cap L_S=\emptyset$. So we know that at least one of $U_S$ and $L_S$ is nonempty. Without loss of generality, suppose there exists an $s \in U_S$. Consider the point $p_s \in S{\setminus }\{s\}$ forming the minimum angle with s. It is easy to check that $p_s \in L_S$, since otherwise we get $\angle (s,p_{p_s}) < \angle (s,p_s)$, which is in contradiction with the choice of $p_s$. Therefore, we also have $L_S\ne \emptyset$. $\square$

Lemma 2.5

Consider the disjoint point sets B, S and let $m,l \ge 3$ be natural numbers. The following statements hold.

• 1. Any l-cap in $B\cup S$ with the rightmost point in $U_S$ and the second rightmost point in S can be extended to an $(l+1)$-cap, by adding an appropriate point of $L_S$ to its right.

• 2. Any m-cup in $B\cup S$ with the leftmost point in $L_S$ and the second leftmost point in S can be extended to an $(m+1)$-cup, by adding an appropriate point of $U_S$ to its left.

Fig. 3

Extension of l-cap $v_1v_2\dots v_l$ by $p_{v_l}$

Proof

We give the sketch of the proof for the first statement; the second one can be proved in a similar way. Denote the l-cap by $v_1v_2\dots v_l$, where $v_{l-1} \in S$ and $v_l \in U_S$. As described in Definition 2.3, consider the point $p_{v_l} \in S{\setminus }\{v_l\}$ forming the minimum angle with $v_l$. By the proof of Lemma 2.4, we have $p_{v_l} \in L_S$. All the points of S lying to the left of $v_l$ are below the line $v_lp_{v_l}$; in particular $v_{l-1}$ is below $v_lp_{v_l}$. See Fig. 3. So we get that $v_1v_2\dots v_{l-1}v_lp_{v_l}$ forms an $(l+1)$-cap. $\square$

Now we state the first upper bound which was obtained by Erdős and Szekeres [3]. First note that in the definition of the function ES(n) given in Theorem 1.1, we can simply assume that the set is non-vertical, since by applying an appropriate rotation, one can make the set non-vertical, by also preserving the convex subsets.

Definition 2.6

((m, l)-Free set) For the natural numbers $m,l \ge 3$, we call a set (m, l)-free if it contains no m-cup and no l-cap.

For the following theorem, we give a modification of the original proof, by using the upper and lower subsets.

Theorem 2.7

(Erdős and Szekeres [3]) Consider the natural numbers m, l and let f(m, l) denote the maximum natural number such that there exists an (m, l)-free set of f(m, l) points in the plane. Then we have $f(m,l)={m+l-4 \atopwithdelims ()l-2}$.

Proof

We only prove $f(m,l) \le {m+l-4 \atopwithdelims ()l-2}$, since this is the part that we need for the rest of the paper. For this, it is enough to prove

$$\begin{aligned} f(m+1,l+1) \le f(m+1,l)+f(m,l+1), \end{aligned}$$

since if it holds for all m, l, one can apply induction to deduce $f(m,l) \le {m+l-4 \atopwithdelims ()l-2}$.

To prove this, we consider a set S with more than $f(m+1,l)+f(m,l+1)$ points in the plane and prove that S must contain either an $(m+1)$-cup or an $(l+1)$-cap. Let $U_S, L_S$ be the associated upper and lower subsets of S, respectively. By Lemma 2.4, we have

$$\begin{aligned} |S|=|U_S|+|L_S| > f(m+1,l)+f(m,l+1), \end{aligned}$$

so we either have $|U_S| > f(m+1,l)$ or $|L_S| > f(m,l+1)$. Without loss of generality, assume that $|U_S| > f(m+1,l)$. By the definition, $U_S$ contains either an $(m+1)$-cup or an l-cap. In the former case, we are done. In the latter one, by Lemma 2.5, we obtain an $(l+1)$-cap in S. So we are done in both cases and the theorem is proved. $\square$

Corollary 2.8

We have ES$(n) \le {2n-4 \atopwithdelims ()n-2}+1$.

Proof

Since n-cups and n-caps are convex n-gons, we have ES$(n) \le f(n,n)+1$. So the result is deduced by Theorem 2.7. $\square$

Now we give a short motivation for the rest of the paper. Consider the point set S with $s \in S$ satisfying the following properties:

• 1. s is the right endpoint of an $(n-2)$-cup in S;

• 2. s is the left endpoint of an $(n-2)$-cap in S;

• 3. s is the left endpoint of an $(n-1)$-cup in S;

• 4. The right endpoint of the $(n-1)$-cup does not coincide with the second point, from the left, of the $(n-2)$-cap.

Then it can be proven that S contains a convex n-gon or an $(n-1)$-cap.

So a set that contains no convex n-gon and no $(n-1)$-cap does not contain any point with all the above 4 properties. Using this fact, for $(n,n-1)$-free sets that contain no convex n-gon, we can improve the upper bound on ES(n) which Corollary 2.8 gives.

As a result, for any given positive integer n, we show the following: Any large enough set of points contains either a convex n-gon, or an $(n-1)$-cap or a point s with the above 4 properties. We construct such a point s inductively for sets of large size. So the cardinality of any $(n,n-1)$-free set that contains no convex n-gon must be small enough that our inductive procedure does not produce such a point s. Therefore, we bound the size of all $(n,n-1)$-free sets that contain no convex n-gon. Next, we combine this bound with a result of Tóth and Valtr [7] to get the improved bound for ES(n).

3 Properties of the Convexification Function

The aim of this section is to obtain an upper bound on the convexification function (Definition 3.2). For this, we first prove some of its most important properties. We start with the definitions of convexifying point and convexification function.

Definition 3.1

((m, l)-Convexifying point) Let $m, l \ge 3$ be natural numbers. Consider a set of points S and a point $s \in S$ which is the leftmost point of an $(l-1)$-cap in S. We call s an (m, l)-convexifying point for S, if for arbitrary $n \ge 4$, the following holds. For any set B with $B \cap S=\emptyset$, if $B \cup S$ contains an $(n-1)$-cup whose left endpoint is s and whose right endpoint is in B, then $B \cup S$ must contain at least one of the followings:

• 1. An m-cup whose two leftmost points belong to S.

• 2. An l-cap whose two rightmost points belong to S.

• 3. A convex n-gon.

Definition 3.2

(Convexification function h(m, l)) For the natural numbers $m,l \ge 3$, define h(m, l) to be the maximum number such that there exists an (m, l)-free set of h(m, l) points in the plane with no (m, l)-convexifying points. The function h(m, l) is called the convexification function.

Lemma 3.3

(Subadditivity) The convexification function is subadditive. In other words, for any natural numbers $m,l \ge 3$, we have

$$\begin{aligned} h(m+1,l+1) \le h(m+1,l)+h(m,l+1). \end{aligned}$$

Proof

Consider the $(m+1,l+1)$-free set S containing more than $h(m+1,l) + h(m,l+1)$ points in the plane. We have to show that S has an $(m+1,l+1)$-convexifying point. Let $U_S, L_S$ be the upper and lower subsets of S, respectively. Since by Lemma 2.4 we have

$$\begin{aligned} |S|=|U_S|+|L_S| > h(m+1,l) + h(m,l+1), \end{aligned}$$

we get either $|U_S| > h(m + 1, l)$ or $|L_S| > h(m, l+ 1)$.

Consider the former case. Note that by Lemma 2.5, $U_S$ is an $(m+1,l)$-free set, since S is $(m+1,l+1)$-free. So $U_S$ has an $(m+1,l)$-convexifying point. Denote this point by s. We show that s is also an $(m+1,l+1)$-convexifying point for S. For this, first note that s is the leftmost point of an $(l-1)$-cap in $U_S$. This cap can be extended to an l-cap in S from right, by Lemma 2.5, so s is the left endpoint of an l-cap in S. Now let $n \ge 4$ be an arbitrary natural number and consider the set B with $B \cap S=\emptyset$, such that $B \cup S$ contains an $(n-1)$-cup whose left endpoint is s and whose right endpoint is in B. Call this $(n-1)$-cup C and construct the set $B'$ as

$$\begin{aligned} B'= (B \cup L_S) \cap C=C {\setminus } U_S. \end{aligned}$$

Clearly, $B' \cap U_S=\emptyset$, and $B' \cup U_S$ contains the $(n-1)$-cup C, whose left endpoint is s and whose right endpoint is in $B'$. So by the Definition 3.1 and $(m+1,l)$-convexifying property of s for $U_S$, $B' \cup U_S$ must contain at least one of the following:

• 1. An $(m+1)$-cup whose two leftmost points belong to $U_S$.

• 2. An l-cap whose two rightmost points belong to $U_S$.

• 3. A convex n-gon.

Since $B' \cup U_S \subset B \cup S$ and $U_S \subset S$, in the cases 1 and 3, we get a desired $(m+1)$-cup and a convex n-gon in $B \cup S$, respectively, which makes s an $(m+1,l+1)$-convexifying point for S. Now consider case 2 and call this l-cap $C'$. Since two rightmost points of $C'$ belong to $U_S$, by Lemma 2.5, $C'$ can be extended to an $(l+1)$-cap by adding an appropriate point of $L_S$ to its right. This way, we get an $(l+1)$-cap in $B \cup S$ whose two rightmost points belong to S, which makes s an $(m+1,l+1)$-convexifying point for S. So s is a convexifying point for S in all of these three cases and we are done. The proof of the second case, where $|L| > h(m, l+ 1)$, is exactly similar to this one. $\square$

Theorem 3.4

For any natural number $m \ge 4$, we have $h(m,4) \le {m-1 \atopwithdelims ()2}+1$.

Proof

The proof consists of two parts. First, we prove that for the (m, 4)-free set S, if it contains an $(m-1)$-cup with a point lying to the right of it, then the second rightmost point of this cup is an (m, 4)-convexifying point of S. Secondly, we prove that if $|S| > {m-1 \atopwithdelims ()2}+1$, then S contains such a cup.

Consider the first part and assume S contains the $(m-1)$-cup $v_1v_2\dots v_{m-1}$, which is ordered in increasing order of x-coordinate, and consider $r \in S$ lying to the right of $v_{m-1}$. Note that r must lie below the line spanned by $v_{m-2}v_{m-1}$, otherwise we get an m-cup which is in contradiction with the (m, 4)-free property of S. We show that $v_{m-2}$ is an (m, 4)-convexifying point for S. For this, note that $v_{m-2}v_{m-1}r$ is a 3-cap, so $v_{m-2}$ is the leftmost point of a 3-cap in S. Now take an arbitrary natural number $n \ge 4$ and consider the set B with $B \cap S=\emptyset$, such that $B \cup S$ contains the $(n-1)$-cup $v_{m-2}u_2u_3\dots u_{n-1}$, again ordered in increasing order of x-coordinate, where $u_{n-1} \in B$. So in particular $v_{m-1} \ne u_{n-1}$. We split the rest of the proof into the following cases:

• Case a: $u_{n-1}$ is to the left of $v_{m-1}$ and above the line $v_{m-2}v_{m-1}$: (Note that in this case we have $v_{m-1} \notin \{u_2,u_3,\dots ,u_{n-2}\}$.)

  • Subcase a1: $u_{n-2}$ is above the line $v_{m-3}v_{m-2}$:

    $v_1v_2\dots v_{m-2}u_{n-2}u_{n-1}$ forms an m-cup with two leftmost points in S. This holds since both $v_{m-3}v_{m-2}u_{n-2}$ and $v_{m-2}u_{n-2}u_{n-1}$ form 3-cups.

  • Subcase a2: $u_{n-2}$ is below the line $v_{m-3}v_{m-2}$ and $v_{m-1}$ is above the line $u_{n-3}u_{n-2}$:

    $v_{m-2}u_2u_3\dots u_{n-2}v_{m-1}u_{n-1}$ forms a convex n-gon. This holds since $v_{m-2}u_2u_3\dots u_{n-1}$ forms a convex $(n-1)$-gon and $v_{m-1}$ is to the right of $u_{n-1}$, lies below $v_{m-2}u_{n-1}$ and above $u_{n-3}u_{n-2}$.

  • Subcase a3: $u_{n-2}$ is below the line $v_{m-3}v_{m-2}$ and $v_{m-1}$ is below the line $u_{n-3}u_{n-2}$:

    $u_{n-3}u_{n-2}v_{m-1}r$ forms a 4-cap with two rightmost points in S. This holds since $u_{n-2}$ is below $v_{m-3}v_{m-2}$, so because it is between $v_{m-2}$ and $v_{m-1}$, it is also below $v_{m-2}v_{m-1}$. On the other hand, r is also below $v_{m-2}v_{m-1}$, by the assumption. So $u_{n-2}v_{m-1}r$ forms a 3-cap. $u_{n-3}u_{n-2}v_{m-1}$ also forms a 3-cap, as well.

• Case b: $u_{n-1}$ is to the left of $v_{m-1}$ and below the line $v_{m-2}v_{m-1}$:

  • Subcase b1: $v_{m-1}$ is above the line $u_{n-2}u_{n-1}$:

    $v_{m-2}u_2u_3\dots u_{n-1}v_{m-1}$ forms an n-cup, and as a result, a convex n-gon.

  • Subcase b2: $v_{m-1}$ is below the line $u_{n-2}u_{n-1}$:

    $u_{n-2}u_{n-1}v_{m-1}r$ forms a 4-cap with two rightmost points in S. This holds since both $u_{n-1}$ and r are below $v_{m-2}v_{m-1}$, $u_{n-1}v_{m-1}r$ forms a 3-cap. $u_{n-2}u_{n-1}v_{m-1}$ also forms a 3-cap.

• Case c: $u_{n-1}$ is to the right of $v_{m-1}$ and above the line $v_{m-2}v_{m-1}$:

  $v_1v_2\dots v_{m-2}v_{m-1}u_{n-1}$ forms an m-cup with two leftmost points in S.

• Case d: $u_{n-1}$ is to the right of $v_{m-1}$ and below the line $v_{m-2}v_{m-1}$:

  $v_{m-2}u_2u_3\dots u_{n-1}v_{m-1}$ forms a convex n-gon. This holds by following the same reasoning as subcase a2. Just note that $u_{n-1}$ is below the line $v_{m-2}v_{m-1}$. Also, all the points $u_2,u_3,\dots ,u_{n-2}$ are below the line $v_{m-2}u_{n-1}$, so we have $v_{m-1} \notin \{u_2,u_3,\dots ,u_{n-2}\}$.

So, according to Definition 3.1, $v_{m-2}$ is an (m, 4)-convexifying point for S (Figs. 4, 5, 6).

Fig. 4

Case a in Theorem 3.4

Fig. 5

Case b in Theorem 3.4

Fig. 6

Cases c, d in Theorem 3.4

Now we prove the second part. Suppose S is an (m, 4)-free set with more than ${m-1 \atopwithdelims ()2}+1$ points in the plane. Let r be the point of S with the largest x-coordinate. Consider the set $S{\setminus }\{r\}$. We have

$$\begin{aligned} |S{\setminus }\{r\}| > \Big (\begin{array}{c}{m-1} \\ {2}\end{array}\Big )=f(m-1,4), \end{aligned}$$

so by Theorem 2.7, $S{\setminus }\{r\}$ must contain either an $(m-1)$-cup or a 4-cap. The latter cannot happen since S is (m, 4)-free, so $S{\setminus }\{r\}$ contains an $(m-1)$-cup. By the choice of r, it must lie to the right of the rightmost point of this cup, so we are done. This completes the proof of the theorem. $\square$

The following theorem gives an upper bound for h(4, l).

Theorem 3.5

For any natural number $l \ge 4$, we have $h(4,l) \le {l-1 \atopwithdelims ()2}+1$.

Proof

We split the proof into two parts as in the proof of Theorem 3.4. First we prove that for the (4, l)-free set S, if it contains an $(l-1)$-cap with a point lying to the left of it, then the leftmost point of this cap is an (4, l)-convexifying point of S. Secondly, we prove that if $|S| > {l-1 \atopwithdelims ()2}+1$, then S contains such a cap.

We proceed with the first part. First note that we cannot deduce this part from Theorem 3.4 by symmetry, since in both of them, we are dealing with $(n-1)$-cups. Assume S contains the $(l-1)$-cap $v_1v_2\dots v_{l-1}$, which is ordered in increasing order of x-coordinate, and consider $r \in S$ lying to the left of $v_1$. Note that r must lie above the line spanned by $v_1v_2$, otherwise we get an l-cap which is in contradiction with the (4, l)-free property of S. We show that $v_1$ is an (4, l)-convexifying point for S. Evidently, $v_1$ is the left endpoint of an $(l-1)$-cap in S. Now take an arbitrary natural number $n \ge 4$ and consider the set B with $B \cap S=\emptyset$, such that $B \cup S$ contains the $(n-1)$-cup $v_1u_2u_3\dots u_{n-1}$, again ordered in increasing order of x-coordinate, where $u_{n-1} \in B$. Note that if there exists $2\le i \le n-3$ such that $u_i \in S$, then $v_1u_iu_{n-2}u_{n-1}$ forms a 4-cup with the two leftmost points belonging to S, which means $v_1$ is an (4, l)-convexifying point for S. On the other hand, if we have $u_{n-2}=v_2$, then $rv_1v_2u_{n-1}$ forms a 4-cup with the required property.

So we can assume that $u_i \in B$ for all $i=2,\dots ,n-3$, and $u_{n-2} \ne v_2$. Now we split the rest of the proof into the following cases:

• Case a: $u_{n-1}$ is to the left of $v_2$ and above the line $v_1v_2$:

  • Subcase a1: $u_{n-2}$ is above the line $v_1v_2$:

    $rv_1u_{n-2}u_{n-1}$ forms a 4-cup with two leftmost points in S. This holds since both of $r, u_{n-2}$ lie above $v_1v_2$, so $rv_1u_{n-2}$ forms a 3-cup. $v_1u_{n-2}u_{n-1}$ also forms a 3-cup, by the assumption.

  • Subcase a2: $u_{n-2}$ is below the line $v_1v_2$ and $v_2$ is above the line $u_{n-3}u_{n-2}$:

    $v_1u_2u_3\dots u_{n-2} v_2u_{n-1}$ forms a convex n-gon. This holds since $v_1u_2u_3\dots u_{n-1}$ forms a convex $(n-1)$-gon, and $v_2$ is below both of $v_1u_{n-1}$ and $u_{n-2}u_{n-1}$, and above $u_{n-3}u_{n-2}$.

  • Subcase a3: $u_{n-2}$ is below the line $v_1v_2$ and $v_2$ is below the line $u_{n-3}u_{n-2}$:

    $u_{n-3}u_{n-2}v_2v_3\dots v_{l-1}$ forms an l-cap with two rightmost points in S. First note that $u_{n-2} \notin \{v_3,\dots ,v_{l-1}\}$, since $x_{u_{n-2}}< x_{u_{n-1}}< x_{v_2} < x_{v_i}$, for all $i\ge 3$. It is enough to show that $u_{n-3}u_{n-2}v_2$ and $u_{n-2}v_2v_3$ form 3-caps. The first one is a 3-cap, since $v_2$ is below $u_{n-3}u_{n-2}$. For the second one, since both of $u_{n-2}$ and $v_3$ are below $v_1v_2$, we get a 3-cap, too.

• Case b: $u_{n-1}$ is to the left of $v_2$ and below the line $v_1v_2$:

  • Subcase b1: $v_2$ is above the line $u_{n-2}u_{n-1}$:

    $v_1u_2u_3\dots u_{n-1}v_2$ forms an n-cup, and as a result, a convex n-gon.

  • Subcase b2: $v_2$ is below the line $u_{n-2}u_{n-1}$:

    $u_{n-2}u_{n-1}v_2v_3\dots v_{l-1}$ forms an l-cap with two rightmost points in S. First note that with a similar reasoning as Subcase a3, we have $u_{n-2} \notin \{v_3,\dots ,v_{l-1}\}$. So it is enough to show that $u_{n-2}u_{n-1}v_2$ and $u_{n-1}v_2v_3$ form 3-caps. The first one is a 3-cap since $v_2$ is below $u_{n-2}u_{n-1}$. For the second one, since $u_{n-1}$ and $v_3$ are both below $v_1v_2$, $u_{n-1}v_2v_3$ must form a 3-cap.

• Case c: $u_{n-1}$ is to the right of $v_2$ and above the line $v_1v_2$:

  $rv_1v_2u_{n-1}$ forms a 4-cup with two leftmost points in S. This holds because $rv_1v_2$ forms a 3-cup, since r is above $v_1v_2$. $u_{n-1}$ is above $v_1v_2$, so $v_1v_2u_{n-1}$ also forms a 3-cup.

• Case d: $u_{n-1}$ is to the right of $v_2$ and below the line $v_1v_2$:

  $v_1u_2u_3\dots u_{n-1}v_2$ forms a convex n-gon. This holds since $v_2$ is to the right of $v_1$, to the left of $u_{n-1}$ and above $v_1u_{n-1}$.

So, according to Definition 3.1, $v_1$ is an (4, l)-convexifying point for S.

The second part can be proved in the same way as the second part in Theorem 3.4, either by following that proof or using that result with symmetry in order to replace cups with caps. $\square$

Fig. 7

Case a in Theorem 3.5

Fig. 8

Case b in Theorem 3.5

Fig. 9

Cases c, d in Theorem 3.5

Now we combine Theorems 3.4, 3.5 with Lemma 3.3 in order to get the following bound on the convexification function h(m, l) (Figs. 7, 8, 9).

Theorem 3.6

For any natural numbers $m,l \ge 4$, we have

$$\begin{aligned} h(m,l) \le \Big (\begin{array}{c}{m+l-4} \\ {l-2}\end{array}\Big )-\Big (\begin{array}{c}{m+l-6} \\ {l-3}\end{array}\Big ). \end{aligned}$$

Proof

First define the function g(m, l) as

$$\begin{aligned} g(m,l)= \Big (\begin{array}{c}{m+l-4} \\ {l-2}\end{array}\Big )-\Big (\begin{array}{c}{m+l-6} \\ {l-3}\end{array}\Big ). \end{aligned}$$

So we need to show that $h(m,l) \le g(m,l)$, for all $m,l\ge 4$. We apply double induction on m and l. For the induction basis, suppose $m=4$. Then according to Theorem 3.5 we have

$$\begin{aligned} h(4,l) \le \Big (\begin{array}{c}{l-1} \\ {2}\end{array}\Big )+1=\Big (\begin{array}{c}{l} \\ {2}\end{array}\Big )-\Big (\begin{array}{c}{l-2} \\ {1}\end{array}\Big )=g(4,l). \end{aligned}$$

Similarly, the other induction basis $l=4$ can be proved by using Theorem 3.4. Now suppose the inequality holds for $(m+1,l)$ and $(m,l+1)$, we prove it for $(m+1,l+1)$. Note that based on the identity

$$\begin{aligned} \Big (\begin{array}{c}{s} \\ {t}\end{array}\Big )=\Big (\begin{array}{c}{s-1} \\ {t}\end{array}\Big )+\Big (\begin{array}{c}{s-1} \\ {t-1}\end{array}\Big ), \end{aligned}$$

we can get that

$$\begin{aligned} g(m+1,l+1)=g(m+1,l)+g(m,l+1). \end{aligned}$$

By Lemma 3.3 we have

$$\begin{aligned} h(m+1,l+1)\le & {} h(m+1,l)+h(m,l+1) \le g(m+1,l)+g(m,l+1)\\= & {} g(m+1,l+1), \end{aligned}$$

where the last inequality holds according to the induction hypothesis. This completes the proof. $\square$

4 Back to the Main Problem

In this section, we prove the main result of this paper, Theorem 1.1. We start with the following lemma which we need for Theorem 4.2.

Lemma 4.1

[3] If a point is the rightmost point of a cup (cap) and also the leftmost point of a cap (cup), then the cup or the cap can be extended to a larger cup or cap, respectively.

Proof

Denote the cup by $v_1v_2\dots v_m$ and the cap by $v_mu_2\dots u_l$. We split the rest of the proof into the following two cases. See Fig. 10.

• Case a: $u_2$ lies above the line spanned by $v_{m-1}v_m$: $v_1v_2\dots v_mu_2$ forms an $(m+1)$-cup.

• Case b: $u_2$ lies below the line spanned by $v_{m-1}v_m$: $v_{m-1}v_mu_2\dots u_l$ forms an $(l+1)$-cap. $\square$

Fig. 10

Case by case analysis in Lemma 4.1

Theorem 4.2

Let $n \ge 6$ be a natural number and consider the set S of $f(n-1,n-1)+g(n,n-2)+1$ points in the plane, where the function g is defined in Theorem 3.6. Then S contains an $(n-1)$-cap or a convex n-gon.

Proof

Consider the partition of S into the upper and lower subsets $U_S,L_S$ as in Definition 2.3. If $|L_S| > f(n-1,n-1)$, then it either contains an $(n-1)$-cup or an $(n-1)$-cap. In the former case, we get an n-cup by Lemma 2.5, and in the latter case, we are immediately done. So we can assume that $|L_S| \le f(n-1,n-1)$. On the other hand, we can assume that $U_S$ is $(n,n-2)$-free, since otherwise we are immediately done or again by Lemma 2.5. We have

$$\begin{aligned} |U_S|=|S|-|L_S|=g(n,n-2)+(f(n-1,n-1)+1-|L_S|), \end{aligned}$$

where the last term is positive. So by applying Theorem 3.6 iteratively, we get $f(n-1,n-1)+1-|L_S|$ $(n,n-2)$-convexifying points for $U_S$. Denote the set of these convexifying points by G. Consider the set $G \cup L_S$. We have

$$\begin{aligned} |G \cup L_S|=f(n-1,n-1)+1, \end{aligned}$$

so it must contain either an $(n-1)$-cup or an $(n-1)$-cap. In the latter case, we are done. In the former case, denote this $(n-1)$-cup by $v_1v_2\dots v_{n-1}$. If $v_1 \in L_S$, by the Lemma 2.5 we get an n-cup in S, which means we are done. On the other hand, every point of G is the leftmost point of an $(n-3)$-cap in $U_S$, which by Lemma 2.5, can be extended to an $(n-2)$-cap in S by adding a point to the right of it. So if $v_{n-1} \in G$, then by Lemma 4.1, we either get an n-cup or an $(n-1)$-cap, which finishes the proof.

So we can assume that $v_1 \in G$ and $v_{n-1} \in L_S$. Now by Definition 3.1, we conclude that S contains at least one of the followings:

• 1. An n-cup;

• 2. An $(n-2)$-cap whose two rightmost points belong to $U_S$;

• 3. A convex n-gon.

In the cases 1, 3, we are done. In case 2, according to Lemma 2.5, we get an $(n-1)$-cap, so we are also done in this case. This completes the proof of the theorem. $\square$

The proof of the following theorem is completely based on and similar to the proof of Theorem 5 in [8].

Theorem 4.3

[7, 8] Define p(n) to be the minimum natural number such that every set with at least p(n) points in the plane contains either an $(n-1)$-cap or a convex n-gon. Then we have

$$\begin{aligned} \mathrm{ES}(n) \le p(n)+1. \end{aligned}$$

Proof

Let S be a set of $p(n)+1$ points in the plane. We have to show that S contains n points in convex position. Let s be a vertex of the convex hull of S, $\mathrm {conv}(S)$, and take the point $s'$ outside $\mathrm {conv}(S)$ such that none of the lines spanned by the points of $S{\setminus } \{s\}$ intersects the segment $ss'$. Also, take a line l through $s'$ which does not intersect $\mathrm {conv}(S)$.

Now consider the projective transformation taking the line l to the line at infinity and also mapping the segment $ss'$ to the vertical half-line emanating downwards from T(s). Since the line l avoided $\mathrm {conv}(S)$, T does not change convexity on the points of S, i.e. $P \subset S$ is in convex position if and only if $T(P) \subset T(S)$ is in convex position.

One can see that none of the lines spanned by the points of $T(S) {\setminus } \{T(s)\}$ intersects the vertical half-line emanating downwards from T(s). Furthermore, $T(S) {\setminus } \{T(s)\}$ is a non-vertical set. So for any natural number l, any l-cap in $T(S) {\setminus } \{T(s)\}$ can be extended to a convex $(l+1)$-gon by adding the point T(s). Therefore, because $|S|=p(n)+1$, we have $|T(S) {\setminus } \{T(s)\}|=p(n)$, and by the definition of the function p(n), we get that $T(S) {\setminus } \{T(s)\}$ must contain either an $(n-1)$-cap or a convex n-gon. Based on what was stated before, T(S) contains a convex n-gon, and as a result, S contains a convex n-gon, as well. This completes the proof.$\square$

Finally, we prove Theorem 1.1, and use it to obtain the asymptotic upper bound (2’).

Proof of Theorem 1.1

Recall the function p(n) from Theorem 4.3. By Theorem 4.2 we get

$$\begin{aligned} p(n)\le & {} f(n-1,n-1)+g(n,n-2)+1\\= & {} \Big (\begin{array}{c}{2n-6} \\ {n-3}\end{array}\Big )+\Big (\begin{array}{c}{2n-6} \\ {n-2}\end{array}\Big )-\Big (\begin{array}{c}{2n-8} \\ {n-3}\end{array}\Big )+1 \\= & {} \Big (\begin{array}{c}{2n-5} \\ {n-2}\end{array}\Big )-\Big (\begin{array}{c}{2n-8} \\ {n-3}\end{array}\Big )+1. \end{aligned}$$

Combining the above with

$$\begin{aligned} \mathrm{ES}(n) \le p(n)+1 \end{aligned}$$

from Theorem 4.3, we get the desired bound. $\square$

Corollary 4.4

We have

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty } \frac{\mathrm{ES}(n)}{{2n-5 \atopwithdelims ()n-2}} \le \frac{7}{8}. \end{aligned}$$

Proof

By Theorem 1.1, it is enough to show that

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty } \frac{{2n-5 \atopwithdelims ()n-2}-{2n-8 \atopwithdelims ()n-3}+2}{{2n-5 \atopwithdelims ()n-2}}=\frac{7}{8}. \end{aligned}$$

But we have

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty } \frac{{2n-5 \atopwithdelims ()n-2}-{2n-8 \atopwithdelims ()n-3}+2}{{2n-5 \atopwithdelims ()n-2}}= & {} 1+\limsup \limits _{n\rightarrow \infty } \frac{-{2n-8 \atopwithdelims ()n-3}}{{2n-5 \atopwithdelims ()n-2}}=1-\liminf \limits _{n\rightarrow \infty } \frac{{2n-8 \atopwithdelims ()n-3}}{{2n-5 \atopwithdelims ()n-2}}\\ {}= & {} 1-\frac{1}{8}=\frac{7}{8}. \end{aligned}$$

$\square$