Shortest Paths in the Plane with Obstacle Violations

Abstract

We study the problem of finding shortest paths in the plane among h convex obstacles, where the path is allowed to pass through (violate) up to k obstacles, for $k \le h$. Equivalently, the problem is to find shortest paths that become obstacle-free if k obstacles are removed from the input. Given a fixed source point s, we show how to construct a map, called a shortest k-path map, so that all destinations in the same region of the map have the same combinatorial shortest path passing through at most k obstacles. We prove a tight bound of $\varTheta (kn)$ on the size of this map, and show that it can be computed in $O(k^2n \log n)$ time, where n is the total number of obstacle vertices.

1 Introduction

Given a set of polygonal obstacles in the plane and an integer parameter k, which k obstacles should we remove to obtain the shortest obstacle-free path between two points s and t? Equivalently, what is the shortest path that is allowed to violate (pass through) up to k obstacles? We call a path violating at most k obstacles a k-path, generalizing a traditional obstacle-free path, which is a 0-path. More precisely, we assume a polygonal environment P containing h disjoint convex obstacles in the plane, with a total of n vertices, all lying inside a rectangle R (the outer boundary). The complement of the obstacles within R is called free space. Given a fixed source point s in free space, we want to compute shortest k-paths, for $k \le h$, to all other points of free space. The description of these shortest paths can be compactly encoded as a finite partition of the plane, called the shortestk-path map. We use the notation $\pi _k (t)$ to denote the shortest k-path from s to t, with the fixed source s being implicit, and denote the length of this path by $d_k (t)$.

In this paper, we investigate structural and computational aspects of shortest k-paths. The problem differs from the 0-path problem in nontrivial ways even in the plane. In particular, two shortest 0-paths originating at a common source cannot intersect, by the triangle inequality, and this non-crossing property of 0-paths is an essential ingredient for computing them in optimal time [19]. In contrast, two shortest k-paths can cross each other, for any $k > 0$. The geometric k-path problem is interesting both theoretically, as part of the broad category of optimization with violations [8, 25] or network augmentation problems [3, 13], and practically, for applications such as robot motion planning, where it may be beneficial to modify a robot’s environment to shorten frequently used paths. (The geometric k-path problem can be seen as a more complex form of network augmentation, since removal of a single obstacle can create many additional “edges” in the path space.) Besides robot motion planning, the problem can also model situations in which the obstacles are “avoidable” at additional cost, for instance by paying a bridge or tunnel toll in a road network.

Our approach to solving the k-path problem is to compute a shortestk-path map${ SPM}_{k}$, which is a partition of the plane into equivalence classes of cells (regions), where all destination points inside a cell have the same combinatorial structure of shortest k-paths to s. Once the map is known, the shortest k-path to any destination can be computed by performing a point location query on the map [10, 22].

1.1 Our Results

We show that ${ SPM}_{k}$ has O(kn) regions and O(kn) edges and that this bound is tight (Sect. 3). We present an $O(k^2 n \log n)$ time and $O(kn \log n)$ space algorithm for computing ${ SPM}_{k}$ (Sect. 4) using the continuous Dijkstra framework, which constructs each ${ SPM}_{j}$ for $0 \le j \le k$ sequentially. The running time of the algorithm is optimal for $k = O(1)$.

1.2 Related Work

The problem of computing shortest paths in the presence of obstacles has a long history in computational geometry, dating back to the 1970s. The case of polygonal obstacles in the plane, in particular, has been a subject of intense research [4, 5, 14, 21, 26, 27, 29, 30, 32], culminating in an optimal $O(n \log n)$ time algorithm using the continuous Dijkstra framework [19]. Many other variations of the problem, including shortest paths inside a simple polygon [15, 18, 23], among weighted regions [28], and among curved obstacles [9, 20], have also been studied. The general flavor of our problem is related to geometric optimization where a small number of constraints can be violated. This line of work has been pursued in [8, 16, 25, 31], in the context of low-dimensional linear programming, separability with outliers, and geometric optimization. Our problem can also be viewed as a form of network augmentation, where the goal is to add edges to the network to improve connectivity, diameter, or spanning ratio, etc. [1, 3, 7, 13].

The prior work most closely related to our problem is a recent result by Maheshwari et al. [24], which presents an $O(n^3)$ time algorithm for computing the 1-violation path inside a simple polygon: that is, a shortest path inside a simple n-gon where at most one edge of the path lies outside the polygon. Our paper deals with a different notion of path violation: we compute a k-violation path, for any value of k, in a polygonal domain with n vertices and h convex holes, where the violation count is the number of holes intersected by the path.

Our problem is also related to the minimum constraint removal problem [6, 11], where given a set of possibly overlapping obstacles in the plane, one would like to compute the minimum number of obstacles that can be removed to create a path in free space from s to t. This problem is known to be intractable even when obstacles are very simple shapes such as rectangles. Note that an important difference from our problem is that we assume the obstacles to be disjoint, so the existence of a free space s–t path is trivial.

The more general version of our problem, in which each obstacle can be removed by paying a fixed cost, was recently studied by Agarwal et al. [2]. Given a cost budget C, the goal now is to remove a set of obstacles with total cost at most C such that the free space admits the shortest possible s–t path. Interestingly, the problem becomes NP-hard even when the obstacles are vertical line segments. The paper [2] also gives polynomial time approximation schemes for this problem.

2 Properties of k-paths

Given a point p in free space, a shortest k-path$\pi _k(p)$ connects s to p, crosses the interiors of at most k obstacles, and has minimum length among all such paths. On occasion, we also need to reason about paths crossing exactlyk obstacles, and we refer to such a path as an $(=k)$-path. We begin with the easy observation that the problem can be solved in polynomial (quadratic) time, using a Dijkstra-like search on a “visibility graph.”

Theorem 1

Given a polygonal domainPwithhconvex obstacles andnvertices, a source pointsand a destinationt, we can compute a shortestk-path fromstotin worst-case time$O((kn + h^2) \log n + kh^2)$.

Proof

By the triangle inequality, each edge of the shortest path $\pi _k(t)$ is either an edge of an obstacle polygon or is a tangent between two obstacles, where we include tangents from s and t. (Each pair of convex obstacles has four tangents.) Let $V_1$ be the set of obstacle vertices (including s and t) and $E_1$ the set of all polygon edges and the tangents. Each edge of $E_1$ is assigned a weight equal to its Euclidean length, and has a label equal to the number of obstacles it crosses. We can compute the set $E_1$, along with the labels, in time $O(n + h^2 \log n)$ [30]. We now construct a graph $G=(V, E)$, with O(kn) vertices and $O(n+ kh^2)$ edges, as follows. For every $v \in V_1$, we create $k+1$ copies $v_0, v_1, \dots , v_k$, corresponding to the number of obstacles crossed on the path to v. For every edge $(u, v) \in E_1$ that passes through $j \le k$ obstacles, we add the edges $(u_0, v_j), (u_1, v_{j+1}), \dots ,(u_{k-j}, v_k)$. We create two new vertices s and t and connect them to their respective copies in G. That is, s connects to $s_0, s_1, \dots , s_k$ and t connects to $t_0, t_1, \dots , t_k$ with zero weight and zero crossing edges. The shortest path from s to t in this graph is the shortest k-path, and the claimed bound follows. $\square$

The visibility graph-based approach is inherently quadratic in the worst case, because the number of obstacles can be $h = \varOmega (n)$. It also is limited to computing the shortest k-path to only one point (or a fixed set of points) at a time, although it can be extended to support queries in $O(h(k + \log n))$ time apiece after quadratic preprocessing.

The main result of our paper is an algorithm to compute shortest k-paths from s to all points of free space in subquadratic time $O(k^2 n \log n )$. We do this by computing a shortestk-path map of free space; we also prove a tight bound of $\varTheta (kn)$ on the combinatorial complexity of ${ SPM}_{k}$. Note that the length of a shortest k-path to a point is unique, although some points (along bisectors forming the boundaries of regions in the shortest path map) can be reached by multiple shortest k-paths. For simplicity, however, we assume that the obstacles are in general position, so that the shortest k-path to each obstacle vertex is unique. (Otherwise, if a vertex is reached from s by multiple shortest k-paths, we pick one of them arbitrarily.)

We begin by highlighting a conceptual difficulty with shortest k-paths. The shortest paths to two different destinations can cross each other, which poses an inherent difficulty for the continuous Dijkstra framework of geometric shortest paths [19], since that method depends on the fact that two Euclidean shortest paths from a common source cannot intersect.

Lemma 1

There exist obstacle configurations such that for two destinations$t_1, t_2$in free space, the shortestk-paths$\pi _k (t_1)$and$\pi _k (t_2)$cross each other, for$k > 0$.

Proof

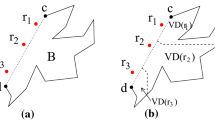
The construction, shown in Fig. 1, has two identical obstacle bundles A and B placed parallel to the y-axis. Each bundle contains four vertical strips with perforations (single-point openings that split the original strip into disjoint sub-strips). The horizontal spacing between the strips in a bundle is infinitesimal, but for clarity the strips are shown separated in the figure. The points s and t both lie on the x-axis at distance 1 to the left and right of bundles A and B, respectively. We show that there are two shortest 1-paths from s to t, which cross each other, as shown in the figure. We then conclude that by perturbing t up and down slightly we obtain two destination points $t_1$ and $t_2$ with their shortest 1-paths crossing, as claimed.

Fig. 1

Two intersecting 1-paths

Within each bundle, the openings form an upper and a lower group. In the upper group, strips 2 and 3 have an opening at $y = (1 + \delta /2)$, and strips 1 and 4 have openings at $y=1$. In the lower group, all except strip 3 have an opening at $y = -1$. If the distance between the bundles is D, then a shortest 0-path has length $2\sqrt{2} + D + 2\delta$, and a shortest 2-path has length $2\sqrt{2} + D$. A path with exactly one crossing in an upper group has length at least $2\sqrt{2} + D + 3\delta /2$, and a shortest path with one crossing in a lower group has length $2\sqrt{2} + \sqrt{D^2 + 4} + \delta \,<\, 2\sqrt{2} + D + 2/D + \delta$. By choosing $D = 10$, say, and $\delta = 4/D$, we can force a shortest 1-path to go through exactly one group of each type. This gives two intersecting shortest k-paths, $\pi _1(t)$ and $\pi '_1(t)$. Now, let $t_1$ (resp. $t_2$) be a destination point obtained by shifting t vertically up (resp. vertically down) infinitesimally. Then it is easy to see that the shortest 1-paths $\pi _1 (t_1)$ and $\pi _1 (t_2)$ cross each other. $\square$

Fortunately, as we show in this section, shortest k-paths can always be decomposed into appropriate non-crossing subpaths to which the continuous Dijkstra method can be applied, working on multiple copies of free space connected using the metaphor of a k-level garage. Toward that goal, we establish a series of lemmas.

Lemma 2

A shortest path with exactly k crossings can be decomposed into a shortest path with exactly $(k-1)$ crossings, a straight line segment inside an obstacle, and a shortest path with zero crossings.

Proof

Let $\pi = (v_1, v_2, \dots , v_m)$ be an $(=k)$-path from $v_1$ to $v_m$. Going backward from $v_m$ along $\pi$, let $v_i$ be the first vertex such that the segment $\overline{v_{i-1}v_i}$ intersects one or more obstacles. Let H be the obstacle that is closest to $v_i$ along the segment $\overline{v_{i-1}v_i}$. By the convexity of H, the segment $\overline{v_{i-1}v_i}$ intersects H at two points, which we call p and q, and the segment $\overline{pq}$ lies entirely within H. By subpath optimality, the path from $v_1$ to p is a shortest path with exactly $k-1$ crossings; by construction, the segment $\overline{pq}$ lies inside the obstacle; and the subpath from q to $v_m$ crosses no obstacles. $\square$

Observe that for any shortest k-path $\pi$, the subpath between any two consecutive vertices $v_{i-1}$ and $v_i$ of $\pi$ is the straight line segment $\overline{v_{i-1}v_i}$. Since the part of $\pi$ that lies inside an obstacle H must be coincident with one such segment, we have the following.

Corollary 1

In a shortest k -path, the path segments preceding and following any obstacle crossing are collinear with the path segment inside the obstacle.

Lemma 2 allows us to break any $\pi _k(t)$ into a $(k-1)$-path $\pi _{k-1}(p)$, a subpath line segment $\overline{pq}$, and an obstacle-free subpath between q and t. We label the last two subpaths with the number of obstacles crossed by the prefix of the path, and call these labels the prefix counts. In particular, the prefix count for the subpath $\overline{pq}$ is $k-1$, and the prefix count for the subpath from q to t is k. By a recursive application of Lemma 2, we can decompose $\pi _k(t)$ into $2k+1$ disjoint subpaths whose labels are in non-decreasing order.

The key consequence of this decomposition is the following lemma, which says that subpaths with the same prefix count cannot cross. The example in Fig. 1 is consistent with the lemma, because the intersecting edges of the two crossing shortest k-paths have different prefix counts.

Lemma 3

Let $\pi _k(t)$ and $\pi '_k(t')$ be two subpaths whose prefix counts are the same. Then $\pi _k(t)$ and $\pi '_k(t')$ do not cross each other.

Proof

The proof follows from a simple application of the triangle inequality: if two subpaths with the same prefix count intersect, then we can reconnect the prefix of each path to the suffix of the other, and possibly perform a local shortcut, either shortening at least one path or leaving them the same length but without a crossing. Since the intersecting subpaths are either both inside some obstacle or in free space, avoiding the intersection does not increase the number of obstacle crossings for either path. $\square$

The next two lemmas establish properties of shortest k-paths that will be useful later.

Definition 1

A point p is k-visible from the source s if the segment $\overline{sp}$ passes through at most k obstacles. A k-visibility edge is a shortest k-path with exactly one edge.

Lemma 4

Ifpis not$(k-1)$-visible froms, then the path$\pi _k(p)$must be an$(=k)$-path.

Proof

By contradiction. Suppose $\pi _k(p)$ passes through fewer than k obstacles. Since p is not $(k-1)$-visible from s, $\pi _k(p)$ must have at least one bend. The path can then be shortened by going through the obstacle causing this bend, thereby increasing the number of crossings by 1. The resulting path is shorter than $\pi _k(p)$ and has at most k crossings, contradicting the optimality of $\pi _k(p)$. $\square$

Let $d_k (p)$ be the length of a shortest k-path to a point p. Clearly, a path that crosses j obstacles and contains at least two segments can be made even shorter if it is allowed to pass through more obstacles. Thus, it follows that for any point p that is not $(k-1)$-visible from s, we must have $d_{j}(p) > d_{j+1}(p)$, for $j < k$.

Lemma 5

For any pointpthat is not$(k-1)$-visible froms, the lengths of the shortestj-paths form a decreasing sequence:

$$\begin{aligned} d_0(p) \;>\; d_1(p) \;>\; \dots \;>\; d_i(p) \;>\; \dots \;>\; d_k(p) \end{aligned}$$

3 Shortest Path Map ${ SPM}_{k}$: Properties and Bounds

Having established the basic properties of shortest k-paths, we now begin our discussion of the shortest k-path map ${ SPM}_{k}$.

Definition 2

Given a shortest k-path $\pi _k(p)$, we define the k-predecessor of p to be the vertex of P (including s) that is adjacent to p in $\pi _k(p)$. The partition of free space into connected regions with the same k-predecessor is called the shortestk-path map, and denoted ${ SPM}_{k}$. The subset of ${ SPM}_{k}$ for which the shortest path $\pi _k(p)$ to every point p has exactly k crossings is called the shortest $(=k)$-path map and denoted by ${ SPM}_{={k}}$. See Fig. 2 for an example.

Unlike ${ SPM}_{0}$, in which the predecessor of a region is always inside or on the boundary of the region, the predecessor of a region in ${ SPM}_{k}$ may lie outside the region. Moreover, multiple regions in ${ SPM}_{k}$ may have the same predecessor. (See Fig. 2.) Thus, we need to maintain additional information with polygon vertices to disambiguate the predecessor relation. In particular, let v be the k-predecessor of p, namely, the vertex adjacent to p in $\pi _k(p)$. Suppose the line segment $\overline{vp}$ crosses $(k-i)$ obstacles, for some $0 \le i \le k$. Then the length $d_k(p)$ of $\pi _k(p)$ is the sum of the length of the i-path to v and the length of segment $\overline{vp}$. We need to maintain the values $d_i(v)$ for all obstacle vertices v and all integers $i=0, 1, \ldots , k$. In other words,

For a point p in ${ SPM}_{={k}}$, we identify the k-predecessor of p by the pair (v, i), where v is a vertex of P and $i \in \{0, 1, \dots , k\}$, such that $d_k(p) = d_i(v) + |\overline{vp}|$ and the segment $\overline{vp}$ crosses $(k-i)$ obstacles.

Thus, the total number of k-predecessors is O(kn). However, this alone does not bound the number of regions in ${ SPM}_{={k}}$ because multiple regions can have the same k-predecessor and the same crossing sequence. Toward our goal of bounding the combinatorial complexity of the map, let us begin with the notion of k-visibility.

Fig. 2

The shaded region denotes the cells of ${ SPM}_{1}$ for which the 1-predecessor is (s, 0). Note that unlike ${ SPM}_{0}$, there are multiple cells with the same predecessor

Fig. 3

The boundary $\partial V_{1}$ of the region $V_{1}$ is dash-dotted, and it encloses the boundary $\partial V_{0}$, which is shown with dotted segments. The region $V_{0}$ is shown in white, $V_{1} \setminus V_{0}$ is shown shaded gray. The blue region denotes $V_{2} \setminus V_{1}$ (Color figure online)

We define $V_{k}$ to be the region consisting of k-visible points, which is star-shaped and therefore simply connected (Fig. 3). Now if $\pi _k(p)$ crosses fewer than k obstacles, then by Lemma 4, p must lie in $V_{k-1}$. The path $\pi _k(p)$ is a straight line segment and the k-predecessor of p is s. Therefore, we have the following.

Lemma 6

All pointspsuch that$\pi _k(p)$has fewer thankcrossings lie in$V_{k-1}$. Outside of$V_{k-1}$, ${ SPM}_{k}$is the same as${ SPM}_{={k}}$, the shortest path map with exactlykcrossings.

This simplifies our discussion and allows us to decompose ${ SPM}_{k}$ into two distinct regions, $V_{k-1}$ and ${ SPM}_{={k}}$. In the following, we study structural properties of these regions and use them to compute upper bounds on their respective sizes. Later, we combine them to compute an upper bound on the size of the map ${ SPM}_{k}$.

3.1 k-Visibility Region

We first bound the complexity of the boundary of $V_{k}$, the region visible from s by a segment crossing at most k obstacles.

Lemma 7

The number of edges on the boundary$\partial V_{k}$is$O(n+h) = O(n)$.

Proof

Every vertex of $\partial V_{k}$ is either a vertex of P or a projection of one of the 2h tangents from s to an obstacle of P. The edges on the boundary $\partial V_{k}$ are therefore sub-segments of the tangents or parts of obstacle boundaries. Each projection vertex belongs to a segment of $\partial V_{k}$ collinear with s, and the endpoint x farther from s is the end of a maximal segment $\overline{sx}$ that crosses exactly k obstacles. Therefore, each of the 2h tangents gives rise to at most one segment of $\partial V_{k}$ and at most two vertices. $\square$

More interestingly, the bound on the total complexity of these regions is less than the sum of the individual bounds.

Lemma 8

The total number of edges on all$\partial V_{i}$, for$0 \le i \le k$, is$O(n + hk)$.

Proof

Any vertex v of P belongs to $\partial V_{i}$ for at most one value of i, namely the i (if any) such that $\overline{sv}$ intersects exactly i obstacles. For $j < i$, v is outside $\partial V_{j}$, and for $j > i$, v is in the interior of $\partial V_{j}$. There are O(h) edges of $\partial V_{i}$ (for any i) not incident to a vertex of P. Summing over all $i \le k$ completes the proof. $\square$

By connecting s to all vertices on boundary $\partial V_{k-1}$, we can easily decompose $V_{k-1}$ into constant complexity regions in ${ SPM}_{k}$.

3.2 The k-Level Garage and the Structure of ${ SPM}_{={k}}$

We now introduce our main idea for computing the shortest k-path map. By Lemma 2, an $(=k)$-path from s to a point p is the concatenation of a $(k-1)$-path to the boundary of some obstacle H, a shortest path inside H, and a shortest path in free space from the other side of H to p. This suggests an incremental construction of ${ SPM}_{={k}}$ from ${ SPM}_{={(k-1)}}$. We describe this construction using the metaphor of a k-level parking garage with elevators.¹ The idea is to create multiple copies of the input polygonal domain and stack them in levels such that the shortest paths at each level have the same prefix count and therefore do not intersect. The planar subdivision of free space at the top level is ${ SPM}_{={k}}$.

Definition 3

(k-garage) We construct the k-garage structure by stacking k copies (or floors) of the input polygonal domain P on top of one another, with special connections at the obstacle boundaries. We connect the obstacle H on floor i to its counterpart on floor $i+1$ such that any path that enters H on floor i can exit only on the next higher floor—in a sense, obstacles act as elevators.

Our algorithm to construct ${ SPM}_{={k}}$ makes use of the continuous Dijkstra method, which simulates the expansion of a unit speed wavefront from the source s in free space. The wavefront at time T contains all points p whose shortest path distance from s is T. The boundary of the wavefront is a set of circular arcs called wavelets, each generated by an obstacle vertex (including s) already covered by the wavefront. The generating vertex v is called the generator of the wavelet and is identified by the pair (v, w), where w is the time at which v was reached by the wavefront. Since the wavefront moves at unit speed, w is precisely the length of the shortest path from s to v. The generators can be thought of as sources additively weighted with delays, since they start emitting wavelets at time w after the start of the simulation. The locus of the meeting points of two adjacent wavelets is a bisector curve. Taken together with the obstacle boundaries, bisector curves partition free space into regions of the shortest path map.

We extend the continuous Dijkstra method to our k-garage structure. Each level of the garage is a plane with polygonal obstacles on which wavefronts propagate as usual, but the wavelets can now move to higher floors by entering the obstacles (elevators). More precisely, when the wavefront hits an obstacle H, it is absorbed by the outer boundary of H and is immediately re-emitted into the interior of H. When that wavefront reaches the inner boundary on the other (previously unreached) side of H, it is absorbed and immediately re-emitted on the next higher floor of the garage. This vertical movement therefore adds no delay. In this modified setting, the wavefront at time T contains points on all floors that are at distance T from the source.

The region $V_{k-1}$ is removed from the polygonal domain on floor k of the k-garage because the shortest k-path is known for every point p in $V_{k-1}$—it is simply the line segment $\overline{sp}$—and leaving these points in the polygonal domain on floor k would create redundant copies of this path. We defer the exact details of our algorithm to Sect. 4. In the following, we note some properties of the k-garage structure useful to our algorithm.

• 1. If $\pi$ is a shortest s–t path from s on floor 0 to t on floor k, then the downward projection $\pi ^{\downarrow }$ of $\pi$, obtained by projecting $\pi$ into the planar domain P, is a shortest k-path to t. (To see this, suppose for contradiction we have another k-path $\pi _c$ from s to t that is shorter. Then by applying Lemma 2 recursively, we can break $\pi _c$ into $2k+1$ disjoint subpaths ordered by their prefix counts. We now lift the paths into the levels of the garage and concatenate them in order: if the prefix counts of the current and the next subpath are the same, join their common endpoint at the same level as the prefix count; otherwise join their common endpoint at the next level. This transforms the path $\pi _c$ into a shortest path $\pi _c^{\uparrow }$ from s on floor 0 to t on floor k. Since the vertical movement between the garage floors incurs no delay, the lifted path $\pi _c^{\uparrow }$ is shorter than $\pi$, which is a contradiction.)

• 2. Since wavefront propagation on floor i is affected only by wavelets coming from floors below it, we can think of wavefront propagation on floor i as occurring in a polygonal domain with multiple sources. On floor $i > 0$, all sources correspond to generators of wavelets coming from lower floors.

• 3. To compute the sources at floor $i > 0$, we need to consider only wavelets coming from floor $i-1$. This follows from Lemma 5, which implies that even if wavelets were allowed to ascend multiple floors in an elevator, a wavelet from floor $i-1$ would reach floor i no later than the wavelets from other lower floors.

• 4. The planar subdivision formed by bisectors of colliding wavelets on floor i is the shortest path map for $(=i)$-paths, ${ SPM}_{={i}}$. Note that since the obstacles are convex, a shortest path to a point on floor i cannot cross the same obstacle (on any floor) more than once, or else it can be made even shorter.

This suggests a natural way of computing the shortest path map ${ SPM}_{={k}}$. We construct maps ${ SPM}_{={i}}$ for $i = 0, 1, \dots , k$ iteratively. Each iteration $i > 0$ is defined by ordinary shortest path propagation with a set of sources that come from the previous iteration. In the following section we use these observations to compute a bound on the size of the shortest k-path map ${ SPM}_{k}$.

3.3 Complexity of ${ SPM}_{k}$

The shortest k-path map ${ SPM}_{k}$ on the top floor of the k-garage is precisely ${ SPM}_{={k}}$ in the portion of free space that is outside $V_{k-1}$, as shown in Lemma 4. The boundary of $V_{k-1}$ has linear size, and so we only need to bound the complexity of ${ SPM}_{={k}}$. To bound the complexity of ${ SPM}_{={k}}$, we consider the embedded planar graph $G_k$ formed by ${ SPM}_{={k}}$, $V_{k-1}$, and the obstacle polygons. We note the following property of planar graphs, which is a direct consequence of Euler’s formula.

Lemma 9

Letfbe the number of faces in a planar graph$G = (V, E)$. If all the vertices ofGhave degree three or more, then the size ofGisO(f).

Proof

Let d(v) be the degree of a vertex v. Since $\sum _{v \in V} d(v) = 2|E|$, and $d(v) \ge 3$, we have $2|E| \ge 3|V|$. Substituting this in Euler’s formula $|V| - |E| + f = 2$ gives us $|V| \;\le \; 2f - 4 \;=\; O(f)$. Since $|E| = |V| + f - 2$, we conclude that $|V| + |E| \;=\; O(f)$. $\square$

Observe that the “interesting” vertices in $G_k$ are the points where bisectors meet obstacle boundaries or meet each other, and therefore have degree at least three. If f is the number of faces, then by Lemma 9 the complexity of the map due to these vertices is O(f). In addition to this, $G_k$ can also have O(n) vertices of degree two corresponding to the vertices of obstacle polygons, giving a total complexity bound of $O(f + n)$.

Therefore, in order to compute a bound on the complexity of ${ SPM}_{={k}}$, it suffices to bound the number of faces f in the graph $G_k$. We begin with the following well-known result [19].

Lemma 10

The shortest path map ofmsources weighted by their delays in a polygonal domain withnvertices andhholes has$f \;\le \; m + n + h \;\le \; m + 2n$faces. By planarity, the total complexity of the map is$O(f + n)$.

The key to the proof of the preceding lemma is that each shortest path map region is star-shaped and connected to the predecessor of all points in the region. Since the total number of predecessors is at most $(m+n)$, the number of faces due to these regions is also at most $(m+n)$. Crucially, this lemma does not immediately apply to ${ SPM}_{={k}}$, because some predecessors of regions on the $k^{{\mathrm{th}}}$ floor belong to regions below the$k^{{\mathrm{th}}}$floor. That is, some of the m sources are not in the polygonal domain, so the argument that each region is connected to its predecessor does not hold. Fortunately, the argument of Lemma 10 is a topological one, and we can create a topological domain in which the argument applies (Fig. 4).

Fig. 4

a–c An example illustration of wavefront propagation across garage floors. The wavefront ascends between floors by entering into obstacles (elevators) and creates boundary sources at the next level. We continue wavefront propagation at the next level using these boundary sources. d Creating a pseudo-polygonal domain by connecting a source on a higher level to its predecessor on an earlier level by a triangular “flap”

Every point $p \in \partial P$ outside of $V_{k-1}$ is labeled by a $(k-1)$-crossing distance $d_{k-1}(p)$. If p belongs to an obstacle H, and there exists some $q\in \partial H$ such that $d_{k-1}(q) + |\overline{qp}| < d_{k-1}(p)$, then $\pi _k(p)$ may reach p by passing through H. The wavefront that determines ${ SPM}_{={k}}$ will be initialized with a weighted source that reaches p by “elevator” passing through H. If $q \in \partial H$ minimizes $d_{k-1}(q) + |\overline{qp}|$, then the predecessor of q on $\pi _{k-1}(q)$ is the generator of the wavelet that first reaches p in the wavefront. We partition each edge of $\partial H$ into maximal sub-edges with the same predecessor. For each sub-edge with predecessor v, we construct a triangular “flap” by drawing the segments from the sub-edge endpoints to v. Shortest paths propagate from v toward the kth garage floor inside the flap, and in the pseudo-polygonal domain obtained by gluing all the flaps onto the boundary of free space, each shortest path map region is connected to its predecessor. If these flaps were projected into the plane, they would likely overlap, but topologically they do not alter the structure of the domain, and they add only two edges per flap.

Lemma 11

LetPbe a polygonal domain withnvertices andhholes. IfPis extended by gluing at mostmtriangular flaps to its boundary, then the shortest path map ofmsources weighted by their delays in this extended polygonal domain has$f \;\le \; m + n + h \;\le \; m + 2n$faces and total complexity$O(m + n)$.

The preceding lemma applies to the propagation of shortest paths on each floor of the k-garage and also to propagation inside the obstacles (elevators). In both cases the key to bounding the complexity of an iterated construction is bounding the number of sources that propagate into the next level, whether elevator or garage floor. In each elevator and on each garage level $i > 0$, the sources are located on the domain boundary. For simplicity we partition the sources at obstacle vertices, so each source is a maximal (sub-)edge $\ell$ on some obstacle boundary $\partial H$, with an associated generator (v, w). We refer to such a source as a boundary source and represent it by the triple $(v, w, \ell )$. Shortest paths from a source $(v, w, \ell )$ enter the domain through edge $\ell$, and their predecessor is vertex v with weight (delay) w. As noted above, each boundary source defines a triangular flap glued onto the boundary of the propagation domain; the flap is the convex hull of $\ell$ and v.

Fig. 5

a Exit claims for the boundary source $(v, w, \ell )$ need to be propagated to next level. b Connecting the sources with their exit claims gives a bipartite planar graph

When boundary sources propagate into some domain (either P or the interior of an obstacle), they define a shortest path map S in the domain. We say that if the region of S corresponding to a source $s = (v,w,\ell )$ intersects a domain edge, then sclaims the intersection interval on that edge. An entry claim of a source $(v, w, \ell )$ is a claim on edge $\ell$ itself; entry claims can be ignored for further propagation, since a path that enters the domain through $\ell$ and exits through the same edge can be shortened. Exit claims (ones on edges other than $\ell$) define the sources for the next level of shortest path propagation. (See Fig. 5.) Within any edge, a maximal sequence of exit claims with the same source is called an exit claim cluster. In other words, exit claims of a source $(v, w, \ell )$ on an edge e may be disconnected and each connected sequence is precisely an exit claim cluster. Note that these exit claim clusters give rise to the boundary sources for subsequent wavefront propagation. That is, for an exit claim cluster on edge e with source $(v, w, \ell )$, the corresponding boundary source at the next level is $(v, w, \ell ')$, where $\ell '$ is the minimal subsegment of e containing the cluster. As noted, entry claims inside $\ell '$ do not affect shortest path propagation at the next level.

Lemma 12

LetSbe the shortest path map obtained by propagatingmboundary sources into a polygonal domain withnvertices. Then the number of exit claim clusters ofSis at most$m + O(n)$.

Proof

Since S is a partition of the domain, the domain boundary is completely covered by claims, which may be either entry claims or exit claims.

We construct an embedded bipartite planar graph whose nodes are claims on the domain boundary. Every source $(v,w,\ell )$ that claims some portion of the domain boundary must have an entry claim on $\ell$; otherwise the shortest path propagation from $(v,w,\ell )$ would not enter the domain. For every exit claim $\tau$ claimed by source $(v, w, \ell )$, we draw an arc from segment $\ell$ to $\tau$, following a shortest path segment across the domain interior. We want to bound the total number of these arcs. Since the shortest paths that define S do not cross, these arcs are non-crossing. (See also Fig. 5.)

We group arcs into bundles whose sources and targets lie on the same pair of domain edges. If we pick one arc from each bundle and regard each domain edge as a node in a planar graph, planarity gives a bound of O(n) on the total number of bundles. This bound on the number of bundles is the first step in bounding the number of arcs.

If a bundle joining edges e and $e'$ has $j > 1$ arcs, we draw $j-1$ cycles, each one defined by two adjacent arcs and the subsegments of e and $e'$ between their endpoints. The cycles for a single bundle are interior-disjoint, but cycles from different bundles may be nested, one containing the other. Note that cycle boundaries cannot cross—they are composed of obstacle boundaries and noncrossing arcs—so nesting is the only possible relation between cycles that are not interior-disjoint.

If a cycle C contains any obstacle, we split the bundle B containing C between the arcs of C, so neither of the resulting two bundles contains C. We charge the splitting of B to one of the obstacles inside C. We choose which obstacle to charge so as to guarantee that each obstacle is charged at most once. If C contains no cycle nested inside it, we charge an arbitrary obstacle inside C. If C contains other cycles, let $C'$ be one at the outermost level of nesting within C. Cycle $C'$ must have at least one of its bounding edges on an obstacle H contained in the interior of C, because otherwise $C'$ would share both obstacle edges with C, which is impossible by construction. Obstacle H is not contained in any cycle $C''$ nested inside C, because $C''$ would necessarily contain $C'$, but $C'$ was chosen outermost. We charge the splitting of B at C to H. Note that H cannot be charged by any cycle inside C (because it is outside all such cycles) or containing C (because it is inside C and hence shielded from such cycles).

Because there are at most O(n) obstacles, each charged for at most one split, the number of bundles after splitting is still O(n). None of the bundles that remain after splitting contains any obstacle inside the quadrilateral it bounds.

Given a bundle incident to edges e and $e'$, we divide it into two sub-bundles, one consisting of arcs directed from e to $e'$ and one consisting of the oppositely directed arcs. Within each sub-bundle, we identify contiguous runs of arcs with the same source. Each maximal run corresponds to an exit claim cluster, so we will call these runs arc clusters. We charge the first and last arc cluster in each sub-bundle to the bundle itself. (There are O(n) such charges.) Crucially, every other arc cluster corresponds to a source that appears only in this bundle, because the arcs before and after it in the sub-bundle confine it and prevent it from claiming edges anywhere else. Hence we can charge each such cluster to the source itself; the source is charged only once.

To recap, we bound the number of exit claim clusters by the number of arc clusters. Arcs belong to bundles, and there are O(n) bundles by planarity. To remove obstacles inside bundles, we split bundles at most O(n) times. We break each bundle into two sub-bundles, and pay explicitly for the first and last arc cluster in each, for a total of O(n). We charge each remaining arc cluster to one of the m sources, charging each source at most once, giving a total bound on the number of arc clusters of $m + O(n)$. $\square$

We are now ready to bound the complexity of ${ SPM}_{={k}}$.

Lemma 13

The number of faces$f_k$in${ SPM}_{={k}}$is$O(n(k+1))$. The complexity of${ SPM}_{={k}}$has the same asymptotic bound.

Proof

The proof is by induction. Our goal is to show that there exists a constant C such that the number of faces $f_k$ in ${ SPM}_{={k}}$ is at most $Cn(k+1)$ for all $k \ge 0$.

We begin with the inductive step. Let m be the number of exit claim clusters in ${ SPM}_{={(k-1)}}$. This is the number of boundary sources in “elevator” propagation across the obstacle interiors, going from level $k-1$ to level k. By Lemma 12, the resulting number of exit claim clusters is $m' = m + O(n)$. But $m'$ is the number of boundary sources in the construction of ${ SPM}_{={k}}$, and once again by Lemma 12, the resulting number of exit claim clusters is $m'' = m'+ O(n) = m + O(n)$, that is, $m'' \le m + c_1 n$ for some constant $c_1$.

To establish the base case, recall that a shortest path map with no crossings (${ SPM}_{0}$) has complexity O(n), which implies that the number of exit claims on its boundary is O(n), i.e., at most $c_2 n$ for some constant $c_2$. Combining the base case and inductive step, we have shown that the number of exit claim clusters on the boundary of ${ SPM}_{={k}}$ is at most $c_2 n + k\cdot c_1 n$. The number of faces of ${ SPM}_{={k}}$ is at most equal to the number of boundary sources, which is at most $Cn(k+1)$, for $C = \max (c_1, c_2)$. Lemma 9 establishes the total complexity bound. $\square$

3.4 A Matching Lower Bound

We will now bound the size of ${ SPM}_{k}$ from below by constructing a map with $\varOmega (nk)$ regions. We construct an arrangement of obstacles as shown in Fig. 6. We start with two obstacle bundles A and B placed parallel to the y-axis. Within each bundle, the horizontal spaces between strips are infinitesimal, but they are shown enlarged for clarity. The source s lies on the x-axis with bundle A placed right next to it. Bundle A consists of 3k perforated strips. In the first 2k strips, the odd numbered ones have openings at $y=0$ and the even numbered ones have openings at $y = -0.5$. The next k strips have an opening at $y=0$. Bundle B is placed at a distance D to the right of A and consists of k strips with no openings.

Fig. 6

A shortest k-path map with complexity $\varOmega (nk)$. Bundle A has 2k black strips and k gray strips; bundle B has k strips. The thick strip S has $\varOmega (n)$ openings. Each opening of S defines k cells in ${ SPM}_{k}$, shown shaded (one to the right of each of the k strips in bundle B). A shortest k-path $\pi (p)$ from s is also shown. Observe that since $\pi (p)$ crosses $(k-1)$ strips in bundle A, it can only cross the first strip in bundle B

The last k strips in bundle A ensure that shortest k-paths starting at s must exit from the opening of the last strip in A (denoted by $y^*$); a path that crosses the last strip in A at some point other than $y^*$ can be shortened while preserving the same number of crossings. Observe that a shortest path starting at s can reach $y^*$ with i crossings, where $0 \le i \le k$. However, each crossing avoided results in an additional length of 1 unit. Therefore a shortest path with i crossings at $y^*$ has an additional length of $(k-i)$ units. Also note that a shortest path with i crossings prior to $y^*$ can cross the first $(k-i)$ of the k strips in bundle B, but cannot cross any farther. Therefore, to the right of strip j in bundle B, we get a region with k-predecessor $(y^*, k-j)$ and a total path length (to a point on the x-axis) of $D+j$. This gives us a total of k regions.

We extend this construction to $\varOmega (nk)$ regions by adding a vertical strip S, which acts as a path splitter. This special strip has a total of m single-point openings at $y = 0, 1, \dots , m$, denoted by $y_i$. We place S at an infinitesimal distance to the left of bundle B, creating k new regions for each opening of S. Note that in the range $0 \le y \le m$, a path that crosses S other than at one of the perforations $y_i$ can be shortened by detouring through the nearest $y_i$ and inserting one more crossing before $y^*$. Hence a shortest k-path always passes through one of the $y_i$. This gives a total of O(mk) regions: the k-predecessor of the region at $y = i$ and to the right of strip j of bundle B will be $(y_i, k-j)$, with a total path length of $\sqrt{D^2 + i^2} + j$.

The total number of vertices in our construction is $3k \times 4 \;+\; k \times 2 \;+\; (m+1) \times 2 \;=\; 14k + 2m + 2$. By choosing $m = (n-14k-2)/2$ and assuming $k < n / 28$, we have $m = \varTheta (n)$ and the total number of regions in ${ SPM}_{k}$ is $\varOmega (nk)$. This gives us the following lemma.

Lemma 14

The worst-case complexity of${ SPM}_{k}$is$\varOmega (nk)$.

Combining Lemmas 7, 13, and 14, we get the main result of this section.

Theorem 2

The shortestk-path map${ SPM}_{k}$has size$\varTheta (kn)$.

4 Computing SPM_k

In this section we describe an $O(k^2 n \log n)$ algorithm to construct ${ SPM}_{k}$. Recall from our discussion about the k-garage (Definition 3), we can construct ${ SPM}_{={k}}$ iteratively, one level at a time. To compute the map at each level, we propagate the sources from the previous level and then perform wavefront propagation at the current level. For this, we use the algorithm for shortest paths in the presence of polygonal obstacles by Hershberger and Suri [19] as a subroutine. Except for a few small modifications required for our setting, most of the algorithm carries over unchanged. In the following, we briefly review the key ideas and discuss the necessary modifications.

The Hershberger–Suri algorithm uses the continuous Dijkstra method, which simulates the propagation of a unit speed wavefront in free space. The wavefront is a collection of circular wavelets. It changes its shape as it propagates and hits obstacles. Each wavelet originates at a generator, which may be a point source or an obstacle vertex (an intermediate source). A generator for a wavelet $\gamma$ is identified by the pair (v, w), where v is an input vertex and w is the time at which v starts emitting $\gamma$. The Hershberger–Suri algorithm simulates wavefront propagation over a planar subdivision called the conforming subdivision of free space. For each subdivision edge e, and every point $p\in e$, the algorithm identifies the generator whose wavelet first reaches p. Combining these results for all $p\in e$ gives the wavefront fore. The key idea of the algorithm is to localize interesting events (such as wavelet collisions) within a constant number of cells in the subdivision. Each free-space edge e of this subdivision is contained in the union of a constant number of cells, called its well-covering region${{{\mathcal {U}}}}(e)$. The wavefront for edge e is computed by combining and propagating the wavefront inside of ${{{\mathcal {U}}}}(e)$. The computed wavefronts are then merged to compute the shortest path map. This is the main result relevant to our algorithm:

Lemma 15

([19]) Given a set of polygonal obstacles withnvertices and a set ofO(n) sources with delays, one can compute the shortest path map in$O(n \log n)$time and$O(n \log n)$space.

From the discussion preceding Lemma 12, recall that the sources on floor i are identified by triples $(v,w,\ell )$, where $\ell$ is a (sub-)edge of some obstacle H, (v, w) is a weighted point source on some floor $j < i$, and the wavelet $\gamma$ generated by (v, w) enters floor i from the interior of H (an elevator) passing through edge $\ell$. Each source $(v,w,\ell )$ defines a triangular flap glued onto the boundary of free space at $\ell$. Conceptually, we think of the wavelet $\gamma$ from $(v,w,\ell )$ as propagating in the flap before it enters floor i. Algorithmically, we can ignore the flap and start the propagation in free space at edge $\ell$. This calls for a slight modification in the initialization step of the Hershberger–Suri algorithm. In particular, we do the following for each edge e of the conforming subdivision:

• 1. Find all boundary sources $(v,w,\ell )$ such that the well-covering region ${{\mathcal {U}}}(e)$ contains $\ell$.

• 2. Initialize covertime(e), which is the time at which e would be engulfed by the wavefront, minimizing over all boundary sources $(v,w,\ell )$ with $\ell \in {{\mathcal {U}}}(e)$, and for each such source considering paths from v with delay w, constrained to pass through $\ell$.

• 3. For each source $(v,w,\ell )$ with $\ell \in {{\mathcal {U}}}(e)$, propagate its wavelet $\gamma$ to e inside ${{\mathcal {U}}}(e)$.

In the following lemma we show how to compute the boundary sources for each step of wavefront propagation.

Lemma 16

Given m boundary sources in a polygonal domain with n vertices, we can compute the exit claims of the sources in $O((m+n) \log (m+n))$ time and space.

Proof

We apply the Hershberger–Suri algorithm, modified for boundary sources as described above. The algorithm computes the shortest path map for the sources inside the polygonal domain in total time and space $O((m+n)\log (m+n))$. The shortest path map partitions the boundary into $O(m+n)$ intervals (claims), each claimed by its own source.

However, some of these intervals may be entry claims, that is, they are claimed by a source that lies on the same segment. Observe that an entry claim interval must have a non-empty intersection with the interval corresponding to its source. We can therefore identify entry claims by overlaying the set of claim intervals with the boundary sources that form another set of m intervals. Overlaying these two sets of intervals takes additional linear time and space. The remainder is the set of all exit claims, that is, those with a claiming source from a different segment. $\square$

With these primitives in place, we are ready to describe our algorithm. The input is a polygonal domain P with convex obstacles. We will use M to denote the set of boundary sources passed as input to the Hershberger–Suri algorithm. The algorithm computes two things: the $(k-1)$-visibility region V and the $(=k)$-path map ${ SPM}_{={k}}$, which combined together form ${ SPM}_{k}$. The length of the shortest path to any point p can then be easily computed by first locating the region containing p in the map ${ SPM}_{k}$ and then connecting p to the k-predecessor of this region as described in the beginning of Sect. 3.

Algorithm to construct${ SPM}_{k}$

• 1. Set $M = \{s\}$ and call the Hershberger–Suri algorithm to compute ${ SPM}_{0}$ for the polygonal domain P. Initialize V to be the empty region $\emptyset$.

• 2. Repeat for each $i \in {1, 2, \dots , k}$:

  • (a) Using Lemma 16, propagate the sources in ${ SPM}_{i-1}$ through the obstacles in P to compute the set of boundary sources $M_{new}$ for ${ SPM}_{={i}}$.

  • (b) Identify all the regions in ${ SPM}_{={(i-1)}}$ for which the predecessor is s. Observe that this is precisely the region $V' = V_{i-1} \setminus V_{i-2}$. Set P to be the new polygonal domain with this region removed.

  • (c) If $V = \emptyset$, then set $V = V'$. Otherwise merge V with $V'$ at the common vertices.

  • (d) Set $M = M_{new}$ and call the Hershberger–Suri algorithm to compute ${ SPM}_{={i}}$ for the polygonal domain P.

• 3. Merge ${ SPM}_{={k}}$ with V at the boundary of regions of ${ SPM}_{={k}}$ that have s as predecessor (i.e. $V' = V_{k} \setminus V_{k-1}$), to obtain ${ SPM}_{k}$.

Observe that after Step 2c of iteration i, the region V is equal to $V_{i-1}$. Because $V_{i-1}$ contains $V_{i-2}$ and because both regions have linear size (by Lemma 7), Step 2c takes linear time. Therefore, the total running time is dominated by k calls to the Hershberger–Suri algorithm with O(nk) sources (Theorem 2). We have the following result.

Theorem 3

If P is a polygonal domain bounded by convex obstacles with a total of n vertices, the shortest k -path map for P with respect to a source point s can be computed in $O(k^2 n \log n)$ time and $(k n \log n)$ space.

5 Conclusion

In this paper, we studied the problem of finding shortest paths that are allowed to pass through a bounded number of convex obstacles. We showed that although two such k-paths may cross each other, they can be decomposed into non-crossing subpaths based on prefix-counts. This decomposition allows us to compute shortest k-paths efficiently, using the continuous Dijkstra framework. We showed that the size of the shortest k-path map is $\varTheta (kn)$ and that it can be computed in worst-case time $O(k^2 n \log n)$ using $(k n \log n)$ space. Our algorithm’s time complexity is optimal when $k = O(1)$.