Computing $L_1$ Shortest Paths Among Polygonal Obstacles in the Plane

Abstract

Given a point s and a set of h pairwise disjoint polygonal obstacles with a total of n vertices in the plane, suppose a triangulation of the space outside the obstacles is given; we present an $O(n+h\log h)$ time and O(n) space algorithm for building a data structure (called shortest path map) of size O(n) such that for any query point t, the length of an $L_1$ shortest obstacle-avoiding path from s to t can be computed in $O(\log n)$ time and the actual path can be reported in additional time proportional to the number of edges of the path. The previously best algorithm computes such a shortest path map in $O(n\log n)$ time and O(n) space. So our algorithm is faster when h is relatively small. Further, our techniques can be extended to obtain improved results for other related problems, e.g., computing the $L_1$ geodesic Voronoi diagram for a set of point sites among the obstacles.

1 Introduction

Computing obstacle-avoiding shortest paths in the plane is a fundamental problem in computational geometry [6, 10, 15, 19, 22, 24, 25, 31, 34, 36]. In this paper, we consider the $L_1$ version of the problem where the path length is measured by the $L_1$ metric. Given a point s and a set of h pairwise disjoint polygonal obstacles, ${\mathcal {P}}=\{P_1,P_2,\ldots ,P_h\}$, with a total of n vertices in the plane, the plane minus the interior of the obstacles is called the free space of ${\mathcal {P}}$. Two obstacles are pairwise disjoint if they do not intersect in their interior. The $L_1$shortest path map problem, denoted by $L_1$-SPM, is to compute a single-source shortest path map (SPM for short) with s as the source point such that for any query point t, an $L_1$ shortest obstacle-avoiding path from s to t can be obtained efficiently.

If the input also includes another point t and the problem only asks for a single $L_1$ shortest path from s to t, then we call this problem version the $L_1$shortest path problem, denoted by $L_1$-SP.

A closely related problem solved by our approach is to find shortest rectilinear paths. A rectilinear path is a path each of whose edges is parallel to a coordinate axis. Rectilinear shortest paths are used widely in VLSI design and network wire-routing applications. As shown in [11, 27, 29, 30], it is easy to convert an arbitrary polygonal path to a rectilinear path with the same $L_1$ length. Thus, in this paper, we focus on computing polygonal paths measured by the $L_1$ distance.

1.1 Previous Work

The $L_1$-SP problem has been studied extensively (e.g., see [7, 8, 11, 12, 27, 29, 30, 37]). In general, there are two approaches for solving this problem: constructing a sparse “path preserving” graph (analogous to a visibility graph), and the continuous Dijkstra paradigm. Clarkson, Kapoor, and Vaidya [11] constructed a graph of $O(n\log n)$ nodes and $O(n\log n)$ edges such that a shortest path can be found in the graph in $O(n\log ^2 n)$ time; subsequently, they gave an algorithm of $O(n\log ^{1.5}n)$ time and $O(n\log ^{1.5}n)$ space [12]. Based on some observations, Chen, Klenk, and Tu [8] showed that the problem was solvable in $O(n\log ^{1.5}n)$ time and $O(n\log n)$ space. By applying the continuous Dijkstra paradigm, Mitchell [29, 30] solved the problem in $O(n\log n)$ time and O(n) space. An $O(n+h\log h)$ time lower bound can be established for solving $L_1$-SP (e.g., based on the results in [13]). Hence, Mitchell’s algorithm is optimal when $h=\Theta (n)$. By using a corridor structure and building a smaller path preserving graph, Inkulu and Kapoor [21] solved the $L_1$-SP problem in $O(n+h\log ^{1.5}n)$ time and $O(n+h\log ^{1.5}h)$ space.

For the query version of the problem, i.e., $L_1$-SPM, Mitchell’s algorithm [29, 30] builds an SPM of size O(n) in $O(n\log n)$ time and O(n) space such that for any query point t, the length of an $L_1$ shortest path from s to t can be reported in $O(\log n)$ time and an actual shortest path can be found in additional time linear in the number of edges of the path. An SPM is a decomposition of the free space into regions (or cells) such that each cell C has a “root” r (which is a vertex of ${\mathcal {P}}$ or the source point s) with the following property: for any point $t\in C$, there is a shortest path from s to t that is a concatenation of a shortest path from s to r and the line segment ${\overline{rt}}$. Refer to [29, 30] for more details.

In addition, for the convex case where all polygonal obstacles in ${\mathcal {P}}$ are convex, to our best knowledge, we are not aware of any previous results better than those mentioned above.

1.2 Our Results

Given a triangulation of the free space of ${\mathcal {P}}$, we present an algorithm that builds an SPM of size O(n) in $O(n+h\log h)$ time and O(n) space, with query time the same as that in [29, 30]. The currently best algorithms can triangulate the free space of ${\mathcal {P}}$ in $O(n\log n)$ time or $O(n+h\log ^{1+\epsilon }h)$ time for any $\epsilon >0$ [2]. Thus, our algorithm is faster than Mitchell’s $O(n\log n)$ time algorithm [29, 30] when h is relatively small, e.g., $h=O(n^{\delta })$ for any positive $\delta <1$.

Fig. 1

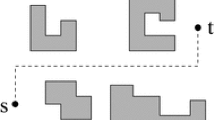
a Three weighted sites (in red) and a simple polygon B with an open edge ${\overline{cd}}$. The goal is to compute the $L_1$ geodesic Voronoi diagram in B with respect to the three sites which influence B only through the edge ${\overline{cd}}$. b Illustrating a possible solution: B is partitioned into three Voronoi regions ${V\!D}(r_i)$ for each $r_i$, $1\le i\le 3$ (Color figure online)

Our approach uses Mitchell’s algorithm [29, 30] as a procedure and further explores the corridor structure of ${\mathcal {P}}$ [25]. One interesting observation we found is that to find an $L_1$ shortest path among convex obstacles, it is sufficient to consider at most four extreme vertices (along the horizontal and vertical directions) of each obstacle (these vertices define a core for each obstacle). We then apply Mitchell’s algorithm to these cores, which takes only $O(h\log h)$ time. More work needs to be done for computing an SPM. For example, one key result we have is that we give an $O(n'+m')$ time algorithm for a special case of constructing the $L_1$ geodesic Voronoi diagram in a simple polygon of $n'$ vertices for $m'$ weighted point sites, where the sites all lie outside the polygon and influence the polygon through one (open) edge (see Fig. 1). We are not aware of any specific previous work on this problem, although an $O((n'+m')\log (n'+m'))$ time solution may be obtained by standard techniques (e.g., sweeping, divide-and-conquer, and continuous Dijkstra scheme). Our linear time algorithm, which is clearly optimal, may be interesting in its own right.

For the convex case where all obstacles in ${\mathcal {P}}$ are convex, we can find a shortest s-t path in $O(n+h\log h)$ time and O(n) space since the triangulation can be done in $O(n+h\log h)$ time (e.g., by the approaches in [2, 20]); this is optimal. A by-product of our techniques is that in $O(n+h\log h)$ time and O(n) space, we can build an SPM of size O(h) (instead of O(n)) such that the shortest path length queries are answered in $O(\log h)$ time each (instead of $O(\log n)$ time).

Our techniques have other applications. The $L_1$geodesic Voronoi diagram problem, denoted by $L_1$-GVD, is defined as follows. Given an obstacle set ${\mathcal {P}}$ and a set of m point sites in the free space, compute the geodesic Voronoi diagram for the m point sites under the $L_1$ metric among the obstacles in ${\mathcal {P}}$, i.e., partition the free space into regions such that each point site q corresponds to a region that consists of all points in the free space whose nearest point site is q with respect to the $L_1$ shortest path distance. Mitchell [29, 30] solved the problem in $O((n+m)\log (n+m))$ time. Our approach can compute the diagram in $O(n+(m+h)\log (m+h))$ time after the free space along with the m point sites is triangulated. Note that the time complexity becomes $O(n+m\log m)$ if it is applied to a simple polygon. In comparison, the Euclidean problem in simple polygons is solvable in $O(n\log n + m\log m)$ time [33], and recently, an $O(n+m\log m\log ^2 n)$ time algorithm was proposed [32].

2 An Overview of Our Approach

Denote by ${\mathcal {F}}$ the free space of ${\mathcal {P}}$, and we assume that ${\mathcal {F}}$ has already been triangulated. Note that we consider s as a point obstacle and include s in the triangulation, which can be done in additional linear time after ${\mathcal {F}}$ is triangulated (in the problem $L_1$-SP, t is also given in the input and we do the same for t). We begin with our algorithm for the convex case, which is a key procedure for solving the general problem.

We first discuss the $L_1$-SP problem. In the convex case, each obstacle in ${\mathcal {P}}=\{P_1,P_2,\ldots ,P_{h}\}$ is convex. For each $P_i\in {\mathcal {P}}$, we compute its core, denoted by $core(P_i)$, which is a constant-size simple polygon by connecting the topmost, leftmost, bottommost, and rightmost points of $P_i$. Let $core({\mathcal {P}})$ be the set of all h cores of ${\mathcal {P}}$. For any point t in the free space ${\mathcal {F}}$, we show that given any shortest s-t path avoiding all cores in $core({\mathcal {P}})$, we can find in O(n) time a shortest s-t path avoiding all obstacles in ${\mathcal {P}}$ with the same $L_1$ length. Based on this observation, our algorithm has two main steps: (1) apply Mitchell’s algorithm [29, 30] on $core({\mathcal {P}})$ to compute a shortest s-t path $\pi _{core}(s,t)$ avoiding the cores in $core({\mathcal {P}})$, which takes $O(h\log h)$ time since each core in $core({\mathcal {P}})$ has at most four vertices; (2) based on $\pi _{core}(s,t)$, compute a shortest s-t path avoiding all obstacles in ${\mathcal {P}}$ in O(n) time. This algorithm runs in $O(n+h\log h)$ time and O(n) space.

To build an SPM in ${\mathcal {F}}$ (for the source point s), similarly, we first apply Mitchell’s algorithm on $core({\mathcal {P}})$ to compute an SPM of O(h) size in the free space with respect to all cores, which can be done in $O(n+h\log h)$ time and O(n) space. Based on the above SPM, in additional O(n) time, we are able to compute an SPM in ${\mathcal {F}}$. Our results for the convex case are given in Sect. 3.

For the general problem where the obstacles in ${\mathcal {P}}$ are not necessarily convex, we first compute a corridor structure [25], which consists of O(h) corridors and O(h) junction triangles. Each corridor possibly has a corridor path. As in [25], the corridor structure can be used to partition the plane into a set ${\mathcal {P}}'$ of O(h) pairwise disjoint convex polygons with a total of O(n) vertices such that a shortest s-t path in ${\mathcal {F}}$ is a shortest s-t path avoiding the convex polygons in ${\mathcal {P}}'$ and possibly containing some corridor paths. Thus, in addition to the corridor paths, finding a shortest path is reduced to an instance of the convex case. By incorporating the corridor path information into Mitchell’s continuous Dijkstra paradigm [29, 30], our algorithm for the convex case can be modified to find a shortest path in $O(n+h\log h)$ time. The above algorithm is presented in Sect. 4.

Sections 4.3, 5, and 6 are together devoted to compute an SPM in ${\mathcal {F}}$ (Sect. 4.3 outlines the algorithm). We use the corridor structure to partition ${\mathcal {F}}$ into the ocean${\mathcal {M}}$, bays, and canals. While the ocean ${\mathcal {M}}$ may be multiply connected, every bay or canal is a simple polygon. Each bay has a single common boundary edge with ${\mathcal {M}}$ and each canal has two common boundary edges with ${\mathcal {M}}$. But two bays or two canals, or a bay and a canal do not share any edge. A common edge of a bay (or canal) with ${\mathcal {M}}$ is called a gate. Thus each bay has one gate and each canal has two gates. Further, the ocean ${\mathcal {M}}$ is exactly the free space with respect to the convex polygonal set ${\mathcal {P}}'$. By modifying our algorithm for the convex case, we can compute an SPM in ${\mathcal {M}}$ in $O(n+h\log h)$ time. This part is discussed in Sect. 4.3.

Denote by $\textit{SPM}({\mathcal {M}})$ the SPM in ${\mathcal {M}}$. To obtain an SPM in ${\mathcal {F}}$, we need to “expand” $\textit{SPM}({\mathcal {M}})$ into all bays and canals through their gates. Here, a challenging subproblem is to solve a special case of the (additively) weighted $L_1$ geodesic Voronoi diagram problem on a simple polygon B: the weighted point sites all lie outside B and influence B through one (open) edge (e.g., see Fig. 1). The subproblem models the procedure of expanding $\textit{SPM}({\mathcal {M}})$ into a bay, where the polygon B is the bay, the point sites are obstacle vertices in ${\mathcal {M}}$, the weight of each site is the length of its shortest path to the source point s, and the edge of the polygon (e.g., ${\overline{cd}}$ in Fig. 1) is the gate of the bay. We give a linear time algorithm for this subproblem in Sect. 5.

Expanding $\textit{SPM}({\mathcal {M}})$ into canals, which is discussed in Sect. 6, is also done in linear time by using our algorithm for the above subproblem as a main procedure. In summary, given $\textit{SPM}({\mathcal {M}})$, computing an SPM for the entire free space ${\mathcal {F}}$ takes additional O(n) time.

In Sect. 7, we generalize our techniques to solve the $L_1$-GVD problem. Section 8 concludes the paper with remark on possibly extending our techniques to solve other related problems.

As in [29, 30], for simplicity of discussion, we assume that the free space ${\mathcal {F}}$ is connected and the point t is always in ${\mathcal {F}}$ (thus, an s-t path always exists). We also make a general position assumption that no two obstacle vertices lie on the same horizontal or vertical line. In the rest of this paper, unless otherwise stated, a shortest path always refers to an $L_1$ shortest path and a path length is always measured by the $L_1$ metric.

3 Shortest Paths Among Convex Obstacles

In this section, we give our algorithms for the convex case, and the techniques will be used for the general case in later sections. Let ${\mathcal {P}}'=\{P_1',P_2'\ldots ,P_{h}'\}$ be a set of h pairwise disjoint convex polygonal obstacles with a total of n vertices. With respect to the source point s, our algorithm builds an SPM of O(n) size in $O(n+h\log h)$ time and O(n) space.

3.1 Notation and Observations

For each convex polygon $P_i'\in {\mathcal {P}}'$, we define its core, denoted by $core(P_i')$, as the simple polygon by connecting the leftmost, topmost, rightmost, and bottommost vertices of $P_i'$ with line segments (see Fig. 2). Note that $core(P_i')$ is contained in $P_i'$ and has at most four edges. Let $core({\mathcal {P}}')$ be the set of the cores of all obstacles in ${\mathcal {P}}'$. Consider a point t in the free space ${\mathcal {F}}$. A key observation (to be proved) is that a shortest s-t path avoiding the cores in $core({\mathcal {P}}')$ can be converted to a shortest s-t path avoiding the obstacles in ${\mathcal {P}}'$ with the same $L_1$ length. Note that a path avoiding the cores in $core({\mathcal {P}}')$ may intersect the interior of some obstacles in ${\mathcal {P}}'$.

We first define some concepts. Consider an obstacle $P_i'$ and $core(P_i')$. For each edge ${\overline{ab}}$ of $core(P_i')$ with vertices a and b, if ${\overline{ab}}$ is not an edge of $P_i'$, then it divides $P_i'$ into two polygons, and we call the one that does not contain $core(P_i')$ an ear of $P'_i$ based on ${\overline{ab}}$, denoted by $ear({\overline{ab}})$ (see Fig. 2). If ${\overline{ab}}$ is also an edge of $P_i$, then $ear({\overline{ab}})$ is not defined. Note that $ear({\overline{ab}})$ has only one edge bounding $core(P_i')$, i.e., ${\overline{ab}}$, which we call its core edge. The other edges of $ear({\overline{ab}})$ are on the boundary of $P_i'$, which we call obstacle edges. There are two paths between a and b along the boundary of $ear({\overline{ab}})$: One path is the core edge ${\overline{ab}}$ and the other consists of all its obstacle edges. We call the latter path the obstacle path of the ear. A line segment is positive-sloped (resp., negative-sloped) if its slope is positive (resp., negative). An ear is positive-sloped (resp., negative-sloped) if its core edge is positive-sloped (resp., negative-sloped). Due to our assumption no two obstacle vertices lie on the same horizontal or vertical line, no ear has a horizontal or vertical core edge. A point p is higher (resp., lower) than another point q if the y-coordinate of p is no smaller (resp., no larger) than that of q. The next observation is self-evident.

Fig. 2

Illustrating the core and ears of a convex obstacle; $ear({\overline{ab}})$ is indicated

Observation 1

For any ear, its obstacle path is monotone in both the x- and y-coordinates. Specifically, consider an ear $ear({\overline{ab}})$ and suppose the vertex a is lower than the vertex b. If $ear({\overline{ab}})$ is positive-sloped, then the obstacle path from a to b is monotonically increasing (i.e., non-decreasing) in both the x- and y-coordinates; if it is negative-sloped, then the obstacle path from a to b is monotonically decreasing in the x-coordinates and monotonically increasing in the y-coordinates.

For an ear $ear({\overline{ab}})$, we define its interior as the region of $ear({\overline{ab}})$ excluding its obstacle edges (the interior of the core edge ${\overline{ab}}$ belongs to the interior of $ear({\overline{ab}})$). We say that a line segment ${\overline{cd}}$penetrates$ear({\overline{ab}})$ if the following hold (see Fig. 3): (1) ${\overline{cd}}$ intersects the interior of $ear({\overline{ab}})$, (2) neither c nor d is in the interior of $ear({\overline{ab}})$, and (3) ${\overline{cd}}$ does not cross ${\overline{ab}}$ at its interior.

Observation 2

Suppose a line segment ${\overline{cd}}$ penetrates an ear $ear({\overline{ab}})$. If ${\overline{cd}}$ is positive-sloped (resp., negative-sloped), then $ear({\overline{ab}})$ is also positive-sloped (resp., negative-sloped).

Clearly, if ${\overline{cd}}$ penetrates the ear $ear({\overline{ab}})$, then ${\overline{cd}}$ intersects the boundary of $ear({\overline{ab}})$ at two points and both points lie on the obstacle path of $ear({\overline{ab}})$ (e.g., see Fig. 3).

Fig. 3

The line segment ${\overline{cd}}$ penetrates $ear({\overline{ab}})$; ${\overline{cd}}$ intersects the obstacle path of $ear({\overline{ab}})$ at e and f

Observation 3

Suppose a line segment ${\overline{cd}}$ penetrates an ear $ear({\overline{ab}})$. Let e and f be the two points on the obstacle path of $ear({\overline{ab}})$ that ${\overline{cd}}$ intersects. Then the $L_1$ length of the line segment ${\overline{ef}}$ is equal to that of the portion of the obstacle path of $ear({\overline{ab}})$ between e and $f\ ($ see Fig. 3).

If ${\overline{cd}}$ penetrates $ear({\overline{ab}})$, then by Observation 3, we can obtain another path from c to d by replacing ${\overline{ef}}$ with the portion of the obstacle path of $ear({\overline{ab}})$ between e and f such that the new path has the same $L_1$ length as ${\overline{cd}}$ and does not intersect the interior of $ear({\overline{ab}})$.

The results in the following lemma have been proved in [29, 30].

Lemma 1

[29, 30] There exists a shortest s-t path in the free space such that if the path makes a turn at a point p, then p is an obstacle vertex.

We call a shortest path in Lemma 1 a vertex-preferred shortest path. Mitchell’s algorithm [29, 30] can find a vertex-preferred shortest s-t path. Denote by ${T\!r\!i}({\mathcal {P}}')$ a triangulation of the free space and the space inside all obstacles. Note that the free space can be triangulated in $O(n+h\log h)$ time [2, 20] and the space inside all obstacles can be triangulated in O(n) time [3]. Hence, ${T\!r\!i}({\mathcal {P}}')$ can be computed in $O(n+h\log h)$ time. The next lemma gives our key observation.

Lemma 2

Given a vertex-preferred shortest s-t path that avoids the polygons in $core({\mathcal {P}}')$, we can find in O(n) time a shortest s-t path with the same $L_1$ length that avoids the obstacles in ${\mathcal {P}}'$.

Proof

Consider a vertex-preferred shortest s-t path for $core({\mathcal {P}}')$, denoted by $\pi _{core}(s,t)$. Suppose it makes turns at $p_1,p_2,\ldots ,p_k$, ordered from s to t along the path, and each $p_i$ is a vertex of a core in $core({\mathcal {P}}')$. Let $p_0=s$ and $p_{k+1}=t$. Then for each $i = 0,1,\ldots , k$, the portion of $\pi _{core}(s,t)$ from $p_i$ to $p_{i+1}$ is the line segment $\overline{p_ip_{i+1}}$, which does not intersect the interior of any core in $core({\mathcal {P}}')$. Below, we first show that we can find a path from $p_i$ to $p_{i+1}$ such that it avoids the obstacles in ${\mathcal {P}}'$ and has the same $L_1$ length as $\overline{p_ip_{i+1}}$.

If $\overline{p_ip_{i+1}}$ does not intersect the interior of any obstacle in ${\mathcal {P}}'$, then $\overline{p_ip_{i+1}}$ is the path we seek. Otherwise, because $\overline{p_ip_{i+1}}$ avoids $core({\mathcal {P}}')$, it can intersect only the interior of some ears. Consider any such ear $ear({\overline{ab}})$. Below, we prove that $\overline{p_ip_{i+1}}$ penetrates $ear({\overline{ab}})$.

First, we already know that $\overline{p_ip_{i+1}}$ intersects the interior of $ear({\overline{ab}})$. Second, it is obvious that neither $p_i$ nor $p_{i+1}$ is in the interior of $ear({\overline{ab}})$. Denote by $A'\in {\mathcal {P}}'$ the obstacle that contains $ear({\overline{ab}})$. Note that ${\overline{ab}}$ is an edge of $core(A')$. Since $\overline{p_ip_{i+1}}$ does not intersect the interior of $core(A')$, $\overline{p_ip_{i+1}}$ cannot cross ${\overline{ab}}$ at its interior. Therefore, $\overline{p_ip_{i+1}}$ penetrates $ear({\overline{ab}})$.

Without loss of generality, assume that $\overline{p_ip_{i+1}}$ is positive-sloped. By Observation 2, $ear({\overline{ab}})$ is also positive-sloped. Let e and f denote the two intersection points between $\overline{p_ip_{i+1}}$ and the obstacle path of $ear({\overline{ab}})$, and ${\widehat{ef}}$ denote the portion of the obstacle path of $ear({\overline{ab}})$ between e and f. By Observation 3, we can replace ${\overline{ef}}$ by ${\widehat{ef}}$ to obtain a new path from $p_i$ to $p_{i+1}$ of the same $L_1$ length as $\overline{p_ip_{i+1}}$. Further, as a portion of the obstacle path of $ear({\overline{ab}})$, ${\widehat{ef}}$ is a boundary portion of the obstacle $A'$ that contains $ear({\overline{ab}})$, and thus ${\widehat{ef}}$ does not intersect the interior of any obstacle in ${\mathcal {P}}'$.

By processing each ear whose interior is intersected by $\overline{p_ip_{i+1}}$ as above, we find a new path from $p_i$ to $p_{i+1}$ such that the path has the same $L_1$ length as $\overline{p_ip_{i+1}}$ and the path does not intersect the interior of any obstacle in ${\mathcal {P}}'$.

By processing each segment $\overline{p_ip_{i+1}}$ in $\pi _{core}(s,t)$ as above for $i=0,1,\ldots ,k$, we obtain another s-t path $\pi (s,t)$ such that the $L_1$ length of $\pi (s,t)$ is equal to that of $\pi _{core}(s,t)$ and $\pi (s,t)$ avoids all obstacles in ${\mathcal {P}}'$. On the other hand, since each core in $core({\mathcal {P}}')$ is contained in an obstacle in ${\mathcal {P}}'$, the length of a shortest s-t path avoiding $core({\mathcal {P}}')$ cannot be longer than that of a shortest s-t path avoiding ${\mathcal {P}}'$. Because the length of $\pi (s,t)$ is equal to that of $\pi _{core}(s,t)$ and $\pi _{core}(s,t)$ is a shortest s-t path avoiding $core({\mathcal {P}}')$, $\pi (s,t)$ is a shortest s-t path avoiding ${\mathcal {P}}'$.

Note that the above discussion also provides a way to construct $\pi (s,t)$, which can be done in O(n) time with the help of the triangulation ${T\!r\!i}({\mathcal {P}}')$. The lemma thus follows. $\square$

In light of Lemma 2, our algorithm for finding a single shortest s-t path works as follows: (1) apply Mitchell’s algorithm [29, 30] on $core({\mathcal {P}}')$ to find a vertex-preferred shortest s-t path avoiding the cores in $core({\mathcal {P}}')$; (2) by Lemma 2, find a shortest s-t path that avoids the obstacles in ${\mathcal {P}}'$. The first step takes $O(h\log h)$ time and O(h) space since the cores in $core({\mathcal {P}}')$ have a total of O(h) vertices. The second step takes O(n) time and O(n) space. Hence, we can find a single shortest s-t path in $O(n+h\log h)$ time and O(n) space.

3.2 Computing the Shortest Path Map

In this subsection, we compute the SPM for ${\mathcal {P}}'$. Mitchell’s algorithm [29, 30] can compute an O(n) size SPM in $O(n\log n)$ time and O(n) space. By applying Mitchell’s algorithm [29, 30] on the core set $core({\mathcal {P}}')$, we can compute an O(h) size SPM in $O(h\log h)$ time and O(h) space, denoted by $\textit{SPM}(core({\mathcal {P}}'))$. With a point location data structure [14, 26], for any query point t in the free space, the length of a shortest s-t path avoiding $core({\mathcal {P}}')$ can be reported in $O(\log h)$ time, which is also the length of a shortest s-t path avoiding ${\mathcal {P}}'$ by Lemma 2.

The above result is superior to Mitchell’s algorithm [29, 30] in three aspects, i.e., the preprocessing time, the SPM size, and the length query time. However, in order to compute an actual shortest path from s to any query point t in an output-sensitive fashion, we build an SPM for ${\mathcal {P}}'$, denoted by $\textit{SPM}({\mathcal {P}}')$, of O(n) size, as follows.

Lemma 3

Given the shortest path map $\textit{SPM}(core({\mathcal {P}}'))$ for the core set $core({\mathcal {P}}')$, we can compute a shortest path map $\textit{SPM}({\mathcal {P}}')$ for the obstacle set ${\mathcal {P}}'$ in O(n) time.

Proof

Consider a cell $C_{core}(r)$ with the root r in $\textit{SPM}(core({\mathcal {P}}'))$. Recall that r is always a vertex of a core in $core({\mathcal {P}}')$ and all points in $C_{core}(r)$ are visible to r with respect to $core({\mathcal {P}}')$ [29, 30]. In other words, for any point p in the cell $C_{core}(r)$, the line segment ${\overline{rp}}$ is contained in $C_{core}(r)$, and further, there exists a shortest s-p path avoiding $core({\mathcal {P}}')$ that contains ${\overline{rp}}$.

Denote by ${\mathcal {F}}({\mathcal {P}}')$ (resp., ${\mathcal {F}}(core({\mathcal {P}}'))$) the free space with respect to ${\mathcal {P}}'$ (resp., $core({\mathcal {P}}')$). Note that $C_{core}(r)$ is a simple polygon in ${\mathcal {F}}(core({\mathcal {P}}'))$. The cell $C_{core}(r)$ may intersect some ears. In other words, certain space in $C_{core}(r)$ may be occupied by ears. Let C(r) be the subregion of $C_{core}(r)$ by removing from $C_{core}(r)$ the space occupied by all ears except their obstacle paths. Thus C(r) lies in ${\mathcal {F}}({\mathcal {P}}')$. However, for each point $p\in C(r)$, p may not be visible to r with respect to ${\mathcal {P}}'$. Our task here is to further decompose C(r) into a set of SPM regions such that each such region has a root visible to all points in the region with respect to ${\mathcal {P}}'$; further, we need to make sure that each point q in an SPM region has a shortest path in ${\mathcal {F}}({\mathcal {P}}')$ from s that contains the line segment connecting q and the root of the region. For this, we first show that C(r) is a connected region.

To show that C(r) is connected, it suffices to show that for any point $p\in C(r)$, there is a path in C(r) that connects r and p. Consider an arbitrary point $p\in C(r)$. Since $p\in C_{core}(r)$, ${\overline{rp}}$ is in $C_{core}(r)$ and there is a shortest path in ${\mathcal {F}}(core({\mathcal {P}}'))$ from s to p that contains ${\overline{rp}}$. If ${\overline{rp}}$ does not intersect the interior of any ear, then we are done since ${\overline{rp}}$ is in C(r). If ${\overline{rp}}$ intersects the interior of some ears, then let $ear({\overline{ab}})$ be one of such ears. By the proof of Lemma 2, ${\overline{rp}}$ penetrates $ear({\overline{ab}})$. Let e and f be the two points on the obstacle path of $ear({\overline{ab}})$ that ${\overline{rp}}$ intersects, and ${\widehat{ef}}$ be the portion of the obstacle path between e and f. Note that if ${\overline{rp}}$ is horizontal or vertical, then it cannot penetrate $ear({\overline{ab}})$ due to the monotonicity of its obstacle path by Observation 1. Without loss of generality, we assume that ${\overline{rp}}$ is positive-sloped. By Observation 2, $ear({\overline{ab}})$ is also positive-sloped. Recall that e and f lie on ${\overline{rp}}$. Without loss of generality, assume that r is higher than p and f is higher than e. Then the segment ${\overline{ef}}$ from e to f is monotonically increasing in both the x- and y-coordinates. By Observation 1, the obstacle path portion ${\widehat{ef}}$ from e to f is also monotonically increasing in both the x- and y-coordinates. As in the proof of Lemma 2, for any point $q\in {\widehat{ef}}$, there is a shortest path in ${\mathcal {F}}(core({\mathcal {P}}'))$ from s to q that contains ${\overline{rf}}$ and the portion of ${\widehat{ef}}$ between f and q. Since ${\overline{ef}}$ is on ${\overline{rp}}$ contained in $C_{core}(r)$, by the properties of the $L_1$ shortest path map [29, 30], ${\widehat{ef}}$ is also contained in the cell $C_{core}(r)$. Thus, ${\widehat{ef}}$ is also contained in C(r). If we process each ear whose interior intersects ${\overline{rp}}$ as above, we find a path in C(r) that connects r and p; further, this path has the same $L_1$ length as ${\overline{rp}}$. Hence, C(r) is a connected region.

Next, we claim that for any point $p\in C(r)$, there is a shortest path in ${\mathcal {F}}({\mathcal {P}}')$ from s to p that contains r. Indeed, since $p\in C_{core}(r)$, there is a shortest path in ${\mathcal {F}}(core({\mathcal {P}}'))$ from s to p that contains ${\overline{rp}}$; let $\pi _{core}(s,r)$ be the portion of this path between s and r. On the one hand, we have shown above that there is a path from r to p in C(r) with the same $L_1$ length as ${\overline{rp}}$. On the other hand, by Lemma 2, there exists a path in ${\mathcal {F}}({\mathcal {P}}')$ from s to r with the same length as $\pi _{core}(s,r)$. Hence, a concatenation of these two paths results in a shortest path from s to p in ${\mathcal {F}}({\mathcal {P}}')$ that contains r. Our claim thus follows.

The above claim and its proof also imply that decomposing C(r) into a set of SPM regions is equivalent to computing an SPM in C(r) with the vertex r as the source point, which we denote by $\textit{SPM}(C(r))$. Since C(r) is a connected region and $C_{core}(r)$ is a simple polygon, we claim that C(r) is a (possibly degenerate) simple polygon. This is because for any ear E that intersects $C_{core}(r)$, the portion $E\cap C_{core}(r)$ lies on the boundary of the simple polygon $C_{core}(r)$; thus, removing E except its obstacle path from $C_{core}(r)$ [to form C(r)] changes only the boundary shape of $C_{core}(r)$ but does not change the nature of the simplicity [from $C_{core}(r)$ to C(r)]. Based on the fact that C(r) is a (possibly degenerate) simple polygon, $\textit{SPM}(C(r))$ can be easily computed in linear time in terms of the number of edges of C(r). For example, since the Euclidean shortest path between any two points in a simple polygon is also an $L_1$ shortest path between the two points [17], an SPM in a simple polygon with respect to the Euclidean distance is also one with respect to the $L_1$ distance. Therefore, we can use a corresponding shortest path algorithm for the Euclidean case (e.g., [16]) to compute each $\textit{SPM}(C(r))$ in our problem.

Note that our discussion above also implies that given $\textit{SPM}(core({\mathcal {P}}'))$, for each cell $C_{core}(r)$ with a root r, we can compute the corresponding $\textit{SPM}(C(r))$ separately. Clearly, the $\textit{SPM}(C(r))$ corresponding to all cells in $\textit{SPM}(core({\mathcal {P}}'))$ constitute a shortest path map $\textit{SPM}({\mathcal {P}}')$ for ${\mathcal {P}}'$.

Due to the planarity of the cell regions involved, the total number of edges of all C(r) is O(n). Given a triangulation ${T\!r\!i}({\mathcal {P}}')$, all regions C(r) can be obtained in O(n) time. Computing all $\textit{SPM}(C(r))$ also takes O(n) time in total. Thus, $\textit{SPM}({\mathcal {P}}')$ can be constructed in O(n) time. $\square$

With Lemma 3, we can obtain following result.

Theorem 1

Given a set of h pairwise disjoint convex polygonal obstacles with a total of n vertices in the plane, in $O(n+h\log h)$ time and O(n) space, we can construct a shortest path map of size O(n) with respect to a source point s, such that given any query point t, the length of an $L_1$ shortest s-t path can be reported in $O(\log h)$ time and an actual shortest path can be found in $O(\log n+k)$ time where k is the number of edges of the path.

4 Shortest Paths Among General Polygonal Obstacles

In the general case, the obstacles in ${\mathcal {P}}$ are not necessarily convex. In Sect. 4.1, we review the corridor structure [25], and introduce the ocean${\mathcal {M}}$. In Sect. 4.2, we present the algorithm for computing a single shortest path and the similar idea also computes an SPM for ${\mathcal {M}}$, i.e., $\textit{SPM}({\mathcal {M}})$. In Sect. 4.3, we outline our algorithm for computing an SPM in the entire free space ${\mathcal {F}}$.

4.1 The Corridor Structure

For ease of discussion, we consider s and t as two point obstacles and assume that all obstacles are contained in a rectangle ${\mathcal {R}}$ (see Fig. 4). Let ${\mathcal {F}}$ be the free space inside ${\mathcal {R}}$. We assume that ${\mathcal {F}}$ has already been triangulated, and let ${T\!r\!i}({\mathcal {F}})$ denote the triangulation.

Fig. 4

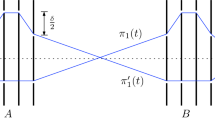
Illustrating a triangulation of the free space among two obstacles and the corridors (with red solid curves). There are two junction triangles indicated by the large dots inside them, connected by three solid (red) curves. Removing the two junction triangles results in three corridors (Color figure online)

Let $G({\mathcal {F}})$ denote the (planar) dual graph of ${T\!r\!i}({\mathcal {F}})$, i.e., each node of $G({\mathcal {F}})$ corresponds to a triangle in ${T\!r\!i}({\mathcal {F}})$ and each edge connects two nodes of $G({\mathcal {F}})$ corresponding to two triangles sharing a diagonal of ${T\!r\!i}({\mathcal {F}})$. The degree of each node in $G({\mathcal {F}})$ is at most three. As in [25], at least one node dual to a triangle incident to each of s and t is of degree three. Based on $G({\mathcal {F}})$, we compute a planar 3-regular graph, denoted by $G^3$ (the degree of each node in $G^3$ is three), possibly with loops and multi-edges, as follows. First, we remove every degree-one node from $G({\mathcal {F}})$ along with its incident edge; repeat this process until no degree-one node exists. Second, remove every degree-two node from $G({\mathcal {F}})$ and replace its two incident edges by a single edge; repeat this process until no degree-two node exists. The resulting graph is $G^3$ (e.g., see Fig. 4), which has O(h) faces, O(h) nodes, and O(h) edges [25]. Each node of $G^3$ corresponds to a triangle in ${T\!r\!i}({\mathcal {F}})$, which is called a junction triangle. The removal of all junction triangles from ${T\!r\!i}({\mathcal {F}})$ results in O(h) corridors, each of which corresponds to one edge of $G^3$.

The boundary of a corridor C consists of four parts (see Fig. 5): (1) a boundary portion of an obstacle $P_i\in {\mathcal {P}}$, from a point a to a point b; (2) a diagonal of a junction triangle from b to a boundary point e on an obstacle $P_j\in {\mathcal {P}}$ ($P_i=P_j$ is possible); (3) a boundary portion of the obstacle $P_j$ from e to a point f; (4) a diagonal of a junction triangle from f to a. The two diagonals ${\overline{be}}$ and ${\overline{af}}$ are called the doors of C, and the other two boundary portions are the two sides of C. Note that C is a (possibly weak) simple polygon. Let $\pi (a,b)$ [resp., $\pi (e,f)$] denote the shortest path from a to b (resp., e to f) inside C. The region $H_C$ bounded by $\pi (a,b), \pi (e,f)$, and the two diagonals ${\overline{be}}$ and ${\overline{fa}}$ is called an hourglass, which is open if $\pi (a,b)\cap \pi (e,f)=\emptyset$ and closed otherwise (see Fig. 5). If $H_C$ is open, then both $\pi (a,b)$ and $\pi (e,f)$ are convex chains and are called the sides of $H_C$; otherwise, $H_C$ consists of two “funnels” and a path $\pi _C=\pi (a,b)\cap \pi (e,f)$ joining the two apices of the two funnels, called the corridor path of C. The two funnel apices connected by the corridor path are called the corridor path terminals. Each funnel side is also convex.

We compute the hourglass for each corridor. With the triangulation ${T\!r\!i}({\mathcal {F}})$, computing the hourglasses for all corridors takes O(n) time.

Let ${\mathcal {Q}}$ be the union of all junction triangles and hourglasses. Then ${\mathcal {Q}}$ consists of O(h) junction triangles, open hourglasses, funnels, and corridor paths. As shown in [21], there exists a shortest s-t path $\pi (s,t)$ avoiding the obstacles in ${\mathcal {P}}$ which is contained in ${\mathcal {Q}}$. We have the following lemma.

Fig. 5

Illustrating an open hourglass (left) and a closed hourglass (right) with a corridor path linking the apices x and y of the two funnels. The dashed segments are diagonals. The paths $\pi (a,b)$ and $\pi (e,f)$ are shown with thick solid curves

Lemma 4

Suppose $\pi (s,t)$ intersects both doors of a corridor C and the hourglass $H_C$ of C is closed, then there exists another shortest s-t path that contains corridor path of C.

Proof

Suppose $\pi (s,t)$ intersects the two doors of C, say, at two points p and q respectively. Then since C is a simple polygon, a Euclidean shortest path between p and q inside C, denoted by $\pi _E(p,q)$, is also an $L_1$ shortest path in C [17], and $\pi _E(p,q)$ must contain the corridor path of C. If we replace the portion of $\pi (s,t)$ between p and q by $\pi _E(p,q)$, then we obtain a new $L_1$ shortest s-t path that contains the corridor path. $\square$

In the following, we assume that $\pi (s,t)$ has the property that if it intersects both doors of C and $H_C$ is closed, then it contains the corridor path of C.

Let ${\mathcal {M}}$ be ${\mathcal {Q}}$ minus the corridor paths. We call ${\mathcal {M}}$ the ocean. Clearly, ${\mathcal {M}}\subseteq {\mathcal {F}}$. The boundary of ${\mathcal {M}}$ consists of O(h) reflex vertices and O(h) convex chains, implying that the complementary region ${\mathcal {R}}\backslash {\mathcal {M}}$ consists of a set of polygons of O(h) reflex vertices and O(h) convex chains. As shown in [25], the region ${\mathcal {R}}\backslash {\mathcal {M}}$ can be partitioned into a set ${\mathcal {P}}'$ of O(h) convex polygons with total of O(n) vertices (e.g., by extending an angle-bisecting segment inward from each reflex vertex). The ocean ${\mathcal {M}}$ is exactly the free space with respect to the convex polygons in ${\mathcal {P}}'$ (i.e., if we consider the polygons of ${\mathcal {P}}'$ as obstacles, then ${\mathcal {M}}$ is the free space). In addition, for each corridor path, no portion of it lies in ${\mathcal {M}}$. Further, the shortest path $\pi (s,t)$ is a shortest s-t path avoiding all convex polygons in ${\mathcal {P}}'$ and possibly containing some corridor paths. The set ${\mathcal {P}}'$ can be obtained in $O(n+h\log h)$ time. Therefore, as in [25], other than the corridor paths, we reduce our original $L_1$-SP problem to the convex case. Note that our algorithms given later can be applied to ${\mathcal {M}}$ directly without partitioning ${\mathcal {R}}\backslash {\mathcal {M}}$ into the convex polygons in ${\mathcal {P}}'$, but for ease of exposition, we will discuss our algorithms on ${\mathcal {P}}'$.

The algorithm in Sect. 4.2 will focus on the space ${\mathcal {M}}$. Note that ${\mathcal {M}}$ is only a subspace of ${\mathcal {F}}$, and we will examine the rest of the space, i.e., ${\mathcal {F}}\backslash {\mathcal {M}}$, later in Sect. 4.3.

4.2 Finding a Single Shortest Path and Computing an SPM for ${\mathcal {M}}$

To find a shortest s-t path in ${\mathcal {F}}$, if there is no corridor path, then we can simply apply our algorithm for the convex case in Sect. 3 to the convex polygon set ${\mathcal {P}}'$. Otherwise, since the corridor paths can give possible “shortcuts” for the sought s-t path, we must take these possible “shortcuts” into consideration while running the continuous Dijkstra paradigm [29, 30], as follows.

First, we compute the core set $core({\mathcal {P}}')$ of ${\mathcal {P}}'$. However, the way we construct $core({\mathcal {P}}')$ here is slightly different from Sect. 3. For each convex polygon $A'\in {\mathcal {P}}'$, in addition to its leftmost, topmost, rightmost, and bottommost vertices, if a vertex v of $A'$ is a corridor path terminal, then v is also kept as a vertex of the core $core(A')$. In other words, $core(A')$ is a simple (convex) polygon whose vertex set consists of the leftmost, topmost, rightmost, and bottommost vertices of $A'$ and all corridor path terminals on $A'$. Since there are O(h) terminal vertices, the cores in $core({\mathcal {P}}')$ still have a total of O(h) vertices and edges. Further, the core set thus defined still has the properties discussed in Sect. 3 for computing shortest $L_1$ paths, e.g., Observation 1, 2, 3, and Lemma 2. Hence, by using our scheme in Sect. 3, we can first find a shortest s-t path avoiding the cores in $core({\mathcal {P}}')$ in $O(h\log h)$ time by applying Mitchell’s algorithm [29, 30], and then obtain a shortest s-t path avoiding ${\mathcal {P}}'$ in O(n) time by Lemma 2. But, the path thus computed may not be a true shortest path in ${\mathcal {F}}$ since the corridor paths are not utilized. To find a true shortest path, we need to modify the continuous Dijkstra paradigm when applying it to $core({\mathcal {P}}')$, as follows.

In Mitchell’s algorithm [29, 30], when an obstacle vertex v is hit by the wavefront for the first time, it will be “permanently labeled” with a value d(v), which is the length of a shortest path from s to v in the free space. The wavefront consists of many “wavelets” (each wavelet is a line segment of slope 1 or $-\,1$). The algorithm maintains a priority queue (called “event queue”), and each element in the queue is a wavelet associated with an “event point” and an “event distance”, which means that the wavelet will hit the event point at the event distance. The algorithm repeatedly takes (and removes) an element from the event queue with the smallest event distance, and processes the event. After an event is processed, some new events may be added to the event queue. The algorithm stops when the point t is hit by the wavefront for the first time.

To handle the corridor paths in our problem, consider a corridor path $\pi _C$ with x and y as its terminals and let l be the length of $\pi _C$. Recall that x and y are vertices of a core in $core({\mathcal {P}}')$. Consider the moment when the vertex x is permanently labeled with the distance d(x). Suppose the wavefront that first hits x is from the funnel whose apex is x. Then according to our discussions above, the only way that the wavelet of the wavefront at x can affect a shortest s-t path is through the corridor path $\pi _C$. If y is not yet permanently labeled, then y has not been hit by the wavefront. We initiate a “pseudo-wavelet” that originates from x with the event point y and event distance $d(x)+l$, meaning that y will be hit by this pseudo-wavelet at the distance $d(x)+l$. We add the pseudo-wavelet to the event queue. If y has been permanently labeled by the time when x is permanently labelled, then the wavefront has already hit y and is currently moving along the corridor path $\pi _C$ from y to x. Thus, the wavelet through x will meet the wavelet through y somewhere on the path $\pi _C$, and these two wavelets will “die” there and never affect the free space outside the corridor. Thus, in this case we do not need to do anything on y. In addition, at the moment when the vertex x is permanently labeled, if the wavefront that first hits x is from the corridor path $\pi _C$ (i.e., through y), then the wavelet at x will keep going to the funnel of x through x; therefore, we process this event on x as usual (i.e., as in [29, 30]), by initiating new wavelets that originate from x.

For a corridor path $\pi _C$ with two terminals x and y, when x is permanently labeled, if the wavefront that first hits x is not from the corridor path $\pi _C$, then we call x a wavefront incoming terminal; otherwise, x is a wavefront outgoing terminal. According to our discussion above, at least one of x and y must be a wavefront incoming terminal. In fact, both x and y can be wavefront incoming terminals, in which case the wavefronts passing through x and y “die” inside the corridor.

Intuitively, the above treatment of corridor path terminals makes corridor paths act as possible “shortcuts” when we propagate the wavefront. The rest of the algorithm proceeds in the same way as in [29, 30] (e.g., processing the segment dragging queries). The algorithm stops when the wavefront first hits the point t, at which moment a shortest s-t path in ${\mathcal {F}}$ has been found.

Since there are O(h) corridor paths, with the above modifications to Mitchell’s algorithm as applied to $core({\mathcal {P}}')$, its running time is still $O(h\log h)$. Indeed, comparing with the original continuous Dijkstra scheme [29, 30] (as applied to $core({\mathcal {P}}')$), there are O(h) additional events on the corridor path terminals, i.e., events corresponding to those pseudo-wavelets. To handle these additional events, we may, for example, as preprocessing, for each corridor path, associate with each its corridor path terminal x the other terminal y as well as the corridor path length l. Thus, during the algorithm, when we process the event point at x, we can find y and l immediately. In this way, each additional event is handled in O(1) time in addition to adding a new event for it to the event queue. Hence, processing all events still takes $O(h\log h)$ time. Note that the shortest s-t path thus computed may penetrate some ears of ${\mathcal {P}}'$. As in Lemma 2, we can obtain a shortest s-t path in the free space ${\mathcal {F}}$ in additional O(n) time. Since applying Mitchell’s algorithm on $core({\mathcal {P}}')$ takes O(h) space, the space used in our entire algorithm is O(n). As a summary, we have the following result.

Theorem 2

Given a set of h pairwise disjoint polygonal obstacles with a total of n vertices in the plane, suppose that the free space has been triangulated; we can find an $L_1$ shortest path between two points in the free space in $O(n+h\log h)$ time and O(n) space.

As Mitchell’s algorithm [29, 30], the above algorithm also computes a shortest path map on the free space of the convex polygons in ${\mathcal {P}}'$, i.e., $\textit{SPM}({\mathcal {M}})$. We should point out that because of the O(h) corridor paths, $\textit{SPM}({\mathcal {M}})$ is different from a “normal” SPM in the following aspect. Consider a corridor path $\pi _C$ with two terminals x and y. Suppose x is a wavefront incoming terminal and y is a wavefront outgoing terminal. Then this means that the algorithm determines a shortest path from s to y which goes through x. Corresponding to the corridor path $\pi _C$, we may put a “pseudo-cell” in $\textit{SPM}({\mathcal {M}})$ with x as the root such that y is the only point in this “pseudo-cell”, and we also associate with the pseudo-cell the corridor path $\pi _C$, which indicates that there is a shortest s-y path that consists of a shortest s-x path and the corridor path $\pi _C$. If x and y are both wavefront incoming terminals, then we need not do anything for this corridor path. Clearly, since there are O(h) corridor paths, the above procedure of building pseudo-cells affects neither the space bound nor the time bound for constructing $\textit{SPM}({\mathcal {M}})$. Therefore, the $\textit{SPM}({\mathcal {M}})$ of size O(n) can be computed in $O(n+h\log h)$ time and O(n) space.

4.3 Computing a Shortest Path Map

Based on $\textit{SPM}({\mathcal {M}})$, in Sect. 4.3, together with Sects. 5 and 6, we will compute in additional O(n) time an SPM on the entire free space ${\mathcal {F}}$ for the source point s, denoted by $\textit{SPM}({\mathcal {F}})$. Our techniques for constructing $\textit{SPM}({\mathcal {F}})$ are independent of those in the earlier sections of this paper.

In the rest of this section, we discuss bays and canals, and outline the algorithm, while the details are given in Sects. 5 and 6.

4.3.1 Bays and Canals

To compute $\textit{SPM}({\mathcal {F}})$, since ${\mathcal {M}}\subseteq {\mathcal {F}}$ and we already have $\textit{SPM}({\mathcal {M}})$, we only need to compute the portion of $\textit{SPM}({\mathcal {F}})$ in the space ${\mathcal {F}}\backslash {\mathcal {M}}$. We first examine the space ${\mathcal {F}}\backslash {\mathcal {M}}$, which we partition into two type of regions, bays and canals, defined as follows. These concepts were also used before for computing visibility polygons [9].

Fig. 6

Illustrating a bay $bay({\overline{cd}})$ in an open hourglass (left) and a canal $canal(x,y)$ in a closed hourglass (right) with a corridor (dotted) path linking the apices x and y of its two funnels. In the right figure, the ${\overline{xd}}$ and ${\overline{yz}}$ are the two gates of $canal(x,y)$ (note that there are three bays in the corridor, one with gate ${\overline{xb}}$ and the other two with gates incident to y and a, respectively)

Consider an hourglass $H_C$ of a corridor C. We first discuss the case in which $H_C$ is open (see Fig. 6). $H_C$ has two sides. Let $S_1(H_C)$ be an arbitrary side of $H_C$. The obstacle vertices on $S_1(H_C)$ all lie on the same side of the corridor C. Let c and d be any two adjacent vertices on $S_1(H_C)$ such that the line segment ${\overline{cd}}$ is not an obstacle edge (see the left figure in Fig. 6). The region enclosed by ${\overline{cd}}$ and a boundary portion of C between c and d is called a bay, denoted by $bay({\overline{cd}})$, which is a simple polygon. We call ${\overline{cd}}$ the gate of the bay.

If the hourglass $H_C$ is closed, then let x and y be the two apices of its two funnels. Consider two adjacent vertices c and d on a side of a funnel such that the line segment ${\overline{cd}}$ is not an obstacle edge. If neither c nor d is a funnel apex, then c and d must lie on the same side of C and the segment ${\overline{cd}}$ also defines a bay as above. However, if either c or d is a funnel apex, say, $c=x$, then x and d may lie on different sides of C. If they lie on the same side of C, then they also define a bay; otherwise, we call ${\overline{xd}}$ a canal gate at x (see Fig. 6). Similarly, there is also a canal gate at the funnel apex y, say ${\overline{yz}}$. The region of C enclosed by the two canal gates ${\overline{xd}}$ and ${\overline{yz}}$ that contains the corridor path of $H_C$ is called a canal, denoted by canal(x, y), which is a simple polygon.

To build $\textit{SPM}({\mathcal {F}})$, we will “expand” $\textit{SPM}({\mathcal {M}})$ to all bays/canals through their gates. Computing an SPM for a bay is a key for solving the problem, and the canal case uses the bay algorithm as a main procedure.

4.3.2 Expanding $\textit{SPM}({\mathcal {M}})$ Into Bays and Canals

Consider a bay $bay({\overline{cd}})$. Let $n'$ be the number of vertices of $bay({\overline{cd}})$. If its gate ${\overline{cd}}$ is in a single cell C(r) of $\textit{SPM}({\mathcal {M}})$ with r as the root, then each point in $bay({\overline{cd}})$ has a shortest path to s via r. Thus, to construct an SPM for $bay({\overline{cd}})$, it suffices to compute an SPM on $bay({\overline{cd}})$ with respect to r, which can be done in $O(n')$ time since $bay({\overline{cd}})$ is a simple polygon.¹

If ${\overline{cd}}$ is not in a single cell of $\textit{SPM}({\mathcal {M}})$, then multiple vertices of $\textit{SPM}({\mathcal {M}})$, i.e., the intersections of the boundaries of the cells of $\textit{SPM}({\mathcal {M}})$ with ${\overline{cd}}$, may lie in the interior of ${\overline{cd}}$. This is actually the challenging subproblem illustrated by Fig. 1. We refer to the vertices of $\textit{SPM}({\mathcal {M}})$ on ${\overline{cd}}$ (including its endpoints c and d) as the $\textit{SPM}({\mathcal {M}})$vertices and let $m'$ be their total number. A straightforward approach for computing an SPM for $bay({\overline{cd}})$ is to use the continuous Dijkstra paradigm [29, 30] to let the wavefront continue to move into $bay({\overline{cd}})$. But, this approach takes $O((n'+m')\log (m'+n'))$ time. Later in Sect. 5, we derive an $O(n'+m')$ time algorithm, as stated in the following lemma.

Lemma 5

For a bay of $n'$ vertices with $m'$$\textit{SPM}({\mathcal {M}})$ vertices on its gate, a shortest path map of size $O(n'+m')$ for the bay can be computed in $O(n'+m')$ time.

Since a canal has two gates which are also edges of ${\mathcal {M}}$, multiple $\textit{SPM}({\mathcal {M}})$ vertices may lie on both its gates. Later in Sect. 6, we prove the following result.

Lemma 6

For a canal of $n'$ vertices with a total of $m'$$\textit{SPM}({\mathcal {M}})$ vertices on its two gates, a shortest path map of size $O(n'+m')$ for the canal can be computed in $O(n'+m')$ time.

By Lemmas 5 and 6, the time for computing the shortest path maps for all bays and canals is linear in terms of the total sum of the numbers of obstacle vertices of all bays and canals, which is O(n), and the total number of the $\textit{SPM}({\mathcal {M}})$ vertices on the gates of all bays and canals, which is also O(n) since the size of $\textit{SPM}({\mathcal {M}})$ is O(n). We hence conclude that given $\textit{SPM}({\mathcal {M}})$, $\textit{SPM}({\mathcal {F}})$ can be computed in additional O(n) time. Thus, we obtain the following result.

Theorem 3

Given a set of h pairwise disjoint polygonal obstacles with a total of n vertices and a source point s in the plane, suppose that a triangulation of the free space is given; we can build a shortest path map of size O(n) with respect to s in $O(n+h\log h)$ time and O(n) space, such that for any query point t, the length of an $L_1$ shortest s-t path can be reported in $O(\log n)$ time and an actual shortest path can be found in additional time linear in the number of edges of the path.

5 Computing a Shortest Path Map for a Bay

Consider a bay $bay({\overline{cd}})$ whose gate is ${\overline{cd}}$ (see Fig. 6). Let $\textit{SPM}(bay({\overline{cd}}))$ be the SPM for $bay({\overline{cd}})$ that we seek to compute. In this section, we give an algorithm for computing $\textit{SPM}(bay({\overline{cd}}))$ in $O(n'+m')$ time, and thus prove Lemma 5.

Let R be the set of roots of the cells of $\textit{SPM}({\mathcal {M}})$ that intersect with ${\overline{cd}}$. To obtain $\textit{SPM}(bay({\overline{cd}}))$, we first compute, for each $r\in R$, the Voronoi region${V\!D}(r)$ inside $bay({\overline{cd}})$ such that for any point $t\in {V\!D}(r)$, there is a shortest s-t path via r; we then compute an SPM on ${V\!D}(r)$ with respect to r. Since every ${V\!D}(r)$ is a simple polygonal region in $bay({\overline{cd}})$, the shortest path map $\textit{SPM}({V\!D}(r),r)$ can be computed in linear time in terms of the number of vertices of ${V\!D}(r)$ (e.g., by using an algorithm in [16]). Thus, the key is to decompose $bay({\overline{cd}})$ into Voronoi regions for the roots of R. Denote by ${\mathcal{VD}}(bay({\overline{cd}}))$ this decomposition of $bay({\overline{cd}})$. We aim to compute ${\mathcal{VD}}(bay({\overline{cd}}))$ in $O(n'+m')$ time.

Without loss of generality, we assume that ${\overline{cd}}$ is positive-sloped, $bay({\overline{cd}})$ is on the right of ${\overline{cd}}$, and the vertex c is higher than d [e.g., $bay({\overline{cd}})=B$ in Fig. 1]. Other cases can be handled similarly. Let $R=\{r_1,r_2,\ldots ,r_k\}$ be the set of roots of the cells of $\textit{SPM}({\mathcal {M}})$ that intersect with ${\overline{cd}}$ in the order from c to d along ${\overline{cd}}$. Note that R may be a multi-set, i.e., two roots $r_i$ and $r_j$ with $i\ne j$ may refer to the same physical point; but this is not important to our algorithm (e.g., we can view each $r_i$ as a distinct copy of the same root). Let $c=v_0, v_1, \ldots , v_k=d$ be the $\textit{SPM}({\mathcal {M}})$ vertices on ${\overline{cd}}$ ordered from c to d (thus $m'=k+1$). Hence, for each $1\le i\le k$, the segment $\overline{v_{i-1}v_{i}}$ is on the boundary of the cell $C(r_i)$ of $\textit{SPM}({\mathcal {M}})$. Note that each cell $C(r_i)$ is a star-shaped polygon, and for each $1\le i\le k-1$, $v_i$ lies on the common boundary of $C(r_i)$ and $C(r_{i+1})$. To compute ${\mathcal{VD}}(bay({\overline{cd}}))$, we need to compute the Voronoi region ${V\!D}(r_i)$ for each $r_i\in R$.

In the following, we begin with an algorithm overview in Sect. 5.1.

5.1 Outline

To compute ${\mathcal{VD}}(bay({\overline{cd}}))$, it turns out that we need to deal with the interactions between some rays, each of which belongs to the bisector of two roots in R. Every such ray is either horizontal or vertical (there are also other types of rays, but they are easy to handle). We process these rays in a certain order (e.g., as to be proved, their origins somehow form a staircase structure). For each ray, if it is vertical, then it is easy (it eventually leads to a ray shooting operation), and its processing does not introduce any new ray. A stack is used to store certain vertical rays that need to be further processed. But, if it is horizontal, then it may intersect the vertical rays in the stack (following the top-bottom order) and the situation is more complicated since its processing may introduce many new horizontal rays and (at most) one vertical ray, also in a certain order along a staircase structure (in addition to causing a ray shooting operation).

The algorithm needs to perform ray shooting operations for some vertical and horizontal rays. Although there are known data structures for ray shooting queries [4, 5, 16, 18], they are not efficient enough for a linear time implementation of the entire algorithm. Based on observations, our approach makes use of the horizontal and vertical visibility maps of $bay({\overline{cd}})$ [3]. More specifically, we prove that all vertical ray shootings are in a “nice” sorted order (called target-sorted). With this property, all vertical ray shootings are performed in totally linear time by using the vertical visibility map of $bay({\overline{cd}})$. The horizontal visibility map is used to guide the overall process of the algorithm. During the algorithm, we march into the bay and the horizontal visibility map allows us to keep track of our current position (i.e., in a trapezoid of the map that contains our current position). The horizontal visibility map also allows each horizontal ray shooting to be done in O(1) time. In addition, in the preprocessing of the algorithm, we also need to perform some other ray shootings (for rays of slope $-\,1$); our linear time solution for this also hinges on the target-sorted property of such rays.

Our algorithm is conceptually simple. As mentioned above, the only data structures we need are linked lists, a stack, and the horizontal and vertical visibility maps. Its correctness relies on the fact that the algorithm implicitly maintains a set of invariant properties in each iteration. To prove the correctness of the algorithm, we need to show that these invariant properties hold iteratively. For this purpose, before presenting the algorithm in Sect. 5.3, we first show a set of observations in Sect. 5.2, which capture some essential properties of this $L_1$ problem.

5.2 Bisector Properties of the Roots of R

In this subsection, we give a number of observations, most of which help capture the behaviors of the bisectors for the roots of R in computing ${\mathcal{VD}}(bay({\overline{cd}}))$.

For a point p, denote by x(p) its x-coordinate and by y(p) its y-coordinate. For two objects $O_1$ and $O_2$ in the plane, if $x(p_1)\le x(p_2)$ for any two points $p_1\in O_1$ and $p_2\in O_2$, then we say $O_1$ is to the left or west of $O_2$; if $y(p_1)\le y(p_2)$ for any two points $p_1\in O_1$ and $p_2\in O_2$, then we say $O_1$ is to the south of $O_2$ or $O_1$ is below$O_2$. Similarly, we can define right, east, north, and above. If $O_1$ is to the left of $O_2$ and is also below $O_2$, then we say $O_1$ is to the southwest of $O_2$. Similarly, we can define northeast, southeast, and northwest.

Fig. 7

Illustrating some cases of the bisector $B(p_1,p_2)$ of two weighted points $p_1$ and $p_2$. In (3), an entire quadrant (the shaded area) can be used as $B(p_1,p_2)$, but we choose $B(p_1,p_2)$ to be the vertical (solid thick) half-line

Each root $r_i\in R$ can be viewed as an additively weighted point whose weight is the $L_1$ length of a shortest path from s to $r_i$. Thus, we need to consider the possible shapes of the bisector of two weighted points. For two weighted points $p_1$ and $p_2$ with weights $w_1$ and $w_2$, respectively, their bisector $B(p_1,p_2)$ consists of all points q such that the $L_1$ length of the line segment $\overline{p_1q}$ plus $w_1$ is equal to the $L_1$ length of $\overline{p_2q}$ plus $w_2$. Figure 7 shows some cases. Note that the bisector can be an entire quadrant of the plane [e.g., see Fig. 7(3)]; in this case, as in [29, 30], we choose a vertical half-line as the bisector. For any pair of consecutive roots $r_{i-1}$ and $r_i$ in R for $2\le i\le k$, since the $\textit{SPM}({\mathcal {M}})$ vertex $v_{i-1}\in {\overline{cd}}$ is on the common boundary of $C(r_{i-1})$ and $C(r_i)$, $v_{i-1}$ lies on the bisector $B(r_{i-1},r_i)$ of $r_{i-1}$ and $r_i$. For two points $p_1$ and $p_2$, denote by $Rec(p_1,p_2)$ the rectangle with $p_1$ and $p_2$ as its two diagonal vertices. The next observation is self-evident.

Observation 4

The bisector $B(p_1,p_2)$ consists of three portions: two half-lines and a line segment connecting them; the line segment has a slope 1 or $-\,1$ and is the intersection of $B(p_1,p_2)$ and the rectangle $Rec(p_1,p_2)$. Each of the two half-lines is perpendicular to an edge of $Rec(p_1,p_2)$ that touches the half-line. Depending on the relative positions and weights of $p_1$ and $p_2$, some portions of $B(p_1,p_2)$ may degenerate and become empty. $B(p_1,p_2)$ is monotone to both the x- and y-axes. For any line l containing one of the three portions of $B(p_1,p_2)$, $p_1$ and $p_2$ cannot lie strictly on the same side of l.

We call the open line segment of $B(p_1,p_2)$ strictly inside $Rec(p_1,p_2)$ its middle segment, denoted by $B_M(p_1,p_2)$, and the two half-lines of $B(p_1,p_2)$ its two rays, each originating at a point on an edge of $Rec(p_1,p_2)$. Thus, the origins of the two rays of $B(p_1,p_2)$ are the two endpoints of $B_M(p_1,p_2)$.

Since each cell in an SPM is a star-shaped simple polygon, the observation below is obvious.

Observation 5

Let C(r) and $C(r')$ be two different cells in $\textit{SPM}({\mathcal {M}})$ with roots r and $r'$. For any two points $p\in C(r)$ and $p'\in C(r')$, the line segments ${\overline{pr}}$ and $\overline{p'r'}$ cannot cross each other.

Recall that we assumed that no two obstacle vertices lie on the same vertical or horizontal line. Since each root in R is an obstacle vertex, no two roots lie on the same vertical or horizontal line. Also recall that the gate ${\overline{cd}}$ of $bay({\overline{cd}})$ is positive-sloped. The next lemma shows the possible relative positions of two consecutive roots in R.

Lemma 7

For any two consecutive roots $r_{i-1}$ and $r_i$ in R with $2\le i\le k$, $r_i$ cannot be to the northeast of $r_{i-1}$.

Proof

Since $v_{i-1}\in {\overline{cd}}$ lies on the common boundary of the two cells $C(r_{i-1})$ and $C(r_i)$, $v_{i-1}$ is on the bisector $B(r_{i-1},r_i)$.

Fig. 8

An example of $r_i$ to the northeast of $r_{i-1}$. The point $p\ne v_{i-1}$ is on $\overline{v_{i-1}v_i}$ and is infinitely close to $v_{i-1}$. The line segment $\overline{r_ip}$ must cross $\overline{r_{i-1}v_{i-1}}$

Assume to the contrary that $r_i$ is to the northeast of $r_{i-1}$. Note that $v_{i-1}$ may lie on either a half-line or the middle segment of $B(r_{i-1},r_i)$. In either case, since $r_i$ is to the northeast of $r_{i-1}$ and ${\overline{cd}}$ is positive-sloped, according to Observation 4, $v_{i-1}$ must be lower than $r_i$, and $v_{i-1}$ must be to the right of $r_{i-1}$ (see Fig. 8).

Since the segment $\overline{v_{i-1}v_i}$ is not a single point and $v_i$ is to the left of $v_{i-1}$, we can find a point $p\in \overline{v_{i-1}v_i}$ such that $p\ne v_{i-1}$ (see Fig. 8). Since $p\in \overline{v_{i-1}v_i}$ and $\overline{v_{i-1}v_i}\subseteq C(r_i)$, we have $p\in C(r_i)$. Note that $v_{i-1}\in C(r_{i-1})\cap C(r_i)$. Below we show that the two line segments $\overline{r_ip}$ and $\overline{r_{i-1}v_{i-1}}$ must cross each other, which contradicts with Observation 5.

Since both $r_i$ and $r_{i-1}$ are obstacle vertices, by our assumption, $r_i$ and $r_{i-1}$ do not lie on a horizontal or vertical line. Hence $r_i$ is strictly to the northeast of $r_{i-1}$. Note that no root in R lies on ${\overline{cd}}$. Since $v_{i-1}$ is lower than $r_i$ and is to the right of $r_{i-1}$, the three points $v_{i-1}$, $r_i$, and $r_{i-1}$ do not lie on the same line (see Fig. 8). In other words, the triangle $\triangle r_iv_{i-1}r_{i-1}$ is not empty. Further, suppose $\rho (r_i,v_{i-1})$ [resp., $\rho (r_i,r_{i-1})$] is the ray originating from $r_i$ and going through $v_{i-1}$ (resp., $r_{i-1}$); then $\rho (r_i,r_{i-1})$ can be obtained by rotating $\rho (r_i,v_{i-1})$ clockwise by an angle $\angle v_{i-1}r_ir_{i-1}>0^{\circ }$. By the definition of the point p, during this rotation, p will be encountered by the rotating ray $\rho (r_i,v_{i-1})$ at an angle $\angle v_{i-1}r_ip$ with $0^{\circ }<\angle v_{i-1}r_ip <\angle v_{i-1}r_ir_{i-1}$, which implies that $\overline{r_ip}$ crosses $\overline{r_{i-1}v_{i-1}}$. The lemma thus follows. $\square$

By Lemma 7, there are three cases on the possible relative positions of $r_{i-1}$ with respect to $r_i$, i.e., $r_{i-1}$ can be to the northwest, southeast, or northeast of $r_{i}$ (e.g., see Fig. 9).

Lemma 8

Consider any two consecutive roots $r_{i-1}$ and $r_i$ in R with $2\le i\le k$.

• 1. If $r_i$ is to the southeast of $r_{i-1}$, then $v_{i-1}$ is on a ray of $B(r_{i-1},r_i)$ that is horizontally going east (i.e., a rightward horizontal ray) and $v_{i-1}$ is to the right of $Rec(r_{i-1},r_i)\ [$see Fig. 9(1)].

• 2. If $r_i$ is to the northwest of $r_{i-1}$, then $v_{i-1}$ is on a ray of $B(r_{i-1},r_i)$ that is vertically going south (i.e., a downward vertical ray) and $v_{i-1}$ is below $Rec(r_{i-1},r_i)\ [$see Fig. 9(2)].

• 3. If $r_i$ is to the southwest of $r_{i-1}$, then $v_{i-1}$ is either on the middle segment $B_M(r_{i-1},r_i)$, or on a ray of $B(r_{i-1},r_i)$ that is either horizontally going east or vertically going south [see Fig. 9(3)]. Further, if $v_{i-1}$ is on the ray horizontally going east, then $v_{i-1}$ is to the right of $Rec(r_{i-1},r_i)$; if $v_{i-1}$ is on the ray vertically going south, then $v_{i-1}$ is below $Rec(r_{i-1},r_i)$.

Proof

We first prove Part 1 of the lemma. If $r_i$ is to the southeast of $r_{i-1}$ [see Fig. 9(1)], then the rectangle $Rec(r_{i-1},r_i)$ cannot intersect ${\overline{cd}}$. Thus, $v_{i-1}$ cannot be on $B_M(r_{i-1},r_i)$, and $v_{i-1}$ must be on a ray of $B(r_{i-1},r_i)$, denoted by $\rho$. By Observation 4, the origin of $\rho$ is on an edge $\alpha$ of $Rec(r_{i-1},r_i)$ and is perpendicular to the edge $\alpha$. Since $v_{i-1}\in \rho$ and $r_{i-1}$ is to the northwest of $r_i$, $\alpha$ must be one of the two edges incident to $r_i$, i.e., the bottom edge or the right edge of $Rec(r_{i-1},r_i)$. In addition, if $\alpha$ is the bottom edge of $Rec(r_{i-1},r_i)$, then $\rho$ must be vertically going south; further, since $r_i$ is to the southeast of $r_{i-1}$, by a similar argument as that for the proof of Lemma 7, we can obtain a contradiction. Thus, $\alpha$ is the right edge of $Rec(r_{i-1},r_i)$ and $\rho$ must be horizontally going east. In addition, it is easy to see that $v_{i-1}$ must be to the right of $Rec(r_{i-1},r_i)$. Part 1 of the lemma thus follows.

Fig. 9

Illustrating the three possible relative positions of $r_{i-1}$ and $r_i$

Part 2 can be proved analogously as Part 1, and we omit it.

For Part 3, if $Rec(r_{i-1},r_i)$ intersects ${\overline{cd}}$, then it is possible that $B_M(r_{i-1},r_i)$ intersects ${\overline{cd}}$ (at $v_{i-1}$). If $B_M(r_{i-1},r_i)$ does not intersect ${\overline{cd}}$, then $v_{i-1}$ lies on a ray of $B(r_{i-1},r_i)$, denoted by $\rho$. Again, the origin of $\rho$ is on either the right edge of $Rec(r_{i-1},r_i)$ or the bottom edge of $Rec(r_{i-1},r_i)$. In the former case, $\rho$ is horizontally going east and $v_{i-1}$ is to the right of $Rec(r_{i-1},r_i)$. In the latter case, $\rho$ is vertically going south and $v_{i-1}$ is below $Rec(r_{i-1},r_i)$. Part 3 thus follows. $\square$

For any two consecutive roots $r_{i-1}$ and $r_i$ in R with $2\le i\le k$, if $v_{i-1}$ is on a ray $\rho$ of $B(r_{i-1},r_i)$, then we let $\rho _{i-1}$ be the ray originating at $v_{i-1}$ with the same direction as $\rho$. If $v_{i-1}$ lies on the middle segment of $B(r_{i-1},r_i)$, then by Lemma 8, $r_{i-1}$ is to the northeast of $r_i$ and ${\overline{cd}}$ intersects $Rec(r_{i-1},r_i)$; in this case, let $\rho _{i-1}$ be the ray of $B(r_{i-1},r_i)$ whose origin is the lower endpoint of $B_M(r_{i-1},r_i)$ (if the origin is at the right edge of $Rec(r_{i-1},r_i)$, then $\rho _{i-1}$ is horizontally going easy; otherwise it is vertically going south). For a ray $\rho$, let $or(\rho )$ denote the origin of $\rho$.

Observation 6

For any $2\le i\le k$, the ray $\rho _{i-1}$ is either horizontally going east or vertically going south. If $v_{i-1}$ is on a ray of $B(r_{i-1},r_i)$, then $or(\rho _{i-1})=v_{i-1}$; if $v_{i-1}$ is on $B_M(r_{i-1},r_i)$, then $or(\rho _{i-1})$ is on either the right edge or the bottom edge of $Rec(r_{i-1},r_i)$.

Lemma 9

Consider any two consecutive roots $r_{i-1}$ and $r_i$ in R with $2\le i\le k$.

• 1. If the ray $\rho _{i-1}$ is horizontal, then $r_{i-1}$ is above $\rho _{i-1}$ and $r_i$ is below $\rho _{i-1}$.

• 2. If $\rho _{i-1}$ is vertical, then $r_{i-1}$ is to the right of $\rho _{i-1}$ and $r_i$ is to the left of $\rho _{i-1}$.

• 3. The origin $or(\rho _{i-1})$ of $\rho _{i-1}$ is always below $r_{i-1}$ and to the right of $r_i$.

Proof

There are three cases on the possible relative positions of $r_{i-1}$ and $r_i$.

• If $r_{i-1}$ is to the northwest of $r_i$ [see Fig. 9(1)], then by the proof of Lemma 8, $\rho _{i-1}$ is horizontal and is contained in the ray of $B(r_{i-1},r_i)$ whose origin is on the right edge of $Rec(r_{i-1},r_i)$. Since $r_{i-1}$ and $r_i$ are two diagonal vertices of $Rec(r_{i-1},r_i)$, $\rho _{i-1}$ is above $r_{i}$ and below $r_{i-1}$.

  Further, the origin $or(\rho _{i-1})$ is $v_{i-1}$, which is below $r_{i-1}$ and to the right of $r_i$.

• If $r_{i-1}$ is to the southeast of $r_i$ [see Fig. 9(2)], then by the proof of Lemma 8, $\rho _{i-1}$ is vertical and lies on the ray of $B(r_{i-1},r_i)$ whose origin is on the bottom edge of $Rec(r_{i-1},r_i)$. Since $r_{i-1}$ and $r_i$ are two diagonal vertices of $Rec(r_{i-1},r_i)$, $\rho _{i-1}$ is to the right of $r_i$ and to the left of $r_{i-1}$. Further, the origin $or(\rho _{i-1})$ is $v_{i-1}$, which is below $r_{i-1}$ and to the right of $r_i$.

• If $r_{i-1}$ is to the northeast of $r_i$ [see Fig. 9(3)], then if $\rho _{i-1}$ is horizontal, then the proof is similar to the first case; otherwise, the proof is similar to the second case.

$\square$

Lemma 10

For any i with $3\le i\le k-1$, if $r_i$ is to the southwest of $r_{i-1}$, then $v_{i-2}$ is to the right of the rectangle $Rec(r_{i-1},r_i)$ and $v_{i}$ is below $Rec(r_{i-1},r_i)$.

Proof

Suppose $r_i$ is southwest of $r_{i-1}$. We only prove that $v_{i-2}$ is to the right of the rectangle $Rec(r_{i-1},r_i)$. The case that $v_{i}$ is below $Rec(r_{i-1},r_i)$ can be proved analogously.

Note that $v_{i-2}\in B(r_{i-2},r_{i-1})$. We discuss the three possible relative positions of $r_{i-2}$ and $r_{i-1}$. By Lemma 7, $r_{i-2}$ may be southeast, northwest, or northeast of $r_{i-1}$. Since $r_i$ is southwest of $r_{i-1}$, to prove $v_{i-2}$ is to the right of $Rec(r_{i-1},r_i)$, it suffices to show that $v_{i-2}$ is to the right of $r_{i-1}$.

• If $r_{i-2}$ is southeast of $r_{i-1}$, then by Lemma 8, $v_{i-2}$ is on the ray of $B(r_{i-1},r_{i-2})$ vertically going south, i.e., $\rho _{i-2}$ is vertical. By Lemma 9, $r_{i-1}$ is to the left of $\rho _{i-2}$. Since $v_{i-2}\in \rho _{i-2}$, $v_{i-2}$ is to the right of $r_{i-1}$.

• If $r_{i-2}$ is northwest of $r_{i-1}$, then by Lemma 8, $v_{i-2}$ is to the right of $Rec(r_{i-2},r_{i-1})$, and thus to the right of $r_{i-1}$.

• If $r_{i-2}$ is northeast of $r_{i-1}$, then the rectangle $Rec(r_{i-2},r_{i-1})$ is to the northeast of $Rec(r_{i-1},r_i)$. If $v_{i-2}$ is on $B_M(r_{i-2},r_{i-1})$, then since $v_{i-2}$ is inside $Rec(r_{i-2},r_{i-1})$, $v_{i-2}$ is to the right of $Rec(r_{i-1},r_i)$; otherwise, the proof is similar to the above two cases. $\square$

Recall that when sketching the algorithm in Sect. 5.1, we claimed that the origins of the rays involved somehow form a staircase structure. The next lemma states this important fact.

Lemma 11

For any i with $2\le i\le k-1$, $or(\rho _{i-1})$ is to the northeast of $or(\rho _i)$.

Proof

We first discuss a scenario that will be used later in this proof. Consider any two consecutive roots $r_j$ and $r_{j+1}$ in R, $1\le j\le k-1$, with $or(\rho _{j})\ne v_{j}$. Then based on our discussion above, it must be the case that $r_{j+1}$ is to the southwest of $r_{j}$, ${\overline{cd}}$ intersects the rectangle $Rec(r_j,r_{j+1})$, and $or(\rho _{j})$ is a point on an edge of $Rec(r_j,r_{j+1})$. Let $z_{j}$ be the intersection of ${\overline{cd}}$ and the right edge of $Rec(r_j,r_{j+1})$ (see Fig. 10). The origin $or(\rho _{j})$ can be either on the right edge or the bottom edge of $Rec(r_j,r_{j+1})$. In either case, $or(\rho _{j})$ must be both below and to the left of $z_{j}$, i.e., $z_{j}$ is to the northeast of $or(\rho _{j})$.

Fig. 10

Illustrating the case when $r_{j}$ is to the northeast of $r_{j+1}$ and $or(\rho _{j})\ne v_{j}$

Consider any i with $2\le i\le k-1$. To prove the lemma, depending on whether $or(\rho _{i-1})=v_{i-1}$ and whether $or(\rho _{i})=v_i$, there are four cases.

• 1. If $or(\rho _{i-1})=v_{i-1}$ and $or(\rho _{i})=v_{i}$, then since $v_{i-1}$ and $v_i$ are on ${\overline{cd}}$ in the order from c to d, $v_{i-1}$ is to the northeast of $v_i$, and thus $or(\rho _{i-1})$ is to the northeast of $or(\rho _{i})$.

• 2. If $or(\rho _{i-1})=v_{i-1}$ and $or(\rho _{i})\ne v_{i}$, then by our discussion at the beginning of this proof, $r_{i+1}$ is to the southwest of $r_{i}$, the rectangle $Rec(r_i,r_{i+1})$ intersects ${\overline{cd}}$, and the point $z_i$ is to the northeast of $or(\rho _{i})$. Further, since $r_{i+1}$ is to the southwest of $r_{i}$, by Lemma 10, $v_{i-1}$ is to the right of $Rec(r_i,r_{i+1})$ and thus to the right of $z_i$. Since $v_{i-1}$ is to the right of $z_i$ and both $v_{i-1}$ and $z_i$ are on ${\overline{cd}}$, $v_{i-1}$ is to the northeast of $z_i$. Therefore, $or(\rho _{i-1})$ (which is $v_{i-1}$) is to the northeast of $or(\rho _{i})$.

• 3. If $or(\rho _{i-1})\ne v_{i-1}$ and $or(\rho _{i})= v_{i}$, then the analysis is analogous to the second case.

• 4. If $or(\rho _{i-1})\ne v_{i-1}$ and $or(\rho _{i})\ne v_{i}$, then $r_{i-1}$ is to the northeast of $r_i$ and $r_{i}$ is to the northeast of $r_{i+1}$. Hence, the rectangle $Rec(r_{i-1},r_i)$ is to the northeast of $Rec(r_i,r_{i+1})$. Since $or(\rho _{i-1})$ is on $Rec(r_{i-1},r_i)$ and $or(\rho _{i})$ is on $Rec(r_i,r_{i+1})$, we also obtain that $or(\rho _{i-1})$ is to the northeast of $or(\rho _{i})$. $\square$

Note that our algorithm may need to process a pair of non-consecutive roots of R. For this, we have the following lemma.

Lemma 12

Consider any root $r_i\in R$ with $1\le i\le k$. For any ray $\rho _{j}$, if $j\le i-1$ and $\rho _{j}$ is vertical, then $\rho _{j}$ is to the right of $r_i$; if $j\ge i$ and $\rho _{j}$ is horizontal, then $\rho _{j}$ is below $r_i$.

Proof

Without loss of generality, assume $i<k$. Consider the ray $\rho _i$, which is on $B(r_i,r_{i+1})$. By Lemma 9, the origin $or(\rho _i)$ is below $r_i$. By Lemma 11, for any ray $\rho _j$ with $j\ge i$, $or(\rho _j)$ is below $or(\rho _i)$ and thus is below $r_i$. Hence, if $\rho _j$ is horizontal, then $\rho _j$ must be below $r_i$.

By an analogous analysis, we can show that if $j\le i-1$ and $\rho _j$ is vertical, then $\rho _j$ is to the right of $r_i$. $\square$

For any two consecutive roots $r_{i-1}$ and $r_i$ in R, $2\le i\le k$, the vertex $v_{i-1}$ divides $B(r_{i-1},r_i)$ into two portions; we denote by $B_{bay}(r_{i-1},r_i)$ the portion that goes inside $bay({\overline{cd}})$ after $v_{i-1}$. A key to building ${\mathcal{VD}}(bay({\overline{cd}}))$ is to compute the interactions among all $B_{bay}(r_{i-1},r_i)$’s, for $i=2,3,\ldots ,k$. Recall that if $v_{i-1}$ is on a ray of $B(r_{i-1},r_i)$, then $B_{bay}(r_{i-1},r_i)$ is the ray $\rho _{i-1}$; otherwise, $v_{i-1}$ is on $B_M(r_{i-1},r_i)$ [i.e., the middle segment of $B(r_{i-1},r_i)$], and $B_{bay}(r_{i-1},r_i)$ consists of a portion of $B_M(r_{i-1},r_i)$ in $Rec(r_{i-1},r_i)$ [i.e., the line segment $\overline{v_{i-1}or(\rho _{i-1})}$] and the ray $\rho _{i-1}$. Lemma 13 below shows that the portion of $B_M(r_{i-1},r_i)$ inside $bay({\overline{cd}})$ appears in $\textit{SPM}({\mathcal {F}})$ [and thus in ${\mathcal{VD}}(bay({\overline{cd}}))$], implying that we can simply keep it when computing ${\mathcal{VD}}(bay({\overline{cd}}))$ and we only need to further deal with the rays $\rho _{i}$ for $i=1,2,\ldots ,k-1$. Thus, dealing with the rays $\rho _{i}$ is the main issue of our algorithm (as discussed in Sect. 5.1).

Lemma 13

For any two consecutive roots $r_{i-1}$ and $r_i$ in R, $2\le i\le k$, if $v_{i-1}$ lies on $B_M(r_{i-1},r_i)$, then the portion of $B_M(r_{i-1},r_i)$ inside $bay({\overline{cd}})$ appears in ${\mathcal{VD}}(bay({\overline{cd}}))$.

Proof

Consider two consecutive roots $r_{i-1}$ and $r_i$ in R, $2\le i\le k$, with $v_{i-1}$ lying on $B_M(r_{i-1},r_i)$.

Denote by $B_M'$ the portion of $B_M(r_{i-1},r_i)$ inside $bay({\overline{cd}})$. Recall that $B_M(r_{i-1},r_i)$ is an open segment that does not contain its endpoints and is strictly inside $Rec(r_{i-1},r_i)$. To prove the lemma, it suffices to show that for any two roots $r_j$ and $r_h$ in R with $\{r_j,r_h\}\ne \{r_{i-1},r_i\}$, if a portion of $B(r_j,r_h)$ appears in $\textit{SPM}({\mathcal {F}})$, then that portion does not intersect $B_M'$.

By Lemma 7, $r_i$ may be to the southeast, or northwest, or southwest of $r_{i-1}$. Since ${\overline{cd}}$ is positive-sloped, if $r_i$ is to the northwest or southeast of $r_{i-1}$, then ${\overline{cd}}$ cannot intersect the rectangle $Rec(r_{i-1},r_i)$ and thus $v_{i-1}$ cannot lie on $B_M(r_{i-1},r_i)$. Therefore, the only possible case is that $r_i$ is to the southwest of $r_{i-1}$.

First, we assume $i-1\ge 2$ and consider the root $r_{i-2}$. We discuss the possible relative positions of $r_{i-2}$ with respect to $r_{i-1}$. Recall that the bisector portion $B_{bay}(r_{i-2},r_{i-1})$ either is $\rho _{i-2}$ or consists of $\overline{v_{i-2}or(\rho _{i-2})}$ and $\rho _{i-2}$. Note that in either case, when moving along $B_{bay}(r_{i-2},r_{i-1})$ from $v_{i-2}$, $B_{bay}(r_{i-2},r_{i-1})$ is monotonically increasing in the x-coordinates. Hence, $v_{i-2}$ is a leftmost point of $B_{bay}(r_{i-2},r_{i-1})$. Since $r_i$ is to the southwest of $r_{i-1}$, by Lemma 10, $v_{i-2}$ is to the right of $Rec(r_{i-1},r_i)$ and thus is strictly to the right of $B_M'$. Hence, $B_{bay}(r_{i-2},r_{i-1})$ cannot intersect $B_M'$.

For any pair of consecutive roots $r_{j-1}$ and $r_j$ in R, $2\le j\le i-2$, similarly, when moving from $v_{j-1}$ along $B_{bay}(r_{j-1},r_j)$, $B_{bay}(r_{j-1},r_j)$ is monotonically increasing in the x-coordinates. Since $v_{i-2}$ is strictly to the right of $B_M'$ and $v_{j-1}$ is to the right of $v_{i-2}$, $B_{bay}(r_{j-1},r_j)$ cannot intersect $B_M'$.

Let $R_1=\{r_1,r_2,\ldots ,r_{i-1}\}$ and $R_2=\{r_{i},r_{i+1},\ldots ,r_{k}\}$. (Note that since R may be a multi-set, $R_1$ and $R_2$ possibly contain the same physical root, but this is not important to our analysis).

For any two different pairs of consecutive roots $r_{j-1},r_j$ and $r_{t-1},r_t$ with $2\le j\le i-1$ and $2\le t\le i-1$, it is possible that $B_{bay}(r_{j-1},r_j)$ and $B_{bay}(r_{t-1},r_t)$ intersect in $\textit{SPM}({\mathcal {F}})$; if that happens, then let $B'$ be the resulting bisector. It is not difficult to see that $B'$ must be going in a direction between the original directions of $B_{bay}(r_{j-1},r_j)$ and $B_{bay}(r_{t-1},r_t)$. Since neither $B_{bay}(r_{j-1},r_j)$ nor $B_{bay}(r_{t-1},r_t)$ intersects $B_M'$, $B'$ cannot intersect $B_M'$. We can further consider the possible intersection between $B'$ and the bisector of another two roots in $R_1$ in the manner as above, and show likewise that the new bisector thus resulted cannot intersect $B_M'$.

The above argument proves the lemma for $R_1$, i.e., for any two roots $r_j$ and $r_t$ in $R_1$ such that a portion of $B(r_j,r_t)$ appears in ${\mathcal{VD}}(bay({\overline{cd}}))$, that portion does not intersect $B_M'$. By a similar argument, we can also prove the lemma for $R_2$, i.e., for any two roots $r_j$ and $r_t$ in $R_2$ such that a portion of $B(r_j,r_t)$ appears in ${\mathcal{VD}}(bay({\overline{cd}}))$, that portion does not intersect $B_M'$. It remains to prove the lemma for two roots in different subsets, i.e., prove that for any two roots $r_j\in R_1$ and $r_t\in R_2$ such that $\{r_j,r_t\}\ne \{r_{i-1},r_i\}$ and a portion of $B(r_j,r_t)$ appears in ${\mathcal{VD}}(bay({\overline{cd}}))$, that portion does not intersect $B_M'$. Note that the case of $B(r_j,r_t)$ (partially) appearing in ${\mathcal{VD}}(bay({\overline{cd}}))$ can occur only after $B_{bay}(r_{i-1},r_i)$ is “blocked” by an intersection between $B_{bay}(r_{i-1},r_i)$ and the bisector of two roots in $R_1$ or two roots in $R_2$. Since the bisector of any two roots in $R_1$ or any two roots in $R_2$ cannot intersect $B_M'$, the portion of $B(r_j,r_t)$ appearing in ${\mathcal{VD}}(bay({\overline{cd}}))$ cannot intersect $B'_M$ either. $\square$

The observations presented above help determine the behaviors of the bisectors for the roots in R (e.g., the properties of the rays $\rho _1,\rho _2,\ldots ,\rho _{k-1}$), which are crucial to constructing ${\mathcal{VD}}(bay({\overline{cd}}))$. They form a basis for both showing the correctness and the efficiency of our algorithm in Sect. 5.3. For example, Lemma 11 can help conduct a set of ray shooting operations in linear time, and Lemma 13 allows us to decompose the problem into certain subproblems with nice properties.

5.3 The Algorithm for Computing ${\mathcal{VD}}(bay({\overline{cd}}))$

In this subsection, we present our algorithm for computing ${\mathcal{VD}}(bay({\overline{cd}}))$, i.e., computing the Voronoi region ${V\!D}(r)$ for each root $r\in R$.

As shown in [29, 30], a key property of the $L_1$ metric is that there exists an SPM such that each edge of the SPM is horizontal, or vertical, or of a slope 1 or $-\,1$. As shown below, the curves involved in specifying ${\mathcal{VD}}(bay({\overline{cd}}))$ consist of only line segments of slopes 0, $\infty$, and $-\,1$ (there is no $+\,1$, which is due to the assumption that ${\overline{cd}}$ is positive-sloped). A line (segment) is said to be ($-\,1$)-sloped if its slope is $-\,1$. Our algorithm needs to perform O(k) vertical, horizontal, and ($-\,1$)-sloped ray shooting queries. By exploiting some properties shown in Sect. 5.2, we conduct all ray shootings in a global manner in $O(n'+k)$ time.

Before describing the main algorithm, we discuss some preprocessing work as well as some basic algorithmic methods that will be used later in the main algorithm.

5.3.1 Preliminaries and Preprocessing

By Lemma 13, for any two consecutive roots $r_{i-1}$ and $r_i$ in R, $2\le i\le k$, if the middle segment $B_M(r_{i-1},r_i)$ of their bisector intersects ${\overline{cd}}$ (at $v_{i-1}$), then we can “separately” process the portion of $B_M(r_{i-1},r_i)$ inside $Rec(r_{i-1},r_i)$, as follows. Let $\partial$ be the boundary of $bay({\overline{cd}})$ excluding ${\overline{cd}}$.

Fig. 11

Illustrating an example of $B_M(r_{i-1},r_i)$ intersecting both ${\overline{cd}}$ (at $v_{i-1}$) and $\partial$ (at p). The line segment $\overline{v_{i-1}p}$ divides $bay({\overline{cd}})$ into $bay_1$ and $bay_2$

Clearly, $v_{i-1}$ divides $B_M(r_{i-1},r_i)$ into two segments, only one of which contains a point in $bay({\overline{cd}})$ [let $B_M'(r_{i-1},r_i)$ denote that segment]. Thus, $B_M'(r_{i-1},r_i)$ is a line segment whose endpoints are $v_{i-1}$ and $or(\rho _{i-1})$. We first determine whether $B_M'(r_{i-1},r_i)$ intersects $\partial$, by performing a $-\,1$-sloped ray shooting operation. Specifically, we shoot a ray $\rho$ originating at $v_{i-1}$ and passing through $or(\rho _{i-1})$. If the length of the portion of $\rho$ between $v_{i-1}$ and the first point p on $\partial$ hit by $\rho$ is larger than the length of $B_M'(r_{i-1},r_i)$, then $B_M'(r_{i-1},r_i)$ does not intersect $\partial$, and we do nothing. Otherwise, $B_M'(r_{i-1},r_i)$ intersects $\partial$ (at the point p). By Lemma 13, the line segment $\overline{v_{i-1}p}$ appears in $\textit{SPM}({\mathcal {F}})$. Also, $\overline{v_{i-1}p}$ partitions $bay({\overline{cd}})$ into two simple polygons (see Fig. 11); one polygon contains $\overline{cv_{i-1}}$ as an edge, which we denote as $bay_1$, and we denote the other polygon as $bay_2$. Let $R_1=\{r_1,r_2,\ldots ,r_{i-1}\}$ and $R_2=\{r_{i},r_{i+1},\ldots ,r_{k}\}$. Since $\overline{v_{i-1}p}$ is in ${\mathcal{VD}}(bay({\overline{cd}}))$, for any point q in $bay_1$, there is a shortest path from s to q that goes through a root $r\in R_1$. Similarly, for any point q in $bay_2$, there is a shortest s-q path that goes through a root $r\in R_2$. This implies that we can divide the original problem of computing ${\mathcal{VD}}(bay({\overline{cd}}))$ on $bay({\overline{cd}})$ and R into two subproblems of computing ${\mathcal{VD}}(bay_1)$ on $bay_1$ and $R_1$ and computing ${\mathcal{VD}}(bay_2)$ on $bay_2$ and $R_2$.

If we process each pair of consecutive roots in R as above, then the original problem may be divided into multiple subproblems, each of which has the following property: for any pair of consecutive roots $r_{i-1}$ and $r_i$ in the root subset of R of a subproblem, if $B_M(r_{i-1},r_i)$ intersects ${\overline{cd}}$, then $B'_M(r_{i-1},r_i)$ does not intersect $\partial$ and is contained in the subpolygon of $bay({\overline{cd}})$ of the subproblem; further, $B'_M(r_{i-1},r_i)$ is in ${\mathcal{VD}}(bay({\overline{cd}}))$ and has been computed.

To perform the above process, a key is to derive an efficient method for the $-\,1$-sloped ray shooting operations. For this, we choose to check all pairs of consecutive roots in R in the order of $r_1,r_2,\ldots ,r_k$. In this way, it is easy to see that the ray shootings are conducted such that the origins of the rays are sorted along ${\overline{cd}}$ from c to d. This is summarized by the next observation.

Observation 7

Partitioning into subproblems conducts O(k) $-\,1$-sloped ray shooting operations that are organized such that the origins of all rays are sorted on ${\overline{cd}}$ from c to d.

We show next that the ray shootings for Observation 7 can be done in $O(n'+k)$ time. Since the origins of all rays in Observation 7 are sorted on ${\overline{cd}}$, we can perform the ray shootings by computing the visible region of $bay({\overline{cd}})$ from ${\overline{cd}}$ along the direction of these rays. This can be easily done by a visibility algorithm on a simple polygon (e.g., [1, 23, 28]). Below, we give a different algorithm for a more general problem; this more general result is needed by the main algorithm.

Given a simple polygon P, the horizontal visibility map of P contains a horizontal line segment inside P through each vertex of P, extending as long as possible without properly crossing the boundary of P (such line segments are called the diagonals; see Fig. 12). The vertical visibility map with vertical diagonals is defined similarly. Each region in a visibility map is a trapezoid (a triangle is a special trapezoid). A visibility map of a simple polygon can be computed in linear time [3].

Fig. 12

Illustrating the horizontal visibility map of a simple polygon

For a ray $\rho$ with its origin in $bay({\overline{cd}})$ (inside it or on the boundary), the boundary point of $bay({\overline{cd}})$ that is not the origin $or(\rho )$ hit by $\rho$ first is called the target point of $\rho$, denoted by $tp(\rho )$. Recall that $\partial$ is the boundary of $bay({\overline{cd}})$ excluding the edge ${\overline{cd}}$. In the rest of this paper, unless otherwise stated, a ray in our discussion always has its origin in $bay({\overline{cd}})$ and its target point on $\partial$.

We say that m parallel rays $\rho _1',\rho _2',\ldots ,\rho _m'$ are target-sorted if we move from c to d (clockwise) on $\partial$, we encounter the target points of these rays on $\partial$ in the order of $tp(\rho '_1),tp(\rho '_2),\ldots ,tp(\rho '_m)$.

Given a set of m target-sorted parallel rays $\rho _1',\rho _2',\ldots ,\rho _m'$ for $bay({\overline{cd}})$ whose origins are in $bay({\overline{cd}})$ and whose target points are on $\partial$, below we present a visibility map based approach for computing their target points in $O(n'+m)$ time (recall that $n'$ is the number of vertices of $bay({\overline{cd}})$).

Without loss of generality, we assume that the rays are all horizontal. We first compute the horizontal visibility map of $bay({\overline{cd}})$ in $O(n')$ time. Then, starting from the vertex c, we scan $\partial$ and check each edge e of $\partial$ and the trapezoid t(e) of the visibility map bounded by e, to see whether the next ray $\rho _i'$ (initially $i=1$) is in the trapezoid t(e) and can hit the edge e. Once the target point of the ray $\rho _i'$ is found, we continue with the next ray $\rho _{i+1}'$. Clearly, the time for computing all target points is $O(n'+m)$. Thus, we have the following result.

Lemma 14

Given a set of m target-sorted parallel rays for $bay({\overline{cd}})$ whose origins are in $bay({\overline{cd}})$ and whose target points are on $\partial$, their target points can be computed in $O(n'+m)$ time.

For the ray shootings in Observation 7, it is easy to see that these rays are target-sorted. Thus, by Lemma 14, their target points can be computed in $O(n'+k)$ time.

In addition, as part of the preprocessing for our main algorithm, we also compute the horizontal visibility map ${H\!M}(bay({\overline{cd}}))$ and the vertical visibility map ${V\!M}(bay({\overline{cd}}))$ of $bay({\overline{cd}})$. Further, for each $1\le i\le k-1$, we compute the trapezoid of the horizontal visibility map ${H\!M}(bay({\overline{cd}}))$ that contains the origin $or(\rho _i)$ of the ray $\rho _i$, in totally $O(n'+k)$ time, in the following way.

Recall that $or(\rho _i)$ is either $v_i$ or in the interior of $bay({\overline{cd}})$. In the latter case, $or(\rho _i)$ is an endpoint of the line segment $B'_M(r_i,r_{i+1}) = \overline{v_ior(\rho _i)}$ whose slope is $-\,1$, and the position of $or(\rho _i)$ has been determined earlier by the $-\,1$-sloped ray shooting operations. By Lemma 11, all origins $or(\rho _1),or(\rho _2),\ldots ,or(\rho _{k-1})$ are ordered from northeast to southwest. Further, $or(\rho _i)$’s are all visible from ${\overline{cd}}$ along the direction of slope $-\,1$. Thus, it is not difficult to show that if we visit the trapezoids of ${H\!M}(bay({\overline{cd}}))$ by scanning the edges of $\partial$ from c to d and looking at the trapezoids bounded by each edge, then the trapezoids containing such $or(\rho _i)$’s are encountered in the same order as $or(\rho _1),or(\rho _2),\ldots ,or(\rho _{k-1})$. This implies that we can use a similar algorithm as for computing the target points of target-sorted parallel rays on $\partial$ (i.e., scanning $\partial$ from c to d and checking the trapezoids of ${H\!M}(bay({\overline{cd}}))$ thus visited along $\partial$) to find all the sought trapezoids, in $O(n'+k)$ time.

The above discussion leads to the following lemma.

Lemma 15

The preprocessing on $bay({\overline{cd}})$ takes $O(n'+k)$ time.

In the main algorithm, the horizontal visibility map ${H\!M}(bay({\overline{cd}}))$ will be used to guide the main process. More specifically, during the algorithm, we traverse inside $bay({\overline{cd}})$ following certain rays, and use ${H\!M}(bay({\overline{cd}}))$ to keep track of where we are (i.e., which trapezoid of ${H\!M}(bay({\overline{cd}}))$ contains our current position). The vertical visibility map ${V\!M}(bay({\overline{cd}}))$ will be used to compute the target points of some target-sorted vertical rays using the above visibility map based approach.

For any two points a and b on $\partial$ with a lying on the portion of $\partial$ from c clockwise to b, we denote by $\partial (a,b)$ the portion of $\partial$ between a and b, and we say that a is beforeb or b is aftera.

5.3.2 The Main Algorithm

After the preprocessing, the problem of computing ${\mathcal{VD}}(bay({\overline{cd}}))$ with the root set R may be divided into multiple subproblems and we need to solve each subproblem. For convenience of the forthcoming discussion, we assume that the original problem on $bay({\overline{cd}})$ with R is merely one such subproblem, i.e., for any two consecutive roots $r_i$ and $r_{i+1}$ in R, if $v_i\in B_M(r_i,r_{i+1})$, then $B'_M(r_i,r_{i+1})$ [$=\overline{v_ior(\rho _i)}$] lies completely in ${\mathcal{VD}}(bay({\overline{cd}}))$ and has been computed. Recall that in the preprocessing, we have already computed the trapezoid of the horizontal visibility map ${H\!M}(bay({\overline{cd}}))$ that contains the origin $or(\rho _i)$ of the ray $\rho _i$, for each $1\le i\le k-1$. Observation 8 below summarizes these facts.

Observation 8

After the preprocessing,

• for any two consecutive roots $r_i$ and $r_{i+1}$ in R, if $v_i\in B_M(r_i,r_{i+1})$, then their bisector portion $B'_M(r_i,r_{i+1})\ [=\overline{v_ior(\rho _i)}]$ has been computed;

• for each $1\le i\le k-1$, the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains the origin $or(\rho _i)$ of the ray $\rho _i$ is known.

As discussed before, our task is to handle the interactions among the rays $\rho _i$ for all $i=1,2,\ldots ,k-1$.

In the algorithm, we need to compute the target points for O(k) horizontal and vertical rays. The main procedure is guided by the horizontal visibility map ${H\!M}(bay({\overline{cd}}))$ so that the target point of each horizontal ray can be determined in amortized constant time. For the vertical ray shootings, we use the visibility map based approach with the vertical visibility map ${V\!M}(bay({\overline{cd}}))$. Note that the vertical ray shootings will occur in an online fashion in the algorithm. We will show that the vertical rays involved are target-sorted. To compute the target points for these vertical rays, the algorithm maintains a reference point, denoted by $p^*$. Initially, $p^*=c$. Then during the algorithm, $p^*$ will be moved forward along $\partial$ from c to d. In this way, the target points of all vertical rays are computed in totally $O(n'+k)$ time [recall that $n'$ is the number of obstacle vertices of $bay({\overline{cd}})$].

Let $\Psi =\{\rho _1,\rho _2,\ldots ,\rho _{k-1}\}$. We process the rays of $\Psi$ incrementally in the order of $\rho _1,\rho _2,\ldots ,\rho _{k-1}$, whose origins are ordered from northeast to southwest by Lemma 11. By Observation 6, each ray in $\Psi$ is either horizontally going east or vertically going south. We say that initially all rays are active and the entire $bay({\overline{cd}})$ is active. In general, the active rays are used to decompose the active region of $bay({\overline{cd}})$. During the algorithm, some portion of $bay({\overline{cd}})$ will be implicitly set as inactive, which means that each point of such a region is in the Voronoi region of a root that has been determined. The active region of $bay({\overline{cd}})$ at any moment of the algorithm always forms a connected simple polygon, a fact that we will not explicitly argue in the following algorithm description. Similarly, some rays will be set as inactive, meaning that they will no longer be involved in the further decomposition of the current active region of $bay({\overline{cd}})$. When the algorithm terminates, the entire $bay({\overline{cd}})$ is inactive and all rays of $\Psi$ are inactive. Note that setting a region or a ray as inactive is done implicitly and is used only for our analysis. Since each ray in $\Psi$ lies on the bisector of two roots in R, we say that the two roots define the ray.

Since our algorithm, and particularly, the argument of its correctness, is quite involved, in the following we first provide a quick sketch of the algorithm. The detailed algorithm including its correctness proof and time analysis will be presented afterwards.

5.3.3 A Quick Sketch of the Algorithm

We start with the first ray $\rho _1$ (i.e., the one whose origin is the northeast most). If $\rho _1$ is horizontal (going east), then we compute its target point $tp(\rho _1)$ on $\partial$ by using ${H\!M}(bay({\overline{cd}}))$ (see Fig. 13). In this case, we can immediately determine ${V\!D}(r_1)$. We move the reference point $p^*$ from c to $tp(\rho _1)$. We then continue with the next ray $\rho _2$.

Fig. 13

Illustrating an example of $\rho _1$ being horizontal

If $\rho _1$ is vertical (going south), then we push $\rho _1$ onto a stack S (initially, $S=\emptyset$), and let the reference point $p^*$ stay at c. We then continue with the next ray $\rho _2$.

In general, suppose our algorithm is about to process a ray $\rho _{i}\in \Psi$, $i>1$, which lies on the bisector $B(r_i,r_{i+1})$. There are a number of cases and subcases to consider, depending on whether $\rho _i$ is vertical or horizontal, whether S is empty, etc. Our algorithm maintains an invariant that the rays in S from bottom to top are target-sorted.

Case 1: $\rho _i$ is vertical (going south). Then we simply push $\rho _i$ onto the top of S and the reference point $p^*$ is not changed. The algorithm then continues with the next ray $\rho _{i+1}\in \Psi$ in this situation.

Case 2: $\rho _i$ is horizontal (going east). We compute the target point $tp(\rho _i)$ of $\rho _i$. We can show that $tp(\rho _i)$ is after the reference point $p^*$ on $\partial$. Depending on whether $S=\emptyset$, there are two subcases.

Subcase 2(a): $S=\emptyset$. In this case, we can determine the Voronoi region ${V\!D}(r_i)$ immediately. We move $p^*$ to $tp(\rho _i)$ and then consider the next ray $\rho _{i+1}$.

Fig. 14

Illustrating Subcase 2(b.1) in which the target points of all rays in S are before $p=tp(\rho _i)$. All vertical rays are in S. The ray $\rho$ is at the top of S and $\rho '$ is at the bottom of S

Subcase 2(b): $S\not =\emptyset$. In this case, for the rays in S whose target points lie on $\partial (p^*,tp(\rho _i))$, we compute their target points by scanning $\partial (p^*,tp(\rho _i))$ from $p^*$ to $tp(\rho _i)$. The target points of some rays in S (e.g., the ray at the top of S) are not yet found if they are on $\partial$ after $tp(\rho _i)$.

Let $\rho$ be the ray at the top of S (e.g., if $\rho _{i-1}$ is vertical, then $\rho$ is $\rho _{i-1}$). Suppose $\rho$ is on the bisector $B(r_{j},r_{j'})$ with $j'>j$. As will be seen later, our algorithm may produce a ray not in $\Psi$ and the two roots defining the ray may not be consecutive in R. Hence, $\rho$ may not be in $\Psi$, and $r_j$ and $r_{j'}$ may not be consecutive. However, it always holds that $i=j'$ and $or(\rho _i)$ is to the southwest of $or(\rho )$. Depending on whether the target point $tp(\rho )$ is before $tp(\rho _i)$, there are two subcases.

Subcase 2(b.1): $tp(\rho )$ is before $tp(\rho _i)$. In this case, the scanning procedure has computed the target points of all rays of S on $\partial (p^*,tp(\rho _i))$ (i.e., all such target points are before $tp(\rho _i)$ on $\partial$; see Fig. 14). In this case, we can readily compute the Voronoi regions of the roots defining the rays in S. Finally, we pop all rays of S out and move $p^*$ to $tp(\rho _i)$. We then consider the next ray $\rho _{i+1}$.

Subcase 2(b.2): $tp(\rho )$ is not before $tp(\rho _i)$. In this case, $tp(\rho )$ was not found on $\partial (p^*,p)$ by the scanning procedure. This is the most involved case since $\rho$ intersects $\rho _i$ before it hits $\partial$ (and so may some other rays in S). We need to consider the consequences of the intersections of such rays of S with $\rho _i$.

First of all, the Voronoi region ${V\!D}(r_i)$ can be readily computed (see Fig. 15). Let $p_1$ be the intersection point of $\rho _i$ and $\rho$, and $q_1$ the intersection of the horizontal line through $r_{i+1}$ and the vertical line through $r_j$ (see Fig. 15). We can show that $q_1$ is to the southeast of $p_1$. Because the rectangle $Rec(p_1,q_1)$ is contained in $Rec(r_j,r_{i+1})$, the portion of $B(r_j,r_{i+1})$ in $Rec(p_1,q_1)$ is a portion of the middle segment of $B(r_j,r_{i+1})$. Further, since $p_1$ is the intersection of $\rho _i$ and $\rho$, $p_1$ is at the intersection of $B(r_i,r_{i+1})$ and $B(r_j,r_i)$. Thus, $p_1$ is on $B(r_j,r_{i+1})$.

Fig. 15

Illustrating an example that the ray $\rho$ at the top of S intersects $\rho _i$ (at $p_1$) before $\rho$ hits $\partial$. The region $VD(r_i)$ is highlighted and $B_M'(r_j,r_{i+1})=\overline{p_1p_1'}$

Fig. 16

Illustrating an example that $B'_M(r_j,r_{i+1})$ ($=\overline{p_1p_1'}$) intersects $\partial$ (first at z)

We can show that $r_{i+1}$ is to the southwest of $r_{j}$, and thus the middle segment of $B(r_j,r_{i+1})$ is $-\,1$-sloped. The portion of $B(r_j,r_{i+1})$ contained in $Rec(p_1,q_1)$ is a segment with an endpoint at $p_1$ and the other endpoint (denoted by $p_1'$) on one of the two edges of $Rec(p_1,q_1)$ incident to $q_1$ (see Fig. 15). We can prove that the portion of $\overline{p_1p_1'}$ contained in $bay({\overline{cd}})$ appears in ${\mathcal{VD}}(bay({\overline{cd}}))$, and thus we should keep this portion of $\overline{p_1p_1'}$. However, $\overline{p_1p_1'}$ may intersect $\partial$. We determine whether such intersection occurs, with the help of ${H\!M}(bay({\overline{cd}}))$.

• 1. If $\overline{p_1p_1'}$ intersects $\partial$, say, at at point z (see Fig. 16). In this case, we can readily compute the Voronoi regions of the roots that define the rays in S. Finally, we move the reference point $p^*$ to z, and continue with the next ray $\rho _{i+1}$.

• 2. If $\overline{p_1p_1'}$ does not intersect $\partial$ (see Fig. 17), then depending on whether the point $p_1'$ is on the right edge or the bottom edge of $Rec(p_1,q_1)$, there are further two cases.

  • (a) If $p_1'$ is on the bottom edge of $Rec(p_1,q_1)$ (see Fig. 17), then let $\rho _i^*$ be the vertical ray originating at $p_1'$ and going south, which is on $B(r_j,r_{i+1})$. We pop $\rho$ out of S and push $\rho _i^*$ onto the top of S. We move $p^*$ to $tp(\rho _i)$), and then continue with the next ray $\rho _{i+1}\in \Psi$.

  • (b) If $p_1'$ is on the right edge of $Rec(p_1,q_1)$ (see Fig. 18), then denote by $\rho _{i1}$ the horizontal ray originating at $p'_1$ and going east, which is on $B(r_j,r_{i+1})$. Then, we pop $\rho$ out of S and move $p^*$ to $tp(\rho _i)$. Finally, we let $\rho _{i1}$ be the next ray to be considered by the algorithm (note that $\rho _{i1}$ is not in $\Psi$).

Fig. 17

Illustrating an example that the point $p_1'$ [$=or(\rho _i^*)$] is on the bottom edge of $Rec(p_1,q_1)$

Fig. 18

Illustrating an example that the point $p_1'$ [$=or(\rho _{i1})$] is on the right edge of $Rec(p_1,q_1)$

5.3.4 The Details of the Algorithm

We now present the full details of the algorithm, including its proof of correctness.

We start with the first ray $\rho _1$. If $\rho _1$ is horizontal (going east), then since $or(\rho _1)$ is the first origin along the northeast direction, no other ray in $\Psi$ can intersect it. Let p be the target point of $\rho _1$ on $\partial$ (see Fig. 13). Clearly, p can be found in O(1) time since we already know the trapezoid in ${H\!M}(bay({\overline{cd}}))$ that contains $or(\rho _1)$ by Observation 8. Denote by $\alpha$ the portion of $B(r_1,r_2)$ between $v_1$ and p. Note that $\alpha$ is either the line segment $\overline{v_1p}$ [if $v_1=or(\rho _1)$], or the concatenation of the two line segments $\overline{v_1or(\rho _1)}$ and $\overline{or(\rho _1)p}$. In either case, $\alpha$ partitions $bay({\overline{cd}})$ into two simple polygons. One of them contains $\overline{cv_1}$ as an edge and we denote it by $bay_1$ (see Fig. 13). We claim that $bay_1$ is the Voronoi region of $r_1$, i.e., ${V\!D}(r_1)=bay_1$. Indeed, by the above analysis and Lemma 13, $\alpha$ is in ${\mathcal{VD}}(bay({\overline{cd}}))$, implying that for any point $q\in bay_1$, there is a shortest path from s to q via $r_1$. The claim thus follows, and ${V\!D}(r_1)$ is determined. We then set the ray $\rho _1$ and the region of $bay_1$ as inactive. Hence, the active region of $bay({\overline{cd}})$ becomes $bay({\overline{cd}})\backslash bay_1$, which needs to be further decomposed. In addition, we move the reference point $p^*$ from c to p [$=tp(\rho _1)$]. We then continue with the next ray $\rho _2$.

If $\rho _1$ is vertical (going south), then we push $\rho _1$ onto a stack S (initially, $S=\emptyset$), and let the reference point $p^*$ stay at c. We then continue with the next ray $\rho _2$.

We will show below that our algorithm maintains the following general invariants, which are used to prove the correctness of the algorithm. Suppose the current moment of the algorithm is right before the next ray $\rho$ is considered, and assume $\rho$ lying on the bisector $B(r_j,r_i)$ with $i>j$. The stack S may be non-empty; if $S=\emptyset$, then the invariants below related to any rays in S are not applicable. Let $\rho '$ be the ray at the top of S, and suppose $\rho '$ lies on $B(r_t,r_{t'})$ with $t'>t$.

Algorithm Invariants

Our algorithm maintains the following invariant properties:

• 1. All rays in S are active and vertically going south.

• 2. The origins of all rays in S from top to bottom are ordered from southwest to northeast.

• 3. The origin of the next ray to be considered by the algorithm (i.e., $\rho )$ is to the southwest of the origin of the ray at the top of $S\ ($i.e., $\rho ')$.

• 4. The two indices j and $t'$ are equal.

• 5. For each ray $\rho ''$ in $S\cup \{\rho \}$, suppose $\rho ''$ lies on the bisector $B(r_{j'},r_{i'})$ of two roots $r_{j'}$ and $r_{i'}$ with $i'>j'$; then the portion of the boundary of the Voronoi region ${V\!D}(r_{i'})\ [$resp., ${V\!D}(r_{j'})]$ from $v_{i'-1}\ ($resp., $v_{j'})$ to the origin $or(\rho '')$ of $\rho ''$ has already been computed [more specifically, the boundary of ${V\!D}(r_{i'})$ is partitioned into two portions by $v_{i'-1}$ and $or(\rho '')$, and the above boundary portion refers to the one that does not include $\overline{v_{i'-1}v_{i'}}$ on ${\overline{cd}}$; the similar applies to the boundary portion of ${V\!D}(r_{j'})]$.

• 6. For each ray $\rho ''$ in S, suppose it lies on the bisector $B(r_{j'},r_{i'})$ of two roots $r_{j'}$ and $r_{i'}$ with $i'>j'$; then $r_{j'}$ is to the right of $\rho ''$ and $r_{i'}$ is to the left of $\rho ''$.

• 7. The root $r_t$ is to the left of all rays in $S\backslash \{\rho '\}\ [$recall that $\rho '\subset B(r_{t},r_{t'})$ with $t'>t]$.

• 8. For any two consecutive rays $\rho '_1$ and $\rho '_2$ in S such that $\rho '_1$ is closer to the top of S, suppose $\rho '_1$ is on $B(r_{i_1},r_{i_2})$ for $i_2>i_1$ and $\rho '_2$ is on $B(r_{j_1},r_{j_2})$ for $j_2>j_1$; then $i_1=j_2$.

• 9. The target points of all rays in S from bottom to top are ordered clockwise on $\partial \ ($i.e., from c to d).

• 10. If $\rho$ is vertical, then the target point $tp(\rho )$ of $\rho$ is after the target point $tp(\rho ')$ of $\rho '$ on $\partial$.

• 11. If the target point of any ray in S has not been computed yet, then the target point of that ray is after the reference point $p^*\ [$i.e., on $\partial (p^*,d)]$.

• 12. The target point $tp(\rho )$ is after $p^*$.

• 13. Suppose $\rho ''$ is the first horizontal ray in $\Psi$ that will be considered by the algorithm in a future time from now; then its target point $tp(\rho '')$ is after $p^*$.

• 14. The trapezoid in the horizontal visibility map ${H\!M}(bay({\overline{cd}}))$ that contains the origin $or(\rho )$ of the ray $\rho$ has been computed.

Now consider the moment that is right after we finish processing $\rho _1$ and before we consider $\rho _2$. Based on the processing of $\rho _1$ discussed above, either $\rho _1$ is horizontal and S is empty, or $\rho _1$ is vertical and $S= \{\rho _1\}$. Lemma 16 below shows that in either case, all invariants of the algorithm hold. We intend to use the proof of Lemma 16 as a “warm-up” for the analysis of the more general situations later. Observation 9 follows from the definitions of the rays in $\Psi$ and Lemma 11.

Observation 9

The target points of all rays in $\Psi$ are on $\partial$. For any two rays $r_j$ and $r_i$ in $\Psi$ with $i>j$, if $r_j$ is horizontal or $r_i$ is vertical, then $tp(r_i)$ is after $tp(r_j)$ on $\partial$.

Lemma 16

At the moment after $\rho _1$ has been processed and before $\rho _2$ is considered, all invariants of the algorithm hold.

Proof

Recall that $\rho _1$ is on $B(r_1,r_2)$ and $\rho _2$ is on $B(r_2,r_3)$, and the reference point $p^*$ is at the target point $tp(\rho _1)$ if $\rho _1$ is horizontal and at the vertex c otherwise.

We first discuss the case when $\rho _1$ is horizontal, in which S is empty and $p^*=tp(\rho _1)$. Invariants (1) through (11) except (5) simply follow since they are all related to some rays in S. For Invariant (5), we only need to consider $\rho _2\subset B(r_2,r_3)$, i.e., we need to show that the portion of the boundary of the Voronoi region ${V\!D}(r_{3})$ from $v_{2}$ to the origin $or(\rho _2)$ of $\rho _2$, which is also the boundary portion of the Voronoi region ${V\!D}(r_{2})$ from $v_{2}$ to $or(\rho _2)$, has already been computed. Denote this boundary portion by $\alpha$. Note that $\alpha$ is the portion of $B(r_2,r_3)$ between $v_2$ and $or(\rho _2)$. Recall that $or(\rho _2)$ is either $v_2$ or not. If $or(\rho _2)=v_2$, then we are done since $\alpha$ is just a single point $v_2$. Otherwise, $v_2$ must be on $B_M(r_2,r_3)$ and $\alpha$ is $B'_M(r_2,r_3)$ [$=\overline{v_2or(\rho _2)}$], which has been computed in our preprocessing by Observation 8. Hence, Invariant (5) follows.

For Invariant (12), we need to show that $tp(\rho _2)$ is after $p^*=tp(\rho _1)$, which is true due to Observation 9 and $\rho _1$ being horizontal. For Invariant (13), let $i>1$ be the smallest index such that $\rho _i\in \Psi$ is horizontal. If there is no such i, then Invariant (13) trivially holds; otherwise, we need to prove that $tp(\rho _i)$ is after $p^*=tp(\rho _1)$, which is true due to Observation 9 and $\rho _1$ being horizontal. For Invariant (14), we need to show that the trapezoid of ${H\!M}(bay({\overline{cd}}))$ containing $or(\rho _2)$ is known, which is true by Observation 8. Hence, when $\rho _1$ is horizontal, all invariants hold.

We then discuss the case when $\rho _1$ is vertical, in which $S= \{\rho _1\}$ and the reference point $p^*=c$. Invariants (1) and (2) simply follow. By Lemma 11, $or(\rho _2)$ is to the southwest of $or(\rho _1)$, and thus Invariant (3) holds. Invariant (4) is obvious. For Invariant (5), we need to consider both $\rho _1$ and $\rho _2$. The proof is similar to that for the case when $\rho _1$ is horizontal, and we omit it. For Invariant (6), we need to show that $r_1$ is to the right of $\rho _1$ and $r_2$ is to the left of $\rho _1$, which is true due to Lemma 9 and $\rho _1$ being vertical. Invariant (7) simply follows since $\rho _1$ is the only ray in S. Invariants (8) and (9) trivially hold since S has only one ray. For Invariant (10), we need to show that if $\rho _2$ is vertical, then $tp(\rho _2)$ is after $tp(\rho _1)$, which is true by Observation 9. For Invariant (11), note that the target point $tp(\rho _1)$ has not been computed. Since $p^*=c$, Invariant (11) trivially holds. Invariants (12) and (13) also easily hold since $p^*=c$ and the target points of all rays in $\Psi$ are on $\partial$. For Invariant (14), we need to show that the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains $or(\rho _2)$ is known, which is true by Observation 8.

We hence conclude that all invariants of the algorithm hold. $\square$

As an implementation detail, although we view S as a stack, we represent S as a doubly-linked list so that we can access the rays in S from both the top and the bottom of S. But, we always pop a ray out of S from its top and push a ray onto S at its top. Next, we discuss the general situations of our algorithm.

Suppose our algorithm just starts to process a ray $\rho _{i}\in \Psi$, $i>1$, which lies on the bisector $B(r_i,r_{i+1})$, and all invariants of the algorithm hold right before $\rho _i$ is processed. There are a number of cases and subcases to consider, depending on whether $\rho _i$ is vertical or horizontal, whether S is empty, and the intersecting consequences between $\rho _i$ and the rays in S (if $S\not =\emptyset$), etc.

Case 1: $\rho _i$ is vertical (going south). Then we simply push $\rho _i$ onto the top of S and the reference point $p^*$ is not changed. The algorithm then continues with the next ray $\rho _{i+1}\in \Psi$ in this situation. Lemma 17 below shows that all invariants of the algorithm hold.

Lemma 17

If the ray $\rho _i\in \Psi$ is vertical, then at the moment after $\rho _i$ is processed and before $\rho _{i+1}$ is considered, all invariants of the algorithm hold.

Proof

Note that $\rho _{i+1}$ is on $B(r_{i+1},r_{i+2})$. Let $\xi$ be the moment right after $\rho _i$ is processed and $\xi '$ be the moment right before $\rho _i$ is considered. Thus, from $\xi '$ to $\xi$, the only change to S is that we push $\rho _i$ onto the top of S. The proof below is based on the assumption that S has at least two rays at the moment $\xi$ (i.e., $\rho _i$ and at least another ray), since otherwise the invariants related to other rays in S than $\rho _i$ trivially hold. This also implies that S is not empty at the moment $\xi '$. Let $\rho$ be the ray at the top of S at the moment $\xi '$, and assume $\rho$ lying on the bisector $B(r_{j},r_{j'})$ with $j'>j$.

Invariant (1) holds since $\rho _i$ is vertical.

For Invariant (2), since all invariants of the algorithm hold at the moment $\xi '$, it suffices to show that $or(\rho _i)$ is to the southwest of $or(\rho )$. Note that at the moment $\xi '$, $\rho _i$ is the next ray to be considered by the algorithm. Thus, by Invariant (3) at the moment $\xi '$, $or(\rho _i)$ is to the southwest of $or(\rho )$. Invariant (2) thus follows.

For Invariant (3), Lemma 11 implies that $or(\rho _{i+1})$ is to the southwest of $or(\rho _i)$.

Invariant (4) trivially holds since $\rho _i\subset B(r_{i},r_{i+1})$ and $\rho _{i+1}\subset B(r_{i+1},r_{i+2})$.

For Invariant (5), it suffices to consider the ray $\rho _{i+1}$, i.e., to show that the portion of the boundary of ${V\!D}(r_{i+1})$ between $v_{i+1}$ and $or(\rho _{i+1})$, which is also the portion of the boundary of ${V\!D}(r_{i+2})$ between $v_{i+1}$ and $or(\rho _{i+1})$, has already been computed. (Note that the case for the ray $\rho _i$ trivially holds due to Invariant (5) at the moment $\xi '$ when $\rho _i$ is the next ray to be considered.) Recall that the above boundary portion is a single point $v_{i+1}$ if $v_{i+1}=or(\rho _{i+1})$ and is the line segment $\overline{v_{i+1}or(\rho _{i+1})}$ otherwise. By Observation 8, if $v_{i+1}\ne or(\rho _{i+1})$, then $\overline{v_{i+1}or(\rho _{i+1})}$ has already been computed in the preprocessing. Thus, Invariant (5) follows.

For Invariant (6), it suffices to prove that $r_{i}$ is to the right of $\rho _i$ and $r_{i+1}$ is to the left of $\rho _i$, which follows from Lemma 9 since $\rho _i$ is vertical.

For Invariant (7), it suffices to show that $r_i$ is to the left of $\rho$. Recall that $\rho$ is on $B(r_{j},r_{j'})$ with $j'>j$. At the moment $\xi '$, by Invariant (4), $j'=i$; by Invariant (6), $r_i$ ($=r_{j'}$) is to the left of $\rho$. Thus, Invariant (7) follows.

For Invariant (8), it suffices to show $j'=i$, which has been proved above for Invariant (7).

For Invariant (9), it suffices to show that $tp(\rho _i)$ is after $tp(\rho )$ on $\partial$. Since $\rho _i$ is vertical, at the moment $\xi '$, by Invariant (10), $tp(\rho _i)$ is after $tp(\rho )$ on $\partial$. Invariant (9) thus follows.

For Invariant (10), we need to prove that if $\rho _{i+1}$ is vertical, then $tp(\rho _{i+1})$ is after $tp(\rho _i)$ on $\partial$, which follows from Observation 9.

For Invariant (11), note that the target point $tp(\rho _i)$ has not been computed. We need to show that $tp(\rho _i)$ is after $p^*$ on $\partial$. At the moment $\xi '$, by Invariant (12), $tp(\rho _i)$ is after $p^*$. Further, $p^*$ has not been moved since the moment $\xi '$. Invariant (11) thus follows.

For Invariant (12), we need to show that $tp(\rho _{i+1})$ is after $p^*$. If $\rho _{i+1}$ is vertical, then by Observation 9, $tp(\rho _{i+1})$ is after $tp(\rho _i)$ on $\partial$, and we have also shown above that $tp(\rho _i)$ is after $p^*$; thus $tp(\rho _{i+1})$ is after $p^*$. If $\rho _{i+1}$ is horizontal, then at the moment $\xi '$, since $\rho _i$ is vertical, the first horizontal ray in $\Psi$ to be considered by the algorithm in future is $\rho _{i+1}$; thus by Invariant (13), $tp(\rho _{i+1})$ is after $p^*$. Invariant (12) then follows.

Invariant (13) trivially holds since $\rho _i$ is vertical. More specifically, suppose the first horizontal ray in $\Psi$ that will be considered by the algorithm after the moment $\xi '$ is $\rho _j$. Note that $j\ge i$. Since all invariants of the algorithm hold at the moment $\xi '$, by Invariant (13), $tp(r_j)$ is after $p^*$ on $\partial$. Then at the moment $\xi$, since $\rho _i$ is vertical, the first horizontal ray in $\Psi$ to be considered by the algorithm is still $\rho _j$. Proving that Invariant (13) holds at the moment $\xi$ is to prove that $tp(r_j)$ is after $p^*$, which has been proved above since $p^*$ has not been moved since the moment $\xi '$.

For Invariant (14), we need to show that the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains $or(\rho _{i+1})$ is known, which is true by Observation 8.

We conclude that all invariants of the algorithm hold at the moment $\xi$. $\square$

Case 2: $\rho _i$ is horizontal (going east). Let $p=tp(\rho _i)$. We claim that we can find p in constant time. Indeed, since $\rho _i$ is the next ray considered by the algorithm, by Invariant (14), the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains $or(\rho _i)$ is known. The claim then follows since p is on the boundary of the above trapezoid. Since $\rho _i$ is horizontal, by Invariant (13) (at the moment right before processing $\rho _i$), p is after the reference point $p^*$. Depending on whether the stack S is empty, there are two subcases to consider.

Subcase 2(a): $S=\emptyset$. Then no ray in S intersects $\rho _i$ before it hits $\partial$ (and thus no ray shooting for any ray $\rho _j\in \Psi$ with $j<i$ intersects $\rho _i$ before hitting $\partial$). Also, for each ray $\rho _j\in \Psi$ with $j>i$, since $or(\rho _j)$ is to the southwest of $or(\rho _i)$ and $\rho _i$ is horizontal, $\rho _j$ cannot intersect $\rho _i$. Hence, the portion $\overline{or(\rho _i)p}$ of the ray $\rho _i$ appears in ${\mathcal{VD}}(bay({\overline{cd}}))$. Recall that $\rho _i$ is on $B(r_i,r_{i+1})$. The portion of $B(r_i,r_{i+1})$ between $v_{i}$ and p divides the current active region of $bay({\overline{cd}})$ into two simple polygons; one of them contains $\overline{v_{i-1}v_i}$ and we denote it by $bay_i$. Further, each point in $bay_i$ has a shortest path to s via $r_i$. Thus, $bay_i$ is the Voronoi region ${V\!D}(r_i)$. We then set $\rho _{i}$ and the region $bay_i$ as inactive. In addition, we move $p^*$ to p. We then consider the next ray $\rho _{i+1}$. We prove below that all invariants of the algorithm hold right after processing $\rho _i$.

Since S is empty, Invariants (1) to (11) except (5) simply hold since they are all related to some rays in S. For Invariant (5), we only need to consider $\rho _{i+1}$, which also holds by Observation 8 (the analysis is similar as before). For Invariant (12), we need to show that $tp(\rho _{i+1})$ is after $p^*$. Since $\rho _i$ is horizontal, by Observation 9, $tp(\rho _{i+1})$ is after $tp(\rho _i)$ ($=p^*$). Thus, Invariant (12) follows. For Invariant (13), suppose $\rho _j\in \Psi$ is the first horizontal ray to be considered by the algorithm. Note that it must be $j>i$. We need to show that $tp(\rho _j)$ is after $p^*$ [$=tp(\rho _i)$], which is true by Observation 9 since $\rho _i$ is horizontal. For Invariant (14), we need to show that the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains $or(\rho _{i+1})$ is known, which is true by Observation 8. Therefore, all invariants of the algorithm hold right after processing $\rho _i$.

Subcase 2(b): $S\not =\emptyset$. Then for the rays in S whose target points lie on $\partial (p^*,p)$, we compute their target points by scanning $\partial (p^*,p)$ from $p^*$ to p [$=tp(\rho _i)$]; this scanning process uses the visibility map based approach with ${V\!M}(bay({\overline{cd}}))$, as described in the preprocessing. By Invariant (9), such vertical rays (from bottom to top in S) are target-sorted. Thus, the scanning procedure takes linear time in terms of the number of edges of $\partial (p^*,p)$ and the number of target points found in this process. Note that the scanning procedure stops when we encounter the point p. This also implies that the target points of some rays in S (e.g., the ray at the top of S) are not yet found if they are on $\partial$ after p.

Let $\rho$ be the ray at the top of S (e.g., if $\rho _{i-1}$ is vertical, then $\rho$ is $\rho _{i-1}$). Suppose $\rho$ is on the bisector $B(r_{j},r_{j'})$ with $j'>j$. Then right before $\rho _i$ is processed, by Invariant (4), $i=j'$ since $\rho _i\subset B(r_{i},r_{i+1})$; by Invariant (3), $or(\rho _i)$ is to the southwest of $or(\rho )$. Depending on whether the target point $tp(\rho )$ is before p or not, there are two subcases.

Subcase 2(b.1): The target point $tp(\rho )$ is before $p=tp(\rho _i)$. In this case, the scanning procedure has found $tp(\rho )$ on $\partial (p^*,p)$. Then by Invariants (9) and (11), the target points of all rays in S have been obtained and all such target points are before p on $\partial$. Since p is the target point of $\rho _i$, the above implies that all rays in S hit $\partial$ before they intersect $\rho _i$ (see Fig. 14). Further, since all other active rays in $\Psi$, i.e., $\rho _{i+1},\rho _{i+2},\ldots ,\rho _{k-1}$, have their origins to the southwest of $or(\rho _i)$, no ray in S can intersect these active rays before it hits $\partial$. This means that for each ray $\rho '$ in S, the portion of $\rho '$ between $or(\rho ')$ and $tp(\rho ')$ appears in ${\mathcal{VD}}(bay({\overline{cd}}))$. Based on the discussion above, we perform a splitting procedure on S, as follows.

Let $\rho '$ be the ray at the bottom of S and $z=tp(\rho ')$ (see Fig. 14). Suppose $\rho '$ is on the bisector $B(r_{t},r_{t'})$ with $t'>t$. By Invariant (5), the boundary portion of ${V\!D}(r_t)$ between $v_t$ and $or(\rho ')$ has been computed. The concatenation of the segment $\overline{or(\rho ')z}$ and this boundary portion of ${V\!D}(r_t)$ splits the current active region of $bay({\overline{cd}})$ into two simple polygons. One of them contains $\overline{v_{t-1}v_t}$ as an edge; further, each point in this polygon has a shortest path to s via $r_t$. Thus, the polygon containing $\overline{v_{t-1}v_t}$ is the Voronoi region ${V\!D}(r_t)$. We also set the region ${V\!D}(r_t)$ as inactive.

We then continue to process the second bottom ray in S, in the similar fashion. This splitting procedure stops once all rays in S are processed. In addition, we set all rays in S as inactive and pop them out of S (S then becomes empty). Finally, we move the reference point $p^*$ to p [$=tp(\rho _i)$], and consider the next ray $\rho _{i+1}$. By the same analysis as that for the Subcase 2(a) when S is empty, we can prove that all invariants of the algorithm hold. We omit the details.

Subcase 2(b.2): The target point $tp(\rho )$ is not before $p=tp(\rho _i)$. In this case, $tp(\rho )$ has not been found on $\partial (p^*,p)$ by the scanning procedure. Then, $\rho$ must intersect $\rho _i$ before it hits $\partial$ (and so may some other rays in S). We need to consider the consequences of the intersections of such rays in S with $\rho _i$. Recall that $\rho _i$ is on $B(r_i,r_{i+1})$ and $\rho$ is on $B(r_j,r_i)$ with $i>j$. Below we show how to determine the Voronoi region ${V\!D}(r_i)$ and the portion of the bisector $B(r_j,r_{i+1})$ in ${\mathcal{VD}}(bay({\overline{cd}}))$. Let $p_1$ be the intersection point of $\rho _i$ and $\rho$ (see Fig. 15).

First of all, we determine the Voronoi region ${V\!D}(r_i)$ (see Fig. 15). Since $\rho$ is the leftmost ray in S by Invariant (2), both the line segments $\overline{or(\rho _i)p_1}$ and $\overline{or(\rho )p_1}$ appear in ${\mathcal{VD}}(bay({\overline{cd}}))$. Since the ray $\rho$ is in the stack S, by Invariant (5), the boundary portion of ${V\!D}(r_i)$ between $v_{i-1}$ and $or(\rho )$ has been computed, which we denote by $\alpha$. At the moment right before $\rho _i$ is processed, since $\rho _i$ is the next ray to be considered, also by Invariant (5), the boundary portion of ${V\!D}(r_i)$ between $v_{i}$ and $or(\rho _i)$ has been computed, which we denote by $\beta$ [i.e., $\beta =v_i$ if $v_i=or(\rho _i)$ and $\beta =\overline{v_ior(\rho _i)}$ otherwise]. As argued similarly in the earlier analysis, ${V\!D}(r_i)$ is the region bounded clockwise by $\alpha$, the segment $\overline{or(\rho )p_1}$, the segment $\overline{or(\rho _i)p_1}$, $\beta$, and $\overline{v_{i-1}v_i}$. This region of ${V\!D}(r_i)$ is then set as inactive.

Second, we determine the portion of the bisector $B(r_j,r_{i+1})$ that appears in ${\mathcal{VD}}(bay({\overline{cd}}))$. Since $\rho _i$ is horizontal, by Lemma 9, the root $r_{i+1}$ is below $\rho _i$. Since $\rho \subset B(r_j,r_i)$ with $i>j$, by Invariant (6), $r_j$ is to the right of $\rho$. Therefore, the intersection point (denoted by $q_1$) of the horizontal line through $r_{i+1}$ and the vertical line through $r_j$ is to the southeast of $p_1$ (see Fig. 15). We first discuss the portion of $B(r_j,r_{i+1})$ contained in the rectangle $Rec(p_1,q_1)$.

Obviously, $Rec(p_1,q_1)$ is contained in the rectangle $Rec(r_j,r_{i+1})$. Thus, the portion of $B(r_j,r_{i+1})$ in $Rec(p_1,q_1)$ is a portion of the middle segment of $B(r_j,r_{i+1})$. Further, since $p_1$ is the intersection of $\rho _i$ and $\rho$, $p_1$ is at the intersection of $B(r_i,r_{i+1})$ and $B(r_j,r_i)$. Thus, $p_1$ is on $B(r_j,r_{i+1})$.

We claim that $r_{i+1}$ is to the southwest of $r_{j}$. This can be proved by showing that $r_{i+1}$ is to the southwest of $p_1$ and $p_1$ is to the southwest of $r_j$. Indeed, since $r_{i+1}$ is below $\rho _i$ and ${\overline{cd}}$ is positive-sloped, $p_1$ must be to the right of $r_{i+1}$, which also implies that $r_{i+1}$ is to the southwest of $p_1$. Similarly, we can show that $p_1$ is to the southwest of $r_j$.

Because $r_{i+1}$ is to the southwest of $r_{j}$, the middle segment of $B(r_j,r_{i+1})$ is $-\,1$-sloped. Denote by $B_M'(r_j,r_{i+1})$ the portion of $B(r_j,r_{i+1})$ contained in $Rec(p_1,q_1)$. Based on the above analysis, $B_M'(r_j,r_{i+1})$ is a $-\,1$-sloped line segment with an endpoint at $p_1$ and the other endpoint on one of the two edges of $Rec(p_1,q_1)$ incident to $q_1$ (see Fig. 15). We have the following lemma.

Lemma 18

$B_M'(r_j,r_{i+1})\cap bay({\overline{cd}})\ ($i.e., the portion of $B_M'(r_j,r_{i+1})$ contained in $bay({\overline{cd}}))$ appears in ${\mathcal{VD}}(bay({\overline{cd}}))$.

Proof

The proof is similar to that for Lemma 13 and hence we only sketch it here. For convenience, we view $B_M'(r_j,r_{i+1})$ as the open segment that does not contain its two endpoints.

It suffices to show that $B_M'(r_j,r_{i+1})$ does not intersect any current active ray. Consider any current active ray $\rho '$, $\rho '\not \in \{\rho ,\rho _{i}\}$. Then $\rho '$ either is in S or is a ray $\rho _t\in \Psi$ with $t>i$.

• If $\rho ' \in S$, then $\rho '$ is vertical by Invariant (1). By Invariant (7), $\rho '$ is to the right of the root $r_j$, and thus to the right of the rectangle $Rec(p_1,q_1)$. Hence, $\rho _t$ does not intersect $B_M'(r_j,r_{i+1})$ since $B_M'(r_j,r_{i+1})$ is strictly inside $Rec(p_1,q_1)$.

• If $\rho '= \rho _t\in \Psi$ with $t>i$, then there are two subcases. If $\rho _t$ is horizontal, then by Lemma 12, $\rho _t$ is below $r_{i+1}$, and is thus below the rectangle $Rec(p_1,q_1)$. Hence, $\rho _t$ does not intersect $B_M'(r_j,r_{i+1})$.

  If $\rho _t$ is vertical, then by Lemma 11, the origin $or(\rho _i)$ is to the northeast of $or(\rho _t)$. Clearly, $or(\rho _i)$ is to the left of $Rec(p_1,q_1)$ and thus $or(\rho _t)$ is to the left of $Rec(p_1,q_1)$. Since $\rho _t$ is vertical, $\rho _t$ is also to the left of $Rec(p_1,q_1)$. Hence, $\rho _t$ does not intersect $B_M'(r_j,r_{i+1})$.

The above argument shows that none of the active rays can intersect $B_M'(r_j,r_{i+1})$. Hence, the portion of $B_M'(r_j,r_{i+1})$ contained in $bay({\overline{cd}})$ must appear in ${\mathcal{VD}}(bay({\overline{cd}}))$. $\square$

The preceding lemma implies that we should report the portion of $B_M'(r_j,r_{i+1})$ that is contained in $bay({\overline{cd}})$ as part of ${\mathcal{VD}}(bay({\overline{cd}}))$.

We compute $B_M'(r_j,r_{i+1})$ in O(1) time, and let $B_M'(r_j,r_{i+1})=\overline{p_1p_1'}$ (see Fig. 15). Note that $p_1'$ is either on the right edge or the bottom edge of $Rec(p_1,q_1)$. However, $\overline{p_1p_1'}$ may intersect $\partial$. To determine whether such intersection occurs, we move among the trapezoids in the horizontal visibility map ${H\!M}(bay({\overline{cd}}))$ from the endpoint $p_1$ of $B_M'(r_j,r_{i+1})$ along the segment $\overline{p_1p_1'}$, as follows.

Note that the portion of the ray $\rho _i$ between its origin $or(\rho _i)$ and its target point $p=tp(\rho _i)$ is contained in a single trapezoid of ${H\!M}(bay({\overline{cd}}))$, i.e., the trapezoid containing $or(\rho _i)$, which is already known according to Invariant (14). Further, this trapezoid is the one that contains $p_1$ since $p_1\in \overline{or(\rho _i)p}$. Starting at $p_1$ in this trapezoid, we move along the segment $\overline{p_1p_1'}$, and enter/exit trapezoids in ${H\!M}(bay({\overline{cd}}))$ one after another, until we encounter either $p_1'$ or an edge of $\partial$ for the first time. In this way, we can determine whether $\overline{p_1p_1'}$ intersects $\partial$. Further, if $\overline{p_1p_1'}$ intersects $\partial$, then the first such intersection point, denoted by z, is also found in this moving process; if $B_M'(r_j,r_{i+1})$ does not intersect $\partial$, then the trapezoid of ${H\!M}(bay({\overline{cd}}))$ containing the point $p_1'$ is determined. It is easy to see that the running time of the above moving procedure is proportional to the number of trapezoids in ${H\!M}(bay({\overline{cd}}))$ that we visit when moving along $\overline{p_1p_1'}$. We will analyze the total running time of the moving process in a global manner later.

Depending on whether $B_M'(r_j,r_{i+1})$ ($=\overline{p_1p_1'}$) intersects $\partial$, there are two cases to consider.

If $B_M'(r_j,r_{i+1})$ intersects $\partial$, then we have found the first intersection point z of $B_M'(r_j,r_{i+1})$ and $\partial$ (see Fig. 16). Note that z must be after p on $\partial$. Also, note that the Voronoi region ${V\!D}(r_i)$ has been computed and set as inactive, and thus $p_1$ lies on the boundary of the current active region of $bay({\overline{cd}})$ (see Fig. 16). Similarly as before, the line segment $\overline{p_1z}$ divides the current active region of $bay({\overline{cd}})$ into two simple polygons; one of them, say $bay'$, contains the point p. Then, the Voronoi regions of the roots that define the rays in S form a decomposition of $bay'$, and we use a procedure similar to the splitting procedure discussed earlier to compute this decomposition of $bay'$, i.e., by considering the rays in S from bottom to top. However, it is possible that the target points of some rays in S have not been computed yet. Recall that all target points of the rays in S before p [$=tp(\rho _i)$] have been computed. But, if the target point of a ray in S is on $\partial (p,z)$, then it is not yet known. To compute these target points, we simply scan $\partial (p,z)$ from p to z. Again, by Invariant (9), the vertical rays in S are target-sorted. Hence this computation can be done in linear time in terms of the number of edges of $\partial (p,z)$ and the number of target points found during this process. In addition, we set the region $bay'$ and all rays in S as inactive, and pop all rays out of S (S becomes empty). Finally, we move the reference point $p^*$ to z, and continue with the next ray $\rho _{i+1}$. Again, since S is empty, similar to the analysis for the subcase 2(a) when S is empty, all invariants of the algorithm hold. We omit the details of the proof.

If $B_M'(r_j,r_{i+1})$ ($=\overline{p_1p_1'}$) does not intersect $\partial$ (see Fig. 17), then as shown above, $B_M'(r_j,r_{i+1})$ appears entirely in ${\mathcal{VD}}(bay({\overline{cd}}))$ since it is contained inside $bay({\overline{cd}})$. Again, the point $p_1'$ is on either the right edge or the bottom edge of $Rec(p_1,q_1)$ (two cases). We discuss these two cases below. Recall that the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains $p_1'$ has been computed. Recall that the ray at the top of S is $\rho$, lying on $B(r_j,r_i)$ with $i>j$.

We first discuss the case when $p_1'$ is on the bottom edge of $Rec(p_1,q_1)$ (see Fig. 17). Let $\rho _i^*$ be the vertical ray originating at $p_1'$ and going south, which is on $B(r_j,r_{i+1})$ by Observation 4. We pop $\rho$ out of S and push $\rho _i^*$ onto the top of S, and set $\rho$ as inactive and $\rho _i^*$ as active. We move $p^*$ to p [$=tp(\rho _i)$]. We then continue to consider the next ray $\rho _{i+1}\in \Psi$. Lemma 19 below shows that all invariants of the algorithm hold.

Lemma 19

At the moment right before the next ray $\rho _{i+1}$ is considered, all invariants of the algorithm hold.

Proof

Let $\xi$ be the moment right before the next ray $\rho _{i+1}$ is considered, and $\xi '$ be the moment right before the ray $\rho _i$ is considered. Thus, the change to S from the time $\xi '$ to $\xi$ is that $\rho$ is popped out and $\rho _i^*$ is pushed in. Recall that at the moment $\xi '$, all invariants of the algorithm hold. Our goal is to prove that all invariants still hold at the moment $\xi$. We assume that S has at least two rays at the moment $\xi$ (otherwise, all invariants related to any other rays in S than $\rho ^*_i$ hold trivially). Let $\rho '$ be the second ray from the top of S (i.e., right below $\rho _i^*$ in S) at the moment $\xi$. Then $\rho '$ is also the second ray from the top of S at the moment $\xi '$ (i.e., right below $\rho$ in S). See Fig. 17 for an example.

Invariant (1) simply follows since $\rho _i^*$ is vertically going south.

For Invariant (2), it suffices to show that $or(\rho ^*_i)$ is to the southwest of $or(\rho ')$. At the moment $\xi '$, since the ray $\rho$ at the top of S is on $B(r_j,r_i)$ with $i>j$, by Invariant (6), $r_j$ is to the left of $or(\rho ')$. Since $or(\rho ^*_i)\in Rec(r_j,r_{i+1})$ is to the left of $r_j$, we obtain that $or(\rho _i^*)$ is to the left of $or(\rho ')$. Further, at the moment $\xi '$, by Invariant (2), $or(\rho )$ is to the southwest of $or(\rho ')$. Since $or(\rho _i^*)$ is below $or(\rho )$, $or(\rho _i^*)$ is below $or(\rho ')$. Since $or(\rho _i^*)$ is both below and to the left of $or(\rho ')$, we obtain that $or(\rho _i^*)$ is to the southwest of $or(\rho ')$. Invariant (2) thus follows.

For Invariant (3), we need to show that $or(\rho _{i+1})$ is to the southwest of $or(\rho _i^*)$. By Lemma 11, $or(\rho _{i+1})$ is to the southwest of $or(\rho _i)$. Since $or(\rho _i^*)$ is to the right of $or(\rho _i)$, $or(\rho _i^*)$ is also to the right of $or(\rho _{i+1})$. By Lemma 9(3), $or(\rho _{i+1})$ is below $r_{i+1}$. Hence, $or(\rho _{i+1})$ is below the rectangle $Rec(p_1,q_1)$ and thus below $or(\rho _i^*)$. Since $or(\rho _{i+1})$ is both below and to the left of $or(\rho _i^*)$, we obtain that $or(\rho _{i+1})$ is to the southwest of $or(\rho _i^*)$. Thus, Invariant (3) follows.

Invariant (4) simply follows since $\rho _i^*\subset B(r_j,r_{i+1})$ and $\rho _{i+1}\subset B(r_{i+1},r_{i+2})$.

For Invariant (5), we need to consider both $\rho _i^*$ and $\rho _{i+1}$. For $\rho _i^*$, since $\rho _i^*\subset B(r_j,r_{i+1})$, we need to show that the boundary portion of the Voronoi region ${V\!D}(r_{i+1})$ [resp., ${V\!D}(r_j)$] from $v_{i}$ (resp., $v_j$) to $or(\rho _i^*)$ has been computed. For this, recall that the boundary portion of ${V\!D}(r_{i+1})$ between $v_i$ and $p_1$ is a common boundary of ${V\!D}(r_{i+1})$ and ${V\!D}(r_i)$, which has been computed. We denote this boundary portion by $\alpha$. Also, the boundary portion of ${V\!D}(r_{j})$ between $v_j$ and $p_1$ has been computed; we denote this boundary portion by $\beta$. Further, after we find the point $p'_1$, the line segment $\overline{p_1p_1'}$ has also been obtained. Since $\overline{p_1p_1'}$ appears entirely in $\textit{SPM}({\mathcal {F}})$, the boundary portion of ${V\!D}(r_{i+1})$ between $v_i$ and $or(\rho _i^*)$ ($=p_1'$) is the concatenation of $\alpha$ and $\overline{p_1p_1'}$, which has been computed. Similarly, the boundary portion of ${V\!D}(r_{j})$ between $v_j$ and $or(\rho _i^*)$ is the concatenation of $\beta$ and $\overline{p_1p_1'}$, which has been computed too. Thus, the case for $\rho _i^*$ holds.

For the ray $\rho _{i+1}$, which is the ray to be considered next by the algorithm, we need to show that the boundary portion of the Voronoi region ${V\!D}(r_{i+1})$ from $v_{i+1}$ to $or(\rho _{i+1})$, which is also the boundary portion of the Voronoi region ${V\!D}(r_{i+2})$ from $v_{i+1}$ to $or(\rho _{i+1})$, has been computed. This simply follows from Observation 8.

In summary, Invariant (5) holds.

For Invariant (6), it suffices to show that $or(\rho _i^*)$ is to the left of $r_j$ and to the right of $r_{i+1}$. Recall that $or(\rho _i^*)$ is on the rectangle $Rec(p_1,q_1)$, $q_1$ is to the southeast of $p_1$, and $q_1$ is the intersection of the vertical line through $r_j$ and the horizontal line through $r_{i+1}$. As shown above, $r_{i+1}$ is to the left of $p_1$. Since $or(\rho _i^*)$ is to the right of $p_1$, $or(\rho _i^*)$ is to the right of $r_{i+1}$. Since $Rec(p_1,q_1)$ is to the left of $r_{j}$, $or(\rho _i^*)$ is to the left of $r_j$. Invariant (6) thus holds.

For Invariant (7), we need to show that $r_j$ is to the left of all rays in $S\backslash \{\rho _i^*\}$. At the moment $\xi '$, the ray $\rho \subset B(r_j,r_i)$ is at the top of S with $i>j$; thus by Invariant (7), $r_j$ is to the left of all rays in $S\backslash \{\rho \}$. Since $S\backslash \{\rho \}=S\backslash \{\rho _i^*\}$, Invariant (7) still holds at the moment $\xi$.

For Invariant (8), recall that $\rho '$ is the second ray from the top of S at both the moments $\xi$ and $\xi '$. We assume $\rho '$ lies on $B(r_t,r_{t'})$ with $t'>t$. To prove Invariant (8) held at $\xi$, it suffices to show $t'=j$ since $\rho _i^*\subset B(r_j,r_{i+1})$. At the moment $\xi '$, since $\rho \subset B(r_j,r_i)$ is the ray at the top of S, by Invariant (8), we have $j=t'$. Thus, Invariant (8) still holds at the moment $\xi$.

For Invariant (9), it suffices to show that $tp(\rho _i^*)$ is after $tp(\rho ')$ on $\partial$. Intuitively this is true due to the following facts: there is a path inside $bay({\overline{cd}})$ from $v_i$ to $or(\rho _i^*)$ [i.e., the concatenation of $\overline{v_ior(\rho _i)}$, $\overline{or(\rho _i)p_1}$, and $\overline{p_1p_1'}$], and both $\rho _i^*$ and $\rho '$ are vertical, and $\rho _i^*$ is to the left of $\rho '$. A detailed analysis is given below.

First, it is easy to see that $tp(\rho _i^*)$ must be after the point p [$=tp(\rho _i)$]. The target point $tp(\rho ')$ may be after p or before p. If $tp(\rho ')$ is before p, then we are done. Thus, we consider the case of $tp(\rho ')$ being after p. By Invariant (2) (at the moment $\xi$) proved above, $or(\rho ')$ is to the northeast of $or(\rho ^*_i)$. Thus, the ray $\rho '$ must cross $\rho _i$ before it hits $\partial$ at $tp(\rho ')$; in other words, the two line segments $\overline{or(\rho ')tp(\rho ')}$ and $\overline{or(\rho _i)tp(\rho _i)}$ intersect inside $bay({\overline{cd}})$. Further, since $\rho '$ is to the right of $\rho ^*_i$ and $p_1$ is to the left of $\rho _i^*$, the intersection point of $\overline{or(\rho ')tp(\rho ')}$ and $\overline{or(\rho _i)tp(\rho _i)}$ is on $\overline{p_1tp(\rho _i)}$.

Recall that $\overline{v_ior(\rho _i)}$ is either a single point or a line segment that is in ${\mathcal{VD}}(bay({\overline{cd}}))$ and does not intersect $\partial$. Consider the region in $bay({\overline{cd}})$ bounded by $\overline{v_ior(\rho _i)}$, $\overline{or(\rho _i)p}$, and $\partial (p,d)$, which we denote by Z. It is easy to see that Z is a simple polygon. Let $\alpha$ be the concatenation of $\overline{p_1p'_1}$ and $\overline{p_1'tp(p_i^*)}$. Note that $\alpha$ is entirely inside Z except that its two endpoints are on the boundary of Z, i.e., $p_1\in \overline{or(\rho _i)p}$ and $tp(p_i^*)\in \partial (p,d)$. Thus, $\alpha$ divides Z into two simple polygons; one of them contains $\overline{p_1p}$ as an edge, which is denoted by $Z'$. Since the intersection of $\overline{or(\rho ')tp(\rho ')}$ and $\overline{or(\rho _i)tp(\rho _i)}$ is on $\overline{p_1tp(\rho _i)}$, the ray $\rho '$ intersects $Z'$. By Invariant (7) (at the moment $\xi$) proved above, the root $r_j$ is to the left of $\rho '$. Thus, $\rho '$ cannot intersect the curve $\alpha$. Hence, the target point $tp(\rho ')$ must be on the boundary of $Z'\cap \partial (p,d)$, which is on $\partial (p,tp(\rho _i^*))$. Thus, $tp(\rho _i^*)$ is after $tp(\rho ')$, and Invariant (9) follows.

For Invariant (10), we need to show that if $\rho _{i+1}$ is vertical, then the target point $tp(\rho _{i+1})$ is after $tp(\rho _i^*)$ on $\partial$. By Invariant (3) (at the moment $\xi$) proved above, $or(\rho _{i+1})$ is to the southwest of $or(\rho _i^*)$. Let Z be the simple polygonal region in $bay({\overline{cd}})$ bounded by $\overline{v_ior(\rho _i)}$, $\overline{or(\rho _i)p_1}$, $\overline{p_1p_1'}$, $\overline{p'_1tp(\rho _i^*)}$, $\partial (tp(\rho _i^*),d)$, and $\overline{dv_i}$. Regardless of whether $or(\rho _{i+1})= v_{i+1}$, the origin $or(\rho _{i+1})$ of $\rho _{i+1}$ is in Z since $or(\rho _{i+1})$ is to the southwest of $or(\rho _i^*)=p_1'$. Further, since both $\rho ^*_i$ and $\rho _{i+1}$ are vertical, $tp(\rho _{i+1})$ must be on $\partial (tp(\rho _i^*),d)$. Invariant (10) thus follows.

For Invariant (11), it suffices to show that $tp(\rho _i^*)$ is after $p^*$ since $tp(\rho _i^*)$ has not been computed. Since $tp(\rho _i^*)$ is after $p=tp(\rho _i)$ ($=p^*$), Invariant (11) simply follows.

For Invariant (12), we need to show that the target point $tp(\rho _{i+1})$ is after $p^*$ [$=p=tp(\rho _i)$]. Let Z be the simple polygonal region in $bay({\overline{cd}})$ bounded by $\overline{v_ior(\rho _i)}$, $\overline{or(\rho _i)p}$, $\partial (p,d)$, and $\overline{dv_i}$. Clearly, $or(\rho _{i+1})$ is in Z. Further, since $or(\rho _{i+1})$ is to the southwest of $or(\rho _i)$, regardless of whether $\rho _{i+1}$ is vertical or horizontal, $tp(\rho _{i+1})$ must be on $\partial (p^*,d)$. Thus, Invariant (12) holds.

For Invariant (13), suppose l is the smallest index with $l>i$ such that $\rho _l\in \Psi$ and $\rho _l$ is horizontal. We need to prove that $tp(\rho _l)$ is after $p^*$ [$=p=tp(\rho _i)$]. Consider the simple polygon Z defined above for proving Invariant (12). Since $\rho _l$ is horizontal, by Lemma 12, $\rho _l$ is below $r_{i+1}$. Thus, it is easy to see that $or(\rho _{l})$ is in Z and $tp(\rho _{l})$ is on $\partial (p^*,d)$. Hence, $tp(\rho _{l})$ is after $p^*$, and Invariant (13) holds.

For Invariant (14), we need to show that the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains $or(\rho _{i+1})$ is known, which is true by Observation 8.

We conclude that all invariants of the algorithm still hold at the moment $\xi$. $\square$

For the purpose of discussing the analysis of the running time of our algorithm later, we call the ray $\rho _i^*$ the termination vertical ray of the (horizontal) ray $\rho _i$.

We have finished the discussion for the case when $p_1'$ is on the bottom edge of $Rec(p_1,q_1)$.

We then discuss the case when the point $p_1'$ is on the right edge of $Rec(p_1,q_1)$ (see Fig. 18). Denote by $\rho _{i1}$ the horizontal ray originating at $p'_1$ and going east, which is on $B(r_j,r_{i+1})$ by Observation 4. Then, we pop $\rho$ out of S and set $\rho$ as inactive. Also, we set $\rho _{i1}$ as active and move the reference point $p^*$ to p [$=tp(\rho _i)$]. Finally, we let $\rho _{i1}$ be the next ray to be considered by the algorithm (note that $\rho _{i1}$ is not in $\Psi$). Lemma 20 below shows that all invariants of the algorithm hold. Recall that the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains $p_1'$ has been computed.

Lemma 20

At the moment right before the next ray $\rho _{i1}$ is considered, all invariants of the algorithm hold.

Proof

Let $\xi$ be the moment right before the next ray $\rho _{i1}$ is considered, and $\xi '$ be the moment right before the ray $\rho _i$ is considered. Thus, the only change to S from the time $\xi '$ to $\xi$ is that $\rho$ is popped out. At the moment $\xi '$, all invariants of the algorithm hold. Our goal is to prove that all invariants still hold at the moment $\xi$. We assume $S\not =\emptyset$ at the moment $\xi$ (otherwise, all invariants related to any rays in S hold trivially). Let $\rho '$ be the ray at the top of S at the moment $\xi$. Then $\rho '$ is the second ray from the top of S (i.e., right below the ray $\rho$ in S) at the moment $\xi '$. Refer to Fig. 18 for an example.

Invariants (1) and (2) simply hold.

For Invariant (3), we need to show that $or(\rho _{i1})$ is to the southwest of $or(\rho ')$. By Invariant (2) at the moment $\xi '$, $or(\rho )$ of the ray $\rho$ at the top of S is to the southwest of $or(\rho ')$. Since $or(\rho _{i1})=p_1'$ is below $or(\rho )$, $or(\rho _{i1})$ is below $or(\rho ')$. Also, by Invariant (7) at the moment $\xi '$, since the top ray $\rho$ in S is on $B(r_j,r_i)$ (with $i>j$), $r_j$ is to the left of $\rho '$ (which is vertical). Since $p_1'$ is on the vertical line through $r_j$, $p_1'=or(\rho _{i1})$ is to the left of $or(\rho ')$. Hence, $or(\rho _{i1})$ is to the southwest of $or(\rho ')$, and Invariant (3) follows.

For Invariant (4), suppose $\rho '$ is on $B(r_{t},r_{t'})$ with $t'>t$; we need to show $j=t'$ since $\rho _{i1}\subset B(r_j,r_{i+1})$ is the next ray to be considered by the algorithm. At the moment $\xi '$, $\rho \subset B(r_j,r_i)$ (with $i>j$) is at the top of S and $\rho '$ is the second ray from the top of S; thus, by Invariant (8) at the moment $\xi '$, $j=t'$. Invariant (4) hence follows.

For Invariant (5), since no new ray is pushed onto S, we only need to consider the ray $\rho _{i1}$. The proof is the same as that for Invariant (5) (for the ray $\rho _i^*$) in the proof of Lemma 19, and we omit it.

Invariants (6), (7), (8), (9), and (11) trivially hold since no new ray is pushed into S.

Invariant (10) simply follows since $\rho _{i1}$ is the next ray to be considered by the algorithm and $\rho _{i1}$ is not vertical.

For Invariant (12), we need to show that the target point $tp(\rho _{i1})$ is after $p^*$ [$=p=tp(\rho _i)$]. Consider the simple polygonal region Z in $bay({\overline{cd}})$ bounded by $\overline{v_ior(\rho _i)}$, $\overline{or(\rho _i)p}$, $\partial (p,d)$, and $\overline{dv_i}$. It is easy to see that $or(\rho _{i1})$ is in Z and $tp(\rho _{i1})$ is on $\partial (p^*,d)$. Thus, $tp(\rho _{i1})$ is after $p^*$.

For Invariant (13), suppose l is the smallest index with $l>i$ such that $\rho _l\in \Psi$ and $\rho _l$ is horizontal. We need to prove that $tp(\rho _l)$ is after $p^*$ [$=p=tp(\rho _i)$]. Consider the simple polygon Z defined above for proving Invariant (12). Since $\rho _l$ is horizontal, by Lemma 12, $\rho _l$ is below $r_{i+1}$. Thus, it is easy to see that $or(\rho _{l})$ is in Z and $tp(\rho _{l})$ is on $\partial (p^*,d)$. Hence, $tp(\rho _{l})$ is after $p^*$, and Invariant (13) holds.

For Invariant (14), recall that the trapezoid of ${H\!M}(bay({\overline{cd}}))$ that contains $p_1'$ ($=or(\rho _{i1})$) has been computed, and thus Invariant (14) holds.

We conclude that all invariants of the algorithm hold at the moment $\xi$. $\square$

For analysis, we refer to the ray $\rho _{i1}$ as a successor horizontal ray of the (horizontal) ray $\rho _i$.

This finished the discussion for the case when $p_1'$ is on the right edge of $Rec(p_1,q_1)$.

Again, $\rho _{i1}$ is the next ray to be considered by the algorithm. Although our earlier discussion on the algorithm processing the next ray is mostly on processing a ray $\rho _i\in \Psi$, the processing for $\rho _{i1}$ ($\not \in \Psi$) is the same, and the proof for all invariants is also very similar. In particular, there may also be a termination vertical ray or a successor horizontal ray generated at the end of processing $\rho _{i1}$, which we still refer to as a termination vertical ray or a successor horizontal ray of $\rho _i$. It is easy to see that a horizontal ray $\rho _i$ may lead to multiple successor horizontal rays but at most one termination vertical ray, i.e., a successor horizontal ray may generate another successor horizontal ray (e.g., see Fig. 19), but a termination vertical ray does not generate another ray.

One might be curious about why the roles of horizontal rays and vertical rays are quite different in our above algorithm, while the $L_1$ metric does not prefer one of these two directions over the other. The asymmetric roles of these two directions are related to the order of $\rho _1,\rho _2,\ldots ,\rho _{k-1}$ in which we process these rays. If one uses a reversed order (i.e., $\rho _{k-1},\rho _{k-2},\ldots ,\rho _1$) in the processing, then the roles of these two types of rays will be reversed.

For the purpose of analyzing the running time of the algorithm later, we discuss more details related to the successor horizontal rays of a horizontal ray $\rho _i\in \Psi$. We process the first successor horizontal ray $\rho _{i1}$ of $\rho _i$ in the same way as $\rho _i$. After $\rho _{i1}$ is processed, we may obtain another successor horizontal ray $\rho _{i2}$. In general, assume all successor horizontal rays we obtain for $\rho _i$ are $\rho _{i1},\rho _{i2},\ldots ,\rho _{it}$, ordered by the time when they are produced (see Fig. 19). Then, after the last ray $\rho _{it}$ is processed, we may or may not obtain the termination vertical ray $\rho _i^*$. For example, when processing $\rho _{it}$, if $S=\emptyset$, then no termination vertical ray is generated. In either case, after $\rho _{it}$ is processed, we continue to consider the next ray $\rho _{i+1}\in \Psi$.

Let $\rho _{i0}=\rho _i$. For each $1\le w\le t$, we define the points $p_{w+1}$, $q_{w+1}$, and $p'_{w+1}$ for the ray $\rho _{iw}$ similarly to the points $p_{1}$, $q_1$, and $p'_{1}$ for $\rho _{i0}$ (see Fig. 19). Note that when processing $\rho _{it}$, depending on the specific situations, the points $p_{t+1}$, $q_{t+1}$, and $p'_{t+1}$ may not exist (e.g., if $S=\emptyset$). In the following, we assume they exist (otherwise, the analysis is actually simpler).

Fig. 19

Illustrating the first two successor horizontal rays $\rho _{i1}$ and $\rho _{i2}$ of a horizontal ray $\rho _i\in \Psi$

It is easy to see that for each $1\le w\le t$, the ray $\rho _{i,w-1}$ contains the top edge of the rectangle $Rec(p_w,p_w')$ and the ray $\rho _{iw}$ touches the bottom edge of $Rec(p_w,p_w')$. In addition, the ray $\rho _{it}$ contains the top edge of $Rec(p_{t+1},p_{t+1}')$. In other words, $\rho _{i0}$ ($=\rho _i$), $Rec(p_1,p_1'), \rho _{i1}, Rec(p_2,p_2'), \rho _{i2}, \ldots , Rec(p_t,p_t')$, $\rho _{it}, Rec(p_{t+1},p_{t+1}')$ are ordered from high to low and left to right (see Fig. 19). Thus, no two different rectangles in the sequence above intersect in their interior. Actually, the rectangles $Rec(p_1,p_1'), Rec(p_2,p_2'), \ldots , Rec(p_{t+1},p_{t+1}')$ are ordered from northwest to southeast. Further, all successor horizontal rays and rectangles involved are higher than $r_{i+1}$. To see this fact, note that for each $1\le w\le t+1$, the point $p_w'$ is higher than the point $q_w$ and $q_w$ is on the horizontal line through $r_{i+1}$ (see Fig. 19). Thus, all these rectangles are contained in the horizontal strip between the horizontal line containing $\rho _i$ and the horizontal line through $r_{i+1}$; we denote this strip by ${H\!Strip}(\rho _i)$. Recall that during our algorithm, the horizontal visibility map ${H\!M}(bay({\overline{cd}}))$ is utilized as a guide and we often move among its trapezoids. When computing and processing these successor horizontal rays, we always follow ${H\!M}(bay({\overline{cd}}))$, e.g., for each $w=0,1,\ldots ,t$, we utilize ${H\!M}(bay({\overline{cd}}))$ to compute the target point $tp(\rho _{iw})$ of the ray $\rho _{iw}$, to determine whether $\overline{p_{w+1}p'_{w+1}}$ intersects $\partial$, and to find the trapezoid in ${H\!M}(bay({\overline{cd}}))$ that contains $p'_{w+1}=or(\rho _{i,w+1})$. The discussion above implies that the time for processing all successor horizontal rays of $\rho _i$ is proportional to O(t) plus the number of trapezoids in ${H\!M}(bay({\overline{cd}}))$ that intersect the horizontal strip ${H\!Strip}(\rho _i)$ as well as the time for computing the target points of some (vertical) rays in S.

In addition, during this process, each of the t successor horizontal rays $\rho _{iw}$ of $\rho _i$ corresponds to a ray in S that is popped out. Thus, there are t vertical rays popped out of S for $\rho _i$. But, at most one ray, i.e., the termination vertical ray $\rho _i^*$, is pushed onto S for $\rho _i$.

We have finished the description of our algorithm for computing $\textit{SPM}(bay({\overline{cd}}))$, which is summarized in the pseudo-code of Algorithm 1.

5.3.5 The Time Complexity

It remains to analyze the running time of the algorithm. First, we show the following lemma.

Lemma 21

The total number of rays ever contained in the stack S throughout the entire algorithm is at most k.

Proof

When processing each ray $\rho _i\in \Psi$, if it is vertical, then we push it onto S; if it is horizontal, then as shown above, although there may be multiple successor horizontal rays of $\rho _i$, at most one ray, i.e., the termination vertical ray, is put into S. Further, according to our algorithm, once a ray in S is popped out, it will never be considered again, and thus never be put into S again. $\square$

We then discuss the total time for computing the target points for all vertical ray shootings in the entire algorithm. We use a reference point $p^*$ on $\partial$ and the vertical visibility map ${V\!M}(bay({\overline{cd}}))$ for this purpose. To conduct the vertical ray shootings, because the rays involved are always target-sorted, we simply scan the edges in a portion of $\partial$ between $p^*$ and another point p that is after $p^*$ on $\partial$. Further, when such a scanning is done, we always move $p^*$ to p. This implies that any portion of $\partial$ is scanned at most once in the entire algorithm. In addition, the number of all vertical ray shootings is at most k. This is because each vertical ray involved is from S, and by Lemma 21, the number of rays ever contained in S is at most k. Therefore, the total time for computing the target points of all vertical rays in the entire algorithm is $O(n'+k)$.

For each ray $\rho _i\in \Psi$, if it is vertical, then processing it takes O(1) time, i.e., pushing $\rho _i$ onto S. If it is horizontal, then assume that $\rho _i$ has t successor horizontal rays. We have discussed that, besides the procedure for computing their target points, the time for processing these t successor horizontal rays is proportional to t plus the number of trapezoids in ${H\!M}(bay({\overline{cd}}))$ intersecting the horizontal strip ${H\!Strip}(\rho _i)$. We have also shown that each successor horizontal ray corresponds to a ray in the stack S that is popped out. Since there are at most k rays ever contained in S by Lemma 21, the total number of successor horizontal rays in the entire algorithm is at most k. On the other hand, consider two different horizontal rays $\rho _i$ and $\rho _j$ in $\Psi$. We claim that the two horizontal strips $HStip(\rho _i)$ and ${H\!Strip}(\rho _j)$ do not intersect each other in their interior. Without loss of generality, assume $i<j$. Indeed, the strip ${H\!Strip}(\rho _i)$ is above the horizontal line through the root $r_{i+1}$ and ${H\!Strip}(\rho _j)$ is below the ray $\rho _j$. Since $\rho _j$ is horizontal and $j>i$, by Lemma 12, $\rho _j$ is below $r_{i+1}$. Our claim thus holds. The above claim implies that, besides the time for computing their target points, the time for processing all successor horizontal rays in the entire algorithm is proportional to the total number of trapezoids in ${H\!M}(bay({\overline{cd}}))$ plus k, which is $O(n'+k)$.

The algorithm performs totally O(k) horizontal ray shootings, for computing the target points of the horizontal rays in $\Psi$ and their successor horizontal rays. Using ${H\!M}(bay({\overline{cd}}))$ and based on the fact that we already know (i.e., have computed) the trapezoid of ${H\!M}(bay({\overline{cd}}))$ containing the origin of each such horizontal ray, all such horizontal ray shootings can be done in O(k) time.

In summary, we have proved the total running time of our algorithm for computing the shortest path map for the bay $bay({\overline{cd}})$ is $O(n'+m')$ (where $m'=k-1$ is the number of $\textit{SPM}({\mathcal {M}})$ vertices on ${\overline{cd}}$). It is easy to see that the size of this SPM is $O(n'+m')$ [e.g., since the running time is $O(n'+m')$]. Lemma 5 is thus proved.

6 Computing a Shortest Path Map for a Canal

In this section, we show how to compute a shortest path map for a canal, which uses our shortest path map algorithm for a bay in Sect. 5 as a main procedure.

Consider a canal $canal(x,y)$ with x and y as the corridor path terminals and two gates ${\overline{xd}}$ and ${\overline{yz}}$ (e.g., see Fig. 6). There may be multiple $\textit{SPM}({\mathcal {M}})$ vertices on both gates. Let $m_1$ (resp., $m_2$) be the number of $\textit{SPM}({\mathcal {M}})$ vertices on ${\overline{xd}}$ (resp., ${\overline{yz}}$), and $n'$ be the number of obstacle vertices of the canal. We show that a shortest path map for the canal can be computed in $O(m_1+m_2+n')$ time. Let $R_1$ (resp., $R_2$) be the set of roots whose cells in $\textit{SPM}({\mathcal {M}})$ intersect ${\overline{xd}}$ (resp., ${\overline{yz}}$).

We recall the definition of wavefront incoming/outgoing terminals in Sect. 4.2. Consider the corridor path terminals x and y of $canal(x,y)$. It is possible that y has a shortest path from s via x [i.e., this path contains the corridor path of $canal(x,y)$], in which case there is a “pseudo-cell” in $\textit{SPM}({\mathcal {M}})$ with x as the root and y being the only other point in this “pseudo-cell”; then x is a wavefront incoming terminal and y is the wavefront-outgoing terminal. If neither y has a shortest path from s via x nor x has a shortest path from s via y, then both x and y are wavefront-incoming terminals. In this case, there is a point on the corridor path of $canal(x,y)$ that has two shortest paths from s, one via x and the other via y [we will use this property to compute an SPM for $canal(x,y)$]. Note that for the two terminals x and y, either both of them are wavefront-incoming terminals, or only one of them is an wavefront-incoming terminal and the other is an wavefront-outgoing terminal. Below, we first discuss the former case; the latter case is very similar.

6.1 Both x and y are Wavefront-Incoming Terminals

If both x and y are wavefront-incoming terminals, by the properties of the corridor path, there is a point $p^*$ on the corridor path of $canal(x,y)$ such that there exist two shortest paths $\pi _1(s,p^*)$ and $\pi _2(s,p^*)$ from s to $p^*$ with $x\in \pi _1(s,p^*)$ and $y\in \pi _2(s,p^*)$. The point $p^*$ can be found in $O(n')$ time since we know the shortest path distances from s to x and to y. More specifically, $p^*$ has the following property: the shortest path distance from s to x plus the length of the sub-path of the corridor path from x to $p^*$ is equal to the shortest path distance from s to y plus the length of the sub-path of the corridor path from y to $p^*$. Since we already know the shortest path distances from s to x and to y, we can compute $p^*$ in time linear in the number of edges of the corridor path, which is bounded by $O(n')$.

Let ${\mathcal{VD}}(canal(x,y),R_1)$ be the (additively) weighted Voronoi diagram of $canal(x,y)$ with respect to the root set $R_1$, i.e., we treat $canal(x,y)$ as a bay with the gate ${\overline{xd}}$. As defined in Sect. 5, ${\mathcal{VD}}(canal(x,y),R_1)$ is the Voronoi decomposition of $canal(x,y)$ with respect to the roots in $R_1$. Similarly, let ${\mathcal{VD}}(canal(x,y),R_2)$ be the weighted Voronoi diagram of $canal(x,y)$ with respect to the root set $R_2$. Using our algorithm in Sect. 5, ${\mathcal{VD}}(canal(x,y),R_1)$ and ${\mathcal{VD}}(canal(x,y),R_2)$ can be computed in totally $O(m_1+m_2+n')$ time. Denote by ${\mathcal{VD}}(canal(x,y),R_1,R_2)$ the weighted Voronoi diagram of $canal(x,y)$ with respect to the roots in $R_1\cup R_2$. As shown in Sect. 5, after ${\mathcal{VD}}(canal(x,y),R_1,R_2)$ is computed, an SPM on $canal(x,y)$ with the source s can be built in $O(m_1+m_2+n')$ time. Thus, the key is to compute ${\mathcal{VD}}(canal(x,y),R_1,R_2)$. Below, we show how to compute ${\mathcal{VD}}(canal(x,y),R_1,R_2)$ in $O(m_1+m_2+n')$ time with the help of the point $p^*$, ${\mathcal{VD}}(canal(x,y),R_1)$, and ${\mathcal{VD}}(canal(x,y),R_2)$.

To compute ${\mathcal{VD}}(canal(x,y),R_1,R_2)$, our strategy is to find a “dividing curve” in $canal(x,y)$ that divides $canal(x,y)$ into two simple polygons $C_1$ and $C_2$, such that each point in $C_1$ has a shortest path from s via a root in $R_1$ and each point in $C_2$ has a shortest path from s via a root in $R_2$. Further, each point on the dividing curve has two shortest paths from s, one path containing a root in $R_1$ and the other path containing a root in $R_2$. Note that the dividing curve is simple and cannot have any loops since $canal(x,y)$ is a simple polygon. After finding $C_1$ and $C_2$, we simply apply the algorithm in Sect. 5 on $C_1$ and $R_1$ to compute the weighted Voronoi diagram of $C_1$ with respect to $R_1$, i.e., ${V\!D}(C_1,R_1)$. We similarly compute ${V\!D}(C_2,R_2)$. Then, ${\mathcal{VD}}(canal(x,y),R_1,R_2)$ consists of ${V\!D}(C_1,R_1)$ and ${V\!D}(C_2,R_2)$. Thus, our remaining task is to compute a dividing curve in $canal(x,y)$, which we denote by $\gamma$.

Note that the point $p^*\in \gamma$. Computing $\gamma$ can be done in $O(n'+m_1+m_2)$ time by a procedure similar to the merge procedure of the divide-and-conquer algorithm for computing the Voronoi diagram of a set of points in the plane [35]. The details are given below.

To compute $\gamma$, we start at the point $p^*$ and trace $\gamma$ out by traversing some corresponding cells in ${\mathcal{VD}}(canal(x,y),R_1)$ and in ${\mathcal{VD}}(canal(x,y),R_2)$ simultaneously. Specifically, we first compute a triangulation of ${\mathcal{VD}}(canal(x,y),R_1)$, denoted by $Tri_1$, and a triangulation of ${\mathcal{VD}}(canal(x,y),R_2)$, denoted by $Tri_2$ [this can be done in linear time [3] since each cell of ${\mathcal{VD}}(canal(x,y),R_1)$ and ${\mathcal{VD}}(canal(x,y),R_2)$ is a simple polygon]. Since $p^*$ is in a triangle (say, $tri_1$) of $Tri_1$ and is in a triangle (say, $tri_2$) of $Tri_2$, we find $tri_1$ in $Tri_1$ and $tri_2$ in $Tri_2$. From the cell of ${\mathcal{VD}}(canal(x,y),R_1)$ [resp., ${\mathcal{VD}}(canal(x,y),R_2)$] that contains $tri_1$ (resp., $tri_2$), we obtain the root $r_1$ (resp., $r_2$) of that cell. We then move along the bisector $B(r_1,r_2)$ inside $canal(x,y)$, starting at $p^*$ and going in each of the two directions along $B(r_1,r_2)$. As following a line segment or a ray of $B(r_1,r_2)$ in a direction, we determine, in O(1) time, which of $tri_1$ or $tri_2$ that we exit first. As we cross from one triangle tri (say, in $Tri_1$) to the next triangle $tri'$, we check which of the following cases occurs: (i) The next triangle $tri'$ (in $Tri_1$) is contained in the same cell of ${\mathcal{VD}}(canal(x,y),R_1)$ as that containing tri; (ii) $tri'$ is contained in a different cell of ${\mathcal{VD}}(canal(x,y),R_1)$ than that containing tri; (iii) the movement touches the boundary of $canal(x,y)$ (thus $tri'$ does not exist). In Case (i), we continue to follow the same bisector [say, $B(r_1,r_2)$]. In Case (ii), we find the root (say, $r'_1$) of the next cell of ${\mathcal{VD}}(canal(x,y),R_1)$; then we compute a new bisector [say, $B(r'_1,r_2)$], and our movement continues along $B(r'_1,r_2)$. In Case (iii), the movement reaches an end of $\gamma$ [on the boundary of $canal(x,y)$]. The dividing curve $\gamma$ is the concatenation of the portions of the bisectors thus traversed.

Due to the properties of the cells of ${\mathcal{VD}}(canal(x,y),R_1)$ and ${\mathcal{VD}}(canal(x,y),R_2)$, our movement above will visit each triangle of $Tri_1$ and $Tri_2$ at most a constant number of times (due to that $\gamma$ is piecewise hyperbolic), each taking O(1) time. Thus, the partition curve $\gamma$ can be computed in $O(n'+m_1+m_2)$ time.

In summary, in this case, an SPM on $canal(x,y)$ can be computed in $O(n'+m_1+m_2)$ time.

6.2 Only One of x and y is a Wavefront-Incoming Terminal

In this case, exactly one of x and y is a wavefront-incoming terminal. The algorithm is similar to that for the former case. The only difference is on how to find a point $p^*$ on the dividing curve $\gamma$ because in this case no such a point $p^*$ can be on the corridor path of $canal(x,y)$.

Without loss of generality, we assume that x is a wavefront-incoming terminal and y is not. Then each point on the corridor path (including y) has a shortest path from s via x. Further, the shortest path through x passes y and goes to the outside of $canal(x,y)$, which means that y is the root of a cell C(y) in $\textit{SPM}({\mathcal {M}})$. If the canal gate ${\overline{yz}}$ is completely contained in the cell C(y), then it is easy to see that ${\mathcal{VD}}(canal(x,y),R_1)$ is ${\mathcal{VD}}(canal(x,y),R_1,R_2)$. Otherwise, as in the former case, we need to find a dividing curve $\gamma$ to divide $canal(x,y)$ into two polygons $C_1$ and $C_2$ such that each point in $C_1$ has a shortest path from s via a root in $R_1$ and each point in $C_2$ has a shortest path from s via a root in $R_2$. To obtain $\gamma$, the key is to find a point $p^* \in \gamma$. Since the canal gate ${\overline{yz}}$ is not completely contained in C(y), there must be a point q on ${\overline{yz}}$ that is on the common boundary of C(y) and another cell C(r) in $\textit{SPM}({\mathcal {M}})$. We claim that q is on $\gamma$. Indeed, note that r is in $R_2$. Hence there is a shortest path $\pi _1(s,q)$ from s to q that contains x, the corridor path in $canal(x,y)$, and the line segment ${\overline{yq}}$, and there is another shortest path $\pi _2(s,q)$ from s to q via the root $r\in R_2$. In other words, q has two shortest paths from s, one via a root in $R_1$ and the other via a root in $R_2$. Therefore, q is on the dividing curve $\gamma$. The rest of the algorithm is similar to that for the former case.

In summary, in this case, an SPM on $canal(x,y)$ can also be built in $O(n'+m_1+m_2)$ time.

Therefore, a shortest path map SPM on $canal(x,y)$ can be computed in $O(n'+m_1+m_2)$ time. Similarly, the size of this SPM is $O(n'+m_1+m_2)$. Lemma 6 is thus proved.

7 The $L_1$ Geodesic Voronoi Diagram

In this section, we extend our techniques to solve the $L_1$ geodesic Voronoi diagram problem (or $L_1$-GVD for short).

Given a set ${\mathcal {P}}$ of h polygonal obstacles with a total of n vertices and a set of m point sites, the $L_1$-GVD problem aims to construct the $L_1$ geodesic Voronoi diagram of for the m point sites. Denote by $G\!V\!D({\mathcal {P}})$ the Voronoi diagram that we want to construct.

Mitchell’s algorithm [29, 30] can be modified to compute $G\!V\!D({\mathcal {P}})$ in $O((n+m)\log (n+m))$ time. Namely, instead of initiating a wavelet at a single source, the modified algorithm for $G\!V\!D({\mathcal {P}})$ initiates a wavelet at each point site. The rest of the algorithm remains the same as before.

We can also extend our SPM algorithm in a similar way to compute $G\!V\!D({\mathcal {P}})$. Generally, since our algorithm makes use of Mitchell’s algorithm [29, 30] as a main procedure when computing the shortest path map $\textit{SPM}({\mathcal {M}})$ for the ocean ${\mathcal {M}}$, to compute $G\!V\!D({\mathcal {P}})$, we can simply replace Mitchell’s algorithm by its modified version for computing $L_1$ geodesic Voronoi diagrams. More specifically, our algorithm for computing $G\!V\!D({\mathcal {P}})$ has the following steps. (1) Compute a triangulation of the free space, in which the m point sites are treated as m point obstacles (hence, more sites lead to more corridors, bays, and canals). (2) Compute the corridor structure on ${\mathcal {P}}$ and the m point obstacles that consists of $O(m+h)$ corridors, which partition the plane into a set ${\mathcal {P}}'$ of $O(m+h)$ convex polygons with a total of $O(n+m)$ vertices. (3) Compute the core set $core({\mathcal {P}}')$ for the convex polygons in ${\mathcal {P}}'$. (4) Apply Mitchell’s modified algorithm [29, 30] to compute the $L_1$ geodesic Voronoi diagram $G\!V\!D(core({\mathcal {P}}'))$ on the core set $core({\mathcal {P}}')$. (5) Based on $G\!V\!D(core({\mathcal {P}}'))$, compute the $L_1$ geodesic Voronoi diagram $G\!V\!D({\mathcal {P}}')$ on the convex polygon set ${\mathcal {P}}'$. Although we have multiple sources, this step is the same as before (i.e., as in Lemma 3). (6) Based on $G\!V\!D({\mathcal {P}}')$, compute the Voronoi regions in all bays and canals, as in Sects. 5 and 6. Again, the algorithms for this step are as before, i.e., as the algorithms in Sects. 5 and 6. We then obtain the final $L_1$ geodesic Voronoi diagram $G\!V\!D({\mathcal {P}})$.

To analyze the running time, Steps (1), (2), and (3) are the same as before except that the number of obstacles becomes $m+h$. Specifically, the triangulation in Step (1) takes $O((n+m)\log (n+m))$ time or $O(n+(h+m)\log ^{1+\epsilon }(h+m))$ time [2]. Steps (2) and (3) together take $O(n+(h+m)\log (h+m))$ time. Step (4) takes $O((m+h)\log (m+h))$ time since the core set $core({\mathcal {P}}')$ has totally $O(m+h)$ vertices. Steps (5) and (6) are also the same as before, which take linear time, i.e., $O(n+m)$. Therefore, we have the following theorem.

Theorem 4

The $L_1$ geodesic Voronoi diagram of m point sites among a set of h pairwise disjoint polygonal obstacles with a total of n vertices in the plane can be computed in $O(n+(h+m)\log (h+m))$ time (suppose a triangulation of the free space is given in the input).

Since the given m sites are points, there is an alternative triangulation algorithm that may be faster (than simply applying the algorithm in [2]) in some situations. The algorithm works as follows: (1) Compute the triangulation of the free space without considering the m sites; (2) find the triangles in the triangulation that contain those m sites (e.g., by a point location data structure); (3) triangulate those triangles that contain at least one point site by considering the point sites as obstacles. The running time of the algorithm is $O(n+h\log ^{1+\epsilon }h+m\log (n+m))$, which is actually bounded by $O(n+h\log ^{1+\epsilon }h+m\log m)$.² Hence, if the m point sites are all inside a simple polygon, then we have the following result.

Corollary 1

The $L_1$ geodesic Voronoi diagram of a set of m point sites in a simple polygon can be computed in $O(n+m\log m)$ time.

In comparison, the Euclidean GVD problem of the simple polygon case is solvable in $O(n\log n+m\log m)$ time [33], and recently, an $O(n+m\log m\log ^2 n)$ time algorithm was proposed [32].

8 Concluding Remarks

As in [29, 30], we conjecture that our algorithms may be generalized to solve the C-oriented shortest path problem [38]. A C-oriented metric defines the distance between two points to be the length of a shortest path with each edge parallel to one of a given set C of fixed orientations. The $L_1$ metric is a special case with only two fixed orientations. Let $c=|C|$. Mitchell’s algorithm [29, 30] can compute a shortest C-oriented path in $O(cn\log n)$ time and O(cn) space among h pairwise disjoint polygons with a total of n vertices in the plane. Similarly, we suspect that our techniques may be extended to solve the problem as well. We sketch the main idea as follows.

We first consider the convex case (i.e., all polygons are convex). We compute a core for each convex polygon based on the orientations in C. Note that in this case a core has O(c) vertices. Thus, we obtain a core set of totally $O(c\cdot h)$ vertices. We then apply Mitchell’s algorithm for the fixed orientations of C on the core set to compute a shortest path avoiding the cores in $O(c^2h\log ch)$ time and $O(c^2h)$ space, after which we find a shortest path avoiding the input polygons in additional O(n) time as in Lemma 2. Thus, a shortest path can be found in $O(n+c^2h\log ch)$ time and $O(n+c^2h)$ space. For the general case, we can use a similar algorithm scheme as our $L_1$ algorithm in Sect. 4. The algorithm runs in $O(n+c^2 h\log ch)$ time and $O(n+c^2h)$ space (provided that the free space has already been triangulated).

This may also yield an approximation algorithm for computing a Euclidean shortest path between two points among polygonal obstacles. Since the Euclidean metric can be approximated within an accuracy of $O(1/c^2)$ if we use c equally spaced orientations, as in [29, 30], our above algorithm computes a path whose length is guaranteed to be within a factor $(1+\delta )$ of the Euclidean shortest path length, where c is chosen such that $\delta =O(1/c^2)$. The algorithm runs in $O(n+(1/\delta ) h\log \frac{h}{\sqrt{\delta }})$ time and $O(n+(1/\delta )h)$ space (given a triangulation of the free space).