Introduction

Thevetia peruviana is a very promising plant for in vitro cultures, because it produces several compounds with applications in pharmaceutical industries [1, 2]. Among the compounds produced from this culture, the cardiac glycosides are particularly important given their applications in the treatment of cardiac diseases. Several studies have obtained cardiac glycosides from this plant. Kohls et al. [3] and Tian et al. [4] isolated several types of cardiac glycosides from seeds of T. peruviana. On the other hand, Arias et al. [1] and Amaringo et al. [5] have reported the production of Peruvoside and Thevetin B, respectively, in plant cell suspensions of this species. Despite of the important metabolites that can be produced from T. peruviana, only very few works reported in the open literature have addressed the in vitro production of these plant cells [1, 2, 5, 6]. Furthermore, to the authors’ knowledge, this work is the first one developing a mechanistic model to describe the cell growth, nutrients uptake, and dynamic behavior of the main metabolites on the central carbon metabolism in plant cell cultures of T. peruviana. The strategy followed for obtaining the model includes the following steps: (a) gathering of experimental data (b) proposal of the kinetic model, (c) parameter estimation, and (d) model validation. In the first step, cultivation of cells was performed under batch operation in shake flask to determine dynamics of cell growth, extracellular sugars and nitrates uptake, and intracellular sugars, nitrates, and phosphates uptake. Second, a mechanistic model for plant cell cultures of T. peruviana, based on the previous works by Cloutier et al. [7] and Leduc et al. [8], is proposed. This model is divided in three compartments: extracellular, intracellular, and central primary metabolism. The model considers the reactions for cell growth and includes a term to describe the initial accumulation of extracellular nitrates in this species. The proposed model includes 28 metabolic species and comprises 33 metabolic reactions, and 61 parameters. Given the issues associated with the over-parametrization of the model, its nonlinear nature and the strong correlation among the effects of the parameters, the parameter estimation routine includes a step of identifiability analysis. In practical identifiability analysis, a subset of parameters for estimation (Subset Selection) is determined considering the influence of the selected parameters on the model and the correlations among the effects of the parameters. Therefore, an ill posed problem is transformed into a well-posed one [9,10,11,12,13,14,15,16,17,18]. In this work, the algorithm for subset selection proposed by Yao et al. [18] to determine the most sensitive and linearly independent parameters is implemented. The proposed model is validated using a new set of experimental data and calculating the confidence intervals for the subset of identifiable parameters. Finally, the validated model is used to determine the distribution of fluxes in plant cell cultures of T. peruviana.

Model development

Many biological processes, such as metabolism of a cell culture and cellular stress responses, are nonstationary in their nature [19]. Therefore, dynamic models are preferred to describe the changes in the main state variables for these processes. In general terms, two types of dynamic structured models can be differentiated in the literature, simple structured models and mechanistic models. In the case of plant cell cultures, some simple structured models have been reported by Bramble et al. [20], Hooker and Lee [21], Van Gulik et al. [22], Takeda et al. [23], Choi et al. [24, 25], Schlatmann et al. [26], Pires Cabral et al. [27], Zhang and Su [28], Li et al. [29], and Cloutier et al. [7] These models are organized in pools that include general information about the activity and functions of the nutrients inside the cells. However, they do not use information about the kinetic reactions for biomass growth and metabolite production, since the cellular reactions are normally empirical and they do not represent the true conversion between components [30, 31]. Mechanistic models give a good representation of the intracellular processes by including balances of intracellular compounds and stoichiometric steps [30]. The metabolic networks are described by ordinary differential equations that represent mass balances of the substrate, biomass, products, and intracellular metabolites, as well as numerous reactions rates corresponding to the pathways [32, 33]. With the solution of this dynamic system, it is possible to obtain information about concentration profiles of each species and flux distribution over time. This information can be useful to evaluate the changes needed to optimize the production of biomass and metabolites of interest based on quantities, such as the flux of different compounds.

Some mechanistic models have been proposed in the literature for plant cell cultures and hairy roots. Leduc et al. [8] presents a model to describe the cell growth and intracellular transport and accumulation of nutrients in Catharanthus roseus hairy roots. The metabolic network includes glycolysis, pentose-phosphate pathway, TCA cycle, energy shuttles, and cofactors. The secondary metabolism is included in the model considering the metabolisms derived from tryptamine and secologanin. The metabolic network is divided into two interlinked subnetworks as the stationary primary metabolism (including glycolysis, TCA cycle, and cell building blocks, such as amino acids, lipids, and organic acids among others) and transient metabolism (including cell growth nutrient transport between medium and intracellular volumes). Cloutier et al. [34] present a dynamic model for the primary metabolism of plant cells and hairy roots based on the modelling approach presented in Leduc et al. [8] but without the steady-state assumption on the primary metabolism. Sigmoid switch functions are multiplied by the reaction rates to reduce discontinuities around the threshold values. Cloutier et al. [35] used the model proposed by Cloutier et al. [34] for the identification and control of intracellular phosphate dynamics in plant cell cultures of Eschscholtiza californica. Cloutier et al. [36] used the model of Cloutier et al. [35] for developing the optimization of the production of alkaloid production from cell cultures of Eschscholtiza californica.

The mechanistic model proposed in this work for plant cell cultures of T. peruviana is based on the works by Cloutier et al. [34] and Leduc et al. [8]. The model is described by the first principles-based model derived from the mass balances, as follows:

$$ \frac{{{\text{d}}\varvec{X}}}{{{\text{d}}t}} = f\left( {\varvec{X},\varvec{t},{\varvec{\uptheta}}} \right)\quad \varvec{X}\left( {t_{0} } \right) = \varvec{X}_{0} $$
(1)
$$ Y = g\left( {\varvec{X},\varvec{t},{\varvec{\uptheta}}} \right) $$
(2)

where \( \varvec{X} = [x_{1} ,x_{2} , \ldots ,x_{r} ] \) indicates the state variable vector, t is the time, \( {\varvec{\uptheta}} = [{\theta }_{1} ,{\theta }_{2} , \ldots ,{\theta }_{m} ] \) is the vector of model parameters, \( \varvec{X}_{0} \) is the vector of initial conditions, and \( \varvec{Y} = [y_{1} ,y_{2} , \ldots ,y_{n} ] \) correspond to the model output vector, with \( n \le r \). The nomenclature used for the state and output variables is presented in Tables 1 and 2, respectively. The initial conditions for the state variables were taken from literature [7, 8, 34, 37] and their values are reported in Table 1.

Table 1 State variables X
Full size table
Table 2 Output variables Y
Full size table

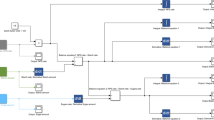
Figure 1 shows the pathway for biomass production, while the reactions considered at each step are presented in Table 3. For this culture, only the reactions of the central carbon metabolism for biomass production were considered. Other considerations considered when formulating the model include

Fig. 1
figure 1

Pathway for biomass production in plant cell cultures of Thevetia peruviana adapted from Cloutier et al. [34] and Leduc et al. [8]

Full size image
Table 3 Reactions of metabolic network considered in the model proposed for plant cell cultures of Thevetia peruviana
Full size table

  • Different to case of Leduc et al. [8], and following the proposal of Cloutier et al. [34], this model does not consider the steady-state hypothesis on the primary metabolism.

  • The extracellular compartment is formed by the main nutrients for cell growth in plant cells: ESUC, ENO3, and EPi. The ESUC is hydrolyzed into EGLUC and EFRUC in reaction (1). According to the experimental results, this hydrolysis is carried out mainly at extracellular level, different to the case reported by Cloutier et al. [35] in which the analysis of the intracellular hydrolysis of sucrose into glucose and fructose for cell cultures of Eschscholtiza californica was included. The extracellular hydrolysis of sucrose into glucose and fructose in plant cell cultures can be due to the presence of the invertase enzyme [38]. Such extracellular hydrolysis has been reported by Choi et al. [39] for cell suspensions of Glycyrrhiza inflate, Shibasaki et al. [24] for cell suspensions of Thalictrum rugosum, Westgate et al. [40] for cell suspensions of Nicotiana tabacum, and Li et al. [41] for cell suspensions of Cephalotaxus harringtonia.

  • In the intracellular compartment, all fructose has turned into glucose, according to reaction (3). All NO3 is formed from ENO3 in reaction (17), and then it is transformed into NH4 in reaction (18). The total Pi is obtained from EPi in reaction (20) and from all intermediate reactions of the central metabolism involving the formation and consumption of this species.

  • Central primary metabolism compartment details the reactions of the precursors for the biomass formation. \( {\text{STH,OP,LIP,ORA, and AA}} \) are considered the biomass precursors according to reaction (31) [7, 8]. The STH and OP are formed through the species GLUC, G6P in reactions (4) and (27), and GLUC, G6P, and R5P in reactions (4), (5), and (26), respectively. The LIP and ORA are formed from reversible reactions from ACOA. The ACOA is formed from the PYR, in reaction (14), which is obtained from glycolysis pathway, in reactions (4), (6), (8), (9), (10), (11), (12), and (13). Finally, the AA are formed from fixation of NH4, and OXO which is formed from TCA cycle, reactions (15) and (16), including the reaction (30), in which the OAA is formed from PEP. In this model, the intracellular STA is considered as a storage carbon source [42]. The AA is only used to form biomass (the endogenous behavior is not considered in the model). Finally, the energy shuttles ADP and ATP, cofactors NADH and NSDPH, and their oxidized forms NAD and NADP are considered in steady state.

Each pathway regulation (reaction rate) is described by multiplicative Michaelis–Menten equation as shown in Eq. (3), indicating the effect of the substrates involved, where each flux has a maximum reaction rate \( v_{max\left( j \right)} \) and an affinity constant \( K_{{m_{i} }} \). The expressions for the fluxes are presented in Table 4. Reaction rate v(17) presents an additional inhibition term expression with a constant of inhibition \( {\text{KIENO}}_{ 3} \) to include the effect of accumulation of extracellular nitrates. The reaction rates for extracellular nitrates and phosphates use simple Michaelis–Menten expressions, different to the reactions rates presented by Cloutier et al. [34] that include double Michaelis–Menten-type expressions. The reaction rates in this work are not multiplied by sigmoid switch functions, since the discontinuities around the threshold are evaluated by the use of sensitivity matrix. Therefore, the kinetic expressions are significantly different to the previous works by Leduc et al. [8] and Cloutier et al. [34]:

Table 4 Kinetic equations proposed in the case of plant cell cultures of Thevetia peruviana
Full size table
$$ v\left( j \right) = v_{\hbox{max} \left( j \right)} \mathop \prod \limits_{i} \frac{{x_{i} }}{{K_{{m_{i} }} + x_{i} }}. $$
(3)

The dynamic model proposed consists of the mass balance equations for extracellular and intracellular nutrients, as presented in the following equation:

$$ \frac{{{\text{d}}X}}{{{\text{d}}t}} = \mathop \sum \limits_{j} r_{ij} v_{j} - \mu x_{i} $$
(4)

where µ is the specific growth rate presented in Eq. (5) and \( r_{ij} \) is the stoichiometric coefficient for each metabolite in the reaction j

$$ \mu = v_{{\hbox{max} \left( {31} \right)}} \times \frac{\text{AA}}{{K_{m} {\text{AA + AA}}}} \times \frac{\text{STH}}{{K_{\text{m}} {\text{STH + STH}}}} \times \frac{\text{LIP}}{{K_{m} {\text{LIP + LIP}}}} \times \frac{\text{ORA}}{{K_{m} {\text{ORA + ORA}}}} \times \frac{\text{OP}}{{K_{m} {\text{OP + OP}}}}. $$
(5)

Parameter estimation and model validation

The objective function used for solving the parameter estimation problem is expressed as the sum of squared errors (MSEY) [Eq. (6)]

$$ \hbox{min} J({\varvec{\uptheta}}) = \mathop \sum \limits_{i = 1}^{n} {\text{MSE}}_{\text{Y}} . $$
(6)

The MSEY for each variable is defined by the following equation:

$$ {\text{MSE}}_{\text{Y}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {Y_{{{ \exp },i}} - Y_{i} } \right)^{2} $$
(7)

where \( Y_{exp,i} \) corresponds to the experimental points. The initial parameter values \( {\varvec{\uptheta}}_{0} \) to solve the optimization problem were taken from other similar works in plant cell cultures [7, 35, 37]. Two sets of experimental data were used for parameter identification, whereas one different data set was used for model validation. Each experimental data set was obtained at different initial sucrose and inoculum concentrations. Simulated Annealing optimization algorithm was used for solving the parameter estimation problem until obtaining an initial pseudo-optimal set of parameter values \( {\varvec{\uptheta}}^{\varvec{*}} \). This set of parameters is presented in Table 5.

Table 5 Initial and pseudo-optimal parameter values for affinity constants K M and maximum reaction rates v max in the proposed model
Full size table

To solve the issues associated with the over-parametrization of the model, its nonlinear nature, and the strong correlation among the effects of the parameters, identifiability analysis was carried out for establishing a new subset of identifiable parameters \( {\varvec{\uptheta}}_{\varvec{k}} \subset {\varvec{\uptheta}}^{*} \) that presents a high effect in the objective function, and low linear dependency. The remaining parameters (i.e., those nonidentifiable) are fixed at their initial values, forming the subset \( {\varvec{\uptheta}}_{{{\mathbf{Fixed}}}} \). A new optimization routine is performed where the decision variables are the parameters in the subset \( {\varvec{\uptheta}}_{\varvec{k}} \), until a new optimal subset of parameters \( {\varvec{\uptheta}}^{*}_{{\mathbf{k}}} \) is obtained. The new set of optimal parameters is \( \left\{ {{\tilde{\mathbf{\theta }}} = {\varvec{\uptheta}}^{*}_{{\mathbf{k}}} \mathop { \cup \;}\nolimits {\varvec{\uptheta}}_{{{\mathbf{Fixed}}}} } \right\} \). If this set of parameters presents a good fit, it will be taken as the final set of optimal parameters, in the opposite case, it will be necessary to re-start the estimation process taking \( {\varvec{\uptheta}}_{0} = {\tilde{\mathbf{\theta }}} \).

To determine the subset of identifiable parameters, a local sensitivity analysis was performed based on the sensitivity matrix. This matrix denotes the relationship between the derivatives of the state variables of the model x i with respect to the parameters \( \theta_{j} \) as it is presented in the following equation [44]:

$$ Z = \frac{\partial X}{\partial \theta } = \left[ {\begin{array}{*{20}c} {\frac{{\partial x_{1} }}{{\begin{array}{*{20}c} {\partial \theta_{1} } \\ {\frac{{\partial x_{2} }}{{\partial \theta_{1} }}} \\ \end{array} }}} & { \frac{{\partial x_{1} }}{{\begin{array}{*{20}c} {\partial \theta_{2} } \\ {\frac{{\partial x_{2} }}{{\partial \theta_{2} }} \cdots } \\ \end{array} }} \cdots } & {\frac{{\partial x_{1} }}{{\begin{array}{*{20}c} {\partial \theta_{m} } \\ {\frac{{\partial x_{2} }}{{\partial \theta_{m} }}} \\ \end{array} }}} \\ \vdots & \vdots & \vdots \\ {\frac{{\partial x_{n} }}{{\partial \theta_{1} }}} & {\frac{{\partial x_{n} }}{{\partial \theta_{2} }} \cdots } & {\frac{{\partial x_{n} }}{{\partial \theta_{m} }}} \\ \end{array} } \right]. $$
(8)

Sensitivity functions were derived by integrating the original model along with the sensitivity equations [45, 46]. This matrix was scaled to ensure dimensional consistency using the following equation [11]:

$$ s_{ij} = z_{ij} \frac{{\Delta \theta_{j} }}{{{\text{SC}}_{i} }} $$
(9)

where \( z_{ij} \) was evaluated at \( {\varvec{\uptheta}}^{*} \), the point in the parameter space where the sensitivity analysis was carried out, \( \Delta \theta_{j} \) is a scaling factor that reflects uncertainty in the initial guess for parameter \( \theta_{j} \), and \( {\text{SC}}_{i} \) is a scaling factor that reflects the uncertainty associated with the measurements. The sensitivity matrix was scaled using \( \Delta \theta_{j} = 0.5 \) according to Brun et al. [11], given that the values obtained in this work are the first ones reported for cell cultures of this specie. The value of SCi was defined as the mean value for the output variables. The scaling of the sensitivity matrix is a central matter for the sensitivity analysis; therefore, in this work, the scaled sensitivity matrix was standardized, subtracting off the mean for each column and dividing it by the standard deviation [47].

The orthogonal method proposed by Yao et al. [18] was used in this work as the routine to determine identifiable parameters. This method sequentially applies orthogonal projections of the sensitivity vectors columns of the standardized sensitivity matrix to select one identifiable parameter at a time. The maximum number of parameters that can be identified was determined from the singularity of fisher information matrix (FIM), because this value indicates when the estimation problem becomes ill posed. The sensitivity matrix is related to the FIM using the following equation [44]:

$$ {\text{FIM}} = S_{{{\varvec{\uptheta}}^{\varvec{*}} }}^{T} QS_{{{\varvec{\uptheta}}^{\varvec{*}} }} $$
(10)

where Q corresponds to the inverse measurement error covariance matrix and \( S_{{{\varvec{\uptheta}}^{\varvec{*}} }} \) is the standardized sensitivity matrix for the pseudo-optimal set of parameters obtained after optimization. This work assumes that the measurement of noise is uncorrelated and constant with the time; therefore, the covariance matrix results in an identity matrix and the FIM becomes the product of the transpose of sensitivity matrix itself [48].

Materials and methods

Cell suspensions

Cell suspensions were obtained from friable callus which were transferred to the shake flask with 80 ml of liquid SH medium. The cultures were maintained in an orbital shaker (IK KS501 digital) at 110 rpm and ambient temperature under natural photoperiod and subcultured every 12–15 days. Experiments were performed in liquid medium supplemented with sucrose [1].

Analytical methods

The samples were initially homogenized. Three milliliters of each sample were taken and filtered in vacuum for biomass determination using the dry weight method. The rest of the sample was centrifuged at 5000 rpm for 10 min in a centrifuge SIGMA 2–16 kPa at 25 °C. The supernatant was separated and used to determine extracellular nutrients. The rest of the sample was rinsed and homogenized three times. Then, this material was again centrifuged at 5000 rpm for 10 min, the supernatant was discarded, and the rest of the material was used for the cellular lysis. These samples were sonicated during 4 h at 37 °C. Then, a solution of NaOH 2 N was added and the mixture was heated to 100 °C for 20 min. The solution was cooled down at ambient temperature and centrifuged at 5000 rpm. Finally, the pH of the supernatant was adjusted between 6.5 and 7.5 to determine the intracellular nutrients.

The extracellular sugars were determined by an HPLC (Agilent), coupled to refractive index detector using a coregel 87P column and water as mobile phase, the testing time was 16 min. The column operates at 80 °C and the RID (infrared) and detector operate at 55 °C. The intracellular glucose was determined using anthrone reagent according to the proposed method by De Bruyn et al. [49]. Nitrates were determined using a method based on salicylic acid [50], and phosphates were determined using the ascorbic acid method [51].

Results and discussion

Results of the final identifiability analysis are presented in Table 6. These results indicate that the subset with the most sensitive and linearly independent parameters corresponds to the subset of size 19. The remaining parameters will conform the subset of fixed parameters \( [{\varvec{\uptheta}}_{{{\mathbf{Fixed}}}} ] \). The re-optimization of each subset (from the least identifiable to the most identifiable) leads to a decrease in the error function reaching a better fit of the predicted values to experimental data, as can be seen in Table 6.

Table 6 Subsets of identifiable parameters according to the orthogonal method
Full size table

The confidence intervals for the identifiable parameters were obtained using the covariance matrix. FIM is the inverse of the parameter estimation error covariance matrix COV and provides the Cramer–Rao lower bound on the parameter estimation errors [52] which can be used to assess the estimation uncertainty of \( \varvec{ }{\varvec{\uptheta}}_{\varvec{K}}^{\varvec{*}} \) [53] as presented in the following equation:

$$ COV \ge FIM^{ - 1} ({\varvec{\uptheta}}_{\varvec{K}}^{\varvec{*}} . ). $$
(11)

Then, approximate standard errors \( \sigma \left( {{\varvec{\uptheta}}_{\varvec{K}}^{\varvec{*}} } \right) \) for the estimated parameters can be calculated as the square root of the diagonal elements of the inverse of \( FIM \), see the following equation:

$$ \sigma \left( {{\varvec{\uptheta}}_{\varvec{K}}^{\varvec{*}} } \right) = \left[ {\sqrt {cov_{11} } ,\sqrt {cov_{22} } , \ldots ,\sqrt {cov_{mm} } } \right]. $$
(12)

In Table 7, the results of the optimal set of parameters \( \left\{ {{\tilde{\mathbf{\theta }}} = {\varvec{\uptheta}}^{*}_{{\mathbf{k}}} \mathop \cup \nolimits \,{\varvec{\uptheta}}_{{{\mathbf{Fixed}}}} } \right\} \) and the confidence intervals for identifiable parameters are reported. The values of the confidence intervals were obtained using the standard deviation calculated by Eq. (12). Most of the identifiable parameters have acceptable values of confidence intervals. However, parameters 22, 24, 49, and 59 have unacceptable confidence intervals, which could indicate that these parameters are insensitive towards the experiments performed. Therefore, it is recommendable to apply strategies of model-based optimal experimental design as a future work for this culture.

Table 7 Optimal parameters for plant cell cultures of T. peruviana and confidence intervals (±) for identifiable parameters
Full size table

The results of the model adjustment using the optimal parameters \( \left[ {{\tilde{\mathbf{\theta }}}} \right] \) are presented in Fig. 2a and b). These results show a good fit for biomass (x), extracellular sucrose (ESUC), intracellular glucose (GLU), and phosphates (Pi). In addition, the model presents a good prediction of the extracellular hydrolysis of sucrose (ESUC) into extracellular glucose (EGLUC) and fructose (EFRUC). However, to get a better fit of nitrates, it is necessary to perform additional studies to determine the effects of accumulation of these nutrients in the plant cell cultures of T. peruviana. The intracellular components reached the steady state by the 16th day approximately. As expected, nutrients as G6P, R5P, PEP, PYR, ACOA, OXO, and OAA increased their concentrations approximately until the 5th day corresponding to lag phase. This behavior is normal given that the cells adapt during this phase with low demands of the nutrients. Then, these nutrients presented a notable decrease in the slope approximately at the 10th day, which corresponds to the start of the exponential phase. This phase implies high requirements of nutrients. Finally, around the 16th day, these nutrients reached steady state close to the time corresponding to the stationary phase. For F6P, an increase was observed until the 10th day where a steady state was reached. G3P then begins to increase from that day. The biomass precursors, STH, OP, ORA, LIP, and AA, follow a similar trend to the cell growth, they are increasing their concentration and reaching the steady state close to the 16th day. This corresponds to the stationary phase for cell growth. The upper and lower bounds in the extracellular components are quite similar to the reported by Cloutier et al. [34]. In the case of intracellular components, similar bounds were found for PEP, PYR, ACOA, and OXO. The reactions for metabolite production presented by Cloutier et al. [34] could generate the differences in the bounds of the other intracellular components with respect to this work, since this research only includes the reactions for biomass production. In Fig. 2c, the results of the model predictions using validation data (i.e. a complete different set from the two used above for identifying the parameters) are presented. Validation results indicate that the model presents good predictive capability in the range of the initial conditions used for the model construction.

Fig. 2
figure 2

Parameter estimation results at the initial inoculum concentration and initial sucrose concentration of a 2.41–22.64 g/L and b 2.41 and 28.21 g/L. c Model results with validation data, at the initial inoculum and initial sucrose concentrations of 3.26–17.50 g/L, respectively. Axis units are (mmolg DW−1), except for x (g/L) and extracellular nutrients (mM)

Full size image

Although the model proposed in this study for plant cell cultures of T. peruviana is based on similar mechanistic models as the presented in Cloutier et al. [34] for cultures of C. roseus hairy root, and Cloutier et al. [35] for plant cell cultures of E. californica, each cellular species present a different set of parameter values. Such differences in the parameter values reflect differences in the cellular physiology among the plant cell cultures studied. For instance, in this work, the value of affinity constant for ACOA correspond to 0.6452 mmolg DW−1, this value is higher than the reported to C. roseus hairy root corresponding to 0.0125 mmolg DW−1, and the reported to E. californica corresponding to 0.0024 mmolg DW−1. The obtained value in the case of T. peruviana indicates its low affinity for this substrate in comparison with the others plant cell cultures analyzed. In the case of biomass precursors, it is possible to conclude that the plant cell cultures of T. peruviana present a high tendency to accumulate nutrients, given its low value of the affinity constant to STA corresponding to 0.0538 mmolg DW−11, which is lower than the reported to C. roseus hairy root which corresponds to 1 mmolg DW−1 and the reported to E. californica corresponds to 0.94 mmolg DW−1.

Fluxes distribution in plant cell cultures of T. peruviana

Figure 3 shows the fluxes distribution for plant cell cultures of T. peruviana for the stationary phase, between the 10th day, when the exponential phase is ending, and 16th day when the stationary phase is ending (before cells dead). The fluxes were evaluated using the results of the kinetics corresponding to an initial inoculum concentration of 2.41 g/L, and an initial sucrose concentration of 22.64 g/L.

Fig. 3
figure 3

Flux distribution for plant cell cultures of Thevetia peruviana. Values in bold correspond to the 10th day of culture

Full size image

It can be seen that the flux of the reaction representing the hydrolysis of sucrose into glucose and fructose v(1) decreases in 96.46% between the 10th day and the 16th day. This decrease suggests that the hydrolysis of sucrose for this plant cell culture is mainly performed at extracellular level. The change in flux v(2) (reaction in which glucose becomes intracellular glucose) shows a decrease of 95.58% between the 10th day and the 16th day. This value is higher than the change experienced in flux v(3) (reaction in which fructose becomes intracellular glucose), for which a decrease of 94.33% was observed. This behavior indicates that the cells consume preferably glucose as source of energy. However, the closeness of the values indicates that the cell is carrying out a parallel uptake of both nutrients, but with preference on glucose. This differentiated uptake of sugars was reported by Krook et al. [54] for cell suspension of Daucus Carota, and could be due to the fact that the glucose is a better substrate in cellular respiration processes than the fructose.

It is observed that the variation in the flux v(20) (extracellular phosphates) is higher than the flux v(17) (extracellular nitrates) with changes the 96.68 and of 32.40%, respectively. This indicates a high demand of phosphates and an initial accumulation of nitrates, which is in agreement with the experimental results obtained in this work.

The main route for the glycolysis pathway is determined through the fluxes: v(8), v(10), v(11), v(13), and v(14). Although in the formation of Glyceraldehido-3-phosphate from Fructose-6-phosphate, the fluxes v(8) and v(9) practically reach the steady state, the change on flux v(8) is slightly higher than the flux v(9). The glyceraldehido-3-phosphate is transformed in phosphoenolpyruvate through the flux v(10) with a change of 76.99%, which is higher than the flux v(11) with a change of 52.41%. In addition, finally, the transformation of phosphoenolpyruvate to pyruvate is preferably carried out through of the flux v(12) with a change of the 77.77% higher than the flux v(13) with a variation of 77.02%.

Analyzing the biomass precursors, it is observed that the fluxes v(26) (organic phosphates), v(27) (structural hexoses), v(21) (amino acids), v(23) (organic acids), and the v(25) (lipids) experienced variations of 95.14, 94.71, 80.55, 77.58, and 55.37%, respectively. The high demand of organic phosphates as precursors of biomass formation could explain the significant changes in the flux of phosphates v(20). The high demand of amino acids is understandable given its important role in protein formation. Between the 10th and the 16th day, the demand of lipids is low in comparison with the other precursors, since the cells could preferably accumulate them, as can be observed in its flux value.

The changes of the flux values found for the flux v(29) corresponding to the reserves of starch were 94.84%, indicating the importance of these reserves for the maintenance of the cells at the end of the growth.

Conclusions

In this work, a new mechanistic model for plant cell cultures of T. peruviana was developed. The identifiability analysis indicated that only 19 parameters of the model are identifiable parameters, suggesting high correlations among parameters effects for this type of models. The analysis of fluxes distributions indicates the behavior and tendencies in the nutrients uptake for this culture. This work is the base for the development of future works in the determination of routes for metabolite production from plant cell cultures of T. peruviana. The information about parameters value for the proposed mechanistic model contributes to the pool of available parameters for the modelling of plant cell cultures. Nonetheless, future work in the application and development of methodologies for identification and strategies for model-based optimal experimental design are required to improve the predictive capabilities of plant cell culture models.