1 Introduction

In the restricted three-body problem (R3BP), the equations of motion describe the dynamics of an infinitesimal mass m under the action of gravitational forces effected by two celestial bodies of giant masses \(M_{Sun}\) and \(m_{ planet}\) (\(m_{ planet} < M_{ Sun}\)), which are rotating around their common center of mass on Keplerian trajectories. The small mass m (satellite) is supposed to be moving as first approximation inside of restricted region of space near the planet of mass \(m_{ planet}\) or inside of so-called Hill sphere [1] radius:

$$\begin{aligned} r_{H} \,\;\cong \,\;a_{p} \cdot \,(1-e^{2})\cdot \left( {\frac{m_\mathrm{planet} }{3(M_\mathrm{Sun} +m_\mathrm{planet} )}} \right) ^{\frac{1}{3}} \end{aligned}$$

where \(a_p\) is semimajor axis of the planet’s orbit, e is the eccentricity of its orbit.

It is worth noting that there is a large number of previous and recent works concerning analytical development with respect to the R3BP equations which should be mentioned accordingly [2,3,4,5].

We should especially emphasize the theory of orbits, which was developed in profound work [5] by V. Szebehely for the case of the circular restricted problem of three bodies (CR3BP) (primaries \(M_{Sun}\) and \(m_{ planet}\) are rotating around their common center of mass on circular orbits) as well as the case of the elliptic restricted problem of three bodies (ER3BP), where the primaries \(M_{Sun}\) and \(m_{ planet}\) are rotating around their common center of mass on elliptic orbits.

$$\begin{aligned} \rho \,\;=\,\;\frac{a_{p} }{1+e\cdot \cos f} \end{aligned}$$

Unlike the CR3BP [6], the position of the primaries is not fixed in the rotating frame as they move along elliptical orbits: Their relative distance \(\rho \) is not constant in time where f is the true anomaly (the unit of distances is chosen so that \(a_p =\) 1).

As for the purpose of the current research, we can formulate it as follows: The main aim is to find a kind of the semi-analytical solution to the system of equations under consideration. Namely, each exact or even semi-analytical solution can clarify the structure, intrinsic code and topology of the variety of possible solutions (from mathematical point of view); here, exact or semi-analytical solution should be treated not only as analytical formulae in quadratures, but a system of ordinary differential equations (each for one appropriate variable) with well-known code for analytical or numerical resolving to be presented in their final form.

2 Mathematical model, equations of motion

According to [6, 7], in the ER3BP equations of motion of the infinitesimal mass m (satellite) can be represented in the synodic co-rotating frame of a Cartesian coordinate system \(\vec {{r}}=\){x, y, z} in non-dimensional form (at given initial conditions):

$$\begin{aligned} \ddot{{x}}\;\;-\;\;2\,\dot{{y}}\,\;= & {} \,\;\;\frac{\partial \,\Omega }{\partial \,x}\,\;,\nonumber \\ \ddot{{y}}\;\;+\;\;2\,\dot{{x}}\,\;= & {} \,\;\;\frac{\partial \,\Omega }{\partial \,y}\,\;,\nonumber \\ \ddot{{z}}= & {} \,\;\;\frac{\partial \,\Omega }{\partial \,z}\;\;, \end{aligned}$$
(1)
$$\begin{aligned} \Omega \;\;= & {} \;\;\frac{1}{1+e\cdot \cos f}\left[ {\frac{1}{2}\,\left( {x^{2}+\,y^{2}-z^{2}\cdot e\cdot \cos f} \right) \;\,+\;\frac{(1-\mu )}{r_{1} }\;\,+\,\;\frac{\mu }{r_{2} }} \right] , \end{aligned}$$
(2)

where dot indicates (d/df) in (1), \(\Omega \) is the scalar function, and

$$\begin{aligned} r_{1}^{2} \;= & {} \;\;(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}\;, \nonumber \\ r_{2}^{2} \;= & {} \;\;(x-\mu +1)^{2}\;+\;y^{2}\;+\;z^{2}\;, \end{aligned}$$
(3)

where \(r_i\) (\(i =\) 1, 2) are distances of the infinitesimal mass m from the primaries \(M_{Sun}\) and \(m_{planet}\), respectively [7].

Now, the unit of mass is chosen in (1) so that the sum of the primary masses is equal to 1. We suppose that \(M_{Sun}\cong 1 - \mu \) and \(m_{ planet} = \mu \), where \(\mu \) is the ratio of the mass of the smaller primary to the total mass of the primaries and 0 \(< \mu \le 1/2\). The unit of time is chosen so that the gravitational constant is equal to 1 in (2).

We neglect the effect of variable masses of the primaries [8] as well as the effect of their oblateness as was considered earlier in [9]. As for the domain where the aforesaid infinitesimal mass m is supposed to be moving, let us consider the Cauchy problem in the whole space. Besides, we should note that the second terms in the left parts of Eq. (1) are associated with the components of the Coriolis acceleration. Finally, let us additionally note that the spatial ER3BP when e  >  0 and \(\mu \)  >  0 is not conservative, and no integrals of motion are known [7].

3 Reduction of the system of equations (1)

Aiming the aforementioned way of constructing the semi-analytical solution, let us present Eq. (1) in a suitable for analysis form as below by appropriately transforming the right parts with regard to partial derivatives with respect to the proper coordinates {x, y, z} [10]

$$\begin{aligned}&\ddot{{x}}\;\;-\;\;2\,\dot{{y}}\,\;=\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )(x-\mu )}{\left( {(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\frac{\mu (x-\mu +1)}{\left( {(x-\mu +1)^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\,\frac{3}{2}}}} \right] \,\;, \nonumber \\&\quad \ddot{{y}}\;\;+\;\;2\,\dot{{x}}\,\;=\,\;\;\frac{1}{1+e\cdot \cos f}\cdot \left[ {y\;\,-\;\,\frac{(1-\mu )y}{\left( {(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\,\frac{\mu y}{\left( {(x-\mu +1)^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\,\frac{3}{2}}}} \right] \,\;,\nonumber \\&\quad {\ddot{{z}}}\;\;\;=\,\;\;\frac{1}{1+e\cdot \cos f}\cdot \left[ {-z\cdot e\cdot \cos f\;\,-\;\,\frac{(1-\mu )z}{\left( {(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\,\frac{\mu z}{\left( {(x-\mu +1)^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\,\frac{3}{2}}}} \right] \;\;, \end{aligned}$$
(4)

Let us transform system of equations (4) to the form which would be convenient for further analysis. From first and second of Eq. (4), we obtain (\(y \ne \) 0):

$$\begin{aligned}&(\ddot{{x}}\;\;-\;\;2\,\dot{{y}})\cdot (1+e\cdot \cos f)\;\,-\;\,x\;\,=\;\,\;(x-{{\upmu }} )\cdot \left\{ {\frac{(\ddot{{y}}\;\;+\;\;2\,\dot{{x}})\,\cdot \,(1+e\cdot \cos f)\;\,-\;\,y}{y}} \right\} \nonumber \\&-\;\frac{{{\upmu }} }{\left( {(x-{{\upmu }} +1)^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\,\frac{3}{2}}}\, \end{aligned}$$
(5)

In (5), \({z^{2}}\) is given as the function of {x, y} , their derivatives {\(\dot{{x}}\), \(\dot{{y}}\)} with respect to the f, accelerations {\(\ddot{{x}}\), \(\ddot{{y}}\)} , and true anomaly f.

But from the second and third of Eq. (4), it follows ({y, z} \(\ne \) 0, {\(\dot{{x}}\), \(\dot{{y}}\), \(\dot{{z}}\)} \(\ne \) 0):

$$\begin{aligned} (1+e\cdot \cos f)\left( {\frac{\;\ddot{{z}}}{z}+1} \right) \;=\,\frac{\;(\ddot{{y}}\;\;+\;\;2\,\dot{{x}})\,\cdot \,(1+e\cdot \cos f)}{y}\,\;,\quad \Rightarrow \quad \frac{\;\ddot{{z}}}{z}\;\,+\;1\;\;=\;\,\frac{\;(\ddot{{y}}\;\;+\;\;2\,\dot{{x}})\,}{y}\,\; \end{aligned}$$
(6)

4 Approximated solutions of Eqs. (1)–(3) for the class of trapped motions

Let us assume that coordinates \(\vec {{r}}=\){x, y, z} of solutions of system (1) belong to the class of trapped motions of the infinitesimal mass m, which is moving near the planet \(m_{ planet}\) (taking into account the equality \(\rho \,\;=\,\;\frac{a_{p} }{1+e\cdot \cos f})\):

$$\begin{aligned} \frac{\left| {\,\vec {{r}}_{2} \,} \right| }{\left| {\,\vec {{r}}_{1} \,} \right| }\;\,<<\,\;1\;,\quad \left| {\,\vec {{r}}_{1} \,} \right| \;\;\cong \;\;\frac{a_{p} }{1+e\cdot \cos f}+\delta \;,\quad \left| {\,\delta \,} \right|<<\;a_{p} \end{aligned}$$
(7)

but the aforementioned infinitesimal mass m is, nevertheless, located on each step of its trajectory at a large distance from the Sun (\(M_{Sun}\)) insofar; here \(\left| {\,\vec {{r}}_{2} \,} \right| \,\;>\;R_{p} \), whereas \(R_{p} \) is the radius of planet \(m_{ planet}\).

Thus, if we take into consideration the additional restriction (7) with respect to the components of solution in Eqs. (1)–(3), the aforesaid assumption should simplify the third of equations (4) accordingly (except the obvious case {z, \(\ddot{{z}}\)} \(=\) 0 in our further analysis):

$$\begin{aligned} \begin{array}{l} \quad \quad \;\ddot{{z}}\,\cdot \,(1+e\cdot \cos f)\;\,+\;\,z\cdot e\cdot \cos f\;=\,\;-\;\frac{z}{\left| {\,\vec {{r}}_{2} \,} \right| ^{\,3}}\cdot \left\{ {(1-\mu )\cdot \frac{\left| {\,\vec {{r}}_{2} \,} \right| ^{\,3}}{\left| {\,\vec {{r}}_{1} \,} \right| ^{3}}\,\;+\;\mu } \right\} \;,\quad \Rightarrow \\ \left\{ {\;\left( {\frac{\left| {\,\vec {{r}}_{2} \,} \right| }{\left| {\,\vec {{r}}_{1} \,} \right| }} \right) ^{\,3}\rightarrow \;\;0\;} \right\} \quad \;\;\Rightarrow \;\;\quad \left| {\,\vec {{r}}_{2} \,} \right| \,\;\cong \,\;\,\frac{\mu ^{\,\frac{1}{3}}}{\left( {-\,\,\frac{\ddot{{z}}}{z}\,\cdot \,(1+e\cdot \cos f)\;\,-\;\,e\cdot \cos f} \right) ^{\,\frac{1}{3}}}\;,\quad \Rightarrow \\ \quad \quad \quad \;y\;\,\;\cong \,\;\,\pm \sqrt{\;\frac{\mu ^{\,\frac{2}{3}}}{\left( {\,\,\frac{\ddot{{z}}}{z}\,\cdot \,(1+e\cdot \cos f)\;\,+\;\,e\cdot \cos f} \right) ^{\,\frac{2}{3}}}\;\;\,-\,\;\,\left( {{\begin{array}{*{20}c} \\ \\ \end{array} }(x-\mu +1)^{2}\;+\;z^{2}\;} \right) } \;, \\ \end{array} \end{aligned}$$
(8)

where appropriate restriction should be valid

$$\begin{aligned} \frac{\mu ^{\,\frac{2}{3}}}{\left( {\,\,\frac{\ddot{{z}}}{z}\,\cdot \,(1+e\cdot \cos f)\;\,+\;\,e\cdot \cos f} \right) ^{\,\frac{2}{3}}}\;\;\,-\,\;\,z^{2} \ge \,\;\,(x-\mu +1)^{2}\;\;, \end{aligned}$$

Thus, we have expressed in (8) the coordinate y via coordinates {x, z} and second derivative of coordinate \(\ddot{{z}}\) with respect to the true anomaly f (as a first approximation).

Now let us present Eq. (6) in a form of the Riccati-type ordinary differential equation [11] for coordinate z, depending on the coordinate y and on the appropriate derivatives of coordinates {\(\dot{{x}}\,,\;\ddot{{y}}\)} with respect to the true anomaly f

$$\begin{aligned} \ddot{{z}}\;\;+\;\,\left( {1\;\,-\;\,\frac{\;(\ddot{{y}}\;\;+\;\;2\,\dot{{x}})\,}{y}} \right) \,\cdot \,z\;\;=\;\,0\,\; \end{aligned}$$
(9)

So, Equation (9) should determine the proper quasi-periodic solution for coordinate z if the solutions for coordinates {x, y} are already obtained.

Let us present further the solutions of Eq. (9)

$$\begin{aligned} \left( {1\;\,-\;\,\frac{\;(\ddot{{y}}\;\;+\;\;2\,\dot{{x}})\,}{y}} \right) \;=\;\alpha \,(f)\quad \Rightarrow \quad \ddot{{z}}\;\;+\;\,\alpha \,\cdot \,z\;\;=\;\,0\,\; \end{aligned}$$
(10)

The aforementioned presentation of solutions in a form (10) for coordinate z is obviously useful from practical point of view in celestial mechanics for the reason that such the solutions, e.g., could be presenting the quasi-periodical dependence of coordinate z with respect to the true anomaly f (if \(\alpha \) is considered to be slowly varying parameter or circa constant, as we can see in our analysis).

The second advance of exploring the differential invariant (6) in a form (10) is that we can reduce one of two equations (second or third) of system (4), which was used at derivation of differential invariant (6). Let us choose the third equation for this aim

$$\begin{aligned} \alpha \;\!=\!\,\;\frac{1}{1\!+\!e\cdot \cos f}\cdot \left[ {e\cdot \cos f\;\!+\;\!\frac{(1-\mu )}{\left( {(x-\mu )^{2}\;\!+\!\;y^{2}\;+\;(z)^{2}} \right) ^{\frac{3}{2}}}\,\;+\;\,\frac{\mu }{\left( {(x-\mu \!+\!1)^{2}\;+\;y^{2}\;+\;(z)^{2}} \right) ^{\,\frac{3}{2}}}} \right] \nonumber \\ \end{aligned}$$
(11)

Meanwhile, equality (11) reveals the quasi-periodic type of the solutions for Eq. (10) (if \(\alpha \) is considered to be slowly varying parameter or circa constant): Indeed, taking into account the additional restriction (7), we can make a reasonable conclusion from (11) that \(\alpha \)  > 0 in any case (for the motions which can be expected according to the additional assumption (7)).

So, in this case Eq. (10) yields the classical periodic type of solutions for coordinate z as presented below (e.g., if \(\alpha \) is considered to be circa constant)

$$\begin{aligned} z\;\;=\;\,C_{1} \,\cos \,\,(f\cdot \,\sqrt{\alpha })\;\;+\;\;C_{2} \,\sin \,\,(f\cdot \,\sqrt{\alpha }) \end{aligned}$$
(12)

where \(\{C_1, C_2\} = \textit{const}\).

We should note also that Eq. (10) reveals the obvious quasi-periodic character of dependence of coordinate y on the derivative of coordinate x (with respect to the true anomaly f). Indeed, we obtain from (10) for coordinate y:

$$\begin{aligned} \ddot{{y}}\;\;+\;(\alpha \;\,-\;\,1)\,\cdot \,y\;=\;-2\,\dot{{x}}\; \end{aligned}$$
(13)

which is, in fact, the equation of forced oscillations ( [10], example 2.36).

For the sake of simplicity, let us consider in our further analysis the partial case \(\alpha =\) 1 in formulae (10)–(13). Then, integrating both the parts of Eq. (13) with respect to the true anomaly f, we could use the result of integrating in the transformation of the left part of first equation of system (4).

Thus, we should obtain in result the nonlinear ordinary differential equation of the second order in regard to the coordinate x(f) in case of the given function (12) for the coordinate z, \(\alpha =\) 1 (whereas the true anomaly f is to be slowly varying independent coordinate). Obviously, such the nonlinear ordinary differential equation of second order (Appendix A1) could be solved by means of numerical methods only. Similar simple case was investigated first in [1] (the well-known Clohessy–Wiltshire equations for relative motion when \(e \ne 0\)) but without obtaining expression for y presented by (8).

Finally, let us note that we should restrict choosing of the obtained solutions for the aforesaid nonlinear ODE of second order with regard to the coordinate x(f) by taking into account the additional condition for the function \(r_{2} \rightarrow R_p\) (while the magnitude of this function should be exceeding the minimal distances within Roche-lobe’s region [4, 5] for the planet with mass \(m_{ planet} = \mu \) around which infinitesimal mass is currently rotating in its trapped motion).

As for expression for the function \(\delta (f)\), we can obtain it from (7) as below

$$\begin{aligned}&\;(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}\;\;\cong \;\;\left( {\frac{a_{p} }{1+e\cdot \cos f}+\delta } \right) ^{2}\;,\quad \left| {\,\delta \,} \right|<<\;a_{p} \quad \Rightarrow \nonumber \\&\;\;\;\delta \;\,\cong \,\;\sqrt{(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}} \;\;-\;\;\left( {\frac{a_{p} }{1+e\cdot \cos f}} \right) \end{aligned}$$
(14)

where expression for y is given in (8) (where expression for \(\frac{\ddot{{z}}}{z}\) could be expressed from (10)), but expression for z is given in (12), \(\alpha =\) 1.

5 Final presentation of the solution

Let us present the solution \(\vec {{r}}=\){x, y, z} for the trapped motion (7) of the infinitesimal mass m satellite, which is moving near the planet \(m_{planet}\) in the ER3BP (1)–(4)

  • The key nonlinear ordinary differential equation of the second order in regard to the coordinate x(f) in case of the given function (12) for the coordinate z (\(\alpha =\) 1) is obtained below:

Let us we substitute expression (8) for coordinate y, expression (12) for coordinate z, and the integrated expression for \(\dot{{y}}\) directly \(\rightarrow \) into the first equation of system (4) to obtain the nonlinear ordinary differential equation of the second order with regard to the unknown coordinate x(f) (\(\alpha = 1, x_0 = {const}\)):

$$\begin{aligned}&\ddot{{x}}\;\;+\;4\,(x-x_{0} )\,\;=\frac{1}{1+e\cdot \cos f}\cdot \left[ {x\;\,-\;\frac{(1-\mu )(x-\mu )}{\left( {(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,\;-\;\frac{\mu (x-\mu +1)}{\left( {\left| {\,\vec {{r}}_{2} \,} \right| } \right) ^{\,3}}} \right] \,\;,\nonumber \\&\quad \left\{ {\;\left| {\,\vec {{r}}_{2} \,} \right| \,\;\cong \,\;\,\mu ^{\,\frac{1}{3}}\;} \right\} \;, \nonumber \\&\quad \ddot{{x}}\;\;+\;4\,(x-x_{0} )\,\;=-\;\frac{(1-\mu )}{1+e\cdot \cos f}\cdot \left[ {1\;\,+\;\frac{(x-\mu )}{\left( {(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,} \right] \,\;,\nonumber \\&\quad \left\{ \;\;y\;\,\;\cong \,\;\,\pm \sqrt{\;\mu ^{\,\frac{2}{3}}\;\;\,-\,\;\,\left( (x-\mu +1)^{2}\;+\;z^{2}\; \right) } \;,\quad \;\mu ^{\,\frac{2}{3}}\;\;\,-\,\;\,\left( (x-\mu +1)^{2}\;+\;z^{2}\; \right) \;\;>\;\;0\;\; \right\} \nonumber \\&\quad \Rightarrow \qquad \ddot{{x}}\;\;+\;4\,(x-x_{0} )\,\;=-\;\frac{(1-\mu )}{1+e\cdot \cos f}\cdot \left[ {1\;\,+\;\frac{(x-\mu )}{\left( {\mu ^{\,\frac{2}{3}}\;-2(x-\mu )-1} \right) ^{\frac{3}{2}}}\,} \right] \,\;, \end{aligned}$$
(15)

  • The expression (8) for coordinate y is given via coordinates {x, z} , true anomaly f, and additional parameter \(\alpha \) in (10) (\(\alpha =\) 1):

$$\begin{aligned} y\;\,\;\cong \,\;\,\pm \sqrt{\;\frac{\mu ^{\,\frac{2}{3}}}{\left( {\,\,\frac{\ddot{{z}}}{z}\,\cdot \,(1+e\cdot \cos f)\;\,+\;\,e\cdot \cos f} \right) ^{\,\frac{2}{3}}}\;\;\,-\,\;\,\left( (x-\mu +1)^{2}\;+\;z^{2}\; \right) } \;\;, \\ \quad \quad \quad \frac{\mu ^{\,\frac{2}{3}}}{\left( {\,\,\frac{\ddot{{z}}}{z}\,\cdot \,(1+e\cdot \cos f)\;\,+\;\,e\cdot \cos f} \right) ^{\,\frac{2}{3}}}\;\;\,-\,\;\,z^{2} \ge \,\;\,(x-\mu +1)^{2}\;\;, \\ \end{aligned}$$

  • expression for z is given in (12) (\(\{C_1, C_2\}= {const}\), \(\alpha =\) 1):

$$\begin{aligned} z\;\;=\;\,C_{1} \,\cos \,\,f\;\;+\;\;C_{2} \,\sin \,\,f \end{aligned}$$

The aforementioned nonlinear ODE of the second order for function x(f) should be solved under the optimizing condition \(r_{2} \rightarrow R_p\), as soon as coordinates {x, y, z} are already calculated (while the magnitude of this function \(r_{2} \) should exceed the minimal distance or Roche limit [4, 5] for the planet with mass \(m_{ planet} =\mu \)).

Let us also consider the case \(\alpha (f) \ne \) const in Eqs. (10)–(11) (which are proved to be valid for the trapped motion (7) of infinitesimal mass m in the ER3BP (1)–(4)).

Using (10), we obtain

$$\begin{aligned} \ddot{{z}}\;\;+\;\,\alpha (f)\,\cdot \,z\;\;=\;\,0\;,\,\; \end{aligned}$$
(16)

where Eq. (16) could be transformed by the change of variables \(\frac{\dot{{z}}}{z}\) to the Riccati ODE of the first order [10] (in case \(z \ne \) 0).

Then, let us simplify the second equation of system (4) by using the left part of (10)

$$\begin{aligned}&\quad \;\;(\ddot{{y}}\;\;+\;\;2\,\dot{{x}})\,\cdot \,(1+e\cdot \cos f)\,\;\,-\;\,y\;=\,\;\;-\;\frac{y}{\left| {\,\vec {{r}}_{2} \,} \right| ^{\,3}}\cdot \left\{ {(1-\mu )\cdot \frac{\left| {\,\vec {{r}}_{2} \,} \right| ^{\,3}}{\left| {\,\vec {{r}}_{1} \,} \right| ^{3}}\,\;+\;\mu } \right\} \;, \nonumber \\&\quad \left\{ {\;\left( {\frac{\left| {\,\vec {{r}}_{2} \,} \right| }{\left| {\,\vec {{r}}_{1} \,} \right| }} \right) ^{\,3}\rightarrow \;\;0\;} \right\} \quad \;\;\Rightarrow \;\;\quad \frac{1}{\left| {\,\vec {{r}}_{2} \,} \right| ^{\,3}}\,\;\cong \,\;\,\frac{1}{\mu }\,\cdot \,\left( {1\,\;\,+(\alpha \;\,-\;\,1)\,\cdot \,(1+e\cdot \cos f)} \right) \end{aligned}$$
(17)

where (in case \(z \ne \) 0)

$$\begin{aligned} \alpha (f)\;\,=\,\,-\,\,\frac{\ddot{{z}}}{z}\; \end{aligned}$$

Furthermore, based on (16)–(17), we can write out the key nonlinear ordinary differential equation of the second order in regard to the coordinate x(f) in case of the given function (16) for the coordinate z

$$\begin{aligned}&\ddot{{x}}\;\;-\;\;2\,\dot{{y}}\,\;+\;\;(\alpha \;\,-\;\,1)\,\cdot \,(x-\mu +1)\,\;\,=\;\;-\;\frac{(1-\mu )}{1+e\cdot \cos f}\cdot \left[ {\;1\;\;+\;\;\frac{(x-\mu )}{\left( {(x-\mu )^{2}\;+\;y^{2}\;+\;z^{2}} \right) ^{\frac{3}{2}}}\,} \right] , \nonumber \\&\quad \,\;\;\quad \quad \Rightarrow \left\{ {\;\;y\;\,\;\cong \,\;\,\pm \sqrt{\;\frac{\mu ^{\,\frac{2}{3}}}{\left( {\,\alpha (f)\,\cdot \,(1+e\cdot \cos f)\;\,-\;\,e\cdot \cos f} \right) ^{\,\frac{2}{3}}}\;\;\,-\,\;\,\left( (x-\mu +1)^{2}\;+\;z^{2}\; \right) } \;\;} \right\} \quad \quad \quad \quad \Rightarrow \nonumber \\&\quad \ddot{{x}}\;-\;2\,\dot{{y}}\;+\;(\alpha \,-\,1)\,\cdot \,(x-\mu +1)\,\,=\;-\;\frac{(1-\mu )}{1+e\cdot \cos f}\cdot \left[ \right. 1\;+\;\;\frac{(x-\mu )}{\left( {\frac{\mu ^{\,\frac{2}{3}}}{\left( {\,\alpha (f)\,\cdot \,(1\!+\!e\cdot \cos f)\;\,\!-\!\;\,e\cdot \cos f} \right) ^{\,\frac{2}{3}}}-\,2(x\!-\!\mu )\,-\,1} \right) ^{\frac{3}{2}}}\left. \right] \,\;,\;\nonumber \\ \end{aligned}$$
(18)
Table 1 Comparison of the averaged parameters of the moons in Solar system
Full size table
Table 2 Results of numerical calculations for Eqs. (16)–(19) (case of Earth)
Full size table
Table 3 Results of numerical calculations for Eqs. (16)–(19) (case of Mars)
Full size table
Table 4 Results of numerical calculations for Eqs. (16)–(19) (case of Venus)
Full size table

where expression (8) for coordinate y in (18) is given via coordinates {x, z} , true anomaly f, and the additional parameter \(\alpha \) in (10) or (16):

$$\begin{aligned} y\;\,\;\cong \,\;\,\pm \sqrt{\;\frac{\mu ^{\,\frac{2}{3}}}{\left( {\,\alpha (f)\,\cdot \,(1+e\cdot \cos f)\;\,-\;\,e\cdot \cos f} \right) ^{\,\frac{2}{3}}}\;\;\,-\,\;\,\left( (x-\mu +1)^{2}\;+\;z^{2}\; \right) } \;\;, \\ \quad \quad \quad \;\;\frac{\mu ^{\,\frac{2}{3}}}{\left( {\,\,\alpha \,\cdot \,(1+e\cdot \cos f)\;\,-\;\,e\cdot \cos f} \right) ^{\,\frac{2}{3}}}\;\;\,-\,\;\,z^{2}\;\,>\,\;\,(x-\mu +1)^{2}\;\;. \\ \end{aligned}$$

The aforementioned nonlinear ODE of the second order for function x(f) should be solved under the optimizing condition \(r_{2} \rightarrow R_p\), as soon as coordinates {x, y, z} are already calculated (while the magnitude of this function \(r_{2} \) should exceed the minimal distances within the Roche-limit [4, 5] for the planet with mass \(m_{ planet}\)).

As for the numerical checking of the proper solutions of Eq. (18), we have tested the cases of Earth, Mars and Venus (see their appropriate parameters at Table 1 in Appendix A1). By the way, for the Earth it means \(z =\) 0 in (16)–(18) where we can choose function \(\alpha (f)\) absolutely arbitrary, but taking into account that it should be the slowly varying function, e.g., as below

$$\begin{aligned} \alpha (f)\;\,\;\cong \,\;\,1000\;\;-\;\;100\cdot \left( {\frac{1-\exp \,(\sin f)}{1+\exp \,(\sin f)}} \right) \; \end{aligned}$$
(19)

Meanwhile, such the same choice of function \(\alpha (f)\) (19) can also be applied for calculations in cases of Mars and Venus as well.

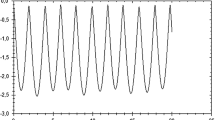
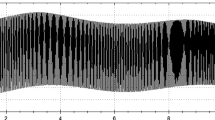
We should note that we have used for calculating the data (Tables 2, 3, 4) the Runge–Kutta fourth-order method with step 0.001 at initial values for Eqs. (16) and (18) as follows: (1) \(x_{0} = - 1.0103652222598\) and \((\dot{{x}})_{0} = 0\) (for Earth; we consider \(z =\) 0); (2) \(x_{0} = - 1, (\dot{{x}})_{0} = 0, z_{0} = 0, (\dot{{z}})_{0} = - 0.1\) (for Mars); 3) \(x_{0} = - 1, (\dot{{x}})_{0} = 0,z_{0} = 0, (\dot{{z}})_{0} = - 0.3\) (for Venus). All the results of numerical calculations for Eqs. (16)–(19) (see Tables 2, 3, 4 in Appendix, A2) we schematically imagine at Figs. 1, 2, 3, 4, and 5.

6 Discussion

As we can see from the derivation above, equations of motion (4) even for the case of trapped motion \(\vec {{r}}=\){x, y, z} (in the sense of additional assumption (7) for the infinitesimal mass m (satellite), which is moving near the planet \(m_{planet}\)) are proved to be very hard to solve analytically.

Fig. 1
figure 1

Results of numerical calculations of the coordinate x by Eq. (18) for Earth

Full size image
Fig. 2
figure 2

Results of numerical calculations of \(r_{2} \) by using (17) and (19) for Earth

Full size image
Fig. 3
figure 3

Results of numerical calculations of \(r_{1} \) by Eqs. (17)–(19) for Earth

Full size image
Fig. 4
figure 4

Results of numerical calculations of \(r_{2} \) by Eqs. (16)–(19) for Mars

Full size image
Fig. 5
figure 5

Results of numerical calculations of \(r_{2} \) by Eqs. (16)–(19) for Venus

Full size image

Nevertheless, at first step we have succeeded in obtaining the elegant expression for the differential invariant (6), which interconnects the second and third equations of system (4). The aforesaid invariant (6) yields Equation (9) of a Riccati-type for the coordinate z which should determine the proper solution (for coordinate z) if the solutions for coordinates {x, y} are already obtained. Then, we suggest a kind of reduction in a form (10) for Eq. (9) which let us obtain the classical analytical (quasi-periodic) solution (12) for coordinate z (if additional function \(\alpha \) is considered to be slowly varying parameter or circa constant), as well as it let us obtain in Equation (8) the approximated solution for coordinate y, which was derived under assumption (7). Hereafter, we have considered the case \(\alpha =\) 1 for the sake of simplicity. The key nonlinear ODE in regard to the coordinate x(f) in case of the given function (12) for the coordinate z, \(\alpha =\) 1 (whereas true anomaly f is to be slowly varying independent coordinate) is obtained to be presented in (15).

Meanwhile, the key nonlinear ODE in regard to coordinate x(f) in case of the given function for coordinate z via (10) is obtained to be presented in a form (18) for \(\alpha \ne \) const. This result outlines the novelty of the paper which should be discussed accordingly. Indeed, results (16)–(18) and (20) in Appendix A1 are obtained as generalization of the simple case \(\alpha =\) 1 which was investigated first in work [1] by F.Cabral (the well-known Clohessy–Wiltshire equations for relative motion when \(e \ne \) 0) but without obtaining expression for y presented by (8) here.

According to our knowledge, semi-analytical solution, obtained by F.Cabral in [1] for simple case \(\alpha =\) 1, is most close to our general case of solutions, presented by formulae (16)–(18) for \(\alpha \ne \) const; moreover, such nontrivial type of solution has not been suggested until the current research and the only way to get some kind of information about the intrinsic properties and behavior of even the particular dynamical system (1) or (4) was to calculate approximated solutions by using various numerical methods. So, any new theoretical method or semi-analytical approach for even the particular solving of such the system of equations would be useful on the level of practical applications.

We also determine the analytical expression which interrelates the coordinate x, depending on the given coordinate z and true anomaly f, relative to the additional function \(\delta (f)\) in (14), which determines deviation of distance of infinitesimal mass m (to \(M_{Sun}\)) from variable relative distance \(\rho \,\;=\,\;\frac{a_{p} }{1+e\cdot \cos f}\) between primaries \(M_{Sun}\) and \(m_{ planet}\).

Ending discussion, let us note also that natural restriction \(r_{2} \rightarrow R_p\) should be valid for the trapped motion \(\vec {{r}}=\{x, y, z\}\) with respect to the aforementioned function \(r_{2} \) in case of the given function for coordinate z in (10) (\(R_p\) is the radius of planet \(m_{planet}\)). It means that we should choose among the solutions of nonlinear ODE of second order in regard to the coordinate x(f) only the optimized solutions, for which the condition \(r_{2} \rightarrow R_p\) is valid accordingly (while its magnitude should exceed the level of minimal distances outside the Roche-lobe’s region [4, 5] for the planet with mass \(m_{planet}\)).

7 Conclusion

In this paper, we present a new ansatz for solving equations of motion for the trapped orbits of the infinitesimal mass m (satellite), which is locked in the space trap to be moving near the planet \(m_{planet}\) in case of the elliptic restricted problem of three bodies, ER3BP (with Keplerian elliptic trajectories of the primaries \(M_{Sun}\) and \(m_{planet}\) around each other): a new type of the solving procedure is implemented here to obtain the coordinates \(\vec {{r}}=\{x, y, z\}\) of the infinitesimal mass m with its orbit located near the planet \(m_{ planet}\). Meanwhile, the system of equations of motion has been successfully explored with respect to the existence of analytical or semi-analytical (approximated) way for presentation of the solution.

We obtain as follows: (1) Equation for coordinate x is given via coordinate y, true anomaly f, and the additional function \(\alpha \), which determines the quasi-periodic (a Riccati-type) character of solution for coordinate z, (2) expression for coordinate y is given via coordinate x, true anomaly f, and the aforementioned parameter \(\alpha \), (3) coordinate z is to be quasi-periodically varying with respect to the true anomaly f.

We have pointed out the optimizing procedure for the nonlinear ordinary differential equation of second order in regard to the aforementioned coordinate x(f) in case of the given function for coordinate z (which is valid only for the optimized solutions \(r_{2} \rightarrow R_p\), while the magnitude of function \(r_{2} \) should exceed the level of minimal distances outside the Roche-limit for the planet).

The suggested approach can be used in future researches for optimizing the maneuvers of spacecraft which is moving near the planet \(m _{planet} = \mu \) in case of the elliptic restricted problem of three bodies (ER3BP).

So, in this case we also could suggest a scheme for \(r_{2} \)-optimizing for the maneuvers of spacecraft which is moving near the planet \(m _{planet}\).

Also, some remarkable articles should be cited, which concern the problem under consideration, [12,13,14,15,16,17,18,19,20,21,22,23,24] and [25,26,27,28,29,30,31,32,33]; the results of the most remarkable and comprehensive works (in the sense of algorithms of obtaining the families of solutions in ER3BP) should be outlined and commented additionally hereto. In [17] Dr. J.Singh and A.Umar describe the motion around the collinear libration points in the elliptic R3BP with a bigger triaxial primary. In work [19] E.I.Abouelmagd and M.A.Sharaf classified trajectories of test particle around the libration points in the restricted three-body problem with the effect of radiation and oblateness. In [21], Kushvah, et al. explored the stability (as authors say, of nonlinear character) in the generalized photogravitational restricted three body problem with additional influence of Poynting–Robertson drag. In [28], Wiegert et al. investigated the problem of stability of quasi-satellites in the outer solar system. In the profound work of Wiesel [29], a lot of theoretical and numerical findings regarding stable orbits around of the martian moons was established thoroughly (he, e.g., found that stable retro-grade orbits exist about both moons, staying in the moon vicinity for at least 25 days, and quite probably longer).