Analysis of multiple parallel cracks in a functionally graded magneto-electro-elastic plane using boundary collocation method

Abstract

The fracture behavior of a functionally graded magneto-elastic plane with multiple parallel cracks is examined in this article. Under anti-plane mechanical, in-plane electric, and magnetic loadings, it is assumed that the cracks are either of the magneto-electrically impermeable or permeable types. Here, three distinct crack configurations are taken into consideration. For each of the three crack configuration cases, the boundary collocation and least square methods are used to obtain the semi-analytical expressions of the stress intensity factors (SIFs) at the crack tips. SIFs are used to calculate the stress magnification factors (SMFs). The novelty of the article is the study of shielding and amplification tendencies of cracks under the impact of functionally graded parameter, geometric size, and electric and magnetic loads. The graphical illustrations of SMFs as a function of gradient parameter, the distance between the cracks, and electric and magnetic loadings for three different crack configurations are the key features of the article.

1 Introduction

Intelligent materials made of piezoelectric and piezomagnetic materials have been widely used in medical ultrasonic imaging, chips of magnetic sensors, magnetic-field probes, acoustic, hydrophones, sensors, electric packaging, and actuators in the smart structures and components of energy harvesters [1]. The coupled properties of piezoelectric and piezomagnetic composites offer the scope to engineers to create intelligent structures, composite materials, and devices that are capable of responding to internal and/or environmental changes. One such composite material is magneto-electro-elastic material having the combined effects of piezoelectric, piezomagnetic, and magneto-electric. Magneto-electro-elastic materials are used in electronic instrumentations and microwave and optoelectronics. Nowadays, the use of functionally graded materials (FGMs) in the engineering field is unavoidable due to their capability of reducing the concentration of stress and increasing fracture toughness.

Eventually, the concept of FGMs is extended to magneto-electro-elastic materials to enhance the reliability of composites. These materials have continuously varying properties which are considered as functionally graded magneto-electro-elastic (FGMEE) materials. These materials have the advantage that they have neither internal seams nor desirable boundaries. However, owing to the brittleness, cracks inevitably exist in FGMEE materials. For such types of materials having cracks subjected to magneto-electro-mechanical loadings, the magneto-electro-elastic field is concentrated near cracks, which causes the advancement of cracks. Also during the manufacturing process, unavoidable initiations of cracks, holes, inclusions, dislocation, and other defects occur. These defects cause premature failure of composites or structures at any moment that finally leads to failure. Therefore, it is very much important to study the fracture behavior of FGMEE materials.

An anti-plane problem for an embedded and edge crack in a functionally graded magneto-electro-elastic strip is studied in [2] by using the integral transform and dislocation density functions. A similar problem for an embedded crack in a functionally graded piezoelectric/piezomagnetic plate was investigated in [3] using the boundary collocation method. In [4], an anti-plane internal crack normal to the edge of a functionally graded piezoelectric/piezomagnetic half-plane was considered in which the theory of energy density is applied to know the fracture behavior. A discussion on the kinking phenomena of impermeable and permeable moving cracks in an FGMEE strip under anti-plane mechanical loading and in-plane electric and also magnetic loadings was presented in [5].

Since FGMEE materials are brittle in nature, they can usually contain multiple cracks with an extremely high crack density. The interaction between these cracks may significantly affect their fracture behavior. However, less number of articles are available in the literature on such multi-crack problems in composites made of piezoelectric and piezomagnetic materials, and only a few studies are conducted [6,7,8,9]. Moreover, due to the vulnerability, edge cracks are more catastrophic in comparison with embedded cracks. The problem of periodic surface cracks under thermal loading in a functionally graded composite was studied in [10, 11].

In general, the finite element method is used to calculate the crack tip SIF for cracked structures [12, 13]. However, due to various difficulties including the determination of a large number of unknowns, and consideration of a large number of node points, this method is sometimes complex to calculate crack tip SIF. To overcome this, the method of the integral equation and others [14,15,16,17] are used. One of them is the boundary collocation method (BCM). In BCM, the exact solutions of governing partial differential equations are used and approximations are restricted only to the boundaries. For approximation, the discretization of boundaries is accomplished. For BCM it is not required to discretize the domain of the problem and therefore the method is applied to problems with arbitrary boundary conditions and irregular domains. Therefore, BCM is an advantageous method to study crack problems due to its simplicity, accuracy, and less computational time. Muskhelishvili [18] has formulated some basic equations for solving the elasticity problem by using the complex variable function. An initiative has been taken by Williams [19] and Isida [20] in their works during solutions of the finite cracked plane problems. If the crack surface is subjected to some loading in a finite cracked plane, then the complex potentials must satisfy the following conditions [21]:

• 1. The equilibrium and compatibility conditions in the occupied region of the crack plane.

• 2. Stress condition on the crack surface.

• 3. For multiply connected cracked plane, the single-valued condition of displacement around the crack.

• 4. The boundary conditions.

In most cases, the first three conditions are automatically satisfied. Only the boundary conditions need to be checked. Along with that for better accuracy, the least square method is used. The least-square technique is used to minimize the resultant force and also the displacement residuals along the boundary [22].

In light of the above discussion, the authors of the current article have concentrated on the issue of multiple parallel cracks in a finite FGMEE plane. According to [2, 3, 5], the material properties are assumed to vary exponentially along the x-axis. Both magneto-electrically impermeable and magneto-electrically permeable crack surface conditions are adopted in this study. Additionally, three distinct crack configuration cases are taken into account. In the first case, multiple parallel embedded cracks of the same length are considered, in the second, multiple parallel edge cracks of the same length are considered, and in the third, multiple parallel edge cracks of alternating lengths are taken into consideration. The problem is then reduced to power series form as per the considered case which is subsequently solved numerically with the aid of BCM and the least square approach. The semi-analytical forms of crack tip SIFs are obtained that help to determine the expressions of crack tip SMFs. The outcome of the current study is also supported by an existing result for a specific case. The shielding and amplification phenomena of cracks can be identified using the semi-analytical forms of SMFs, which can be used to determine the likelihood of crack arrest. Through visual presentations for the three different crack configurations under consideration, an effort has been made to illustrate the effects of the gradient parameter, the distance between the cracks, and the electric and magnetic loadings on SMFs.

2 Problem formulation

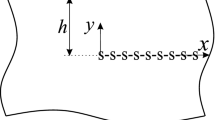
Consider a finite number $(2 N + 1)$ of parallel cracks having length $b_m - a_m$ $(m=0, \pm 1,...,\pm N)$ in a finite magneto-electro-elastic plane of width w and height 2h as shown in Fig. 1a. Any two parallel cracks are separated by a distance of $h_0$. The magneto-electro-elastic plane exhibits transversely isotropic behavior and is poled in the $z-$direction. The surfaces of the cracks are subjected to anti-plane mechanical $\tau _0$, in-plane electric $D_0$, and magnetic $B_0$ loadings, as shown in Fig. 1b. Therefore, this article addresses the problem of an anti-plane elastic field coupled with in-plane electric and magnetic fields and the model is based on the framework of magneto-electrostatics.

Fig. 1

Functionally graded magneto-electro-elastic plane with multiple parallel cracks

The constitutive equations for infinitely small deformations are given by

$$\begin{aligned}&\tau _{ m z k}=c_{4 4} \frac{\partial w_m}{\partial k} + e_{1 5} \frac{\partial \phi _m}{\partial k} + f_{1 5} \frac{\partial \psi _m}{\partial k}, \end{aligned}$$

(1)

$$\begin{aligned}&D_{ m k}=e_{1 5} \frac{\partial w_m}{\partial k} - \epsilon _{1 1} \frac{\partial \phi _m}{\partial k} - g_{1 1} \frac{\partial \psi _m}{\partial k}, \end{aligned}$$

(2)

$$\begin{aligned}&B_{ m k}=f_{1 5} \frac{\partial w_m}{\partial k} - g_{1 1} \frac{\partial \phi _m}{\partial k} - \mu _{1 1} \frac{\partial \psi _m}{\partial k}, \end{aligned}$$

(3)

where $\tau _{ m z k}$, $D_{ m k}$, $B_{ m k}\; (k=x,y)$ are the anti-plane shear stress, in-plane electric displacement, and magnetic inductions, respectively. Throughout the article $m=0, \pm 1,...,\pm N$ denote the $2 N + 1$ number of parallel edge cracks. The mechanical displacement, electric and magnetic potentials are denoted by $w_m$, $\phi _m$, and $\psi _m$, respectively. $c_{4 4}$, $e_{1 5}$, $f_{1 5}$, $\epsilon _{1 1}$, $g_{1 1}$, $\mu _{1 1}$ are the material constants viz., shear modulus, magnetic permeability, dielectric, piezoelectric, piezomagnetic and magneto-electric constants, respectively, and expressed as

$$\begin{aligned}&c_{4 4}(x)=c_{4 4 0} e^{\beta x},\; e_{1 5}(x)=e_{1 5 0} e^{\beta x},\; f_{1 5}(x)=f_{1 5 0} e^{\beta x}, \end{aligned}$$

(4)

$$\begin{aligned}&\epsilon _{1 1}(x)=\epsilon _{1 1 0} e^{\beta x},\; g_{1 1}(x)=g_{1 1 0} e^{\beta x},\; \mu _{1 1}(x)=\mu _{1 1 0} e^{\beta x}, \end{aligned}$$

(5)

where $\beta$ is the functionally graded parameter and $c_{4 4 0}$, $\mu _{1 1 0}$, $\epsilon _{1 1 0}$, $e_{1 5 0}$, $f_{1 5 0}$, $g_{1 1 0}$ represent the material constants at $x=0$.

The equilibrium equations of the FGMEE plane for $m=0, \pm 1,...,\pm N$ in the absence of body force and free charge can be written as

$$\begin{aligned}&\frac{\partial \tau _{m x z}}{\partial x} + \frac{\partial \tau _{m y z}}{\partial y}=0, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial D_{m x}}{\partial x} + \frac{\partial D_{m y}}{\partial y}=0, \end{aligned}$$

(7)

$$\begin{aligned}&\frac{\partial B_{m x}}{\partial x} + \frac{\partial B_{m y}}{\partial y}=0. \end{aligned}$$

(8)

With the aid of auxiliary functions ${\eta _m}, \chi _m, \zeta _m$ defined by

$$\begin{aligned}&{\eta _m}=c_{4 4 0} w_m + e_{1 5 0} \phi _m + f_{1 5 0} \psi _m, \end{aligned}$$

(9)

$$\begin{aligned}&\chi _m=e_{1 5 0} w_m - \epsilon _{1 1 0} \phi _m - g_{1 1 0} \psi _m, \end{aligned}$$

(10)

$$\begin{aligned}&\zeta _m=f_{1 5 0} w_m - g_{1 1 0} \phi _m - \mu _{1 1 0} \psi _m, \end{aligned}$$

(11)

the following relations can be obtained employing Eqs. (1)–(3) as

$$\begin{aligned}&\tau _{m z k} = e^{\beta x} \frac{\partial {\eta _m}}{\partial k},\; D_{m k} = e^{\beta x} \frac{\partial \chi _{m}}{\partial k},\; B_{m k} = e^{\beta x} \frac{\partial \zeta _{m}}{\partial k}.&\end{aligned}$$

(12)

Therefore, Eqs. (6)–(8) reduce to

$$\begin{aligned}&\nabla ^{2} {\eta _m} + \beta \frac{\partial {\eta _m}}{\partial x} = 0, \end{aligned}$$

(13)

$$\begin{aligned}&\nabla ^{2} \chi _m + \beta \frac{\partial \chi _m}{\partial x} = 0, \end{aligned}$$

(14)

$$\begin{aligned}&\nabla ^{2} \zeta _m + \beta \frac{\partial \zeta _m}{\partial x} = 0. \end{aligned}$$

(15)

The considered problem is solved for two different crack boundary conditions which are impermeable and permeable types. The boundary conditions for the magneto-electrically impermeable cracks are given by

$$\begin{aligned} y \in [-h, h]:&\tau _{m z x} (a_m, y) = D_{m x} (a_m, y)= B_{m x} (a_m, y) \nonumber \\&= \tau _{m z x} (b_m, y) = D_{m x} (b_m, y)= B_{m x} (b_m, y) = 0, \end{aligned}$$

(16)

$$\begin{aligned}&x \in (a_m, b_m): \tau _{m z y} (x, h_m) = -\tau _0, \; D_{m y} (x, h_m) = -D_0, B_{m y} (x, h_m) = -B_0,&\end{aligned}$$

(17)

$$\begin{aligned}&x \notin (a_m, b_m): w_m (x, h_m)=\phi _m (x, h_m)=\psi _m (x, h_m)=0,&\end{aligned}$$

(18)

and for magneto-electrically permeable cracks those are given by

$$\begin{aligned} y \in [-h, h]:&\tau _{m z x} (a_m, y) = D_{m x} (a_m, y) = B_{m x} (a_m, y)&\nonumber \\ {}&= \tau _{m z x} (b_m, y) = D_{m x} (b_m, y) = B_{m x} (b_m, y) = 0,&\end{aligned}$$

(19)

$$\begin{aligned}&x \in (a_m, b_m): \tau _{m z y} (x, h_m) = -\tau _0, \end{aligned}$$

(20)

$$\begin{aligned}&x \notin (a_m, b_m): w_m (x, h_m)=0, \end{aligned}$$

(21)

$$\begin{aligned}&x \in [0, w]: \phi _m (x, h_m)=\psi _m (x, h_m)=0, \end{aligned}$$

(22)

where $h_m=m h_0$.

3 Problem solution

3.1 Solution for magneto-electrically impermeable cracks

Case I: Multiple parallel embedded cracks of equal length

Keeping in mind the geometry of the considered problem and the contributions of the articles [3, 23, 24], the complex functions $\varPhi _{m j}\;(j=1,2,3)$ for magneto-electrically impermeable parallel cracks are defined as

$$\begin{aligned} \varPhi _{m j}&= \sum _{n=1}^{M} i A_{m j n} \sqrt{\{z-(a_m+i h_m)\}\{z-(b_m+i h_m)\}} (z- i h_m)^{n-1}, \end{aligned}$$

(23)

where $A_{m j n}$ are the real unknowns to be determined, M is the number of summation term and z is a complex number defined as $z=x+i y$ for $x,y\in \Re$. Since the problem deals with the real-valued functions, the mechanical displacement, electric and magnetic potentials are given by

$$\begin{aligned}&w_m=\text {Re}(\varPhi _{m 1}), \phi _m=\text {Re}(\varPhi _{m 2}), \psi _m=\text {Re}(\varPhi _{m 3}). \end{aligned}$$

(24)

It is clear that by the above choice of complex functions, the first three conditions as mentioned in section 1 is already satisfied. Only the boundary condition needs to be taken care of. Using (24), Eqs. (1)–(3) reduce to

$$\begin{aligned}&\tau _{ m z k}=c_{4 4} \frac{\partial \text {Re}(\varPhi _{m 1})}{\partial k} + e_{1 5} \frac{\partial \text {Re}(\varPhi _{m 2})}{\partial k} + f_{1 5} \frac{\partial \text {Re}(\varPhi _{m 3})}{\partial k}, \end{aligned}$$

(25)

$$\begin{aligned}&D_{ m k}=e_{1 5} \frac{\partial \text {Re}(\varPhi _{m 1})}{\partial k} - \epsilon _{1 1} \frac{\partial \text {Re}(\varPhi _{m 2})}{\partial k} - g_{1 1} \frac{\partial \text {Re}(\varPhi _{m 3})}{\partial k}, \end{aligned}$$

(26)

$$\begin{aligned}&B_{ m k}=f_{1 5} \frac{\partial \text {Re}(\varPhi _{m 1})}{\partial k} - g_{1 1} \frac{\partial \text {Re}(\varPhi _{m 2})}{\partial k} - \mu _{1 1} \frac{\partial \text {Re}(\varPhi _{m 3})}{\partial k}. \end{aligned}$$

(27)

The following expressions can be obtained with the help of Cauchy–Riemann equations

$$\begin{aligned} \tau _{ m z k}&=c_{4 4} \text{ Re }\left( \frac{\partial \varPhi _{m 1}}{\partial k}\right) + e_{1 5} \text{ Re }\left( \frac{\partial \varPhi _{m 2}}{\partial k}\right) + f_{1 5} \text{ Re }\left( \frac{\partial \varPhi _{m 3}}{\partial k}\right) , \end{aligned}$$

(28)

$$\begin{aligned} D_{ m k}&=e_{1 5} \text{ Re }\left( \frac{\partial \varPhi _{m 1}}{\partial k}\right) - \epsilon _{1 1} \text{ Re }\left( \frac{\partial \varPhi _{m 2}}{\partial k}\right) - g_{1 1} \text{ Re }\left( \frac{\partial \varPhi _{m 3}}{\partial k}\right) , \end{aligned}$$

(29)

$$\begin{aligned} B_{ m k}&=f_{1 5} \text{ Re }\left( \frac{\partial \varPhi _{m 1}}{\partial k}\right) - g_{1 1} \text{ Re }\left( \frac{\partial \varPhi _{m 2}}{\partial k}\right) - \mu _{1 1} \text{ Re }\left( \frac{\partial \varPhi _{m 3}}{\partial k}\right) . \end{aligned}$$

(30)

Equation (23) gives

$$\begin{aligned}&\frac{\partial \varPhi _{m j}}{\partial x}=\sum _{n=1}^{M} i A_{m j n} P_{m n}, \quad \frac{\partial \varPhi _{m j}}{\partial y}=\sum _{n=1}^{M} i^2 A_{m j n} P_{m n}, \nonumber \\\text{ where } \; P_{m n}=&[2 n (x + i y - i h_m)^n - (2 n -1) (a_m + b_m)&\nonumber \\&\times (x+i y-i h_m)^{n-1} + 2 (n-1) a_m b_m (x+i y-i h_m)^{n-2}] \nonumber \\ {}&/[2 \sqrt{\{x+i y-(a_m+i h_m)\}\{x+i y-(b_m+i h_m)\}}]. \end{aligned}$$

(31)

Utilizing (31), Eqs. (28)–(30) can be expressed as

$$\begin{aligned} \tau _{ m z x}&=\sum _{n=1}^{M} \left[ c_{4 4} A_{m 1 n} + e_{1 5} A_{m 2 n} + f_{1 5} A_{m 3 n}\right] \text{ Re } (i P_{m n}), \end{aligned}$$

(32)

$$\begin{aligned} D_{ m x}&=\sum _{n=1}^{M} \left[ e_{1 5} A_{m 1 n} - \epsilon _{1 1} A_{m 2 n} - g_{1 1} A_{m 3 n}\right] \text{ Re } (i P_{m n}), \end{aligned}$$

(33)

$$\begin{aligned} B_{ m x}&=\sum _{n=1}^{M} \left[ f_{1 5} A_{m 1 n} - g_{1 1} A_{m 2 n} - \mu _{1 1} A_{m 3 n}\right] \text{ Re } (i P_{m n}), \end{aligned}$$

(34)

$$\begin{aligned} \tau _{ m z y}&=\sum _{n=1}^{M} \left[ c_{4 4} A_{m 1 n} + e_{1 5} A_{m 2 n} + f_{1 5} A_{m 3 n}\right] \text{ Re } (i^2 P_{m n}), \end{aligned}$$

(35)

$$\begin{aligned} D_{ m y}&=\sum _{n=1}^{M} \left[ e_{1 5} A_{m 1 n} - \epsilon _{1 1} A_{m 2 n} - g_{1 1} A_{m 3 n}\right] \text{ Re } (i^2 P_{m n}), \end{aligned}$$

(36)

$$\begin{aligned} B_{ m y}&=\sum _{n=1}^{M} \left[ f_{1 5} A_{m 1 n} - g_{1 1} A_{m 2 n} - \mu _{1 1} A_{m 3 n}\right] \text{ Re } (i^2 P_{m n}). \end{aligned}$$

(37)

Case II: Multiple parallel edge cracks of equal length

Fig. 2

Comparison of normalized SIFs at the crack tip a $a_0$ and b $b_0$ as a function of $(b_0-a_0) / (2 h)$ for distinct values of $\beta h$ between the obtained results and existing results [2] for a single embedded crack in a functionally graded magneto-electro-elastic strip

Fig. 3

Comparison of normalized SIFs at the crack tip $b_0$ as a function of $b_0 / h$ for distinct values of $\beta h$ between the obtained results and existing results [2] for a single edge crack in a functionally graded magneto-electro-elastic strip

For this crack configuration the complex functions $\varPhi _{m j}\;(j=1,2,3)$ for magneto-electrically impermeable parallel cracks are defined as

$$\begin{aligned}&\varPhi _{m j}=\sum _{n=1}^{M} i A_{m j n} \sqrt{\{z-(b_m+i h_m)\}} (z- i h_m)^{n-1}, \end{aligned}$$

(38)

Following a similar procedure as of Case I, Eqs. (28)–(30) can be expressed as

$$\begin{aligned} \tau _{ m z x}&=\sum _{n=1}^{M} \left[ c_{4 4} A_{m 1 n} + e_{1 5} A_{m 2 n} + f_{1 5} A_{m 3 n}\right] \text{ Re } (i Q_{m n}), \end{aligned}$$

(39)

$$\begin{aligned} D_{ m x}&=\sum _{n=1}^{M} \left[ e_{1 5} A_{m 1 n} - \epsilon _{1 1} A_{m 2 n} - g_{1 1} A_{m 3 n}\right] \text{ Re } (i Q_{m n}), \end{aligned}$$

(40)

$$\begin{aligned} B_{ m x}&=\sum _{n=1}^{M} \left[ f_{1 5} A_{m 1 n} - g_{1 1} A_{m 2 n} - \mu _{1 1} A_{m 3 n}\right] \text{ Re } (i Q_{m n}), \end{aligned}$$

(41)

$$\begin{aligned} \tau _{ m z y}&=\sum _{n=1}^{M} \left[ c_{4 4} A_{m 1 n} + e_{1 5} A_{m 2 n} + f_{1 5} A_{m 3 n}\right] \text{ Re } (i^2 Q_{m n}), \end{aligned}$$

(42)

$$\begin{aligned} D_{ m y}&=\sum _{n=1}^{M} \left[ e_{1 5} A_{m 1 n} - \epsilon _{1 1} A_{m 2 n} - g_{1 1} A_{m 3 n}\right] \text{ Re } (i^2 Q_{m n}), \end{aligned}$$

(43)

$$\begin{aligned} B_{ m y}&=\sum _{n=1}^{M} \left[ f_{1 5} A_{m 1 n} - g_{1 1} A_{m 2 n} - \mu _{1 1} A_{m 3 n}\right] \text{ Re } (i^2 Q_{m n}). \nonumber \\ \text{ where } \; Q_{m n}&=[(2 n -1) (x+i y-i h_m)^{n-1} - 2 (n-1) b_m (x+i y-i h_m)^{n-2}] \nonumber \\ {}&\quad /[2 \sqrt{\{x+i y-(b_m+i h_m)\}}]. \end{aligned}$$

(44)

Fig. 4

Variations of SMFs at the crack tip a as a function of $\beta / h$ under magneto-electrically a impermeable and b permeable condition for Case I

Fig. 5

Variations of SMFs at the crack tip b as a function of $\beta / h$ under magneto-electrically a impermeable and b permeable condition for Case I

Fig. 6

Variations of SMFs at the crack tip b as a function of $\beta / h$ under magneto-electrically a impermeable and b permeable condition for Case II

Fig. 7

Variations of SMFs at the crack tip b as a function of $\beta / h$ under magneto-electrically a impermeable and b permeable condition for Case III

Case III: Multiple parallel edge cracks of alternating length

In this case the expressions of complex functions, anti-plane shear stress, in-plane electric displacement, and magnetic inductions are the same as obtained for the case of multiple parallel edge cracks of equal length. The only change is in the value of $b_m$ whose value is same for all m in Case II whereas for this case $b_{2\,m}<b_{2\,m + 1}$ $(m=0, \pm 1,...,\pm N)$.

3.2 Solution for magneto-electrically permeable cracks

Case I: Multiple parallel embedded cracks of equal length

The complex functions $\varPhi _{m j}\;(j=1,2,3)$ for magneto-electrically permeable cracks are given by

$$\begin{aligned} \varPhi _{m 1}&=\sum _{n=1}^{M} i [A_{m 1 n} \sqrt{\{z-(a_m+i h_m)\}\{z-(b_m+i h_m)\}}&\nonumber \\&-(p A_{m 2 n} + q A_{m 3 n}) (z- i h_m)] (z - i h_m)^{n-1}, \end{aligned}$$

(45)

$$\begin{aligned} \varPhi _{m j}&=\sum _{n=1}^{M} i A_{m j n} (z - i h_m)^{n}, \; j=2,3, \end{aligned}$$

(46)

where $p=e_{150} / c_{440}$ and $q=f_{150} / c_{440}$. Analogous to the impermeable case, the following expressions are obtained.

$$\begin{aligned} \frac{\partial \varPhi _{m 1}}{\partial x}&=\sum _{n=1}^{M} i \left[ A_{m 1 n} P_{m n} - (p A_{m 2 n} + q A_{m 3 n}) R_{m n}\right] , \end{aligned}$$

(47)

$$\begin{aligned} \frac{\partial \varPhi _{m 1}}{\partial y}&=\sum _{n=1}^{M} i^2 \left[ A_{m 1 n} P_{m n} - (p A_{m 2 n} + q A_{m 3 n}) R_{m n} \right] , \end{aligned}$$

(48)

$$\begin{aligned} \frac{\partial \varPhi _{m j}}{\partial x}&=\sum _{n=1}^{M} i A_{m j n} R_{m n},\quad \frac{\partial \varPhi _{m j}}{\partial y}=\sum _{n=1}^{M} i^2 A_{m j n} R_{m n}, \nonumber \\&j=2,3, \nonumber \\ \text {where}&\quad R_{m n}=n (x+i y-i h_m)^{n-1}. \end{aligned}$$

(49)

Using (40)–(42), Eqs. (28)–(30) for permeable type cracks can be expressed as

$$\begin{aligned} \tau _{ m z x}&=\sum _{n=1}^{M} c_{4 4} A_{m 1 n} \text{ Re } (i P_{m n}) - [c_{4 4} p A_{m 2 n} + c_{4 4} q A_{m 3 n}- e_{1 5} A_{m 2 n} - f_{1 5} A_{m 3 n}] \text{ Re } (i R_{m n}), \end{aligned}$$

(50)

$$\begin{aligned} D_{ m x}&=\sum _{n=1}^{M} e_{1 5} A_{m 1 n} \text{ Re } (i P_{m n}) - [e_{1 5} p A_{m 2 n} + e_{1 5} q A_{m 3 n} + \epsilon _{1 1} A_{m 2 n} + g_{1 1} A_{m 3 n}] \text{ Re } (i R_{m n}), \end{aligned}$$

(51)

$$\begin{aligned} B_{ m x}&=\sum _{n=1}^{M} f_{1 5} A_{m 1 n} \text{ Re } (i P_{m n}) - [f_{1 5} p A_{m 2 n} + f_{1 5} q A_{m 3 n} + g_{1 1} A_{m 2 n} + \mu _{1 1} A_{m 3 n}] \text{ Re } (i R_{m n}), \end{aligned}$$

(52)

$$\begin{aligned} \tau _{ m z y}&=\sum _{n=1}^{M} c_{4 4} A_{m 1 n} \text{ Re } (i^2 P_{m n}) - [c_{4 4} p A_{m 2 n} + c_{4 4} q A_{m 3 n}- e_{1 5} A_{m 2 n} - f_{1 5} A_{m 3 n}] \text{ Re } (i^2 R_{m n}), \end{aligned}$$

(53)

$$\begin{aligned} D_{ m y}&=\sum _{n=1}^{M} e_{1 5} A_{m 1 n} \text{ Re } (i^2 P_{m n}) - [e_{1 5} p A_{m 2 n} + e_{1 5} q A_{m 3 n}+ \epsilon _{1 1} A_{m 2 n} + g_{1 1} A_{m 3 n}] \text{ Re } (i^2 R_{m n}), \end{aligned}$$

(54)

$$\begin{aligned} B_{ m y}&=\sum _{n=1}^{M} f_{1 5} A_{m 1 n} \text{ Re } (i^2 P_{m n}) - [f_{1 5} p A_{m 2 n} + f_{1 5} q A_{m 3 n}+ g_{1 1} A_{m 2 n} + \mu _{1 1} A_{m 3 n}] \text{ Re } (i^2 R_{m n}). \end{aligned}$$

(55)

Case II: Multiple parallel edge cracks of equal length

Fig. 8

Variations of SMFs at the crack tip a as a function of $h_0 / h$ under magneto-electrically a impermeable and b permeable condition for Case I

Fig. 9

Variations of SMFs at the crack tip b as a function of $h_0 / h$ under magneto-electrically a impermeable and b permeable condition for Case I

Fig. 10

Variations of SMFs at the crack tip b as a function of $h_0 / h$ under magneto-electrically a impermeable and b permeable condition for Case II

Fig. 11

Variations of SMFs at the crack tip b as a function of $h_0 / h$ under magneto-electrically a impermeable and b permeable condition for Case III

Fig. 12

Variations of SMFs as a function of $\lambda _d$ for Case I at the crack tip a a and b b

Fig. 13

Variations of SMFs at the crack tip b as a function of $\lambda _d$ for a Case II and b Case III

Fig. 14

Variations of SMFs as a function of $\lambda _b$ for Case I at the crack tip a a and b b

Fig. 15

Variations of SMFs at the crack tip b as a function of $\lambda _b$ for a Case II and b Case III

For this case the complex functions $\varPhi _{m j}\;(j=1,2,3)$ for magneto-electrically permeable cracks are given by

$$\begin{aligned}&\varPhi _{m 1}=\sum _{n=1}^{M} i [A_{m 1 n} \sqrt{\{z-(b_m+i h_m)\}} -(p A_{m 2 n} + q A_{m 3 n}) (z- i h_m)] (z - i h_m)^{n-1}, \end{aligned}$$

(56)

$$\begin{aligned}&\varPhi _{m j}=\sum _{n=1}^{M} i A_{m j n} (z - i h_m)^{n}, \; j=2,3. \end{aligned}$$

(57)

Thus, Eqs. (28)–(30) reduce to

$$\begin{aligned} \tau _{ m z x}&=\sum _{n=1}^{M} c_{4 4} A_{m 1 n} \text{ Re } (i Q_{m n}) - [c_{4 4} p A_{m 2 n} + c_{4 4} q A_{m 3 n} - e_{1 5} A_{m 2 n} - f_{1 5} A_{m 3 n}] \text{ Re } (i R_{m n}), \end{aligned}$$

(58)

$$\begin{aligned} D_{ m x}&=\sum _{n=1}^{M} e_{1 5} A_{m 1 n} \text{ Re } (i Q_{m n}) - [e_{1 5} p A_{m 2 n} + e_{1 5} q A_{m 3 n} + \epsilon _{1 1} A_{m 2 n} + g_{1 1} A_{m 3 n}] \text{ Re } (i R_{m n}), \end{aligned}$$

(59)

$$\begin{aligned} B_{ m x}&=\sum _{n=1}^{M} f_{1 5} A_{m 1 n} \text{ Re } (i Q_{m n}) - [f_{1 5} p A_{m 2 n} + f_{1 5} q A_{m 3 n} + g_{1 1} A_{m 2 n} + \mu _{1 1} A_{m 3 n}] \text{ Re } (i R_{m n}), \end{aligned}$$

(60)

$$\begin{aligned} \tau _{ m z y}&=\sum _{n=1}^{M} c_{4 4} A_{m 1 n} \text{ Re } (i^2 Q_{m n}) - [c_{4 4} p A_{m 2 n} + c_{4 4} q A_{m 3 n} - e_{1 5} A_{m 2 n} - f_{1 5} A_{m 3 n}] \text{ Re } (i^2 R_{m n}), \end{aligned}$$

(61)

$$\begin{aligned} D_{ m y}&=\sum _{n=1}^{M} e_{1 5} A_{m 1 n} \text{ Re } (i^2 Q_{m n}) - [e_{1 5} p A_{m 2 n} + e_{1 5} q A_{m 3 n} + \epsilon _{1 1} A_{m 2 n} + g_{1 1} A_{m 3 n}] \text{ Re } (i^2 R_{m n}), \end{aligned}$$

(62)

$$\begin{aligned} B_{ m y}&=\sum _{n=1}^{M} f_{1 5} A_{m 1 n} \text{ Re } (i^2 Q_{m n}) - [f_{1 5} p A_{m 2 n} + f_{1 5} q A_{m 3 n} + g_{1 1} A_{m 2 n} + \mu _{1 1} A_{m 3 n}] \text{ Re } (i^2 R_{m n}). \end{aligned}$$

(63)

Case III: Multiple parallel edge cracks of alternating length

Again, in this case, the expressions of complex functions, anti-plane shear stress, in-plane electric displacement, and magnetic inductions are the same as of Case II with only a change in the value of $b_m$.

4 Stress magnification factors

The stress intensity factors at the crack tips are determined by

$$\begin{aligned}&K_{III}^{(m)} (a_m) = \lim \limits _{x \rightarrow a_m} \sqrt{2 \pi (a_m-x)}\; \tau _{m z y} (x, h_m), \end{aligned}$$

(64)

$$\begin{aligned}&K_{III}^{(m)} (b_m) = \lim \limits _{x \rightarrow b_m} \sqrt{2 \pi (x-b_m)}\; \tau _{m z y} (x, h_m). \end{aligned}$$

(65)

In terms of $A_{m j n}$, the crack tip stress intensity factors for multiple parallel embedded cracks of equal length for magneto-electrically impermeable cracks are given by

$$\begin{aligned}&K_{III}^{(m)} (a_m) = e^{\beta a_m} \sqrt{\frac{\pi (b_m - a_m)}{2}} \; \sum _{n=1}^{M} a_m^{n-1} \left( c_{4 4 0} A_{m 1 n} + e_{1 5 0} A_{m 2 n} + f_{1 5 0} A_{m 3 n}\right) , \end{aligned}$$

(66)

$$\begin{aligned}&K_{III}^{(m)} (b_m) = -e^{\beta b_m} \sqrt{\frac{\pi (b_m - a_m)}{2}} \; \sum _{n=1}^{M} b_m^{n-1} \left( c_{4 4 0} A_{m 1 n} + e_{1 5 0} A_{m 2 n} + f_{1 5 0} A_{m 3 n}\right) , \end{aligned}$$

(67)

and for magneto-electrically permeable cracks those are given by

$$\begin{aligned}&K_{III}^{(m)} (a_m) = e^{\beta a_m} \sqrt{\frac{\pi (b_m - a_m)}{2}} \; \sum _{n=1}^{M} a_m^{n-1} c_{4 4 0} A_{m 1 n}, \end{aligned}$$

(68)

$$\begin{aligned}&K_{III}^{(m)} (b_m) = -e^{\beta b_m} \sqrt{\frac{\pi (b_m - a_m)}{2}} \; \sum _{n=1}^{M} b_m^{n-1} c_{4 4 0} A_{m 1 n}. \end{aligned}$$

(69)

The crack tip stress intensity factors for multiple parallel edge cracks of equal as well as alternating lengths for magneto-electrically impermeable cracks are determined by

$$\begin{aligned} K_{III}^{(m)} (b_m)&= -e^{\beta b_m} \sqrt{\frac{\pi }{2}} \; \sum _{n=1}^{M} b_m^{n-1} \left( c_{4 4 0} A_{m 1 n} + e_{1 5 0} A_{m 2 n} + f_{1 5 0} A_{m 3 n}\right) , \end{aligned}$$

(70)

and for magneto-electrically permeable cracks they are determined by

$$\begin{aligned}&K_{III}^{(m)} (b_m) = -e^{\beta b_m} \sqrt{\frac{\pi }{2}} \; \sum _{n=1}^{M} b_m^{n-1} c_{4 4 0} A_{m 1 n}. \end{aligned}$$

(71)

The stress magnification factors at the crack tips [14, 15] are determined by

$$\begin{aligned}&M^{(m)} (a_m) = \frac{K_{III}^{(m)} (a_m)}{K_{III}^{(m)*} (a_m)},\; M^{(m)} (b_m) = \frac{K_{III}^{(m)} (b_m)}{K_{III}^{(m)*} (b_m)}, \end{aligned}$$

(72)

where $K_{III}^{(m)*} (a_m)$ and $K_{III}^{(m)*} (b_m)$ are the crack tip SIFs of the $m^{th}$ crack in the absence of remaining cracks for the concerned case.

5 Numerical results and discussion

The boundary collocation method is used to solve Eqs.  (31)–(36), (39)–(44), (46)–(47). It is sufficient to take into account only the positive portion of the y-axis due to geometric symmetry. For numerical computation, some points on the external boundaries of the plane and crack surfaces are chosen. Here, $A_{m j n}$’s are the unknowns to be determined. If the number of equations is equal to the total number of unknowns, then the unknowns can be determined by using the concept of matrix inversion [24]. Usually, to improve the accuracy more points are to be taken so that the number of equations is greater than the total number of unknowns, and the least square method is employed to obtain the coefficients [22]. The parameters are assumed to be $c_{4 4 0}=54\; \text {GPA}$, $e_{1 5 0}=7.8\;\text {C}/ \text {m}^2$, $\epsilon _{1 1 0}=3.64 \times 10^{-9}\;\text {C}^{2} / \text {Nm}^{2}$, $f_{1 5 0}=175\;\text {N} / \text {Am}$, $\mu _{1 1 0}=-1.97 \times 10^{-4}\;\text {Ns}^{2} / \text {C}^{2}$, $g_{1 1 0}=0.8 \times 10^{-11}\;\text {Ns} / (\text {VC})$, $\tau _{0}=4.2 \times 10^{6}\;\text {N} / \text {m}^2$ [7]. While determining $A_{m j n}$’s, M is chosen in such a way that three decimal digit accurate values of crack tip SMFs are acquired. For Case I $a_m / h = 0.2$, $b_m / h = 0.4$, Case II $b_m / h = 0.4$ and Case III $b_{2m} / h = b_{01} = 0.2$, $b_{2m+1} / h = b_{02} = 0.4$ are taken.

5.1 Validation

This section of the article presents a validation to compare the acquired results with the results provided in [2]. The integral transform and dislocation density functions were used in [2] to tackle the problem of a magneto-electrically impermeable or permeable embedded and edge crack perpendicular to the boundary of a functionally graded magneto-electro-elastic strip.

By taking into consideration a single crack, $N=0$ in the direction of x-axis, and for $h>>b_0$, the current problem is reduced to [2]. For $c_{4 4 0}=44\; \text {GPA}$, $e_{1 5 0}=5.8\;\text {C}/ \text {m}^2$, $\epsilon _{1 1 0}=6.46 \times 10^{-9}\;\text {C}^2 / \text {Nm}^2$, $f_{1 5 0}=275\;\text {N} / \text {Am}$, $\mu _{1 1 0}=-2.97 \times 10^{-4}\;\text {Ns}^2 / \text {C}^2$, $g_{1 1 0}=0.5 \times 10^{-11}\;\text {Ns} / (\text {VC})$, $\tau _{0}=4.2 \times 10^{6}\;\text {N} / \text {m}^2$, $\lambda _d=0$ and $\lambda _b=0$ [7], the findings of both the studies are compared for both embedded and edge crack configurations. It can be seen from Figs. 2 and 3 that the results obtained by our proposed method are in good agreement with the existing results provided in [2] when the normalizing factor of SIFs for embedded and edge crack is taken into account as $\tau _0 \sqrt{\pi (b_0-a_0) / 2}$ and $\tau _0 \sqrt{\pi b_0}$, respectively.

5.2 SMFs vs. functionally graded parameter $\beta$

Figures 4, 5, 6, and 7 illustrate how functionally graded parameters affect crack tip SMFs in both magneto-electrically impermeable and permeable conditions. As $\beta / h$ increases, SMF increases at the left crack tips in Case I, as shown in Fig. 4. In contrast, it decreases at the right crack tips with the increasing value of $\beta / h$ for all three cases as demonstrated from Figs. 5, 6 and 7. This shows that the likelihood of crack amplification increases at the left crack tip as the value of the functionally graded parameter increases, whereas the likelihood of crack shielding increases at the right crack tip.

Upon examination of the results, it is evident that for the negative value of $\beta / h$ the possibility of crack shielding is high for inner cracks in comparison with the outer ones whereas for the positive value of $\beta / h$ the possibility of crack amplification is high for outer cracks in comparison with the inner ones at the left crack tips under Case I. On the other hand at the right crack tip for the negative value of $\beta / h$ the possibility of crack amplification is high for inner cracks while for the positive value of $\beta / h$ the possibility of crack shielding is high for outer cracks for the Cases I and II. In Case III, it is noted that for negative values of the functionally graded parameter, the crack amplification phenomenon is high for longer cracks, while for positive values, the shielding phenomenon is high for shorter cracks.

Additionally, under magneto-electrically impermeable and permeable conditions, the magnitude of the SMFs at the crack tips varies in all cases. This indicates that the crack arrest tendency differs between magneto-electrically impermeable and permeable conditions.

5.3 SMFs versus crack spacing $h_0$

Figures 8, 9, 10, and 11 illustrate how crack spacing affects the likelihood of crack arrest. For both the impermeable and permeable type cracks, it is observed that as the spacing between the cracks increases the crack tip SMFs started to decrease which arises the possibility of cracks’ arrest. In Cases I and III only shielding behavior is noticed while both shielding and amplification behavior is noticed in Case II.

Additionally, in Cases I and II, under both magneto-electrically impermeable and permeable conditions, the magnitude of the crack tip SMFs for outer cracks is greater than that for inner cracks. For Case III, it can be shown that the shorter cracks have an elevated magnitude of crack tip SMFs than the longer ones. The magneto-electrically impermeable and permeable conditions significantly affect the tendency of cracks to arrest, as shown in Figs. 8, 9, 10, and 11.

5.4 SMFs versus electric load $\lambda _d$ and magnetic load $\lambda _b$

The shielding and amplification behavior of permeable type cracks is unaffected by the electric and magnetic loads. However, the effects of both loads are depicted in Figs. 12, 13, 14 and 15 for the impermeable type cracks. As per the figure keeping the magnetic load fixed, if the electric load increases, then the cracks started to arrest at both crack tips, whereas, for fixed electric load and increasing magnetic load, the cracks are started to propagate. In other words, electric loads resist the propagation of cracks, whereas magnetic load enhances the propagation of cracks.

6 Concluding remarks

The possibility of multiple parallel magneto-electrically impermeable and permeable cracks being arrested for three different configurations of cracks is examined in this article under the impact of gradient parameter, the distance between the cracks, and electric and magnetic loadings. The semi-analytical forms of SIFs and therefore SMFs are obtained for all three crack configuration cases by expressing the displacement and potential functions in terms of power series and applying boundary collocation and least square methods. The following are the findings of the current study:

• The semi-analytical expressions of SIFs aid in calculating the crack tip SMFs for the cases under consideration.

• In all three crack configuration scenarios, the change in the values of the functionally graded parameter has a considerable impact on the likelihood of crack arrest.

• The graphical displays of SMFs as a function of crack distance show that the interaction of cracks plays a non-negligible role in the shielding and amplifying nature of parallel cracks of different configurations. The crack arrest is less likely to occur as the distance between the cracks gets smaller because the cracks start to amplify.

• With an increase in the electric load and a decrease in the magnetic load, the cracks have a greater tendency to arrest.

• The distinction between parallel cracks, which are magneto-electrically impermeable and permeable for different cases, is graphically illustrated using SMFs.

• The innermost cracks have the smallest magnitude, and the outermost cracks have the largest magnitude when there are multiple parallel embedded and edge cracks of equal length. The shorter edge cracks have a magnitude greater than the longer ones when there are multiple parallel edge cracks of varying lengths.