1 Introduction

Today the study of intelligent materials is at the cutting edge of the current science and is a hot topic. Predictably, the successful development of intelligent materials would be a revolution event for many traditional industries. As one kind of intelligent materials, such as magneto-electric materials or multiferroic composite, the piezoelectric/piezomagnetic (PE/PM) composite material is made up of a variety of piezoelectric and piezomagnetic elements, which are more remarkable in terms of the magneto-electric effect than single-phase magneto-electric materials’ [1, 2]. Due to their advantages, intelligent materials containing the PE/PM elements, which are widely used in the manufacture of the intelligent products or intelligent structures, such as the disk-type transducer of ultrasonic transducers, the chips of magnetic sensors, magnetic-filed probes, and sensitive components of energy harvesters [1,2,3].

The PE/PM composites and their products are usually layered and brittle structures. Not only does the concentrated stress caused by electric, magnetic and external forces easily lead to serious cracks in PE/PM composites, but also the process of production or development of PE/PM composites would lead to unavoidable initiation of cracks, holes, inclusions, dislocation and other defects. It is not difficult to imagine these defects would bring about the premature failure of a device at any moment, finally leading to the failure of the products [4, 5]. Therefore, it is imperative to study the fracture behavior. In order to solve the "defect" problem of the devices, such as the screw dislocation, crack, and so on, which has attracted much attention about the fracture problem of such material or structure [6,7,8,9,10], some numerical methods are usually employed to solve these fracture problems with multi-physical fields coupling, and these methods can be classified into two kinds of methods, weighted residuals and analytical method. Generally, the exact solutions of multi fields problems are not easy to obtain, Wang [10] used classical elastic theory, Muskhelishvili theory, to derive out the exact solutions of the screw dislocation and anti-plane crack of the magneto-electro-elastic material. Additionally, the closed-forms expressions of these similar problems of FGM can also be derived [8, 9]. Besides, for the crack problems, complex analysis method is also employed to obtain the analytical results [11, 12]. As for obtaining the numerical results of the fracture problem, finite element method and integral equation method are often used [13, 14], which can simulate and compute some complex issues. Besides, there exists many results on the fracture problem of PE/PM functionally graded materials [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18].

Meanwhile, according to our knowledge, a crack starts from inclusion and exclusion of surface and this is a process. Simultaneously, in terms of the process of crack growth, the boundary condition is changing from infinite to finite region with the crack growth in a finite body. There exists some situations, for example, when a macro-crack exists in a very long tube or aircraft skin, the boundary condition can be absolutely defined as an infinite or semi-infinite region. However, in fact, some manufactured items, such as monitors, are typically fabricated as rectangular structures [19]. However, although not a few research have studied the crack problem of the PE/PM FGM rectangular plate, but when adopting mechanical strategy most of them would assume the infinite boundary [10,11,12,13,14,15,16,17,18,19,20,21]. Therefore, based on our experience in solving the fracture problem of the finite region, boundary collocation method is also employed in this paper [22]. The fracture problem of PE/PM FGM plate with a central crack inside and the influences of piezoelectricity and piezomagnetism on the impermeable or permeable crack are investigated. Finally, we obtain some corresponding results.

2 Magneto-electric FGM plate boundary condition and governing equations

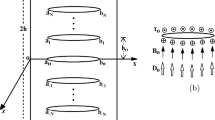
In FGM manufacture, many basic components are commonly designed for regular shapes. However, rectangular plate is one of the very common types of structure, and some sensor applications, additionally fracture tests of FGM are manufactured in rectangular configuration as shown in Fig. 1 [19, 20]. From Fig. 1, one could clearly observe that the crack in the rectangular plate, which should be defined finite region fracture problem.

Fig. 1
figure 1

Schematics diagram of sensor application and FGM fracture test in rectangular configuration [19, 20]

Full size image

Now, consider a finite magneto-electro-elastic plate that contains a Griffith crack in reference to the rectangular coordinate system x, y, z, as shown in Fig. 2. The plate exhibits transversely isotropic behavior, and the poling direction is in z-axis. It is assumed that the body is transversely isotropic, and the constitutive equation is

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{zk} =c_{44} \frac{\partial w}{\partial k}+e_{15} \frac{\partial \phi }{\partial k}+f_{15} \frac{\partial \psi }{\partial k} \\ \\ D_k =e_{15} \frac{\partial w}{\partial k}-\varepsilon _{11} \frac{\partial \phi }{\partial k}-\hbox {g}_{{11}} \frac{\partial \psi }{\partial k} \\ \\ B_k =f_{15} \frac{\partial w}{\partial k}-\hbox {g}_{{11}} \frac{\partial \phi }{\partial k}-\mu _{11} \frac{\partial \psi }{\partial k} \\ \end{array}} \right. \end{aligned}$$
(1)

where \(\tau _{zk} ,D_k ,B_k (k=x,y)\) are the anti-plane shear stress, in-plane electric displacement and magnetic induction, respectively. \(c_{44} ,\varepsilon _{11} ,e_{15} ,f_{15} ,g_{11} ,\mu _{11} \) are the shear modulus, the dielectric constant, the piezoelectric constant, the piezomagnetic constant, the magneto-electric constant and the magnetic permeability, respectively. \(w,\phi ,\psi \) are the mechanical displacement, electric potential and magnetic potential.

Fig. 2
figure 2

FGM rectangle plate with a central crack applied in magneto-electro-mechanical load

Full size image

The material parameters depend on x-axis with the exponent properties, which is one-dimensionally dependent. They are

$$\begin{aligned} \left\{ {\begin{array}{l} c_{44} =c_{440} e^{\beta x},\varepsilon _{11} =\varepsilon _{110} e^{\beta x} \\ e_{15} =e_{150} e^{\beta x},f_{15} =f_{150} e^{\beta x} \\ g_{11} =g_{110} e^{\beta x},\mu _{11} =\mu _{110} e^{\beta x} \\ \end{array}} \right. \end{aligned}$$
(2)

where \(\beta \) is a function of gradient parameter.

The body force and free charge are ignored here. Thus, the equilibrium equation of magneto-electrical FGM is

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\partial \tau _{zx} }{\partial x}+\frac{\partial \tau _{zy} }{\partial y}=0 \\ \\ \frac{\partial D_x }{\partial x}+\frac{\partial D_y }{\partial y}=0 \\ \\ \frac{\partial B_x }{\partial x}+\frac{\partial B_y }{\partial y}=0 \\ \end{array}} \right. \end{aligned}$$
(3)

The following auxiliary functions \(\omega ,\chi ,\zeta \) are introduced as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \omega =c_{440} w+e_{150} \phi +f_{150} \psi \\ \\ \chi =e_{150} w-\varepsilon _{110} \phi -g_{110} \psi \\ \\ \zeta =f_{150} w-g_{110} \phi -\mu _{110} \psi \\ \end{array}} \right. \end{aligned}$$
(4)

From Feng [23], the governing equation can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{l} \nabla ^{2}\omega +\beta \frac{\partial \omega }{\partial x}=0 \\ \\ \nabla ^{2}\chi +\beta \frac{\partial \chi }{\partial x}=0 \\ \\ \nabla ^{2}\zeta +\beta \frac{\partial \zeta }{\partial x}=0 \\ \\ \end{array}} \right. \end{aligned}$$
(5)

where, \(\nabla ^{2}=\frac{\partial ^{2}}{\partial \hbox {x}^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\), it is a two-dimensional Laplace operator.

Substituting Eqs. (2) and (4) into Eq. (1), one can obtain the following equations:

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{zx} =e^{\beta x}\omega _{,x} ,\tau _{zy} =e^{\beta x}\omega _{,y} \\ \\ D_x =e^{\beta x}\chi _{,x} ,D_y =e^{\beta x}\chi _{,y} \\ \\ B_x =e^{\beta x}\zeta _{,x} ,B_y =e^{\beta x}\zeta _{,y} \\ \\ \end{array}} \right. \end{aligned}$$
(6)

When the crack is in the center of the plate, the rectangular coordinate system x, y, z is shown in Fig. 1. As mentioned before, many researches only analyze one type of crack magneto-electrical boundary conditions, which is permeable or impermeable. Here, considering more sufficient cases for investigating the differences between the two crack boundary conditions.

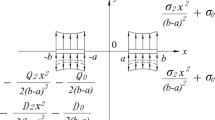
According to the characteristics of the magneto-electrically impermeable/permeable crack, the boundary conditions are

  1. (a)

    for magneto-electrically impermeable crack

$$\begin{aligned} \left\{ {\begin{array}{l} x\in (-a,a):\tau _{zy} (x,0)=-\tau _0 ,D_y (x,0)=-D_0 ,B_y (x,0)=-B_0 \\ x\notin (-a,a):w(x,0)=\phi (x,0)=\psi (x,0) \\ -h<y<h:\tau _{zx} (-a,y)=D_x (-a,y)=B_x (-a,y)=0 \\ -h<y<h:\tau _{zx} (a,y)=D_x (a,y)=B_x (a,y)=0 \\ \end{array}} \right. \end{aligned}$$
(7)
  1. (b)

    for magneto-electrically permeable crack:

$$\begin{aligned} \left\{ {\begin{array}{l} x\in (-a,a):\tau _{zy} (x,0)=-\tau _o \\ x\notin (-a,a):w(x,0)=0 \\ x\in (-b,b):\phi (x,0)=\psi (x,0)=0 \\ -h<y<h:\tau _{zx} (-a,y)=D_x (-a,y)=B_x (-a,y)=0 \\ -h<y<h:\tau _{zx} (a,y)=D_x (a,y)=B_x (a,y)=0 \\ \end{array}} \right. \end{aligned}$$
(8)

3 Stress intensity factors and energy release rate

For the derivation of the stress fields, the stress intensity factors and the energy release rate, the semi-inverse method is used. Besides, the displacement function is assumed as the form of power series.

Since the geometry structure is rectangular, a central crack is in finite region. Hence, by these conditions, the trial functions could be obtained as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \varphi _1 =\sum _{k=1}^M {iA_k \sqrt{z^{2}-a^{2}}z^{k-1}}\\ \varphi _2 =\sum _{k=1}^M {iB_k \sqrt{z^{2}-a^{2}}z^{k-1}} \\ \varphi _3 =\sum _{k=1}^M {iC_k \sqrt{z^{2}-a^{2}}z^{k-1}} \\ \end{array}} \right. \end{aligned}$$
(9)

Meanwhile, it is assumed that the functions as follows are the real part of the trial functions, respectively,

$$\begin{aligned} w=\hbox {Re}(\varphi _1 ),\phi =\hbox {Re}(\varphi _2 ),\psi =\hbox {Re}(\varphi _3 ) \end{aligned}$$
(10)

Thus, the functions can be expressed as:

$$\begin{aligned} \left\{ {\begin{array}{l} w(r,\theta )=-\sum _{k=1}^M {A_k r^{k-1}\sqrt{\hbox {r}_1 r_2 }\sin \left[ (k-1)\theta +\frac{\theta _1 +\theta _2 }{2}\right] } \\ \phi (r,\theta )=-\sum _{k=1}^M {B_k r^{k-1}\sqrt{\hbox {r}_1 r_2 }\sin \left[ (k-1)\theta +\frac{\theta _1 +\theta _2 }{2}\right] } \\ \psi (r,\theta )=-\sum _{k=1}^M {C_k r^{k-1}\sqrt{\hbox {r}_1 r_2 }\sin \left[ (k-1)\theta +\frac{\theta _1 +\theta _2 }{2}\right] } \\ \end{array}} \right. \end{aligned}$$
(11)

Substituting Eq. (10) into Eq. (1), one could obtain

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{yz} =\tau _{zy} =c_{44} \frac{\partial }{\partial y}\hbox {Re}\varphi _1 +e_{15} \frac{\partial }{\partial y}\hbox {Re}\varphi _2 +f_{15} \frac{\partial }{\partial y}\hbox {Re}\varphi _3 \\ \tau _{xz} =\tau _{zx} =c_{44} \frac{\partial }{\partial x}\hbox {Re}\varphi _1 +e_{15} \frac{\partial }{\partial x}\hbox {Re}\varphi _2 +f_{15} \frac{\partial }{\partial x}\hbox {Re}\varphi _3 \\ D_y =D_y =e_{15} \frac{\partial }{\partial y}\hbox {Re}\varphi { }_1-\varepsilon _{11} \frac{\partial }{\partial y}\hbox {Re}\varphi _2 -\hbox {g}_{{11}} \frac{\partial }{\partial y}\hbox {Re}\varphi _3 \\ D_x =D_x =e_{15} \frac{\partial }{\partial x}\hbox {Re}\varphi { }_1-\varepsilon _{11} \frac{\partial }{\partial x}\hbox {Re}\varphi _2 -\hbox {g}_{{11}} \frac{\partial }{\partial x}\hbox {Re}\varphi _3 \\ B_y =B_y =f_{15} \frac{\partial }{\partial y}\hbox {Re}\varphi { }_1-\hbox {g}_{{11}} \frac{\partial }{\partial y}\hbox {Re}\varphi { }_2-\mu _{11} \frac{\partial }{\partial y}\hbox {Re}\varphi { }_3 \\ B_x =B_x =f_{15} \frac{\partial }{\partial x}\hbox {Re}\varphi { }_1-\hbox {g}_{{11}} \frac{\partial }{\partial x}\hbox {Re}\varphi { }_2-\mu _{11} \frac{\partial }{\partial x}\hbox {Re}\varphi { }_3 \\ \end{array}} \right. \end{aligned}$$
(12)

By the Cauchy–Riemann Law, Eq. (12) could be changed as

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{zx} -i\tau _{zy} =C_{44} (\partial _1 w_3 -i\partial _2 w_3 )+e_{15} (\partial _1 \phi _3 -i\partial _2 \phi _3 )+f_{15} (\partial _1 \psi _3 -i\partial _2 \psi _3 ) \\ =C_{44} \varphi _1^{\prime } +e_{15} \varphi _2^{\prime } +f_{15} \varphi _3^{\prime } \\ D_x -iD_y =e_{15} (\partial _1 w_3 -i\partial _2 w_3 )-\varepsilon _{11} (\partial _1 \phi _3 -i\partial _2 \phi _3 )-g_{11} (\partial _1 \psi _3 -i\partial _2 \psi _3 ) \\ =e_{15} \varphi _1^{\prime } -\varepsilon _{11} \varphi _2^{\prime } -g_{11} \varphi _3^{\prime } \\ B_x -iB_y =f_{15} (\partial _1 w_3 -i\partial _2 w_3 )-g_{11} (\partial _1 \phi _3 -i\partial _2 \phi _3 )-\mu _{11} (\partial _1 \psi _3 -i\partial _2 \psi _3 ) \\ =f_{15} \varphi _1^{\prime } -g_{11} \varphi _2^{\prime } -\mu _{11} \varphi _3^{\prime } \\ \end{array}} \right. \end{aligned}$$
(13)

and applying Eqs. (10) and (13), one could obtain

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{zx} =\frac{1}{2}\left[ C_{44} (\varphi _1^{\prime } +\overline{\varphi _1^{\prime } } )+e_{15} (\varphi _2^{\prime } +\overline{\varphi _2^{\prime } } )+f_{15} (\varphi _2^{\prime } +\overline{\varphi _2^{\prime } } )\right] \\ \tau _{zy} =-\frac{1}{2i}\left[ C_{44} (\varphi _1^{\prime } -\overline{\varphi _1^{\prime } } )+e_{15} (\varphi _2^{\prime } -\overline{\varphi _2^{\prime } } )+f_{15} (\varphi _2^{\prime } -\overline{\varphi _2^{\prime } } )\right] \\ D_x =\frac{1}{2}\left[ e_{15} (\varphi _1^{\prime } +\overline{\varphi _1^{\prime } } )-\varepsilon _{11} (\varphi _2^{\prime } +\overline{\varphi _2^{\prime } } )-g_{11} (\varphi _3^{\prime } +\overline{\varphi _3^{\prime } } )\right] \\ D_y =-\frac{1}{2i}\left[ e_{15} (\varphi _1^{\prime } -\overline{\varphi _1^{\prime } } )-\varepsilon _{11} (\varphi _2^{\prime } -\overline{\varphi _2^{\prime } } )-g_{11} (\varphi _3^{\prime } -\overline{\varphi _3^{\prime } } )\right] \\ B_x =\frac{1}{2}\left[ f_{15} (\varphi _1^{\prime } +\overline{\varphi _1^{\prime } } )-g_{11} (\varphi _2^{\prime } +\overline{\varphi _2^{\prime } } )-\mu _{11} (\varphi _3^{\prime } +\overline{\varphi _3^{\prime } } )\right] \\ B_y =-\frac{1}{2i}\left[ f_{15} (\varphi _1^{\prime } -\overline{\varphi _1^{\prime } } )-g_{11} (\varphi _2^{\prime } -\overline{\varphi _2^{\prime } } )-\mu _{11} (\varphi _3^{\prime } -\overline{\varphi _3^{\prime } } )\right] \\ \end{array}} \right. \end{aligned}$$
(14)

Simplifying Eq. (14) one could obtain the anti-plane shear stress, in-plane electric displacement and magnetic induction, respectively, as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{zx} =-c_{44} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}A_k \left\{ k\hbox {sin}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ -\,e_{15} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}B_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ -\,f_{15} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}C_k \left\{ k\hbox {sin}(k\theta -\frac{\theta _1 +\theta _2 }{2})-(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ D_x =-e_{15} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}A_k \left\{ k\hbox {sin}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ +\,\varepsilon _{11} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}B_k \left\{ k\hbox {sin}(k\theta -\frac{\theta _1 +\theta _2 }{2})-(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ +\,g_{11} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}C_k \left\{ k\hbox {sin}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ B_x =-f_{15} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}A_k \left\{ k\hbox {sin}(k\theta -\frac{\theta _1 +\theta _2 }{2})-(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\,\theta _2 }{2}\right] \right\} } \\ +g_{11} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}B_k \left\{ k\hbox {sin}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ +\,\mu _{11} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}C_k \left\{ k\hbox {sin}(k\theta -\frac{\theta _1 +\theta _2 }{2})-(\frac{a}{r})^{2}(k-1)\sin \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ \end{array}} \right. \end{aligned}$$
(15a)
$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{zy} =-c_{44} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}A_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ -\,e_{15} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}B_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ -\,f_{15} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}C_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ \hbox {D}_y =-e_{15} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}A_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ +\,\varepsilon _{11} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}B_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ +\,g_{11} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}C_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ B_y =-f_{15} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}A_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ +\,g_{11} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}B_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ +\,\mu _{11} \sum _{k=1}^M {\frac{\hbox {r}^{k}}{\sqrt{r_1 r_2 }}C_k \left\{ k\hbox {cos}\left( k\theta -\frac{\theta _1 +\theta _2 }{2}\right) -(\frac{a}{r})^{2}(k-1)\cos \left[ (k-2)\theta -\frac{\theta _1 +\theta _2 }{2}\right] \right\} } \\ \end{array}} \right. \end{aligned}$$
(15b)

Due to the crack tip owning the stress singularity and the boundary condition, the stress intensity factor \(K_\mathrm{III}^\tau \), the electric displacement intensity factor \(K_\mathrm{III}^D\) and the magnetic flux intensity \(K_\mathrm{III}^B\) at the tip of crack could be expressed as matrix form

$$\begin{aligned} K^{\tau }=[K_\mathrm{III}^\tau \,\,K_\mathrm{III}^D \,\,K_\mathrm{III}^B ]^\mathrm{T}\,=\mathop {\lim }\limits _{r\rightarrow \pm \hbox {a}} e^{\beta }\sqrt{2\pi (r\mp a)}[\tau _{zy} \,\,D_y \,\,B_y ]^\mathrm{T}_{\theta =0} \end{aligned}$$
(16)

Substituting Eq. (15) into Eq. (16), one could obtain

$$\begin{aligned}&\left[ K_\mathrm{III}^\tau \,\,K_\mathrm{III}^D \,\,K_\mathrm{III}^B \right] ^\mathrm{T}\,=-\sum _{k=1}^M {e^{\beta }\sqrt{\pi }a^{k-0.5}} \nonumber \\&\quad \times \left[ \hbox {c}_{44{0}} A_k +e_{15{0}} B_k +f_{15{0}} C_k \,\,e_{15{0}} A_k -\varepsilon _{11{0}} B_k -g_{11{0}} C_k \,\,f_{15{0}} A_k -g_{11{0}} B_k -\mu _{11{0}} C_k\right] ^\mathrm{T} \end{aligned}$$
(17)

According to Pak’s [24] definition of energy release rate, there is

$$\begin{aligned} G=\frac{1}{2}\left[ {{\begin{array}{l} {K_\mathrm{III}^\tau } \\ {K_\mathrm{III}^D } \\ {K_\mathrm{III}^B } \\ \end{array} }} \right] ^\mathrm{T}\left[ {{\begin{array}{lll} {C_{44} }&{} {B_1 }&{} {f_{15} } \\ {e_{15} }&{} {-\varepsilon _{11} }&{} {-g_{11} } \\ {f_{15} }&{} {-g_{11} }&{} {-\mu _{11} } \\ \end{array} }} \right] ^{-1}\left[ {{\begin{array}{l} {K_\mathrm{III}^\tau } \\ {K_\mathrm{III}^D } \\ {K_\mathrm{III}^B } \\ \end{array} }} \right] \end{aligned}$$
(18)

where the above inverse matrix \(\left[ {{\begin{array}{lll} {C_{44} }&{} {B_1 }&{} {f_{15} } \\ {e_{15} }&{} {-\varepsilon _{11} }&{} {-g_{11} } \\ {f_{15} }&{} {-g_{11} }&{} {-\mu _{11} } \\ \end{array} }} \right] ^{-1}\) is positive, for different magnetic or electric loads, the energy release rate is always positive. If the crack surface only been allowed to be applied by mechanical loads, the form of energy release rate could be simplified as elastic material. From Anderson [25], the energy release rate of classical elasticity is

$$\begin{aligned} G=\frac{(K^{\tau })^{2}}{C_{44} } \end{aligned}$$
(19)

For the type of permeable crack, the methods are similar as above. Due to the limit of the space, the relative results are presented directly as follows

Here, the trial functions should be

$$\begin{aligned} \left\{ {\begin{array}{l} \varphi _1 =\sum _{k=1}^M {iA_k \sqrt{z^{2}-a^{2}}z^{k-1}} -\sum _{k=1}^M {iPB_k z^{k}} -\sum _{k=1}^M {iQC_k z^{k}} \\ \varphi _2 =\sum _{k=1}^M {iB_k z^{k}} \\ \varphi _3 =\sum _{k=1}^M {iC_k z^{k}} \\ \end{array}} \right. \end{aligned}$$
(20)

where \(P=\frac{e_{150} }{C_{440} },Q=\frac{f_{150} }{C_{440} }.\)

The intensity factors in matrix form are

$$\begin{aligned}{}[K_\mathrm{III}^\tau \,\,K_\mathrm{III}^D \,\,K_\mathrm{III}^B ]^\mathrm{T} =-\sum _{k=1}^M {e^{\beta }\sqrt{\pi }a^{k-0.5}[\hbox {C}_{440} A_k \,\,e_{150} A_k \,\,f_{150} A_k ]^\mathrm{T}} \end{aligned}$$
(21)

The energy release rate is

$$\begin{aligned} G=\frac{K_\mathrm{III}^\tau K_\mathrm{III}^\omega }{2}=\frac{(K_\mathrm{III}^\tau )^{2}}{C_{44} } \end{aligned}$$
(22)

4 Numerical results and discussion

The boundary collocation method is used to solve Eqs. (15), (17) or (21). Since the parameters of the above equations are constant, they could all be determined by the previous experiments. The values of the parameters can be extracted from [26] and as follows: \(C_{440} =54.0\,\mathrm{Gpa}\), \(e_{150} =7.8\,\mathrm{c/m}^{2}\), \(\varepsilon _{110} =3.64\times 10^{-9}\,\mathrm{C}^{2}/\mathrm{Nm}^{2}\), \(f_{150} =175.0\,\mathrm{N}/\mathrm{Am}\), \(\mu _{110} =-1.97\times 10^{-4}\,\mathrm{Ns}^{2}/\mathrm{C}^{2}\), \(g_{110} =0.8\times 10^{-11}\,\mathrm{Ns}/(\mathrm{V}\cdot \mathrm{C})\), \(\tau _{0} ={4.2}\times {10}^{{6}}\,\mathrm{N/m}^{2}\), \(B_0 f_{150} /\tau _0 \mu _{110} =0.00\), \(D_0 e_{150} /\tau _0 \varepsilon _{110} =0.00\). Due to the geometric symmetry and using boundary collocation, it just only needs to match points in half boundary region. Usually, in order to obtain better results, more points are taken and the least square method is used in this calculation. On the other side, for investigating the effect of the various crack size or the plate size on the fracture behavior, so the width is \(b=1\), and half-height \(h=0.1,\,0.25,\,1\), respectively. The crack length is \(a=0.1\rightarrow 0.9\). In the step of numerical calculation, for Eqs. (9–17), (20) or (21), the number of summation terms \(M=20\), the number on the right or left side, \(N_1 =80\), and the number on the upper side \(N_2 =40\). The results can then be achieved by programs in MATLAB. The schematic diagram is shown in Fig. 3.

Fig. 3
figure 3

Boundary collocation method used in FGM rectangle plate with a central crack

Full size image

To make the stress intensity factor and the energy release rate (ERR) dimensionless

$$\begin{aligned} \left\{ {\begin{array}{l} Y_\mathrm{III}^i =K^{i}/K_o^i \\ G_\mathrm{III}^i =G/G_o^i \\ \end{array}} \right. \end{aligned}$$
(23)

where

$$\begin{aligned} \left\{ {\begin{array}{l} K_o^i =i\sqrt{\pi a} \\ G_o^i =\frac{\pi ai^{2}}{2}\left( C_{440} +\frac{e_{150}^2 \mu _{150} -2e_{150} f_{150} g_{110} +f_{150}^2 \varepsilon _{110} }{\mu _{110} \varepsilon _{110} -g_{110}^2 }\right) \\ i=\tau _0 ,D_0 ,B_0 \\ \end{array}} \right. \end{aligned}$$
(24)

\(i=\tau _0 ,D_0 ,B_0\) stand for mechanical load, electric load and magnetic load.

4.1 The verification of numerical results

In this subsection, the numerical results we obtained were tested by comparing them with those of Wang [27]; their accuracy is confirmed. Figure 4 shows that the solid lines are largely in great agreement with the points, where the lines represent our numerical results, the degenerating model of FGM, and the points represent the solution of elastic model.

Fig. 4
figure 4

Comparison of normalized SIFs between the present results and Wang’s results [27]

Full size image
Fig. 5
figure 5

Our model degenerated into semi-infinite plate model [28]

Full size image
Table 1 A comparison between the numerical results and semi-infinite plane mode
Full size table

Moreover, for validating sufficiently the correctness of the equations and the programs, the numerical results should be compared with the analytical solution, where the analytical solution of SIFs of the infinite plate with a single central crack can be found in the classic Handbook [28]. The analytical formula of SIFs is expressed as

$$\begin{aligned} K_\mathrm{III} =\tau _o \sqrt{\pi a}\sqrt{\frac{2b}{\pi a}tg\left( {\frac{\pi a}{2b}} \right) } \end{aligned}$$
(25)

By dividing \(\tau _o \sqrt{\pi a}\) into the above expression, normalized SIFs is defined by

$$\begin{aligned} Y_\mathrm{III} =\sqrt{\frac{2b}{\pi a}tg\left( {\frac{\pi a}{2b}} \right) } \end{aligned}$$
(26)

In order to describe the numerical calculation more specifically, the present model degenerates into a semi-infinite model as shown in Fig. 5. Besides, the calculated values are given in Table 1 which presents the normalized SIFs of the solutions and results of their analysis. To further test correctness and accuracy, the relative errors that between this numerical results and the analytical results are calculated in Table 1. It shows that when the dimension ratio h / b is large enough, it approaches an infinite region solution (e.g. when it equals to 10), with the maximum of the relative error is less than \(0.2\% \). There is good agreement between the numerical solutions and the analytic solutions, proving the accuracy of the numerical results used in FGM. Meanwhile, for the finite boundary condition, the results show that stress intensity factors increase with increases in the relative length of crack. In another word, cracks within finite region boundary are more likely to fracture than in the infinite boundary solution.

Fig. 6
figure 6

The convergence study of term numbers and collocation node numbers in different graded parameters

Full size image
Fig. 7
figure 7

Variation of the normalized SIF \(K_\mathrm{III}^\tau \)a for the different crack length vs the ratio \(\beta /h\), b for the different ratio \(\beta /a\) versus the height–width ratio

Full size image
Fig. 8
figure 8

Normalized ERR for magneto-electrically impermeable crack in a functionally graded material rectangle plate (the graded coefficient \(\beta =0.5\), \(\lambda _D =D_0 e_{150} /(\tau _0 \varepsilon _{110} ),\lambda _B =B_0 f_{150} /(\tau _0 \mu _{110} ))\) under a various electric loads in the cases (b) various magnetic loads in the cases

Full size image
Fig. 9
figure 9

Electric displacement simulation a, b comparison between magneto-electrically impermeable crack and magneto-electrically permeable crack. Electric potential simulation c, d comparison between magneto-electrically impermeable crack and magneto-electrically permeable crack

Full size image

4.2 The convergence of numerical results of the terms and node numbers

The trial function of power series is employed for the derivation and numerical calculation. In terms of the convergence of this approach to this kind problem, Figure 6 illustrates the effect of term numbers and the collocation nodes on the numerical results. From Fig. 6a, it shows that when the number of collocation nodes \(N1=100\) and \(N2=200\), the term numbers M can be at least from 10 to 100; meanwhile the results have good convergence for different graded parameters. Besides, the convergence of the results in terms of the number of collocation nodes also represents good convergence as shown in Fig. 6b. When the number of terms M is 25, the collocation nodes N1 can be 10–150; meanwhile it performs good convergence in terms of different graded parameters. Fig. 6 can illustrate that this proposed method is suitable for FGM.

Fig. 10
figure 10

Magnetic flux simulation a, b comparison between magneto-electrically impermeable crack and magneto-electrically permeable crack. Magnetic potential simulation c, d comparison between magneto-electrically impermeable crack and magneto-electrically permeable crack

Full size image

4.3 Effects of graded parameters and crack surface boundary condition under the magneto-electricity load

4.3.1 Effect of graded parameters

Numerical results revealed in Fig. 7 illustrate that the normalized SIF versus the functionally graded parameter \(\beta \). It indicates that the SIFs always increase as the graded constant \(\beta \) decreasing, and it also shows that when the boundary condition tends to finite region, the SIF would also tend to increase. In another side, Fig. 7b indicates the SIF always decrease as the plate thickness h increases. Besides, the SIFs will tend to be stable when the height–width ratio is greater than about 0.3.

4.3.2 Effect of electromagnetic quantity

Since the combine action of the electromagnetic load is common mechanism in PE/PM materials, it is necessary to investigate the effect of the magnitude of the electric load and the magnetic load, respectively, on the ability of the crack tip stress value. For this purpose, it could make one of the two loads be constant, and study the other load effects on the crack energy release rate G. Figure 8a shows that, in the specified magnetic loads, increasing electrical loads could generally lead to hinder the propagation of cracks. However, Fig. 8b depicts that, for the solution of the constant electrical loads, increasing magnetic loads would always promote to increase the value of ERR. Meantime, Fig. 8 also illustrates that when the boundary condition tends to the finite region, the ERR would also tend to decrease.

4.4 The effects of the electromagnetic loads on the permeable/impermeable crack surface boundaries

Figures 9 and 10 shows the distinctions between the magneto-electrically permeable crack and the magneto-electrically impermeable crack for the PE/PM properties of FGM. Figure 9a, b illustrates electric displacement and electric potential simulation under two different crack surface boundary conditions but with the same loads \(\tau _o ,D_o ,B_o \) and the same size h, b, a. Figure 10a, b shows magnetic flux and magnetic potential simulation under two different crack boundary conditions but with the same loads \(\tau _o ,D_o ,B_o \) and the same size h, b, a. Obviously, those results show that the electric displacement and magnetic flux can hardly be distinguished in the two different crack surface conditions. However, the electric potential simulation and the magnetic potential simulation are obviously different. The electric/magnetic potentials of the plate are too weak in terms of the permeable crack surface boundary so that there is no crack singularity effect. Furthermore, it proves that the potential values are always bigger with impermeable crack surfaces than with permeable crack surfaces.

5 Summary

Fracture analysis is performed for a FGPM rectangular plate with a central crack. By using the semi-inverse method, the fracture parameters are derived into power-series forms, following which the numerical results are obtained using boundary collocation method. The results are summarized as follows.

  1. (1)

    The gradient parameter has a great influence on the behavior of fracture. When one increases the value of gradient parameter, it would be helpful in reducing the behavior of structure or materials’ fracture.

  2. (2)

    How the electric load and the magnetic loads affect the behavior of fractures is contrary. Increasing the electric load would be beneficial in impeding the growth of the crack, but increasing the magnetic load would make the energy release rate improve.

  3. (3)

    For impermeable type crack, both the electric and the magnetic loads have critical roles in the crack tip singularity. However, the electric load and the magnetic load have no influence on the crack tip for permeable type crack.