1 Introduction

The photoacoustic (PA) technology is based on the physics of heat and elastic waves, that is, the waves generated and scattered through the medium. The absorption of an intensely modulated light beam by a material is the most common wave-producing process. Periodic thermal and mechanical vibrations, often known as heat and elastic waves, may take different forms. An example of this phenomenon is a sound wave produced by gas in contact with a sample’s surface. The PA signal can be detected either on the front side of the material, which is irradiated by a modified light beam, or on the backside of the material, which is irradiated by an unmodified light beam (i.e., the so-called heat transfer configuration).

Wave propagation in semiconductor materials has several applications in atomic physics, industrial engineering, thermal power plants, underwater constructions, pressure vessels, aircraft, chemical pipelines and metallurgy science, among others. Several applications, including the evaluation of thermal diffusion processes in solids [1], can benefit from a heat transfer detection setup. When this method is used in semiconductors, more information about the carrier transport properties can be obtained [2]. This is because of the mechanisms of thermal conversion in which recombination process will create the heat waves due to the production of periodic redundant carriers in a semiconductor. When electron–hole pairs are formed, semiconductor materials also display mechanical stress. The photo-generated free carriers cause periodic elastic stress in the sample, which leads to the production of an acoustic wave [3]. Moreover, the elastic constants of the semiconductor materials will be perturbed due to the density of free carrier, but this effect may be neglected [4].

Some materials, such as semiconductors, offer a variety of useful physical properties which may be useful in modern engineering applications. According to the principle of thermoelasticity, semiconductor materials may only be classified as elastic materials. The importance of semiconductors in current technologies has been recently highlighted when these materials were used to produce electrical energy from sunlight while being exposed to laser pulses [5]. Semiconductor materials are used as nanomaterials in various fields of mechanical and electrical engineering, and have a variety of applications in modern industry, including transistors and solar cells. Photothermal theory has recently been applied to semiconductor media to produce sustainable energy technologies. To characterize the overlap between the thermoelectric and thermoelastic equations, several physic-based mathematical models have been developed. Gordon et al. [6] first introduced the electronic deformations for photothermal spectroscopy. While using a laser source, photoacoustic spectroscopy is utilized in the context of sensitive analytical procedures to measure the sound velocity of some semiconductor materials [7]. Many applications in engineering industries use wave propagation during electrical deformations of an elastic semiconductor medium by photothermal processing techniques [8]. Abouelregal [9] studied the time-dependent heat flow reaction in a rotating solid cylinder of semiconductor silicon. Using Green and Naghdi method, Abouelregal et al. [10,11,12] investigated the effect of an additional carrier on an infinite semiconductor subject to a normal force and rotating semiconductor materials.

Thermoelasticity is a branch of elasticity theory that considers the temperature changes. The interaction between the thermal field and elastic medium is addressed by the theory of thermoelasticity. Due to its applications in advanced structural design issues, the classical and extended theories of thermoelasticity have been widely explored in recent years. The conventional theory of thermoelasticity assumes that the mechanical forces acting on a solid do not affect its temperature change due to external or internal heat loading. As a result, obtaining deformation and temperature distributions in structures subject to the thermal shock loads is critical from theoretical point of view. In order to address this weakness of the coupled classic theory of thermoelasticity, different theories of thermoelasticity have been recently developed [13,14,15,16,17,18,19,20,21]. Green and Naghdi [22,23,24] proposed the idea of thermoelasticity with or without energy dissipation named Green–Naghdi theories of type II and III as the generalized thermoelastic theories.

Thanks to its insightful interpretation and merits, in recent years, the Moore–Gibson–Thompson (MGT) equation has been developed by many researchers. This theory was founded based on a third-order differential equation, which is beneficial in many fluidic and viscoelastic materials [25]. Quintanilla [26, 27] constructed a novel heat conduction model in the context of the MGT equation. Generally speaking, when a relaxation modulus is introduced into the Green–Naghdi type III model, the new equation can be produced. Abouelregal et al. [28,29,30] prepared the proposed modified heat equation after incorporating the relaxation parameter into the GN-III model by utilizing the energy equation. It should be emphasized that, since the advent of the MGT equation, the number of researches on this theory has significantly increased [31,32,33,34].

When the temperature gradient occurs due to light absorption in flexible semiconductor materials, it causes an electric potential difference between the end points in the semiconductor. Several authors have analyzed the coupled and uncoupled systems of plasma, thermodynamic and elastic equations as well as different effects of thermal and electronic deformation in semiconductors using classical models. According to the knowledge of the authors of this study, there is no research work on the transient examination of semiconductor materials subject to thermal loading and photo-generated plasma by taking into account the temperature-dependent material properties.

It is well known that the use the classical Fourier’s law to describe the heat flux results in an infinite signal speed paradox. The contribution of the present study is to introduce a new photothermal model incorporating Moore–Gibson–Thompson photothermal (MGTPT) equations, which explains photoexcited carriers and acoustic waves in semiconductor materials. These equations are of the third order in time evolutions of a predominantly hyperbolic type. The MGTPT model accounts for a finite speed propagation due to the presence of the thermal relaxation coefficient behind of the third-order time derivatives. This is the first attempt dealing with the mathematical analysis of the photothermal model which may be useful to develop a new theoretical framework into the thermoelastic and photothermal mechanisms.

As an application of the proposed model, disturbances that occur during a photothermal process in a homogeneous solid sphere of thermal semiconductor are investigated using the Moore–Gibson–Thompson photothermal (MGTPT) equation for photothermal conductivity. The governing equations involving the correlated plasmas, thermal mechanisms and elastic waves are presented in the field of Laplace transforms, and the analytical solution is achieved by employing numerical reflection methods. To this end, physical field quantities and distinct analytic comparisons are drawn and the results are compared with other findings in the literature.

2 Mathematical formulation

Thermoelastic and electronic deformation processes can be described by the following equations of motion with an external force:

$$\sigma _{{{\text{ij}},\;{\text{j}}}} + F_{{\text{i}}} = \varrho \ddot{u}_{{\text{i}}} .$$
(1)

The constitutive equations:

$$\sigma_{{{\text{ij}}}} = C_{{{\text{ijkl}}}} e_{{{\text{kl}}}} - \left( {\beta_{{{\text{ij}}}} \theta + d_{{{\text{nij}}}} N} \right)$$
(2)

The strain–displacement relations:

$$e_{{{\text{ij}}}} = \frac{1}{2}\left( {u_{i,\;j} + u_{j,\;i} } \right)$$
(3)

The rise in carrier density N is denoted by the following associated plasma–thermal–elastic wave equation [35, 36]

$$\left( {D_{{{\text{Eij}}}} N_{,j} } \right)_{,i} = \varrho \frac{\partial N}{{\partial t}} + \frac{1}{\tau }N + \kappa \theta + G$$
(4)

In the case of harmonic modulation lasers, Vasilev and Sandomirskii [37] initially found that the thermal activation coupling parameter k is insignificant at low temperatures.

The classical law of Fourier results in the endless propagation speeds. From this viewpoint, a small perturbation in the starting data may emerge to affect the complete solution over the entire space. Cattaneo-Vernotte [38, 39] introduced a more comprehensive Fourier law by incorporating the thermal relaxation \(\tau_{0}\) into the heat flow vector \(\vec{q}\) as follows:

$$\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\vec{q} = - K_{{{\text{ij}}}} \vec{\nabla }\theta$$
(5)

The material-dependent constant \(\tau_{0}\) is known as the parameter for thermal relaxation or temporal relaxation which is the essential objective of this study. From physical point of view, the parameter \(\tau_{0}\) is the time required to establish the constant conduct of heat when a volume element is subject to a temperature gradient. This time delay can be interpreted by many phenomena and settings, like when models are used to investigate difficulties with lithotripsy, heat treatment, ultrasonic filtering and high-frequency ultrasound (HFU) chemistry.

The improved Fourier law based on the GN-III model can be represented by [23]

$$\vec{q} = - K_{{{\text{ij}}}} \,\vec{\nabla }\theta - K_{{{\text{ij}}}}^{*} \vec{\nabla }\vartheta$$
(6)

where the function \(\vartheta\) denotes the thermal displacement which satisfies \(\dot{\vartheta } = \theta\) and the parameters \(K_{ij}^{*}\) refer to the thermal conductivity rates. The energy balance equation can be written as [40, 41]

$$\varrho C_{E} \frac{\partial \theta }{{\partial t}} + T_{0} \frac{\partial }{\partial t}\left( {\beta_{{{\text{ij}}}} e_{{{\text{ij}}}} } \right) = - \vec{\nabla } \cdot \vec{q} + Q$$
(7)

The combination of improved Fourier law proposed in (6) together with the energy Eq. (7) has the same weakness as the Fourier’s normal theory, predicting that thermal waves are spreading immediately. Quintanilla [26, 27] and Abouelregal et al. [28,29,30] prepared a modified heat equation after incorporating the relaxation parameter into the GN-III model. The modified Fourier’s law would then take the following form [26, 27]

$$\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\vec{q} = - K_{{{\text{ij}}}} \,\vec{\nabla }\theta - K_{{{\text{ij}}}}^{*} \vec{\nabla }\vartheta$$
(8)

Consider that the semiconductor elastic media are exposed to light beams from the outside while the excited free electrons create a carrier-free charge density with the semiconductor gap energy \(E_{g}\). Due to the absorbed light energy, there is a change in the electronic deformation and elastic vibrations. In this case, thermal–elastic–plasma waves will affect the overall form of the heat conductivity equation.

When the recombination of electron–hole pairs is considered, the fraction of the absorbed optical energy is thermalized. With this conditions, the modified Fourier’s law for a semiconductor material with plasma effect can be expressed as follows:

$$\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\vec{q} = - K_{{{\text{ij}}}} \,\vec{\nabla }\theta - K_{{{\text{ij}}}}^{*} \vec{\nabla }\vartheta - \int {\frac{{E_{g} }}{\tau }} Nd\vec{x}$$
(9)

The photo-excitation effect is represented by the final term in Eq. (9). When the above equation is differentiated with respect to \(\vec{x}\), the resulting equation would be

$$\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left( {\vec{\nabla } \cdot \vec{q}} \right) = - \vec{\nabla } \cdot \left( {K_{{{\text{ij}}}} \,\vec{\nabla }\theta } \right) - \vec{\nabla } \cdot \left( {K_{{{\text{ij}}}}^{*} \vec{\nabla }\vartheta } \right) - \frac{{E_{g} }}{\tau }N$$
(10)

By substituting Eq. (10) into Eq. (7), the modified heat conduction equation with thermal memory that explains the interaction between the thermal–plasma–elastic waves may be derived as

$$\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left[ {\varrho C_{E} \frac{{\partial^{2} \theta }}{{\partial t^{2} }} + T_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\beta_{{{\text{ij}}}} u_{i,\;j} } \right) - \varrho \frac{\partial Q}{{\partial t}}} \right] = \left( {K_{{{\text{ij}}}} \dot{\theta }_{,j} } \right)_{,i} + \left( {K_{{{\text{ij}}}}^{*} \theta_{,j} } \right)_{,i} + \frac{{E_{g} }}{\tau }\frac{\partial N}{{\partial t}}$$
(11)

It is assumed that the adjacent free space is permeated by an initial magnetic field \(\vec{H}\). This term generates an induced electric field \(\vec{E}\) and magnetic field \(\overrightarrow { h}\) that satisfy the Maxwell’s magnetic equations which are sufficient for slowly moving media:

$$\vec{J} = \nabla \times \vec{h},\;\nabla \times \vec{E} = - \mu_{0} \frac{{\partial \vec{h}}}{\partial t},\;\vec{E} = - \mu_{0} \left( {\frac{{\partial \vec{h}}}{\partial t} \times \vec{H}} \right),\;\nabla \cdot \vec{h} = 0,$$
(12)
$$\tau_{{{\text{ij}}}} = \mu_{0} \left[ {H_{i} h_{j} + H_{j} h_{i} - H_{k} h_{k} \delta_{{{\text{ij}}}} } \right],$$
(13)

where \(\mu_{0}\) is the magnetic permeability, \(\vec{J}\) is the current density, and \(\tau_{{{\text{ij}}}}\) is the Maxwell stress tensor.

3 Statement of the problem

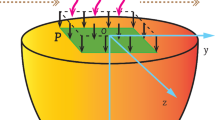
In the current section, an application of the proposed model is described. We will examine a homogeneous, isotropic, infinitesimal, semiconducting solid sphere of radius R where the outer surface is subjected to a time-dependent, traction-free variable heat. Furthermore, it is assumed that there are no heat sources or body forces applied within the body. It is useful to employ a spherical coordinate system \(\left( {r,\;\vartheta ,\;\phi } \right)\) in which \(0 \le r \le R\), \(0 \le \vartheta \le 2\pi\) and \(0 \le \phi \le 2\pi\) (See Fig. 1). It is also supposed that all defined functions depend on distance r and time t due to the symmetry of the problem. The components of the displacement vector and displacement–strain relations can be written as follows:

- The displacement–strain relationships are:

$$\begin{array}{*{20}c} {u_{\rho } = u\left( {r,\;t} \right),\; u_{\phi } \left( {r,\;t} \right) = 0 = u_{\vartheta } \left( {r,\;t} \right), } \\ {e_{{{\text{rr}}}} = \frac{u}{r}, \;e_{\phi \phi } = e_{{{\text{zz}}}} = \frac{\partial u}{{\partial r}},\;e_{r\phi } = e_{r\vartheta } = e_{\phi \vartheta } = 0. } \\ \end{array}$$
(14)

- The dilatation \(e\) is given by

$$e = \frac{1}{{r^{2} }}\frac{{\partial \left( {r^{2} u} \right)}}{\partial r}$$
(15)

- The stress–strain–temperature–carrier relations (2) can be written as

$$\begin{array}{*{20}c} {\sigma_{{{\text{rr}}}} = \left( {\lambda + 2\mu } \right)\frac{\partial u}{{\partial r}} + 2\lambda \frac{u}{r} - \left( {3\lambda + 2\mu } \right)\left( {\alpha_{t} \theta + \delta_{n} N} \right),} \\ {\sigma_{\vartheta \vartheta } = \sigma_{\phi \phi } = \lambda \frac{\partial u}{{\partial r}} + 2\left( {\mu + \lambda } \right)\frac{u}{r} - \left( {3\lambda + 2\mu } \right)\left( {\alpha_{t} \theta + \delta_{n} N} \right),} \\ \end{array}$$
(16)

where \(\alpha_{t}\) is the linear thermal expansion coefficient, \(\delta_{n}\) is the electronic deformation coefficient, and \(\lambda\), \(\mu\) denote the Lame’s constants. When the Lorentz force \(F_{r}\) is taken into account, the dynamic equation of motion becomes

$$\frac{{\partial \sigma_{{{\text{rr}}}} }}{\partial r} + \frac{2}{r}\left( {\sigma_{{{\text{rr}}}} - \sigma_{\vartheta \vartheta } } \right) + F_{r} = \varrho \frac{{\partial^{2} u}}{{\partial t^{2} }}.$$
(17)

Assume that the surface cavity is immersed in a magnetic field of constant strength \(\vec{H}_{0} = \left( {0,\;0,\;H_{0} } \right)\) acting in \(\phi\)-direction. According to Eq. (12), one obtains

$$\vec{E} = \left( {0,\;\mu_{0} H_{0} \frac{\partial u}{{\partial t}},\;0} \right),\;\vec{J} = \left( {0,\;\frac{\partial }{\partial r}\left( {\frac{1}{{r^{2} }}\frac{{\partial \left( {r^{2} u} \right)}}{\partial r}} \right),\;0} \right),\;\vec{h} = \left( {0,\;0,\;\frac{1}{{r^{2} }}\frac{{\partial \left( {r^{2} u} \right)}}{\partial r}} \right).$$
(18)

The magnetic field \(\vec{H}_{0}\) induces the radial component of Lorentz force \(F_{r}\), which is given by

$$F_{r} = \mu_{0} \left( {\vec{J} \times \vec{H}_{0} } \right)_{r}$$
(19)

Thus, from Eqs. (18) and (19), the radial force \(F_{r}\) and Maxwell’s stress \(\tau_{{{\text{rr}}}}\) can be expressed as:

$$F_{r} = \mu_{0} H_{0}^{2} \frac{\partial }{\partial r}\left( {\frac{1}{{r^{2} }}\frac{{\partial \left( {r^{2} u} \right)}}{\partial r}} \right),\;\;\;\tau_{{{\text{rr}}}} = \frac{{\mu_{0} H_{0}^{2} }}{{r^{2} }}\frac{{\partial \left( {r^{2} u} \right)}}{\partial r}$$
(20)

Inserting Eqs. (16) and (20) into Eq. (17) results in

$$\left( {\lambda + 2\mu + \mu_{0} H_{0}^{2} } \right)\frac{\partial }{\partial r}\left( {\frac{1}{{r^{2} }}\frac{{\partial \left( {r^{2} u} \right)}}{\partial r}} \right) - \gamma \frac{\partial \theta }{{\partial r}} - d_{n} \frac{\partial N}{{\partial r}} = \varrho \frac{{\partial^{2} u}}{{\partial t^{2} }}.$$
(21)

in which \(\left\{ {\gamma ,\; d_{n} } \right\} = \left( {3\lambda + 2\mu } \right)\left\{ {\alpha_{t} ,\;\delta_{n} } \right\}\).

Equation (21) can be rewritten as

$$\left( {\lambda + 2\mu + \mu_{0} H_{0}^{2} } \right)\nabla^{2} e - \gamma \nabla^{2} \theta - d_{n} \nabla^{2} N = \varrho \frac{{\partial^{2} e}}{{\partial t^{2} }}.$$
(22)

Without any heat sources (\(Q = 0\)), the generalized modified MGTE heat conduction Eq. (11) will be expressed as follows:

$$\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left[ {\varrho C_{E} \frac{{\partial^{2} \theta }}{{\partial t^{2} }} + \gamma T_{0} \frac{{\partial^{2} e}}{{\partial t^{2} }}} \right] = K\nabla^{2} \dot{\theta } + K^{*} \nabla^{2} \theta + \frac{{E_{g} }}{\tau }\frac{\partial N}{{\partial t}}.$$
(23)

In the spherical coordinate system, the Laplacian operator is given by \(\nabla^{2} = \frac{{\partial^{2} }}{{\partial r^{2} }} + \frac{2}{r}\frac{\partial }{\partial r} = \frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} \frac{\partial }{\partial r}} \right)\).

Fig. 1
figure 1

Schematic configuration of a homogeneous, isotropic, infinitesimal, semiconducting solid sphere

Full size image

The governing equations can be easily transformed into the dimensionless forms. As a result, the dimensionless variables listed below are presented:

$$\begin{array}{*{20}c} {\left\{ {r^{\prime } ,\;u^{\prime } } \right\} = v_{0} \eta \left\{ {r,\;u} \right\}, \left\{ {t^{\prime } ,\;\tau_{0}^{\prime } ,\;\tau^{\prime } } \right\} = v_{0}^{2} \eta \left\{ {t,\;\tau_{0} ,\;\tau } \right\},\;\left\{ {\theta^{\prime } ,\;N^{\prime } } \right\} = \frac{1}{{\rho v_{0}^{2} }}\left\{ {\gamma \theta ,\;d_{n} n} \right\},} \\ {\left\{ {\sigma_{{{\text{ij}}}}^{\prime } ,\;\tau_{{{\text{rr}}}}^{\prime } } \right\} = \frac{1}{{\varrho v_{0}^{2} }}\left\{ {\sigma_{{{\text{ij}}}} ,\;\tau_{{{\text{rr}}}} } \right\},\;\eta = \frac{{\rho C_{E} }}{K},\;v_{0}^{2} = v_{1}^{2} + v_{a}^{2} .} \\ \end{array}$$
(24)

In Eq. (25), the parameter \(v_{1} = \sqrt {\frac{\lambda + 2\mu }{\varrho }}\) represents the dilatational wave speed, and the factor \(v_{a} = \sqrt {\frac{{\mu_{0} H_{0}^{2} }}{\varrho }}\) symbolizes the Alfven wave speed. The governing equations can be then rewritten in the following forms when the prime’s symbols are omitted

$$\left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left[ {\frac{{\partial^{2} \theta }}{{\partial t^{2} }} + \varepsilon_{1} \frac{{\partial^{2} e}}{{\partial t^{2} }}} \right] = \left( {\frac{\partial }{\partial t} + \omega^{*} } \right)\nabla^{2} \theta + \varepsilon_{2} \frac{{\partial^{2} N}}{{\partial t^{2} }},$$
(25)
$$\nabla^{2} e - \nabla^{2} \theta - \nabla^{2} {\rm N} = \frac{{\partial^{2} e}}{{\partial t^{2} }},$$
(26)
$$\nabla^{2} {\rm N} = g_{1} \frac{{\partial {\rm N}}}{\partial t} + g_{2} {\rm N} + g_{3} \theta ,$$
(27)
$$\begin{array}{*{20}c} {\sigma_{{{\text{rr}}}} = \beta^{2} \frac{\partial u}{{\partial r}} + \left( {1 - \beta^{2} } \right)e - \theta - {\rm N},} \\ {\sigma_{\vartheta \vartheta } = \beta^{2} \frac{u}{r} + \left( {1 - \beta^{2} } \right)e - \theta - {\rm N},} \\ \end{array}$$
(28)

where

$$\begin{array}{*{20}c} {\beta^{2} = \frac{2\mu }{{\lambda + 2\mu }},\;\varepsilon_{1} = \frac{{\gamma^{2} T_{0} }}{{\varrho^{2} C_{E} c_{0}^{2} }},\;\omega^{*} = \frac{{K^{*} }}{{v_{0}^{2} \eta K}},\;\varepsilon_{2} = \frac{{\gamma E_{g} v_{0}^{2} }}{{\tau d_{n} K}} ,} \\ {{ }g_{1} = \frac{\varrho }{{D_{E} \eta }},\;g_{2} = \frac{1}{{D_{E} \eta \tau_{1} }},\;g_{3} = \frac{{\kappa d_{n} }}{{\gamma \eta^{2} D_{E} c_{0}^{2} }}.} \\ \end{array}$$
(29)

The initial conditions of the problem take the following forms

$$\begin{array}{*{20}c} {u\left( {r,0} \right) = 0 = \frac{{\partial u\left( {r,\;0} \right)}}{\partial r},\;\;{\rm N}\left( {r,\;0} \right) = 0 = \frac{{\partial {\rm N}\left( {r,\;0} \right)}}{\partial r}, } \\ {\theta \left( {r,\;0} \right) = 0 = \frac{{\partial \theta \left( {r,\;0} \right)}}{\partial r}.} \\ \end{array}$$
(30)

It is also assumed that the boundary conditions satisfy the following terms:

$$\theta \left( {R,\;t} \right) = \theta_{0} H\left( t \right),\; t > 0$$
(31)
$$\sigma_{{{\text{rr}}}} \left( {R,\;t} \right) = 0$$
(32)

where \(H\left( t \right)\) stands for the Heaviside function and \(\theta_{0}\) is a constant coefficient.

The carriers can reach the sample’s surface during the diffusion phase with a finite probability of recombination. As a result, the carrier density boundary condition can be written as:

$$D_{E} \frac{\partial N}{{\partial r}} = s_{v} N\;{\text{at}}\;r = R,$$
(33)

where \(s_{v}\) is the surface recombination velocity.

4 Solution in the transformation domain

To solve the linear differential equations with constant coefficients, the Laplace transform technique is utilized. Laplace transforms of various functions should be performed to examine the control system. In order to analyze the dynamic control system, both characteristics of the Laplace transform and the inverse Laplace transform are employed. The Laplace transform of function \(g\left( t \right)\), which is denoted by \({\mathcal{L}}\left[ {g\left( t \right) } \right]\) or by \(\overline{g}\left( s \right)\), is defined by the following equation

$${\mathcal{L}}\left[ {g\left( t \right) } \right] = \overline{g}\left( s \right) = \mathop \smallint \limits_{0}^{\infty } g\left( t \right)e^{ - st} dt,\;s > 0.$$
(34)

The following equations are also obtained by applying the Laplace transform on Eqs. (25) to (28):

$$\left( {\nabla^{2} - \psi } \right)\overline{\theta } = \psi \varepsilon_{1} \overline{e} - \varepsilon_{2} s^{2} \overline{N},$$
(35)
$$\left( {\nabla^{2} - s^{2} } \right)\overline{e} = \nabla^{2} \overline{\theta } + \nabla^{2} \overline{\rm N},$$
(36)
$$\left( {\nabla^{2} - g_{4} } \right)\overline{\rm N} = g_{3} \overline{\theta },$$
(37)
$$\overline{\sigma }_{{{\text{rr}}}} = \beta^{2} \frac{{d\overline{u}}}{dr} + \left( {1 - \beta^{2} } \right)\overline{e} - \overline{\theta } - \overline{\rm N},$$
(38)
$$\overline{\sigma }_{\vartheta \vartheta } = \beta^{2} \frac{{\overline{u}}}{r} + \left( {1 - \beta^{2} } \right)\overline{e} - \overline{\theta } - \overline{\rm N},$$
(39)

where \(\psi = s^{2} \left( {1 + \tau_{0} s} \right)/\left( {s + \omega^{*} } \right)\).

When Eqs. (35) to (37) are decoupled, one gets

$$\left( {\nabla^{6} - \alpha_{2} \nabla^{4} + \alpha_{1} \nabla^{2} - \alpha_{0} } \right)\left\{ {\overline{\theta },\;\overline{N},\;\overline{e}} \right\} = 0,$$
(40)

where \(\alpha_{2}\), \(\alpha_{1}\) and \(\alpha_{0}\) are specified by

$$\begin{aligned} \alpha _{2} = & s^{2} + g_{7} + \frac{{g_{6} }}{{g_{3} }},\;\alpha _{1} = s^{2} g_{7} + g_{8} + \frac{{g_{6} g_{5} }}{{g_{3} }},\;\alpha _{0} = s^{2} g_{8} , \\ g_{4} = & sg_{1} + g_{2} ,\;g_{5} = g_{4} - g_{3} ,\;g_{6} = ~g_{3} \psi \varepsilon _{1} , \\ g_{7} = g_{4} + \psi ,\;g_{8} = g_{4} \psi + ~s^{2} g_{3} \varepsilon _{2} . \\ \end{aligned}$$
(41)

Presenting \(\lambda_{i} ,\) \(\left( {i = 1,\;2,\;3} \right)\) into Eq. (40) yields

$$\left( {\nabla^{2} - \lambda_{1}^{2} } \right)\left( {\nabla^{2} - \lambda_{2}^{2} } \right)\left( {\nabla^{2} - \lambda_{3}^{2} } \right)\left\{ {\overline{e},\;\overline{\theta },\;\overline{N}} \right\} = 0,$$
(42)

where \(\lambda_{1}^{2}\), \(\lambda_{2}^{2}\) and \(\lambda_{3}^{2}\) are the roots of below equation

$$\lambda^{6} - \alpha_{2} \lambda^{3} + \alpha_{1} \lambda^{2} - \alpha_{0} = 0,$$
(43)

which are given by

$$\begin{gathered} \lambda _{2}^{2} = - \frac{1}{3}\beta _{0} \left[ {\sin \left( {\gamma _{0} } \right) + \sqrt 3 \cos \left( {\gamma _{0} } \right)} \right] + \frac{1}{3}\alpha _{2} , \hfill \\ \lambda _{1}^{2} = \frac{1}{3}\left[ {2\beta _{0} \sin \left( {\gamma _{0} } \right) + \alpha _{2} } \right], \hfill \\ \lambda _{2}^{2} = \frac{1}{3}\beta _{0} \left[ {\sqrt 3 \cos \left( {\gamma _{0} } \right) - \sin \left( {\gamma _{0} } \right)} \right] + \frac{1}{3}\alpha _{2} , \hfill \\ \end{gathered}$$
(44)

with

$$\beta_{0} = \sqrt {\alpha_{2}^{2} - 3\alpha_{1} } ,\;\gamma_{0} = \frac{1}{3}\sin^{ - 1} \left( { - \frac{{2\alpha_{2}^{3} - 9\alpha_{2} \alpha_{1} + 27\alpha_{0} }}{{2\beta_{0}^{3} }}} \right).$$
(45)

The general solution of Eq. (42) can be written in the following form

$$\left\{ {\overline{e},\;\overline{\theta },\;\overline{\rm N}} \right\} = \frac{1}{\sqrt r }\mathop \sum \limits_{i = 1}^{3} \left\{ {1,\;L_{i} ,\;H_{i} } \right\}A_{i} I_{1/2} \left( {\lambda_{i} r} \right).$$
(46)

where \(I_{n} \left( { . } \right)\) indicates the second type of modified Bessel functions of order n. \(A_{i} ,\) \(\left( {i = 1,2,3} \right)\) are three parameters depending on s. In addition, \(L_{i}\) and \(M_{i}\) are two distinct factors which are correlated to \(A_{i}\). Thereby, the following relations can be obtained by inserting Eq. (46) into Eqs. (35) to (37)

$$H_{i} = \frac{{g_{3} \left( {\lambda_{i}^{2} - s^{2} } \right)}}{{\lambda_{i}^{4} - g_{5} \lambda_{i}^{2} }},\;\;L_{n} = \frac{{\left( {\lambda_{i}^{2} - s^{2} } \right)\left( {\lambda_{i}^{2} - g_{4} } \right)}}{{\lambda_{i}^{4} - g_{5} \lambda_{i}^{2} }},\;\;i = 1,\;2,\;3.$$
(47)

The displacement \(\overline{u}\) can be achieved by using the following so-called Bessel function

$$\int {x^{\frac{3}{2}} I_{\frac{1}{2}} \left( x \right)dx} = x^{\frac{3}{2}} I_{\frac{3}{2}} \left( x \right)$$
(48)

Then, one has

$$\overline{u} = \frac{1}{\sqrt r }\mathop \sum \limits_{i = 1}^{3} \frac{1}{{\lambda_{i} }}A_{i} I_{3/2} \left( {\lambda_{i} r} \right).$$
(49)

For any positive number x, it is found that the modified Bessel \(I_{n}\) fulfills the following relations

$$I_{\frac{1}{2}} \left( x \right) = \sqrt {\frac{2}{\pi x}} \sinh \left( x \right),\;\;I_{\frac{3}{2}} \left( x \right) = \sqrt {\frac{2}{\pi x}} \left( {\cosh \left( x \right) - \frac{\sinh \left( x \right)}{{\sqrt x }}} \right).$$
(50)

Introducing Eq. (50) into Eqs. (46) and (49), one obtains

$$\left\{ {\overline{e}, \;\overline{\theta },\;\overline{\rm N}} \right\} = \sqrt {\frac{2}{\pi r}} \mathop \sum \limits_{i = 1}^{3} \left\{ {1,\;L_{i} ,\;H_{i} } \right\}\frac{{A_{i} }}{{\sqrt {\lambda_{i} r} }}\sinh \left( {\lambda_{i} r} \right)$$
(51)
$$\overline{u} = \sqrt {\frac{2}{\pi }} \mathop \sum \limits_{i = 1}^{2} \frac{{A_{i} }}{{r\lambda_{i}^{\frac{3}{2}} }}\left( {\cosh \left( {\lambda_{i} r} \right) - \frac{{\sinh \left( {\lambda_{i} r} \right)}}{{\lambda_{i} r}}} \right)$$
(52)

As a result, the final solutions for thermal stresses are derived by the following closed-form relations:

$$\overline{\sigma }_{rr} = \sqrt {\frac{2}{\pi }} \mathop \sum \limits_{i = 1}^{3} \frac{{A_{i} }}{{\sqrt r \left( {\lambda_{i} r} \right)^{5/2} }}\left( { - 2\beta^{2} \lambda_{i} r\cosh \left( {\lambda_{i} r} \right) + \left( {2\beta^{2} + \Omega_{i} \lambda_{i}^{2} r^{2} } \right)\sinh \left( {\lambda_{i} r} \right)} \right),$$
(53)
$$\begin{array}{*{20}c} {\overline{\sigma }_{\vartheta \vartheta } = \sqrt {\frac{2}{\pi }} \mathop \sum \limits_{i = 1}^{3} \frac{{A_{i} }}{{\sqrt r \left( {\lambda_{i} r} \right)^{5/2} }}\left( {\left( { - 2 + 3\beta^{2} } \right)\lambda_{i} r\cosh \left( {\lambda_{i} r} \right)} \right.} \\ { + \left. {\left( {2 + \Omega_{i} \lambda_{i}^{2} r^{2} + \beta^{2} \left( {3 + \lambda_{i}^{2} r^{2} } \right)} \right)\sinh \left( {\lambda_{i} r} \right)} \right)} \\ \end{array}$$
(54)

where \(\Omega_{i} = 1 - L_{i} - H_{i}\).

The non-dimensional Maxwell’s stress \(\tau_{{{\text{rr}}}}\) is given by

$$\tau_{{{\text{rr}}}} = \frac{{v_{a}^{2} }}{{v_{0}^{2} }}\sqrt {\frac{2}{\pi r}} \mathop \sum \limits_{i = 1}^{3} \frac{{A_{i} }}{{\sqrt {\lambda_{i} r} }}\sinh \left( {\lambda_{i} r} \right)$$
(55)

The boundary conditions (31) to (33) possess the following forms after performing the Laplace transform

$$\begin{gathered} \bar{\theta } = \frac{{\theta _{0} }}{s},~~~ \hfill \\ \bar{\sigma }_{{{\text{rr}}}} \left( {R,\;s} \right) = 0, \hfill \\ D_{E} \left. {\frac{{\partial \bar{N}}}{{\partial r}}} \right|_{{r = R}} = s_{f} \bar{N}\left( {R,s} \right). \hfill \\ \end{gathered}$$
(56)

Equations (46) and (53) are substituted into Eq. (56) and give

$$\sqrt {\frac{2}{\pi R}} \mathop \sum \limits_{i = 1}^{3} L_{i} \frac{{A_{i} }}{{\sqrt {\lambda_{i} R} }}\sinh \left( {\lambda_{i} R} \right) = \frac{{\theta_{0} }}{s},$$
(57)
$$\mathop \sum \limits_{i = 1}^{3} \frac{{A_{i} }}{{\sqrt R \left( {\lambda_{i} R} \right)^{5/2} }}\left( {\left( {2\beta^{2} + \Omega_{i} \lambda_{i}^{2} R^{2} } \right)\sinh \left( {\lambda_{i} R} \right) - 2\beta^{2} \lambda_{i} R\cosh \left( {\lambda_{i} R} \right)} \right) = 0,$$
(58)
$$\begin{array}{*{20}c} {\sqrt {\frac{2}{\pi }} \mathop \sum \limits_{i = 1}^{3} \frac{{A_{i} }}{{\sqrt R \left( {\lambda_{i} R} \right)^{5/2} }}\left( {\left( {2 + \lambda_{i}^{2} R^{2} } \right)\sinh \left( {\lambda_{i} R} \right) - 2\lambda_{i} R\cosh \left( {\lambda_{i} R} \right)} \right)} \\ { = \frac{{s_{f} }}{{D_{E} }}\sqrt {\frac{2}{\pi R}} \mathop \sum \limits_{i = 1}^{3} H_{i} \frac{{A_{i} }}{{\sqrt {\lambda_{i} R} }}\sinh \left( {\lambda_{i} R} \right),} \\ \end{array}$$
(59)

The values of parameters \(A_{i} ,\) \(\left( {i = 1,\;2,\;3} \right)\) can be derived by solving the systems (57) to (59).

The inversion of Laplace transforms is obtained in this study using an accurate and efficient numerical approach based on the Fourier series expansion [42]. Any function in the Laplace domain can be inverted to the time domain by using the following operator:

$$\Gamma \left( {\rho ,\;t} \right) = \frac{{e^{{{\text{ct}}}} }}{t}\left( {\frac{1}{2}\overline{\Gamma }\left( {\rho ,\;c} \right) + {\text{Re}} \mathop \sum \limits_{j = 1}^{{N_{f} }} \overline{\Gamma }\left( {\rho ,\;c + \frac{{{\text{ij}}\pi }}{t}} \right)\left( { - 1} \right)^{j} } \right)$$
(60)

where \(N_{f}\) denotes the number of terms, \({\text{Re}}\) represents the real part, and i stands for the imaginary number unit. Several numerical tests have demonstrated that the value of the parameter c fulfills the relation \(c\tau \cong 4.7\), allowing for quick convergence [43].

5 Numerical results

In order to demonstrate the theoretical results achieved in the previous sections, we will now provide some numerical simulations. The effect of the modified Moore–Gibson–Thompson photothermal (MGTPT) heat equation on the considered physical fields is exhibited through diagrams and tables using Mathematica software.

When compared to typical covalent semiconductors such as silicon (Si), metal oxide semiconductors constitute a distinct class of materials due to their electronic charge transfer properties. Metal oxide semiconductors are valence compounds with strong ionic bonding strength. Isotropic silicone (Si) is used as a semiconductor solid for theoretical analysis. The physical parameters considered at \(T_{0} = 300 K\) are as follows [12]:

$$\begin{array}{*{20}c} {\lambda = 3.64 \times 10^{10} {\text{kg}}\;{\text{m}}^{ - 1} {\text{s}}^{ - 2} ,\;\mu = 5.46 \times 10^{10} {\text{kg}}\;{\text{m}}^{ - 1} {\text{s}}^{ - 2} ,\;\rho = 2330\;{\text{kg}}\;{\text{m}}^{ - 3} ,} \\ {K = 1.51\;{\text{W}}\;{\text{m}}^{ - 1} {\text{K}}^{ - 1} ,\;C_{E} = 6.95 \times 10^{2} {\text{J}}\;{\text{kg}}\;{\text{K}}^{ - 1} ,\;d_{n} = - 9 \times 10^{ - 31} {\text{m}}^{3} , } \\ {E_{g} = 1.11 {\text{eV}},\;D_{E} = 2.5 \times 10^{ - 3} {\text{m}}^{2} {\text{s}}^{ - 1} ,\;s_{f} = 2 {\text{m}}\;{\text{s}}^{ - 1} ,\;\tau = 5 \times 10^{ - 5} {\text{s}}.} \\ \end{array}$$

The numerical approach described by Eq. (60) is used to exhibit the distribution of non-dimensional temperature \(\theta\), radial displacement u, radial and hoop stresses \(\sigma_{{{\text{rr}}}}\) and \(\sigma_{\vartheta \vartheta }\), Maxwell’s stress \(\tau_{{{\text{rr}}}}\) and absolute carrier density N along the radial cylindrical direction. The numerical results at time \(t = 0.12{\text{s}}\) and \(R = 1\) are graphically illustrated in Figs. 2, 3, 4, 5, 6 and 7. All domain variables are numerically calculated in three cases.

Fig. 2
figure 2

Temperature variation \(\theta\) with \(r\) for different models of photo-thermoelasticity

Full size image
Fig. 3
figure 3

Displacement variation \(u\) with \(r\) for different models of photo-thermoelasticity

Full size image
Fig. 4
figure 4

Carrier density \(N\) variation with \(r\) for different models of photo-thermoelasticity

Full size image
Fig. 5
figure 5

Radial stress variation \(\sigma_{{{\text{rr}}}}\) with \(r\) for different models of photo-thermoelasticity

Full size image
Fig. 6
figure 6

Hoop stress variation \(\sigma_{\vartheta \vartheta }\) with \(r\) for different models of photo-thermoelasticity

Full size image
Fig. 7
figure 7

Maxwell’s stress \(\tau_{{{\text{rr}}}}\) with \(r\) for different models of photo-thermoelasticity

Full size image

5.1 Comparison of several photo-thermoelastic models

As previously stated, the Moore–Gibson–Thompson photothermal (MGTPT) model is assumed as a generalization of several earlier photothermal-elasticity models. It is introduced not only to generalize but also to resolve some of physical problems and flaws found in the previous models. In Sects. 1 and 2, these inconsistencies are noted and addressed. Before making comparisons between different models, we will first explain how the previous models can be obtained from the photo-thermoelastic Moore–Gibson–Thompson model as special cases.

  1. 1.

    The coupling photo-thermoelastic theory (CPTE) can be produced when the thermal parameters are ignored (\(\tau_{0} = K^{*} = 0\)).

  2. 2.

    The generalized Lord and Shulman photothermal-elasticity model (PLS) is obtained as the Green and Naghdi parameter takes the value \(K^{*} = 0\).

  3. 3.

    If the relaxation parameter \(\tau_{0} = 0\) is missing, the photothermal model (PGN-III) based on Green and Naghdi theory III can be constructed.

  4. 4.

    If the term containing the parameter K is omitted in the heat equation, the photothermal Green and Naghdi model (PGN-II) may be concluded.

  5. 5.

    When \(\tau_{0} ,\;K^{*} > 0\), the proposed Moore–Gibson–Thompson photothermal model (PTPM) can be deduced.

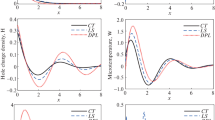
The present subsection intends to examine the comparison between the newly proposed model (MGTPT) and the previous thermo-photovoltaic models (CPTE, PLS, PGN-II and PGN-III). To better illustrate the comparisons and for practical purposes, our findings are exhibited through some figures and tables. Tables 1, 2, 3, 4, 5 and 6 and Figs. 2, 3, 4, 5, 6 and 7 show the variations of the considered fields against the radial distance r for different photothermal models. In this case, the non-dimensional parameter of carrier lifetime \(\tau\) and instantaneous time t are fixed (\(\tau = 0.01,\;t = 0.15\)). To this end, some noteworthy facts should be pointed out:

  • It is clear that the differences in the values of the vector fields evolve over the time within the solid sphere. It is also emphasized that the MGTPT photothermal model has an important impact on the distribution of all profiles of the examined fields.

  • The thermal parameters \(\tau_{0}\) and \(K^{*}\) introduced into the heat equation have significant influences on all studied fields.

  • The velocity limitation of heat waves in the case of MGTPT photothermal-elasticity theory is evident in all presented results. The distributions of different field have a finite spread we further go away from the surface of the solid sphere. This phenomenon is in contrast to the traditional photo-thermoelasticity theory in which the propagation rate of thermal and mechanical waves is infinite, resulting in nonzero values for all studied functions within the medium.

  • The coupled photothermal model (CPTE) and the generalized photothermal models (PLS, PGN-II, PGN-III and MGTPT) yield such values that are different in magnitude and similar in behavior at the surface of the semiconducting sphere.

  • For all physical fields, the curves converge while the parameter r approaches to zero to meet the regularity requirement.

  • This result indicates that the non-dimensional radial displacement u grows with decreasing distance r until it reaches its maximum values and then decays rapidly to reach its minimum points, and then gradually decreases to be finally stable.

  • Figure 4 demonstrates that the displacement u starts with zero value at the surface \(r = 1\), which corresponds to the boundary condition, imposed on the problem for all cases.

  • It is also found that the temperature curve and other vector fields in the case of the GN-III model are higher than those of the modified MGTPT model in addition to the generalized PLS and GN-II models.

  • The results of the frequently used GN-III thermal elasticity model show that it varies significantly from the GN-II thermal elasticity models in terms of reduced energy dissipation.

  • In the case of PLS and MGTPT models, the inclusion of the thermal relaxation coefficient \(\tau_{0}\) may reduce the propagation of heat waves within the medium.

  • Over time t, only a small area near the surface of the solid sphere in the case of all the examined distributions has nonzero values. Changes appear in the early stages of the reactions because of the thermal shock, and then, the values of the distributions almost disappear outside this region, indicating that the region which is far from the surface has not yet been subjected to thermal perturbations.

  • There is a satisfactory convergence in the values of the obtained results in the case of the PGN-III and the traditional elasticity (CPTE) models, in contrast to the other generalized photo-thermoelastic models. In other words, the thermal waves do not disappear quickly inside the body due to the thermal shock. This phenomenon is fully consistent with the claims of Quintanilla [26] and the observations of Abouelregal et al. [28,29,30,31].

  • Near the surface of the solid sphere, all types of stresses are compressive, while by approaching to the center of the sphere, they may take the positive values. The tensile stress shows that the medium adjacent to the sphere surface is positioned throughout the time and this consistent with the findings reported by Ref. [44]. Moreover, the higher values of the considered fields on the cavity surface are evident with higher radial magnitudes. More explanations on this phenomena are given in Ref. [45].

Table 1 Variations of temperature \(\theta\) with \(r\) for different models of photo-thermoelasticity
Full size table
Table 2 Variations of displacement \(u\) with \(r\) for different models of photo-thermoelasticity
Full size table
Table 3 Variations of carrier density \(N\) with \(r\) for different models of photo-thermoelasticity
Full size table
Table 4 Variations of radial stress \(\sigma_{{{\text{rr}}}}\) with \(r\) for different models of photo-thermoelasticity
Full size table
Table 5 Variations of hoop stress \(\sigma_{\vartheta \vartheta }\) with \(r\) for different models of photo-thermoelasticity
Full size table
Table 6 Variations of Maxwell’s stress \(\tau_{rr}\) with \(r\) for different models of photo-thermoelasticity
Full size table

5.2 The effect of time instant and carrier lifetime

Semiconductors may excite electrons to higher energy levels (for example, due to photon absorption), resulting in the formation of electron–hole pairs which is known as a generation process. Recombination will eventually return these electrons to their ground states. The lifetime parameter \(\tau\) of a charge carrier is usually defined as the average time which takes electrons and holes to recombine following stimulation. Therefore, the lifetime parameter \(\tau\) must be calculated from a property that includes both generation and recombination, such as photoluminescence, photoconductivity or photoelectric response. In a solar cell, one of the most fundamental factors is the lifetime of the charge carrier. The mobility of the charge carrier is used to characterize the propagation length and, consequently, the chance of the photo-generated charge carrier reaching the corresponding electrode.

According to the above, minority carrier lifetime parameter \(\tau\) is an important physical feature associated with semiconductor recombination processes. The minority carrier life of high-quality semiconductors with few defects is long, while the minority carrier life of poor-quality semiconductors is short and the defect density is large. Thus, the lifetime parameter \(\tau\) of the minority carrier is essential in semiconductor devices.

Table 7 shows the changes in the photothermal fields as a function of the instant time \(t\) and the photo-generated carrier lifetime parameter \(\tau\) at \(r = 0.9\). The study in this subsection will be conducted in light of Moore–Gibson–Thomson photo-thermoelastic modified theory (MGTPT).

Table 7 The effect of time instant \(t\) and carrier lifetime \(\tau\) on photothermal physical fields
Full size table

From the presented numerical values in Table 7, it is concluded that:

  • The carrier lifetime coefficient \(\tau\) has a significant influence on the distribution of all studied variables.

  • In the case of constant time, the temperature values increase with increase in the carrier lifetime coefficient \(\tau\).

  • The magnitude of carrier density \(N\) decreases by increase in the lifetime \(\tau\), while the magnitude of the thermal stress \(\sigma_{rr}\) decreases.

  • In the case of constant time, the Maxwell stress \(\tau_{rr}\) curves increase as the carrier lifetime factor \(\tau\) shifts upward.

  • Theoretical and practical methods for obtaining the information about intrinsic carrier concentrations and long carrier lifetime \(\tau\) are critical criteria for modeling of the semiconductor devices in order to understand and improve the properties and performance of devices.

  • In the investigation of the macroscopic outputs of some materials related to thermo-photovoltaic materials, which dominate the determination of material properties, the carrier lifetime parameter \(\tau\) will play an important role.

  • Instantaneous time \(t\) has a considerable effect on the changes of different physical fields. At constant lifetime \(\tau\), with any increase in the instantaneous time value \(t\), the magnitudes of all examined variables also increase.

  • Over time \(t\), only a small area near the surface of the solid sphere in the case of all the examined distributions has nonzero values. Changes appear in the early stages of the reactions because of the thermal shock, and then, the values of the distributions almost disappear outside this region, indicating that the region far from the surface has not yet been subjected to thermal perturbations.

All the observations and results of this study clarify the concept of finite heat dissipation rates. For designers of new materials and other disciplines like materials science and physical engineering, the results obtained in this example may be useful in the presence of plasma waves and elastic materials. Because of the flaws and lack of information in material properties, measurement of carrier life in many thin-film ferroelectric materials can be challenging. Rapidly changing contraction and expansion leads to temperature fluctuations in materials subject to heat transfer by conduction [41]. Since the pulsed laser techniques are widely used in material processing, nondestructive testing and characterization, this mechanism has attracted much attention in recent years [8].

6 Conclusion

This article presented a new thermal heat conduction model based on the Moore–Gibson–Thompson equation. In the restructured photothermal model, type III Green–Naghdi, as well as Lord and Shulman heat transfer equations, was incorporated. The modified model will be used to explore the interaction between heat, plasma and elastic waves in semiconductor materials. There have been only a few articles in the literature about the new proposal. Various models of thermoelastic and photothermal models can be obtained as special cases of the proposed model.

The following important observations can be drawn from the previous discussions:

  • The comparison between the solutions illustrates the fact that thermal parameters have a significant influence on the distribution of the physical field variables. There are also considerable impacts on the variables examined from instantaneous time and lifetime characteristics.

  • According to the new model (MGTPT), heat waves move and propagate within the medium at finite speeds instead of the infinite speed predicted by previous models of photothermal elasticity (CPTE and PGN-III).

  • The results in the case of the PGN-III model showed a satisfactory convergence with the results of the conventional model of photo-thermoelasticity (CPTE), in which heat waves propagate at finite velocities within the medium, in contrast to the other generalized thermoelastic models. It can also be observed that with the decrease in the radial distance and with the evolution of time, for all different photo-thermoelastic models, we found the convergence of the values of the physical quantities.

  • The results presented in this study will be useful to scientists who are working in the related fields such as physics, materials design, thermal efficiency and geophysics. A wide range of thermodynamic problems can also be solved by utilizing the method proposed in the present work.