1 Introduction

Laser-induced damage to optical materials is a distinct field. For more than 50 years, several publications have attempted to address the topic from a theoretical and experimental standpoint. As pulsed laser technologies are widely used in material processing and non-destructive detection and characterization, the excitation of thermoelastic waves by a pulsed laser in solids is of significant interest. When a solid material absorbs a laser pulse, it creates a localized temperature rise, which causes thermal expansion and heat wave formation in the material. There are two important effects in heating the ultra-short pulsed laser [1]. A focused, high-powered laser beam can heat materials to thousands of degrees Kelvin. The temperature of continuous-wave laser heating can be monitored remotely with great accuracy by fitting the spectrum radiation to a blackbody curve. Heating with a pulsed laser offers several benefits, but the temperature increases and falls in nanoseconds, necessitating quick electronics and time-consuming methods for temperature estimation [2].

Metal softening and/or hardness, annealing of crystalline or polycrystalline materials, diffusion of dopants in semiconductors, synthesis of compounds and thin films, polymerization of polymers, and other applications of laser heating are all possible. Thermally triggered processes, bulk diffusion, and phase transitions have all been aided by laser annealing. Laser heating has the benefit of being both spatially and temporally localized. Additionally, by establishing thermal gradients, sample temperatures considerably above the sample chamber's capacity can be obtained, such as heated samples in diamond anvil cells [3, 4].

Laser heating has a number of benefits over traditional techniques, including accuracy, local therapy, and cheap cost. Absorption occurs when a high-intensity laser interacts with a solid surface. As a result, the substrate material gains internal energy and the irradiated zone releases heat. The temperature gradients in the irradiated zone remain considerable since the process is often rapid. As a result, there is a lot of thermal stress and thermally generated tension in this area. Moreover, from the point of view of application, the end result is decisive in the laser treatment procedure. High stress levels in the irradiated zone may cause the surface to fail due to stress-induced cracking. As a result, caution should be exercised while performing laser therapy [5].

There is no elastic component in the heat conduction equation of the classical uncoupled thermoelasticity theory. Furthermore, the heat conduction equation is a parabolic, which means that heat waves will propagate at limitless rates. The physical facts contradict these two occurrences anticipated by the conventional uncoupled thermoelasticity theory. The goal of developing generalized thermoelasticity theories was to eliminate the above two phenomena. Biot [6] developed the coupled theory of thermoelasticity to resolve the contradiction that elastic changes have no influence on the temperature change in the conventional uncoupled theory. The heat equation for the coupled theory, on the other hand, is of mixed parabolic/hyperbolic type; therefore, both theories share the second flaw.

Several theories of thermoelasticity have been established in order to eliminate the shortcoming of the traditional coupled dynamic theory of thermoelasticity. Lord Shulman's theory (LS) [7] and Green-Lindsay's model (GL) [8] are the first two generalized models of thermoelasticity. Theoretically, one coefficient of thermal relaxation is given in the traditional Fourier law of thermal conductivity, while the G-L theory introduces two thermal relaxation times in the constituent relationships of force-pressure tensor and in the entropy equation. Green and Naghdi [9,10,11] postulated three new models of thermal elasticity allowing for a larger class of issues with heat flow, identified as GN Models I, II and III. For these three models, the first model (GN-I) will be the same as the conventional thermal conduction theory, the second model (GN-II) will forecast the finite rate of the thermal propagation without energy dissipation, and the third model (GN-III) indicates the transmission of limited heat signals and involving dissipate energy. Several researchers including Abouelregal [12,13,14,15] have studied several interesting thermoelastic problems using thermoelastic theories [16,17,18,19,20].

The Moore–Gibson–Thompson (MGT) equation has grown more important in recent years, as evidenced by numerous academic articles devoted to its study and interpretation. The theory was founded on a third-order differential equation, which is crucial to many fluid dynamics [21]. Quintanilla [22, 23] constructed a novel heat conduction model within the MGT equation. Abouelregal et al. [24,25,26] prepared the proposed modified heat equation after adding the relaxation parameter in the GN-III model and used the energy equation. The number of articles on this theory has increased significantly since the advent of the MGT equation [27,28,29,30].

Some materials, such as semiconductors, offer a variety of physical characteristics that are useful during research. According to the principle of thermoelasticity, semiconductor materials may only be classed as elastic materials. The relevance of semiconductors in current technology was recently highlighted when they were utilized to produce electrical energy from sunlight while also being subjected to laser pulses [31]. Semiconductor materials are utilized as nanomaterials in various fields of mechanical and electrical engineering, and they have a variety of uses in modern industry, including transistors, screens, and solar cells. The photothermal theory has recently been applied to semiconductor mediums to produce sustainable energy technologies. To characterize the overlap between the photothermal equations and the thermoelasticity equations, several mathematical-physical models were studied. Gordon et al. [32] first introduced electronic deformations to photothermal spectroscopy. While using a laser source, photoacoustic spectroscopy is utilized in the context of sensitive analytical procedures to measure the velocity of sound of some semiconductor materials [33]. Many applications in engineering industries employ wave propagation during electro-deformations of elastic semiconductor medium in the photothermal processing techniques [34]. Acoustic velocity, thermal diffusion coefficients, sample temperatures, bulk sample flow rates, specific heats, and volume expansion coefficients in materials have all been measured using photothermal spectroscopy.

The sample is uniformly elastic and electrically deformed by excited photo-carriers. The mechanism of electronic deformation is founded on the fact that photogenerated plasma in the semiconductor produces lattice crystal deformation, that is, the deformation of the conductive potential, and valence bands in the semiconductor. This can result in local stress in the sample via photo-stimulated carriers. This strain in turn can create plasma waves in the semiconductor by regular elastic locally similar to thermal wave production [35].

The mechanical, electric, and thermal properties of semiconductors materials vary with changes in temperature. When a temperature gradient due to absorption of light occurs in semiconductor, elastic materials causes an electric potential difference between endpoints in the semiconductor. Several authors have analyzed the uncoupled and coupled system of plasma, thermodynamic and elastic equations as well as different effects of thermal as well as electronic deformation in semiconductors using classical models. According to a review of the literature, there is no work on the transient examination of the semiconductor cylinders subjected to ultra-short pulsed laser heating and photogenerated plasma, as well as temperature-dependent material characteristics. The importance of the issue is the primary motivation for a thorough examination of it in this study. The discovery of a highly helpful technique for investigating solid materials has reignited attention in the photoacoustic impact in solids since then. In the disciplines of physics, biology, engineering, chemistry, and medicine, a great deal of theoretical and experimental research has been published. Semiconducting materials have become increasingly popular in modern engineering, as technology has advanced. Wave propagation in a semiconducting material will be of significant academic and practical importance. Photoluminescence, for instance, is a possible result of optical absorption, and when this occurs in conjunction with radiative trapping, delayed heat generation can occur. In addition, the photochemical mechanism is a non-thermal deexcitation pathway for absorbed light energy. The chain reaction produced by the absorbed photons has resulted in the formation of a new chemical.

The purpose of this paper is to investigate disturbances in infinite, isotropic, homogeneous thermoelastic semiconductor materials using the new Moore–Gibson–Thompson (MGT) heat conduction model. The propagation of waves in semiconductor materials has many applications in various fields of science and technology, namely atomic physics, industrial engineering, thermal power plants, submarine structures, pressure vessel, aerospace, chemical pipes, and metallurgy. The effect of thermo-electronic deformation in semiconductors has been investigated, including partially coupled plasma, thermal mechanism, and elastic waves. Under proper boundary conditions, we used the normal mode method analysis to solve a system of partial differential equations in this phenomenon. Physical field quantities are introduced analytically and graphed, along with some analytical comparisons. The results obtained were compared with the results of the work of other researchers.

2 Basic equations

The generalized coupled hyperbolic plasma, generalized thermal and elastic equations, for thermoelastic semiconductors with isotropic and homogeneous electronic, thermal and elastic properties, are given by:

Equations of motion:

$$ \sigma _{{ij,j}} + F_{i} = \rho {\text{\"u }}_{i} $$
(1)

The constitutive equations [26, 27]:

$$ \sigma_{ij} = C_{ijkl} e_{kl} - \left( {\beta_{ij} \theta + d_{nij} N} \right). $$
(2)

The strain–displacement relations:

$${e}_{ij}=\frac{1}{2}\left({u}_{i,j}+{u}_{j,i}\right).$$
(3)

In Eqs. (1)-(3), \({\sigma }_{ij}\) are the components of stress, \(\varrho \) is the density of the material, \({u}_{i}\) are the displacement components, \({F}_{i}\) are the components of body forces and \(i,j,k=\mathrm{1,2},3\), \({e}_{ij}\) is the strain tensor, \({e}_{kk}=e\) is the cubical dilatation, \({d}_{nij}={d}_{ni}{\delta }_{ij}\) are the difference in deformation potential of the conduction and valence bands, \({C}_{ijkl}\) are the elastic constants for material, and \({\beta }_{ij}={\beta }_{i}{\delta }_{ij}\) are the stress-temperature coefficients. Also, \(\theta =T-{T}_{0}\) denotes the thermodynamical temperature, \({T}_{0}\) is the reference temperature, and \(N\) is the carrier density.

The coupled plasma-thermal-elastic wave equation can be written as [35, 36]

$$ \left( {D_{Eij} N_{,j} } \right)_{,i} = \rho \frac{\partial N}{{\partial t}} + \frac{1}{\tau }N + \kappa \theta + G, $$
(4)

where \(D_{Eij}\) are the diffusion coefficients, \(\kappa \) is the thermal activation coupling parameter, \(\tau \) is the lifetime of photogenerated electron–hole pairs, and \(G\) is the carrier photogeneration “source” term. In the case of harmonic modulation lasers, Vasilev and Sandomirskii [37] initially found that the thermal activation coupling parameter \(\kappa \) is insignificant at low temperatures.

Cattaneo–Vernotte in [38,39,40] introduced a wider Fourier law by adding the thermal relaxation \({\tau }_{0}\) to the vector of the heat flow \(\overrightarrow{q}\) as

$$ \left( {1 + \tau_{0} { }\frac{\partial }{\partial t}} \right)\vec{q} = - K_{ij} \vec{\nabla }\theta . $$
(5)

In Eq. (1), \({K}_{ij}\) refers to the thermal conductivity tensor.

The improved Fourier law based on the GN-III model can be represented as [11]

$$ \vec{q} = - K_{ij} \,\vec{\nabla }\theta - K_{ij}^{*} \vec{\nabla }\vartheta , $$
(6)

where the function \(\vartheta \) denotes thermal displacement which satisfies \(\dot{\vartheta }=\theta \) and the parameters \({K}_{ij}^{*}\) refer to the thermal conductivity rates. The equation of the energy balance can be written as [41, 42]

$$ \rho C_{E} \frac{\partial \theta }{{\partial t}} + T_{0} \frac{\partial }{\partial t}\left( {\beta_{ij} e_{ij} } \right) = - \vec{\nabla } \cdot \vec{q} + Q, $$
(7)

where \({C}_{E}\) is the specific heat at constant volume and \(Q\) is the heat source.

The combination of improved Fourier law proposed in (6) with the energy Eq. (7) has the same weakness as Fourier's normal theory, predicting that thermal waves are spreading immediately. Quintanilla [22, 23] and Abouelregal et al. [24,25,26] prepared the proposed modified heat equation after adding the relaxation parameter in the GN-III model. The modified Fourier's law would then take the following form [22, 23]

$$ \left( {1 + \tau_{0} { }\frac{\partial }{\partial t}} \right)\vec{q} = - K_{ij} \,\vec{\nabla }\theta - K_{ij}^{*} \vec{\nabla }\vartheta . $$
(8)

Consider that the semiconductor elastic media is subjected to light beams from the outside and that the excited free electrons create a carrier-free charge density with semiconductor gap energy \(E_{g}\). Because of the absorbed optical energy, there is a change in electronic deformation and elastic vibrations. Thermal-elastic-plasma waves will affect the overall form of the heat conductivity equation in this situation. The modified Fourier law for semiconductor materials with plasma effect in a generalized version can be written as follows:

$$ \left( {1 + \tau_{0} { }\frac{\partial }{\partial t}} \right)\vec{q} = - K_{ij} \,\vec{\nabla }\theta - K_{ij}^{*} \vec{\nabla }\vartheta - \int {\frac{{E_{g} }}{\tau }} Nd\vec{x}. $$
(9)

The photo-excitation effect is represented by the final term in Eq. (9). When the above equation is differentiated with respect to \(\vec{x}\), the result is

$$ \left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left( {\vec{\nabla } \cdot \vec{q}} \right) = - \vec{\nabla } \cdot \left( {K_{ij} \,\vec{\nabla }\theta } \right) - \vec{\nabla } \cdot \left( {K_{ij}^{*} \vec{\nabla }\vartheta } \right) - \frac{{E_{g} }}{\tau }N. $$
(10)

By substituting Eq. (10) into Eq. (7), the modified heat conduction equation with thermal memory that explains the interaction between the thermal-plasma-elastic waves may be derived as

$$ \left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left[ {\rho C_{E} \frac{{\partial^{2} \theta }}{{\partial t^{2} }} + T_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\beta_{ij} u_{i,j} } \right) - \rho \frac{\partial Q}{{\partial t}}} \right] = \left( {K_{ij} \dot{\theta }_{,j} } \right)_{,i} + \left( {K_{ij}^{*} \theta_{,j} } \right)_{,i} + \frac{{E_{g} }}{\tau }\frac{\partial N}{{\partial t}}. $$
(11)

We assumed that the adjacent free space is permeated by an initial magnetic field \(\vec{H}\). This generates an induced electro field \(\vec{E}\) and induced magnetic field \(\vec{h}\) that fulfills the magnetic equations of Maxwell and is sufficient for slowly moving media [43]:

$$ \vec{J} = \nabla \times \vec{h},{ }\nabla \times \vec{E} = - \mu_{0} \frac{{\partial \vec{h}}}{\partial t},{ }\vec{E} = - \mu_{0} \left( {\frac{{\partial \vec{h}}}{\partial t} \times \vec{H}} \right),{ }\nabla \cdot \vec{h} = 0, $$
(12)
$$ \tau_{ij} = \mu_{0} \left[ {H_{i} h_{j} + H_{j} h_{i} - H_{k} h_{k} \delta_{ij} } \right], $$
(13)

where \({\mu }_{0}\) is the magnetic permeability, \(\overrightarrow{J}\) is the current density, and \({\tau }_{ij}\) is the Maxwell stress tensor.

3 Statement of the problem

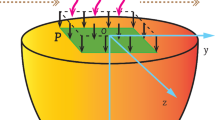
This section presents case formulation and theoretical analyses of a semiconductor medium based on the interaction of plasma, heat waves, and elastic waves. The model developed for this paper has been directly applied to the mentioned problem. A one-dimensional (1D) problem of a thermally homogenous, isotropic, electrically conducting solid cylinder of radius \({\rho }_{0}\) owing to symmetry is considered. As a result, all studied field variables are assumed to be dependent on time \(t\) and radial distance \(\rho \). The outer surface of the solid cylinder is constrained and has been illuminated using a laser pulse heating system. The \(z\)-axis is aligned with the cylinder axis with the use of the cylindrical coordinate system \(\left( {\rho ,\phi ,z} \right)\). The temperature in the cylinder is initially constant and uniform (\(T_{0}\)). Furthermore, all examined fields are assumed to be finite within the medium for the regularity condition. The displacement components for the 1D problem and displacement–strain relations are given by

$$ \begin{array}{*{20}l} {u_{\rho } = u\left( {\rho ,t} \right), u_{\phi } \left( {\rho ,t} \right) = 0 = u_{z} \left( {\rho ,t} \right), } \hfill \\ {e_{\rho \rho } = \frac{u}{\rho }, e_{\phi \phi } = \frac{\partial u}{{\partial \rho }},e_{\rho \phi } = e_{\rho z} = e_{zz} = e_{\phi z} = 0.} \hfill \\ \end{array} $$
(14)

The stress–strain–temperature–carrier relations (2) will be the form

$$ \begin{gathered} \sigma_{\rho \rho } = 2\mu \frac{\partial u}{{\partial \rho }} + \lambda e - \left( {3\lambda + 2\mu } \right)\left( {\alpha_{t} \theta + \delta_{n} N} \right), \hfill \\ \sigma_{\phi \phi } = 2\mu \frac{u}{\rho } + \lambda e - \left( {3\lambda + 2\mu } \right)\left( {\alpha_{t} \theta + \delta_{n} N} \right), \hfill \\ \sigma_{zz} = \lambda e - \left( {3\lambda + 2\mu } \right)\left( {\alpha_{t} \theta + d_{n} N} \right), \hfill \\ \end{gathered} $$
(15)

where \({\alpha }_{t}\) is the linear thermal expansion coefficient, \(\delta_{n}\) is the electronic deformation coefficient, \(\lambda\), \(\mu \) are the Lame’s constants, and \(e = \frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }\). When the Lorentz force \(F_{\rho }\) is taken into account, the dynamic motion equation becomes

$$ \frac{{\partial \sigma_{\rho \rho } }}{\partial \rho } + \frac{1}{\rho }\left( {\sigma_{\rho \rho } - \sigma_{\phi \phi } } \right) + F_{\rho } = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}. $$
(16)

Assume the cylinder is immersed in a magnetic field of constant strength \(\vec{H}_{0} = \left( {0,0,H_{0} } \right)\). According to Eq. (12), we obtain

$$ \vec{E} = \left( {0,\mu_{0} H_{0} \frac{\partial u}{{\partial t}},0} \right),{ }\vec{J} = \left( {0,\frac{\partial }{\partial \rho }\left( {\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }} \right),0} \right),\vec{h} = \left( {0,0,\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }} \right). $$
(17)

The magnetic field \({\overrightarrow{H}}_{0}\) induces the radial component of Lorentz force \({F}_{\rho }\), which is given by.

$$ F_{\rho } = \mu_{0} \left( {\vec{J} \times \vec{H}_{0} } \right)_{\rho } . $$
(18)

Thus, we have \({F}_{\rho }\) and Maxwell's stress \({\tau }_{\rho \rho }\) from Eqs. (13) and (17) as

$$ F_{r} = \mu_{0} H_{0}^{2} \frac{\partial }{\partial \rho }\left( {\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }} \right),{ }\tau_{\rho \rho } = \mu_{0} H_{0}^{2} \frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho } $$
(19)

Inserting Eqs. (15) and (19) into Eq. (16), we have

$$ \left( {\lambda + 2\mu + \mu_{0} H_{0}^{2} } \right)\frac{\partial }{\partial \rho }\left( {\frac{1}{\rho }\frac{{\partial \left( {\rho u} \right)}}{\partial \rho }} \right) - \gamma \frac{\partial \theta }{{\partial \rho }} - d_{n} \frac{\partial N}{{\partial \rho }} = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}. $$
(20)

where \(\left\{ {\gamma ,{ }d_{n} } \right\} = \left( {3\lambda + 2\mu } \right)\left\{ {\alpha_{t} ,\delta_{n} } \right\}\).

When we apply the operator \(\frac{1}{\rho }\frac{\partial (\rho u)}{\partial \rho }\) to both sides of Eq. (20), we obtain

$$ \left( {\lambda + 2\mu + \mu_{0} H_{0}^{2} } \right)\nabla^{2} e - \gamma \nabla^{2} \theta - d_{n} \nabla^{2} N = \rho \frac{{\partial^{2} e}}{{\partial t^{2} }}. $$
(21)

In the cylindrical coordinate system, the Laplacian operator is given by \({\nabla }^{2}=\frac{{\partial }^{2}}{\partial {\rho }^{2}}+\frac{1}{\rho }\frac{\partial }{\partial \rho }\). Without any heat sources (\(Q=0\)), the generalized modified MGTE heat conduction Eq. (11) will be as follows:

$$ \left( {1 + \tau_{0} { }\frac{\partial }{\partial t}} \right)\left[ {\rho C_{E} \frac{{\partial^{2} \theta }}{{\partial t^{2} }} + \gamma T_{0} \frac{{\partial^{2} e}}{{\partial t^{2} }}} \right] = K\nabla^{2} \dot{\theta } + K^{*} \nabla^{2} \theta + \frac{{E_{g} }}{\tau }\frac{\partial N}{{\partial t}}. $$
(22)

The governing equations can easily be transformed into dimensionless forms. As a result, the dimensionless variables listed below are presented:

$$ \begin{array}{*{20}c} {\left\{ {\rho^{\prime}, u^{\prime}} \right\} = v_{0} \eta \left\{ {\rho ,u} \right\}, \left\{ {t^{\prime},\tau^{\prime}_{0} ,\tau^{\prime}} \right\} = v_{0}^{2} \eta \left\{ {t,\tau_{0} ,\tau } \right\},\left\{ {\theta^{\prime},N^{\prime}} \right\} = \frac{1}{{\rho v_{0}^{2} }}\left\{ {\gamma \theta ,d_{n} n} \right\},} \\ {\left\{ {\sigma^{\prime}_{ij} ,\tau^{\prime}_{\rho \rho } } \right\} = \frac{1}{{\rho v_{0}^{2} }}\left\{ {\sigma_{ij} ,\tau_{\rho \rho } } \right\}, \eta = \frac{{\rho C_{E} }}{K}, v_{0}^{2} = v_{1}^{2} + v_{a}^{2} .} \\ \end{array} $$
(23)

In Eq. (23), the parameter \({v}_{1}=\sqrt{\frac{\lambda +2\mu }{\varrho }}\) represents the dilatational wave speed, and the factor \({v}_{a}=\sqrt{\frac{{\mu }_{0}{H}_{0}^{2}}{\varrho }}\) symbolizes the medium Alfven wave speed. The governing equations can be rewritten in the following forms if the primes are ignored

$$ \left( {1 + \tau_{0} { }\frac{\partial }{\partial t}} \right)\left[ {\frac{{\partial^{2} \theta }}{{\partial t^{2} }} + \varepsilon_{1} \frac{{\partial^{2} e}}{{\partial t^{2} }}} \right] = \left( {\frac{\partial }{\partial t} + \omega^{*} } \right)\nabla^{2} \theta + \varepsilon_{2} \frac{\partial N}{{\partial t}}, $$
(24)
$$ \nabla^{2} e - \nabla^{2} \theta - \nabla^{2} {\rm N} = \frac{{\partial^{2} e}}{{\partial t^{2} }}, $$
(25)
$$ \nabla^{2} {\rm N} = g_{1} \frac{{\partial {\rm N}}}{\partial t} + g_{2} {\rm N} + g_{3} \theta , $$
(26)
$$ \begin{array}{*{20}l} {\sigma_{\rho \rho } = 2\beta^{2} \frac{\partial u}{{\partial \rho }} + \left( {1 - 2\beta^{2} } \right)e - \theta - {\rm N},} \hfill \\ {\sigma_{\phi \phi } = 2\beta^{2} \frac{u}{\rho } + \left( {1 - 2\beta^{2} } \right)e - \theta - {\rm N},} \hfill \\ {\sigma_{zz} = \left( {1 - 2\beta^{2} } \right)e - \theta - {\rm N},} \hfill \\ \end{array} $$
(27)

where

$$ \begin{array}{*{20}l} {\beta^{2} = \frac{\mu }{\lambda + 2\mu }, \varepsilon_{1} = \frac{{\gamma^{2} T_{0} }}{{\rho^{2} C_{e} c_{0}^{2} }}, \omega^{*} = \frac{{K^{*} }}{{c_{0}^{2} K}},\varepsilon_{2} = \frac{{\gamma E_{g} v_{0}^{2} \eta }}{{\tau d_{n} \rho C_{E} }} ,} \hfill \\ {\eta_{0} = \left( {c_{0} \eta } \right)^{2} , g_{1} = \frac{\rho }{{D_{E} \eta_{0} }}, g_{2} = \frac{1}{{D_{E} \eta_{0} \tau_{1} }}, g_{3} = \frac{{\kappa d_{n} }}{{\gamma D_{E} \eta_{0} }}.} \hfill \\ \end{array} $$
(28)

4 Initial and boundary conditions

The initial conditions of the problem are taken as

$$ \begin{array}{*{20}l} {u\left( {\rho ,0} \right) = 0 = \frac{{\partial u\left( {\rho ,0} \right)}}{\partial \rho },{ }{\rm N}\left( {\rho ,0} \right) = 0 = \frac{{\partial {\rm N}\left( {\rho ,0} \right)}}{\partial \rho },{ }} \hfill \\ {\theta \left( {\rho ,0} \right) = 0 = \frac{{\partial \theta \left( {\rho ,0} \right)}}{\partial \rho }.} \hfill \\ \end{array} $$
(29)

We suppose that the cylinder's exterior surface is constrained. Then the mechanical boundary condition in this case can be expressed as

$$ u\left( {\rho ,t} \right) = 0\, {\text{at}}\, \rho = \rho_{0} . $$
(30)

Also, we assume that a variable heat flux in the form of exponentially laser pulsed heat is applied to the boundary surface \(\rho ={\rho }_{0}\). As a result, the following boundary condition may be applied [44]:

$$ q_{\rho } = q_{0} \frac{{t^{2} }}{{16t_{p}^{2} }}{ }e^{{ - t/t_{p} }} , {\text{ at }} \rho = \rho_{0} , $$
(31)

where \({q}_{0}\) is a constant and \({t}_{p}\) is the pulsing heat flux duration time.

Using the modified Fourier’s law (8) after using dimensionless variables (23) will be

$$ \left( {1 + \tau_{0} { }\frac{\partial }{\partial t}} \right)\dot{q}_{\rho } = - \,\left( {\frac{\partial }{\partial t} + \omega^{*} } \right) \frac{\partial \theta }{{\partial \rho }} $$
(32)

Equations (31) and (32) are decoupled to provide the following boundary condition

$$ \frac{{q_{0} }}{{16t_{p}^{2} }}\left( {1 + \tau_{0} { }\frac{\partial }{\partial t}} \right)\frac{\partial }{\partial t}\left( {t^{2} { }e^{{ - t/t_{p} }} } \right) = - \,\left( {\frac{\partial }{\partial t} + \omega^{*} } \right){ }\frac{\partial \theta }{{\partial \rho }}{\text{ at }}\rho = \rho_{0} $$
(33)

The carriers can reach the sample surface during the diffusion phase, with a finite probability of recombination. As a result, the carrier density boundary condition may be written as follows:

$$ D_{E} \frac{\partial N}{{\partial \rho }} = s_{v} N{\text{ at }} \rho = \rho_{0} , $$
(34)

where \({s}_{v}\) is the surface recombination velocity.

5 Solution in the domain of the Laplace transform

For solving linear differential equations with constant coefficients, the Laplace transform is utilized. In control system engineering, the Laplace transformation is very important. Laplace transforms of various functions must be performed to examine the control system. In order to analyze the dynamic control system, both the characteristics of the Laplace transform and the inverse Laplace transformation are employed. The Laplace transform of function \(g(t)\), which is denoted by \(\mathcal{L}\left[g(t)\right]\) or by \(\overline{g }(s)\), is defined by the following equation:

$$ {\mathcal{L}}\left[ {g\left( t \right){ }} \right] = \overline{g}\left( s \right) = \mathop \int \limits_{0}^{\infty } g\left( t \right)e^{ - st} dt, s > 0. $$
(35)

We get the following results by using the Laplace transform approach to Eqs. (24) to (27):

$$ \left( {\nabla^{2} - \psi } \right)\overline{\theta } = \psi \varepsilon_{1} \overline{e} - \varepsilon_{2} s\overline{N}, $$
(36)
$$ \left( {\nabla^{2} - s^{2} } \right)\overline{e} = \nabla^{2} \overline{\theta } + \nabla^{2} \overline{\rm N}, $$
(37)
$$ \left( {\nabla^{2} - g_{4} } \right)\overline{\rm N} = g_{3} \overline{\theta }, $$
(38)
$$ \left[ {\begin{array}{*{20}c} {\overline{\sigma }_{\rho \rho } } \\ {\overline{\sigma }_{\phi \phi } } \\ {\overline{\sigma }_{zz} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {2\beta^{2} } & 0 & {\left( {1 - 2\beta^{2} } \right)} & { - 1} & { - 1} \\ 0 & {2\beta^{2} } & {\left( {1 - 2\beta^{2} } \right)} & { - 1} & { - 1} \\ 0 & 0 & {\left( {1 - 2\beta^{2} } \right)} & { - 1} & { - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{\partial \overline{u}}}{\partial \rho }} \\ {\frac{{\overline{u}}}{\rho }} \\ {\overline{\theta }} \\ {\overline{\rm N}} \\ \end{array} } \right] . $$
(39)

where \(\psi ={s}^{2}\left(1+{\tau }_{0} s\right)/\left(\mathrm{s}+{\omega }^{*}\right)\).

When Eqs. (36, 37, 38) are decoupled, we get

$$ \left( {\nabla^{6} - \alpha_{2} \nabla^{4} + \alpha_{1} \nabla^{2} - \alpha_{0} } \right)\left\{ {\overline{\theta },\overline{N},\overline{e}} \right\} = 0, $$
(40)

where \({\alpha }_{2}\), \({\alpha }_{1},\) and \({\alpha }_{0}\) are specified by

$$ \begin{array}{*{20}l} {\alpha_{2} = s^{2} + g_{7} + \frac{{g_{6} }}{{g_{3} }},\alpha_{1} = s^{2} g_{7} + g_{8} + \frac{{g_{6} g_{5} }}{{g_{3} }},\alpha_{0} = s^{2} g_{8} ,} \hfill \\ {g_{4} = sg_{1} + g_{2} , g_{5} = g_{4} - g_{3} , g_{6} = g_{3} \;\psi \;\varepsilon_{1} ,} \hfill \\ {g_{7} = g_{4} + \psi , g_{8} = g_{4} \;\psi + sg_{3} \varepsilon_{2} ,} \hfill \\ \end{array} $$
(41)

Presenting \({\lambda }_{i},\) \((i=\mathrm{1,2},3)\) into Eq. (40), we obtain

$$ \left( {\nabla^{2} - \lambda_{1}^{2} } \right)\left( {\nabla^{2} - \lambda_{2}^{2} } \right)\left( {\nabla^{2} - \lambda_{3}^{2} } \right)\left\{ {\overline{\theta },\overline{N},\overline{e}} \right\} = 0, $$
(42)

where \({\lambda }_{1}^{2}\), \({\lambda }_{2}^{2}\), and \({\lambda }_{3}^{2}\) are the roots of the equation

$$ \lambda^{6} - \alpha_{2} \lambda^{3} + \alpha_{1} \lambda^{2} - \alpha_{0} = 0, $$
(43)

which are given by

$$ \begin{array}{*{20}l} {\lambda_{1}^{2} = \frac{1}{3}\left[ {2\beta_{0} \sin \left( {\gamma_{0} } \right) + \alpha_{2} } \right],} \hfill \\ {\lambda_{2}^{2} = - \frac{1}{3}\beta_{0} \left[ {\sin \left( {\gamma_{0} } \right) + \sqrt 3 \cos \left( {\gamma_{0} } \right)} \right] + \frac{1}{3}\alpha_{2} ,} \hfill \\ {\lambda_{2}^{2} = \frac{1}{3}\beta_{0} \left[ {\sqrt 3 \cos \left( {\gamma_{0} } \right) - \sin \left( {\gamma_{0} } \right)} \right] + \frac{1}{3}\alpha_{2} ,} \hfill \\ \end{array} $$
(44)

with

$$ \beta_{0} = \sqrt {\alpha_{2}^{2} - 3\alpha_{1} } , \gamma_{0} = \frac{1}{3}\sin^{ - 1} \left( { - \frac{{2\alpha_{2}^{3} - 9\alpha_{2} \alpha_{1} + 27\alpha_{0} }}{{2\beta_{0}^{3} }}} \right). $$
(45)

The general solution of Eq. (40) can be written in the form

$$ \left\{ {\overline{e}, \overline{\theta },\overline{\rm N}} \right\} = \mathop \sum \limits_{i = 1}^{3} \left\{ {1,L_{i} ,H_{i} } \right\}A_{i} I_{0} \left( {\lambda_{i} \rho } \right). $$
(46)

where \({I}_{\mathrm{n}}( . )\) indicates the second types of modified Bessel functions of order\(n\). \({A}_{i}\) \((i=\mathrm{1,2},3)\) are three parameters that are dependent on\(s\). In addition, \({L}_{i}\) and \({M}_{i}\) are two distinct factors that are correlated with\({A}_{i}\). We get the following relations by inserting Eq. (46) into Eqs. (36–38)

$$ H_{i} = \frac{{g_{3} \left( {\lambda_{i}^{2} - s^{2} } \right)}}{{\lambda_{i}^{4} - g_{5} \lambda_{i}^{2} }},{ }L_{n} = \frac{{\left( {\lambda_{i}^{2} - s^{2} } \right)\left( {\lambda_{i}^{2} - g_{4} } \right)}}{{\lambda_{i}^{4} - g_{5} \lambda_{i}^{2} }}, i = 1,2,3. $$
(47)

The displacement \(\overline{u }\) may be represented as follows in the Laplace transform domain:

$$ \overline{u} = \mathop \sum \limits_{i = 1}^{3} \frac{1}{{m_{i} }}A_{i} I_{1} \left( {\lambda_{i} \rho } \right). $$
(48)

The following well-known Bessel function relation was utilized to obtain Eq. (48):

$$ \int xI_{0} \left( x \right)dx = xI_{1} \left( x \right) $$
(49)

When we differentiate Eq. (48) in terms of \(\rho \), we get

$$ \frac{{\partial \overline{u}}}{\partial \rho } = \sum\limits_{i = 1}^{3} {A_{i} \left( {I_{0} \left( {\lambda_{i} \rho } \right) - \frac{1}{{\rho \lambda_{i} }}I_{1} \left( {\lambda_{i} \rho } \right)} \right).} $$
(50)

As a result, the final solutions for thermal stresses are derived in the closed form as

$$ \begin{array}{*{20}l} {\overline{\sigma }_{\rho \rho } = \sum\limits_{i = 3}^{3} {A_{i} \left( {{\Omega }_{i} I_{0} \left( {\lambda_{i} \rho } \right) - \frac{{2\beta^{2} }}{{\rho { }\lambda_{i} }}I_{1} \left( {\lambda_{i} \rho } \right)} \right)} } \hfill \\ {\overline{\sigma }_{\phi \phi } = \sum\limits_{i = 1}^{3} {A_{i} \left( {{\Phi }_{i} I_{0} \left( {\lambda_{i} \rho } \right) + \frac{{2\beta^{2} }}{{\rho { }\lambda_{i} }}I_{1} \left( {\lambda_{i} \rho } \right)} \right)} } \hfill \\ {\overline{\sigma }_{zz} = \sum\limits_{i = 1}^{3} {A_{i} {\Phi }_{i} I_{0} \left( {\lambda_{i} \rho } \right).} } \hfill \\ \end{array} $$
(51)

where

$$ \Omega_{i} = 1 - L_{i} - H_{i,} \Phi_{i} = 1 - 2\beta^{2} - L_{i} - H_{i} . $$
(52)

The non-dimensional Maxwell's stress \({M}_{\rho \rho }\) is given by

$$ \tau_{\rho \rho } = \frac{{v_{a}^{2} }}{{v_{0}^{2} }}e = \frac{{v_{a}^{2} }}{{v_{0}^{2} }}\sum\limits_{i = 1}^{3} {A_{i} I_{0} \left( {\lambda_{i} \rho } \right)} $$
(53)

The boundary conditions (30), (33) and (34) have the following forms after performing the Laplace transform

$$ \begin{array}{*{20}l} {\left. {\frac{{\partial \overline{\theta }}}{\partial \rho }} \right|_{{\rho = \rho_{0} }} = - \frac{{sq_{0} \left( {1 + st0} \right)tp^{3} }}{{8t_{p}^{2} \left( {s + \omega^{*} } \right)\left( {1 + stp} \right)^{3} }} = - \overline{G}\left( s \right)} \hfill \\ {\overline{u}\left( {\rho_{0} ,s} \right) = 0} \hfill \\ {D_{E} \left. {\frac{{\partial \overline{N}}}{\partial \rho }} \right|_{{\rho = \rho_{0} }} = s_{f} \overline{N}\left( {\rho_{0} ,s} \right)} \hfill \\ \end{array} $$
(54)

Equations (46) and (49) are substituted into Eq. (54), giving

$$ \begin{array}{*{20}l} {\mathop \sum \limits_{i = 1}^{3} \lambda_{i} A_{i} I_{1} \left( {\rho_{0} \lambda_{i} } \right) = - \overline{G}\left( s \right)} \hfill \\ {\mathop \sum \limits_{i = 1}^{3} \frac{1}{{m_{i} }}A_{i} I_{1} \left( {\rho_{0} \lambda_{i} } \right) = 0} \hfill \\ {\mathop \sum \limits_{i = 1}^{3} A_{i} M_{i} \left( {\left( {D_{E} - s_{v} } \right)I_{0} \left( {\lambda_{i} \rho_{0} } \right) - \frac{{D_{E} }}{{\rho_{0} \lambda_{i} }}I_{1} \left( {\lambda_{i} \rho_{0} } \right)} \right) = 0} \hfill \\ \end{array} $$
(55)

We derive the values of the parameters \({A}_{i},\) \((i=\mathrm{1,2},3)\) by solving the system (54).

The inversion of Laplace transforms was obtained in this study using an accurate and efficient numerical approach based on Fourier series expansion [45]. Any function in the Laplace domain can be inverted to the time domain using this method as follows:

$$ \Gamma \left( {\rho ,t} \right) = \frac{{e^{ct} }}{t}\left( {\frac{1}{2}\overline{\Gamma }\left( {\rho ,c} \right) + Re\mathop \sum \limits_{j = 1}^{{N_{f} }} \overline{\Gamma }\left( {\rho ,c + \frac{ij\pi }{t}} \right)\left( { - 1} \right)^{j} } \right) $$
(56)

where \({N}_{f}\) denotes the number of terms, \(Re\) denotes the real part, and \(i\) denotes the imaginary number unit. Numerous numerical tests have demonstrated that the value of the parameter \(c\) fulfills the relation \(c\tau \cong 4.7\), allowing for quicker convergence [46].

6 Numerical results

We will now show some numerical findings in order to demonstrate the theoretical results gained in the previous sections. The influence of the modified photothermal heat equation (MGTPT), which is defined by the Moore–Gibson–Thompson (MGT) equation, on the studied physical fields is now shown in the form of graphical representations and tables using Mathematica software. For theoretical analysis, isotropic silicon (Si) is utilized as the semiconductor solid material.

At \({T}_{0}=300\mathrm{ K}\), the following physical parameters are used [35]:

$$ \begin{array}{*{20}l} {\lambda = 3.64 \times 10^{10} kg m^{ - 1} s^{ - 2} , \mu = 5.46 \times 10^{10} kg m^{ - 1} s^{ - 2} , \rho = 2330 kg m^{ - 3} ,} \hfill \\ {K = 1.51 W m^{ - 1} K^{ - 1} , C_{E} = 6.95 \times 10^{2} J kg K^{ - 1} , d_{n} = - 9 \times 10^{ - 31} m^{3} , } \hfill \\ {E_{g} = 1.11 eV, D_{E} = 2.5 \times 10^{ - 3} m^{2} s^{ - 1} , s_{f} = 2 m s^{ - 1} , \tau = 5 \times 10^{ - 5} s.} \hfill \\ \end{array} $$

In the context of the coupled theory of thermal-plasma-elastic waves under MGTE model, the numerical approach described in (57) has been used to distribute the distribution of non-dimensional temperature \(\theta \), the radial displacement \(u\), the radial and hoop stresses \({\sigma }_{\rho \rho }\) and \({\sigma }_{\phi \phi }\), Maxwell's stress \({\tau }_{\rho \rho }\) and the absolute carrier density \(N\) along the radial direction of the cylinder. Figures 1, 2, 3, 4, 5, 6 graphically depict the numerical findings for time t \(t=0.12\mathrm{s}\) and \({\rho }_{0}=1\). In three cases, numerical calculations are made for all the studied field variables.

Fig. 1
figure 1

The temperature variation \(\theta \) for different models of photo-thermoelasticity

Full size image
Fig. 2
figure 2

The displacement variation \(u\) for different models of photo-thermoelasticity

Full size image
Fig. 3
figure 3

The carrier density \(N\) variation for different models of photo-thermoelasticity

Full size image
Fig. 4
figure 4

The radial stress variation \({\sigma }_{\rho \rho }\) for different models of photo-thermoelasticity

Full size image
Fig. 5
figure 5

The hoop stress variation \({\sigma }_{\phi \phi }\) for different models of photo-thermoelasticity

Full size image
Fig. 6
figure 6

The Maxwell's stress \({\tau }_{\rho \rho }\) for different models of photo-thermoelasticity

Full size image

6.1 Comparison of several thermoelasticity models

The suggested Moore–Gibson–Thompson photothermal (MGTPT) model is a generalization of several photo-thermoelasticity models used in this study. It was provided not only to generalize but also to solve some of the physical consequences found in some earlier models. In the first and second sections, many inconsistencies are addressed.

Many earlier models of photo-thermoelasticity can be derived as special instances by reference to the modified Moore–Gibson–Thompson heat conduction equation (MGTPT). When \({{\tau }_{0}=K}^{*}=0\), the coupled photo-thermoelasticity theory (CPTE) is obtained, and when \({K}^{*}=0\), the generalized Lord and Shulman photo-thermoelasticity model (PLS) is obtained. Furthermore, the photothermal Green and Naghdi model (PGN-III) can be obtained if the relaxation parameter \({\tau }_{0}=0\) is omitted, and the photothermal Green and Naghdi model (PGN-II) may be obtained if the term that contains the parameter \(K\) is absent. If \({{\tau }_{0},K}^{*}>0\), this indicates that the photothermal model (MGTPT) is used.

The present subsection will examine the comparison of the newly given model with other previous photothermal models in order to verify them. To illustrate comparison and research, as well as for practical purposes, tables and figures will be used to illustrate discussions and comparisons. Tables 1, 2, 3, 4, 5, 6 show the changes in investigated studied fields against radial distance \(\rho \) for the CPTE, PLS, PGN-II, PGN-III, and MGTPT models. In this case, the non-dimensional carrier lifetime parameter \(\tau \) and the pulsing heat flux duration time \({t}_{p}\) are fixed (\(\tau =0.01,{t}_{p}=0.15\)). From the figures and tables, we can mention some noteworthy facts:

  • The existence of variations in the fields is obviously developing over time in the photothermal MGTPT model and has an important influence across all domain profiles examined.

  • The thermal parameters \({\tau }_{0}\) and \({K}^{*}\) have a significant impact on all of the domains investigated, as seen in the graphs.

  • The phenomena of restricted thermal transmissions velocity of photo-thermoelasticity MGTPT theory is well understood in all figures and tables.

  • Different domain distributions have a limited prevalence. This is in contrast to cases where coupling and decoupling theorems on photo-thermoelasticity have an infinite propagation rate, which results in nonzero values for all functions anywhere in the medium.

  • The coupled photothermal model (CPTE), as well as modified and generalized photothermal models (PLS, PGNII, PGNIII, and MGTPT), give values that are different in magnitude and similar in behavior at the surface of the semiconducting cylinder, where the boundary conditions appear.

  • For all physical domains, all curves converge, where \(\rho \) tends to zero to meet the regularity requirement.

  • The result indicates that the non-dimensional radial displacement \(u\) grows with decreasing distance \(r\) until it reaches its maximum values, then declines rapidly to reach minimum points, and then gradually decreases to seem stable.

  • Fig. 3 shows that the displacement \(u\) begins with the value of zero for all surface \(\rho =1\) situations that are consistent with the limiting condition and progressively decrease to their lowest value.

  • The temperature of GN-III is likewise found to be higher than that of MGTE, with comparable results for the PLS and MGTPT models.

  • The results of the frequently used GN-III thermoelastic model show that it differs significantly from the GN-II thermoelastic models in terms of reduced energy dissipation. In the LS and MGTE models, the inclusion of the relaxation parameter might result in a slower temperature decline.

  • The PGN-III results also show convergence from the conventional elasticity model (CPTE), which, unlike other generalized thermoelasticity models, does not vanish fast inside the body due to heat. This is fully consistent with the claims of Quintanilla [22] and the observations of Abouelregal et al. [25,26,27].

  • In one section of the cylinder, all kinds of pressure are compressed, while in another area there is tension. Tensile highlights that the medium next to the cylinder surface is positioned throughout time and this conforms to the information given in [47]. Furthermore, the higher value and amplitude of fields measured at the cavity surface are obvious with the rise in radial breadth. The explanations for this occurrence are included in [48].

Table 1 The variation of the temperature \(\theta \) against the radial distance \(\rho \)
Full size table
Table 2 The variation of the displacement \(u\) against the radial distance \(\rho \)
Full size table
Table 3 The variation of the carrier density \(N\) against the radial distance \(\rho \)
Full size table
Table 4 The variation of the radial stress \({\sigma }_{\rho \rho }\) against the radial distance \(\rho \)
Full size table
Table 5 The variation of the hoop stress \({\sigma }_{\phi \phi }\) against the radial distance \(\rho \)
Full size table
Table 6 The Maxwell's stress \({\tau }_{\rho \rho }\) against the radial distance \(\rho \)
Full size table

6.2 The effect of carrier lifetime and laser pulse duration parameters

Exploration of lasers was useful to understand the properties of a material's inner structure, and as a result, various modern applications in physical sciences, engineering, and medicine have emerged. The thermal effect of a non-Gaussian laser on a thermoelastic material that is employed as a heat source is highly relevant under the influence of extended thermoelastic theories.

The use of photothermal excitation of shorter elastic pulses (high-frequency elastic waves) for various fields of practical physics is now of great interest. When a laser beam (laser light sources) hit a sample inside the cavity, the laser pulses caused the temperature to increase. The intensities of free carrier charge are shown after all photo-excited electrons have been excited. The fact that the ultrasound produced by photothermal contains information about the medium produced and the surrounding media has enabled the creation of one-dimensional theoretical models.

Theoretical and practical ways of obtaining information on carrier intrinsic concentrations and a long carrier lifetime \(\tau \) are critical criteria for modeling semiconductor devices in order to comprehend and improve device physics and performance. Minority carrier movement and effective carrier lifetime parameter \(\tau \) of the absorber material for solar cells affect the open-circuit voltage and photo-generated current density \(N\) in particular.

The phenomena of microwave heating using pulsed lasers is investigated in this section. The solid cylinder is constructed of silicon and heated by a pulsed non-Gaussian laser beam with a duration \({t}_{p}\), causing the vibration to be dampened by thermoelasticity. Energy dissipation occurs when temperature and stress combine, turning mechanical energy into permanent heat energy. Table 7 shows how the duration of a laser pulse \({t}_{p}\) and the lifespan parameter \(\tau \) influence the dimensionless thermo-physical investigated fields at \(\rho =0.9\). The study in this subsection will be carried out in light of Moore–Gibson–Thomson's photo-thermoelastic modified theory (MGTPT).

Table 7 Effects of carrier lifetime and laser pulse duration parameters on the dimensionless physical fields
Full size table

The investigated fields, comprising temperature, displacement carrier density, and thermal stress components, are dependent not only on distance \(\rho \) and time \(t\) but also on the duration of the laser pulse \({t}_{p}\) and the photo-generated carrier lifespan parameter \(\tau \), as shown in Table 7. Moreover, thermal and mechanical waves are more sensitive with the change of laser duration \({t}_{p}\) than with the change of lifetime \(\tau \).

The values of the temperature \(\theta \), carrier density \(N\), and radial displacement \(u\) have all been demonstrated to decrease as the time of the laser pulse \({t}_{p}\) grows, but the values of thermal stress \({\sigma }_{\rho \rho }\) and Maxwell's stress \({\tau }_{\rho \rho }\) have both increased. From the table, it can be seen that by increasing the photo-generated carrier lifetime parameter \(\tau \), we find that there is an increase in the temperature, carrier density \(N\), the magnitudes of the thermal stress \({\sigma }_{\rho \rho },\) and Maxwell's stress \({\tau }_{\rho \rho }\). However, the radial displacement \(u\) distribution decreases with the increase in value of the lifetime parameter \(\tau \).

In the investigation of the macroscopic output of some materials pertaining to photothermal materials, which dominate in the determination of material characteristics, the carrier lifetime parameter \(\tau \) will play a significant role. All of these findings demonstrate the concept of limited heat dispersion rates. For designers of novel materials and other disciplines of materials science and physical engineering, the results obtained in this example might be useful in the presence of plasma waves and elasticity. Because of flaws and a lack of information about material characteristics, measuring carrier lifetime in many thin-film photovoltaic materials may be challenging.

Rapidly varying contraction and expansion cause temperature fluctuations in materials susceptible to heat transmission by conduction [49]. Because pulsed laser technologies are widely utilized in material processing, nondestructive testing, and characterization, this mechanism has attracted a lot of attention [50].

7 Conclusion

This paper proposes a new photo-thermoelastic heat conduction model based on the Moore–Gibson–Thompson equation. The Green–Naghdi type III model, in addition to the Lord and Shulman heat transfer equation, was included in the modified thermos-photovoltaic model. The interplay of heat, plasma, and elastic waves in semiconducting materials is investigated using this extended model. Only a few literature reviews have been published on our model. From the suggested model, several thermoelastic and photothermal models may be derived as special cases.

According to the discussions, thermal factors have a great influence on the distributions of photothermal fields. The effects of laser pulse length and lifetime characteristics on the investigated fields are also important. In the new extended photo-thermoelastic model (MGTPT), heat travels through the medium as a wave of finite velocity rather than as a wave of unlimited velocity. Compared with the PGN-III model, the generalized MGTPT model is better at explaining the photo-thermoelastic process. The results of PGN-III also show convergence with the conventional elasticity model (CPTE), which, unlike other generalized thermoelastic models, does not disappear rapidly within the body due to heat.

The photothermal approach can provide simple and sensitive ways for measuring optical absorption in materials, as well as some insight into deexcitation processes. Scientists working in disciplines such as physics, material design, thermal efficiency, and geophysics will benefit greatly from ideas presented in this paper. The technique utilized in the preceding study may be applied to solve a wide range of photo-thermoelasticity and thermodynamic issues.